Оба метода нахождения энергии решетки — экспериментальный и теоретический — требуют данных, получение которых сопряжено с определенными трудностями. Так, для вычисления коэффициента Маделунга необходимо знать кристаллическую структуру вещества, которая определяется посредством сложной расшифровки рентгенограмм кристаллов, а также величину сжимаемости х, измерение которой связано с техникой высоких давлений, доступной лишь немногим лабораториям. Поэтому широко используется уравнение, предложенное для расчета энергий решеток А. Ф. Капустинским вычисление 1)д при помощи этого уравнения требует знания только ионных радиусов. [c.269]
Входящий в уравнение (IV. 13) коэффициент борновского отталкивания п находят из данных ио сжимаемости кристаллов рассмотрим принцип этого расчета. [c.267]
Наконец, величина п может быть получена из уравнения для сжимаемости кристалла [c.137]
Величина п в уравнении 25.13 может быть вычислена из уравнения для сжимаемости кристалла [c.327]
Величина п в уравнении (I, 15) или (I, 16) может быть вычислена на основании данных о сжимаемости кристалла. [c.38]
Так как А я мы можем считать известными, уравнение (7) дает нам одно соотношение между В п п. Если бы мы могли найти еще одно соотношение между ними, то обе эти величины могли бы быть определены экспериментально . Это второе соотношение получается путем измерения сжимаемости кристалла. Сжимаемостью называют относительное уменьшение объема на единицу приложенного давления, что можно записать в форме [c.227]
Все величины в числителе уравнения (82) рассчитаны для некоторых ионов и помещены в табл. 10. Необходимо оценить значение т. Для этого в литературе ко времени появления работы [70] был предложен единственный путь, основанный на использовании экспериментальных данных по сжимаемости, который нашел себе удачное применение при оценке сил отталкивания в ионных кристаллах [76[. [c.94]
В противоположность идеальным газам коэффициенты уравнения состояния для кристаллов не удается оценить простым образом. Коэффициенты расширения, сжимаемости и давления зависят от температуры и давления. Для достаточно широкого диапазона температур нельзя составить простое уравнение состояния. Только с приближением к предельному идеальному состоянию при низких температурах и высоких давлениях коэффициенты термического уравнения состояния принимают простую форму, так как тогда термические свойства по существу не зависят от температуры. Это означает, что объем и давление принимают постоянное значение. Производные этих величин по температуре, термические коэффициенты расширения и напряжения, а также температурные коэффициенты расширения и сжимаемости становятся равными нулю. Поэтому в предельном состоянии с приближением к абсолютному нулю температуры справедливо [c.36]
Изменение сжимаемости при изменении температуры тем меньше, чем больше гидростатическое давление. По-казано что при давлениях больше Ю кгс смР- сжимаемость практически не зависит от температуры. Это объясняется тем, что уменьшение сжимаемости сопровождается уменьшением коэффициента объемного расширения, и доля термического давления в общем сопротивлении сжатию становится незначительной. Аналогичное явление наблюдается при сжатии молекулярных и ионных кристаллов 2°. Уменьшение влияния температуры следует и из уравнения состояния полимерных материалов, полученного в работе . [c.10]
Возможно, что уравнение (120), по которому вычисляется кинетическое давление, преувеличивает значение чисто гармонических колебаний, но его предельная форма, по-видимому, подтверждается опытами по влиянию давления на сжимаемость. Вопрос о том, соответствует ли плавление предельной устойчивости упорядоченного кристалла или же его постепенно возрастающей неупорядоченности, можно надеяться решить только после введения в теорию межмолекулярной энергии квантовых условий и введения значений п, отличающихся от 12. [c.150]
Межионные расстояния в реальных кристаллах. Поскольку ион не является просто жесткой сферой, подобной биллиардному шару, а обладает известной сжимаемостью, реальные расстояния между ионами в кристалле зависят не только от протяженности электронных облаков ионов в пространстве, но также и от сил, с которыми ионы действуют друг на друга , как это выражено, например, уравнением (7). Радиусы ионов щелочного металла и галоида были определены из расстояний в кристаллах, состоящих из одновалентных ионов и имеющих структуру хлористого натрия, а радиусы других ионов в табл. 16 в действительности представляют протяженность в пространстве электронного облака вокруг иона, определенного сравнением с ионами галоида и щелочного металла. Отсюда следует, что расстояния в кристалле должны передаваться такими радиусами только в том случае, если кристалл состоит из одновалентных ионов и имеет структуру хлористого натрия. Но, понятно, поливалентные ионы не могут образовать кристалл, состоящий из одновалентных ионов, а также кристаллы могут и не иметь структуры хлористого натрия. Поэтому определим величину, которую можно назвать приведенной постоянной Маделунга, с помощью уравнения [c.230]
Если кристаллы относительно симметричны, в уравнение (У-5) можно подставлять усредненные значения г я у. Если сжимаемость кристалла обозиачть 3, то изменение давления на поверхности раздела можно выразить уравнением [c.206]
При расчетах энергий кристаллов Борном и Майером к чему мы вернемся позже. Потекцнзл отталкивания возрастает тем более внезапно и быстро, чем меньше р, и поэтому г 1р (безразл1ерная величина) соответствует в известном смысле п в уравнении (6) и также может быть вычислена по данным о сжимаемости кристалла. Детали расчета читатель найдет в статье Борна и Майера. Выражая потенциал уравнением (11), лш вместо (8) получаем [c.229]
Выведите формулу, связываюшую параметр р в уравнении (1.74) с коэффициентом сжимаемости кристалла к = – / йУ/йр) V — объем, р — внешнее давление). Чему равен расчетный коэффициент сжимаемости для кристалла Na l (кратчайшее расстояние Na—С1 составляет [c.88]
Термохимический радиус. Для многоатомных ионных соединений из-за сложности их структуры рассчитать энергию рещетки по уравнению (4.23) трудно. А. Ф. Капустинский предложил полуэмпирическую формулу, дающую довольно точные значения. Обычно МдД, частное от деления постоянной Маделунга на среднее координационное число ионов в кристалле, обратно пропорционально расстоянию между центрами аниона и катиона Го. Отсюда Мд пропорциональна v/ro, где го = г+ + г— с другой стороны, для соединений, содержащих крупные анионы, вместо уравнения (4.23) выполняется уравнение Борна — Мейера, и при подстановке у/го вместо Ма получают следующее уравнение (р — константа, связанная с коэффициентом сжимаемости) [c.197]
Жидкости отличаются от газов на три порядка большими значениями плотности и очень незначительной сжимаемостью. Они не сохраняют определенной формы (кроме некоторых стеклообразных жидкостей) и обладают вблизи точки кипенйя неупорядоченной структурой, в которой, однако, при приближении к температуре пдавАения возникают области ближнего порядка. Органические вещества с длинными п бчёч-ными молекулами могут образовывать жидкие кристаллы, главным признаком которых является дальнодействующая параллельная ориентация молекул однако вследствие отсутствия строгой кристаллической структуры сохраняется более или менее высокая подвижность частиц. Для жидкостей не существует уравнений состояния е универсально действующими константами (как для газов), но применяются индивидуальные константы. [c.439]
В настояш,ем кристалле положение, конечно, гораздо сложнее. Так, например, в хлористом натрии действует сила притяжения между каждым ионом натрия и шестью ионами хлора, являющимися его ближайшими соседями, и сила отталкивания от восьми ионов натрия, которые расположены лишь немного дальше. Тем не менее, зная геометрию ионного кристалла, можно без большого труда вычислить его полную энергию, выраженную через постоянные в уравнениях для сил притяжения и отталкивания. Эти постоянные можно найти путем сопоставления вычисленных и измеренных значений таких свойств кристалла, как сжимаемость, и полученное таким образом значение энергии кристалла (его энергия решетки) может быть использовано для термохимических расчетов типа, приведенного на стр. 81. Для галогенидов щелочных металлов и для некоторых других простых ионных кристаллов получаются согласующиеся результаты, но для полного соответствия необходимо добавить небольшие члены, отвечающие а) вандерваальсовым силам и б) небольшой степени ковалентности связей между ионами (см. стр. 316). [c.241]
Сжимаемость кристаллических тел очень невелика, действие сил отталкивания убывает с ростом расстояния между взаимодействующими частицами очень быстро. Показатель степени п в уравнении энергии решетки колеблется от 3 (для металлов) до 12 (для некоторых ионных кристаллов). Поэтому следует ожидать, что пространство кристалла организовано достаточно компактно. Рассмотрим возможности компактной укладки сфер. Плотноупакованный узловой ряд — это ряд равновеликих сфер, уложенных так, что их центры лежат на одной прямой. Такой ряд возможен только как трансляционный. Для создания плотноупакованной плоской узловой сетки (рис. 4.4) на плоскости следует уложить три пересекающихся в одном узле трансляционно плотных ряда сфер. Прямые, проведенные через их центры, разобьют плоскость на равносторонние треугольники, стянутые по шесть к одной вершине (рис. 4.5). Описывают такие сетки символом Шлэфли, указывая число вершин элементарной петли 3 и верхний индекс 6 по числу треугольников, сводимых к одной вершине 3 . Плотноупакованный ряд и нлотноупакованная плоская сетка могут быть уложены единственным способом. [c.95]
Расплавы. Для анализа структурных проблем, связанных с процессом плавления, используют параметры термического и калорического уравнений состояния, в частности, относительное изменение молярного объема АУпл/ кр (АКпл — разность молярных объемов расплава и кристалла в точке плавления Гпл, 1 кр — молярный объем кристалла), сжимаемость х, коэффициент теплового расширения а и молярные теплоемкости. По изменению величин Дх, Асе и Ас , можно получить сведения о процессе плавления. [c.205]
Совокупность уравнений (VII.7, VII.10) дает величину Су кристалла. Для перехода к Ср применяется формула (11.20). Далее авторы [640 распространяют на молекулярные решетки соотношение Грюнайзена [642] для атомных решеток aF/Риз = onst, где а — коэффициент термического расширения V — мольный объем Риз — изотермическая сжимаемость. Отсюда получается [c.181]
В этом выводе пренебрегают ван-дер-ваальсовскими силами, тепловой энергией и нулевой энергией. Можно допустить, что все они входят в член, выражающий отталкивание, и затем определять р таким образом, чтобы уравнение (12) дало величину 11 равную указанной в табл. 20. Этот путь подобен пути определения п по л1етоду II. Борн и Майер и Хэггинс учли отдельно ван-дер-вааль-совские силы, тепловую и нулевую энергии, и вычисленные ими величины включают специальные поправки на эти факторы величина р получена ими из сжимаемости при учете этих факторов. Разница между величинами р, полученными нами и ими, до известной степени объясняется тем, что мы не полностью учитывали эти факторы . Тем не менее, ясно, что член, представляющий сумму потенциала отталкивания, ван-дер-ваальсовского потенциала и поправки на кинетическую энергию, может выражаться экспоненциальной функцией только приближенно кроме того, эти слагаемые могут быть различными для кристалла и для газа. [c.251]
Как в случае ионных кристаллов, так и в этом случае можно получить выражение для сжимаемости путем двукратного ди-ференцирования выражения для энергии (уравнение 10, гл. XIV). Если проделать это, то получается неудовлетворительное совпадение с экспериментальными данными. Объясняется это частично тем, что экспериментальные величины получены при комнатных температурах в то же время имеются указания на то, что величины, полученные таким образом, могут довольно значительно отличаться от величин, соответствующих абсолютному нулю. Но, во всяком случае, относительно небольшие изменения в выражении для энергии могут настолько сильно изменить вычисленную величину сжимаемости, что последняя не имеет существенного значения с точки зрения приведенного расчета. При введении поправок, необходимых для получения правильных величин сжимаемости, величина А , необходимая для приведения теоретически вычисленных величин энергий в соответствие с экспериментально найденными, несколько меняется, и совпадение, какое имеет место у различных щелочных металлов, становится несколько менее точным. Тем не менее, общая картина и допущение, что А1 имеет нормальную величину, практически одинаковую для всех щелочных металлов, повидимому, вполне удовлетворительны. Небольшие расхождения выявляются в случае щелочноземельных металлов, а у металлов более высокой валентности отклонения от металлического характера возрастают, и в конце концов наблюдается полный переход металлических связей в атомные или ковалентные. Некоторые из элементов, расположенных вправо от [c.372]
Представив отклонение кристалла от идеального состояния (соответствующего температуре О К) как набор квазичастиц, можно выразить его статистическую сумму как произведение множителей, отвечающих тому или иному типу квазичастиц. Причем вместо исключительно сложного расчета набора значений g и е, для макроскопической системы достаточно рассчитать их для существенно более простой подсистемы, соответствующей тому или иному типу квазичастиц. При этом вклад разных квазичастиц в физические и химические свойства кристалла будет существенно различен. Так, упоминавщиеся точечные дефекты кристаллической рещетки играют исключительно важную роль в химических (как термодинамических, так и кинетических) свойствах твердого тела и их рассмотрению будет посвящена отдельная глава. В данной главе будет рассмотрено статистическое описание фононов (как квазичастиц, дающих наибольший вклад в статистическую сумму кристалла, а следовательно, и в, определяемые температурой (а не значением Щ термодинамические свойства — энтропию и теплоемкость) и электронов (определяющих не только электропроводность кристалла, но и в значительной степени зависимость [ о от объема, а значит — и уравнение состояния). Проявление вращательных степеней свободы для твердых тел мало характерно. Одним из интересных примеров таких тел является кристаллический фуллерен Сбо (другие фуллерены менее доступны в макроскопических количествах), для которого при температуре выше 60 К наблюдается свободное вращение почти сферических молекул вокруг своих кристаллографических позиций, которое при более низких температурах замораживается . Эта особенность проявляется в ряде интересных свойств фуллеренов, например сжимаемости и пластической деформируемости, и делает порошки на основе фуллеренов перспективными твердофазными смазочными материалами. [c.93]
полученных разными методами (табл. 2). Эти данные указывают на согласие различных методов определения зарядов в пределах обычной погрешности 0,1-0,2 е, которая свойственна большинству методов.
Отметим, что сжимаемости катионов в целом значительно меньше по величине, чем сжимаемости анионов. Так, сжимаемость мелкого Li+ почти на порядок (в 8 раз) меньше сжимаемости самого маленького из анионов F– и в 15 раз меньше, чем сжимаемость крупного I–. Даже крупный Cs+ несколько менее сжимаем, чем F–, а почти столь же крупный Ba2+ в два раза менее сжимаем, чем мелкий анион O2-. Таким образом, на основании этих результатов можно заключить, что сжимаемость кристалла определяется, в основном, сжимаемостью входящих в его состав анионов.
Известной формулой Лоренц – Лорентца поляризуемость α (рефракция R) некоторого вещества связана с показателем преломления п:
|
R =V |
n2 |
−1 |
= (4 / 3)πNα . |
(17) |
|
|
n2 |
+ 2 |
||||
Для ковалентного кристалла или металла отыскание экспериментальных значений
αi не представляет трудностей, как и установление их радиуса. Рефракцию кристалла нужно просто разделить на число атомов в мольном объеме. Значения α для нейтральных атомов даны в Приложении 1-2.
На близость поляризуемости и объема молекулы (атома) было впервые указано еще Г. Лорентцем в 1879 г. В 50-х годах прошлого века было обнаружено, что существует прямая пропорциональность между поляризуемостью атома в ковалентных
иметаллических кристаллах и кубом его ковалентного радиуса: αК = drК3 .
Действительно, поскольку основной вклад в электронную поляризуемость дают электроны внешней наименее прочно связанной оболочки, то атом, в первом и достаточно грубом приближении можно рассматривать как классическую проводящую сферу, поляризуемость которой пропорциональна кубу радиуса этой сферы. Отклонения от этого правила обусловлены эффектами расширения катионов и сжатия анионов в кристалле. Особенно сильно этот эффект отражается на размерах (объемах) анионов и их поляризуемости.
86

|
Согласно Куртису и Вильсону существует линейная зависимость вида: |
|
|
α =α0 −k ln R−2 , |
(18) |
где α0 – поляризуемость свободного иона, R – межатомное расстояние. Это уравнение получено на основе предположения, что на анион действует электростатический потенциал со стороны кристаллической решетки. Таким образом, поляризация свободного аниона α0 может быть найдена из уравнения (18) при R → ∞.
На рис. 45 показана зависимость анионной поляризуемости от R-2 для фторидов,
хлоридов, бромидов и йодидов щелочных металлов. Можно видеть, что lnαi
действительно практически линейно зависят от R-2. Экстраполяция на очень большие расстояния R−2 → 0 дает следующие оценки αi0 : 1,83; 4,67; 6,13 и 9,16 Å3 для
«свободных» F–, Сl–, Вr– и I–, соответственно.
Рис. 45. Поляризуемость анионов в щелочных галогенидах как функция силы электростатического поля: 1 – йодиды, 2 –
бромиды, 3 – хлориды, 4 – фториды. Значенияαданывлогарифмическойшкале.
Необходимо также иметь в виду про огромное различие в поляризуемостях аниона и нейтрального атома. Сравните, например, α(Н–) = 31,4 и α(Н) = 0,66 Å3; α(F–) = 2,2 и α(F) = 0,6 Å3. Особенно велика эта разница для катионов: например, α(Li+) = 0,028; α(Li) = 24,3 Å3. Следовательно, даже очень малая доля ковалентности связи должна внести существенные коррективы в распределение общей поляризуемости кристалла между катионом и анионом. Поскольку поглощение световых волн кристаллом поляризует электронные оболочки атомов, то собственная окраска кристалла сильно зависит от ионности-ковалентности. Так, если ионные хлориды и бромиды прозрачные, то более ковалентные сульфиды и теллуриды обычно непрозрачны.
87
Московский государственный университет им. М.В.Ломоносова Геологический факультет
Кафедра кристаллографии и кристаллохимии
В.С.Урусов, Н.Н.Еремин
КРИСТАЛЛОХИМИЯ
(краткий курс)
Часть 2
Допущено УМС по “Геологии” УМО классических университетов в качестве учебного пособия для студентов вузов, обучающихся по направлению 511000 “Геология” и
естественнонаучным геологическим специальностям
Издательство Московского университета
2005
УДК 548.0 ББК 24.5 У 73
Урусов В.С., Еремин Н.Н. Кристаллохимия. Краткий курс. Часть 2. Учебное пособие. – М.: Изд–во Московского университета, 2005. – 125 с.
У73
ISBN 5-211-05056-8
Пособие охватывает тематику лекций второй половины курса «кристаллохимия».
В нем содержится последовательный анализ основных категорий кристаллохимии: морфотропии, полиморфизма, структурной гомологии и изоморфизма. В пособии продемонстрирована их тесная взаимосвязь, указаны современные методические приемы их изучения, описаны количественные модели представлений об устойчивости структурного типа.
Для студентов специальностей «геохимия», а также для магистрантов магистерской программы «кристаллография и кристаллохимия».
Рецензенты:
Член–корреспондент РАН, профессор Д.Ю.Пущаровский Кандидат геолого–минералогических наук, доцент Ю.К.Егоров–Тисменко
Печатается по решению Ученого совета Геологического факультета МГУ от
20.10.2005 г.
УДК 548.0 ББК 24.5
|
ISBN 5-211-05056-8 |
© Геологический факультет МГУ, 2004. |
2
Содержание
|
Предисловие |
5 |
|
Введение. Основные категории теоретической кристаллохимии и |
6 |
|
соотношения между ними |
|
|
Глава V. Морфотропия, как категория кристаллохимии |
9 |
|
5-1. История изучения морфотропии |
9 |
|
5-2. Критерии устойчивости структурного типа для ионных кристаллов |
10 |
|
5-3. Фактор толерантности и модельные структуры Гольдшмидта |
21 |
|
5-4. Критерии устойчивости структурного типа для существенно ковалентных |
25 |
|
кристаллов |
|
|
5-5. Обобщение понятия морфотропии на примере кристаллохимии силикатов |
32 |
|
Глава VI. Cтруктурная гомология |
35 |
|
6-1. Предварительные замечания |
35 |
|
6-2. Структуры вычитания и внедрения |
35 |
|
6-3. Псевдосимметрия. Производные и вырожденные структуры |
37 |
|
6-4. Структурная гомология силикатов |
38 |
|
6-5. Другие примеры структурной гомологии халькогенидов |
42 |
|
6-6. Гомологические серии некоторых оксидов и фторидов |
43 |
|
Глава VII. Полиморфизм и политипия |
48 |
|
7-1. Определения и исторический обзор |
48 |
|
7-2. Систематика полиморфных переходов |
50 |
|
7-3. Изменение симметрии при изменении температуры и давления |
58 |
|
Координационные правила полиморфизма |
|
|
7-4. Термодинамические основы теории полиморфизма |
66 |
|
7-5. Политипизм |
67 |
|
Глава VIII. Изоморфизм |
72 |
|
8-1. Определения |
72 |
|
8-2. Краткие исторические сведения |
72 |
|
8-3. Классификация изоморфизма |
75 |
|
8-4. Эмпирические правила изоморфизма и их современная трактовка |
79 |
|
3 |
|
8-5. Физико–химические основы изоморфизма |
84 |
|||||
|
8-6. Кристаллохимическая трактовка правил изоморфизма |
88 |
|||||
|
Глава IX. Современные методы кристаллохимического прогноза |
93 |
|||||
|
9-1. Предварительные замечания. |
93 |
|||||
|
9-2. |
Симметрийные и геометрические ограничения |
94 |
||||
|
9-3. |
Принципы |
плотнейшей |
упаковки. |
Конструирование |
пробных |
95 |
|
кристаллических структур заданного состава |
||||||
|
9-4. |
Принципы полного и локального валентного и координационного баланса. |
97 |
||||
|
Современный метод валентности связи (МВС) |
||||||
|
9-5. |
Возможные методы уточнения пробной структуры кристалла |
102 |
9-6. Компьютерное моделирование с использованием атомистических 104
|
потенциалов межатомного взаимодействия |
||
|
9-7. Расчеты ab-initio (из первых принципов) |
108 |
|
|
Приложения |
112 |
|
|
Приложение 1. Предметный указатель |
113 |
|
|
Приложение 2. |
Контрольные вопросы по 2-ой части |
117 |
|
Приложение 3. |
Примерный список вопросов на экзамен |
120 |
|
Литература |
124 |
.
4
Предисловие
Это учебное пособие создавалось на основе переработанного материала учебника В.С.Урусова «Теоретическая кристаллохимия» (МГУ, 1987 г.) и отражает содержание курса лекций, который читается на Геологическом факультете МГУ для студентов специальности «геохимия» во 2-ом и 3-ем семестрах. Оно включает также минимальные сведения для самостоятельных занятий и коллоквиумов (задачи, вопросы) и примерный набор экзаменационных вопросов.
Краткий курс состоит из двух частей: 1-ая часть содержит описание понятий и аппарата кристаллохимии, 2-ая часть дает представление обо всех главных категориях кристаллохимии, которые рассматриваются, в основном, на примерах из структурной минералогии. 1-ая часть включает материал обучения в течение 2-ого семестра, 2-ая часть
– в течение 3-его семестра.
5
Введение. ОСНОВНЫЕ КАТЕГОРИИ
ТЕОРЕТИЧЕСКОЙ КРИСТАЛЛОХИМИИ
И СООТНОШЕНИЯ МЕЖДУ НИМИ
Как и любая другая научная дисциплина, кристаллохимия располагает определенным набором понятий и определений. Наиболее крупные и общие понятия называются категориями. Химическая кристаллография передала кристаллохимии три крупнейших эмпирических обобщения, которые можно назвать категориями этой науки:
морфотропию, полиморфизм, изоморфизм.
Морфотропией называется резкое изменение кристаллической структуры в закономерном ряду химических соединений при сохранении количественного соотношения структурных единиц. Например, сфалерит ZnS, троилит FeS, ольдгамит СаS принадлежат к трем различным структурным типам: сфалерита, никелина и галита соответственно. Изменение структуры вызвано заменой катиона при том же анионе и отношений атомных количеств катиона и аниона 1:1.
По существу, только морфотропия полностью соответствует закону Гаюи: химически различные вещества обладают и различным кристаллическим строением. Кристаллохимические закономерности, объединяемые понятиями изоморфизма и полиморфизма, ограничивают действие закона Гаюи. Изоморфизм – взаимное замещение
химически различных компонентов в эквивалентных позициях кристаллической структуры. Например, сфалерит ZnS и метациннабарит НgS изоструктурны и изоморфны, так как возможно образование смешанных кристаллов (твердого раствора замещения) состава (Zn, Нg)S с различным соотношением количеств Zn и Нg. Полиморфизмом
называют изменение кристаллической структуры некоторого вещества при изменении термодинамических условий. Например, при высокой температуре ZnS стабилен в гексагональной структуре вюртцита, при низкой – в кубической сфалеритовой. Низкотемпературная форма НgS – тригональная киноварь.
В. М. Гольдшмидт указал на то, что при внешнем различии все три категории кристаллохимии связаны между собой взаимными переходами. Действительно, структура
изоморфной смеси может скачком перестроиться при достижении некоторой определенной концентрации примеси (изодиморфизм). Так, при относительно небольших
6
примесях кадмия твердый раствор (Zn, Сd)S имеет структуру сфалерита, а при больших его содержаниях (Сd, Zn)S переходит в структуру вюртцита (гринокит). Этот переход можно рассматривать условно как морфотропное превращение, при частичном замещении катионной структурной единицы. Оно является следствием деформации структуры твердого раствора под влиянием изменения среднего размера катиона.
Относительные размеры структурных единиц изменяются и под действием внешних факторов. Так, давление относительно сильнее уменьшает радиус крупного и рыхлого аниона, чем катиона в ионных кристаллах. Повышение температуры, наоборот, сильнее увеличивает размер аниона, чем катиона. Поэтому полиморфизм можно рассматривать
как следствие изменения отношения размеров катиона и аниона при постоянном составе и назвать, вслед за В. М. Гольдшмидтом, автоморфотропией. Следует помнить, однако, что эта трактовка не является исчерпывающей и не объясняет, например, полиморфизм простых веществ. Она, скорее, может служить иллюстрацией мысли Гольдшмидта о существовании скрытых связей между основными категориями кристаллохимии. Наличие
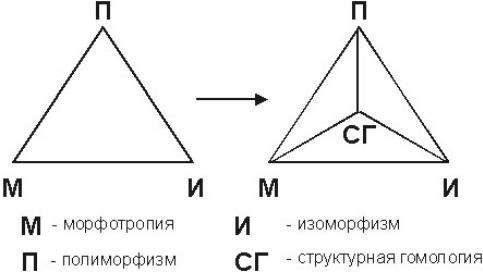
таких связей и взаимных переходов категорий кристаллохимии можно изобразить в виде треугольника.
Накопленный в прошлом веке теоретический и экспериментальный кристаллохимический материал позволил от треугольника категорий перейти к
«тетраэдру кристаллохимии». Этой четвертой вершиной служит СГ – структурная гомология, которую можно определить как существование гомологических рядов кристаллических структур (структурных типов), связанных между собой промежуточными членами ряда. Структурная гомология, таким образом, имеет дело с
7
постепенностью структурных изменений дискретных членов ряда в противоположность морфотропии, которая описывает резкие изменения структуры. Типичные гомологические ряды химических составов и кристаллических структур известны для пирротинов Fen-1Sn (n³8), уранинитов UO2+x, оксидов титана ТinО2n-1 (n=4-9), молибдена МоnО3n-1 (фазы Магнели).
В тех случаях, когда в морфотропном ряду соединений сохраняется сходство кристаллических структур, понятия морфотропии и структурной гомологии совпадают. В качестве примера подобного совпадения можно указать на ряд фаз Лавеса МgCu2– МgNi2– МgZn2, близко родственных по структуре. В некоторых типах полиморфизма структуры модификаций связаны друг с другом четкими гомологическими отношениями. Структурная гомология, в свою очередь, часто также является условием изоморфных замещений. Это, в конечном счете, ведет к взаимным перекрытиям между СГ и остальными категориями (М, И, П), что и выражается «тетраэдром кристаллохимии».
8

Глава 5. МОРФОТРОПИЯ, КАК КАТЕГОРИЯ КРИСТАЛЛОХИМИИ
5-1. ИСТОРИЯ ИЗУЧЕНИЯ МОРФОТРОПИИ
Основоположником кристаллохимического понятия морфоторпии является немецкий кристаллограф П.Грот (рис. 1), который в 1870 г. обратил внимание на то, что
под влиянием закономерного замещения химических составных частей некоторого ряда соединений в определенном месте наступает изменение кристаллической формы. Он обобщил эти наблюдения введением понятия морфотропии (буквально – поворот формы). Типичным примером морфотропии является широко известный ряд карбонатных минералов: магнезит МgСО3, сидерит FeСО3, родохрозит МnСО3, кальцит и арагонит СаСО3, стронцианит SrСО3, церуссит PbСО3 и витерит ВаСО3. В этом ряду магнезит, сидерит, родохрозит и кальцит кристаллизуются в структуре типа кальцита, а
арагонит, стронцианит, церуссит и витерит – в
Рис. 1. П. Грот (1843 – 1927)
структуре типа арагонита. Значит, именно карбонат кальция, имеющий две структурные модификации, попадает в этом ряду на границу морфотропного перехода.
В дальнейшем особенно мюнхенская школа кристаллографов под руководством П.
Грота в течение нескольких десятилетий накапливала и обрабатывала огромный фактический материал, который лег в основу пятитомной «Химической кристаллографии» Грота (1906-1919). В Берлине в те же годы плодотворно работал К. Ф. Раммельсберг, ученик и преемник Митчерлиха. Норвежский ученый В. Брёгер описал морфотропию в минеральных рядах, а в Англии А. Туттон провел очень точные исследования соотношений углов между гранями и оптических свойств с составом сульфатов.
Количественное изучение закономерностей морфотропии сильно продвинулось вперед благодаря введению понятия топических осей почти одновременно разными учеными: Ф. Бекке (1893), В. Мутманном (1894) и А. Туттоном (1893). Топические оси
9

характеризовали размеры кристаллического тела, имеющего форму параллелепипеда и содержащего 1 моль вещества. Эти величины позволили разобраться в многочисленных примерах морфотропии, которые до этого, по выражению А. Е. Арцруни (1893), как бы «складывались в чулан для ненужных и разнородных вещей».
Однако применение топических осей в химической кристаллографии продолжалось недолго, ибо появление рентгеноструктурного анализа (1912) сделало возможным прямое определение параметров элементарной ячейки кристаллического вещества. Основные закономерности морфотропии, которые вошли в современную теоретическую кристаллохимию, установлены в первые десятилетия после этого открытия и принадлежат в основном В. М. Гольдшмидту и его сотрудникам (1923-1927), П. Ниггли и его сотрудникам, особенно Ф. Лавесу (1930) и др. На их достижения опираются разработки современных исследователей.
5-2. КРИТЕРИИ УСТОЙЧИВОСТИ СТРУКТУРНОГО ТИПА ДЛЯ ИОННЫХ КРИСТАЛЛОВ
Вместе с накоплением эмпирических фактов кристаллохимия обогащалась правилами и законами, определяющими условия стабильного существования кристаллической структуры (или ее фрагментов) того или иного типа. Очевидно, те же правила способны с
определенной долей вероятности предсказать характер изменения структуры при заданном изменении состава,
|
т. е. указать место и тип морфотропного перехода. |
|||||
|
На |
основании |
обобщения |
довольно |
||
|
ограниченного экспериментального материала Л. |
|||||
|
Полинг (рис. 2) еще в 1928 г. вывел пять правил, или |
|||||
|
принципов, которым должны подчиняться стабильные |
|||||
|
структуры существенно ионных кристаллов: |
|||||
|
1) |
расстояние |
катион |
– |
анион |
в |
|
Рис. 2. Л. Полинг (1901 – 1994). |
координационном |
полиэдре |
(КП) |
||
определяется суммой ионных радиусов, а координационное число (КЧ) – их отношением;
2)сумма валентных усилий катионов, сходящихся на анионах, должна быть численно равна или почти равна валентности аниона;
3)устойчивость структуры снижается при наличии общих ребер и особенно
10
граней КП;
4)высоковалентные и особенно мелкие по размеру катионы стремятся не иметь общих анионов;
5)число разных по конструкции структурных фрагментов стремится к минимуму.
Первое из этих правил суммирует более ранние правила Магнуса (1922) – Гольдшмидта (1926), согласно которым КЧ катиона определяется тем отношением его радиуса к радиусу аниона, при котором наступает соприкосновение между собой и «расталкивание» соседних анионов. Эти отношения, найденные из простых геометрических соображений, приведены в табл. 1 для разных КЧ.
Таблица 1. Минимальные отношения ионных радиусов для разных КЧ
|
КЧ |
КП |
r+ / r− |
|
|
12 |
кубооктаэдр |
1,000 |
|
|
9 |
центрированная по вертикальным граням |
0,732 |
|
|
тригональная призма |
|||
|
8 |
куб |
0,732 |
|
|
8 |
квадратная антипризма |
0,645 |
|
|
7 |
октаэдр с одной центрированной гранью |
0,592 |
|
|
6 |
октаэдр |
0,414 |
|
|
4 |
тетраэдр |
0,215 |
|
|
3 |
треугольник |
0,155 |
|
Это правило намечает правильную тенденцию к уменьшению КЧ с уменьшением отношения r+/r–, но «критические» значения из табл. 1 не имеют смысла абсолютных границ. Например, среди щелочных галогенидов со структурой типа NaСl (КЧ = 6, октаэдр) целый ряд веществ (например, CsF, RbF, КF, RbCl) по этому критерию должны были бы кристаллизоваться в структуре типа СsСl (КЧ = 8, куб) или даже давать плотнейшие упаковки одинаковых по размеру сфер (КЧ=12), а многие другие (например, LiСl, LiBr, LiI) – в структуре с КЧ=4.
Подобным образом этот подход предсказывает КЧ = 8 для ВаО, SrО, СаО, которые на самом деле имеют структуру типа NaCl. Среди оксидов щелочноземельных металлов только периклаз МgО «выбирает» разрешенную для него критериями Магнуса– Гольдшмидта структуру NaCl. Однако в других кислородных соединениях магний
11

размещается не только в октаэдрах, но и в полиэдрах с иными КЧ: 8 (пироп Мg3Аl2 [SiO4]3) и 4 (благородная шпинель МgА12О4).
Тем не менее использование «критических условий» Магнуса–Гольдшмидта позволило Полингу указать на важные случаи пограничного (неустойчивого) поведения некоторых катионов в кислородных соединениях. К ним относятся Аl и В с отношениями r+/r– = 0,4 и 0,2 соответственно. Действительно, в трех модификациях Аl2SiO5 (кианите, андалузите и силлиманите) Аl находится в КП с КЧ = 6, 5 и 4. Бор одинаково охотно окружает себя как тремя лигандами (треугольник), так и четырьмя (тетраэдр). Подобным образом двуокись германия GeO2 (r+/r– ≈ 0,4) диморфна: она имеет полиморфные модификации со структурами кварца (КЧ = 4) и рутила (КЧ = 6). Таким образом, морфотропный ряд кислородных соединений с общей формулой МО2 можно успешно рассмотреть с позиций критерия Магнуса–Гольдшмидта (r+/r– в скобках):
Дело обстоит не так просто в других морфотропных рядах; выше уже говорилось, что в ряду ВаО – SrО– СаО – МgО только структура периклаза находится в соответствии с правилами Магнуса–Гольдшмидта, а СаО должен находиться на границе устойчивости структурного типа NaСl. Радиус Сd2+ близок к радиусу Са2+, поэтому монтепонит СdO имеет структуру типа NaСl в соответствии с правилами устойчивости. Но цинкит ZnО при радиусе Zn2+ несколько большем, чем радиус Мg2+, кристаллизуется в структуре типа вюртцита (КЧ=4) в противоречии с ожидаемой устойчивостью структуры типа NaCl.
Объяснение этого несоответствия заключается в том, что структуры с низкими КЧ типа сфалерита – вюртцита или куприта Сu2О (4:2) стабилизируются высокой долей ковалентности химической связи, когда проявляется ее направленный характер. По этой
причине правила устойчивости существенно ковалентных кристаллов будут рассмотрены в следующем разделе этой главы.
Особое место в морфотропных рядах занимают слоистые структуры. Они возникают обычно при высокой поляризуемости аниона, когда его несимметричное ближайшее
окружение индуцирует анионный диполь и дает дополнительную энергию взаимодействия – энергию анионной поляризации. Действительно, фториды и оксиды редко образуют слоистые структуры из–за низкой поляризуемости аниона, но хлориды, бромиды, сульфиды и особенно йодиды и теллуриды обычны в слоистых кристаллических
12
структурах (например, структурные типы СdI2, СdCl2, МоS2, FeCl3 и т. п.). Особенно характерна слоистость для гидроксидов в связи с тем, что гидроксил ОН– имеет постоянный диполь: брусит Мg(ОН)2, гиббсит Аl(ОН)3, хэггит V2О2(ОН)3 и т. п. Бруситовые и гиббситовые слои, связывающие в трехэтажные пакеты кремнекислородные слои, являются причиной хорошо известной способности слюд расщепляться на тонкие пластинки.
Для гидроксидов типа АХ Ф. Гунд теоретически предвидел возможность образования слоистых структур, и в 1933 г. была экспериментально найдена тетрагональная слоистая структура LiOH. Эффективный размер гидроксил–иона ОН– очень близок к радиусу F–. Поэтому отношения r+/r– для LiOH и LiF практически одинаковы и предсказание типа структуры в этом случае становится неоднозначным. Иначе говоря, наличие постоянных диполей, склонность к поляризуемости анионов, зависимость
радиусов ионов от многих факторов и частичная ковалентность химической связи являютcя причинами, осложняющими простое применение правил Магнуса–Гольдшмидта.
Второе правило Полинга – так называемое электростатическое правило валентностей – считается наиболее важным из пяти. Оно отражает один из фундаментальных принципов кристаллохимии: в устойчивой существенно ионной структуре валентность каждого аниона, взятая с обратным знаком, точно или приближенно равна сумме валентных усилий катионов первой координационной сферы:
|
z− = åvi |
= åzi+ /νi , |
(1) |
|
i |
i |
где z− – заряд аниона, vi – валентное усилие i–катиона, равное отношению его заряда zi+ к
KЧ(νi ).
Для многих простых и даже довольно сложных структур это правило выполняется точно. Рассмотрим его на примере перовскита СаТiO3. Ион О2- в структуре перовскита окружен двумя Ti4+ (КЧ = 6) и четырьмя Са2+ (КЧ=12), валентные усилия которых равны
vTi=4/6=2/3 и vСa=2/12=1/6. Сумма åvi =2(2/3)+4(1/6)=2 точно соответствует заряду
i
аниона.
Это простое правило сильно ограничивает число приемлемых для данного вещества структур. Оно может служить также для контроля правильности определения кристаллической структуры. Л. Полинг считал, что для устойчивых кристаллических построек, особенно минералов, отклонения от предсказаний его правила не превышают ±10% и встречаются редко, но они могут быть больше для полученных в лаборатории кристаллов, среди которых нередки метастабильные и просто неустойчивые.
13

В первоначальной формулировке Полинга валентные усилия катиона распределяются поровну между окружающими его анионами вне зависимости от расстояния катион – анион. Строго говоря, это верно только для правильных КП, в которых все расстояния от центра до вершин равны. Для искаженных КП валентные усилия катиона должны распределяться между анионами не равномерно, а каким–то образом зависеть от величины расстояния катион – анион.
Еще в конце 50-х годов прошлого века было обнаружено при анализе некоторых кристаллических структур (цоизит, бадделиит), что «недосыщенные» катионными
валентными усилиями анионы характеризуются в среднем более короткими связями с катионом, а «пересыщенные», наоборот, более длинными. Позже появились попытки (Пятенко, 1970-1972; Браун, Шэннон, 1973), количественно выразить обратную
зависимость между величиной пая валентности и межатомным расстоянием в форме
где λ – эмпирический показатель степени, который изменяется от 2 для электроположительных химических элементов до 7 для электроотрицательных. Параметр b находят из условия равенства суммы валентных усилий катиона его заряду:
|
b = zi+ / å(1/ Rijλ ) j |
(3) |
|
j |
В случае надежно уточненных кристаллических структур этот метод обеспечивает отклонение от значений формальной валентности аниона не более чем на 10%.
Рассмотрим применение детализированного таким образом второго правила Полинга на примере соединений А22+В25+О7, принадлежащих структурному типу пирохлора (Пятенко, 1970). В этой структуре КЧ(А)=8, КЧ(В)=6. Атомы кислорода занимают две позиции – О1 и О2. На каждом атоме О1 сходятся только четыре восьмивершинника вокруг атомов А2+ (v =2/8), а каждый О2 принадлежит одновременно двум восьмивершинникам (v = 2/8) и двум октаэдрам (v = 5/6). Формальный баланс
валентностей в соответствии с первоначальным вариантом правила Полинга дает сумму валентных усилий катионов на О1 только 4(2/8) = 1, а на О2 – 2(2/8) +2(5/6) =2,17 вместо 2. Расхождение, особенно в случае О1, недопустимо велико для устойчивой структуры.
Решение этой задачи можно найти, если обратиться к анализу конкретных межатомных расстояний в структуре пирохлора. Все шесть расстояний В–О в ней точно равны друг другу, так как В занимает правильную систему точек с симметрией 3m .
Следовательно, v(В) остается равным 5/6. Однако А–восьмивершинники характеризуются резким различием отдельных расстояний. Так, в структуре Cd2Nb2O7 два расстояния CdO1 равны 2,25 Å, а остальные шесть расстояний Cd-O2 составляют 2,73 Å. С учетом того,
14
что в величина λ для Cd равна 6, найдем, что валентное усилие в связи Cd-O1 оказывается равным 0,52, а в связи Cd-O2 только 0,16. С этими vi сумма валентных усилий на О1 составит 4·0,52=2,08, а на O2 – 2(0,16)+2(5/6) = 1,99. Оба новых значения весьма близки к валентности аниона 2, т. е. отвечают условию локального баланса валентностей.
Любопытно, что если место Cd в структуре пирохлора занимает более электроотрицательный атом Hg, для которого λ = 7, перепад межатомных расстояний в восьмивершиннике становится меньше (0,36 Å вместо 0,48 Å). Наоборот, в случае более электроположительных атомов Са (l = 3) в А–позиции локальный баланс достигался бы лишь при 1 Å. Такое сильное искажение восьмивершинника должно сталкиваться с большими стерическими препятствиями, и кристаллизация Ca2Nb2O7 в структурном типе пирохлора оказывается невозможной. Постоянное присутствие в природных пирохлорах Na и Са компенсируется одновременным замещением О на F, что требует меньших значений v катионов.
Отметим, что хотя свое второе правило Л. Полинг отнес к ионным структурам,
условие локального баланса валентностей должно соблюдаться и для ковалентных кристаллов. Его можно использовать формально прежним способом. Например, для ZnS с тетраэдрической координацией обоих атомов vZn = 1/2 и ∑v =4×1/2= 2, что равно валентности S, как требует правило.
Однако в этих случаях, по существу, более правильно использовать не валентное усилие катиона, а порядок (кратность) k ковалентной связи. Самое простое, хотя и не самое строгое, определение порядка связи есть отношение валентности к координационному числу. Тогда порядок связи в структуре сфалерита k=1/2, и правило Полинга вновь будет выполняться.
В случае существенно ковалентных кристаллов со сложными структурами, в
которых межатомные расстояния оказываются различными даже между атомами одного сорта, для расчета порядка связи k в зависимости от ее длины Rk можно применить уравнение Полинга, например, в следующем виде для металлических кристаллов:
|
R1 − Rk = 0,30 ln k , |
(4) |
где R1 – длина связи с кратностью k=1. В табл. 2 приведены результаты расчета порядков связей в структуре Sb2Se3 (Тайдесвелл и др., 1957). При выборе R1(Sb-Se)=2,63 Å, видно, что кристаллографически различные атомы Sb и Se обнаруживают постоянные валентности 3 и 2, равные приблизительно сумме кратностей связей для каждого из них, причем некоторый вклад в локальный баланс дают и соседи, расположенные от центрального атома примерно на 40% дальше, чем ближайшие.
15
Таблица 2. Локальный баланс валентностей в кристалле Sb2Se3
|
Атом |
Лигаид |
Rk*, Å |
k |
|
Sb 1 |
Se 2 |
2,66(2) |
0,89 |
|
Se 3 |
2,66(1) |
0,89 |
|
|
Se 1 |
3,22(2) |
0,10 |
|
|
Se 2 |
3,26(1) |
0,09 |
|
|
Se 3 |
3,74(1) |
0,01 |
|
|
Σ=2,97 |
|||
|
Sb2 |
Se 1 |
2,58(1) |
1,21 |
|
Se 3 |
2,78(2) |
0,56 |
|
|
Se 1 |
2,98(2) |
0,26 |
|
|
Se 2 |
3,46(2) |
0,04 |
|
|
Σ= 2,93 |
|||
|
Se 1 |
Sb 2 |
2,58(1) |
1,21 |
|
Sb 2 |
2,98(2) |
0,26 |
|
|
Sb 1 |
3,22(2) |
0,10 |
|
|
Σ=1,93 |
|||
|
Se 2 |
Sb 1 |
2,66(2) |
0,89 |
|
Sb 1 |
3,26(1) |
0,09 |
|
|
Sb 2 |
3,46(2) |
0,04 |
|
|
Σ=1,95 |
|||
|
Se 3 |
Sb 1 |
2,66(1) |
0,89 |
|
Sb 2 |
2,78(2) |
0,56 |
|
|
Sb 1 |
3,74(1) |
0,01 |
|
|
Σ=2,02 |
|||
* Цифра в скобках – число одинаковых связей.
Уравнение (4) с общим (универсальным) множителем 0,37 Å сейчас широко
используется для анализа выполнения локального баланса валентностей в кристаллах самых различных типов, вне зависимости от характера химической связи. Оно позволяет
указать на неверное определение кристаллической структуры в случае очень сильного отклонения рассчитанных валентностей от реальных, на замещение O2- одновалентными ионами F– и OH–, на возможное положение атомов H в структуре (эти последние случаи представляют трудности для рентгеноструктурного анализа из–за близости атомных факторов рассеяния O, OH и F).
Условие локального баланса валентностей может служить хорошим критерием выбора КЧ в тех случаях, когда приходится иметь дело с сильно искаженным КП и целым набором близких друг к другу межатомных расстояний. Приведем пример использования такого критерия. Нетрудно проверить, что вошедшая в справочники и учебники
16
кристаллохимическая формула фергюссонита Y[8]Nb[4]O4[3] при КЧ (Nb)=4 полностью удовлетворяет первоначальному варианту второго правила Полинга. Однако Ю. А. Пятенко показал (1972), что при учете конкретных межатомных расстояний в этой структуре KЧ(Nb)=6 лучше соответствует балансу валентностей на обоих сортах анионов O1 и О2, чем КЧ(Nb)=4 (табл. 3). Этот выбор, конечно, меняет и среднее КЧ (О): оно становится 3,5 вместо 3.
Таблица 3. Локальный баланс валентных усилий на анионах в структуре фергюссонита при КЧ (Nb) = 4 и КЧ (Nb) = 6 (в скобках)
|
Анион |
v (Y3+) |
v (Nb5+) |
åvi |
||
|
О1 |
0,39+0,34 |
{ |
1,12(4) |
1,85 |
0,15 |
|
0,98+0,31(6) |
2,02 |
0,02 |
|||
|
О2 |
0,37+0,40 |
{ |
1,38(4) |
2,15 |
0,15 |
|
1,21(6) |
1,98 |
0,02 |
Г. Донней и Р. Альманн (1970) предложили оценивать максимальный радиус каждого иона, на котором его валентное усилие становится равным нулю. Это можно сделать, если экстраполировать к нулю значения vi для разных КЧ, отложенные против соответствующих значений ионного радиуса ri. Сказанное было проиллюстрировано ими для К+ и О2-. Полученные таким способом rмакс равны 1,88 и 1,45 Å соответственно. Значит, расстояние К–О = 1,88+1,45=3,33 Å является критическим рубежом, который ограничивает первую координационную сферу. Замечено также, что эти критические значения в среднем на 0,25 Å меньше суммы ван–дер–ваальсовых радиусов (см. часть 1 пособия) и в сомнительных случаях можно использовать просто эту сумму в качестве предельного радиуса первой координационной сферы.
Третье и четвертое правила Полинга тесно связаны между собой и имеют прямое отношение к тому факту, что появление общих ребер и особенно граней КП приводит к сильному уменьшению расстояний между катионами, находящимися в их центрах. Так, расстояния, между центрами октаэдров с общими вершинами, ребрами и гранями относятся как 1:0,71:0,58, а тетраэдров соответственно 1:0,53:0,33. При столь значительном сближении резко возрастают силы отталкивания между катионами, что делает структуру неустойчивой. По этой причине SiO4–тетраэдры связываются друг с другом только вершинами. Более крупные ТiO6–октаэдры могут иметь по два (рутил), три (брукит) и четыре (анатаз) общих ребра, но только рутил является стабильной модификацией ТiO2.
В силикатах с отношением О/Si³4 SiO4–тетраэдры не имеют общих вершин.
17
Исключения наблюдаются в случае смешанных анионных радикалов, в которых, кроме кремния участвуют мелкие и высокозаряженные катионы другого сорта. Так, в структуре боросиликата данбурита СаВ2Si2О8 (О/Si = 4) встречены сдвоенные по общим вершинам SiO4– и ВО4–тетраэдры; диортогруппы Si2O7 и B2O7, чередуясь друг с другом, образуют общий каркас этой структуры.
Если КП вокруг катионов с большим зарядом все–таки вынуждены иметь общие ребра или грани, то отталкивание между ними. ведет к деформации КП, при которой расстояние между катионами было бы как можно больше. Это достигается за счет уменьшения длины общих ребер КП. Известно, что стандартная длина ребра правильного кислородного октаэдра в оксидах и силикатах составляет 2,7-2,9 Å, т. е. приблизительно равна удвоенному значению ионного (или ван–дер–ваальсового) радиуса кислорода. Но длина ребер октаэдров в корунде Аl2О3, которые окаймляют обобществленные между ними грани, уменьшается почти до 2,5 Å.
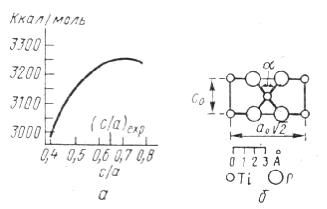
Электростатическая природа этих эффектов иллюстрируется рис. 3, а, где показана зависимость электростатической энергии решетки рутила ТiO2 как функции отношения осей с/а тетрагональной ячейки.
Рис. 3. Электростатическая энергия
структуры типа рутила как функция величины отношения с/а (а); сечение элементарной ячейки рутила (110) (б).
Изменение угла α обусловливает изменение величины с/а.
Если бы кислородные октаэдры были правильными, то с/а было бы равно 0,586. Опыт дает с/а = 0,644, а максимуму электростатической энергии соответствует с/а = 0,721.
На рис. 3, б показано, что увеличение с/а достигается при уменьшении угла α в результате отталкивания между Тi4+ и соответствующего стягивания ионов кислорода на общем ребре. Отношению с/а = 0,721 отвечало бы очень короткое расстояние О–О около 2,4 Å. Отталкивание между ионами кислорода, резко возрастающее при их сближении, препятствует этому, и устанавливается компромиссное расстояние О–О, составляющее около 2,5 Å.
18

Третье и четвертое правила Полинга, строго говоря, относятся только к КП вокруг ионов с заполненной оболочкой типа инертного газа. Незаполненные оболочки ионов переходных металлов оставляют возможности для металл – металл валентных взаимодействий, которые становятся более эффективными при сближении катионов друг с другом. Поэтому многие переходные металлы в соединениях типа АХ склонны кристаллизоваться в структуре типа NiAs, в которой октаэдры вокруг атомов металла имеют общие грани (см. рис. 12 из первой части пособия). Следующий морфотропный ряд иллюстрирует сказанное: МgS – FeS – СоS – МnS – CaS. Найнинджерит МgS имеет структуру типа NaСl, а пирротин FeS и джайпурит СоS с очень близкими отношениями r+/r– – структуру типа NiAs. Ольдгамит СаS с большим значением r+/r– тем не менее снова «предпочитает» структуру NaСl. Образование непрерывных «стержней» со связями Ме– Ме, проходящими через всю структуру, хорошо объясняет магнитные (ферромагнетик) и электрические (проводник) свойства пирротина (см. рис. 12 первой части). Такие связи типичны для переходных металлов с незаполненными электронными оболочками, и поэтому они часто образуют структуру пирротина. Интересно, однако, что алабандин МnS имеет структуру типа NaCl, а две нестабильные модификации – структуры типа сфалерита и вюртцита. Отсутствие структуры типа NiAs для МnS находит объяснение в том, что Мn2+ обладает наполовину заполненной d5–оболочкой, которая по правилу Гунда представляет собой устойчивую конфигурацию, и поэтому соседние атомы Мn не стремятся обобществить свои d–электроны за счет образования связей металл–металл.
Пятое правило Полинга иногда называют «правилом экономичности» (парсимонии). Оно имеет большое число исключений, но от него было бы преждевременно отказаться. Примерами таких исключений являются четыре (!)
неэквивалентные октаэдрические позиции для катионов одной и той же группы элементов в амфиболах, кислородные октаэдры и тетраэдры вокруг Аl в силлиманите и слюдах, октаэдрические и тетраэдрические позиции FeIII в синтетическом гранате
Y3Fe2[6]Fe[4]O12 и т. п.
Рис. 4. В. М. Гольдшмидт
(1888 – 1947).
Итоговое эмпирическое обобщение многочисленных наблюдений над атомным строением существенно ионных кристаллов выражено В. М. Гольдшмидтом (рис. 4) в форме «основного закона
19

кристаллохимии»: структура кристалла определяется количественным соотношением его структурных единиц, отношением их размеров и их поляризационными свойствами.
Окончание этой формулировки в современном понимании отражает не только склонность сильно поляризующихся анионов (Сl–, Br–, Se2-, Te2- и др.) к образованию слоистых структур, но и к образованию существенно ковалентных связей при больших поляризуемостях (больших значениях электроотрицательностей) катионов. Правила устойчивости существенно ковалентных кристаллов будут рассмотрены в разделе 5-4.
5-3. ФАКТОР ТОЛЕРАНТНОСТИ И МОДЕЛЬНЫЕ СТРУКТУРЫ ГОЛЬДШМИДТА
Геометрические правила Магнуса – Гольдшмидта указывают условия образования устойчивого КП из двух различных по размерам ионов. Только для простых бинарных
соединений они совпадают с геометрическими критериями устойчивости структурного типа.
Если кристалл состоит из КП разного сорта, то ставится задача определить критерии наилучшего (в смысле плотности упаковки) сочетания их друг с другом. Пример решения такой задачи привел В. М. Гольдшмидт (1927) для кристаллов типа АВХ3 со структурой перовскита. Она имеет кубическую или псевдокубическую ячейку (рис. 5). Ионы А расположены в ее вершинах, В – в центре, а X – в центре граней; КЧ(А) = 12 (кубооктаэдр), КЧ(В)=6 (октаэдр), КЧ (X) =6 (4А+2В). Если ячейка кубическая, то расстояние А – X
должно быть в 
 2 раза больше, чем В– X, т. е.
2 раза больше, чем В– X, т. е.
|
rA + rX = |
2( |
rB + rX ) |
(5). |
Поскольку большинство перовскитов не являются кубическими, то Гольдшмидт заменил это условие более общим:
rA + rX = t
 2(rB + rX )
2(rB + rX )
(6),
где t – фактор толерантности
(приспособляемости), учитывающий искажение структуры. Если использовать стандартные ионные радиусы для КЧ = 6, то t
для реальных структур находится в пределах 0,8-1,0. Для истинно кубического
20
представителя перовскитов таусонита SrTiO3 значение t находится как раз в середине этого интервала (0,9). Если учесть, далее, что расстояние А-X в кубооктаэдре примерно на 6% больше, чем сумма стандартных радиусов, то фактор t приблизится к 1 для строго кубических перовскитов (SrTiO3, KNiF3, LaAlO3, NaTaO3 и др.).
Когда фактор толерантности t выходит за указанные пределы, структура перовскита перестает существовать и заменяется другими структурными типами соединений АВХ3. В
табл. 4 показана смена структурных типов в ряду ильменит → перовскит → кальцит → арагонит → RbNO3 по мере увеличения фактора толерантности t.
На границах между различными структурными типами находятся диморфные вещества, например СаСО3 и KNO3 со структурами кальцита и арагонита. Структура арагонита с более высокими КЧ одновременно и более плотная, поэтому она стабилизируется при повышенных давлениях.
Морфотропные ряды, подобные приведенным в табл. 4, указывают на возможность направленной перестройки структуры как при изменении состава (изодиморфизм, см. гл. VIII), так и при изменении термодинамических условий (полиморфизм, см.гл. VII). Так, давно известно, что Sr постоянно присутствует в арагоните в гораздо больших количествах, чем в кальците, стабилизируя эту модификацию, подобно повышению давления.
Таблица 4. Смена структурных типов АВХ3 с изменением фактора толерантности t
|
Минерал |
t |
Структурный |
|
|
тип; КЧ |
|||
|
MgTiO3, гейкилит |
0,76 |
ильменит 6:6:4 |
|
|
FeTiO3, ильменит |
0,78 |
||
|
МnТiO3, пирофанит |
0,80 |
||
|
СаТiO3, перовскит |
0,86 |
перовскит 12:6:6 |
|
|
SrTiO3, таусонит |
0,91 |
||
|
ВаТiO3 |
0,99 |
||
|
MgCO3, магнезит |
1,20 |
кальцит 6:3:3 |
|
|
MnCO3, родохрозит |
1,26 |
||
|
СаСО3, кальцит |
1,35 |
||
|
СаСО3, арагонит |
1,35 |
арагонит 9:3:4 |
|
|
SrCO3, стронцианит |
1,47 |
||
|
ВаСО3, витерит |
1,56 |
||
|
RbNO3 |
1,65 |
RbNO3 12:3:5 |
|
|
CsNO3 |
1,75 |
||
21

Идею Гольдшмидта нетрудно распространить и на другие типы соединений. Рассмотрим в качестве нового примера кристаллы стехиометрического типа АВ2Х4. Начнем с кубического структурного типа нормальной шпинели, в которой катионы В заселяют половину октаэдров, а катионы А четверть тетраэдров плотнейшей кубической упаковки из атомов кислорода. В идеальной структуре шпинели расстояние В-X равно (1/4) а, а расстояние А–Х=(1/8) a 
 3 . Следовательно, для нее справедливо следующее
3 . Следовательно, для нее справедливо следующее
|
соотношение: |
|
|
rA + rX = 0,87(rB + rX ) или rT + rX = 0,87(rO + rX ) , |
(7) |
rT и rO – радиусы катионов в тетраэдрах и октаэдрах соответственно. Из–за изменения кислородного позиционного параметра (u, u, u) в структуре шпинели возможны отклонения от идеального значения 0,87, которые можно учесть с помощью фактора
|
толерантности t: |
|
|
rT + rX = 0,87t(rO + rX ) . |
(8) |
Для стабильных шпинелей (как нормальных, так и обращенных) t обычно находится в интервале 1,0-1,2. Это, во–первых, означает что катионы А и В в шпинелях должны быть весьма близки по размерам ( rT » rO ), и, во–вторых, обусловливает возможность их неупорядоченного распределения по октаэдрическим и тетраэдрическим позициям. Действительно, для кислородных шпинелей характерны катионы с радиусами 0,6-0,9 Å (А13+, Mg2+, Zn2+, Fe2+, Fe3+, Ge4+, Mn2+, Mn3+, Co2+, Sn4+, Ti4+, Ni2+, Cr3+, V3+), и многие из
них дают частично обращенные структуры с неупорядоченным распределением ионов разного заряда по октаэдрическим и тетраэдрическим позициям (например, MgFe2O4 или
MnFe2O4).
Если фактор t становится меньше 1, что можно достигнуть либо увеличением rO ,
либо уменьшением rT , то структурный тип шпинели сменяется структурным типом оливина Mg2SiO4. В нем кристаллизуются многие ортосиликаты и ортогерманаты, для которых rT < rO из–за относительно малых размеров A (Si, Ge). Критическим значением t=0,97 характеризуется диморфный Mg2GeO4, который при повышении температуры переходит из структуры оливина в структуру шпинели. Ситуация, когда rT < rO ,
реализуется и при другом распределении валентностей в хризоберилле ВеА12О4 со структурой оливина. Здесь в качестве более мелкого катиона выступает Ве2+, занимающий тетраэдрические позиции, тогда как более крупный и высокозаряженный Al3+ находится в октаэдрах.
Наоборот, при t > l,2, что достигается, если rA ³ rB , соединения типа АВ2О4
22

тортвейтита Sc2Si2O7
Рис. 7. Cочленение шестичленных
колец из октаэдров с помощью
приобретают структуру фенакита Be2SiO4, в которой оба катиона имеют почти равные размеры и находятся в тетраэдрических позициях. Кажущееся противоречие с этим выводом представляет виллемит Zn2SiO4 ( rB > rA ), но следует учесть, что тетраэдрическая координация более крупного цинка стабилизируется его стремлением оказаться в sр3– гибридном состоянии и дать четыре направленных связи.
По существу, на той же гольдшмидтовской идее соизмеримости структурных элементов основано деление кристаллохимии силикатов на два раздела (две главы, по Н. В. Белову, рис. 6). В первую («брэгговскую») главу попадают кристаллические структуры силикатов, которые представляют собой плотнейшую упаковку (большей частью кубическую) из атомов О, ОН, F и в которых октаэдрические пустоты заселены катионами Mg, Al, FeII, FeIII, Ti, а тетраэдрические – атомами Si и Al.
Ребра октаэдров с этими относительно мелкими (r < 1 Å) катионами длиной 2,7-2,9 Å хорошо приспосабливаются к ребрам соседних (Si, Al) – тетраэдров длиной 2,55-2,75 Å.
«Вторая глава» кристаллохимии силикатов, создание которой связано с именем Н. В. Белова,
описывает кристаллические постройки с крупными катионами, главным образом Na, Ca, TR (r>1 Å). В том случае, когда они находятся в кислородных
Рис. 6. Н.В.Белов (1891 – 1982). октаэдрах, ребра последних равны 3,7-3,8 Å и ребро одиночного SiO4–тетраэдра не соизмеримо с ними.
Поэтому основной кремнекислородной «строительной единицей» во «второй главе» становится диортогруппа [Si2O7] – два связанных
«мостиком» тетраэдра. Сумма высот двух тетраэдров близка к 4 Å, т. е. действительно соизмерима с ребром (Ca, Na, ТR)О6–октаэдра. На рисунке 7 показан способ сочленения такой
группой октаэдров в структуре тортвейтита
Sc2Si2O7.
Близкие значения фактора толерантности
допускают существование в одном структурном диортогруппы Si2O7 в структуре
типе различных химических веществ одного
стехиометрического типа. Например, известны перовскиты КIO3, СаТiO3, LaAlO3, KNiF3;
23
шпинели MgAl2O4, Zn2TiO4, Co3S4, K2Cd(CN)4, нитраты (LiNO3), карбонаты (MgCO3) и
бораты (ScBO3) со структурой кальцита и т. д. Это дало основание В. М. Гольдшмидту ввести представление о кристаллохимических аналогах, или модельных структурах
(1926).
Хорошо известными кристаллохимическими аналогами силикатов являются германаты и фторбериллаты. Например, в структуре оливина кристаллизуются Mg2SiO4, Ca2GeO4 и Na2BeF4. Значение модельных структур состоит в том, что с ними часто гораздо легче экспериментировать, чем с моделируемыми объектами. Так, фторбериллаты гораздо более легкоплавки и растворимы, чем силикаты. Германаты из–за большего размера Ge по сравнению с Si находятся ближе к критическому значению фактора толерантности и легко моделируют структуры силикатов, устойчивых при высоких давлениях. Вспомним о диморфизме GeO2 (структуры кварца и рутила) и Mg2GeO4 (структуры оливина и шпинели), который является прототипом (моделью) переходов кварца SiO2 в стишовит и оливина (Mg, Fe)2SiO4 в силикатную шпинель при высоких давлениях.
5-4. КРИТЕРИИ УСТОЙЧИВОСТИ СТРУКТУРНОГО ТИПА ДЛЯ СУЩЕСТВЕННО КОВАЛЕНТНЫХ КРИСТАЛЛОВ
Другая группа правил определяет условия устойчивости структурных типов ковалентных и существенно ковалентных кристаллов. Для них, в отличие от ионных кристаллов, ведущим фактором становится направленность химических связей, которая обусловливает как КЧ, так и геометрическую конфигурацию ближайшего окружения – тип КП.
В качестве меры направленного характера химической связи между атомами можно использовать среднее главное квантовое число n самых наружных занятых электронных оболочек. По мере увеличения n атомные орбитали, участвующие в образовании связей, и, следовательно, сами связи постепенно теряют свою направленность. Однако это свойство зависит не только от n , но и от разности электроотрицательностей атомов–
партнеров Δχ. По мере возрастания Δχ связи становятся все более ионными, т. е. ненаправленными, вне зависимости от величины n . На диаграмме Музера-Пирсона,
построенной в координатах n -Δχ (рис. 8), четыре важнейших структурных типа МХ –
В2(СsСl) В1(NaCl), ВЗ (сфалерит), В4 (вюртцит) – занимают свои поля. Правее и выше
24

(большие n и Δχ) находится область стабильности В2 (СsС1) – структуры с высокими КЧ
(8:8) и ионностью связи, левее и ниже других (малые n и Δχ) – область стабильности ВЗ
(сфалерит) с низкими КЧ (4:4) и высокой долей ковалентности связи. На рис. 9 показаны аналогичные соотношения для структурных типов МХ2.
|
Рис. 8. Диаграмма Музера–Пирсона для соединений |
Рис. 9. Диаграмма Музера–Пирсона для МХ2. |
|
|
МХ: 1 – структура NaCl (В1); 2 – структура СsС1 |
Структурные типы: 1 |
– котуннит РbCl2, 2 – флюорит, |
|
(В2); 3 – структура сфалерита; 4 – структура |
3 –рутил, 4 – СdI2, 5 |
–МоS2, б – СdCl2, 7 – GeS2 и |
|
вюртцита. |
различные модификации SiO2. КЧ катионов |
|
|
уменьшаются от 9 до 4 в этом ряду. |
Впервой части пособия уже упоминалось правило октета Юм-Розери, согласно которому КЧ в структурах простых ковалентных веществ (IV-VII группы Периодической системы) равно 8 – N, где N – номер группы. В отношении бинарных соединений МХ с существенно ковалентной связью X. Гримм и А. Зоммерфельд в 1926 г. отметили особую устойчивость структуры типа сфалерита (вюртцита), если сумма номеров группы NM + NX
=8. Другими словами, атомы М и X так расположены в Периодической системе, что атом М на столько клеток предшествует атомам IVгруппы Si, Ge, Sn, на сколько клеток позади них расположен атом X. Отметим, что правило Гримма–Зоммерфельда не выполняется для соединений переходных металлов. Так, ТiС и ScN имеют структуру типа NaCl, а не ZnS.
Вболее общей форме правило Гримма – Зоммерфельда можно выразить как nе/m = 4, где nе – число валентных электронов, а m – число атомов на формулу соединения. Отношение nе/m можно назвать также «концентрацией валентных электронов». Это правило легко понять с точки зрения теории направленных валентностей, если допустить sр3–гибридизацию валентных оболочек обоих партнеров, что и приводит к тетраэдрической конфигурации окружения. Четыре связи между атомом и его
25

ближайшими соседями оказываются ординарными σ-связями, и на каждый из них размещаются два валентных электрона. Примечательно, что величина межатомного расстояния в таких изоэлектронных рядах (сумма атомных номеров åZ =соnst) почти не
зависит от того, в какой группе данного периода находятся атомы М и X (табл. 5). Оно хорошо передается суммой ковалентных радиусов.
Таблица 5. Межатомные расстояния в кристаллах со структурой алмаза–сфалерита (в скобках сумма радиусов)
|
åZ |
кристалл |
R, Å |
åZ |
кристалл |
R, Å |
|
28{ |
AlP |
2,35 (2,25) |
CuI |
2,62 (2,75) |
|
|
Si |
2,35 (2,40) |
82{ |
ZnTe |
2,64 (2,75) |
|
|
CuCl |
2,34 (2,35) |
GaSb |
2,64 (2,75) |
||
|
46{ |
|||||
|
ZnS |
2,35 (2,35) |
AgI |
2,808 (3,00) |
||
|
GaP |
2,35 (2,30) |
100{ |
CdTe |
2,805 (2,95) |
|
|
CuBr |
2,46 (2,45) |
InSb |
2,806 (3,00) |
||
|
64{ |
ZnSe |
2,45 (2,50) |
β-Sn |
2,810 (2,90) |
|
|
GaAs |
2,44 (2,45) |
||||
|
Ge |
2,45 (2,50) |
||||
Дальнейшим обобщением правила октета для существенно ковалентных соединений типа МkХl, обычно обладающих полупроводниковыми свойствами, является правило Музера–Пирсона (1960):
где l – число анионов, b – число связей, образуемых между одноименными атомами. Например, в тетрагональной фазе ZnP2 имеются спиральные цепочки из атомов Р. Следовательно, каждый атом Р связан с двумя другими и b = 2 (каждая связь принадлежит данному атому наполовину). Правило выполняется при nе = 2+(2·5)=12, l = 2.
Обобщенному правилу Пирсона для сложных соединений можно придать следующий вид:
|
( ne + nXX − nMM l = 8 ). |
(10) |
Здесь nе – сумма валентных электронов всех атомов в химической формуле соединения, nXX – число электронов, участвующих в связях анион – анион, nMM – число электронов, образующих связи катион – катион или остающихся на неподеленных L–парах. Например в галените РbS из четырех валентных электронов Рb два остаются в качестве неподеленной L-пары. Значит, nе = 6 + 4 = 10, nXX = 0, nMM = 2, l = 1, и правило выполняется. Для кристалла In2Те3 nе = (2·3)+(3·6)=24, nXX = nMM = 0, l = 3, и правило
26

Пирсона также действует.
Иные варианты правила октета для тетраэдрических структур халькогенидов дал Э.
Партэ (1972):
|
bL m = (ne / m) − 4 , |
(11) |
|
где bL – число неподеленных пар, и |
|
|
ne / l = 8(k / l)bMM + bXX , |
(12) |
где k – число катионов, l – число анионов, bMM и bXX – числа связей катион – катион (и неподеленных электронных пар катионов) и анион – анион. При ne/m = 4 bL = 0 и первое правило Партэ переходит в правило Гримма – Зоммерфельда для «нормальных» тетраэдрических структур. При 4 < ne/m ≤ 6 появляются дефектные тетраэдрические структуры. Например, ZnIn2S4 (ne/m = 4,57) имеет дефектную тетрагональную структуру типа халькопирита СuFeS2(Сu2Fe2S4), в которой остается вакантной одна из четырех тетраэдрических катионных позиций. Если ne/m > 6, то образуются молекулярные структуры.
Свое второе правило (12) Партэ применил к так называемым полианионным и поликатионным соединениям, в которых помимо частично ионных связей катион – анион возникают и предельно ковалентные связи анион – анион и катион – катион. При ne/l = 8 образуются нормальные валентные соединения, взаимодействия анион – анион и катион – катион отсутствуют (bXX = bMM = 0). Это условие отвечает, очевидно, возможности для аниона создать устойчивую восьмиэлектронную оболочку, т. е. стать подобным соседнему инертному газу, хотя это, конечно, не означает, что все 8 валентных электронов принадлежат безраздельно аниону. Тип связи по той классификации, которая была дана в первой части пособия, в этом случае ближе всего к донорно–акцепторной разновидности ковалентного взаимодействия.
Если ne/l < 8, т. е. электронов недостаточно, то появляется возможность анион – анионных взаимодействий. Например, ауростибит АuSb2 (ne/l = 5,5) имеет структуру типа пирита с «молекулярной» гантелью Sb2. Структура карбида кальция СаС2 (ne/l =5) содержит молекулярные группы С2.
В другом случае, когда ne/l > 8, возникает общий «избыток» электронов для завершения по донорно – акцепторному механизму анионной оболочки и возможно образование катион – катионных связей. Типичным примером является миллерит NiS (ne/l = 16, если считать валентной всю незаконченную d–подоболочку никеля). В структуре миллерита КЧ никеля 5, а КП – полуоктаэдр. Такие полуоктаэдры объединяются по три своими квадратными основаниями в бесконечные «пустые» внутри каналы тригонального сечения
27

(рис. 10). По образному выражению Н. В. Белова, атомы Ni «выглядывают» из оснований полуоктаэдров и осуществляют взаимодействие Ni-Ni.
Этот пример показывает, что в существенно ковалентных соединениях переходных металлов с незаполненными d–оболочками электронная конфигурация металла (катиона)
|
должна служить не менее важным |
|||||||||
|
критерием выбора устойчивой |
взаимной |
||||||||
|
координации |
атомов, |
чем |
условие |
||||||
|
завершения электронной оболочки аниона. |
|||||||||
|
Именно на это обстоятельство обратил |
|||||||||
|
внимание Н.В.Белов, который предложил |
|||||||||
|
так называемые «числовые законы» |
|||||||||
|
строения сульфидов и сульфосолей (1973- |
|||||||||
|
1976). Согласно этим правилам, наиболее |
|||||||||
|
Рис. 10. Ромбоэдрическая упаковка троек из Ni- |
устойчивыми |
являются |
18-электронные |
||||||
|
«криптоновые» и «ксеноновые» оболочки |
|||||||||
|
полуоктаэдров |
в |
миллерите, |
атомы |
Ni |
|||||
|
«выглядывают» |
из |
их |
оснований |
в |
катионов, которые формируются по |
||||
|
пронизывающие |
структуру |
каналы |
и |
донорно–акцепторному механизму. Так, в |
|||||
|
объединяются в металлические тройки. |
предыдущем |
примере |
с миллеритом |
||||||
образование Ni-Ni связей обязано стремлению атома Ni получить 18-электронную конфигурацию. В этой структуре КЧ Ni и S равны 5. Мысленно завершим сначала оболочку аниона до S2-, для чего потребуется временно «занять» два валентных электрона у каждого Ni. Во внешней оболочке последнего остается 8 электронов, и необходимо еще 10 для устойчивой 18-электропной конфигурации. Однако S2-, окруженный пятью Ni2+, способен дать только четыре донорные электронные пары вместо требующихся пяти. Это вынуждает атомы металлов образовать кластеры из троек Ni, чтобы восполнить недостаток электронов для завершения своих оболочек. Своеобразные «объемные» кластеры образуются атомами Ni, находящимися в тетраэдрическом окружении в структурах хизлевудита Ni3S2, орегонита Ni2FeAs2 и пентландита Ni9S8. В последнем, например, металлический кластер создается путем «прилипания» восьми NiS4–тетраэдров к пустому октаэдру, внутри которого и размещается 8-ядерный кластер.
Типична кластеризация атомов Fе в пирротине Fe7S8, кубаните СuFe2S3. Fе в пирротине со структурой NiAs (рис. 12, часть 1) получает недостающие ему для построения 18-электронной оболочки электроны путем обобществления граней соседних FeS6–октаэдров, которые образуют цепочечные кластеры. В минералах талнахите Сu9Fe8S16, мойхуките Сu9Fe9S16 образуются смешанные Сu-, Fe-кластеры.
28
Другое «число» Белова – 13. Оно отвечает относительной устойчивости (по правилу Гунда) наполовину занятой d5–оболочки, характерной для переходных элементов из середины соответствующих групп – Fe3+, Mn2+, Mo2+, Re2+. Поэтому для Fe3+ достаточно только четырех донорных пар электронов, что и осуществляется в халькопирите CuIFeIIIS2, где FeIII находится в тетраэдрической координации. Н. В. Белов считал, что стремление к 13 электронам объясняет частое для СuII и AgII КЧ = 2. Добавление двух пар донорных электронов к собственным девяти d–электронам этих металлов достаточно для достижения 13-электронной оболочки.
Своеобразны соотношения между структурным типом пирита FeS2 (см. рис. 14, часть 1) и слоистыми структурами типа молибденита MoS2 и CdI2 (см. рис. 13, часть 1) для существенно ковалентных халькогенидов. В. М. Гольдшмидт заметил еще в 1931 г., что соединение МХ2 кристаллизуется в слоистой структуре, если металлический радиус атома М относительно велик, а если он меньше 1,35 Å, то стабильной становится структура пирита. Он считал, что большие металлические атомы легче отдают сере электроны для завершения ее электронной оболочки, а малые – с трудом, что заставляет атомы серы объединяться в молекулярную гантель S2.
Сейчас можно добавить к этому, что электронная концентрация для кристаллов со структурой пирита обычно меньше, чем для слоистых кристаллов. Это иллюстрируется сопоставлением соединений платины: PtS2, PtSe2 и PtTe2 (ne/l = 11) кристаллизуются в слоистых структурах, тогда как PtP2, сперрилит PtAs2, геверсит PtSb2 (ne/l = 10) – в структуре типа пирита. Относительный недостаток валентных электронов во втором случае приводит к образованию псевдомолекулярных анионных группировок Р2, As2, Sb2.
Наоборот, относительный избыток валентных электронов катиона ведет к появлению катионных группировок. Такова структура «антипирита» (по Н. В. Белову) InSe, в которой гантели In2 находятся внутри тригональных призм из атомов Se. Кристаллохимическая формула этого соединения [In2]Se2, а его структура аналогична слоистой структуре молибденита MoS2, в которой на местах одиночных атомов Мо размещаются двухъядерные кластеры In2.
Особое место занимает кристаллохимия существенно ковалентных соединений с неполновалентными катионами: PbII, TlI, AsIII, SbIII, BiIII. В этих валентных состояниях последние обладают одной неподеленной парой электронов – L-парой. Не участвуя непосредственно в образовании связи, L-napa тем не менее принимает участие в гибридизации валентной оболочки, т. е. в большинстве случаев приобретает
направленный в пространстве характер и по этой причине становится стереохимически активной. В меньшей мере это относится к более тяжелым катионам (TlI, PbII, BiIII), L –
29

пара которых чаще всего не имеет определенной пространственной локализации и стереохимически инертна.
Как упоминалось в первой части, L-пары выступают как некие аналоги отрицательно заряженных лигандов, занимающие определенное пространство. Их эффективный объем соизмерим с объемом таких мелких анионов, как F– или О2-. По этой причине L-пары отталкиваются друг от друга и от других отрицательно заряженных лигандов, стремясь занять по возможности наиболее удаленное положение. Их можно изобразить в качестве достраивающих КП лигандов, например, тройная «зонтичная»
координация As, Sb, Bi может формально рассматриваться как тетраэдрическая YLX3, где Y = As, Sb, Bi, X = S и ее аналоги, L – неподеленная пара, занимающая четвертую вершину тетраэдра.
Если атомы Y имеют КЧ = 5 и КП – полуоктаэдр, то L-napa
направлена от основания полуоктаэдра в мнимую шестую вершину октаэдра, и координацию можно изобразить в виде
YLX5..
Рассмотренные выше комплексы входят в состав сульфосолей, которые составляют почти половину известных сейчас природных
халькогенидов (более 100 минеральных видов). Они могут выступать как в изолированном виде, так и конденсироваться в более сложные сульфосолевые комплексы – цепочки, ленты, слои.
Сульфосоли с островными изолированными группами YS3 зонтичного строения – так называемые тетраэдрические сульфосоли, к ним относятся, например, блеклые руды: теннантит Cu12As8S12 и тетраэдрит Cu12Sb8S12. В сфалеритоподобном каркасе блеклых руд по сравнению со сфалеритом часть атомов серы «пропущена» и четверть тетраэдров замещается на условные тетраэдры YLS3. На элементарную ячейку блеклых руд приходится 32 тетраэдра, восемь из которых дефектные YLS3; формула такой ячейки имеет вид Cu24Y8L8S24. Мнимые L-вершины собраны в структуре в тетраэдрические четвёрки и образуют в каркасе крупные полости, по две на ячейку (Белов, Годовиков, Бакакин,1982).
Несмотря на всю сложность проблемы стабильности структурных типов, эмпирические «числовые» правила позволяют по крайней мере в рамках теории
направленных валентностей и модели валентного состояния атома понять причины изменения кристаллической структуры, например, в морфотропном ряду MS:
30

Структура реальгара AsS состоит из изломанных кольцевых молекул As4S4, в которых каждый атом As связан не только с двумя атомами S, но и с другим атомом As. Итак, KЧ(As)=3, KЧ(S)=2 в полном соответствии с правилом Юм–Розери. Структура ZnS – типичный пример действия правила Гримма – Зоммерфельда. Структуры миллерита NiS и пирротина FeS подчиняются «числовому закону 18» Н. В. Белова, а алабандин MnS со структурой типа NaCl – «числовому закону 13».
5-5. ОБОБЩЕНИЕ ПОНЯТИЯ МОРФОТРОПИИ НА ПРИМЕРЕ КРИСТАЛЛОХИМИИ СИЛИКАТОВ
Кристаллохимия силикатов – наиболее разработанный раздел структурной минералогии. Строение силиката, как впервые показал Ф. Махачки (1928), зависит от отношения числа атомов кислорода к числу атомов кремния O/Si в формульной единице. Если O/Si>4, то могут образоваться изолированные SiO4–тетраэдры, а если O/Si<4, то они должны соединяться между собой общими вершинами (мостиками), образуя большое разнообразие конденсированных (полимерных) форм кремнекислородных радикалов.
Систематику силикатов, которую начал на этой основе разрабатывать Е. Шибольд (1932, 1933), сейчас можно считать практически законченной благодаря трудам многих выдающихся ученых (В. Брэгг, Л. Полинг, В. Захариасен, Н. В. Белов и др.).
В табл. 6 приводится ряд важнейших кремнекислородных радикалов от изолированных SiO4–тетраэдров до трехмерного каркаса SiO2 в зависимости от O/Si.
Покажем теперь, что множество силикатов можно представить как типичный морфотропный ряд, если за основу взять не «классическое» отношение O/Si, а отношение суммы двухвалентных эквивалентов электроположительных катионов (обозначим ее обобщенно М) к числу атомов кремния M/Si. Для этой цели удобно выразить химическую формулу силиката в виде (МxSiy)О2, так что M/Si = x/y. Например, формула форстерита будет MgSi0,5O2; энстатита Mg2/3Si2/3O2 и т. д. Отношение M/Si в таком ряду меняется от 2 для ортосиликатов до 0 для кварца (см. табл. 6). В такой записи силикаты (MxSiy)O2 образуют морфотропный ряд, в котором выделяется действительная химическая причина перестройки кристаллической структуры – изменение киелотно–основных свойств
31
катионов, связанных с кислородом. Действительно, средняя электроотрицательность катионов, как нетрудно убедиться, изменяется с M/Si, а именно: она тем меньше, чем больше это отношение. Вообще атом кремния устойчиво сохраняет тетраэдрическую координацию до тех пор, пока другие катионы в структуре более электроположительны. Если он сам оказывается в роли наименее электроотрицательного катиона, как, например, в SiP2O7, он меняет координацию на октаэдрическую.
Таблица 6. Основные типы кремнекислородных радикалов как функция атомных отношений O/Si и M/Si
|
O/Si |
Формула анионного радикала |
Форма радикала |
M/Si |
|
|
4:1 |
[SiO4]4- |
изолированный тетраэдр |
2:1 |
|
|
7:2 |
[Si2O7]6- |
диортогруппа |
3:2 |
|
|
3:1 |
[Si3O9]6-, [Si4O12]8-, [Si6O18]12- |
кольца |
1:1 |
|
|
3:1 |
∞ [SiO3]2- |
цепь |
1:1 |
|
|
11:4 |
∞ [Si4O11]6- |
лента |
3:4 |
|
|
5:2 |
∞ [Si4O10]4- |
слой |
1:2 |
|
|
∞ |
||||
|
2:1 |
∞ [SiO2] |
каркас |
0:1 |
|
|
∞ |
||||
|
∞ |
Другое преимущество такого подхода заключается в том, что он представляет
возможность вскрыть характер изменения вдоль морфотропного ряда некоторых важных свойств. Как было отмечено в первой части пособия, эффективный заряд атома кремния в силикатах несколько увеличивается от островных к каркасным структурам. Это наблюдение соответствует упомянутому ранее правилу взаимного влияния связей: чем более ионный характер имеет связь М-X в системе М-X-L, тем более ковалентна связь X- L(O-Si). Параллельно увеличивается средняя длина связи Si-О от 1,61 до 1,64 Å (рис. 11).
Обычно отмечается увеличение доли мостиковых атомов кислорода, приходящихся на один SiO4–тетраэдр, от 0 до 4 в рассматриваемом ряду силикатов. К этому следует добавить и зависимость среднего КЧ кислорода от отношения M/Si: оно уменьшается от 4 (или более) до 2 при уменьшении M/Si до нуля, сопровождаясь уменьшением среднего расстояния Si-О (см. рис. 11).
Возможность анализа с точки зрения морфотропии не является, конечно, спецификой только кристаллохимии силикатов. Подобный подход можно легко применить и для выявления кристаллохимических закономерностей в классах боратов, фосфатов, сульфатов и т. д.
32

Рис. 11. Связь среднего расстояния Si-О со средней электроотрицательностью χ катионов в амфиболах (а): 1 – тремолит, 2 – марганцевый куммингтонит, 3 – глаукофан, 4 – грюнерит; зависимость расстояния Si-О от среднего КЧ кислорода (б).
33
Глава VI. СТРУКТУРНАЯ ГОМОЛОГИЯ
6-1. ПРЕДВАРИТЕЛЬНЫЕ ЗАМЕЧАНИЯ
Морфотропия, как ясно из сказанного выше, описывает резкое изменение кристаллической структуры при закономерном (но дискретном) изменении химического состава. С другой стороны, кристаллохимия знает много примеров родства кристаллических структур соединений даже тогда, когда их химическая конституция не имеет близкого сходства. Крайним случаем такого родства является тождество – изоструктурность соединений разных классов (NaCl, MgO, PbS, SnSb, TiN со структурой типа NaCl и т. п.). Модельные структуры Гольдшмидта возникли как следствие такого тождества строения (ТiO2 и MgF2, Zn2SiO4 и Li2BeF4, CaMgSi2O6 и NaLiBe2F6,
Са3А12[SiO4]3 и Na3Al2[LiF4]3 и т. п.). Еще большее число наблюдений может быть охвачено понятием структурной гомологии – родственности кристаллического строения некоторого гомологического ряда соединении, отдельные члены которого связаны друг с другом промежуточными формами. Роль этого понятия в кристаллохимии нельзя недооценивать.
Гомология, как известно, занимает важное место в биологии, химии, математике и других науках. В кристаллографию это понятие ввел итальянский ученый К. М. Виола (1904) и развил Е. С. Федоров в 1907 г. при рассмотрении генеалогии различных кристаллических структур (их решеток) в результате деформации исходных тетрагональной или гексагональной структур. Это учение Федорова было развито и систематически изложено в 1961 г. В. И. Михеевым (точечные группы гомологии) и В. В. Нардовым и др. (пространственные группы гомологии).
В кристаллохимии к представлениям о гомологии обращались неоднократно (Е. С. Макаров, 1947; А. Магнели, 1953; В. Пирсон, 1957; П. И. Крипякевич, 1963; Н. Л. Смирнова, 1961; И. Лима–де–Фариа, 1969; и многе другие).
6-2. СТРУКТУРЫ ВЫЧИТАНИЯ И ВНЕДРЕНИЯ
Существует неочевидная на первый взгляд родственность структур в ряду CdI2– NiAs-Ni2In. Действительно, характер расположения и число атомов в элементарной ячейке, стоящих на втором месте в формулах этих соединений, одинаковы: они образуют гексагональную плотнейшую упаковку. В структуре CdI2 (рис. 13, часть 1) атомы Cd
34

занимают половину октаэдрических пустот через слой, в структуре NiAs (рис. 12, часть 1) заняты все октаэдрические пустоты, а в структуре Ni2In вторая половина атомов никеля Ni2 занимает центры тригональных призм из атомов Nil, находящихся в октаэдрических пустотах плотнейшей упаковки атомов In.
Эти особенности структурных соотношений приводят к тому, что оказывается возможным непрерывный переход от структуры типа CdI2 к структуре типа Ni2In через структуру типа NiAs в системах Ni-Те, Ni-Sb, Ni-Sn и Ni-In при переменном соотношении количеств компонентов. Если рассматривать структуру NiAs как основную (исходную), то структуру типа Ni2In можно считать «заполненной», или фазой внедрения, по отношению к ней, а структуру типа CdI2 «дефектной» структурой, или фазой вычитания.
Дефектные и заполненные структуры часто образуют гомологические серии на основе некоторой исходной структуры. Так, пирротины с общей формулой Fe1-xS являются дефектными производными структуры NiAs (троилит FeS). Фазы Fe9S10, Fe10S11 и другие гексагональные, а фаза состава Fe7S8 (клинопирротин) является моноклинным искажением этой структуры. Ураниниты UО2+х (x<0,38), образующиеся за счет частичного окисления UIV→UVI, обладают структурой, которую можно описать условно как
промежуточную между флюоритовой (рис. 6,
|
часть 1) и структурой типа СО2 (рис. 14, часть |
|||
|
1) за счет образования уранильных |
групп |
||
|
UO22+. При составах UO2-U4O9 структура фаз |
|||
|
кубическая, в области составов U4O9-U3O8 – |
|||
|
тетрагональная, |
гексагональная |
или |
|
|
ромбическая. Ряд заполненных структур |
|||
|
приводит от структуры типа ReO3 к структуре |
|||
|
типа перовскита в случае натрий (калий, |
|||
|
цезий)-вольфрамовых бронз. Структура WO3 |
|||
|
(тип ReO3) (рис. 12) геометрически подобна |
|||
|
Рис. 12. Структурный тип ReO3 |
структуре СаТiO3 |
(связанные вершинами |
|
|
октаэдры), но позиции крупного катиона в ней |
вакантны. В них и внедряются атомы Na, и при составе NaWO3 структура становится перовскитоподобной (WVI→WV, т.е. вольфрам переходит в пятивалентную форму).
35
6-3. ПСЕВДОСИММЕТРИЯ. ПРОИЗВОДНЫЕ И ВЫРОЖДЕННЫЕ СТРУКТУРЫ
Искаженные структуры часто можно поставить в гомологическое соответствие с некоторой исходной структурой, которую часто называют прототипом (архетипом). Так, структуры CrS (монокл.), МnР (ромб.), NiP (ромб.) являются результатом той или иной деформации прототипической структуры типа NiAs (гекс.). Структура SnS является ромбически, a SnSe – ромбоэдрически искаженными формами структуры типа NaCl и т. д.
Многочисленные соотношения такого рода часто объединяются понятием
псевдосимметрии.
В общем случае одна исходная система эквивалентных точек в пространственной группе, описывающей структуру прототипа, делится в структурном гомологе на две или большее число точек или, наоборот, две или несколько правильных систем точек, описывающих структуру некоторого гомолога, можно соединить в одну в исходной струкутуре прототипа. В первом случае, который можно объединить термином «производные структуры», симметрия обычно понижается, а размеры ячейки увеличиваются, во втором случае, которому соответствует понятие «вырожденных структур», симметрия становится более высокой. Если состав фазы с производной структурой тот же, что и у исходной, то такой переход от прототипа к производной структуре принято называть образованием сверхструктуры. Он сводится к упорядочению атомов в структуре твердого раствора (см. гл. VII). Если же в подобном ряду родственных структур состав изменяется, то мы переходим к тем структурным гомологам, которые возникают как производные структуры при мысленно упорядоченном замещении атомов в исходной структуре. Такой ряд, например, образуют минералы с тетраэдрической координацией атомов: С (алмаз) – ZnS (сфалерит) – CuFeS2 (халькопирит) – Cu2FeSnS4 (станнин). Симметрия в этом ряду понижается от кубической до тетрагональной. Подобный ряд дают и гексагональные сульфидные аналоги: С (лонсдейлит) – ZnS (вюртцит) – CuFe2S3 (кубанит) – Cu3Fe2SnS6 (гексастаннин). В этом ряду симметрия понижается от гексагональной у алмаза (лонсдейлита) и вюртцита до ромбической у кубанита и гексастаннина. В обоих примерах одна исходная правильная система точек, занятая углеродом в алмазе и лонсдейлите, расщепляется сначала на две (в сфалерите и вюртците), затем на три (в халькопирите и кубаните), и, наконец, на четыре различные позиции в станине и гексастаннине.
36
6.4. СТРУКТУРНАЯ ГОМОЛОГИЯ СИЛИКАТОВ
Много примеров гомологических соотношений дает структурная минералогия силикатов.
Один из наиболее ранних и очень ярких примеров был найден при структурном изучении в 1928-29 г.г. минералов группы хондродита–гумита, которые еще в конце XIX и начале XX века рассматривались как образующие морфотропный ряд. В таблице 7
приведены составы и периоды ячеек пяти основных минералов этой гомологической серии. Из нее видно, что их составы могут быть получены из переменных количеств брусита Mg(F,OH)2 и форстерита Mg2SiO4, а параметры a и b ромбических или моноклинных ячеек практически одинаковы, тогда как параметры c кратны величине около 1,5 Å, которая лишь несколько превышает ионные радиусы кислорода, фтора и гидроксила (см. приложение 1-9, часть 1) и может служить для оценки числа слоев кислородной упаковки между противоположными гранями (001) элементарной ячейки.
Таблица 7. Гомологические серии гумита и лейкофёницита.
|
Минерал |
Формула |
Пр. гр. |
a, Å |
b, Å |
c, Å |
α, град. |
|
Норбергит |
Mg3SiO4(F,OH)2 |
Pbnm |
4,71 |
10,27 |
8,73 |
– |
|
Хондродит |
Mg5[SiO4]2(F,OH)2 |
P21/b |
4,75 |
10,27 |
7,80 |
109,2 |
|
Гумит |
Mg7[SiO4]3(F,OH)2 |
Pbnm |
4,74 |
10,24 |
20,72 |
– |
|
Клиногумит |
Mg9[SiO4]4(F,OH)2 |
P21/b |
4,74 |
10,23 |
13,58 |
|
|
Форстерит |
Mg2SiO4 |
Pbnm |
4,76 |
10,20 |
5,98 |
100,9 |
|
Лейкофёницит |
Mn7[SiO4]3(OH)2 |
P21/b |
4,83 |
10,84 |
11,32 |
103,7 |
|
Джерригиббсит |
Mn9[SiO4]4(OH)2 |
Pbn21 |
4,85 |
10,70 |
28,17 |
– |
|
Риббеит |
Mn5[SiO4]2(OH)2 |
Pbnm |
4,80 |
10,73 |
15,67 |
– |
|
Аллеганит |
Mn5[SiO4]2(OH)2 |
P21/b |
4,85 |
10,72 |
8,28 |
108,6 |
|
Мангангумит |
Mn7[SiO4]3(OH)2 |
Pbnm |
4,82 |
10,58 |
21,45 |
– |
|
Соналит |
Mn9[SiO4]3(OH, F)2 |
P21/b |
4,85 |
10,54 |
14,02 |
100,3 |
Таким образом, по Брэггу и Кларингбуллу (1965), число слоев плотнейшей гексагональной упаковки составляет 4 для оливина, 6 для норбергита, 5 для хондродита, 14 для гумита и 9 для клиногумита.
При использовании полиэдрического изображения кристаллических структур этой гомологической серии (рис. 13) они могут быть представлены в виде слоев из зигзагообразных цепочек соединенных ребрами октаэдров (связанных между собой одиночными тетраэдрами SiO4). В элементарной ячейке оливина (форстерита) вдоль оси c помещается один целый октаэдр и две его половины, в структуре брусита – только две половинки, в структуре норбергита – два целых октаэдра и две половинки. Следовательно,
структура этой гомологической серии может быть понята и как упорядоченное взаимное прорастание слоев толщиной из трех и двух октаэдров. Тогда структуру оливина можно
37

изобразить как октаэдрическую последовательность 22, клиногумит как 3222, гумит как 322(322), хондродит как 32 и норбергит как 33.
a) б)
Рис. 13 а) полиэдрическая модель кристаллической структуры форстерита; б) полиэдрическая модель кристаллической структуры клиногумита.
Существуют и Mn-аналоги этих минералов, и они образуют так называемую лейкофёницитовую гомологическую серию (табл. 7). Однако, в отличие от гумитовой серии, в ней присутствуют октаэдрические слои толщиной в один октаэдр. Родоночальниками и конечными членами этой серии можно считать тефроит Mn2SiO4 cо структурой оливина (последовательность 22) и граутит MnOOH (11). Тогда джерригиббсит Mn9[SiO4]4(OH)2 имеет октаэдрическую последовательность 22221,
лейкофёницит Mn7[SiO4]3(OH)2 – 2221, риббеит Mn5[SiO4]2(OH)2 – 221. Вместе с тем имеются и такие члены этой серии, которые содержат слои толщиной в три октаэдра:
аллеганит Mn5[SiO4]2(OH)2 – 32, мангангумит Mn7[SiO4]3(OH)2 –322 (в отличие от близкого по составу лейкофёницита он является, как и гумит, ромбическим), соналит Mn9[SiO4]3(OH, F)2 (Mn-аналог моноклинного клиногумита) – 3222.
У. Брэгг (1965) обратил также внимание на близкое соответствие между структурой слюды и структурами пироксенов и амфиболов. Он рассматривал слюды как следующий
этап превращения пироксена в амфибол в результате соединения пироксеновых кремнекислородных цепочек сначала в ленты (амфибол), а затем в слои (слюды).
Подобная аналогия между этими структурами отражается в размерах элементарных ячеек типичных представителей каждой группы:
|
диопсид |
тремолит |
мусковит |
|||
|
а(Å) |
9,71 |
а |
9,78 |
с |
10,06 |
|
в(Å) |
8,89 |
b/2 |
8,90 |
b |
9,02 |
38
с(Å) 5,24 с 5,26 a 5,19
Именно это структурное родство и объясняет существование гибридных построек – биопириболов (от «биотит + пироксен + амфибол»), обнаруженных около 30 лет назад методами электронной микроскопии высокого разрешения (Веблен и др., 1977).
Общая химическая формула для чисто магниевых по составу и ромбических по структуре биопириболов может быть представлена в виде Mg3n+1Si4nO10n+2(OH)2n-2, где n = Si/(4Mg-3Si). При n=1 эта формула превращается в формулу ортопироксена Mg4Si4O12 = 4 MgSiO3, при n=2 получается состав ортоамфибола Mg7Si8O22(OH)2, при n=3 – “биопирибол” – джимтомсонит, при n=∞ – тальк Mg3Si4O10(OH)2. Если для некоторого минерала из этого гомологического ряда n имеет нецелочисленное значение, следовательно, такой член ряда, скорее всего, представляет собой тесное срастание модулей двух или более членов ряда. Например, состав честерита Mg17Si20O54(OH)6 отвечает значению n ≈ 2,5, т.е. структура этого биопирибола представляет собой срастание модулей амфибола и джимтомсонита. Это отражается и в величине параметров элементарной ячейки; если параметр b амфибола удваивается по сравнению с параметром b пироксена, а джимтомсонита – утраивается, то для честерита параметр b в пять раз больше величины этого параметра для пироксена.
Общую гомологическую серию сейдозерита (или бафертисита) дают титано– силикатные слюды и их синтетические аналоги. Это около 30 кристаллических соединений разного состава, в которых основными строительными единицами, или модулями, служат сейдозерит Na(Mn,Ti)2(Ti,Zr)[Si2O7](O,F) и накафит Na2Ca[PO4]F (рис. 14), которые переслаиваются друг с другом в различных соотношениях, так что толщина
смешанного блока увеличивается в три раза по мере роста количества накафитового компонента в промежутке между сейдозеритовыми модулями.
С помощью структурной гомологии удобно описывать явления полимеризации или конденсации кремнекислородных радикалов, например, в ряду радикалов [Si8O22] (власовит) – [Si8O20] (эканит) – [Si8O19] (делхаалит) – [Si8O18] (карлстонит) – [(Si, Al)8O16] (жисмондин), построенных из различным образом сочлененных между собой четверных колец SiO4–тетраэдров (Пущаровский, 1986).
39

Рис. 14. Блоки сейдозерита (a), ломоносовита (б), квадруфита (в), полифита (г) и накафита (д).
6-5. ДРУГИЕ ПРИМЕРЫ СТРУКТУРНОЙ ГОМОЛОГИИ
40

Рис. 15. Кристаллические структуры козалита (а),
буланжерита (б) и джемсонита (с).
ХАЛЬКОГЕНИДОВ
Гомологические соотношения легко прослеживаются и в группе дисульфидов: FeS2 (пирит) – CoAsS (кобальтин) – NiSbS (ульманит).
Другая модификация дисульфида железа (марказит) также дает ряд производных структур: FeS2 (марказит) – FeAs2 (леллингит) – FeAsS (арсенопирит). Структуры марказита и леллингита ромбические, но с разным осевым отношением с/b: 0,61 и 0,48 соответственно. Структура арсенопирита – моноклинно искаженная форма этого структурного типа.
Другие варианты искажения структуры марказита можно обнаружить в структурах IrSe2
и CoSb2.
Большое разнообразие гомологических соотношений дают такие сложные по составу минералы и их неорганические аналоги, как сульфосоли, т.е. соединения, в которых присутствуют одновременно два халькогена: из
6-ой (S, Se, Te) и 5-ой групп (As, Sb, Bi)
Периодической системы. Рассмотрим только один пример таких серий, а именно серию буланжерита Pb5Sb4S11 – козалита Pb2Bi2S5 (таблица 8). В этих структурах присутствуют бесконечные стержни из структур прототипов PbS (вдоль направления [011]) или SnS (вдоль направления [001]), рис. 15.
Такие стержни образуют в структуре своеобразные зигзагообразные слои с расширениями и сужениями. Соседние слои связываются друг с другом через часть вершин полиэдров, так что образуются тупые углы и «пропуски» некоторых из связей на границах слоев.
Таблица 8. Гомологическая серия буланжерита–козалита.
|
Минерал |
Формула |
Пр. |
Параметры элементарной |
Углы, |
|
группа |
ячейки, Å |
градусы |
41

|
Джемсонит |
FePb4Sb6S14 |
P21/a |
a = 15,57 |
b =18,98 |
c =4,03 |
91,8 |
|
Синт. фаза |
Pb4Sb4S11 |
Pbam |
b =15,56 |
a = 15,01 |
c =4,03 |
– |
|
Буланжерит |
Pb5Sb4S11 |
P21/a |
b =23,54 |
a = 21,61 |
c =8,08 |
100,7 |
|
Синт. фаза |
Sn3Sb2S6 |
Pnma |
c =34,91 |
a = 23,15 |
b =3,96 |
|
|
Робинсонит |
Pb4Sb6S13 |
Pnam |
b =17,69 |
a = 16,56 |
c =3,98 |
|
|
Синт. фаза |
Sn4Sb6S13 |
I2/m |
a = 24,31 |
b =23,49 |
c =3,92 |
94,0 |
|
Дадсонит |
Pb10+xSb14-xS31-xCl |
? |
c =17,33 |
a = 19,04 |
b =8,23 |
96,3 |
|
Синт. фаза |
Pb5Sb6S14 |
? |
a = 28,37 |
b =22,04 |
c =4,02 |
92,3 |
|
Козалит |
Pb2Bi2S5 |
Pbnm |
b =23,89 |
a = 19,10 |
c =4,06 |
6.6. ГОМОЛОГИЧЕСКИЕ СЕРИИ НЕКОТОРЫХ ОКСИДОВ И ФТОРИДОВ
Особенно благоприятной дли построения на ее основе различных производных (вторичных) мотивов является структура типа флюорита как во фторидном (CaF2), так и оксидном (ZrO2, CeO2) рядах. Близкородственными структуре флюорита являются тригональный тисонит LaF3 и ромбический β-YF3. В этих структурах в роли ведущих,
выстраивающих плотную упаковку, выступают не анионы, как обычно, а катионы. Катионные каркасы построены из треугольных сеток по плоскостям (111) во флюорите, по плоскостям (002) в тисоните и (020) в β-YF3. Во флюорите они образуют кубическую (трехслойную) плотнейшую упаковку, а в LaF3 и YF3 – гексагональную (двухслойную) укладку. Последние две структуры можно считать «заполненными» по отношению к флюориту, поскольку число анионов в «пустотах» в 1,5 раза больше.
Интересный анализ гомологических связей в группе флюоритоподобных структур, иногда даже на первый взгляд неожиданных, дал Н. В. Белов. Он включил в рассмотрение флюорит, пирохлоры с общей формулой А2В2Х7, сенармонтит Sb2O3 и арсенолит Аs2О3, биксбиит (Mn, Fe)2O3 и целый ряд редкоземельных оксидов (Sc2O3, Y2O3, Sm2O3, Eu2O3), а также Тl2О3.
Рис. 16. Многогранники, возникающие из куба за счет усечения вершин (удаления анионов): а – куб, б – семивершинник, в – тригональная призма, г – уплощенный октаэдр, д – шестивершинник с одной квадратной
гранью
42
Общую формулу представителей этого семейства он предложил записать в виде А4Х8-x. Для флюорита x=0, для пирохлоров х=1, для остальных оксидов х=2. Таким образом, все члены этого ряда являются дефектными структурами (вычитания) по отношению к флюориту, причем из кубической упаковки (структура CaF2) выпадает часть анионов: одна восьмая (x=1) или одна четвертая (х=2).
Исходным КП является куб, за счет «усечения» вершин которого можно получить различные другие КП (рис. 16). Такое «усечение» вершин и происходит фактически при вычитании анионов из флюоритоподобной структуры. Если последняя строится из кубов, расположенных по принципу трехмерной шахматной доски (рис. 17, а), то в структуре
пирохлоров в половине кубов срезаны две вершины и из них получились уплощенные октаэдры (рис. 16, г). В сохранившихся кубах располагаются атомы Са, Na, TR, а в уплощенных октаэдрах – Nb, Та, Ti (рис. 17, б).
Вструктуре сенармонтита Sb2O3 – арсенолита As2O3 все кубы структуры флюорита срезаны до уплощенных октаэдров, которые ориентированы четырьмя различными способами (рис. 17, в). Внутри каждых четырех уплощенных октаэдров образуется крупный правильный пустой октаэдр (рис. 17, г). Атомы Sb(As) несколько сдвинуты из центров уплощенных октаэдров к тому из оснований, которое является гранью крупного пустого октаэдра. Поэтому более частое изображение структуры сенармонтита – арсенолита: укладка из октаэдрических «молекул» [Sb4O6] или [As4O6] октаэдров из шести атомов О и «прилипших» к каждому из них по четырем граням атомов Sb или As.
Вструктуре биксбиита (Mn, Fe)2O3 только четверть кубов исходного флюорита срезана по двум вершинам до уплощенного октаэдра. У прочих кубов исходного мотива CaF2 усекаются по две вершины, связанные не телесной диагональю куба, а диагональю одной из его граней (рис. 18). При этом возникает шестивершинник с одной квадратной гранью. Эти КП располагаются через слой: в одном слое все кубы усечены по диагонали грани, а в следующем – половина по телесной диагонали и половина по диагонали грани. Интересно, что и в этой структуре каждая четверка усеченных кубов окружает крупный правильный пустой октаэдр. Постоянное присутствие такой структурной детали в
производных флюорита приводит к характерной спайности по октаэдру для всего рассматриваемого семейства.
43

Рис. 17. Удвоенная элементарная ячейка флюорита, представленная 32 кубами (а); структура пирохлора (б); структура сенармонтита – арсенолита (в); пустой октаэдр внутри октанта этой структуры (г).
44
На первый взгляд нити родства, протянутые между различными структурами, происходящими от флюоритового мотива, могут показаться искусственными,
результатом разгадки чисто геометрической головоломки. Однако это не так, в чем легко убедиться. Родство структур CaF2 и LaF3, YF3 сказывается в образовании между ними твердых растворов Ca1-xTRxF2+x. Этот случай был назван В. М. Гольдшмидтом
изоморфизмом с заполнением пространства (ср. – заполненные структуры) из–за
появления в пустых кубах структуры флюорита добавочных ионов F–. Подобном
образом становятся объяснимыми и обычные твердые растворы ZrO2(CeO2, UO2) – TR2O3,
которые, однако, приводят к образованию дефектных структур (вакансии в кислородных позициях). Многие другие наблюдения, с которыми мы столкнемся позже в гл. VIII, получают логичное
истолкование на основе структурной гомологии.
Рис. 18. Слои элементарной ячейки биксбиита: а – слой, в котором все кубы усечены по диагонали грани; б – слой, в котором половина кубов усечена по пространственной диагонали, а другая половина – по диагонали куба; в – половина (два слоя) элементарной ячейки объединяются в металлические тройки.
45
Среди новых синтетических оксидов меди, обладающих сверхпроводящими свойствами при температурах, близких к комнатным (такие вещества называются ВТСП –
высокотемпературные сверхпроводники), существует целый ряд гомологических серий. К ним относятся, например Tl-
купраты с общей формулой
Рис. 19. Фрагменты кристаллических структур Талиевых купратов: a) n=1; b) n=2; c) n=3; d) n=4; e) n=5.
TlmBa2Can-1CunO2n+m+2 (m=1, n=1-5; m=2, n=1-4). В этих структурах (рис. 19) два главных модуля
представляют собой слои состава СuO2 с преимущественно
квадратной координацией атомов меди и вырезки из искаженной структуры перовскита, в которой
преобладают координационные полиэдры в форме полуоктаэдров
(квадратных пирамид).
Различные представители таких гомологических серий отличаются друг от друга числом плоских сеток СuO2 и крупных катионов Ca, Ba и Tl в промежутках между двумя основными модулями. В результате такого характера взаимной укладки модулей размеры всех тетрагональных членов этой серии в плоскости (001) приблизительно одинаковы и соответствуют удвоенной длине связи Cu-O. При переходе от n-ного члена серии к следующему (n+1)-му члену параметр c увеличивается на 3,1 Å. Таким образом, знание чисел n и m позволяет предсказывать основные черты строения соответствующего члена этой гомологической серии.
46
Глава VII. ПОЛИМОРФИЗМ И ПОЛИТИПИЯ.
7-1. ОПРЕДЕЛЕНИЯ И ИСТОРИЧЕСКИЙ ОБЗОР.
Полиморфизмом называется существование различных кристаллических структур одного и того же вещества при разных термодинамических условиях. Под полиморфным переходом понимают структурное превращение, происходящее при изменении интенсивных параметров состояния (температуры, давления, электрических или других силовых полей). Различные кристаллические фазы одного вещества называются полиморфными модификациями. Равновесно могут сосуществовать согласно правилу фаз не более трех полиморфных модификаций. Обычно же одна из фаз является термодинамически стабильной при данных условиях, остальные – метастабильные.
Полиморфная модификация имеет поле стабильности на фазовой диаграмме в Р–Т координатах, и ее линии равновесия с другими модификациями или с расплавом и паром могут быть определены экспериментально или рассчитаны теоретически, если известны термодинамические свойства фаз, находящихся в равновесии.
Эти предварительные замечания необходимы для ограничения круга явлений, относящихся к собственно полиморфизму, и выделения в самостоятельные объекты исследования политипов, магнитоупорядоченных фаз и нестабильных (промежуточных) кристаллических модификаций.
Хотя отдельные примеры полиморфных разновидностей были известны минералогам еще в конце XVIII в., представления о полиморфизме проникали в науку с большим трудом. Так, из обнаружения фактов существования в природе двух кристаллических разновидностей карбоната кальция – кальцита и арагонита (Клапрот, 1798), двух разновидностей дисульфида железа – пирита и марказита, двух разновидностей двуокиси титана – рутила и анатаза не было сделано никаких выводов общего характера. Это объясняется глубоким влиянием закона Р. Ж. Гаюи, согласно которому каждому веществу должна быть свойственна определенная кристаллографическая форма. Так, Гаюи ссылался на наличие стронция в арагоните, чтобы доказать «принудительный» характер изменения формы карбоната кальция под влиянием примеси. Подобные аргументы в 1811 г. выдвинул Гаюи в споре с К–Л. Бертолле, который в своих работах приводил отдельные известные в начале XIX в. случаи различия форм одного вещества.
Честь открытия полиморфизма принадлежит Э. Митчерлиху, который
экспериментальным путем обнаружил диморфизм кристаллов фосфорнокислого натрия (1821), а затем фосфора и серы (1823). Однако Митчерлих считал полиморфизм довольно
47
случайным и редким явлением, располагая еще очень незначительным материалом. К 1844 г. было известно лишь 15 примеров полиморфизма, а через четыре года Л. Пастер сообщает о тридцати подобных случаях. Признание широкого распространения полиморфизма принадлежит М. Франкенгейму, который в 30-х годах XIX в. дал закону Гаюи современную формулировку: каждому химическому соединению соответствует одна кристаллическая форма при данных температуре и давлении.
Всамом начале своей деятельности в Московском университете в 1890 г В. И. Вернадский насчитывал три–четыре сотни полиморфных модификаций разных веществ, но смело утверждал, что это число должно быть сильно увеличено, если принять во
внимание факты образования изоморфных смесей между веществами с различной кристаллической формой. Он высказывал мнение, что всякий раз, когда исследователь
поставит перед собой задачу найти полиморфную разновидность некоторого кристаллического вещества, он найдет ее или верные признаки ее существования. Справедливость этих слов великого ученого мы особенно осознаем сейчас, когда
благодаря возможности вести эксперименты в широких пределах температур и давлений исследователи непрерывно пополняют список полиморфных превращений.
Впрошлом веке рентгеноструктурный анализ отчетливо выявил, что полиморфное превращение связано с перестройкой атомного строения кристалла, а изменение
кристаллической формы есть следствие перестройки пространственной конфигурации атомов. Достижения первых десятилетий этого нового этапа развития учения о полиморфизме суммировал В. М. Гольдшмидт, который особенно подчеркнул связи между полиморфизмом, морфотропией и изоморфизмом.
При полиморфных переходах легко возникают метастабильные состояния. Впервые подобные наблюдения сделал еще в начале прошлого века Ж. Л. Гей–Люссак, а в конце его В. Оствальд обобщил их и сформулировал следующее правило, которое получило название правила «ступенчатых переходов» Оствальда: при любом процессе сначала возникает не наиболее устойчивое состояние с наименьшей свободной энергией, а
наименее устойчивое и наиболее близкое по величине свободной энергии к исходному состоянию. Например, при кристаллизации из низкотемпературного водного раствора вначале появляется неустойчивая модификация карбоната кальция – арагонит, которая лишь постепенно переходит в устойчивую форму–кальцит. Подобным образом из
гидротермальных растворов часто осаждается сульфид цинка в метастабильной форме вюртцита, которая способна длительное время сохраняться без превращения в устойчивую модификацию – сфалерит. Кристаллизацией из раствора йодида ртути всегда
впервый момент получают метастабильную желтую модификацию вместо стабильной
48
красной. Третью, еще более неустойчивую бесцветную модификацию HgI2 наблюдал Тамман в 1910 г. Она образуется при быстрой конденсации паров и менее чем через минуту превращается в красную модификацию.
7-2. СИСТЕМАТИКА ПОЛИМОРФНЫХ ПЕРЕХОДОВ
Огромный экспериментальный материал, накопленный сейчас при изучении полиморфизма, требует систематизации и классификации. Существует несколько схем классификации типов полиморфизма, из которых наиболее известна структурная классификация М. Бюргера (1951). Как в схеме Бюргера, так и в более поздних классификациях (Г. Б. Бокий, 1954; Р. Эванс, 1964; А. С. Поваренных, 1966; и др.) основой
для выделения различных видов полиморфизма служат степень и характер изменения структуры в процессе перехода: меняются или не меняются первое КЧ, структурный тип, структурный мотив и т. п. В них обычно находится место и для политипных модификаций, которые рассматриваются на равных правах с полиморфными. Хотя с чисто
структурной точки зрения политипизм можно рассматривать как одномерный полиморфизм, политипные модификации возникают, вероятно, в процессе роста и для них нельзя указать полей существования на фазовой диаграмме. Поэтому в физико–
химическом отношении полиморфизм и политипизм совершенно различны и должны рассматриваться отдельно (см. раздел 7-4 «Политипия»).
Учитывая эти замечания, можно представить сводную структурную классификацию типов и разновидностей полиморфизма, которая приведена в табл. 9.
Тип I (с изменением первого КЧ) присутствует во всех схемах и в согласии с рассмотрением Бюргера в нем выделяются два вида: реконструктивные и дисторсионные переходы. К реконструктивным относятся также превращения, в которых
для перехода от структуры одной модификации к другой необходимы разрыв связей и полная перестройка структуры. Таковы переходы графит → алмаз, кальцит → арагонит,
кварц → стишовит (тип рутила) и т. п.
Разрыв всех связей в первой координационной сфере требует большой затраты энергии (порядка энергии связи), и, следовательно, энергетический барьер такого процесса очень высок.
Таблица 9. Классификация полиморфизма.
49
|
Тип |
Подтип или вид |
Примеры |
|||
|
a) реконструктивный переход |
сер. Sn→ бел.. Sn |
||||
|
I. С изменением |
графит→алмаз |
||||
|
кварц→стишовит |
|||||
|
первого КЧ |
|||||
|
б) дисторсионный переход |
B1→B2 |
||||
|
α-Fe→γ-Fe |
|||||
|
a) |
изменение |
типа укладки |
сфалерит→ вюртцит |
||
|
II. C изменением |
координационных |
полиэдров |
рутил→ брукит→ анатаз |
||
|
(реконструктивный переход) |
кварц→кристобалит→тридимит |
||||
|
взаимного |
|||||
|
расположения КП |
б) поворот отдельных атомных |
α-→β-модификации кремнезема |
|||
|
групп друг относительно |
друга |
||||
|
(дисторсионный переход) |
|||||
|
а) |
замещение |
атомов |
с |
(Cu,Au) →Cu,Au |
|
|
образованием сверхструктуры |
колумбит FeNb2O6→иксиолит 3(Fe, Nb)O2 |
||||
|
III. Превращения типа |
микроклин→санидин |
||||
|
порядок–беспорядок |
б) вращение молекул или |
парафины, NH4NO3 |
|||
|
радикалов |
|||||
|
в) электронное или магнитное |
магнетит (переход Вервея), CoO |
||||
|
упорядочение |
|||||
|
IV. Переходы типа |
перовскиты |
||||
|
смятия или сдвига |
|||||
|
V. Изоструктурные |
Сe, EuO, SmS, Fe2O3, MnS2 |
||||
|
переходы |
|||||
Поскольку энергия связей, которые нужно разорвать, обычно гораздо больше, чем разность энергий обеих полиморфных модификаций, то для таких превращений необходима большая энергия активации и они обычно протекают медленно. Поэтому метастабильный арагонит не является минералогической редкостью, а алмаз, как известно, не испытывает никаких самопроизвольных изменений в условиях земной поверхности. Известно, однако, что желтую ромбическую форму йодида ртути HgI2
можно легко перевести в стабильную красную тетрагональную модификацию даже простым механическим воздействием (царапанием). Тем не менее структурная перестройка и в этом случае достаточно глубокая: в красной модификации HgI2 атомы Hg
занимают послойно четверть тетраэдрических пустот искаженной плотнейшей кубической (трехслойной) упаковки атомов I, а в желтой (тип CdI2) – половину (через слой) октаэдрических пустот четырехслойной упаковки атомов I.
Изменение координационного числа при полиморфном превращении может осуществляться и за счет простого растяжения или сжатия всей структуры в некотором
50

направлении. Это деформационные, или дисторсионные, переходы. Так, превращение при 460° С CsCl из структуры В2 с КЧ=8:8 в структуру типа NaCl (В1) с КЧ=6:6 можно представить как растяжение В2 вдоль тройной оси и сжатие в перпендикулярном направлении (рис. 20).
Рис. 20. Превращение структуры типа CsCl в структуру типа NаCl путем растяжения вдоль оси L3
В результате такого растяжения атомы В7 и B8 удаляются от центрального атома А и его координация постепенно приближается к шестерной. Если такую деформацию производить до тех пор, пока не получится ромбоэдрическая ячейка с острым углом между ребрами, равными 60°, нетрудно перейти к кубической решетке В1, как показано на рис. 20, б. Это не просто мысленный геометрический способ перехода от структуры В2 к В1, а реальный физический процесс, как показано в последние годы путем прямого рентгенографического изучения подобных превращений.
Механизм превращения объемно–центрированной кубической модификации α-Fe с
КЧ=8 в гранецентрированную кубическую γ-Fe (при 920° С) во многом подобен только что рассмотренному. На рис. 21 показано, что в кластере из четырех ячеек α-Fe можно выбрать тетрагональную гранецентрированную ячейку, основание которой в 
 2 раз больше высоты. Ее растяжение и сжатие в соответствующих направлениях, показанных стрелками, приводят к кубической гранецентрированной ячейке γ-Fe.
2 раз больше высоты. Ее растяжение и сжатие в соответствующих направлениях, показанных стрелками, приводят к кубической гранецентрированной ячейке γ-Fe.
51

Рис. 21. Механизм превращения объемно–
центрированной кубической структуры в гранецентрированную.
Другой механизм был рассмотрен Г. В. Курдюмовым в 1930 г. Согласно ему диагональ грани [101] структуры γ-Fe наследуется от телесной диагонали [111] α-Fe.
Таким образом, три атома Fe, находящиеся на этой диагонали, сохраняют свои позиции. Остальные атомы должны сместиться на небольшие расстояния, чтобы занять позиции гранецентрированной структуры. Деформационные переходы не требуют преодоления высокого энергетического барьера, и поэтому они протекают относительно быстро.
При изменении только способа взаимной упаковки КП (II тип полиморфизма) ближайшие группировки атомов в структуре сохраняются. Однако и в этом типе возможно разделить превращения на реконструктивные и дисторсионные. В первом
случае могут оказаться необходимыми разрыв связей в первой координационной сфере и перестройка структуры. Такие переходы совершаются медленно, и полиморфные
модификации не связаны непрерывно одна с другой и могут не иметь ничего общего в отношении симметрии. Примеры таких превращений: 1) любая пара модификаций SiO2 в ряду кварц – тридимит – кристобалит; 2) вюртцит – сфалерит ZnS; 3) пирит – марказит FeS2; 4) сенармонтит – валентинит Sb2O3; 5) арсенолит – клодетит As2O3.
Структуры всех форм кремнезема, кроме стишовита, представляют собой трехмерные каркасы из тетраэдров SiO4, соединенных вершинами. Структуры высокотемпературных модификаций трех основных форм – кристобалита, тридимита и кварца – изображены на рис. 22. В кристобалите и тридимите мостиковые связи Si-О-Si линейны, а в модификациях кварца они образуют тупой угол (~140°).
52

Рис. 22. Укладка SiO4 –тетраэдров в высокотемпературных β-модификациях кремнезема: кристобалита (a),
тридимите (б) и кварце (в).
Структуры кристобалита и тридимита можно рассматривать как построенные из слоев тетраэдров. В первом из них каждый слой повернут по отношению к нижележащему на 120°, так что одинаковая ориентировка повторяется через три слоя и элементарная ячейка имеет кубическую симметрию (см. рис. 22, а). В тридимите каждый следующий слой представляет собой зеркальное отражение предыдущего (см. рис. 22, б). Структура
тридимита имеет гексагональную симметрию и тройные оси тетраэдров параллельны оси с. (Структуры высокотемпературных β-тридимита и β-кристобалита отличаются друг от друга примерно как вюртцит от сфалерита). Однако в гексагональной структуре β-кварца вдоль оси с направлены двойные оси тетраэдров (см. рис. 22, в).
Таким образом, три основные формы кремнезема существенно отличаются по способу укладки тетраэдрических «кирпичиков», и переход из одной модификации в другую должен сопровождаться разрывом связей Si-О-Si. Поэтому такие превращения относятся к реконструктивным, протекают медленно, с чем связано сохранение нестабильных форм кремнезема в течение геологического времени.
Иное положение с α→β превращениями кварца, тридимита и кристобалита. Они протекают без разрушения каких–либо связей, только в результате небольшого разворота отдельных тетраэдров друг относительно друга. Такие превращения называются переходами со смещением или искажением (дисторсионные или деформационные).
53

сплава CuAu.
Рис. 24. Послойное упорядочение
Рис. 23. Превращение верхней структуры (а) в любую нижнюю требует разрыва связей первой сферы, тогда как взаимные превращения структур б, в и г сопровождаются только искажениями.
Рис. 23 иллюстрирует, по М. Бюргеру, соотношение между реконструктивными и деформационными превращениями без изменения первого КЧ. Ясно, что
деформационные превращения происходят гораздо легче и быстрее, чем реконструктивные. Так, например, β-кварц не сохраняется при температуре ниже 573° С и быстро переходит в α-кварц. В свою очередь, монокристалл α-
кварца при нагревании выше 573° С без разрушения приобретает структуру β-кварца.
Большое число полиморфных превращений обязано разнообразным процессам упорядочения (см. III тип в
табл. 9). Наиболее известны среди них полиморфные
атомов Cu и Au в структуре
переходы с образованием сверхструктуры благодаря упорядочению атомов, замещающих друг друга в кристаллической структуре. Классический пример – переход ниже критической точки
(температуры Кюри) 408° С сплава Сu, Аu (1:1) с кубической гранецентрированной структурой и случайным размещением Сu и Аu по узлам в сверхструктуру тетрагональной
54

симметрии с послойным чередованием атомов обоих сортов (рис. 24). Хорошо известный из минералогии пример – упорядочение Аl и Si в структуре К–полевого шпата с переходом от моноклинного санидина к триклинному микроклину.
В минералах группы колумбита (Fe, Mn) (Nb, Та)2Oб
со структурой так называемого трирутилового типа параметр с увеличен в 3 раза по сравнению с рутиловым из–за упорядоченного размещения катионов (рис. 25, а).
При повышенных температурах возникает неупорядоченная структура иксиолита (Та, Mb, Fe, Mn)O2 типа α-РbO2 (см. рис. 25, б). Таким образом,
упорядочение катионов в колумбите дает сверхструктуру по отношению к иксиолиту.
К превращениям типа порядок–беспорядок логично отнести и те, которые возникают в результате
вращательного или крутильного разупорядочения отдельных молекул или радикалов. Давно известны (Дж. Бернал) явления вращения молекул при повышении температуры в органических кристаллах (парафинах,
Рис. 25. Кристаллическая структура спиртах). Они сопровождаются структурным переходом
|
колумбита (а) и α-PbO2 |
с повышением симметрии. |
В неорганических кристаллах вращение отдельных групп и радикалов (NH4+, NO3–, СО32-, Н2O и др.) – довольно обычное явление. Хорошо изучен полиморфизм NH4NO3 благодаря вращению отдельных групп. При температуре от комнатной до 84°С это соединение кристаллизуется в ромбической структуре. В интервале 84-125° С оно приобретает тригональную симметрию в результате вращения NО3 вокруг тройной оси. При T=125° оно становится кубическим из–за беспорядочного вращения NH4+ и NO3– вокруг своих центров, что делает их форму псевдосферической.
К типу III (см. табл. 9) можно отнести также весьма своеобразный способ изменения структуры кристалла, который возникает в результате упорядоченного распределения валентных электронов в соединениях атомов со смешанной валентностью. Характерный пример – магнетит FeIII[FeIIFeIII]O4 с кубической структурой обращенной шпинели. При повышенных температурах в октаэдрических позициях, занятых равными количествами двух– и трехвалентного железа, невозможно разделить валентные состояния FeII и FeIII из– за быстрого электронного обмена между ними. Однако ниже 120 К октаэдрические позиции расщепляются на несколько сортов, по которым атомы FeII и FeIII распределяются
55
порознь друг от друга: возникает полиморфное превращение, называемое переходом Вервея, в сверхструктуру низкой (триклинной?) симметрии.
Когда магнитное упорядочение приводит к изменению структуры, оно может с полным правом рассматриваться как причина полиморфного перехода. Так, при понижении температуры в СоО происходит антиферромагнитное упорядочение; при этом кубическая структура (тип NaCl) превращается в тетрагональную.
Переходы IV типа, в которых не изменяются структурный тип и число атомов в ячейке, а в
результате незначительных подвижек атомов изменяется симметрия ячейки при малом изменении ее объема, можно назвать
полиморфными переходами типа сдвига или смятия. Известный пример – переходы в кристаллах со структурой типа перовскита. На
|
рис. 26 показаны формы элементарных ячеек |
Рис. 26. Смятие кубической ячейки |
|
|
перовскита (a) в направлениях, указанных |
||
|
четырех фаз титаната бария ВаТiO3, стабильных |
||
|
стрелками (б, в, г) |
||
|
при разных температурах. К таким превращениям |
приводит небольшое смещение атомов Ti в направлениях, показанных на рис. 26 стрелками. Так, при переходе от кубической к тетрагональной ячейке (120° С) атомы Ti смещаются всего на 0,06 Å вдоль оси 4-го порядка. Отношение с/а в тетрагональной ячейке равно 1,01, а изменение объема составляет только 0,1%. В результате таких атомных сдвигов возникает спонтанная электрическая поляризация, и поэтому многие
соединения с некубической структурой перовскитового типа являются сегнетоэлектриками.
Особый V тип полиморфных превращений вообще не связан с изменением структуры двух модификаций, но сопровождается скачкообразным изменением параметров ячейки, объема и других свойств кристалла в точке перехода. Примером таких превращений является изоструктурное превращение Се под действием давления около 7 кбар со значительным (16%) скачкообразным уменьшением объема. Выше и ниже точки превращения структура одна и та же – ГЦК. Это превращение обусловлено электронным переходом 4f → 5d ( E 0,04 эВ по спектроскопическим данным) в валентной оболочке Се и уменьшением радиуса последнего, который стимулируется внешним давлением. Этот же переход наблюдается в Се при низких Т (-180° С) и атмосферном давлении.
Отсюда можно сделать вывод о характере изменения температуры перехода с ростом давления: при возрастании Т растет и Р перехода, т. е. дР/дТ>0. Подобного рода
56
изоструктурные полиморфные переходы под давлением наблюдаются и для оксидов и халькогенидов редкоземельных металлов (EuO, SmS, SmSe). Изоструктурное превращение двух ГЦК–форм металлического цезия CsII → CsIII в районе 40 кбар,
сопровождающееся резким уменьшением параметра ячейки от 5,98 Å (CsII), до 5,80 Å (CsIII), связывается с электронным переходом 6s → 5d и уменьшением радиуса Cs.
Разными методами обнаружен скачок объема приблизительно на 10% при давлении около 500 кбар в гематите Fe2O3. Структура типа корунда при этом сохраняется. Такое
изоструктурное фазовое превращение можно объяснить с позиций теории кристаллического поля переходом Fe3+ из высокоспинового в низкоспиновое состояние (см. главу III, часть 1). Низкоспиновое состояние оказывается более стабильным, когда
|
расщепление |
d–уровней в кристаллическом поле |
становится под действием давления |
|
больше, чем |
энергия спаривания электронов π. |
В точке перехода = π . Уменьшение |
объема связано с тем, что ионный радиус Fe3+ (нс) много меньше, чем Fe3+ (вс): 0,55 и 0,78 Å соответственно (см. приложение 1-9, часть 1). Изоструктурный переход той же природы недавно обнаружен для гауерита MnS2.
7-3. ИЗМЕНЕНИЕ СИММЕТРИИ ПРИ ИЗМЕНЕНИИ ТЕМПЕРАТУРЫ И ДАВЛЕНИЯ. КООРДИНАЦИОННЫЕ ПРАВИЛА ПОЛИМОРФИЗМА
Правилом, из которого, правда, имеется довольно много исключений, можно считать повышение симметрии более высокотемпературных полиморфных модификаций. Некоторые примеры такого повышения симметрии приведены в табл. 8. Его причины весьма различны со структурной точки зрения, хотя почти всегда оно сопровождается возрастанием объема при нагревании кристалла, его термическим расширением. Наиболее эффективный способ увеличения объема состоит в уменьшении КЧ. Примеры полиморфных переходов с уменьшением КЧ многочисленны: α-CsCl (8:8) → β-CsCl (6:6),
α-GeO2 (6:3) → β-GeO2 (4:2), α-ВаСl2 (9:4,5) → β-BaCl2 (8:4), арагонит (9:4) → кальцит СаСО3 (6:3). В последнем примере в скобках даны КЧ кальция и кислорода, КЧ углерода не изменяется (3). Многие металлы при повышении температуры испытывают переход от ГЦК– и ГПУ–структур (12) к ОЦК–структуре (8).
Таблица 10. Примеры повышения симметрии с повышением Т
57
|
Вещество |
Симметрия модификации |
|||
|
α |
β |
γ |
||
|
Cu2S |
ромб. (халькозин) |
гекс. (выc. халькозин) |
куб. (выc. дигенит) |
|
|
Ag2S |
ромб. (акантит) |
куб. (аргентит) |
куб. |
|
|
FeS2 |
ромб. (марказит) |
куб. (пирит) |
||
|
HgS |
триг. (киноварь) |
куб. (метациннабарит) |
||
|
AgBiS2 |
ромб. (матильдит) |
куб. |
||
|
AgI |
гекс. (йодаргирит) |
куб. |
куб. |
|
|
PbF2 |
ромб. |
куб. |
||
|
BaCl2 |
ромб. |
куб. |
||
|
LnF3 (Ln = Eu, Ho) |
ромб. |
гекс. |
||
|
TiO2 |
ромб. (брукит) |
тетр. (анатаз) |
тетр. (рутил) |
|
|
ZrO2 |
мон. (бадделеит) |
тетр. |
куб. |
|
|
Fe2O3 |
гекс. (гематит) |
куб. |
||
|
SiO2 |
ромб. (α-тридимит) |
гекс. (β-тридимит) |
||
|
SiO2 |
тетр. (α-кристобалит) |
куб. (β-кристобалит) |
||
|
GeO2 |
тетр. |
гекс. |
||
|
Bi2O3 |
мон. (бисмит) |
куб. (силленит) |
||
|
K2SO4 |
ромб. |
гекс. |
||
|
СаСОз |
ромб. (арагонит) |
триг. (кальцит) |
||
|
NH4NO3 |
ромб. |
тетр. |
куб. |
|
|
KNO3 |
ромб. |
триг. |
Тенденция к уменьшению КЧ имеет довольно много исключений. Например, высокотемпературная (>2700°С) кубическая модификация ZrO2 имеет флюоритовую структуру (8:4), а низкотемпературная (бадделиит) – моноклинную (7:3;4). Таким образом, повышение симметрии с ростом Т – более общее явление, чем уменьшение КЧ (таблица 10). Это можно понять как стремление кристалла распределить напряжения, возникающие при большой амплитуде колебаний атомов, по возможности более равномерно между отдельными связями.
С другой стороны, смена симметрии скачком на более низкую при понижении T часто вызывает противодействие кристалла, которое проявляется в двойниковании.
Таково происхождение дофинейских двойников, образующися при α-β-превращении кварца, таковы альбитовые или периклиновые полисинтетические двойники, образующиеся при переходе моноклинного (неупорядоченного) в триклинный (упорядоченный) полевой шпат, и многие другие. Плоскость двойникования как бы
частично восполняет исчезновение ряда элементов симметрии в низкотемпературной
58

модификации.
Среди других структурных изменений при повышении температуры,
сопровождающихся повышением симметрии, поворот групп атомов (α-β-кварц, α-β-
тридимит, α-β-кристобалит), вращение радикалов (NH4NO3), неупорядоченное распределение атомов в общих позициях структуры (матильдит (Ag,Bi)S2) в высокотемпературных модификациях. Вообще, как мы подчеркивали выше, различные
процессы упорядочения обычно ведут к потере некоторых элементов симметрии в структуре и, следовательно, ее понижению даже тогда, когда сингония не меняется
(Cu,Zn).
В противоположность случаю повышения температуры увеличение давления сопровождается уменьшением объема кристалла. При достаточно высоком давлении сжатие кристалла приводит, как правило, к более высокой координации в первой и последующих координационных сферах. Примеры увеличения первого КЧ в полиморфных превращениях, происходящих при высоких давлениях, даны в табл. 11.
Кажущееся противоречие фактам, приведенным в этой таблице, представляет
увеличение под действием давления поля стабильности киновари HgS (2:2) относительно метациннабарита (4:4) или аналогичный переход при 7 кбар HgSe из структуры типа сфалерита в структуру киновари. Это тот случай, когда первое
КЧ оказывается не вполне адекватной характеристикой структуры. Дело в том, что в структуре киновари (рис. 27), которую можно
Рис. 27. Структура киновари HgS
рассматривать как построенную из параллельных оси с спиральных атомных цепочек, два расстояния Hg-S в спиралях по 2,39 Å, однако имеются еще две пары довольно близких соседей: 2х3,10 и 2х3,30 Å. Таким образом, координационное окружение в киновари можно описать как сильно искаженный (сжатый по одной из осей 4-ого порядка) октаэдр, и поэтому структура киновари на 6% более плотная, чем метациннабарита с тетраэдрической координацией (4х2,53 Å). Становится понятным, почему при 344° С киноварь превращается в метациннабарит с неожиданным на первый взгляд увеличением КЧ.
Таблица 11. Увеличение первого КЧ при повышении давления
59
|
Вещество |
Давление перехода, кбар |
Структура низкого давления |
Структура высокого давления |
|
С |
75 |
графит (3) |
алмаз (4) |
|
P |
100 |
мышьяк (3) |
простая кубич. (6) |
|
Sn |
120 |
бел. олово (6) |
ОЦК (8) |
|
Ge |
120 |
алмаз (4) |
бел. олово (6) |
|
Ва |
58 |
ОЦК (8) |
ГЦК (12) |
|
ZnO |
100 |
вюртцит (4:4) |
NaCl (6:6) |
|
InSb |
30 |
сфалерит (4:4) |
бел. олово (6:6) |
|
CdS |
20 |
вюртцит (4:4) |
NaCl (6:6) |
|
ZnS |
245 |
сфалерит (4:4) |
NaCl (6:6) |
|
RbI |
4 |
NaCl (6:6) |
CsCl (8:8) |
|
KC1 |
20 |
NaCl.(6:6) |
CsCl (8:8) |
|
RbF |
35 |
NaCl (6:6) |
CsCl (8:8) |
|
NaCl |
300 |
NaCl (6:6) |
CsCl (8:8) |
|
SiO2 |
90 |
кварц (4:2) |
рутил (стишовит (6:3) |
|
AlAsO4 |
90 |
кварц (4:2) |
рутил (6:3) |
|
TiO2 |
≈ 300 |
рутил (6:3) |
иск. флюорит (8:4) |
Более правильной, чем КЧ, характеристикой относительной плотности структуры являются упаковочные коэффициенты, которые определяют долю занятого атомами кристаллического пространства. Эту долю легко найти, когда атомы одинакового размера и формы (металлы, ковалентные кристаллы простых веществ и т. п.). Тогда отношение
объема сферических атомов к полному объему ячейки есть коэффициент компактности структуры γ: γ = 0,74 для плотнейших шаровых упаковок (КЧ=12); 0,68 для ОЦК–
структуры (8), 0,52 для простой кубической (6), 0,34 для структуры типа алмаза (4). Затруднения возникают для кристаллов, состоящих из атомов разных сортов.
Например, для структуры типа CsCl (8:8) γ = 0,68 при условии одинакового размера обоих сортов атомов и 0,73 – при максимально допустимом их различии. Еще больше диапазон этого свойства для структуры типа NaCl: если при одинаковых размерах атомов разного сорта γ = 0,52, то для максимально возможного из геометрических соображений различия размеров γ = 0,79. По этой причине был введен (Лиу, 1981) более объективный критерий компактности гетероатомной структуры, так называемый индекс упаковки α :
V = αR3 , где V – мольный объем (в см3/моль), R – ближайшее расстояние катион – анион (в Å). Индекс упаковки α является функцией не только КЧ, но в общем случае также функцией отношения периодов вдоль кристаллографических осей, угла между осями и координат атомов в структуре (например, кислородного позиционного параметра для
60

таких кубических структур, как структура шпинели или граната), α изменяется от 0,43
для наиболее плотно упакованных металлов с кубической гранецентрированной или гексагональной плотной упаковкой до 17,16 для гораздо более рыхлой молекулярной структуры «сухого льда» СО2.
Однако сравнение между различными типами соединений с помощью индекса упаковки затруднительно. Например, α для алмаза составляет 0,926, а для близкородственной ему структуры сфалерита – 1,854. По этой причине более удобно
|
использовать средний |
атомный индекс |
упаковки α |
(Урусов, |
Пущаровский, 1984) |
|
|
V m = α |
R3 (т – число |
атомов в формуле |
соединения). |
Тогда α |
= 0,93 для алмаза и |
сфалерита. Подобным образом устраняется слишком большое различие в индексах упаковки между структурами типа NaCl и флюорита CaF2: если α для них равны 1,204 и 1,654 соответственно, то α составляют 0,602 и 0,618, что указывает на их близость в отношении эффективности укладки атомов, в соответствии с близостью средних значений КЧ (6 и 5,3). На рис. 28 показан ход α (угол наклона прямых) для некоторых обычных структурных типов.
Знание индекса упаковки α позволяет правильно расположить структуры в
некотором морфотропном ряду соединений и использовать его для анализа «автоморфотропии» – полиморфизма. Например, для MX2 можно построить морфотропный ряд, изображенный на рисунке 29.
Повышение давления приводит к структурному переходу справа налево. Например, SiO2 при высоких давлениях экспериментально получен в структурах рутила TiO2
(стишовит) и α-РbO2. Следующей, и гораздо более трудной, экспериментальной задачей стало получение SiO2 в структуре флюорита CaF2 при сверхвысоких давлениях. В последние годы такие эксперименты были проведены и при давлениях, близких а 1 Мбар (миллион атмосфер), была получена модификация SiO2, структуру которой можно представить как промежуточную между структурой флюорита (рис. 6, часть 1) и пирита
(рис. 14, часть 1).
61

Рис. 28. Средний атомный индекс упаковки – угол наклона прямых в координатах V/m-R3. A1 – беспараметрические структуры с гранецентрированной кубической ячейкой; А4 – алмаз; А7 – мышьяк; B1 – NaCl; B2 – CsCl; В3 – сфалерит; 1 – рутилоподобные структуры; 2 – α–РbО2; 3 – бадделиит; 4 – флюорит; 5 – коттунит; Q – кварц.
Наоборот, повышение температуры стимулирует то структурное превращение, которое предсказывается направлением слева направо в таком ряду. Например, GeO2 при
обычной температуре имеет структуру типа рутила и при высоких температурах переходит в структуру кварца, кварц – в кристобалит и т. д.
Рис. 29. Морфотропный ряд соединений MX2. В скобках указаны средние атомные индексы упаковки.
Анализ свойств атома в кристалле (см. Главу IV, часть 1) показал, что анионы обладают большей сжимаемостью (и термическим расширением), чем катионы. Значит, можно думать, что повышение давления увеличивает отношение r+/r–, а рост температуры уменьшает его для данного вещества. Достижение некоторого критического значения этого отношения в соответствии с правилами Магнуса – Гольдшмидта приводит к автоморфотропному переходу, т. е. изменение термодинамических условий как бы
62
передвигает кристалл с одного места на другое в морфотропном ряду.
Подобные рассуждения полезны главным образом из–за своей наглядности, но они не имеют общего характера. Во многих случаях причины изменения плотности упаковки
атомов в кристалле можно понять только после детального анализа исходной и конечной структур. Рассмотрим в качестве примера важный для глубин мантии Земли переход при высоких давлениях порядка 100 кбар форстерита Mg2SiO4 из структуры оливинового типа в структуру типа шпинели. Несмотря на значительное уменьшение объема (~9%), первые КЧ не изменяются: магний занимает октаэдрические, а кремний – тетраэдрические позиции как в оливине α-Mg2SiO4, так и в шпинельной модификации – рингвудите γ- Mg2SiO4 (существует еще промежуточная искаженная шпинелеподобная модификация β- Mg2SiO4). Однако вторые (катионные) координационные сферы различны. В оливине атомы Si располагаются в центре тригональных призм, образованных шестью атомами Mg. Вокруг призмы находятся еще 3 атома Mg, что приводит к КЧ Si относительно Mg, равному 9. В структуре шпинели атомы Si занимают центры усеченных тетраэдров из 12 атомов Mg. Таким образом, переход оливин → шпинель связан с увеличением второго КЧ
Si от 9 до 12.
Еще более характерно изменение взаимной координации одноименных атомов. Так, в оливине среднее КЧ Mg относительно других Mg (двух сортов – Mgl и Mg2) равно 3 (вокруг Mgl располагаются 2Mgl и 2Mg2, а вокруг Mg2 – 2Mgl), а в шпинели 6. Следовательно, рассматриваемый переход сопровождается значительным увеличением КЧ в катионной подрешетке. Именно более плотная катионная упаковка и является основной причиной повышения плотности γ-модификации.
Хотя при изменении температуры и давления КЧ изменяются в противоположных направлениях, тенденции в изменении симметрии одинаковы. Действительно, как при повышении температуры, так и при увеличении давления полиморфные превращения
обычно идут в сторону образования кристаллических модификаций более высокой симметрии. Например, ромбический Ва–перовскит ВаТiO3 переходит в кубическую модификацию как при T>120°С, так и при Р>34 кбар, моноклинный бадделиит ZrO2 как при повышении Т, так и с ростом Р превращается сначала в тетрагональную, а затем в кубическую флюоритовые модификации.
Обширные экспериментальные исследования превращений низкоcимметричных минеральных фаз земной коры (ромбических оливинов, ромбических и моноклинных пироксенов и амфиболов, моноклинных и триклинных полевых шпатов) показали, что в
условиях верхней мантии и переходного слоя они превращаются в более симметричные и
63
более плотно упакованные кубические шпинели, гранаты, периклаз, гексагональные типы ильменита и корунда, тетрагональный стишовит. Эти наблюдения позволили подойти (Доливо–Добровольский, 1984; Юшкин, 1984) к выделению кристаллических оболочек с повышением симметрии от поверхности в недра Земли: гранито–метаморфический слой коры с преобладанием полевых шпатов – триклинная оболочка, гранулит–базальтовый слой с клинопироксенами в качестве главных минеральных фаз – моноклинная оболочка, верхняя мантия (оливины) – ромбическая оболочка, переходный слой и нижняя мантия (силикатные шпинель, перовскит, периклаз MgO) – кубическая оболочка.
Известно, что среди минералов (около 4000 минеральных видов) значительно
больше половины видов встречается только в самой поверхностной и самой тонкой оболочке Земли – земной коре. Неоднократно, начиная с 1860 г., повторявшаяся симметрийная статистика минералов (Шафрановский, 1982, 1983, Урусов, 2003) показывает, что на долю моноклинных и триклинных видов приходится около 40%, а вместе с ромбическими – больше 60%. Это подтверждает вывод о том, что при обычных
температурах и давлениях резко преобладают кристаллические постройки низкой и средней категорий симметрии.
64
7.4. Термодинамические основы теории полиморфизма.
Очевидно, наиболее устойчивой при данных термодинамических условиях является та полиморфная модификация вещества, которая обладает минимальной свободной энергией Гиббса. При некоторых других условиях две полиморфные модификации оказываются в равновесии друг с другом, если их свободные энергии равны:
|
G1 (T , P) = G2 (T , P) . |
(13) |
Для области давлений, близких к атмосферному, можно пренебречь изменением энергии за счет изменения объема, и условием равновесия становится равенство свободных энергий Гельмгольца:
|
F1 (T ) = F2 (T ) ; |
|
|
E1 − TS1 = E2 − TS2 или E −T S = 0 , |
(14) |
где Е – внутренняя энергия, S – энтропия кристалла. При абсолютном нуле устойчива полиморфная форма с наименьшей внутренней энергией. При повышении температуры модификация с более высокой энтропией может сделаться более стабильной. Это
|
произойдет при температуре перехода Ttr, когда E = (E2 − E1)tr = Ttr (S2 − S1) = Ttr |
S . Отсюда |
|
следует, что для всех превращений, которые совершаются при росте Т, S и |
E имеют |
положительные значения. Другими словами, в соответствии с принципом Лешателье
фазовые превращения при повышении температуры должны сопровождаться поглощением тепла. Это означает, что структурная перестройка проходит таким образом,
чтобы новообразованная структура допускала тепловые колебания атомов с большей энергией при меньшем напряжении связей. Это осуществляется при увеличении объема кристалла и часто сопровождается уменьшением КЧ. Типичный пример дает CsCl (8:8), который при нагревании до 450° С переходит в структуру типа NaCl (6:6) с увеличением объема на 8,85 см3/моль (~17%), возрастанием энтропии на 1,06±0,04 энтропийных единиц и поглощением тепла около 700 кал/моль.
При высоком давлении равенство свободных энергий полиморфных модификаций представляется в виде:
|
Etr −Ttr Str + Ptr Vtr = 0 . |
(15) |
Эти превращения всегда связаны с уменьшением объема фазы высокого давления ( Vtr < 0). Оно должно компенсироваться повышением внутренней энергии и (или) снижением энтропии. Сжатие приводит, как мы видели в предыдущем разделе, к более высокой координации в первой или более далеких координационных сферах. Понижение энтропии
65
связано с уменьшением объема (сокращением свободы колебаний атомов) и частично с повышением степени упорядоченности структуры.
7-5. ПОЛИТИПИЗМ
Политипизм (политипию) можно определить как способность одного и того же вещества кристаллизоваться в нескольких слоистых структурных модификациях, которые различаются только порядком чередования или поворотом одинаковых слоев. Размеры элементарных ячеек в плоскости слоя одинаковы для всех политипных модификаций. Период повторяемости в направлении, перпендикулярном слоям, зависит от последовательности наложения слоев, но всегда в целое число раз больше толщины одного слоя.
Это явление было открыто Г. Баумгауэром в 1912 г. при изучении карбида кремния SiC. Сейчас для этого вещества известны многие десятки политипных модификаций. Во всех этих модификациях гекcагональная элементарная ячейка имеет параметр а==3,078 Å, тогда как переменный параметр с всегда кратен одной и той же величине 2,518 Å – толщине элементарного слоя. Высота элементарных ячеек различных политипов SiC
изменяется от с ≈ 5Å у двухслойного политипа 2Н до с ≈ 1500Å у 594-слойного ромбоэдрического политипа 594R. Наиболее же обычна шестислойная гекcагональная модификация 6H.
Политипизм иногда рассматривают как особый одномерный полиморфизм. Но
помимо этого не очень существенного структурного отличия от полиморфизма политипизм имеет и свои физико–химические особенности. В противоположность полиморфным модификациям, которые обладают своими полями устойчивости и образуются при разных Т и Р, для политипов пока невозможно точно указать границы их существования. Кроме того, обычно одновременно кристаллизуется смесь нескольких политипов, которые могут образовывать срастания друг с другом даже в одном монокристалле. Более того, в отличие от полиморфных модификаций политипы имеют почти точно совпадающие физические свойства. Так, плотность всех политипов SiC составляет 3,217 г/см3, а показатели преломления No и Ne колеблются от 2,6467 до 2,6487 и от 2,6889 до 2,6930 соответственно. Поскольку плотность всех политипов одинакова, то, вероятно, давление не может обусловливать их переходы друг в друга. В разности энергий Гиббса (15) двух политипных модификаций P V исчезает из–за одинакового объема обеих фаз ( V ≈ 0 ).
По отношению к другому фактору равновесия (температуре) нельзя сделать столь же
66
определенного заключения, поскольку энтропии различных политипов все же несколько различаются. Максимальной энтропией и наименьшей свободной энергией при данной Т должна характеризоваться наиболее разупорядоченная структура, конфигурационная энтропия которой S ≈ kN ln 2, где k – постоянная Больцмана, N – общее число слоев в структуре. С этой точки зрения существование упорядоченных политипов вообще представляется аномальным. Пока нет единого объяснения этого феномена. Можно думать, что существует некоторое небольшое различие внутренних энергий разных политипов. Но с этих позиций трудно понять образование политипов с большим периодом с, особенно для таких существенно ковалентных кристаллов, как SiC, в которых дальнодействующие электростатические силы очень слабы. Как структура воспроизводит себя, повторяя чередование слоев с большой точностью после длинного и как будто случайного их набора? Возможно, что более реальна та гипотеза образования политипов, которая связывает их с механизмом роста кристалла на винтовых дислокациях (Верма, 1957). В этом случае различные политипы вообще нельзя рассматривать как термодинамически стабильные фазы.
В связи с тем что структуры всех политипов слоистые, их удобно описывать с помощью теории плотнейших упаковок. Например, две полиморфные модификации сульфида цинка ZnS (сфалерит и вюртцит) обычно описываются соответственно как кубическая и гексагональная плотнейшие упаковки атомов серы, половина тетраэдрических пустот которых занята атомами Zn. Гексагональная структура вюртцита двухслойная …АВАВАВ…, а кубическая структура сфалерита – трехслойная
…АВСАВСАВС… . Соседние слои плотнейшей упаковки следуют друг за другом в направлении [001] в гексагональной элементарной ячейке и [111] – в кубической.
Этим классическим способом удобно обозначать и различные политипы. Так,
наиболее распространенный шестислойный политип будет выражаться повторяющейся последовательностью букв …АВСАСВ… Этот политип, обычный для SiC и ZnS, обозначается также символом Рамсделла 6Н, где число указывает период повторяемости слоев вдоль оси с, а Н – гексагональную ячейку. В тех же обозначениях символ 15R соответствует 15-слойному политипу с примитивной ромбоэдрической элементарной ячейкой. Структуры нескольких распространенных политипов ZnS с этими обозначениями изображены на рис. 30.
Имеется еще много других обозначений тех же политипов (символы Хегга, последовательность интервалов по Отту, операторы Наборро – Франка и др.). Рассмотрим только более удобные и более широко известные числовые символы Г. С. Жданова и буквенные обозначения Л. Полинга. Символ Жданова состоит из пары чисел: первое
67

A
обозначает число слоев, которые следуют друг за другом в последовательности B  C а
C а
A
второе – число слоев, которые сменяют друг друга в обратной последовательности B  C. Например, классическая последовательность АВСВ… будет в символах Жданова обозначаться цифрами 22. В обозначениях Полинга каждый слой характеризуется ориентировкой слоев, находящихся по обе стороны от него: к и г (см. главу V).
C. Например, классическая последовательность АВСВ… будет в символах Жданова обозначаться цифрами 22. В обозначениях Полинга каждый слой характеризуется ориентировкой слоев, находящихся по обе стороны от него: к и г (см. главу V).
Соотношения между различными обозначениями некоторых политипов приводятся в табл. 12.
Рис. 30. Различные политипы ZnS (SiC)
Подстрочный индекс 3 в обозначениях Жданова и Полинга относится к ромбоэдрическим структурам политипов. Для длиннопериодических структур удобнее обозначения Рамсделла и Жданова. Иногда используют также степень «гексагональности» политипа h, имея в виду относительное количество (в процентах) слоев в структуре, находящихся в гексагональной ориентировке. Так, для кубической модификации 3C h = 0, гексагональной 2Н h = 100, а для 6H h = 33, для 15R h = 40 и т. д.
Таблица 12. Различные обозначения некоторых политипов
|
Символ Рамсделла |
Классическая последовательность |
Символы |
Обозначения |
|
слоев |
Жданова |
Полинга |
|
|
2H |
AB |
11 |
(г)2 |
|
4H |
АВСВ |
22 |
(гк)2 |
|
6H |
АВСАСВ |
33 |
(гкк)2 |
|
15R |
АВСВАСАВАСВСАСВ |
(23)3 |
(гкгкк)3 |
68

|
21R |
АВСАСВАСАВСВАСВССАВАСВ |
(34)3 |
(гкгкккк)3 |
Политипизм особенно характерен для кристаллов со слоистыми структурами (CdI2, CdBr2, PbI2, NbSe2, TaSe2 и др.). Так, хорошо известен политипизм CdI2, имеющего более сотни различных политипов. Самой распространенной структурной модификацией этого соединения является политип 4Н. Как и в случаях SiC и ZnS, для CdI2 обычным является
присутствие в кристалле в синтаксических срастаниях нескольких политипов одновременно. Кроме того, часто встречаются случаи статистической неупорядоченности слоев, а полностью упорядоченные политипы с большими периодами с являются скорее исключениями.
Политипизм имеет много примеров и среди минералов с гексагональными (псевдогексагональными) структурами. Интересны с этой точки зрения политипы гексагональных Ti-шпинелей – хэгбомитов (Mg, Fe)2(Al, Ti)4(O,OH)8. Установлены следующие политипные модификации: 4Н, 5Н, 6Н, 15H, 15R, 18R и D. Символом D
описывается полностью неупорядоченная в отношении упаковки кислородных слоев разновидность. Исходная структура 4Н основана на 8-слойной плотнейшей упаковке атомов О (гкккгккк) вдоль 6-ной оси, в отличие от шести слоев (по диагонали куба) в кубической благородной шпинели MgAl2O4. Степень гексагональности политипа 4H h = 26, 15R h = 20 и т. д.
Изученные несколько политипов гексагонального тридимита представляют собой чередование двухэтажных «слоев» SiO4–тeтpaэдpoв тридимита и трехэтажных «слоев» кристобалита. Слоистая гексагональная структура графита допускает существование в ней участков ромбоэдрической симметрии («трехслойной» в отличие от «двухслойной» обычного графита). Подобным образом наряду с обычной двуслойной гексагональной
|
модификацией 2Н молибденита |
MoS2 в природе встречается трехслойная |
||||
|
ромбоэдрическая модификация 3R. |
|||||
|
Широко проявляется политипизм в структурах |
|||||
|
слоистых силикатов: слюд, хлоритов, глинистых |
|||||
|
минералов. Эти силикаты построены из различных |
|||||
|
сочетаний между собой двумерных тетраэдрических |
|||||
|
и октаэдрических сеток (рис. 31). Первые состоят из |
|||||
|
сцепленных вершинами тетраэдров, в которых |
|||||
|
находятся атомы Si, A1, иногда FeIII. Вторые |
|||||
|
построены из соединенных боковыми ребрами |
|||||
|
Рис. 31. Сочетание в |
слоистом |
октаэдров, которые заселяются либо полностью |
|||
|
силикате пирофиллите |
корундового |
||||
|
слоя из октаэдров с двумя слоями из |
69 |
||||
|
тетраэдров. Треть атомов |
О |
в среднем |
(триоктаэдрические сетки), либо только 2/3 из них (диоктаэдрические сетки) атомами Al, FeII, FeIII, Mg, Zn, Li и др. Центры этих многогранников образуют гексагональный мотив.
Различные способы сочленения сеток и их взаимной ориентировки практически эквивалентны результату поворота слоев на углы, кратные 60° (в большинстве случаев кратные 120°). На этом основана систематика политипов слоистых силикатов (Смит и Иодер, 1956; Радослович, 1959; Звягин, 1961; и др.). В ней обозначения политипов содержат буквы и цифры: буквы Тк, М, Т, Н, О обозначают сингонию (триклинную, моноклинную, тригональную, гексагональную и ромбическую ортогональную), а цифры перед ними обозначают период повторяемости слоев. Буквы имеют также подстрочные индексы 1 или 2, которые относятся к структурам с моноклинной осью а или b соответственно. Так, символ 2M1 обозначает политипную модификацию слюды с моноклинной симметрией, образованную поворотом слоев относительно исходного политипа 1М на 120° (или 240°), и моноклинной осью а. В природе наиболее часто встречаются модификации 1М, 2M1 и 3Т из шести возможных структур слюд: для мусковита характерна модификация 2M1, для биотита и флогопита – 1М.
При структурно–химической трансформации слоистых минералов, проходящей под действием гидротермальных растворов, наследуется политипная модификация: в Mg – карбонатной среде по мусковиту 2M1 образуется флогопит 2M1, по мусковиту 1М – флогопит 1М, по диккиту 2M1 – серпентин 2M1, по каолиниту 1Тк – серпентин 1М (ЗТ) и т. п. (Франк–Каменецкий и др., 1983). Это означает, что изменение химического состава октаэдрических сеток не влечет за собой смещения (поворота) тетраэдрического слоя относительно октаэдрического.
70
Глава VIII. ИЗОМОРФИЗМ
8-1. ОПРЕДЕЛЕНИЯ
Изоморфизмом называется взаимное замещение атомов (или их групп) разных химических элементов в эквивалентных позициях кристаллической структуры.
Изоморфизм приводит к образованию смешанных кристаллов, состав которых в определенных пределах изменяется непрерывно и постепенно. У термина «смешанный кристалл» имеются еще два синонима, используемых чаще. Один из них – изоморфная смесь – встречается в основном в минералогической и геохимической литературе. Второй – твердый раствор замещения – широко употребляется в физической химии и физике твердого тела.
Содержание указанных терминов совпадает не полностью. Так, понятия «изоморфизм»
и«изоморфная смесь» включают в себя и те сложные случаи замещения, когда бывает трудно указать, какие именно компоненты образуют смешанный кристалл, Кроме того, изоморфизм допускает как статическую, так и динамическую трактовку. Изоморфизм с
точки зрения динамики заключается в описании распределения изоморфной примеси между фазами в различных процессах кристаллизации.
От изоморфизма следует отличать изоструктурность, которой отвечает отсутствие изоморфных замещений, несмотря на одинаковые кристаллические структуры. Уже
известный нам пример изоструктурности дают три минерала со структурой хлористого натрия – галит NaCl, периклаз MgO, галенит PbS. В отличие от этого, галит и сильвин KCl
иизоструктурны, и изоморфны.
8-2. КРАТКИЕ ИСТОРИЧЕСКИЕ СВЕДЕНИЯ
К началу XIX в. в кристаллографической науке торжествовала концепция Р. Ж. Гаюи, основное положение которой предписывало каждому кристаллическому веществу свойственную лишь ему «полиэдрическую молекулу» (т. е. структуру). Основным противником этой крайней точки зрения в теории был другой французский ученый, К–Л. Бертолле, обращавший внимание на известные минералогам XVIII в. факты непостоянства состава кристаллов и совпадения их форм при разных составах. Но этот спор, в котором победителем казался для современников Гаюи, не мог быть решен окончательно до тех пор, пока на помощь теоретическому умозрению и эмпирическому наблюдению минералога не пришла лабораторная практика химика.
71

Опыты по кристаллизации дали к началу XIX века тот необходимый фактический материал, который привел к открытию изоморфизма.
На точную экспериментальную основу эти опыты были впервые поставлены французским химиком Николя Лебланом (1742-1806) и петербургским академиком Товием Ловицем (1757-1804). Большая часть их достижений оказалась надолго забытой, и только в
прошлом столетии они смогли получить достойную оценку. Однако ни Леблану («великому неудачнику», как его назвал В. И. Вернадский), ни его ближайшим
последователям не удалось сделать открытия изоморфизма из–за давления идей Гаюи. Только Э. Митчерлиху (рис. 32) удалось, наконец, избавиться от
|
Рис. 32. Э. Митчерлих (1794 – 1863) |
гипноза этих идей, когда в 1819 г. он пришел к |
|
следующему выводу: те тела изоморфны, которые: 1) |
при аналогичном химическом составе имеют подобную кристаллическую форму и 2) способны образовать смешанные кристаллы в произвольных, непостоянных отношениях. От первой части этого вывода происходит и название «изоморфизм», которое было дано Митчерлихом открытому им явлению в 1821 г.
Экспериментальной основой для открытия изоморфизма были многочисленные опыты Митчерлиха над сокристаллизацией мышьяковокислых и фосфорнокислых солей калия и аммония и целым рядом других солей. Митчерлих имел дело только с изовалентным изоморфизмом типа: К+-NH4+, Ba2+-Sr2+, Fe2+–Со2+ и т. д. Но уже через несколько лет (1826) догадка И. Гесселя о том, что единственный известный тогда полевой шпат (лабрадор) представляет собой изоморфную смесь двух полевых шпатов состава NaAlSi3O8 (альбит) и CaAlSi2O8 (анортит), могла бы привести к обнаружению гетеровалентного изоморфизма: NaSi-CaAl. Однако эта работа, как и многие другие исследования этого ученого, оставалась неизвестной вплоть до конца XIX в. Верные
соображения о возможности гетеровалентных замещений содержались и в магистерской диссертации Д. И. Менделеева (1855-1856).
Окончательное становление этих представлений связано с именем австрийского минералога Г. Чермака, который в 1865-1871 гг. объяснил сложный и переменный состав таких породообразующих минералов, как плагиоклазы, пироксены и амфиболы, взаимными замещениями не отдельных атомов, а атомных пар (Na+Si4+↔Ca2+Al3+, Mg2+Si4+↔AlAl3+ и т. п.) с общей суммарной валентностью.
72
Вторая половина XIX века ознаменована интенсивным изучением зависимости физических свойств изоморфной смеси от ее состава. Была обнаружена линейная зависимость от состава угла между осями и показателя преломления: М. Шустер предложил (1880) использовать ориентацию осей оптической индикатриссы для определения состава полевых штапов, Г. Н. Вырубов указал на линейную связь угла оптических осей смешанного кристалла с его составом, Бодлендер – на
|
пропорциональность между составом и вращением плоскости поляризации. |
||||||||
|
И. |
В. |
Ретгерс |
установил |
(1889) |
||||
|
пропорциональность между удельным весом (удельным |
||||||||
|
объемом) и составом (правило Ретгерса). Он пришел к |
||||||||
|
следующему общему положению: два вещества только |
||||||||
|
тогда действительно изоморфны, когда физические |
||||||||
|
свойства их смешанных кристаллов являются |
||||||||
|
непрерывными (обычно линейными) функциями их |
||||||||
|
химического состава (рис. 33). |
||||||||
|
В. |
Мутманн |
(1894) |
рассмотрел |
связь |
||||
|
Рис. 33. Иллюстрация к правилам молекулярного |
объема, |
равного |
отношению |
|||||
|
Ретгерса и Вегарда: |
молекулярного |
веса |
к удельному весу, с |
составом и |
||||
|
а) изоморфизм; б – изодиморфизм. |
||||||||
|
нашел, |
что в изоморфной серии вместе с увеличением |
|||||||
молекулярного веса наблюдается увеличение молекулярного объема, но только если члены ряда принадлежат одной группе Периодической системы.
Случаи, когда вместо непрерывной зависимости удельного объема от состава наблюдаются два отрезка, примыкающих к чистым компонентам и смещенных друг – относительно друга (см. рис. 33), Ретгерс назвал изодиморфизмом. Очевидно, здесь образуется не один, а два ряда смешанных кристаллов, каждый со своей кристаллической формой. Изодиморфизм возникает, когда чистые компоненты обладают разной кристаллической структурой.
П. Грот в 90-х годах XIX века настойчиво указывал на то, что объем, занимаемый атомами, есть главное свойство, допускающее или запрещающее взаимное замещение. Он проводил такое сравнение: при постройке здания можно заменить кирпичи камнями совсем других физических и химических свойств, но только при условии, что по форме и по величине эти камни будут сравнимы с основными кирпичами.
Попытки объединить те химические элементы, которые чаще других образуют друг с другом изоморфные смеси, в группы или ряды были начаты еще Митчерлихом. Т. Грэм и Ф. Отто, по–видимому, впервые в 1847 г. собрали химические элементы,
73
преимущественно изовалентные, в одиннадцать групп по признаку их изоморфизма в простых телах и соединениях. Д. И. Менделеев подверг критическому пересмотру таблицу Грэма, собрав вместе более сходные элементы. А. Е. Арцруни разместил (1893) элементы по десяти изоморфным рядам, пытаясь соблюдать признак изовалентности, однако, с точки зрения современного исследователя, некоторые его ряды необоснованно расширены. Чисто историческое значение имеют теперь и 18 изоморфных рядов В. И. Вернадского (1909). Однако в той же работе Вернадский выдвинул идею о подвижности границ внутри ряда в зависимости от термодинамических условий: «изоморфные ряды перемещаются и изменяются под влиянием температуры и давления». Он едва ли не впервые обратил внимание на важность изучения явлений распада изоморфных смесей, несомненно, под влиянием успехов физической химии в изучении кристаллического состояния. Я. Г. Вант–Гофф в 1890 г. вводит представление о твердых растворах, а В. Розебомом, В. Нернстом и другими исследователями создается учение о фазовых равновесиях. В 1907 г. Н. С. Курнаков и С. Ф. Жемчужный с помощью физико– химического анализа изучили область распада твердых растворов в системе NaCl-KCl и положили начало учению об устойчивости изоморфных смесей.
8-3. КЛАССИФИКАЦИЯ ИЗОМОРФИЗМА
Изоморфизм делится на два типа: изовалентный и гетеровалентный. В изовалентном изоморфизме можно найти только два подтипа: 1) собственно изоморфизм, если компоненты смеси изоструктурны; 2) изодиморфизм, если компоненты обладают различными структурами.
Гораздо сложнее и разветвленнее классификация гетеровалентного изоморфизма. Всю совокупность гетеровалентных замещений можно разбить на два основных подтипа: 1) без изменения общего числа атомов в элементарной ячейке (собственно гетеровалентный изоморфизм); 2) с изменением числа атомов (гетеровалентный изодиморфизм). Оба этих подтипа объединяются обязательным условием баланса (или компенсации) валентностей при изоморфных замещениях гетеровалентного типа. Однако способы компенсации могут быть различными, и это позволяет провести выделение видов и разновидностей гетеровалентного изоморфизма. Так, среди замещений с сохранением числа атомов имеются три вида: а) сопряженное замещение в анионной и катионной подрешетках с одновременным изменением валентностей катиона и аниона (например, ZnS-GaAs, K2BeF4-K2SO4, KNbO3-KMgF3); б) замещение двух одинаковых атомов в
эквивалентных структурных позициях на два различных атома с той же суммарной
74
валентностью (например, 2SnO2-FeNbO4, Fe2O3-FeTiO3, 2PbS-AgBiS2, 2ZnS-CuFeS2); в)
замещение двух пар различных атомов в неэквивалентных структурных положениях с одинаковой суммарной валентностью (например, ряд плагиоклазов NaAlSi3O8-CaAl2Si2O8,
пироксены CaMgSi2O6-NaFeSi2O6).
Замещения с изменением числа атомов в ячейке распадаются на два основных вида: а) с вычитанием (образованием вакансий); б) с внедрением (заселением интерстиций) – «с заполнением пространства», по В. М. Гольдшмидту.
Такие изоморфные замещения с вычитанием, как 2Li+ ← Mg2+ +v(Li) (LiCl-MgCl2), 3Mg2+ ← 2Al3+ + v (Mg) (в биотите), 3Fe2+← 2Sc3+ + v (Fe) (в вольфрамите), приводят к образованию вакантных позиций v в кристаллической структуре, чтобы удовлетворить требованиям электронейтральности кристалла. Классичеcким представителем изоморфных замещений c внедрением (заполнением пространства) является флюорит CaF2 с редкими землями (и иттрием), в котором замещение идет по следующей схеме: Са2+ ← Y3+ + [F–], где [F–] обозначает внедренный в кубическое междоузлие ион [F–].
Знание способов и механизмов кристаллохимической компенсации при гетеровалентном изоморфизме играет большую роль в управляемом синтезе необходимых для современной техники монокристаллов с примесями.
Следует подчеркнуть, что нет резкой границы между замещениями с вычитанием и внедрением, скорее, это две стороны одного и того же процесса. Действительно, замещение Mg2+ ←2Li+ в области системы LiCl-MgCl2, богатой MgCl2, осуществляется, вероятно, за счет внедрения дополнительного атома Li (компенсатора) в свободную октаэдрическую пустоту ромбоэдрической ячейки MgCl2 (рис. 34). Очевидное родство между структурами LiCl (тип NaCl, рис 34 а) и MgCl2 (тип CdCl2, рис 34 б) обусловливает реализацию непрерывных замещений в системах LiCl-MeCl2 (Ме – Mg, Mn, Fe, Zn, Ni, Co).
Подобным образом замещение 2Al3+ ← 3Mg2+ в мусковите есть замещение с заполнением пространства в отличие от замещения с вычитанием 3Mg2+ ← 2Al3+ в биотите. Своеобразным видом замещений с внедрением компенсаторов валентности в крупные пустоты некоторых каркасных, кольцевых и слоистых структур, главным образом силикатов и алюмосиликатов, являются замещения типа Si4+ ← Al3+ + Na+ в кварце, Be2+ ← Li+ + Na+ (или Li+ + Cs+) в берилле, Ca2+← 2Na+ в катаплеите и цеолитах.
75

Рис. 34. Связь между элементарными ячейками LiCl (а) и MgCl2 (б). В последней свободен каждый второй
катионный слой в направлении тройной оси элементарного ромбоэдра
Гетеровалентные замещения с сохранением числа атомов в структуре часто бывают собственно изоморфными, т. е. компоненты смеси либо изоструктурны, либо принадлежат к родственным структурным типам. Примерами полной изоструктурности компонентов являются замещения в системах циркон ZrSiO4 – ксенотим YPO4, сфалерит ZnS – GaAs (сопряженный катион–анионный изоморфизм).
Примерами второго рода служат системы 3SnO2 – FeNb2O6, 2ZnS – CuGaS2. При обычных условиях Nb-тапиолит FeNb2O6 имеет полирутиловую структуру с утроенным параметром с, но при высоких температурах (выше 1300° С) она переходит в структуру типа рутила TiO2 – касситерита SnO2 (очевидно, с неупорядоченным расположением атомов Fe3+ и Nb5+ в одних и тех же рутиловых октаэдрах). Галлит CuGaS2 имеет тетрагональную структуру халькопирита, которая, будучи родственной кубической структуре сфалерита, отличается от нее лишь упорядоченным распределением тетраэдров меди и галлия. Нетрудно видеть, что в этих примерах структура одного из компонентов смеси является производной от структуры другого.
Вотличие от замещений с сохранением числа атомов гетеровалентный изоморфизм
сизменением числа атомов практически всегда относится к изодиморфизму. Редкие
76
исключения из этого правила связаны с теми случаями, которые можно рассматривать как промежуточные между изо– и гетеровалентным изоморфизмом (например, непрерывные замещения анионов CO32- ↔ SO42- в канкрините Na6Ca2[AlSiO4]6(CO3, SO4)(ОН)2. Однако твердые растворы в системе К2СО3– K2SO4 – типичный случай изодиморфизма. Другой пример «изоструктурности» компонентов гетеровалентной смеси дают непрерывные анионные замещения в системе КСl – КВН4, обусловленные, вероятно, вращением и псевдосферической формой комплексного аниона ВН4–.
Кроме тех взаимных замещений между отдельными атомами и их изолированными группами, которые были рассмотрены выше, иногда выделяют и более сложные случаи «аномального» изоморфизма (Никитин, 1944; Франк–Каменецкий, 1969, 1971). Они относятся к замещениям между протяженными в одном (смешанноцепность), в двух
(смешаннослойность) и в трех (смешанноблочность) измерениях структурными элементами. Особенно распространены такие замещения в цепочечных структурах биополимеров (смешанноцепность), слоистых силикатах (смешаннослойность) и т. д. «Аномальный» изоморфизм часто сопровождает структурные преобразования в твердом состоянии с четким «наследованием» структурных элементов в продуктах реакции. Он
образует постепенные переходы к ориентированным срастаниям эпитаксической природы. Очевидно, что так называемый «аномальный» изоморфизм может описывать те случаи структурной гомологии, когда существует беспорядок во взаимном размещении структурных единиц (модулей).
77
8-4. ЭМПИРИЧЕСКИЕ ПРАВИЛА ИЗОМОРФИЗМА И ИХ СОВРЕМЕННАЯ ТРАКТОВКА
Основы современных представлений об изоморфизме были созданы в первой половине прошлого века и опираются на рентгеноструктурное изучение атомного строения смешанных кристаллов. Первые систематические исследования в этом направлении привели шведского ученого Л. Вегарда в 1921 г. к установлению правила аддитивности размеров элементарной ячейки твердого раствора (правило Вегарда):
где х1 и х2 – мольные доли, а1 и а2 – параметры ячейки чистых компонентов. Под символом
а можно понимать любой из параметров ячейки или любое среднее межатомное расстояние. На первый взгляд правило Вегарда совершенно идентично правилу Ретгерса (см. рис. 33), которое можно записать в виде:
где V, V1 и V2 – мольные объемы твердого раствора и чистых компонентов соответственно. Нетрудно убедиться, однако, на примере кубического кристалла (V=ka3), что уравнения (16) и (17) не тождественны.
Соответствие измерений правилу Вегарда является очень удобным приемом, чтобы установить самое существование твердого раствора. Однако строго прямолинейная зависимость параметров ячейки от состава наблюдается довольно редко. Наоборот, весьма обычны отклонения от него, которые можно выразить с помощью параболической
|
функции от состава смеси: |
|
|
a = x1a1 + x2 a2 + x1 x2δ , |
(18) |
где δ – некоторый параметр, который может иметь как знак плюс (для положительных отклонений), так и знак минус (для отрицательных отклонений). В табл. 13 на примере системы NaCl-KCl показано, что измеренные экспериментально межатомные расстояния заметно отклоняются от правила Вегарда ( R = x1R1 + x2 R2 ), меньше – от правила Ретгерса
( R3 = x1 R13 + x2 R23 ) и согласуются в пределах экспериментальной ошибки (±0,0005 Å) с
уравнением (18) при δ = 0,05 Å.
Таблица 13. Межатомные расстояния в твердых растворах NaCl – KCl
78
|
NaCl, |
R, Å |
Отклонение от правил |
|||
|
мол. доля |
|||||
|
Вегарда |
Ретгерса |
δ = 0,05 Å |
|||
|
0,0000 |
3,1458 |
– |
– |
– |
|
|
0,1002 |
3,1177 |
0,0045 |
0,0015 |
0,0000 |
|
|
0,2997 |
3,0593 |
0,0111 |
0,0039 |
0,0006 |
|
|
0,3835 |
3,0327 |
0,0118 |
0,0036 |
0,0000 |
|
|
0,4999 |
2,9956 |
0,0127 |
0,0038 |
0,0002 |
|
|
0,5037 |
2,9942 |
0,0125 |
0,0036 |
0,0000 |
|
|
0,5981 |
2,9628 |
0,0118 |
0,0032 |
-0,0002 |
|
|
0,6990 |
2,9286 |
0,0105 |
0,0027 |
0,0000 |
|
|
0,8243 |
2,8852 |
0,0080 |
0,0038 |
0,0007 |
|
|
0,9003 |
2,8578 |
0,0053 |
0,0018 |
0,0008 |
|
|
1,0000 |
2,8200 |
– |
– |
– |
|
В более сложных случаях отклонения от правила Вегарда могут иметь знакопеременный характер. Такое поведение параметров ячейки обычно указывает на изменение положения изоморфной примеси в структуре.
После создания систем эффективных радиусов атомов и ионов (1920-1927)
появилась возможность для целого ряда обобщений в области кристаллохимии изоморфизма. Они принадлежат главным образом В. М. Гольдшмидту, а также X. Гримму, В. Юм–Розери, А. Е. Ферсману и другим исследователям
Заслугой В. М. Гольдшмидта является формулировка основных эмпирических правил изоморфизма. Среди них наиболее известно следующее эмпирическое правило 15% разницы радиусов: изоморфные смеси образуются в широких пределах при температурах, лежащих далеко от точки плавления, если (ионные) радиусы взаимозамещающихся структурных единиц различаются не более чем на 15% (от меньшего значения).
Гольдшмидт относил это правило к «прозрачным», т.е. существенно ионным, кристаллам. Аналогом его для металлических и ковалентных кристаллов можно считать
правило 15%-ной разности атомных диаметров В. Юм–Розери (1934).
Опыт показывает, что если разница атомных радиусов превышает предельное значение 15%, существование широких областей твердых растворов становится очень маловероятным, когда же она меньше 15%, важное значение могут приобрести другие факторы, которые могут помешать ожидаемой высокой растворимости. Так, Л. Даркен и Р. Гурри (1953) установили на большом эмпирическом материале по изучению взаимной растворимости в металлических сплавах, что область, наиболее благоприятная для
79

образования твердых растворов, ограничивается разностью злектроотрицательностей ±0,4 и 15%-ной разницей атомных радиусов.
Дальнейшие уточнения размерных критериев были сделаны В. С. Соболевым (1948) и А. С. Поваренных (1964). Они наметили корреляцию между типом диаграммы
|
плавкости, по Розебоому, и относительной разницей размеров r r1 или |
R R1 (r – |
|
радиусы ионов, R – межатомные расстояния). Так, по А. С. Поваренных, если |
R R1 < 4- |
5%, то изоморфные замещения непрерывны при всех температурах. При 4-5%< R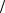 R1 <8- 10% изоморфизм совершенный (непрерывный) только при средних и высоких Т (> 100400° С). При 8-10%< R
R1 <8- 10% изоморфизм совершенный (непрерывный) только при средних и высоких Т (> 100400° С). При 8-10%< R R1 <14-16% изоморфизм ограниченный, с понижением Т
R1 <14-16% изоморфизм ограниченный, с понижением Т
|
происходит распад изоморфных смесей. Если 14-16%< R R1 <20-25%, |
изоморфизм |
|
становится ограниченным даже при самых высоких температурах, а при |
R R1 >20-25% |
|
заметных замещений обычно не наблюдается. |
В. М. Гольдшмидт, А. Е. Ферсман и их последователи хорошо понимали, что, хотя близость размеров замещающих друг друга атомов или ионов – очень важное и обязательное условие, оно не является достаточным. Так, А. Е. Ферсман писал: «Вообще явление замещения… представляет одно из самых замечательных проявлений сходства радиусов, но и оно много более сложно, чем простое применение равенства радиусов или их отклонения (не свыше 10-15% от среднего)». Одно из главных дополнительных условий изоморфизма, по мнению этих исследований, близость поляризационных свойств ионов. Так, ионы благородногазового строения (Na+, Са2+ и т. п.) не замещаются или замещаются с трудом ионами типа «купро» (с 18-электронной оболочкой), даже если их размеры очень близки (Cu+, Hg2+, … соответственно). И позже, когда кислотно–основные свойства ионов стали характеризовать не поляризуемостями, а электроотрицательностями, много раз было замечено (Файф, 1951; Рамберг, 1952; Поваренных, 1964; Нокколдс, 1966),
что с увеличением разности ЭО χ уменьшаются изоморфные возможности данной пары ионов. Например, почти одинаковые по ионным радиусам Na+ и Сu+ практически не изоморфны из–за большого значения χ =0,9.
Другим важным эмпирическим обобщением явились представления Гольдшмидта о направленности, «полярности» изоморфизма. Так, в случае изовалентных замещений правило полярности гласит: ион с меньшим радиусом будет входить в общую кристаллическую структуру легче, чем ион с большим радиусом занимающий ту же позицию. Например, Na+ (r = 0,98Å) должен охотнее замещать К+ (r = 1,33 Å) в КСl, чем более крупный К+ будет замещать Na+ в NaCl.
В случае гетеровалентных замещений действует другое правило полярности
80
Гольдшмидта: ион с большим зарядом входит в кристалл легче, чем ион с меньшим зарядом, занимающий ту же кристаллографическую позицию. Например, Mg2+ может замещаться на Sc3+, а обратное замещение маловероятно.
По отношению к процессам кристаллизации правила полярности удобно выразить с помощью коэффициента распределения K = cкр  сж , где cкр – концентрация
сж , где cкр – концентрация
изоморфной примеси в кристалле, cж – в жидкой фазе (растворе или расплаве), Если К>1,
то примесь «захватывается», а если К<1, то «допускается» кристаллом. Из правил полярности следует, что ион с меньшим радиусом или большим зарядом должен «захватываться», а ион с большим радиусом или меньшим зарядом «допускается» кристаллом.
В. В. Щербина обратил внимание на то, что пределы замещений очень ограничиваются в случае изодиморфизма – различия кристаллических структур компонентов. Например, изоморфизм Са2+ и Sr2+ ( r r1 = 16%) обычен для изоструктурных силикатов (полевые шпаты), фосфатов (апатиты), карбонатов (арагонит) и т. п., но отсутствует в природных сульфатах, поскольку гипс CaSO4·2H2O – моноклинный кристаллогидрат, а безводный целестин SrSO4 имеет ромбическую структуру типа барита BaSO4. В последнем примесь стронция в том или ином количестве присутствует всегда при той же разнице размеров ионов ( r
r1 = 16%) обычен для изоструктурных силикатов (полевые шпаты), фосфатов (апатиты), карбонатов (арагонит) и т. п., но отсутствует в природных сульфатах, поскольку гипс CaSO4·2H2O – моноклинный кристаллогидрат, а безводный целестин SrSO4 имеет ромбическую структуру типа барита BaSO4. В последнем примесь стронция в том или ином количестве присутствует всегда при той же разнице размеров ионов ( r r1 = 15%).
r1 = 15%).
В 1937 г. В. В. Щербина предположил, что селен (промежуточный по размеру между серой и теллуром) играет в сульфидах «посредническую» роль. Изоморфно замещая серу, селен увеличивает параметры решетки и способствует вхождению еще более крупного теллура, которому самостоятельно трудно войти в структуру сульфида из– за слишком большого различия в размерах серы и теллура. Это предположение в
дальнейшем было оправдано экспериментальными исследованиями и теоретическими расчетами.
Детальную разработку современного ему учения об изоморфизме сделал в 19331937 гг. А. Е. Ферсман (рис. 35). На основе работ В. Гольдшмидта, X. Гримма и др. он пришел к новым важнейшим обобщениям. В частности, он обратил внимание на то, что
именно в диагональных направлениях Периодической системы увеличение радиуса иона на 6-10% сопровождается одновременным увеличением заряда. Это обеспечивает наиболее благоприятные условия для гетеровалентного изоморфизма. Продолжая историческую линию Митчерлих–Грэм–Менделеев–Арцруни–Вернадский, он обосновал
диагональные ряды изоморфизма, носящие его имя (1933).
81
Рис. 35. А.Е.Ферсман (1883 – 1945)
Стрелки в этой схеме указывают на направленность (полярность) изоморфизма. Преимущественно диагональное направление стрелок (справа налево и вверх в
соответствии с правилом полярности) заменяется на вертикальное особенно для таких
|
пар, |
как |
Zr-Hf, |
Nb-Та, |
Mo-W. |
Это |
следствие |
|
|
«лантаноидного сжатия» (см. Главу II, часть 1) – |
|||||||
|
уменьшения радиусов четырнадцати Ln-элементов с |
|||||||
|
ростом Z приблизительно на 0,2 Å, в результате которого |
|||||||
|
размеры указанных выше пар атомов оказываются |
|||||||
|
чрезвычайно близки. По этой причине Hf, например, |
|||||||
|
вообще не образует в природе собственных минералов и |
|||||||
|
был обнаружен в рудах циркония. |
|||||||
|
Рис. 36. Звезда изоморфизма |
В итоге А. Е. |
Ферсман |
построил так |
называемые |
|||
|
для иона Ba2+. |
«звезды |
изоморфизма», которые |
показывают в |
||||
обобщенной форме изоморфные связи между элементами. Например, для Ba она имеет вид, изображенный на рис. 36. Наиболее тесные изоморфные отношения Ba обнаруживает со своими ближайшими соседями (K, Rb, Sr) и менее прочные – с более далекими (Na, Cs).
Из анализа подобных «звезд» следует и правило кристаллохимической компенсации:
если Ва2+ замещается на Ln3+, то лучшей компенсацией избыточной валентности является одновременное замещение другого иона Ва2+ на K+: 2Ba2+ ↔Ln3+ + K+.
И Гольдшмидт, и Ферсман неоднократно подчеркивали энергетическое обоснование правил изоморфизма: на фоне стремления смешанного кристалла к минимуму
электростатической энергии вхождение в структуру иона с меньшим размером или большим зарядом «укрепляет решетку», т. е. является «энергетически выгодным». Обосновывая свой закон диагональных рядов, Ферсман писал: «…энергетический выигрыш имеет место тогда, когда в кристаллическую решетку вместо иона низкого
82
заряда входит такой же по размеру ион и того же знака, но более высокого заряда». Классики теории изоморфизма вполне отдавали себе отчет в сложности задачи. Так, А. Е. Ферсман писал: «Анализ явлений изоморфизма с точки зрения энергетики представляет
очень важную задачу и намечает совершенно новые пути в изучении геохимических процессов. Изоморфизм есть не просто случайная замена одних элементов другими на основании их объема и закона масс, а один из способов достижения более устойчивых энергетических комплексов… Однако анализ этой проблемы с точки зрения энергетики пока невозможен и частично наталкивается на ряд противоречий» (1934).
8-5. Физико-химические основы изоморфизма
За прошедшие с тех пор, как написаны эти слова, 70 с лишним лет были не только созданы возможности такого анализа, но и устранены многие из его противоречий. Были уточнены многие эмпирические правила изоморфизма, добавилось много новых наблюдений. В частности стало понятно, что изоморфизм – явление, которое, как и полиморфизм не может быть понято только на языке кристаллохимии. Это понимание должно быть основано на общих физико–химических термодинамических законах. Равновесное состояние изоморфной смеси, как и любой другой физико–химической системы, определяется стремлением к минимуму ее гиббсовской свободной энергии:
|
G = H − T S = U + P V −T S . |
(19) |
Более точно говоря, поведение изоморфной смеси (состава х1 мольных долей первого компонента и х2 мольных долей второго компонента) управляется термодинамическими функциями смешения – разностями термодинамических функций твердого раствора и механической смеси компонентов того же состава:
Gсм (x1, x2 ) = Gтв. р− р (x1, x2 ) − x1 G1 − x2 G2 = H − T Sсм ,
|
Нсм (x1 , x2 ) = H тв. р− р (x1 , x2 ) − x1 H1 − x2 H 2 , |
|
|
Sсм (x1 , x2 ) = Sтв.р− р (x1 , x2 ) − x1 S1 − x2 S2 . |
(20) |
Здесь Н см и Sсм – теплота и энтропия смешения соответственно.
Обратимся к тем связям между термодинамическими функциями смешения и кристаллохимической моделью изоморфной смеси, которые составляют основу рассматриваемой теории. Наиболее простой представляется трактовка физического
смысла конфигурационной части энтропии смешения Sсм . Эта мера
неупорядоченности системы может быть рассчитана из уравнения Больцмана:
83

где k – постоянная Больцмана; W – число способов распределения замещающих друг друга атомов по N эквивалентным позициям кристаллической структуры. W рассчитывается с помощью правил математической комбинаторики. Если распределение атомов чисто
случайное, то Sконф равна энтропии идеальной
смеси, например для двухкомпонентной системы (любого агрегатного состояния):
|
S Ид. |
= −kN(x ln x + x |
2 |
ln x |
2 |
) |
. |
(22) |
|
конф |
1 |
1 |
Здесь kN – универсальная газовая постоянная (N – число Авогадро).
На рис. 37 изображена энтропия смешения
Рис. 37. Конфигурационная энтропия двухкомпонентного идеального (или регулярного)
идеального раствора
раствора. Она имеет положительные значения во всем ряду составов и достигает максимума (1,38 э. е.) при равенстве концентраций компонентов. Существенно, отметить, что при х1 → 0 и х2 → 0 ход кривой становится очень крутым и ее производная в этих областях максимальна. Это означает, что энтропия чистого вещества сильно возрастает при попадании в него следов примеси. Отсюда понятна принципиальная трудность получения сверхчистых веществ. По образному выражению Б. Ф. Ормонта, «природа боится чистоты». Напомним, что впервые еще В. И. Вернадский в статье «Парагенезис химических элементов в земной коре» (1910) выдвинул представление о «всюдности» распространения химических элементов, о «микрокосмическом» характере рассеяния: «В пылинке или капле, как в микрокосмосе, отражается общий состав космоса». В настоящее время этот феномен носит название «эффекта улавливания микропримеси». Помимо энтропийного фактора в случае
микроскопических концентраций примеси важную роль также играет и несовершенство реального кристалла: «собственные дефекты» кристалла тоже способствуют захвату микропримеси.
Из уравнения (20) следует, что энтропийный член –T∆Scм вносит в свободную энергию смешения ∆Gcм отрицательный вклад, который увеличивается с температурой. Поэтому энтропийный эффект всегда способствует смешению компонентов, т. е. увеличению степени беспорядка в системе. Кроме того, можно заключить, что взаимная смесимость должна увеличиваться с температурой, что, как известно, и имеет место в большинстве случаев. Итак, в идеальной системе нет сил, противодействующих
84
смешению. Однако в реальных ситуациях такие силы обычно возникают, и они связаны с различием химических и физических свойств компонентов смеси. Чем больше различия радиусов и электронных характеристик замещающих друг друга атомов, тем больше силы,
искажающие кристаллическую структуру твердого раствора по сравнению с чистым кристаллом. Эти деформации приводят к повышению внутренней энергии кристалла твердого раствора по сравнению с суммой энергий чистых компонентов (уменьшению ее абсолютной величины), что объясняет положительный знак ∆Hcм, соответствующий эндотермическому эффекту (поглощению тепла) при образовании смешанного кристалла.
На рис. 38 показано несколько вариантов соотношения отдельных функций
смешения и зависимости от состава двухкомпонентной системы в субсолидусной области (т. е. при повышенных температурах) и соответствующие им типы диаграмм состояния. Вариант а (∆Gcм<0 во всем интервале концентраций) соответствует непрерывным твердым растворам при повышенных температурах и области несмесимости (куполообразная незаштрихованная площадь на нижней части рисунка) при более низких температурах. Вариант б (∆Gcм имеет ω–образную форму с двумя перегибами) соответствует распаду твердых растворов при температуре эвтектики на две фазы, составы которых определяются положением минимумов кривой ∆Gcм. Вариант в (∆Gcм >0 во всем интервале составов) приводит к диаграмме состояния с простой эвтектикой без взаимной растворимости компонентов в твердом состоянии. Заметим, что ∆Hcм >0 во всех вариантах и возрастает от а к в. Следовательно, можно утверждать: чем больше ∆Hcм, тем меньше взаимная растворимость в твердом состоянии, т. е. тем уже пределы изоморфизма при одной и той же T. Поскольку при уменьшении величины ∆Hcм пределы смесимости расширяются, то при ∆Hcм<0 переходим к ситуации, когда на диаграмме состояния 1 типа (см. рис. 38, а) твердые растворы устойчивы до очень низких температур, т. е. купол распада практически исчезает.
85
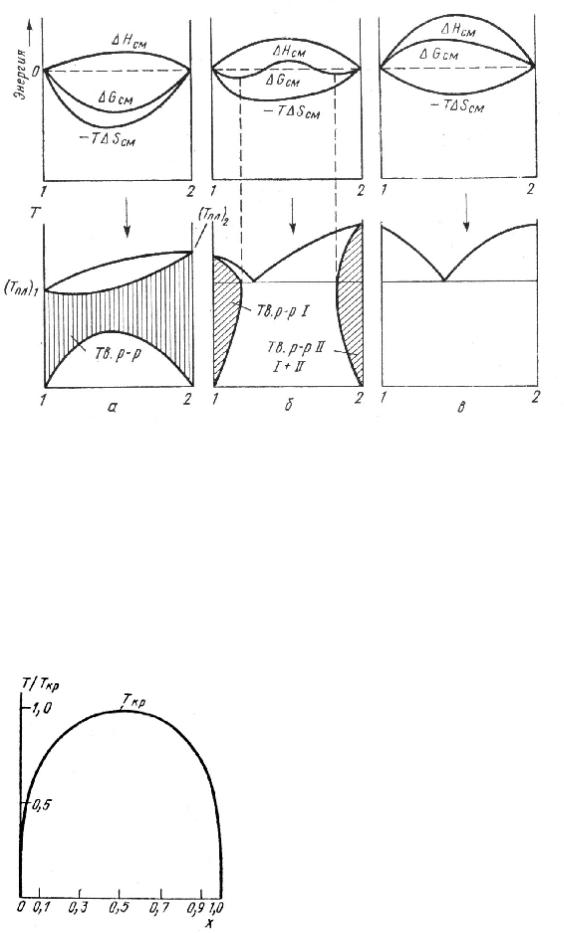
Рис. 38. Соотношение между термодинамическими функциями смешения и типами диаграмм состояния.
Таким образом, два фактора – энтропия смешения ∆Scм, понижающая свободную энергию на величину –T∆Scм и всегда способствующая смесимости, и энтальпия смешения ∆Hcм, в большинстве случаев повышающая свободную энергию и поэтому препятствующая взаимной растворимости компонентов смеси, вступают в конкуренцию между собой. Результат их «борьбы» выражается в той или иной, но вполне определенной области существования изоморфной смеси.
Как видно из рис. 38, энтальпия смешения является параболической функцией состава:
Hcм = x1x2Q ,
(23)
где Q – так называемый параметр взаимодействия.
Решение задачи о распаде твердых растворов в рамках теории регулярных растворов (∆Scм
=∆Sконфид. и Q = const) было дано еще в 1937 г. Р. Беккером. Полученная им кривая распада в
86
Рис. 39. Кривая распада регулярного
координатах Т/Ткр – х изображена на рис. 39. Под симметричным куполом находится область сосуществования двух твердых растворов, составы которых при данной Т определяются положением точек на кривой распада. Критическая температура Tкр связана c энергией смешения параметром взаимодействия Q простым соотношением:
втом случае, если Q выразить в калориях на моль.
8.6.Кристаллохимическая трактовка правил изоморфизма.
Первая попытка наметить связь между физико–химическим и кристаллохимическим пониманием изоморфизма принадлежит В. С. Соболеву (1948). Он отметил, что сопоставление результатов физико–химического и кристаллохимического исследования твердых растворов «в конечном счете должно привести к постановке задачи расчета и построения физико–химических диаграмм на основании простейших кристаллохимических свойств изучаемых веществ». В его работе была установлена приближенная корреляция между типом диаграммы состояния (положением областей распада твердых растворов по отношению к кривым плавкости – ликвидусу и солидусу) и относительным различием радиусов замещающих друг друга ионов. При r r1 <10-15%
r1 <10-15%
диаграммы состояния относятся к I типу, по Розебому (непрерывный ряд твердых растворов); простого эвтектического типа диаграммы состояния следует ожидать при
r r1 > 40%.
r1 > 40%.
Значительно позднее, начиная с середины 60-ых годов прошлого века, была детально разработана современная количественная теория изоморфизма, основанная на расчетах параметра взаимодействия Q. Оба основных условия изоморфизма – близость размеров составляющих кристалл структурных единиц (атомов, ионов, радикалов, молекул) и величин их поляризации (или характеров химической связи) – выражены в энергетическом уравнении:
|
Q = a(δ )2 + b( )2 , |
(25) |
где δ = r R ( r – разность ионных или атомных радиусов замещающих друг друга структурных единиц, R – среднее межатомное расстояние между катионом и анионом),
R ( r – разность ионных или атомных радиусов замещающих друг друга структурных единиц, R – среднее межатомное расстояние между катионом и анионом),
– разность степеней ионности связи в компонентах изоморфной смеси, а и b некоторые положительные параметры. Действительно, чем больше δ, или , или обе эти величины вместе, тем больше значение Q, а значит, выше критическая температура Ткр по уравнению (24) и тем меньше возможность широких или заметных пределов изоморфных
87
замещений. Таким образом, можно считать, что главные правила изоморфизма являются простым следствием тех причин, которые вызывают повышение энергии в результате геометрической (структурной) или электронной («химической») деформации твердого раствора при образовании его из чистых кристаллов. Структурная деформация происходит из–за различия размеров, а электронная – из–за различия в строении
электронных оболочек замещающих друг друга атомов и возникающего вследствие этого «возмущения».
Именно различием электронного строения атомов и разным характером образуемых ими химических связей нужно объяснить отсутствие или чрезвычайную ограниченность изоморфизма таких весьма близких по размерам, но отличающихся по
|
электроотрицательности пар, как К+ и Ag+ ( r =18%, χ =1,1), Са2+ и Cd2+ ( |
r =5%, Δχ |
|
|
=0,6), Са2+ и Hg2+ ( |
r =8%, Δχ =0,9), Mg2+ и Zn2+ ( r =12%, Δχ =0,4), несмотря на наличие |
|
|
широких или даже непрерывных изоморфных рядов соединений Na+ и К+ ( |
r =36%, Δχ |
|
|
=0,1), К+ и Rb+ ( r =12%, Δχ =0,0), Са2+ и Sr2+ ( r =16%, Δχ =0,1), Sr2+ и Ва2+ ( |
r =15%, Δχ |
|
|
=0,1), Zn2+ и Cd2+ ( |
r =19%, Δχ =0,1), с той же или большей разностью в размерах r , но с |
|
|
меньшей разностью |
χ . |
Еще один энергетический эффект появится, если смешиваются твердые вещества, обладающие разными кристаллическими структурами, т. е. в случае изодиморфизма. Этот эффект очень близко связан с энергией полиморфного превращения. Действительно, если, например, основной кристалл имеет структуру типа сфалерита ZnS с КЧ=4, а примесь вне твердого раствора кристаллизуется как пирротин в структуре NiAs с КЧ = 6, то процесс растворения можно представить в виде нескольких последовательных этапов: сначала нужно перевести кристалл примесного компонента в структуру типа ZnS, т. е. мысленно «заставить» его совершить полиморфный переход, затратив на это некоторую энергию, а лишь затем позволить ему заместить основной компонент в кристалле типа ZnS, на что потребуется дополнительное поглощение энергии, связанной с геометрическим и электронным видами деформации смешанного кристалла. Подобный ряд замещений дают такие двухвалентные примесные элементы в сфалерите ZnS, как Mn, FeII, Co, Ni, сульфиды которых имеют структуру либо типа NaCl (алабандин MnS), либо типа NiAs (пирротин FeS и джайпурит CoS), либо миллерита NiS с КЧ=5. Во всех случаях для вхождения в сфалерит необходимо структурное превращение «гостевого» компонента с уменьшением КЧ.
Теперь мы столкнулись уже с достаточном кругом примеров, когда 15%-ный критерий различия радиусов Гольдшмидта оказывался недействительным. И вообще
88
следует иметь в виду, что этот критерий не только не является достаточным, но подчас даже не является и необходимым. Это связано с тем, что согласно ему различие размеров
рассматривается как собственное внутреннее свойство данной пары элементов и полностью игнорируется влияние химического (кристаллического) окружения. Если воспринимать правило «15%» слишком буквально, то нужно было бы ожидать одной и той же способности к взаимным замещениям данной пары элементов А и В, в какой бы системе это ни происходило. Однако уже давно и разными исследователями были обнаружены факты влияния кристаллической среды на степень проявления изоморфизма. Так, разность ионных радиусов Mg2+ и Са2+ составляет почти 40%, что по критерию В. М. Гольдшмидта исключает широкую смесимость в их соединениях. Действительно, в системе MgO-CaO взаимная растворимость весьма ограничена: максимальная концентрация MgO в СаО составляет 10,8 мол. % при очень высокой температуре (2700 К), а СаО в MgO – только 3,1 мол.% при 2900 К. Область твердых растворов резко сужается с понижением температуры и ниже 1600° С становится совершенно незначительной. Однако в системе форстерит Mg2SiO4 – монтичеллит CaMgSiO4 существуют довольно широкие области твердых растворов (монтичеллит растворяет до 10 мол. % форстерита). Подобным образом широкие области смесимости экспериментально установлены в системе магнезит MgCO3 – кальцит CaCO3. Вообще, более сложные по составу соединения обладают большей изоморфной емкостью. Для иллюстрации этого положения приведем пример ограниченного изоморфизма Аl-FeIII в оксидах Аl2О3-Fe2O3 и непрерывного – в кальциевых гранатах Са3(Аl, Fe)2Si3O2.
Многочисленные подобные факты объясняются на основе уравнения (25)
|
следующим образом. Запишем различие размеров компонентов |
смеси в таком виде: |
|
δ = r / R = (r2 − r1 ) /(x1r1 + x2 r2 + r) . В этом выражении r – |
размер (радиус) той |
структурной единицы смеси, которая остается неизменной при замещении. Например, в системе MgO-CaO это ион кислорода O2-, а в системе MgCO3 – CaCO3 – ион CO32-. Радиус иона O2- равен 1,32 Å, а радиус иона CO32- – почти на 1 Å больше. Следовательно, значение δ для второй системы значительно меньше, чем для первой, значение параметра взаимодействия Q меньше, а пределы изоморфной смесимости шире (24).
Таким образом, современная энергетическая теория дает естественное и разумное объяснение этим наблюдениям. В общем виде это правило формулируется следующим образом: общая структурная единица изоморфной смеси не является нейтральной, увеличение ее размера расширяет смесимость (а увеличение заряда сужает). Это правило
можно назвать правилом содействия (ассистирования).
То же развернутое выражение для различия размеров δ позволяет найти объяснение
89
|
правилу полярности изоморфизма. Допустим, |
что r2 > r1 , Тогда при большем содержании |
|||
|
компонента с крупным ионом или атомом ( x2 |
→ 1, x1 → 0), знаменательв выражении для |
|||
|
δ относительно больше, а значение |
Q меньше, чем |
для большего |
содержаничя |
|
|
компонента с мелким ионом (атомом) |
( x2 → 0 , x1 → 1). |
Таким образом, |
мы получили |
объяснение того, почему ион (атом) меньшего размера легче замещает ион (атом) более крупного размера, чем наоборот.
Cовременная теория хорошо описывает эффект уменьшения изоморфной смесимости с понижением температуры (ферсмановская «автолизия» или «самоочистка» минералов в ходе посткристаллизационной термической истории), Вопрос о влиянии давления на изоморфизм разработан несколько хуже, хотя в последнее время эта проблема
привлекает к себе пристальное внимание в связи с усилением интереса к глубинным процессам в мантии Земли и синтезом новых материалов с помощью техники высоких давлений. Наиболее просто и естественно решается вопрос о влиянии давления на изодиморфизм. В соответствии с принципом Лешателье рост давления должен увеличить
поле устойчивости твердого раствора на основе компонента с более плотной атомной упаковкой. Если КЧ компонентов различны, то расширяется поле устойчивости на основе
твердого раствора с большими КЧ за счет уменьшения поля устойчивости твердого раствора с меньшими КЧ. Таким образом, изоморфная примесь как бы «вдавливается» в кристалл, если при этом ее КЧ повышается, и, наоборот, как бы «выдавливается» из него, если ее КЧ уменьшается.
Сложнее обстоит дело в том случае, если компоненты изоструктурны. В общем, давление ограничивает ее и приводит к распаду смесей. Этот эффект можно было ожидать заранее, так как сжатие кристалла твердого раствора вызывает рост сил межатомного
отталкивания и затрудняет возможности совместного вхождения атомов разных элементов в общую кристаллическую структуру. Теоретический анализ и экспериментальные факты позволяют сформулировать правило, которое можно назвать
правилом депрессии (подавления) изоморфизма (не изодиморфизма!) с ростом Р.
Однако подобные рассуждения остаются справедливыми только до тех пор, пока не принимаются во внимание возможные осложняющие эффекты, например, правильные (когерентные) срастания фаз распада, которые могут привести к противоречию с только что сформулированным правилом.
В настоящее время существует целый ряд полуэмпирических теорий изоморфизма,
способные достаточно точно предсказывать области смесимости и распада твердых растворов. Так, разрабатываемая на протяжении многих лет одним из авторов настоящего
90

пособия (см. Урусов В.С., 1977, 1997) феноменологическая теория твердых растворов
замещения достаточно точно указывает границы взаимной растворимости компонентов. В качестве примера на рис. 40 приведены хорошо согласующиеся между собой экспериментальные и теоретические кривые распада в системе рутил–касситерит. Более того, современный уровень развития математической кристаллохимии и бурно прогрессирующее компьютерное обеспечение энергетической кристаллохимии (см. Главу IX) позволяют в ряде случаев заменять физический эксперимент математическим, в том числе и в области изоморфизма. В качестве примера (рис. 41) приведем недавно проведенные расчеты изоморфных замещений в системе CaO-SrO. Видно, что расчетные данные хорошо воспроизводят экспериментальную информацию.
|
Рис. 40. Экспериментальные и теоретические |
Рис. 41. Экспериментальные (точки) и расчетные |
|
(пунктир) кривые распада в системе TiO2-SnO2. |
(Петрова Т.Г., 2004, программа GULP) кривые |
|
распада в системе CaO-SrO. |
Глава IX. СОВРЕМЕННЫЕ МЕТОДЫ КРИСТАЛЛОХИМИЧЕСКОГО ПРОГНОЗА
9.1. Предварительные замечания
Последние два десятилетия прошлого века ознаменовались гигантским прогрессом в области теоретического предвидения структуры и свойств кристаллических веществ. Несмотря на это, основная задача кристаллохимии – проблема предсказания вероятности
существования и устойчивости той или иной кристаллической структуры для заданного химического состава – все еще остается не до конца решенной. Современные методы и
приемы предсказания наиболее вероятной структуры для соединения с заданным химическим составом могут быть выстроены в иерархический ряд в соответствии со следующей схемой:
1. Топологический отбор, благодаря которому только относительно небольшое число сочетаний основных структурных элементов (координационных полиэдров) устойчиво повторяется в различных кристаллических структурах. В соответствии с пятым
91
правилом экономичности (парсимонии) Л.Полинга, число существенно различных структурных единиц в кристалле стремится быть минимальным.
2.Учет симметрийных и геометрических ограничений, среди которых наиболее
важную и не до конца еще понятую роль играет резкое предпочтение одних пространственных групп симметрии перед другими.
3.Использование принципа плотнейшей упаковки, фактора толерантности, диаграмм сортировки структурных типов и др. для построения пробной структуры.
4.Введение критериев вероятности реализации выбранной топологической схемы (пробной структуры) на основе принципов электронейтральности и наилучшего валентного и координационного соответствия (баланса). Построение матриц связанности
играфов связей, нахождение валентностей связи и идеальных (ненапряженных) длин связей. Сравнение различных моделей на основе минимума дисторсии связей и полиэдров
имаксимума энтропии.
5.Уточнение наиболее вероятной топологической конструкции с применением целого ряда эмпирических и полуэмпирических методов (метод напряженных связей, DLS, VLS, DVLS, см. ниже).
6.Поиск атомной конфигурации, отвечающей минимуму энергии сцепления кристалла. Компьютерное моделирование структуры и свойств (упругих, термодинамических и др.) с использованием атомистических потенциалов межатомного взаимодействия.
7.Квантово–механические расчеты «из первых принципов» (ab initio), воспроизводящие атомную структуру, энергию межатомного взаимодействия, распределение электронной плотности и основные свойства кристалла.
Впринципе, все перечисленные этапы теоретического выбора и определения структуры и свойств кристалла могут быть использованы последовательно, один за другим, ибо каждый следующий и более высокий уровень такого анализа существенно ограничивает рамки поиска.
9.2. Симметрийные и геометрические ограничения
Напомним, что главным законом вероятного строения кристаллической структуры
является непременное подчинение геометрического узора распределения атомов в кристаллическом пространстве одной из 230 пространственных групп симметрии. Однако не все пространственные группы имеют одинаковую распространенность. С одной стороны, при прочих равных условиях структуры с более высокой симметрией
92
образуются чаще. Из рис. 42 видно, что кристаллы триклинной сингонии среди большого числа неорганических соединений наименее распространенные, их более чем в 3 раза меньше, чем кубических. Относительный максимум приходится на ромбические и моноклинные кристаллы, а самой распространенной пространственной группой является
P21/c.
Рис 42. Распространенность 56000 неорганических соединений по сингониям (Урусов и Тереньтева, 2003). 1
– триклинная сингония; 2 – моноклинная, 3 – ромбическая, 4 – тригональная; 5 – тетрагональная; 6 – гексагональная, 7 – кубическая.
На рисунке 43 приведено распределение минералов по сингониям. Видно, что в этом случае резко преобладают кристаллические постройки низкой и средних категорий.
Рис 43. Распространенность 2900 минералов по сингониям. (Урусов и Тереньтева, 2003). 1 – триклинная сингония; 2 – моноклинная, 3 – ромбическая, 4 – тригональная; 5 – тетрагональная; 6 – гексагональная, 7 – кубическая.
93
Кристаллов с триклинной сингонией становится больше, чем тригональных и гексагональных, а моноклинная сингония выходит в «лидеры», опережая ромбическую по распространенности. Это связано с тем, что большая часть из минеральных видов встречается только в самой поверхностной оболочке Земли – Земной коре, образуясь в результате реакций выветривания и изменения глубинных пород под действием воды, атмосферы и солнечного света. Это приводит к сильному усложнению состава и ограниченному полю устойчивости таких минералов. Таким образом, нестабильные или
малоустойчивые кристаллические постройки отличаются относительно низкой симметрией.
9-3. Принципы плотнейшей упаковки. Конструирование пробных кристаллических структур заданного состава
Другой важный принцип, который ограничивает возможное многообразие кристаллических структур, заключается в стремлении атомов или молекул заполнить пространство не только наиболее симметрично, но и наиболее плотно. Поэтому такую
значительную роль в описании и топологическом конструировании кристаллических структур, особенно интерметаллических и ионных соединений, играет теория плотнейших упаковок. Согласно этой теории, имеются всего два типа плотнейшего расположения атомов (ионов) одинакового размера: кубическая и гексагональная плотнейшие упаковки.
Все многообразие кристаллических структур, которые подчиняются законам плотнейших упаковок, создается различными узорами заполнения другими атомами пустот между атомами плотнейших упаковок. Эти пустоты с различным числом ближайших соседей (шестью – октаэдрические, четырьмя – тетраэдрические, тремя – треугольные и др.) характеризуются разным размером (радиусом и объемом), причем увеличение числа ближайших соседей сопровождается ростом размера пустоты. Поэтому во многих, хотя и далеко не всех случаях можно предсказать, какой тип пустот будет заполняться тем или иным атомом, зная соотношение радиусов ионов разного сорта (первое правило Полинга, глава V). Например, для отношения радиусов ионов в интервале от 0,414 до 0,215 наиболее вероятным является попадание более мелкого иона в тетраэдрическую пустоту между более крупными. Если это отношение больше 0,414, то более вероятным становится заполнение октаэдрической пустоты, а если меньше 0,215, то треугольной и т.п. .
Второе правило Полинга (глава V) позволяет наиболее рационально распределить в структуре атомы разной валентности. Оно требует, чтобы в стабильной структуре соблюдался локальный баланс валентностей, то есть сумма валентных усилий (отношение
94
валентности атома к его координационному числу) всех ближайших соседей данного атома была бы равна или приблизительно равна его собственной валентности. Это
правило делает маловероятным заполнение позиций с большим отклонением от локального баланса (больше 10-20 %). В следующих разделах это правило будет рассматриваться особенно подробно.
Третье и четвертое правила Полинга (глава V) относятся к характеру сочленения между собой одинаковых или разных полиэдров. В частности, они указывают на то, что координационные полиэдры стремятся иметь минимальное количество общих элементов, то есть вершин, ребер и граней, принадлежащих одновременно двум или более соседним полиэдрам. Например, в структурах силикатов основными строительными кирпичиками являются тетраэдры SiO4, которые либо отделены друг от друга, либо соединяются с помощью общих вершин (мостиковых атомов кислорода), но никогда не имеют общих ребер и тем более граней. Это жесткое условие значительно ограничивает возможное число форм кремнекислородных радикалов, хотя и так их насчитывается более ста.
Пятое правило Полинга, так называемое правило экономичности, утверждает, что
число различных структурных элементов в одной кристаллической структуре стремится быть небольшим. Это позволяет пойти дальше и сконструировать устойчивые группировки координационных полиэдров, называемые вторичными структурными элементами, из которых можно построить большое семейство кристаллических структур.
В конечном счете можно выделить три группы методов начального конструирования вероятных кристаллических структур: первая из них, основанная на принципе плотнейших упаковок, сводится к методике построения пробной кристаллической структуры на основании заполнения пустот и вывода сверхструктур, либо путем табулирования известных структурных типов. Ко второй группе относятся методики, использующие заданную упаковку базисных атомов. Здесь можно выделить следующие приемы: 1) задание структуры с помощью заполняющих пространство полиэдров, либо 2) с использованием сеток атомов. Наконец, третья группа методов использует для кристаллического конструирования отдельные фрагменты структур: 1) из отдельных полиэдров; 2) c использованием атомных сеток; 3) c использованием вторичных структурных единиц.
9-4. Принципы полного и локального валентного и координационного баланса. Современный метод валентностей
связи (МВС)
На указанном этапе конструирования топологической схемы кристаллической
95
структуры задача решается путем последовательного перебора всех допустимых сочетаний валентностей V и координационных чисел (к.ч.) катионов А и анионов Х в формуле типа АnХm (под А подразумеваются все катионные, под Х – все анионные составляющие, включая атомы одного и того же химического элемента в неэквивалентных кристаллографических положениях – позициях Уайкоффа). В таком переборе обязательным является выполнение двух естественных условий:
а) электронейтральности кристалла (или его формульной единицы)
где слева стоит сумма валентностей всех катионов, а справа – сумма валентностей всех анионов;
б) баланса КЧ (числа связей)
где νij – число j–анионов в ближайшем окружении i–катиона (к.ч. i–катиона), νji – число i–
катионов в ближайшем окружении j–аниона (к.ч. j–аниона). Равенство (27) отвечает очевидному требованию, чтобы число связей от катионов к анионам точно равнялось числу связей от анионов к катионам при том непременном условии, что более электроположительные атомы (“катионы”) окружены только более электроотрицательными атомами (“анионами”). Однако совершенно не требуется, чтобы
соединение было полностью ионным по характеру химической связи или чтобы эффективные заряды катионов и анионов равнялись их формальным валентностям. Таким образом, условия (26) и (27) оказываются применимыми к громадному большинству неорганических соединений и минералов. Очевидными исключениями являются интерметаллические и поликатионные (полианионные) соединения.
Перебор всех значений валентностей и КЧ даже для заранее заданного и относительно простого стехиометрического типа, например, АВХ3, требует большой затраты времени без предварительной автоматизации этого процесса. Для решения
подобной задачи используются метод графов связей и метод построения матриц связанности. В современном варианте этот метод позволяет довести решение до предсказания длин связей в отдельных координационных полиэдрах (КП) и ввести
критерии отбора наиболее вероятных структур из большого числа принципиально разрешенных.
В своей первоначальной «полинговской» форме
96
условие локального баланса валентностей выполняется точно только для простых структур, обычно состоящих из правильных координационных полиэдров одного типа. Если в структуре имеются несколько разных типов координационных полиэдров, связанных между собой общими элементами (вершинами, ребрами или гранями), то
искажение таких полиэдров почти неизбежно и второе правило Полинга почти всегда нарушается. Однако можно потребовать, чтобы и в таких случаях второе правило выполнялось точно, если отказаться от первоначального определения валентного усилия как простого отношения валентности к координационному числу и допустить, что оно является некоторой функцией длины связи. На основе большого экспериментального материала установлено, что эффективное валентное усилие является экспоненциальной или обратно степенной функцией межатомного расстояния. Эмпирические значения
параметров в этих зависимостях для многих сочетаний пар атомов даются в соответствующих таблицах. Теперь можно поставить перед собой две задачи: прямую и обратную. Для известной структуры, можно определить значения валентных усилий, используя экспериментальные значения длин связи. Суммы этих значений для каждого из атомов должны быть практически точно равны их валентностям. В противном случае можно заподозрить, что структура определена не совсем правильно или же что исходные
допущения о валентности или даже химическом составе некоторых из позиций были неверны. Например, вместо иона кислорода О2- на том же месте могут оказаться практически неотличимые от него с помощью рентгеновских методов ионы ОН– или F– с вдвое меньшими значениями валентностей (зарядов). Такой прием позволяет также установить валентность тех атомов, которые в одной кристаллической структуре проявляют разные валентные состояния: это относится, например, к атомам меди в структурах купратных высокотемпературных сверхпроводников.
Для решения задачи предсказания деталей структуры с известной или гипотетической топологией на основе модифицированного второго правила нужно вначале определить эффективные значения валентных усилий (валентностей) всех связей, а затем вычислить по соответствующим формулам ожидаемые значения длин связей. Поскольку, как правило, различных связей в кристалле существенно больше, чем различных атомов, то для решения этой задачи недостаточно только уравнений баланса
валентностей и необходимо добавить к ним условия наименьшего отклонения эффективных валентностей связей от “средних” полинговских значений. Эти условия
приводят к появлению новых уравнений связи между валентностями индивидуальных связей и задача отыскания всех значений эффективных валентных усилий сводится к решению системы линейных уравнений. Доказано, что такая задача всегда имеет
97
единственное решение. На завершающем этапе топологическая схема строения кристалла дополняется предсказанием ожидаемых длин отдельных связей и размеров ячейки.
Описанная методика реализована в программном продукте BONDVAL, который
разработан на кафедре Кристаллографии и Кристаллохимии Геологического факультета МГУ (Урусов и Орлов) для использования на IBM-совместимых PC в среде Windows. Для
решения системы линейных уравнений используется метод последовательного исключения неизвестных (модифицированный метод Гаусса).
Ограничимся здесь в качестве примера только случаем, который предполагает для соединения типа АВХ3 следующий набор КЧ катионов: А[8] – атом А находится в восьмивершиннике АХ8, В[6] – атом В находится в окружении шести анионов ВХ6. Тогда координационный баланс (27) накладывает следующее условие на среднее КЧ Х: `ν(Х) = (8+6)/3 = 14/3.
Нецелочисленное значение`ν означает, что анионы должны занимать не одну, а две или несколько неэквивалентных позиций. Предположим, что возможны только два неэквивалентных по координации сорта анионов – Х1 и Х2 в соотношении 2:1. Если допустить также, что V(Х) равна типичному значению 2 (кислород, сера и их аналоги), то валентности катионов в согласии с условием электронейтральности (26) могут изменяться в интервале от 1 до 5.
Рассмотрим тот случай, когда валентности катионов в заданной ранее стехиометрической формуле составляют 2 для атомов А и 4 для атомов В, так что традиционная химическая формула может быть записана в виде А2+В4+Х12-2X22-, где знаки «плюс» и «минус» означают электроположительный и электроотрицательный характеры соответствующих частиц. Построение и решение матрицы связанности для предполагаемой модели сводится к следующей процедуре. Сначала определяются средние валентности связей `s , совпадающие с полинговскими валентными усилиями катионов:
`s (А) = VA/νA = 2/8 = 0/25, `s (B) = VB/νB = 4/6 = 0.67. Для того частного случая, когда КЧ анионов Х1 равно 4, а анионов Х2 равно 6, в табл. 14 перечислены все возможные
координационные окружения обоих анионов и отклонения валентностей аниона от суммы валентных усилий окружающих его катионов (отклонение от точного выполнения второго
|
правила Полинга): |
||
|
Vj = V’j – Vj |
= ` åνi=1 `si − Vj |
(29) |
|
В свою очередь, истинные значения валентностей анионов равны сумме |
||
|
валентностей всех |
его ненапряженных (идеальных) связей, согласно |
правилу сумм |
98
|
Модели Валентностей Связей (МВС): |
|
|
Vj = åνi=1 sij . |
(30) |
|
По условию электронейтральности кристалла (26) допустимы только такие |
|
|
сочетания ближайших окружений анионов, для которых åmj |
Vj = 0. Это обстоятельство |
резко ограничивает число возможных кристаллохимических формул и соответствующих матриц связанности.
|
Таблица 14. Возможные |
катионные окружения анионов X1 и X2 |
для структурной схемы |
|||||
|
A2+B4+X12[4]X2[6] и соответствующие отклонения |
V от правила Полинга. |
||||||
|
X1 |
V |
X2 |
V |
||||
|
4A |
-1.00 |
6A |
-0.50 |
||||
|
3A,B |
-0.58 |
5A,B |
-0,08 |
||||
|
2A,2B |
-0.16 |
4A,2B |
0.34 |
||||
|
A,3B |
0.25 |
3A,3B |
0.76 |
||||
|
4A |
0.68 |
2A,4B |
1.18 |
||||
|
A,5B |
1.60 |
||||||
|
6B |
2.00 |
||||||
Используя значения Vj из табл. 14, легко показать, что в рассматриваемом случае возможны лишь четыре варианта распределения связей, которые можно выразить в виде следующих матриц (цифры обозначают числа соответствующих связей, а sij – их валентности, которые выступают в роли неизвестных):
|
1) |
2Х1 |
Х2 |
2) |
2Х1 |
Х2 |
3) |
2Х1 |
Х2 |
4) |
2Х1 |
Х2 |
|
А2+ |
А2+ |
А2+ |
А2+ |
||||||||
|
6s11 |
2s12 |
4s11 |
4s12 |
2s11 |
6s12 |
8s11 |
0 |
||||
|
В4+ |
В4+ |
В4+ |
В4+ |
||||||||
|
2s21 |
4s22 |
4s21 |
2s22 |
6s21 |
0 |
0 |
6s22 |
Два последних случая 3) и 4) отбраковываются сразу, поскольку они не обеспечивают связи между структурными единицами АХ8 и ВХ6, то есть их сочлененность (linkedness), которая выражается как доля общих анионов (из полного их числа) для обоих полиэдров, равна нулю: L = 0. Для случая 4) это видно непосредственно из матрицы связанности. Для случая 3) из трех уравнений для сумм валентностей связей V = Σ sij
находим, что s11= 0, s12 = 0.33, s21 = 0.67 и, следовательно, значение L также оказывается равным нулю.
Для матриц 1) и 2), которые содержат по четыре неизвестных значения sij, решения
99
могут быть получены из трех независимых уравнений сумм валентностей связей и одного уравнения петли (замкнутого контура) связей:
|
s11– s21 + s22 – s21 = 0. |
(31) |
Заметим, что в уравнении (31) валентности связей рассматриваются как векторы, знак которых меняется на противоположный в зависимости от того, в каком направлении идет связь – от катиона к аниону или от аниона к катиону. В результате решения системы четырех линейных уравнений получаем следующие значения валентностей связей: 1) s11= 0.308, s12 = 0.077, s21 = 1.077, s22 = 0.461; 2) s11= 0.280, s12 = 0.220, s21 = 0.720, s22 = 0.560.
Сочлененность L = 1 для обоих последних случаев, поскольку все три аниона участвуют в образовании связей между обоими катионами. Однако, чтобы выбрать наиболее вероятное распределение связей из двух оставшихся вариантов, необходимо ввести некоторый критерий сравнения, в качестве которого может служить отклонение (дисторсия) связей от идеального варианта. Таким критерием является
среднеквадратичное отклонение рассчитанных валентностей связей от их средних (полинговских) значений (индекс дисторсии):
Здесь sij = sij – `s. Для случая 1) D = 0.22, а для случая 2) D = 0.05, то есть второй вариант
распределения чисел связей между катионами и анионами гораздо более предпочтительный, чем первый. Кроме того, для случая 2) распределение связей между обоими катионами А и В анионами Х1 и Х2 гораздо более равномерное (симметричное), чем в случае 1).
Обобщая сказанное выше, можно утверждать, что устойчивая кристаллическая структура должна подчиняться принципу минимальной диссиметризации, под которым
понимается минимальное отклонение реализуемой структуры от идеализированной (предельно симметричной) модели распределения связей во всех координационных полиэдрах.
9.5. Возможные методы уточнения пробной структуры кристалла.
После того, как геометрическая модель вероятного строения кристалла вчерне построена, неизбежно встает вопрос о ее уточнении. Здесь, в настоящее время, можно использовать метод постройки или подгонки длин отдельных связей друг к другу.
Такой подход достигается с помощью процедуры DLS – математической
100
оптимизации структуры и подгонки длин отдельных связей к некоторым стандартным длинам, например к тем же суммам радиусов атомов или ионов. В результате такой
подгонки оптимизированные длины отдельных связей и размеры элементарной ячейки обычно существенно отличаются от исходных и, как правило, приближаются к экспериментальным значениям. В программе DLS реализуется минимизация следующего функционала:
|
ρw = åωij2 [Dijo − Dij ]2 |
, |
(33) |
|
ij |
где Dij0 – стандартные значения межатомных расстояний (например, сумма ионных или атомных радиусов), а Dij – рассчитанные оптимальные расстояния связи между атомами i и j, ωij – весовой множитель для каждой i–j связи. Этот метод DLS подгонки структуры впервые был подробно описан в работе Майера и Виллинджера в 1969 году. В качестве
исходных данных необходимо иметь лишь очень приблизительную топологическую модель кристаллической структуры. Программа DLS, таким образом, может быть применена для:
1)определения гипотетических и предварительное уточнение пробных структур;
2)изучения геометрических конструкций в сложных кристаллических каркасах;
3)анализа и уточнения псевдосимметричных кристаллических структур.
Таблица 15. Результаты уточнения структуры магнезиально–силикатного перовскита MgSiO3
методом ДЛС (весовая схема: ω(Si-O) = 2.0, ω(Mg-O) = 1.5, ω(O-O) = 1.0).
|
Атом |
Координаты, теор. |
Координаты, эксп. |
|||||||
|
x |
y |
z |
x |
y |
z |
||||
|
Mg |
0.526 |
0.605 |
0.25 |
0.514 |
0.557 |
0.25 |
|||
|
Si |
0.5 |
0 |
0.5 |
0.5 |
0 |
0.5 |
|||
|
O1 |
0.093 |
0.502 |
0.25 |
0.102 |
0.465 |
0.25 |
|||
|
O2 |
0.184 |
0.189 |
0.547 |
0.195 |
0.208 |
0.555 |
|||
|
Связь |
R, теор., Å |
R, эксп., Å |
Связь |
R, теор., Å |
R, эксп., Å |
||||
|
Si-O1 |
(2)1.765 |
(2)1.784 |
Mg-O1 |
2.022 |
1.999 |
||||
|
Si-O2 |
(2)1.782 |
(2)1.767 |
Mg-O1 |
2.108 |
2.070 |
||||
|
Si-O2 |
(2)1.785 |
(2)1.784 |
Mg-O2 |
(2)2.139 |
(2)2.030 |
||||
|
Mg-O2 |
(2)2.196 |
(2)2.252 |
|||||||
|
Mg-O2 |
(2)2.295 |
(2)2.413 |
В качестве математической модели DLS используются 2 алгоритма – Ньютона– Рафсона и Гаусса–Ньютона. Стандартная версия программы параметризирована для 100 атомов (независимых и связанных симметрийными операциями), 200 расстояний и 150 переменных. Программа функционирует в DOS-режиме (операционная система Windows 95-98 –NT) и не требует существенных аппаратных ресурсов. В качестве примера такого
101
расчета в таблице 15 приведены результаты DLS-подгонки структуры магнезиального силикатного перовскита в сравнении с экспериментальными данными.
9-6. Компьютерное моделирование с использованием атомистических межатомных потенциалов взаимодействия
Даже самые усовершенствованные из геометрических методов конструирования кристаллических структур используют очень приближенные критерии устойчивости атомных конфигураций. Безусловно, и минимум функционала квадрата отклонений расстояний от стандартных (табличных) значений, и учет реального распределения валентности связей приближают модель к правильной структуре, но единственно верным
критерием нахождения устойчивого варианта кристаллической структуры является условие минимума структурной энергии кристаллического ансамбля. Все современные
методы компьютерного моделирования основаны на общем термодинамическом положении – среди всех возможных вариантов размещения атомов в кристаллической структуре любого химического соединения реализуется тот, который при заданных давлении и температуре отвечает минимуму его свободной энергии. Следовательно,
ведущий принцип при нахождении этого устойчивого варианта кристаллической структуры – минимизация его структурной энергии по отношению ко всем варьируемым величинам (параметрам решетки, координатам атомов, их зарядам и т.д.) и последующий расчет термодинамических и физических свойств, являющихся функциями энергии межатомного взаимодействия. Эта задача решается, в принципе, как квантово– химическими методами, исходящими из так называемых «первых принципов» (ab initio), так и с помощью полуэмпирических (атомистических) методов структурного моделирования.
Квантовая химия твердого тела пытается решить эту задачу путем поиска минимума энергии взаимодействия всех электронов и ядер в рассматриваемой системе. В отличие от них, полуэмпирические методы, ориентируясь на понятийный аппарат кристаллохимии, не требуют рассмотрения внутриатомных взаимодействий, что сразу существенно облегчает вычислительную задачу поиска минимума энергии системы. Поэтому они получили большое распространение в конце прошлого – начале нашего века.
Для кристаллов с различным типом химической связи структурная энергия может быть выражена через различные энергетические величины. Так, для чисто ионных соединений удобно использовать энергию решетки U, для ковалентных и металлических кристаллов – энергию атомизации E, а для молекулярных неорганических соединений – энергию
102
сублимации L.
Процедура минимизации энергии межатомного взаимодействия с успехом используется для моделирования структур и свойств широкого круга кристаллов, расчета дефектов, локализации позиции примесных ионов, предсказания фазовой стабильности, расчета габитусов кристаллов, релаксации кристаллической поверхности и решения ряда других задач кристаллохимии, химии и физики твердого тела.
В исследованиях по структурному моделированию неорганических кристаллов используется ряд программ, имеющих между собой ряд общих черт, а именно:
маделунговская составляющая энергии суммируется в обратном пространстве методом Эвальда, короткодействующие потенциалы суммируются в пределах той сферы, где они остаются существенными (обычно 15-20 Å), энергия сцепления выражается как сумма парных и многочастичных потенциалов. Поиск минимума энергии осуществляется варьированием атомных координат и параметров элементарной ячейки. Обычно в качестве алгоритма минимизации используют метод Ньютона–Рафсона.
Наиболее мощной программой для подобного рода вычислений является комплекс GULP (General Utility Lattice Program) Дж. Гэйла. Этот программный продукт позволяет проводить практически все возможные вычисления в данной области кристаллохимии. Основные возможности программы следующие:
–выбор алгоритма минимизации;
–использование подавляющего большинства различных потенциалов межатомного взаимодействия;
–подгонка параметров потенциала и зарядов атомов под различные экcпериментальные характеристики кристаллов;
–проведение моделирования при заданных P-T условиях;
–использование молекулярно–динамических расчетов;
–расчет фононных спектров кристаллов; ИК– и рамановских спектров.
–расчет упругих и диэлектрических свойств кристалла, градиентов электрических
полей;
–расчет дефектных областей кристалла;
–расчет парциальных зарядов атомов в кристалле по методу выравнивания орбитальных электроотрицательностей;
–расчет конечных непериодических молекул;
–расчет путей миграции атомов в кристалле.
Кроме того, в программе присутствует большое число опций, позволяющих контролировать сам процесс расчета, что делает ее достаточно гибкой, особенно для
103
моделирования сложных объектов. Все это ставит GULP на первое место среди таких программ. Отметим, что все программы подобного класса изначально ориентированы на большие ЭВМ, что связано с чрезвычайной трудоемкостью вычислений, особенно в случае большого числа атомов в элементарной ячейке. Однако, быстрый рост производительности персональных IBM-совместимых станций позволили адаптировать эти программы и для них, без критического ухудшения производительности.
В качестве примера таких расчетов приведем результаты моделирования по программе GULP стишовита – SiO2 со структурой типа рутила (КЧ (Si)=6), устойчивой при высоких давлениях. Для этого соединения проводилась серия расчетов при различных значениях зарядов атомов (степени ионности связи Si-O). Оказалось, что структура стишовита воспроизводима при степенях ионности приблизительно от 0.45 до 0.70. На рис. 44 для стишовита показаны зависимости от степени ионности связи Si-O энергии атомизации и объема элементарной ячейки (a), отношения c/a элементарной ячейки и координаты атома кислорода x (=y) (b), а также упругих свойств (с). Как видно из рисунка, предсказаная энергия сцепления при оптимальных зарядах атомов оказывается весьма близкой к эксперименту. Рассчитанные значения упругих констант также
достигают максимального согласия с экспериментальными значениями именно при оптимальных зарадах: +2,08 (Si) и -1,04 (O).
Большим достоинством парных потенциалов является их трансферабельность. Это значит, что определенный на конкретном соединении потенциал межатомного
взаимодействия для пары атомов может быть с успехом перенесен в родственные структуры, где эта пара атомов также контактирует друг с другом. Так, например, потенциал парного взаимодействия Сu-O был разработан при моделировании структуры ВТСП Ca2CuO3. Его структура построена на основе двух CuO4 квадратов, лежащих в одной плоскости и связанных между собой общей вершиной. Результаты моделирования этого соединения приведены в таблице 16. Полученный на этом соединении потенциальный набор позволил хорошо воспроизвести и все родственные структуры: CaCuO2, SrCuO3, (Sr1.19Ca0.73) Cu2O4 и BaCuO2. Это говорит об устойчивом характере взаимодействия в Cu-O4–квадрате вне зависимости от типа щелочноземельного катиона.
104

a)
E, eV
Eexp.=
-18.92
f
с/a*103 b)
c/a exp.=
-638
f
Cij, GPa c)
|
C33 |
||
|
C11 |
||
|
C66 |
||
|
C12 |
C13 |
|
|
C44 |
||
f
Vexp.=
46.6
V, Е3
Exp. x=0.306
x(O)*103
Exp. Cij
Kv K
Gv G
Рис. 44. Энергия атомизации и объем элементарной ячейки (a), отношение c/a элементарной ячейки и координата атома кислорода x (=y) (b), упругие свойства (с) стишовита как функция ионности f связи Si-O.
Таблица 16.Результаты моделирования Ca2CuO3.
105
|
Параметр |
Эксперимент |
Расчет |
Разность |
||
|
a , Å |
12,230 |
12.230 |
0.000 (0.00%) |
||
|
b , Å |
3,770 |
3.763 |
-0.007 (-0.19%) |
||
|
c , Å |
3,250 |
3.252 |
0.002 (0.07%) |
||
|
α=β=γ, Град. |
90 |
90 |
0 |
||
|
Объем эл. ячейки, Å3 |
149,848 |
149.681 |
-0.167 (-0.11%) |
||
|
Сa x, |
0,150 |
0.161 |
0.011 |
||
|
y |
0 |
0 |
0 |
||
|
z |
0,5 |
0.5 |
0 |
||
|
Cu x |
0 |
0 |
0 |
||
|
y |
0,5 |
0.5 |
0 |
||
|
z |
0 |
0 |
0 |
||
|
O1 x |
0,345 |
0.339 |
0.006 |
||
|
y |
0 |
0 |
0 |
||
|
z |
0,5 |
0.5 |
0 |
||
|
O2 x |
0 |
0 |
0 |
||
|
y |
0 |
0 |
0 |
||
|
z |
0 |
0 |
0 |
||
|
Межатомные расстояния, Å |
|||||
|
Связь |
Эксперимент |
Расчет |
|||
|
Ca-O |
2,385 x 1, |
2,186 x 1, |
|||
|
2,490 x 4, |
2,487 x 4, |
||||
|
2,451 x 2 |
2,551 x 2 |
||||
|
Cu-O |
1,885 x 2, |
1,882 x 2, |
|||
|
1,896 x 2 |
1,964 x 2 |
||||
|
O-O |
2,673 x 4 |
2,720 x 4 |
|||
|
Предсказанные свойств соединения |
|||||
|
Межатомная энергия U, эВ |
-109,878 |
||||
|
Упругие константы,1011 Дин/см2 |
С11=28,74, С33=21,16, С12=19,50,С13=3,64, С44=-0.34, С66=18,97 |
9-7. Расчеты ab initio (из первых принципов)
Квантовая химия твердого тела пытается решить задачу нахождения стабильной атомной конфигурации заданного состава поиском минимума энергии взаимодействия всех электронов и ядер в рассматриваемой системе. В основе современной квантовой химии лежит уравнение Шредингера. Хотя его и не трудно записать даже для молекулы из нескольких сотен атомов, однако, численное решение уравнения представляет собой крайне сложную задачу. Во–первых, даже в самом простом случае оно сводится к уравнению в частных производных, число переменных в котором равно утроенному числу электронов. В случае же твердого тела число переменных составляет n*1023 и, следовательно, без приближений здесь не обойтись.
Во–вторых, межатомные взаимодействия, ответственные за пространственное размещение атомов в элементарной ячейке на несколько порядков слабее внутриатомных.
Например, энергия связи кристалла алмаза составляет менее 1% от всей электронно– ядерной энергии. А ведь алмаз является рекордсменом прочности среди всех
кристаллических веществ и состоит из легких атомов с небольшим числом электронов и
106
относительно небольшой внутриатомной энергией, тогда как для других неорганических кристаллов доля энергии межатомной связи в полной электронно–ядерной энергии гораздо меньше. Из этого примера ясно, какой огромной точностью должны обладать квантово–механические расчеты кристаллической структуры, чтобы правильно предсказать ее энергию и те свойства, которые являются ее производными. Отметим, что к ним относятся практически все важнейшие свойства кристалла, которыми интересуются физики, химики, технологи и другие специалисты: тепловые, упругие, механические, диэлектрические свойства.
В последние годы все большее значение получают расчеты структуры и свойств кристаллов современными неэмпирическими квантово–механическими методами (из первых принципов). Среди них наибольшую распространенность имеют методы самосогласованного поля Хартри–Фока (HF) и теории функционала плотности (DFT) в различных вариантах.- от приближения локальной плотности (LDA) до более точных приближений обобщенных градиентов (GGA). На практике задача компьютерного
моделирования в квантовой химии сводится к построению поверхностей потенциальной энергии. Потенциальная поверхность – это графическое представление потенциала сил, действующих между ядрами (атомы, молекулы), как функции геометрических параметров, определяющих атомную конфигурацию. Очевидно, эти методы выходят за
рамки кристаллохимических подходов и используют предсказания и выводы этой науки только на предварительном этапе отбора наиболее вероятных структурных моделей. Из программных продуктов наиболее известны различные версии программы CRYSTAL, основанной на нерелятивистской теории Хартри–Фока для периодических структур, а также SIESTA и WIEN, реализующие теорию функционала плотности. Отметим, что все
они ориентированы на наиболее производительные и быстродействующие вычислительные комплексы.
Не вдаваясь в детальное описание сравнительных возможностей и вычислительной методологии методов ab initio, приведем для иллюстрации в табл. 17 результаты расчетов структуры и многих свойств ромбического MgSiO3, которые выполнены в простейшем варианте DFT LDA. Как легко убедиться, эти расчеты воспроизводят структуру и свойства хотя и несколько хуже метода атомных потенциалов, но уже в весьма неплохом согласии с экспериментом.
Таблица 17. Результаты моделирования структуры и свойств магнезиально–силикатного перовскита MgSiO3 с помощью методов полуклассических потенциалов (Atomistic Potentials) и «из первых принципов» (Ab initio) в сравнении с экспериментом.
107
|
Свойство |
Atomistic |
Ab initio |
Эксперимент |
|
|
potentials |
||||
|
V0 Å3 |
162.31 |
157.87 |
162.45 |
|
|
a0, Å |
4.7822 |
4.7272 |
4.7747 |
|
|
b0, Å |
4.8960 |
4.8889 |
4.9319 |
|
|
c0, Å |
6.9322 |
6.8311 |
6.8987 |
|
|
Mg x |
0.5056 |
0.5160 |
0.5143 |
|
|
y |
0.5267 |
0.5576 |
0.5556 |
|
|
z |
¼ |
¼ |
¼ |
|
|
Si (x; y; z) |
(0; ½; 0) |
(0; 1/2; 0) |
(0; 1/2; 0) |
|
|
O1 |
x |
0.1026 |
0.1044 |
0.1037 |
|
y |
0.4620 |
0.4654 |
0.4655 |
|
|
z |
¼ |
¼ |
¼ |
|
|
O2 |
x |
0.1982 |
0.1969 |
0.1974 |
|
y |
0.2014 |
0.2015 |
0.2011 |
|
|
z |
0.5526 |
0.5539 |
0.5538 |
|
|
C11, ГПа |
500 |
499 |
482 |
|
|
C22, ГПа |
509 |
561 |
537 |
|
|
C33, ГПа |
398 |
466 |
485 |
|
|
C12 , ГПа |
116 |
123 |
144 |
|
|
C13 , ГПа |
210 |
137 |
147 |
|
|
C23, ГПа |
188 |
142 |
146 |
|
|
C44 , ГПа |
174 |
217 |
204 |
|
|
C55 , ГПа |
189 |
186 |
186 |
|
|
C66 , ГПа |
102 |
160 |
147 |
|
|
K, ГПа |
270.4 |
258.3 |
264.0 |
|
|
G, ГПа |
146.3 |
187.3 |
178.4 |
|
|
CV, Дж/(моль.K) |
80.88 |
80.6 |
||
|
α, 10-5 К-1 |
2.09 |
1.57;2.2 |
||
|
CL, м/сек. |
– |
10953 |
11042 |
|
|
S, Дж/(моль.K) |
61.81 |
57.2 |
||
|
θD, K |
984 |
1097 |
1078 |
|
Если вспомнить с какой скоростью повышается быстродействие компьютеров (для наиболее массового IBM-совместимого модельного ряда компьютеров за 10 лет с 1982 по 1992 скорость счета выросла порядка на 3 (от XT до Pentium); c 1993 по 2003 появились Pentium-II, Pentium-III¸ Pentium-IV и производительности операций с плавающей точкой выросла опять на 3 порядка), можно утверждать, что прямые методы расчета ждет бурное развитие уже в самое ближайшее будущее.
Кроме того, привлечение методов молекулярной динамики дает возможность перейти к предсказанию поведения кристалла во всем поле его стабильности, т.е.
108
построить полное уравнение состояния и изучить условия стабильности кристаллической фазы.
109
Приложение 1. Предметный указатель
|
стр. |
|
|
автоморфотропия |
7 |
|
аномальный изоморфизм |
78 |
|
архетип |
37 |
|
биопириболы |
40 |
|
валентное усилие |
13 |
|
вторая глава кристаллохимии |
24 |
|
силикатов |
|
|
вторичный структурный элемент |
92 |
|
второе правило Полинга |
13 |
|
вырожденные структуры |
37 |
|
гетеровалентный изоморфизм |
75 |
|
дефектная структура |
36 |
|
диагональные ряды Ферсмана |
83 |
|
диаграмма Музера–Пирсона |
25 |
|
дисторсионный переход |
51 |
|
замещение с внедрением |
76 |
|
замещение с вычитанием |
76 |
|
заполненная структура |
36 |
|
звезды изоморфизма |
83 |
|
изовалентный изоморфизм |
75 |
|
изодиморфизм |
6 |
|
изоморфизм |
6 |
|
изоморфная смесь |
72 |
|
изоструктурность |
72 |
|
категории кристаллохимии |
6 |
|
критерий компактности Лиу |
62 |
|
критическая температура |
88 |
|
кубическая оболочка Земли |
65 |
|
модельные структуры |
25 |
|
моноклинная оболочка Земли |
65 |
|
морфотропия |
6 |
|
обозначения политипов Полинга |
69 |
|
основной закон кристаллохимии |
20 |
|
параметр взаимодействия |
87 |
|
первое правило Полинга |
11 |
|
переход Вервея |
57 |
|
полиморфизм |
6 |
|
полиморфные модификации |
48 |
|
полиморфный переход |
41 |
|
политипизм |
50 |
|
порядок ковалентной связи |
16 |
|
правила Магнуса – Гольдшмидта |
11 |
|
правило «ступенчатых |
49 |
|
переходов» Оствальда |
|
|
правило 15% разницы ионных |
80 |
|
радиусов |
|
правило 15% разницы атомных |
80 |
|
радиусов |
|
|
правило Вегарда |
79 |
|
правило взаимного влияния |
34 |
|
связей |
|
|
правило Гримма – Зоммерфельда |
26 |
|
правило депрессии |
91 |
|
правило кристаллохимической |
83 |
|
компенсации |
|
|
правило октета Юм–Розери |
26 |
|
правило Пирсона |
27 |
|
правило полярности |
81 |
|
правило Ретгерса |
74 |
|
правило содействия |
91 |
|
производные структуры |
37 |
|
прототип |
37 |
|
процедура DLS |
93 |
|
псевдосимметрия |
37 |
|
пятое правило Полинга |
20 |
|
пять правил Полинга |
10 |
|
расчет ab-initio |
97 |
|
реконструктивный переход |
51 |
|
ромбическая оболочка Земли |
65 |
|
сверхструктура |
37 |
|
символ Жданова |
69 |
|
символ Рамсделла |
68 |
|
смешанноблочность |
78 |
|
смешаннослойность |
78 |
|
смешанноцепность |
78 |
|
смешанный кристалл |
72 |
|
средний индекс упаковки |
62 |
|
степень «гексагональности» |
69 |
|
политипа |
|
|
структурная гомология |
7 |
|
твердый раствор замещения |
72 |
|
теория регулярных растворов |
88 |
|
тетраэдр кристаллохимии |
7 |
|
третье правило Полинга |
18 |
|
триклинная оболочка Земли |
65 |
|
фаза внедрения |
36 |
|
фаза вычитания |
36 |
|
фактор толерантности |
21 |
|
феноменологическая теория |
92 |
|
твердых растворов |
|
|
четвертое правило Полинга |
18 |
|
числовые законы Белова |
29 |
|
энергия анионной поляризации |
13 |
111
|
энтальпия смешения |
87 |
|
энтропия смешения |
85 |
|
эффект улавливания |
86 |
|
микропримеси |
|
|
Cтруктуры |
|
|
α-Fe |
51,53 |
|
γ-Fe |
51,53 |
|
β-Sn |
27,51,61 |
|
α-Sn |
51,61 |
|
(Sr1.19Ca0.73)Cu2O4 106 |
|
|
β-YF3 |
43 |
|
α-кварц |
12,25,33,51,53-55,60,61,63, |
|
β-кварц |
77 |
|
51,53-55,60,63 |
|
|
α-кристобалит |
51,53,54,59,60,63 |
|
β-кристобалит |
51,53,54,59,60,63 |
|
α-РbO2 |
56,63 |
|
α-тридимит |
51,53,54,59,60,63,70 |
|
β-тридимит |
51,53,54,59,60,63,70 |
|
AgBiS2 |
59 |
|
AlAsO4 |
61 |
|
AlP |
27 |
|
As |
63 |
|
Ba |
61 |
|
BaCl2 |
59 |
|
BaCuO2 |
106 |
|
BаО |
12 |
|
BаТiO3 |
22,64,59 |
|
Ca2CuO3 |
106,108 |
|
Ca2GeO4 |
25 |
|
Ca3(Аl, Fe)2Si3O2 |
90 |
|
Ca3Al2[SiO4]3 |
35 |
|
CaCuO2 |
106 |
|
CaMgSi2O6 |
35,72 |
|
CaО |
12,90-92 |
|
CaС2 |
28 |
|
CdBr2 |
70 |
|
CdCl2 |
13,26 |
|
CdI2 |
13,26,30,36,52,70 |
|
CdS |
61 |
|
CdTe |
27 |
|
Ce |
51,57 |
|
CeO2 |
42,46 |
|
Co3S4 |
25 |
|
CoO |
51,57 |
|
CoSb2 |
42 |
|
CrS |
37 |
|
CsF |
11 |
|
CsII |
58 |
|
CsIII |
58 |
|
CsNO3 |
22 |
|
CsСl |
11,26,52,59,61-63,65 |
|
Cu,Au |
51,55 |
|
Cu,Zn |
60 |
|
CuBr |
27 |
|
CuCl |
27 |
|
CuI |
27 |
|
CО2 |
12,36,63 |
|
Eu2O3 |
43 |
|
EuO |
51,58 |
|
Fe10S11 |
36 |
|
Fe9S10 |
36 |
|
FeCl3 |
13 |
|
FeNbO4 |
76 |
|
GaAs |
27,76,77 |
|
GaP |
27 |
|
GaSb |
27 |
|
Ge |
27,61 |
|
GeO2 |
12,25,59,63 |
|
GeS2 |
26 |
|
HgI2 |
50,52 |
|
HgSe |
60 |
|
In2Те3 |
28 |
|
InSb |
27,61 |
|
InSe |
30 |
|
IrSe2 |
42 |
|
K2Cd(CN)4 |
25 |
|
K2SO4 |
59,78,74 |
|
K2СО3 |
78 |
|
KF |
11 |
|
KIO3 |
24 |
|
KMgF3 |
76 |
|
KNbO3 |
76 |
|
KNiF3 |
21,24 |
|
KNO3 |
59 |
|
KВН4 |
78 |
|
LaAlO3 |
21,24 |
|
LaF3 |
59 |
|
Li2BeF4 |
35 |
|
LiBr |
11 |
|
LiI |
11 |
|
LiNO3 |
25 |
|
LiOH |
13 |
|
LiСl |
11,76,77 |
|
Mg2Cu |
63 |
|
Mg2GeO4 |
23 |
|
MgAl2O4 |
25 |
|
MgCl2 |
76,77 |
|
MgFe2O4 |
23 |
|
MnFe2O4 |
23 |
|
MnР |
37 |
|
Na2BeF4 |
25 |
112
|
Na3Al2[LiF4]3 |
35 |
Zn2TiO4 |
25 |
|
NaFeSi2O6 |
76 |
ZnIn2S4 |
28 |
|
NaLiBe2F6 |
35 |
ZnP2 |
27 |
|
NaTaO3 |
21 |
ZnSe |
27 |
|
NaWO3 |
36 |
ZnTe |
27 |
|
NbSe2 |
70 |
ZrO2 |
12,42,46,59,63 |
|
NH4NO3 |
51,56,59,60 |
акантит |
59 |
|
Ni2In |
35,36,63 |
алабандин |
19,32,90 |
|
Ni2Sn |
63 |
аллеганит |
38,39 |
|
NiP |
37 |
алмаз |
27,37,51,61,63 |
|
P |
61 |
альбит |
73,76 |
|
Pb4Sb4S11 |
43 |
анатаз |
18,48,51,59 |
|
Pb5Sb6S14 |
43 |
андалузит |
12 |
|
PbF2 |
59 |
анортит |
73,76 |
|
PbI2 |
70 |
апатит |
82 |
|
PtP2 |
30 |
арагонит |
9,22,48,59,82 |
|
PtS2 |
30 |
аргентит |
59 |
|
PtSe2 |
30 |
арсенолит |
43,44,45,53 |
|
PtTe2 |
30 |
арсенопирит |
42 |
|
RbCl |
11 |
ауростибит |
28 |
|
RbF |
11 |
бадделиит |
12,14,59,63,64 |
|
RbF |
61 |
барит |
82 |
|
RbI |
61 |
бафертисит |
40 |
|
RbNO3 |
22 |
берилл |
77 |
|
ReO3 |
36 |
биксбиит |
43,44,46 |
|
Sb2Se3 |
16 |
биотит |
40,72 |
|
Sc2O3 |
43 |
бисмит |
59 |
|
ScBO3 |
25 |
брукит |
18,51,59,98 |
|
ScN |
26 |
брусит |
13 |
|
Si |
27 |
буланжерит |
42,43 |
|
SiP2O7 |
33 |
валентинит |
53 |
|
Sm2O3 |
43 |
виллемит |
24 |
|
SmS |
51,58 |
витерит |
9,22 |
|
SmSe |
58 |
власовит |
40 |
|
Sn3Sb2S6 |
43 |
вольфрамит |
76 |
|
Sn4Sb6S13 |
43 |
вюртцит |
6,26,37,51,53,61,68 |
|
SnS |
37,42 |
галенит |
28,35,42,72,89 |
|
SnSb |
35 |
галит |
6,26,35,37,52,57,61,62, 63, |
|
SnSe |
37 |
65,72,75,79,80,82,89 |
|
|
SrCuO3 |
106 |
галлит |
77 |
|
SrО |
12,92 |
гауэрит |
51, 58 |
|
TaSe2 |
70 |
геверсит |
30 |
|
ThO2 |
12 |
гейкилит |
22 |
|
TiN |
35 |
гексастаннин |
37 |
|
Tl2О3 |
43 |
гематит |
51,58,59,90 |
|
TR2O3 |
46 |
гиббсит |
13 |
|
UO2 |
36,41 |
гипс |
82 |
|
WO3 |
36 |
глаукофан |
34 |
|
Y2O3 |
43 |
граутит |
39 |
|
YF3 |
43 |
графит |
51,61,70 |
|
YFe2FeO12 |
20 |
гринокит |
7 |
|
Zn2SiO4 |
35 |
грюнерит |
34 |
113
|
гумит |
38,39 |
монтепонит |
12 |
|
дадсонит |
43 |
монтичеллит |
90 |
|
данбурит |
18 |
мусковит |
40,71,76 |
|
делхаалит |
40 |
найнинджерит |
19 |
|
джайпурит |
19,90 |
накафит |
40,41 |
|
джемсонит |
42,43 |
никелин |
6,19,30,35,36,37,90 |
|
джерригиббсит |
38,39 |
норбергит |
38,39 |
|
джимтомсонти |
40 |
оксиды титана |
8 |
|
дигенит выc. |
59 |
оливин |
23,25,64 |
|
диккит |
71 |
ольдгамит |
6,19 |
|
диопсид |
40 |
орегонит |
30 |
|
жисмондин |
40 |
парафины |
51,56 |
|
иксиолит |
51,56 |
пентландит |
29 |
|
ильменит |
22 |
периклаз |
12,35,64,72,90,91 |
|
йодогардит |
27,59 |
перовскит |
14,21,22,24,36,51,57, 64 |
|
кальцит |
9,22,48,59,90,91 |
пирит |
28,30,42,48,53,59 |
|
канкринит |
78 |
пироп |
12 |
|
каолинит |
71 |
пирофанит |
22 |
|
карборунд |
67-70 |
пирофиллит |
71 |
|
карлстонит |
40 |
пирохлор |
15,43,44,45 |
|
касситерит |
77,92 |
пирротин |
8,19,30,32,36,90 |
|
катаплеит |
77 |
полифит |
41 |
|
квадруфит |
41 |
реальгар |
32 |
|
кианит |
12 |
риббеит |
38,39 |
|
киноварь |
6,59,60 |
рингвудит |
64 |
|
клиногумит |
38,39 |
робинсонит |
43 |
|
клинопирротин |
36 |
родохрозит |
9,22 |
|
клодетит |
53 |
рутил |
12,18,19,25,48,51,59, 61,63, |
|
кобальтин |
42 |
77,92 |
|
|
козалит |
42,43 |
санидин |
51,56 |
|
колумбит |
51,56 |
сейдозерит |
40,41 |
|
корунд |
18,71,90 |
сенармонтит |
43,44,45,53 |
|
котуннит |
26,63 |
серпентин |
71 |
|
ксенотим |
77 |
сидерит |
9 |
|
кубанит |
30,38 |
силленит |
59 |
|
куммингтонит |
34 |
силлиманит |
12,20 |
|
куприт |
12 |
сильвин |
61,72,75,78-80,82 |
|
лабрадор |
73 |
соналит |
38,39 |
|
лейкофёницит |
38,39 |
сперрилит |
30 |
|
леллингит |
42 |
спирты |
56 |
|
ломоносовит |
41 |
станнин |
37 |
|
лонсдейлит |
37 |
стишовит |
25,51,61,63,106,107 |
|
магнезит |
9,22,25,90,91 |
стронцианит |
9,22 |
|
магнетит |
51,56 |
сфалерит |
6,16,26,27,32,37,51,53,61, |
|
мангангумит |
38,39 |
63,68,77,78,89,90 |
|
|
марказит |
42,48,53,59 |
талнахит |
30 |
|
матильдит |
59,60 |
тальк |
40 |
|
метациннаборит |
6,59,60 |
тапиолит |
77 |
|
микроклин |
51,56 |
таусонит |
21,22 |
|
миллерит |
29,32,90 |
теннантит |
31 |
|
мойхукит |
30 |
тетраэдрит |
31 |
|
молибденит |
13,26,30,31,70 |
тефроит |
39 |
114
|
тисонит |
43 |
|
тисонит |
43,46 |
|
тортвейтит |
24 |
|
тремолит |
34,40 |
|
троилит |
6,36 |
|
ульманит |
42 |
|
уранинит |
8,36 |
|
фазы Лавеса |
8 |
|
фазы Магнели |
8 |
|
фенакит |
23 |
|
фергюссонит |
17 |
|
флогопит |
71 |
|
флюорит |
12,26,43,44,46,61-63 |
|
форстерит |
33,38,39,64,90 |
|
халькозин |
59 |
|
халькозин выc. |
59 |
|
халькопирит |
28,30,37,78 |
|
хизлевудит |
30 |
|
хондродит |
38,39 |
|
хризоберилл |
23 |
|
хэгбомит |
70 |
|
хэггит |
13 |
|
целестин |
82 |
|
цеолиты |
77 |
|
церуссит |
9 |
|
цинкит |
12,61 |
|
циркон |
77 |
|
цоизит |
14 |
|
честерит |
40 |
|
шпинель |
12,23,24,25,56,64,70 |
|
эканит |
40 |
|
энстатит |
33,103,110 |
115
Приложение 2. Контрольные вопросы по 2-ой части
1.Дайте определения основных категорий кристаллохимии.
2.Почему взаимосвязь между категориями удобно изображать в виде тетраэдра?
3.Какие наблюдения подвели П.Грота к введению понятия морфотропия
4.В чем был смысл введения понятия топических осей?
5.Cформулируйте принципов, которым должны подчиняться стабильные структуры существенно ионных кристаллов.
6.В чем геометрический смысл правил Магнуса–Гольдшмидта и 1-ого Правила Полинга?
7.Какой фундаментальный принцип отражает второе правило Полинга?
8.Каковы с точки зрения Полинга максимальные отклонения допустимы от суммы валентных усилий для существования устойчивой кристаллической постройки?
9.Возможно ли применять 2-ое правило Полинга для структур с существенной долей ковалентности связи?
10.Каким образом можно выделить первую координационную сферу центрального атома?
11.Во сколько раз вырастут силы отталкивания если тетраэдры соединить не по вершине, а по ребру (по грани)?
12.Во сколько раз вырастут силы отталкивания если октаэдры соединить не по вершине, а по ребру (по грани)? Каким образом кристалл компенсирует это увеличение сил отталкивания?
13.В чем геометрический смысл фактора толерантности?
14.В чем (с точки зрения фактора толерантности) причина неупорядоченного
вхождения различных катионов как в тетраэдрическую так и в октаэдрическую позицию структуры шпинели?
15.На чем основано деление кристаллохимии силикатов на 2 части «Брэгговскую» и «Беловскую»?
16.В чем практическая польза введения Гольдшмидтом понятия «модельных структур»?
17.В какие правила трансформируется Правило Юм–Розери для простых веществ в случае бинарных соединений? Соединений типа МkХl?
18.Приведите примеры поликатионных и полианионных кристаллических соединений. Каковы их структурные особенности?
19.Почему помимо числа 18 Белов ввел еще одно «магическое число 13(14)?
20.Как были объяснены кардинальные отличия структур FeS2 с одной стороны и MoS2 и CdI2, с другой стороны?
21.К каким структурным образованиям ведет избыток валентных электронов катионов? Приведите примеры.
22.В чем особенность кристаллохимии существенно ковалентных соединений с неполновалентными катионами? Приведите примеры.
23.До каких пор атом кремния устойчиво сохраняет в структуре тетраэдрическую координацию? В каком случае он меняет ее на октаэдрическую?
24.Поясните действие правила взаимного влияния связей на примере силикатов.
25.В чем выражается родственность структур CdI2-NiAs-Ni2In?
26.В чем выражается родственность структур WO3 и перовскита?
27.Каковы структурные причины существования гибридных построек – биопириболов?
28.Напишите последовательный ряд вырождеенных структур для станнина.
29.Напишите последовательный ряд производных структур для лонсдейлита.
30.Какие полиэдры могут возникнуть, если удалить 1 или 2 вершины у куба? Приведите примеры соединений с такими полиэдрами.
31.В чем отличие реконструктивных и дисторсионных переходов?
32.В чем отличие монотропных и энантиотропных переходов?
33.Возможно ли изменить первое координационное число без разрыва химических связей? Если возможно, то каким образом? Приведите примеры.
34.Что такое переход Вервея?
35.К каким типам полиморфных переходов относятся следующие структурные превращения: α-кварц – β-кварц – тридимит – кристобалит – стишовит?
36.Увеличивается или уменьшается симметрия при образовании сверхструктур?
37.Увеличивается или уменьшается симметрия при появлении эффектов вращения радикалов?
38.В чем причина резкого скачка объема элементарной ячейки Се под действием давления около 7 кбар?
39.В чем причина резкого скачка объема элементарной ячейки гематита под действием давления около 500 кбар?
40.В чем заключаются структурные причины повышения симметрии более высокотемпературных полиморфных модификаций?
41. Приведите примеры поижения симметрии более высокотемпературных полиморфных модификаций.
42. .Как влияет давление на структуры полиморфных модификаций?
43.Как объяснить увеличение под действием давления поля стабильности киновари HgS (координационые числа 2 и 2) относительно метациннабарита (координационые числа 4 и 4)?
44.Какие параметры являются более правильными, чем КЧ, характеристиками относительной плотности структуры?
45.В чем причины резкого преобладания среди минералов кристаллов низших и средних сингоний? Отличается ли симметрийная статистика минералов от статистики неорганических соединений?
46.Каковы принципиальные особенности потитипии, не позволяющие ее
классифицировать как полиморфизм
47.Опишите по Жданову 15 слойную модификацию карборунда АВСВАСАВАСВСАСВ. В чем основа его классификации?
48.Опишите по Жданову 21 слойную модификацию карборунда АВСАСВАСАВСВАСВССАВАСВ. В чем основа его классификации?
49.В чем отличия понятий «изоморфная смесь» и «твердый раствор замещения»?
50.В чем отличия понятий «изоморфизм», «изотипность» и «изоструктурность»?
51.Почему В. И. Вернадский назвал Леблана «великим неудачником»?
52.Какие тела Митчерлих считал изоморфными?
53.Опишите возможные схемы гетеровалентных замещений без изменения общего числа атомов в элементарной ячейке.
54.Опишите два основных вида гетеровалентных замещений с изменением числа атомов в ячейке. Насколько принципиально они отличаются друг от друга?
55.Укажите основные эипирические правила изоморфизма.
56.На что может указывать знакопеременный характер отклонения от правила Вегарда?
57.Кто должен легче входить в чужую кристаллическую структуру: Na+ в сильвин, или К+ в галит? Обоснуйте ответ.
58.Приведите примеры действия правила ассистирования, правила депрессии.
59.В чем заключается эффект влияния микропримеси?
60.Какие два фактора обеспечивают типы диаграмм состояния изоморфной смеси?
Приложение 3. Примерный список вопросов на экзамен
∙Основные вехи истории кристаллохимии. Кристаллохимия среди других наук о веществе. Основные задачи кристаллохимии.
∙Свойства атомов, важные для кристаллохимии: угловая форма орбиталей, орбитальные радиусы, потенциалы ионизации и сродство к электрону, орбитальные электроотрицательности, поляризуемость, кислотно–основные свойства.
∙Структурные особенности разных типов связи: ионной, ковалентной, металлической, ван–дер–ваальсовой
∙Переходные типы химической связи в кристаллах. Степень ионности химической связи и разность электроотрицательностей. Структуры кристаллов, переходные от ионных к ковалентным.
∙Строение электронных оболочек атомов (их протяженность, угловая ориентация). Орбитальные радиусы атомов и ионов. Лантаноидное сжатие.
∙Остаточная (вандерваальсова) связь. Вандерваальсовы радиусы. Молекулярные кристаллы.
∙Водородная связь. Строение кристаллогидратов. Структура льда. Структуры гидрооксидов и слоистых силикатов.
∙Понятие об электроотрицательности. Шкала электроотрицательности Полинга.
Связь электроотрицательности с потенциалом ионизации и сродством к электрону (формула Малликена). Степень ионности связи и разность электроотрицательностей.
∙Поляризуемость атомов и ионов. Ее связь с размерами атомов и ионов. Слоистые структуры как результат поляризации анионов. Структуры гидрооксидов.
∙Структуры гомодесмические и гетеродесмические. Структурные мотивы, примеры структур с разными мотивами.
∙Ионная связь. Энергия решетки ионных кристаллов. Формулы Борна, Капустинского, ЭКи и ВЭКи Ферсмана.
∙Энергия связи в кристаллах: энергия решетки, энергия атомизации. Потенциальная кривая химической связи.
∙Металлическая связь. Радиусы Металлических атомов. Основные структуры металлов.
∙Структуры, переходные между металлическими и ковалентными.
∙Координационные полиэдры и координационные числа. Связи между координационными числами разных атомов в структуре. Среднее координационное число.
∙Структурный тип. Изоструктурность, изотипность, структурный класс. Гомеотипия.
∙Распределение электронной плотности и «кристаллические» радиусы атомов. Сжатие аниона и расширение катиона в кристаллическом поле.
∙Эффективные заряды атомов в кристалле и методы их определения
∙Построение периодической системы элементов: принцип Паули, правило Гунда.
∙Потенциалы ионизации и сродство к электрону. Периодическая зависимость от порядкового номера Z. Химические свойства и классификация элементов: металлы, полуметаллы и неметаллы.
∙Диполь–дипольные взаимодействиия. Поляризация аниона в низкосимметричных позициях структуры (пример: O в структуре шпинели). Причина образования слоистых структур: структурные типы CdI2 и MoS2
∙Ионы переходных металлов в кристаллическом поле. Расщепление d–электронов в октаэдрическом окружениях. Энергия стабилизации в кристаллическом поле.
Радиусы ионов переходных металлов в высокоспиновом и низкоспиновом состояниях.
∙Кислотно–основные свойства атомов и ионов
∙Соотношение между атомными и ионными радиусами
∙Орбитальные радиусы и орбитальные электроотрицательности атомов и ионов.
∙Изоморфизм, определение, история открытия и изучения. Классификация.
∙Классические правила изоморфизма (Вегарда, полярности, диагональных рядов, эвезды изоморфизма).
∙Основы количественной теории изоморфизма. Принципы расчета областей распада изоморфных смесей.
∙Правила изоморфизма с точки зрения количественной теории: полярность (ассиметрия области распада), влияние общей структурной единицы и т.д.
∙Изоморфные ряды. Роль лантанидного сжатия в изоморфизме.
∙Внешние и внутренние факторы изоморфизма: роль различия свойств атомов (ионов), влияние температуры и давления на смесимость.
∙Основные физико–химические принципы теории изоморфизма: роль энтропии и энтальпии смешения.
∙Критическая температура распада и ее связь с энергией смешения.
∙Структурная классификация полиморфизма.
∙Полиморфизм: определение, история открытия и изучения, классификация
∙Политипизм. Отличие от полиморфизма. Основные способы обозначения. Примеры.
∙Изменение симметрии кристалла при изменении T и P. Координационные правила полиморфизма.
∙Основной закон кристаллохимии в формулировке Гольдшмидта и его современное понимание.
∙Структурная гомология. Производные и вырожденные структуры.
∙Локальный баланс валентностей (второе правило Полинга), примеры.
∙Морфотропия, ее закономерности и их кристаллохимические причины (отношение радиусов катиона и аниона, поляризуемость и т.п.
∙Элементы теории кристаллического поля. Предпочтение иона переходного металла к октаэдру или тетраэдру. Спиновое состояние.
∙Фактор толерантности и модельные структуры Гольдшимдта. Примеры.
∙Критерии устойчивости структурных типов ковалентных кристаллов: правила Юма–Розери, Гримма–Зоммерфельда, Пирсона, Белова.
∙Основные категории кристаллохимии и соотношения между ними. «Тетраэдр» кристаллохимии.
∙Эффективные радиусы ионов. Критерии вывода радиусов Ланде, Гольдшимдта, Полинга.
∙Зависимость ионного радиуса от заряда, координационного числа, спинового состояния.
∙Периодические зависимости ионных радиусов. Лантаноидное сжатие.
∙Атомные и ковалентные радиусы. Их периодические зависимости.
∙Ван–дер–ваальсовы радиусы.
∙Структурные единицы кристалла. Мотив структуры. Кристаллохимические формулы.
∙Критерии устойчивости структур ионных кристаллов.
∙Правила Магнуса–Гольдшимдта, Полинга.
∙Современный подход к конструированию возможных кристаллических структур заданного состава.
∙Возможные варианты уточнения пробных кристаллических структур.
∙Методы моделирования кристаллических структур, основанные на поиске минимума энергии межатомного взаимодействия.
∙Кристаллохимия сульфатов
∙Кристаллохимия боратов
∙Кристаллохимия карбонатов
∙Структура льда и кристаллогидратов (гипс)
∙Структура никелина NiAs и роль взаимодействий металл–металл в ее стабильности и свойствах.
∙Структуры каркасных силикатов (полиморфные модификации SiO2 и цеолиты).
∙Кристаллохимия полевых шпатов.
∙Кристаллохимия слоистых силикатов.
∙Кристаллохимия ленточных силикатов.
∙Кристаллохимия цепочечных силикатов.
∙Силикаты с островными кремнекислородными комплексами.
∙Структурные типы силикатов с изолированными тетраэдрами SiO4.
∙Структуры сульфосолей
∙Сульфиды неполновалентных элементов (реальгар, аурипигмент, антимонит).
∙Сульфиды с кластерными полиэдрическими группами.
∙Структуры дисульфидов (пирит, арсенопирит).
∙Тетраэдрические структуры сульфидов (сфалерит, вюртцит и их производные).
∙Структурные типы самородных металлов.
∙Структуры элементов YII, YI и Y групп Периодической системы.
∙Структурные типы элементов Y группы Периодической системы.
∙Структурные типы интерметаллидов.
∙Структурные типы галогенидов.
∙Структурные типы гидрооксидов и оксидов флюминия и железа (гиббсит–бемит– диаспор–корунд). Структура ильменита.
∙Каркасные и слоистые структуры минералов железо–марганцевых конкреций.
∙Структурные типы сложных оксидов (пирохлор, шпинель, перовскит).
ЛИТЕРАТУРА
Основная
∙Бокий Г. Б. Кристаллохимия. М., 1971.
∙Загальская Ю. Г., Литвинская Г. П. Геометрическая микрокристаллография. –
М., 1976.
∙Загальская Ю. Г., Литвинская Г. П., Егоров – Тисменко Ю. К. Руководство к практическим занятиям по кристаллохимии.- М., 1983.
∙Полинг Л. Общая химия. М., Мир. 1974.
∙Пущаровский Д.Ю. Структура и свойства кристаллов. М., 1982.
∙Пущаровский Д.Ю., Урусов В.С. Структурные типы минералов. М., 1990.
∙Современная кристаллография. Под ред. Вайнштейна Б. К, Т. 2. Структура кристаллов, М., 1979.
∙Урусов В.С. Теоретическая кристаллохимия. М., 1987.
Дополнительная
∙Белов Н. В. Очерки по структурной минералогии. – М., 1976.
∙Белов Н. В. Структура ионных кристаллов и металлических фаз. М., 1947.
∙Верма А., Кришна П. Полиморфизм и политипизм в кристаллах. М., 1969.
∙Земан И. Кристаллохимия. М., 1969.
∙Зоркий П М. Симметрия молекул и кристаллических структур. – М., 1986.
∙Зоркий П. М. Архитектура кристаллов. М., 1968. .
∙Китайгородский А. И. Смешанные кристаллы. М., 1983.
∙Макаров Е. С. Изоморфизм атомов в кристаллах. М., 1973.
∙Мейер К. Физико–химическая кристаллография. М., 1972.
∙Урусов В. С. Теория изоморфной смесимости. М., 1977.
∙Урусов В.С., Дубровинский Л.С. ЭВМ – моделирование структур и свойств кристаллов. М., 1989.
∙Урусов В.С., Дубровинский Л.С., Дубровинская Н.А. Конструирование вероятных кристаллических структур. М., 1990.
∙Урусов В.С., Таусон В.Л., Акимов В.В. Геохимия твердого тела. М. 1997.
Сжимаемость – кристалл
Cтраница 2
Величина п в уравнении ( I, 15) или ( I, 16) может быть вычислена на основании данных о сжимаемости кристалла.
[16]
Потенциал отталкивания возрастает тем более внезапно и быстро, чем меньше р, и поэтому г0 / р ( безразмерная величина) соответствует в известном смысле п в уравнении ( 6) и также может быть вычислена по данным о сжимаемости кристалла. Детали расчета читатель найдет в статье Борна и Майера.
[17]
В и п, известны, оно дает второе соотношение между этими ьеличинами. Сжимаемость кристаллов галогенидов щелочных металлов измерил Слэтер [41 ], экстраполировавший полученные им данные к абсолютному нулю.
[18]
Конденсированные системы – твердые тела н жидкости вдали от критической точки – характеризуются сжимаемостью в миллион раз меньшей, чем сжимаемость газов. Так, сжимаемость кристалла NaCl равна 0ЗХ Х10 – 12 см2 / дин, жидкой ртути – 3 8 – 1СН2 см2 / днн, тогда как сжимаемость воздуха при атмосферном давлении равна 10 – 6 см2 / днн.
[19]
Здесь опущены второстепенные члены, учитывающие поляризацию, ван-дер-ваальсово взаимодействие и нулевую энергию. Коэффициент р может быть найден из сжимаемости кристаллов.
[20]
Если бы мы могли найти еще одно соотношение между ними, то обе эти величины могли бы быть определены экспериментально. Это второе соотношение получается путем измерения сжимаемости кристалла.
[21]
С помощью соотношений Сягети – Оделевского и Дорзнц – До – ренца вычислена частота реаеточнюс колебаний кристаллов типа корунда, обладающих сложным фононнам спектром. Установлена юр-реляция мввду этой частотой и сжимаемостью кристалла.
[22]
Кривые 1, 2 и 3 получены Вильямсом [74, 75] из структуры и теп лот сублимации кристаллических углеводородов: кривая 1 – из свойств алифатических углеводородов, кривая 2 – из свойств ароматических углеводородов, кривая 3 – из свойств алифатических и ароматических углеводородов. Кривая 4 получена Китайгородским и Мирской [71, 103] из кристаллической структуры, сжимаемости кристаллов и теплоты сублимации ряда ароматических и алифатических соединений. Кривая 5 получена Крауэллом [40] из межплоскостного расстояния и сжимаемости решетки графита. Кривая 6 получена в работе [104] при использовании экспериментальных значений второго вириального коэффициента газообразного метана. Полученные Киселевым, Пошкусом и Афреймовичем [9, 10] кривые 7 и 8 близки к кривой 5, полученной Крауэлом из свойств решетки графита, и к кривой 4, полученной Китайгородским и Мирской из свойств кристаллических углеводородов.
[23]
Фуллерен в кристаллическом состоянии является полупроводником с шириной запрещенной зоны АЕ около 2 1 эВ и довольно узкими ( порядка 0 5 эВ) ширинами валентной зоны и зоны проводимости. Молекулы Сео связаны, в основном, ван-дер-ваальсовским взаимодействием, и сжимаемость кристаллов Сео очень велика. Можно ожидать, что ширины валентной зоны и зоны проводимости, экспоненциально зависящие от расстояния между молекулами, должны быстро увеличиваться с ростом давления. Ширина запрещенной зоны при этом должна уменьшаться, и при некотором давлении кристалл может перейти в металлическое состояние.
[25]
Келлерман [94] применил вышеизложенную теорию, где силы притяжения берутся в виде суммы кулоновских взаимодействий между точечными ионами с зарядами е, а силы отталкивания вида (7.3) действуют только между ближайшими ионами, при изучении кристалла хлористого натрия. В его расчеты входит только один параметр, выбираемый так, чтобы по нему можно было определить сжимаемость кристалла.
[26]
При этом ддя описания частоты решеточных колебаний используются как кванто-вомеханические [1-4], так и полуэмпирические [1,5-8] подходы. В частности, в работах [1,5-8] было показано, что с помощью простых моделей удается рассчитать частоту фоконного спектра щелочно-галоидных кристаллов, которая находится в хорошем согласии с экспериментом, и установить корреляцию между этой частотой и сжимаемостью кристалла.
[27]
Предметом исследований Борна в этих работах были ионные решетки, для которых по меньшей мере часть взаимодействия должна иметь очевидную электростатическую природу. Предполагалось, что постоянная решетки и коэффициент сжимаемости кристалла могут быть вычислены при некоторых простых допущениях о законе взаимодействия. Борн рассказывал о том, как он и Ланде, упорно пытавшиеся решить задачу суммирования кулоновских потенциалов, были поражены и восхищены тем ее решением, которое получил Маделунг. Однако после того, как эта в сущности математическая трудность была преодолена, главной проблемой, представляющей наибольший интерес, становилось построение модели для определения короткодействующих сил, обеспечивающих стабильность ионной решетки.
[28]
Аномально высокая сжимаемость кристалла политетрафторэтилена ( рис. VI. Например, можно ожидать, что несмотря на более высокую ( на 60 %) сжимаемость кристалла политетрафторэтилена по сравнению с кристаллом полиэтилена, вследствие различия эффективных масс осциллятора т, ( как показано в табл. III.
[29]
При этом если выбор значения т – 6 является в какой-то мере обоснованным ( если иметь в виду лондоновские диполь-дипольные дисперсионные силы), то значение п 12 взято совершенно произвольно. Было показано, что параметр р почти не меняется для большинства галогенидов щелочных металлов и составляет приближенно 0 35 А. Позднее Блейк и Майер [3] подтвердили преимущества использования экспоненциального закона перед степенным. Они вычислили по методу Гайтлера – Лондона отталкивание между двумя атомами с заполненными оболочками ( с восемью электронами) и установили, что во всем интервале межатомных расстояний от 1 8 А до 3 1 А экспоненциальная функция приводит к лучшему соответствию с экспериментом. Однако значение р, вычисленное этими авторами, оказалось несколько меньшим ( на 0 2 А), чем это следовало из экспериментов по сжимаемости кристаллов галогенидов щелочных металлов.
[30]
Страницы:
1
2
3
Предложите, как улучшить StudyLib
(Для жалоб на нарушения авторских прав, используйте
другую форму
)
Ваш е-мэйл
Заполните, если хотите получить ответ
Оцените наш проект
1
2
3
4
5
Рис.1.3.1.
Кристалл NaCl
Экспериментально определенная из опытов по
сжимаемости кристаллов величина n = 3,4 для NaCl. В качестве N обычно берут NA – число Авогадро и получают энергию связи на моль.
Константа Маделунга a учитывает то обстоятельство, что каждый ион
связан в решетке с окружающими ионами I и II
координационных сфер (рис.1.3.1). Иногда для уточнения рассматривают и другие
взаимодействия, однако на величине Uc они сказываются
мало. Константа Маделунга изменяется в пределах 1,6<a< 1,8 и вообще определяется кристаллической
структурой.
В табл. 1.3.3 приведены экспериментальные
значения энергии связи Uc и значения, вычисленные теоретически для 1 моля
решетки, а также некоторые другие сведения об ионных кристаллах.
Таблица 1.3.3
Некоторые сведения о
кристаллах с ионным типом связей
|
Вещество |
Параметр решетки |
Константа Маделунга |
Uc, Дж/моль |
Температура плавления, 0 С |
|
|
Теорет. значение |
Эксперим. значение |
||||
|
NaCl |
2,81 |
1,748 |
183,1 |
182,8 |
800 |
|
LiCl |
2,56 |
1,748 |
199,2 |
198,1 |
614 |
|
KCl |
3,14 |
1,748 |
165,4 |
164,4 |
770 |
|
KBr2 |
2,80 |
1,748 |
159,3 |
156,2 |
735 |
|
CsI |
2,28 |
1,763 |
139,1 |
145,3 |
621 |
|
AgCl |
2,78 |
1,748 |
203 |
205,7 |
455 |
|
CuCl |
2,71 |
1,638 |
216 |
221,9 |
430 |
|
BeO |
1,64 |
1,641 |
– |
4521; 4601 |
2520… 2570 |
|
CaF2 |
2,38 |
– |
– |
2613,3 |
1418 |
|
TiO2 |
– |
1,600 |
– |
12158,5 |
1870±15 |
|
CaO |
2,4 |
– |
– |
3572 |
2600 |
|
MgO |
2,10 |
– |
– |
3935,6 |
2800 |
В справочной литературе иногда в качестве
параметра решетки приводят величину r = a0, равную кратчайшему расстоянию между двумя идентичными
ионами одного знака.
Устойчивость межмолекулярных связей в некоторой
мере характеризует температура плавления вещества. У ионных кристаллов она
довольно высока (см. табл. 1.3.3), наивысшие температуры плавления у следующих
окислов, 0C: ZrO- 2900; HfO – 2780±30; ThO2 – 3050.
Следует отметить, что наблюдается неплохое
соответствие теоретических и экспериментальных значений, но только для
кристаллов галогенидов щелочных металлов.
Значительно хуже соответствие теоретических и
экспериментальных результатов для кристаллов с валентностью более 1. Причина
заключается в кулоновском характере сил притяжения. Сферическая симметрия электростатического
поля ионов приводит к отсутствию избирательности и стремлению каждого иона
окружить себя возможно большим числом соседей противоположного знака. Ионы
располагаются по принципу наиболее плотной упаковки. Координационное число К и
тип структуры зависят от радиусов взаимодействующих ионов. Так, вокруг очень
маленького иона натрия размещаются 6 ионов хлора большего радиуса (К=6) .
Чтобы было выполнено условие
электронейтральности, вокруг иона хлора располагаются также 6 ионов натрия (см.
рис. 1.3.1). В кристалле хлористого цезия оба иона сравнимы по величине и
поэтому ион цезия размещается в центре октаэдрической поры, в центре куба, в вершинах
которого размещены ионы хлора (рис. 1.3.2).
Рис. 1.3.2. Элементарная
ячейка решетки CsCl
Таким образом, в определении типа структуры большую
роль играют геометрические соотношения.
При взаимодействии двухвалентных ионов
сферическая симметрия электростатического поля ионов нарушается, и это резко
ухудшает применимость потенциалов Маделунга и Борна-Майера для расчета энергии
связи.
1.3.2. Ковалентная связь (гомеополярная)
Резкое разграничение ионной и ковалентной, а
также ковалентной и металлической связей неоправданно. Условность этого
разделения подчеркивается следующими фактами: энергия связи в этих кристаллах
близка и составляет порядка 10 эВ на атом, температуры плавления и кипения отличаются
мало (менее, чем в 10 раз); близки
во многих случаях механические свойства – твердость, пластичность, прочность.
Наконец, в основе микромеханизма их возникновения лежат отторжение и
обобществление электронов, имеющие в каждом конкретном случае лишь некоторые
особенности.
В ионной связи в результате взаимодействия возникает
ситуация, когда электрон, обеспечивающий связь, принадлежит одному (отрицательному)
иону более, чем другому. В случае ковалентной связи происходит спаривание
электронов у соседних атомов, образующих кристаллическую или аморфную
конденсированную структуру.
Классическими примерами кристаллов с ковалентной
связью служат элементы IV группы периодической таблицы: С, Si и Ge, а
также многие их соединения, в частности, широко распространенный в практике
керамического производства карбид кремния SiС.
Полностью или частично ковалентный характер имеют связи кремния во многих
силикатах. Ковалентная связь преобладает также в кристаллах типа АNB8-N, т.е. в кристаллах, образованных из элементов А и В, атомы которых
содержат N и (8 -N) валентных электронов
соответственно, так что на одну пару взаимодействующих атомов приходится восемь
s-p электронов валентных
орбиталей. Однако в этом случае межатомная связь включает в себя как
ковалентную, так и ионную составляющую.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание – внизу страницы.
