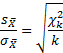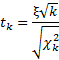t-критерий Стьюдента – общее название для класса методов статистической проверки гипотез (статистических критериев), основанных на распределении Стьюдента.
Таблица значений критерия Стьюдента в теории вероятностей и математической статистике используется довольно часто. На сайте можно посмотреть примеры ее использования в следующих задачах:
-
Доверительные интервалы для среднего и дисперсии
-
Проверка гипотезы о равенстве средних
Ниже размещена таблица критический точек t-критерия Стьюдента для односторонней и двусторонней критической области.
|
Число степеней свободы k |
Уровень значимости α (двусторонняя критическая область) | |||||
| 0,1 | 0,05 | 0,02 | 0,01 | 0,002 | 0,001 | |
| 1 | 6,31 | 12,70 | 31,82 | 63,70 | 318,30 | 637,00 |
| 2 | 2,92 | 4,30 | 6,97 | 9,92 | 22,33 | 31,60 |
| 3 | 2,35 | 3,18 | 4,54 | 5,84 | 10,22 | 12,90 |
| 4 | 2,13 | 2,78 | 3,75 | 4,60 | 7,17 | 8,61 |
| 5 | 2,01 | 2,57 | 3,37 | 4,03 | 5,89 | 6,86 |
| 6 | 1,94 | 2,45 | 3,14 | 3,71 | 5,21 | 5,96 |
| 7 | 1,89 | 2,36 | 3,00 | 3,50 | 4,79 | 5,40 |
| 8 | 1,86 | 2,31 | 2,90 | 3,36 | 4,50 | 5,04 |
| 9 | 1,83 | 2,26 | 2,82 | 3,25 | 4,30 | 4,78 |
| 10 | 1,81 | 2,23 | 2,76 | 3,17 | 4,14 | 4,59 |
| 11 | 1,80 | 2,20 | 2,72 | 3,11 | 4,03 | 4,44 |
| 12 | 1,78 | 2,18 | 2,68 | 3,05 | 3,93 | 4,32 |
| 13 | 1,77 | 2,16 | 2,65 | 3,01 | 3,85 | 4,22 |
| 14 | 1,76 | 2,14 | 2,62 | 2,98 | 3,79 | 4,14 |
| 15 | 1,75 | 2,13 | 2,60 | 2,95 | 3,73 | 4,07 |
| 16 | 1,75 | 2,12 | 2,58 | 2,92 | 3,69 | 4,01 |
| 17 | 1,74 | 2,11 | 2,57 | 2,90 | 3,65 | 3,95 |
| 18 | 1,73 | 2,10 | 2,55 | 2,88 | 3,61 | 3,92 |
| 19 | 1,73 | 2,09 | 2,54 | 2,86 | 3,58 | 3,88 |
| 20 | 1,73 | 2,09 | 2,53 | 2,85 | 3,55 | 3,85 |
| 21 | 1,72 | 2,08 | 2,52 | 2,83 | 3,53 | 3,82 |
| 22 | 1,72 | 2,07 | 2,51 | 2,82 | 3,51 | 3,79 |
| 23 | 1,71 | 2,07 | 2,50 | 2,81 | 3,59 | 3,77 |
| 24 | 1,71 | 2,06 | 2,49 | 2,80 | 3,47 | 3,74 |
| 25 | 1,71 | 2,06 | 2,49 | 2,79 | 3,45 | 3,72 |
| 26 | 1,71 | 2,06 | 2,48 | 2,78 | 3,44 | 3,71 |
| 27 | 1,71 | 2,05 | 2,47 | 2,77 | 3,42 | 3,69 |
| 28 | 1,70 | 2,05 | 2,46 | 2,76 | 3,40 | 3,66 |
| 29 | 1,70 | 2,05 | 2,46 | 2,76 | 3,40 | 3,66 |
| 30 | 1,70 | 2,04 | 2,46 | 2,75 | 3,39 | 3,65 |
| 40 | 1,68 | 2,02 | 2,42 | 2,70 | 3,31 | 3,55 |
| 60 | 1,67 | 2,00 | 2,39 | 2,66 | 3,23 | 3,46 |
| 120 | 1,66 | 1,98 | 2,36 | 2,62 | 3,17 | 3,37 |
| ∞ | 1,64 | 1,96 | 2,33 | 2,58 | 3,09 | 3,29 |
|
Число степеней свободы k |
0,05 | 0,025 | 0,01 | 0,005 | 0,001 | 0,0005 |
| Уровень значимости α (односторонняя критическая область) |
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Пример решения задачи
Задача
Имеется
три независимых реализации нормальной случайной величины: 0.8, 3.2, 2.0.
Построить
доверительный интервал для среднего.
Указание:
воспользоваться таблицами Стьюдента
Решение
Вычислим
среднее и
исправленную дисперсию:
Найдем
доверительный интервал для оценки неизвестного среднего.
Он считается по формуле:
По таблице распределения Стьюдента:
Искомый доверительный интервал для среднего:
Предположим, что надо сравнить между собой результаты выполнения тестов на внимание в двух группах. Чтобы узнать различаются ли группы между собой необходимо вычислить t-критерий Стьюдента для независимых выборок.
1. Внесем данные по группам в таблицу:
| № | Результаты группы №1 (сек.) | Результаты группы №2 (сек.) |
| 1 | 30 | 46 |
| 2 | 45 | 49 |
| 3 | 41 | 52 |
| 4 | 38 | 55 |
| 5 | 34 | 56 |
| 6 | 36 | 40 |
| 7 | 31 | 47 |
| 8 | 30 | 51 |
| 9 | 49 | 58 |
| 10 | 50 | 46 |
| 11 | 51 | 46 |
| 12 | 46 | 56 |
| 13 | 41 | 53 |
| 14 | 37 | 57 |
| 15 | 36 | 44 |
| 16 | 34 | 42 |
| 17 | 33 | 40 |
| 18 | 49 | 58 |
| 19 | 32 | 54 |
| 20 | 46 | 53 |
| 21 | 41 | 51 |
| 22 | 44 | 57 |
| 23 | 38 | 56 |
| 24 | 50 | 44 |
| 25 | 37 | 42 |
| 26 | 39 | 49 |
| 27 | 40 | 50 |
| 28 | 46 | 55 |
| 29 | 42 | 43 |
Шаг 2. Проверить распределения на нормальность.
Шаг 3. Рассчитать среднее арифметическое, стандартное отклонение и количество человек в каждой группе.
Шаг 4. Вычисляем эмпирическое значения по формуле t-критерия Стьюдента для независимых выборок
Шаг 5. Вычисляем степени свободы.
Шаг 6. Определяем по таблице критических значений t-Стьюдента уровень значимости.
Значение 6,09 больше чем значение 3,473 следовательно уровень значимости меньше 0,001
Шаг 7. Если уровень значимости меньше 0,05 делается вывод о наличи различий между группами. Таким образом между двумя группами есть различия в скорости выполнения тестов на внимание.
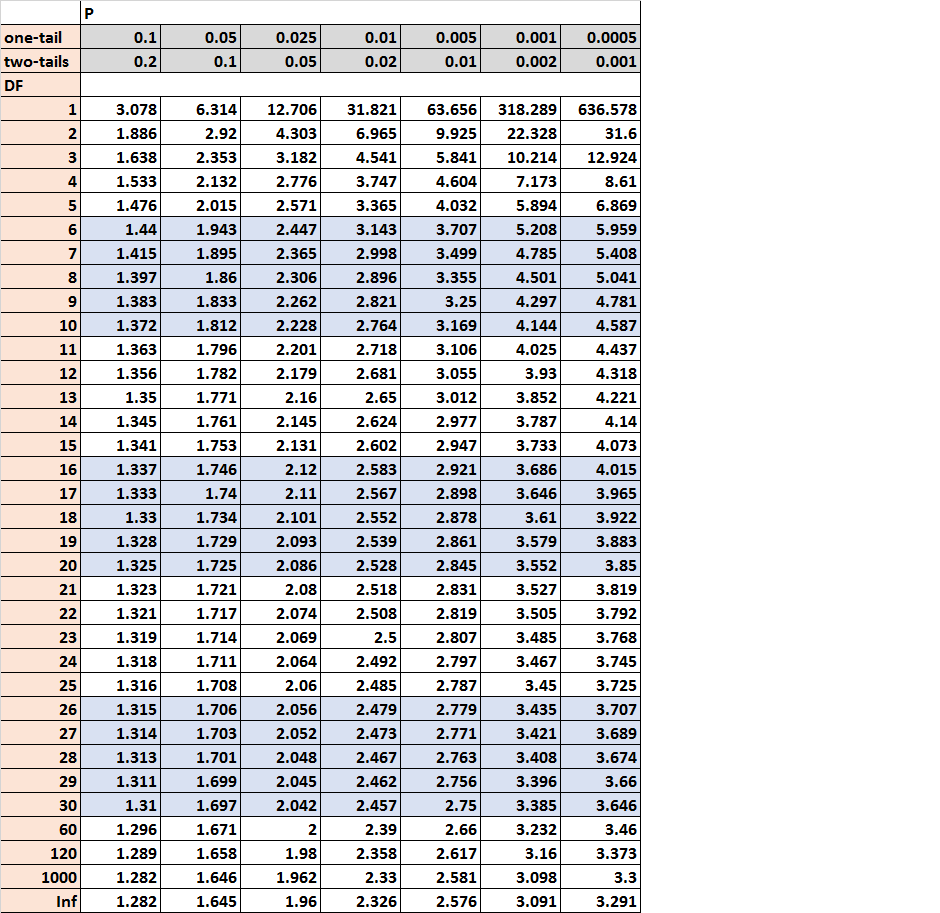
В этом руководстве объясняется, как читать и интерпретировать таблицу t-Distribution .
Что такое таблица t-распределения?
Таблица t-распределения — это таблица, которая показывает критические значения t-распределения. Чтобы использовать таблицу t-распределения, вам нужно знать только три значения:
- Степени свободы t-критерия
- Количество хвостов t-теста (односторонний или двусторонний)
- Альфа-уровень t-теста (обычно выбирают 0,01, 0,05 и 0,10).
Вот пример таблицы t-Distribution со степенями свободы, указанными в левой части таблицы, и альфа-уровнями, указанными в верхней части таблицы:
Когда вы проводите t-тест, вы можете сравнить статистику теста из t-теста с критическим значением из таблицы t-распределения. Если статистика теста больше критического значения, найденного в таблице, то вы можете отклонить нулевую гипотезу t-критерия и сделать вывод, что результаты теста статистически значимы.
Давайте рассмотрим несколько примеров использования таблицы t-Distribution.
Примеры использования таблицы t-распределения
В следующих примерах показано, как использовать таблицу t-Distribution в нескольких различных сценариях.
Пример № 1: Односторонний t-критерий для среднего
Исследователь набирает 20 субъектов для исследования и проводит односторонний t-критерий для среднего значения, используя альфа-уровень 0,05.
Вопрос: после того, как она проведет свой односторонний t-критерий и получит тестовую статистику t , с каким критическим значением она должна сравнить t ?
Ответ: Для t-критерия с одной выборкой степени свободы равны n-1 , что в данном случае 20-1 = 19. Задача также сообщает нам, что она проводит односторонний тест и использует альфа-уровень 0,05, поэтому соответствующее критическое значение в таблице t-распределения равно 1,729 .
Пример № 2: Двусторонний t-критерий для среднего
Исследователь набирает 18 субъектов для исследования и проводит двусторонний t-критерий для среднего значения, используя альфа-уровень 0,10.
Вопрос: После того, как она проведет свой двусторонний t-критерий и получит тестовую статистику t , с каким критическим значением она должна сравнить t ?
Ответ: Для t-критерия с одной выборкой степени свободы равны n-1 , что в данном случае 18-1 = 17. Задача также сообщает нам, что она проводит двусторонний тест и использует альфа-уровень 0,10, поэтому соответствующее критическое значение в таблице t-распределения равно 1,74 .
Пример №3: Определение критического значения
Исследователь проводит двусторонний t-критерий для среднего значения, используя размер выборки 14 и альфа-уровень 0,05.
Вопрос: Каким должно быть абсолютное значение ее тестовой статистики t , чтобы она отвергла нулевую гипотезу?
Ответ: Для t-критерия с одной выборкой степени свободы равны n-1 , что в данном случае 14-1 = 13. Задача также сообщает нам, что она проводит двусторонний тест и использует альфа-уровень 0,05, поэтому соответствующее критическое значение в таблице t-распределения равно 2,16.Это означает, что она может отклонить нулевую гипотезу, если тестовая статистика t меньше -2,16 или больше 2,16.
Пример №4: Сравнение критического значения с тестовой статистикой
Исследователь проводит правосторонний t-критерий для среднего значения, используя размер выборки 19 и альфа-уровень 0,10.
Вопрос: Тестовая статистика t оказывается равной 1,48. Может ли она отвергнуть нулевую гипотезу?
Ответ: Для t-критерия с одной выборкой степени свободы равны n-1 , что в данном случае 19-1 = 18. Задача также сообщает нам, что она проводит правосторонний тест (который является односторонним тестом) и что она использует альфа-уровень 0,10, поэтому соответствующее критическое значение в таблице t-распределения равно 1,33.Поскольку ее тестовая статистика t больше 1,33, она может отклонить нулевую гипотезу.
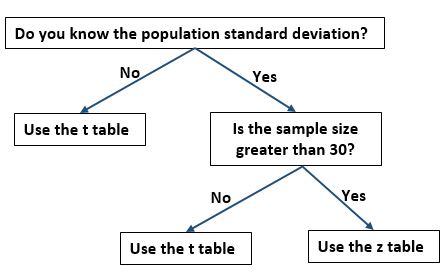
Должны ли вы использовать таблицу t или таблицу z?
Одной из проблем, с которой часто сталкиваются учащиеся, является определение того, следует ли им использовать таблицу t-распределения или таблицу z для нахождения критических значений для конкретной задачи. Если вы застряли на этом решении, вы можете использовать следующую блок-схему, чтобы определить, какую таблицу вам следует использовать:
Дополнительные ресурсы
Полный список таблиц критических значений, включая таблицу биномиального распределения, таблицу распределения хи-квадрат, z-таблицу и другие, см. на этой странице .
-
Определить
расчетное значение t-критерия
по формуле
где
f
– степень свободы, которая определяется
как
-
Определить
критическое значение t-критерия
с использованием таблицы 1 приложения,
при заданном уровне значимости и
степени свободы. -
Сравнить
расчетное и критическое значение t
– критерия. Если расчетное значение
больше или равно критическому, то
гипотеза равенства средних значений
в двух выборках изменений отвергается
(Но). Во всех других случаях она
принимается на заданном уровне
значимости.
Пример.
Две
группы студентов обучались по двум
различным методикам. В конце обучения
с ними был проведен тест по всему курсу.
Необходимо оценить, насколько существенны
различия в полученных знаниях. Результаты
тестирования представлены в таблице
4.
Таблица
4
|
25 |
18 |
9 |
13 |
8 |
20 |
25 |
18 |
6 |
12 |
|
19 |
13 |
12 |
12 |
18 |
9 |
7 |
10 |
18 |
20 |
Рассчитаем
выборочное среднее, дисперсию и
стандартное отклонение:
Определим
значение tp
по
формуле tp
= 0,45
По
таблице 1 (см. приложение) находим
критическое значение tk
для уровня значимости р = 0,01
tk
= 2,88
Вывод:
так как расчетное значение критерия
меньше критического 0,45<2,88 гипотеза
Но подтверждается и существенных
различий в методиках обучения нет на
уровне значимости 0,01.
Алгоритм расчета t-критерия Стьюдента для зависимых выборок измерений
1.
Определить расчетное значение t-критерия
по формуле
,
где
2.
Рассчитать степень свободы f
3.
Определить критическое значение
t-критерия
по таблице 1 приложения.
4.
Сравнить расчетное и критическое
значение t-критерия.
Если расчетное значение больше или
равно критическому, то гипотеза равенства
средних значений в двух выборках
изменений отвергается (Но). Во всех
других случаях она принимается на
заданном уровне значимости.
U–критерий
Манна–Уитни
Назначение
критерия
Критерий
предназначен для оценки различий между
двумя
непараметрическими
выборками по уровню
какого-либо
признака, количественно измеренного.
Он позволяет выявлять различия между
малыми
выборками,
когда n
< 30.
Описание критерия
Этот
метод определяет, достаточно ли мала
зона пересекающихся значений между
двумя рядами. Чем меньше эта область,
тем более вероятно, что различия
достоверны. Эмпирическое значение
критерия U
отражает то, насколько велика зона
совпадения между рядами. Поэтому чем
меньше U,
тем
более вероятно,
что различия достоверны.
Гипотезы
НО:
Уровень признака в группе 2 не ниже
уровня признака в
группе
1.
HI:
Уровень признака в группе 2 ниже уровня
признака в группе 1.
Алгоритм расчета критерия Манна-Уитни (u)
-
Перенести
все данные испытуемых на индивидуальные
карточки. -
Пометить
карточки испытуемых выборки 1 одним
цветом, скажем красным, а все карточки
из выборки 2 – другим, например, синим.
-
Разложить
все карточки в единый ряд по степени
нарастания признака, не считаясь с
тем, к какой выборке они относятся, как
если бы мы работали с одной большой
выборкой.
-
Проранжировать
значения на карточках, приписывая
меньшему значению меньший ранг. -
Вновь
разложить карточки на две группы,
ориентируясь на цветные обозначения:
красные карточки в один ряд, синие –
в другой. -
Подсчитать
сумму рангов отдельно на красных
карточках (выборка 1) и на синих карточках
(выборка 2). Проверить, совпадает ли
общая сумма рангов с расчетной. -
Определить
большую из двух ранговых сумм. -
Определить
значение U
по формуле:
где
n1
– количество
испытуемых в выборке 1;
n2
– количество
испытуемых в выборке 2,
Тх
– большая из двух рантовых сумм;
nх
– количество испытуемых в группе с
большей суммой рангов.
9.
Определить критические значения U
по таблице 2 (см. приложение).
Если
Uэмп.>
Uкр0,05,
то гипотеза Но
принимается.
Если Uэмп.≤
Uкр,
то отвергается. Чем меньше значения U,
тем достоверность различий выше.
Пример.
Сравнить
эффективность двух методов обучения
в двух группах. Результаты испытаний
представлены в таблице 5.
Таблица 5
|
18 |
10 |
7 |
15 |
14 |
11 |
13 |
||||
|
15 |
20 |
10 |
8 |
16 |
10 |
19 |
7 |
15 |
14 |
29 |
Перенесем
все данные в другую таблицу, выделив
данные второй группы подчеркиванием
и сделаем ранжирование общей выборки
(см. алгоритм ранжирования в методических
указаниях к заданию 3).
|
Значения |
7 |
7 |
8 |
10 |
10 |
10 |
11 |
13 |
14 |
14 |
15 |
15 |
15 |
16 |
18 |
19 |
20 |
29 |
|
Ранги |
1,5 |
1,5 |
3 |
5 |
5 |
5 |
7 |
8 |
9,5 |
9,5 |
12 |
12 |
12 |
14 |
15 |
16 |
17 |
18 |
|
Номер |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
Найдем
сумму рангов двух выборок и выберем
большую из них: Тх
= 113
Рассчитаем
эмпирическое значение критерия по
формуле 2: Up
= 30.
Определим
по таблице 2 приложения критическое
значение критерия при уровне значимости
р = 0.05 : Uk
= 19.
Вывод:
так
как расчетное значение критерия U
больше критического при уровне значимости
р = 0.05 и 30 > 19, то гипотеза о равенстве
средних принимается и различия в
методиках обучения несущественны.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Проверка статистической гипотезы позволяет сделать строгий вывод о характеристиках генеральной совокупности на основе выборочных данных. Гипотезы бывают разные. Одна из них – это гипотеза о средней (математическом ожидании). Суть ее в том, чтобы на основе только имеющейся выборки сделать корректное заключение о том, где может или не может находится генеральная средняя (точную правду мы никогда не узнаем, но можем сузить круг поиска).
Распределение Стьюдента
Общий подход в проверке гипотез описан здесь, поэтому сразу к делу. Предположим для начала, что выборка извлечена из нормальной совокупности случайных величин X с генеральной средней μ и дисперсией σ2. Средняя арифметическая из этой выборки, очевидно, сама является случайной величиной. Если извлечь много таких выборок и посчитать по ним средние, то они также будут иметь нормальное распределение с математическим ожиданием μ и дисперсией
Тогда случайная величина
имеет стандартное нормальное распределение со всеми вытекающими отсюда последствиями. Например, с вероятностью 95% ее значение не выйдет за пределы ±1,96.
Однако такой подход будет корректным, если известна генеральная дисперсия. В реальности, как правило, она не известна. Вместо нее берут оценку – несмещенную выборочную дисперсию:
где
Возникает вопрос: будет ли генеральная средняя c вероятностью 95% находиться в пределах ±1,96sx̅. Другими словами, являются ли распределения случайных величин
и
эквивалентными.
Впервые этот вопрос был поставлен (и решен) одним химиком, который трудился на пивной фабрике Гиннесса в г. Дублин (Ирландия). Химика звали Уильям Сили Госсет и он брал пробы пива для проведения химического анализа. В какой-то момент, видимо, Уильяма стали терзать смутные сомнения на счет распределения средних. Оно получалось немного более размазанным, чем должно быть у нормального распределения.
Собрав математическое обоснование и рассчитав значения функции обнаруженного им распределения, химик из Дублина Уильям Госсет написал заметку, которая была опубликована в мартовском выпуске 1908 года журнала «Биометрика» (главред – Карл Пирсон). Гиннесс строго-настрого запретил выдавать секреты пивоварения, и Госсет подписался псевдонимом Стьюдент.
Несмотря на то что, К. Пирсон уже изобрел распределение Хи-квадрат, все-таки всеобщее представление о нормальности еще доминировало. Никто не собирался думать, что распределение выборочных оценок может быть не нормальным. Поэтому статья У. Госсета осталась практически не замеченной и забытой. И только Рональд Фишер по достоинству оценил открытие Госсета. Фишер использовал новое распределение в своих работах и дал ему название t-распределение Стьюдента. Критерий для проверки гипотез, соответственно, стал t-критерием Стьюдента. Так произошла «революция» в статистике, которая шагнула в эру анализа выборочных данных. Это был краткий экскурс в историю.
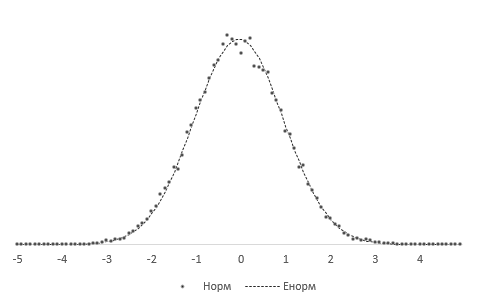
Посмотрим, что же мог увидеть У. Госсет. Сгенерируем 20 тысяч нормальных выборок из 6-ти наблюдений со средней (X̅) 50 и среднеквадратичным отклонением (σ) 10. Затем нормируем выборочные средние, используя генеральную дисперсию:
Получившиеся 20 тысяч средних сгруппируем в интервалы длинной 0,1 и подсчитаем частоты. Изобразим на диаграмме фактическое (Norm) и теоретическое (ENorm) распределение частот выборочных средних.
Точки (наблюдаемые частоты) практически совпадают с линией (теоретическими частотами). Оно и понятно, ведь данные взяты из одной и то же генеральной совокупности, а отличия – это лишь ошибки выборки.
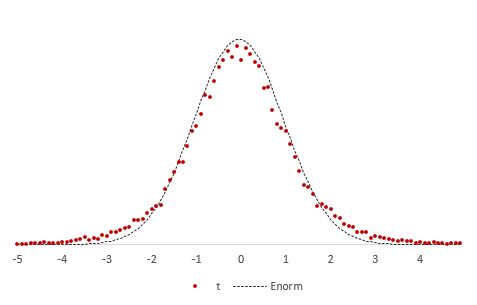
Проведем новый эксперимент. Нормируем средние, используя выборочную дисперсию.
Снова подсчитаем частоты и нанесем их на диаграмму в виде точек, оставив для сравнения линию стандартного нормального распределения. Обозначим эмпирическое частоты средних, скажем, через букву t.
Видно, что распределения на этот раз не очень-то и совпадают. Близки, да, но не одинаковы. Хвосты стали более «тяжелыми».
У Госсета-Стьюдента не было последней версии MS Excel, но именно этот эффект он и заметил. Почему так получается? Объяснение заключается в том, что случайная величина
зависит не только от ошибки выборки (числителя), но и от стандартной ошибки средней (знаменателя), которая также является случайной величиной.
Давайте немного разберемся, какое распределение должно быть у такой случайной величины. Вначале придется кое-что вспомнить (или узнать) из математической статистики. Есть такая теорема Фишера, которая гласит, что в выборке из нормального распределения:
1. средняя X̅ и выборочная дисперсия s2 являются независимыми величинами;
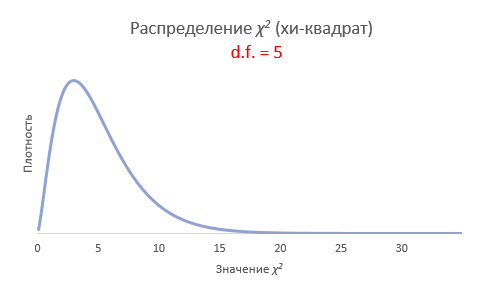
2. соотношение выборочной и генеральной дисперсии, умноженное на количество степеней свободы, имеет распределение χ2(хи-квадрат) с таким же количеством степеней свободы, т.е.
где k – количество степеней свободы (на английском degrees of freedom (d.f.))
Вернемся к распределению средней. Разделим числитель и знаменатель выражения
на σX̅. Получим
Числитель – это стандартная нормальная случайная величина (обозначим ξ (кси)). Знаменатель выразим из теоремы Фишера.
Тогда исходное выражение примет вид
Это и есть t-критерий Стьюдента в общем виде (стьюдентово отношение). Вывести функцию его распределения можно уже непосредственно, т.к. распределения обеих случайных величин в данном выражении известны. Оставим это удовольствие математикам.
Функция t-распределения Стьюдента имеет довольно сложную для понимания формулу, поэтому не имеет смысла ее разбирать. Вероятности и квантили t-критерия приведены в специальных таблицах распределения Стьюдента и забиты в функции разных ПО вроде Excel.
Итак, вооружившись новыми знаниями, вы сможете понять официальное определение распределения Стьюдента.
Случайной величиной, подчиняющейся распределению Стьюдента с k степенями свободы, называется отношение независимых случайных величин
где ξ распределена по стандартному нормальному закону, а χ2k подчиняется распределению χ2 c k степенями свободы.
Таким образом, формула критерия Стьюдента для средней арифметической
есть частный случай стьюдентова отношения
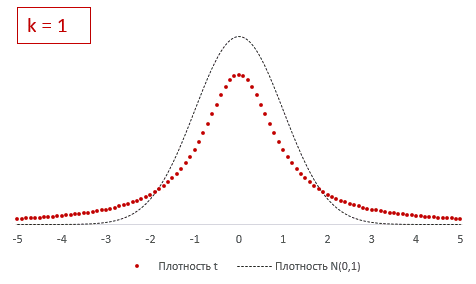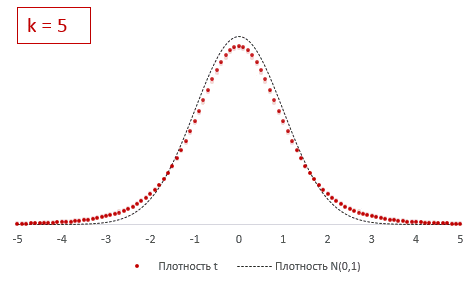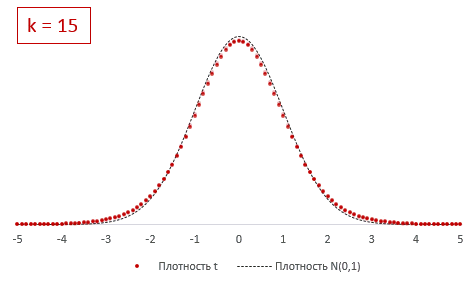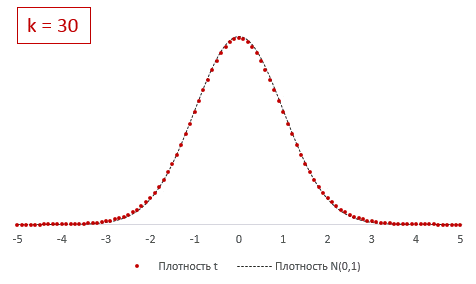
Из формулы и определения следует, что распределение т-критерия Стьюдента зависит лишь от количества степеней свободы.
При k > 30 t-критерий практически не отличается от стандартного нормального распределения.
В отличие от хи-квадрат, t-критерий может быть одно- и двусторонним. Обычно пользуются двусторонним, предполагая, что отклонение может происходить в обе стороны от средней. Но если условие задачи допускает отклонение только в одну сторону, то разумно применять односторонний критерий. От этого немного увеличивается мощность критерия.
Несмотря на то, что открытие Стьюдента в свое время совершило переворот в статистике, t-критерий все же довольно сильно ограничен в возможностях применения, т.к. сам по себе происходит из предположения о нормальном распределении исходных данных. Если данные не являются нормальными (что обычно и бывает), то и t-критерий уже не будет иметь распределения Стьюдента. Однако в силу действия центральной предельной теоремы средняя даже у ненормальных данных быстро приобретает колоколообразную форму распределения.
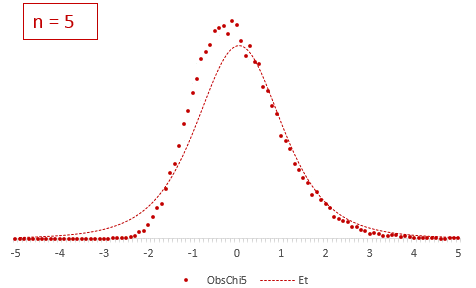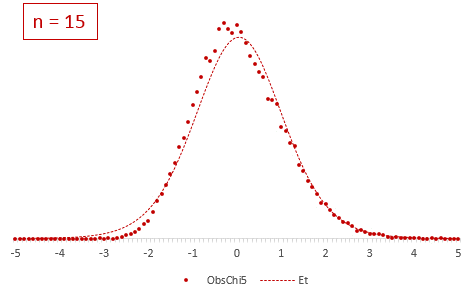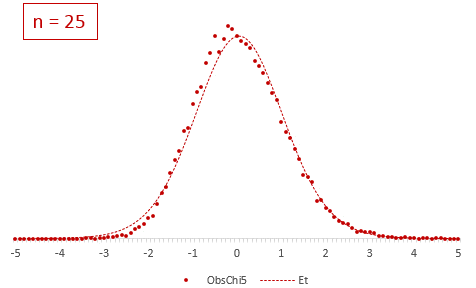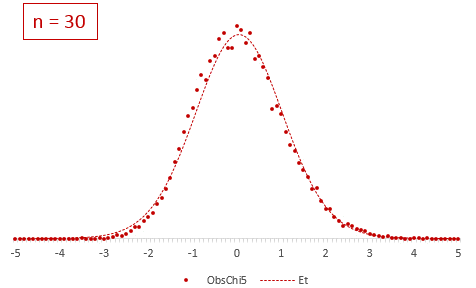
Рассмотрим, для примера, данные, имеющие выраженный скос вправо, как у распределения хи-квадрат с 5-ю степенями свободы.
Теперь создадим 20 тысяч выборок и будет наблюдать, как меняется распределение средних в зависимости от их объема.
Отличие довольно заметно в малых выборках до 15-20-ти наблюдений. Но дальше оно стремительно исчезает. Таким образом, ненормальность распределения – это, конечно, нехорошо, но некритично.
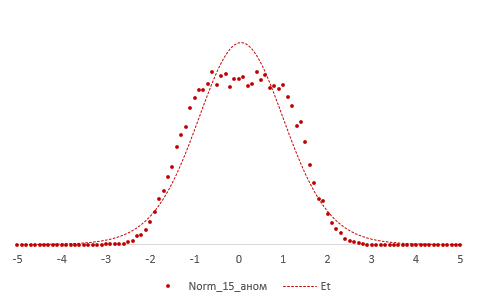
Больше всего t-критерий «боится» выбросов, т.е. аномальных отклонений. Возьмем 20 тыс. нормальных выборок по 15 наблюдений и в часть из них добавим по одному случайном выбросу.
Картина получается нерадостная. Фактические частоты средних сильно отличаются от теоретических. Использование t-распределения в такой ситуации становится весьма рискованной затеей.
Итак, в не очень малых выборках (от 15-ти наблюдений) t-критерий относительно устойчив к ненормальному распределению исходных данных. А вот выбросы в данных сильно искажают распределение t-критерия, что, в свою очередь, может привести к ошибкам статистического вывода, поэтому от аномальных наблюдений следует избавиться. Часто из выборки удаляют все значения, выходящие за пределы ±2 стандартных отклонения от средней.
Пример проверки гипотезы о математическом ожидании с помощью t- критерия Стьюдента в MS Excel
В Excel есть несколько функций, связанных с t-распределением. Рассмотрим их.
СТЬЮДЕНТ.РАСП – «классическое» левостороннее t-распределение Стьюдента. На вход подается значение t-критерия, количество степеней свободы и опция (0 или 1), определяющая, что нужно рассчитать: плотность или значение функции. На выходе получаем, соответственно, плотность или вероятность того, что случайная величина окажется меньше указанного в аргументе t-критерия, т.е. левосторонний p-value.
СТЬЮДЕНТ.РАСП.2Х – двухсторонне распределение. В качестве аргумента подается абсолютное значение (по модулю) t-критерия и количество степеней свободы. На выходе получаем вероятность получить такое или еще больше значение t-критерия (по модулю), т.е. фактический уровень значимости (p-value).
СТЬЮДЕНТ.РАСП.ПХ – правостороннее t-распределение. Так, 1-СТЬЮДЕНТ.РАСП(2;5;1) = СТЬЮДЕНТ.РАСП.ПХ(2;5) = 0,05097. Если t-критерий положительный, то полученная вероятность – это p-value.
СТЬЮДЕНТ.ОБР – используется для расчета левостороннего обратного значения t-распределения. В качестве аргумента подается вероятность и количество степеней свободы. На выходе получаем соответствующее этой вероятности значение t-критерия. Отсчет вероятности идет слева. Поэтому для левого хвоста нужен сам уровень значимости α, а для правого 1 — α.
СТЬЮДЕНТ.ОБР.2Х – обратное значение для двухстороннего распределения Стьюдента, т.е. значение t-критерия (по модулю). Также на вход подается уровень значимости α. Только на этот раз отсчет ведется с двух сторон одновременно, поэтому вероятность распределяется на два хвоста. Так, СТЬЮДЕНТ.ОБР(1-0,025;5) = СТЬЮДЕНТ.ОБР.2Х(0,05;5) = 2,57058
СТЬЮДЕНТ.ТЕСТ – функция для проверки гипотезы о равенстве математических ожиданий в двух выборках. Заменяет кучу расчетов, т.к. достаточно указать лишь два диапазона с данными и еще пару параметров. На выходе получим p-value.
ДОВЕРИТ.СТЬЮДЕНТ – расчет доверительного интервала средней с учетом t-распределения.
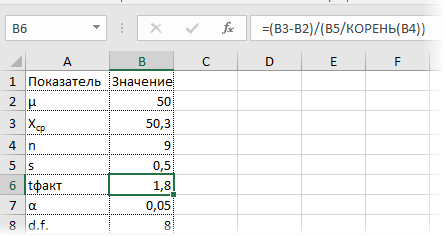
Рассмотрим такой учебный пример. На предприятии фасуют цемент в мешки по 50кг. В силу случайности в отдельно взятом мешке допускается некоторое отклонение от ожидаемой массы, но генеральная средняя должна оставаться 50кг. В отделе контроля качества случайным образом взвесили 9 мешков и получили следующие результаты: средняя масса (X̅) составила 50,3кг, среднеквадратичное отклонение (s) – 0,5кг.
Согласуется ли полученный результат с нулевой гипотезой о том, что генеральная средняя равна 50кг? Другими словами, можно ли получить такой результат по чистой случайности, если оборудование работает исправно и выдает среднее наполнение 50 кг? Если гипотеза не будет отклонена, то полученное различие вписывается в диапазон случайных колебаний, если же гипотеза будет отклонена, то, скорее всего, в настройках аппарата, заполняющего мешки, произошел сбой. Требуется его проверка и настройка.
Краткое условие в обще принятых обозначениях выглядит так.
H0: μ = 50 кг
Ha: μ ≠ 50 кг
Есть основания предположить, что распределение заполняемости мешков подчиняются нормальному распределению (или не сильно от него отличается). Значит, для проверки гипотезы о математическом ожидании можно использовать t-критерий Стьюдента. Случайные отклонения могут происходить в любую сторону, значит нужен двусторонний t-критерий.
Вначале применим допотопные средства: ручной расчет t-критерия и сравнение его с критическим табличным значением. Расчетный t-критерий:
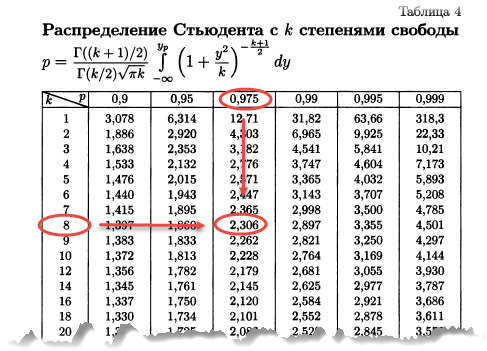
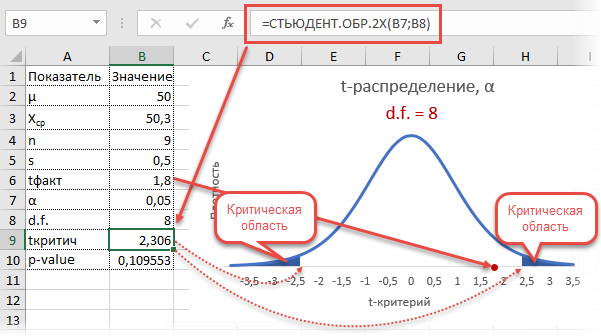
Теперь определим, выходит ли полученное число за критический уровень при уровне значимости α = 0,05. Воспользуемся таблицей для критерия Стьюдента (есть в любом учебнике по статистике).
По столбцам идет вероятность правой части распределения, по строкам – число степеней свободы. Нас интересует двусторонний t-критерий с уровнем значимости 0,05, что равносильно t-значению для половины уровня значимости справа: 1 — 0,05/2 = 0,975. Количество степеней свободы – это объем выборки минус 1, т.е. 9 — 1 = 8. На пересечении находим табличное значение t-критерия – 2,306. Если бы мы использовали стандартное нормальное распределение, то критической точкой было бы значение 1,96, а тут она больше, т.к. t-распределение на небольших выборках имеет более приплюснутый вид.
Сравниваем фактическое (1,8) и табличное значение (2.306). Расчетный критерий оказался меньше табличного. Следовательно, имеющиеся данные не противоречат гипотезе H0 о том, что генеральная средняя равна 50 кг (но и не доказывают ее). Это все, что мы можем узнать, используя таблицы. Можно, конечно, еще p-value попробовать найти, но он будет приближенным. А, как правило, именно p-value используется для проверки гипотез. Поэтому далее переходим в Excel.
Готовой функции для расчета t-критерия в Excel нет. Но это и не страшно, ведь формула t-критерия Стьюдента довольно проста и ее можно легко соорудить прямо в ячейке Excel.
Получили те же 1,8. Найдем вначале критическое значение. Альфа берем 0,05, критерий двусторонний. Нужна функция обратного значения t-распределения для двухсторонней гипотезы СТЬЮДЕНТ.ОБР.2Х.
Полученное значение отсекает критическую область. Наблюдаемый t-критерий в нее не попадает, поэтому гипотеза не отклоняется.
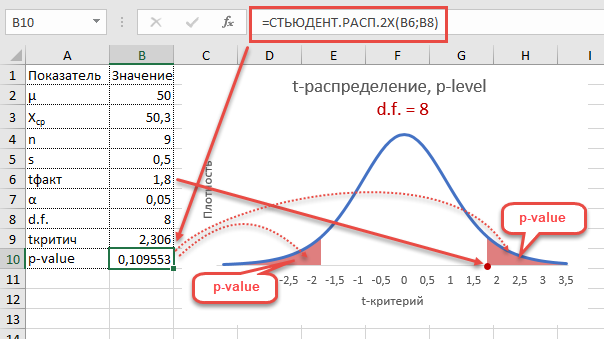
Однако это тот же способ проверки гипотезы с помощью табличного значения. Более информативно будет рассчитать p-value, т.е. вероятность получить наблюдаемое или еще большее отклонение от средней 50кг, если эта гипотеза верна. Потребуется функция распределения Стьюдента для двухсторонней гипотезы СТЬЮДЕНТ.РАСП.2Х.
P-value равен 0,1096, что больше допустимого уровня значимости 0,05 – гипотезу не отклоняем. Но теперь можно судить о степени доказательства. P-value оказался довольно близок к тому уровню, когда гипотеза отклоняется, а это наводит на разные мысли. Например, что выборка оказалась слишком мала для обнаружения значимого отклонения.
Пусть через некоторое время отдел контроля снова решил проверить, как выдерживается стандарт заполняемости мешков. На этот раз для большей надежности было отобрано не 9, а 25 мешков. Интуитивно понятно, что разброс средней уменьшится, а, значит, и шансов найти сбой в системе становится больше.
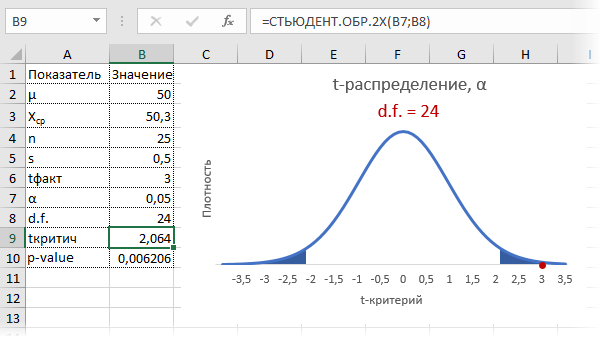
Допустим, были получены те же значения средней и стандартного отклонения по выборке, что и в первый раз (50,3 и 0,5 соответственно). Рассчитаем t-критерий.
Критическое значение для 24-х степеней свободы и α = 0,05 составляет 2,064. На картинке ниже видно, что t-критерий попадает в область отклонения гипотезы.
Можно сделать вывод о том, что с доверительной вероятностью более 95% генеральная средняя отличается от 50кг. Для большей убедительности посмотрим на p-value (последняя строка в таблице). Вероятность получить среднюю с таким или еще большим отклонением от 50, если гипотеза верна, составляет 0,0062, или 0,62%, что при однократном измерении практически невозможно. В общем, гипотезу отклоняем, как маловероятную.
Расчет доверительного интервала для математического ожидания с помощью t-распределения Стьюдента в Excel
С проверкой гипотез тесно связан еще один статистический метод – расчет доверительных интервалов. Если в полученный интервал попадает значение, соответствующее нулевой гипотезе, то это равносильно тому, что нулевая гипотеза не отклоняется. В противном случае, гипотеза отклоняется с соответствующей доверительной вероятностью. В некоторых случаях аналитики вообще не проверяют гипотез в классическом виде, а рассчитывают только доверительные интервалы. Такой подход позволяет извлечь еще больше полезной информации.
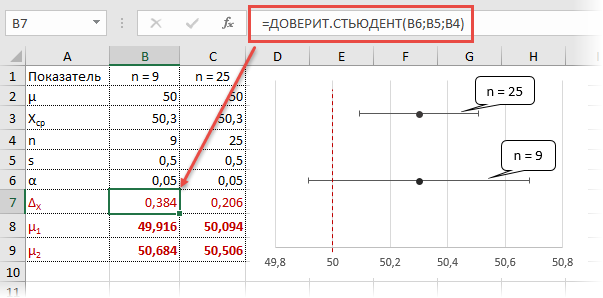
Рассчитаем доверительные интервалы для средней при 9 и 25 наблюдениях. Для этого воспользуемся функцией Excel ДОВЕРИТ.СТЬЮДЕНТ. Здесь, как ни странно, все довольно просто. В аргументах функции нужно указать только уровень значимости α, стандартное отклонение по выборке и размер выборки. На выходе получим полуширину доверительного интервала, то есть значение которое нужно отложить по обе стороны от средней. Проведя расчеты и нарисовав наглядную диаграмму, получим следующее.
Как видно, при выборке в 9 наблюдений значение 50 попадает в доверительный интервал (гипотеза не отклоняется), а при 25-ти наблюдениях не попадает (гипотеза отклоняется). При этом в эксперименте с 25-ю мешками можно утверждать, что с вероятностью 97,5% генеральная средняя превышает 50,1 кг (нижняя граница доверительного интервала равна 50,094кг). А это довольно ценная информация.
Таким образом, мы решили одну и ту же задачу тремя способами:
1. Древним подходом, сравнивая расчетное и табличное значение t-критерия
2. Более современным, рассчитав p-value, добавив степень уверенности при отклонении гипотезы.
3. Еще более информативным, рассчитав доверительный интервал и получив минимальное значение генеральной средней.
Важно помнить, что t-критерий относится к параметрическим методам, т.к. основан на нормальном распределении (у него два параметра: среднее и дисперсия). Поэтому для его успешного применения важна хотя бы приблизительная нормальность исходных данных и отсутствие выбросов.
Напоследок предлагаю видеоролик о том, как рассчитать критерий Стьюдента и проверить гипотезу о генеральной средней в Excel.
Иногда просят объяснить, как делаются такие наглядные диаграммы с распределением. Ниже можно скачать файл, где проводились расчеты для этой статьи.
Скачать файл с примером.
Всего доброго, будьте здоровы.
Поделиться в социальных сетях:
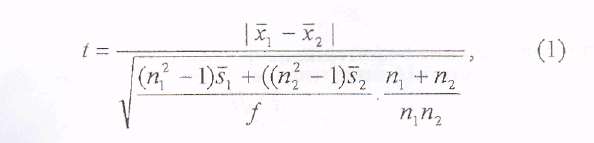
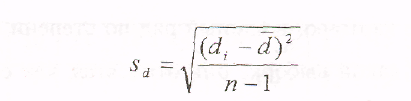
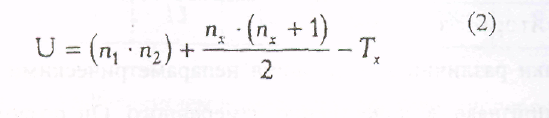 Определить
Определить