Как найти таблицу абсолютных частот

Статистические исследования числовых рядов. Статистические характеристики числовых рядов

Очень часто из-за дороговизны или слишком большого числа наблюдений невозможно получить полной информации об объектах, событиях или наблюдениях. По этой причине информацию получают на основе анализа части всего множества объектов, событий или наблюдений, называемой рядом числовых данных, рядом выборочных данных или, просто, выборкой.

Выборка представляет собой конечный ряд чисел (выборочных данных), количество чисел в котором называют объемом выборки

Для обеспечения достоверности информации об объектах, событиях или наблюдениях, полученных на основе статистических исследований числовых рядов (анализа выборочных данных), отбор выборочных данных должен носить случайный характер и иметь достаточно большой объем, то есть выборка должны быть репрезентативной (представительной).

Статистические исследования числовых рядов (рядов чисел, рядов выборочных данных) удобно проводить в соответствии со следующей схемой, которую мы изложим на примере следующей выборки   X :

1. Определяем объем выборки (число чисел в числовом ряде).

   В числовом ряде (1) десять чисел, поэтому объем выборки равен   10.

2. Вычисляем среднее арифметическое числового ряда   X   (среднее выборочное значение), которое обозначают .

   Для числового ряда (1)

   

   

   

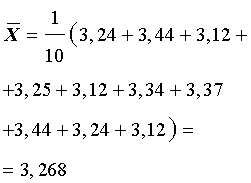
3. Производим упорядочение числового ряда по возрастанию (ранжирование числовых данных). Полученный числовой ряд, который обозначим   X₁ ,   называют вариационным рядом.

   Для числового ряда   X   вариационный ряд   X₁   имеет следующий вид:

   X₁ = {3,12;   3,12;   3,12;   3,24;   3,24;   3,25;   3,34;   3,37;   3,44;   3,44}

4. Вычисляем размах числового ряда   X ,   то есть разность между наибольшим числом из числового ряда и наименьшим числом из числового ряда.

   В числовом ряде   X ,  как и в вариационном ряде   X₁ ,   число   3,44   является наибольшим числом, а число   3,12   является наименьшим числом. Поэтому размах числового ряда   X   равен

   3,44 – 3,12 = 0,32

5. Вычисляем медиану числового ряда.

   В случае, когда объем выборки (число членов числового ряда) – чётное число, медианой числового ряда является число, равное половине суммы двух чисел, стоящих в середине вариационного ряда.

   Число членов ряда   X   равно чётному числу   10 ,   а в середине вариационного ряда   X₁  стоят числа   3,24   и   3,25 .   Поэтому медиана числового ряда, которую обычно обозначают символом   Me ,   равна

   

   В случае, когда объем выборки (число членов числового ряда) –нечётное число, медианой числового ряда является число, стоящее в середине вариационного ряда.

   Например, медианой числового ряда

   {2;   3;   7;   9;   15}

   является число   7 .

6. Составляем таблицу частот числового ряда.

   Если взглянуть на числа (выборочные данные), составляющие вариационный ряд   X₁ ,   то можно заметить, некоторые числа повторяются, а другие встречаются лишь по одному разу. Это наблюдение приводит к следующему определению.

   ОПРЕДЕЛЕНИЕ 1. Если выборочное данное встречается в вариационном ряде   m   раз, то число   m   называют частотой (абсолютной частотой) этого выборочного данного.

   Воспользовавшись определением 1, сформируем для числового ряда   X   таблицу, содержащую две строки, которую называют таблицей частот (абсолютных частот) числового ряда. Для этого в первой строке таблицы запишем числа, составляющие вариационный ряд   X₁ ,   причем запишем числа в порядке возрастания и без повторений. Во второй строке таблицы запишем частоты (абсолютные частоты), соответствующие числам из первой строки таблицы.

   ТАБЛИЦА ЧАСТОТ ЧИСЛОВОГО РЯДА

   Числа, составляющие вариационный ряд (без повторений)	3,12	3,24	3,25	3,34	3,37	3,44
   Частоты	3	2	1	1	1	2

   Числа, составляющие вариационный ряд (без повторений)	Частоты
   3,12	3
   3,24	2
   3,25	1
   3,34	1
   3,37	1
   3,44	2

   ЗАМЕЧАНИЕ. Сумма частот, то есть сумма чисел, записанных во второй строке таблицы частот числового ряда, равна объему выборки (числу чисел в числовом ряде). В рассматриваемом случае это число   10 .

7. Составляем таблицу относительных частот (в процентах).

   ОПРЕДЕЛЕНИЕ 2. Относительной частотой (в процентах) выборочного данного называют число процентов, которое составляет частота этого выборочного данного от всего объема выборки (количества членов числового ряда).

   Для того, чтобы сформировать таблицу относительных частот числового ряда, заменим частоты, записанные во второй строке таблицы частот числового ряда, на соответствующие им относительные частоты. В результате получим следующую таблицу.

   ТАБЛИЦА ОТНОСИТЕЛЬНЫХ ЧАСТОТ (В ПРОЦЕНТАХ)

   Числа, составляющие вариационный ряд (без повторений)	3,12	3,24	3,25	3,34	3,37	3,44
   Относительные частоты (%)	30%	20%	10%	10%	10%	20%

   Числа, составляющие вариационный ряд (без повторений)	Относительные частоты (%)
   3,12	30%
   3,24	20%
   3,25	10%
   3,34	10%
   3,37	10%
   3,44	20%

8. Находим моду числового ряда.

   ОПРЕДЕЛЕНИЕ 3. Модой числового ряда называют выборочное данное с наибольшей частотой.

   Из таблицы частот числового ряда видно, что модой числового ряда   X   является число   3,12 ,   поскольку его частота   3   является наибольшей. Очевидно, что и относительная частота этого выборочного данного является самой большой   (30%) .

   ЗАМЕЧАНИЕ. Объем выборки, среднее выборочное значение, размах, медиана и мода числового ряда являются одними из статистических характеристик числовых рядов.

Как
правило, анализ данных начинается с
изучения того, как часто встречаются
те или иные значения интересующего
исследователя признака (переменной) в
имеющемся множестве наблюдений. Для
этого строятся таблицы
и графики распределения частот. Нередко
они являются основой для получения
ценных содержательных выводов
исследования.

Если
признак принимает всего лишь несколько
возможных значений (до 10-15), то таблица
распределения частот показывает частоту
встречаемости каждого значения признака.
Если указывается, сколько раз встречается
каждое значение признака, то это –
таблица абсолютных
частот
распределения, если указывается доля
наблюдений, приходящихся на то или иное
значение признака, то говорят об
относительных
частотах
распределения.

Пример.
Предположим,
исследователя в нашем примере (табл.
4.1) интересует, как распределяются ответы
всех учеников до проведения тренинга.
Для этого он подсчитает частоту
встречаемости каждого из ответов и
составит таблицу распределения частот
(табл. 4.2). Таблица показывает, что чаще
встречаются средние значения выраженности
признака и реже – крайние значения.

Таблица
4.2

Таблица
распределения частот

Абсолютная
и относительная частоты связаны
соотношением:

где
f_a
–
абсолютная частота некоторого значения
признака, N
–
число
наблюдений, f_о
–
относительная частота этого значения
признака. Очевидно, что сумма всех
абсолютных частот равна числу наблюдений
– N,
а
сумма всех относительных частот равна
1. Нередко относительная частота
применяется для оценки вероятности
встречаемости значения.

Во
многих случаях признак может принимать
множество различных значений, например,
если мы измеряем время решения тестовой
задачи. В этом случае о распределении
признака позволяет судить таблица
сгруппированных частот, в
которых частоты группируются по разрядам
или интервалам значений признака.

Пример.
Предположим,
в группе испытуемых численностью 40
человек измерено время решения тестовой
задачи. Максимальное время составило
67 секунд, минимальное – 32 секунды.
Построение таблицы распределения частот
в этом случае производится поэтапно.

Построение
таблицы сгруппированных частот

1. Определение
   размаха: 67 – 32 = 35.

2. Выбор
   желаемого числа разрядов и интервала
   разрядов. Определяется произвольно.
   Обычное число разрядов – от 6 до 15.
   Удобным интервалом разрядов в нашем
   случае может быть 5. 35 делим на 5, получаем
   число разрядов – 7. Учитывая, что начинать
   лучше с 30 или с 31 и заканчивать на 69 или
   70, уточняем размах (70 – 30 = 40) и число
   разрядов (40 : 5 = 8).

3. Определение
   границ разрядов. Если мы начнем с 30, то
   первый разряд будете 30 до 34, второй –
   с 35 до 49 и т. д., до восьмого – с 65 до 69.
   Границы соседних
   разрядов
   не должны совпадать!

1. Подсчет
   частот встречаемости значений признака
   для каждого интервала.

Таблица
4.3 содержит результат подсчета
сгруппированных таким образом частот
по разрядам (интервалам) значений
признака – времени решения тестовой
задачи.

Таблица
4.3

Таблица
частот, сгруппированных по интервалам
времени

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Мода и медиана

Модой ряда чисел называется число, наиболее часто встречающееся в данном ряду.

Обратимся снова к нашему примеру со сборной по футболу:

Чему в данном примере равна мода? Какое число наиболее часто встречается в этой выборке?

Все верно, это число ( displaystyle 181), так как два игрока имеют рост ( displaystyle 181) см; рост же остальных игроков не повторяется.

Тут все должно быть ясно и понятно, да и слово знакомое, правда?

Перейдем к медиане, ты ее должен знать из курса геометрии. Но мне не сложно напомнить, что в геометрии медиана (в переводе с латинского- «средняя») — отрезок внутри треугольника, соединяющий вершину треугольника с серединой противоположной стороны.

Ключевое слово – СЕРЕДИНА. Если ты знал это определение, то тебе легко будет запомнить, что такое медиана в статистике.

Медианой ряда чисел с нечетным числом членов называется число, которое окажется посередине, если этот ряд упорядочить (проранжировать, т.е. расположить значения в порядке убывания или возрастания).

Медианой ряда чисел с четным числом членов называется среднее арифметическое двух чисел, записанных посередине, если этот ряд упорядочить.

Ну что, вернемся к нашей выборке футболистов?

Ты заметил в определении медианы важный момент, который нам еще здесь не встречался? Конечно, «если этот ряд упорядочить»!

Для того, чтобы в ряду чисел был порядок, можно расположить значения роста футболистов как в порядке убывания, так и в порядке возрастания. Мне удобней выстроить этот ряд в порядке возрастания (от самого маленького к самому большому).

Вот, что у меня получилось:

Так, ряд упорядочили, какой еще есть важный момент в определении медианы? Правильно, четное и нечетное количество членов в выборке.

Заметил, что для четного и нечетного количества даже определения отличаются? Да, ты прав, не заметить – сложно. А раз так, то нам надо определиться, четное у нас количество игроков в нашей выборке или нечетное?

Все верно – игроков ( displaystyle 11), значит, количество нечетное! Теперь можем применять к нашей выборке менее заковыристое определение медианы для нечетного количества членов в выборке.

Ищем число, которое оказалось посередине в нашем упорядоченном ряду:

Ну вот, чисел у нас ( displaystyle 11), значит, по краям остается по пять чисел, а рост ( displaystyle 183) см будет медианой в нашей выборке.

Не так уж и сложно, правда?

Частота и относительная частота

Частота представляет собой число повторений, сколько раз за какой-то период происходило некоторое событие, проявлялось определенное свойство объекта либо наблюдаемый параметр достигал данной величины.

То есть частота определяет то, как часто повторяется та или иная величина в выборке.

Разберемся на нашем примере с футболистами. Перед нами вот такой вот упорядоченный ряд:

Частота – это число повторений какой-либо величины параметра. В нашем случае, это можно считать вот так. Сколько игроков имеет рост ( 176)?

Все верно, один игрок. Таким образом, частота встречи игрока с ростом ( 176) в нашей выборке равна ( 1).

Сколько игроков имеет рост ( 178)? Да, опять же один игрок. Частота встречи игрока с ростом ( 178) в нашей выборке равна ( 1).

Задавая такие вопросы и отвечая на них, можно составить вот такую табличку:

Ну вот, все довольно просто. Помни, что сумма частот должна равняться количеству элементов в выборке (объему выборки).

То есть в нашем примере: ( 1+1+1+2+1+1+1+1+1+1=11)

Перейдем к следующей характеристике – относительная частота.

Относительная частота – это отношение частоты к общему числу данных в ряду. Как правило, относительная частота выражается в процентах.

Обратимся опять к нашему примеру с футболистами. Частоты для каждого значения мы рассчитали, общее количество данных в ряду мы тоже знаем ( left( n=11 right)) .

Рассчитываем относительную частоту для каждого значения роста и получаем вот такую табличку:

А теперь сам составь таблицы частот и относительных частот для примера с 9-классниками, решающими задачи.