Утверждение. Если для двух вершин существует маршрут, связывающий их, то обязательно найдется минимальный маршрут, соединяющий эти вершины. Обозначим длину этого маршрута через d(v, w).
Определение. Величину d(v, w) (конечную или бесконечную) будем называть расстоянием между вершинами v, w. Это расстояние удовлетворяет аксиомам метрики:
1) d(v, w) ![]() 0, причем d(v, w) = 0 тогда и только тогда, когда v=w;
0, причем d(v, w) = 0 тогда и только тогда, когда v=w;
2) d(v, w) = d(w, v);
3) d(v, w) ![]() d(v, u) + d(u, w).
d(v, u) + d(u, w).
Определение. Диаметром связного графа называется максимально возможное расстояние между двумя его вершинами.
Определение. Центром графа называется такая вершина, что максимальное расстояние между ней и любой другой вершиной является наименьшим из всех возможных; это расстояние называется радиусом графа.
Пример 82.
Для графа G, изображенного на рис. 3.16, найти радиус, диаметр и центры.
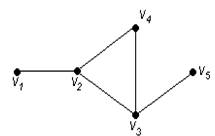
Рис. 3.16. Граф для примера 82
Решение.
Чтобы определить центры, радиус, диаметр графа G, найдем матрицу D(G) расстояний между вершинами графа, элементами dij которой будут расстояния между вершинами vi и vj. Для этого воспользуемся графическим представлением графа. Заметим, что матрица D(G) симметрична относительно главной диагонали. 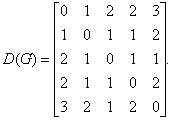
С помощью полученной матрицы для каждой вершины графа G определим наибольшее удаление из выражения: ![]() для i, j = 1, 2, …, 5. В результате получаем: r(v1) = 3, r(v2) = 2, r(v3) = 2, r(v4) = 2, r(v5) = 3. Минимальное из полученных чисел является радиусом графа G, максимальное – диаметром графа G. Значит, R(G) = 2 и D(G) = 3, центрами являются вершины v2, v3, v4.
для i, j = 1, 2, …, 5. В результате получаем: r(v1) = 3, r(v2) = 2, r(v3) = 2, r(v4) = 2, r(v5) = 3. Минимальное из полученных чисел является радиусом графа G, максимальное – диаметром графа G. Значит, R(G) = 2 и D(G) = 3, центрами являются вершины v2, v3, v4.
Пусть
![]() –
–
граф (или псевдограф).
Расстояние в графе удовлетворяют
аксиомам метрики
1)
![]() ,
,![]()
2)
![]() (не
(не
в ориентированном графе)
3)
![]()
4)
![]() в
в
связном графе (не в ориентированном
графе).
Пусть
![]() связный
связный
граф (или псевдограф).
-
Определение
Диаметром графа G
называется величина
 .
.
Пусть
![]() .
.
-
Определение
Максимальным удалением (эксцентриситетом)
в графе G
от вершины
 называется
называется
величина
 .
. -
Определение
Радиусом графа G
называется величина

-
Определение
Центром графа Gназывается
любая вершина
 такая,
такая,
что
 .
.
Алгоритм фронта волны
Пусть
![]() ориентированный
ориентированный
граф с n³2 вершинами и v,w
(v¹w)
– заданные вершины из V.
Алгоритм поиска
минимального пути из
![]() в
в
![]() в
в
ориентированном графе
(алгоритм
фронта волны).
1) Помечаем
вершину
![]() индексом
индексом
0, затем помечаем вершины Î образу вершины
![]() индексом
индексом
1. Обозначаем их FW1
(v).
Полагаем k=1.
2)
Если
![]() или
или
k=n-1,
и одновременно![]()
то вершина
![]() не
не
достижима из
![]() .
.
Работа алгоритма заканчивается.
В противном случае продолжаем:
3)
Если
![]() ,
,
то переходим к шагу 4.
В противном случае мы нашли
минимальный путь из
![]() в
в
![]() и
и
его длина равна k.
Последовательность вершин

есть этот минимальный путь. Работа
завершается.
4)
Помечаем индексом k+1
все непомеченные вершины, которые
принадлежат образу множества вершин c
индексом k.
Множество вершин с индексом k+1
обозначаем
![]() .
.
Присваиваем k:=k+1
и переходим к 2).
-
Замечания
Множество
 называется
называется
фронтом волны kго
уровня.
·
Вершины
![]() могут
могут
быть выделены неоднозначно, что
соответствует случаю, если
![]() несколько
несколько
минимальных путей из
![]() в
в
![]() .
.
Чтобы найти расстояния в
ориентированном графе, необходимо
составить матрицу минимальных расстояний
R(D)между
его вершинами. Это квадратная матрица
размерности
![]() ,
,
элементы главной диагонали которой
равны нулю (![]() ,
,
i=1,..,n).
Сначала составляем матрицу
смежности. Затем переносим единицы из
матрицы смежности в матрицу минимальных
расстояний (![]() ,
,
если
![]() ).
).
Далее построчно заполняем матрицу
следующим образом.
Рассматриваем первую строку,
в которой есть единицы. Пусть это строка
− i-тая
и на пересечении с j-тым
столбцом стоит единица (то есть
![]() ).
).
Это значит, что из вершины
![]() можно
можно
попасть в вершину
![]() за
за
один шаг. Рассматриваем j-тую
сроку (строку стоит вводить в рассмотрение,
если она содержит хотя бы одну единицу).
Пусть элемент
![]() .
.
Тогда из вершины
![]() в
в
вершину
![]() можно
можно
попасть за два шага.
Таким образом, можно записать
![]() .
.
Следует заметить, что если в рассматриваемых
строках две или более единиц, то следует
прорабатывать все возможные варианты
попадания из одной вершины в другую,
записывая в матрицу длину наикратчайшего
из них.
-
Пример Найдем
расстояния в ориентированном графе D,
изображенном на рис. 7. В данной задаче
количество вершин n=7,
следовательно, матрицы смежности
и минимальных расстояний между вершинами
ориентированного графа Dбудут
иметь размерность 7×7.
 Рис.7.
Рис.7.
Матрица смежности:
 .
.
Начинаем заполнять матрицу
R(D)
минимальных расстояний: сначала ставим
нули по главной диагоналии rij=aij,
если aij=1,
(т.е. переносим единицы из матрицы
смежности). Рассматриваем первую строку.
Здесь есть две единицы, то есть из первой
вершины за один шаг можно попасть во
вторую и шестую. Из второй вершины можно
попасть за один шаг в третью (путь в
первую вершину нас не интересует),
следовательно, можно записать
![]() .
.
Из шестой вершины можем добраться за
один шаг в пятую и седьмую, а значит,
![]() ,
,
![]() .
.
Теперь ищем маршруты, исходящие из
первой вершины, состоящие из 3 шагов: за
2 шага идем в третью вершину, оттуда за
один шаг попадаем в четвертую, поэтому
![]() .
.
В итоге получаем следующую матрицу:

Таким образом, диаметром
исследуемого ориентированного графа
будет
![]() .
.
Для каждой вершины заданного
ориентированного графа найдем максимальное
удаление (эксцентриситет) в графе G от
вершины нее по формуле, которая была
приведена выше
![]() :
:
r(vi)
− максимальное из расстояний, стоящих
в i-той
строке. Таким образом,
r(v1)=3,
r(v2)=3,
r(v3)=5,
r(v4)=4,
r(v5)=2,
r(v6)=2,
r(v7)=3.
Значит, радиусом графа G
будет
![]()
Соответственно, центрами
графа G будут
вершины v5
иv6
, так как величины их эксцентриситетов
совпадают с величиной радиуса![]() .
.
Опишем теперь нахождение
минимального пути из вершины v3
в вершинуv6
по алгоритму фронта волны. Обозначим
вершину v3
как V0,
а вершину v6–
как W
(см. рис. 8). Множество вершин, принадлежащих
образу V0,
состоит из одного элемента – это вершина
v4,
которую, согласно алгоритму, обозначаем
как V1:
FW1(v3)={v4}.
Поскольку искомая вершина
не принадлежит фронту волны первого
уровня
![]() ,
,
продолжаем работу алгоритма. Строим
фронт волны второго уровня – это множество
вершин, принадлежащих образу вершиныV1:
FW2(v3)={v7},
обозначаем v7≡V2.
В образ вершины V2
входят две вершины –v5
и v4,
но, так как v4
уже была помечена как V0,
то фронт волны третьего уровня состоит
из одного элемента: FW3(v3)={v5},
v5≡V3.
Из непомеченных вершин в образ вершины
V3
входят v1
и v2,
соответственно, FW4(v3)={v1,
v2},
v1≡V4,
v2≡V4.
Теперь помечены все вершины, кроме v6,
которая входит в образ вершины
![]() ,
,
то есть FW5(v3)={v6≡W},
работа алгоритма закончена. Минимальный
путь (5 шагов) из вершины v3
в вершинуv6
выглядит так: v3v4v7v5v1v6.
 Рис.8.
Рис.8.
Минимальный путь в
нагруженном ориентированном графе по
методу Форда-Беллмана
Найти минимальный путь в
нагруженном ориентированном графе из
вершины
![]() в
в
вершину
![]() по
по
методу Форда-Беллмана.
Рассмотрим сначала общую
задачу – нахождения минимального пути
из вершины vнач
в vкон.
Пусть D=(V,X)
– нагруженный ориентированный граф,
V={v1,…,vn},
n>1.
Введем величины
![]() ,
,
где i=1,…,n,
k=0,1,2,…,n–1.
Для каждого фиксированного
i и
k
величина
![]() равна
равна
длине минимального пути среди путей из
vнач
в vi
содержащих не более k
дуг. Если путей нет, то
![]() .
.
Положим также
![]() .
.
Составляем матрицу длин
дуг C(D)=[cij]
порядка n:

Утверждение.
При i=2,…,n,
k³0
выполняется равенство
![]() .
.
(3.1)
Алгоритм Форда-Беллмана
нахождения минимального пути в нагруженном
ориентированном графе D из vнач
в vкон.(
vнач
≠ vкон).
(![]()
записываем в виде матрицы, i–
строка, k-столбец).
1) Составляем
таблицу
![]() ,
,
i=1,…,n,
k=0,…,n-1.
Если
![]() ,
,
то пути из vнач
в vкон
нет. Конец алгоритма.
2) Если
![]() то
то
это число выражает длину любого
минимального пути из vнач
в vкон.
Найдем минимальное k1³1,
при котором
![]() .
.
По определению
![]() получим,
получим,
что k1–
минимальное число дуг в пути среди всех
минимальных путей из vначв
vкон.
3) Затем
определяем номера i2,…,
![]() такие,
такие,
что
![]() ,
,
![]() ,
,
![]()
![]()
![]() ,
,
то есть восстанавливаем по
составленной таблице и матрице стоимости
искомый минимальный путь из vнач
в vкон.
-
Пример
Найдем минимальный путь из
вершины v2
в v6
в ориентированном нагруженном графе
D,
изображенном на рис. 9. В рассматриваемом
графе количество вершин n=7,
следовательно, матрица длин дуг
ориентированного графа Dбудет
иметь размерность 7×7.
 Рис.
Рис.
9.
Матрица длин дуг для рассматриваемого
графа будет выглядеть следующим образом:
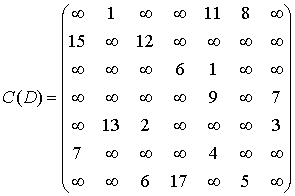 .
.
Согласно алгоритму, составляем
таблицу стоимости минимальных путей
из вершины v2
в вершину vi
не более, чем за k
шагов, k=0,…n-1
(n=7,
следовательно, k=0,…6).
Как было определено выше,
![]() ,
,
и
![]() для
для
всех остальных вершин vi≠
v2,
то есть первый столбец таблицы состоит
из элементов, равных
![]() ,
,
кроме элемента
![]() .
.
Второй столбец таблицы повторяет вторую
строку матрицы стоимости, поскольку
представляет собой стоимость возможных
путей из вершины v2
за один шаг. Далее по формуле (3.1) находим
по столбцам все оставшиеся элементы
таблицы. Например, чтобы найти элемент
![]() ,
,
складываем элементы столбца
![]() и
и
первого столбца матрицы стоимости и
выбираем минимальное из получившихся
чисел:
![]() .
.
В конечном итоге получаем следующую
таблицу:

Теперь необходимо по
построенной таблице и по матрице C(D)
восстановить минимальный путь из вершины
v2
в v6,
который будет строиться с конца, то
есть, начиная с вершины v6.
Для этого выбираем минимальное из чисел,
стоящих в строке, соответствующей v6
в таблице. Это число – 21 – длина
минимального искомого пути. В первый
раз такая длина была получена при
количестве шагов, равном 4. В вершину v6
мы можем попасть за один шаг из вершин
v1
и v7
(длина соответствующих дуг 8 и 5
соответственно – данные из матрицы
C(D)).
Выбираем минимальную по длине из этих
дуг. Далее, в вершину v7
можно попасть из v4
и v5(длина
соответствующих дуг 7 и 3 соответственно).
Продолжая аналогичным образом, найдем
искомый путь за 4 шага минимальной длины
из вершины v2
в v6:
v2v3v5v7v6.
78
Необходимо по определенном условию найти кратчайший путь из одной точки в другую. При этом данные представлены в таблице с указанием длины пути. Решение задач на определение кратчайшего пути — это задание № 4 в ОГЭ.
Это задание можно решить двумя способами:
- При помощи алгоритма Дейкстры
- При помощи построения графа по таблице расстояний.
Для ОГЭ удобнее второй способ, т.к. в заданиях ОГЭ этот способ быстрее и удобнее.
Задача 1 Определить кратчайший путь

Мы видим, что на пересечении двух населенных пунктов, например, А и B есть какая-то цифра, то это значит, что есть дорога на данном участке и ее протяженность 3 км (в нашей задаче).
Все, что осталось сделать – это построить граф, чтобы визуально найти самую короткую дорогу.
Графы составляйте как можно просторнее, чтобы самим не запутаться.

На рисунке мы видим сразу, что из А в F есть прямая дорога = 15 км
АВDF = 3+4+6 = 13
Но если мы будем так искать руками, то это будет чуть подольше.
Давайте определимся с вами с ключевыми точками. Точка D – ключевая точка через которую мы идем по дороге от А в F.
Теперь нужно посмотреть, а как же попасть в точку D быстрее?
Это может быть через пункт В 3+4 = 7 км
Или через пункт С 5+2 = 7 км.
Такой пример попался, что расстояние двух дорог одинаково.
Далее из D в F можем попасть напрямую DF = 6 км, а можем через Е 3+4 = 7 км
Соответственно, единственно короткая дорога в данной задаче будет:
АВDF 3 км + 4 км + 6 км = 13 км
Ответ: 13
Основное состоит в том, что когда построили граф, то необходимо ориентироваться на точки, которые встречаются на пути. В этой задача определяем ключевую точку D, т.к. через нее проходит больше всего дорог при переходе от А до F. И определяем наиболее короткую дорогу до ключевой точки сначала, а потом от ключевой точки до конечной.
Задача 2. Определить кратчайший путь

По условию нам необходимо найти кратчайший путь между пунктами В и D, но граф нам также нужно строить.

На графе видно, что один прямой путь у нас уже есть из D в E равный 4. Эта дорога из Е единственная.
Далее мы идем из В и видим, что можно пройти через А, а можем пройти и через С.
Если проходим через А, то будет 1 + 4 = 5
Если проходим через А и С, то будет 1+2+1 = 4
Третья дорога ВСЕ = 4+1 = 5
Следовательно, самый короткий путь будет:
ВАСЕD= 1+2+1+4=8 км
Ответ: 8
Следующее задание выглядит необычно, т.к. присутствуют непривычные нам переменные. Здесь у нас названия населенных пунктов.
Задание 3. Определить кратчайший путь

В результате задача стоит следующим образом: нужно пройти из Вершков в Ивановское.
Проще всего это задание сделать, если присвоить названиям поселка те же английские буквы для того, чтобы не запутаться.
Можно поставить и русские буквы по первым буквам названий, но тут могут быть совпадения, например, в нашем задании два поселка с названием с буквы Д.
Поэтому просто ставим английские буквы по алфавиту.


Еще раз замечаем, что мы ищем короткий путь из деревни Вершки (В) в поселок Ивановский (F).
Что видим?
Прямой путь сразу видно через пункт D 4+5=9
Теперь проверяем другие пути, вдруг будет короче.
Идти через А и С нет смысла, т.к. АС = 8 км.
Можем пойти из В в Е 2 км, далее в пункт С и в пункт F.
ВЕС = 2+1+3 = 6 км
Ответ: 6
Граф не такой точный метод решения, но он очень простой для понимания: можно визуально нарисовать граф и отследить все дороги.
Да, может понадобиться время для тренировки, чтобы научиться быстро определять. Но даже если решать это задание, ведя по графу пальцем, время на решение уйдет всего 2-3 минуты и несколько минут на оформление графа.
Задание 4. Определение кратчайшего пути

В этом задании мы также должны найти кратчайший путь, но есть ограничение – надо обязательно пройти через пункт С.
Задание становится проще, т.к. мы понимаем, как будет строиться наш путь.
Строим граф:

Причем путь из А в Е можно не строить, так как эта дорога прямая и через пункт С не проходит, т.е. не выполняется условие.
Граф получился у нас менее нагружен. Нарисовали пути, подписали. Обязательно выберите время и проверьте еще раз правильность графа по таблице, чтобы ничего не упустить.
Граф построен. Мы должны пройти из пункта А через точку С в пункт Е.
В пункт С можно попасть либо через пункт В 1+2 = 3; либо из А в С – это 4 км. Через D пройти не сможем, т.к. один пункт посещать два раза нельзя, а в этом случае будет именно этот вариант.
Соответственно, самой короткой дорогой будет дорога через В: АВС 1+2 = 3
Затем из С можно попасть только в D, а затем в Е:
ADCDE = 1+2+3+2 = 8 км
Ответ 8 км.
Примеры решения задач по информационным моделям (подготовка к ЕГЭ) по ссылке.
Автор – Лада Борисовна Есакова.
В своей деятельности человек повсеместно использует модели, то есть создает образ, упрощенную копию того объекта, с которым ему приходится иметь дело.
Модель – это искусственно созданный объект, дающий упрощенное представление о реальном объекте, процессе или явлении, отражающий существенные стороны изучаемого объекта с точки зрения цели моделирования.
Моделирование – это построение моделей, предназначенных для изучения и объектов, процессов или явлений.
Распространенными информационными моделями являются графики, схемы, таблицы, диаграммы. Одним из распространенных видов моделей являются графы. Граф – это один из способов графического едставления информации. Объекты представлены в нем как вершины (узлы), а связи между объектами как ребра (дуги). Т.е. граф – это набор вершин и связывающих их ребер.
Путь в графе – это конечная последовательность вершин, каждая из которых (кроме последней) соединена со следующей ребром. Граф может содержать циклы (первая вершина пути может совпадать с последней).
Обычно в задачах используют взвешенный граф, т.е. граф, в котором с каждым ребром связано число (вес). Например, расстояние, стоимость и т.д.

Граф может задаваться таблицей, в которой на пересечении строки и столбца с наименованиями вершин записано числовое значение (вес) ребра, соединяющего эти вершины.

Дерево – это граф, не имеющий циклов. В дереве существует один единственный путь между любой парой вершин. Одна из вершин дерева (корень) не имеет входящих ребер, все остальные имеют ровно одно входящее ребро. Вершины, у которых нет исходящих ребер, называются листьями.

1. Поиск графа, соответствующего таблице
Пример 1.
В таблице приведена стоимость перевозок между соседними железнодорожными станциями. Укажите схему, соответствующую таблице.


Решение:
Сравним значения таблицы и схем:
Согласно таблице вершина A должна быть связана с вершинами B (значение 4) и D (значение 5). Т.е. AB=4, AD=5. На схеме значения указаны около соответствующего ребра. Сразу отбрасываем 1),2),3) схемы, т.к. на них AD не равно 5.
Для уверенности проверим все остальные ребра схемы 4): BC=3, BD=6, что совпадает со значениями таблицы. Правильная схема 4).
Ответ: 4
2. Анализ информации в таблице и графе
Пример 2.
На рисунке справа схема дорог Н-ского района изображена в виде графа, в таблице содержатся сведения о длинах этих дорог (в километрах).

Так как таблицу и схему рисовали независимо друг от друга, то нумерация населенных пунктов в таблице никак не связана с буквенными обозначениями на графе. Определите, какова длина дороги из пункта В в пункт Е. В ответе запишите целое число – так, как оно указано в таблице.
Решение:
На графе из вершины В выходит 5 ребер, значит в таблице соответствующий пункт должен иметь дороги в 5 других (строка должна содержать 5 заполненных клеток). Такой пункт в таблице один: П6.
На графе из вершины Е выходит 4 ребра, значит в таблице соответствующий пункт должен иметь дороги в 4 других (строка должна содержать 4 заполненные клетки). Такой пункт в таблице один: П4.
Таким образом, нам нужно найти расстояние между П6 и П4. Согласно таблице оно равно 20.
Ответ: 20
3. Поиск информации в таблице по условию
Пример 3.
Между четырьмя местными аэропортами: ЛУГОВОЕ, ДЯТЛОВО, НИКИТИНО и ОРЕХОВО, ежедневно выполняются авиарейсы. Приведён фрагмент расписания перелётов между ними:

Путешественник оказался в аэропорту ЛУГОВОЕ в полночь. Определите самое раннее время, когда он может попасть в аэропорт ОРЕХОВО. Считается, что путешественник успевает совершить пересадку в аэропорту, если между временем прилета в этот аэропорт и временем вылета проходит не менее часа.
1) 12:05 2) 12:50 3)12:55 4) 13:30
Решение:
Можно, конечно, решить эту задачу просто глядя на таблицу и перебирая подходящие варианты, но есть риск ошибиться или пропустить нужную строчку. Поэтому рекомендую нарисовать дерево всех возможных путей из аэропорта ЛУГОВОЕ в ОРЕХОВО:

Средняя ветка не подходит, т.к. между прилетом в аэропорт ДЯТЛОВО (11:15) и вылетом из ДЯТЛОВО в ОРЕХОВО (12:00) интервал меньше часа.
Из оставшихся двух выбираем раннее время прилета: 12:55.
Ответ: 3
4. Выбор таблицы по условию
Пример 4.
В таблицах приведена протяженность автомагистралей между соседними населенными пунктами. Если пересечение строки и столбца пусто, то соответствующие населенные пункты не являются соседними. Укажите номер таблицы, для которой выполняется условие «Максимальная протяженность маршрута от пункта C до пункта B не больше 6». Протяженность маршрута складывается из протяженности автомагистралей между соответствующими соседними населенными пунктами. При этом через любой насеченный пункт маршрут должен проходить не более одного раза.

Решение:
По каждой из схем построим дерево с корнем в точке C и листьями в точке B. При этом нам не нужно строить дерево полностью. Как только найдена ветка с протяженностью больше 6, делаем вывод, что таблица не удовлетворяет указанному условию:

Таблицы 1), 2) и 4) отвергаем уже при анализе первой ветки дерева.
В таблице 3) две ветки вообще не приведут в B, а две другие имеют суммарную длину, не превышающую 6.
Ответ: 3
5. Поиск кратчайшего пути по таблице
Пример 5.
Между населёнными пунктами A, B, C, D, E, F, Z построены дороги, протяжённость которых приведена в таблице. (Отсутствие числа в таблице означает, что прямой дороги между пунктами нет.)

Определите длину кратчайшего пути между пунктами A и Z (при условии, что передвигаться можно только по построенным дорогам).
1) 13 2) 16 3) 19 4) 21
Решение:
При решении этой задачи тоже не следует полагаться на простой визуальный анализ таблицы. Чтобы избежать ошибок, построим дерево с корнем в вершине A и листьями в вершине Z. При этом нам не нужно выписывать все ветки. Второй путь из A в С (AC=6) длиннее первого (ABC=5), значит и весь маршрут через него будет длиннее.
Второй путь из C в E (CE=10) длиннее первого (CDE=6), значит и весь маршрут через него будет длиннее.

Нам остается сложить длины всех отрезков и выбрать маршрут с наименьшей длиной.
Это верхняя ветка дерева с длиной 16.
Ответ: 2
Благодарим за то, что пользуйтесь нашими статьями.
Информация на странице «Задача №3. Таблицы и схемы, поиск оптимального маршрута по таблице и по расписанию.» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.
Публикация обновлена:
08.05.2023
Графы. Нахождение кратчайшего расстояния между двумя вершинами с помощью алгоритма Дейкстры
- Подробности
- Категория: Сортировка и поиск
Алгоритм Дейкстры (англ. Dijkstra’s algorithm) — алгоритм на графах, изобретённый нидерландским учёным Эдсгером Дейкстрой в 1959 году. Находит кратчайшие пути от одной из вершин графа до всех остальных. Алгоритм работает только для графов без рёбер отрицательного веса.

Лекция 2: Алгоритмы и методы сортировки. Алгоритмы нахождения кратчайшего пути в графе
Лекция 5: Поиск в графах и обход. Алгоритм Дейкстры
Алгоритмы и структуры данных, лекция 13
Рассмотрим выполнение алгоритма на примере графа, показанного на рисунке.
Пусть требуется найти кратчайшие расстояния от 1-й вершины до всех остальных.
Кружками обозначены вершины, линиями — пути между ними (рёбра графа). В кружках обозначены номера вершин, над рёбрами обозначена их «цена» — длина пути. Рядом с каждой вершиной красным обозначена метка — длина кратчайшего пути в эту вершину из вершины 1.
Первый шаг. Рассмотрим шаг алгоритма Дейкстры для нашего примера. Минимальную метку имеет вершина 1. Её соседями являются вершины 2, 3 и 6.
Первый по очереди сосед вершины 1 — вершина 2, потому что длина пути до неё минимальна. Длина пути в неё через вершину 1 равна сумме значения метки вершины 1 и длины ребра, идущего из 1-й в 2-ю, то есть 0 + 7 = 7. Это меньше текущей метки вершины 2, бесконечности, поэтому новая метка 2-й вершины равна 7.
Аналогичную операцию проделываем с двумя другими соседями 1-й вершины — 3-й и 6-й.
Все соседи вершины 1 проверены. Текущее минимальное расстояние до вершины 1 считается окончательным и пересмотру не подлежит (то, что это действительно так, впервые доказал Э. Дейкстра). Вычеркнем её из графа, чтобы отметить, что эта вершина посещена.
Второй шаг. Шаг алгоритма повторяется. Снова находим «ближайшую» из непосещённых вершин. Это вершина 2 с меткой 7.
Снова пытаемся уменьшить метки соседей выбранной вершины, пытаясь пройти в них через 2-ю вершину. Соседями вершины 2 являются вершины 1, 3 и 4.
Первый (по порядку) сосед вершины 2 — вершина 1. Но она уже посещена, поэтому с 1-й вершиной ничего не делаем.
Следующий сосед вершины 2 — вершина 3, так как имеет минимальную метку из вершин, отмеченных как не посещённые. Если идти в неё через 2, то длина такого пути будет равна 17 (7 + 10 = 17). Но текущая метка третьей вершины равна 9, а это меньше 17, поэтому метка не меняется.
Ещё один сосед вершины 2 — вершина 4. Если идти в неё через 2-ю, то длина такого пути будет равна сумме кратчайшего расстояния до 2-й вершины и расстояния между вершинами 2 и 4, то есть 22 (7 + 15 = 22). Поскольку 22< , устанавливаем метку вершины 4 равной 22.
, устанавливаем метку вершины 4 равной 22.
Все соседи вершины 2 просмотрены, замораживаем расстояние до неё и помечаем её как посещённую.
Третий шаг. Повторяем шаг алгоритма, выбрав вершину 3. После её «обработки» получим такие результаты:
Дальнейшие шаги. Повторяем шаг алгоритма для оставшихся вершин. Это будут вершины 6, 4 и 5, соответственно порядку.
Завершение выполнения алгоритма. Алгоритм заканчивает работу, когда нельзя больше обработать ни одной вершины. В данном примере все вершины зачёркнуты, однако ошибочно полагать, что так будет в любом примере — некоторые вершины могут остаться незачёркнутыми, если до них нельзя добраться, т. е. если граф несвязный. Результат работы алгоритма виден на последнем рисунке: кратчайший путь от вершины 1 до 2-й составляет 7, до 3-й — 9, до 4-й — 20, до 5-й — 20, до 6-й — 11.
Реализация алгоритма на различных языках программирования :
C++
#include "stdafx.h"
#include <iostream>
using namespace std;
const int V=6;
//алгоритм Дейкстры
void Dijkstra(int GR[V][V], int st)
{
int distance[V], count, index, i, u, m=st+1;
bool visited[V];
for (i=0; i<V; i++)
{
distance[i]=INT_MAX; visited[i]=false;
}
distance[st]=0;
for (count=0; count<V-1; count++)
{
int min=INT_MAX;
for (i=0; i<V; i++)
if (!visited[i] && distance[i]<=min)
{
min=distance[i]; index=i;
}
u=index;
visited[u]=true;
for (i=0; i<V; i++)
if (!visited[i] && GR[u][i] && distance[u]!=INT_MAX &&
distance[u]+GR[u][i]<distance[i])
distance[i]=distance[u]+GR[u][i];
}
cout<<"Стоимость пути из начальной вершины до остальных:tn";
for (i=0; i<V; i++) if (distance[i]!=INT_MAX)
cout<<m<<" > "<<i+1<<" = "<<distance[i]<<endl;
else cout<<m<<" > "<<i+1<<" = "<<"маршрут недоступен"<<endl;
}
//главная функция
void main()
{
setlocale(LC_ALL, "Rus");
int start, GR[V][V]={
{0, 1, 4, 0, 2, 0},
{0, 0, 0, 9, 0, 0},
{4, 0, 0, 7, 0, 0},
{0, 9, 7, 0, 0, 2},
{0, 0, 0, 0, 0, 8},
{0, 0, 0, 0, 0, 0}};
cout<<"Начальная вершина >> "; cin>>start;
Dijkstra(GR, start-1);
system("pause>>void");
}
kvodo
Pascal
program DijkstraAlgorithm;
uses crt;
const V=6; inf=100000;
type vektor=array[1..V] of integer;
var start: integer;
const GR: array[1..V, 1..V] of integer=(
(0, 1, 4, 0, 2, 0),
(0, 0, 0, 9, 0, 0),
(4, 0, 0, 7, 0, 0),
(0, 9, 7, 0, 0, 2),
(0, 0, 0, 0, 0, 8),
(0, 0, 0, 0, 0, 0));
{алгоритм Дейкстры}
procedure Dijkstra(GR: array[1..V, 1..V] of integer; st: integer);
var count, index, i, u, m, min: integer;
distance: vektor;
visited: array[1..V] of boolean;
begin
m:=st;
for i:=1 to V do
begin
distance[i]:=inf; visited[i]:=false;
end;
distance[st]:=0;
for count:=1 to V-1 do
begin
min:=inf;
for i:=1 to V do
if (not visited[i]) and (distance[i]<=min) then
begin
min:=distance[i]; index:=i;
end;
u:=index;
visited[u]:=true;
for i:=1 to V do
if (not visited[i]) and (GR[u, i]<>0) and (distance[u]<>inf) and
(distance[u]+GR[u, i]<distance[i]) then
distance[i]:=distance[u]+GR[u, i];
end;
write('Стоимость пути из начальной вершины до остальных:'); writeln;
for i:=1 to V do
if distance[i]<>inf then
writeln(m,' > ', i,' = ', distance[i])
else writeln(m,' > ', i,' = ', 'маршрут недоступен');
end;
{основной блок программы}
begin
clrscr;
write('Начальная вершина >> '); read(start);
Dijkstra(GR, start);
end.
kvodo
Java
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.io.PrintWriter;
import java.util.ArrayList;
import java.util.Arrays;
import java.util.StringTokenizer;
public class Solution {
private static int INF = Integer.MAX_VALUE / 2;
private int n; //количество вершин в орграфе
private int m; //количествое дуг в орграфе
private ArrayList<Integer> adj[]; //список смежности
private ArrayList<Integer> weight[]; //вес ребра в орграфе
private boolean used[]; //массив для хранения информации о пройденных и не пройденных вершинах
private int dist[]; //массив для хранения расстояния от стартовой вершины
//массив предков, необходимых для восстановления кратчайшего пути из стартовой вершины
private int pred[];
int start; //стартовая вершина, от которой ищется расстояние до всех других
private BufferedReader cin;
private PrintWriter cout;
private StringTokenizer tokenizer;
//процедура запуска алгоритма Дейкстры из стартовой вершины
private void dejkstra(int s) {
dist[s] = 0; //кратчайшее расстояние до стартовой вершины равно 0
for (int iter = 0; iter < n; ++iter) {
int v = -1;
int distV = INF;
//выбираем вершину, кратчайшее расстояние до которого еще не найдено
for (int i = 0; i < n; ++i) {
if (used[i]) {
continue;
}
if (distV < dist[i]) {
continue;
}
v = i;
distV = dist[i];
}
//рассматриваем все дуги, исходящие из найденной вершины
for (int i = 0; i < adj[v].size(); ++i) {
int u = adj[v].get(i);
int weightU = weight[v].get(i);
//релаксация вершины
if (dist[v] + weightU < dist[u]) {
dist[u] = dist[v] + weightU;
pred[u] = v;
}
}
//помечаем вершину v просмотренной, до нее найдено кратчайшее расстояние
used[v] = true;
}
}
//процедура считывания входных данных с консоли
private void readData() throws IOException {
cin = new BufferedReader(new InputStreamReader(System.in));
cout = new PrintWriter(System.out);
tokenizer = new StringTokenizer(cin.readLine());
n = Integer.parseInt(tokenizer.nextToken()); //считываем количество вершин графа
m = Integer.parseInt(tokenizer.nextToken()); //считываем количество ребер графа
start = Integer.parseInt(tokenizer.nextToken()) - 1;
//инициализируем списка смежности графа размерности n
adj = new ArrayList[n];
for (int i = 0; i < n; ++i) {
adj[i] = new ArrayList<Integer>();
}
//инициализация списка, в котором хранятся веса ребер
weight = new ArrayList[n];
for (int i = 0; i < n; ++i) {
weight[i] = new ArrayList<Integer>();
}
//считываем граф, заданный списком ребер
for (int i = 0; i < m; ++i) {
tokenizer = new StringTokenizer(cin.readLine());
int u = Integer.parseInt(tokenizer.nextToken());
int v = Integer.parseInt(tokenizer.nextToken());
int w = Integer.parseInt(tokenizer.nextToken());
u--;
v--;
adj[u].add(v);
weight[u].add(w);
}
used = new boolean[n];
Arrays.fill(used, false);
pred = new int[n];
Arrays.fill(pred, -1);
dist = new int[n];
Arrays.fill(dist, INF);
}
//процедура восстановления кратчайшего пути по массиву предком
void printWay(int v) {
if (v == -1) {
return;
}
printWay(pred[v]);
cout.print((v + 1) + " ");
}
//процедура вывода данных в консоль
private void printData() throws IOException {
for (int v = 0; v < n; ++v) {
if (dist[v] != INF) {
cout.print(dist[v] + " ");
} else {
cout.print("-1 ");
}
}
cout.println();
for (int v = 0; v < n; ++v) {
cout.print((v + 1) + ": ");
if (dist[v] != INF) {
printWay(v);
}
cout.println();
}
cin.close();
cout.close();
}
private void run() throws IOException {
readData();
dejkstra(start);
printData();
cin.close();
cout.close();
}
public static void main(String[] args) throws IOException {
Solution solution = new Solution();
solution.run();
}
}
cybern.ru
Ещё один вариант:
import java.io.*;
import java.util.*;
public class Dijkstra {
private static final Graph.Edge[] GRAPH = {
new Graph.Edge("a", "b", 7),
new Graph.Edge("a", "c", 9),
new Graph.Edge("a", "f", 14),
new Graph.Edge("b", "c", 10),
new Graph.Edge("b", "d", 15),
new Graph.Edge("c", "d", 11),
new Graph.Edge("c", "f", 2),
new Graph.Edge("d", "e", 6),
new Graph.Edge("e", "f", 9),
};
private static final String START = "a";
private static final String END = "e";
public static void main(String[] args) {
Graph g = new Graph(GRAPH);
g.dijkstra(START);
g.printPath(END);
//g.printAllPaths();
}
}
class Graph {
private final Map<String, Vertex> graph; // mapping of vertex names to Vertex objects, built from a set of Edges
/** One edge of the graph (only used by Graph constructor) */
public static class Edge {
public final String v1, v2;
public final int dist;
public Edge(String v1, String v2, int dist) {
this.v1 = v1;
this.v2 = v2;
this.dist = dist;
}
}
/** One vertex of the graph, complete with mappings to neighbouring vertices */
public static class Vertex implements Comparable<Vertex> {
public final String name;
public int dist = Integer.MAX_VALUE; // MAX_VALUE assumed to be infinity
public Vertex previous = null;
public final Map<Vertex, Integer> neighbours = new HashMap<>();
public Vertex(String name) {
this.name = name;
}
private void printPath() {
if (this == this.previous) {
System.out.printf("%s", this.name);
} else if (this.previous == null) {
System.out.printf("%s(unreached)", this.name);
} else {
this.previous.printPath();
System.out.printf(" -> %s(%d)", this.name, this.dist);
}
}
public int compareTo(Vertex other) {
return Integer.compare(dist, other.dist);
}
}
/** Builds a graph from a set of edges */
public Graph(Edge[] edges) {
graph = new HashMap<>(edges.length);
//one pass to find all vertices
for (Edge e : edges) {
if (!graph.containsKey(e.v1)) graph.put(e.v1, new Vertex(e.v1));
if (!graph.containsKey(e.v2)) graph.put(e.v2, new Vertex(e.v2));
}
//another pass to set neighbouring vertices
for (Edge e : edges) {
graph.get(e.v1).neighbours.put(graph.get(e.v2), e.dist);
//graph.get(e.v2).neighbours.put(graph.get(e.v1), e.dist); // also do this for an undirected graph
}
}
/** Runs dijkstra using a specified source vertex */
public void dijkstra(String startName) {
if (!graph.containsKey(startName)) {
System.err.printf("Graph doesn't contain start vertex "%s"n", startName);
return;
}
final Vertex source = graph.get(startName);
NavigableSet<Vertex> q = new TreeSet<>();
// set-up vertices
for (Vertex v : graph.values()) {
v.previous = v == source ? source : null;
v.dist = v == source ? 0 : Integer.MAX_VALUE;
q.add(v);
}
dijkstra(q);
}
/** Implementation of dijkstra's algorithm using a binary heap. */
private void dijkstra(final NavigableSet<Vertex> q) {
Vertex u, v;
while (!q.isEmpty()) {
u = q.pollFirst(); // vertex with shortest distance (first iteration will return source)
if (u.dist == Integer.MAX_VALUE) break; // we can ignore u (and any other remaining vertices) since they are unreachable
//look at distances to each neighbour
for (Map.Entry<Vertex, Integer> a : u.neighbours.entrySet()) {
v = a.getKey(); //the neighbour in this iteration
final int alternateDist = u.dist + a.getValue();
if (alternateDist < v.dist) { // shorter path to neighbour found
q.remove(v);
v.dist = alternateDist;
v.previous = u;
q.add(v);
}
}
}
}
/** Prints a path from the source to the specified vertex */
public void printPath(String endName) {
if (!graph.containsKey(endName)) {
System.err.printf("Graph doesn't contain end vertex "%s"n", endName);
return;
}
graph.get(endName).printPath();
System.out.println();
}
/** Prints the path from the source to every vertex (output order is not guaranteed) */
public void printAllPaths() {
for (Vertex v : graph.values()) {
v.printPath();
System.out.println();
}
}
}
rosettacode.org
C
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
//#define BIG_EXAMPLE
typedef struct node_t node_t, *heap_t;
typedef struct edge_t edge_t;
struct edge_t {
node_t *nd; /* target of this edge */
edge_t *sibling;/* for singly linked list */
int len; /* edge cost */
};
struct node_t {
edge_t *edge; /* singly linked list of edges */
node_t *via; /* where previous node is in shortest path */
double dist; /* distance from origining node */
char name[8]; /* the, er, name */
int heap_idx; /* link to heap position for updating distance */
};
/* --- edge management --- */
#ifdef BIG_EXAMPLE
# define BLOCK_SIZE (1024 * 32 - 1)
#else
# define BLOCK_SIZE 15
#endif
edge_t *edge_root = 0, *e_next = 0;
/* Don't mind the memory management stuff, they are besides the point.
Pretend e_next = malloc(sizeof(edge_t)) */
void add_edge(node_t *a, node_t *b, double d)
{
if (e_next == edge_root) {
edge_root = malloc(sizeof(edge_t) * (BLOCK_SIZE + 1));
edge_root[BLOCK_SIZE].sibling = e_next;
e_next = edge_root + BLOCK_SIZE;
}
--e_next;
e_next->nd = b;
e_next->len = d;
e_next->sibling = a->edge;
a->edge = e_next;
}
void free_edges()
{
for (; edge_root; edge_root = e_next) {
e_next = edge_root[BLOCK_SIZE].sibling;
free(edge_root);
}
}
/* --- priority queue stuff --- */
heap_t *heap;
int heap_len;
void set_dist(node_t *nd, node_t *via, double d)
{
int i, j;
/* already knew better path */
if (nd->via && d >= nd->dist) return;
/* find existing heap entry, or create a new one */
nd->dist = d;
nd->via = via;
i = nd->heap_idx;
if (!i) i = ++heap_len;
/* upheap */
for (; i > 1 && nd->dist < heap[j = i/2]->dist; i = j)
(heap[i] = heap[j])->heap_idx = i;
heap[i] = nd;
nd->heap_idx = i;
}
node_t * pop_queue()
{
node_t *nd, *tmp;
int i, j;
if (!heap_len) return 0;
/* remove leading element, pull tail element there and downheap */
nd = heap[1];
tmp = heap[heap_len--];
for (i = 1; i < heap_len && (j = i * 2) <= heap_len; i = j) {
if (j < heap_len && heap[j]->dist > heap[j+1]->dist) j++;
if (heap[j]->dist >= tmp->dist) break;
(heap[i] = heap[j])->heap_idx = i;
}
heap[i] = tmp;
tmp->heap_idx = i;
return nd;
}
/* --- Dijkstra stuff; unreachable nodes will never make into the queue --- */
void calc_all(node_t *start)
{
node_t *lead;
edge_t *e;
set_dist(start, start, 0);
while ((lead = pop_queue()))
for (e = lead->edge; e; e = e->sibling)
set_dist(e->nd, lead, lead->dist + e->len);
}
void show_path(node_t *nd)
{
if (nd->via == nd)
printf("%s", nd->name);
else if (!nd->via)
printf("%s(unreached)", nd->name);
else {
show_path(nd->via);
printf("-> %s(%g) ", nd->name, nd->dist);
}
}
int main(void)
{
#ifndef BIG_EXAMPLE
int i;
# define N_NODES ('f' - 'a' + 1)
node_t *nodes = calloc(sizeof(node_t), N_NODES);
for (i = 0; i < N_NODES; i++)
sprintf(nodes[i].name, "%c", 'a' + i);
# define E(a, b, c) add_edge(nodes + (a - 'a'), nodes + (b - 'a'), c)
E('a', 'b', 7); E('a', 'c', 9); E('a', 'f', 14);
E('b', 'c', 10);E('b', 'd', 15);E('c', 'd', 11);
E('c', 'f', 2); E('d', 'e', 6); E('e', 'f', 9);
# undef E
#else /* BIG_EXAMPLE */
int i, j, c;
# define N_NODES 4000
node_t *nodes = calloc(sizeof(node_t), N_NODES);
for (i = 0; i < N_NODES; i++)
sprintf(nodes[i].name, "%d", i + 1);
/* given any pair of nodes, there's about 50% chance they are not
connected; if connected, the cost is randomly chosen between 0
and 49 (inclusive! see output for consequences) */
for (i = 0; i < N_NODES; i++) {
for (j = 0; j < N_NODES; j++) {
/* majority of runtime is actually spent here */
if (i == j) continue;
c = rand() % 100;
if (c < 50) continue;
add_edge(nodes + i, nodes + j, c - 50);
}
}
#endif
heap = calloc(sizeof(heap_t), N_NODES + 1);
heap_len = 0;
calc_all(nodes);
for (i = 0; i < N_NODES; i++) {
show_path(nodes + i);
putchar('n');
}
#if 0
/* real programmers don't free memories (they use Fortran) */
free_edges();
free(heap);
free(nodes);
#endif
return 0;
}
rosettacode.org
PHP
<?php
function dijkstra($graph_array, $source, $target) {
$vertices = array();
$neighbours = array();
foreach ($graph_array as $edge) {
array_push($vertices, $edge[0], $edge[1]);
$neighbours[$edge[0]][] = array("end" => $edge[1], "cost" => $edge[2]);
$neighbours[$edge[1]][] = array("end" => $edge[0], "cost" => $edge[2]);
}
$vertices = array_unique($vertices);
foreach ($vertices as $vertex) {
$dist[$vertex] = INF;
$previous[$vertex] = NULL;
}
$dist[$source] = 0;
$Q = $vertices;
while (count($Q) > 0) {
// TODO - Find faster way to get minimum
$min = INF;
foreach ($Q as $vertex){
if ($dist[$vertex] < $min) {
$min = $dist[$vertex];
$u = $vertex;
}
}
$Q = array_diff($Q, array($u));
if ($dist[$u] == INF or $u == $target) {
break;
}
if (isset($neighbours[$u])) {
foreach ($neighbours[$u] as $arr) {
$alt = $dist[$u] + $arr["cost"];
if ($alt < $dist[$arr["end"]]) {
$dist[$arr["end"]] = $alt;
$previous[$arr["end"]] = $u;
}
}
}
}
$path = array();
$u = $target;
while (isset($previous[$u])) {
array_unshift($path, $u);
$u = $previous[$u];
}
array_unshift($path, $u);
return $path;
}
$graph_array = array(
array("a", "b", 7),
array("a", "c", 9),
array("a", "f", 14),
array("b", "c", 10),
array("b", "d", 15),
array("c", "d", 11),
array("c", "f", 2),
array("d", "e", 6),
array("e", "f", 9)
);
$path = dijkstra($graph_array, "a", "e");
echo "path is: ".implode(", ", $path)."n";
Output is:
path is: a, c, f, e
rosettacode.org
Python
from collections import namedtuple, queue
from pprint import pprint as pp
inf = float('inf')
Edge = namedtuple('Edge', 'start, end, cost')
class Graph():
def __init__(self, edges):
self.edges = edges2 = [Edge(*edge) for edge in edges]
self.vertices = set(sum(([e.start, e.end] for e in edges2), []))
def dijkstra(self, source, dest):
assert source in self.vertices
dist = {vertex: inf for vertex in self.vertices}
previous = {vertex: None for vertex in self.vertices}
dist[source] = 0
q = self.vertices.copy()
neighbours = {vertex: set() for vertex in self.vertices}
for start, end, cost in self.edges:
neighbours[start].add((end, cost))
#pp(neighbours)
while q:
u = min(q, key=lambda vertex: dist[vertex])
q.remove(u)
if dist[u] == inf or u == dest:
break
for v, cost in neighbours[u]:
alt = dist[u] + cost
if alt < dist[v]: # Relax (u,v,a)
dist[v] = alt
previous[v] = u
#pp(previous)
s, u = deque(), dest
while previous[u]:
s.pushleft(u)
u = previous[u]
s.pushleft(u)
return s
graph = Graph([("a", "b", 7), ("a", "c", 9), ("a", "f", 14), ("b", "c", 10),
("b", "d", 15), ("c", "d", 11), ("c", "f", 2), ("d", "e", 6),
("e", "f", 9)])
pp(graph.dijkstra("a", "e"))
Output:
['a', 'c', 'd', 'e']
rosettacode.org
