Демографические таблицы – один из основных методов анализа демографических процессов. Они бывают общими – для повторяющихся демографических событий, и специальными – для неповторяющихся, а также простыми – для одного демографического процесса, и комбинированными – для нескольких процессов одновременно.
Таблица смертности – простая специальная таблица – числовая модель смертности, представляющая собой систему взаимосвязанных, упорядоченных по возрасту рядов чисел, отражающих процесс вымирания некоторого условного или реального поколения с фиксированной начальной численностью. Идея таблицы смертности впервые появилась в середине XVII века в работе Дж.Граунта (http://www.demoscope.ru/weekly/2006/0261/biblio05.php), современный вид таблицы смертности был рекомендован в конце XIX века Лондонским институтом актуариев.
Для построения таблиц смертности реального поколения необходимо собрать информацию за почти 100-летний период – период жизни одного поколения, она будет отражать закономерности вымирания определенной когорты, но с опозданием. Таблицы смертности для календарного года – это оценки смертности условного поколения. Они оперативно отражают изменения уровня смертности во времени и влияние на смертность особенностей текущего года.
В основу построения таблицы смертности положен принцип стационарного населения (ссылка на главу 13): «закрытое население», в котором отсутствует миграция; число рождений равно числу смертей, неизменная возрастная структура; любая совокупность новорожденных имеет тот же порядок вымирания (возрастные коэффициенты смертности), что и все остальные.
Как и любая демографическая таблица, таблица смертности имеет шкалу. Шкала приведена в первой колонке таблицы и отражает точное число полных лет, прошедших с момента рождения. Начальный возраст в таблице – 0 лет (момент рождения), конечный – w лет (возраст, к которому вымирает вся совокупность родившихся). Первая колонка таблицы – точный возраст х. Это единственная независимая переменная, которая может измеряться в днях, месяцах (при изучении младенческой смертности), но, как правило, измеряется в годах. В зависимости от длины возрастного интервала n выделяют полные (n=1) и краткие (n=5 или n=10) таблицы смертности. В таблице 1 приведен пример краткой таблицы смертности.
Таблица 1. Пример краткой таблицы смертности
| Точный возраст | число доживших до точного возраста х | число умирающих в интервале возраста от х до х+n | вероятность умереть в интервале возраста от x до х+n | вероятность выжить к возрасту х+n для всех тех, кто дожил до возраста х | среднее число человеко-лет, прожитое в интервале возраста от х до х+n теми, кто дожил до начала данного интервала | число человеко-лет жизни в возрасте х лет и старше | ожидаемая продолжительность жизни в точном возрасте х лет |
|---|---|---|---|---|---|---|---|
| х | lх | ndх | nqх | npх | nLх | Tх | Eх |
| 0 | 100000 | 525 | 0,00525 | 0,99475 | 99561 | 6550537 | 65,51 |
| 1 | 99475 | 133 | 0,001337 | 0,998663 | 397588 | 6450976 | 64,85 |
| 5 | 99342 | 93 | 0,000936 | 0,999064 | 496477 | 6053388 | 60,93 |
| 10 | 99249 | 143 | 0,001441 | 0,998559 | 495938 | 5556911 | 55,99 |
| 15 | 99106 | 397 | 0,004006 | 0,995994 | 494703 | 5060973 | 51,07 |
| 20 | 98709 | 722 | 0,007314 | 0,992686 | 491874 | 4566270 | 46,26 |
| 25 | 97987 | 1041 | 0,010624 | 0,989376 | 487542 | 4074396 | 41,58 |
| 30 | 96946 | 1796 | 0,018526 | 0,981474 | 480682 | 3586854 | 37,00 |
| 35 | 95150 | 2871 | 0,030173 | 0,969827 | 469182 | 3106172 | 32,65 |
| 40 | 92279 | 4105 | 0,044485 | 0,955515 | 451638 | 2636990 | 28,58 |
| 45 | 88174 | 5025 | 0,05699 | 0,94301 | 428702 | 2185352 | 24,78 |
| 50 | 83149 | 6185 | 0,074385 | 0,925615 | 401078 | 1756650 | 21,13 |
| 55 | 76964 | 8263 | 0,107362 | 0,892638 | 365235 | 1355572 | 17,61 |
| 60 | 68701 | 10947 | 0,159343 | 0,840657 | 317506 | 990337 | 14,42 |
| 65 | 57754 | 13293 | 0,230166 | 0,769834 | 256357 | 672831 | 11,65 |
| 70 | 44461 | 13955 | 0,313871 | 0,686129 | 187652 | 416474 | 9,37 |
| 75 | 30506 | 12072 | 0,395725 | 0,604275 | 122149 | 228822 | 7,50 |
| 80 | 18434 | 9809 | 0,532115 | 0,467885 | 66172 | 106673 | 5,79 |
| 85 | 8625 | 5506 | 0,638377 | 0,361623 | 27703 | 40501 | 4,70 |
| 90 | 3119 | 2207 | 0,707599 | 0,292401 | 9201 | 12798 | 4,10 |
| 95 | 912 | 493 | 0,54057 | 0,45943 | 2977 | 3597 | 3,94 |
| 100 | 419 | 419 | 1 | 0 | 620 | 620 | 1,48 |
Таблица смертности для календарного года строится на основе возрастных коэффициентов смертности (ссылка на главу 6 про показатели) (m(x) = frac{M(x)}{overline{P}(x) bullet T}), которые рассчитывают как отношение умерших по возрастам за год к среднегодовому населению. Эти коэффициенты смертности преобразуют в вероятности умереть, и после выбора корня таблицы l0 разворачивается вся таблица смертности – это так называемый демографический метод построения таблицы смертности. Численность населения, для которого строится таблица смертности, должна быть достаточно большой, чтобы исключить случайные колебания возрастных коэффициентов.
Первые формулы перехода от возрастных коэффициентов смертности к вероятностям умереть были предложены практически одновременно в середине XIX века У.Фаром и А.Кетле:
({_{n}^{}q}_{x} = frac{2 cdot {_{n}^{}m}_{x}}{2 + {_{n}^{}m}_{x}}) для однолетних возрастных интервалов
({_{n}^{}q}_{x} = frac{2n cdot {_{n}^{}m}_{x}}{2 + n cdot {_{n}^{}m}_{x}}) для n-летних возрастных интервалов.
Эти формулы перехода от возрастных коэффициентов смертности к вероятностям умереть основаны на гипотезе линейного изменения числа смертей в возрастных интервалах.
Формулы для ситуаций, когда гипотеза линейного изменения числа смертей работает плохо
В 1968 году американский демограф Чанг (Chiang) модифицировал эту формулу, введя в нее параметр (a_{x}), который показывает, какую долю возрастного интервала прожили умершие в этом интервале:
(q(x) = frac{n bullet m(x)}{1 + (n – a(x)) bullet m(x)})
Если (a_{x})=0,5, получим формулу Кетле-Фарра.
Для оценки параметра (a_{x}) в возрастном интервале 1-4 года используется эмпирическая формула, предложенная Коулом и Демени (Coale, Demeny, 1983). В таблице П1 приведены результаты оценок на основе этой формулы. Для остальных возрастов можно использовать гипотезу линейности функции дожития.
Таблица П1. Оценки параметра (a_{x} )в возрастном интервале 1-4 года
Мужчины Женщины Значения 1a0 Если 1m0 ≥ 0,107 0,330 0,350 Если 1m0 < 0,107 0,045+2,6841m0 0,053+2,8001m0 Значения 4a1 Если 1m0 ≥ 0,107 0,338 0,340 Если 1m0 < 0,107 0,413-0,7041m0 0,381-0,3801m0 Источник: Preston, Heuveline, Guillot Demography, p. 48. adapted from Coale and Demeny (1983), West modal life tables https://www.gwern.net/docs/statistics/2001-preston-demography.pdf
Часть показателей таблицы смертности рассчитывается для точных возрастов (lx, Ex), остальные – для возрастных интервалов.
lx – число доживших до точного возраста х из начальной численности когорты. Начальная численность когорты (поколения) или корень таблицы l0 обычно принимается равной 100000 человек (но может встречаться 1000, 10000 и даже 1). Корень таблицы задает масштаб расчетов. Ряд чисел доживающих называют функцией дожития. График функции дожития (см. Рис. 1) по мере снижения смертности стремится принять прямоугольную форму, это явление получило название квадратизации функции дожития.
ndx – числа умирающих в интервале возраста от х до (х+n). Сумма значений ndx равна числу родившихся l0.
nqx – вероятность умереть в интервале возраста от x до х+n; nqx=ndx/lx для всех тех, кто дожил до возраста х. Вероятность наступления смерти в возрастном интервале представляет собой усредненный риск смерти, относящийся ко всем членам когорты, дожившим до начала данного интервала.
Чтобы оценить вероятность смерти на первом году жизни, Росстат оценивает так называемый фактор сепарации f на основе числа смертей до 1 года в текущем и предыдущем годах:
(f = frac{M^{t – 1}}{M^{t – 1} + M^{t}})
где (M^{t – 1})– число младенцев, умерших в данном году, но родившихся в предыдущем году, (M^{t})– число младенцев, умерших в данном году и родившихся в данном году.
Вероятность смерти на первом году жизни рассчитывается на основании фактора сепарации, числа родившихся в текущем и предыдущем году и суммарного числа умерших детей до года в текущем году:
(q_{0} = frac{M_{0} bullet (1 – f)}{N_{t}} + frac{M_{0} bullet f}{N_{t – 1}})
где (N_{t} )и (N_{t – 1} )– числа родившихся в текущем и предыдущем годах, (M_{0})– число детей, умерших в текущем году в возрасте до 1 года, f – фактор сепарации.
В последнем возрастном интервале вероятность умереть приравнивается к 1.
npx – вероятность выжить к возрасту х+n для всех тех, кто дожил до возраста х; nqx+npx = 1.
nLx – среднее число человеко-лет, прожитое в интервале возраста от х до х+n теми, кто дожил до начала данного интервала (lx). Приближенно, при использовании гипотезы равномерного распределения смертей в возрастном интервале, этот показатель рассчитывается как полусумма чисел доживающих до начала и конца возрастного интервала, умноженная на длину возрастного интервала n. Эта гипотеза будет слишком грубой для детских и старших возрастов, где число смертей как правило смещено к началу возрастного интервала.
Согласно методике Росстата, в возрастном интервале от 0 до 1 года число человеко-лет рассчитывается по формуле:
(L_{0} = f bullet l_{0} + (1 – f) bullet l_{1})
Если в последней возрастной группе значение коэффициента смертности оказывается ниже коэффициента смертности в предыдущей возрастной группе, то значение Lω рассчитывается по формуле:
(L_{w} = frac{l_{w}}{2})
Тх – число человеко-лет жизни в возрасте х лет и старше, Tx=Lx+Lx+n+…+Lw.
Еx – ожидаемая продолжительность жизни в точном возрасте х лет, ее можно оценить на основе одной из формул. Формула (2) подразумевает линейное распределение смертей в возрастных интервалах.
(Е_{х} = frac{Т_{х}}{l_{x}} = frac{sum_{x}^{w}{_{n}^{}L}_{x}}{l_{x}}) (1) или (Е_{х} = frac{Т_{х}}{l_{x}} = frac{sum_{x}^{w}{{_{n}^{}d}_{x}(x + frac{n}{2})}}{l_{x}}) (2)
На рис. 1 приведены графики основных функций таблицы смертности.
Рис. 1. Графики функций таблицы смертности (слева направо и сверху вниз): числа доживающих, числа умерших, вероятность умереть, ожидаемая продолжительность жизни
Для оценки уровня смертности чаще всего пользуются важнейшей интегральной характеристикой смертности населения – ожидаемой продолжительностью жизни при рождении Е0. Этот показатель отражает число лет, которое в среднем предстоит прожить новорожденному при условии, что на протяжении всей жизни этого поколения возрастные уровни смертности останутся такими же, как в году, для которого рассчитан данный показатель. Е0 зависит только от распределения возрастных коэффициентов смертности и не может интерпретироваться как средний возраст смерти населения в данном году, который, в свою очередь, зависит еще и от возрастной структуры населения.
Например, в 2021 году ожидаемая продолжительность жизни при рождении у мужчин в России составила 65,51 года. Это означает, что новорожденные 2021 года в среднем проживут 60,51 года, но только при условии, что таблица смертности 2021 года на протяжении их жизни останется неизменной.
Когда число умирающих на первом году жизни достаточно велико, может проявиться так называемый парадокс младенческой смертности, при котором Е1›Е0. В настоящее время в большинстве экономически развитых стран этот парадокс отсутствует из-за низкого уровня младенческой смертности.
Кроме основных показателей, на основе таблицы смертности можно определить:
- отсроченную (интервальную) продолжительность жизни в интервале возраста. Например, отсроченная продолжительность жизни мужчин в трудоспособных возрастах будет рассчитываться по формуле: (frac{T_{15} – T_{65}}{l_{15}}), если за границы трудоспособного возраста принять 15 и 65 лет. На основе этого показателя можно оценить потери ожидаемой продолжительности жизни (в годах) для возрастного контингента на основе текущих характеристик смертности.
- медианную продолжительность жизни – возраст, к которому в живых остается ровно половина исходной численности поколения (0,5 bullet l(0)).
- модальную продолжительность предстоящей жизни – возраст, в котором умирает большая часть поколения.
Видео G-1-5-1+ Минуты 2.58 – до конца И Видео G-1-5-2+ 15.37-до конца Демографические таблицы. Таблица смертности
6.5.1. Построение полной таблицы смертности
Построение таблиц смертности является
в принципе несложной, но достаточно
трудоемкой вычислительной процедурой.
Она включает в себя несколько этапов3:
-
расчет значений
исходного показателя для всех возрастов
на основе данных статистики смертности
(распределения умерших
по возрастам); -
если необходимо, обработку этого ряда
значений для уст
ранения
искажений, вызванных возрастной
аккумуляцией; -
интерполяцию ряда
значений для устранения возможных
пропусков
или экстраполяцию для расчета значений
для самых
старших
возрастов; -
вычисление остальных
функций таблицы смертности.
Основная
методическая проблема построения
таблиц смертности,
как уже говорилось, связана с переходом
от реальных показателей повозрастной
смертности к табличным вероятностям
умереть в данном возрасте, т.е. оттх*
кqx.
Методы построения таблиц смертности
занимают большое место в демографии.
Можно повторить уже сказанное выше, что
история демографии в значительной мере
совпадает с историей
разработки и совершенствования этих
методов.
Современные таблицы
смертности рассчитываются с помощью
т.н. косвенного,
или
демографического,
метода. Демографический
метод назван так потому, что в его основе
лежат данные о повозрастной
смертности, а также о возрастно-половойструктуре населения,
получаемые во время переписей и текущего
учета.Косвенным этот метод назван,
чтобы противопоставить
его т.н. прямому
методу, или,
иначе, методу Р. Бека, основанному
на непосредственном расчете показателей
таблицысмертности
в ситуации, когда известно распределение
смертей на элементарные совокупности
сетки Лексиса4.
Исходным показателем
здесь служит повозрастной коэффициент
смертности, который приравнивается к
табличному
коэффициенту
смертности
(dx/Lx)
и на основе
которого определяются все функции
таблицы смертности, начиная, разумеется,
с вероятности умереть в возрастех
лет. Демографический метод позволяет
строить таблицы смертности, наиболее
адекватноотражающие
ее уровень. При этом на величину итоговых
показателей не влияют колебания
чисел родившихся и умерших вгоды,
предшествовавшие расчету5.
Проблема, связанная с переходом от
повозрастных коэффициентов смертности
к вероятностям смерти на возрастном
интервале (х,
х+п) лет,
состоит в том, что первые, как известно,
рассчитываются
по отношению к общему числу человеко-лет,
прожитых населением на этом возрастном
интервале, или к его приближению, т.е.
среднегодовому населению. Вторые же
рассчитываются по отношению к численности
населения в началевозрастного
интервала. Чтобы построить таблицу
смертности, надо установить
соотношение между ними, т.е. междутх
иqx.
Иначе говоря, нужно перейти оттх
кqx6.
Пусть Nx
– число
доживающих до возраста х
лет в реальном
населении. Из этого числа до следующего
возрастах+1 летне
доживет Dx.
Тогда, по
определению:
![]()
Вместе с тем повозрастной коэффициент
смертности тх равен
отношениюDx
к числу человеко-лет, прожитыхNx
в течение интервала
(х, х + 1).
Это число человеко-лет, в свою очередь,
равно сумме двух слагаемых:
Первое слагаемое
– это (Nx
– Dx,
т.е. число человеко-лет, прожитых на этом
интервале возраста теми, кто дожил до
возраста (х,
х + 1).
Второе слагаемое
– это число человеко-лет, прожитых на
этом интервале возраста теми, кто
не дожил до возраста(х, х + 1),т.е.
умер на этом интервале возраста. Это
число равно a‘x–Dx.

Последнее выражение есть знакомая
формула расчета повозрастного
коэффициента смертности.
Решим уравнение Рх
= (NX
–Dx)
+ a‘xDx
относительно
Nx:
Nx=Px+(1-a‘xDx).
Подставим
это выражение в приведенную выше формулу
для qx.
![]()
Если числитель и знаменатель этого
выражения разделить на Рx
, то получим искомое базисное соотношение
междуqx
итх:
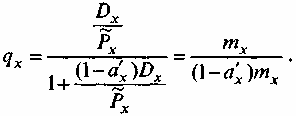
Величины
а0
а1
…варьируют от страны к стране в
зависимости от уровня смертности.
Для развивающихся
стран, в которых смертность высока,
обычно принимается
а0
– 0,3, a1
– 0,4 и 0,5 для всех остальных. Там же,
где смертность низка, наилучшей величиной
для а0является 0,1. В целом выбранная
величина не является критичной, за
исключением а0.
Более того, существует альтернативный
путь определенияq0без использования вышеприведенной
формулы. Речь идет о простом приравниванииq0к коэффициенту
младенческой смертности.Newell
С. Methods
and
Models
in
Demography.
London.
1988. P.
69.
Приведенное выше
уравнение является фундаментальным
для построения современных таблиц
смертности. Зная всеqx
ивыбрав корень
таблицы смертности
l0
, можно,
используя приведенные
выше соотношения между ними, построить
все остальные
функции таблиц смертности.
Соседние файлы в папке Медков Демография
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 6 августа 2021 года; проверки требует 1 правка.
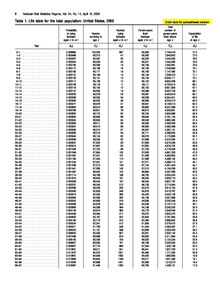
Пример таблицы смертности
Таблица смертности (также таблица дожития) — упорядоченный по возрасту ряд чисел, характеризующий порядок вымирания поколения людей, один из важнейших инструментов демографической статистики, широко используется на практике в страховании (см. Актуарные расчёты).
Классификация таблиц смертности[править | править код]
- по полу;
- по типу поселения (таблицы смертности городского и сельского населения);
- полные (включающие все возраста) и краткие (включающие возраста 0, 1, 5, 10, 15,…) таблицы смертности;
- таблицы смертности условного и реального поколения (последние рассчитываются крайне редко и только в научных целях).
Показатели таблицы и их общепринятые обозначения[править | править код]

Графики функции дожития lx для мужского населения Швеции за разные годы (ось абсцисс — возраст, ось ординат — доля доживающих, l0=1).
- х — возраст (от 0 до 100 лет; встречаются и другие верхние границы, например, 80 или 85 лет);
- lx («эль малое икс») — точное число доживающих до возраста х лет (l0 обычно принимается за 100000);
- dx= lx –lx+1— число умирающих при переходе от возраста х к возрасту х+1 лет;
- qx=dx / lx — вероятность умереть при переходе от возраста х к возрасту х+1 лет;
- рx=1-qx — вероятность дожития до возраста х+1 лет для лиц в точном возрасте х лет;
- Lx («эль большое икс») — среднее число живущих в возрасте х (с точки зрения демографии, это число человеко-лет, прожитых поколением в возрасте х), обычно[1] рассчитывается как среднее арифметическое между lx и lx+1 для всех возрастов, кроме 0 (L0 рассчитывается по особой формуле ввиду крайней неравномерности распределения младенческой смертности);
- Тx — число человеко-лет, которое предстоит прожить совокупности людей, находящихся в возрасте х лет (сумма Lx от возраста х до верхнего возрастного предела таблицы);
- еx=Тx / lx — средняя ожидаемая продолжительность предстоящей жизни в возрасте х лет. Как правило, под ожидаемой продолжительностью жизни (ОПЖ) понимают ожидаемую продолжительность жизни при рождении, то есть е0, которая и является итоговым показателем таблицы смертности. ОПЖ — вовсе не средний возраст смерти, а число лет, которое в среднем предстоит прожить индивидам данного возраста, если на протяжении всей их жизни, до полного вымирания поколения, сохранится данный режим смертности[2], то есть повозрастные коэффициенты смертности останутся неизменными. Таким образом, ОПЖ при рождении является интегральным индикатором смертности в данный момент времени, не зависящим от возрастной структуры населения. Снижение или рост ОПЖ обуславливается динамикой смертности во всех возрастных группах населения.
Методы построения таблиц смертности[править | править код]
- Метод Бёка
- Метод Буняковского
Исторический очерк[править | править код]
Древнейшей дошедшей до нас таблицей смертности является таблица Ульпиана (II—III век н. э.)[3].
Первая[уточнить] попытка построения таблицы смертности (для населения Лондона) принадлежит Джону Граунту (1662 год), однако только в 1693 году Э. Галлей построил достаточно полную таблицу. В России первую таблицу в начале XIX века построил К. Ф. Герман.[4]
См. также[править | править код]
- Смертность
- Модель смертности Гомперца-Мейкхема
- Популяционная динамика старения
- Страхование жизни
Примечания[править | править код]
- ↑ Это, вообще говоря, некорректно, так как функция дожития не является прямой, напоминая скорее кривую третьего порядка. Уточнить значение Lx можно, например, с помощью [demography.academic.ru/1419/%D0%91%D0%9E%D0%A0%D0%A2%D0%9AE%D0%92%D0%98%D0%A7%D0%90_%D0%9F%D0%9E%D0%9F%D0%A0%D0%90%D0%92%D0%9A%D0%90 поправки] Борткевича
- ↑ Вандескрик К. Демографический анализ. С. 135.
- ↑ В. И. Колесник. Таблица Ульпиана // Демографический энциклопедический словарь. — М.: Советская энциклопедия. Главный редактор Д. И. Валентей. 1985.
- ↑ Демографический энциклопедический словарь. С. 542.
Литература[править | править код]
- Демографический энциклопедический словарь. — М.: Советская энциклопедия. Главный редактор Д. И. Валентей. 1985.
- Вандескрик К. Демографический анализ. — М.: Академический проект; Гаудеамус, 2005. — 272 с. ISBN 5-8291-0500-4, 5-98426-024-7.
Ссылки[править | править код]
- Human Life Table Database (HLD)
- Human Mortality Database (HMD)
- Australian Human Mortality Database (AHMD)
- Canadian Human Mortality Database (CHMD)
- The Japanese Mortality Database (JMD)
- United States Mortality Database (USMDB)
- Latin American Human Mortality Database (LAHMD)
- Latin American Mortality Database (LAMBdA)
- UN Model Life Tables for Developing Countries
- UN Extended Model Life Tables
- WHO-Global Health Observatory Life Tables
- UK Government Actuary Department’s Interim Life Tables
- Actuarial Life Table from the U.S. Social Security department
- US CDC Vital Statistics Reports
- Ehemu Database
- World Health Organisation Life Tables
|
|
Некоторые внешние ссылки в этой статье ведут на сайты, занесённые в спам-лист. Эти сайты могут нарушать авторские права, быть признаны неавторитетными источниками или по другим причинам быть запрещены в Википедии. Редакторам следует заменить такие ссылки ссылками на соответствующие правилам сайты или библиографическими ссылками на печатные источники либо удалить их (возможно, вместе с подтверждаемым ими содержимым). Список проблемных ссылок
|
A diagram that shows the death rate for a defined population within a specific rate of time
What is a Mortality Table?
A mortality table is a diagram that shows the death rate for a defined population within a specific rate of time. Also known as a life table or an actuarial table, mortality tables are used in business by insurance companies to price insurance products and schemes for individuals.
Also, mortality tables can be used to develop complex mathematical models that represent the survival rates of different populations. They are also useful in the study of biology and medicine. The tables can help in the development of diagnostic criteria for certain drugs, as well as the type of treatment an individual should receive.
Summary
- A mortality table is a diagram that shows the death rate for a defined population within a specific period of time. It predicts the likelihood that an individual will die within the current year.
- One type of mortality table is the period life table, which determines mortality rates for a specific population during a defined period of time.
- The second type of mortality table is the cohort life table, which determines the overall mortality rate of a group of people with the same year of birth (a cohort).
Features of Mortality Tables
Mortality tables are very complex grids of numbers that predict the probability that an individual will die before their next birthday for each age based on a selection of variables.
Using certain characteristics such as gender and age, mortality tables provide probabilities of death based on thousands or the number of people in a group of 1,000 expected to die within a certain year. They usually cover ages in one-year increments from birth through age 100, with the probability of death increasing with age.
Mortality tables usually consist of separate data for men and women due to the substantial difference in mortality rates and the average lifespan for each gender.
Several statistics can be drawn as a result, including:
- Probability of surviving past a particular year of age
- Remaining life expectancy for people at different ages
- Proportion of the original birth cohort still living
Types of Mortality Tables
There are two main types of mortality tables – the period life table and the cohort life table.
1. Period life table
The period life table determines mortality rates for a specific population during a defined period of time, such as a single year or a group of years. It also assumes that mortality rates apply throughout the remainder of a person’s life, and as such, it does not take into consideration any future developments or changes to mortality rates.
Period life tables are useful in measuring mortality rates over a specific period and enable statistics to be drawn objectively by comparing mortality rates and trends over time both among different regions of a country, as well as among different countries.
2. Cohort life table
Also known as a generation life table, the cohort life table determines the overall mortality rate of a group of people with the same year of birth (a cohort). It shows the probability for an individual from the given cohort dying at each age over the course of their lifespan.
The cohort life table is based on age-specific probabilities of one dying, which are determined using a combination of mortality data for the specific cohort from past years long with estimates about mortality rates for the cohort in the future.
The cohort life table takes into account evolutions in observed and estimated mortality rates for the cohort throughout its lifetime, and as a result, it is regarded as a more accurate and appropriate measure of how long a person of a certain age would be expected to live on average.
Since mortality rates constantly change over time as a result of the development in the global health of populations and can be negatively impacted by deadly global pandemics, cohort life tables are typically preferred over period life tables.
It should be noted, however, that cohort life tables typically involve an element of subjectivity, as it requires estimates of future mortality rates in their calculations and is therefore vulnerable to any errors that may plague the projections.
It does result in period life tables to be used in favor of cohort life tables to compare life expectancies of different population sub-groups or predict how long people with generally good health will live.
Using Mortality Tables in Business
In business, mortality tables are generally used by insurance agencies to determine prices for insurance products. It requires a thorough process involving not only insurance agents but also actuaries who need to develop projections of future insured events, such as death, sickness, and disability.
Actuaries are responsible for developing mathematical models of the rates and timings of events, such as death or sickness, by studying historical data of the occurrence of such events in the past.
Actuaries also take into account how expectations will evolve, as well as age and other population characteristics to derive expected rates of deaths, sickness, and disability for the future. It enables them to form a comparison between people at risk of death and those that actually die to determine the probability of death at each age.
As mentioned previously, mortality tables play a significant role in helping insurance agencies determine the prices of various insurance products. The collection and accurate use of data are pivotal in developing such tables to be deployed in the insurance industry, as the more accurate data one can find, the stronger the actuarial structure of the insurance company will be.
Mortality Tables as Projections – Uses in Public Health
Mortality tables serve as actuarial resources to make projections on matters of public health, which are used to generate policy and epidemiological strategy. The mathematical tools help to determine disease and survival outcomes that help to better educate doctors and patients involving health concerns and diseases they may have contracted.
The tables lead to better-educated patients who can help make more informed decisions that determine professional care and treatment options. It is important, as often, individuals find themselves in positions where they have to make difficult decisions regarding which types of treatment they are to receive when they are unexpectedly diagnosed with a potentially life-threatening disease.
More Resources
CFI offers the Commercial Banking & Credit Analyst (CBCA)™ certification program for those looking to take their careers to the next level. To keep learning and advancing your career, the following resources will be helpful:
- Actuarial Life Table
- Variable Life Insurance
- Accidental Death and Dismemberment Insurance (AD&D)
- Property and Casualty Insurers
- See all wealth management resources
Имеются следующие данные о возрастных коэффициентах смертности:
для детей, в возрасте до одного года – 26,2‰ (К0),
для детей, достигших возраста один год – 6,5‰ (К1),
для детей, достигших возраста два года – 4,0‰ (К2),
для детей, достигших возраста три года – 2,5‰ (К3),
для детей, достигших возраста четыре года – 0,6‰ (К4).
Сумма предстоящих человеко-лет жизни для совокупности родившихся (10 тыс. чел.) составляет 636 600.
Составьте таблицу смертности для данных возрастных групп и определите среднюю ожидаемую продолжительность предстоящей жизни для возраста 0, 1, 2, 3 и 4 года.
Решение:
Таблицы смертности и средней продолжительности жизни, таблицы дожития – система взаимосвязанных упорядоченных по возрасту рядов чисел, организованных как описание процесса уменьшения с возрастом под действием смертности некоторого абстрактного поколения с фиксированной начальной численностью, именуемой корнем таблицы.
Макет таблицы смертности имеет вид:
| Возраст, лет | Число доживших до возраста х, лет | Вероятность дожить до следующего возраста | Вероятность смерти в течение года | Число живущих в возрасте х | Предстоящее число чел.-лет жизни | Средняя продолжительность предстоящей жизни | Коэффициент дожития |
|---|---|---|---|---|---|---|---|
| х | lx | px | qx | Lx | Tx | ex0 | Px |
В нашей задаче численность поколения условно равна 10 000 чел.
На основе возрастных коэффициентов смертности можно определить вероятность смерти в течение года для каждого года жизни (qх):
q0 = 0,0262
q1 = 0,0065
q2 = 0,0040
q3 = 0,0025
q4 = 0,0006
Затем определим вероятность дожития от возраста х до возраста х + 1 (рх):
p0 = 1 – q0 = 1 – 0,0262 = 0,9738
p1 = 1 – q1 = 1 – 0,0065 = 0,9935
p2 = 1 – q2 = 1 – 0,0040 = 0,9960
p3 = 1 – q3 = 1 – 0,0025 = 0,9975
p4 = 1 – q4 = 1 – 0,0006 = 0,9994
Теперь рассчитаем число доживающих до возраста х (lx) :
l0 = 10 000 (по условию)
l1 = l0 × p0 = 10 000 × 0,9738 = 9 738
l2 = l1 × p1 = 9 738 × 0,9935 = 9 675
l3 = l2 × p2 = 9 675 × 0,9960 = 9 636
l4 = l3 × p3 = 9 636 × 0,9975 = 9 612
l5 = l4 × p4 = 9 612 × 0,9994 = 9 606
Найдём число живущих в возрасте х лет (Lх), представляющее собой среднюю арифметическую из числа доживающих до возраста х и до возраста х + 1:
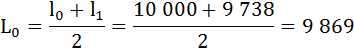
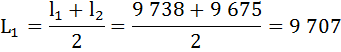
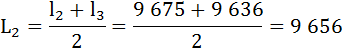
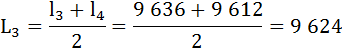
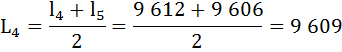
Определим число предстоящих человеко-лет жизни (Тх) для разных возрастов.
По условию задания
Т0 = 636 600
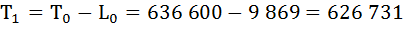
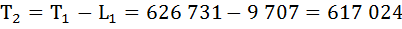
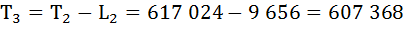
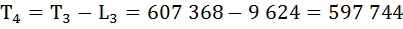
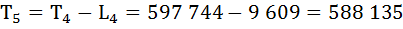
Рассчитаем среднюю продолжительность предстоящей жизни населения по формуле:
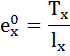
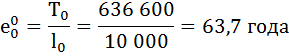
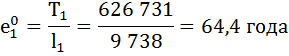
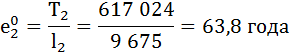
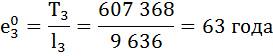
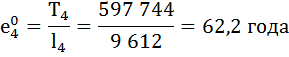
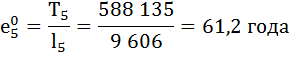
Коэффициент передвижки Px – вероятность для индивидуума в интервале возраста от х до х+1 прожить 1 год и попасть в интервал от х+1 до х+2 – определяется по формуле:
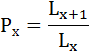
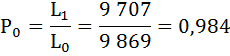
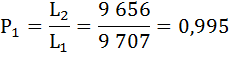
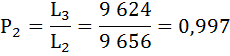
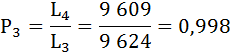
Полученные результаты занесём в таблицу:
| х | lx | px | qx | Lx | Tx | e0x | Px |
|---|---|---|---|---|---|---|---|
| 0 | 10 000 | 0,9738 | 0,0262 | 9 869 | 636 600 | 63,7 | 0,984 |
| 1 | 9 738 | 0,9935 | 0,0065 | 9 707 | 626 731 | 64,4 | 0,995 |
| 2 | 9 675 | 0,9960 | 0,0040 | 9 656 | 617 024 | 63,8 | 0,997 |
| 3 | 9 636 | 0,9975 | 0,0025 | 9 624 | 607 368 | 63 | 0,998 |
| 4 | 9 612 | 0,9994 | 0,0006 | 9 609 | 597 744 | 62,2 | – |
| 5 | – | – | – | – | 588 135 | 61,2 | – |
| – | – | – | – | – | – | – | – |
| 100 | – | – | – | – | – | – | – |
| 636 600 |
Условие задачи взято из: Социально-экономическая статистика: Практикум/Под ред. В. Н. Салина, Е. П. Шпаковской: Учеб. пособие. – М.:Финансы и статистика, 2003. – 192 с.
