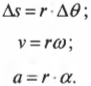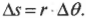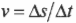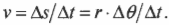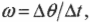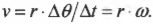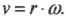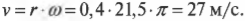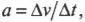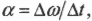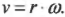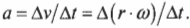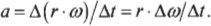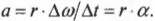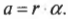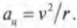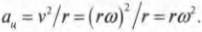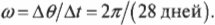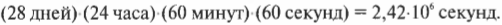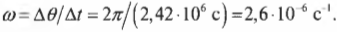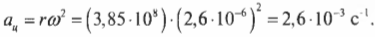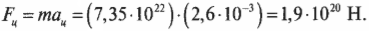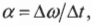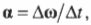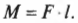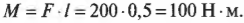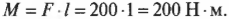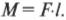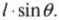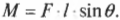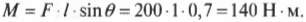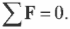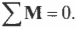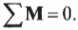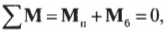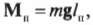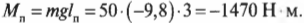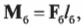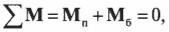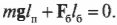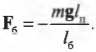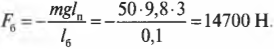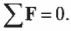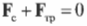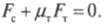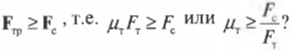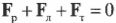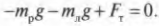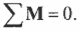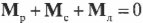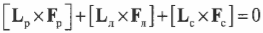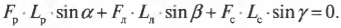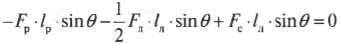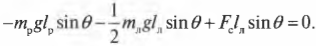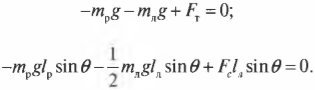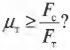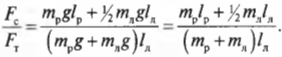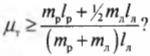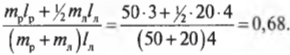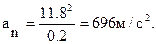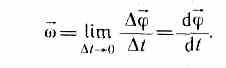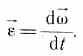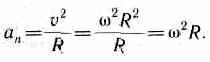Как найти тангенциальное ускорение колеса - Сайт, где вы сможете решить свои вопросы

В этой главе…

Переходим от поступательного движения к вращательному движению
Вычисляем тангенциальную скорость и тангенциальное ускорение
Выясняем связь между угловым ускорением и угловой скоростью
Разбираемся с моментом силы
Поддерживаем вращательное движение

Эта и следующая главы посвящены вращательному движению объектов самой разной природы: от космических станций до пращи. Именно такое движение стало причиной того, что наша планета имеет круглую форму. Если вам известны основные свойства прямолинейного движения и законы Ньютона (они подробно описываются в двух первых частях этой книги), то вы сможете быстро овладеть основами вращательного движения. Даже если вы позабыли некоторые сведения из прежних глав, не беда, ведь к ним всегда можно вернуться в случае необходимости. В этой главе представлены основные понятия вращательного движения: угловая скорость угловое ускорение, тангенциальное ускорение, момент силы и т.п. Однако довольно слов, приступим к делу!

Содержание

Переходим от прямолинейного движения к вращательному
Разбираемся с параметрами вращательного движения
- Вычисляем линейную скорость вращательного движения
- Вычисляем тангенциальное ускорение
- Вычисляем центростремительное ускорение
Используем векторы для изучения вращательного движения
- Определяем направление угловой скорости
- Определяем направление углового ускорения
Поднимаем грузы: момент силы
- Знакомимся с формулой момента силы
- Разбираемся с направлением приложенной силы и плечом силы
- Размышляем над тем, как создается момент силы
- Определяем направление момента силы
Уравновешиваем моменты сил
- Простой пример: вешаем рекламный плакат
- Более сложный пример: учитываем силу трения при расчете равновесия

Переходим от прямолинейного движения к вращательному

Для такого перехода нужно изменить уравнения, которые использовались ранее для описания прямолинейного движения. В главе 7 уже упоминались некоторые эквиваленты (или аналоги) из мира прямолинейного и вращательного движения.

Вот как выглядят основные формулы прямолинейного движения, которые подробно описываются в главе 3:

( v=Delta{s}/Delta{t} ), где ( v ) — это скорость, ( Delta{s} ) — перемещение, a ( Delta{t} ) — время перемещения;
( a=Delta{v}/Delta{t} ), где ( a ) — это ускорение, ( Delta{v} ) — изменение скорости, a ( Delta{t} ) — время изменения скорости;
( Delta{s}=v_0(t_1-t_0)+{}^1!/!_2a(t_1-t_0)^2 ), где ( v_0 ) — это начальная скорость, ( t_0 ) — это начальный момент времени, a ( t_1 ) — это конечный момент времени;
( v^2_1-v^2_0=2aDelta{s} ), где ( v_1 ) — это конечная скорость.

По аналогии можно легко вывести основные формулы вращательного движения:

( omega=Delta{theta}/Delta{t} ), где ( omega ) — угловая скорость, ( Delta{theta} ) — угол поворота, ( Delta{t} ) — время поворота на угол ( Delta{theta} );
( alpha=Delta{omega}/Delta{t} ), где ( alpha ) — угловое ускорение, ( Delta{omega} ) — изменение угловой скорости, ( Delta{t} ) — время изменения угловой скорости;
( theta=omega_0(t_1-t_0)+{}^1!/!_2a(t_1-t_0)^2 ), где ( omega_0 ) — это начальная скорость;
( omega^2_1-w^2_0=2as ), где ( omega_1 ) — это конечная скорость.

Разбираемся с параметрами вращательного движения

В физике движение принято разделять на поступательное и вращательное. При поступательном движении любая прямая, связанная с движущимся объектом, остается параллельной самой себе. При вращательном движении все точки тела движутся по окружностям. Тангенциальным движением называется часть вращательного движения, происходящего по касательной к окружности вращения, а радиальным (или нормальным) движением — часть вращательного движения, происходящего перпендикулярно (по нормали) к касательной, т.е. вдоль радиуса окружности.

Параметры прямолинейного поступательного и вращательного движений можно связать следующими формулами:

Допустим, колеса мотоцикла вращаются с угловой скоростью ( omega ), равной 21,5( 21,5pi ) радиан в секунду. С какой скоростью едет мотоцикл? Чтобы дать ответ на этот вопрос, достаточно воспользоваться простой формулой связи линейной и угловой скорости.

Вычисляем линейную скорость вращательного движения

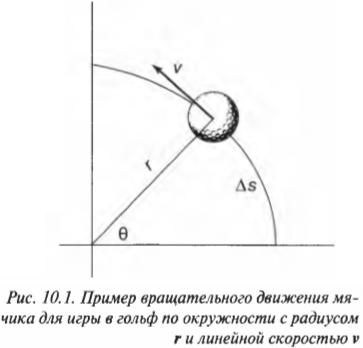
Скорость тангенциального движения материальной точки принято называть линейной скоростью вращательного движения. На рис. 10.1 приведен пример вращения мячика для игры в гольф по окружности с радиусом ( mathbf{r} ) и линейной скоростью ( mathbf{v} ). Скорость ( mathbf{v} ) является векторной величиной, т.е. обладает величиной и направлением (подробнее о векторах рассказывается в главе 4), перпендикулярным радиус-вектору ( mathbf{r} ).

Угловая скорость связана с линейной скоростью соотношением ( v=romega ), которое легко интуитивно понять. При одинаковой угловой скорости, чем дальше материальная точка от центра окружности вращения, тем больше ее линейная скорость.

Попробуем получить уже упомянутую выше формулу связи линейной и угловой скорости ( v=romega ). Длина окружности ( L ) радиуса ( r ) выражается известной формулой ( L=2pi r ), а полный угол, который охватывает окружность, равен ( 2pi ) радиан. Соответственно, длина дуги окружности длиной ( Delta s ), охватывающая угол ( Deltatheta ), равна:

Из формулы прямолинейного движения

путем подстановки выражения для ( Delta s ) получим:

Поскольку:

где ( omega ) — угловая скорость, ( Delta{theta} )— угол поворота, ( Delta{t} ) — время поворота на угол ( Delta{theta} ), то:

Теперь можно легко и просто дать ответ на вопрос, поставленный в конце предыдущего раздела, т.е. определить скорость мотоцикла по угловой скорости вращения его колес. Итак, колеса мотоцикла вращаются с угловой скоростью ( omega ), равной 21,5( pi ) радиан в секунду. Пусть радиус колеса ( r ) равен 40 см, тогда достаточно использовать следующую формулу:

Подставляя в нее значения, получим:

Итак, скорость мотоцикла равна 27 м/с или 97 км/ч.

Вычисляем тангенциальное ускорение

Тангенциальным ускорением называется скорость изменения величины линейной скорости вращательного движения. Эта характеристика вращательного движения очень похожа на линейное ускорение прямолинейного движения (см. главу 3). Например, точки на колесе мотоцикла в момент старта имеют нулевую линейную скорость, а спустя некоторое время после разгона ускоряются до некоторой ненулевой линейной скорости. Как определить это тангенциальное ускорение точки колеса? Переформулируем вопрос: как связать линейное ускорение

где ( a ) — это ускорение, ( Delta v ) — изменение скорости, a ( Delta t ) — время изменения скорости, с угловым ускорением

где ( Deltaomega ) — изменение угловой скорости, ( Delta t ) — время изменения угловой скорости?

Как мы уже знаем, линейная и угловая скорости связаны равенством

Подставим это выражение в предыдущую формулу линейного ускорения:

Поскольку радиус остается постоянным, то его можно вынести за скобки:

Поскольку угловое ускорение ( alpha=Deltaomega/Delta t ), то:

Итак, получаем следующую формулу связи между линейным и угловым ускорением:

Иначе говоря, тангенциальное ускорение равно произведению радиуса на угловое ускорение.

Вычисляем центростремительное ускорение

Центростремительнным ускорением называется ускорение, необходимое для удержания объекта на круговой орбите вращательного движения. Как связаны угловая скорость и центростремительное ускорение? Формула для центростремительного ускорения уже приводилась ранее (см. главу 7):

Теперь, используя известную формулу связи линейной и угловой скорости ( v=romega ), получим:

По этой формуле можно определить величину центростремительного ускорения по известной угловой скорости и радиусу. Например, для вычисления центростремительного ускорения Луны, вращающейся вокруг Земли, удобно использовать именно эту формулу.

Луна делает полный оборот вокруг Земли за 28 дней, т.е. за 28 дней Луна проходит ( 2pi ) радиан. Отсюда получаем угловую скорость Луны:

Чтобы получить значение угловой скорости в привычных единицах, следует преобразовать дни в секунды:

После подстановки этого значения в предыдущую формулу получим:

Средний радиус орбиты Луны равен 3,85·10⁸ м. Подставляя эти значения угловой скорости и радиуса в формулу центростремительного ускорения, получим:

Зная это ускорение и массу Луны, которая равна 7,35·10²² кг, можно определить центростремительную силу, необходимую для удержания Луны на ее орбите:

Используем векторы для изучения вращательного движения

В предыдущих разделах этой главы угловая скорость и угловое ускорение рассматривались как скаляры, т.е. как параметры, характеризующиеся только величиной. Однако эти параметры вращательного движения, на самом деле, являются векторами, т.е. они обладают величиной и направлением (см. главу 4). В этом разделе рассматривается величина и направление некоторых параметров вращательного движения.

Определяем направление угловой скорости

Как нам уже известно, вращающееся колесо мотоцикла имеет не только угловую скорость, но и угловое ускорение. Что можно сказать о направлении вектора угловой скорости? Оно не совпадает с направлением линейной тангенциальной скорости, а… перпендикулярно плоскости колеса!

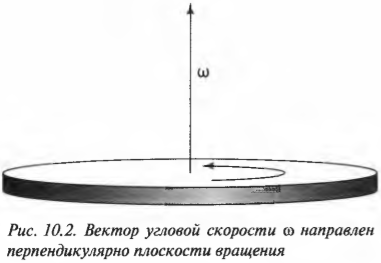
Эта новость всегда приводит к некоторому замешательству среди новичков: угловая скорость ( omega ), оказывается, направлена вдоль оси вращающегося колеса (рис. 10.2). Во вращающемся колесе единственной неподвижной точкой является его центр. Поэтому начало вектора угловой скорости принято располагать в центре окружности вращения.

Для определения направления вектора угловой скорости ( omega ) часто используют правило правой руки. Если охватить ладонью ось вращения, а пальцы свернуть так, чтобы они указывали на направление тангенциальной скорости, то вытянутый большой палец укажет направление вектора угловой скорости ( omega ).

Теперь угловую скорость можно использовать так же, как и остальные векторные характеристики движения. Направление вектора угловой скорости можно найти по правилу правой руки, а величину — по приведенной ранее формуле. То, что вектор угловой скорости направлен перпендикулярно плоскости вращательного движения, часто вызывает некоторые трудности у начинающих, но к этому можно быстро привыкнуть.

Определяем направление углового ускорения

Если вектор угловой скорости направлен перпендикулярно плоскости вращательного движения, то куда направлен вектор углового ускорения в случае замедления или ускорения вращения объекта? Как известно (см. предыдущие разделы), угловое ускорение определяется формулой:

где ( alpha ) — угловое ускорение, ( Deltaomega ) — изменение угловой скорости, ( Delta t )— время изменения угловой скорости.

В векторной форме оно имеет следующий вид:

где ( mathbf{alpha} ) — вектор углового ускорения, а ( Deltamathbf{omega} ) — изменение вектора угловой скорости. Отсюда ясно, что направление вектора углового ускорения совпадает с направлением изменения вектора угловой скорости.

Если вектор угловой скорости меняется только по величине, то направление вектора углового ускорения параллельно направлению вектора угловой скорости. Если величина угловой скорости растет, то направление вектора углового ускорения совпадает с направлением вектора угловой скорости, как показано на рис. 10.3.

А если величина угловой скорости падает, то направление вектора углового ускорения противоположно направлению вектора угловой скорости, как показано на рис. 10.4.

Поднимаем грузы: момент силы

В физике большое значение имеет не только время, но и место приложения силы. Всем когда-либо приходилось пользоваться рычагом для перемещения тяжелых грузов. Чем длиннее рычаг, тем легче сдвинуть груз. На языке физики применение силы с помощью рычага характеризуется понятием момент силы.

Приложение момента силы неразрывно связано с вращательным движением объектов. Если приложить силу к краю карусели, то карусель начнет вращательное движение. Чем дальше точка приложения силы, тем легче раскрутить карусель до заданной угловой скорости (параметры вращательного движения описываются в главе 1 1 ).

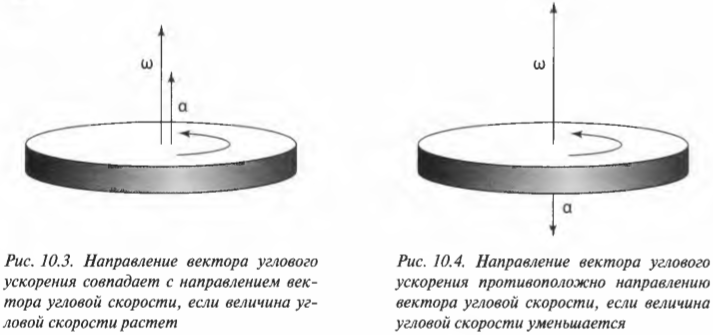
В верхней части рис. 10.5 показаны весы-качели с грузом массы ( m_1 ) на одном конце и грузом большей массы ( m_2=2m_1 ) посередине. Чтобы уравновесить весы-качели, нужно сместить груз с большей массой ( m_2 ) к другому концу весов, как показано в нижней части рис. 10.5. Как известно из опыта, размещение груза в точке вращения весов не приводит к уравновешиванию весов. Чтобы уравновесить весы, нужно сдвинуть груз с большей массой ( m_2=2m_1 ) к другому концу весов на расстояние вдвое меньшее, чем расстояние от точки вращения до второго груза с массой ( m_1 ).

Знакомимся с формулой момента силы

Для уравновешивания весов важно не только, какая сила используется, но и где она прикладывается. Расстояние от точки приложения силы до точки вращения называется плечом силы.

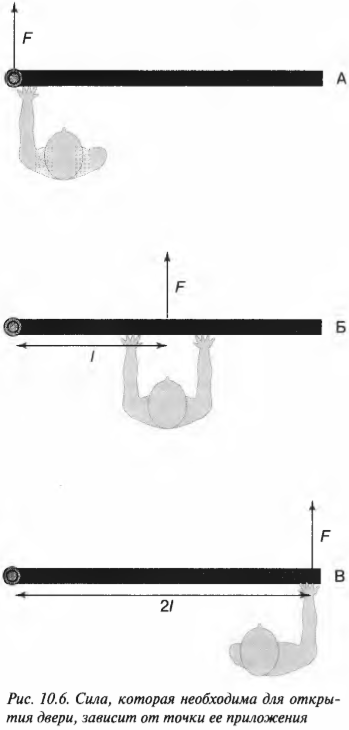
Предположим, что нам нужно открыть дверь, схематически показанную на рис. 10.6. Как известно из опыта, дверь практически невозможно открыть, если прилагать силу вблизи петель (см. схему А на рис. 10.6). Однако, если приложить силу посередине двери, то открыть ее будет гораздо проще (см. схему Б на рис. 10.6). Наконец, прилагая силу у противоположного края двери по отношению к расположению петель, ее можно открыть с еще меньшим усилием (см. схему В на рис. 10.6).

На рис. 10.6 расстояние от мест расположения петель до точки приложения силы и есть плечо силы. Моментом силы называется произведение прилагаемой силы ( F ) на плечо силы ( l ):

Момент силы в системе СИ измеряется в Н·м, а в системе СГС — в дин·см (подробнее эти системы единиц измерения описываются в главе 2).

Вернемся к примеру на рис. 10.6, где требуется открыть дверь шириной 1 м с помощью силы величиной 200 Н. В случае А (см. рис. 10.6) плечо силы равно нулю и произведение этого плеча на силу любой величины (включая и силу 200 Н) даст нулевой момент силы. В случае Б (см. рис. 10.6) плечо силы равно половине ширины двери, т.е. плечо силы ( l ) равно 0,5 м и момент силы будет равен:

В случае В (см. рис. 10.6) плечо силы равно ширине двери, т.е. плечо силы ( l ) равно 1 м и момент силы будет равен:

Итак, увеличение вдвое длины плеча при той же силе дает нам такое же увеличение момента силы. До сих пор сила прилагалась перпендикулярно к линии, соединяющей точку приложения силы и точку вращения. А что будет с моментом силы, если дверь будет немного приоткрыта и направление силы уже будет не перпендикулярным?

Разбираемся с направлением приложенной силы и плечом силы

Допустим, что сила приложена не перпендикулярно к поверхности двери, а параллельно, как показано на схеме А на рис. 10.7. Как известно из опыта, таким образом дверь открыть невозможно. Дело в том, что у такой силы нет проекции, которая бы могла вызвать вращательное движение. Точнее говоря, у такой силы нет ненулевого плеча для создания вращательного момента силы.

Размышляем над тем, как создается момент силы

Момент силы из предыдущего примера требуется создавать всегда для открытия двери независимо от того, какую дверь приходится открывать: легкую калитку изгороди или массивную дверь банковского сейфа. Как вычислить необходимый момент силы? Сначала нужно определить плечо сил, а потом умножить его на величину силы.

Однако не всегда все так просто. Посмотрите на схему Б на рис. 10.7. Как видите, сила прилагается под некоторым углом ( theta ). Как в таком случае определить плечо силы? Если бы угол ( theta ) был прямым, то мы могли бы воспользоваться уже известно нам формулой:

Однако в данном случае угол ( theta ) не является прямым.

В таком случае нужно просто помнить следующее правило: плечом силы называется длина перпендикуляра, опущенного из предполагаемой точки вращения на прямую, относительно которой действует сила.

Попробуем применить это правило определения плеча силы для схемы Б на рис. 10.7. Нужно продлить линию, вдоль которой действует сила, а потом опустить на нее перпендикуляр из точки вращения двери. Из полученного прямоугольного треугольника легко определить искомое плечо силы:

Если угол ( theta ) равен нулю, то никакого момента силы не возникает (см. схему А на рис. 10.7).

Итак, получаем для момента силы для схемы Б на рис. 10.7:

Например, если требуется открыть дверь шириной 1 м с помощью силы величиной 200 Н, приложенной под углом ( theta ) = 45°, то создаваемый момент этой силы будет равен:

Как видите, этот момент силы 140 Н·м меньше, чем момент силы 200 Н·м, созданный под прямым углом на схеме В на рис. 10.6.

Определяем направление момента силы

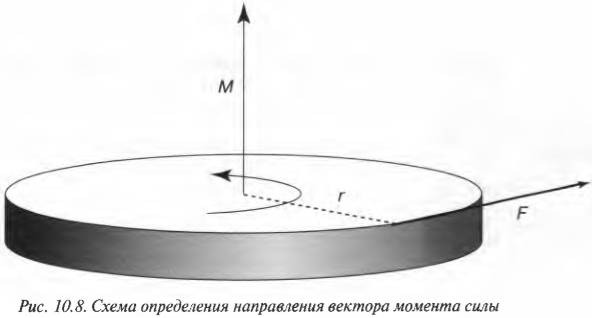
Учитывая все приведенные выше сведения о моменте силы, у читателя вполне может возникнуть подозрение, что момент силы обладает направлением. И это действительно так. Момент силы является векторной величиной, направление которой определяется по правилу правой руки. Если охватить ладонью ось вращения, а пальцы свернуть так, чтобы они указывали на направление силы, то вытянутый большой палец укажет направление вектора момента силы.

На рис. 10.8 показан пример силы ( mathbf{F} ) с плечом ( mathbf{l} ) и соответствующего вектора момента сил ( mathbf{M} ).

Уравновешиваем моменты сил

В жизни нам часто приходится сталкиваться с равновесными состояниями. Как равновесное механическое состояние определяется с точки зрения физики? Обычно физики подразумевают под равновесным состоянием объекта то, что он не испытывает никакого ускорения (но может двигаться с постоянной скоростью).

Для поступательного движения равновесное состояние означает, что сумма всех сил, действующих на объект равна нулю:

Иначе говоря, результирующая действующая сила равна нулю.

Вращательное движение также может быть равновесным, если такое движение происходит без углового ускорения, т.е. с постоянной угловой скоростью.

Для вращательного движения равновесное состояние означает, что сумма всех моментов сил, действующих на объект, равна нулю:

Как видите, это условие равновесного вращательного движения аналогично условию равновесного поступательного движения. Условия равновесного вращательного движения удобно использовать для определения момента силы, необходимого для уравновешивания неравномерно вращающегося объекта.

Простой пример: вешаем рекламный плакат

Предположим, что у входа в магазин нужно повесить большой и тяжелый рекламный плакат, как показано на рис. 10.9. Хозяин магазина пытался сделать это и раньше, но у него ничего не выходило, поскольку он использовал очень непрочный болт.

Попробуем определить силу, с которой болт должен удерживать всю конструкцию, показанную на рис. 10.9. Пусть плакат имеет массу 50 кг и висит на шесте 3 м от точки опоры шеста, а массу шеста в данном примере будем считать пренебрежимо малой. Болт находится в 10 см от точки опоры шеста.

Согласно условиям равновесия, сумма всех моментов сил должна быть равна нулю:

Иначе говоря:

где ( mathbf{M_п} ) — это момент силы со стороны плаката, а ( mathbf{M_б} ) — это момент силы со стороны болта.

Чему равны упомянутые моменты? Момент силы со стороны плаката можно легко определить по формуле:

где ( m ) = 50 кг — это масса плаката, ( mathbf{g} ) — ускорение свободного падения под действием силы гравитационного притяжения (силы тяжести), ( mmathbf{g} ) — сила тяжести плаката, а ( l_п ) = 3 м — это плечо силы тяжести плаката.

Подставляя значения, получим:

Обратите внимание, что здесь перед ускорением свободного падения под действием силы гравитационного притяжения стоит знак “минус”. Это значит, что вектор ускорения свободного падения направлен вниз, т.е. в сторону, противоположную выбранному направлению оси координат.

Момент силы со стороны болта определяется формулой:

где ( mathbf{F_б} ) — это искомая сила, с которой болт должен удерживать всю конструкцию, а ( l_б ) = 0,1 м — это ее плечо.

Подставляя полученные выражения для моментов сил в формулу:

получим, что:

Отсюда с помощью простых алгебраических преобразований получим искомую силу:

Как видите сила, с которой болт должен удерживать всю конструкцию, направлена противоположно вектору ускорения свободного падения, т.е. вверх.

Подставляя значения, получим искомый ответ:

Более сложный пример: учитываем силу трения при расчете равновесия

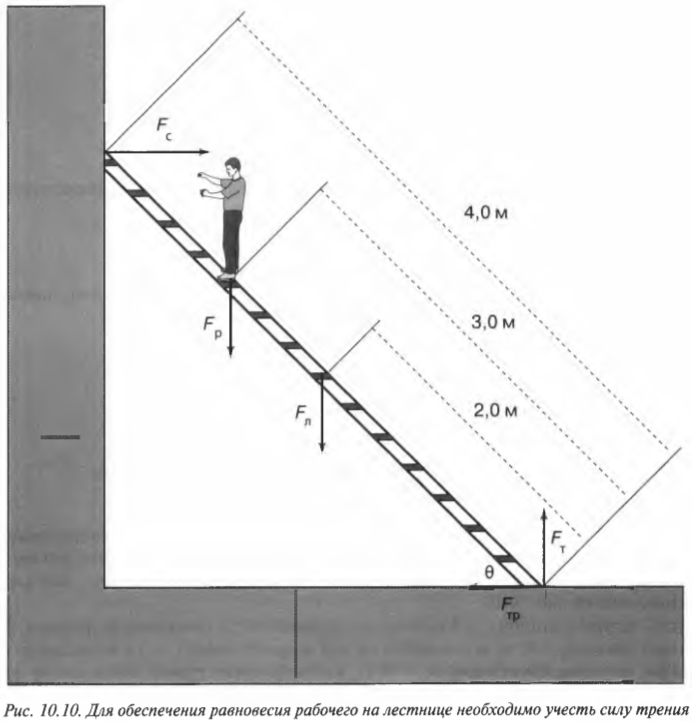
Рассмотрим теперь другую более сложную задачу, в которой для расчета равновесия системы объектов нужно учесть силу трения. Предположим, что работник магазина решил использовать переносную лестницу для монтажа рекламного плаката, как схематически показано на рис. 10.10.

Пусть лестница длиной ( l_л ) = 4 м стоит под углом ( theta ) = 45° к поверхности тротуара, работник имеет массу ( m_р ) = 45 кг и находится на ней на расстоянии ( l_р ) = 3 м от нижнего конца лестницы, лестница имеет массу (m_л ) = 20 кг, а коэффициент трения покоя между поверхностью тротуара и концами лестницы равен ( mu_п ) = 0,7. Вопрос: будет ли такая система объектов находиться в состоянии равновесия? Попросту говоря, достаточной ли будет сила трения, чтобы лестница вместе с рабочим не соскользнула и упала?

Итак, для ответа на этот вопрос нам нужно учесть следующие силы, действующие на лестницу:

( mathbf{F_с} ) — нормальная сила со стороны стены;
( mathbf{F_р} ) — вес рабочего;
( mathbf{F_л} ) — вес лестницы;
( mathbf{F_{тр}} ) — сила трения между поверхностью тротуара и концами лестницы;
( mathbf{F_т} ) — нормальная сила со стороны тротуара.

Согласно условиям равновесного поступательного движения, сумма всех сил, действующих на лестницу, должна быть равна нулю:

Это значит, что сумма всех сил вдоль горизонтальной оси, а именно нормальной силы со стороны стены ( mathbf{F_с} ) и силы трения между поверхностью тротуара и концами лестницы ( mathbf{F_{тр}} ), должна быть равна нулю, то есть:

или

Перефразируя поставленный выше вопрос о достаточности силы трения, получим: выполняется ли условие

Кроме того, сумма всех сил вдоль вертикальной оси, а именно веса рабочего ( mathbf{F_р} ), веса лестницы ( mathbf{F_л} ) и нормальной силы со стороны тротуара ( mathbf{F_т} ), должна быть равна нулю, то есть:

или

Согласно условиям равновесного вращательного движения, также необходимо равенство нулю всех моментов сил, действующих на лестницу:

Пусть предполагаемой точкой вращения является нижний конец лестницы, тогда должна быть равна нулю сумма моментов сил, создаваемых весом рабочего ( mathbf{M_р=[L_р!times! F_р]} ), весом лестницы ( mathbf{M_л=[L_л!times!F_л]} ) и нормальной силой со стороны стены ( mathbf{M_с=[L_с!times! F_с]} ):

или

Поскольку ( L_р=l_р ), ( L_л=l_л/2 ) (центр тяжести лестницы находится посередине лестницы), ( L_с=l_л ), ( alpha=360^{circ}-theta ), ( beta=360^{circ}-theta ) и ( gamma=theta ), то получим:

или

Таким образом, мы получили систему из двух уравнений с двумя неизвестными сил ( mathbf{F_с} ) и ( mathbf{F_т} ):

Зададимся вопросом: соблюдается ли условие

Из системы двух уравнений получим:

Итак, остается выяснить, соблюдается ли условие:

После подстановки значений получим:

Поскольку ( mu_т ) = 0,7, то упомянутое условие соблюдается, и лестница с рабочим не упадет.

Глава 10. Вращаем объекты: момент силы

3.4 (68.5%) 40 votes

Источник

Рассмотри твердое тело, вращающееся вокруг неподвижной оси z . Сделаем рисунок. Ось вращения направим перпендикулярно плоскости рисунка, на нас. Пусть φ – угол поворота тела вокруг оси, отсчитываемый от некоторого начального положения. За положительное направление выберем направление против часовой стрелки. Угловая скорость ω равна производной угла поворота по времени t :
.
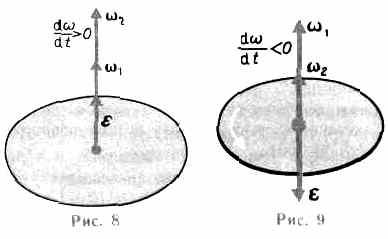
При , тело вращается против часовой стрелки; при – по часовой. Вектор угловой скорости направлен перпендикулярно плоскости рисунка. При он направлен на нас; при – от нас.

Угловое ускорение ε равно производной угловой скорости по времени:
.
Вектор углового ускорения также направлен перпендикулярно плоскости рисунка. При он направлен на нас; при – от нас.

Рассмотрим точку A , принадлежащую твердому телу. Опустим из нее перпендикуляр OA на ось вращения. Пусть – расстояние от точки до оси. Траекторией движения точки A является окружность (или дуга) с центром в точке O радиуса .

Абсолютное значение скорости точки A определяется по формуле:
.
Вектор скорости направлен по касательной к траектории (окружности), перпендикулярно отрезку OA . При этом вектор должен производить закручивание в ту же сторону, что и вектор угловой скорости .

Касательное (или тангенциальное) ускорение точки A определяется аналогично скорости:
.
Оно направлено по касательной к окружности, перпендикулярно OA . При этом вектор должен производить закручивание в ту же сторону, что и вектор углового ускорения .

Нормальное ускорение всегда направлено к центру окружности и имеет абсолютную величину
.

Полное ускорение точки A , или просто ускорение, равно векторной сумме касательного и нормального ускорений:
.
Поскольку векторы и перпендикулярны, то абсолютная величина ускорения точки A определяется по формуле:
.

Теперь рассмотрим прямолинейное поступательное движение тела. Направим ось x вдоль его линии движения. Пусть s есть перемещение тела вдоль этой оси относительно некоторого начального положения. Тогда скорость движения всех точек тела равна производной перемещения по времени:
.
При , вектор скорости направлен вдоль оси x . При – противоположно этой оси.

Ускорение точек тела равно производной скорости по времени, или второй производной перемещения по времени:
.
При , вектор ускорения направлен вдоль оси x . При – противоположно.

Рассмотрим два тела, находящиеся в зацеплении без проскальзывания. Пусть точка A принадлежит первому телу, а точка B – второму. И пусть, в рассматриваемый момент времени, положения этих точек совпадают. Тогда, если между телами нет проскальзывания, то скорости этих точек равны:
.
Если каждое из тел вращается вокруг неподвижной оси, то равны соответствующие касательные ускорения:
.
Если одно из тел движется поступательно (пусть это второе тело), то ускорение его точек равно касательному ускорению точки соприкосновения первого тела:
.

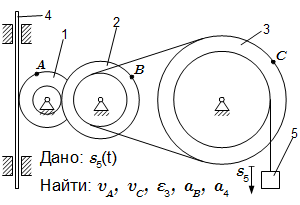
Механизм состоит из ступенчатых колес 1, 2, 3, находящихся в зацеплении и связанных ременной передачей, зубчатой рейки 4 и груза 5, привязанного к концу нити, намотанной на одно из колес. Радиусы ступеней колес равны соответственно: у колеса 1 – r₁ = 2 см, R₁ = 4 см, у колеса 2 – r₂ = 6 см, R₂ = 8 см, у колеса 3 – r₃ = 12 см, R₃ = 16 см. На ободьях колес расположены точки A, B и C. Задан закон движения груза: s₅ = t 3 – 6t (см). Положительное направление для s₅ – вниз.

Определить в момент времени t = 2 скорости точек A, C; угловое ускорение колеса 3; ускорение точки B и ускорение рейки 4.

Указания. Эта задача – на исследование вращательного движения твердого тела вокруг неподвижной оси. При решении задачи учесть, что проскальзывание в ременной передаче и в точках сцепления колес отсутствует. То есть скорости точек колес, находящихся в зацеплении равны, а скорости точек ремня равны скорости точек, лежащих на ободе колес, связанных ременной передачей.

Дано:
t = 2 с; r₁ = 2 см, R₁ = 4 см; r₂ = 6 см, R₂ = 8 см; r₃ = 12 см, R₃ = 16 см; s₅ = t 3 – 6t (см).

Груз 5 совершает поступательное движение. Поэтому скорости (и ускорения) всех его точек равны. В условии задачи задано смещение s груза относительно некоторого начального положения. Дифференцируя по времени t , находим зависимость скорости точек груза от времени:
.
Дифференцируя скорость груза по времени, находим зависимость ускорения груза от времени:
.

Находим скорость и ускорение груза в заданный момент времени :
см/с;
см/с 2 .

Груз 5 связан нитью с внутренним ободом колеса 3. Поэтому скорости точек внутреннего обода колеса 3 равны скорости груза:
.
Отсюда находим угловую скорость колеса 3 для произвольного момента времени:
.
Здесь подразумевается, что и являются функциями от времени t . Дифференцируя по t , находим угловое ускорение колеса 3:
.
Находим значения угловой скорости и углового ускорения в момент времени с. Для этого подставляем найденные значения и при с:
с –1 ;
с –2 .

Рассмотрим колесо 2. Его внутренний обод связан нитью с внешним ободом колеса 3. Поэтому скорости точек на этих ободьях равны:
. Отсюда
.
Дифференцируя по времени, находим угловое ускорение колеса 2 в произвольный момент времени:
.
Подставляем значения для с:
с –1 ;
с –2 .

Рассмотрим колесо 1. Его внутренний обод находится в зацеплении с внешним ободом колеса 2. Поэтому скорости точек на этих ободьях равны:
. Отсюда
.
Дифференцируя по времени, находим угловое ускорение колеса 1 в произвольный момент времени:
.
Подставляем значения для с:
с –1 ;
с –2 .

Итак, мы нашли:
ω ₁ = 5.3333 с –1 , ω ₂ = 1.3333 с –1 , ω ₃ = 0.5 с –1 , ε ₁ = 10.6667 с –2 , ε ₂ = 2.6667 с –2 , ε ₃ = 1 с –2 .

Точка A лежит на окружности радиуса R₁ с центром в точке O₁, расположенной на оси вращения. Поэтому скорость этой точки направлена по касательной к окружности и по абсолютной величине равна
см/с.

Точка C лежит на окружности радиуса R₃ с центром O₃ на оси вращения. Скорость этой точки:
см/с.

Точка B лежит на окружности радиуса R₂ с центром O₂, расположенном на оси вращения. Касательное (или тангенциальное) ускорение этой точки направлено по касательной к окружности в сторону, на которую указывает угловое ускорение (по часовой стрелке). По абсолютной величине оно равно
см/с 2 .

Нормальное ускорение всегда направлено к центру окружности. По абсолютной величине оно равно
см/с 2 .

Полное ускорение равно векторной сумме касательного и нормального ускорений:
.
Поскольку касательное ускорение перпендикулярно нормальному, то для абсолютной величины полного ускорения имеем:
см/с 2 .

Рейка 4 движется поступательно по направляющим. Она находится в зацеплении с внешним ободом колеса 1. Поэтому ее скорость равна скорости точек внешнего обода колеса 1:
.
Дифференцирую по времени, получаем ускорение рейки в произвольный момент времени:
.
Подставляем численные значения для момента времени t = 2 с :
см/с 2 .

см/с; см/с; с –2 ; см/с 2 ; см/с 2 .

Автор: Олег Одинцов . Опубликовано: 25-10-2019

Вот как выглядят основные формулы прямолинейного движения, которые подробно описываются в главе 3:

По аналогии можно легко вывести основные формулы вращательного движения:

( omega=Delta<theta>/Delta ) , где ( omega ) — угловая скорость, ( Delta <theta>) — угол поворота, ( Delta ) — время поворота на угол ( Delta <theta>) ;

( alpha=Delta<omega>/Delta ) , где ( alpha ) — угловое ускорение, ( Delta <omega>) — изменение угловой скорости, ( Delta ) — время изменения угловой скорости;

( theta=omega_0(t_1-t_0)+<>^1!/!_2a(t_1-t_0)^2 ) , где ( omega_0 ) — это начальная скорость;

( omega^2_1-w^2_0=2as ) , где ( omega_1 ) — это конечная скорость.

Разбираемся с параметрами вращательного движения

В физике движение принято разделять на поступательное и вращательное. При поступательном движении любая прямая, связанная с движущимся объектом, остается параллельной самой себе. При вращательном движении все точки тела движутся по окружностям. Тангенциальным движением называется часть вращательного движения, происходящего по касательной к окружности вращения, а радиальным (или нормальным) движением — часть вращательного движения, происходящего перпендикулярно (по нормали) к касательной, т.е. вдоль радиуса окружности.

Параметры прямолинейного поступательного и вращательного движений можно связать следующими формулами:

Допустим, колеса мотоцикла вращаются с угловой скоростью ( omega ) , равной 21,5 ( 21,5pi ) радиан в секунду. С какой скоростью едет мотоцикл? Чтобы дать ответ на этот вопрос, достаточно воспользоваться простой формулой связи линейной и угловой скорости.

Вычисляем линейную скорость вращательного движения

Скорость тангенциального движения материальной точки принято называть линейной скоростью вращательного движения. На рис. 10.1 приведен пример вращения мячика для игры в гольф по окружности с радиусом ( mathbf ) и линейной скоростью ( mathbf ) . Скорость ( mathbf ) является векторной величиной, т.е. обладает величиной и направлением (подробнее о векторах рассказывается в главе 4), перпендикулярным радиус-вектору ( mathbf ) .

Угловая скорость связана с линейной скоростью соотношением ( v=romega ) , которое легко интуитивно понять. При одинаковой угловой скорости, чем дальше материальная точка от центра окружности вращения, тем больше ее линейная скорость.

Попробуем получить уже упомянутую выше формулу связи линейной и угловой скорости ( v=romega ) . Длина окружности ( L ) радиуса ( r ) выражается известной формулой ( L=2pi r ) , а полный угол, который охватывает окружность, равен ( 2pi ) радиан. Соответственно, длина дуги окружности длиной ( Delta s ) , охватывающая угол ( Deltatheta ) , равна:

Из формулы прямолинейного движения

путем подстановки выражения для ( Delta s ) получим:

где ( omega ) — угловая скорость, ( Delta <theta>) — угол поворота, ( Delta ) — время поворота на угол ( Delta <theta>) , то:

Теперь можно легко и просто дать ответ на вопрос, поставленный в конце предыдущего раздела, т.е. определить скорость мотоцикла по угловой скорости вращения его колес. Итак, колеса мотоцикла вращаются с угловой скоростью ( omega ) , равной 21,5 ( pi ) радиан в секунду. Пусть радиус колеса ( r ) равен 40 см, тогда достаточно использовать следующую формулу:

Подставляя в нее значения, получим:

Итак, скорость мотоцикла равна 27 м/с или 97 км/ч.

Вычисляем тангенциальное ускорение

Тангенциальным ускорением называется скорость изменения величины линейной скорости вращательного движения. Эта характеристика вращательного движения очень похожа на линейное ускорение прямолинейного движения (см. главу 3). Например, точки на колесе мотоцикла в момент старта имеют нулевую линейную скорость, а спустя некоторое время после разгона ускоряются до некоторой ненулевой линейной скорости. Как определить это тангенциальное ускорение точки колеса? Переформулируем вопрос: как связать линейное ускорение

где ( a ) — это ускорение, ( Delta v ) — изменение скорости, a ( Delta t ) — время изменения скорости, с угловым ускорением

где ( Deltaomega ) — изменение угловой скорости, ( Delta t ) — время изменения угловой скорости?

Как мы уже знаем, линейная и угловая скорости связаны равенством

Подставим это выражение в предыдущую формулу линейного ускорения:

Поскольку радиус остается постоянным, то его можно вынести за скобки:

Поскольку угловое ускорение ( alpha=Deltaomega/Delta t ) , то:

Итак, получаем следующую формулу связи между линейным и угловым ускорением:

Иначе говоря, тангенциальное ускорение равно произведению радиуса на угловое ускорение.

Вычисляем центростремительное ускорение

Центростремительнным ускорением называется ускорение, необходимое для удержания объекта на круговой орбите вращательного движения. Как связаны угловая скорость и центростремительное ускорение? Формула для центростремительного ускорения уже приводилась ранее (см. главу 7):

Теперь, используя известную формулу связи линейной и угловой скорости ( v=romega ) , получим:

По этой формуле можно определить величину центростремительного ускорения по известной угловой скорости и радиусу. Например, для вычисления центростремительного ускорения Луны, вращающейся вокруг Земли, удобно использовать именно эту формулу.

Луна делает полный оборот вокруг Земли за 28 дней, т.е. за 28 дней Луна проходит ( 2pi ) радиан. Отсюда получаем угловую скорость Луны:

Чтобы получить значение угловой скорости в привычных единицах, следует преобразовать дни в секунды:

После подстановки этого значения в предыдущую формулу получим:

Средний радиус орбиты Луны равен 3,85·10 8 м. Подставляя эти значения угловой скорости и радиуса в формулу центростремительного ускорения, получим:

Зная это ускорение и массу Луны, которая равна 7,35·10 22 кг, можно определить центростремительную силу, необходимую для удержания Луны на ее орбите:

Используем векторы для изучения вращательного движения

В предыдущих разделах этой главы угловая скорость и угловое ускорение рассматривались как скаляры, т.е. как параметры, характеризующиеся только величиной. Однако эти параметры вращательного движения, на самом деле, являются векторами, т.е. они обладают величиной и направлением (см. главу 4). В этом разделе рассматривается величина и направление некоторых параметров вращательного движения.

Определяем направление угловой скорости

Как нам уже известно, вращающееся колесо мотоцикла имеет не только угловую скорость, но и угловое ускорение. Что можно сказать о направлении вектора угловой скорости? Оно не совпадает с направлением линейной тангенциальной скорости, а… перпендикулярно плоскости колеса!

Эта новость всегда приводит к некоторому замешательству среди новичков: угловая скорость ( omega ) , оказывается, направлена вдоль оси вращающегося колеса (рис. 10.2). Во вращающемся колесе единственной неподвижной точкой является его центр. Поэтому начало вектора угловой скорости принято располагать в центре окружности вращения.

Для определения направления вектора угловой скорости ( omega ) часто используют правило правой руки. Если охватить ладонью ось вращения, а пальцы свернуть так, чтобы они указывали на направление тангенциальной скорости, то вытянутый большой палец укажет направление вектора угловой скорости ( omega ) .

Теперь угловую скорость можно использовать так же, как и остальные векторные характеристики движения. Направление вектора угловой скорости можно найти по правилу правой руки, а величину — по приведенной ранее формуле. То, что вектор угловой скорости направлен перпендикулярно плоскости вращательного движения, часто вызывает некоторые трудности у начинающих, но к этому можно быстро привыкнуть.

Определяем направление углового ускорения

Если вектор угловой скорости направлен перпендикулярно плоскости вращательного движения, то куда направлен вектор углового ускорения в случае замедления или ускорения вращения объекта? Как известно (см. предыдущие разделы), угловое ускорение определяется формулой:

где ( alpha ) — угловое ускорение, ( Deltaomega ) — изменение угловой скорости, ( Delta t ) — время изменения угловой скорости.

В векторной форме оно имеет следующий вид:

где ( mathbf <alpha>) — вектор углового ускорения, а ( Deltamathbf <omega>) — изменение вектора угловой скорости. Отсюда ясно, что направление вектора углового ускорения совпадает с направлением изменения вектора угловой скорости.

Если вектор угловой скорости меняется только по величине, то направление вектора углового ускорения параллельно направлению вектора угловой скорости. Если величина угловой скорости растет, то направление вектора углового ускорения совпадает с направлением вектора угловой скорости, как показано на рис. 10.3.

А если величина угловой скорости падает, то направление вектора углового ускорения противоположно направлению вектора угловой скорости, как показано на рис. 10.4.

Поднимаем грузы: момент силы

В физике большое значение имеет не только время, но и место приложения силы. Всем когда-либо приходилось пользоваться рычагом для перемещения тяжелых грузов. Чем длиннее рычаг, тем легче сдвинуть груз. На языке физики применение силы с помощью рычага характеризуется понятием момент силы.

Приложение момента силы неразрывно связано с вращательным движением объектов. Если приложить силу к краю карусели, то карусель начнет вращательное движение. Чем дальше точка приложения силы, тем легче раскрутить карусель до заданной угловой скорости (параметры вращательного движения описываются в главе 1 1 ).

В верхней части рис. 10.5 показаны весы-качели с грузом массы ( m_1 ) на одном конце и грузом большей массы ( m_2=2m_1 ) посередине. Чтобы уравновесить весы-качели, нужно сместить груз с большей массой ( m_2 ) к другому концу весов, как показано в нижней части рис. 10.5. Как известно из опыта, размещение груза в точке вращения весов не приводит к уравновешиванию весов. Чтобы уравновесить весы, нужно сдвинуть груз с большей массой ( m_2=2m_1 ) к другому концу весов на расстояние вдвое меньшее, чем расстояние от точки вращения до второго груза с массой ( m_1 ) .

Знакомимся с формулой момента силы

Для уравновешивания весов важно не только, какая сила используется, но и где она прикладывается. Расстояние от точки приложения силы до точки вращения называется плечом силы.

Предположим, что нам нужно открыть дверь, схематически показанную на рис. 10.6. Как известно из опыта, дверь практически невозможно открыть, если прилагать силу вблизи петель (см. схему А на рис. 10.6). Однако, если приложить силу посередине двери, то открыть ее будет гораздо проще (см. схему Б на рис. 10.6). Наконец, прилагая силу у противоположного края двери по отношению к расположению петель, ее можно открыть с еще меньшим усилием (см. схему В на рис. 10.6).

На рис. 10.6 расстояние от мест расположения петель до точки приложения силы и есть плечо силы. Моментом силы называется произведение прилагаемой силы ( F ) на плечо силы ( l ) :

Момент силы в системе СИ измеряется в Н·м, а в системе СГС — в дин·см (подробнее эти системы единиц измерения описываются в главе 2).

Вернемся к примеру на рис. 10.6, где требуется открыть дверь шириной 1 м с помощью силы величиной 200 Н. В случае А (см. рис. 10.6) плечо силы равно нулю и произведение этого плеча на силу любой величины (включая и силу 200 Н) даст нулевой момент силы. В случае Б (см. рис. 10.6) плечо силы равно половине ширины двери, т.е. плечо силы ( l ) равно 0,5 м и момент силы будет равен:

В случае В (см. рис. 10.6) плечо силы равно ширине двери, т.е. плечо силы ( l ) равно 1 м и момент силы будет равен:

Итак, увеличение вдвое длины плеча при той же силе дает нам такое же увеличение момента силы. До сих пор сила прилагалась перпендикулярно к линии, соединяющей точку приложения силы и точку вращения. А что будет с моментом силы, если дверь будет немного приоткрыта и направление силы уже будет не перпендикулярным?

Разбираемся с направлением приложенной силы и плечом силы

Допустим, что сила приложена не перпендикулярно к поверхности двери, а параллельно, как показано на схеме А на рис. 10.7. Как известно из опыта, таким образом дверь открыть невозможно. Дело в том, что у такой силы нет проекции, которая бы могла вызвать вращательное движение. Точнее говоря, у такой силы нет ненулевого плеча для создания вращательного момента силы.

Размышляем над тем, как создается момент силы

Момент силы из предыдущего примера требуется создавать всегда для открытия двери независимо от того, какую дверь приходится открывать: легкую калитку изгороди или массивную дверь банковского сейфа. Как вычислить необходимый момент силы? Сначала нужно определить плечо сил, а потом умножить его на величину силы.

Однако не всегда все так просто. Посмотрите на схему Б на рис. 10.7. Как видите, сила прилагается под некоторым углом ( theta ) . Как в таком случае определить плечо силы? Если бы угол ( theta ) был прямым, то мы могли бы воспользоваться уже известно нам формулой:

Однако в данном случае угол ( theta ) не является прямым.

В таком случае нужно просто помнить следующее правило: плечом силы называется длина перпендикуляра, опущенного из предполагаемой точки вращения на прямую, относительно которой действует сила.

Попробуем применить это правило определения плеча силы для схемы Б на рис. 10.7. Нужно продлить линию, вдоль которой действует сила, а потом опустить на нее перпендикуляр из точки вращения двери. Из полученного прямоугольного треугольника легко определить искомое плечо силы:

Если угол ( theta ) равен нулю, то никакого момента силы не возникает (см. схему А на рис. 10.7).

Итак, получаем для момента силы для схемы Б на рис. 10.7:

Например, если требуется открыть дверь шириной 1 м с помощью силы величиной 200 Н, приложенной под углом ( theta ) = 45°, то создаваемый момент этой силы будет равен:

Как видите, этот момент силы 140 Н·м меньше, чем момент силы 200 Н·м, созданный под прямым углом на схеме В на рис. 10.6.

Определяем направление момента силы

Учитывая все приведенные выше сведения о моменте силы, у читателя вполне может возникнуть подозрение, что момент силы обладает направлением. И это действительно так. Момент силы является векторной величиной, направление которой определяется по правилу правой руки. Если охватить ладонью ось вращения, а пальцы свернуть так, чтобы они указывали на направление силы, то вытянутый большой палец укажет направление вектора момента силы.

На рис. 10.8 показан пример силы ( mathbf ) с плечом ( mathbf ) и соответствующего вектора момента сил ( mathbf ) .

Уравновешиваем моменты сил

В жизни нам часто приходится сталкиваться с равновесными состояниями. Как равновесное механическое состояние определяется с точки зрения физики? Обычно физики подразумевают под равновесным состоянием объекта то, что он не испытывает никакого ускорения (но может двигаться с постоянной скоростью).

Для поступательного движения равновесное состояние означает, что сумма всех сил, действующих на объект равна нулю:

Иначе говоря, результирующая действующая сила равна нулю.

Вращательное движение также может быть равновесным, если такое движение происходит без углового ускорения, т.е. с постоянной угловой скоростью.

Для вращательного движения равновесное состояние означает, что сумма всех моментов сил, действующих на объект, равна нулю:

Как видите, это условие равновесного вращательного движения аналогично условию равновесного поступательного движения. Условия равновесного вращательного движения удобно использовать для определения момента силы, необходимого для уравновешивания неравномерно вращающегося объекта.

Простой пример: вешаем рекламный плакат

Предположим, что у входа в магазин нужно повесить большой и тяжелый рекламный плакат, как показано на рис. 10.9. Хозяин магазина пытался сделать это и раньше, но у него ничего не выходило, поскольку он использовал очень непрочный болт.

Попробуем определить силу, с которой болт должен удерживать всю конструкцию, показанную на рис. 10.9. Пусть плакат имеет массу 50 кг и висит на шесте 3 м от точки опоры шеста, а массу шеста в данном примере будем считать пренебрежимо малой. Болт находится в 10 см от точки опоры шеста.

Согласно условиям равновесия, сумма всех моментов сил должна быть равна нулю:

где ( mathbf ) — это момент силы со стороны плаката, а ( mathbf ) — это момент силы со стороны болта.

Чему равны упомянутые моменты? Момент силы со стороны плаката можно легко определить по формуле:

где ( m ) = 50 кг — это масса плаката, ( mathbf ) — ускорение свободного падения под действием силы гравитационного притяжения (силы тяжести), ( mmathbf ) — сила тяжести плаката, а ( l_п ) = 3 м — это плечо силы тяжести плаката.

Подставляя значения, получим:

Обратите внимание, что здесь перед ускорением свободного падения под действием силы гравитационного притяжения стоит знак “минус”. Это значит, что вектор ускорения свободного падения направлен вниз, т.е. в сторону, противоположную выбранному направлению оси координат.

Момент силы со стороны болта определяется формулой:

где ( mathbf ) — это искомая сила, с которой болт должен удерживать всю конструкцию, а ( l_б ) = 0,1 м — это ее плечо.

Подставляя полученные выражения для моментов сил в формулу:

Отсюда с помощью простых алгебраических преобразований получим искомую силу:

Как видите сила, с которой болт должен удерживать всю конструкцию, направлена противоположно вектору ускорения свободного падения, т.е. вверх.

Подставляя значения, получим искомый ответ:

Более сложный пример: учитываем силу трения при расчете равновесия

Рассмотрим теперь другую более сложную задачу, в которой для расчета равновесия системы объектов нужно учесть силу трения. Предположим, что работник магазина решил использовать переносную лестницу для монтажа рекламного плаката, как схематически показано на рис. 10.10.

Пусть лестница длиной ( l_л ) = 4 м стоит под углом ( theta ) = 45° к поверхности тротуара, работник имеет массу ( m_р ) = 45 кг и находится на ней на расстоянии ( l_р ) = 3 м от нижнего конца лестницы, лестница имеет массу (m_л ) = 20 кг, а коэффициент трения покоя между поверхностью тротуара и концами лестницы равен ( mu_п ) = 0,7. Вопрос: будет ли такая система объектов находиться в состоянии равновесия? Попросту говоря, достаточной ли будет сила трения, чтобы лестница вместе с рабочим не соскользнула и упала?

Итак, для ответа на этот вопрос нам нужно учесть следующие силы, действующие на лестницу:

( mathbf ) — нормальная сила со стороны стены;

( mathbf ) — вес рабочего;

( mathbf ) — вес лестницы;

( mathbf> ) — сила трения между поверхностью тротуара и концами лестницы;

( mathbf ) — нормальная сила со стороны тротуара.

Согласно условиям равновесного поступательного движения, сумма всех сил, действующих на лестницу, должна быть равна нулю:

Это значит, что сумма всех сил вдоль горизонтальной оси, а именно нормальной силы со стороны стены ( mathbf ) и силы трения между поверхностью тротуара и концами лестницы ( mathbf> ) , должна быть равна нулю, то есть:

Перефразируя поставленный выше вопрос о достаточности силы трения, получим: выполняется ли условие

Кроме того, сумма всех сил вдоль вертикальной оси, а именно веса рабочего ( mathbf ) , веса лестницы ( mathbf ) и нормальной силы со стороны тротуара ( mathbf ) , должна быть равна нулю, то есть:

Согласно условиям равновесного вращательного движения, также необходимо равенство нулю всех моментов сил, действующих на лестницу:

Пусть предполагаемой точкой вращения является нижний конец лестницы, тогда должна быть равна нулю сумма моментов сил, создаваемых весом рабочего ( mathbf ) , весом лестницы ( mathbf ) и нормальной силой со стороны стены ( mathbf ) :

Поскольку ( L_р=l_р ) , ( L_л=l_л/2 ) (центр тяжести лестницы находится посередине лестницы), ( L_с=l_л ) , ( alpha=360^<circ>-theta ) , ( beta=360^<circ>-theta ) и ( gamma=theta ) , то получим:

Таким образом, мы получили систему из двух уравнений с двумя неизвестными сил ( mathbf ) и ( mathbf ) :

Зададимся вопросом: соблюдается ли условие

Из системы двух уравнений получим:

Итак, остается выяснить, соблюдается ли условие:

После подстановки значений получим:

Поскольку ( mu_т ) = 0,7, то упомянутое условие соблюдается, и лестница с рабочим не упадет.

Тангенциальное уравнение при вращательном движении

лЙОЕНБФЙЛБ ЙЪХЮБЕФ ТБЪМЙЮОЩЕ НЕИБОЙЮЕУЛЙЕ ДЧЙЦЕОЙС ФЕМ ВЕЪ ТБУУНПФТЕОЙС РТЙЮЙО ЧЩЪЩЧБАЭЙИ ЬФЙ ДЧЙЦЕОЙС.

1.1.1 лЙОЕНБФЙЛБ РПУФХРБФЕМШОПЗП ДЧЙЦЕОЙС

рТЙ РПУФХРБФЕМШОПН ДЧЙЦЕОЙЙ ФЕМБ ЧУЕ ФПЮЛЙ ФЕМБ ДЧЙЦХФУС ПДЙОБЛПЧП, Й, ЧНЕУФП ФПЗП ЮФПВЩ ТБУУНБФТЙЧБФШ ДЧЙЦЕОЙЕ ЛБЦДПК ФПЮЛЙ ФЕМБ, НПЦОП ТБУУНБФТЙЧБФШ ДЧЙЦЕОЙЕ ФПМШЛП ПДОПК ЕЗП ФПЮЛЙ.

пУОПЧОЩЕ ИБТБЛФЕТЙУФЙЛЙ ДЧЙЦЕОЙС НБФЕТЙБМШОПК ФПЮЛЙ: ФТБЕЛФПТЙС ДЧЙЦЕОЙС, РЕТЕНЕЭЕОЙЕ ФПЮЛЙ, РТПКДЕООЩК ЕА РХФШ, ЛППТДЙОБФЩ, УЛПТПУФШ Й ХУЛПТЕОЙЕ.

мЙОЙА, РП ЛПФПТПК ДЧЙЦЕФУС НБФЕТЙБМШОБС ФПЮЛБ Ч РТПУФТБОУФЧЕ, ОБЪЩЧБАФ ФТБЕЛФПТЙЕК.

рЕТЕНЕЭЕОЙЕН НБФЕТЙБМШОПК ФПЮЛЙ ЪБ ОЕЛПФПТЩК РТПНЕЦХФПЛ ЧТЕНЕОЙ ОБЪЩЧБЕФУС ЧЕЛФПТ РЕТЕНЕЭЕОЙС ∆r=r-r₀, ОБРТБЧМЕООЩК ПФ РПМПЦЕОЙС ФПЮЛЙ Ч ОБЮБМШОЩК НПНЕОФ ЧТЕНЕОЙ Л ЕЕ РПМПЦЕОЙА Ч ЛПОЕЮОЩК НПНЕОФ.

уЛПТПУФШ НБФЕТЙБМШОПК ФПЮЛЙ РТЕДУФБЧМСЕФ УПВПК ЧЕЛФПТ, ИБТБЛФЕТЙЪХАЭЙК ОБРТБЧМЕОЙЕ Й ВЩУФТПФХ РЕТЕНЕЭЕОЙС НБФЕТЙБМШОПК ФПЮЛЙ ПФОПУЙФЕМШОП ФЕМБ ПФУЮЕФБ. чЕЛФПТ ХУЛПТЕОЙС ИБТБЛФЕТЙЪХЕФ ВЩУФТПФХ Й ОБРТБЧМЕОЙЕ ЙЪНЕОЕОЙС УЛПТПУФЙ НБФЕТЙБМШОПК ФПЮЛЙ ПФОПУЙФЕМШОП ФЕМБ ПФУЮЕФБ.

1.1.2 тБЧОПНЕТОПЕ РТСНПМЙОЕКОПЕ ДЧЙЦЕОЙЕ

тБЧОПНЕТОЩН РТСНПМЙОЕКОЩН ДЧЙЦЕОЙЕН ОБЪЩЧБЕФУС ФБЛПЕ РТСНПМЙОЕКОПЕ ДЧЙЦЕОЙЕ, РТЙ ЛПФПТПН НБФЕТЙБМШОБС ФПЮЛБ (ФЕМП) ДЧЙЦЕФУС РП РТСНПК Й Ч МАВЩЕ ТБЧОЩЕ РТПНЕЦХФЛЙ ЧТЕНЕОЙ УПЧЕТЫБЕФ ПДЙОБЛПЧЩЕ РЕТЕНЕЭЕОЙС.

чЕЛФПТ УЛПТПУФЙ ТБЧОПНЕТОПЗП РТСНПМЙОЕКОПЗП ДЧЙЦЕОЙС НБФЕТЙБМШОПК ФПЮЛЙ ОБРТБЧМЕО ЧДПМШ ЕЕ ФТБЕЛФПТЙЙ Ч УФПТПОХ ДЧЙЦЕОЙС. чЕЛФПТ УЛПТПУФЙ РТЙ ТБЧОПНЕТОПН РТСНПМЙОЕКОПН ДЧЙЦЕОЙЙ ТБЧЕО ЧЕЛФПТХ РЕТЕНЕЭЕОЙС ЪБ МАВПК РТПНЕЦХФПЛ ЧТЕНЕОЙ, РПДЕМЕООПНХ ОБ ЬФПФ РТПНЕЦХФПЛ ЧТЕНЕОЙ:

рТЙНЕН МЙОЙА, РП ЛПФПТПК ДЧЙЦЕФУС НБФЕТЙБМШОБС ФПЮЛБ, ЪБ ПУШ ЛППТДЙОБФ пи, РТЙЮЕН ЪБ РПМПЦЙФЕМШОПЕ ОБРТБЧМЕОЙЕ ПУЙ ЧЩВЕТЕН ОБРТБЧМЕОЙЕ ДЧЙЦЕОЙС ФПЮЛЙ. фПЗДБ, УРТПЕГЙТПЧБЧ ЧЕЛФПТЩ r Й v, ОБ ЬФХ ПУШ, ДМС РТПЕЛГЙК ∆r_x = |∆r| Й ∆v_x = |∆v| ЬФЙИ ЧЕЛФПТПЧ НЩ НПЦЕН ЪБРЙУБФШ:

, ПФУАДБ РПМХЮБЕН ХТБЧОЕОЙЕ ТБЧОПНЕТОПЗП ДЧЙЦЕОЙС: ∆r_x = v_x · t .

ф.Л. РТЙ ТБЧОПНЕТОПН РТСНПМЙОЕКОПН ДЧЙЦЕОЙЙ S = |∆r|, НПЦЕН ЪБРЙУБФШ: S_x = v_x · t. фПЗДБ ДМС ЛППТДЙОБФЩ ФЕМБ Ч МАВПК НПНЕОФ ЧТЕНЕОЙ ЙНЕЕН:

ЗДЕ И₀ – ЛППТДЙОБФБ ФЕМБ Ч ОБЮБМШОЩК НПНЕОФ t = 0.

рТЙНЕТ 1. хТБЧОЕОЙЕ ДЧЙЦЕОЙС ФЕМБ ДБОП Ч ЧЙДЕ И = 4 – 3t. пРТЕДЕМЙФШ ОБЮБМШОХА ЛППТДЙОБФХ ФЕМБ, УЛПТПУФШ ДЧЙЦЕОЙС Й РЕТЕНЕЭЕОЙС ФЕМБ ЪБ 2 УЕЛХОДЩ.

тЕЫЕОЙЕ: уТБЧОЙН ДБООПЕ ХТБЧОЕОЙЕ ДЧЙЦЕОЙС ФЕМБ У ХТБЧОЕОЙЕН ДЧЙЦЕОЙС Ч ПВЭЕН ЧЙДЕ: И = И₀ + v_x t Й И = 4 – 3t.

пЮЕЧЙДОП, ЮФП И₀ = 4Н, v_x = – 3Н/У (ЪОБЛ “-” ПЪОБЮБЕФ, ЮФП ОБРТБЧМЕОЙЕ УЛПТПУФЙ ОЕ УПЧРБДБЕФ У ОБРТБЧМЕОЙЕН ПУЙ пи, Ф.Е. ПОЙ РТПФЙЧПРПМПЦОП ОБРТБЧМЕОЩ). рЕТЕНЕЭЕОЙЕ ФЕМБ ОБКДЕН РП ЖПТНХМЕ: S = И – И₀. лПОЕЮОХА ЛППТДЙОБФХ И НПЦОП ПРТЕДЕМЙФШ, РПДУФБЧМСС Ч ХТБЧОЕОЙЕ ДЧЙЦЕОЙС ЧТЕНС t₁: И = 4 – 3t₁. ч ПВЭЕН ЧЙДЕ ЖПТНХМБ РЕТЕНЕЭЕОЙС: S = 4 – 3t₁ – И₀ = 4 – 3t₁ – 4 = – 3t₁ = -3 · 2 = – 6 Н (фЕМП ДЧЙЦЕФУС Ч ПФТЙГБФЕМШОПН ОБРТБЧМЕОЙЙ ПУЙ пи).

рТЙНЕТ 2.мПДПЮОЙЛ РЕТЕЧПЪЙФ РБУУБЦЙТПЧ У ПДОПЗП ВЕТЕЗБ ОБ ДТХЗПК ЪБ ЧТЕНС t =10 НЙО. РП ФТБЕЛФПТЙЙ бч. уЛПТПУФШ ФЕЮЕОЙС ТЕЛЙ vТ = 0,3 Н/У, ЫЙТЙОБ ТЕЛЙ 240 Н. у ЛБЛПК УЛПТПУФША v ПФОПУЙФЕМШОП ЧПДЩ Й РПД ЛБЛЙН ХЗМПН α Л ВЕТЕЗХ ДПМЦОБ ДЧЙЗБФШУС МПДЛБ, ЮФПВЩ ДПУФЙЮШ ДТХЗПЗП ВЕТЕЗБ ЪБ ХЛБЪБООПЕ ЧТЕНС?

t = 10 НЙО = 660 У.

v’ – ? α – ?

тЕЫЕОЙЕ: рТЙНЕН ВЕТЕЗ ЪБ ОЕРПДЧЙЦОХА УЙУФЕНХ ПФУЮЕФБ. фПЗДБ ПФОПУЙФЕМШОП ВЕТЕЗБ УЛПТПУФШ МПДЛЙ ТБЧОБ:

ьФБ УЛПТПУФШ (ТЙУХОПЛ 1.1), СЧМСЕФУС УХННПК ДЧХИ УЛПТПУФЕК: УЛПТПУФЙ МПДЛЙ ПФОПУЙФЕМШОП ЧПДЩ v’ (УЛПТПУФЙ ПФОПУЙФЕМШОП РПДЧЙЦОПК УЙУФЕНЩ ПФУЮЕФБ) Й УЛПТПУФЙ ТЕЛЙ v_Т (УЛПТПУФЙ УБНПК РПДЧЙЦОПК УЙУФЕНЩ ПФУЮЕФБ ПФОПУЙФЕМШОП ОЕРПДЧЙЦОПК). рП ЪБЛПОХ УМПЦЕОЙС УЛПТПУФЕК: v =v_Т + v’. фБЛ ЛБЛ РП ХУМПЧЙА ЪБДБЮЙ УЛПТПУФШ МПДЛЙ ПФОПУЙФЕМШОП ВЕТЕЗБ ОБРТБЧМЕОБ ЧДПМШ бч, Б УЛПТПУФШ ТЕЛЙ РЕТРЕОДЙЛХМСТОП бч, ФП УЛПТПУФШ МПДЛЙ ПФОПУЙФЕМШОП ЧПДЩ(РП ФЕПТЕНЕ рЙЖБЗПТБ):

йУЛПНЩК ХЗПМ НПЦОП ОБКФЙ ЙЪ ЧЩТБЦЕОЙС:

пФЧЕФ: v’ = 0.5 Н /У, α = arctg ≈ 53 0 .

1.1.3 оЕТБЧОПНЕТОПЕ ДЧЙЦЕОЙЕ

дЧЙЦЕОЙЕ, РТЙ ЛПФПТПН ЪБ ТБЧОЩЕ РТПНЕЦХФЛЙ ЧТЕНЕОЙ ФЕМП УПЧЕТЫБЕФ ОЕТБЧОЩЕ РЕТЕНЕЭЕОЙС ОБЪЩЧБАФ ОЕТБЧОПНЕТОЩН ЙМЙ РЕТЕНЕООЩН. уТЕДОЕК УЛПТПУФША v_УТ ОБЪЩЧБЕФУС ЧЕМЙЮЙОБ, ТБЧОБС ПФОПЫЕОЙА РЕТЕНЕЭЕОЙС ФЕМБ ∆r ЪБ ОЕЛПФПТЩК РТПНЕЦХФПЛ ЧТЕНЕОЙ ∆t Л ЬФПНХ РТПНЕЦХФЛХ:

нПДХМШ УТЕДОЕК УЛПТПУФЙ ПРТЕДЕМСЕФУС ЛБЛ ПФОПЫЕОЙЕ РХФЙ ∆S, РТПКДЕООПЗП ФЕМПН ЪБ ОЕЛПФПТЩК РТПНЕЦХФПЛ ЧТЕНЕОЙ, Л ЬФПНХ РТПНЕЦХФЛХ:

оБРТБЧМЕОЙЕ ЧЕЛФПТБ УТЕДОЕК УЛПТПУФЙ v_УТ УПЧРБДБЕФ У ОБРТБЧМЕОЙЕН ∆r (ТЙУХОПЛ 1.2).

рТЙ ОЕПЗТБОЙЮЕООПН ХНЕОШЫЕОЙЙ ∆t, v_УТ УФТЕНЙФУС Л РТЕДЕМШОПНХ ЪОБЮЕОЙА, ЛПФПТПЕ ОБЪЩЧБЕФУС НЗОПЧЕООПК УЛПТПУФША. йФБЛ, НЗОПЧЕООБС УЛПТПУФШ v ЕУФШ РТЕДЕМ, Л ЛПФПТПНХ УФТЕНЙФУС УТЕДОСС УЛПТПУФШ v_УТ, ЛПЗДБ РТПНЕЦХФПЛ ЧТЕНЕОЙ ДЧЙЦЕОЙС УФТЕНЙФУС Л ОХМА:

йЪ ЛХТУБ НБФЕНБФЙЛЙ ЙЪЧЕУФОП, ЮФП РТЕДЕМ ПФОПЫЕОЙС РТЙТБЭЕОЙС ЖХОЛГЙЙ Л РТЙТБЭЕОЙА БТЗХНЕОФБ, ЛПЗДБ РПУМЕДОЙК УФТЕНЙФУС Л ОХМА РТЕДУФБЧМСЕФ УПВПК РЕТЧХА РТПЙЪЧПДОХА ЬФПК ЖХОЛГЙЙ РП ДБООПНХ БТЗХНЕОФХ. рПЬФПНХ:

нЗОПЧЕООБС УЛПТПУФШ v ЕУФШ ЧЕЛФПТОБС ЧЕМЙЮЙОБ, ТБЧОБС РЕТЧПК РТПЙЪЧПДОПК ТБДЙХУБ – ЧЕЛФПТБ ДЧЙЦХЭЕКУС ФПЮЛЙ РП ЧТЕНЕОЙ. фБЛ ЛБЛ УЕЛХЭБС Ч РТЕДЕМЕ УПЧРБДБЕФ У ЛБУБФЕМШОПК, ФП ЧЕЛФПТ УЛПТПУФЙ v ОБРТБЧМЕО РП ЛБУБФЕМШОПК Л ФТБЕЛФПТЙЙ Ч УФПТПОХ ДЧЙЦЕОЙС (ТЙУХОПЛ 1.2).

рП НЕТЕ ХНЕОШЫЕОЙЕ ∆t РХФШ ∆S ЧУЕ ВПМШЫЕ ВХДЕФ РТЙВМЙЦБФШУС Л |∆r|, РПЬФПНХ НПДХМШ НЗОПЧЕООПК УЛПТПУФЙ:

фБЛЙН ПВТБЪПН, НПДХМШ НЗОПЧЕООПК УЛПТПУФЙ v ТБЧЕО РЕТЧПК РТПЙЪЧПДОПК РХФЙ РП ЧТЕНЕОЙ :

рТЙ ОЕТБЧОПНЕТОПН ДЧЙЦЕОЙЙ ФЕМБ ЕЗП УЛПТПУФШ ОЕРТЕТЩЧОП ЙЪНЕОСЕФУС. лБЛ ВЩУФТП ЙЪНЕОСЕФУС УЛПТПУФШ ФЕМБ, РПЛБЪЩЧБЕФ ЧЕМЙЮЙОБ, ЛПФПТБС ОБЪЩЧБЕФУС ХУЛПТЕОЙЕН. уТЕДОЙН ХУЛПТЕОЙЕН ОЕТБЧОПНЕТОПЗП ДЧЙЦЕОЙС Ч ЙОФЕТЧБМЕ ПФ t ДП t + ∆t ОБЪЩЧБЕФУС ЧЕЛФПТОБС ЧЕМЙЮЙОБ, ТБЧОБС ПФОПЫЕОЙА ЙЪНЕОЕОЙС УЛПТПУФЙ ∆v Л ЙОФЕТЧБМХ ЧТЕНЕОЙ ∆t:

нЗОПЧЕООЩН ХУЛПТЕОЙЕН Б Ч НПНЕОФ ЧТЕНЕОЙ t ВХДЕФ РТЕДЕМ УТЕДОЕЗП ХУЛПТЕОЙС:

фБЛЙН ПВТБЪПН, ХУЛПТЕОЙЕ ∆Б ЕУФШ ЧЕЛФПТОБС ЧЕМЙЮЙОБ, ТБЧОБС РЕТЧПК РТПЙЪЧПДОПК УЛПТПУФЙ РП ЧТЕНЕОЙ. ч ДБООПК УЙУФЕНЕ ПФУЮЕФБ ЧЕЛФПТ ХУЛПТЕОЙС НПЦЕФ ВЩФШ ЪБДБО РТПЕЛГЙСНЙ ОБ УППФЧЕФУФЧХАЭЙЕ ЛППТДЙОБФОЩЕ ПУЙ (РТПЕЛГЙСНЙ Б_И, Б_Х, Б_z).

уПУФБЧМСАЭБС Б_τ ЧЕЛФПТБ ХУЛПТЕОЙС, ОБРТБЧМЕООБС ЧДПМШ ЛБУБФЕМШОПК Л ФТБЕЛФПТЙЙ Ч ДБООПК ФПЮЛЕ, ОБЪЩЧБЕФУС ФБОЗЕОГЙБМШОЩН (ЛБУБФЕМШОЩН) ХУЛПТЕОЙЕН. фБОЗЕОГЙБМШОПЕ ХУЛПТЕОЙЕ ИБТБЛФЕТЙЪХЕФ ЙЪНЕОЕОЙЕ ЧЕЛФПТБ УЛПТПУФЙ РП НПДХМА. чЕЛФПТ Б_τ ОБРТБЧМЕО Ч УФПТПОХ ДЧЙЦЕОЙС ФПЮЛЙ РТЙ ЧПЪТБУФБОЙЙ ЕЕ УЛПТПУФЙ (ТЙУХОПЛ 1.3 – Б) Й Ч РТПФЙЧПРПМПЦОХА УФПТПОХ – РТЙ ХВЩЧБОЙЙ УЛПТПУФЙ (ТЙУХОПЛ 1.3 – В).

фБОЗЕОГЙБМШОБС УПУФБЧМСАЭБС ХУЛПТЕОЙС Б_τ ТБЧОБ РЕТЧПК РТПЙЪЧПДОПК РП ЧТЕНЕОЙ ПФ НПДХМС УЛПТПУФЙ, ПРТЕДЕМСС ФЕН УБНЩН ВЩУФТПФХ ЙЪНЕОЕОЙС УЛПТПУФЙ РП НПДХМА:

чФПТБС УПУФБЧМСАЭБС ХУЛПТЕОЙС, ТБЧОБС:

ОБЪЩЧБЕФУС ОПТНБМШОПК УПУФБЧМСАЭЕК ХУЛПТЕОЙС Й ОБРТБЧМЕОБ РП ОПТНБМЙ Л ФТБЕЛФПТЙЙ Л ГЕОФТХ ЕЕ ЛТЙЧЙЪОЩ (РПЬФПНХ ЕЕ ОБЪЩЧБАФ ФБЛ ЦЕ ГЕОФТПУФТЕНЙФЕМШОЩН ХУЛПТЕОЙЕН).

рПМОПЕ ХУЛПТЕОЙЕ ЕУФШ ЗЕПНЕФТЙЮЕУЛБС УХННБ ФБОЗЕОГЙБМШОПК Й ОПТНБМШОПК УПУФБЧМСАЭЙИ:

рТЙНЕТ 1. рХУФШ И ЧПЪТБУФБЕФ РТПРПТГЙПОБМШОП ЛЧБДТБФХ ЧТЕНЕОЙ, Ф.Е. И = б·t 2 . юЕНХ ТБЧОБ НЗОПЧЕООБС УЛПТПУФШ Ч НПНЕОФ ЧТЕНЕОЙ t₁ – ?

тЕЫЕОЙЕ: ч ПВЭЕН УМХЮБЕ РТПЙЪЧПДОБС ПФ УФЕРЕООПК ЖХОЛГЙЙ t n ЪБРЙУЩЧБЕФУС Ч ЧЙДЕ:

нЗОПЧЕООБС УЛПТПУФШ ПРТЕДЕМСЕФУС:

пФЧЕФ: ч НПНЕОФ ЧТЕНЕОЙ t₁ ЙНЕЕН v = 2·Б·t₁.

рТЙНЕТ 2. ъБЧЙУЙНПУФШ РТПКДЕООПЗП ФЕМПН РХФЙ S ПФ ЧТЕНЕОЙ t ЪБДБЕФУС ХТБЧОЕОЙЕН S = At – Bt 2 + Ct 3 , ЗДЕ б = 2 Н/У, ч = 3 Н/У 2 , у = 4 Н/У 3 .

оБКФЙ: Б) ЪБЧЙУЙНПУФШ УЛПТПУФЙ v Й ХУЛПТЕОЙС a ФЕМБ ПФ ЧТЕНЕОЙ t;

В) ТБУУФПСОЙЕ S, УЛПТПУФШ v Й ХУЛПТЕОЙЕ Б ФЕМБ ЮЕТЕЪ ЧТЕНС t =2 У РПУМЕ ОБЮБМБ ДЧЙЦЕОЙС.

S = At – Bt 2 + Ct 3 , б = 2 Н/У, ч = 3 Н/У 2 , у = 4 Н/У 3 ;

В) S -? , V -? , a-? РТЙ t = 2 c.

Б) уЛПТПУФШ ФЕМБ: v = ds /dt ; v = A – 2Bt + 3Ct 2 ; v = 2 – 6t + 12t 2 Н/У. хУЛПТЕОЙЕ ФЕМБ: Б = dv /dt; Б= – 2B + 6уt; a = – 6 + 24t Н/У 2 .

В) тБУУФПСОЙЕ, РТПКДЕООПЕ ФЕМПН, S = 2t – 3t 2 + 4t 3 . фПЗДБ ЮЕТЕЪ ЧТЕНС t = 2c ЙНЕЕН: S = 24 Н; v = 38 Н/У; Б = 42 Н/У 2 .

пФЧЕФ: v = 2 – 6t + 12t 2 ; a = – 6 + 24 t Н/У 2 ; S = 24 Н; v = 38 Н/У; Б = 42 Н/У 2 .

1.1.4 тБЧОПРЕТЕНЕООПЕ РТСНПМЙОЕКОПЕ ДЧЙЦЕОЙЕ

тБЧОПРЕТЕНЕООЩН ОБЪЩЧБЕФУС ДЧЙЦЕОЙЕ, РТЙ ЛПФПТПН УЛПТПУФШ ФЕМБ (НБФЕТЙБМШОПК ФПЮЛЙ) ЪБ МАВЩЕ ТБЧОЩЕ РТПНЕЦХФЛЙ ЧТЕНЕОЙ ЙЪНЕОСЕФУС ПДЙОБЛПЧП, Ф.Е. ОБ ТБЧОЩЕ ЧЕМЙЮЙОЩ. ьФП ДЧЙЦЕОЙЕ НПЦЕФ ВЩФШ ТБЧОПХУЛПТЕООЩН Й ТБЧОПЪБНЕДМЕООЩН.

еУМЙ ОБРТБЧМЕОЙЕ ХУЛПТЕОЙС Б УПЧРБДБЕФ У ОБРТБЧМЕОЙЕН УЛПТПУФЙ v ФПЮЛЙ, ДЧЙЦЕОЙЕ ОБЪЩЧБЕФУС ТБЧОПХУЛПТЕООЩН. еУМЙ ОБРТБЧМЕОЙЕ ЧЕЛФПТПЧ Б Й v РТПФЙЧПРПМПЦОЩ, ДЧЙЦЕОЙЕ ОБЪЩЧБЕФУС ТБЧОПЪБНЕДМЕООЩН.

рТЙ ТБЧОПРЕТЕНЕООПН РТСНПМЙОЕКОПН ДЧЙЦЕОЙЙ ХУЛПТЕОЙЕ ПУФБЕФУС РПУФПСООЩН Й РП НПДХМА Й РП ОБРТБЧМЕОЙА (Б = const). рТЙ ЬФПН УТЕДОЕЕ ХУЛПТЕОЙЕ Б_УТ ТБЧОП НЗОПЧЕООПНХ ХУЛПТЕОЙА Б ЧДПМШ ФТБЕЛФПТЙЙ ФПЮЛЙ. оПТНБМШОПЕ ХУЛПТЕОЙЕ РТЙ ЬФПН ПФУХФУФЧХЕФ ( Б_n=0 ).

йЪНЕОЕОЙЕ УЛПТПУФЙ ∆v = v – v₀ Ч ФЕЮЕОЙЙ РТПНЕЦХФЛБ ЧТЕНЕОЙ ∆t = t – t₀ РТЙ ТБЧОПРЕТЕНЕООПН РТСНПМЙОЕКОПН ДЧЙЦЕОЙЙ ТБЧОП: ∆v = a·∆t, ЙМЙ v – v₀ = a·(t – t₀). еУМЙ Ч НПНЕОФ ОБЮБМБ ПФУЮЕФБ ЧТЕНЕОЙ (t₀) УЛПТПУФШ ФПЮЛЙ ТБЧОБ v₀ (ОБЮБМШОБС УЛПТПУФШ) Й ХУЛПТЕОЙЕ Б ЙЪЧЕУФОП, ФП УЛПТПУФШ v Ч РТПЙЪЧПМШОЩК НПНЕОФ ЧТЕНЕОЙ t: v = v₀ + a·t. рТПЕЛГЙС ЧЕЛФПТБ УЛПТПУФЙ ОБ ПУШ пи УЧСЪБОБ У УППФЧЕФУФЧХАЭЙНЙ РТПЕЛГЙСНЙ ЧЕЛФПТПЧ ОБЮБМШОПК УЛПТПУФЙ Й ХУЛПТЕОЙС ХТБЧОЕОЙЕН: v_И = v_0И ± a_И·t. бОБМПЗЙЮОП ЪБРЙУЩЧБАФУС ХТБЧОЕОЙС ДМС РТПЕЛГЙК ЧЕЛФПТБ УЛПТПУФЙ ОБ ДТХЗЙЕ ЛППТДЙОБФОЩЕ ПУЙ.

чЕЛФПТ РЕТЕНЕЭЕОЙС ∆r ФПЮЛЙ ЪБ РТПНЕЦХФПЛ ЧТЕНЕОЙ ∆t = t – t₀ РТЙ ТБЧОПРЕТЕНЕООПН РТСНПМЙОЕКОПН ДЧЙЦЕОЙЙ У ОБЮБМШОПК УЛПТПУФША v₀ Й ХУЛПТЕОЙЕН Б ТБЧЕО:

Б ЕЗП РТПЕЛГЙС ОБ ПУШ пи (ЙМЙ РЕТЕНЕЭЕОЙЕ ФПЮЛЙ ЧДПМШ УППФЧЕФУФЧХАЭЕК ПУЙ ЛППТДЙОБФ) РТЙ t₀ = 0 ТБЧОБ:

рХФШ S_x, РТПКДЕООЩК ФПЮЛПК ЪБ РТПНЕЦХФПЛ ЧТЕНЕОЙ ∆t = t – t₀ Ч ТБЧОПРЕТЕНЕООПН РТСНПМЙОЕКОПН ДЧЙЦЕОЙЙ У ОБЮБМШОПК УЛПТПУФША v₀ Й ХУЛПТЕОЙЕН Б, РТЙ t₀ = 0 ТБЧЕО:

фБЛ ЛБЛ ЛППТДЙОБФБ ФЕМБ ТБЧОБ И = И₀ + S, ФП ХТБЧОЕОЙЕ ДЧЙЦЕОЙС ФЕМБ ЙНЕЕФ ЧЙД:

чПЪНПЦОП ФБЛ ЦЕ РТЙ ТЕЫЕОЙЙ ЪБДБЮ ЙУРПМШЪПЧБФШ ЖПТНХМХ:

рТЙНЕТ 1. хУЛПТЕОЙЕ БЧФПНПВЙМС ТБЧОП Б = – 4 Н/У₂. юФП ЬФП ПЪОБЮБЕФ?

тЕЫЕОЙЕ: хУЛПТЕОЙЕ БЧФПНПВЙМС ПФТЙГБФЕМШОП, УМЕДПЧБФЕМШОП, УЛПТПУФШ ЕЗП ХНЕОШЫБЕФУС, Ф.Е. БЧФПНПВЙМШ ФПТНПЪЙФ. еЗП УЛПТПУФШ ХНЕОШЫБЕФУС ОБ 4 Н/У ЪБ ЛБЦДХА УЕЛХОДХ.

рТЙНЕТ 2. дЧБ ЧЕМПУЙРЕДЙУФБ ЕДХФ ОБЧУФТЕЮХ ДТХЗ ДТХЗХ. пДЙО, ЙНЕС УЛПТПУФШ 18 ЛН/Ю, ДЧЙЦЕФУС ТБЧОПЪБНЕДМЕООП, У ХУЛПТЕОЙЕН 20 УН/У 2 , ДТХЗПК, ЙНЕС УЛПТПУФШ 5,4 ЛН/Ю, ДЧЙЦЕФУС ТБЧОПХУЛПТЕООП У ХУЛПТЕОЙЕН 0,2 Н/У 2 . юЕТЕЪ ЛБЛПЕ ЧТЕНС ЧЕМПУЙРЕДЙУФЩ ЧУФТЕФСФУС Й ЛБЛПЕ РЕТЕНЕЭЕОЙЕ УПЧЕТЫЙФ ЛБЦДЩК ЙЪ ОЙИ ДП ЧУФТЕЮЙ, ЕУМЙ ТБУУФПСОЙЕ НЕЦДХ ОЙНЙ Ч ОБЮБМШОЩК НПНЕОФ ЧТЕНЕОЙ 130 Н?

v₀₁ = 18 ЛН/Ю = 5 Н/У,

a₁ = 20 УН/У 2 = 0,2 Н/У 2 ,

Б) В)

тЕЫЕОЙЕ: рХУФШ ПУШ пи УПЧРБДБЕФ У ОБРТБЧМЕОЙЕН ДЧЙЦЕОЙС РЕТЧПЗП ЧЕМПУЙРЕДЙУФБ, Б ОБЮБМП ЛППТДЙОБФ У ФПЮЛПК O, Ч ЛПФПТПК ПО ОБИПДЙМУС Ч НПНЕОФ ЧТЕНЕОЙ t = 0 (ТЙУХОПЛ 1.4). фПЗДБ ХТБЧОЕОЙС ДЧЙЦЕОЙС ЧЕМПУЙРЕДЙУФБ ФБЛПЧЩ :

(Ф.Л. Б_1И= – Б₁; И₀₁ = 0);

(Ф.Л. v_2x = – v₀₂ Й a_2x = – a₂).

ч НПНЕОФ ЧУФТЕЮЙ Ч ФПЮЛЕ б: t = t₁; x₁ = x₂. фПЗДБ РПМХЮЙН ТБЧЕОУФЧП:

, ПФЛХДБ v₀₁·t₁ + v₀₂·t₁ = И₀₂, Ф.Л. Б₁ = Б₂,

пРТЕДЕМЙН РЕТЕНЕЭЕОЙЕ ЛБЦДПЗП ДП ЧУФТЕЮЙ.

1.1.5 уЧПВПДОПЕ РБДЕОЙЕ ФЕМ. дЧЙЦЕОЙЕ ФЕМБ, ВТПЫЕООПЗП ЧЕТФЙЛБМШОП ЧЧЕТИ

уЧПВПДОЩН РБДЕОЙЕН ОБЪЩЧБЕФУС ДЧЙЦЕОЙЕ, ЛПФПТПЕ УПЧЕТЫЙМП ВЩ ФЕМП ФПМШЛП РПД ДЕКУФЧЙЕН УЙМЩ ФСЦЕУФЙ ВЕЪ ХЮЕФБ УПРТПФЙЧМЕОЙС ЧПЪДХИБ. рТЙ УЧПВПДОПН РБДЕОЙЙ ФЕМБ У ОЕВПМШЫПК ЧЩУПФЩ h ПФ РПЧЕТИОПУФЙ ъЕНМЙ (h ≪R_Ъ, ЗДЕ R_Ъ – ТБДЙХУ ъЕНМЙ) ПОП ДЧЙЦЕФУС У РПУФПСООЩН ХУЛПТЕОЙЕН g, ОБРТБЧМЕООЩН ЧЕТФЙЛБМШОП ЧОЙЪ.

хУЛПТЕОЙЕ g ОБЪЩЧБЕФУС ХУЛПТЕОЙЕН УЧПВПДОПЗП РБДЕОЙС. пОП ПДОП Й ФПЦЕ ДМС ЧУЕИ ФЕМ Й ЪБЧЙУЙФ МЙЫШ ПФ ЧЩУПФЩ ОБД ХТПЧОЕН НПТС Й ПФ ЗЕПЗТБЖЙЮЕУЛПК ЫЙТПФЩ. еУМЙ Ч НПНЕОФ ОБЮБМБ ПФУЮЕФБ ЧТЕНЕОЙ (t₀ = 0) ФЕМП ЙНЕМП УЛПТПУФШ v₀, ФП РП ЙУФЕЮЕОЙЙ РТПЙЪЧПМШОПЗП РТПНЕЦХФЛБ ЧТЕНЕОЙ ∆t = t – t₀ УЛПТПУФШ ФЕМБ РТЙ УЧПВПДОПН РБДЕОЙЙ ВХДЕФ: v = v₀ + g·t.

рХФШ h, РТПКДЕООЩК ФЕМПН Ч УЧПВПДОПН РБДЕОЙЙ, Л НПНЕОФХ ЧТЕНЕОЙ t:

нПДХМШ УЛПТПУФЙ ФЕМБ РПУМЕ РТПИПЦДЕОЙС Ч УЧПВПДОПН РБДЕОЙЙ РХФЙ h ОБИПДЙФУС ЙЪ ЖПТНХМЩ:

рТПДПМЦЙФЕМШОПУФШ ∆t УЧПВПДОПЗП РБДЕОЙС ВЕЪ ОБЮБМШОПК УЛПТПУФЙ (v₀ = 0) У ЧЩУПФЩ h:

рТЙНЕТ 1. фЕМП РБДБЕФ ЧЕТФЙЛБМШОП ЧОЙЪ У ЧЩУПФЩ 20 Н ВЕЪ ОБЮБМШОПК УЛПТПУФЙ. пРТЕДЕМЙФШ:

1) РХФШ h, РТПКДЕООЩК ФЕМПН ЪБ РПУМЕДОАА УЕЛХОДХ РБДЕОЙС,

2) УТЕДОАА УЛПТПУФШ РБДЕОЙС v_УТ,

3) УТЕДОАА УЛПТПУФШ ОБ ЧФПТПК РПМПЧЙОЕ РХФЙ v_УТ2.

тЕЫЕОЙЕ: оБРТБЧЙН ПУШ Х ЧЕТФЙЛБМШОП ЧОЙЪ, Й РХУФШ ОБЮБМП ЛППТДЙОБФ УПЧРБДБЕФ У ОБЮБМШОЩН РПМПЦЕОЙЕН ФЕМБ (ТЙУХОПЛ 1.5).

1) уПЗМБУОП ЖПТНХМЕ:

ХТБЧОЕОЙЕ ДЧЙЦЕОЙС ЪБРЙЫЕФУС Ч ЧЙДЕ:

Ч НПНЕОФ РБДЕОЙС ОБ ЪЕНМА Х = h₀. пФУАДБ ЧТЕНС ДЧЙЦЕОЙС ФЕМБ:

ъБ ЧТЕНС ( t – ∆t) ФЕМП РТПЫМП РХФШ

рХФШ ЪБ РПУМЕДОАА УЕЛХОДХ ТБЧЕО:

2) фЕМП РТПЫМП РХФШ h₀. чТЕНС ДЧЙЦЕОЙС . фПЗДБ УТЕДОСС УЛПТПУФШ РБДЕОЙС

3) дМС ПРТЕДЕМЕОЙС УТЕДОЕК УЛПТПУФЙ ОБ ЧФПТПК РПМПЧЙОЕ РХФЙ, ОЕПВИПДЙНП ХЪОБФШ ЧТЕНС, ЪБ ЛПФПТПЕ ЬФБ ЮБУФШ РХФЙ РТПКДЕОБ. чТЕНС ДЧЙЦЕОЙС ОБ ЧФПТПК РПМПЧЙОЕ РХФЙ ТБЧОП РПМОПНХ ЧТЕНЕОЙ РПМЕФБ t НЙОХУ ЧТЕНС t₁, ЪБФТБЮЕООПЕ ОБ РТПИПЦДЕОЙЕ РЕТЧПК РПМПЧЙОЩ РХФЙ. чТЕНС t₁ ОБИПДЙФУС ЙЪ ХТБЧОЕОЙС:
,Ф.Е.

фБЛЙН ПВТБЪПН,

уМЕДПЧБФЕМШОП,

рТЙ ДЧЙЦЕОЙЙ ФЕМБ ЧЕТФЙЛБМШОП ЧЧЕТИ У ОБЮБМШОПК УЛПТПУФША v₀, ХУЛПТЕОЙЕ ФЕМБ ТБЧОП ХУЛПТЕОЙА УЧПВПДОПЗП РБДЕОЙС g. оБ ХЮБУФЛЕ ДП ОБЙЧЩУЫЕК ФПЮЛЙ РПДЯЕНБ ДЧЙЦЕОЙЕ ФЕМБ СЧМСЕФУС ТБЧОПЪБНЕДМЕООЩН, Б РПУМЕ ДПУФЙЦЕОЙС ЬФПК ФПЮЛЙ – УЧПВПДОЩН РБДЕОЙЕН ВЕЪ ОБЮБМШОПК УЛПТПУФЙ.

уЛПТПУФШ ФЕМБ Ч РТПЙЪЧПМШОЩК НПНЕОФ ЧТЕНЕОЙ t ПФ ОБЮБМБ ДЧЙЦЕОЙС ОЕЪБЧЙУЙНП ПФ ФПЗП, ТБУУНБФТЙЧБЕФУС МЙЫШ РПДЯЕН ФЕМБ ЙМЙ ЕЗП ПРХУЛБОЙЕ РПУМЕ ДПУФЙЦЕОЙС ОБЙЧЩУЫЕК ФПЮЛЙ, ТБЧОБ v = v₀ + g·t.

чЕЛФПТ РЕТЕНЕЭЕОЙС ∆r ФЕМБ ЪБ РТПЙЪЧПМШОЩК РТПНЕЦХФПЛ ЧТЕНЕОЙ ∆t = t – t₀, РТЙ ХУМПЧЙЙ t₀ = 0, ТБЧЕО:

ч НПНЕОФ ЧТЕНЕОЙ t_РПД, УППФЧЕФУФЧХАЭЙК ОБЙВПМШЫЕНХ РПДЯЕНХ ФЕМБ ОБД ФПЮЛПК ВТПУБОЙС (ЛПЗДБ Х = Х_НБИ ЙМЙ ЧЩУПФБ РПДЯЕНБ ФЕМБ НБЛУЙНБМШОБ h = h_max = Х_max – Х₀) УЛПТПУФШ ФЕМБ УФБОЕФ ТБЧОБ ОХМА: v = v₀ – g·t_РПД = 0, ПФЛХДБ t_РПД = v₀/g, Ч ЬФПФ НПНЕОФ ОБРТБЧМЕОЙЕ ДЧЙЦЕОЙС ФЕМБ ЙЪНЕОСЕФУС ОБ РТПФЙЧПРПМПЦОПЕ.

нБЛУЙНБМШОБС ЧЩУПФБ РПДЯЕНБ ФЕМБ ОБД ФПЮЛПК ВТПУБОЙС:

1.1.6 дЧЙЦЕОЙЕ ФЕМБ, ВТПЫЕООПЗП РПД ХЗМПН Л ЗПТЙЪПОФХ Й ВТПЫЕООПЗП ЗПТЙЪПОФБМШОП У ОЕЛПФПТПК ЧЩУПФЩ

дЧЙЦЕОЙЕ ФЕМБ, ВТПЫЕООПЗП У ОЕЛПФПТПК ЧЩУПФЩ, НПЦОП ТБЪМПЦЙФШ ОБ ДЧБ ОЕЪБЧЙУЙНЩИ ДЧЙЦЕОЙС: ТБЧОПНЕТОПЕ РТСНПМЙОЕКОПЕ, РТПЙУИПДСЭЕЕ Ч ЗПТЙЪПОФБМШОПН ОБРТБЧМЕОЙЙ УП УЛПТПУФША υ_И , ТБЧОПК ОБЮБМШОПК УЛПТПУФЙ ВТПУБОЙС υ₀ (υ_И = υ₀), Й УЧПВПДОПЕ РБДЕОЙЕ У ЧЩУПФЩ, ОБ ЛПФПТПК ОБИПДЙМПУШ ФЕМП Ч НПНЕОФ ВТПУБОЙС, У ХУЛПТЕОЙЕН g. дМС ПРЙУБОЙС ЬФПЗП ДЧЙЦЕОЙС ЧЩВЙТБАФ РТСНПХЗПМШОХА УЙУФЕНХ ЛППТДЙОБФ ИпХ. фТБЕЛФПТЙС ДЧЙЦЕОЙС СЧМСЕФУС ЧЕФЧШ РБТБВПМЩ (ТЙУХОПЛ 1.6).

хТБЧОЕОЙЕ ДЧЙЦЕОЙС РП ПУСН пИ Й пХ:

уЛПТПУФШ ФЕМБ Ч МАВПК ФПЮЛЕ ФТБЕЛФПТЙЙ НПЦОП ПРТЕДЕМЙФШ РП ЖПТНХМЕ:

рТЙ ЬФПН ЧТЕНС РПМЕФБ УЧСЪБОП У ЧЕТФЙЛБМШОПК УПУФБЧМСАЭЕК ДЧЙЦЕОЙС. дБМШОПУФШ РПМЕФБ – У ЗПТЙЪПОФБМШОПК.

рТЙНЕТ 1. у ВБЫОЙ ЧЩУПФПК о = 25 Н ЗПТЙЪПОФБМШОП ВТПЫЕО ЛБНЕОШ УП УЛПТПУФША υ₀ = 15 Н/У. оБКФЙ: УЛПМШЛП ЧТЕНЕОЙ ЛБНЕОШ ВХДЕФ Ч ДЧЙЦЕОЙЙ; ОБ ЛБЛПН ТБУУФПСОЙЙ S_x ПФ ПУОПЧБОЙЙ ВБЫОЙ ПО ХРБДЕФ ОБ ЪЕНМА; У ЛБЛПК УЛПТПУФША υ ПО ХРБДЕФ ОБ ЪЕНМА; ЛБЛПК ХЗПМ φ УПУФБЧЙФ ФТБЕЛФПТЙС ЛБНОС У ЗПТЙЪПОФПН Ч ФПЮЛЕ ЕЗП РБДЕОЙС ОБ ЪЕНМА.

рЕТЕНЕЭЕОЙЕ ВТПЫЕООПЗП ЗПТЙЪПОФБМШОП ЛБНОС НПЦОП ТБЪМПЦЙФШ ОБ ДЧБ (ТЙУХОПЛ 1.7): ЗПТЙЪПОФБМШОПЕ S_x Й ЧЕТФЙЛБМШОПЕ S_y.

рТЙНЕОСС ЪБЛПО ОЕЪБЧЙУЙНПУФЙ ДЧЙЦЕОЙС, ЙНЕЕН:

, , ПФУАДБ,

1)

2) S_x = L = v₀·t = 15 · 2,26 = 33,9 Н;

3) v_Х = g · t = 9,81 · 2,26 = 22,1 Н/У,

4)

дЧЙЦЕОЙЕ ФЕМБ, ВТПЫЕООПЗП РПД ХЗМПН Л ЗПТЙЪПОФХ, ФБЛЦЕ НПЦОП ТБЪМПЦЙФШ ОБ ДЧБ ОЕЪБЧЙУЙНЩИ ДЧЙЦЕОЙС: ТБЧОПНЕТОПЕ РТСНПМЙОЕКОПЕ, РТПЙУИПДСЭЕЕ Ч ЗПТЙЪПОФБМШОПН ОБРТБЧМЕОЙЙ У ОБЮБМШОПК УЛПТПУФША v_0И = v₀·Cosα Й УЧПВПДОПЕ РБДЕОЙЕ У ОБЮБМШОПК УЛПТПУФША v_0Х = v₀·Sinα, (ТЙУХОПЛ 1.8). зДЕ α – ХЗПМ НЕЦДХ ОБРТБЧМЕОЙСНЙ ЧЕЛФПТБ УЛПТПУФЙ υ₀ Й ПУША пИ. фТБЕЛФПТЙЕК ФБЛПЗП ДЧЙЦЕОЙС СЧМСЕФУС РБТБВПМБ. хТБЧОЕОЙС ДЧЙЦЕОЙС РТЙНХФ ЧЙД:

уЛПТПУФШ ФЕМБ Ч МАВПК ФПЮЛЕ ФТБЕЛФПТЙЙ:

рТЙНЕТ 2. фЕМП ВТПЫЕОП РПД ХЗМПН α Л ЗПТЙЪПОФХ У ОБЮБМШОПК УЛПТПУФША υ₀. пРТЕДЕМЙФШ ЧТЕНС РПМЕФБ t, НБЛУЙНБМШОХА ЧЩУПФХ о РПДЯЕНБ Й ДБМШОПУФШ L РПМЕФБ.

тЕЫЕОЙЕ: лБЛ ПВЩЮОП ЪБДБЮБ ОБЮЙОБЕФУС У ЧЩСЧМЕОЙС УЙМ, ДЕКУФЧХАЭЙИ ОБ ФЕМП. оБ ФЕМП ДЕКУФЧХЕФ ФПМШЛП УЙМБ ФСЦЕУФЙ, РПЬФПНХ Ч ЗПТЙЪПОФБМШОПН ОБРТБЧМЕОЙЙ ПОП РЕТЕНЕЭБЕФУС ТБЧОПНЕТОП, Б Ч ЧЕТФЙЛБМШОПН – ТБЧОПРЕТЕНЕООП У ХУЛПТЕОЙЕН g.

вХДЕН ТБУУНБФТЙЧБФШ ЧЕТФЙЛБМШОХА Й ЗПТЙЪПОФБМШОХА УПУФБЧМСАЭЙЕ ДЧЙЦЕОЙС ФЕМБ РП ПФДЕМШОПУФЙ, ДМС ЬФПЗП ТБЪМПЦЙН ЧЕЛФПТ ОБЮБМШОПК УЛПТПУФЙ ОБ ЧЕТФЙЛБМШОХА ( υ₀·Sinα ) Й ЗПТЙЪПОФБМШОХА ( υ₀·Cosα ) УПУФБЧМСАЭЙЕ (ТЙУХОПЛ 1.9).

оБЮОЕН ТБУУНБФТЙЧБФШ ЧЕТФЙЛБМШОХА УПУФБЧМСАЭХА ДЧЙЦЕОЙС. чТЕНС РПМЕФБ t = t₁ + t₂, ЗДЕ t₁ – ЧТЕНС РПДЯЕНБ (ФЕМП ДЧЙЦЕФУС РП ЧЕТФЙЛБМЙ ТБЧОПЪБНЕДМЕООП), t₂ – ЧТЕНС УРХУЛБ (ФЕМП ДЧЙЦЕФУС РП ЧЕТФЙЛБМЙ ТБЧОПХУЛПТЕООП).

чЕТФЙЛБМШОБС УЛПТПУФШ ФЕМБ Ч ОБЙЧЩУЫЕК ФПЮЛЕ ФТБЕЛФПТЙЙ (РТЙ t = t₁) ТБЧОБ ПЮЕЧЙДОП ОХМА. у ДТХЗПК УФПТПОЩ, ЬФБ УЛПТПУФШ НПЦЕФ ВЩФШ ЧЩТБЦЕОБ РТЙ РПНПЭЙ ЖПТНХМЩ ЪБЧЙУЙНПУФЙ УЛПТПУФЙ ТБЧОПЪБНЕДМЕООПЗП ДЧЙЦЕОЙС ПФ ЧТЕНЕОЙ.

пФУАДБ, РПМХЮБЕН: 0 = υ₀Sinα – g·t₁ ЙМЙ

(1.2)

рПДУФБЧЙН (1.1) Ч (1.2)

чТЕНС УРХУЛБ t₂ НПЦОП ЧЩЮЙУМЙФШ, ТБУУНПФТЕЧ РБДЕОЙЕ ФЕМБ У ЙЪЧЕУФОПК ЧЩУПФЩ о ВЕЪ ОБЮБМШОПК ЧЕТФЙЛБМШОПК УЛПТПУФЙ:

рПМОПЕ ЧТЕНС РПМЕФБ:

дМС ОБИПЦДЕОЙС ДБМШОПУФЙ РПМЕФБ L ОЕПВИПДЙНП ПВТБФЙФШУС Л ЗПТЙЪПОФБМШОПК УПУФБЧМСАЭЕК ДЧЙЦЕОЙС ФЕМБ. лБЛ ХЦЕ ПФНЕЮБМПУШ, РП ЗПТЙЪПОФБМЙ ФЕМП РЕТЕНЕЭБЕФУС ТБЧОПНЕТОП.

1.1.7 тБЧОПРЕТЕНЕООПЕ ДЧЙЦЕОЙЕ ФПЮЛЙ РП ПЛТХЦОПУФЙ

дЧЙЦЕОЙЕ РП ПЛТХЦОПУФЙ СЧМСЕФУС РТПУФЕКЫЙН РТЙНЕТПН ЛТЙЧПМЙОЕКОПЗП ДЧЙЦЕОЙС. уЛПТПУФШ υ ДЧЙЦЕОЙС РП ПЛТХЦОПУФЙ ОБЪЩЧБЕФУС МЙОЕКОПК (ПЛТХЦОПК) УЛПТПУФША. рТЙ ТБЧОПНЕТОПН ДЧЙЦЕОЙЙ РП ПЛТХЦОПУФЙ НПДХМШ НЗОПЧЕООПК УЛПТПУФЙ НБФЕТЙБМШОПК ФПЮЛЙ У ФЕЮЕОЙЕН ЧТЕНЕОЙ ОЕ ЙЪНЕОСЕФУС. дЧЙЦХЭБСУС ФПЮЛБ ЪБ ТБЧОЩЕ РТПНЕЦХФЛЙ ЧТЕНЕОЙ РТПИПДЙФ ТБЧОЩЕ РП ДМЙОЕ ДХЗЙ ПЛТХЦОПУФЙ. фБОЗЕОГЙБМШОПЕ ХУЛПТЕОЙЕ РТЙ ТБЧОПНЕТОПН ДЧЙЦЕОЙЙ ФПЮЛЙ РП ПЛТХЦОПУФЙ ПФУХФУФЧХЕФ ( a_τ ). йЪНЕОЕОЙЕ ЧЕЛФПТБ УЛПТПУФЙ υ РП ОБРТБЧМЕОЙА ИБТБЛФЕТЙЪХЕФУС ОПТНБМШОЩН ХУЛПТЕОЙЕН a_n, ЛПФПТПЕ ОБЪЩЧБЕФУС ФБЛЦЕ ГЕОФТПУФТЕНЙФЕМШОЩН ХУЛПТЕОЙЕН.

ч ЛБЦДПК ФПЮЛЕ ФТБЕЛФПТЙЙ ЧЕЛФПТ a_n ОБРТБЧМЕО РП ТБДЙХУХ Л ГЕОФТХ ПЛТХЦОПУФЙ, Б ЕЗП НПДХМШ ТБЧЕО:

рТЙ ПРЙУБОЙЙ НЕИБОЙЮЕУЛПЗП ДЧЙЦЕОЙС, Ч ЮБУФОПУФЙ ДЧЙЦЕОЙС РП ПЛТХЦОПУФЙ, ОБТСДХ У РТСНПХЗПМШОПК ДЕЛБТФПЧПК УЙУФЕНПК ЛППТДЙОБФ ЙУРПМШЪХЕФУС РПМСТОБС УЙУФЕНБ ЛППТДЙОБФ. рПМПЦЕОЙЕ ФПЮЛЙ н ОБ ЛБЛПК-ФП РМПУЛПУФЙ (ОБРТЙНЕТ, ипх) ПРТЕДЕМСЕФУС ДЧХНС РПМСТОЩНЙ ЛППТДЙОБФБНЙ: НПДХМЕН r ТБДЙХУБ ЧЕЛФПТБ ФПЮЛЙ Й ХЗМПН φ – ХЗМПЧПК ЛППТДЙОБФПК, ЙМЙ РПМСТОЩН ХЗМПН (ТЙУХОПЛ 1.10).

хЗПМ φ ПФУЮЙФЩЧБЕФУС ПФ ПУЙ пи ДП ТБДЙХУБ-ЧЕЛФПТБ r РТПФЙЧ ЮБУПЧПК УФТЕМЛЙ. фПЮЛХ п Ч ЬФПН УМХЮБЕ ОБЪЩЧБАФ РПМАУПН УЙУФЕНЩ ЛППТДЙОБФ. уПЧНЕУФЙН РПМАУ ЛППТДЙОБФ УЙУФЕНЩ У ГЕОФТПН ПЛТХЦОПУФЙ, РП ЛПФПТПК ДЧЙЦЕФУС НБФЕТЙБМШОБС ФПЮЛБ; ФПЗДБ r = R (ТЙУХОПЛ 1.11), Б ЙЪНЕОЕОЙЕ РПМПЦЕОЙС ФПЮЛЙ ОБ ПЛТХЦОПУФЙ НПЦЕФ ВЩФШ ПИБТБЛФЕТЙЪПЧБОП ЙЪНЕОЕОЙЕН ∆φ ХЗМПЧПК ЛППТДЙОБФЩ ФПЮЛЙ: ∆φ = φ₂ -φ₁.

хЗПМ ∆φ ОБЪЩЧБЕФУС ХЗМПН РПЧПТПФБ ТБДЙХУБ – ЧЕЛФПТБ ФПЮЛЙ. ьМЕНЕОФБТОЩЕ (ВЕУЛПОЕЮОП НБМЩЕ) ХЗМЩ РПЧПТПФБ ТБУУНБФТЙЧБАФУС ЛБЛ ЧЕЛФПТЩ.

нПДХМШ ЧЕЛФПТБ dφ ТБЧЕО ХЗМХ РПЧПТПФБ. оБРТБЧМЕОЙЕ ЧЕЛФПТБ dφ УПЧРБДБЕФ У ОБРТБЧМЕОЙЕН РПУФХРБФЕМШОПЗП ДЧЙЦЕОЙС ПУФТЙС ЧЙОФБ, ЗПМПЧЛБ ЛПФПТПЗП, ЧТБЭБЕФУС Ч ОБРТБЧМЕОЙЙ ДЧЙЦЕОЙС ФПЮЛЙ РП ПЛТХЦОПУФЙ, Ф.Е. РПДЮЙОСЕФУС РТБЧЙМХ РТБЧПЗП ЧЙОФБ (ТЙУХОПЛ 1.12).

CТЕДОЕК ХЗМПЧПК УЛПТПУФША ДЧЙЦЕОЙС ФПЮЛЙ РП ПЛТХЦОПУФЙ ЧПЛТХЗ ПУЙ ОБЪЩЧБЕФУС ЧЕМЙЮЙОБ ω_cp, ТБЧОБС ПФОПЫЕОЙА ХЗМБ РПЧПТПФБ ∆φ ТБДЙХУ-ЧЕЛФПТБ ФПЮЛЙ ЪБ РТПНЕЦХФПЛ ЧТЕНЕОЙ ∆t Л ДМЙФЕМШОПУФЙ ЬФПЗП РТПНЕЦХФЛБ:

хЗМПЧПК УЛПТПУФША (НЗОПЧЕООПК ХЗМПЧПК УЛПТПУФША) ω ОБЪЩЧБЕФУС РТЕДЕМ, Л ЛПФПТПНХ УФТЕНЙФУС УТЕДОСС ХЗМПЧБС УЛПТПУФШ РТЙ ВЕУЛПОЕЮОПН ХНЕОШЫЕОЙЙ РТПНЕЦХФЛБ ЧТЕНЕОЙ ∆t, ЙМЙ РЕТЧБС РТПЙЪЧПДОБС ПФ ХЗМБ РПЧПТПФБ РП ЧТЕНЕОЙ:

чЕЛФПТ ω ОБРТБЧМЕО ЧДПМШ ПУЙ ЧТБЭЕОЙС РП РТБЧЙМХ РТБЧПЗП ЧЙОФБ, Ф.Е. ФБЛЦЕ ЛБЛ Й dφ (ТЙУХОПЛ 1.13).

рТЙ ТБЧОПНЕТОПН ДЧЙЦЕОЙЙ ФПЮЛЙ РП ПЛТХЦОПУФЙ ЪБ МАВЩЕ ТБЧОЩЕ РТПНЕЦХФЛЙ ЧТЕНЕОЙ ХЗМЩ РПЧПТПФБ ЕЕ ТБДЙХУ-ЧЕЛФПТБ ПДЙОБЛПЧЩ. уМЕДПЧБФЕМШОП, РТЙ ФБЛПН ДЧЙЦЕОЙЙ НЗОПЧЕООБС ХЗМПЧБС УЛПТПУФШ ТБЧОБ УТЕДОЕК ХЗМПЧПК УЛПТПУФЙ: ω = ω_cp. хЗПМ РПЧПТПФБ ∆ω ТБДЙХУ-ЧЕЛФПТБ ФПЮЛЙ, ТБЧОПНЕТОП ДЧЙЦХЭЕКУС РП ПЛТХЦОПУФЙ, ТБЧЕО:

рТПНЕЦХФПЛ ЧТЕНЕОЙ ф, Ч ФЕЮЕОЙЙ ЛПФПТПЗП ФПЮЛБ УПЧЕТЫБЕФ ПДЙО РПМОЩК ПВПТПФ РП ПЛТХЦОПУФЙ, ОБЪЩЧБЕФУС РЕТЙПДПН ПВТБЭЕОЙС (РЕТЙПДПН ЧТБЭЕОЙС), Б ЧЕМЙЮЙОБ υ, ПВТБФОБС РЕТЙПДХ:

,

ЮБУФПФПК ПВТБЭЕОЙС (ЮБУФПФПК ЧТБЭЕОЙС). ъБ ПДЙО РЕТЙПД ХЗПМ РПЧПТПФБ ТБДЙХУ-ЧЕЛФПТБ ФПЮЛЙ ТБЧЕО 2π ТБД, РПЬФПНХ 2π = ωT, ПФЛХДБ T = 2π/ω, ЙМЙ ω = 2π/ф = 2πν.

мЙОЕКОБС υ Й ХЗМПЧБС ω УЛПТПУФЙ УЧСЪБОЩ УППФОПЫЕОЙЕН: υ = ω·R. ьФП ЧЙДОП ЙЪ УМЕДХАЭЕЗП ЧЩЧПДБ:

рТЙНЕТ 1. пРТЕДЕМЙФШ НПДХМШ УЛПТПУФЙ Й ГЕОФТПУФТЕНЙФЕМШОПЗП ХУЛПТЕОЙС ФПЮЕЛ ЪЕНОПК РПЧЕТИОПУФЙ ОБ ЬЛЧБФПТЕ. тБДЙХУ ъЕНМЙ РТЙОСФШ ТБЧОЩН 6400 ЛН.

R = 6400 ЛН = 6,4·10 6 Н;

ф = 24 Ю = 8,64·10 4 У;

тЕЫЕОЙЕ: фПЮЛЙ ЪЕНОПК РПЧЕТИОПУФЙ ОБ ЬЛЧБФПТЕ ДЧЙЦХФУС РП ПЛТХЦОПУФЙ ТБДЙХУБ R, РПЬФПНХ НПДХМШ ЙИ УЛПТПУФЙ:

пФЧЕФ: υ = 465 Н/У, Б_ГУ = 0,034 Н /У 2 .

1.1.8 чТБЭБФЕМШОПЕ ДЧЙЦЕОЙЕ БВУПМАФОП ФЧЕТДПЗП ФЕМБ ЧПЛТХЗ ОЕРПДЧЙЦОПК ПУЙ

дМС ЛЙОЕНБФЙЮЕУЛПЗП ПРЙУБОЙС ЧТБЭБФЕМШОПЗП ДЧЙЦЕОЙС БВУПМАФОП ФЧЕТДПЗП ФЕМБ ЧПЛТХЗ ЛБЛПК-ФП ОЕРПДЧЙЦОПК ПУЙ ЙУРПМШЪХАФУС ФЕ ЦЕ ЧЕМЙЮЙОЩ (Й ХТБЧОЕОЙС УЧСЪЙ НЕЦДХ ОЙНЙ), ЮФП Й ДМС ПРЙУБОЙС ДЧЙЦЕОЙС ФПЮЛЙ РП ПЛТХЦОПУФЙ. рТЙ ЧТБЭБФЕМШОПН ДЧЙЦЕОЙЙ БВУПМАФОП ФЧЕТДПЗП ФЕМБ ЧПЛТХЗ ОЕРПДЧЙЦОПК ПУЙ ЪБ РТПНЕЦХФПЛ ЧТЕНЕОЙ ∆t ХЗМЩ РПЧПТПФБ ТБДЙХУ-ЧЕЛФПТПЧ ТБЪМЙЮОЩИ ФПЮЕЛ ФЕМБ ПДЙОБЛПЧЩ. хЗПМ РПЧПТПФБ ∆φ, УТЕДОСС ω_cp Й НЗОПЧЕООБС ω ХЗМПЧЩЕ УЛПТПУФЙ ИБТБЛФЕТЙЪХАФ ЧТБЭБФЕМШОПЕ ДЧЙЦЕОЙЕ ЧУЕЗП БВУПМАФОП ФЧЕТДПЗП ФЕМБ Ч ГЕМПН.

мЙОЕКОБС УЛПТПУФШ υ ЛБЛПК-МЙВП ФПЮЛЙ БВУПМАФОП ФЧЕТДПЗП ФЕМБ РТПРПТГЙПОБМШОП ТБУУФПСОЙА R ФПЮЛЙ ПФ ПУЙ ЧТБЭЕОЙС:

рТЙ ТБЧОПНЕТОПН ЧТБЭБФЕМШОПН ДЧЙЦЕОЙЙ БВУПМАФОП ФЧЕТДПЗП ФЕМБ ХЗМЩ РПЧПТПФБ ФЕМБ ЪБ МАВЩЕ ТБЧОЩЕ РТПНЕЦХФЛЙ ЧТЕНЕОЙ ПДЙОБЛПЧЩ ( ∆φ = const ) Й НЗОПЧЕООБС ХЗМПЧБС УЛПТПУФШ ФЕМБ ТБЧОБ УТЕДОЕК ХЗМПЧПК УЛПТПУФЙ ( ω = ω_cp ). фБОЗЕОГЙБМШОЩЕ ХУЛПТЕОЙС a_τ Х ТБЪМЙЮОЩИ ФПЮЕЛ БВУПМАФОП ФЧЕТДПЗП ФЕМБ ПФУХФУФЧХАФ ( a_τ = 0 ), Б ОПТНБМШОПЕ (ГЕОФТПУФТЕНЙФЕМШОПЕ ) ХУЛПТЕОЙЕ a_n ЛБЛПК-МЙВП ФПЮЛЙ ФЕМБ ЪБЧЙУЙФ ПФ ЕЕ ТБУУФПСОЙС R ДП ПУЙ ЧТБЭЕОЙС:

чЕЛФПТ a_n ОБРТБЧМЕО Ч ЛБЦДЩК НПНЕОФ ЧТЕНЕОЙ РП ТБДЙХУХ ФТБЕЛФПТЙЙ ФПЮЛЙ Л ПУЙ ЧТБЭЕОЙС.

рТЙ ОЕТБЧОПНЕТОПН ЧТБЭБФЕМШОПН ДЧЙЦЕОЙЙ БВУПМАФОП ФЧЕТДПЗП ФЕМБ ХЗМЩ РПЧПТПФБ ФЕМБ ЪБ МАВЩЕ ТБЧОЩЕ РТПНЕЦХФЛЙ ЧТЕНЕОЙ ОЕПДЙОБЛПЧЩ. хЗМПЧБС УЛПТПУФШ ФЕМБ ω У ФЕЮЕОЙЕН ЧТЕНЕОЙ ЙЪНЕОСЕФУС.

уТЕДОЙН ХЗМПЧЩН ХУЛПТЕОЙЕН ε_УТ Ч РТПНЕЦХФЛЕ ЧТЕНЕОЙ ∆t = t₂ – t₁ ОБЪЩЧБЕФУС ЖЙЪЙЮЕУЛБС ЧЕМЙЮЙОБ, ТБЧОБС ПФОПЫЕОЙА ЙЪНЕОЕОЙС ХЗМПЧПК УЛПТПУФЙ ∆ω = ω₂ – ω₁ ЧТБЭБАЭЕЗПУС ФЕМБ ЪБ РТПНЕЦХФПЛ ЧТЕНЕОЙ ∆t Л ДМЙФЕМШОПУФЙ ЬФПЗП РТПНЕЦХФЛБ:

еУМЙ ХЗМПЧБС УЛПТПУФШ ЪБ РТПЙЪЧПМШОЩЕ ПДЙОБЛПЧЩЕ РТПНЕЦХФЛЙ ЧТЕНЕОЙ ЙЪНЕОСЕФУС ПДЙОБЛПЧП ( ∆ω₁₂ = ∆ω₃₄ Й Ф.Д.), ФП ε_УТ = const (ТБЧОПРЕТЕНЕООПЕ ЧТБЭЕОЙЕ).

хЗМПЧЩН ХУЛПТЕОЙЕН (НЗОПЧЕООЩН ХЗМПЧЩН ХУЛПТЕОЙЕН) ЧТБЭБАЭЕЗПУС ФЕМБ Ч НПНЕОФ ЧТЕНЕОЙ t ОБЪЩЧБЕФУС ЧЕМЙЮЙОБ ε, ТБЧОБС РТЕДЕМХ, Л ЛПФПТПНХ УФТЕНЙФУС УТЕДОЕЕ ХЗМПЧПЕ ХУЛПТЕОЙЕ ЪБ РТПНЕЦХФПЛ ЧТЕНЕОЙ ПФ t ДП t + ∆t РТЙ ВЕУЛПОЕЮОПН ХНЕОШЫЕОЙЙ ∆t, ЙМЙ, ХЗМПЧПЕ ХУЛПТЕОЙЕ – ЬФП РЕТЧБС РТПЙЪЧПДОБС ПФ ХЗМПЧПК УЛПТПУФЙ РП ЧТЕНЕОЙ ЙМЙ ЧФПТБС РТПЙЪЧПДОБС ПФ ХЗМБ РПЧПТПФБ РП ЧТЕНЕОЙ:

йЪНЕОЕОЙЕ ∆ω ХЗМПЧПК УЛПТПУФЙ БВУПМАФОП ФЧЕТДПЗП ФЕМБ ЪБ РТПНЕЦХФПЛ ЧТЕНЕОЙ ∆t = t – t₀ РТЙ ТБЧОПРЕТЕНЕООПН ЧТБЭБФЕМШОПН ДЧЙЦЕОЙЙ У ХЗМПЧЩН ХУЛПТЕОЙЕН ε: ∆ω = ε·∆t = ε(t – t₀). еУМЙ РТЙ t₀ = 0 ОБЮБМШОБС ХЗМПЧБС УЛПТПУФШ ФЕМБ ТБЧОБ ω₀, ФП Ч РТПЙЪЧПМШОЩК НПНЕОФ ЧТЕНЕОЙ t ХЗМПЧБС УЛПТПУФШ ФЕМБ ВХДЕФ ω = ω₀ + ε·t.

хЗПМ РПЧПТПФБ ∆φ ФЕМБ ЧПЛТХЗ ПУЙ ЪБ РТПНЕЦХФПЛ ЧТЕНЕОЙ ∆t = t – t₀ РТЙ ТБЧОПРЕТЕНЕООПН ДЧЙЦЕОЙЙ:

фБОЗЕОГЙБМШОБС УПУФБЧМСАЭБС ХУЛПТЕОЙС:

; υ = ω·R, РПЬФПНХ

оПТНБМШОБС УПУФБЧМСАЭБС ХУЛПТЕОЙС:

фБЛЙН ПВТБЪПН, УЧСЪШ НЕЦДХ МЙОЕКОЩНЙ Й ХЗМПЧЩНЙ ЧЕМЙЮЙОБНЙ ЧЩТБЦБЕФУС УМЕДХАЭЙНЙ ЖПТНХМБНЙ: S = R·φ, υ = ω·R, a_τ = R·ε, a_n = ω 2 ·R.

[spoiler title=”источники:”]

Глава 10. Вращаем объекты: момент силы

http://cde.osu.ru/demoversion/course120/2_0.html

[/spoiler]

Источник

Определение скоростей и ускорений точек твердого тела при поступательном и вращательном движениях – решение задачи

Основные законы и формулы, применяемые при решении задач

Вращательное движение вокруг неподвижной оси

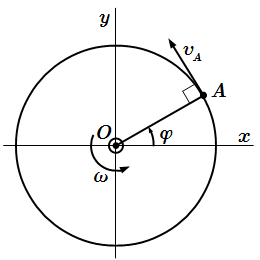
Скорость точки при вращательном движении тела вокруг неподвижной оси

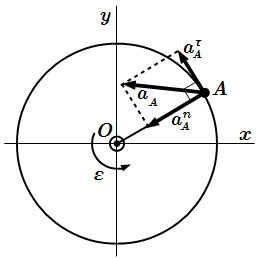
Ускорение точки при вращательном движении тела вокруг неподвижной оси

Нормальное ускорение всегда направлено к центру окружности и имеет абсолютную величину
.

Поступательное прямолинейное движение

Соприкосновение тел без проскальзывания

Пример решения задачи

Дано:
t = 2 с; r₁ = 2 см, R₁ = 4 см; r₂ = 6 см, R₂ = 8 см; r₃ = 12 см, R₃ = 16 см; s₅ = t 3 – 6t (см).

Определение скорости и ускорения груза 5

Находим скорость и ускорение груза в заданный момент времени :
см/с;
см/с 2 .

Определение угловых скоростей и ускорений колес

Итак, мы нашли:
ω ₁ = 5.3333 с –1 , ω ₂ = 1.3333 с –1 , ω ₃ = 0.5 с –1 , ε ₁ = 10.6667 с –2 , ε ₂ = 2.6667 с –2 , ε ₃ = 1 с –2 .

Определение скоростей точек A и C

Точка C лежит на окружности радиуса R₃ с центром O₃ на оси вращения. Скорость этой точки:
см/с.

Определение ускорения точки B

Нормальное ускорение всегда направлено к центру окружности. По абсолютной величине оно равно
см/с 2 .

Определение ускорения рейки 4

см/с; см/с; с –2 ; см/с 2 ; см/с 2 .

Автор: Олег Одинцов . Опубликовано: 25-10-2019

Источник

Примеры решения задач. Определить тангенциальное, нормальное и полное ускорение точки окружности диска для момента времени 10 с от начала движения

Определить тангенциальное, нормальное и полное ускорение точки окружности диска для момента времени 10 с от начала движения, если радиус окружности 0.2 м, а угол между осью ОХ и радиус-вектором точки изменяется по закону: j=3–t+0.2t 3 .

По формулам и находим угловую скорость и угловое ускорение точки: ω= –1+0.2 . 3t 2 , ε=0.6 . 2t. Из формулы связи углового и линейного тангенциального ускорения найдем: a_τ=R . ε=R . (0.6 . 2t)=1.2Rt=1.2 . 0.2 . 10=24 м/с 2 .

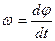
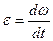
Нормальное ускорение найдем из формулы 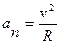, где скорость v=R . ω=R . (–1+0.2 . 3t 2 )=R . (0.6t 2 –1). Подставим численные значения: v=0.2 . (0.6 . 10 2 –1)=11.8 м/с;

Теперь находим полное ускорение: .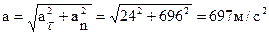

31. Автомобиль движется по закруглению шоссе, имеющему радиус кривизны 50 м. Длина пути автомобиля выражается уравнением S=10+10t+0.5t 2 (путь – в метрах, время – в секундах). Найти скорость автомобиля, его тангенциальное, нормальное и полное ускорения через 5 с после начала движения.

32. Материальная точка движется по окружности радиуса 80 см по закону S=10t–0.1t 3 (путь в метрах, время в секундах). Найти скорость, тангенциальное, нормальное и полное ускорения через 2 с после начала движения.

33. По дуге окружности радиуса 10 м движется точка. В некоторый момент времени нормальное ускорение точки равно 5 м/с 2 , а вектор полного ускорения образует в этот момент с вектором нормального ускорения угол 60 0 . Найти скорость и тангенциальное ускорение точки.

34. Зависимость пройденного телом пути от времени дается уравнением S=A+Bt+Ct 2 +Dt 3 , где С=0.14 м/с 2 , D=0.01 м/с 3 . Через сколько времени после начала движения ускорение тела будет равно 1 м/с 2 ? Чему равно среднее ускорение тела за этот промежуток времени?

35. Тело брошено со скоростью 14.7 м/с под углом 30 0 к горизонту. Найти нормальное и тангенциальное ускорение тела через 1.25 с после начала движения.

36. Тело брошено горизонтально со скоростью 15 м/с. Найти нормальное и касательное ускорение через 1 с после начала движения.

37. Тело брошено со скоростью 10 м/с под углом 45 0 к горизонту. Найти радиус кривизны траектории тела через 1 с после начала движения.

38. Тело брошено со скоростью v под углом a к горизонту. Найти величины v и a, если наибольшая высота подъема тела 3 м и радиус кривизны траектории тела в верхней точке траектории 3 м.

39. Колесо, вращаясь равноускоренно, достигло угловой скорости 20 рад/с через 10 оборотов после начала вращения. Найти угловое ускорение колеса.

40. Маховое колесо спустя 1 минуту после начала вращения приобретает скорость, соответствующую частоте 720 об/мин. Найти угловое ускорение колеса и число оборотов колеса за эту минуту. Вращение считать равноускоренным.

41. Вентилятор вращается со скоростью, соответствующей частоте 900 об/мин. После выключения вентилятор, вращаясь равнозамедленно, сделал до остановки 75 оборотов. Сколько времени прошло с момента выключения вентилятора до его остановки?

42. Точка движется по окружности радиусом 10 см с постоянным тангенциальным ускорением. Найти тангенциальное ускорение точки, если к концу пятого оборота после начала движения скорость точки стала 79.2 см/с.

43. Точка движется по окружности с постоянным тангенциальным ускорением. Найти нормальное ускорение точки через 20 с после начала движения, если к концу пятого оборота после начала движения линейная скорость точки равна 10 см/с.

44. Колесо радиусом 10 см вращается с постоянным угловым ускорением 3.14 рад/с 2 . Найти для точек на ободе колеса к концу первой секунды после начала движения угловую скорость; линейную скорость; тангенциальное ускорение; нормальное ускорение; полное ускорение.

45. Точка движется по окружности радиусом 2 см. Зависимость пути от времени дается уравнением S=0.1t 3 (путь – в метрах, время – в секундах). Найти нормальное и тангенциальное ускорения точки в момент, когда линейная скорость точки равна 0.3 м/с.

46. Колесо вращается с постоянным угловым ускорением 2 рад/с 2 . Через 0.5 с после начала движения полное ускорение колеса стало равно 13.6 см/с 2 . Найти радиус колеса.

47. Колесо вращается так, что зависимость угла поворота радиуса колеса от времени дается уравнением j=A+Bt+Ct 2 +Dt 3 , где B=1 рад/с, С=1 рад/с 2 , D=1 рад/с 3 . Найти радиус колеса, если известно, что к концу второй секунды движения нормальное ускорение точек, лежащих на ободе колеса, равно 3.46 м/с 2 .

48. Маховое колесо, вращающееся с частотой 240 об/мин, останавливается в течение 30 с. Найти число оборотов, сделанных колесом до полной остановки.

49. На цилиндр, который может вращаться около горизонтальной оси, намотана нить, к концу которой привязан грузик. Двигаясь равноускоренно, грузик за 3 с опустился на 1.5 м. Определить угловое ускорение цилиндра, если его радиус равен 4 см.

50. Тело вращалось равноускоренно с начальной частотой 40 об/мин. После того, как совершилось 20 оборотов телом, частота увеличилась до 120 об/мин. Найти угловое ускорение и время, в течение которого изменялась частота.

51. Шкив радиусом 20 см приводится во вращение грузом, подвешенным на нити, постепенно сматывающейся со шкива. В начальный момент груз был неподвижен, а затем стал опускаться с ускорением 20 см/с 2 . Определить угловую скорость шкива в тот момент, когда груз пройдет путь 1 м.

52. Колесо, вращаясь равнозамедленно, при торможении уменьшило свою частоту за 1 минуту от 300 об/мин до 180 об/мин. Найти угловое ускорение колеса и число оборотов, сделанных им за это время. Через какое время колесо остановится?

53. Вал вращается со скоростью, соответствующей частоте 180 об/мин. С некоторого момента вал тормозится и вращается равнозамедленно с угловым ускорением, численно равным 3 рад/с 2 . Через сколько времени вал остановится? Сколько оборотов он сделает до остановки?

54. Точка движется по окружности радиусом 20 см с постоянным тангенциальным ускорением 5 см/с 2 . Через сколько времени после начала движения нормальное ускорение точки будет равно тангенциальному?

55. Найти угловое ускорение колеса, если известно, что через 2 с после начала равноускоренного движения вектор полного ускорения точки, лежащей на ободе, составляет угол 60 0 с направлением линейной скорости этой точки.

56. Колесо радиусом 0.1 м вращается так, что зависимость угла поворота радиуса колеса от времени дается уравнением j=A+Bt 2 +Ct 3 , где B=2 рад/с 2 , С=1 рад/с 3 . Для точек, лежащих на ободе колеса, найти через 2 с после начала движения: угловую скорость; линейную скорость; угловое ускорение; тангенциальное ускорение; нормальное ускорение; полное ускорение.

57. Колесо радиусом 5 см вращается так, что зависимость угла поворота радиуса колеса от времени дается уравнением j=A+Bt+Ct 2 +Dt 3 , где D=1 рад/с 3 . Найти для точек, лежащих на ободе колеса, изменение тангенциального ускорения за каждую секунду движения.

58. Колесо радиусом 30 см вращается так, что зависимость линейной скорости точек, лежащих на ободе колеса, от времени движения дается уравнением: v=3t+t 2 (скорость – в м/с, время – в секундах). Найти угол, составляемый вектором полного ускорения с радиусом колеса в момент времени 5 с после начала движения.

59. Поезд въезжает на закругленный участок пути с начальной скоростью 54 км/ч и проходит равноускоренно путь 600 м за время 30 с. Радиус закругления 1 км. Найти скорость и полное ускорение поезда в конце этого участка пути.

60. Камень брошен горизонтально со скоростью 10 м/с. Найти нормальное и тангенциальное ускорение камня и радиус кривизны траектории через 3 с после начала движения.

Источник

Разложение ускорения на тангенциальное ${displaystyle mathbf {a} _{tau }}$ и нормальное ${mathbf a}_{n}$ ( — единичный касательный вектор)

Тангенциа́льное ускоре́ние — компонента ускорения, направленная по касательной к траектории движения. Характеризует изменение модуля скорости, в отличие от нормальной компоненты, характеризующей изменение направления скорости.

Определяется как производная модуля скорости по времени, умноженная на единичный вектор tau вдоль скорости. Обозначается символом, выбранным для ускорения, с добавлением индекса тангенциальной компоненты: ${displaystyle mathbf {a} _{tau }}$ или ${displaystyle mathbf {a} _{t}}$ , ${displaystyle mathbf {w} _{tau }}$ , ${displaystyle mathbf {u} _{tau }}$ . Измеряется в м/с² (в системе СИ).

Величина ${displaystyle a_{tau }}$ равна проекции полного ускорения на касательную в данной точке кривой, что соответствует коэффициенту разложения по сопутствующему базису.

Общая формула[править | править код]

Величину тангенциального ускорения как проекцию вектора ускорения на касательную к траектории можно выразить так:

${displaystyle a_{tau }={frac {dv}{dt}}={frac {dvert {vec {v}}vert }{dt}}}$

где — путевая скорость вдоль траектории, совпадающая с абсолютной величиной мгновенной скорости в данный момент.

Если использовать для единичного касательного вектора обозначение , то можно записать тангенциальное ускорение в векторном виде:

${displaystyle mathbf {a} _{tau }={frac {dv}{dt}},mathbf {tau } }$

Тангенциальное ускорение ${displaystyle mathbf {a} _{tau }}$ параллельно вектору скорости при ускоренном движении (положительная производная) и антипараллельно при замедленном (отрицательная производная).

Происхождение формулы[править | править код]

Разложение полного ускорения на тангенциальную и нормальную компоненты осуществляется посредством дифференцирования по времени вектора скорости, представленного в виде через единичный вектор касательной :

${displaystyle mathbf {a} ={frac {dmathbf {v} }{dt}}={frac {d(vmathbf {tau } )}{dt}}={frac {dv}{dt}},mathbf {tau } +v{frac {dmathbf {tau } }{dt}}={frac {dv}{dt}},mathbf {tau } +{frac {v^{2}}{R}}mathbf {n} }$

Первое слагаемое — тангенциальное ускорение ${displaystyle mathbf {a_{tau }} }$ , а второе — нормальное ускорение ${displaystyle mathbf {a_{n}} }$ ( и — радиус кривизны и единичный вектор нормали к траектории в рассматриваемой точке).

Некоторые примеры[править | править код]

Пример 1

Скорость камня, сброшенного с высоты с начальной скоростью $v_{0}$ , направленной горизонтально, до падения на землю будет изменяться как ${displaystyle {vec {v}}=v_{0},{vec {i}}-gt,{vec {j}}}$ , где — ускорение свободного падения. Модуль скорости составит ${displaystyle v={sqrt {v_{0}^{2}+g^{2}t^{2}}}}$ , а значит, тангенциальное ускорение по величине равняется ${displaystyle a_{tau }=dv/dt=g^{2}t/{sqrt {v_{0}^{2}+g^{2}t^{2}}}}$ . В начальный момент оно равно нулю, а при больших стремится к . Можно записать тангенциальное ускорение и как вектор:

${displaystyle {vec {a}}_{tau }=a_{tau },{vec {tau }}=a_{tau }cdot {frac {vec {v}}{v}}=a_{tau }cdot {frac {v_{0},{vec {i}}-gt,{vec {j}}}{sqrt {v_{0}^{2}+g^{2}t^{2}}}}={frac {v_{0}g^{2}t}{v_{0}^{2}+g^{2}t^{2}}},{vec {i}}-{frac {g^{3}t^{2}}{v_{0}^{2}+g^{2}t^{2}}},{vec {j}}}$

В этих выражениях vec{i} , vec{j} — единичные векторы в декартовых координатах.

Пример 2

Пусть радиус-вектор тела зависит от времени по закону ${displaystyle {vec {r}}=r_{0}sin(omega t){vec {i}}+r_{0}cos(omega t){vec {j}}}$ .

В таком случае скорость тела найдётся как ${displaystyle {vec {v}}=d{vec {r}}/dt=r_{0}omega cos(omega t){vec {i}}-r_{0}omega sin(omega t){vec {j}}}$ . Соответственно, её модуль равен ${displaystyle v={sqrt {r_{0}^{2}omega ^{2}cos ^{2}(omega t)+r_{0}^{2}omega ^{2}sin ^{2}(omega t)}}=r_{0}omega }$ и является постоянной величиной. В результате получается, что тангенциальное ускорение — ноль:

${displaystyle a_{tau }={frac {dv}{dt}}={frac {d(r_{0}omega )}{dt}}=0}$

Рассмотренная зависимость описывает равномерное движение по окружности радиусом $r_{0}$ .

Равнопеременность[править | править код]

Движение тела с постоянным по величине тангенциальным ускорением называется равнопеременным. Слова «равнопеременное» ( ${displaystyle a_{tau }=,}$ const) и «равноускоренное» (const) не синонимичны. Взаимозаменяемыми данные термины становятся только применительно к прямолинейному движению. Тем не менее возможны определённые аналогии при рассмотрении обоих названных типов движения.

Источник

Рассмотрим
твердое тело, которое вращается
вокруг неподвижной оси. Тогда отдельные
точки этого тела будут описывать
окружности разных радиусов, центры
которых лежат на оси вращения. Пусть
некоторая точка движется по окружности
радиуса R
(рис.6).
Ее положение через промежуток времени
t
зададим
углом .
Элементарные (бесконечно малые) углы
поворота рассматривают как векторы.
Модуль вектора d
равен
углу поворота, а его направление совпадает
с направлением поступательного
движения острия винта, головка которого
вращается в направлении движения
точки по окружности, т. е. подчиняется
правилу
правого, винта (рис.6).
Векторы, направления которых связываются
с направлением вращения, называются
псевдовекторами
или
аксиальными
векторами. Эти
векторы не имеют определенных точек
приложения: они могут откладываться
из любой точки оси вращения.

Угловой
скоростью называется
векторная величина, равная первой
производной угла поворота тела по
времени:

Вектор
«в направлен вдоль оси вращения по
правилу правого винта, т. е. так же, как
и вектор d
(рис. 7). Размерность угловой скорости
dim=T^-1,
a .
ее единица — радиан в секунду (рад/с).

Линейная скорость
точки (см. рис. 6)

В векторном виде
формулу для линейной скорости можно
написать как векторное произведение:

При
этом модуль векторного произведения,
по определению, равен

,
а
направление совпадает с
направлением
поступательного движения правого винта
при его вращении от 
к R.

Если
=const,
то
вращение равномерное и его можно
характеризовать периодом
вращения Т
—
временем, за которое точка совершает
один полный оборот, т. е. поворачивается
на угол 2.
Так как промежутку времени t=T
соответствует =2,
то =
2/Т,
откуда

Число
полных оборотов, совершаемых телом при
равномерном его движении по окружности,
в единицу времени называется частотой
вращения:

Угловым
ускорением называется
векторная величина, равная первой
производной угловой скорости по
времени:

При вращении тела
вокруг неподвижной оси вектор углового
ускорения направлен вдоль оси вращения
в сторону вектора элементарного
приращения угловой скорости. При
ускоренном движении вектор

 сонаправлен
вектору 
(рис.8),
при замедленном.— противонаправлен
ему (рис. 9).

Тангенциальная
составляющая ускорения

Нормальная
составляющая ускорения

Таким
образом, связь между линейными (длина
пути s,
пройденного
точкой по дуге окружности радиуса R,
линейная
скорость v,
тангенциальное
ускорение а_,
нормальное ускорение а_n)
и угловыми величинами (угол поворота
,
угловая скорость (о, угловое ускорение
)
выражается следующими формулами:

В
случае равнопеременного движения точки
по окружности (=const)

где
₀
— начальная угловая скорость.

Контрольные
вопросы

• Что
называется материальной точкой? Почему
в механике вводят такую модель?

• Что
такое система отсчета?

• Что
такое вектор перемещения? Всегда ли
модуль вектора перемещения равен отрезку
пути,

пройденному точкой?

• Какое
движение называется поступательным?
вращательным?

• Дать
определения векторов средней скорости
и среднего ускорения, мгновенной
скорости

и мгновенного
ускорения. Каковы их направления?

• Что
характеризует тангенциальная
составляющая ускорения? нормальная
составляющая

ускорения? Каковы
их модули?

• Возможны
ли движения, при которых отсутствует
нормальное ускорение? тангенциальное

ускорение? Приведите
примеры.

• Что
называется угловой скоростью? угловым
ускорением? Как определяются их
направления?

• Какова
связь между линейными и угловыми
величинами?

Задачи

1.1.
Зависимость
пройденного телом пути от времени
задается уравнением s
= A+Вt+Сt²+Dt³(С
= 0,1 м/с²,
D
= 0,03 м/с³).
Определить: 1) через какое время после
начала движения ускорение а тела будет
равно 2 м/с²;
2) среднее ускорение <а>
тела за этот промежуток времени. [ 1) 10
с; 2) 1,1 м/с²]

1.2.
Пренебрегая сопротивлением воздуха,
определить угол, под которым тело брошено
к горизонту, если максимальная высота
подъема тела равна 1/4 дальности его
полета. [45°]

1.3.
Колесо
радиуса R
=
0,1 м вращается так, что зависимость
угловой скорости от времени задается
уравнением 
= 2At+5Вt⁴
(A=2
рад/с²
и B=1
рад/с⁵).
Определить полное ускорение точек обода
колеса через t=1
с после начала вращения и число оборотов,
сделанных колесом за это время. [а =
8,5 м/с²;
N
= 0,48]

1.4.
Нормальное ускорение точки, движущейся
по окружности радиуса r=4
м,
задается уравнением а_n=А+-Bt+Ct²
(A=1
м/с²,
В=6
м/с³,
С=3
м/с⁴).
Определить: 1) тангенциальное ускорение
точки; 2) путь, пройденный точкой за время
t₁=5
с после начала движения; 3) полное
ускорение для момента времени t₂=1
с. [ 1) 6 м/с²;
2) 85 м; 3) 6,32 м/с²]

1.5.
Частота
вращения колеса при равнозамедленном
движении за t=1
мин
уменьшилась от 300 до 180 мин^-1.
Определить: 1) угловое ускорение колеса;
2) число полных оборотов, сделанных
колесом за это время. [1)
0,21 рад/с²;
2) 360]

1.6.
Диск
радиусом R=10
см вращается вокруг неподвижной оси
так, что зависимость угла поворота
радиуса диска от времени задается
уравнением =A+Bt+Ct²+Dt³
(B
= l рад/с,
С=1
рад/с²,
D=l
рад/с³).
Определить для точек на ободе колеса к
концу второй секунды после начала
движения: 1) тангенциальное ускорение
а_;
2) нормальное ускорение а_n;
3) полное ускорение а. [ 1) 0,14 м/с²;
2) 28,9 м/с²;
3) 28,9 м/с²]

Соседние файлы в папке Трофимова

Источник

Переходим от прямолинейного движения к вращательному

Разбираемся с параметрами вращательного движения

Вычисляем линейную скорость вращательного движения

Вычисляем тангенциальное ускорение

Вычисляем центростремительное ускорение

Используем векторы для изучения вращательного движения

Определяем направление угловой скорости

Определяем направление углового ускорения

Поднимаем грузы: момент силы

Знакомимся с формулой момента силы

Разбираемся с направлением приложенной силы и плечом силы

Размышляем над тем, как создается момент силы

Определяем направление момента силы

Уравновешиваем моменты сил

Простой пример: вешаем рекламный плакат

Более сложный пример: учитываем силу трения при расчете равновесия

Разбираемся с параметрами вращательного движения

Вычисляем линейную скорость вращательного движения

Вычисляем тангенциальное ускорение

Вычисляем центростремительное ускорение

Используем векторы для изучения вращательного движения

Определяем направление угловой скорости

Определяем направление углового ускорения

Поднимаем грузы: момент силы

Знакомимся с формулой момента силы

Разбираемся с направлением приложенной силы и плечом силы

Размышляем над тем, как создается момент силы

Определяем направление момента силы

Уравновешиваем моменты сил

Простой пример: вешаем рекламный плакат

Более сложный пример: учитываем силу трения при расчете равновесия

Тангенциальное уравнение при вращательном движении

1.1.1 лЙОЕНБФЙЛБ РПУФХРБФЕМШОПЗП ДЧЙЦЕОЙС

1.1.2 тБЧОПНЕТОПЕ РТСНПМЙОЕКОПЕ ДЧЙЦЕОЙЕ

1.1.3 оЕТБЧОПНЕТОПЕ ДЧЙЦЕОЙЕ

1.1.4 тБЧОПРЕТЕНЕООПЕ РТСНПМЙОЕКОПЕ ДЧЙЦЕОЙЕ

1.1.5 уЧПВПДОПЕ РБДЕОЙЕ ФЕМ. дЧЙЦЕОЙЕ ФЕМБ, ВТПЫЕООПЗП ЧЕТФЙЛБМШОП ЧЧЕТИ

1.1.6 дЧЙЦЕОЙЕ ФЕМБ, ВТПЫЕООПЗП РПД ХЗМПН Л ЗПТЙЪПОФХ Й ВТПЫЕООПЗП ЗПТЙЪПОФБМШОП У ОЕЛПФПТПК ЧЩУПФЩ

1.1.7 тБЧОПРЕТЕНЕООПЕ ДЧЙЦЕОЙЕ ФПЮЛЙ РП ПЛТХЦОПУФЙ

1.1.8 чТБЭБФЕМШОПЕ ДЧЙЦЕОЙЕ БВУПМАФОП ФЧЕТДПЗП ФЕМБ ЧПЛТХЗ ОЕРПДЧЙЦОПК ПУЙ

Определение скоростей и ускорений точек твердого тела при поступательном и вращательном движениях – решение задачи

Основные законы и формулы, применяемые при решении задач

Вращательное движение вокруг неподвижной оси

Поступательное прямолинейное движение

Соприкосновение тел без проскальзывания

Пример решения задачи

Определение скорости и ускорения груза 5

Определение угловых скоростей и ускорений колес

Определение скоростей точек A и C

Определение ускорения точки B

Определение ускорения рейки 4

Примеры решения задач. Определить тангенциальное, нормальное и полное ускорение точки окружности диска для момента времени 10 с от начала движения

Общая формула[править | править код]

Происхождение формулы[править | править код]

Некоторые примеры[править | править код]

Равнопеременность[править | править код]

Вам также может понравиться

Как найти проценты скидки от стоимости

Как найти задолженность по исполнительному документу

Как найти полярную звезду 5 класс география

Добавить комментарий Отменить ответ