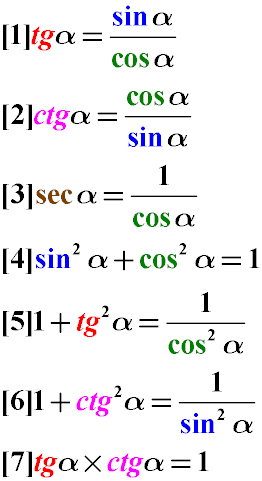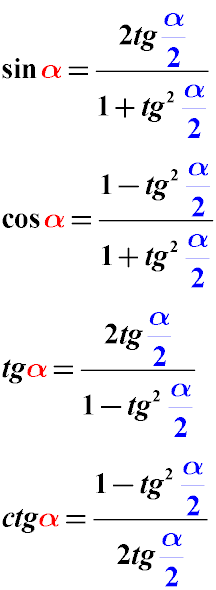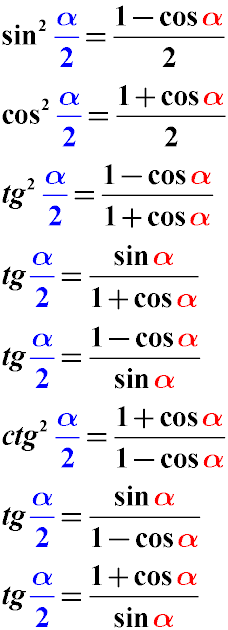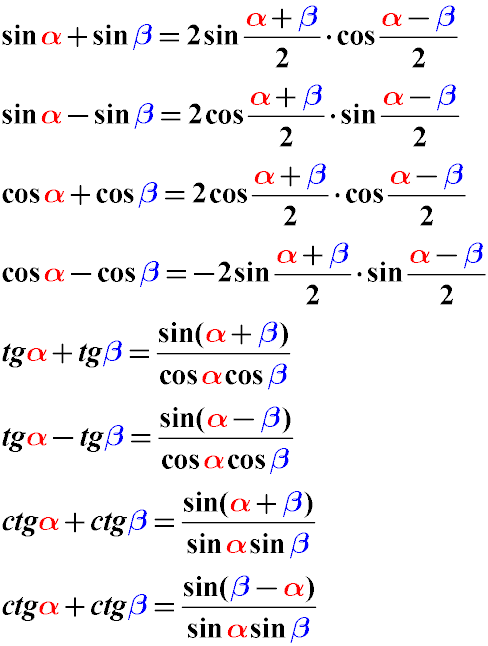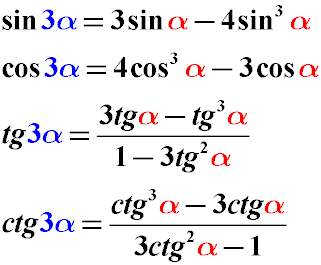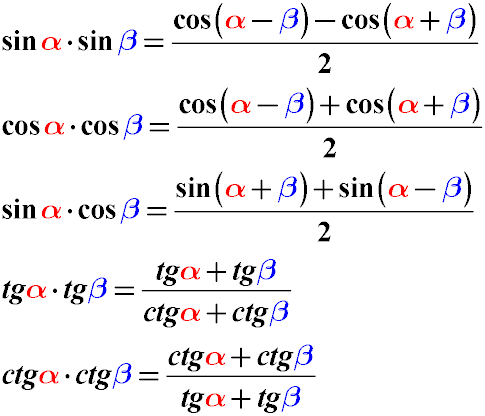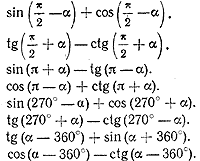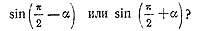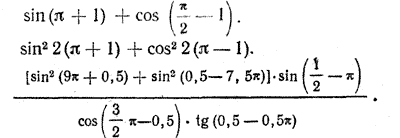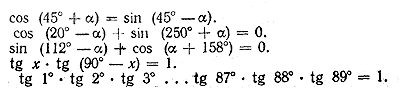Вот есть в геометрии одиничное коло.
anonym )))
Ученик
(31),
закрыт
4 года назад
в нем рисуеться система координат. Оттуда пишут формулу cos(180-альфа) =sinаАьфа. Что это значит? Как тогда искать sin(180-альфа)? Или tg(180-альфа)?
Лучший ответ
Spink
Знаток
(416)
9 лет назад
Это называются формулы приведения.
косинус (180 – альфа) = – косинус (альфа) <– МИНУС КОСИНУС АЛЬФА
синус (180 – альфа) = синус (альфа)
тангенс (180 – альфа) = МИНУС тангенс (альфа)
Остальные ответы
Похожие вопросы
Тангенс онлайн калькулятор
Введите число от 0 до 360.
(обязательное поле)
Введите число от 0 до 59.
(не обязательное поле, по умолчанию – 0)
Введите число от 0 до 59.
(не обязательное поле, по умолчанию – 0)
Математика, Геометрия 9 класс.
Тангенс минус 180 градусов таблица.
Тангенс минус 180 градусов 0 минут равен = 0
Тангенс минус 180 градусов 1 минут равен = -0.0003
Тангенс минус 180 градусов 2 минут равен = -0.0006
Тангенс минус 180 градусов 3 минут равен = -0.0009
Тангенс минус 180 градусов 4 минут равен = -0.0012
Тангенс минус 180 градусов 5 минут равен = -0.0015
Тангенс минус 180 градусов 6 минут равен = -0.0017
Тангенс минус 180 градусов 7 минут равен = -0.002
Тангенс минус 180 градусов 8 минут равен = -0.0023
Тангенс минус 180 градусов 9 минут равен = -0.0026
Тангенс минус 180 градусов 10 минут равен = -0.0029
Тангенс минус 180 градусов 11 минут равен = -0.0032
Тангенс минус 180 градусов 12 минут равен = -0.0035
Тангенс минус 180 градусов 13 минут равен = -0.0038
Тангенс минус 180 градусов 14 минут равен = -0.0041
Тангенс минус 180 градусов 15 минут равен = -0.0044
Математика, Геометрия 9 класс.
Тангенс угла минус 180 градусов
Тангенс минус 180 таблица.
Тангенс минус 180 градусов 16 минут равен = -0.0047
Тангенс минус 180 градусов 17 минут равен = -0.0049
Тангенс минус 180 градусов 18 минут равен = -0.0052
Тангенс минус 180 градусов 19 минут равен = -0.0055
Тангенс минус 180 градусов 20 минут равен = -0.0058
Тангенс минус 180 градусов 21 минут равен = -0.0061
Тангенс минус 180 градусов 22 минут равен = -0.0064
Тангенс минус 180 градусов 23 минут равен = -0.0067
Тангенс минус 180 градусов 24 минут равен = -0.007
Тангенс минус 180 градусов 25 минут равен = -0.0073
Тангенс минус 180 градусов 26 минут равен = -0.0076
Тангенс минус 180 градусов 27 минут равен = -0.0079
Тангенс минус 180 градусов 28 минут равен = -0.0081
Тангенс минус 180 градусов 29 минут равен = -0.0084
Тангенс минус 180 градусов 30 минут равен = -0.0087
Математика, Геометрия 9 класс.
Тангенс минус 180 равен:
Таблица значений Тангенсов минус 180 градусов.
Тангенс минус 180 градусов 31 минут равен = -0.009
Тангенс минус 180 градусов 32 минут равен = -0.0093
Тангенс минус 180 градусов 33 минут равен = -0.0096
Тангенс минус 180 градусов 34 минут равен = -0.0099
Тангенс минус 180 градусов 35 минут равен = -0.0102
Тангенс минус 180 градусов 36 минут равен = -0.0105
Тангенс минус 180 градусов 37 минут равен = -0.0108
Тангенс минус 180 градусов 38 минут равен = -0.0111
Тангенс минус 180 градусов 39 минут равен = -0.0113
Тангенс минус 180 градусов 40 минут равен = -0.0116
Тангенс минус 180 градусов 41 минут равен = -0.0119
Тангенс минус 180 градусов 42 минут равен = -0.0122
Тангенс минус 180 градусов 43 минут равен = -0.0125
Тангенс минус 180 градусов 44 минут равен = -0.0128
Тангенс минус 180 градусов 45 минут равен = -0.0131
Математика, Геометрия 9 класс.
Найти Тангенс минус 180 градусов:
Tg минус 180 градусов равен:
Тангенс минус 180 градусов 46 минут равен = -0.0134
Тангенс минус 180 градусов 47 минут равен = -0.0137
Тангенс минус 180 градусов 48 минут равен = -0.014
Тангенс минус 180 градусов 49 минут равен = -0.0143
Тангенс минус 180 градусов 50 минут равен = -0.0145
Тангенс минус 180 градусов 51 минут равен = -0.0148
Тангенс минус 180 градусов 52 минут равен = -0.0151
Тангенс минус 180 градусов 53 минут равен = -0.0154
Тангенс минус 180 градусов 54 минут равен = -0.0157
Тангенс минус 180 градусов 55 минут равен = -0.016
Тангенс минус 180 градусов 56 минут равен = -0.0163
Тангенс минус 180 градусов 57 минут равен = -0.0166
Тангенс минус 180 градусов 58 минут равен = -0.0169
Тангенс минус 180 градусов 59 минут равен = -0.0172
Тангенс минус 180 градусов 60 минут равен = -0.0175
Недавние расчеты
Тангенс -180 градусов 9 минут и 43 секунд равен = 0.0028264712876695
(-3.1387661898289 радиан)
Тангенс -180 градусов 38 минут и 21 секунд равен = 0.011156025582585
(-3.1304370907875 радиан)
Тангенс -180 градусов 14 минут и 30 секунд равен = 0.0042179040385615
(-3.1373747745641 радиан)
Тангенс -180 градусов 9 минут и 13 секунд равен = 0.0026810260801577
(-3.1389116339333 радиан)
Тангенс -180 градусов 58 минут и 18 секунд равен = 0.016960408535949
(-3.1246338710246 радиан)
Тангенс -180 градусов 29 минут и 33 секунд равен = 0.0085959582765667
(-3.1329969070237 радиан)
Тангенс -180 градусов 57 минут и 22 секунд равен = 0.016688836021151
(-3.124905366686 радиан)
Тангенс -180 градусов 56 минут и 18 секунд равен = 0.016378470443881
(-3.1252156474419 радиан)
Тангенс -180 градусов 6 минут и 53 секунд равен = 0.0020022831787857
(-3.1395903730868 радиан)
Тангенс -180 градусов 37 минут и 54 секунд равен = 0.011025109787746
(-3.1305679904814 радиан)
Для решения некоторых задач будет полезной таблица тригонометрических тождеств, которая позволит гораздо проще совершать преобразования функций:
Простейшие тригонометрические тождества
Частное от деления синуса угла альфа на косинус того же угла равно тангенсу этого угла (Формула 1). См. также доказательство правильности преобразования простейших тригонометрических тождеств.
Частное от деления косинуса угла альфа на синус того же угла равно котангенсу этого же угла (Формула 2)
Секанс угла равен единице, деленной на косинус этого же самого угла (Формула 3)
Сумма квадратов синуса и косинуса одного и того же угла равна единице (Формула 4). см. также доказательство суммы квадратов косинуса и синуса.
Сумма единицы и тангенса угла равна отношению единицы к квадрату косинуса этого угла (Формула 5)
Единица плюс котангенс угла равна частному от деления единицы на синус квадрат этого угла (Формула 6)
Произведение тангенса на котангенс одного и того же угла равно единице (Формула 7).
Преобразование отрицательных углов тригонометрических функций (четность и нечетность)
Для того, чтобы избавиться от отрицательного значения градусной меры угла при вычислении синуса, косинуса или тангенса, можно воспользоваться следующими тригонометрическими преобразованиями (тождествами), основанными на принципах четности или нечетности тригонометрических функций.
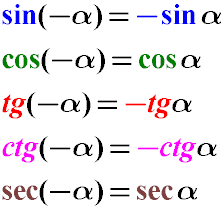
Как видно, косинус и секанс является четной функцией, синус, тангенс и котангенс – нечетные функции.
Синус отрицательного угла равен отрицательному значению синуса этого же самого положительного угла (минус синус альфа).
Косинус “минус альфа” даст тоже самое значение, что и косинус угла альфа.
Тангенс минус альфа равен минус тангенс альфа.
Формулы приведения двойного угла (синус, косинус, тангенс и котангенс двойного угла)
Если необходимо разделить угол пополам, или наоборот, перейти от двойного угла к одинарному, можно воспользоваться следующими тригонометрическими тождествами:
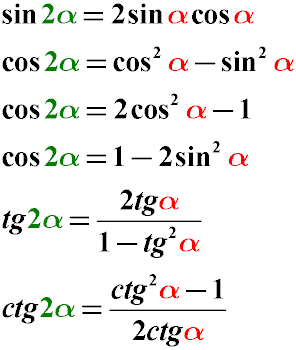
Преобразование двойного угла (синуса двойного угла, косинуса двойного угла и тангенса двойного угла) в одинарный происходит по следующим правилам:
Синус двойного угла равен удвоенному произведению синуса на косинус одинарного угла
Косинус двойного угла равен разности квадрата косинуса одинарного угла и квадрата синуса этого угла
Косинус двойного угла равен удвоенному квадрату косинуса одинарного угла минус единица
Косинус двойного угла равен единице минус двойной синус квадрат одинарного угла
Тангенс двойного угла равен дроби, числитель которой – удвоенный тангенс одинарного угла, а знаменатель равен единице минус тангенс квадрат одинарного угла.
Котангенс двойного угла равен дроби, числитель которой – квадрат котангенса одинарного угла минус единица, а знаменатель равен удвоенному котангенсу одинарного угла
Формулы универсальной тригонометрической подстановки
Указанные ниже формулы преобразования могут пригодиться, когда нужно аргумент тригонометрической функции ( sin α, cos α, tg α) разделить на два и привести выражение к значению половины угла. Из значения α получаем α/2 .
Данные формулы называются формулами универсальной тригонометрической подстановки. Их ценность заключается в том, что тригонометрическое выражение с их помощью сводится к выражению тангенса половины угла, вне зависимости от того, какие тригонометрические функции (sin cos tg ctg) были в выражении изначально. После этого уравнение с тангенсом половины угла решить гораздо проще.
Тригонометрические тождества преобразования половины угла
Указанные ниже формулы тригонометрического преобразования половинной величины угла к его целому значению.
Значение аргумента тригонометрической функции α/2 приводится к значению аргумента тригонометрической функции α.
Тригонометрические формулы сложения углов
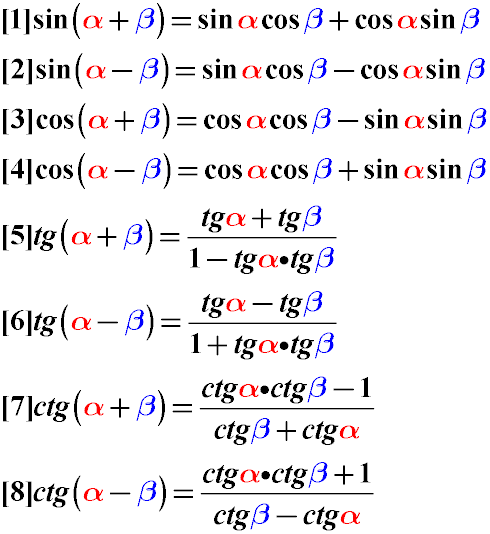
cos (α – β) = cos α · cos β + sin α · sin β
sin (α + β) = sin α · cos β + sin β · cos α
sin (α – β) = sin α · cos β – sin β · cos α
cos (α + β) = cos α · cos β – sin α · sin β
Тангенс и котангенс суммы углов альфа и бета могут быть преобразованы по следующим правилам преобразования тригонометрических функций:
Тангенс суммы углов равен дроби, числитель которой – сумма тангенса первого и тангенса второго угла, а знаменатель – единица минус произведение тангенса первого угла на тангенс второго угла.
Тангенс разности углов равен дроби, числитель которой равен разности тангенса уменьшаемого угла и тангенса вычитаемого угла, а знаменатель – единице плюс произведение тангенсов этих углов.
Котангенс суммы углов равен дроби, числитель которой равен произведению котангенсов этих углов плюс единица, а знаменатель равен разности котангенса второго угла и котангенса первого угла.
Котангенс разности углов равен дроби, числитель которой – произведение котангенсов этих углов минус единица, а знаменатель равен сумме котангенсов этих углов.
Данные тригонометрические тождества удобно применять, когда нужно вычислить, например, тангенс 105 градусов (tg 105). Если его представить как tg (45 + 60), то можно воспользоваться приведенными тождественными преобразованиями тангенса суммы углов, после чего просто подставить табличные значения тангенса 45 и тангенса 60 градусов.
Формулы преобразования суммы или разности тригонометрических функций
Выражения, представляющие собой сумму вида sin α + sin β можно преобразовать с помощью следующих формул:
Формулы тройного угла – преобразование sin3α cos3α tg3α в sinα cosα tgα
Иногда необходимо преобразовать тройную величину угла так, чтобы аргументом тригонометрической функции вместо 3α стал угол α.
В этом случае можно воспользоваться формулами (тождествами) преобразования тройного угла:
Формулы преобразования произведения тригонометрических функций
Если возникает необходимость преобразовать произведение синусов разных углов косинусов разных углов или даже произведения синуса на косинус, то можно воспользоваться следующими тригонометрическими тождествами:
В этом случае произведение функций синуса, косинуса или тангенса разных углов будет преобразовано в сумму или разность.
Формулы приведения тригонометрических функций
Пользоваться таблицей приведения нужно следующим образом. В строке выбираем функцию, которая нас интересует. В столбце – угол. Например, синус угла (α+90) на пересечении первой строки и первого столбца выясняем, что sin (α+90) = cos α .
См. также Полный список формул приведения тригонометрических функций.
| Угол |
α + 90 α + π/2 |
α + 180 α + π |
α + 270 α + 3π/2 |
90 – α π/2- α |
180 – α π- α |
270 – α 3π/2- α |
360 – α 2π- α |
| sin | cos α | -sin α | -cos α | cos α | sin α | -cos α | -sin α |
| cos | -sin α | -cos α | sin α | sin α | -cos α | -sin α | cos α |
| tg | -ctg α | tg α | -ctg α | ctg α | -tg α | ctg α | -tg α |
| ctg | -tg α | ctg α | -tg α | tg α | -ctg α | tg α | -ctg α |
0
Начать курс обучения
tg(0°)=tg(360°)=0 точная, но чуть более сложная таблица ( с точностью до 1′) здесь.
|
Углы |
Углы |
Углы |
Углы |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
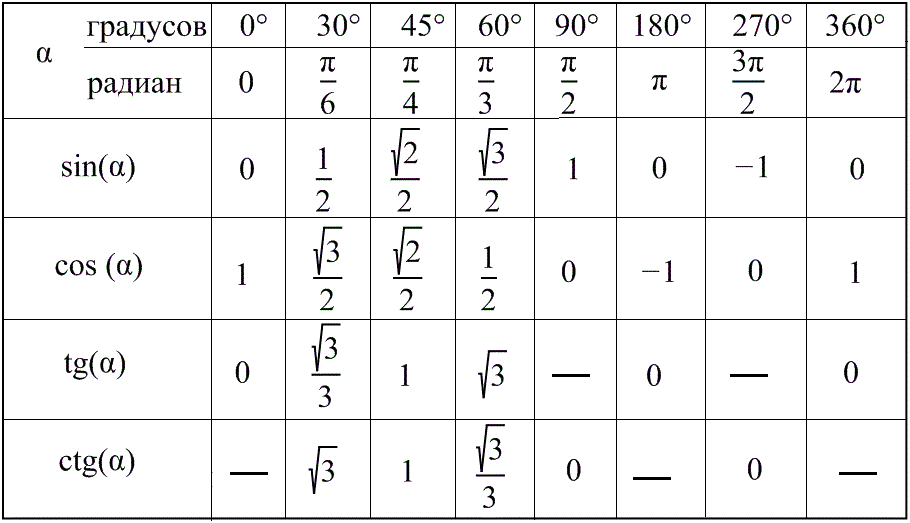
Углы 0°,30°,45°,60°,90°,180°,270°,360°,(π/6,π/4,π/3,π/2,π,3π/2,2π).
Синусы, косинусы, тангенсы и котангенсы. Таблица значений тригонометрических функций
Доп. Инфо:
- Таблица косинусов углов от 0° – 360°. Углы с шагом в 1°. Таблица значений косинусов.
- Таблица синусов углов от 0° – 360°. Углы с шагом в 1°. Таблица значений синусов.
- Таблица синусов, она-же косинусов точная.
- Таблица тангенсов углов углов от 0° – 360°. Углы с шагом в 1°. Таблица значений тангенса, tg
- Таблица котангенсов углов углов от 0° – 360°. Углы с шагом в 1°. Таблица значений котангенса, ctg
- Таблица тангенсов, она же котангенсов точная.
- Углы 0°,30°,45°,60°,90°,180°,270°,360°,(π/6,π/4,π/3,π/2,π,3π/2,2π).
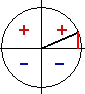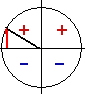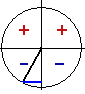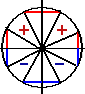
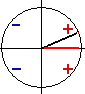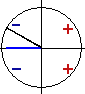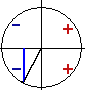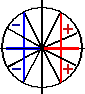
Синусы, косинусы, тангенсы и котангенсы. Таблица значений тригонометрических функций. - Знаки тригонометрических функций синус, косинус, тангенс и котангенс по четвертям в тригонометрическом круге.
- Определение и численные соотношения между единицами измерения углов в РФ.
Тысячные, угловые градусы, минуты, секунды, радианы, обороты. - Таблица соответствия угловых градусов, радиан, оборотов, тысячных (артиллерийских РФ). 0-360 градусов, 0-2π радиан.
| 3ГОНОМЕТРИЯ В НАЧАЛО | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ФОРМУЛЫ ПРИВЕДЕНИЯ. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Теорема. Для любого угла φ sin (90° — φ) = cosφ. (1) |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Доказательство. Если угол φ оканчивается в 1-й четверти, то угол 90° + φ должен оканчиваться во 2-й четверти. Используя единичный круг, получаем: sin (90° + φ) = BD, cos φ = ОС. Но треугольники ОАС и BOD равны; поэтому BD = ОС. Отсюда и вытекает равенство (1). |
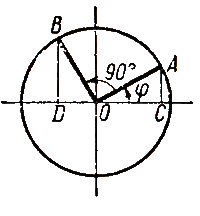 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
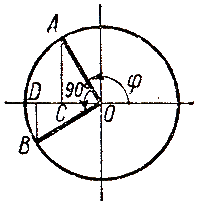
Если угол φ оканчивается во 2-й четверти, то угол 90° +φ должен оканчиваться в 3-й четверти. Используя единичный круг, получаем: sin (90°+φ) = — BD, cos φ = —ОС. Треугольники ОАС и BOD равны; поэтому BD = ОС. Следовательно, —BD = —ОС, или sin (90° +φ) = cos φ. |
 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Аналогично можно рассмотреть случаи, когда угол φ оканчивается в 3-й или в 4-й четверти. Тождество (1) легко проверить и в случае, когда конечная сторона угла φ лежит на какой-нибудь оси координат. Предлагаем учащимся самостоятельно убедиться в этом. Из доказанного тождества (1) вытекает ряд других важных тождеств. Заменив в (1) φ на — φ, получаем: sin (90° — φ) = cos (—φ) = cos φ. (2) Чтобы получить аналогичную формулу для cos (90° — φ), заменим в (2) φ на 90° — φ. В результате получаем: или sin [90° — (90° — φ)] = cos (90° — φ), Итак, sin φ = cos (90° — φ). cos (90° — φ) = sin φ. (3) Из (2) и (3) вытекает: tg (90° — φ) = ctg φ. . (4) Аналогично, Формулы sin (90° — φ) = cos φ, tg (90° — φ) == ctg φ, cos (90° — φ) = sin φ, ctg (90° — φ) = tg φ. иногда называют формулами дополнительного угла. Это связано с тем, что углы 90° — φ и φ дополняют друг друга до прямого угла. Эти формулы очень просто запомнить: одна функция заменяется на другую, сходную с ней (синус на косинус, косинус на синус, тангенс на котангенс, котангенс на тангенс). Например, sin 40° = cos 50°; tg 70° = ctg 20° и т. д. Теперь получим формулы для угла 90° + φ. Одну из таких формул мы уже доказали выше: sin (90° + φ) = cos φ. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Остальные формулы легко получаются из формул дополнительного угла и свойства четности (нечетности) тригонометрических функций. Имеем: cos (90° + φ) = cos [90° — (— φ)] = sin (— φ) = —sin φ; tg (90° + φ) = tg [90°— (— φ)] = ctg(— φ) = —ctg φ; ctg (90° + φ) = ctg [90° — (— φ)] = tg (— φ) = — tg φ. Исходя из этих формул, можно получить формулы для углов 180° ± φ. Например, sin (180° + φ) = sin [90° + (90°+ φ)] = cos (90° + φ) = —sin φ; sin (180° — φ) = sin [90° + (90° — φ)] = cos (90° — φ) = sin φ. Аналогично доказываются формулы cos (180° + φ) = — cos φ; cos (180° — φ) = — cos φ. Чтобы получить соответствующие формулы для тангенса и котангенса, можно воспользоваться выведенными соотношениями для синуса и косинуса, учитывая, что tg φ = sin φ/cos φ, ctg φ = cos φ/sin φ. Однако в данном случае лучше всего исходить из того, что угол 180° является периодом функций tg φ и ctg φ. Отсюда сразу же получаем: tg (180° + φ) = tg φ, tg (180° — φ) == tg (—φ) = — tg φ, ctg (180° + φ) = ctg φ, ctg (180° — φ) = ctg (— φ) = — ctg φ. Из формул для углов 180° ± φ можно получить аналогичные формулы для углов 270° ± φ. Формулы для углов 360° ± φ легко получаются, если учесть, что угол 360° является общим периодом тригонометрических функций. Подробно останавливаться на этом мы не будем. В таблице приведены нужные нам формулы. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Заучивать эти формулы нет нужды. Достаточно помнить следующее: 1) если в формуле содержатся углы 180° и 360° (π и 2π), то наименование функции не изменяется; если же в формуле содержатся углы 90° и 270° (π/2 и 3π/2), то наименование функции меняется на сходное (синус на косинус, тангенс на котангенс и т. д.); 2) чтобы определить знак в правой части формулы (+ или—), достаточно, считая угол φ острым, определить знак выражения, стоящего в левой части формулы. Пусть, например, нужно определить tg (90° + φ). Прежде всего мы замечаем, что в формуле содержится угол 90°. Поэтому в правой части искомой формулы должен стоять ctg φ. Итак, tg (90° + φ) = — ctg φ. Аналогично устанавливается формула cos (180° — φ) = — cos φ. Поскольку в формуле содержится угол в 180°, наименование функции не изменяется. Если угол φ острый, то угол 180°—φ должен оканчиваться во 2-й четверти. Но косинус угла, оканчивающегося во 2-й четверти, отрицателен. Поэтому в правой части формулы должен стоять знак —. Полученные выше формулы носят название формул приведения. Причины такого названия будут выяснены далее. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Упражнения 1.Упростить выражения 2. Доказать, что если прямые у = k1x и у = k2x взаимно перпендикулярны, то k1k2 = — 1. 6.Упростить выражения 7. Доказать тождества 8. Доказать, что синус суммы двух углов треугольника равен синусу третьего угла. 10. Что больше: а) sin 26° или cos 40°; в) sin 0,63 или cos 0,87 ; б) tg57° или ctg20°; г) tg 3/8 π или ctg 5/16 π? . |