Ангелина158
Ученик
(216),
на голосовании
11 лет назад
Голосование за лучший ответ
Julia Tarasevich
Ученик
(116)
11 лет назад
1 – косинус альфа / синус альфа
Похожие вопросы
Уравнения разложения тригонометрических функций:квадрат синус альфа, косинус альфа, тангенс альфа, котангенс альфа.
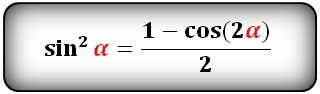
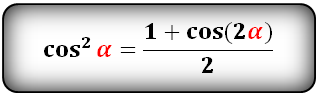
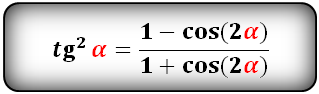
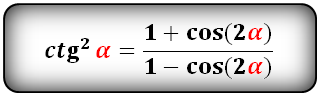
Формулы преобразования функций двойного угла (2α) в выражение через одинарный угол (α)
sin(2α)- через sin и cos:
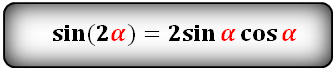
sin(2α)- через tg и ctg:
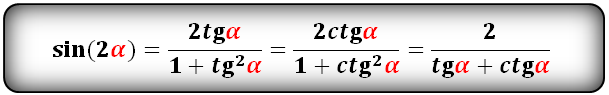
cos(2α)- через sin и cos:
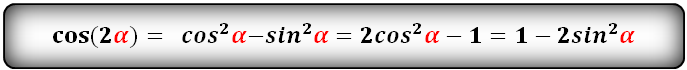
cos(2α)- через tg и ctg:
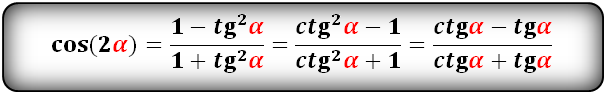
tg(2α) и сtg(2α):
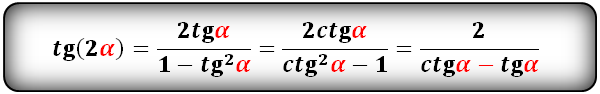
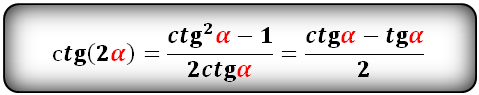
Формулы преобразования функций (синус, косинус, тангенс, котангенс), тройного угла (3α) в выражение через одинарный угол (α):


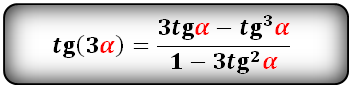
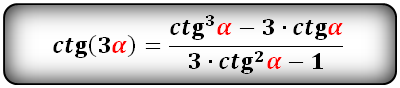
Тригонометрические формулы преобразования разности аргументов


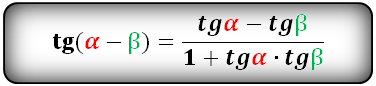
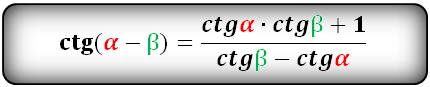
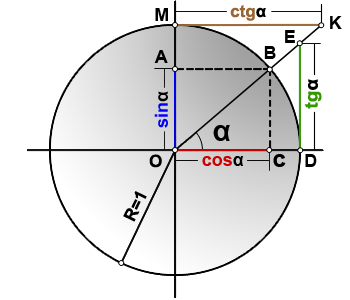
sin(α)=OA
cos(α)=OC
tg(α)=DE
ctg(α)=MK
R=OB=1
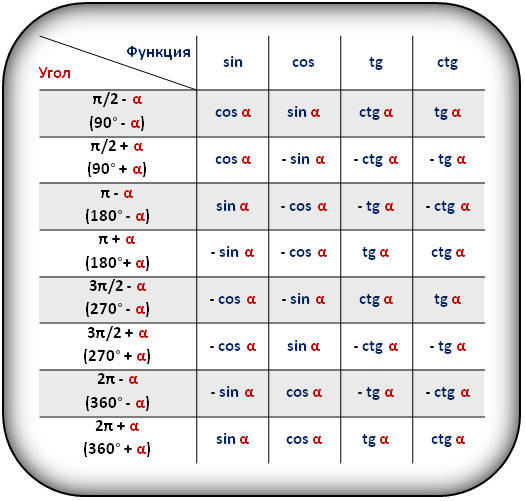
Значения функций для некоторых углов, α
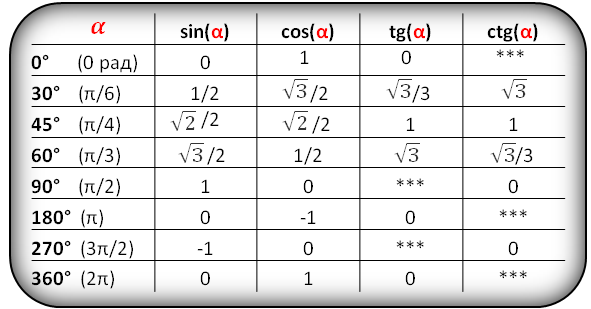
В таблице показаны формулы приведения для тригонометрических функций (sin, cos, tg, ctg).
| tg(2α) = | 2tg(α)
1 – tg2(α) |
| ctg(2α) = | ctg2(α) – 1
2ctg(α) |
© Школяр. Математика (при поддержке «Ветвистого древа») 2009—2021
tg(0°)=tg(360°)=0 точная, но чуть более сложная таблица ( с точностью до 1′) здесь.
|
Углы |
Углы |
Углы |
Углы |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
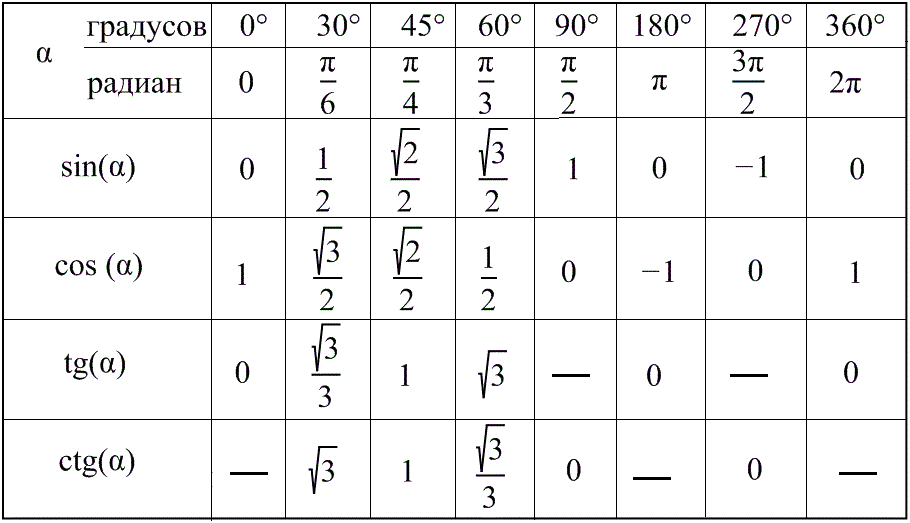
Углы 0°,30°,45°,60°,90°,180°,270°,360°,(π/6,π/4,π/3,π/2,π,3π/2,2π).
Синусы, косинусы, тангенсы и котангенсы. Таблица значений тригонометрических функций
Доп. Инфо:
- Таблица косинусов углов от 0° – 360°. Углы с шагом в 1°. Таблица значений косинусов.
- Таблица синусов углов от 0° – 360°. Углы с шагом в 1°. Таблица значений синусов.
- Таблица синусов, она-же косинусов точная.
- Таблица тангенсов углов углов от 0° – 360°. Углы с шагом в 1°. Таблица значений тангенса, tg
- Таблица котангенсов углов углов от 0° – 360°. Углы с шагом в 1°. Таблица значений котангенса, ctg
- Таблица тангенсов, она же котангенсов точная.
- Углы 0°,30°,45°,60°,90°,180°,270°,360°,(π/6,π/4,π/3,π/2,π,3π/2,2π).
Синусы, косинусы, тангенсы и котангенсы. Таблица значений тригонометрических функций. - Знаки тригонометрических функций синус, косинус, тангенс и котангенс по четвертям в тригонометрическом круге.
- Определение и численные соотношения между единицами измерения углов в РФ.
Тысячные, угловые градусы, минуты, секунды, радианы, обороты. - Таблица соответствия угловых градусов, радиан, оборотов, тысячных (артиллерийских РФ). 0-360 градусов, 0-2π радиан.
Основные формулы тригонометрии – это формулы, устанавливающие связи между основными тригонометрическими функциями. Синус, косинус, тангенс и котангенс связаны между собой множеством соотношений. Ниже приведем основные тригонометрические формулы, а для удобства сгруппируем их по назначению. С использованием данных тригонометрических формул можно находить и решать практически любую задачу из стандартного курса тригонометрии. Сразу отметим, что ниже приведены лишь все тригонометрические формулы, а не их вывод, которому будут посвящены отдельные статьи.
Основные тождества тригонометрии
Тригонометрические тождества дают связь между синусом, косинусом, тангенсом и котангенсом одного угла, позволяя выразить одну функцию через другую (посредством преобразования).
sin2a+cos2a=1tgα=sinαcosα, ctgα=cosαsinαtgα·ctgα=1tg2α+1=1cos2α, ctg2α+1=1sin2α
Эти тождества напрямую вытекают из определений единичной окружности, синуса (sin), косинуса (cos), тангенса (tg) и котангенса (ctg) и их свойств.
Основные формулы приведения в тригонометрии
Формулы приведения позволяют переходить от работы с произвольными и сколь угодно большими углами к работе с углами в пределах от 0 до 90 градусов, то есть, преобразовывать их.
sinα+2πz=sinα, cosα+2πz=cosαtgα+2πz=tgα, ctgα+2πz=ctgαsin-α+2πz=-sinα, cos-α+2πz=cosαtg-α+2πz=-tgα, ctg-α+2πz=-ctgαsinπ2+α+2πz=cosα, cosπ2+α+2πz=-sinαtgπ2+α+2πz=-ctgα, ctgπ2+α+2πz=-tgαsinπ2-α+2πz=cosα, cosπ2-α+2πz=sinαtgπ2-α+2πz=ctgα, ctgπ2-α+2πz=tgαsinπ+α+2πz=-sinα, cosπ+α+2πz=-cosαtgπ+α+2πz=tgα, ctgπ+α+2πz=ctgαsinπ-α+2πz=sinα, cosπ-α+2πz=-cosαtgπ-α+2πz=-tgα, ctgπ-α+2πz=-ctgαsin3π2+α+2πz=-cosα, cos3π2+α+2πz=sinαtg3π2+α+2πz=-ctgα, ctg3π2+α+2πz=-tgαsin3π2-α+2πz=-cosα, cos3π2-α+2πz=-sinαtg3π2-α+2πz=ctgα, ctg3π2-α+2πz=tgα
Формулы приведения являются следствием периодичности тригонометрических функций.
Все формулы сложения в тригонометрии
Формулы сложения в тригонометрии позволяют выразить тригонометрическую функцию суммы или разности углов через тригонометрические функции этих углов.
sinα±β=sinα·cosβ±cosα·sinβcosα+β=cosα·cosβ-sinα·sinβcosα-β=cosα·cosβ+sinα·sinβtgα±β=tgα±tgβ1±tgα·tgβctgα±β=-1±ctgα·ctgβctgα±ctgβ
На основе формул сложения выводятся тригонометрические формулы кратного угла.
Формулы кратного угла: двойного, тройного и т.д.
sin2α=2·sinα·cosαcos2α=cos2α-sin2α, cos2α=1-2sin2α, cos2α=2cos2α-1tg2α=2·tgα1-tg2α сtg2α=сtg2α-12·сtgα sin3α=3sinα·cos2α-sin3α, sin3α=3sinα-4sin3αcos3α=cos3α-3sin2α·cosα, cos3α=-3cosα+4cos3αtg3α=3tgα-tg3α1-3tg2αctg3α=ctg3α-3ctgα3ctg2α-1
Формулы половинного угла
Формулы половинного угла в тригонометрии являются следствием формул двойного угла и выражают соотношения между основными функциями половинного угла и косинусом целого угла.
sin2α2=1-cosα2cos2α2=1+cosα2tg2α2=1-cosα1+cosαctg2α2=1+cosα1-cosα
Формулы понижения степени
sin2α=1-cos2α2cos2α=1+cos2α2sin3α=3sinα-sin3α4cos3α=3cosα+cos3α4sin4α=3-4cos2α+cos4α8cos4α=3+4cos2α+cos4α8
Часто при расчетах действовать с громоздкими степенями неудобно. Формулы понижения степени позволяют понизить степень тригонометрической функции со сколь угодно большой до первой. Приведем их общий вид:
для четных n решение
sinnα=Cn2n2n+12n-1∑k=0n2-1(-1)n2-k·Ckn·cos((n-2k)α)cosnα=Cn2n2n+12n-1∑k=0n2-1Ckn·cos((n-2k)α)
для нечетных n
sinnα=12n-1∑k=0n-12(-1)n-12-k·Ckn·sin((n-2k)α)cosnα=12n-1∑k=0n-12Ckn·cos((n-2k)α)
Сумма и разность тригонометрических функций
Разность и сумму тригонометрических функций можно представить в виде произведения. Разложение на множители разностей синусов и косинусов очень удобно для применения при решении тригонометрических уравнений и упрощении выражений.
sinα+sinβ=2sinα+β2·cosα-β2sinα-sinβ=2sinα-β2·cosα+β2cosα+cosβ=2cosα+β2·cosα-β2cosα-cosβ=-2sinα+β2·sinα-β2, cosα-cosβ=2sinα+β2·sinβ-α2
Произведение тригонометрических функций
Если формулы суммы и разности функций позволяют перейти к их произведению или умножению, то формулы произведения (здесь нужно умножать) тригонометрических функций осуществляют обратный переход – от произведения к сумме. Рассматриваются формулы произведения синусов, косинусов и синуса на косинус.
sinα·sinβ=12·(cos(α-β)-cos(α+β))cosα·cosβ=12·(cos(α-β)+cos(α+β))sinα·cosβ=12·(sin(α-β)+sin(α+β))
Универсальная тригонометрическая подстановка
Все основные тригонометрические функции – тангенс, котангенс, синус, косинус – могут быть выражены через тангенс половинного угла.
sinα=2tgα21+tg2α2cosα=1-tg2α21+tg2α2tgα=2tgα21-tg2α2ctgα=1-tg2α22tgα2
![]()
Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта
