Тимофей Поляков
27 марта, 12:25
0
Если опустить высоту из границы меньшего основания на большее, то тангенс острого угла при основании трапеции численно будет равен отношению высоты трапеции на проекцию боковой стороны на большее основание.
Высота нам известна, а проекция боковой стороны на большее основание равна разности длин большего и меньшего оснований трапеции, разделенной на 2.
Получим:
tg A = 2 * h / (a – b) = 2 * 8 / (13 – 5) = 2.
- Комментировать
- Жалоба
- Ссылка
Версия для печати и копирования в MS Word
1
Тангенс острого угла прямоугольной трапеции равен
Найдите её большее основание, если меньшее основание равно высоте и равно 58.
2
Тангенс острого угла прямоугольной трапеции равен 2. Найдите её большее основание, если меньшее основание равно высоте и равно 78.
3
Тангенс острого угла прямоугольной трапеции равен
Найдите её бóльшее основание, если меньшее основание равно высоте и равно 14.
4
Тангенс острого угла прямоугольной трапеции равен
Найдите её большее основание, если меньшее основание равно высоте и равно 55.
5
Тангенс острого угла прямоугольной трапеции равен
Найдите её большее основание, если меньшее основание равно высоте и равно 40.
6
Тангенс острого угла прямоугольной трапеции равен
Найдите её большее основание, если меньшее основание равно высоте и равно 14.
7
Тангенс острого угла прямоугольной трапеции равен
Найдите её большее основание, если меньшее основание равно высоте и равно 90.
8
Тангенс острого угла прямоугольной трапеции равен
Найдите её бóльшее основание, если меньшее основание равно высоте и равно 86.
9
Тангенс острого угла прямоугольной трапеции равен
Найдите её большее основание, если меньшее основание равно высоте и равно 55.
10
Тангенс острого угла прямоугольной трапеции равен
Найдите её большее основание, если меньшее основание равно высоте и равно 54.
11
Тангенс острого угла прямоугольной трапеции равен
Найдите её большее основание, если меньшее основание равно высоте и равно 77.
12
Тангенс острого угла прямоугольной трапеции равен
Найдите её большее основание, если меньшее основание равно высоте и равно 8.
13
Тангенс острого угла прямоугольной трапеции равен
Найдите её большее основание, если меньшее основание равно высоте и равно 39.
14
Тангенс острого угла прямоугольной трапеции равен
Найдите её большее основание, если меньшее основание равно высоте и равно 14.
15
Тангенс острого угла прямоугольной трапеции равен
Найдите её большее основание, если меньшее основание равно высоте и равно 54.
16
Тангенс острого угла прямоугольной трапеции равен
Найдите её большее основание, если меньшее основание равно высоте и равно 7.
17
Тангенс острого угла прямоугольной трапеции равен
Найдите её большее основание, если меньшее основание равно высоте и равно 63.
18
Тангенс острого угла прямоугольной трапеции равен
Найдите её большее основание, если меньшее основание равно высоте и равно 66.
19
Тангенс острого угла прямоугольной трапеции равен
Найдите её большее основание, если меньшее основание равно высоте и равно 54.
20
Тангенс острого угла прямоугольной трапеции равен
Найдите её большее основание, если меньшее основание равно высоте и равно 58.
21
Тангенс острого угла прямоугольной трапеции равен
Найдите её большее основание, если меньшее основание равно высоте и равно 99.
22
Тангенс острого угла прямоугольной трапеции равен
Найдите её большее основание, если меньшее основание равно высоте и равно 97.
23
Тангенс острого угла прямоугольной трапеции равен
Найдите её большее основание, если меньшее основание равно высоте и равно 4.
Задание
В равнобедренной трапеции одно из оснований равно 5, а другое — 9. Высота трапеции равна 6. Найдите тангенс острого угла трапеции.
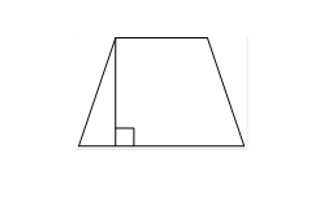
Решение
- Для удобства введем буквенное обозначение ABCDF (см. рисунок):
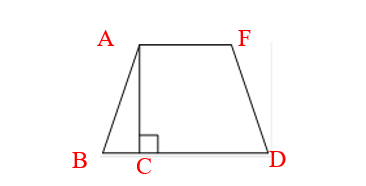
Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.
- Нам необходимо найти тангенс острого угла трапеции (угол В = угол D – острые углы трапеции). Для этого рассмотрим прямоугольный треугольник ACB (угол С прямой, так как АС – высота трапеции). В данном треугольнике:
ВС = (ВD – AF)/2 = (9 – 5)/2 = 2
АС = 6 (по условию, АС – высота трапеции)
- Осталось найти тангенс острого угла. Из определения тангенса (см. выше) следует:
tgАВС = АС / ВС = 6 / 2 = 3
Ответ: 3
![]()
Углы равнобедренной трапеции. Здравствуйте! В этой статье речь пойдёт о решении задач с трапецией. Данная группа заданий входит в состав экзамена, задачки простые. Будем вычислять углы трапеции, основания и высоты. Решение ряда задач сводится к решению прямоугольного треугольника, как говориться: куда мы без теоремы Пифагора, синуса и косинуса?
Работать будем с равнобедренной трапецией. У неё равны боковые стороны и углы при основаниях. О трапеции есть статья на блоге, посмотрите.

Отметим небольшой и важный нюанс, который в процессе решения самих заданий подробно расписывать не будем. Посмотрите, если у нас дано два основания, то большее основание высотами, опущенными к нему, разбивается на три отрезка – один равен меньшему основанию (это противолежащие стороны прямоугольника), два других равны друг другу (это катеты равных прямоугольных треугольников):

Простой пример: дано два основания равнобедренной трапеции 25 и 65. Большее основание разбивается на отрезки следующим образом:
![]()
*И ещё! В задачах не введены буквенные обозначения. Это сделано умышленно, чтобы не перегружать решение алгебраическими изысками. Согласен, что это математически неграмотно, но цель донести суть. А обозначения вершин и прочих элементов вы всегда можете сделать сами и записать математически корректное решение.
Рассмотрим задачи:

27439. Основания равнобедренной трапеции равны 51 и 65. Боковые стороны равны 25. Найдите синус острого угла трапеции.
Для того чтобы найти угол необходимо построить высоты. На эскизе обозначим данные в условии величины. Нижнее основание равно 65, высотами оно разбивается на отрезки 7, 51 и 7:

В прямоугольном треугольнике нам известна гипотенуза и катет, можем найти второй катет (высоту трапеции) и далее уже вычислить синус угла.
По теореме Пифагора указанный катет равен:
![]()
Таким образом:

Ответ: 0,96

27440. Основания равнобедренной трапеции равны 43 и 73. Косинус острого угла трапеции равен 5/7. Найдите боковую сторону.
Построим высоты и отметим данные в условии величины, нижнее основание разбивается на отрезки 15, 43 и 15:

Ответ: 21

27441. Большее основание равнобедренной трапеции равно 34. Боковая сторона равна 14. Синус острого угла равен (2√10)/7. Найдите меньшее основание.
Построим высоты. Для того чтобы найти меньшее основание нам необходимо найти чему равен отрезок являющийся катетом в прямоугольном треугольнике (обозначен синим):

Можем вычислить высоту трапеции, а затем найти катет:

По теореме Пифагора вычисляем катет:

Таким образом, меньшее основание равно:
![]()
Ответ: 22

27442. Основания равнобедренной трапеции равны 7 и 51. Тангенс острого угла равен 5/11. Найдите высоту трапеции.
Построим высоты и отметим данные в условии величины. Нижнее основание разбивается на отрезки:

Что делать? Выражаем тангенс известного нам угла при основании в прямоугольном треугольнике:
![]()
Ответ: 10

27443. Меньшее основание равнобедренной трапеции равно 23. Высота трапеции равна 39. Тангенс острого угла равен 13/8. Найдите большее основание.
Строим высоты и вычисляем чему равен катет:

Таким образом большее основание будет равно:
![]()
Ответ: 71

27444. Основания равнобедренной трапеции равны 17 и 87. Высота трапеции равна 14. Найдите тангенс острого угла.
Строим высоты и отмечаем известные величины на эскизе. Нижнее основание разбивается на отрезки 35, 17, 35:

По определению тангенса:

Ответ: 0,4

77152. Основания равнобедренной трапеции равны 6 и 12. Синус острого угла трапеции равен 0,8. Найдите боковую сторону.
Построим эскиз, построим высоты и отметим известные величины, большее основание разбивается на отрезки 3, 6 и 3:

Выразим гипотенузу обозначенную как х через косинус:

Из основного тригонометрического тождества найдём cosα
![]()
Таким образом:

Ответ: 5

27818. Чему равен больший угол равнобедренной трапеции, если известно, что разность противолежащих углов равна 500? Ответ дайте в градусах.

Из курса геометрии нам известно, что если имеем две параллельные прямые и секущую, что сумма внутренних односторонних углов равна 1800. В нашем случае это
![]()
C условии сказано, что разность противолежащих углов равна 500, то есть
![]()
Так как у равнобедренной трапеции углы при основании равны, то есть угол А равен углу В, то можем записать
![]()
Имеем два уравнения с двумя неизвестными, можем решить систему:

*Конечно, эту задачу можно было легко решить просто перебирая пары углов )

27833. В равнобедренной трапеции большее основание равно 25, боковая сторона равна 10, угол между ними 600. Найдите меньшее основание.

Построим высоты DE и CF:

Меньшее основание равно отрезку EF, так как DC и EF это противолежащие стороны прямоугольника. Отрезок EF мы можем найти если вычислим АЕ. Выразим этот катет прямоугольного треугольника ADE через функцию косинуса:

Так как AE=FB=5, то EF=25–5–5=15. Следовательно и DC=15.
Ответ: 15

27837. Основания равнобедренной трапеции равны 15 и 9, один из углов равен 450. Найдите высоту трапеции.

Из точек D и C опустим две высоты:

Как уже сказано выше они разбивают большее основание на три отрезка: один равен меньшему основанию, два других равны друг другу.
В данном случае они равны 3, 9 и 3 (в сумме 15). Кроме того, отметим что высотами отсекаются прямоугольные треугольники, причём они являются равнобедренными, так как углы при основании равны по 450. Отсюда следует, что высота трапеции будет равна 3.
Ответ: 3
На этом всё! Успеха вам!
С уважением, Александр.
P.S: Расскажите о сайте в социальных сетях!
поделиться знаниями или
запомнить страничку
- Все категории
-
экономические
43,655 -
гуманитарные
33,653 -
юридические
17,917 -
школьный раздел
611,944 -
разное
16,904
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
