Найти тангенс фи , если известен косинус фи
Калькулятор коэффициент мощности cos fi в tg fi
Как найти тангенс фи, если известен косинус фи формула:
- tg φ = (√(1-cos²φ))/cos φ
Калькулятор онлайн – косинус в тангенс
cos φ:
tg φ:
Поделиться в соц сетях:
Популярные сообщения из этого блога
Индекс Руфье калькулятор
Проба Руфье калькулятор онлайн. Первые упоминания теста относиться к 1950 году. Именно в это время мы находим первое упоминание доктора Диксона о “Использование сердечного индекса Руфье в медико-спортивном контроле”. Проба Руфье – представляет собой нагрузочный комплекс, предназначенный для оценки работоспособности сердца при физической нагрузке. Индекс Руфье для школьников и студентов. У испытуемого, находящегося в положении лежа на спине в течение 5 мин, определяют число пульсаций за 15 сек (P1); После чего в течение 45 сек испытуемый выполняет 30 приседаний. После окончания нагрузки испытуемый ложится, и у него вновь подсчитывается число пульсаций за первые 15 с (Р2); И в завершении за последние 15 сек первой минуты периода восстановления (Р3); Оценку работоспособности сердца производят по формуле: Индекс Руфье = (4(P1+P2+P3)-200)/10; Индекс Руфье для спортсменов Измеряют пульс в положении сидя (Р1); Спортсмен выполняет 30 глубоких приседаний в
Найти косинус фи (cos φ), через тангенс фи (tg φ)
tg фи=… чему равен cos фи? Как перевести тангенс в косинус формула: cos(a)=(+-)1/sqrt(1+(tg(a))^2) Косинус через тангенс, перевести tg в cos, калькулятор – онлайн tg φ: cos φ: ± Поделиться в соц сетях:
Уведомление
Cookie
Калькулятор приведения тригонометрических функций
Калькулятор выполняет приведение к тригонометрическим функциям выражений, содержащих такие функции как: синус, косинус, тангенс, котангенс, секанс, косеканс. Помимо выражения тригонометрических функций через другие, калькулятор также выполнит тригонометрические преобразования, через тригонометрические тождества.
Тригонометрические функции записываются как:
синус sin(x), косинус cos(x), тангенс tan(x), котангенс cot(x), секанс sec(x), косеканс csc(x).
Примеры: sin(5π/6), cos(π/3), sin(2π-t), tan(π + t), x-sin(π/5)+cos(π/3), sin(x)^2 + cos(x)^2 и т.д.
Что такое тангенс угла
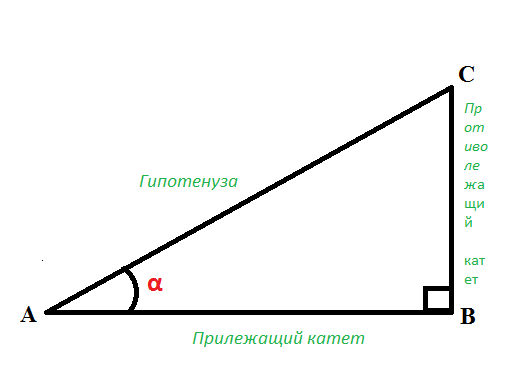
Пусть задан прямоугольный треугольник ABC с острым углом α, тогда тангенсом угла α будет отношение противолежащего катета к прилежащему tg α = BC/AB.
Тангенс угла можно определить как отношение синуса угла к косинусу данного угла
tg α = sin α / cos α
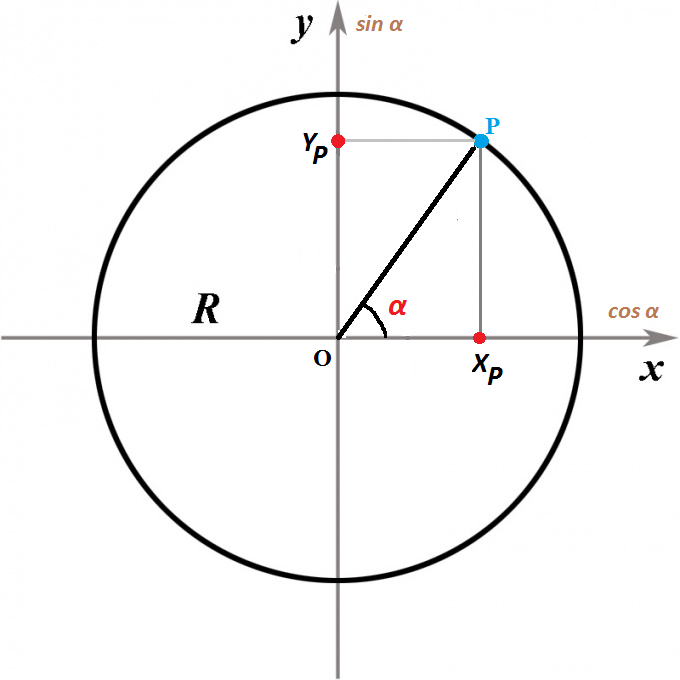
Так же для определения тангенса угла можно воспользоваться окружностью, построенной в декартовой системе координат, радиуса R и центром в начале координат O.
На окружности отметим точку P с координатами (1;0), теперь повернем луч OP на некоторый угол α. Направление против часовой стрелки считается положительным, по часовой стрелки – отрицательным.
Тангенсом угла α будет отношение ординаты точки YP к абсциссе точки XP.
tg α = YP/XP.
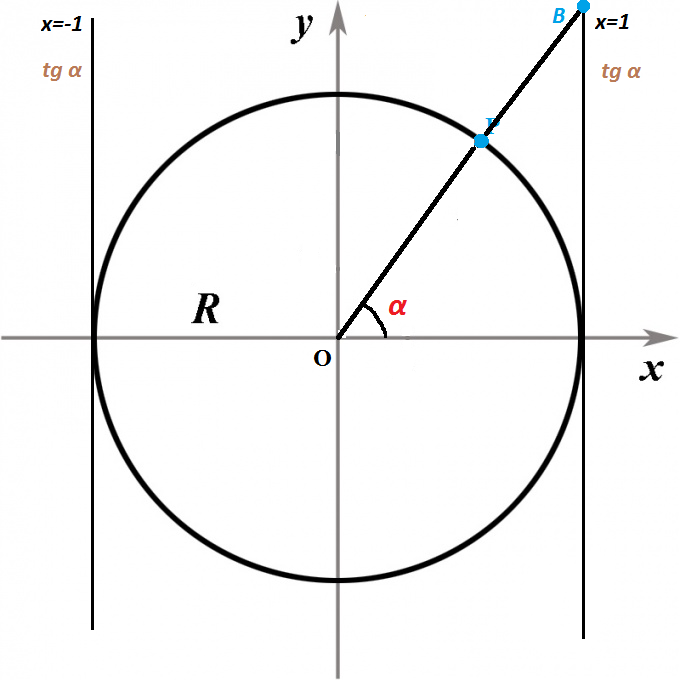
Для вычисления тангенса угла, можно также воспользоваться осью тангенсов. Определим окружность радиуса R как единичную с центром в начале координат O.
Параллельно оси y, на расстоянии равном радиусу окружности расположим прямую x=1. На окружности отметим точку P с координатами (1;0), теперь повернем луч OP на некоторый угол α и
продолжим луч OP до пересечения с прямой x=1. Тангенсу угла α будет соответствовать значение в точке B.
Найти синус через косинус, тангенс, котангенс, секанс, косеканс угла
Онлайн калькулятор тригонометрических функций предназначен для того, чтобы быстро найти ответ на задачу, в которой нужно рассчитать, чему равен синус, косинус, тангенс онлайн.
Здесь также выполняется расчет котангенса, секанса, косеканса, версинуса, коверсинуса, гаверсинуса, экссеканса и экскосеканса. Единицы измерения – градусы, минуты, секунды. Ответ вычисляется после нажатия на кнопку “Решить”.
Пример задачи. Используем онлайн калькулятор синуса, косинуса, тангенса для того, чтобы найти синус и тангенс, зная косинус угла А в виде дроби Cos A = 1/3. В поле “тригонометрическая функция” указывается “cos”, “числитель” — число “1”, “знаменатель” — число “3”.
Решение синусов и тангенсов:
По таблице “Косинусы” находим значение угла A с градусами и минутами = 70,528779° = 70°32′.
Так как Sin2 + Cos2 = 1, то, используя тригонометрический калькулятор синусов онлайн:
1) значение синуса Sin A = √1 – (1/3)2 = √9/9 – 1/9 = √(9 – 1)/9 = √8/9 = 2,828427 / 3 = 0,942809;
2) значение тангенса tg A = Sin A / Cos A = (2,828427 / 3) • (3/1) = 8,485281/3 = 2,828427.
Пример задачи. Найти синус, тангенс через косинус угла А = Cos A = -0,5 с помощью онлайн калькулятора синусов, косинусов, тангенсов, котангенсов. В поле “тригонометрическая функция” указывается “cos”, “числитель” — число “- 0,5”.
Решение синусов и тангенсов:
По таблице “Косинусы” находим угол A в градусах = 120° = 120°0′.
Используем формулу основного тригонометрического тождества
Sin2 + Cos2 = 1. Далее требуется вычислить синус.
1) значение синуса Sin A = √1 – (-0,5)2 = √1 – 0,25 = √0,75 = 0,866025;
2) значение тангенса tg A = Sin A / Cos A = 0,866025 / -0,5 = -1,732051.
Пример задачи.
Используем калькулятор синусов и косинусов градусов, минут, секунд онлайн, чтобы найти значение синуса, косинуса, тангенса, котангенса угла A = 12°34’56” = 12 градусов 34 минуты 56 секунд.
Решение:
A = 12°34’56” = 12,582222°
Синус угла sin 12°34’56” = 0,2178404227.
Косинус угла cos 12°34’56” = 0,9759844015.
Тангенс угла tg 12°34’56” = sin 12°34’56” / cos 12°34’56” = 0,2232007218.
Котангенс угла ctg 12°34’56” = cos 12°34’56” / sin 12°34’56” = 4,4802722491.
Секанс sec 12°34’56” = 1 / cos 12°34’56” = 1,0246065402.
Косеканс cosec 12°34’56” = 1 / sin 12°34’56” = 4,5905162484.
Версинус versin 12°34’56” = 1 – cos 12°34’56” = 0,0240155994.
Коверсинус coversin 12°34’56” = 1 – sin 12°34’56” = 0,7821595773.
Гаверсинус haversin 12°34’56” = 0,0240155994 / 2 = 0,0120077997.
Экссеканс exsec 12°34’56” = 1,0246065402 – 1 = 0,0246065402.
Экскосеканс excsc 12°34’56” = 4,5905162484 – 1 = 3,5905162484.
Дано:
ΔABC – прямоугольный треугольник,
гипотенуза AB = c,
катет BC = a,
катет AC = b,
Таблица значений синуса угла
В геометрии синус угла A – отношение противолежащего катета “a” к гипотенузе “c”.
Математическая формула синуса. sin A = a/c

Синус угла 0 градусов: sin 0° = sin 0 = 0
Синус угла 30 градусов: sin 30° = sin (π/6) = 1/2
Синус угла 45 градусов: sin 45° = sin (π/4) = √2/2
Синус угла 60 градусов: sin 60° = sin (π/3) = √3/2
Синус угла 90 градусов: sin 90° = sin (π/2) = 1
Синус угла 180 градусов: sin 180° = 0
Таблица косинуса угла
Косинус угла A – отношение прилежащего катета “b” к гипотенузе “c”.
Формула косинуса. cos A = b/c
Косинус угла 0 градусов: cos 0° = cos 0 = 1
Косинус угла 30 градусов: cos 30° = cos (π/6) = √3/2
Косинус угла 45 градусов: cos 45° = cos (π/4) = √2/2
Косинус угла 60 градусов: cos 60° = cos (π/3) = 1/2
Косинус угла 90 градусов: cos 90° = cos (π/2) = 0
Косинус угла 180 градусов: cos 180° = –1
Таблица тангенса угла
В тригонометрии тангенс угла A – отношение противолежащего катета “a” к прилежащему катету “b”.
Геометрическая формула тангенса. tg A = a/b
Тангенс угла 0 градусов: tg 0° = tg 0 = 0
Тангенс угла 30 градусов: tg 30° = tg (π/6) = √3/3
Тангенс угла 45 градусов: tg 45° = tg (π/4) = 1
Тангенс угла 60 градусов: tg 60° = tg (π/3) = √3
Тангенс угла 90 градусов: tg 90° = tg (π/2) = не определяется
Тангенс угла 180 градусов: tg 180° = 0
Котангенс угла
Котангенс угла A – отношение длины прилежащего катета “b” к противолежащему катету “a”.
Формула котангенса. ctg A = b/a
Секанс
Секанс угла A равен отношению гипотенузы “c” к длине прилежащего катета “b”.
Формула секанса. sec A = c/b
Косеканс
Косеканс угла A – отношение гипотенузы “c” к противолежащему катету “a”.
Формула косеканса. cosec A = c/a
Версинус
Формула версинуса. versin A = 1 — cos A.
Коверсинус
Коверсинус рассчитывается как coversin A = 1 — sin A.
Гаверсинус
Формула гаверсинуса. haversin A = (versin A)/2.
Экссеканс
Экссеканс вычисляется по формуле: exsec A = sec A — 1.
Экскосеканс
Формула экскосеканса. excsc A = cosec A — 1.
Тригонометрические функции
Онлайн калькулятор тригонометрических функций вычисляет синус (sin), косинус (cos), тангенс (tg), котангенс (ctg), секанс (sec), косеканс (cosec) для угла заданного в градусах, радианах, градах, минутах или секундах.
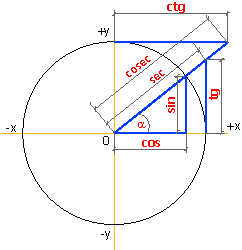
Тригонометрические функции — вид элементарных функций, к которым относятся следующие функции:
sin — синус
cos — косинус
tg — тангенс
ctg — котангенс
sec — секанс
cosec — косеканс
versin — версинус (синус-верзус)
vercos — коверсинус (косинус-верзус)
haversin — гаверсинус (половина от синус-верзус)
exsec — экссеканс
excsc — экскосеканс
Для того чтобы вычислить все эти тригонометрические функции сразу для заданного угла, введите значение угла в поле Угол и получите результат в виде таблицы значений всех функций для этого угла. Угол можно задать в градусах, радианах, градах, минутах и секундах, для выбора единицы измерения — просто щелкните на ее название.
![]()
Тригонометрические функции
Точность вычисления
Знаков после запятой: 10
Файл очень большой, при загрузке и создании может наблюдаться торможение браузера.
Как известно из школы, синус угла (sin) — это отношение длины противоположного этому углу катета к гипотенузе, а косинус (cos) — это отношение прилежащего этому углу катета к гипотенузе.
Остальные тригонометрические функции можно выразить через синус и косинус:
Тангенс: (отношение длины противоположного углу катета к прилежащему катету)
Котангенс: (отношение длины прилежащего к углу катета к противоположному катету)
Секанс: (отношение длины гипотенузы к прилежащему к углу катету)
Косеканс: (отношение длины гипотенузы к противоположному катету)
Редко используемые тригонометрические функции:
Версинус:
Коверсинус:
Гаверсинус:
Экссеканс:
Экскосеканс:
