Что такое тангенс угла и как его найти
Живущим людям на Земле
всегда хотелось знать,
как путь найти в пустыне, море,
и можно к звёздам ли попасть.
Хотелось труд свой облегчить,
создать машины, чтоб летать.
И чтоб вопросы разрешить,
пришлось про тангенс всем узнать.
Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. Впервые встречаясь с тригонометрией в восьмом классе на геометрии, школьники оглядываются на свою жизнь, задавая вопрос, насколько пригодится им эта область науки в дальнейшем.
Редко кто задумывается, что раздел математики, позволяющий рассказать о заданном треугольнике всё (найти все его стороны и углы, выделить особенности), позволил в своё время сделать великие открытия.
Тригонометрия, дав возможность строить корабли и самолёты, отправлять человека в космос, создавать приборы для ориентирования на море, в лесу, в пустыне, определять расстояния, не измеряя их непосредственно линейкой, шагами или чем-то иным, помогла упростить жизнь человечества, раскрыть новые горизонты знаний.
Тангенс угла
Первые встречи с тангенсом происходят при изучении прямоугольных треугольников.
В них соотношения сторон, образующих прямой угол (катетов), и стороны, лежащей напротив угла в 90º (гипотенузы), задают важные параметры для изучения углов.
Для понимания связи между объектами рассматриваются отношения различных отрезков. Задавая связь между ними, вводят понятия синуса, косинуса (это что?), тангенса, котангенса.
Важно, что это отвлечённые понятия, не связанные с какими-либо единицами измерения.
Введя функции угла, определяют их свойства. Некоторые полученные формулы могут иметь довольно громоздкий вид. Чтобы избежать затруднённого чтения, вводятся другие объекты.
Так произошло и с тангенсом. Ему посчастливилось получить два определения. Каждое характеризует заданное отношение по-своему. С одной стороны, рассматривается связь между катетами и острыми углами прямоугольного треугольника, с другой – даётся возможность упростить формулы, содержащие синусы и косинусы.
Мало кто задумывается, изучая тангенс в школе, что первоначально он был необходим, чтобы найти касательные линии к заданной кривой. Само понятие возникло от латинского слова tangens, которое означает «трогающий», «касающийся» и является причастием настоящего времени от tangere («трогать», «касаться»).
Тангенс — это отношение…
Итак, есть два определения:
-
Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.
Это определение удобно использовать при изучении геометрических фигур. Оно даёт возможность, минуя вычисления гипотенузы, находить углы или катеты. Выделяя прямоугольные треугольники в произвольных фигурах, задача по изучению свойств исследуемых объектов становится проще.
-
Тангенс – это отношение синуса к косинусу.
Благодаря этому определению, многие тригонометрические формулы принимают более удобный вид, становятся легче воспринимаемыми.
Приняты обозначения:
Вместо «тангенс угла альфа» пишут: tgα. На калькуляторах, в различных программах ЭВМ и ПК закрепилось другое обозначение: tan(α).
Как найти тангенс угла (формулы)
Первое свойство тангенса вытекает из его определения как отношения катетов.
Сумма двух непрямых углов прямоугольного треугольника равна 90º. Поэтому
![]()
Так как тангенс – это отношение катетов, то
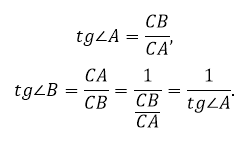
Получается, что
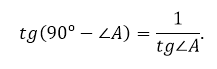
Учитывая особенности некоторых треугольников (равностороннего, прямоугольного, равнобедренного), а также записанное свойство, была составлена таблица значений тангенса для углов 30º, 45º, 60º.
В частности,
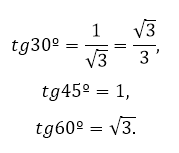
Задача нахождения других углов по значению тангенса была решена с помощью составления более обширных таблиц. За счёт появления современных вычислительных средств необходимость применения табулированных значений уменьшилась.
Как найти тангенс по клеточкам
Учитывая первое определение, можно определить, как найти его по клеточкам. Рисунок дополняется перпендикулярными линиями (строится высота), затем считается количество клеточек в полученном прямоугольном треугольнике на катетах, противолежащем и прилежащем искомому углу, а затем берётся их отношение.
Благодаря второму определению, задачу, как найти тангенс угла, можно решить, минуя таблицы и построение прямоугольных треугольников. Достаточно знать синус и косинус, связанные между собой основным тригонометрическим тождеством:
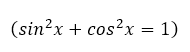
Из формулы тангенсов, записывающей кратко второе определение
![]()
и основного тригонометрического тождества можно понять, как найти тангенс, зная только косинус или синус угла.
Достаточно поделить основное тригонометрическое тождество на квадрат косинуса, подставить формулу тангенса. В результате получится его зависимость от косинуса:
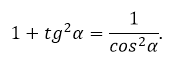
Если выразить в последнем случае косинус, то запишется связь между тангенсом и синусом:
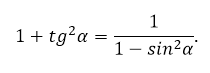
В статье мы рассмотрим, как найти значения:
(tg, frac{π}{3}), (ctg, (-frac{7π}{3})), (tg ,0), (ctg, frac{5π}{6})
и других тангенсов и котангенсов без тригонометрической таблицы.
Есть два способа вычислять тангенсы и котангенсы. Первый – через синусы и косинусы, второй – через оси тангенсов и котангенсов. Первый способ проще в освоении, второй – быстрее в применении.
Но в любом случае вам нужно уметь уверенно расставлять числа с пи на тригонометрическом круге и откладывать углы.
Способ 1 – вычисление тангенсов и котангенсов через синусы и косинусы
Конечно, этот способ подразумевает, что вы уже умеете вычислять синус и косинус. Не умеете? Тогда бегом читать эту статью, и эту тоже.
Уже умеете? Тогда ловите два определения:
– тангенс равен отношению синуса к косинусу числа.
(tg ,t=)(frac{sin,t}{cos,t})
– котангенс равен отношению косинуса к синусу числа.
(ctg ,t=)(frac{cos,t}{sin,t})
Пример. Вычислите (tg, frac{π}{3}) и (ctg, frac{π}{3}).
Решение:
Ищем сначала (frac{π}{3}), а после вычисляем (sin,frac{π}{3}) и (cos,frac{π}{3}).

(sin, frac{π}{3}=frac{sqrt{3}}{2}); (cos, frac{π}{3}=frac{1}{2});
(tg , frac{π}{3}=) (frac{frac{sqrt{3}}{2}}{frac{1}{2}})(=frac{sqrt{3}}{2}:frac{1}{2}=frac{sqrt{3}}{2}cdot frac{2}{1}=sqrt{3}).
(ctg,frac{π}{3}=)(frac{frac{1}{2}}{frac{sqrt{3}}{2}})(=frac{1}{2}:frac{sqrt{3}}{2}=frac{1}{2}cdotfrac{2}{sqrt{3}}=frac{1}{sqrt{3}}).
Пример. Вычислите (tg, frac{5π}{6}) и (ctg, frac{5π}{6}).
Решение:
Найдем сначала (frac{5π}{6}) на круге: (frac{5π}{6}=frac{6π}{6}-frac{π}{6}=π-frac{π}{6}).

(ctg, frac{5π}{6}=)(frac{cos frac{5π}{6}}{sinfrac{5π}{6}})(=-frac{sqrt{3}}{2}:frac{1}{2}=-frac{sqrt{3}}{2} cdot frac{2}{1}=-sqrt{3});
(tg,frac{5π}{6}=)(frac{sinfrac{5π}{6}}{cosfrac{5π}{6}})(=frac{1}{2}:(-frac{sqrt{3}}{2})=frac{1}{2}cdot(-frac{2}{sqrt{3}})=-frac{1}{sqrt{3}}).
Пример. Вычислите (tg, 0) и (ctg, 0).
Решение:

(0) на тригонометрическом круге совпадает с (1) на оси косинусов, значит (cos,0=1).
Если из точки (0) на тригонометрическом круге провести перпендикуляр (красная пунктирная линия) к оси синусов, то мы попадем в (0), получается (sin,0=0). Следовательно: (tg, 0=)(frac{sin,0}{cos,0}) (=frac{0}{1}=0).
С котангенсом интереснее: (ctg, 0=)(frac{cos,0}{sin,0}) (=frac{1}{0}=???). На ноль делить нельзя – это железное правило математики. Поэтому и посчитать такой котангенс не получится. (ctg,0) – не вычислим в принципе.
Пример. Вычислите (tg,120^°) и (ctg, 120^°).
Решение:

(ctg,120^°=)(frac{cos,120^°}{sin,120^°})(=-frac{1}{2}:frac{sqrt{3}}{2}=-frac{1}{2}cdotfrac{2}{sqrt{3}}=-frac{1}{sqrt{3}});
(tg,120^°=)(frac{sin,120^° }{cos,120^°})(=frac{sqrt{3}}{2}:(-frac{1}{2})=frac{sqrt{3}}{2}cdot(-frac{2}{1})=-sqrt{3}).
Способ 2 – вычисление тангенсов и котангенсов с использованием осей
Прямая, проходящая через начало отсчета тригонометрического круга и параллельная оси синусов (ось (y)), называется осью тангенсов. Направление оси тангенсов и оси синусов совпадает.
Прямая проходящая через (frac{π}{2}) ((90^°)) тригонометрического круга и параллельная оси косинусов (ось (x)) называется осью котангенсов. Направление оси котангенсов и оси косинусов совпадает.

Ось тангенсов – сдвинутая копия оси синусов, ось котангенсов – копия оси косинусов. Единицы на осях котангенсов и тангенсов совпадают.
Чтобы определить тангенс и котангенс с помощью тригонометрического круга, нужно:
1) Начертить тригонометрический круг и оси тангенсов и котангенсов;
2) Отметить аргумент тангенса или котангенса на тригонометрическом круге;
3) Соединить прямой эту точку, соответствующую аргументу и начало координат;
4) Продлить прямую до осей и найти координаты пересечения, как показано на картинке ниже:

О том, как просто запомнить где какое значение стоит на осях, можно прочитать в статье «Как запомнить тригонометрический круг».
Пример. Вычислите (tg, frac{π}{4}) и (ctg, frac{π}{4}).
Решение:
1) Строим круг, оси и отмечаем аргумент на окружности;

2) Соединяем точку, соответствующую аргументу, и начало координат;

3) Продляем до осей;

И на оси тангенсов, и на оси котангенсов мы пришли в единицу, поэтому (tg, frac{π}{4}=1) и (ctg, frac{π}{4}=1).
Пример. Вычислите (tg, frac{2π}{3}) и (ctg, frac{2π}{3}).
Решение: (frac{2π}{3}=frac{3π}{3}-frac{π}{3}=π-frac{π}{3})



(ctg ,frac{2π}{3}=-frac{1}{sqrt{3}}); (tg,frac{2π}{3}=-sqrt{3}).
Пример. Найдите значения выражений (tg,(-30^°)) и (ctg,(-30^°)).
Решение:



Понятно, что во время ЕГЭ такой красивой картинки не будет, но она и не нужна. Если вы будете знать, как правильно расставлять значения на тригонометрическом круге и будете помнить расположение чисел на осях, то вам будет достаточно нарисованного от руки круга.
Пример (ЕГЭ). Найдите значение выражения (2sqrt{3} tg,(-300^°)).
Решение: (-300^°=-360^°+60^°).

(2sqrt{3}tg(-300^° )=2sqrt{3}cdotsqrt{3}=2cdot 3=6).
Ответ: (6).
Смотрите также:
Как найти синус и косинус без тригонометрической таблицы?
Из градусов в радианы и наборот
Тригонометрическая таблица с кругом
Почему в тригонометрической таблице такие числа?
Для тех кто хочет закрепить знания:
Задание на вычисление синусов, косинусов, тангенсов и котангенсов
Тригонометрия — это раздел математики, в котором изучаются тригонометрические функции, их свойства, взаимосвязи и применение.
Слово «тригонометрия» образовано от греческих слов «trigonom» (треугольник) и «metreo» (измерять).
Возникновение и развитие тригонометрии связаны с практическими потребностями в измерении и вычислении сначала элементов треугольников на местности, а позднее — в строительстве, мореплавании и астрономии. Современная тригонометрия широко применяется в разных областях математики, в частности в геометрии, других науках, в технике. Например, тригонометрические функции используются при решении задач оптики, задач кинематического анализа и синтеза механизмов, гармонического анализа и других.
Cинус, косинус, тангенс, котангенс острого угла прямоугольного треугольника
Нет понятий «просто синус» или «просто косинус», не имеют смысла записи типа «sin» и «cos» сами по себе, они сами по себе никакой величины не обозначают (точно так же, как и, например, значок квадратного корня сам по себе). Те, кто этого не понимает, часто делает грубую ошибку типа: sin x /cos x = in /co
Есть понятие синуса, косинуса, тангенса, котангенса как тригонометрических функций угла. Здесь угол — аргумент функции. Он может обозначаться «х», «а», «альфа», «бета», «гамма», «фи», «дельта» или ещё какой-нибудь буквой. Суть от этого не меняется.
Для того, чтобы более наглядно представить приведенные ниже определения, начертите прямоугольный треугольник. Это треугольник, один из углов которого — прямой (т.е. один из углов равен 90 градусов). Стороны, прилежащие к прямому углу (перпендикулярные друг другу стороны) — это катеты данного прямоугольного треугольника. Противолежащая прямому углу сторона — это гипотенуза.
Теперь выберите любой из двух других (острых) углов треугольника и обозначьте его, например, альфа. Один из катетов будет примыкать к вершине этого угла (и, собственно, образовывать этот угол вместе с гипотенузой). Это — прилежащий катет. Другой катет не примыкает к вершине этого угла, он находится как бы напротив данной вершины. Это — противолежащий катет.
Кстати, почему-то не все представляют, что такое угол треугольника при данной вершине. У треугольника (обозначим его ABC) есть три вершины: А, В и С. Когда говорят об угле А треугольника, то подразумевают угол, образованный сторонами ВА и АС. Это и есть угол при вершине А.
Итак,
Синусом острого угла называется отношение противолежащего этому углу катета к гипотенузе.
Косинусом острого угла называется отношение прилежащего к этому углу катета к гипотенузе.
Тангенсом острого угла называется отношение противолежащего этому углу катета к прилежащему катету.
Котангенсом острого угла называется отношение прилежащего этому углу катета к противолежащему катету.
Секансом острого угла называется отношение гипотенузы к прилежащему к этому углу катету. Обозначается: sec x.
Косекансом острого угла называется отношение гипотенузы к противолежащему этому углу катету. Обозначается: cosec x.
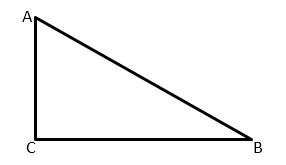
Как найти углы в прямоугольном треугольнике, если известны стороны?
Дан треугольник АВС, угол С — прямой.
Стороны АВ, АС и ВС известны.
Т.к. угол С — прямой, он равен 90 градусам.
Другие углы можно найти, например, так:
если известен катет и гипотенуза
sinA = BC / AB,
sinB = AC / AB,
если известны два катета
tg A = BC / AC
tg B = AC / BC
Предположим, получили, что sin A = ½. По таблице смотрим, что такому значению sin x соответствует величина угла 30 градусов.
Или, к примеру, получили, что tg B = 1. Значит, угол В равен 45 градусов.
Или, к примеру, мы получили, что sin B = 0,259. По таблице Брадиса или с помощью калькулятора находим, что угол В равен 15 градусов.
sin 15° = 0,259
arcsin0,259 = 15°
Как найти углы в прямоугольном треугольнике, если известен один угол?
Поскольку треугольник прямоугольный, то один из его углов равен 90 градусов. Величина второго угла известна (по условию задачи, обозначим её альфа). В сумме углы треугольника составляют 180 градусов. Значит, третий угол равен 180—90—альфа.
Еединичная окружность (единичный круг)
Единичный круг — это круг с центром в начале координат и радиусом, равным единице (R = 1).
Единичная окружность — это окружность единичного круга (т.е. окружность с центром в начале координат и с радиусом, равным единице).
Единичный радиус-вектор — это вектор, начало которого совпадает с началом координат, а его длина равна единице.
Углы отсчитывают от начального положения подвижного радиуса-вектора (совпадает с положением Ох).
Координатные четверти отсчитываются так:
y
|
|
(II четверть) | (I четверть)
|
________________________ x
|0
|
(III четверть) | (IV четверть)
|
|
Угол первой четверти — от 0 до 90 градусов (от 0 до пи/2).
Угол второй четверти — от 90 до 180 градусов (от пи/2 до пи).
Угол третьей четверти — от 180 до 270 градусов (от пи до 2пи/3).
Угол четвертой четверти — от 270 до 360 градусов (от 2пи/3 до 2пи).
Например:
- углы первой четверти: 30 градусов, 85 градусов, пи/4;
- углы второй четверти: 120 градусов, 178 градусов;
- углы третьей четверти: 205 градусов, 260 градусов;
- углы четвертой четверти: 272 градуса, 305 градусов.
Тригонометрические функции
К тригонометрическим функциям относятся функции:
y = sin x;
y = cos x;
y = tg x;
y = ctg x;
y = sec x;
y = cosec x.
Синусом угла, образованного осью Ох и произвольным радиусом-вектором ОА, называется отношение проекции этого вектора на ось Оу к его длине.
Косинусом угла, образованного осью Ох и произвольным радиусом-вектором ОА, называется отношение проекции этого вектора на ось Ох к его длине.
Тангенсом угла, образованного осью Ох и произвольным радиусом-вектором ОА, называется отношение проекции этого вектора на ось Оу к его проекции на ось Ох.
Котангенсом угла, образованного осью Ох и произвольным радиусом-вектором ОА, называется отношение проекции этого вектора на ось Ох к его проекции на ось Оу.
Секансом угла, образованного осью Ох и произвольным радиусом-вектором ОА, называется отношение длины этого вектора к его проекции на ось Ох.
Косекансом угла, образованного осью Ох и произвольным радиусом-вектором ОА, называется отношение длины этого вектора к его проекции на ось Оу.
Тригонометрические функции связаны между собой, и этим можно воспользоваться для нахождения синуса угла по его косинусу или котангенсу или косинуса угла по его синусу или тангенсу.
Как найти синус угла, если известен косинус?
Нужно воспользоваться основным тригонометрическим тождеством:
sin2a + cos2a = 1
sin2a = 1 − cos2a
|sin a| = КОРЕНЬ(1 − cos2a)
sin a = ± КОРЕНЬ(1 − cos2a)
знак перед корнем нужно выбрать в соответствии с четвертью данного угла (синус положительный в I и II четвертях, косинус положительный в I и IV четвертях)
Как найти косинус угла, если известен синус?
Нужно воспользоваться основным тригонометрическим тождеством:
sin2a + cos2a = 1
cos2a = 1 − sin2a
|cos a| = КОРЕНЬ(1 − sin2a)
cos a = ± КОРЕНЬ(1 − sin2a)
знак перед корнем нужно выбрать в соответствии с четвертью данного угла (синус положительный в I и II четвертях, косинус положительный в I и IV четвертях)
Как найти синус угла, если известен котангенс?
Нужно воспользоваться тригонометрическим тождеством
1 + ctg2 a = 1/sin2 a
sin2 a = 1 / (1 + ctg2 a)
|sin a| = 1/ КОРЕНЬ(1 + ctg2 a)
sin a = ±1/ КОРЕНЬ(1 + ctg2 a)
знак перед корнем нужно выбрать в соответствии с четвертью данного угла (синус положительный в I и II четвертях, котангенс положительный в I и III четвертях)
Как найти косинус угла, если известен тангенс?
Нужно воспользоваться тригонометрическим тождеством
1 + tg2 a = 1/cos2 a
cos2 a = 1 / (1 + tg2 a)
|cos a| = 1/ КОРЕНЬ(1 + tg2 a)
cos a = ±1/ КОРЕНЬ(1 + tg2 a)
знак перед корнем нужно выбрать в соответствии с четвертью данного угла (косинус положительный в I и IV четвертях, тангенс положительный в I и III четвертях)
Тригонометрическое тождество
Тригонометрическим тождеством называется равенство, в которое входят тригонометрические функции и которое удовлетворяется произвольным допустимым значением угла — аргумента тригонометрических функций, но не удовлетворяется, если каждую в отдельности тригонометрическую функцию заменить произвольной величиной.
Основные тригонометрические тождества:
sin2a + cos2a = 1
tg a = sin a / cos a
ctg a = cos a / sin a
sec a = 1 / cos a
cosec a = 1 / sin a
Arcsin, arcos, arctg, arcctg (обратные тригонометрические функции)
- arcsin — читается: арксинус;
- arcos — читается: арккосинус;
- arctg — читается: арктангенс;
- arcctg — читается: арккотангенс.
arcsin, arcos, arctg, arcctg — это обратные тригонометрические функции.
Обратной тригонометрической функцией y = arcsin x называют угол у, взятый на отрезке от –пи/2 до +пи/2, синус которого равен х:
y = arcsin x sin y = x
Обратной тригонометрической функцией y = arccos x называют угол у, взятый на отрезке от –пи до +пи, косинус которого равен х:
y = arccos x cos y = x
Обратной тригонометрической функцией y = arctg x называют угол у, взятый на промежутке от –пи/2 до +пи/2 (исключая концы), тангенс которого равен х:
y = arctg x tg y = x
Обратной тригонометрической функцией y = arcctg x называют угол у, взятый на промежутке от 0 до пи (исключая концы), котангенс которого равен х:
y = arctg x tg y = x
Например,
sin 30° = 0,5
arcsin0,5 = 30°
Синусоида и косинусоида
График функции y = sin x называется синусоидой.
График функции y = cos x называется косинусоидой.
Источники информации:
- Справочник по элементарной математике. Геометрия, тригонометрия, векторная алгебра. Под редакцией П.Ф. Фильчакова. —К.: Наукова думка, 1967. — 442 с.
- В.Д. Гетманцев, О.Ф. Саушкiн. Математика: Тригонометрiя: Посiбник для слухачiв пiдотовчих вiддiлень, вступникiв до вищих навчальних закладiв, студентiв педагогiчних iнститутiв (на укр.). —К.: Либiдь, 1994. — 144 с.
- docme.ru — зачем нужна тригонометрия?
- ru.wikipedia.org — Википедия — тригонометрия;
- ru.wikihow.com — как изучать тригонометрию?
Содержание:
- Тангенс угла в треугольнике
- Тангенс произвольного угла
Тангенс угла в треугольнике
Определение
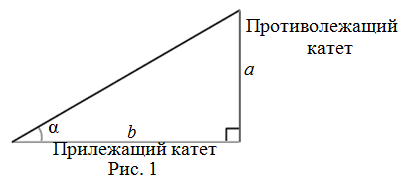
Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего
этому углу катета к прилежащему катету (рис. 1):
$$operatorname{tg} alpha=frac{a}{b}$$
Замечание
Сравнивая определения для тангенса и
котангенса угла, можно заметить, что тангенс и котангенс угла связаны между собой соотношением:
$$
operatorname{tg} alpha=frac{1}{operatorname{ctg} alpha}
$$
Пример
Задание. Найти тангенс острого угла прямоугольного треугольника, если известно, что
прилежащий к этому углу катет равен 3 см, а противолежащий ему – на 2 сантиметра длиннее.
Решение. Вначале найдем длину противолежащего катета:
$a = 3 + 2 = 5$ (см)
Тогда тангенс угла
$$
operatorname{tg} alpha=frac{5}{3}
$$
Ответ.
$$
operatorname{tg} alpha=frac{5}{3}
$$
Тангенс произвольного угла
Определение
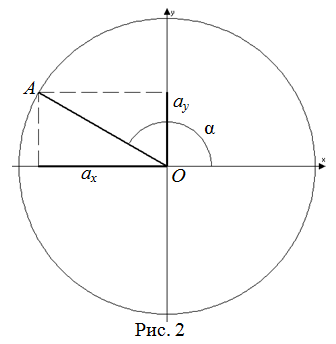
Тангенс произвольного угла
$alpha$, образованного осью
$O_x$ и произвольным радиус-вектором $overrightarrow{O A}=left(a_{x} ; a_{y}right)$ (рис. 2), – отношение
проекции этого вектора на ось
$O_y$ к его проекции на ось
$O_x$:
$$operatorname{tg} alpha=frac{a_{y}}{a_{x}}$$

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Найти тангенс угла, образованного вектором
$bar{a}=(1 ;-1)$ и осью абсцисс.
Решение. Проекция на ось абсцисс равна
$a_x=1$, а на ось ординат – $a_y=-1$, тогда
$$operatorname{tg} alpha=frac{-1}{1}=-1$$
Ответ. $operatorname{tg} alpha=-1$
Читать дальше: что такое котангенс угла.
Как найти тангенс угла
Тригонометрия – тема, которую многие обходят стороной. Несмотря на это, если найти к ней правильный подход она станет очень интересной для вас. Тригонометрические формулы, в том числе и формулы для нахождения тангенса, используются во многих сферах реальной жизни. Данная статья расскажет о способах нахождения тангенса угла и приведет примеры применения данной величины в жизни. Это даст вам мотивацию на пути изучения данной темы.
Несмотря на мнение, которые бытует среди большинства школьников, тригонометрия достаточно часто применяется в жизни. Наглядный пример практического применения даст вам стимул не лениться. Вот несколько сфер деятельности где используются тригонометрические вычисления, в том числе и нахождение тангенса угла:
- Экономика.
- Астрономия.
- Авиация.
- Инженерия.
Итак, ниже будут приведены способы нахождения tg.
2
Как найти tg угла
Нахождение тангенса угла достаточно просто. Вы можете изучить данную тему и просто вызубрить правила, но все это может вылететь из головы на экзамене. Поэтому стоит подходить к данному вопросу осмысленно. Основные формулы для запоминания:
- tg0° = 0
- tg30° = 1/√3
- tg45° = 1
- tg60° = √3
- tg90° = ∞ (бесконечность/неопределенно)
Обратите внимание, что величины идут по возрастанию: чем больше угол – тем больше значение тангенса. Соответственно, при градусном значении угла в 0° мы получим 0. При значении в тридцать градусов – единица поделенная на корень из трех и т.д., пока мы не достигнем отметки в 90°. При нем величина тангенса равна бесконечности или неопределенности (исходя из конкретной ситуации).
Данные выражения вытекают из правила нахождения тангенса через прямоугольный треугольник. Так, тангенс угла A (tgA) равен соотношению противолежащего катета к прилежащему. Представьте, что дан прямоугольный треугольник, в котором известны все стороны, но не известны углу. По решению задачи требуется найти тангенс угла A. Величина стороны, которая лежит напротив угла – 1, а прилежащего катета – √3. Их соотношение дает 1/√3. Мы уже знаем, что величина угла при данном показателе равна 30 градусам. Соответственно, угол A = 30°.
В прямоугольном треугольнике у прямоугольного угла оба тангенса – прилежащие. Противолежащая сторона данного угла – гипотенуза. Именно потому, что мы не можем разделить два катета друг на друга (нарушится условие нахождения), тангенс 90° в данном случае не существует.
Помимо всего этого, часто приходится находить тангенс тупого угла. Обычно в задачах встречаются тупые углы с величиной в 120 или 150 градусов. Формула нахождения тангенса тупого угла выглядит следующим образом: tg(180-a) = tga.
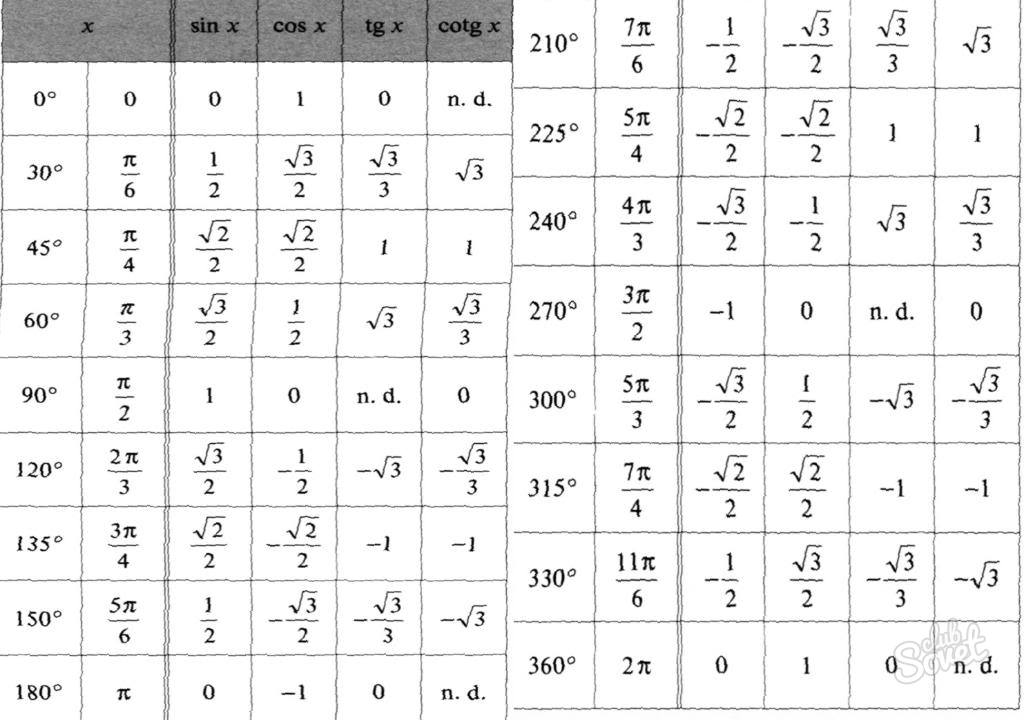
К примеры, нам необходимо найти тангенс 120°. Необходимо задать себе следующий вопрос: сколько нужно отнять от 180, чтобы получить 120? Однозначно, 60°. Отсюда следует, что тангенс 120° и тангенс 60° равны друг другу и tg120° = √3. По такой же логике можно найти тангенс в 150 и 180 градусов. Их значения будут соответственно равны 1/√3 и 0. Величины тангенсов других углов приведены в тригонометрической таблицы, но используются они крайне редко.
3
Как найти tg угла онлайн
Существует много онлайн ресурсов для нахождения тангенса угла. Одним из таких является сайт FXYZ. Перейдите по ссылке. Перед вами выйдет страница, где будут приведены основные формулы, связанные с тангенсом, а также калькулятор. Пользоваться калькулятором достаточно просто. Необходимо ввести соответствующие и калькулятор вычислит ответ. Этот несложный алгоритм поможет вам в случае, если вы что-то забыли. На данном сайте есть два калькулятора. Один – для нахождения величины тангенса исходя из длин катетов треугольника, а второй исходя из величины угла. Используйте тот вычислитель, который требует задача.
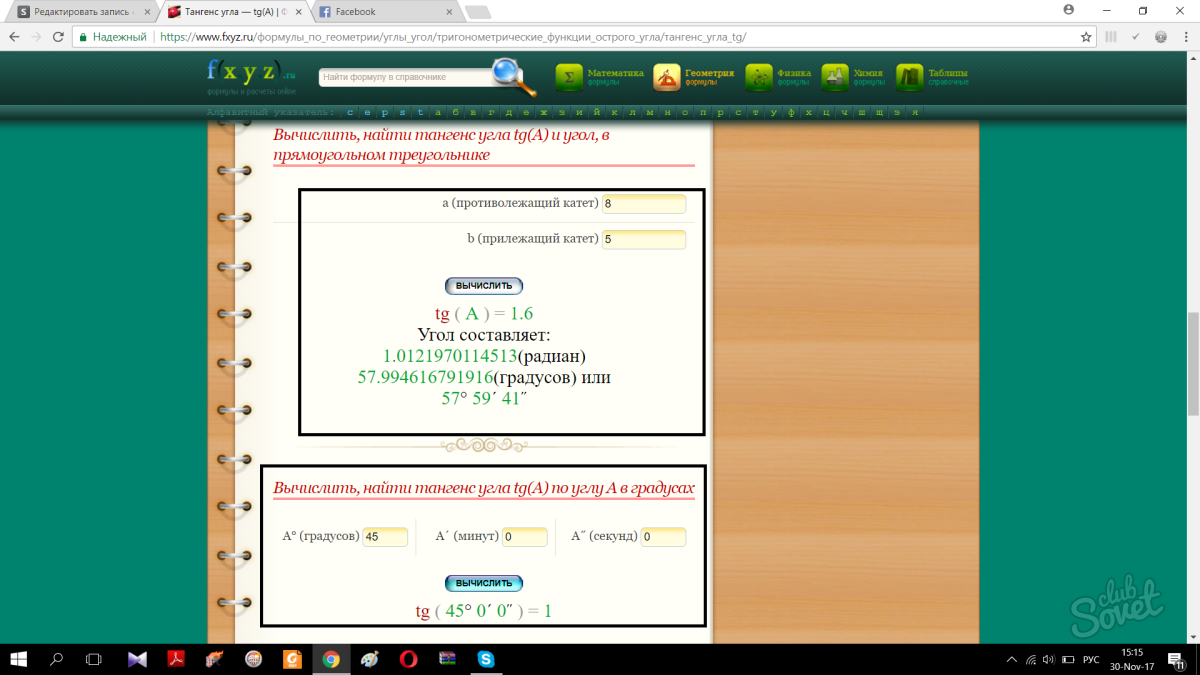
Как вы могли заметить, нахождения тангенса и других тригонометрических показателей очень часто применяется в реальной жизни, а находить эти значения совсем несложно. Если вы поймете суть нахождения, то что-либо зазубривать вам не придется – вы сами сможете дойти до правильного ответа. Если все-таки что-то не получается, воспользуйтесь калькулятором, но не злоупотребляйте. На экзамене, зачете или школьной контрольной работе такой возможности вам никто не предоставит. Более того, если вы поступите на факультет, где изучается тригонометрия высшей математики, без базовых знаний вам придется серьезно попотеть чтобы не срезаться.
