Тригонометрия – это наука, изучающая свойства тригонометрических формул (trigwnon – треугольник и метр – мера).
Тригонометрич. формулы — это элементарные функции, выражающие зависимость всех сторон прямоугольного треугольника от острых углов к гипотенузе (или зависимость хорд и высот от его центрального угла в окружности).
К прямым функциям тригонометрии относятся: sin x (синус), cos x (косинус). К производным: tg x (тангенс), ctg x (котангенс). В дополнение к другим тригонометрическим функциям: sec x (секанс) и cosec x (косеканс).
Косинус и синус в тригонометрии — бесконечно дифференцируемые и периодически непрерывные вещественные функции. Остальные, наоборот, дифференцируются в области определения, однако, как и прямые тригонометрические функции, непрерывны.
Основные тригонометрич. тождества:
Зная синус или косинус числа, можно найти его тангенс или котангенс: tg a = sin a / cos a
Вы можете найти синус числа, если известен его косинус, и наоборот: sin2 a + cos2 a = 1
Можно найти тангенс через синус с известным косинусом: 1 + tg2 a = 1 / cos2 a
Вы можете найти котангенс через синус с известным косинусом: 1 + 1 / tg2 a = 1 / sin2
sin(90o – а) = cos а
cos(90o – а) = sin а
И еще, любую формулу в математике можно применять не только слева направо, но и наоборот. В тригонометрии это же применяется при преобразовании суммы в произведение или при переходе от произведения к сумме.
Ответы Mail.ru
Образование
ВУЗы, Колледжи
Детские сады
Школы
Дополнительное образование
Образование за рубежом
Прочее образование
Вопросы – лидеры.
Где найти ответы на ОГЭ 2023?
1 ставка
Написать экологическое обоснование изделия из кольца
1 ставка
Помогите с английским 21 упражнением, расставить a,an,the.
1 ставка
Чем на ваш взгляд лучше заменить ЕГЭ?
1 ставка
Лидеры категории
Лена-пена
Искусственный Интеллект
М.И.
Искусственный Интеллект
Y.Nine
Искусственный Интеллект
•••
Как найти Тангенс числа, зная косинус? Напишите формулу, пожалуйста.!!!
Митяй
Мудрец
(16354),
закрыт
12 лет назад
Лучший ответ
Vlad Boikov
Профи
(739)
12 лет назад
sin^2+Cos^2=1
а дальше сам
Остальные ответы
BuHT
Мастер
(1169)
12 лет назад
tg=sin/cos=((1-cos^2)^1/2)/cos
Екатерина Максимова
Мыслитель
(5442)
12 лет назад
Роза Марковна
Просветленный
(35806)
12 лет назад
Пожалуй вот так
tg=sin/cos
sin^2+cos^2=1
sin= корень (1-cos^2)
тогда tg=(корень (1-cos^2))/cos
Похожие вопросы
Как найти тангенс, если известен косинус
Понятие тангенса является одним из основных в тригонометрии. Оно обозначает некую тригонометрическую функцию, которая является периодической, но не непрерывной в области определения, как синус и косинус. И имеет разрывы в точках (+,-)Пи*n+Пи/2, где n – это период функции. В России он обозначается как tg(x). Его можно представить через любую тригонометрическую функцию, так как все они тесно взаимосвязаны между собой.

Вам понадобится
- Учебник по тригонометрии.
Инструкция
Для того, чтобы выразить тангенс угла через синус, нужно вспомнить геометрическое определение тангенса. Итак, тангенсом острого угла в прямоугольном треугольнике, называют отношение противолежащего катета к прилежащему.
С другой стороны, рассмотрите декартову систему координат, на которой начерчена единичная окружность с радиусом R=1, и центром О в начале координат. Примите поворот против часовой стрелки, как положительный, а в обратную сторону отрицательный.
Отметьте некую точку M на окружности. Из нее опустите перпендикуляр на ось Ох, назовите ее точкой N. Получился треугольник OMN, у которого угол ONM является прямым.
Теперь рассмотрите острый угол MON, по определению синуса и косинуса острого угла в прямоугольном треугольнике
sin(MON) = MN/OM, cos(MON) = ON/OM. Тогда MN= sin(MON)*OM, а ON = cos(MON)*OM.
Вернувшись к геометрическому определению тангенса (tg(MON) = MN/ON), подставьте полученные выше выражения. Тогда:
tg(MON) = sin(MON)*OM/cos(MON)*OM, сократите OM, тогда tg(MON) = sin(MON)/cos(MON).
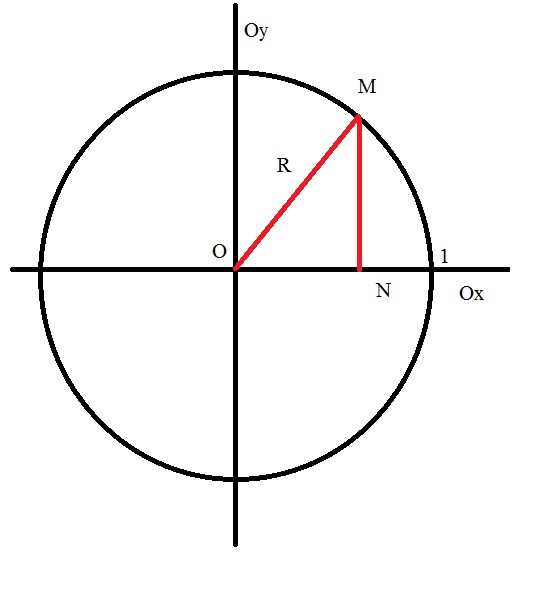
Из основного тригонометрического тождества (sin^2(x)+cos^2(x)=1) выразите косинус, через синус: cos(x)=(1-sin^2(x))^0,5 Подставьте это выражение в полученное на шаге 5. Тогда tg(MON) = sin(MON)/(1-sin^2(MON))^0,5.
Иногда существует потребность в вычисление тангенса двойного и половинчатого угла. Тут тоже выведены соотношения:tg(x/2) = (1-cos(x))/sin(x) = (1-(1-sin^2(x))^0,5)/sin(x);tg(2x) = 2*tg(x)/(1-tg^2(x)) = 2*sin(x)/(1-sin^2(x))^0,5/(1-sin(x)/(1-sin^2(x))^0,5)^2) =
= 2*sin(x)/(1-sin^2(x))^0,5/(1-sin^2(x)/(1-sin^2(x)).
Также возможно выразить квадрат тангенса через двойной угол косинуса, либо синус. tg^2(x) = (1-cos(2x))/(1+cos(2x)) = (1-1+2*sin^2(x))/(1+1-2*sin^2(x)) = (sin^2(x))/(1-sin^2(x)).
Обратите внимание
Обратите внимание на области допустимых значений при решение уравнений и неравенств.
Полезный совет
Знание наизусть основных тождеств, поможет быстро переходить от одних тригонометрических функций к другим.
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.

Внимание! Эти формулы работают только если аргументы у тригонометрических функций одинаковые, т.е.
(sin^2 776^° +cos^2 776^° =1)
(tg, 3xcdot ctg, 3x=1)
Но:
(sin^2x+cos^23x≠1)
(tg, xcdot ctg, y≠1)
Все формулы связи тригонометрических функций учить не надо, потому что они достаточно легко получаются друг из друга несложными преобразованиями (подробности в этих видео). Кроме того, при частом использовании они постепенно запоминаются сами.
Примеры применения формул связи
Зачем нужны формулы связи? Они позволяют найти все тригонометрические функции угла, если известна лишь одна из них, а также дают возможность упрощать выражения, доказывать тождества, решать тригонометрические уравнения, заменяя одну функцию другой и так далее.
Пример. Найдите (5sin,α), если (cos,α=frac{2sqrt{6}}{5}) и (α∈(frac{3π}{2};2π)).
Решение. Нам известен косинус, найти надо синус. А что связывает синус и косинус? Основное тригонометрическое тождество:
(sin^2α+cos^2α=1).
Подставим вместо косинуса его значение:
(sin^2α+)((frac{2sqrt{6}}{5}))(^2=1)
(sin^2α+)(frac{4cdot 6}{25})(=1)
(sin^2α+)(frac{24}{25})(=1)
(sin^2α=1-)(frac{24}{25})
(sin^2α=)(frac{1}{25})
(sinα=±)(frac{1}{5})
Внимание! Последняя строчка – место, где теряется огромное количество баллов на ЕГЭ! Это одна из самых популярных ошибок – забыть отрицательный корень. Пожалуйста, раз и навсегда запомните, что у неполного квадратного уравнения вида (x^2=a) (при (a>0)) два корня (x_1=sqrt{a}) и (x_2=-sqrt{a}). Пусть двойка над иксом (та которая «квадрат») будет вам вечным маяком, сигнализирующим: «тут ДВА корня! Два! Не забудь!»
Вернемся к задаче. Получилось, что синус может иметь значение (frac{1}{5}), а может (-)(frac{1}{5}). И какое значение нам надо выбрать – с минусом или плюсом? Тут нам на помощь приходит информация, что (α∈(frac{3π}{2};2π)). Давайте нарисуем числовую окружность и отметим отрезок ((frac{3π}{2};2π)).

Обратите внимание – в этой четверти синус принимает только отрицательные значения (можно провести перпендикуляры до оси синусов и убедиться, что это так).

Значит, в нашем случае (sin,α=-frac{1}{5}) т.е. (5sin,α=5cdot(-frac{1}{5})=-1).
Ответ: (-1).
Пример.Найдите (tg,α), если (cos,α=)(frac{sqrt{10}}{10}) и (α∈(frac{3π}{2};2π)).
Решение. Есть 2 пути решения этой задачи:
– напрямую вычислить тангенс через формулу (tg^2α+1=)(frac{1}{cos^2α});
– сначала с помощью тождества (sin^2α+cos^2α=1) найти (sin,α), а потом через формулу (tg,α=)(frac{sin,α}{cos,α}) получить тангенс.
В учебниках обычно идут первым путем, поэтому мы пойдем вторым.
Вычисляем синус:
(sin^2α+)((frac{sqrt{10}}{10})^2)(=1)
(sin^2α+)(frac{10}{100})(=1)
(sin^2α+)(frac{1}{10})(=1)
(sin^2α=1-)(frac{1}{10})
(sin^2α=)(frac{9}{10});
(sin,α=±)(frac{3}{sqrt{10}})
Опять (α∈(frac{3π}{2};2π)), значит в итоге синус может быть только отрицательным. То есть, (sin,α=-)(frac{3}{sqrt{10}}).
А теперь вычисляем тангенс: (tg,α=-)(frac{3}{sqrt{10}})(:)(frac{sqrt{10}}{10})(=)(-frac{3}{sqrt{10}}cdotfrac{10}{sqrt{10}})(=-)(frac{30}{10})(=-3).
Ответ: (-3).
Пример. Известно, что (tg,α=-frac{3}{4}) и (frac{π}{2}<α<π). Найдите значения трех других тригонометрических функций угла (α).
Решение. Проще всего из тангенса найти котангенс:
(ctg, α=)(frac{1}{tg, α})
(ctg,α=1:(-frac{3}{4})=1cdot(-frac{4}{3})=-frac{4}{3}).
Теперь вычислим косинус по упомянутой выше формуле:
(tg^2 α+1=)(frac{1}{cos^2α})
((-)(frac{3}{4}))(^2+1=)(frac{1}{cos^2α})
(frac{9}{16})(+1=)(frac{1}{cos^2α})
(frac{9+16}{16})(=)(frac{1}{cos^2α})
(frac{25}{16})(=)(frac{1}{cos^2α})
(cos^2α=)(frac{16}{25})
(cosα=±)(frac{4}{5})
Опять перед нами стоит выбор плюс или минус. Отметим отрезок ((frac{π}{2};π)) на тригонометрической окружности и посмотрим какие значения принимает косинус в этой четверти, чтобы определится со знаком.

Очевидно, что косинус отрицателен в этой четверти, а значит (cos,α=-)(frac{4}{5}).
Осталось найти синус:
(sin^2α+cos^2α=1)
(sin^2α+(-)(frac{4}{5})()^2=1)
(sin^2α+)(frac{16}{25})(=1)
(sin^2α=1-)(frac{16}{25})
(sin^2α=)(frac{9}{25})
(sin,α=±)(frac{3}{5})
Опять используем круг, чтобы определить знак.

Получается, что (sin,α=)(frac{3}{5}).
Ответ: (ctg,α=-)(frac{4}{3}); (cos,α=-)(frac{4}{5}); (sin,α=)(frac{3}{5}).
Пример (ЕГЭ). Найдите (tg^2 α), если (5 sin^2α+13 cos^2α=6).
Решение. Давайте пойдем от того, что известно. В равенстве (5 sin^2α+13 cos^2α=6) синус заменим на косинус:
(5(1-cos^2α)+13 cos^2α=6)
(5-5 cos^2α+13 cos^2α=6)
(5+8 cos^2α=6)
(8 cos^2α=1)
(cos^2α=)(frac{1}{8})
Поняли почему именно синус заменили на косинус, а не наоборот? И почему не надо извлекать корень, досчитывая до «чистого» косинуса? Потому что для нахождения (tg^2α) хорошо подходит формула (tg^2α+1=)(frac{1}{cos^2α}) :
(tg^2 α+1=1:)(frac{1}{8})
(tg^2 α+1=1cdot)(frac{8}{1})
(tg^2 α+1=8)
(tg^2 α=7)
Ответ: (7).
Теперь еще одна задача из ЕГЭ, для наглядности мы ее решение оформили картинкой.

Пример. Упростите выражение (frac{1}{sin^2 α})(-ctg^2 α-cos^2 β).
Решение.
|
(frac{1}{sin^2 α})(-ctg^2 α-cos^2 β) |
Самое очевидное, что можно сделать – это представить котангенс как отношение косинуса к синусу. |
|
|
(=)(frac{1}{sin^2 α})(-)(frac{cos^2α}{sin^2 α})(-cos^2 β=) |
Приводим дроби к общему знаменателю. |
|
|
(=)(frac{1-cos^2α}{sin^2 α})(-cos^2 β=) |
(1-cos^2α) можно заменить на (sin^2 α). |
|
|
(=)(frac{sin^2 α}{sin^2 α})(-cos^2 β=) |
Сокращаем синусы. |
|
|
(=1-cos^2 β=sin^2 β). |
Пример. Докажите тождество (frac{cos^4α-sin^4α}{(1-sinα)(1+sinα)})(+2tg^2 α=)(frac{1}{cos^2 α}).
Решение.
|
(frac{cos^4α-sin^4α}{(1-sinα)(1+sinα)})(+2tg^2 α=)(frac{1}{cos^2 α}) |
Чтобы доказать это тождество, будем преобразовывать левую часть, пытаясь свести ее к правой. Поехали. Разложим числитель левой дроби по формуле разности квадратов, а знаменатель, наоборот, соберем по ней же. |
|
|
(frac{(cos^2α-sin^2α )(cos^2 α+sin^2α)}{1-sin^2α})(+2tg^2 α=)(frac{1}{cos^2 α}) |
Очевидно, что вторая скобка числителя равна (1) (по основному тригонометрическому тождеству), а знаменатель можно заменить на (cos^2 α). |
|
|
(frac{cos^2α-sin^2α}{cos^2 α})(+2tg^2 α=)(frac{1}{cos^2 α}) |
Теперь разложим тангенс по формуле (tg, α=)(frac{sin,α}{cos,α}). |
|
|
(frac{cos^2α-sin^2α}{cos^2 α})(+2)(frac{sin^2α}{cos^2α})(=)(frac{1}{cos^2 α}) |
Приводим дроби к общему знаменателю. |
|
|
(frac{cos^2α-sin^2α+2 sin^2α}{cos^2 α})(=)(frac{1}{cos^2 α}) |
Приводим подобные слагаемые. |
|
|
(frac{cos^2α+sin^2α}{cos^2 α})(=)(frac{1}{cos^2 α}) |
И вновь нас выручает основное тригонометрическое тождество |
|
|
(frac{1}{cos^2 α}) (=)(frac{1}{cos^2 α}) |
Левая часть полностью идентична правой, то есть тождество доказано.
Как доказать все формулы связи
Найти тангенс фи , если известен косинус фи
Калькулятор коэффициент мощности cos fi в tg fi
Как найти тангенс фи, если известен косинус фи формула:
- tg φ = (√(1-cos²φ))/cos φ
Калькулятор онлайн – косинус в тангенс
cos φ:
tg φ:
Поделиться в соц сетях:
Популярные сообщения из этого блога
Индекс Руфье калькулятор
Проба Руфье калькулятор онлайн. Первые упоминания теста относиться к 1950 году. Именно в это время мы находим первое упоминание доктора Диксона о “Использование сердечного индекса Руфье в медико-спортивном контроле”. Проба Руфье – представляет собой нагрузочный комплекс, предназначенный для оценки работоспособности сердца при физической нагрузке. Индекс Руфье для школьников и студентов. У испытуемого, находящегося в положении лежа на спине в течение 5 мин, определяют число пульсаций за 15 сек (P1); После чего в течение 45 сек испытуемый выполняет 30 приседаний. После окончания нагрузки испытуемый ложится, и у него вновь подсчитывается число пульсаций за первые 15 с (Р2); И в завершении за последние 15 сек первой минуты периода восстановления (Р3); Оценку работоспособности сердца производят по формуле: Индекс Руфье = (4(P1+P2+P3)-200)/10; Индекс Руфье для спортсменов Измеряют пульс в положении сидя (Р1); Спортсмен выполняет 30 глубоких приседаний в
Найти косинус фи (cos φ), через тангенс фи (tg φ)
tg фи=… чему равен cos фи? Как перевести тангенс в косинус формула: cos(a)=(+-)1/sqrt(1+(tg(a))^2) Косинус через тангенс, перевести tg в cos, калькулятор – онлайн tg φ: cos φ: ± Поделиться в соц сетях:

