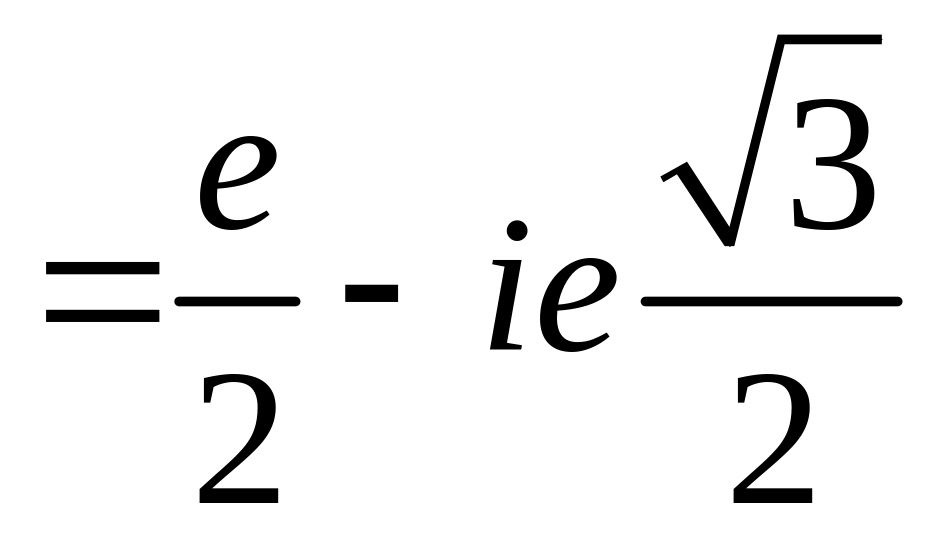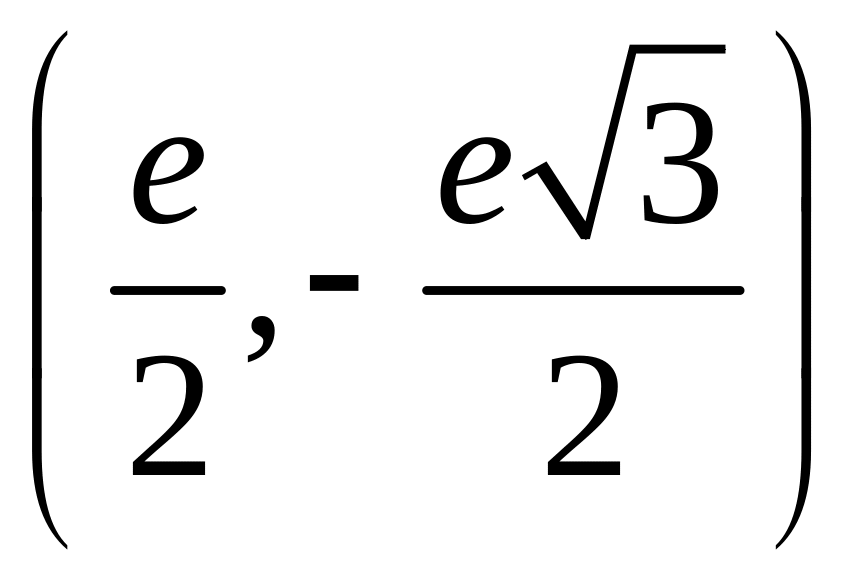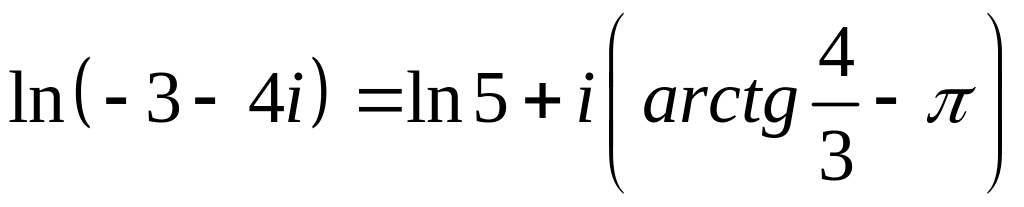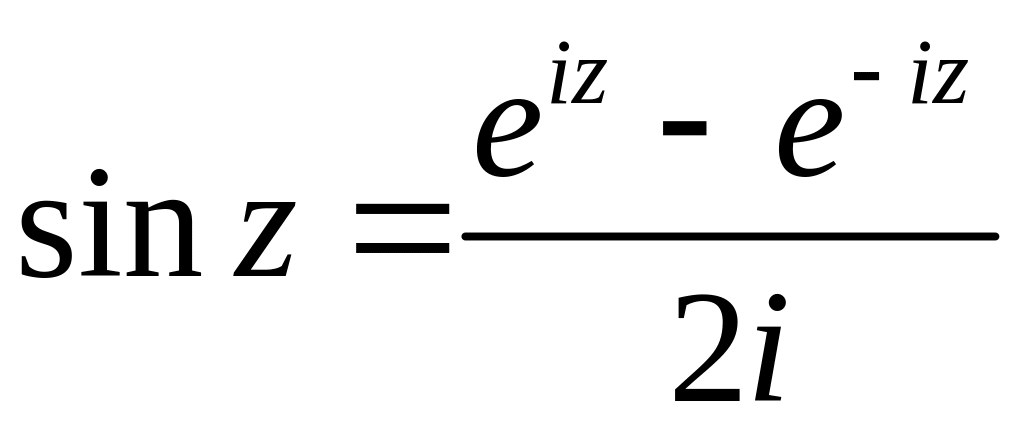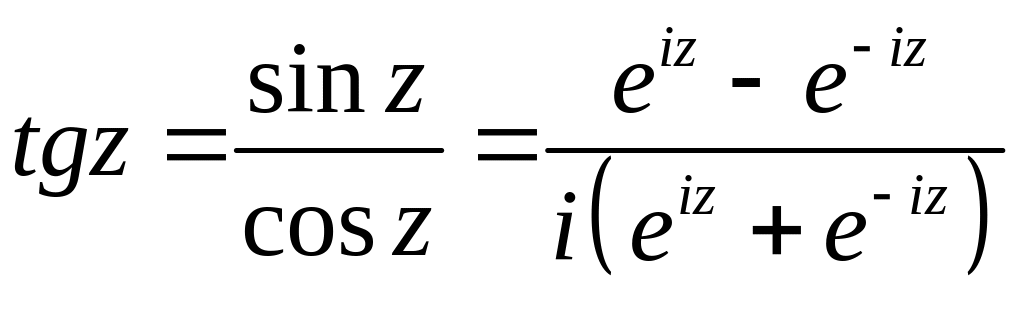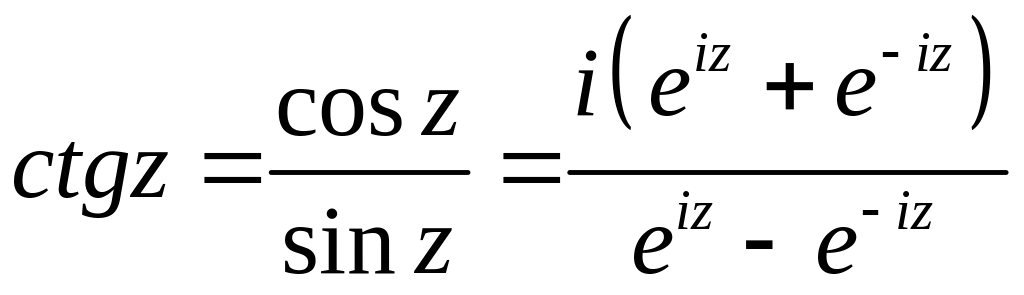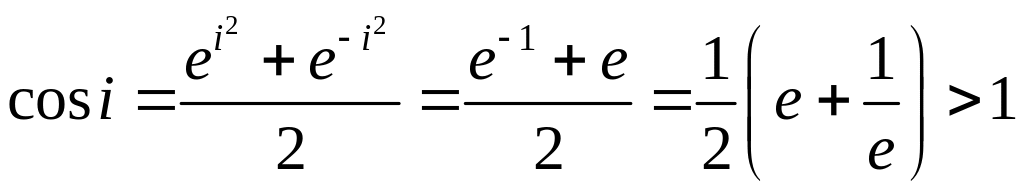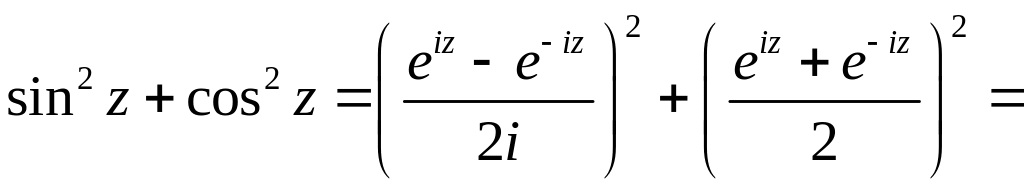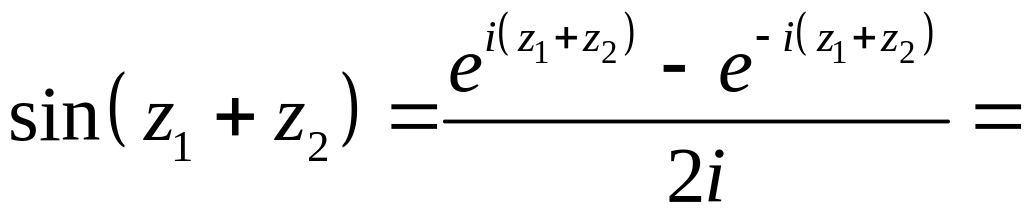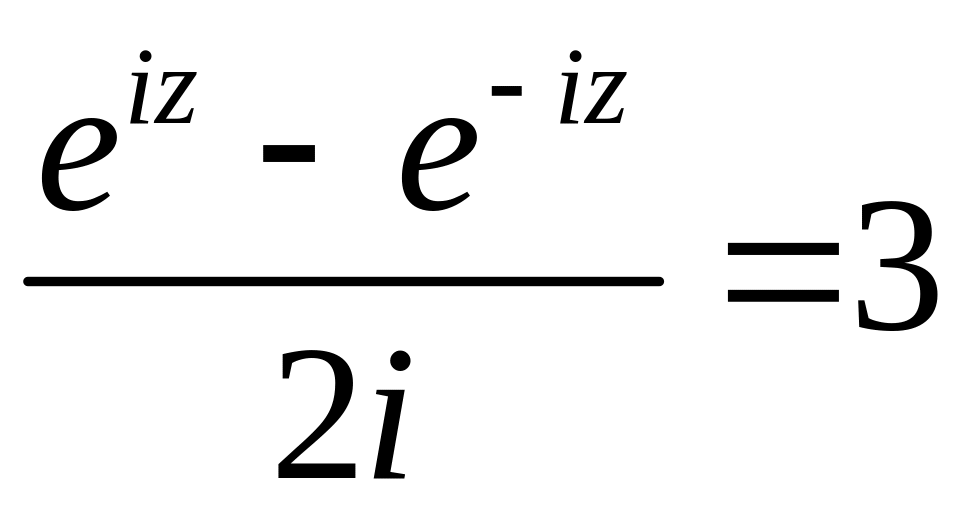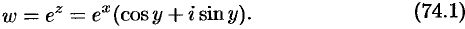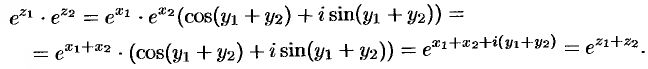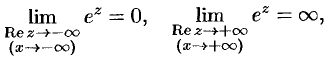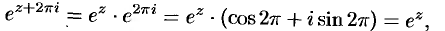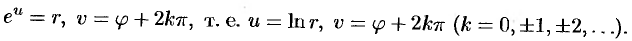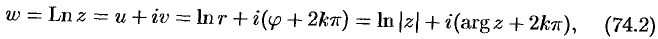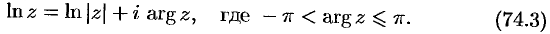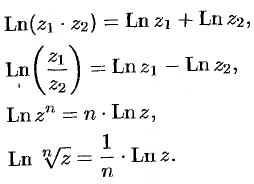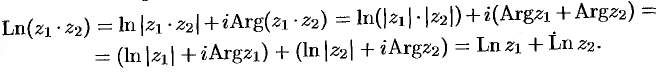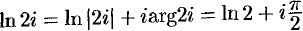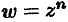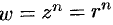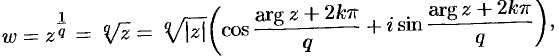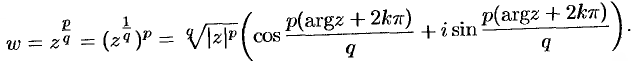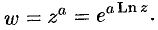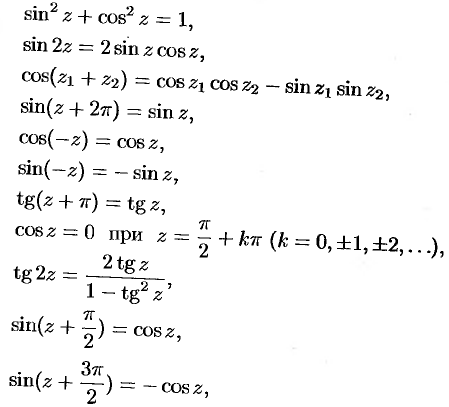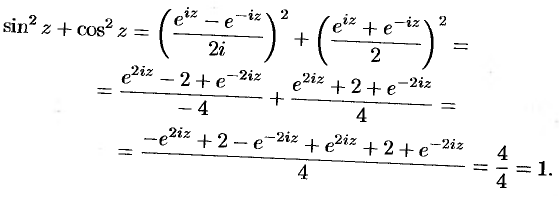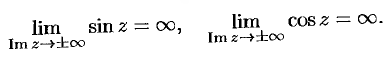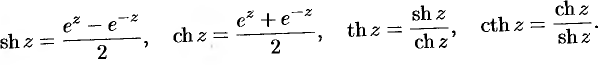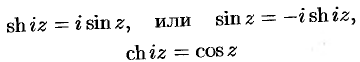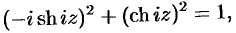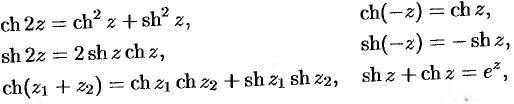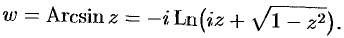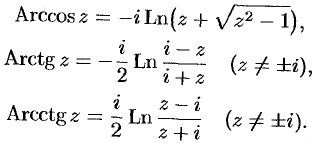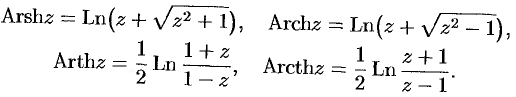Получил просьбу разобрать, как вычислять арксинус и другие функции сложнее экспоненты, если аргумент комплексный. Давайте разберем.
Начнем с общих вопросов. Аналитическая функция (заданная хоть где-нибудь сходящимся степенным рядом) может быть продолжена на всю свою область определения (которая ей присуща, а не задается извне), и, соответственно, представлена в данной точке из области определения некоторым сходящимся степенным рядом. Возможно, не одним. Подставив туда данное комплексное число, найдем значение функции. Их может быть несколько, если рядов больше одного.
Впрочем, не все функции во всех точках аналитические, даже среди элементарных. Корень, например, не аналитичен в нуле, хотя определен там…
Если функция задана через четыре действия арифметики (конечное число операций), то проблем с вычислением нет: арифметика определена полностью и однозначно.
Это многочлены и дробно-рациональные функции, то есть отношение двух многочленов. Довольно обширный и хороший класс функций. В него входят, в частности, все целые степени.
Если приходится делить на нуль, то либо получится полюс, если предел бесконечен, либо устранимая особая точка, если предел конечен. Других вариантов в данном случае не будет, хотя в общем случае бывают еще существенно особые точки, в которых предел по разным кривым может быть вообще любой, и в любой окрестности такой точки функция принимает все значения, или все кроме одного. Про особые точки я рассказывал.
Пример устранимой точки: нуль для z/z или sin(z)/z. Пример полюса: нуль для 1/z или (z+1)/z².
Примером функции с существенно особой точкой является exp(1/z): нуль именно такая точка, причем экспонента принимает в любой окрестности нуля все значения, кроме нулевого. А sin(1/z) тоже имеет существенно особую точку в нуле, но принимает в окрестности вообще все значения, без исключений.
Если мы добавим рациональные или вещественные степени, то тоже все делается, только теперь значений может быть много, и может теряться аналитичность: функция может быть определена в точке, но не быть аналитичной.
Комплексные степени вводятся через формулу Эйлера, которую я уже много раз приводил:
Что делает формула Эйлера — вопрос, кстати, очень тонкий. Я планирую скоро выпустить материал на эту тему. Можно сказать, что она задает функцию “экспонента”, особенно если записать формулу так:
Хотя обычно определение экспоненты другое, через ряд, например. Экспонента однозначна, так что все в порядке. Еще можно сказать, что формула Эйлера задает одно из значений (главное значение) степени числа е с показателем ix. Как найти остальные значения, я рассказывал.
Наконец, можно сказать, что формула Эйлера позволяет выразить комплексное число, записанное в тригонометрической форме, в форме экспоненциальной. Аналог: теорема Лагранжа о том, что любое натуральное представимо в виде суммы четырех квадратов. Ну а здесь любое комплексное с модулем единица представимо в виде числа е в некоторой мнимой степени (которая есть аргумент числа, умноженный на i).
В любом случае, формула Эйлера дает правило, как возводить число e в мнимую степень. По обычным правилам степени можно научиться возводить е в любую комплексную степень (получая, впрочем, только одно из значений), что вторая из приведенных формул и описывает.
Теперь мы можем любое комплексное число записать в экспоненциальной форме через модуль и аргумент:
Традиционно с большой буквы пишут многозначные функции, а они же с малой означают “главное значение” или одну из “ветвей”.
После этого легко определить логарифм (который всегда бесконечнозначен) для всех ненулевых чисел:
А умея вычислять логарифм, можно вычислить любую степень любого числа (кроме нуля):
Нет только степеней нуля, кроме положительных. Причем все степени, кроме целых, всегда многозначны.
Теперь тригонометрия. Из формулы Эйлера для x и –x получаем формулы для синуса и косинуса, которые распространяем на любые комплексные x:
Поделив одну на другую, получим тангенс:
Теперь обратные тригонометрические функции. Арксинус x=arcsin(z) определяется уравнением z=sin(x) относительно x. Решаем:
Записываем корни квадратного уравнения (в комплексных числах всё так же, через дискриминант, как в школе учили):
Ну, и логарифмируем (с учетом, что 1/i=-i):
Аналогично с арккосинусом:
С тангенсом еще проще. Уравнение tg(x)=z; подставляем, преобразуем, выражаем x:
У арктангенса есть особые точки в ±i. Именно поэтому разложение в ряд в окрестности нуля сходится в круге радиуса 1. Так что тангенс не может равняться i или -i.
Вычислим арктангенс числа 1. Для этого поделим i+1 на i-1, домножив на i+1 сверху и снизу. Снизу получим квадрат модуля, это 2, а сверху, по формуле квадрата суммы, 2i. Под логарифмом стоит i, число с модулем 1 и аргументом π/2. Получаем π/4, как и положено.
Замечу, что никто не мешает использовать эти формулы без всякой ТФКП, если у вас в программной библиотеке (или калькуляторе) логарифм есть, а арккосинуса нету. Главное, аккуратно обработать все вхождения i, чтобы они самоистребились, а не выдали ошибку.
Путеводитель по каналу
Элементарные функции комплексного переменного
Показательная функция комплексного переменного
В действительной области показательная функция вводится обычно в связи с обобщением понятия степени
. В комплексной области функцию требуется определить так, чтобы при
ее свойства совпадали с известными свойствами функции
. Одно из важнейших свойств функции
— представление ее рядом Тейлора: она является суммой сходящегося на всей числовой прямой ряда
.
Учитывая это, рассматриваем ряд и убеждаемся, что он абсолютно сходится при любом
, т.е. во всей комплексной плоскости
определена некоторая функция — сумма этого ряда. Так как при
имеем
, то вводим следующее определение: показательной функцией
в комплексной области называется функция, которая является суммой сходящегося во всей комплексной плоскости ряда
(2.3)
Из определения следует, что показательная функция определена во всей комплексной плоскости. В частности, при , где
— действительное число, имеем
. Используя свойства абсолютно сходящихся рядов (возможность перестановки и группировки членов ряда), ряд можно записать в виде алгебраической суммы двух рядов с действительными членами отделить действительную и мнимую части ряда:
Полученные ряды являются рядами Тейлора для функций и
. В результате имеем равенство
, или, обозначив
через
(2.4)
Формула (2.4) — формула Эйлера была использована для записи комплексного числа в показательной форме.
Функция обладает, очевидно, рядом свойств, справедливость которых установлена в действительной области, т.е. для
.
С другой стороны, в силу расширения множества, следует ожидать, что имеют место и другие свойства, аналога которых в действительной области нет.
К свойствам первой группы нужно отнести прежде всего формулу сложения:
(2.5)
Доказательство формулы сводится, согласно определению показательной функции, к доказательству справедливости при любых и
равенства
которое устанавливается путем перемножения абсолютно сходящихся рядов, записанных слева (см. пример 1.44).
Если в равенстве (2.5) положить — любое комплексное число, то, учитывая тождество
, можно записать
. Это равенство, справедливое при любых значениях
, означает, что функция
является периодической и ее период — чисто мнимое число
. Аналога этому свойству в действительной области нет, функция
— непериодическая.
Так же, как и в действительной области, показательная функция не обращается в нуль ни при каком значении аргумента. Действительно, если предположить противное, что существует
, при котором
, то из тождества
, где
— любое комплексное число, получили бы,
при любом
, что неверно. Однако это единственное исключение, т.е. нуль — единственное значение, которое не может принимать функция
. В отличие от
значение функции в комплексной области может быть отрицательным, например
. Вообще
может принимать любые значения в
, за исключением нуля. Это свойство доказывается просто, если в формуле (2.5) положить
и сравнить равенство
с показательной формой записи комплексного числа. В результате получим, что при фиксированном z , т.е. при фиксированных
и
, модуль числа
равен
, а аргумент равен
, т.е.
(2.6)
Отсюда получаем, что может принимать любые значения
, так как
— любое число.
Пример 2.13. Найти для чисел: а)
; б)
.
Решение
а) Находим модуль числа и аргумент
. После этого можно записать
, то есть
.
Можно записать решение иначе, используя формулу сложения (2.5) и формулу Эйлера (2.4):
Полому , а из показательной формы записи числа
находим
.
б) Представим число в виде произведения , а множитель
в показательной форме:
. Тогда
Поэтому имеем , или
, так как для
данного значения аргумента имеет место ограничение . После этого записываем
.
Пример 2.14. Найти , если
.
Решение
Применяя последовательно формулы (2.5),(2.6), находим
, то есть
.
Поэтому .
Пример 2.15. Показать, что функция является периодической и ее период — действительное число.
Решение
Нужно показать, что существует число такое, что
для любого
. Но из формулы (2.5) имеем
, поэтому число
должно быть таким, чтобы выполнялось равенство
, а это верно при
. Следовательно, период функции
— действительное число
.
Пример 2.16. Доказать, что функция является неоднолистной на множестве
. Найти область однолистности.
Решение
Неоднолистность функции следует из определения, так как существуют не равные значения аргумента, такие, что в них совпадают значения функции. Например, для и
получается
.
Чтобы определить область однолистности, запишем разность
или
.
Значения функции совпадают для тех и
, для которых выполняется равенство
, то есть
.
Однолистным отображение будет в любой области, принадлежащей горизонтальной полосе ширины , в частности полосе
или
(рис. 2.9).
Любая прямая , параллельная действительной оси отображается в луч
, так как из
получаем
. В частности, действительная ось
, то есть
, переходит в луч
— действительную положительную полуось, а прямая
, то есть
, — в луч
, геометрически это — та же действительная полуось
Для однозначности отображения на границе проведем разрез по лучу. При этом точкам прямой будут соответствовать точки нижнего “берега” оси
, а точкам прямой
точки верхнего “берега”.
Такой же результат получим и для следующей полосы . Она отображается также в плоскость с разрезом
.
Вообще любая полоса с помощью функции
переходит в плоскость с разрезом по действительной положительной полуоси.
Нарушенную разрезом непрерывность отображения можно восстановить, построением римановой поверхности функции по такому же принципу как сделано для
.
Полученный результат (см. решение примера 2.16) запишем в виде утверждения: функция взаимно однозначно отображает:
1) любую полосу — в плоскость с разрезом по лучу
;
2) полосу в плоскость с разрезом по действительной отрицательной полуоси;
3) полосу во всю комплексную плоскость с разрезом по действительной положительной полуоси.
Тригонометрические и гиперболические комплексные функции
Функции вводятся аналогично показательной функции — как суммы соответствующих абсолютно сходящихся во всей комплексной плоскости рядов:
(2.7)
(2.8)
На основе этих функций определяются и другие тригонометрические и гиперболические:
Из определений следует, что функции являются четными, а остальные — нечетными.
Сравнивая формулы (2.7) и (2.8) с формулой (2.3) — определением функции , получаем следующие формулы, справедливые при любом
(2.9)
(2.10)
Формулы (2.9) и (2.10) — формулы Эйлера; они связывают тригонометрические и гиперболические функции с показательной. Формула (2.9) при , где
— действительная переменная, рассмотрена выше (см. формулу (2.4)).
Так как формулы (2.9) и (2.10) верны при любых значениях , то, заменяя
на
и учитывая, что
и
— нечетные, a
и
— четные функции, можем записать
Комбинируя эти формулы с (2.9) и (2.10), получаем представление тригонометрических и гиперболических функций через показательную:
(2.11)
(2.12)
Эти формулы позволяют использовать при исследовании гиперболических и тригонометрических функций в комплексной области свойства показательной функции и не обращаться к определениям (2.7),(2.8), т.е. не рассматривать более сложные операции — действия с рядами.
Так, с помощью (2.11) и (2.12) устанавливается справедливость таких формул сложения, как
и других формул, в частности формул тригонометрии.
Кроме того, что тригонометрические и гиперболические функции выражаются через , они еще и связаны между собой. Соответствующие формулы получаются из (2.11) и (2.12):
(2.13)
Отсюда, в частности, получаются такие формулы, как
Как и в действительной области, тригонометрические функции и
являются периодическими и их период равен
. Это следует из формул (2.11) (см. пример 2.15). А гиперболические функции, не будучи периодическими в действительной области, в комплексной области являются периодическими, их период, как и у функции
, — мнимое число
(это следует из рассмотрения равенств (2.12)).
Замечательным свойством, не имеющим аналога в действительной области, является свойство неограниченности (по модулю) функций и
. Эти функции могут принимать любые значения, в частности большие единицы. Например, для числа
по формуле (2.11) имеем:
.
Можно показать и в общем виде, что для любого числа найдется такое число
, что для всех
, удовлетворяющих условию
, выполняется неравенство
. Для доказательства следует использовать формулы (2.11).
Пример 2.17. Найти и
для чисел: а)
; б)
.
Решение
а) Используем формулу (2.13): , поэтому
, а так как
, то
и, следовательно,
.
б) Учитывая равенство , используем, как и выше, формулу (2.13):
Поэтому и, следовательно,
.
Пример 2.18. Найти , если a)
; б)
.
Решение
Для решения используем формулу сложения, обозначая , а также формулу (2.13).
а) Решим первый пример:
поэтому .
б) Решим второй пример:
поэтому .
Для решения можно использовать формулу сложения непосредственно для гиперболической функции:
Пример 2.19. Найти модуль и аргумент числа , если a)
; 6)
.
Решение
а) Используем определение функции и формулу (2.13):
поэтому .
б) Представим число в виде произведения двух чисел:
и найдем модуль и аргумент каждого. Для числа имеем
. Число
является действительным, причем отрицательным, так как
Поэтому . Окончательно, используя правило умножения комплексных чисел в тригонометрической форме, получаем
Пример 2.20. Найти мнимую часть числа , где
— тот корень уравнения
, который расположен в третьей четверти.
Решение
Корнями уравнения , или
, являются четыре комплексных числа, которые могут быть найдены по правилу извлечения корня из комплексного числа:
Для того чтобы отобрать корень, которому соответствует точка в третьей четверти, нужно взять . Искомым корнем будет число
, или в алгебраической форме
.
Вычислим теперь или, что то же,
. Можно перейти к показательной функции по формуле (2.12) или использовать формулу сложения для гиперболической функции и формулу (2.13):
Получаем ответ: .
Комплексный логарифм
Понятие функции, обратной показательной функции, как и в действительной области, связано с понятием логарифма числа.
Логарифмом комплексного числа называется число
такое, что справедливо равенство
; обозначается
. Таким образом,
.
Для нахождения логарифма числа , т.е. для нахождения действительной и мнимой частей числа
, запишем число
в показательной форме, и число
будем искать в алгебраической форме:
.
Тогда равенство или
есть равенство чисел, записанных в показательной форме, и из него находим
и
, а именно
, то есть
. Для искомого числа
получаем выражение:
, где
.
Из этого следует, что логарифм комплексного числа определяется неоднозначно; полученное выражение определяет множество значений логарифма данного числа ; обозначается
(2.14)
Для каждого фиксированного значения получаем определенное число — значение логарифма числа
; при
оно называется главным значением логарифма:
(2.15)
Пример 2.21. Найти — главные значения и
для следующих чисел:
а) ; б)
; в)
.
Решение
а) Находим модуль и аргумент числа . По формулам (2.14) и (2.15) получаем:
б) Для числа находим модуль и аргумент:
. Поэтому имеем результат:
в) Находим модуль и аргумент числа . Получаем ответ:
Пример 2.22. Найти модуль, аргумент, действительную и мнимую части числа .
Решение
Находим модуль и аргумент числа . По формуле (2.14) получаем
. Поэтому:
Точка расположена в первой четверти, так как
и
. Поэтому
Замечание 2.4. Введение понятия логарифма числа позволяет определить в комплексной области степень с любым комплексным показателем и показательную функцию с любым комплексным основанием
.
При и
, где
— натуральное число, степени
и
рассмотрены выше; при
и
, где
— целое число
, определение к также очевидно.
В общем случае при любом комплексном степень определяется формулой
(2.16)
Аналогично вводится функция с любым комплексным основанием
(2.17)
В силу бесконечной значности логарифма, каждому числу соответствует бесконечное множество значений степени
, определяемой по формуле (2.16), и бесконечное множество чисел, определяемых по формуле (2.17) при
. Среди этих множеств выделяются главные значения, которые соответствуют главным значениям логарифмов.
Пример 2.23. Показать, что выражение принимает только действительные значения.
Решение
Пример 2.24. Найти , где
— корень уравнения
, удовлетворяющий условию
.
Решение
Замечание 2.5. Введение понятия логарифма комплексного числа позволяет решать в комплексной области показательные уравнения. Простейшим таким уравнением является уравнение вида . Решение этого уравнения сводится к нахождению значений выражения
, то есть
.
Пример 2.25. Решить уравнения: a) ; б)
; в)
.
Решение
а) Из равенства по определению логарифма получаем
. Далее, учитывая равенства
, по формуле (2.14) находим
. Уравнение имеет бесчисленное множество решений, которые геометрически изображаются точками, расположенными на расстоянии
друг от друга на прямой
, параллельной мнимой оси. Среди решений есть действительное число
— точка на оси
.
б) Все решения уравнения получаются, как значения выражения , то есть
.
в) Из равенства получаем
. Находим модуль и аргумент числа
. Множество решений уравнения описывается равенством
В случаях “б” и “в” уравнения не имеют действительных решений, так как ни при каких значениях среди полученных множеств нет действительных чисел. Геометрически же соответствующие точки расположены на той же прямой
, что и в случае “а”, на расстоянии
друг от друга; начальными значениями (при
) для них являются
и
. Решения уравнений “б” и “в” изображены на рис. 2.10 (по осям масштабы разные).
Пример 2.26. Найти из уравнения
.
Решение
Используя формулу (2.12), сведем задачу к решению показательного уравнения . Получим квадратное уравнение относительно функции
, корнями которого являются числа
. Далее нужно найти значения выражений
. Для этого используем формулу (2.14):
Получили два множества решений исходного уравнения:
Геометрически — это точки, лежащие на прямых
параллельных мнимой оси; расстояние между любыми соседними точками на каждой прямой равны ; начальные значения (при
):
или
и
(рис. 2.11).
Логарифмическая функция комплексного переменного
Логарифмическая функция вводится, как функция, обратная к показательной, т.е. как решение уравнения , значения функции при любом
определяются по формуле (2.14).
Функция, очевидно, многозначная и отображает плоскость на каждую из полос:
, или
.
В плоскости с разрезом по лучу возможно выделение однозначных ветвей, каждая из которых однозначно отображает эту плоскость на одну из полос
, в частности функция
— главное значение логарифмической функции отображает плоскость на полосу
(см. рис. 2.9). В плоскости с разрезом
также возможно выделение однозначных ветвей, каждая из которых однозначно отображает эту плоскость на одну из полос
, в частности функция
— главное значение логарифмической функции отображает плоскость на полосу
. Выделение ветви определяется заданием значения функции в одной из точек области.
Пример 2.27. Найти решение уравнения при условии
.
Решение
Обратные тригонометрические и гиперболические комплексные функции
Функции, обратные к тригонометрическим и гиперболическим функциям, определяются, как и в действительной области.
Например, обратным тригонометрическим синусом числа называется число
такое, что выполняется равенство
. Отображение обозначается, как и в действительной области,
.
Аналогично определяются и другие тригонометрические функции комплексного аргумента:
Из определений могут быть получены формулы для нахождения числа по заданному числу
.
Рассмотрим эту задачу на примере нахождения . По определению имеем
. Заменим
по формуле Эйлера (2.11), и из соотношения
или
, т.е. квадратного уравнения относительно
, находим
. Перед радикалом записан только знак плюс, так как в комплексной области
— двузначное выражение. Далее, используя определение логарифма, находим
Для каждого числа получаем бесконечное множество значений для
в силу двузначности
и бесконечной значности логарифма. Все это множество значений
обозначается
. Окончательный результат:
(2.18)
Формулы, аналогичные (2.18), могут быть получены и для других функций:
Все эти формулы, как и (2.18), дают бесконечнозначные выражения — определяют многозначные функции. Выделяя однозначную ветвь выражения , можно получить однозначные функции в каждом случае.
Большого практического значения эти формулы, как и (2.18), не имеют. Для нахождения значений обратных тригонометрических и обратных гиперболических функций можно использовать их определения и формулы связи тригонометрических и гиперболических функций с показательной функцией (формулы Эйлера (2.11)-(2.12)), т.е. применять метод, с помощью которого выведена формула (2.18). Этим методом решен пример 2.26, где найдено значение .
Замечание 2.6. Рассмотрим уравнения, содержащие тригонометрические и гиперболические функции. Простейшими из них являются уравнения:
Решение их, согласно определению, сводится к нахождению обратных тригонометрических и обратных гиперболических функций.
Пример 2.28. Решить уравнение .
Решение
Множество решений уравнения определяется выражением , или с помощью формулы (2.18):
. Выражение в скобках, в силу двузначности корня, записывается в виде
и
. Для каждого из этих чисел по сформулированному выше правилу находим логарифм:
а) для числа имеем
, поэтому
б) для числа имеем
, поэтому
Получаем два множества решений уравнения:
Геометрически — это множество точек, расположенных на расстоянии друг от друга на прямых, параллельных мнимой оси (рис. 2.12):
и
,
Действительных решений уравнение не имеет, так как ни при каком значении среди чисел
нет действительных. Это соответствует известному свойству функции
в действительной области
.
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.
Элементарные функции комплексного переменного.
Рассмотрим некоторые
элементарные функции комплексного
переменного, а именно, показательную
функцию
,
логарифмическую функцию
,
тригонометрические –
,
,
,
и,
обратные тригонометрические функции
,
,
,
,а
также гиперболические функции
,
,
,
и обратные к ним функции
,
,
,
).
1. Показательная функция комплексного переменного.
Показательная
функция
определяется как
или
(12)
Очевидны следующие
свойства функции
.
1)
;
2)
.
Так как
,
то показательная функция
– периодическая функция периода
.
Пример 24.
Найти значение функции
в точке
и указать координаты точки комплексной
плоскости, соответствующей найденному
значению.
Решение.
,
откуда координаты искомой точки
.●
2. Логарифмическая функция комплексного переменного.
Логарифмическая
функция
определяется как обратная к показательной.
Определение.
Натуральным логарифмом
(
)
комплексного числа
называется показатель степени
,
в которую необходимо возвести число
,
чтобы получить число
.
Пусть
,
,
где
.
Тогда
,
откуда
,
,
,
,
.
,
где
(13)
Определение.
Выражение
называется главным
значением натурального логарифма числа
.
Из формулы (13)
следует, что действительная часть
натурального логарифма определяется
однозначно, а мнимая часть содержит
неопределенное слагаемое, кратное
,
т. е. существует бесконечное множество
значений натурального логарифма любого
числа
,
отличного от нуля.
Логарифм нуля не
существует.
Пример 25.
Вычислить
и
.
Решение.
Найдем модуль и аргумент числа
.
.
Так
как действительная и мнимая части числа
отрицательны, то главное значение
аргумента равно
.
Тогда
–
главное
значение логарифма данного числа и
.●
Пример 26.
Вычислить
и
.
Решение.
Модуль числа
равен
,
а главное значение аргумента равно
,
следовательно,
,
.●
С помощью логарифма
может быть определена любая степень
комплексного числа.
Пример 27.
Вычислить
.
Решение.
,
где
.
Обратите внимание,
что
-действительные числа.●
3. Тригонометрические функции комплексного переменного.
Тригонометрические
функции синус и косинус определены
ранее (см. формулы (6)).
Определение.
Тригонометрическая функция синус
комплексного переменного определяется
как
,
где
,
(14)
функция косинус
как
,
где
, (15)
функция тангенс
как
,
где
, (16)
функция котангенс
как
,
где
. (17)
Пример 28.
Вычислить
.
Решение.
.●
Пример 29.
Вычислить
.
Пример
28.
Вычислить
.
Решение.
●
Пример 30.
Доказать, что
.
Решение.
.●
Замечание.
Для тригонометрических функций
комплексной переменной имеют место и
другие тождества, справедливые для
тригонометрических функций действительного
аргумента
(см. пример 31).
Пример 31.
Доказать, что
.
Решение.
.
Пример 32.
Решить уравнение
.
Решение.
,
откуда
,
и
.
Решая квадратное
относительно
,
имеем
или
,
откуда
и
.
Ответ:
Замечание.
Числа
при
имеют одинаковые мнимые части, поэтому
они лежат на прямой, параллельной
действительной оси и отстоящей от нее
на расстоянии
.●
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Основные элементарные функции комплексного переменного
Определим основные элементарные функции комплексного переменного 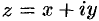
Показательная функция
Показательная функция 
Положив в этом равенстве 
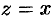
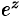
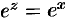
Показательная функция 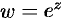
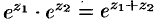
Аналогично можно убедиться в справедливости свойств: 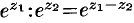
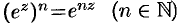
Учитывая, что 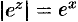
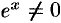
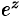
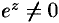
Исходя из определения (74.1), легко убедиться, что
выражение 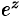
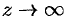
Положив в равенстве (74.1) 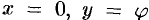
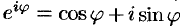
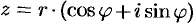
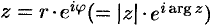
Показательная функция комплексного переменного обладает и специфическим свойством: она является периодической с мнимым основным периодом 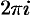
Действительно,
т.е. 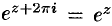
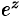
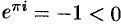
Логарифмическая функция
Эта функция определяется как функция, обратная показательной: число 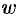
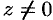
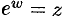
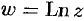
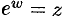
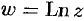

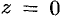
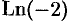
Положив 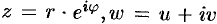
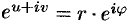
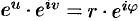
Следовательно,
т.е. 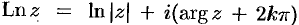
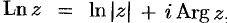
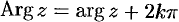
Формула (74.2) показывает, что логарифмическая функция комплексного переменного имеет бесчисленное множество значений, т. е. 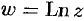
Однозначную ветвь этой функции можно выделить, подставив в формулу (74.2) определенное значение 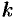
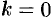
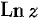
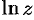
Если 
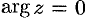
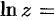
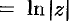
Формулу (74.2) можно переписать так: 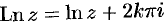
Из формулы (74.2) следует, что логарифмическая функция 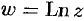
Докажем, например, первое свойство:
Пример №74.2.
Вычислить 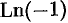
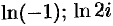
Решение:
Для числа 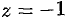
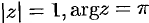
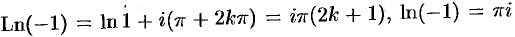
Степенная функция 
Если 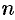
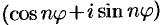
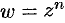
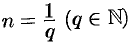
где 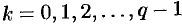
Здесь функция 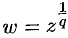
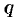
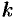
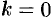
Если 
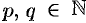
Функция 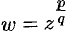
Степенная функция 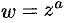
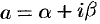
Функция 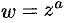
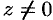
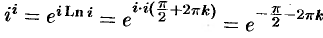
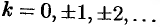
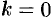
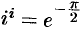
Тригонометрические функции
Тригонометрические функция комплексного аргумента 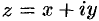
При действительных 
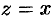
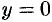
Тригонометрические функции комплексного переменного сохраняют многие свойства тригонометрических функций действительного переменного. В частности,
и т.д. Докажем, например, первое свойство:
Отметим, что тригонометрические функции 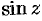
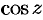

Так, например, 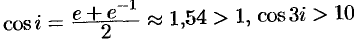
Гиперболические функции
Эти функции определяются равенствами
Легко заметить связь между гиперболическими и тригонометрическими функциями. Заменяя в указанных функциях 
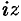
(а также 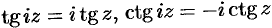
Пользуясь этими равенствами, можно получить ряд формул, связывающих гиперболические функции. Так, заменяя в формуле 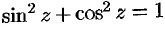
или — 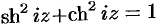

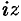

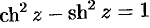
и т.д.
Из определения гиперболических функций следует, что функции 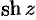
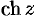
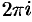
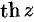
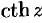
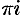
Обратные тригонометрические и гиперболические функции
Число 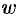

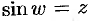
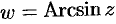
Используя определение синуса, имеем 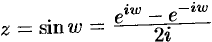
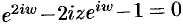
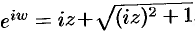
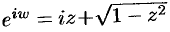
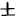
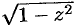
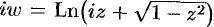
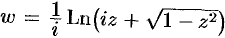
Функция 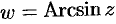
Функции, обратные гиперболическим, обозначаются-соответственно 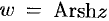
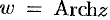
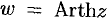
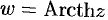
Обратные гиперболические функции имеют следующие выражения:
Все эти функции бесконечнозначны.
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
- Решение задач по высшей математике
Другие темы по высшей математике возможно вам они будут полезны: