пт., 2015-05-22 11:11 — eg_r
Чему равен tg 0? Много раз учил таблицу значений тригонометрических функций, и все впустую. Ну, не могу я ее запомнить. Вот так, каждый раз, ищу ответ в интернете. Даже не знаю, что буду делать на контрольной(((((
пт., 2015-05-22 11:33 — солнце
Не обязательно запоминать всю таблицу. Выучите только табличные значения sinx и cosx, а зная их, tgх и сtgх всегда можно найти по формулам
tgх = sinx/cosx
сtgх = cosx/sinx
- ответить
сб., 2015-05-23 14:02 — belost
Согласен с солнцем, что значения функции тангенс запоминать не нужно. Внимательно посмотрите на табличные значения функций синус и косинус, вы увидите, что они повторяются, в обратном порядке, после 90 градусов, только в косинусе еще знак меняется на минус. Там учить нечего.
- ответить
вс., 2015-05-24 14:51 — vedomur
Тангенс нуля равен нулю, и это можно вычислить по формуле
sin0/cos0= 0/1=0
Функция тангенс не имеет значения, только, если cosх=0, т.е при х= 90+пи
- ответить
ср., 2015-05-27 18:50 — Alenka
А может быть вам будет проще, если запомните, как проходит график функции тангенс? Здесь очень хорошо видно, что tg 0=0. График проходит через начало координат.

- ответить
ср., 2015-05-27 19:34 — Изюмина
Тангенс нуля всегда равен нулю, это легко запомнить.
- ответить
Отправить комментарий

Примеры:
(tg:30^° =frac{1}{sqrt{3}})
(tg:(frac{π}{3})=sqrt{3})
(tg:2=-2,185…)
Содержание:
- Аргумент и значение
Тангенс острого угла
Тангенс числа или любого угла
Знаки по четвертям
Связь с другими функциями
Аргумент и значение тангенса

Аргументом тангенса может быть:
– как число или выражение с Пи: (1,3), (frac{π}{4}), (π), (-frac{π}{3}) и т.п.
– так и угол в градусах: (45^°), (360^°),(-800^°), (1^° ) и т.п.
Для обоих случаев тангенс вычисляется одинаковым способом – либо через значения синуса и косинуса, либо через тригонометрический круг (см. ниже).
Значение тангенса – всегда действительное число (возможно, иррациональное): (1), (sqrt{3}), (-frac{1}{sqrt{3}}), (-0,1543…)
Тангенс острого угла
Тангенс можно определить с помощью прямоугольного треугольника – он равен отношению противолежащего катета к прилежащему.
Пример:
1) Пусть дан угол и нужно определить тагенс этого угла.

2) Достроим на этом угле любой прямоугольный треугольник.

3) Измерив, нужные стороны, можем вычислить тангенс.

Вычисление тангенса числа или любого угла
Для чисел, а также для тупых, развернутых углов и углов больших (360°) тангенс чаще всего определяют с помощью синуса и косинуса, через их отношение:
(tg: t=)(frac{sin:t}{cos:t})
Пример. Вычислите (tg:0).
Решение: Чтобы найти тангенс нуля нужно найти сначала синус и косинус (0). И то, и другое найдем с помощью тригонометрического круга:

Точка (0) на числовой окружности совпадает с (1) на оси косинусов, значит (cos:0=1). Если из точки (0) на числовой окружности провести перпендикуляр к оси синусов, то мы попадем в точку (0), значит (sin:0=0). Получается: (tg:0=)(frac{sin:0}{cos:0}) (=)(frac{0}{1})(=0).
Ответ: (0).
Пример. Вычислите (tg:(-765^circ)).
Решение: (tg: (-765^circ)=)(frac{sin:(-765^circ)}{cos:(-765^circ)})
Что бы вычислить синус и косинус (-765^°). Отложим (-765^°) на тригонометрическом круге. Для этого надо повернуть в отрицательную сторону на (720^°) , а потом еще на (45^°).

(sin(-765^°)=-frac{sqrt{2}}{2});
(cos(-765^°)=frac{sqrt{2}}{2}) ;
получается (tg(-765^°)= -frac{sqrt{2}}{2} ∶ frac{sqrt{2}}{2}=-1).
Ответ: (-1).
Пример. Вычислите (tg:frac{π}{3}).
Решение: (tg: frac{π}{3}=)(frac{sin:frac{π}{3}}{cos:frac{π}{3}}). Опять находим синус пи на 3 и косинус пи на 3 (хоть с помощью тригонометрического круга, хоть по таблице):
(sin(frac{π}{3})=frac{sqrt{3}}{2});
(cos(frac{π}{3})=frac{1}{2}) ;
получается (tg(frac{π}{3})= frac{sqrt{3}}{2} ∶ frac{1}{2}= frac{sqrt{3}}{2} cdot frac{2}{1}=sqrt{3}).
Ответ: (sqrt{3}).
Однако можно определять тангенс и напрямую через тригонометрический круг – для этого надо на нем построить дополнительную ось:
Прямая проходящая через начало отсчета на числовой окружности и параллельная оси ординат (синусов) называется осью тангенсов. Направление оси тангенсов и оси синусов совпадает.

Ось тангенсов – это фактически копия оси синусов, только сдвинутая. Поэтому все числа на ней расставляются так же как на оси синусов.
Чтобы определить тангенс с помощью числовой окружности, нужно:
1) Отметить соответствующую аргументу тангенса точку на числовой окружности.
2) Провести прямую через эту точку и начало координат и продлить её до оси тангенсов.
3) Найти координату пересечения этой прямой и оси тангенсов.
Пример. Вычислите (tg:frac{π}{4}).
Решение:
1)Отмечаем (frac{π}{4}) на окружности.

2) Проводим через данную точку и начало координат прямую.

3) В данном случае координату долго искать не придется – она равняется (1).
Ответ: (1).
Пример. Вычислите (tg: 45°) и (tg: (-240°)).
Решение:
Для угла (45°) ((∠KOA)) тангенс будет равен (1), потому что именно в таком значении сторона угла, проходящая через начало координат и точку (A), пересекает ось тангесов. А для угла (-240°) ((∠KOB)) тангенс равен (-sqrt{3}) (приблизительно (-1,73)).

Значения для других часто встречающихся в практике углов смотри в тригонометрической таблице.
В отличие от синуса и косинуса значение тангенса не ограничено и лежит в пределах от (-∞) до (+∞), то есть может быть любым.

При этом тангенс не определен для:
1) всех точек (A) (значение в Пи: …(-)(frac{7π}{2}),(-)(frac{3π}{2}),(frac{π}{2}), (frac{5π}{2}), (frac{9π}{2}) …; и значение в градусах: …(-630°),(-270°),(90°),(450°),(810°)…)
2) всех точек (B) (значение в Пи: …(-)(frac{9π}{2}),(-)(frac{5π}{2}),(-)(frac{π}{2}), (frac{3π}{2}), (frac{7π}{2}) …; и значение в градусах: …(-810°),(-450°),(-90°),(270°)…) .
Так происходит потому, что прямая проходящая через начало координат и любую из этих точек никогда не пересечет ось тангенсов, т.к. будет идти параллельно ей. Поэтому в этих точках тангенс – НЕ СУЩЕСТВУЕТ (для всех остальных значений тангенс может быть найден).
Из-за этого при решении тригонометрических уравнений и неравенств с тангенсом необходимо учитывать ограничения на ОДЗ.
Знаки по четвертям
С помощью оси тангенсов легко определить знаки по четвертям тригонометрической окружности. Для этого надо взять любую точку на четверти и определить знак тангенса для нее описанным выше способом. У всей четверти знак будет такой же.
Для примера на рисунке нанесены две зеленые точки в I и III четвертях. Для них значение тангенса положительно (зеленые пунктирные прямые приходят в положительную часть оси), значит и для любой точки из I и III четверти значение тангенса будет положительно (знак плюс).
С двумя фиолетовыми точками в II и IV четвертях – аналогично, но с минусом.

Связь с другими тригонометрическими функциями:
– косинусом того же угла: формулой (1+tg^2x=)(frac{1}{cos^2x})
– синусом и косинусом того же угла: (tg:x=)(frac{sin:x}{cos:x})
– котангенсом того же угла: формулой (ctg:x=)(frac{1}{tg:x})
Другие наиболее часто применяемые формулы смотри здесь.
Смотрите также:
Формулы приведения
Значения тангенса и котангенса на тригонометрическом круге
В прошлой статье мы познакомились с тригонометрическим кругом и научились находить значения синуса и косинуса основных углов.
Как же быть с тангенсом и котангенсом ? Об этом и поговорим сегодня.
Где же на тригонометрическом круге оси тангенсов и котангенсов?
Ось тангенсов параллельна оси синусов (имеет тоже направление, что ось синусов) и проходит через точку (1; 0).
Ось котангенсов параллельна оси косинусов (имеет тоже направление, что ось косинусов) и проходит через точку (0; 1).
На каждой из осей располагается вот такая цепочка основных значений тангенса и котангенса: Почему так?
Я думаю, вы легко сообразите и сами. 🙂 Можно по-разному рассуждать. Можете, например, использовать тот факт, что и
Собственно, картинка за себя сама говорит.
Если не очень все же понятно, разберем примеры:
Пример 1.
Вычислить
Находим на круге . Эту точку соединяем с точкой (0;0) лучом (начало – точка (0;0)) и смотрим, где этот луч пересекает ось тангенсов. Видим, что
Ответ:
Пример 2.
Вычислить
Находим на круге . Точку (0;0) соединяем с указанной точкой лучом. И видим, что луч никогда не пересечет ось тангенсов.
не существует.
Ответ: не существует
Пример 3.
Вычислить
Находим на круге точку (это та же точка, что и ) и от нее по часовой стрелке (знак минус!) откладываем (). Куда попадаем? Мы окажемся в точке, что на круге у нас (см. рис.) названа как . Эту точку соединяем с точкой (0;0) лучом. Вышли на ось тангенсов в значение .
Так значит,
Ответ:
Пример 4.
Вычислить
Поэтому от точки (именно там будет ) откладываем против часовой стрелки .
Выходим на ось котангенсов, получаем, что
Ответ:
Пример 5.
Вычислить
Находим на круге . Эту точку соединяем с точкой (0; 0). Выходим на ось котангенсов. Видим, что
Ответ:
Теперь, умея находить по тригонометрическому кругу значения тригонометрических функций (а я надеюсь, что статья, где мы начинали знакомство с кругом и учились вычислять значения синусов и косинусов, вами прочитана…), вы можете пройт и тест по теме «Нахождение значений косинуса, синуса, тангенса и котангенса различных углов».
Чтобы не потерять страничку, вы можете сохранить ее у себя:
Таблица ТАНГЕНСОВ для углов от 0° до 360° градусов
ТАНГЕНС (Tg α) острого угла в прямоугольном треугольнике равняется отношение противолежащего катета к прилежащему катету.
| α (радианы) | 0 | π/6 | π/4 | π/3 | π/2 | π | √3π/2 | 2π |
|---|---|---|---|---|---|---|---|---|
| α (градусы) | 0° | 30° | 45° | 60° | 90° | 180° | 270° | 360° |
| tg α (Тангенс) | 0 | 1/√3 | 1 | √3 | — | 0 | — | 0 |
Малая таблица значений тригонометрических функций (в радианах и градусах)
| Угол в градусах | tg (Тангенс) |
|---|---|
| 0° | 0 |
| 1° | 0.0175 |
| 2° | 0.0349 |
| 3° | 0.0524 |
| 4° | 0.0699 |
| 5° | 0.0875 |
| 6° | 0.1051 |
| 7° | 0.1228 |
| 8° | 0.1405 |
| 9° | 0.1584 |
| 10° | 0.1763 |
| 11° | 0.1944 |
| 12° | 0.2126 |
| 13° | 0.2309 |
| 14° | 0.2493 |
| 15° | 0.2679 |
| 16° | 0.2867 |
| 17° | 0.3057 |
| 18° | 0.3249 |
| 19° | 0.3443 |
| 20° | 0.364 |
| 21° | 0.3839 |
| 22° | 0.404 |
| 23° | 0.4245 |
| 24° | 0.4452 |
| 25° | 0.4663 |
| 26° | 0.4877 |
| 27° | 0.5095 |
| 28° | 0.5317 |
| 29° | 0.5543 |
| 30° | 0.5774 |
| 31° | 0.6009 |
| 32° | 0.6249 |
| 33° | 0.6494 |
| 34° | 0.6745 |
| 35° | 0.7002 |
| 36° | 0.7265 |
| 37° | 0.7536 |
| 38° | 0.7813 |
| 39° | 0.8098 |
| 40° | 0.8391 |
| 41° | 0.8693 |
| 42° | 0.9004 |
| 43° | 0.9325 |
| 44° | 0.9657 |
| 45° | 1 |
| 46° | 1.0355 |
| 47° | 1.0724 |
| 48° | 1.1106 |
| 49° | 1.1504 |
| 50° | 1.1918 |
| 51° | 1.2349 |
| 52° | 1.2799 |
| 53° | 1.327 |
| 54° | 1.3764 |
| 55° | 1.4281 |
| 56° | 1.4826 |
| 57° | 1.5399 |
| 58° | 1.6003 |
| 59° | 1.6643 |
| 60° | 1.7321 |
| 61° | 1.804 |
| 62° | 1.8807 |
| 63° | 1.9626 |
| 64° | 2.0503 |
| 65° | 2.1445 |
| 66° | 2.246 |
| 67° | 2.3559 |
| 68° | 2.4751 |
| 69° | 2.6051 |
| 70° | 2.7475 |
| 71° | 2.9042 |
| 72° | 3.0777 |
| 73° | 3.2709 |
| 74° | 3.4874 |
| 75° | 3.7321 |
| 76° | 4.0108 |
| 77° | 4.3315 |
| 78° | 4.7046 |
| 79° | 5.1446 |
| 80° | 5.6713 |
| 81° | 6.3138 |
| 82° | 7.1154 |
| 83° | 8.1443 |
| 84° | 9.5144 |
| 85° | 11.4301 |
| 86° | 14.3007 |
| 87° | 19.0811 |
| 88° | 28.6363 |
| 89° | 57.29 |
| 90° | ∞ |
Полная таблица тангенсов для углов от 0° до 360°
| Угол | tg (Тангенс) |
|---|---|
| 91° | -57.29 |
| 92° | -28.6363 |
| 93° | -19.0811 |
| 94° | -14.3007 |
| 95° | -11.4301 |
| 96° | -9.5144 |
| 97° | -8.1443 |
| 98° | -7.1154 |
| 99° | -6.3138 |
| 100° | -5.6713 |
| 101° | -5.1446 |
| 102° | -4.7046 |
| 103° | -4.3315 |
| 104° | -4.0108 |
| 105° | -3.7321 |
| 106° | -3.4874 |
| 107° | -3.2709 |
| 108° | -3.0777 |
| 109° | -2.9042 |
| 110° | -2.7475 |
| 111° | -2.6051 |
| 112° | -2.4751 |
| 113° | -2.3559 |
| 114° | -2.246 |
| 115° | -2.1445 |
| 116° | -2.0503 |
| 117° | -1.9626 |
| 118° | -1.8807 |
| 119° | -1.804 |
| 120° | -1.7321 |
| 121° | -1.6643 |
| 122° | -1.6003 |
| 123° | -1.5399 |
| 124° | -1.4826 |
| 125° | -1.4281 |
| 126° | -1.3764 |
| 127° | -1.327 |
| 128° | -1.2799 |
| 129° | -1.2349 |
| 130° | -1.1918 |
| 131° | -1.1504 |
| 132° | -1.1106 |
| 133° | -1.0724 |
| 134° | -1.0355 |
| 135° | -1 |
| 136° | -0.9657 |
| 137° | -0.9325 |
| 138° | -0.9004 |
| 139° | -0.8693 |
| 140° | -0.8391 |
| 141° | -0.8098 |
| 142° | -0.7813 |
| 143° | -0.7536 |
| 144° | -0.7265 |
| 145° | -0.7002 |
| 146° | -0.6745 |
| 147° | -0.6494 |
| 148° | -0.6249 |
| 149° | -0.6009 |
| 150° | -0.5774 |
| 151° | -0.5543 |
| 152° | -0.5317 |
| 153° | -0.5095 |
| 154° | -0.4877 |
| 155° | -0.4663 |
| 156° | -0.4452 |
| 157° | -0.4245 |
| 158° | -0.404 |
| 159° | -0.3839 |
| 160° | -0.364 |
| 161° | -0.3443 |
| 162° | -0.3249 |
| 163° | -0.3057 |
| 164° | -0.2867 |
| 165° | -0.2679 |
| 166° | -0.2493 |
| 167° | -0.2309 |
| 168° | -0.2126 |
| 169° | -0.1944 |
| 170° | -0.1763 |
| 171° | -0.1584 |
| 172° | -0.1405 |
| 173° | -0.1228 |
| 174° | -0.1051 |
| 175° | -0.0875 |
| 176° | -0.0699 |
| 177° | -0.0524 |
| 178° | -0.0349 |
| 179° | -0.0175 |
| 180° | 0 |
Таблица тангенсов для углов от 91° до 180°
| Угол | tg (Тангенс) |
|---|---|
| 181° | 0.0175 |
| 182° | 0.0349 |
| 183° | 0.0524 |
| 184° | 0.0699 |
| 185° | 0.0875 |
| 186° | 0.1051 |
| 187° | 0.1228 |
| 188° | 0.1405 |
| 189° | 0.1584 |
| 190° | 0.1763 |
| 191° | 0.1944 |
| 192° | 0.2126 |
| 193° | 0.2309 |
| 194° | 0.2493 |
| 195° | 0.2679 |
| 196° | 0.2867 |
| 197° | 0.3057 |
| 198° | 0.3249 |
| 199° | 0.3443 |
| 200° | 0.364 |
| 201° | 0.3839 |
| 202° | 0.404 |
| 203° | 0.4245 |
| 204° | 0.4452 |
| 205° | 0.4663 |
| 206° | 0.4877 |
| 207° | 0.5095 |
| 208° | 0.5317 |
| 209° | 0.5543 |
| 210° | 0.5774 |
| 211° | 0.6009 |
| 212° | 0.6249 |
| 213° | 0.6494 |
| 214° | 0.6745 |
| 215° | 0.7002 |
| 216° | 0.7265 |
| 217° | 0.7536 |
| 218° | 0.7813 |
| 219° | 0.8098 |
| 220° | 0.8391 |
| 221° | 0.8693 |
| 222° | 0.9004 |
| 223° | 0.9325 |
| 224° | 0.9657 |
| 225° | 1 |
| 226° | 1.0355 |
| 227° | 1.0724 |
| 228° | 1.1106 |
| 229° | 1.1504 |
| 230° | 1.1918 |
| 231° | 1.2349 |
| 232° | 1.2799 |
| 233° | 1.327 |
| 234° | 1.3764 |
| 235° | 1.4281 |
| 236° | 1.4826 |
| 237° | 1.5399 |
| 238° | 1.6003 |
| 239° | 1.6643 |
| 240° | 1.7321 |
| 241° | 1.804 |
| 242° | 1.8807 |
| 243° | 1.9626 |
| 244° | 2.0503 |
| 245° | 2.1445 |
| 246° | 2.246 |
| 247° | 2.3559 |
| 248° | 2.4751 |
| 249° | 2.6051 |
| 250° | 2.7475 |
| 251° | 2.9042 |
| 252° | 3.0777 |
| 253° | 3.2709 |
| 254° | 3.4874 |
| 255° | 3.7321 |
| 256° | 4.0108 |
| 257° | 4.3315 |
| 258° | 4.7046 |
| 259° | 5.1446 |
| 260° | 5.6713 |
| 261° | 6.3138 |
| 262° | 7.1154 |
| 263° | 8.1443 |
| 264° | 9.5144 |
| 265° | 11.4301 |
| 266° | 14.3007 |
| 267° | 19.0811 |
| 268° | 28.6363 |
| 269° | 57.29 |
| 270° | ∞ |
Таблица тангенсов для углов от 181° до 270°
| Угол | tg (Тангенс) |
|---|---|
| 271° | -57.29 |
| 272° | -28.6363 |
| 273° | -19.0811 |
| 274° | -14.3007 |
| 275° | -11.4301 |
| 276° | -9.5144 |
| 277° | -8.1443 |
| 278° | -7.1154 |
| 279° | -6.3138 |
| 280° | -5.6713 |
| 281° | -5.1446 |
| 282° | -4.7046 |
| 283° | -4.3315 |
| 284° | -4.0108 |
| 285° | -3.7321 |
| 286° | -3.4874 |
| 287° | -3.2709 |
| 288° | -3.0777 |
| 289° | -2.9042 |
| 290° | -2.7475 |
| 291° | -2.6051 |
| 292° | -2.4751 |
| 293° | -2.3559 |
| 294° | -2.246 |
| 295° | -2.1445 |
| 296° | -2.0503 |
| 297° | -1.9626 |
| 298° | -1.8807 |
| 299° | -1.804 |
| 300° | -1.7321 |
| 301° | -1.6643 |
| 302° | -1.6003 |
| 303° | -1.5399 |
| 304° | -1.4826 |
| 305° | -1.4281 |
| 306° | -1.3764 |
| 307° | -1.327 |
| 308° | -1.2799 |
| 309° | -1.2349 |
| 310° | -1.1918 |
| 311° | -1.1504 |
| 312° | -1.1106 |
| 313° | -1.0724 |
| 314° | -1.0355 |
| 315° | -1 |
| 316° | -0.9657 |
| 317° | -0.9325 |
| 318° | -0.9004 |
| 319° | -0.8693 |
| 320° | -0.8391 |
| 321° | -0.8098 |
| 322° | -0.7813 |
| 323° | -0.7536 |
| 324° | -0.7265 |
| 325° | -0.7002 |
| 326° | -0.6745 |
| 327° | -0.6494 |
| 328° | -0.6249 |
| 329° | -0.6009 |
| 330° | -0.5774 |
| 331° | -0.5543 |
| 332° | -0.5317 |
| 333° | -0.5095 |
| 334° | -0.4877 |
| 335° | -0.4663 |
| 336° | -0.4452 |
| 337° | -0.4245 |
| 338° | -0.404 |
| 339° | -0.3839 |
| 340° | -0.364 |
| 341° | -0.3443 |
| 342° | -0.3249 |
| 343° | -0.3057 |
| 344° | -0.2867 |
| 345° | -0.2679 |
| 346° | -0.2493 |
| 347° | -0.2309 |
| 348° | -0.2126 |
| 349° | -0.1944 |
| 350° | -0.1763 |
| 351° | -0.1584 |
| 352° | -0.1405 |
| 353° | -0.1228 |
| 354° | -0.1051 |
| 355° | -0.0875 |
| 356° | -0.0699 |
| 357° | -0.0524 |
| 358° | -0.0349 |
| 359° | -0.0175 |
| 360° | 0 |
Таблица тангенсов для углов от 271° до 360°
Как распечатать таблицу? Левой кнопкой на компьютерной мишке выделите нужную часть таблицы, на выделенном фоне нажмите правую кнопку мишки и в появившемся меню перейдете в пункт «Печать».
Чему равен тангенс 30? …
— Ищем в таблице соответствующее значение. Правильный ответ: 0.5774
Тангенс
Тангенс – одна из тригонометрических функций. Как и для всех других функций, значение тангенса определяется для конкретного угла или числа (в этом случае используют числовую окружность.
Аргумент и значение тангенса
Аргументом тангенса может быть:
– как число или выражение с Пи: (1,3), (frac<π><4>), (π), (-frac<π><3>) и т.п.
– так и угол в градусах: (45^°), (360^°),(-800^°), (1^° ) и т.п.
Для обоих случаев тангенс вычисляется одинаковым способом – либо через значения синуса и косинуса, либо через тригонометрический круг (см. ниже).
Тангенс острого угла
Тангенс можно определить с помощью прямоугольного треугольника – он равен отношению противолежащего катета к прилежащему.
1) Пусть дан угол и нужно определить тагенс этого угла.
2) Достроим на этом угле любой прямоугольный треугольник.
3) Измерив, нужные стороны, можем вычислить тангенс.
Вычисление тангенса числа или любого угла
Для чисел, а также для тупых, развернутых углов и углов больших (360°) тангенс чаще всего определяют с помощью синуса и косинуса, через их отношение:
Пример. Вычислите (tg:0).
Решение: Чтобы найти тангенс нуля нужно найти сначала синус и косинус (0). И то, и другое найдем с помощью тригонометрического круга :
Точка (0) на числовой окружности совпадает с (1) на оси косинусов, значит (cos:0=1). Если из точки (0) на числовой окружности провести перпендикуляр к оси синусов, то мы попадем в точку (0), значит (sin:0=0). Получается: (tg:0=) (frac) (=) (frac<0><1>) (=0).
Пример. Вычислите (tg:(-765^circ)).
Решение: (tg: (-765^circ)=) (frac)
Что бы вычислить синус и косинус (-765^°). Отложим (-765^°) на тригонометрическом круге. Для этого надо повернуть в отрицательную сторону на (720^°) , а потом еще на (45^°).
Однако можно определять тангенс и напрямую через тригонометрический круг – для этого надо на нем построить дополнительную ось:
Прямая проходящая через начало отсчета на числовой окружности и параллельная оси ординат (синусов) называется осью тангенсов. Направление оси тангенсов и оси синусов совпадает.
Ось тангенсов – это фактически копия оси синусов, только сдвинутая. Поэтому все числа на ней расставляются так же как на оси синусов.
Чтобы определить тангенс с помощью числовой окружности, нужно:
1) Отметить соответствующую аргументу тангенса точку на числовой окружности.
2) Провести прямую через эту точку и начало координат и продлить её до оси тангенсов.
3) Найти координату пересечения этой прямой и оси тангенсов.
2) Проводим через данную точку и начало координат прямую.
3) В данном случае координату долго искать не придется – она равняется (1).
Пример. Вычислите (tg: 45°) и (tg: (-240°)).
Решение:
Для угла (45°) ((∠KOA)) тангенс будет равен (1), потому что именно в таком значении сторона угла, проходящая через начало координат и точку (A), пересекает ось тангесов. А для угла (-240°) ((∠KOB)) тангенс равен (-sqrt<3>) (приблизительно (-1,73)).
Значения для других часто встречающихся в практике углов смотри в тригонометрической таблице.
В отличие от синуса и косинуса значение тангенса не ограничено и лежит в пределах от (-∞) до (+∞), то есть может быть любым.
При этом тангенс не определен для:
1) всех точек (A) (значение в Пи: …(-) (frac<7π><2>) ,(-) (frac<3π><2>) , (frac<π><2>) , (frac<5π><2>) , (frac<9π><2>) …; и значение в градусах: …(-630°),(-270°),(90°),(450°),(810°)…)
2) всех точек (B) (значение в Пи: …(-) (frac<9π><2>) ,(-) (frac<5π><2>) ,(-) (frac<π><2>) , (frac<3π><2>) , (frac<7π><2>) …; и значение в градусах: …(-810°),(-450°),(-90°),(270°)…) .
Так происходит потому, что прямая проходящая через начало координат и любую из этих точек никогда не пересечет ось тангенсов, т.к. будет идти параллельно ей. Поэтому в этих точках тангенс – НЕ СУЩЕСТВУЕТ (для всех остальных значений тангенс может быть найден).
Из-за этого при решении тригонометрических уравнений и неравенств с тангенсом необходимо учитывать ограничения на ОДЗ .
Знаки по четвертям
С помощью оси тангенсов легко определить знаки по четвертям тригонометрической окружности. Для этого надо взять любую точку на четверти и определить знак тангенса для нее описанным выше способом. У всей четверти знак будет такой же.
Для примера на рисунке нанесены две зеленые точки в I и III четвертях. Для них значение тангенса положительно (зеленые пунктирные прямые приходят в положительную часть оси), значит и для любой точки из I и III четверти значение тангенса будет положительно (знак плюс).
С двумя фиолетовыми точками в II и IV четвертях – аналогично, но с минусом.
Связь с другими тригонометрическими функциями:
– котангенсом того же угла: формулой (ctg:x=) (frac<1>)
Другие наиболее часто применяемые формулы смотри здесь .
[spoiler title=”источники:”]
http://kvn201.com.ua/table-tangensov.htm
http://cos-cos.ru/math/186/
[/spoiler]
Тангенс — одна из тригонометрических функций, обозначется tg (в англоязычной традиции — tan).
В прямоугольном треугольнике тангенс острого угла равен отношению противолежащего катета к прилежащему. Значение тангенса легко найти, зная синус и косинус угла:
tg(α) = sin(α)/cos(α).
Значения тангенсов для часто встречающихся углов (π — число пи, √ — корень квадратный):
- tg (0°) = 0
- tg (30°) = tg (π/6) = (√3)/3 = 1/√3
- tg (45°) = tg (π/4) = 1
- tg (60°) = tg (π/3) = √3
- tg (90°) = tg (π/2) = +∞ (значение не определено, вблизи 90° тангенс стремится к бесконечности)
- tg (180°) = tg (π) = 0
- tg (270°) = tg (3π/2) = –∞ (значение не определено, вблизи 90° тангенс стремится к бесконечности)
- tg (360°) = tg (2π) = 0
Другие тригонометрические функции:
- Что такое синус? Значения синусов
- Что такое косинус? Значения косинусов
- Что такое котангенс? Значения котангенсов
- Что такое секанс? Значения секансов
- Что такое косеканс? Значения косекансов
Дополнительно от Генона:
- Что такое теорема косинусов?
- Что такое теорема синусов?
- Где найти тригонометрические формулы двойного угла?
- Как разложить квадрат синуса, косинуса и тангенса?
- Как найти площадь прямоугольного треугольника?
Последнее редактирование ответа: 27.03.2010
-

Оставить отзывОставить отзыв
Вы можете написать свои замечания к ответу, предложения об улучшении или просто поблагодарить автора. Комментарий, после проверки, увидят автор и редактор ответа. Будьте, пожалуйста, вежливыми. Спасибо!
Если Вы хотите получить уведомление об
исправлении ответа укажите свой e-mail:Неправильный формат адреса электронной почты
 Похожие вопросы
Похожие вопросы
- Что такое косинус?
- Что такое синус?
- Что такое arcctg?
- Как найти тангенс?
- Что такое арксинус?
- Что такое синус а?
- Что такое arctg?
- Что такое arcsin?
- Как найти синус?
- Что такое arccos?
В соответствии с пользовательским соглашением администрация не несет ответственности за содержание материалов, которые размещают пользователи. Для урегулирования спорных вопросов и претензий Вы можете связаться с администрацией сайта genon.ru.
Размещенные на сайте материалы могут содержать информацию, предназначенную для пользователей старше 18 лет, согласно Федерального закона №436-ФЗ от 29.12.2010 года “О защите детей от информации, причиняющей вред их здоровью и развитию”. Обращение к пользователям 18+.
tg(0°)=tg(360°)=0 точная, но чуть более сложная таблица ( с точностью до 1′) здесь.
|
Углы |
Углы |
Углы |
Углы |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
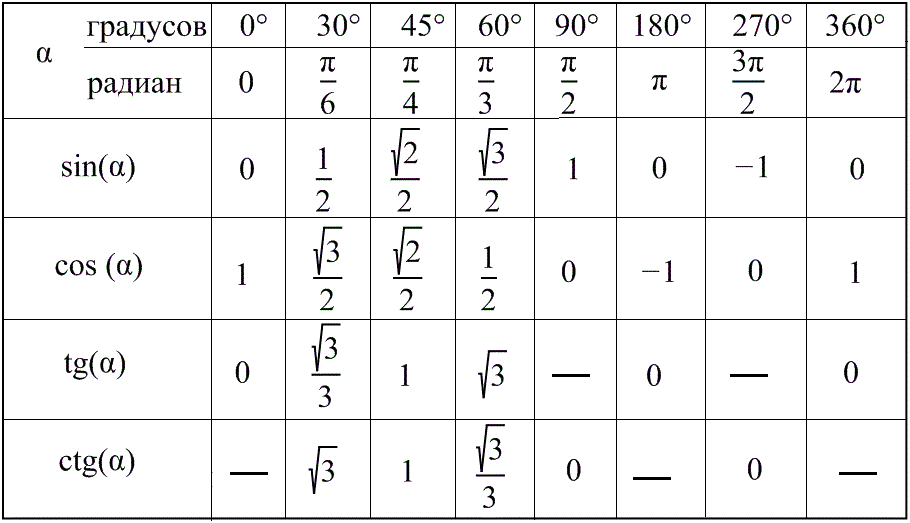
Углы 0°,30°,45°,60°,90°,180°,270°,360°,(π/6,π/4,π/3,π/2,π,3π/2,2π).
Синусы, косинусы, тангенсы и котангенсы. Таблица значений тригонометрических функций
Доп. Инфо:
- Таблица косинусов углов от 0° – 360°. Углы с шагом в 1°. Таблица значений косинусов.
- Таблица синусов углов от 0° – 360°. Углы с шагом в 1°. Таблица значений синусов.
- Таблица синусов, она-же косинусов точная.
- Таблица тангенсов углов углов от 0° – 360°. Углы с шагом в 1°. Таблица значений тангенса, tg
- Таблица котангенсов углов углов от 0° – 360°. Углы с шагом в 1°. Таблица значений котангенса, ctg
- Таблица тангенсов, она же котангенсов точная.
- Углы 0°,30°,45°,60°,90°,180°,270°,360°,(π/6,π/4,π/3,π/2,π,3π/2,2π).
Синусы, косинусы, тангенсы и котангенсы. Таблица значений тригонометрических функций. - Знаки тригонометрических функций синус, косинус, тангенс и котангенс по четвертям в тригонометрическом круге.
- Определение и численные соотношения между единицами измерения углов в РФ.
Тысячные, угловые градусы, минуты, секунды, радианы, обороты. - Таблица соответствия угловых градусов, радиан, оборотов, тысячных (артиллерийских РФ). 0-360 градусов, 0-2π радиан.
