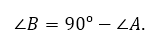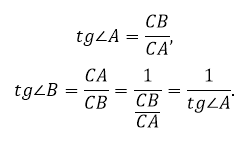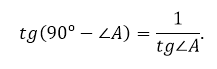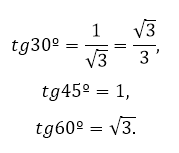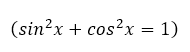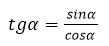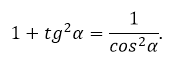|
Как найти тангенс угла, если известен косинус? Как найти котангенс угла, если известен косинус? Итак, читаем внимательно условие вопроса, и вспоминаем, чему нас учили в школе, у нас есть косинус угла, и этого окажется вполне достаточным для того, чтобы мы выполнили задание автора вопроса и нашли тангенс и котангенс данного угла. Вспоминаем, что мы можем найти, зная косинус, конечно-же, мы сразу можем найти синус, это очень легко, и в этом нам поможет вот это волшебное тождество и то, что из него следует, – формула для нахождения синуса: Теперь, зная чему равен синус угла, через косинус, проще простого решать дальше по известным формулам для нахождения тангенса и котангенса, просто подставляя в них эти формулы для синуса, которые я разместила выше: система выбрала этот ответ лучшим Ксарфакс 5 лет назад Для того, чтобы найти тангенс и котангенс через косинус, достаточно вспомнить тригонометрические формулы: tgα = sinα / cosα. ctgα = cosα / sinα. Так как косинус известен, то синус можно найти из основного тригонометрического тождества: sin²α + cos²α = 1. sinα = √(1 – cos²α), если угол α находится в 1 и 2 четверти. sinα = – √(1 – cos²α), если угол α находится в 3 и 4 четверти. Таким образом: tgα = ± √(1 – cos²α) / cosα. ctgα = ± cosα / √(1 – cos²α). Так как произведение тангенса и котангенса = 1, то ctgα также можно найти из формулы: ctgα = 1 / tgα. Пример Косинус угла α равен 0,94, при этом α находится в 1 четверти (0 < α < 90). Нужно найти тангенс и котангенс. Воспользуемся формулой: tgα = √(1 – cos²α) / cosα. В первой четверти синус и косинус больше 0, поэтому тангенс и котангенс также будут положительными. tgα ≈ 0,34 / 0,94 ≈ 0,36. Соответственно ctgα ≈ 1 / 0,36 ≈ 2,78. Лара Изюминка 6 месяцев назад В школе изучают следующую тригонометрическую формулу: Косинус в квадрате альфа равно единица разделить на сумму единицы и тангенса в квадрате альфа. Из этой формулы легко выразить тангенс в квадрате альфа. Он очевидно равен 1 деленная на косинус в квадрате альфа и из этой дроби нужно вычесть один, а можно еще преобразовать как на картинке. Ну, а для того чтобы выразить котангенс, нужно вспомнить , что произведение тангенса и котангенса равно единице, тогда просто меняем числитель и знаменатель местами и получается формула для нахождения котангенса через косинус. Ну, а знак тангенса и котангенса определяем по той четверти, в которой находится угол. Если это первая и третья четверти, то плюс, иначе минус. bezdelnik 5 лет назад tg а = Sin a/Cos a. Чтобы выразить тангенс через косинус осталось выразить синус через косинус. Для этого воспользуемся основной тригонометрической формулой (Sin a)^2 +/(Cos a)^2 = 1. Тогда (Sin a)^2 = 1 – (Cos a)^2, Sin a = √(1 – (Cos a)^2), а tg = √(1 – (Cos a)^2)/Cos a. Например, при а= 60 градусов Cos 60° = 0,5, tg = √(1 – 0,25)/0,5 = √(0,75)/0,5 = √(3*0,25)/0,5 = (0,5*√3)/0,5 = √3 = 1,732… . ctg a = Cos a/Sin a, то-есть величина обратная tg а, и при а = 60° ctg 60° = 1/√3 = √3/3 = 0,57735… . 127771 3 года назад Первым делом стоит вспомнить определение тангенса и котангенса, а именно: То есть получаются следующие формулы: tg(x) = sin(x) / cos(x) ctg(x) = cos(x) / sin(x) Из условия задачи нам известен косинус, значит нам нужно будет найти синус. Для этого есть такая формула: sin^2(x) + cos^2(x) = 1 Значит: sin^2(x) = 1 – cos^2(x) sin(x) = √(1 – (Cos a)^2) Теперь у нас есть значения синуса и косинуса, которые можно будет подставить в следующие формулы: Rafail 5 лет назад Наверное все помнят основное тождество тригонометрии: sin^2(x)+cos^2(x)=1. Почему-то также чётко я запомнил следующие простые формулы: tg^2(x)+1=sec^2(x) и ctg^2(x)+1=cosec^2(x). Ну и три определения: sec(x)=1/cos(x), cosec(x)=1/sin(x) и ctg(x)=1/tg(x). Теперь осталось выбрать нужные и применить. Допустим, cos(x)=(√3)/2, тогда sec(x)=2/√3, sec^2(x)=4/3, tg^2(x)=1/3, tg(x)=1/√3, ctg(x)=√3. Зайцевана 5 лет назад Пусть cosa = 1/2, тогда tga^2 = 1/(cosa)^2-1, (tga)^2 =1/0,25 – 1 = 3, tga =корень квадратный из 3, (со знаком + или – в зависимости в какой четверти находится а). ctga = 1/корень из 3. Синус, косинус, тангенс и котангенс угла – это тригонометрические функции. Можно сказать, что все они связаны между собой. Часто для нахождения одной из этих функций при условии, что известна другая, приходится вспоминать основные тригонометрические равенства или тождества, а также определение самих этих понятий. Зная все перечисленное выше, несложно выразить одну функцию через другую. Тангенс угла – это отношение синуса этого угла к его косинусу. Котангенс угла – это отношение косинуса угла к его синусу. Нам известен косинус, из основного тригонометрического тождества ( sin²α + cos²α = 1 ) выразим синус: sinα = √(1 – cos²α) для α из 1 и 2 четвертей, sinα = -√(1 – cos²α) для α из 3 и 4 четвертей. Подставив формулу для синуса угла в формулу тангенса и котангенса, получим формулы для вычисления значений этих функций: tgα = ± √(1 – cos²α) / cosα, ctgα = ± cosα / √(1 – cos²α). Котангенс, впрочем, можно вычислить путем попроще, вспомнив, что тангенс и котангенс – функции обратные, то есть ctgα = 1 / tgα. Подставляем в формулу значение тангенса и вычисляем котангенс. Если вам требуется найти тангенс и котангенс при помощи косинуса, то вам предстоит воспользоваться определенной тригонометрической формулой: при которой вы сможете отыскать синус из данной формулы, при том, что мы имеем известный косинус. Получившаяся формула выглядит таким образом: Теперь, нам следует подставить значение синуса в формулу вычисления тангенса, а именно речь идет о : Теперь подставим аналогичную формулу через косинус для котангенса: TheSun 3 года назад Для нахождения тангенса и котангенса через косинус необходимо воспользоваться приведенной ниже тригонометрической формулой: Находим синус из формулы указанной выше (при условии, что косинус нам известен), получается: Подставляем в формулу вычисления тангенса значение синуса: tg? = sin? / cos? = ± ?(1 – cos??) / cos?. Теперь аналогично для котангенса через косинус. ctg? = cos? / sin? = ± cos? / ?(1 – cos??). Все функции мы знаем из курса тригонометрии, и в это же время проходят и алгоритм нахождения тангенса/котангенса через косинус. Ну как следует из вопроса косинус нам известен. Если нет, то находим по формулам – Имея на руках значения двух вводных – синуса и косинуса, далее еще проще действовать по формулам нахождения тангенса и котангенса. Знаете ответ? |
Ответы Mail.ru
Образование
ВУЗы, Колледжи
Детские сады
Школы
Дополнительное образование
Образование за рубежом
Прочее образование
Вопросы – лидеры.
Где найти ответы на ОГЭ 2023?
1 ставка
Написать экологическое обоснование изделия из кольца
1 ставка
Помогите с английским 21 упражнением, расставить a,an,the.
1 ставка
Чем на ваш взгляд лучше заменить ЕГЭ?
1 ставка
Распредели данные словосочетания в два столбика в зависимости от того, переходный глагол или непереходный
1 ставка
Лидеры категории
Лена-пена
Искусственный Интеллект
М.И.
Искусственный Интеллект
Y.Nine
Искусственный Интеллект
•••
Как найти Тангенс числа, зная косинус? Напишите формулу, пожалуйста.!!!
Митяй
Мудрец
(16354),
закрыт
12 лет назад
Лучший ответ
Vlad Boikov
Профи
(739)
12 лет назад
sin^2+Cos^2=1
а дальше сам
Остальные ответы
BuHT
Мастер
(1169)
12 лет назад
tg=sin/cos=((1-cos^2)^1/2)/cos
Екатерина Максимова
Мыслитель
(5442)
12 лет назад
Роза Марковна
Просветленный
(35806)
12 лет назад
Пожалуй вот так
tg=sin/cos
sin^2+cos^2=1
sin= корень (1-cos^2)
тогда tg=(корень (1-cos^2))/cos
Похожие вопросы
Как найти тангенс, если известен косинус
Понятие тангенса является одним из основных в тригонометрии. Оно обозначает некую тригонометрическую функцию, которая является периодической, но не непрерывной в области определения, как синус и косинус. И имеет разрывы в точках (+,-)Пи*n+Пи/2, где n – это период функции. В России он обозначается как tg(x). Его можно представить через любую тригонометрическую функцию, так как все они тесно взаимосвязаны между собой.

Вам понадобится
- Учебник по тригонометрии.
Инструкция
Для того, чтобы выразить тангенс угла через синус, нужно вспомнить геометрическое определение тангенса. Итак, тангенсом острого угла в прямоугольном треугольнике, называют отношение противолежащего катета к прилежащему.
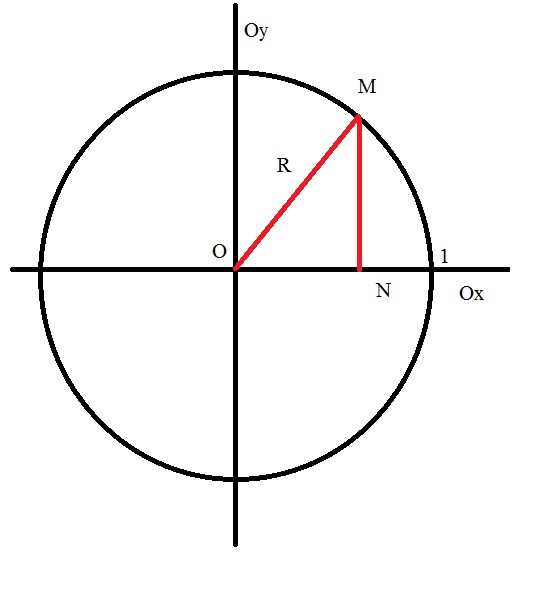
С другой стороны, рассмотрите декартову систему координат, на которой начерчена единичная окружность с радиусом R=1, и центром О в начале координат. Примите поворот против часовой стрелки, как положительный, а в обратную сторону отрицательный.
Отметьте некую точку M на окружности. Из нее опустите перпендикуляр на ось Ох, назовите ее точкой N. Получился треугольник OMN, у которого угол ONM является прямым.
Теперь рассмотрите острый угол MON, по определению синуса и косинуса острого угла в прямоугольном треугольнике
sin(MON) = MN/OM, cos(MON) = ON/OM. Тогда MN= sin(MON)*OM, а ON = cos(MON)*OM.
Вернувшись к геометрическому определению тангенса (tg(MON) = MN/ON), подставьте полученные выше выражения. Тогда:
tg(MON) = sin(MON)*OM/cos(MON)*OM, сократите OM, тогда tg(MON) = sin(MON)/cos(MON).
Из основного тригонометрического тождества (sin^2(x)+cos^2(x)=1) выразите косинус, через синус: cos(x)=(1-sin^2(x))^0,5 Подставьте это выражение в полученное на шаге 5. Тогда tg(MON) = sin(MON)/(1-sin^2(MON))^0,5.
Иногда существует потребность в вычисление тангенса двойного и половинчатого угла. Тут тоже выведены соотношения:tg(x/2) = (1-cos(x))/sin(x) = (1-(1-sin^2(x))^0,5)/sin(x);tg(2x) = 2*tg(x)/(1-tg^2(x)) = 2*sin(x)/(1-sin^2(x))^0,5/(1-sin(x)/(1-sin^2(x))^0,5)^2) =
= 2*sin(x)/(1-sin^2(x))^0,5/(1-sin^2(x)/(1-sin^2(x)).
Также возможно выразить квадрат тангенса через двойной угол косинуса, либо синус. tg^2(x) = (1-cos(2x))/(1+cos(2x)) = (1-1+2*sin^2(x))/(1+1-2*sin^2(x)) = (sin^2(x))/(1-sin^2(x)).
Обратите внимание
Обратите внимание на области допустимых значений при решение уравнений и неравенств.
Полезный совет
Знание наизусть основных тождеств, поможет быстро переходить от одних тригонометрических функций к другим.
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Как найти тангенс зная косинус
Содержание
- Линии тригонометрических функций
- Значения основных функций тригонометрии
- Сведение к углу
- Использование формул
- Частные случаи
- Тангенс угла
- Тангенс — это отношение.
- Как найти тангенс угла (формулы)
- Как найти тангенс по клеточкам
Для того, чтобы определить значение угла α, необходимо воспользоваться подходящей функции из тригонометрии. Во время решения задач постоянно возникает необходимость в том, чтобы узнать значение углов. Для некоторых углов можно найти точные значения, для других сложно определить точную цифру и можно вывести только приблизительное значение.
В этой статье мы подробно поговорим о функциях из тригонометрии. Мы не только расскажем о свойствах синуса, тангенса и других функций, но и узнаем, как правильно вычислять значения для каждого отдельного случая.
Рассмотрим подробно каждый случай.
Приближенное число для каждой из известных функций можно найти по определению. Для одних можно указать точные значения, для других – только приблизительные.
Соотношения сторон и углов фигуры используются для того, чтобы определить значения для 30 ° , 45 ° , 60 ° . Если угол выходит за пределы 90 ° , то перед вычислением значения следует воспользоваться специальной формулой для того, чтобы привести угол к нужному виду.
Если известно значение синуса для α , можно быстро узнать значение косинуса для этого же угла. Это легко выполнить с помощью основных тождеств, которые представлены в геометрии.
В некоторых случаях для того, чтобы узнать sin или cos угла, можно использовать подходящую тригонометрическую формулу. Например, по известному значению синуса 45 ° , мы сможем определить значение синуса 30 ° , воспользовавшись правилом из тригонометрии.
Если для примера не подходит ни одно из приведенных выше решений, можно найти приближенное значение. В этом вам помогут таблицы основных тригонометрических функций, которые легко можно найти.
Если взять за основу определения, возможно определить значения для определенного угла α . Также можно вычислить значения тангенса и котангенса для определенного случая. Можно найти значений основных функций из тригонометрии для частных вариантов. Это углы 0 ° , 90 ° , 180 ° , 270 ° , 360 ° .
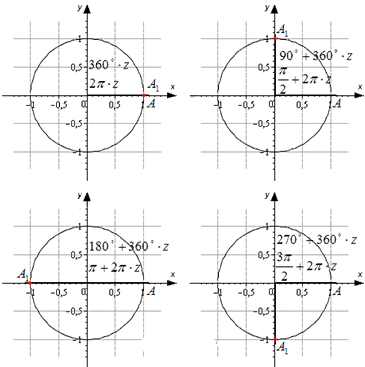
Разобьем эти углы на четыре группы: 360 · z градусов ( 2 π · z рад), 90 + 360 · z градусов ( π 2 + 2 π · z рад), 180 + 360 · z градусов ( π + 2 π · z рад) и 270 + 360 · z градусов ( 3 π 2 + 2 π · z рад), где z — любое целое число.
Изобразим данные формулы на рисунке:
Для каждой группы соответствуют свои значения.
При повороте из точки A на 360 · z ° , она переходит в себя. А 1 ( 1 , 0 ) . Синус 0 ° , 360 ° , 720 ° равен 0 , а косинус равен 1 . Представим это в виде формулы: sin ( 360 ° · z ) = 0 и cos ( 360 ° · z ) = 1 .
Можно определить, что t g ( 360 ° · z ) = 0 1 = 0 , а котангенс не определен.
Если А ( 1 , 0 ) повернуть на 90 + 360 · z ° , то она перейдет в А 1 ( 0 , 1 ) . По определению: sin ( 90 ° + 360 ° · z ) = 1 и cos ( 90 ° + 360 ° · z ) = 0 . Мы не сможем определить значение тангенса, но котангенс рассчитывается по данной формуле: c t g ( 90 ° + 360 ° · z ) = 0 1 = 0 .
Рассмотрим особенности для третьей группы углов. После поворота точки А ( 1 , 0 ) на любой из углов 180 + 360 · z ° , она перейдет в A 1 ( − 1 , 0 ) . Мы находим значения функций кроме тангенса.
Рассмотрим правила для четвертой группы углов. При повороте точки на 270 + 360 · z ° мы попадем в A 1 ( 0 , − 1 ) . Мы находим значения всех функций кроме тангенса.
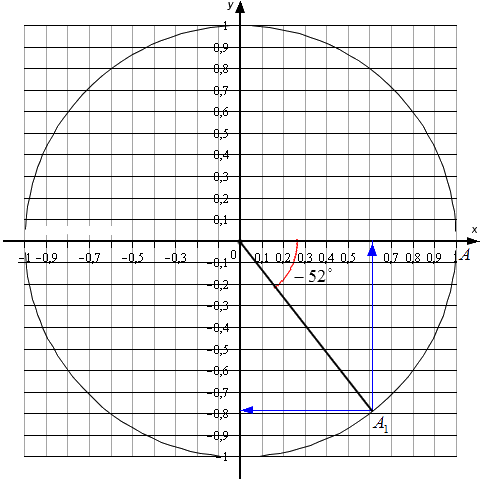
Для углов, которые не относятся к перечню от 0 ° , 90 ° , 180 ° , 270 ° , 360 ° … , точных значений нет. Мы можем найти лишь приближенные значения. Рассмотрим пример. Условия – найти основные значения для угла − 52 ° . Выполним построения.
Согласно рисунку, абсцисса А 1 ≈ 0 , 62 , а ордината ≈ − 0 , 78 . Соответственно, sin ( — 52 ° ) ≈ — 0 , 78 и cos ( — 52 ° ) ≈ 0 , 62 . Осталось определиться с тангенсом и котангенсом.
Выполняем вычисления: t g ( — 52 ° ) ≈ — 0 , 78 0 , 62 ≈ — 1 , 26 и c t g ( — 52 ° ) ≈ 0 , 62 — 0 , 78 ≈ — 0 , 79 .
Чем точнее выполняется чертеж, тем более точными будут значения для каждого индивидуального случая. Выполнять вычисления удобно только в теории, так как на практике довольно сложно и долго выполнять рисунки.
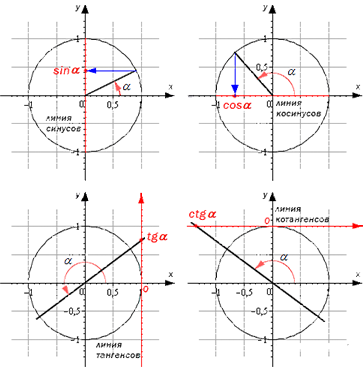
Линии тригонометрических функций
Линии тригонометрических функций – это линии, которые изображаются вместе с единичной окружностью. Они имеют точку отсчета и единичный отрезок, которая равна единице в координатной системе. Они используются для наглядного изображения значений.
Рассмотрим их на подробном рисунке
Как найти sin α , cos α , t g α , c t g α
Для тридцати-, сорокопяти-, шестидесятиградусных углов мы имеем определенные значения. Чтобы найти их, можно воспользоваться правилами о прямоугольном треугольнике с острыми углами. Для этого используется теорема Пифагора.
Для того, чтобы узнать значения для углов тридцати- и шестидесятиградусных углов изображаем прямоугольный треугольник с углами данной величины. Длина гипотенузы должна быть равна 1 . Согласно теореме Пифагора, катет, лежащий напротив тридцатиградусного угла, равен половине гипотенузы. Воспользуемся теоремой: 1 2 — 1 2 2 = 3 2 . Так как синус угла – это катет, деленный на гипотенузу, вычисляем, что sin 30 ° = 1 2 1 = 1 2 и sin 60 ° = 3 2 1 = 3 2 .
Косинус можно найти по формуле, которая предполагает деление прилежащего катета на гипотенузу. Вычисляем: cos 30 ° = 3 2 1 = 3 2 и cos 60 ° = 1 2 1 = 1 2 .
Тангенс можно найти по формуле, которая предполагает деление противолежащего катета на прилежащий. Котангенс находим по такой же схеме – делим прилежащий катет на противолежащий.
Вычисляем: t g 30 ° = 1 2 3 2 = 1 3 = 3 3 и t g 60 ° = 3 2 1 2 = 3 . Находим котангенс по подобной схеме: с t g 30 ° = 3 2 1 2 = 3 и с t g 60 ° = 1 2 3 2 = 1 3 = 3 3 . После этого приступаем к вычислению значений основных тригонометрических функций для сорока пятиградусного угла. Используем равнобедренный треугольник с углами 45 ° и гипотенузой, которая равна 1 . Используем теорему Пифагора. Согласно формуле, длины катетов равны 2 2 . Т
Теперь мы сможем найти значения для основных тригонометрических функций. Используем формулу, которая предполагает деление длин соответствующих сторон рассматриваемого треугольника.
Выводим формулу: c t g 45 ° = 2 2 2 2 = 1 .
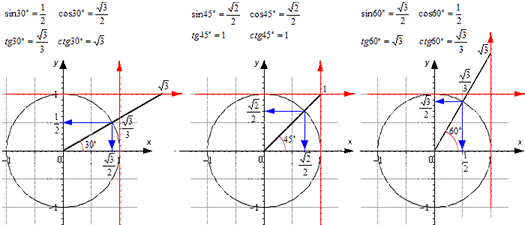
Полученные значения для тридцати-, сорокапяти-, шестидесятиградусных углов будут использоваться для решения различных задач. Запишите их – они часто будут использоваться. Для удобства можно использовать таблицу значений.
Проиллюстрируем значения для тридцати-, сорокапяти-, шестидесятиградусных углов с использованием окружности и линий.
Значения основных функций тригонометрии
Основные тождества из геометрии связывают с собой sin α , cos α , t g α , c t g α для определенного угла. С помощью одной функции вы легко сможете найти другую.
Для того, чтобы найти синус по известному косинусу, sin 2 α + cos 2 α = 1 .
Тангенс по известному косинусу t g 2 α + 1 = 1 cos 2 α .
Котангенс по известному синусу или наоборот 1 + c t g 2 α = 1 sin 2 α .
Тангенс через котангенс или наоборот можно найти благодаря удобной формуле: t g α · c t g α = 1 .
Для того, чтобы закрепить полученные знания, рассмотрим их на подробном примере
Необходимо найти значение синуса угла π 8 , если t g π 8 = 2 — 1 .
Сначала найдем котангенс угла: c t g π 8 = 1 t g π 8 = 1 2 — 1 = 2 + 1 ( 2 — 1 ) · ( 2 + 1 ) = 2 + 1 ( 2 ) 2 — 1 2 = 2 + 1 Воспользуемся формулой 1 + c t g 2 α = 1 sin 2 α . Благодаря этому мы вычисляем значение синуса. Имеем
sin 2 π 8 = 1 1 + c t g 2 π 8 = 1 1 + ( 2 + 1 ) 2 = 1 4 + 2 2 = 1 2 · ( 2 + 2 ) = 2 — 2 2 · ( 2 + 2 ) · ( 2 — 2 ) = = 2 — 2 2 · ( 2 2 — ( 2 ) 2 ) = 2 — 2 4
Для завершения необходимо определить значение синуса. Угол π 8 является углом первой четверти, то синус является положительным. Чтобы точно определить знак, вы можете воспользоваться таблицей, в которой определены знаки по четвертям координатной плоскости. Таким образом, sin π 8 = sin 2 π 8 = 2 — 2 4 = 2 — 2 2 . sin π 8 = 2 — 2 2 .
Сведение к углу
Удобнее всего находить значения для угла от 0 до 90 ° . Сведение к углу из интервала от 0 до 90 ° . Если угол не соответствует заданному интервалу, можно использовать законы и тождества, которые мы учили на уроках геометрии. Тогда мы сможем найти значение, которое будет равно для угла указанных пределах.
Задача заключается в том, чтобы найти синус 210 ° . Представим 210 как разность или сумму, разложив число на несколько. Воспользуемся соответствующей формулой для приведения. Используем формулу для нахождения значения синуса 30 ° : sin 210 ° = sin ( 180 ° + 30 ° ) = — sin 30 ° = — 1 2 , или косинуса 60 ° sin 210 ° = sin ( 270 ° — 60 ° ) = — cos 60 ° = — 1 2 .
Для того, чтобы решать задачи было намного проще, при нахождении значений переходите к углам из интервала от 0 до 90 ° с помощью формул приведения, если угол не находится в этих пределах.
Использование формул
Раннее мы рассмотрели подробности, касающиеся нахождению значений основных функций с использованием формул тригонометрии. Для того, чтобы определить значение для определенного угла, используйте формулы и значения основных функций для известных углов.
Для примера вычислим значение тангенса π 8 , который был использован в предыдущем примере. Возьмем за основу основные формулы тригонометрии.
Найдите значение t g π 8 .
Используя формулу тангенса, преобразуем уравнение до следующего равенства t g 2 π 8 = 1 — cos π 4 1 + cos π 4 . Значения косинуса угла π 4 известны из предыдущего примера. Благодаря этому мы быстро найдем значения тангенса.
t g 2 π 8 = 1 — cos π 4 1 + cos π 4 = 1 — 2 2 1 + 2 2 = 2 — 2 2 + 2 = = ( 2 — 2 ) 2 ( 2 + 2 ) · ( 2 — 2 ) = ( 2 — 2 ) 2 2 2 — ( 2 ) 2 = ( 2 — 2 ) 2 2
Угол π 8 является углом первой четверти. Согласно таблице основных тригонометрических функций по четвертям координатной плоскости, тангенс этого угла положителен. Продолжаем вычисления для дальнейшего решения: t g π 8 = t g 2 π 8 = ( 2 — 2 ) 2 2 = 2 — 2 2 = 2 — 1
Частные случаи
Тригонометрия – довольно сложная наука. Далеко не всегда можно найти формулы, используемые для вычисления. Существует множество уравнений, которые не поддаются стандартным формулам. Некоторые значения очень сложно обозначить точной цифрой. Это не так просто, как может показаться.
Однако точные значения не всегда нужны. Хватает и тех, что не претендуют на высокую точность. Благодаря существующим таблицам, которые можно найти в математических учебниках, можно найти любое приближенное значение основных функций. Благодаря справочным материалам вычислять формулы будет намного проще. В таблицах содержатся значения с высокой точностью.
- 10 — 11 классы
- Алгебра
- 5 баллов
ребят, как найти тангенс если известен косинус? и как косинус перевести в синус? напомните. плиз
Живущим людям на Земле
всегда хотелось знать,
как путь найти в пустыне, море,
и можно к звёздам ли попасть.
Хотелось труд свой облегчить,
создать машины, чтоб летать.
И чтоб вопросы разрешить,
пришлось про тангенс всем узнать.
Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. Впервые встречаясь с тригонометрией в восьмом классе на геометрии, школьники оглядываются на свою жизнь, задавая вопрос, насколько пригодится им эта область науки в дальнейшем.
Редко кто задумывается, что раздел математики, позволяющий рассказать о заданном треугольнике всё (найти все его стороны и углы, выделить особенности), позволил в своё время сделать великие открытия.
Тригонометрия, дав возможность строить корабли и самолёты, отправлять человека в космос, создавать приборы для ориентирования на море, в лесу, в пустыне, определять расстояния, не измеряя их непосредственно линейкой, шагами или чем-то иным, помогла упростить жизнь человечества, раскрыть новые горизонты знаний.
Тангенс угла
Первые встречи с тангенсом происходят при изучении прямоугольных треугольников.
В них соотношения сторон, образующих прямой угол (катетов), и стороны, лежащей напротив угла в 90º (гипотенузы), задают важные параметры для изучения углов.
Для понимания связи между объектами рассматриваются отношения различных отрезков. Задавая связь между ними, вводят понятия синуса, косинуса, тангенса, котангенса.
Важно, что это отвлечённые понятия, не связанные с какими-либо единицами измерения.
Введя функции угла, определяют их свойства. Некоторые полученные формулы могут иметь довольно громоздкий вид. Чтобы избежать затруднённого чтения, вводятся другие объекты.
Так произошло и с тангенсом. Ему посчастливилось получить два определения. Каждое характеризует заданное отношение по-своему. С одной стороны, рассматривается связь между катетами и острыми углами прямоугольного треугольника, с другой – даётся возможность упростить формулы, содержащие синусы и косинусы.
Мало кто задумывается, изучая тангенс в школе, что первоначально он был необходим, чтобы найти касательные линии к заданной кривой. Само понятие возникло от латинского слова tangens, которое означает «трогающий», «касающийся» и является причастием настоящего времени от tangere («трогать», «касаться»).
Тангенс — это отношение.
Итак, есть два определения:
Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.
Тангенс – это отношение синуса к косинусу.
Вместо «тангенс угла альфа» пишут: tgα. На калькуляторах, в различных программах ЭВМ и ПК закрепилось другое обозначение: tan(α).
Как найти тангенс угла (формулы)
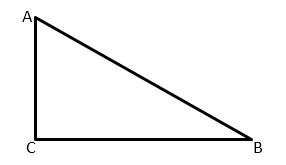
Первое свойство тангенса вытекает из его определения как отношения катетов.
Сумма углов прямоугольного треугольника равна 90º. Поэтому
Так как тангенс – это отношение катетов, то
Учитывая особенности некоторых треугольников (равностороннего, прямоугольного, равнобедренного), а также записанное свойство, была составлена таблица значений тангенса для углов 30º, 45º, 60º.
Задача нахождения других углов по значению тангенса была решена с помощью составления более обширных таблиц. За счёт появления современных вычислительных средств необходимость применения табулированных значений уменьшилась.
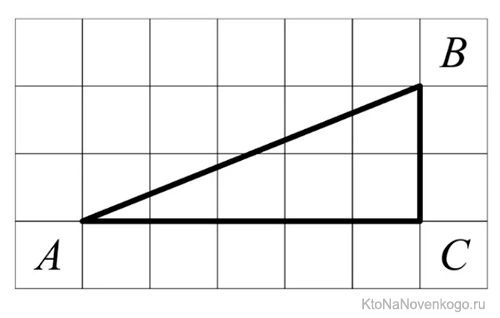
Как найти тангенс по клеточкам
Учитывая первое определение, можно определить, как найти тангенс угла по клеточкам. Рисунок дополняется перпендикулярными линиями (строится высота), затем считается количество клеточек в полученном прямоугольном треугольнике на катетах, противолежащем и прилежащем искомому углу, а затем берётся их отношение.
Благодаря второму определению, задачу, как найти тангенс угла, можно решить, минуя таблицы и построение прямоугольных треугольников. Достаточно знать синус и косинус, связанные между собой основным тригонометрическим тождеством:
Из формулы тангенсов, записывающей кратко второе определение
и основного тригонометрического тождества можно понять, как найти тангенс, зная только косинус или синус угла.
Достаточно поделить основное тригонометрическое тождество на квадрат косинуса, подставить формулу тангенса. В результате получится зависимость тангенса и косинуса:
Если выразить в последнем случае косинус, то запишется связь между тангенсом и синусом:
«>
Как найти тангенс, если известен косинус
Понятие тангенса является одним из основных в тригонометрии. Оно обозначает некую тригонометрическую функцию, которая является периодической, но не непрерывной в области определения, как синус и косинус. И имеет разрывы в точках (+,-)Пи*n+Пи/2, где n – это период функции. В России он обозначается как tg(x). Его можно представить через любую тригонометрическую функцию, так как все они тесно взаимосвязаны между собой.
Для того, чтобы выразить тангенс угла через синус, нужно вспомнить геометрическое определение тангенса. Итак, тангенсом острого угла в прямоугольном треугольнике, называют отношение противолежащего катета к прилежащему.
С другой стороны, рассмотрите декартову систему координат, на которой начерчена единичная окружность с радиусом R=1, и центром О в начале координат. Примите поворот против часовой стрелки, как положительный, а в обратную сторону отрицательный.
Отметьте некую точку M на окружности. Из нее опустите перпендикуляр на ось Ох, назовите ее точкой N. Получился треугольник OMN, у которого угол ONM является прямым.
Теперь рассмотрите острый угол MON, по определению синуса и косинуса острого угла в прямоугольном треугольнике
sin(MON) = MN/OM, cos(MON) = ON/OM. Тогда MN= sin(MON)*OM, а ON = cos(MON)*OM.
Вернувшись к геометрическому определению тангенса (tg(MON) = MN/ON), подставьте полученные выше выражения. Тогда:
tg(MON) = sin(MON)*OM/cos(MON)*OM, сократите OM, тогда tg(MON) = sin(MON)/cos(MON).
Из основного тригонометрического тождества (sin^2(x)+cos^2(x)=1) выразите косинус, через синус: cos(x)=(1-sin^2(x))^0,5 Подставьте это выражение в полученное на шаге 5. Тогда tg(MON) = sin(MON)/(1-sin^2(MON))^0,5.
Иногда существует потребность в вычисление тангенса двойного и половинчатого угла. Тут тоже выведены соотношения:tg(x/2) = (1-cos(x))/sin(x) = (1-(1-sin^2(x))^0,5)/sin(x);tg(2x) = 2*tg(x)/(1-tg^2(x)) = 2*sin(x)/(1-sin^2(x))^0,5/(1-sin(x)/(1-sin^2(x))^0,5)^2) =
= 2*sin(x)/(1-sin^2(x))^0,5/(1-sin^2(x)/(1-sin^2(x)).
Также возможно выразить квадрат тангенса через двойной угол косинуса, либо синус. tg^2(x) = (1-cos(2x))/(1+cos(2x)) = (1-1+2*sin^2(x))/(1+1-2*sin^2(x)) = (sin^2(x))/(1-sin^2(x)).