Improve Article
Save Article
Like Article
Improve Article
Save Article
Like Article
In Python, math module contains a number of mathematical operations, which can be performed with ease using the module. math.tan() function returns the tangent of value passed as argument. The value passed in this function should be in radians.
Syntax: math.tan(x)
Parameter:
x : value to be passed to tan()Returns: Returns the tangent of value passed as argument
Code #1:
import math
a = math.pi / 6
print ("The value of tangent of pi / 6 is : ", end ="")
print (math.tan(a))
Code #2:
import math
import numpy as np
import matplotlib.pyplot as plt
in_array = np.linspace(0, np.pi, 10)
out_array = []
for i in range(len(in_array)):
out_array.append(math.tan(in_array[i]))
i += 1
print("in_array : ", in_array)
print("nout_array : ", out_array)
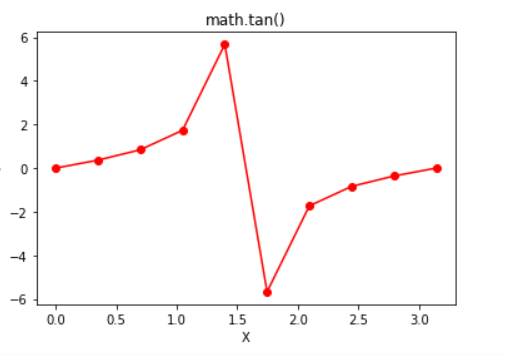
plt.plot(in_array, out_array, color = 'red', marker = "o")
plt.title("math.tan()")
plt.xlabel("X")
plt.ylabel("Y")
plt.show()
Output:
in_array : [0. 0.34906585 0.6981317 1.04719755 1.3962634 1.74532925
2.0943951 2.44346095 2.7925268 3.14159265]out_array : [0.0, 0.36397023426620234, 0.8390996311772799, 1.7320508075688767, 5.671281819617707, -5.671281819617711, -1.7320508075688783, -0.8390996311772804, -0.36397023426620256, -1.2246467991473532e-16]
Last Updated :
20 Mar, 2019
Like Article
Save Article
В этом разделе представлены тригонометрические функции модуля math.
Содержание:
- Функция
math.sin(); - Функция
math.cos(); - Функция
math.tan(); - Функция
math.asin(); - Функция
math.acos(); - Функция
math.atan(); - Функция
math.atan2(); - Функция
math.hypot().
math.sin(x):
Функция math.sin() возвращает синус угла x значение которого задано в радианах.
>>> from math import * >>> sin(pi/2) # 1.0 >>> sin(pi/4) # 0.7071067811865475)
math.cos(x):
Функция math.cos() возвращает косинус угла x значение которого задано в радианах.
>>> from math import * >>> cos(pi/3) # 0.5000000000000001 >>> cos(pi) # -1.0
math.tan(x):
Функция math.tan() возвращает тангенс угла x значение которого задано в радианах.
>>>from math import * >>> tan(pi/3) # 1.7320508075688767 >>> tan(pi/4) # 0.9999999999999999
При определенных значениях углов тангенс должен быть равен либо −∞ либо +∞, скажем tan(3π/2)=+∞, a tan(−π/2)=−∞, но вместо этого мы получаем либо очень большие либо очень маленькие значения типа float:
>>> tan(-pi/2) # -1.633123935319537e+16 >>> tan(3*pi/2) # должно быть Inf, но # 5443746451065123.0
math.asin(x):
Функция math.asin() возвращает арксинус значения x, т. е. такое значение угла y, выраженного в радианах при котором sin(y) = x.
>>> from math import * >>> asin(sin(pi/6)) # 0.5235987755982988 >>> pi/6 # 0.5235987755982988
math.acos(x):
Функция math.acos() возвращает арккосинус значения x, т. е. возвращает такое значение угла y, выраженного в радианах, при котором cos(y) = x.
>>> from math import * >>> acos(cos(pi/6)) 0.5235987755982987 >>> pi/6 0.5235987755982988
math.atan(x):
Функция math.atan() возвращает арктангенс значения x, т. е. возвращает такое значение угла y, выраженного в радианах, при котором tan(y) = x.
>>> from math import * >>> atan(tan(pi/6)) # 0.5235987755982988 >>> pi/6 # 0.5235987755982988
math.atan2(y, x):
Функция math.atan2() возвращает арктангенс значения y/x, т. е. возвращает такое значение угла z, выраженного в радианах, при котором tan(z) = x. Результат находится между -pi и pi.
>>> from math import * >>> y = 1 >>> x = 2 >>> atan2(y, x) # 0.4636476090008061 >>> atan(y/x) # 0.4636476090008061 >>> tan(0.4636476090008061) # 0.49999999999999994
Данная функция, в отличие от функции math.atan(), способна вычислить правильный квадрант в котором должно находиться значение результата. Это возможно благодаря тому, что функция принимает два аргумента (x, y) координаты точки, которая является концом отрезка начатого в начале координат. Сам по себе, угол между этим отрезком и положительным направлением оси X не несет информации о том где располагается конец этого отрезка, что приводит к одинаковому значению арктангенса, для разных отрезков, но функция math.atan2() позволяет избежать этого, что бывает очень важно в целом ряде задач. Например, atan(1) и atan2(1, 1) оба имеют значение pi/4, но atan2(-1, -1) равно -3 * pi / 4.
math.hypot(*coordinates):
Функция math.hypot() возвращает евклидову норму, sqrt(sum(x**2 for x in coordinates)). Это длина вектора от начала координат до точки, заданной координатами.
Для двумерной точки (x, y) это эквивалентно вычислению гипотенузы прямоугольного треугольника с использованием теоремы Пифагора sqrt(x*x + y*y).
Изменено в Python 3.8: Добавлена поддержка n-мерных точек. Раньше поддерживался только двумерный случай.
Модуль math – один из наиважнейших в Python. Этот модуль предоставляет обширный функционал для работы с числами.
math.ceil(X) – округление до ближайшего большего числа.
math.copysign(X, Y) – возвращает число, имеющее модуль такой же, как и у числа X, а знак – как у числа Y.
math.fabs(X) – модуль X.
math.factorial(X) – факториал числа X.
math.floor(X) – округление вниз.
math.fmod(X, Y) – остаток от деления X на Y.
math.frexp(X) – возвращает мантиссу и экспоненту числа.
math.ldexp(X, I) – X * 2i. Функция, обратная функции math.frexp().
math.fsum(последовательность) – сумма всех членов последовательности. Эквивалент встроенной функции sum(), но math.fsum() более точна для чисел с плавающей точкой.
math.isfinite(X) – является ли X числом.
math.isinf(X) – является ли X бесконечностью.
math.isnan(X) – является ли X NaN (Not a Number – не число).
math.modf(X) – возвращает дробную и целую часть числа X. Оба числа имеют тот же знак, что и X.
math.trunc(X) – усекает значение X до целого.
math.exp(X) – eX.
math.expm1(X) – eX – 1. При X → 0 точнее, чем math.exp(X)-1.
math.log(X, [base]) – логарифм X по основанию base. Если base не указан, вычисляется натуральный логарифм.
math.log1p(X) – натуральный логарифм (1 + X). При X → 0 точнее, чем math.log(1+X).
math.log10(X) – логарифм X по основанию 10.
math.log2(X) – логарифм X по основанию 2.
math.pow(X, Y) – XY.
math.sqrt(X) – квадратный корень из X.
math.acos(X) – арккосинус X. В радианах.
math.asin(X) – арксинус X. В радианах.
math.atan(X) – арктангенс X. В радианах.
math.atan2(Y, X) – арктангенс Y/X. В радианах. С учетом четверти, в которой находится точка (X, Y).
math.cos(X) – косинус X (X указывается в радианах).
math.sin(X) – синус X (X указывается в радианах).
math.tan(X) – тангенс X (X указывается в радианах).
math.hypot(X, Y) – вычисляет гипотенузу треугольника с катетами X и Y (math.sqrt(x * x + y * y)).
math.degrees(X) – конвертирует радианы в градусы.
math.radians(X) – конвертирует градусы в радианы.
math.cosh(X) – вычисляет гиперболический косинус.
math.sinh(X) – вычисляет гиперболический синус.
math.tanh(X) – вычисляет гиперболический тангенс.
math.acosh(X) – вычисляет обратный гиперболический косинус.
math.asinh(X) – вычисляет обратный гиперболический синус.
math.atanh(X) – вычисляет обратный гиперболический тангенс.
math.erf(X) – функция ошибок.
math.erfc(X) – дополнительная функция ошибок (1 – math.erf(X)).
math.gamma(X) – гамма-функция X.
math.lgamma(X) – натуральный логарифм гамма-функции X.
math.pi – pi = 3,1415926…
math.e – e = 2,718281…
Содержание
- 1. Особенности применения тригонометрических функций. Преобразование радиан в градусы и наоборот
- 2. Средства языка Python для конвертирования из градусов в радианы и наоборот. Функции math.degrees(x) и math.radians(x)
- 3. Ограничения на использование тригонометрических функций
- 4. Функция math.acos(x). Арккосинус угла
- 5. Функция math.asin(x). Арксинус
- 6. Функция math.atan(x). Арктангенс
- 7. Функция math.atan2(x, y). Арктангенс от x/y
- 8. Функция math.cos(x). Косинус угла
- 9. Функция math.sin(x)
- 10. Функция math.hypot(x, y). Евклидовая норма (Euclidean norm)
- 11. Функция math.tan(x). Тангенс угла x
- Связанные темы
Поиск на других ресурсах:
1. Особенности применения тригонометрических функций. Преобразование радиан в градусы и наоборот
Чтобы использовать тригонометрические функции в программе, нужно подключить модуль math
import math
Все тригонометрические функции оперируют радианами. Зависимость между радианами и градусами определяется по формуле:
1 радиан = 180°/π = 57.2958°
Если известен угол в градусах, то для корректной работы тригонометрических функций, этот угол нужно преобразовать в радианы.
Например. Задан угол, имеющий n градусов. Найти арккосинус этого угла. В этом случае формула вычисления результата будет следующей:
... n_rad = n*3.1415/180 # получить угол в радианах ac = math.acos(n_rad) # вычислить арккосинус ...
Чтобы получить более точное значение результата, в программе можно использовать константу math.pi, которая определяет число π. В этом случае текст программы будет иметь следующий вид
n_rad = n*math.pi/180 # получить угол в радианах ac = math.acos(n_rad) # вычислить арккосинус
⇑
2. Средства языка Python для конвертирования из градусов в радианы и наоборот. Функции math.degrees(x) и math.radians(x)
В языке Python существуют функции преобразования из градусов в радианы и, наоборот, из радиан в градусы.
Функция math.degrees(x) конвертирует значение параметра x из радиан в градусы.
Функция math.radians(x) конвертирует значение параметра x из градусов в радианы.
Пример.
# Функция math.degrees(x) import math x = 1 # x - угол в радианах y = math.degrees(x) # y = 57.29577951308232 - угол в градусах x = math.pi # x = 3.1415... y = math.degrees(x) # y = 180.0 # Функция math.radians(x) x = 180.0/math.pi y = math.radians(x) # y = 1.0 x = 45 # x - угол в градусах y = math.radians(x) # y = 0.7853981633974483
⇑
3. Ограничения на использование тригонометрических функций
При использовании тригонометрических функций следует учитывать соответствующие ограничения, которые следуют из самой сущности этих функций. Например, не существует арксинуса из числа, которое больше 1.
Если при вызове функции задать неправильный аргумент, то интерпретатор выдаст соответствующее сообщение об ошибке
ValueError: math domain error
⇑
4. Функция math.acos(x). Арккосинус угла
Функция acos(x) возвращает арккосинус угла x. Аргумент x задается в радианах и может быть как целым числом, так и вещественным числом.
Пример.
# Функция math.acos(x) import math n = float(input('n = ')) # ввести n n_rad = n*math.pi/180 # получить угол в радианах ac = math.acos(n_rad) # вычислить арккосинус print('n_rad = ', n_rad) print('ac = ', ac)
Результат работы программы
n = 35 n_rad = 0.6108652381980153 ac = 0.913643357298706
⇑
5. Функция math.asin(x). Арксинус
Функция math.asin(x) вычисляет арксинус угла от аргумента x. Значение аргумента x задается в радианах.
Пример.
# Функция math.asin(x) import math n = 10 # n - угол в градусах # конвертировать из градусов в радианы n_rad = n*math.pi/180 # n_rad = 0.17453292519943295 # вычислить арксинус asn = math.asin(n_rad) # asn = 0.17543139267904395
⇑
6. Функция math.atan(x). Арктангенс
Функция math.atan(x) возвращает арктангенс аргумента x, значение которого задается в радианах. При использовании функции важно помнить допустимые значения x, которые можно задавать при вычислении арктангенса.
Пример.
# Функция math.atan(x) import math n = 60 # n - угол в градусах # конвертировать из градусов в радианы n_rad = n*math.pi/180 # n_rad = 1.0471975511965976 # вычислить арктангенс atn = math.atan(n_rad) # atn = 0.808448792630022
⇑
7. Функция math.atan2(x, y). Арктангенс от x/y
Функция math.atan2(x, y) вычисляет арктангенс угла от деления x на y. Функция возвращает результат от —π до π. Аргументы x, y определяют координаты точки, через которую проходит отрезок от начала координат. В отличие от функции atan(x), данная функция правильно вычисляет квадрант, влияющий на знак результата.
Пример.
# Функция math.atan2(x,y) import math x = -2 y = -1 res = math.atan2(x, y) # res = -2.0344439357957027
⇑
8. Функция math.cos(x). Косинус угла
Функция math.cos(x) вычисляет косинус угла для аргумента x. Значение аргумента x задается в радианах.
Пример.
# Функция math.cos(x) import math x = 0 y = math.cos(x) # y = 1.0 x = math.pi y = math.cos(x) # y = -1.0 x = 2 # 2 радианы y = math.cos(x) # y = -0.4161468365471424
⇑
9. Функция math.sin(x)
Функция math.sin(x) возвращает синус угла от аргумента x, заданного в радианах.
Пример.
# Функция math.sin(x) import math x = math.pi y = math.sin(x) # y = 1.2246467991473532e-16 x = 0 y = math.sin(x) # y = 0.0 x = 2 # 2 радиана y = math.sin(x)
⇑
10. Функция math.hypot(x, y). Евклидовая норма (Euclidean norm)
Функция возвращает Евклидовую норму, которая равна длине вектора от начала координат до точки x, y и определяется по формуле
Пример.
# Функция math.hypot(x, y) import math x = 1.0 y = 1.0 z = math.hypot(x, y) # z = 1.4142135623730951 x = 3.0 y = 4.0 z = math.hypot(x, y) # z = 5.0
⇑
11. Функция math.tan(x). Тангенс угла x
Функция math.tan(x) возвращает тангенс от аргумента x. Аргумент x задается в радианах.
Пример.
# Функция math.tan(x, y) import math x = 1.0 y = math.tan(x) # y = 1.5574077246549023 x = 0.0 y = math.tan(x) # y = 0.0
⇑
Связанные темы
- Теоретико-числовые функции и функции представления
- Степенные и логарифмические функции
- Гиперболические функции
- Специальные функции и константы
⇑
Содержание:развернуть
- Синтаксис и подключение
- Константы модуля Math
- Список функций
-
Теоретико-числовые функции и функции представления
-
Степенные и логарифмические функции
-
Тригонометрические функции
-
Угловые преобразования
-
Гиперболические функции
-
Специальные функции
Python библиотека math содержит наиболее применяемые математические функции и константы. Все вычисления происходят на множестве вещественных чисел.
Если вам нужен соответствующий аппарат для комплексного исчисления, модуль math не подойдёт. Используйте вместо него cmath. Там вы найдёте комплексные версии большинства популярных math-функций.
Синтаксис и подключение
Чтобы подключить модуль, необходимо в начале программы прописать следующую инструкцию:
import math
Теперь с помощью точечной нотации можно обращаться к константам и вызывать функции этой библиотеки. Например, так:
math.log()
Константы модуля Math
math.pi
Представление математической константы π = 3.141592…. “Пи” — это отношение длины окружности к её диаметру.
print(math.pi)
> 3.141592653589793
math.e
Число Эйлера или просто e. Иррациональное число, которое приблизительно равно 2,71828.
print(math.e)
> 2.718281828459045
math.tau
Число τ — это отношение длины окружности к её радиусу. Т.е
import math
> print(math.tau)
print(math.tau == 2 * math.pi)
> True
math.inf
Положительная бесконечность.
print(math.inf)
> inf
Для оперирования отрицательной бесконечно большой величиной, используйте -math.inf
Константа math.inf эквивалента выражению float("inf").
math.nan
NaN означает — “не число”.
print(math.nan)
> nan
Аналогичная запись: float("nan").
Список функций
Теоретико-числовые функции и функции представления
math.ceil()
Функция округляет аргумент до большего целого числа.
print(math.ceil(3.0001))
> 4
math.comb(n, k)
Число сочетаний из n по k. Показывает сколькими способами можно выбрать k объектов из набора, где находится n объектов. Формула:
Решим задачу: На столе лежат шесть рубинов. Сколько существует способов выбрать два из них?
print(math.comb(6,2))
> 15
💭 Можете подставить числа в формулу, и самостоятельно проверить правильность решения.
math.copysign()
Функция принимает два аргумента. Возвращает первый аргумент, но со знаком второго.
print(math.copysign(-6, 2))
> 6.0
math.fabs()
Функция возвращает абсолютное значение аргумента:
print(math.fabs(-42))
> 42.0
math.factorial()
Вычисление факториала. Входящее значение должно быть целочисленным и неотрицательным.
print(math.factorial(5))
> 120
math.floor()
Антагонист функции ceil(). Округляет число до ближайшего целого, но в меньшую сторону.
print(math.floor(3.99))
> 3
math.fmod(a, b)
Считает остаток от деления a на b. Является аналогом оператора “%” с точностью до типа возвращаемого значения.
print(math.fmod(75, 4))
> 3.0
math.frexp(num)
Возвращает кортеж из мантиссы и экспоненты аргумента. Формула:
, где M — мантисса, E — экспонента.
print(math.frexp(10))
> (0.625, 4)
# проверим
print(pow(2, 4) * 0.625)
> 10.0
math.fsum()
Вычисляет сумму элементов итерируемого объекта. Например, вот так она работает для списка:
summable_list = [1, 2, 3, 4, 5]
print(math.fsum(summable_list))
> 15.0
math.gcd(a, b)
Возвращает наибольший общий делитель a и b. НОД — это самое большое число, на которое a и b делятся без остатка.
a = 5
b = 15
print(math.gcd(a, b))
> 5
math.isclose(x, y)
Функция возвращает True, если значения чисел x и y близки друг к другу, и False в ином случае. Помимо пары чисел принимает ещё два необязательных именованных аргумента:
rel_tol— максимально допустимая разница между числами в процентах;abs_tol— минимально допустимая разница.
x = 10
y = 11
print(math.isclose(x, y))
> False
print(math.isclose(x, y, rel_tol=1))
> True
math.isfinite()
Проверяет, является ли аргумент NaN, False или же бесконечностью. True, если не является, False — в противном случае.
norm = 3
inf = float('inf')
print(math.isfinite(norm))
> True
print(math.isfinite(inf))
> False
math.isinf()
True, если аргумент — положительная/отрицательная бесконечность. False — в любом другом случае.
not_inf = 42
inf = math.inf
print(math.isinf(not_inf))
> False
print(math.isinf(inf))
> True
math.isnan()
Возврат True, если аргумент — не число (nan). Иначе — False.
not_nan = 0
nan = math.nan
print(math.isnan(not_nan))
> False
print(math.isnan(nan))
> True
math.isqrt()
Возвращает целочисленный квадратный корень аргумента, округлённый вниз.
print(math.isqrt(44))
> 6
math.ldexp(x, i)
Функция возвращает значение по формуле:
возвращаемое значение = x * (2 ** i)print(math.ldexp(3, 2))
> 12.0
math.modf()
Результат работы modf() — это кортеж из двух значений:
- Дробная часть аргумента;
- Целая часть аргумента;
print(math.modf(3.14))
> (0.14000000000000012, 3.0)
math.perm(n, k)
Возвращает число размещений из n по k. Формула:
Задача: Посчитать количество вариантов распределения трёх билетов на концерт Стаса Михайлова для пяти фанатов.
print(math.perm(5, 3))
> 60
Целых 60 способов! Главное — не запутаться в них, и не пропустить концерт любимого исполнителя!
math.prod()
Принимает итерируемый объект. Возвращает произведение элементов.
multiple_list = [2, 3, 4]
print(math.prod(multiple_list))
> 24
math.remainder(m, n)
Возвращает результат по формуле:
Результат = m – x * n,
где x — ближайшее целое к выражению m/n число.
print(math.remainder(55, 6))
> 1.0
print(math.remainder(4, 6))
> -2.0
math.trunc()
trunc() вернёт вам целую часть переданного в неё аргумента.
print(math.trunc(4.6))
> 4
Степенные и логарифмические функции
math.exp(x)
Возвращает e в степени x. Более точный аналог pow(math.e, x).
print(math.exp(3))
> 20.085536923187668
math.expm1(x)
Вычисляет значение выражения exp(x) - 1 и возвращает результат.
print(math.expm1(3))
> 19.085536923187668
print(math.expm1(3) == (math.exp(3) - 1))
> True
math.log()
Функция работает, как с одним, так и с двумя параметрами.
1 аргумент: вернёт значение натурального логарифма (основание e):
print(math.log(math.e))
> 1.0
2 аргумента: вернёт значение логарифма по основанию, заданному во втором аргументе:
print(math.log(16, 4))
> 2.0
☝️ Помните, это читается, как простой вопрос: “в какую степень нужно возвести число 4, чтобы получить 16“. Ответ, очевидно, 2. Функция log() с нами согласна.
math.log1p()
Это натуральный логарифм от аргумента (1 + x):
print(math.log(5) == math.log1p(4))
> True
math.log2()
Логарифм по основанию 2. Работает точнее, чем math.log(x, 2).
math.log10()
Логарифм по основанию 10. Работает точнее, чем math.log(x, 10).
math.pow(a, b)
Функция выполняет возведение числа a в степень b и возвращает затем вещественный результат.
print(math.pow(2,4))
> 16.0
Подробнее о возведении в степень в Python:
math.sqrt()
Возврат квадратного корня из аргумента
print(math.sqrt(16))
> 4.0
Про квадратные корни в Python:
Тригонометрические функции
math.acos()
Функция возвращает арккосинус в радианах:
print(math.acos(-1))
> 3.141592653589793
math.asin()
Возврат арксинуса (угол в радианах):
# π/2
print(math.asin(1))
> 1.5707963267948966
math.atan()
Арктангенс:
# π/4
print(math.atan(1))
> 0.7853981633974483
math.atan2(y, x)
Функция принимает на вход два аргумента и возвращает арктангенс y/x. Значение будет в радианах. atan2() учитывает четверть, в которой находится точка (x, y).
print(math.atan2(-12, 13))
> -0.7454194762741583
math.cos()
Косинус угла, который следует указывать в радианах:
print(math.cos(math.pi))
> -1.0
math.dist(p, q)
Функция возвращает значение евклидова расстояния между точками p и q. У точек должны совпадать измерения. В прямоугольной системе координат dist(p, q) эквивалентна следующей формуле:
# аналогично sqrt(8)
print(math.dist((0, 0), (2, 2)))
> 2.8284271247461903
math.hypot(x, y)
Возвращает длину вектора от начала координат до точки, заданной координатами. Иначе — функция вычисляет гипотенузу треугольника c катетами x и y.
print(math.hypot(3, 4))
> 5.0
math.sin()
Функция вернёт синус угла. Угол следует задавать в радианах:
print(math.sin(0))
> 0.0
math.tan()
Тангенс угла. Аргумент указываем в радианах.
print(math.tan(math.radians(315)))
> -1.0000000000000004
Угловые преобразования
math.degrees()
Функция переводит радианное значение угла в градусы.
print(math.degrees(math.pi))
> 180.0
math.radians()
Наоборот: из градусов — в радианы.
# функция отрабатывает прямо, как по табличке синусов =)
print(math.radians(30))
> 0.5235987755982988
print(math.pi / 6)
> 0.5235987755982988
Гиперболические функции
Гиперболические функции являются аналогами тригонометрических и тесно с ними связаны. Но тригонометрические функции основаны на окружностях, а гиперболические, соответственно, на гиперболах.
Для Python все они принимают один аргумент — точку, в которой вычисляется значение функции.
math.acosh()
Обратный гиперболический косинус:
print(math.acosh(1))
> 0.0
math.asinh()
Обратный гиперболический синус:
print(math.asinh(0))
> 0.0
math.atanh()
Обратный гиперболический тангенс:
print(math.atanh(0))
> 0.0
math.cosh()
Гиперболический косинус:
print(math.cosh(1.2))
> 1.8106555673243747
math.sinh()
Гиперболический синус:
print(math.sinh(2.5))
> 6.0502044810397875
math.tanh()
Гиперболический тангенс:
print(math.tanh(6))
> 0.9999877116507956
Специальные функции
math.erf(x)
Возвращает в x функцию ошибки Гаусса.
math.erfc(x)
Возвращает в x комплементарную функцию ошибки.
math.gamma()
Возвращает значение гамма-функции в точке x.
print(math.gamma(4))
> 6.0
math.lgamma()
Аналогично возвращается натуральный логарифм модуля значения гамма-функции в точке x.
print(math.log(math.gamma(4)))
> 1.791759469228055
print(math.lgamma(4))
> 1.7917594692280554
–