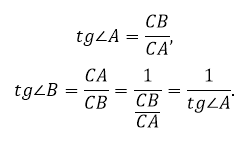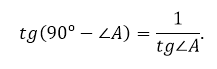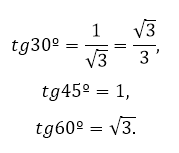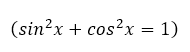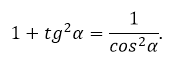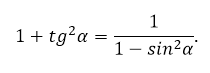Как найти тангенс по смотреть - Сайт, где вы сможете решить свои вопросы

29
Июн 2013

Категория: Справочные материалы

Значения тангенса и котангенса на тригонометрическом круге

2013-06-29
2016-08-04

В прошлой статье мы познакомились с тригонометрическим кругом и научились находить значения синуса и косинуса основных углов.

Как же быть с тангенсом и котангенсом? Об этом и поговорим сегодня.

Где же на тригонометрическом круге оси тангенсов и котангенсов?

Ось тангенсов параллельна оси синусов (имеет тоже направление, что ось синусов) и проходит через точку (1; 0).

Ось котангенсов параллельна оси косинусов (имеет тоже направление, что ось косинусов) и проходит через точку (0; 1).

На каждой из осей располагается вот такая цепочка основных значений тангенса и котангенса: $-sqrt3,;;-1,;frac{-sqrt3}{3},;0,;frac{sqrt3}{3},;1,;sqrt3.$ Почему так?

Я думаю, вы легко сообразите и сами. 🙂 Можно по-разному рассуждать. Можете, например, использовать тот факт, что $tgalpha=frac{sinalpha}{cosalpha}$ и $ctgalpha=frac{cosalpha}{sinalpha}.$

Изучаем картинку:

Собственно, картинка за себя сама говорит.

Если не очень все же понятно, разберем примеры:

Пример 1.

Вычислить $tg :300^{circ}$

Решение:

Находим на круге $300^{circ}$ . Эту точку соединяем с точкой (0;0) лучом (начало – точка (0;0)) и смотрим, где этот луч пересекает ось тангенсов. Видим, что $tg :300^{circ}=-sqrt3.$

Ответ:

Пример 2.

Вычислить $tg :90^{circ}$

Решение:

Находим на круге $90^{circ}$ . Точку (0;0) соединяем с указанной точкой лучом. И видим, что луч никогда не пересечет ось тангенсов.

$tg :90^{circ}$ не существует.

Ответ: не существует

Пример 3.

Вычислить $tg:frac{11pi}{4}$

Решение:

$frac{11pi}{4}=frac{12pi}{4}-frac{pi}{4}=3pi-frac{pi}{4}.$

Находим на круге точку (это та же точка, что и ) и от нее по часовой стрелке (знак минус!) откладываем $frac{pi}{4}$ ( $45^{circ}$ ). Куда попадаем? Мы окажемся в точке, что на круге у нас (см. рис.) названа как $135^{circ}$ . Эту точку соединяем с точкой (0;0) лучом. Вышли на ось тангенсов в значение .

Так значит, $tg:frac{11pi}{4}=-1.$

Ответ:

Пример 4.

Вычислить $ctg:840^{circ}$

Решение:

$840^{circ}=2cdot 360^{circ}+120^{circ}.$

Поэтому от точки $0^{circ}$ (именно там будет $2cdot 360^{circ}$ ) откладываем против часовой стрелки $120^{circ}$ .

Выходим на ось котангенсов, получаем, что $ctg:840^{circ}=-frac{sqrt3}{3}.$

Ответ: $-frac{sqrt3}{3}.$

Пример 5.

Вычислить $ctg:270^{circ}$

Решение:

Находим на круге $270^{circ}$ . Эту точку соединяем с точкой (0; 0). Выходим на ось котангенсов. Видим, что $ctg:270^{circ}=0.$

Ответ:

Теперь, умея находить по тригонометрическому кругу значения тригонометрических функций (а я надеюсь, что статья, где мы начинали знакомство с кругом и учились вычислять значения синусов и косинусов, вами прочитана…), вы можете пройти тест по теме «Нахождение значений косинуса, синуса, тангенса и котангенса различных углов».

Автор: egeMax |

комментариев 6

Печать страницы

Источник

В статье мы рассмотрим, как найти значения:

(tg, frac{π}{3}), (ctg, (-frac{7π}{3})), (tg ,0), (ctg, frac{5π}{6}⁡)

и других тангенсов и котангенсов без тригонометрической таблицы.

Есть два способа вычислять тангенсы и котангенсы. Первый – через синусы и косинусы, второй – через оси тангенсов и котангенсов. Первый способ проще в освоении, второй – быстрее в применении.

Но в любом случае вам нужно уметь уверенно расставлять числа с пи на тригонометрическом круге и откладывать углы.

Способ 1 – вычисление тангенсов и котангенсов через синусы и косинусы

Конечно, этот способ подразумевает, что вы уже умеете вычислять синус и косинус. Не умеете? Тогда бегом читать эту статью, и эту тоже.

Уже умеете? Тогда ловите два определения:

– тангенс равен отношению синуса к косинусу числа.

(tg ,t=)(frac{sin⁡,t}{cos,⁡t})

– котангенс равен отношению косинуса к синусу числа.

(ctg ,t=)(frac{cos⁡,t}{sin,⁡t})

Пример. Вычислите (tg, frac{π}{3}) и (ctg, frac{π}{3}).
Решение:

Ищем сначала (frac{π}{3}), а после вычисляем (sin,⁡frac{π}{3}) и (cos⁡,frac{π}{3}).

(sin⁡, frac{π}{3}=frac{sqrt{3}}{2}); (cos⁡, frac{π}{3}=frac{1}{2});
(tg , frac{π}{3}=) (frac{frac{sqrt{3}}{2}}{frac{1}{2}})(=frac{sqrt{3}}{2}:frac{1}{2}=frac{sqrt{3}}{2}cdot frac{2}{1}=sqrt{3}).
(ctg,frac{π}{3}=)(frac{frac{1}{2}}{frac{sqrt{3}}{2}})(=frac{1}{2}:frac{sqrt{3}}{2}=frac{1}{2}cdotfrac{2}{sqrt{3}}=frac{1}{sqrt{3}}).

Пример. Вычислите (tg, frac{5π}{6}) и (ctg, frac{5π}{6}).
Решение:

Найдем сначала (frac{5π}{6}) на круге: (frac{5π}{6}=frac{6π}{6}-frac{π}{6}=π-frac{π}{6}).

(ctg, frac{5π}{6}=)(frac{cos⁡ frac{5π}{6}}{sin⁡frac{5π}{6}})(=-frac{sqrt{3}}{2}:frac{1}{2}=-frac{sqrt{3}}{2} cdot frac{2}{1}=-sqrt{3});
(tg,frac{5π}{6}=)(frac{sin⁡frac{5π}{6}}{cos⁡frac{5π}{6}})(=frac{1}{2}:(-frac{sqrt{3}}{2})=frac{1}{2}cdot(-frac{2}{sqrt{3}})=-frac{1}{sqrt{3}}).

Пример. Вычислите (tg, 0) и (ctg, 0).
Решение:

(0) на тригонометрическом круге совпадает с (1) на оси косинусов, значит (cos⁡,0=1).
Если из точки (0) на тригонометрическом круге провести перпендикуляр (красная пунктирная линия) к оси синусов, то мы попадем в (0), получается (sin,⁡0=0). Следовательно: (tg, 0=)(frac{sin,⁡0}{cos⁡,0}) (=frac{0}{1}=0).

С котангенсом интереснее: (ctg, 0=)(frac{cos,⁡0}{sin⁡,0}) (=frac{1}{0}=???). На ноль делить нельзя – это железное правило математики. Поэтому и посчитать такой котангенс не получится. (ctg,⁡0) – не вычислим в принципе.

Пример. Вычислите (tg,120^°) и (ctg, 120^°).
Решение:

(ctg,120^°=)(frac{cos⁡,120^°}{sin,120^°})(=-frac{1}{2}:frac{sqrt{3}}{2}=-frac{1}{2}cdotfrac{2}{sqrt{3}}=-frac{1}{sqrt{3}});
(tg,120^°=)(frac{sin⁡,120^° }{cos⁡,120^°})(=frac{sqrt{3}}{2}:(-frac{1}{2})=frac{sqrt{3}}{2}cdot(-frac{2}{1})=-sqrt{3}).

Способ 2 – вычисление тангенсов и котангенсов с использованием осей

Прямая, проходящая через начало отсчета тригонометрического круга и параллельная оси синусов (ось (y)), называется осью тангенсов. Направление оси тангенсов и оси синусов совпадает.

Прямая проходящая через (frac{π}{2}) ((90^°)) тригонометрического круга и параллельная оси косинусов (ось (x)) называется осью котангенсов. Направление оси котангенсов и оси косинусов совпадает.

Ось тангенсов – сдвинутая копия оси синусов, ось котангенсов – копия оси косинусов. Единицы на осях котангенсов и тангенсов совпадают.

Чтобы определить тангенс и котангенс с помощью тригонометрического круга, нужно:
1) Начертить тригонометрический круг и оси тангенсов и котангенсов;
2) Отметить аргумент тангенса или котангенса на тригонометрическом круге;
3) Соединить прямой эту точку, соответствующую аргументу и начало координат;
4) Продлить прямую до осей и найти координаты пересечения, как показано на картинке ниже:

О том, как просто запомнить где какое значение стоит на осях, можно прочитать в статье «Как запомнить тригонометрический круг».

Пример. Вычислите (tg, frac{π}{4}) и (ctg, frac{π}{4}).
Решение:

1) Строим круг, оси и отмечаем аргумент на окружности;

2) Соединяем точку, соответствующую аргументу, и начало координат;

3) Продляем до осей;

И на оси тангенсов, и на оси котангенсов мы пришли в единицу, поэтому (tg, frac{π}{4}=1) и (ctg, frac{π}{4}=1).

Пример. Вычислите (tg, frac{2π}{3}) и (ctg, frac{2π}{3}).
Решение: (frac{2π}{3}=frac{3π}{3}-frac{π}{3}=π-frac{π}{3})

(ctg ,frac{2π}{3}=-frac{1}{sqrt{3}}); (tg,frac{2π}{3}=-sqrt{3}).

Пример. Найдите значения выражений (tg,(-30^°)) и (ctg,(-30^°)).
Решение:

Понятно, что во время ЕГЭ такой красивой картинки не будет, но она и не нужна. Если вы будете знать, как правильно расставлять значения на тригонометрическом круге и будете помнить расположение чисел на осях, то вам будет достаточно нарисованного от руки круга.

Пример (ЕГЭ). Найдите значение выражения (2sqrt{3} tg,(-300^°)).
Решение: (-300^°=-360^°+60^°).

(2sqrt{3}tg(-300^° )=2sqrt{3}cdotsqrt{3}=2cdot 3=6).
Ответ: (6).

Смотрите также:
Как найти синус и косинус без тригонометрической таблицы?
Из градусов в радианы и наборот
Тригонометрическая таблица с кругом
Почему в тригонометрической таблице такие числа?

Для тех кто хочет закрепить знания:
Задание на вычисление синусов, косинусов, тангенсов и котангенсов

Источник

Определение тангенса угла

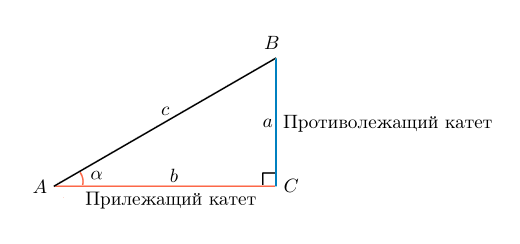
Тангенсом угла в прямоугольном треугольнике называют отношение противолежащего катета к прилежащему.

Катетами являются стороны, которые образуют прямой угол в треугольнике, соответственно, гипотенузой является третья (самая длинная) сторона.

Для простоты запоминания можно дать такое определение: тангенс угла — это отношение дальнего от рассматриваемого угла катета к ближнему катету.

В случае с рисунком, описанным выше: tg⁡α=abtgalpha=frac{a}{b}

Тангенс можно найти напрямую пользуясь данной формулой, а можно и через тригонометрические тождества. Разберем подробнее задачи.

Задача 1

В прямоугольном треугольнике катеты равны 6 см6text{ см} и 8 см8text{ см}. Найдите тангенс угла, близлежащего к меньшей стороне.

Решение

a=8a=8
b=6b=6

tg⁡α=ab=86≈1.33tgalpha=frac{a}{b}=frac{8}{6}approx1.33

Ответ

1.331.33

Формулу:

tg⁡α=abtgalpha=frac{a}{b}

Можно записать в следующем виде:

tg⁡α=sin⁡αcos⁡αtgalpha=frac{sinalpha}{cosalpha}

Проверим истинность данного выражения. Подставим вместо синуса и косинуса их определения:

tg⁡α=sin⁡αcos⁡α=acbc=abtgalpha=frac{sinalpha}{cosalpha}=frac{frac{a}{c}}{frac{b}{c}}=frac{a}{b}

Получили первичное равенство, значит выражение для тангенса через отношение синуса к косинусу верно.

Решим задачу, пользуясь этой формулой.

Задача 2

По условию задачи известен косинус угла, равный 32frac{sqrt{3}}{2} и синус того же угла, равный 12frac{1}{2}. Найдите тангенс данного угла.

Решение

cos⁡α=32cosalpha=frac{sqrt{3}}{2}

sin⁡α=12sinalpha=frac{1}{2}

tg⁡α=sin⁡αcos⁡α=1232=13tgalpha=frac{sinalpha}{cosalpha}=frac{frac{1}{2}}{frac{sqrt{3}}{2}}=frac{1}{sqrt{3}}

Ответ

13frac{1}{sqrt{3}}

Еще одно тождество помогает решить задачи, связанные с тангенсом:

1+tg⁡2α=1cos⁡2α1+tg^2alpha=frac{1}{cos^2alpha}

Оно появляется путем деление каждого слагаемого основного тождества тригонометрии на квадрат косинуса.

Задача 3

Известен квадрат косинуса угла в прямоугольном треугольнике, равный 0.80.8. Нужно найти тангенс этого угла.

Решение

cos⁡2α=0.8cos^2alpha=0.8

1+tg⁡2α=1cos⁡2α1+tg^2alpha=frac{1}{cos^2alpha}

1+tg⁡2α=10.81+tg^2alpha=frac{1}{0.8}

1+tg⁡2α=1.251+tg^2alpha=1.25

tg⁡2α=0.25tg^2alpha=0.25

tg⁡α=0.25tgalpha=sqrt{0.25}

tg⁡α=0.5tgalpha=0.5

Ответ

0.50.5

У вас есть трудности с вычислением тангенса? Можете заказать задачу по математике у наших экспертов!

Тест по теме “Вычисление тангенса”

Источник

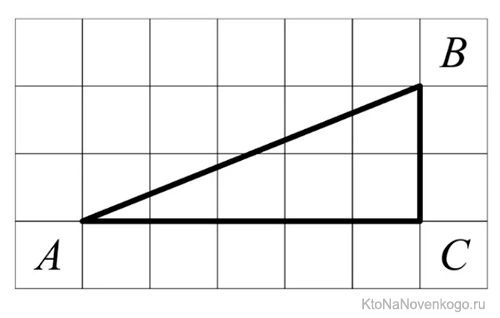
Обычно в задачах требуется найти тангенс именно острого угла, как, допустим, на этом примере:

Для этого мы строим прямоугольный треугольник, проведя линию (перпендикуляр) BD:

Далее вспоминаем определение тангенса, это отношение противолежащего катета к прилежащему.

То есть tg(BOA) = DB / DO.

Чтобы найти DO и DB достаточно будет посчитать количество клеточек.

DO = 2.

DB = 5.

Значит, tg(BOA) = 5 / 2 = 2,5.

Зная тангенс, мы можем легко найти и котангенс:

ctg(BOA) = 1 / tg(BOA) = 1 / 2,5 = 0,4.

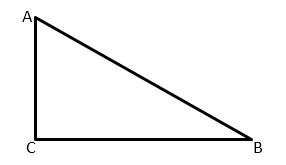
А вот задача на нахождение тангенса угла по клеточкам немного другого плана (ищем тангенс угла AOB):

Если соединить точки A и B, то угол ABO будет прямым.

И тангенс можно вычислить как отношение BA к BO.

Как же нам их найти?

И BO, и BA будут гипотенузами 2 совершенно равных прямоугольных треугольников (для наглядности я их выделил красным).

Длина катетов их равна 2 и 8, а квадрат гипотенузы, как известно, равен сумме квадратов катетов.

Таким образом, у нас получится следующее:

tg(BOA) = BA / BO = √(2² + 8²) / √(2² + 8²) = 1.

И нетрудно догадаться, что треугольник этот равнобедренный с равными углами BOA и BAO по 45 градусов.

Источник

Что такое тангенс угла и как его найти

Живущим людям на Земле
всегда хотелось знать,
как путь найти в пустыне, море,
и можно к звёздам ли попасть.

Хотелось труд свой облегчить,
создать машины, чтоб летать.
И чтоб вопросы разрешить,
пришлось про тангенс всем узнать.

Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. Впервые встречаясь с тригонометрией в восьмом классе на геометрии, школьники оглядываются на свою жизнь, задавая вопрос, насколько пригодится им эта область науки в дальнейшем.

Редко кто задумывается, что раздел математики, позволяющий рассказать о заданном треугольнике всё (найти все его стороны и углы, выделить особенности), позволил в своё время сделать великие открытия.

Тригонометрия, дав возможность строить корабли и самолёты, отправлять человека в космос, создавать приборы для ориентирования на море, в лесу, в пустыне, определять расстояния, не измеряя их непосредственно линейкой, шагами или чем-то иным, помогла упростить жизнь человечества, раскрыть новые горизонты знаний.

Тангенс угла

Первые встречи с тангенсом происходят при изучении прямоугольных треугольников.

В них соотношения сторон, образующих прямой угол (катетов), и стороны, лежащей напротив угла в 90º (гипотенузы), задают важные параметры для изучения углов.

Для понимания связи между объектами рассматриваются отношения различных отрезков. Задавая связь между ними, вводят понятия синуса, косинуса (это что?), тангенса, котангенса.

Важно, что это отвлечённые понятия, не связанные с какими-либо единицами измерения.

Введя функции угла, определяют их свойства. Некоторые полученные формулы могут иметь довольно громоздкий вид. Чтобы избежать затруднённого чтения, вводятся другие объекты.

Так произошло и с тангенсом. Ему посчастливилось получить два определения. Каждое характеризует заданное отношение по-своему. С одной стороны, рассматривается связь между катетами и острыми углами прямоугольного треугольника, с другой – даётся возможность упростить формулы, содержащие синусы и косинусы.

Мало кто задумывается, изучая тангенс в школе, что первоначально он был необходим, чтобы найти касательные линии к заданной кривой. Само понятие возникло от латинского слова tangens, которое означает «трогающий», «касающийся» и является причастием настоящего времени от tangere («трогать», «касаться»).

Тангенс — это отношение…

Итак, есть два определения:

Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.

Это определение удобно использовать при изучении геометрических фигур. Оно даёт возможность, минуя вычисления гипотенузы, находить углы или катеты. Выделяя прямоугольные треугольники в произвольных фигурах, задача по изучению свойств исследуемых объектов становится проще.
Тангенс – это отношение синуса к косинусу.

Благодаря этому определению, многие тригонометрические формулы принимают более удобный вид, становятся легче воспринимаемыми.

Приняты обозначения:

Вместо «тангенс угла альфа» пишут: tgα. На калькуляторах, в различных программах ЭВМ и ПК закрепилось другое обозначение: tan⁡(α).

Как найти тангенс угла (формулы)

Первое свойство тангенса вытекает из его определения как отношения катетов.

Сумма двух непрямых углов прямоугольного треугольника равна 90º. Поэтому

Так как тангенс – это отношение катетов, то

Получается, что

Учитывая особенности некоторых треугольников (равностороннего, прямоугольного, равнобедренного), а также записанное свойство, была составлена таблица значений тангенса для углов 30º, 45º, 60º.

В частности,

Задача нахождения других углов по значению тангенса была решена с помощью составления более обширных таблиц. За счёт появления современных вычислительных средств необходимость применения табулированных значений уменьшилась.

Как найти тангенс по клеточкам

Учитывая первое определение, можно определить, как найти его по клеточкам. Рисунок дополняется перпендикулярными линиями (строится высота), затем считается количество клеточек в полученном прямоугольном треугольнике на катетах, противолежащем и прилежащем искомому углу, а затем берётся их отношение.

Благодаря второму определению, задачу, как найти тангенс угла, можно решить, минуя таблицы и построение прямоугольных треугольников. Достаточно знать синус и косинус, связанные между собой основным тригонометрическим тождеством:

Из формулы тангенсов, записывающей кратко второе определение

и основного тригонометрического тождества можно понять, как найти тангенс, зная только косинус или синус угла.

Достаточно поделить основное тригонометрическое тождество на квадрат косинуса, подставить формулу тангенса. В результате получится его зависимость от косинуса:

Если выразить в последнем случае косинус, то запишется связь между тангенсом и синусом:

Источник

Значения тангенса и котангенса на тригонометрическом круге

Способ 1 – вычисление тангенсов и котангенсов через синусы и косинусы

Способ 2 – вычисление тангенсов и котангенсов с использованием осей

Тест по теме “Вычисление тангенса”

Тангенс угла

Тангенс — это отношение…

Как найти тангенс угла (формулы)

Как найти тангенс по клеточкам

Вам также может понравиться

Как найти моль через реакцию

Как составить жалобу в роспотребнадзор на автосалон

Как можно перенести слово найти

Добавить комментарий Отменить ответ