Тригонометрия – это наука, изучающая свойства тригонометрических формул (trigwnon – треугольник и метр – мера).
Тригонометрич. формулы — это элементарные функции, выражающие зависимость всех сторон прямоугольного треугольника от острых углов к гипотенузе (или зависимость хорд и высот от его центрального угла в окружности).
К прямым функциям тригонометрии относятся: sin x (синус), cos x (косинус). К производным: tg x (тангенс), ctg x (котангенс). В дополнение к другим тригонометрическим функциям: sec x (секанс) и cosec x (косеканс).
Косинус и синус в тригонометрии — бесконечно дифференцируемые и периодически непрерывные вещественные функции. Остальные, наоборот, дифференцируются в области определения, однако, как и прямые тригонометрические функции, непрерывны.
Основные тригонометрич. тождества:
Зная синус или косинус числа, можно найти его тангенс или котангенс: tg a = sin a / cos a
Вы можете найти синус числа, если известен его косинус, и наоборот: sin2 a + cos2 a = 1
Можно найти тангенс через синус с известным косинусом: 1 + tg2 a = 1 / cos2 a
Вы можете найти котангенс через синус с известным косинусом: 1 + 1 / tg2 a = 1 / sin2
sin(90o – а) = cos а
cos(90o – а) = sin а
И еще, любую формулу в математике можно применять не только слева направо, но и наоборот. В тригонометрии это же применяется при преобразовании суммы в произведение или при переходе от произведения к сумме.
Содержание:
Пусть в прямоугольном треугольнике гипотенуза равна с, один из острых углов равен 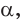
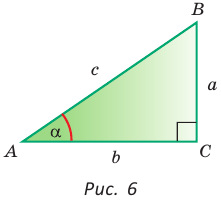
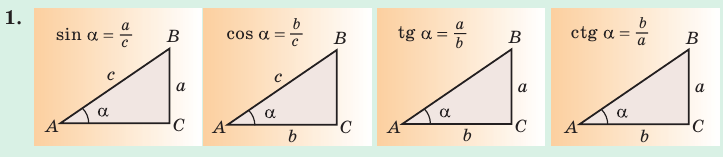
Определения синуса, косинуса, тангенса и котангенса острого угла
Определение. Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе:
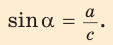
Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе:
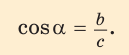
Определение. Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему:
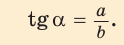
Котангенсом острого угла прямоугольного треугольника называется отношение прилежащего катета к противолежащему:
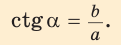
Пример:
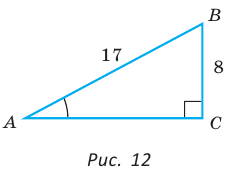
Угол К в  равен 90° (рис. 7).
равен 90° (рис. 7).
Тогда:
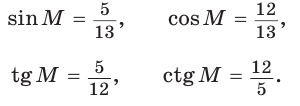
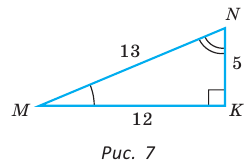
Для угла N катет МК — противолежащий, а катет NK — прилежащий (см. рис. 7, с. 11). Поэтому согласно определениям получаем:
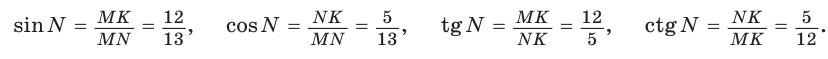
Можно заметить, что синус острого угла а прямоугольного треугольника и косинус другого острого угла этого треугольника, содержащего  равны, т. е.
равны, т. е. 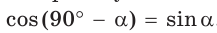 . Так же
. Так же 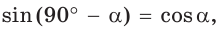
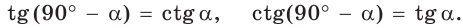 Например,
Например, 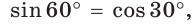
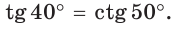
А теперь выполните Тест 1 и Тест 2.
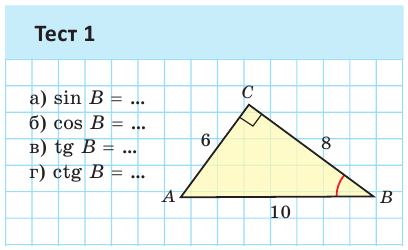
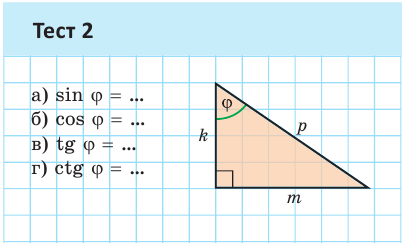
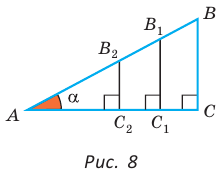
Значение синуса острого угла, а также косинуса, тангенса и котангенса зависит только от величины угла и не зависит от размеров и расположения прямоугольного треугольника с указанным острым углом.
Это следует из того, что прямоугольные треугольники с равным острым углом подобны, а у подобных треугольников соответствующие стороны пропорциональны. Так, в  (рис. 8)
(рис. 8) 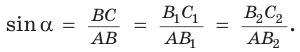
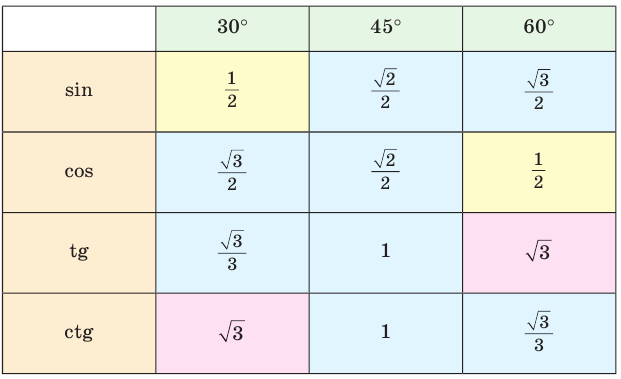
Значения синуса, косинуса, тангенса и котангенса углов 30°, 45°, 60°
Рассмотрим прямоугольный треугольник АВС, у которого 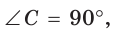
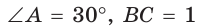 (рис. 9). Так как катет, лежащий против угла в 30°, равен половине гипотенузы, то АВ = 2. По теореме Пифагора
(рис. 9). Так как катет, лежащий против угла в 30°, равен половине гипотенузы, то АВ = 2. По теореме Пифагора
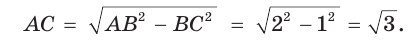 Тогда:
Тогда:
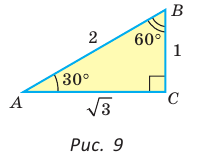
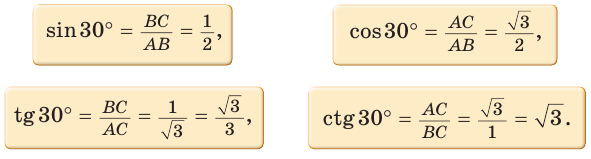
Так как 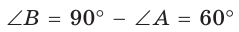 (см. рис. 9), то
(см. рис. 9), то

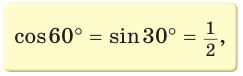
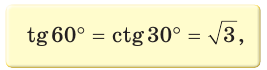
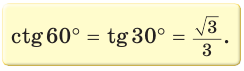
Рассмотрим равнобедренный прямоугольный треугольник АВС, у которого 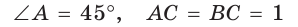 (рис. 10). По теореме Пифагора
(рис. 10). По теореме Пифагора
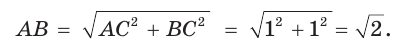
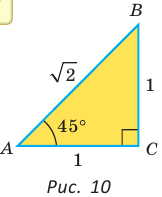
Тогда:
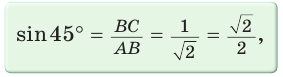
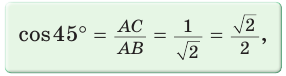
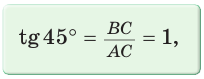
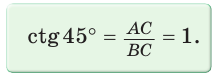
Составим таблицу значений синусов, косинусов, тангенсов и котангенсов для углов 30°, 45° и 60°.
Нахождение значений тригонометрических функций
Значения синуса, косинуса, тангенса и котангенса данного угла можно приближенно находить при помощи специальных тригонометрических таблиц* либо калькулятора.
Например, с помощью калькулятора, компьютера или мобильного телефона (смартфона) находим: sin45° = 0,707106… . Приближенное значение тригонометрических функций при решении задач будем брать с округлением до четырех знаков после запятой: sin45° = 0,7071.
Итак, точное значение sin 45° равно 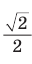 . а приближенное — 0,7071.
. а приближенное — 0,7071.
Таблицы и калькулятор также позволяют находить величину острого угла по значению синуса, косинуса или тангенса. Например, найдем острый угол, синус которого равен 0,4175. Выбрав на компьютере вид калькулятора «инженерный», далее «градусы», нужно ввести последовательно  . На экране появится ответ: 24,676… . Округлим его до десятых долей градуса и получим 24,7°. Учитывая, что 1° содержит 60 угловых минут, получим: 0,7° = 0,7 • 60′ = 42′. Искомый угол, синус которого 0,4175, приближенно равен 24°42′.
. На экране появится ответ: 24,676… . Округлим его до десятых долей градуса и получим 24,7°. Учитывая, что 1° содержит 60 угловых минут, получим: 0,7° = 0,7 • 60′ = 42′. Искомый угол, синус которого 0,4175, приближенно равен 24°42′.
А теперь выполните Тест 3.

Тригонометрические функции острого угла
Синус, косинус, тангенс и котангенс являются функциями угла, так как каждому острому углу 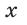 соответствует единственное значение синуса, косинуса, тангенса и котангенса. Они называются тригонометрическими функциями и записываются так:
соответствует единственное значение синуса, косинуса, тангенса и котангенса. Они называются тригонометрическими функциями и записываются так: 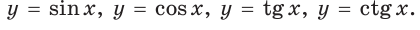
Поскольку в прямоугольном треугольнике катет меньше гипотенузы, то для острого угла 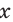 справедливо:
справедливо: 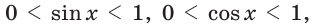 следовательно синус и косинус острого угла положительны и меньше 1.
следовательно синус и косинус острого угла положительны и меньше 1.
Тангенс и котангенс острого угла могут принимать любое положительное значение. Например, tg85° ~ 11,4.
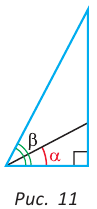
С увеличением острого угла синус и тангенс возрастают, а косинус и котангенс убывают (рис. 11), то есть если 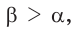 то
то
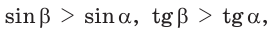 но
но 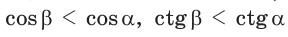 (cm. c. 28, задачу 2*). Это гарантирует, что синус (косинус, тангенс и котангенс) острого угла определяют этот угол однозначно.
(cm. c. 28, задачу 2*). Это гарантирует, что синус (косинус, тангенс и котангенс) острого угла определяют этот угол однозначно.
Пример №1
В прямоугольном треугольнике АВС, где 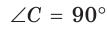 , катет ВС равен 8 см, гипотенуза АВ равна 17 см. Найти косинус угла А (рис. 12).
, катет ВС равен 8 см, гипотенуза АВ равна 17 см. Найти косинус угла А (рис. 12).
Решение:
По теореме Пифагора найдем катет 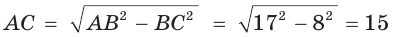 (см). Косинус острого угла прямоугольного треугольника равен от ношению прилежащего катета к гипотенузе. Тогда
(см). Косинус острого угла прямоугольного треугольника равен от ношению прилежащего катета к гипотенузе. Тогда 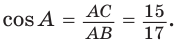
Ответ: 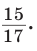
Пример №2
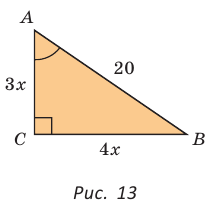
Гипотенуза АВ прямоугольного треугольника АВС равна 20 см, 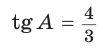 (рис. 13). Найти площадь треугольника.
(рис. 13). Найти площадь треугольника.
Решение:
Так как 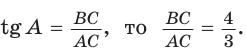 Обозначим
Обозначим 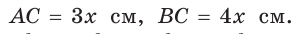 По теореме Пифагора
По теореме Пифагора 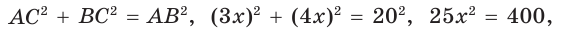
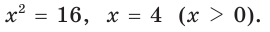 Тогда
Тогда 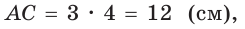 ВС = 4 • 4 = 16(см),
ВС = 4 • 4 = 16(см), 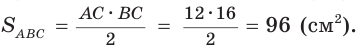
Ответ: 96 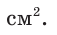
Пример №3
При помощи циркуля и линейки построить угол, синус которого равен 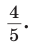
Решение:
Идея решения. Построим прямоугольный треугольник с катетом, равным 4 единицы, и гипотенузой, равной 5 единиц. Синус угла, противолежащего указанному катету, будет равен 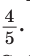
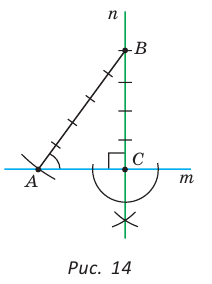
Построение. 1) Строим прямой угол С (рис. 14), для чего проводим произвольную прямую  отмечаем на ней точку С и строим прямую
отмечаем на ней точку С и строим прямую  проходящую через точку С перпендикулярно прямой
проходящую через точку С перпендикулярно прямой  (вспомните по рисунку алгоритм построения). 2) На прямой
(вспомните по рисунку алгоритм построения). 2) На прямой  от точки С откладываем последовательно четыре равных отрезка. Получаем отрезок ВС, который содержит 4 единицы. 3) Строим окружность с центром в точке В радиусом, равным пяти единицам. В пересечении этой окружности и прямой
от точки С откладываем последовательно четыре равных отрезка. Получаем отрезок ВС, который содержит 4 единицы. 3) Строим окружность с центром в точке В радиусом, равным пяти единицам. В пересечении этой окружности и прямой 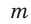 получаем точку А.
получаем точку А.
Угол ВАС — искомый.
Доказательство:
Из 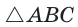 находим
находим 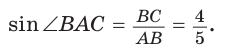
Алгоритм решения прямоугольного треугольника
Под решением прямоугольного треугольника понимают нахождение его неизвестных сторон и углов по некоторым элементам, определяющим этот треугольник. Рассмотрим три задачи:
- нахождение катета по гипотенузе и острому углу;
- нахождение катета по другому катету и острому углу;
- нахождение гипотенузы по катету и острому углу.
Пример №4
Гипотенуза прямоугольного треугольника равна 6, острый угол равен 32° (рис. 23). Найти катет, прилежащий к данному углу. Ответ округлить до 0,1.
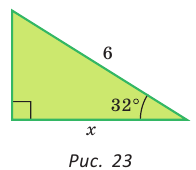
Решение:
Примем длину искомого катета за 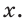
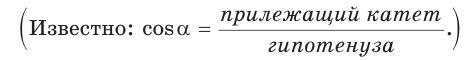
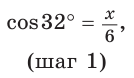


Ответ: 5,1.
Пример №5
Катет прямоугольного треугольника равен 2,5, а прилежащий к нему угол равен 68° (рис. 24). Найти другой катет. Ответ округлить до 0,1.
Решение:
Примем длину неизвестного катета за 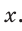
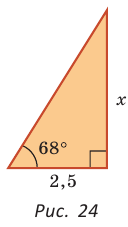
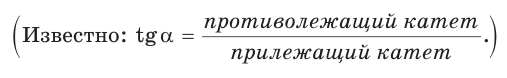
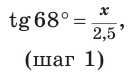
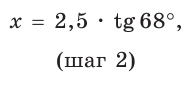

Ответ: 6,2.
Пример №6
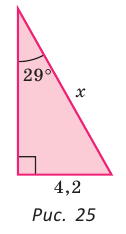
Катет прямоугольного треугольника равен 4,2, противолежащий ему угол равен 29° (рис. 25). Найти гипотенузу треугольника. Ответ округлить до 0,1.
Решение:
Примем длину гипотенузы за 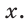
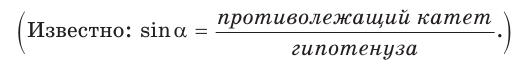
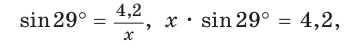
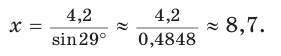
Ответ: 8,7.
Правила решения прямоугольного треугольника
Преобразуем формулы синуса, косинуса, тангенса и котангенса и запишем результаты для треугольника на рисунке 26:
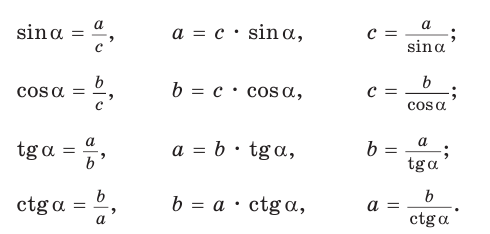
Удобно пользоваться следующими правилами:
- Катет равен гипотенузе, умноженной на синус противолежащего или на косинус прилежащего угла (рис. 27, а).
- Гипотенуза равна катету, деленному на синус противолежащего или на косинус прилежащего угла (рис. 27, б).
- Катет равен другому катету, умноженному на тангенс противолежащего или на котангенс прилежащего к первому катету угла (рис. 27, в).
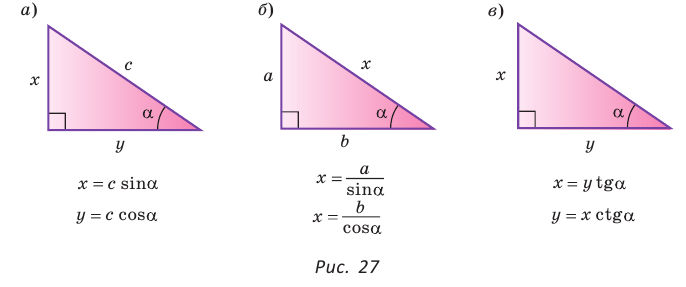
Пример №7
В 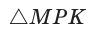 известно:
известно: 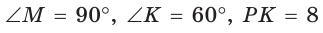 (рис. 28).
(рис. 28).
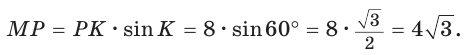
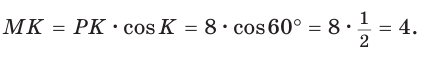
Полезно запомнить!
Если в прямоугольном треугольнике с углом 30° (или 60°) дан меньший катет а, то больший
катет 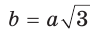 (рис. 29, а). А если дан больший катет
(рис. 29, а). А если дан больший катет 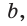 то меньший катет
то меньший катет 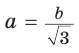 (рис. 29, б).
(рис. 29, б).
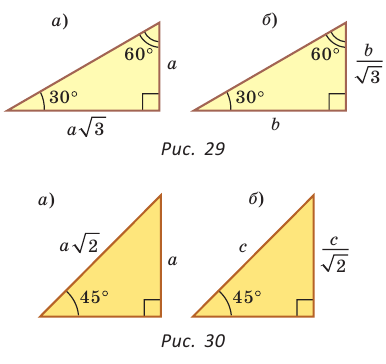
Если в прямоугольном треугольнике с углом 45° дан катет а,
то гипотенуза 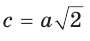 (рис. 30, а), а если дана гипотенуза с, то катет
(рис. 30, а), а если дана гипотенуза с, то катет 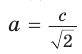 (рис. 30, б).
(рис. 30, б).
Пример №8
В прямоугольном треугольнике АВС известно: 
 — высота, проведенная к гипотенузе (рис. 31). Найти проекцию НВ катета ВС на гипотенузу.
— высота, проведенная к гипотенузе (рис. 31). Найти проекцию НВ катета ВС на гипотенузу.
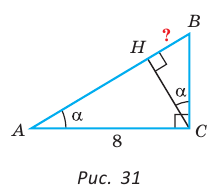
Решение:
Заметим, что  так как эти углы дополняют
так как эти углы дополняют  Из
Из 
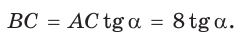 Из
Из 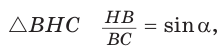
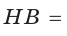
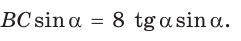
Ответ: 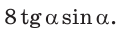
Пример №9
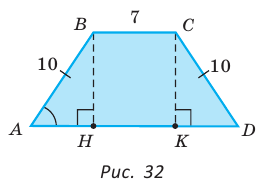
В равнобедренной трапеции ABCD меньшее основание ВС равно 7, боковая сторона АВ равна 10, sinA = 0,8. Найти площадь трапеции.
Решение:
Площадь трапеции находится по формуле 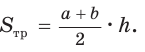 Найдем большее основание и высоту трапеции. Проведем в трапеции высоты ВН и СК (рис. 32). Так как НВСК — прямоугольник (все углы — прямые), то НК = ВС = 7. Из равенства прямоугольных треугольников АНВ и DKC (по катету и гипотенузе) АН = KD. Из прямоугольного треугольника АНВ находим:
Найдем большее основание и высоту трапеции. Проведем в трапеции высоты ВН и СК (рис. 32). Так как НВСК — прямоугольник (все углы — прямые), то НК = ВС = 7. Из равенства прямоугольных треугольников АНВ и DKC (по катету и гипотенузе) АН = KD. Из прямоугольного треугольника АНВ находим: 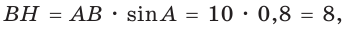 откуда АН = 6 (пифагорова тройка 6, 8, 10). Тогда
откуда АН = 6 (пифагорова тройка 6, 8, 10). Тогда 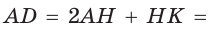
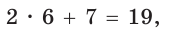
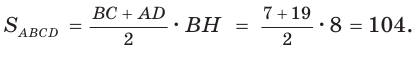
Ответ: 104.
Тригонометрические формулы
Используя формулы 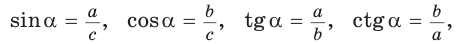 где
где 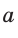 и
и 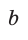 — катеты, с — гипотенуза прямоугольного треугольника, можно получить формулы, связывающие значения тригонометрических функций острого угла.
— катеты, с — гипотенуза прямоугольного треугольника, можно получить формулы, связывающие значения тригонометрических функций острого угла.
1. Основное тригонометрическое тождество
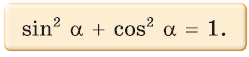
Доказательство:
По теореме Пифагора 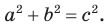
Тогда 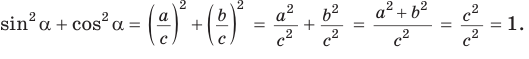
Следствие:
Так как синус и косинус острого угла а положительны, то
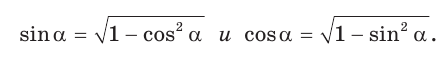
2. Выражение тангенса и котангенса через синус и косинус
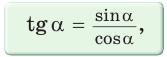
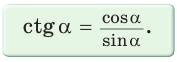
Доказательство:
a)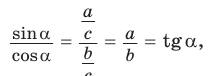 б)
б)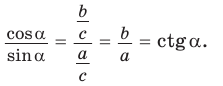
Следствие:
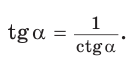
Проверим справедливость основного тригонометрического тождества.
Верно ли, например, что 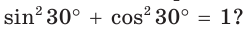 Да, это верно, так как
Да, это верно, так как 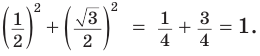
3. Основная задача
Дано: 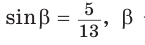 — острый угол.
— острый угол.
Найти: 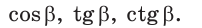
Решение:
Способ 1. Используем основное тригонометрическое тождество: 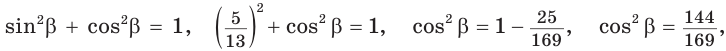
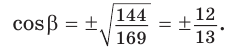 Так как косинус острого угла больше нуля, то
Так как косинус острого угла больше нуля, то 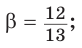 откуда
откуда 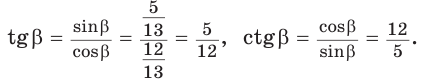
Способ 2. Изобразим прямоугольный треугольник с катетом 5 и гипотенузой 13 (рис. 41). Синус угла, противолежащего данному катету, равен 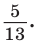 Поэтому этот угол равен
Поэтому этот угол равен 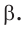 По теореме Пифагора другой катет равен
По теореме Пифагора другой катет равен 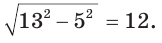 Тогда
Тогда 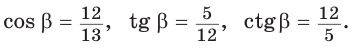
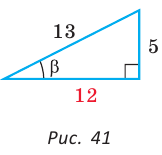
Способ 3. Пусть катет, противолежащий углу 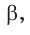 равен 5х, тогда гипотенуза равна
равен 5х, тогда гипотенуза равна 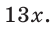 По теореме Пифагора прилежащий катет равен
По теореме Пифагора прилежащий катет равен 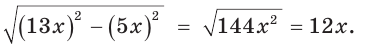 Отсюда
Отсюда 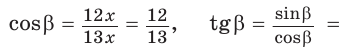
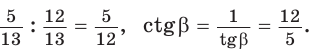
Ответ: 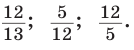
Пример №10
В параллелограмме ABCD (рис. 42) сторона ВС = 50 см, высота ВК = 30 см, 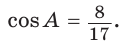 . Найти периметр параллелограмма.
. Найти периметр параллелограмма.
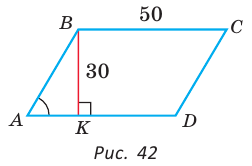
Решение:
Из треугольника АВК находим: 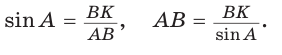 Из основного тригонометрического тождества следует:
Из основного тригонометрического тождества следует: 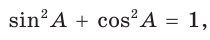
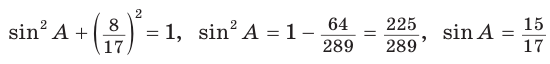 (так как угол А — острый, то sinA > 0). Тогда
(так как угол А — острый, то sinA > 0). Тогда 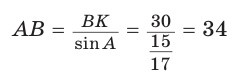 (см )
(см ) 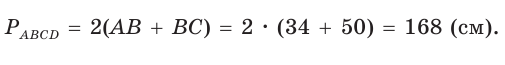
Ответ: 168 см.
Пример №11
Доказать, что при увеличении угла от 0° до 90°:
а) синус угла увеличивается от 0 до 1, а косинус — уменьшается от 1 до 0;
б) тангенс угла увеличивается от О до бесконечности.
Решение:
а) Рассмотрим прямоугольные треугольники с гипотенузой, равной 1. Для этого опишем радиусом ОМ, равным 1, четверть окружности — дугу МК (рис. 43). Пусть 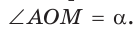 Опустим из точки А перпендикуляр АВ на ОМ. Тогда
Опустим из точки А перпендикуляр АВ на ОМ. Тогда 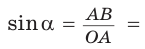
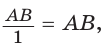
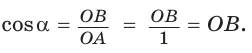 При повороте радиуса ОМ вокруг центра О против часовой стрелки, начиная от ОМ и заканчивая ОК, угол
При повороте радиуса ОМ вокруг центра О против часовой стрелки, начиная от ОМ и заканчивая ОК, угол 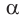 будет увеличиваться от 0° до 90° (образуя указанные на чертеже углы:
будет увеличиваться от 0° до 90° (образуя указанные на чертеже углы:  и т. д.). Величина катета АВ, противолежащего углу
и т. д.). Величина катета АВ, противолежащего углу 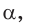 будет увеличиваться от 0 до 1. А величина катета ОВ, наоборот, будет уменьшаться от 1 до 0. Таким образом, при увеличении угла от 0° до 90° его синус увеличивается от 0 до 1, а косинус уменьшается от 1 до 0.
будет увеличиваться от 0 до 1. А величина катета ОВ, наоборот, будет уменьшаться от 1 до 0. Таким образом, при увеличении угла от 0° до 90° его синус увеличивается от 0 до 1, а косинус уменьшается от 1 до 0.
Из формулы 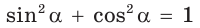 также следует (учитывая положительность синуса и косинуса острого угла), что с увеличением синуса от 0 до 1 косинус уменьшается от 1 до 0.
также следует (учитывая положительность синуса и косинуса острого угла), что с увеличением синуса от 0 до 1 косинус уменьшается от 1 до 0.
б) Для определения изменения тангенса угла удобно рассматривать треугольники, у которых прилежащий катет не изменяется и остается равным 1, а противолежащий катет изменяется. Рассмотрим прямоугольный треугольник АОМ, у которого отрезок ОМ = 1, 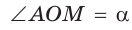 (рис. 44). По определению
(рис. 44). По определению 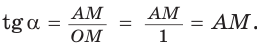 Угол
Угол 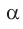 станем изменять, перемещая точку А по прямой MN, начиная от точки М и проходя через точки
станем изменять, перемещая точку А по прямой MN, начиная от точки М и проходя через точки 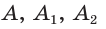 и т. д. При этом угол
и т. д. При этом угол 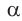 и его тангенс начнут возрастать. Таким образом, когда угол
и его тангенс начнут возрастать. Таким образом, когда угол 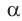 при движении точки А вверх будет стремиться к углу КОМ, равному 90°, то тангенс этого угла будет неограниченно возрастать.
при движении точки А вверх будет стремиться к углу КОМ, равному 90°, то тангенс этого угла будет неограниченно возрастать.
К такому же выводу можно прийти, рассматривая формулу 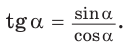 При увеличении угла
При увеличении угла 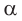 от 0° до 90° числитель дроби будет увеличиваться от 0 до 1, а знаменатель — уменьшаться от 1 до 0, значит, вся дробь будет увеличиваться от 0 до бесконечности. Таким образом, при увеличении угла от 0° до 90° его тангенс увеличивается от 0 до бесконечности.
от 0° до 90° числитель дроби будет увеличиваться от 0 до 1, а знаменатель — уменьшаться от 1 до 0, значит, вся дробь будет увеличиваться от 0 до бесконечности. Таким образом, при увеличении угла от 0° до 90° его тангенс увеличивается от 0 до бесконечности.
Пример №12
В основании прямоугольного параллелепипеда  лежит квадрат, диагональ которого
лежит квадрат, диагональ которого 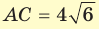 см. Диагональ
см. Диагональ 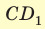 боковой грани составляет с ребром основания
боковой грани составляет с ребром основания 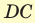 угол
угол  (рис. 46). Найдите объем параллелепипеда.
(рис. 46). Найдите объем параллелепипеда.
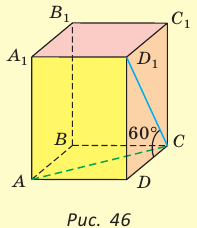
Решение:
Объем прямоугольного параллелепипеда находится по формуле 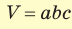 , где а, b и с — его измерения. Так как ABCD — квадрат, то
, где а, b и с — его измерения. Так как ABCD — квадрат, то 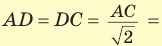
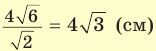 . Из прямоугольного треугольника
. Из прямоугольного треугольника 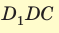 находим
находим 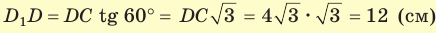 . Искомый объем
. Искомый объем 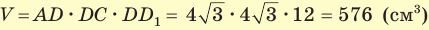 .
.
Ответ: 576 см3.
Синус, косинус, тангенс и котангенс тупого угла
1. Определение значений 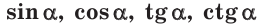 для любого угла а от 0° до 180°
для любого угла а от 0° до 180°
Ранее мы дали определения синуса, косинуса, тангенса и котангенса острого угла через отношение сторон прямоугольного треугольника. Сделаем теперь это для углов от 0° до 180°.
Рассмотрим полуокружность с центром в начале координат и радиусом, равным 1 (рис. 48). От положительной полуоси  против часовой стрелки отложим острый угол
против часовой стрелки отложим острый угол 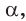 сторона которого пересекает полуокружность в точке
сторона которого пересекает полуокружность в точке 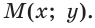 . Из прямоугольного треугольника OMN, где ОМ = 1, ON = х, MN = у, получаем:
. Из прямоугольного треугольника OMN, где ОМ = 1, ON = х, MN = у, получаем: 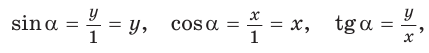
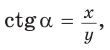 то есть синус, косинус,
то есть синус, косинус,
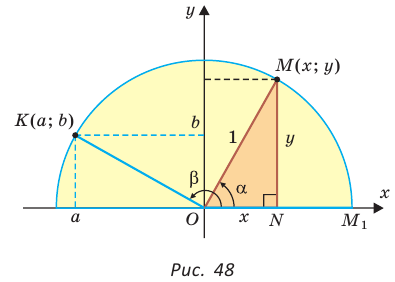
тангенс и котангенс острого угла а выражаются через координаты  точки
точки  Точно так же определяются значения
Точно так же определяются значения 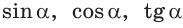 и
и 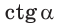 для любого угла а из промежутка
для любого угла а из промежутка 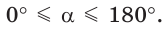 Таким образом, синусом угла а называется ордината
Таким образом, синусом угла а называется ордината 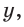 косинусом — абсцисса
косинусом — абсцисса 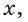 тангенсом — отношение ординаты к абсциссе
тангенсом — отношение ординаты к абсциссе 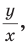 а котангенсом — отношение абсциссы к ординате
а котангенсом — отношение абсциссы к ординате 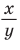 точки М единичной полуокружности.
точки М единичной полуокружности.
Например, для тупого 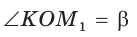 (рис. 48), где
(рис. 48), где 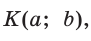 получим:
получим:
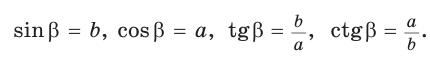
Для любого положения точки 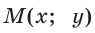 на единичной полуокружности верно равенство
на единичной полуокружности верно равенство 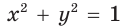 (докажите самостоятельно). Поэтому для углов
(докажите самостоятельно). Поэтому для углов  где
где  верно основное тригонометрическое тождество
верно основное тригонометрическое тождество 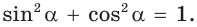
Также верны тождества: 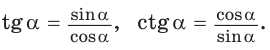
Нахождение синуса, косинуса, тангенса и котангенса тупых углов
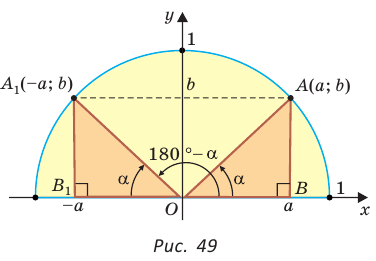
Пусть 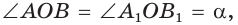 откуда
откуда 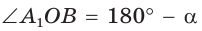 (рис. 49). Так как
(рис. 49). Так как 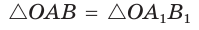 по гипотенузе и острому углу, то
по гипотенузе и острому углу, то 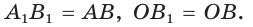 Точки
Точки 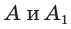 имеют координаты:
имеют координаты: 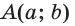 и
и 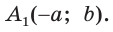 Тогда
Тогда 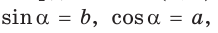
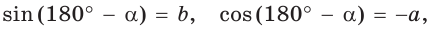 то есть для углов от 0° до 180° справедливы равенства:
то есть для углов от 0° до 180° справедливы равенства:
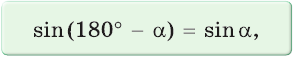
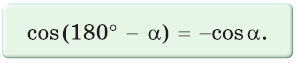
Можно пользоваться следующим правилом:
Синус тупого угла равен синусу смежного с ним острого угла.
Косинус тупого угла равен косинусу смежного с ним острого угла, взятому со знаком «минус».
Пример 1. 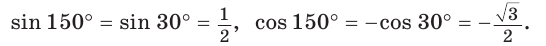
Разделив почленно равенство 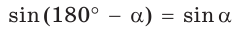 на равенство
на равенство 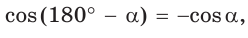 а затем наоборот, получим равенства:
а затем наоборот, получим равенства:
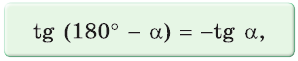
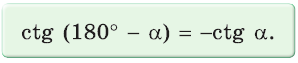
Можно пользоваться следующим правилом:
Тангенс (котангенс) тупого угла равен тангенсу (котангенсу) смежного с ним острого угла, взятому со знаком «минус».
Пример 2. 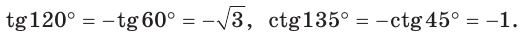
Указанные формулы и правила позволяют находить значения тригонометрических функций тупого угла через значения тригонометрических функций острого угла, который дополняет данный тупой угол до 180°: синусы углов, дополняющих друг друга до 180°, равны между собой, а косинусы, тангенсы и котангенсы — противоположны. Так как синус, косинус, тангенс и котангенс острого угла положительные, то синус тупого угла положительный, а косинус, тангенс и котангенс — отрицательные.
Значения тригонометрических функций для углов 0°, 90°, 180°
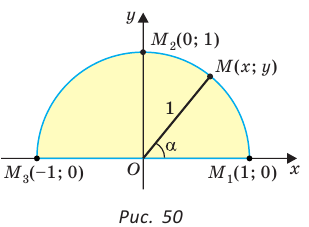
Если луч ОМ совпадет с лучом 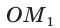 (рис. 50), то будем считать, что
(рис. 50), то будем считать, что 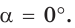 Тогда:
Тогда:
а) 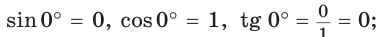 значение
значение 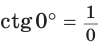 не определено, так как деление на нуль невозможно;
не определено, так как деление на нуль невозможно;
б) 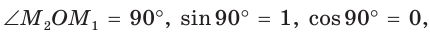
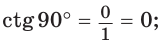 значение
значение 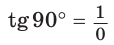 не определено, так как деление на нуль невозможно; в)
не определено, так как деление на нуль невозможно; в) 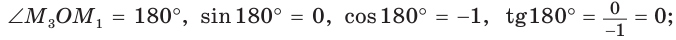 значение
значение 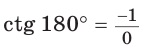 не определено, так как деление на нуль невозможно.
не определено, так как деление на нуль невозможно.
Поскольку проекции радиуса, равного 1, на оси координат меньше либо равны 1, то для углов 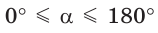 справедливы неравенства:
справедливы неравенства: 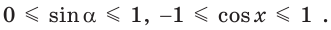
Пример №13
Найти 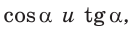 если
если 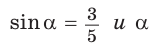 – тупой угол.
– тупой угол.
Решение:
Способ 1. Так как 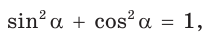 то
то 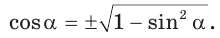 Поскольку угол
Поскольку угол 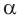 — тупой, то его косинус отрицательный. Поэтому
— тупой, то его косинус отрицательный. Поэтому 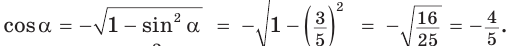 Тогда
Тогда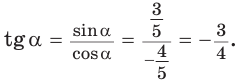
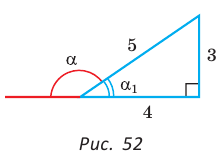
Способ 2. Синус острого угла 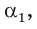 смежного с данным тупым углом
смежного с данным тупым углом 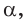 равен также
равен также 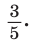 Построим прямоугольный треугольник со сторонами 3, 4 и 5 (рис. 52). В нем
Построим прямоугольный треугольник со сторонами 3, 4 и 5 (рис. 52). В нем 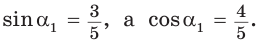 Так как косинусы смежных углов противоположны, то
Так как косинусы смежных углов противоположны, то 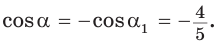 . Аналогично,
. Аналогично, 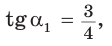
Ответ:
Формулы площади треугольника и площади параллелограмма
Тригонометрические функции позволяют получить формулы для вычисления площади треугольника и площади параллелограмма. Сформулируем их в виде двух теорем.
Теорема. Площадь треугольника равна половине произведения двух его сторон на синус угла между ними, т. е. 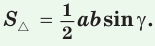
Доказательство:
Пусть в треугольнике  — острый,
— острый,  — высота (рис. 56, а).
— высота (рис. 56, а).
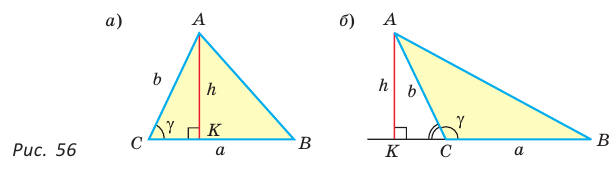
Из прямоугольного треугольника 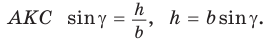 Тогда
Тогда 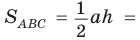
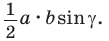
Если угол  тупой (рис. 56,
тупой (рис. 56, 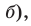 то
то 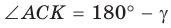 — острый. Из прямоугольного треугольника АКС следует, что
— острый. Из прямоугольного треугольника АКС следует, что 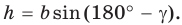 Так как
Так как 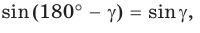 то
то 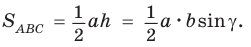
Если 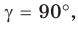 то
то 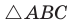 — прямоугольный с катетами
— прямоугольный с катетами 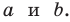 Учитывая, что
Учитывая, что  получим:
получим: 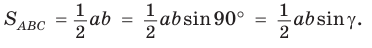
Теорема доказана.
Теорема. Площадь параллелограмма равна произведению двух его соседних сторон на синус угла между ними, т. е. 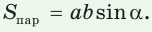
Используя рисунок 57, докажите эту теорему самостоятельно.
Замечание. Если 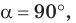 то параллелограмм является прямоугольником. Его площадь
то параллелограмм является прямоугольником. Его площадь 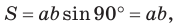 так как
так как  Таким образом, формула площади прямоугольника
Таким образом, формула площади прямоугольника 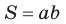 — частный случай формулы площади параллелограмма
— частный случай формулы площади параллелограмма 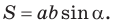

Известно, что слово «синус» в переводе с латинского имеет множество значений: изгиб, дуга, пазуха, бухта, впадина, залив, хорда, забота и нежная любовь. При помощи Интернета выясните:
а) какое из значений подходит к математическому понятию «синуса»;
б) какие из значений относятся к медицине и почему насморк врачи иногда называют синуситом.
Пример №14
Дан параллелограмм ABCD, площадь которого 40 см2, а периметр 36 см. Найти стороны параллелограмма, если его угол D равен 150° (рис. 58).
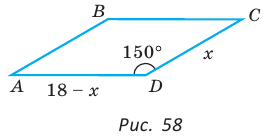
Решение:
Полупериметр параллелограмма равен 18 см. Если 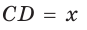 см, то
см, то 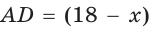 см.
см.
Тогда
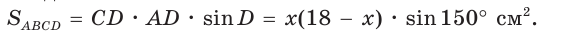
Так как 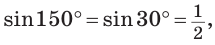 то
то 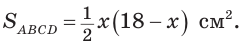
По условию 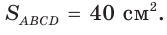 Составим и решим уравнение:
Составим и решим уравнение: 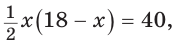
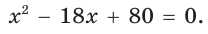 По теореме Виета (обратной)
По теореме Виета (обратной) 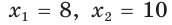 — корни.
— корни.
Если CD = 8 см, то AD = 10 см, если CD = 10 см, то AD = 8 см.
Ответ: 8 см, 10 см.
Пример №15
Доказать, что площадь выпуклого четырехугольника равна половине произведения его диагоналей на синус угла между ними, т.е. 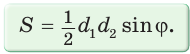
Доказательство:
Пусть диагонали 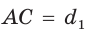 и
и 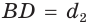 четырехугольника ABCD (рис. 59) пересекаются в точке О,
четырехугольника ABCD (рис. 59) пересекаются в точке О, 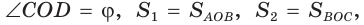
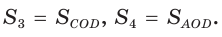 Докажем, что
Докажем, что 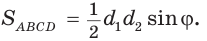
Обозначим 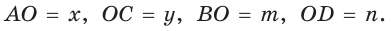 Заметим, что
Заметим, что 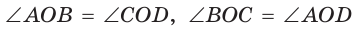 как вертикальные,
как вертикальные, 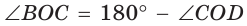 по свойству смежных углов. Поэтому
по свойству смежных углов. Поэтому 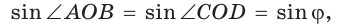
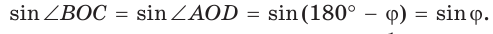 По формуле площади треугольника
По формуле площади треугольника 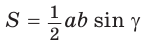 у получим:
у получим:
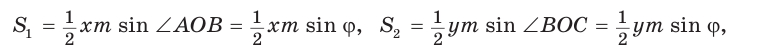
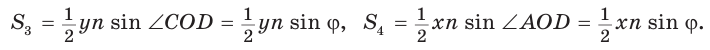
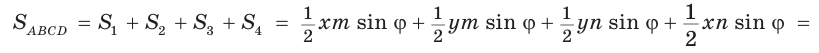
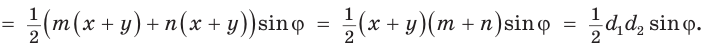
Утверждение доказано
Среднее пропорциональное (среднее геометрическое) в прямоугольном треугольнике
Если для положительных чисел 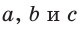 выполняется пропорция
выполняется пропорция 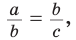 то число
то число 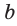 называется средним пропорциональным чисел а и с (между числами а и с). Из указанной пропорции
называется средним пропорциональным чисел а и с (между числами а и с). Из указанной пропорции 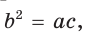 откуда
откуда 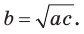 В такой форме записи число
В такой форме записи число 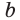 еще называют средним геометрическим чисел а и с.
еще называют средним геометрическим чисел а и с.
Пример №16
Число 4 является средним пропорциональным, или средним геометрическим чисел 2 и 8, так как = 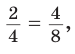 или
или 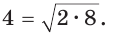
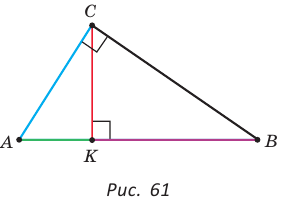
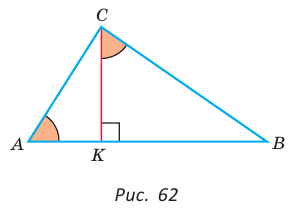
В прямоугольном треугольнике АВС, где 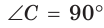 , проведем высоту СК (рис. 61). Отрезок АК является проекцией катета АС на гипотенузу, а отрезок ВК — проекцией катета ВС на гипотенузу. Катеты, гипотенуза, высота и проекции катетов на гипотенузу связаны отношениями, которые мы сформулируем в виде следующей теоремы.
, проведем высоту СК (рис. 61). Отрезок АК является проекцией катета АС на гипотенузу, а отрезок ВК — проекцией катета ВС на гипотенузу. Катеты, гипотенуза, высота и проекции катетов на гипотенузу связаны отношениями, которые мы сформулируем в виде следующей теоремы.
Теорема (о среднем пропорциональном в прямоугольном треугольнике).
а) Высота прямоугольного треугольника, проведенная к гипотенузе, есть среднее пропорциональное между проекциями катетов на гипотенузу, т. е. 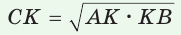 (см. рис. 61).
(см. рис. 61).
б) Катет есть среднее пропорциональное между гипотенузой и проекцией этого катета на гипотенузу, т. е. 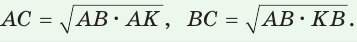
Доказательство:
а)3аметим, что если 
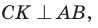 то
то 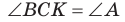 (эти углы дополняют
(эти углы дополняют 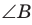 до 90°) (рис. 62). Из
до 90°) (рис. 62). Из 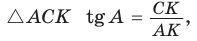 из
из 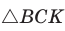
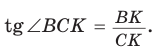 Отсюда
Отсюда 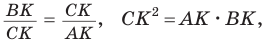
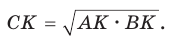
б) Из 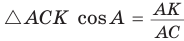 , из
, из 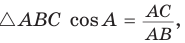 откуда
откуда 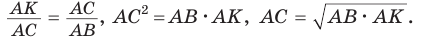
Аналогично доказывается, что 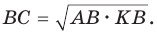 Теорема доказана.
Теорема доказана.
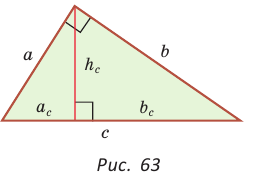
Обозначив катеты 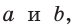 гипотенузу с, высоту
гипотенузу с, высоту 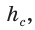 проекции катетов на гипотенузу
проекции катетов на гипотенузу 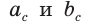 (рис. 63), получим следующие формулы:
(рис. 63), получим следующие формулы:
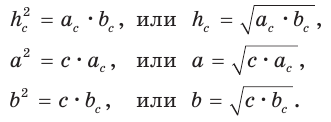
Пример №17
Найти площадь прямоугольного треугольника, если проекции катетов на гипотенузу равны 2 см и 8 см.
Решение:
Пусть СН — высота прямоугольного треугольника АВС  АН = 2 см — проекция катета АС на гипотенузу, НВ = 8 см —
АН = 2 см — проекция катета АС на гипотенузу, НВ = 8 см —
проекция катета СВ на гипотенузу (рис. 64). Так как высота СН есть среднее геометрическое между проекциями катетов на гипотенузу, то 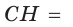
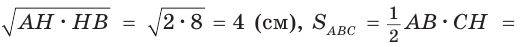
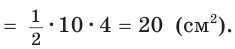
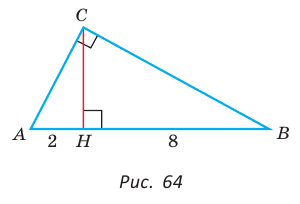
Ответ: 20 см2.
Пример №18
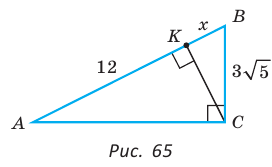
В прямоугольном треугольнике АВС из вершины прямого угла С проведена высота 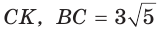 см, АК = 12 см (рис. 65). Найти гипотенузу АВ.
см, АК = 12 см (рис. 65). Найти гипотенузу АВ.
Решение:
Пусть 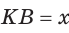 см, тогда
см, тогда 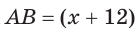 см.
см.
Катет есть среднее пропорциональное между гипотенузой и проекцией катета на гипотенузу. Поэтому 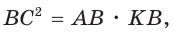 т. е.
т. е. 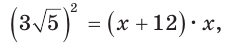
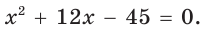 По теореме Виета (обратной)
По теореме Виета (обратной) 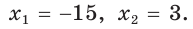 По смыслу задачи
По смыслу задачи 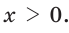 Значит, КВ = 3 см, АВ = 15 см.
Значит, КВ = 3 см, АВ = 15 см.
Ответ: 15 см.
Пример №19
При помощи циркуля и линейки построить отрезок, равный среднему геометрическому отрезков т и п .
Решение:
Пусть даны отрезки т и п . Необходимо построить отрезок 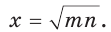
Построение.
1) На произвольной прямой откладываем данные отрезки: 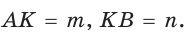
2) На отрезке АВ как на диаметре строим полуокружность, для чего находим середину О отрезка АВ, откуда ОА — радиус данной окружности.
3) Из точки К восстанавливаем перпендикуляр к прямой АВ до пересечения с полуокружностью в точке М (рис. 66).
Отрезок 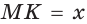 — среднее пропорциональное отрезков
— среднее пропорциональное отрезков 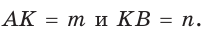
Доказательство:
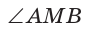 — прямой как вписанный угол, опирающийся на диаметр. В прямоугольном треугольнике АМВ высота МК является средним пропорциональным проекций катетов AM и МВ на гипотенузу
— прямой как вписанный угол, опирающийся на диаметр. В прямоугольном треугольнике АМВ высота МК является средним пропорциональным проекций катетов AM и МВ на гипотенузу 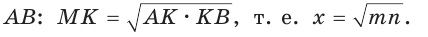
Повторение*
В 8-м классе мы доказали следующую теорему:
Теорема (о касательной и секущей). Если из одной точки к окружности проведены касательная и секущая, то квадрат отрезка касательной, соединяющего данную точку и точку касания, равен произведению отрезков се кущей, соединяющих данную точку и точки пересечения секущей с окружностью, т. е. 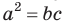 (рис. 70).
(рис. 70).
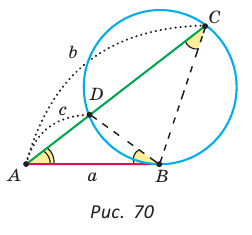
Как видим, отрезок 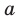 является средним пропорциональным между отрезками
является средним пропорциональным между отрезками 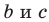 секущей. Глядя на рисунок 70, вспомните идею доказательства теоремы.
секущей. Глядя на рисунок 70, вспомните идею доказательства теоремы.
Теорема о площадях треугольников с общим (равным) углом
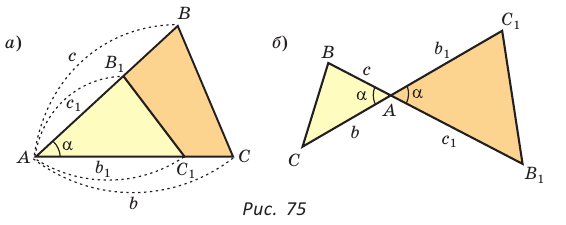
Площади треугольников, имеющих общий угол (или равный угол), относятся как произведения сторон, заключающих этот угол (рис. 75),
т.е. 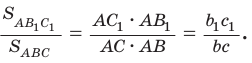
Доказательство:
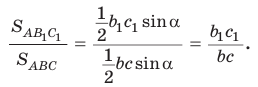
Следствие: Верно:
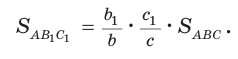
Пример №20
Площадь треугольника АВС равна 16, АК : КС = 3 :1 , AM : МВ = 1 :2 (рис. 76). Найти 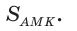
Решение:
Способ 1. По следствию из теоремы о площадях треугольников с общим углом получаем:
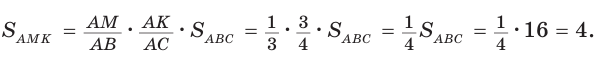
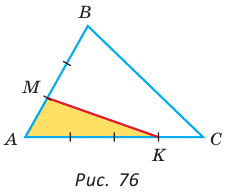
Способ 2. 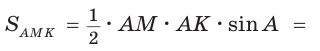
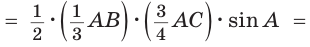
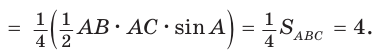
Ответ: 4.
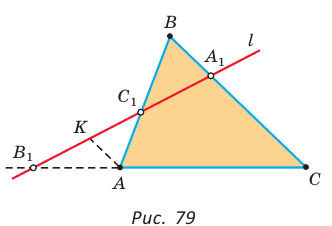
Теорема Менелая
Если дан треугольник АВС и прямая 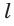 пересекает стороны ВС, АВ и продолжение стороны АС в точках
пересекает стороны ВС, АВ и продолжение стороны АС в точках 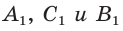 соответственно (рис. 79), то
соответственно (рис. 79), то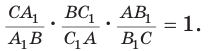
Доказательство:
Проведем отрезок 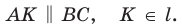 Так как
Так как 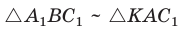 и
и  (по двум углам), то
(по двум углам), то 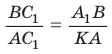 и
и 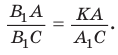 Перемножив почленно указанные пропорции, получим
Перемножив почленно указанные пропорции, получим
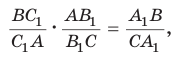 откуда
откуда 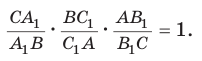
Замечание. При составлении произведения трех отношений теоремы Менелая можно начинать с любой из шести точек (трех вершин треугольника и трех точек пересечения прямой  с прямыми, содержащими стороны треугольника) и двигаться по контуру либо по часовой, либо против часовой стрелки. При этом вершины треугольника и точки пересечения должны чередоваться.
с прямыми, содержащими стороны треугольника) и двигаться по контуру либо по часовой, либо против часовой стрелки. При этом вершины треугольника и точки пересечения должны чередоваться.
Пример №21
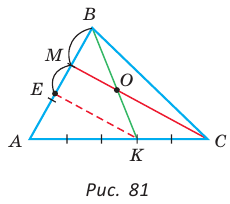
В треугольнике АВС на сторонах АВ и АС взяты соответственно точки М и К, такие, что AM : МВ = 2 :1 , АК : КС = 3 :2 . Отрезки СМ и ВК пересекаются в точке О. Найти ВО : ОК.
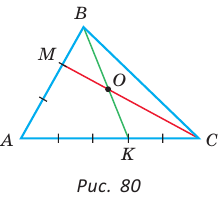
Решение:
Способ 1 (теорема Менелая). Рассмотрим 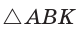 (рис. 80). Прямая
(рис. 80). Прямая 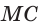 пересекает две его стороны АВ и ВК соответственно в точках М и О и продолжение третьей стороны АК в точке С. По теореме Менелая
пересекает две его стороны АВ и ВК соответственно в точках М и О и продолжение третьей стороны АК в точке С. По теореме Менелая 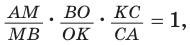 откуда
откуда 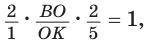
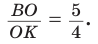
Способ 2 (теорема Фалеса обобщенная). Проведем 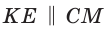 (рис. 81). По теореме Фалеса
(рис. 81). По теореме Фалеса 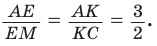 Тогда АЕ — три части, ЕМ — две части, AM — пять частей, откуда
Тогда АЕ — три части, ЕМ — две части, AM — пять частей, откуда 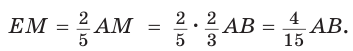
Но 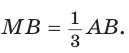 Отсюда
Отсюда 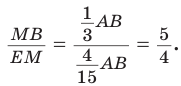 Для
Для 
по теореме Фалеса 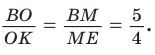
Ответ: 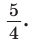
Пример №22
Дан равнобедренный треугольник АВС (АВ = ВС), площадь которого равна 80. Точка К делит высоту ВН в отношении 1 : 3, считая от основания. Прямая АК пересекает сторону ВС в точке М. Найти площадь четырехугольника НКМС (рис. 82).
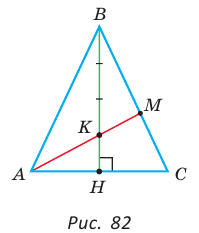
Решение:
1) 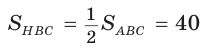 (ВН — высота и медиана треугольника АВС).
(ВН — высота и медиана треугольника АВС).
2) Применим теорему Менелая к треугольнику НВС.
Прямая AM пересекает его стороны ВН и ВС соответственно в точках К и М и продолжение стороны НС в точке  Тогда
Тогда 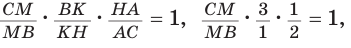
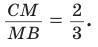 Откуда
Откуда 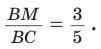
3) 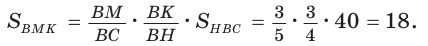
4) 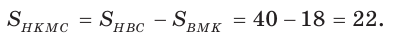
Ответ: 22.
Неравенство Коши
Среднее арифметическое двух неотрицательных чисел больше либо равно их среднему геометрическому, т. е.
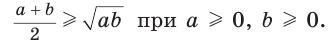
Например, 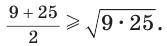 Действительно,
Действительно, 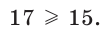
Алгебраическое доказательство указанного неравенства таково. Рассмотрим разность левой и правой частей неравенства 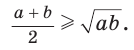 Получим:
Получим: 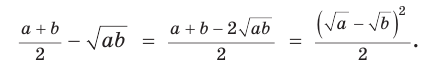 Так как
Так как 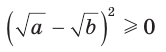 при всех допустимых
при всех допустимых 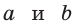 , то
, то 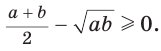 Следовательно, неравенство
Следовательно, неравенство 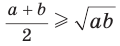 верно.
верно.
Неравенство 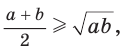 где
где 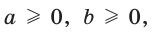 называется неравенством Коши по имени известного французского математика и часто используется при решении олимпиадных задач.
называется неравенством Коши по имени известного французского математика и часто используется при решении олимпиадных задач.
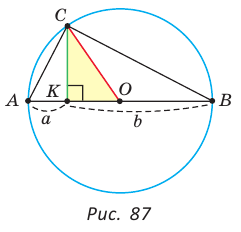
Приведем геометрическое доказательство указанного неравенства. Изобразим окружность с диаметром АВ и центром в точке О (рис. 87). На диаметре возьмем точку К (для определенности левее центра О). Пусть 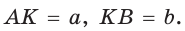 Из точки К восстановим перпендикуляр КС, где точка С принадлежит окружности. Проведем радиус ОС. Так как вписанный угол, опирающийся на диаметр, прямой, то
Из точки К восстановим перпендикуляр КС, где точка С принадлежит окружности. Проведем радиус ОС. Так как вписанный угол, опирающийся на диаметр, прямой, то  прямоугольный, СК — его высота, проведенная к гипотенузе. По теореме о среднем пропорциональном в прямоугольном треугольнике
прямоугольный, СК — его высота, проведенная к гипотенузе. По теореме о среднем пропорциональном в прямоугольном треугольнике 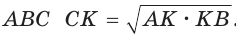 . Но радиус ОС равен половине диаметра АВ, т. е.
. Но радиус ОС равен половине диаметра АВ, т. е. 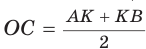 . В
. В 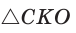 катет меньше гипотенузы, т. е.
катет меньше гипотенузы, т. е. 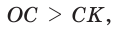 так как катет меньше гипотенузы. Отсюда
так как катет меньше гипотенузы. Отсюда 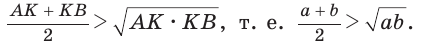
Равенство левой и правой частей неравенства достигается, когда точка К совпадает с точкой О и 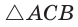 становится равнобедренным и прямоугольным. Поэтому справедливо неравенство
становится равнобедренным и прямоугольным. Поэтому справедливо неравенство 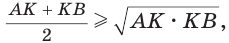 т. е
т. е 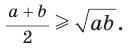
ЗАПОМИНАЕМ
2. Значения тригонометрических функций углов 30 45°, 60°:
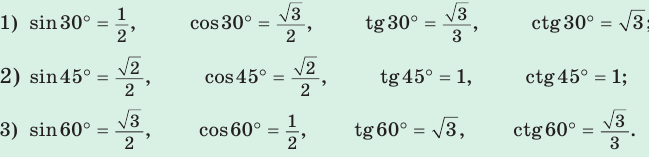
3. Тригонометрические формулы (тождества):
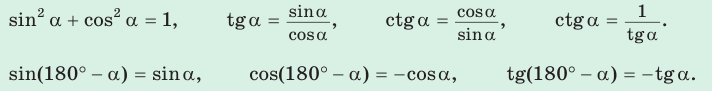
Примеры: 
4. Формулы площади треугольника и параллелограмма:

5. Среднее пропорциональное в прямоугольном треугольнике:
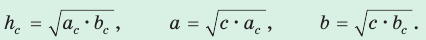
- Сумма углов треугольника
- Внешний угол треугольника
- Свойство точек биссектрисы угла
- Свойство катета прямоугольного треугольника, лежащего против угла в 30°
- Угол – определение, виды, как обозначают с примерами
- Перпендикулярные прямые в геометрии
- Признаки равенства треугольников
- Признаки равенства прямоугольных треугольников
Как найти тангенс, если известен косинус
Понятие тангенса является одним из основных в тригонометрии. Оно обозначает некую тригонометрическую функцию, которая является периодической, но не непрерывной в области определения, как синус и косинус. И имеет разрывы в точках (+,-)Пи*n+Пи/2, где n – это период функции. В России он обозначается как tg(x). Его можно представить через любую тригонометрическую функцию, так как все они тесно взаимосвязаны между собой.

Вам понадобится
- Учебник по тригонометрии.
Инструкция
Для того, чтобы выразить тангенс угла через синус, нужно вспомнить геометрическое определение тангенса. Итак, тангенсом острого угла в прямоугольном треугольнике, называют отношение противолежащего катета к прилежащему.
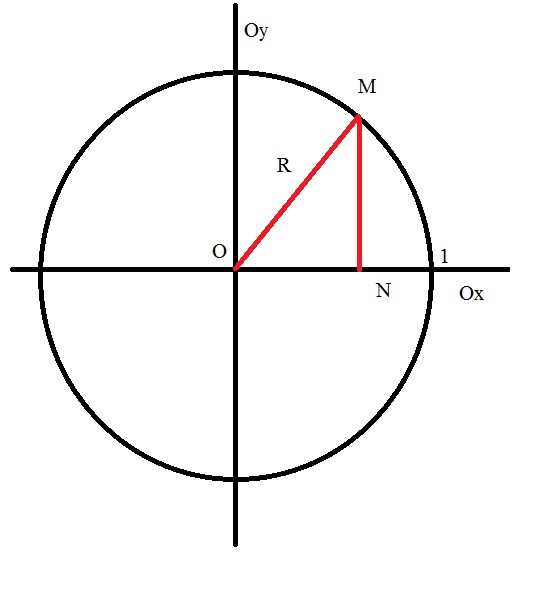
С другой стороны, рассмотрите декартову систему координат, на которой начерчена единичная окружность с радиусом R=1, и центром О в начале координат. Примите поворот против часовой стрелки, как положительный, а в обратную сторону отрицательный.
Отметьте некую точку M на окружности. Из нее опустите перпендикуляр на ось Ох, назовите ее точкой N. Получился треугольник OMN, у которого угол ONM является прямым.
Теперь рассмотрите острый угол MON, по определению синуса и косинуса острого угла в прямоугольном треугольнике
sin(MON) = MN/OM, cos(MON) = ON/OM. Тогда MN= sin(MON)*OM, а ON = cos(MON)*OM.
Вернувшись к геометрическому определению тангенса (tg(MON) = MN/ON), подставьте полученные выше выражения. Тогда:
tg(MON) = sin(MON)*OM/cos(MON)*OM, сократите OM, тогда tg(MON) = sin(MON)/cos(MON).
Из основного тригонометрического тождества (sin^2(x)+cos^2(x)=1) выразите косинус, через синус: cos(x)=(1-sin^2(x))^0,5 Подставьте это выражение в полученное на шаге 5. Тогда tg(MON) = sin(MON)/(1-sin^2(MON))^0,5.
Иногда существует потребность в вычисление тангенса двойного и половинчатого угла. Тут тоже выведены соотношения:tg(x/2) = (1-cos(x))/sin(x) = (1-(1-sin^2(x))^0,5)/sin(x);tg(2x) = 2*tg(x)/(1-tg^2(x)) = 2*sin(x)/(1-sin^2(x))^0,5/(1-sin(x)/(1-sin^2(x))^0,5)^2) =
= 2*sin(x)/(1-sin^2(x))^0,5/(1-sin^2(x)/(1-sin^2(x)).
Также возможно выразить квадрат тангенса через двойной угол косинуса, либо синус. tg^2(x) = (1-cos(2x))/(1+cos(2x)) = (1-1+2*sin^2(x))/(1+1-2*sin^2(x)) = (sin^2(x))/(1-sin^2(x)).
Обратите внимание
Обратите внимание на области допустимых значений при решение уравнений и неравенств.
Полезный совет
Знание наизусть основных тождеств, поможет быстро переходить от одних тригонометрических функций к другим.
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Тангенс в прямоугольном треугольнике
Что такое тангенс в прямоугольном треугольнике? Как найти тангенс? От чего зависит значение тангенса?
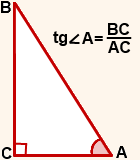
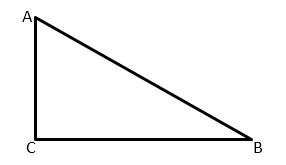
Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.
Например, для угла A треугольника ABC
Поэтому тангенс угла A в треугольнике ABC — это
Для угла B треугольника ABC
противолежащим является катет AC,
Соответственно, тангенс угла B в треугольнике ABC
равен отношению AC к BC:
Таким образом, тангенс острого угла прямоугольного треугольника — это некоторое число, получаемое при делении длины противолежащего катета на длину прилежащего катета.
Так как длины катетов — положительные числа, то и тангенс острого угла прямоугольного треугольника является положительным числом.
Тангенс угла треугольника зависит от величины угла, но не зависит от катетов (важно лишь их отношение).
Если в треугольнике изменить длины катетов, не меняя угол, то величина тангенса не изменится.
Тангенс в прямоугольном треугольнике – свойства, формула и примеры нахождения
Геометрические фигуры завораживают количеством своих свойств и функций, таких как тангенс в прямоугольном треугольнике. Это происходит в основном из-за двух факторов.
Во-первых, нам уже известен один из углов, который равен 90 градусам. Во-вторых, есть много свойств с применением прямоугольников. А из двух прямоугольных треугольников как раз получается именно такая фигура.
Из этого вытекает многое, но сегодня мы поговорим об одном очень интересном свойстве такого треугольника, как тангенс. В данной статье мы подробно рассмотрим определение тангенса, узнаем, как его можно найти и как его можно использовать.
Если вы уже что-то слышали про отношения одной из сторон к гипотенузе, то здесь все просто. Если же нет – то ниже дано краткое объяснение.
Что такое тангенс в прямоугольном треугольнике
Синусом угла в треугольнике называют отношение противолежащей данному углу стороны к гипотенузе треугольника, а косинусом – прилежащего к гипотенузе.
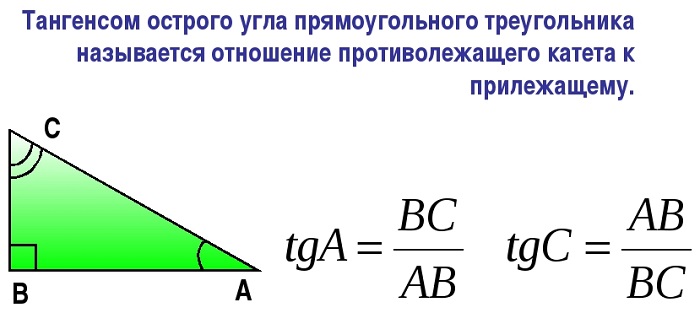
И если мы поделим синус угла на косинус, то получим тангенс (обозначается как tg), а если косинус на синус – то котангенс. Здесь все очень просто, главное знать катеты и гипотенузу треугольника.

Также бывают и тригонометрические тангенсы на окружности со своими графиками, разностью показателей числа π, но в данной статье мы их не рассматриваем, так как к треугольнику они имеют лишь косвенное отношение.
Таблица тангенсов углов от 0° до 360°
Ниже представлена таблица значений, которая пригодится для быстрого нахождения необходимых значений.
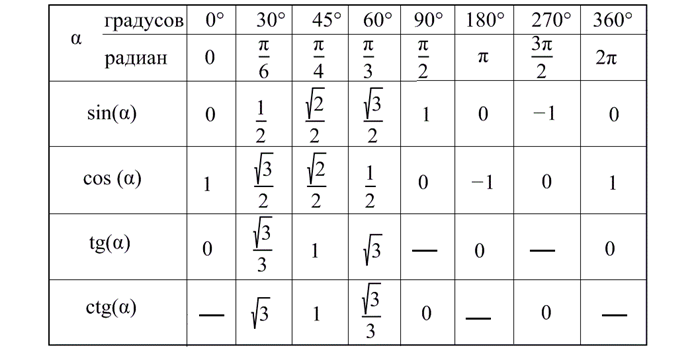
В качестве альтернативы предлагаем либо искать значения онлайн, либо запоминать их. Самым же эффективным способом математики считают вывод этих значений, но это будет удобно далеко не для всех.
Примеры вычислений тангенса в прямоугольном треугольнике
Существует довольно много способов и несложных формул для нахождения тангенса в прямоугольном треугольнике. Мы же рассмотрим только некоторые из них.
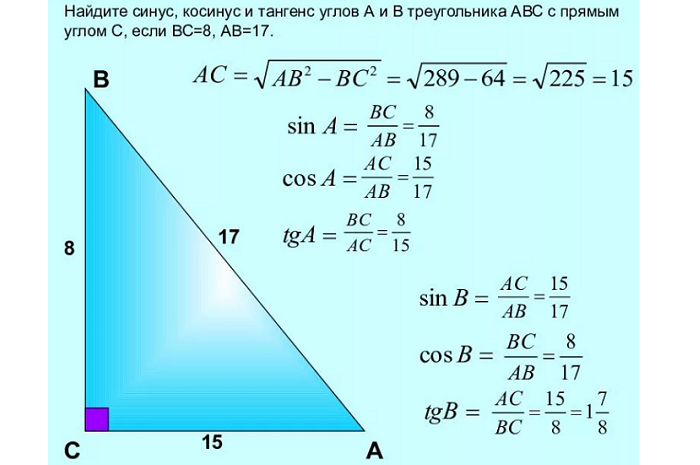
Все способы упираются в нахождение сторон, поэтому здесь секрет прост – если вы знаете значения всех сторон, то тангенс угла A в треугольнике находится по следующему правилу: tgA = BC : AC, что означает, что tg A равен отношению противолежащей стороны углу к прилежайщей.
Легче всего найти тангенс именно острого угла. Если даже это не угол прямоугольного треугольника, то дополнить его до прямоугольного не составит труда.
Это то, на чем построена сама сущность тангенса, но если нужно найти стороны, то это уже точно задача не про тангенсы.
Что такое тангенс угла и как его найти
Живущим людям на Земле
всегда хотелось знать,
как путь найти в пустыне, море,
и можно к звёздам ли попасть.
Хотелось труд свой облегчить,
создать машины, чтоб летать.
И чтоб вопросы разрешить,
пришлось про тангенс всем узнать.
Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. Впервые встречаясь с тригонометрией в восьмом классе на геометрии, школьники оглядываются на свою жизнь, задавая вопрос, насколько пригодится им эта область науки в дальнейшем.
Редко кто задумывается, что раздел математики, позволяющий рассказать о заданном треугольнике всё (найти все его стороны и углы, выделить особенности), позволил в своё время сделать великие открытия.
Тригонометрия, дав возможность строить корабли и самолёты, отправлять человека в космос, создавать приборы для ориентирования на море, в лесу, в пустыне, определять расстояния, не измеряя их непосредственно линейкой, шагами или чем-то иным, помогла упростить жизнь человечества, раскрыть новые горизонты знаний.
Тангенс угла
Первые встречи с тангенсом происходят при изучении прямоугольных треугольников.
В них соотношения сторон, образующих прямой угол (катетов), и стороны, лежащей напротив угла в 90º (гипотенузы), задают важные параметры для изучения углов.
Для понимания связи между объектами рассматриваются отношения различных отрезков. Задавая связь между ними, вводят понятия синуса, косинуса (это что?), тангенса, котангенса.
Важно, что это отвлечённые понятия, не связанные с какими-либо единицами измерения.
Введя функции угла, определяют их свойства. Некоторые полученные формулы могут иметь довольно громоздкий вид. Чтобы избежать затруднённого чтения, вводятся другие объекты.
Так произошло и с тангенсом. Ему посчастливилось получить два определения. Каждое характеризует заданное отношение по-своему. С одной стороны, рассматривается связь между катетами и острыми углами прямоугольного треугольника, с другой – даётся возможность упростить формулы, содержащие синусы и косинусы.
Мало кто задумывается, изучая тангенс в школе, что первоначально он был необходим, чтобы найти касательные линии к заданной кривой. Само понятие возникло от латинского слова tangens, которое означает «трогающий», «касающийся» и является причастием настоящего времени от tangere («трогать», «касаться»).
Тангенс — это отношение.
Итак, есть два определения:
Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.
Это определение удобно использовать при изучении геометрических фигур. Оно даёт возможность, минуя вычисления гипотенузы, находить углы или катеты. Выделяя прямоугольные треугольники в произвольных фигурах, задача по изучению свойств исследуемых объектов становится проще.
Тангенс – это отношение синуса к косинусу.
Благодаря этому определению, многие тригонометрические формулы принимают более удобный вид, становятся легче воспринимаемыми.
” alt=””>
Вместо «тангенс угла альфа» пишут: tgα. На калькуляторах, в различных программах ЭВМ и ПК закрепилось другое обозначение: tan(α).
Как найти тангенс угла (формулы)
Первое свойство тангенса вытекает из его определения как отношения катетов.
Сумма двух непрямых углов прямоугольного треугольника равна 90º. Поэтому
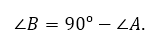
Так как тангенс – это отношение катетов, то
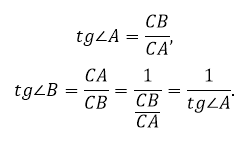
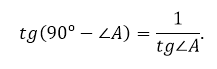
Учитывая особенности некоторых треугольников (равностороннего, прямоугольного, равнобедренного), а также записанное свойство, была составлена таблица значений тангенса для углов 30º, 45º, 60º.
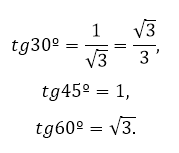
Задача нахождения других углов по значению тангенса была решена с помощью составления более обширных таблиц. За счёт появления современных вычислительных средств необходимость применения табулированных значений уменьшилась.
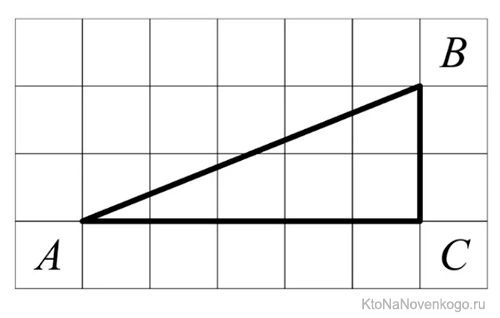
Как найти тангенс по клеточкам
Учитывая первое определение, можно определить, как найти тангенс угла по клеточкам. Рисунок дополняется перпендикулярными линиями (строится высота), затем считается количество клеточек в полученном прямоугольном треугольнике на катетах, противолежащем и прилежащем искомому углу, а затем берётся их отношение.
Благодаря второму определению, задачу, как найти тангенс угла, можно решить, минуя таблицы и построение прямоугольных треугольников. Достаточно знать синус и косинус, связанные между собой основным тригонометрическим тождеством:
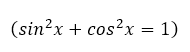
Из формулы тангенсов, записывающей кратко второе определение
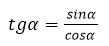
и основного тригонометрического тождества можно понять, как найти тангенс, зная только косинус или синус угла.
Достаточно поделить основное тригонометрическое тождество на квадрат косинуса, подставить формулу тангенса. В результате получится зависимость тангенса и косинуса:
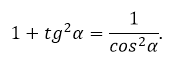
Если выразить в последнем случае косинус, то запишется связь между тангенсом и синусом:
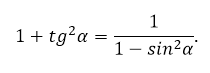
Удачи вам! До скорых встреч на страницах блога KtoNaNovenkogo.ru
Эта статья относится к рубрикам:
Комментарии и отзывы (5)
Я Очень Люблю Правила, Теоремы, Формулы по Предмету «Математика», «Алгебра».
Прочитал статью и остался один главный вопрос, а собственно без вспомогательных таблиц найти угол В ГРАДУСАХ вообще возможно и есть ли у вас статья, где рассказыввается как это сделать? Спасибо.
Я ни разу не математик, но почему у вас сумма углов прямоугольного треугольника равна 90 градусов. А так все хорошо начиналось. Объясняете хорошо, но после таких ошибок у меня сомнения что информация верная.
Спасибо. Уточнил в тексте, что это сумма двух непрямых углов прямоугольного треугольника.
Пишу стихи. Востребован тангенс для решения жизненных ситуаций поскольку состоит из тех же функций,как-то, касающийся,прилежащий, трогающий. Куда без них денешься.
[spoiler title=”источники:”]
http://nauka.club/matematika/geometriya/tangens.html
http://ktonanovenkogo.ru/voprosy-i-otvety/tangens-chto-ehto-takoe-otnoshenie-najti-formulam-kletochkam.html
[/spoiler]
Ответы Mail.ru
Образование
ВУЗы, Колледжи
Детские сады
Школы
Дополнительное образование
Образование за рубежом
Прочее образование
Вопросы – лидеры.
Где найти ответы на ОГЭ 2023?
1 ставка
Написать экологическое обоснование изделия из кольца
1 ставка
Помогите с английским 21 упражнением, расставить a,an,the.
1 ставка
Чем на ваш взгляд лучше заменить ЕГЭ?
1 ставка
Лидеры категории
Лена-пена
Искусственный Интеллект
М.И.
Искусственный Интеллект
Y.Nine
Искусственный Интеллект
•••
Как найти Тангенс числа, зная косинус? Напишите формулу, пожалуйста.!!!
Митяй
Мудрец
(16354),
закрыт
12 лет назад
Лучший ответ
Vlad Boikov
Профи
(739)
12 лет назад
sin^2+Cos^2=1
а дальше сам
Остальные ответы
BuHT
Мастер
(1169)
12 лет назад
tg=sin/cos=((1-cos^2)^1/2)/cos
Екатерина Максимова
Мыслитель
(5442)
12 лет назад

Роза Марковна
Просветленный
(35806)
12 лет назад
Пожалуй вот так
tg=sin/cos
sin^2+cos^2=1
sin= корень (1-cos^2)
тогда tg=(корень (1-cos^2))/cos
Похожие вопросы
