Всего: 40 1–20 | 21–40
Добавить в вариант
Тип 18 № 40 

i
Найдите тангенс угла AOB, изображенного на рисунке.
Найдите тангенс угла AOB, изображённого на рисунке.
Найдите тангенс угла AOB.
Найдите тангенс угла AOB, в треугольнике, изображённом на рисунке.
Найдите тангенс угла AOB, изображённого на рисунке.
Найдите тангенс угла AOB.
Найдите тангенс угла AOB, изображённого на рисунке.
Найдите тангенс угла AOB.
Найдите тангенс угла AOB, изображённого на рисунке.
Найдите тангенс угла AOB. Размер клетки 1 × 1.
Найдите тангенс угла AOB.
Найдите тангенс угла AOB, изображённого на рисунке.
Найдите тангенс угла AOB, изображённого на рисунке.
Найдите тангенс угла AOB
Найдите тангенс угла AOB, изображённого на рисунке.
Найдите тангенс угла AOB, изображённого на рисунке.
Найдите тангенс угла AOB, изображённого на рисунке.
Найдите тангенс угла AOB
Найдите тангенс угла AOB, изображённого на рисунке.
Найдите тангенс AOB
Всего: 40 1–20 | 21–40
Обычно в задачах требуется найти тангенс именно острого угла, как, допустим, на этом примере:

Для этого мы строим прямоугольный треугольник, проведя линию (перпендикуляр) BD:

Далее вспоминаем определение тангенса, это отношение противолежащего катета к прилежащему.
То есть tg(BOA) = DB / DO.
Чтобы найти DO и DB достаточно будет посчитать количество клеточек.
DO = 2.
DB = 5.
Значит, tg(BOA) = 5 / 2 = 2,5.
Зная тангенс, мы можем легко найти и котангенс:
ctg(BOA) = 1 / tg(BOA) = 1 / 2,5 = 0,4.
_
А вот задача на нахождение тангенса угла по клеточкам немного другого плана (ищем тангенс угла AOB):

Если соединить точки A и B, то угол ABO будет прямым.

И тангенс можно вычислить как отношение BA к BO.
Как же нам их найти?

И BO, и BA будут гипотенузами 2 совершенно равных прямоугольных треугольников (для наглядности я их выделил красным).
Длина катетов их равна 2 и 8, а квадрат гипотенузы, как известно, равен сумме квадратов катетов.
Таким образом, у нас получится следующее:
tg(BOA) = BA / BO = √(2² + 8²) / √(2² + 8²) = 1.
И нетрудно догадаться, что треугольник этот равнобедренный с равными углами BOA и BAO по 45 градусов.
Здравствуйте, дорогие читатели. В этом выпуске поговорим о задании, которое иногда доставляет неожиданные неприятности на экзамене. Задания довольно простые, но бывают промахи. Это задания, которые сделаны как бы на тетрадном листочке в клеточку. Итак, давайте начнем.
Задание №1. УГЛЫ
Задача №1
Запомните, чтобы найти тангенс острого угла на таких картинках, обязательно нужно достроить до прямоугольного треугольника.
Вспомним, что такое тангенс острого угла прямоугольного треугольника?
Определение тангенса острого угла:
Тангенсом острого угла прямоугольного треугольника, называется отношение противолежащего катета к прилежащему. Катет BF- противолежащий угла FОВ, OF – прилежащий к углу FOB.
Задача №2
Чтобы найти тангенс угла АОВ на этой картинке, нужно достроить до прямоугольного треугольника, и найти стороны этого треугольника.
1. Достроим до треугольника ОВН и докажем, что он прямоугольный.
2. Для этого достроим на стороне ОН, ОВ и ВН прямоугольные треугольники ОСВ, ОНК и BDH. Докажем, что треугольник АВН прямоугольный.
Найдем гипотенузу ОВ прямоугольного треугольника ОСВ, гипотенузу ОН прямоугольного треугольника ОКН и гипотенузу ВН прямоугольного треугольника ВDH через теорему Пифагора: квадрат гипотенузы равен сумме квадратов катетов.
Теперь докажем, что треугольник ОВН прямоугольный. Воспользуемся обратной теоремой Пифагора: если квадрат одной стороны равен сумме квадратов двух других сторон, то треугольник прямоугольный.
Так как равенство верно, то треугольник ОВН прямоугольный.
Теперь найдем тангенс угла АОВ
Задание №2 Расстояние
Для выполнения этого задания, проведите отрезок ВС, найдите середину его и отметим точкой К. Проведите отрезок АК, который равен 4. Ответ 4
Задание №3 Площадь
Задача №1
Задание простое, но есть ошибки по невнимательности.
Задача №2
а) Площадь треугольника и параллелограмма
Запомните! Площадь треугольника от площади параллелограмма отличается только тем, что площадь треугольника нужно делить на 2, а площадь параллелограмма нет.
б) Площадь трапеции. Чтобы найти площадь трапеции, нужно сложить основания трапеции, умножить на высоту и поделить на 2.
в) Площадь ромба равна половине произведения диагоналей.
Это не все типы заданий, что встречаются на экзамене. Продолжение следует.
Спасибо что дочитали. Вы меня очень поддержите, если поставите лайк и подпишитесь на мой блог.
 Подготовка
Подготовка
к ОГЭ: нахождение тангенса угла по клеткам.
1. Источник: МА-9 ДЕМО 2017
Найдите тангенс угла АОВ треугольника,
изображённого на рисунке.
Решение:
Тангенсом
угла прямоугольного треугольника называется отношение противолежащего катета к
прилежащему. Воспользовавшись клеточками, нетрудно найти нужные величины: АВ=4 АО=2
![]() =
= ![]() = 2
= 2
Ответ: 2
2. Источник: Открытый банк заданий по математике
Прототип задания 12 (№
27450)
 |
На клетчатой бумаге с размером клетки ![]()
изображён угол. Найдите тангенс этого угла
 |
Решение:
Находим прямоугольный треугольник
(как
показано на рисунке). Далее по п1.
Ответ: 2,5
3. Источник: Открытый банк
заданий по математике
Прототип задания 12 (№
27456)
 |
На клетчатой бумаге с размером клетки ![]()
изображён угол. Найдите тангенс этого угла
 |
Решение:
Находим прямоугольный треугольник
(как
показано на рисунке).
 |
Находим по т. Пифагора
противолежащий катет
(красный треугольник),
прилежащий катет
(жёлтый треугольник).
![]() = 1
= 1
 |
Замечание: обучающиеся
обычно решают это
задание следующим образом: кладут
снизу
клетчатый лист, чтобы на просвет
задача
стала аналогичной п.1.
(как показано на рисунке).
Ответ:
1
Обычно в задачах требуется найти тангенс именно острого угла, как, допустим, на этом примере:

Для этого мы строим прямоугольный треугольник, проведя линию (перпендикуляр) BD:

Далее вспоминаем определение тангенса, это отношение противолежащего катета к прилежащему.
То есть tg(BOA) = DB / DO.
Чтобы найти DO и DB достаточно будет посчитать количество клеточек.
DO = 2.
DB = 5.
Значит, tg(BOA) = 5 / 2 = 2,5.
Зная тангенс, мы можем легко найти и котангенс:
ctg(BOA) = 1 / tg(BOA) = 1 / 2,5 = 0,4.
_
А вот задача на нахождение тангенса угла по клеточкам немного другого плана (ищем тангенс угла AOB):

Если соединить точки A и B, то угол ABO будет прямым.

И тангенс можно вычислить как отношение BA к BO.
Как же нам их найти?

И BO, и BA будут гипотенузами 2 совершенно равных прямоугольных треугольников (для наглядности я их выделил красным).
Длина катетов их равна 2 и 8, а квадрат гипотенузы, как известно, равен сумме квадратов катетов.
Таким образом, у нас получится следующее:
tg(BOA) = BA / BO = √(2² + 8²) / √(2² + 8²) = 1.
И нетрудно догадаться, что треугольник этот равнобедренный с равными углами BOA и BAO по 45 градусов.
Каталог заданий.
Углы
Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
Задание 18 № 40
Найдите тангенс угла AOB, изображенного на рисунке.
Аналоги к заданию № 40: 348424 348519 352779 357581 369740 369808 Все
Источник: Демонстрационная версия ГИА—2013 по математике., Демонстрационная версия ГИА—2014 по математике.
Раздел кодификатора ФИПИ: 5.1 Планиметрия. Нахождение геометрических величин.
Решение
·
·
Сообщить об ошибке · Помощь
2
Задание 18 № 311485
На квадратной сетке изображён угол A. Найдите .
Источник: ГИА-2013. Математика. Тренировочная работа № 4.(1 вар.)
Раздел кодификатора ФИПИ: 5.1 Планиметрия. Нахождение геометрических величин.
Решение
·
·
Сообщить об ошибке · Помощь
3
Задание 18 № 316348
Найдите тангенс угла, изображённого на рисунке.
Аналоги к заданию № 316348: 316374 323618 348622 348734 349410 349506 349517 349574 349593 340982 … Все
Раздел кодификатора ФИПИ: 5.1 Планиметрия. Нахождение геометрических величин.
Решение
·
·
Сообщить об ошибке · Помощь
4
Задание 18 № 316374
Найдите тангенс угла, изображённого на рисунке.
Аналоги к заданию № 316348: 316374 323618 348622 348734 349410 349506 349517 349574 349593 340982 … Все
Раздел кодификатора ФИПИ: 5.1 Планиметрия. Нахождение геометрических величин.
Решение
·
·
Сообщить об ошибке · Помощь
5
Задание 18 № 323618
Найдите тангенс угла AOB, изображённого на рисунке.
Аналоги к заданию № 316348: 316374 323618 348622 348734 349410 349506 349517 349574 349593 340982 … Все
Раздел кодификатора ФИПИ: 5.1 Планиметрия. Нахождение геометрических величин.
Решение
·
·
Сообщить об ошибке · Помощь
Пройти тестирование по этим заданиям
О проекте · Редакция · Правовая информация · О рекламе
© Гущин Д. Д., 2011—2022
Найдите тангенс угла, изображённого на рисунке.
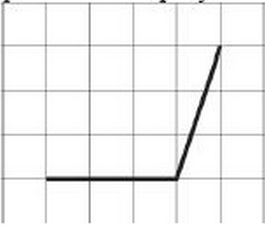
Решение задачи
В данном уроке рассматривается пример решения задачи на определение значения тригонометрических функций. Решением данной задача целесообразно будет воспользоваться при подготовке к ОГЭ.
Для решения задачи на заданном рисунке проводятся дополнительные построения: проводится прямая, совпадающая с одной из сторон заданного угла, а от другой стороны заданного угла на эту прямую опускается перпендикуляр. Для наглядности заданный угол обозначается , смежный с ним угол –
. Анализируя рисунок, определяется, что верно равенство и решение задачи сводится к определению
. Согласно определению, тангенс острого угла прямоугольного треугольника равен отношению противолежащего катета к прилежащему. Далее по рисунку определяется значение катетов образованного в результате построения треугольника. Таким образом, вычисляется значение
и соответственно , что и является решением задачи.
Задание 18 в ОГЭ — это задачи на квадратной решётке, которые, в свою очередь, объединяют в себе очень много геометрического материала. Здесь и нахождение длин отрезков (медиан, биссектрис, средних линий, радиусов, расстояний до прямой), и вычисление площадей, и нахождение тригонометрических функций углов.
Рассмотрим задачи последнего типа. Стороны квадратных клеток равны 1
.
Задача 1. Найдите тангенс угла АОВ.
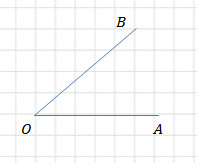
Эта задача легко решится, если увидеть прямоугольный треугольник и вспомнить, что тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.
Опустим из точки В перпендикуляр ВН на сторону ОА.

Из рисунка видно, что катет ВН = 4, а катет ОН = 5. Значит,

Ответ: 0,8.
Теперь решим задачу посложней.
Задача 2. Найдите тангенс угла АОВ.

Казалось бы, условие тоже, но посмотрите на расположение угла. Можно ли здесь увидеть прямоугольный треугольник? Можно и нужно.
Что мы знаем? Из любой точки к прямой можно провести перпендикуляр, и притом только один. Перпендикуляр — это кратчайшее расстояние от точки до прямой.
Вполне достаточно.
Из точки В к прямой ОА можно провести отрезки (важно: проводить надо в узлы клеток).
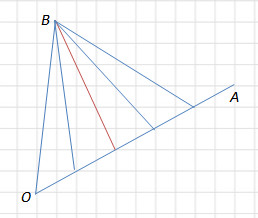
Однако, только один из отрезков перпендикулярен прямой ОА. На рисунке он красного цвета. Уберём с чертежа ненужные элементы.

Перед нами треугольник ОВН. Но, чтобы не было никаких сомнений, проверим, будет ли он прямоугольным. Найдём каждую из сторон треугольника, используя теорему Пифагора.
Для этого достроим наш чертёж.

Используя рисунок, получим

По теореме, обратной теореме Пифагора, если для треугольника выполняется равенство a² + b² = c², то треугольник прямоугольный.
В нашем случае,


Теперь ответим на вопрос задачи (не забыли ещё?).

Ответ: 1,5.
Эти две задачи показывают, что одинаковые условия не гарантируют ещё, что решения также будут один в один. В каждом случае нужно «нащупать» свой путь. Наверное, это самое трудное в этих задачах.
Решите самостоятельно.
1. На квадратной сетке изображён угол . Найдите .
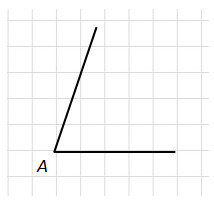
2. Найдите тангенс угла . Размер клетки 1 × 1.
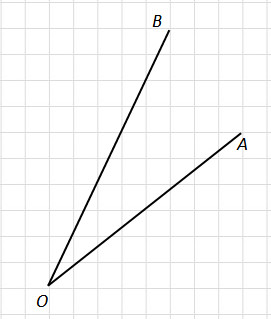
Желаю вам успешной и плодотворной работы по подготовке к экзамену!
