Всего: 40 1–20 | 21–40
Добавить в вариант
Тип 18 № 40
i
Найдите тангенс угла AOB, изображенного на рисунке.
Найдите тангенс угла AOB, изображённого на рисунке.
Найдите тангенс угла AOB.
Найдите тангенс угла AOB, в треугольнике, изображённом на рисунке.
Найдите тангенс угла AOB, изображённого на рисунке.
Найдите тангенс угла AOB.
Найдите тангенс угла AOB, изображённого на рисунке.
Найдите тангенс угла AOB.
Найдите тангенс угла AOB, изображённого на рисунке.
Найдите тангенс угла AOB. Размер клетки 1 × 1.
Найдите тангенс угла AOB.
Найдите тангенс угла AOB, изображённого на рисунке.
Найдите тангенс угла AOB, изображённого на рисунке.
Найдите тангенс угла AOB
Найдите тангенс угла AOB, изображённого на рисунке.
Найдите тангенс угла AOB, изображённого на рисунке.
Найдите тангенс угла AOB, изображённого на рисунке.
Найдите тангенс угла AOB
Найдите тангенс угла AOB, изображённого на рисунке.
Найдите тангенс AOB
Всего: 40 1–20 | 21–40
Здравствуйте, дорогие читатели. В этом выпуске поговорим о задании, которое иногда доставляет неожиданные неприятности на экзамене. Задания довольно простые, но бывают промахи. Это задания, которые сделаны как бы на тетрадном листочке в клеточку. Итак, давайте начнем.
Задание №1. УГЛЫ
Задача №1
Запомните, чтобы найти тангенс острого угла на таких картинках, обязательно нужно достроить до прямоугольного треугольника.
Вспомним, что такое тангенс острого угла прямоугольного треугольника?
Определение тангенса острого угла:
Тангенсом острого угла прямоугольного треугольника, называется отношение противолежащего катета к прилежащему. Катет BF- противолежащий угла FОВ, OF – прилежащий к углу FOB.
Задача №2
Чтобы найти тангенс угла АОВ на этой картинке, нужно достроить до прямоугольного треугольника, и найти стороны этого треугольника.
1. Достроим до треугольника ОВН и докажем, что он прямоугольный.
2. Для этого достроим на стороне ОН, ОВ и ВН прямоугольные треугольники ОСВ, ОНК и BDH. Докажем, что треугольник АВН прямоугольный.
Найдем гипотенузу ОВ прямоугольного треугольника ОСВ, гипотенузу ОН прямоугольного треугольника ОКН и гипотенузу ВН прямоугольного треугольника ВDH через теорему Пифагора: квадрат гипотенузы равен сумме квадратов катетов.
Теперь докажем, что треугольник ОВН прямоугольный. Воспользуемся обратной теоремой Пифагора: если квадрат одной стороны равен сумме квадратов двух других сторон, то треугольник прямоугольный.
Так как равенство верно, то треугольник ОВН прямоугольный.
Теперь найдем тангенс угла АОВ
Задание №2 Расстояние
Для выполнения этого задания, проведите отрезок ВС, найдите середину его и отметим точкой К. Проведите отрезок АК, который равен 4. Ответ 4
Задание №3 Площадь
Задача №1
Задание простое, но есть ошибки по невнимательности.
Задача №2
а) Площадь треугольника и параллелограмма
Запомните! Площадь треугольника от площади параллелограмма отличается только тем, что площадь треугольника нужно делить на 2, а площадь параллелограмма нет.
б) Площадь трапеции. Чтобы найти площадь трапеции, нужно сложить основания трапеции, умножить на высоту и поделить на 2.
в) Площадь ромба равна половине произведения диагоналей.
Это не все типы заданий, что встречаются на экзамене. Продолжение следует.
Спасибо что дочитали. Вы меня очень поддержите, если поставите лайк и подпишитесь на мой блог.
№8. Найдите тангенс угла AOB, изображенного на рисунке.
Решение:
Опустим перпендикуляр AH на сторону OB.
Рассмотрим прямоугольный △ A O H :
Тангенс угла – отношение противолежащего катета к прилежащему.
tg ∠ A O H = A H O H = 4 2 = 2
Ответ: 2
№9. Найдите тангенс угла A треугольника ABCб изображённого на рисунке.
Решение:
Тангенс угла – это отношение противолежащего катета к прилежащему.
tg ∠ B A C = B C A C = 2 5 = 0,4
Ответ: 0,4
№10. На рисунке изображена трапеция ABCD. Используя рисунок, найдите sin ∠ B A H .
Решение:
Рассмотрим прямоугольный △ A B H :
Синус угла – отношение противолежащего катета к гипотенузе.
sin ∠ A = B H A B
Найдем AB по теореме Пифагора:
A B 2 = A H 2 + B H 2
A B 2 = 3 2 + 4 2
A B 2 = 9 + 16 = 25
A B = ± 25 = [ − 5 не подходит 5 подходит
A B = 5
sin ∠ A = B H A B = 4 5 = 0,8
Ответ: 0,8
№11. На рисунке изображен ромб ABCD. Используя рисунок, найдите tg ∠ O B C .
Решение:
Тангенс угла – это отношение противолежащего катета к прилежащему.
tg ∠ O B C = O C B O = 3 4 = 0,75
Ответ: 0,75
№12. На рисунке изображена трапеция ABCD. Используя рисунок, найдите cos ∠ H B A .
Решение:
Рассмотрим прямоугольный △ A B H :
Косинус угла – отношение прилежащего катета к гипотенузе.
cos ∠ A B H = B H A B
Найдем A B по теореме Пифагора:
A B 2 = A H 2 + B H 2
A B 2 = 6 2 + 8 2
A B 2 = 36 + 64 = 100
A B = ± 100 = [ − 10 не подходит 10 подходит
A B = 10
cos ∠ A B H = B H A B = 8 10 = 0,8
Ответ: 0,8
№13. Найдите тангенс угла, изображенного на рисунке.
Решение:
tg β = tg ( 180 ° − α ) = − tg α
Рассмотрим прямоугольный △ B C H .
Тангенс угла – отношение противолежащего катета к прилежащему.
tg α = C H B H = 3 1
tg β = − tg α = − 3
Ответ: -3
№14. Найдите тангенс угла AOB.
Решение:
Опустим высоту BH на сторону OA.
Рассмотрим прямоугольный △ O B H :
tg ∠ O = B H O H
Найдем B H и O H по теореме Пифагора:
B H 2 = 2 2 + 8 2 = = 4 + 64 = 68
B H = ± 68 = ± 4 ⋅ 17 = ± 4 ⋅ 17 = ± 2 17 = [ − 2 17 не подходит 2 17 подходит
B H = 2 17
O H 2 = 1 2 + 4 2 = 1 + 16 = 17
O H = ± 17 = [ − 17 не подходит 17 подходит
O H = 17
tg ∠ O = B H O H = 2 17 17 = 2
Ответ: 2
|
Найдите тангенс угла AOB, изображенного на рисунке Тангенс — это отношение противолежащего катета к прилежащему. Противолежащим является перпендикуляр, проведённый из точки B на сторону AO. Прилежащий катет — отрезок от точки O до точки пересечения AO с перпендикуляром. Из рисунка очевидно, что противолежащий катет в два раза больше прилежащего. Значит, тангенс угла AOB = 2. автор вопроса выбрал этот ответ лучшим Stan1711 3 года назад Тангенс угла определяется как отношение значения величины катета противо угла к катету прилежащему к углу.Из чертежа, если провести линию с какой нибудь точки одного луча угла на другой под углом 90°,можно определить такие значения – 2 и 1 или 4 и 2. Отсюда видно что величина тангенса этого угла АОВ будет 2. Знаете ответ? |
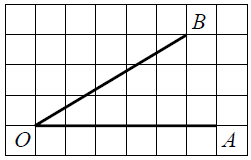
Найдите тангенс угла AOB, изображённого на рисунке.
Источник: statgrad
Решение:
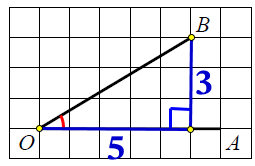
Дорисуем угол АОВ до прямоугольного треугольника:
Тангенс угла – это отношение противолежащего (дальнего) катета к прилежащему (близкому).
tgangle AOB=frac{3}{5}=0,6
Ответ: 0,6.
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 5 / 5. Количество оценок: 4
Оценок пока нет. Поставь оценку первым.
Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️
Вступай в группу vk.com 😉
Расскажи, что не так? Я исправлю в ближайшее время!
В отзыве оставь любой контакт для связи, если хочешь, что бы я тебе ответил.