Как найти тангенс угла aoc

№8. Найдите тангенс угла AOB, изображенного на рисунке.

Решение:

Опустим перпендикуляр AH на сторону OB.

Рассмотрим прямоугольный △ A O H :

Тангенс угла – отношение противолежащего катета к прилежащему.

tg ∠ A O H = A H O H = 4 2 = 2

Ответ: 2

№9. Найдите тангенс угла A треугольника ABCб изображённого на рисунке.

Решение:

Тангенс угла – это отношение противолежащего катета к прилежащему.

tg ∠ B A C = B C A C = 2 5 = 0,4

Ответ: 0,4

№10. На рисунке изображена трапеция ABCD. Используя рисунок, найдите sin ∠ B A H .

Решение:

Рассмотрим прямоугольный △ A B H :

Синус угла – отношение противолежащего катета к гипотенузе.

sin ∠ A = B H A B

Найдем AB по теореме Пифагора:

A B 2 = A H 2 + B H 2

A B 2 = 3 2 + 4 2

A B 2 = 9 + 16 = 25

A B = ± 25 = [ − 5 не подходит 5 подходит

A B = 5

sin ∠ A = B H A B = 4 5 = 0,8

Ответ: 0,8

№11. На рисунке изображен ромб ABCD. Используя рисунок, найдите tg ∠ O B C .

Решение:

Тангенс угла – это отношение противолежащего катета к прилежащему.

tg ∠ O B C = O C B O = 3 4 = 0,75

Ответ: 0,75

№12. На рисунке изображена трапеция ABCD. Используя рисунок, найдите cos ∠ H B A .

Решение:

Рассмотрим прямоугольный △ A B H :

Косинус угла – отношение прилежащего катета к гипотенузе.

cos ∠ A B H = B H A B

Найдем A B по теореме Пифагора:

A B 2 = A H 2 + B H 2

A B 2 = 6 2 + 8 2

A B 2 = 36 + 64 = 100

A B = ± 100 = [ − 10 не подходит 10 подходит

A B = 10

cos ∠ A B H = B H A B = 8 10 = 0,8

Ответ: 0,8

№13. Найдите тангенс угла, изображенного на рисунке.

Решение:

tg β = tg ( 180 ° − α ) = − tg α

Рассмотрим прямоугольный △ B C H .

Тангенс угла – отношение противолежащего катета к прилежащему.

tg α = C H B H = 3 1

tg β = − tg α = − 3

Ответ: -3

№14. Найдите тангенс угла AOB.

Решение:

Опустим высоту BH на сторону OA.

Рассмотрим прямоугольный △ O B H :

tg ∠ O = B H O H

Найдем B H и O H по теореме Пифагора:

B H 2 = 2 2 + 8 2 = = 4 + 64 = 68

B H = ± 68   = ± 4 ⋅ 17 = ± 4 ⋅ 17 = ± 2 17 = [ − 2 17 не подходит 2 17 подходит

B H   =   2 17

O H 2 = 1 2 + 4 2 = 1 + 16 = 17

O H = ± 17 = [ − 17 не подходит 17 подходит

O H   =   17

tg ∠ O = B H O H = 2 17 17 = 2

Ответ: 2

Каталог заданий.
Углы

Пройти тестирование по этим заданиям
Вернуться к каталогу заданий

Версия для печати и копирования в MS Word

Пройти тестирование по этим заданиям

Как находить тангенс угла на окружности

Значения тангенса и котангенса на тригонометрическом круге

В прошлой статье мы познакомились с тригонометрическим кругом и научились находить значения синуса и косинуса основных углов.

Как же быть с тангенсом и котангенсом ? Об этом и поговорим сегодня.

Где же на тригонометрическом круге оси тангенсов и котангенсов?

Ось тангенсов параллельна оси синусов (имеет тоже направление, что ось синусов) и проходит через точку (1; 0).

Ось котангенсов параллельна оси косинусов (имеет тоже направление, что ось косинусов) и проходит через точку (0; 1).

На каждой из осей располагается вот такая цепочка основных значений тангенса и котангенса: Почему так?

Я думаю, вы легко сообразите и сами. 🙂 Можно по-разному рассуждать. Можете, например, использовать тот факт, что и

Собственно, картинка за себя сама говорит.

Если не очень все же понятно, разберем примеры:

Пример 1.

Вычислить

Находим на круге . Эту точку соединяем с точкой (0;0) лучом (начало – точка (0;0)) и смотрим, где этот луч пересекает ось тангенсов. Видим, что

Ответ:

Пример 2.

Вычислить

Находим на круге . Точку (0;0) соединяем с указанной точкой лучом. И видим, что луч никогда не пересечет ось тангенсов.

не существует.

Ответ: не существует

Пример 3.

Вычислить

Находим на круге точку (это та же точка, что и ) и от нее по часовой стрелке (знак минус!) откладываем (). Куда попадаем? Мы окажемся в точке, что на круге у нас (см. рис.) названа как . Эту точку соединяем с точкой (0;0) лучом. Вышли на ось тангенсов в значение .

Так значит,

Ответ:

Пример 4.

Вычислить

Поэтому от точки (именно там будет ) откладываем против часовой стрелки .

Выходим на ось котангенсов, получаем, что

Ответ:

Пример 5.

Вычислить

Находим на круге . Эту точку соединяем с точкой (0; 0). Выходим на ось котангенсов. Видим, что

Ответ:

Теперь, умея находить по тригонометрическому кругу значения тригонометрических функций (а я надеюсь, что статья, где мы начинали знакомство с кругом и учились вычислять значения синусов и косинусов, вами прочитана…), вы можете пройт и тест по теме «Нахождение значений косинуса, синуса, тангенса и котангенса различных углов».

Чтобы не потерять страничку, вы можете сохранить ее у себя:

Тангенс

Тангенс – одна из тригонометрических функций. Как и для всех других функций, значение тангенса определяется для конкретного угла или числа (в этом случае используют числовую окружность.

Аргумент и значение тангенса

Аргументом тангенса может быть:
— как число или выражение с Пи: (1,3), (frac ), (π), (-frac ) и т.п.
— так и угол в градусах: (45^°), (360^°),(-800^°), (1^° ) и т.п.

Для обоих случаев тангенс вычисляется одинаковым способом – либо через значения синуса и косинуса, либо через тригонометрический круг (см. ниже).

Тангенс острого угла

Тангенс можно определить с помощью прямоугольного треугольника — он равен отношению противолежащего катета к прилежащему.

1) Пусть дан угол и нужно определить тагенс этого угла.

2) Достроим на этом угле любой прямоугольный треугольник.

3) Измерив, нужные стороны, можем вычислить тангенс.

Вычисление тангенса числа или любого угла

Для чисел, а также для тупых, развернутых углов и углов больших (360°) тангенс чаще всего определяют с помощью синуса и косинуса, через их отношение:

Пример. Вычислите (tg:0).
Решение: Чтобы найти тангенс нуля нужно найти сначала синус и косинус (0). И то, и другое найдем с помощью тригонометрического круга :

Точка (0) на числовой окружности совпадает с (1) на оси косинусов, значит (cos:0=1). Если из точки (0) на числовой окружности провести перпендикуляр к оси синусов, то мы попадем в точку (0), значит (sin:⁡0=0). Получается: (tg:0=) (frac ) (=) (frac ) (=0).

Пример. Вычислите (tg:(-765^circ)).
Решение: (tg: (-765^circ)=) (frac )
Что бы вычислить синус и косинус (-765^°). Отложим (-765^°) на тригонометрическом круге. Для этого надо повернуть в отрицательную сторону на (720^°) , а потом еще на (45^°).

Однако можно определять тангенс и напрямую через тригонометрический круг — для этого надо на нем построить дополнительную ось:

Прямая проходящая через начало отсчета на числовой окружности и параллельная оси ординат (синусов) называется осью тангенсов. Направление оси тангенсов и оси синусов совпадает.

Ось тангенсов – это фактически копия оси синусов, только сдвинутая. Поэтому все числа на ней расставляются так же как на оси синусов.

Чтобы определить тангенс с помощью числовой окружности, нужно:
1) Отметить соответствующую аргументу тангенса точку на числовой окружности.
2) Провести прямую через эту точку и начало координат и продлить её до оси тангенсов.
3) Найти координату пересечения этой прямой и оси тангенсов.

2) Проводим через данную точку и начало координат прямую.

3) В данном случае координату долго искать не придется – она равняется (1).

Пример. Вычислите (tg: 45°) и (tg: (-240°)).
Решение:
Для угла (45°) ((∠KOA)) тангенс будет равен (1), потому что именно в таком значении сторона угла, проходящая через начало координат и точку (A), пересекает ось тангесов. А для угла (-240°) ((∠KOB)) тангенс равен (-sqrt ) (приблизительно (-1,73)).

Значения для других часто встречающихся в практике углов смотри в тригонометрической таблице.

В отличие от синуса и косинуса значение тангенса не ограничено и лежит в пределах от (-∞) до (+∞), то есть может быть любым.

При этом тангенс не определен для:
1) всех точек (A) (значение в Пи: …(-) (frac ) ,(-) (frac ) , (frac ) , (frac ) , (frac ) …; и значение в градусах: …(-630°),(-270°),(90°),(450°),(810°)…)
2) всех точек (B) (значение в Пи: …(-) (frac ) ,(-) (frac ) ,(-) (frac ) , (frac ) , (frac ) …; и значение в градусах: …(-810°),(-450°),(-90°),(270°)…) .

Так происходит потому, что прямая проходящая через начало координат и любую из этих точек никогда не пересечет ось тангенсов, т.к. будет идти параллельно ей. Поэтому в этих точках тангенс – НЕ СУЩЕСТВУЕТ (для всех остальных значений тангенс может быть найден).

Из-за этого при решении тригонометрических уравнений и неравенств с тангенсом необходимо учитывать ограничения на ОДЗ .

Знаки по четвертям

С помощью оси тангенсов легко определить знаки по четвертям тригонометрической окружности. Для этого надо взять любую точку на четверти и определить знак тангенса для нее описанным выше способом. У всей четверти знак будет такой же.

Для примера на рисунке нанесены две зеленые точки в I и III четвертях. Для них значение тангенса положительно (зеленые пунктирные прямые приходят в положительную часть оси), значит и для любой точки из I и III четверти значение тангенса будет положительно (знак плюс).
С двумя фиолетовыми точками в II и IV четвертях – аналогично, но с минусом.

Связь с другими тригонометрическими функциями:

— котангенсом того же угла: формулой (ctg⁡:x=) (frac )
Другие наиболее часто применяемые формулы смотри здесь .

Алгебра

Лучшие условия по продуктам Тинькофф по этой ссылке

Дарим 500 ₽ на баланс сим-карты и 1000 ₽ при сохранении номера

. 500 руб. на счет при заказе сим-карты по этой ссылке

Лучшие условия по продуктам
ТИНЬКОФФ по данной ссылке

План урока:

Синус и косинус угла на единичной окружности

Впервые мы познакомились с синусом, косинусом и другими тригонометрическими функциями ещё в 8 класс на уроках геометрии, при изучении прямоугольного треугольника. Пусть есть некоторый треуг-ник АВС, у которого∠ С – прямой, а ∠ВАС принимается за α. Тогда sinα – это отношение ВС к АВ, а cosα– это отношение АС к АВ. В свою очередь tgα– это отношение ВС к АС:

С помощью тригонометрических функций удобно было находить стороны прямоугольного треугол-ка. Например, пусть известно, что гипотенуза АВ равна 5, а sinα = 0,8. Тогда из формулы sinα = ВС/АВ легко получить, что

ВС = АВ•sinα = 5•0,8 = 4

Если известно, что cosα = 0,6, то мы сможем найти и второй катет:

АС = АВ•cosα = 5•0,6 = 3

Отдельно заметим, что тангенс угла может быть рассчитан не как отношение двух катетов, а как отношение синуса к косинусу:

tgα = ВС/ АС = (АВ•sinα)/(АВ•cosα) = (sinα)/(cosα)

Отметим на единичной окружности произвольную точку А, которой соответствует некоторый угол α. У этой точки есть свои координаты х_А и у_А:

Попытаемся определить, чему равны координаты точки А. Для этого обозначим буквой B точку, в которой перпендикуляр, опущенный из А, пересекает горизонтальную ось Ох, и рассмотрим треугольник ОАВ:

Ясно, что ОАВ – это прямоугольный треугольник, ведь∠ АОВ = 90°. Значит, отрезок АВ можно рассчитать по формуле

Но ОА – это радиус единичной окружности. Это значит, что ОА = 1. Тогда

АВ = sinα•ОА = sinα•1 = sinα

С другой стороны, видно, что величина отрезка АВ равна координате у_А. Получается, что у_А = АВ = sinα, или

Отрезок ОВ также можно найти из прямоугольного треугольника АОВ, используя косинус:

Учитывая, что ОА = 1, а длина ОВ равна координате х_А, мы получим следующее:

х_А = ОВ = cosα•ОА = cosα•1 = cosα

то есть координата х_А равна cos α:

Итак, мы выяснили, что координаты точки, лежащей на единичной окружности, равны синусу и косинусу угла, соответствующего этой точке.

Таким образом, нам удалось дать новое определение синусу и косинусу угла:

Заметим, что в прямоугольном треугольнике углы, помимо самого прямого угла, могут быть только острыми. Поэтому предыдущее определение синуса и косинуса, данное в 8 классе в курсе геометрии, было пригодно лишь для углов из диапазона 0 1 I и II четверть

Что такое тангенс угла и как его найти

Живущим людям на Земле
всегда хотелось знать,
как путь найти в пустыне, море,
и можно к звёздам ли попасть.

Хотелось труд свой облегчить,
создать машины, чтоб летать.
И чтоб вопросы разрешить,
пришлось про тангенс всем узнать.

Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. Впервые встречаясь с тригонометрией в восьмом классе на геометрии, школьники оглядываются на свою жизнь, задавая вопрос, насколько пригодится им эта область науки в дальнейшем.

Редко кто задумывается, что раздел математики, позволяющий рассказать о заданном треугольнике всё (найти все его стороны и углы, выделить особенности), позволил в своё время сделать великие открытия.

Тригонометрия, дав возможность строить корабли и самолёты, отправлять человека в космос, создавать приборы для ориентирования на море, в лесу, в пустыне, определять расстояния, не измеряя их непосредственно линейкой, шагами или чем-то иным, помогла упростить жизнь человечества, раскрыть новые горизонты знаний.

Тангенс угла

Первые встречи с тангенсом происходят при изучении прямоугольных треугольников.

В них соотношения сторон, образующих прямой угол (катетов), и стороны, лежащей напротив угла в 90º (гипотенузы), задают важные параметры для изучения углов.

Для понимания связи между объектами рассматриваются отношения различных отрезков. Задавая связь между ними, вводят понятия синуса, косинуса (это что?), тангенса, котангенса.

Важно, что это отвлечённые понятия, не связанные с какими-либо единицами измерения.

Введя функции угла, определяют их свойства. Некоторые полученные формулы могут иметь довольно громоздкий вид. Чтобы избежать затруднённого чтения, вводятся другие объекты.

Так произошло и с тангенсом. Ему посчастливилось получить два определения. Каждое характеризует заданное отношение по-своему. С одной стороны, рассматривается связь между катетами и острыми углами прямоугольного треугольника, с другой – даётся возможность упростить формулы, содержащие синусы и косинусы.

Мало кто задумывается, изучая тангенс в школе, что первоначально он был необходим, чтобы найти касательные линии к заданной кривой. Само понятие возникло от латинского слова tangens, которое означает «трогающий», «касающийся» и является причастием настоящего времени от tangere («трогать», «касаться»).

Тангенс — это отношение.

Итак, есть два определения:

Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.

Это определение удобно использовать при изучении геометрических фигур. Оно даёт возможность, минуя вычисления гипотенузы, находить углы или катеты. Выделяя прямоугольные треугольники в произвольных фигурах, задача по изучению свойств исследуемых объектов становится проще.

Тангенс – это отношение синуса к косинусу.

Благодаря этому определению, многие тригонометрические формулы принимают более удобный вид, становятся легче воспринимаемыми.

” alt=””>

Вместо «тангенс угла альфа» пишут: tgα. На калькуляторах, в различных программах ЭВМ и ПК закрепилось другое обозначение: tan⁡(α).

Как найти тангенс угла (формулы)

Первое свойство тангенса вытекает из его определения как отношения катетов.

Сумма двух непрямых углов прямоугольного треугольника равна 90º. Поэтому

Так как тангенс – это отношение катетов, то

Учитывая особенности некоторых треугольников (равностороннего, прямоугольного, равнобедренного), а также записанное свойство, была составлена таблица значений тангенса для углов 30º, 45º, 60º.

Задача нахождения других углов по значению тангенса была решена с помощью составления более обширных таблиц. За счёт появления современных вычислительных средств необходимость применения табулированных значений уменьшилась.

Как найти тангенс по клеточкам

Учитывая первое определение, можно определить, как найти тангенс угла по клеточкам. Рисунок дополняется перпендикулярными линиями (строится высота), затем считается количество клеточек в полученном прямоугольном треугольнике на катетах, противолежащем и прилежащем искомому углу, а затем берётся их отношение.

Благодаря второму определению, задачу, как найти тангенс угла, можно решить, минуя таблицы и построение прямоугольных треугольников. Достаточно знать синус и косинус, связанные между собой основным тригонометрическим тождеством:

Из формулы тангенсов, записывающей кратко второе определение

и основного тригонометрического тождества можно понять, как найти тангенс, зная только косинус или синус угла.

Достаточно поделить основное тригонометрическое тождество на квадрат косинуса, подставить формулу тангенса. В результате получится зависимость тангенса и косинуса:

Если выразить в последнем случае косинус, то запишется связь между тангенсом и синусом:

Удачи вам! До скорых встреч на страницах блога KtoNaNovenkogo.ru

Эта статья относится к рубрикам:

Комментарии и отзывы (5)

Я Очень Люблю Правила, Теоремы, Формулы по Предмету «Математика», «Алгебра».

Прочитал статью и остался один главный вопрос, а собственно без вспомогательных таблиц найти угол В ГРАДУСАХ вообще возможно и есть ли у вас статья, где рассказыввается как это сделать? Спасибо.

Я ни разу не математик, но почему у вас сумма углов прямоугольного треугольника равна 90 градусов. А так все хорошо начиналось. Объясняете хорошо, но после таких ошибок у меня сомнения что информация верная.

Спасибо. Уточнил в тексте, что это сумма двух непрямых углов прямоугольного треугольника.

Пишу стихи. Востребован тангенс для решения жизненных ситуаций поскольку состоит из тех же функций,как-то, касающийся,прилежащий, трогающий. Куда без них денешься.

Найдите величину угла ABC. Ответ дайте в градусах

27887. Найдите величину угла ABC. Ответ дайте в градусах.

Отметим центр окружности. Обозначим его точкой О, построим центральный угол АОС:

Угол АОС равен 90 0 . Это видно по тому как проходят АО и ОС относительно клетчатой сетки. Угол АВС это вписанный угол, построенный на той же дуге.

По свойству вписанного угла:

27888. Найдите величину угла ABC. Ответ дайте в градусах.

Отметим центр окружности. Обозначим его точкой О, построим центральный угол АОС и вписанный угол ADC:

Центральный угол АОС равен 90 0 . По свойству вписанного угла

Известно, что у четырёхугольника вписанного в окружность сумма противоположных углов равна 180 градусам, следовательно:

27889. Найдите величину угла ABC. Ответ дайте в градусах.

Отметим центр окружности (видно о клетчатой сетке). Обозначим его точкой О, построим центральный угол АОС:

Угол АОС равен 90 градусов. Угол АВС это вписанный угол, построенный на той же дуге. По свойству вписанного угла:

[spoiler title=”источники:”]

http://ktonanovenkogo.ru/voprosy-i-otvety/tangens-chto-ehto-takoe-otnoshenie-najti-formulam-kletochkam.html

http://matematikaege.ru/vpisaniy-ugol/27887-najdite-velichinu-ugla-abc-otvet-dajte-v-gradusax.html

[/spoiler]

2. Определение тангенса угла

Что нужно вспомнить:

•      Тан­генс угла в пря­мо­уголь­ном
тре­уголь­ни­ке — отноше­ние про­ти­во­ле­жа­ще­го ка­те­та к прилежащему.

Нужно рассмотреть
прямоугольный треугольник.

              

Задача 1

Най­ди­те тангенс угла А тре­уголь­ни­ка ABC,
изображённого на рисунке 1.

Решение:   Ответ: 0,4.

Рис.1

Задача 2

Найдите тангенс угла B треугольника ABC,
изображённого на рисунке 2.

Решение: 5 Ответ: 3,5.

Рис. 2

Задача 3

Найдите тангенс угла AOB, изображённого 
на рисунке 3.

Решение: 1.   Достроим до прямо-угольного треугольника СОВ. 2. Ответ: 2.

Рис. 3

Задача 4

На квадратной сетке изображён угол А
(рис.4). Найдите .

Решение: 1. Достроим до прямо-угольного треугольника АВС так, чтобы т.В и т.С попали в уголки клеток. 2. Ответ: 3.

Рис. 4

Задача 5

Найдите тан­генс угла, изображённого
на рисунке 5.

Решение: 1.   Достроим до прямого угла (рис. 5.1) 2.  Углы и в сумме об­ра­зу­ют развёрнутый угол     Значит,      Ответ: -3.

Рис. 5 Рис. 5.1

Задача 6

Найдите тан­генс угла АОВ (рис. 6).

Решение: Найдём каждую из сторон треугольника АОВ, чтобы показать, что он прямоугольный:              Таким образом Ответ: 0,5.

Рис. 6

8. Определение градусной меры
вписанного угла

Что нужно вспомнить:

•      Вписанный угол – угол, вершина которого
лежит на окружности, а стороны её пересекают.

•      Центральный угол – угол, вершина которого
совпадает с центром окружности, а стороны её пересекают.

Вписанный угол равен половине дуги, на которую опирается.

Задача 1:

Найдите угол ABC (рис.
20). Ответ дайте в градусах.

Решение: Проведём вспомогательное построение. Заметим, что дуга AC составляет ровно четверть окружности, следовательно, она равна 360°/4 = 90°. Угол ABC — вписанный, поэтому он равен половине дуги, на которую опирается, значит, он равен половине дуги AC: 90°/2 = 45°. Ответ: 45.

Рис. 20

Задача 2:

Найдите угол ABC (рис.
21). Ответ дайте в градусах.

Решение: Проведём вспомогательное построение. Заметим, что дуга BC составляет ровно четверть окружности, следовательно, она равна 360°/4 = 90°. Угол BAC — вписанный, поэтому он равен половине дуги, на которую опирается, значит, он равен половине дуги BC: 90°/2 = 45°. Треугольник ABC  Ответ: 67,5.

Рис. 21

Задача 3:

Найдите угол ABC (рис.22).
Ответ дайте в градусах.

Решение: Угол ABC  – опирается на большую дугу АC. Проведём вспомогательное построение. Заметим, что дуга АC составляет  всей окружности, следовательно, она равна Угол AВC — вписанный, поэтому он равен половине дуги, на которую опирается, значит, он равен половине большой дуги АC: 270°/2 = 135°. Ответ: 135.

Рис. 22

Задача 4:

Найдите угол ABC (рис.
23). Ответ дайте в градусах.

Решение: Проведём вспомогательное построение. Угол АОС – центральный и равен . Угол АВС опирается на ту же дугу, что и угол АОС, но является вписанным, поутому равен половине угла АОС, т.е. . Ответ: 22,5.

Рис. 23

9. Задачи для самостоятельно решения

     I.           
Определение
тангенса угла

1.  
 Найдите тангенс угла А треугольника, изображённого на
рисунке.

2.  
Найдите тангенс угла С треугольника ABC, изображённого
на рисунке.

3.  
Найдите тангенс угла AOB, изображённого на рисунке.

4.  
 Найдите тангенс угла AOB, изображённого на рисунке.

5.  
Найдите тангенс угла AOB, изображённого на рисунке.

6.  
Найдите
тангенс угла AOB, изображённого на рисунке.

7.  
Найдите тангенс угла AOB.

8.  
Найдите тангенс угла AOB.

9.  
Найдите тангенс угла  AOB.

10.                      
Найдите
тангенс угла, изображённого на рисунке.

 

 II.           
Определение
площади фигуры (ромба, трапеции, параллелограмма, треугольника)

1.  
На
клетчатой бумаге с размером клетки 1х1 изображён параллелограмм. Найдите его
площадь.

2.  
На клетчатой бумаге с размером клетки 1х1 изображён
треугольник. Найдите его площадь.

3.  
На
клетчатой бумаге с размером клетки 1х1 изображён прямоугольный треугольник.

4.  
На клетчатой бумаге с размером клетки 1х1 изображён
ромб. Найдите его площадь.

5.  
На клетчатой бумаге с размером клетки 1×1 изображён
ромб. Найдите длину его большей диагонали.

6.  
На клетчатой бумаге с размером клетки 1х1 изображена
трапеция. Найдите её площадь.

7.  
На клетчатой бумаге с размером клетки 1х1 изображена
трапеция. Найдите её площадь.

III.           
Определение
расстояния от точки до прямой (отрезка)

1.  
На клет­ча­той
бу­ма­ге с раз­ме­ром клет­ки 1см x 1см от­ме­че­ны точки А, В и С.
Най­ди­те рас­сто­я­ние от точки А до пря­мой ВС. Ответ вы­ра­зи­те
в сантиметрах.

2.  
На клет­ча­той бу­ма­ге с раз­ме­ром клет­ки 1см x 1см
от­ме­че­ны точки А, В и С. Най­ди­те рас­сто­я­ние
от точки А до пря­мой ВС. Ответ вы­ра­зи­те в
сантиметрах. 

3.  
На клет­ча­той
бу­ма­ге с раз­ме­ром клет­ки 1см x 1см от­ме­че­ны точки А, В и С.
Най­ди­те рас­сто­я­ние от точки А до се­ре­ди­ны от­рез­ка ВС.
Ответ вы­ра­зи­те в сантиметрах.

4.  
На клет­ча­той бу­ма­ге с раз­ме­ром клет­ки 1 см × 1
см от­ме­че­ны точки А, В и С. Най­ди­те
рас­сто­я­ние от точки А до се­ре­ди­ны от­рез­ка ВС.
Ответ вы­ра­зи­те в сантиметрах.

5.  
На клет­ча­той
бу­ма­ге с раз­ме­ром клет­ки 1 см × 1 см от­ме­че­ны точки А, В и С.
Най­ди­те рас­сто­я­ние от точки А до пря­мой BC. Ответ вы­ра­зи­те
в сантиметрах.

IV.           
Определение
длины средней линии треугольника и трапеции

1.  
На клет­ча­той бу­ма­ге с раз­ме­ром клет­ки 1×1
изображён тре­уголь­ник ABC. Най­ди­те длину его средней линии,
параллельной сто­ро­не AC.

2.  
На клет­ча­той бу­ма­ге с раз­ме­ром клет­ки 1×1
изображён тре­уголь­ник ABC. Най­ди­те длину его средней линии,
параллельной сто­ро­не AC.

3.  
На клет­ча­той бу­ма­ге с раз­ме­ром клет­ки 1×1
изображён тре­уголь­ник ABC. Най­ди­те длину его средней линии,
параллельной сто­ро­не AC.

4.  
На клетчатой бумаге с размером клетки 1х1 изображена
трапеция. Найдите длину её средней линии.

5.  
На клетчатой бумаге с размером клетки 1х1 изображена
трапеция. Найдите длину её средней линии.

6.  
На клетчатой бумаге с размером клетки 1х1 изображена
трапеция. Найдите длину её средней линии.

 
V.           
Определение
длины большего катета, большей диагонали

1.  
На клетчатой бумаге с размером клетки 1×1 изображен
прямоугольный треугольник. Найдите длину его большего катета.

2.  
На клетчатой бумаге с размером клетки 1×1 изображен
прямоугольный треугольник. Найдите длину его большего катета.

3.  
На клетчатой бумаге с размером клетки 1х1 изображён
прямоугольный треугольник. Найдите длину его большего катета.

4.  
На
клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите длину его
большей диагонали.

5.  
На клетчатой бумаге с размером клетки 1×1 изображён
ромб. Найдите длину его большей диагонали.

VI.           
Определение
площади сложных или составных фигур

1.  
На клетчатой бумаге с размером клетки 1х1 изображена
фигура. Найдите её площадь.

2.  
На клетчатой бумаге с размером клетки 1х1 изображена
фигура. Найдите её площадь.

3.  
На
клетчатой бумаге с размером клетки 1х1 изображена фигура. Найдите её площадь.

 

4.  
На клетчатой
бумаге с размером клетки 1х1 изображена фигура. Найдите её площадь.

 

5.  
Пло­щадь одной клет­ки равна 1. Най­ди­те пло­щадь фи­гу­ры,
изоб­ражённой на ри­сун­ке.

6.  
Пло­щадь одной клет­ки равна 1. Най­ди­те пло­щадь фи­гу­ры,
изоб­ражённой на ри­сун­ке.

VII.           
Определение
площади сложных или составных фигур

1.  
Найдите
угол ABC. Ответ дайте в градусах.

2.  
Найдите угол ABC. Ответ дайте в градусах.

3.  
Найдите угол ABC. Ответ дайте в градусах.

4.  
Найдите
угол ABC. Ответ дайте в градусах.

5.  
Найдите
угол ABC. Ответ дайте в градусах.

6.  
Найдите
угол ABC. Ответ дайте в градусах.

Геометрия,


вопрос задал 1213145,


7 лет назад

Приложения:

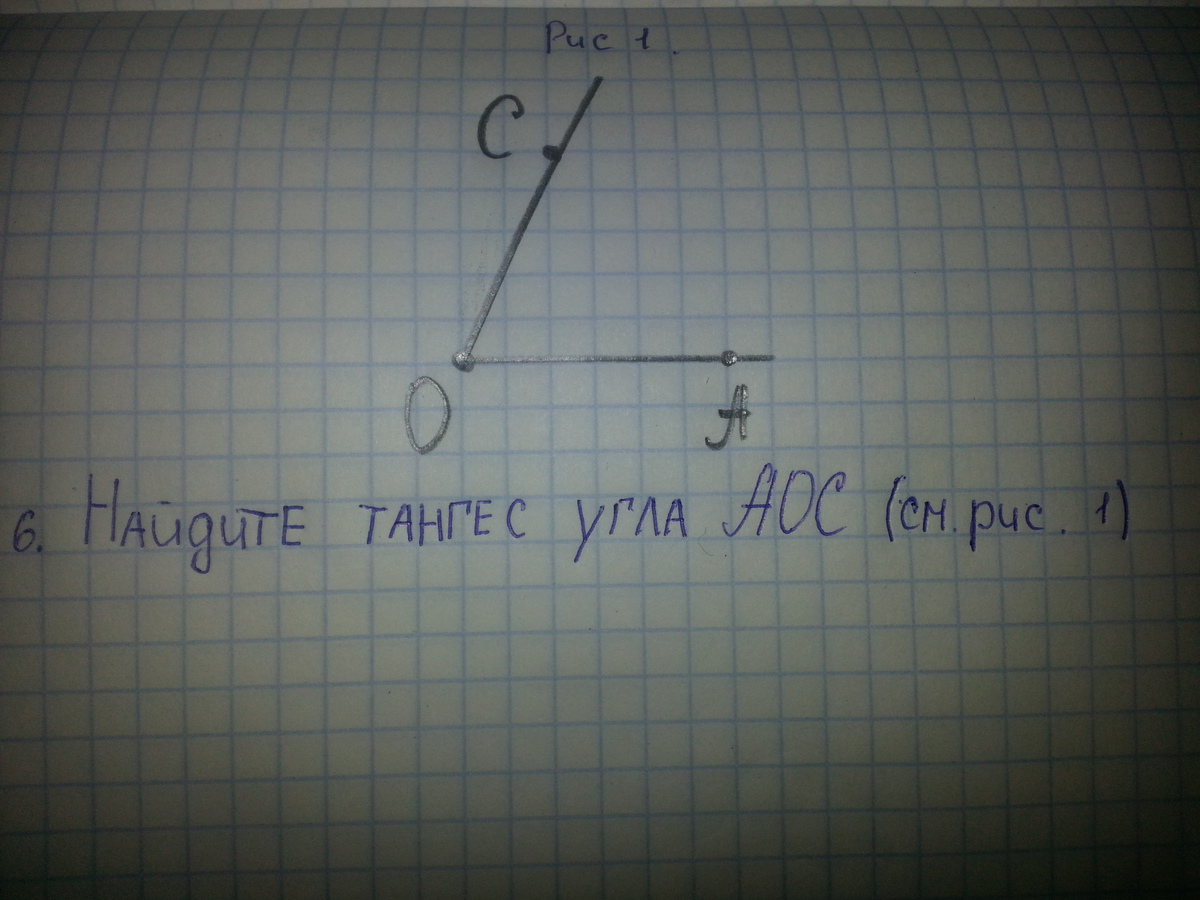
Ответы на вопрос

Ответил sumerki213

0

tg-отношение противолежащего к прилежащему катетов,дострой угол до прямоугольного треугольника и увидешь, что tgAOC=6/3=2

Ответил 1213145

0

А почему 6/3? Можете объяснить?

Ответил sumerki213

0

да,треугольник я построила таким образом: опустила перпендикуляр на прямую АО из прямой ОС,точку на прямой ОС бери такую,где прямая проходит через вершину клетки,и тогда у тебя получается катеты 6 и 3

Ответил mymurkin

0

тангенс 5/2=2,5, опустить перпендикуляр с ОС на ОА и посчитать клетки

Новые вопросы

Математика,
5 лет назад

2) сосна и ель – основные хвойные породы северного казахстана. каждые 10 месяцев сосна вырастает на 80 см, а ель на 20 см. сколько сантиметров прибавляется к высоте сосны и ели за год?​

Литература,
5 лет назад

основная мысль илья муромец и соллвей разбойник9​…

Алгебра,
7 лет назад

решите уравнение -4 +x/5 =x+4/2…

Математика,
7 лет назад

11/12- 5/18. Пожалуйста…

Математика,
8 лет назад

4 кг варенья разложили в 5 банок поровну. Сколько килограммов варенья в каждом банке?

Литература,
8 лет назад

Характеристика персонажа “Татьяна” из произведения  Му-Му…