Всего: 129 1–20 | 21–40 | 41–60 | 61–80 …
Добавить в вариант
Тип 18 № 40 

i
Найдите тангенс угла AOB, изображенного на рисунке.
Тип 18 № 66 

i
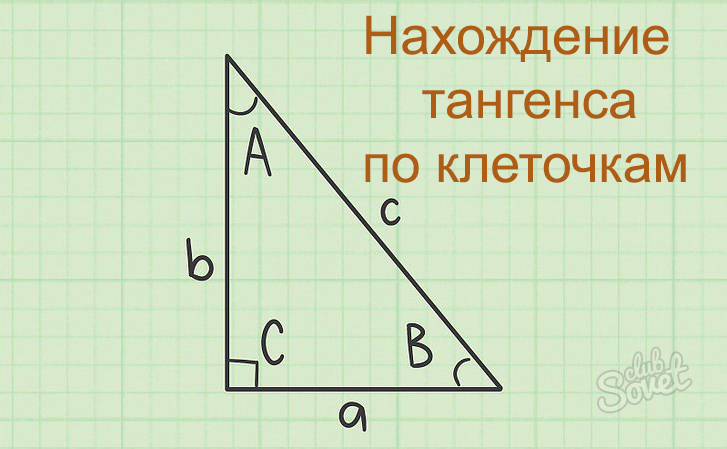
Найдите тангенс угла А треугольника ABC, изображённого на рисунке.
Тип 18 № 92 

i
Найдите тангенс угла B треугольника ABC, изображённого на рисунке.
Из вершины прямого угла C треугольника ABC проведена высота CP. Радиус окружности, вписанной в треугольник BCP, равен 8, тангенс угла BAC равен Найдите радиус вписанной окружности треугольника ABC.
Найдите тангенс угла С треугольника ABC , изображённого на рисунке.
В треугольнике одна из сторон равна 12, другая равна 10, а тангенс угла между ними равен Найдите площадь треугольника.
Периметр ромба равен 24, а тангенс одного из углов равен Найдите площадь ромба.
Одна из сторон параллелограмма равна 12, другая равна 5, а тангенс одного из углов равен Найдите площадь параллелограмма.
Основания трапеции равны 18 и 12, одна из боковых сторон равна 6, а тангенс угла между ней и одним из оснований равен Найдите площадь трапеции.
В прямоугольном треугольнике один из катетов равен угол, лежащий напротив него, равен 60°, а гипотенуза равна 20. Найдите площадь треугольника, делённую на
На рисунке изображен ромб ABCD. Используя рисунок, найдите
Источник: 9 класс. Математика. Краевая диагностическая работа. Краснодар (вар. 2)
На рисунке изображен ромб ABCD. Используя рисунок, найдите
Источник: 9 класс. Математика. Краевая диагностическая работа. Краснодар (вар.6)
Найдите тангенс угла A треугольника ABC, изображённого на рисунке.
Источник: ГИА-2013. Математика. Экзамен. Вариант 1
Найдите тангенс угла A треугольника ABC, изображённого на рисунке.
Источник: ГИА-2013. Математика. Экзамен. Вариант 2
Найдите тангенс угла C треугольника ABC, изображённого на рисунке.
Источник: ГИА-2013. Математика. Экзамен. Вариант 3
В треугольнике ABC угол C равен 90°, AC = 20, tgA = 0,5. Найдите BC.
В треугольнике ABC угол C равен 90°, BC = 20, = 0,5. Найдите AC.
В треугольнике ABC угол C равен 90°, BC = 18, tgA = 3. Найдите AC.
Тангенс острого угла прямоугольной трапеции равен
Найдите её большее основание, если меньшее основание равно высоте и равно 15.
Найдите тангенс угла В треугольника ABC, изображённого на рисунке.
Источник: Банк заданий ФИПИ
Всего: 129 1–20 | 21–40 | 41–60 | 61–80 …
Обычно в задачах требуется найти тангенс именно острого угла, как, допустим, на этом примере:

Для этого мы строим прямоугольный треугольник, проведя линию (перпендикуляр) BD:

Далее вспоминаем определение тангенса, это отношение противолежащего катета к прилежащему.
То есть tg(BOA) = DB / DO.
Чтобы найти DO и DB достаточно будет посчитать количество клеточек.
DO = 2.
DB = 5.
Значит, tg(BOA) = 5 / 2 = 2,5.
Зная тангенс, мы можем легко найти и котангенс:
ctg(BOA) = 1 / tg(BOA) = 1 / 2,5 = 0,4.
_
А вот задача на нахождение тангенса угла по клеточкам немного другого плана (ищем тангенс угла AOB):

Если соединить точки A и B, то угол ABO будет прямым.

И тангенс можно вычислить как отношение BA к BO.
Как же нам их найти?

И BO, и BA будут гипотенузами 2 совершенно равных прямоугольных треугольников (для наглядности я их выделил красным).
Длина катетов их равна 2 и 8, а квадрат гипотенузы, как известно, равен сумме квадратов катетов.
Таким образом, у нас получится следующее:
tg(BOA) = BA / BO = √(2² + 8²) / √(2² + 8²) = 1.
И нетрудно догадаться, что треугольник этот равнобедренный с равными углами BOA и BAO по 45 градусов.
Здравствуйте, дорогие читатели. В этом выпуске поговорим о задании, которое иногда доставляет неожиданные неприятности на экзамене. Задания довольно простые, но бывают промахи. Это задания, которые сделаны как бы на тетрадном листочке в клеточку. Итак, давайте начнем.
Задание №1. УГЛЫ
Задача №1
Запомните, чтобы найти тангенс острого угла на таких картинках, обязательно нужно достроить до прямоугольного треугольника.
Вспомним, что такое тангенс острого угла прямоугольного треугольника?
Определение тангенса острого угла:
Тангенсом острого угла прямоугольного треугольника, называется отношение противолежащего катета к прилежащему. Катет BF- противолежащий угла FОВ, OF – прилежащий к углу FOB.
Задача №2
Чтобы найти тангенс угла АОВ на этой картинке, нужно достроить до прямоугольного треугольника, и найти стороны этого треугольника.
1. Достроим до треугольника ОВН и докажем, что он прямоугольный.
2. Для этого достроим на стороне ОН, ОВ и ВН прямоугольные треугольники ОСВ, ОНК и BDH. Докажем, что треугольник АВН прямоугольный.
Найдем гипотенузу ОВ прямоугольного треугольника ОСВ, гипотенузу ОН прямоугольного треугольника ОКН и гипотенузу ВН прямоугольного треугольника ВDH через теорему Пифагора: квадрат гипотенузы равен сумме квадратов катетов.
Теперь докажем, что треугольник ОВН прямоугольный. Воспользуемся обратной теоремой Пифагора: если квадрат одной стороны равен сумме квадратов двух других сторон, то треугольник прямоугольный.
Так как равенство верно, то треугольник ОВН прямоугольный.
Теперь найдем тангенс угла АОВ
Задание №2 Расстояние
Для выполнения этого задания, проведите отрезок ВС, найдите середину его и отметим точкой К. Проведите отрезок АК, который равен 4. Ответ 4
Задание №3 Площадь
Задача №1
Задание простое, но есть ошибки по невнимательности.
Задача №2
а) Площадь треугольника и параллелограмма
Запомните! Площадь треугольника от площади параллелограмма отличается только тем, что площадь треугольника нужно делить на 2, а площадь параллелограмма нет.
б) Площадь трапеции. Чтобы найти площадь трапеции, нужно сложить основания трапеции, умножить на высоту и поделить на 2.
в) Площадь ромба равна половине произведения диагоналей.
Это не все типы заданий, что встречаются на экзамене. Продолжение следует.
Спасибо что дочитали. Вы меня очень поддержите, если поставите лайк и подпишитесь на мой блог.
Как найти тангенс угла по клеточкам
Вычисление такой величины как тангенс может потребоваться как в ходе решения тригонометрических уравнений, так и при поиске ответа задачи по геометрии. Именно во втором случае хорошим подспорьем может оказаться наличие графического изображения угла, тангенс которого необходимо найти, на разлинованной в клеточку бумаге. Как это сделать – читайте в данной статье.
1
Работа с прямоугольными треугольниками
Прежде, чем приступить к нахождению такой величины как тангенс, необходимо определиться с терминологией. Так понятие “тангенс угла” характеризует отношение противолежащего данному угла катета к прилежащему. Т. о. работа ведется в пределах прямоугольного треугольника.
Суть описанного далее алгоритма заключается в работе с прямоугольными треугольниками в рамках непосредственно определения тангенса.
Задача – определить тангенс ∠AOB.
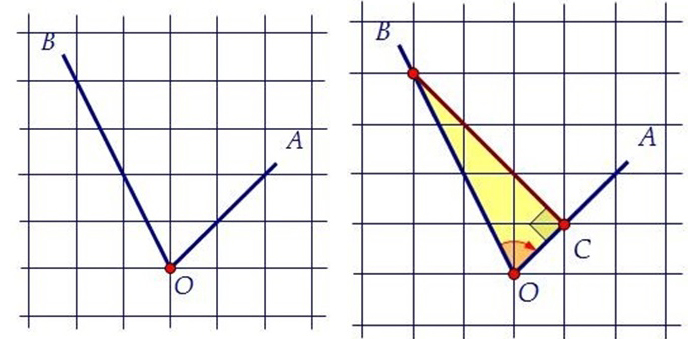
- Установите т. B на луче OB в месте его прохождения через вершину клетки.
- Из т. B опускаете перпендикуляр на луч OA. Место пересечения отмечаете как т. C.
- В результате получается прямоугольный ΔBOC, в котором находится угол ∠AOB (очевидно, что ∠BOC = ∠AOB), тангенс которого необходимо найти.
- Исходя из определения тангенса, tg∠AOB = BC / OC. Глядя на рисунок, несложно заметить что длина катета BC складывается из трех диагоналей клеток. При этом длина катета OC соответствует диагонали одной клетки. Следовательно, BC = 3OC.
- tg∠AOB = 3OC/OC = 3.
Задача – определить тангенс ∠AOB.

Расчет tg∠AOB будет основан на том, что tg(η – λ) = (tgη – tgλ) / (1 + tgη*tgλ).
- В одной из точек прохождения лучами OA и OB вершин клеток-квадратов отмечаете т. A и т. B соответственно.
- Опускаете из них перпендикуляры. В результате вы получаете 2 прямоугольных треугольника – ΔOMB и ΔOLA.
- “Расчетный” ∠AOB является разностью углов ∠AOL и ∠BOM: ∠AOB = ∠AOL – ∠BOM.
- tg∠AOB = tg(∠AOL – ∠BOM) = (tg∠AOL – tg∠BOM) / (1 + tg∠AOL*tg∠BOM). Т. о. нахождение искомой величины сводится к нахождению тангенсов углов в построенных прямоугольных треугольниках.
- tg∠AOL = AL / OL. Обратившись к рисунку заметно, что AL = 2OL. Поэтому tg∠AOL= 2OL / OL = 2.
- tg∠BOM = BM / OM. Обратившись к рисунку видно, что OM=6BM. Поэтому tg∠BOM = BM / 6BM = 1/6.
tg∠AOB = (2 – 1/6) / (1 + 2/6) = 11*3 / 6*4 = 11/8 ⇒ tg∠AOB = 1,375.
2
Использование теоремы косинусов
Задача – определить тангенс ∠AOB.
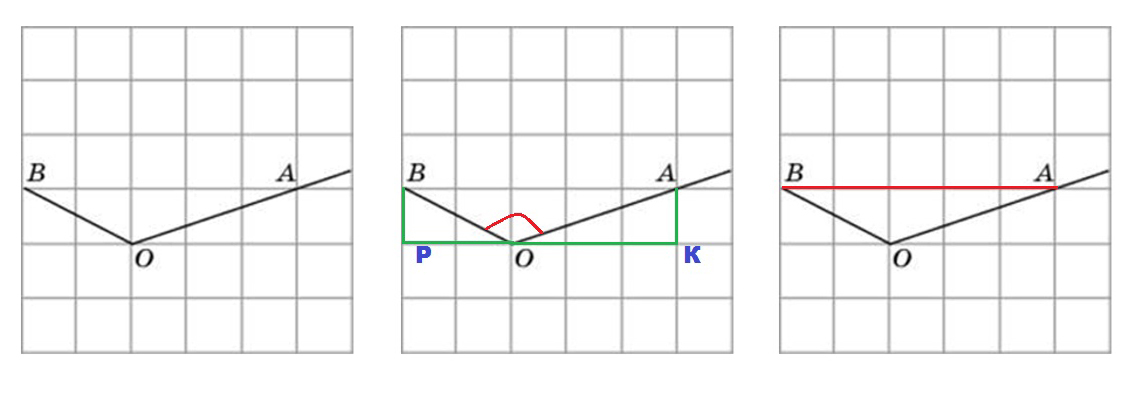
- т. A и т. B устанавливаете в точках прохождения лучей заданного угла через вершины клеток-квадратов. Опускаете из них перпендикуляры. Также отрезком соединяете между собой т. A и т. B.
- Ваша задача – вычислить длины сторон получившегося ΔAOB. Для этого обращаемся к теореме Пифагора.
- AO = √OK2 + AK2, установив длину стороны клетки как условную 1, получаем AO = √9 + 1=√10.
- OB = √BP2 + OP2, т. к. длина стороны клетки равна 1, получаем OB = √4 + 1 = √5.
- Согласно теореме косинусов, AB2 = AO2 + OB2 – 2AO*OB*cos∠AOB ⇒ cos∠AOB = (AO2 + OB2 – AB2) / 2AO*OB. Подставив числовые значения, получаем:
cos∠AOB = (10 + 5 – 25) / 2√5√10;
cos∠AOB = -10/2√5√10;
cos∠AOB = -1/√2.
- Далее воспользуемся основным тождеством тригонометрии: sinβ2 + cosβ2 = 1.
sin∠AOB = √1-1/2 = 1/√2.
- Известно, что tg∠AOB = sin∠AOB / cos∠AOB = -√2 / √2 ⇒ tg∠AOB = -1.
В зависимости от угла, тангенс которого необходимо найти, выбирайте наиболее подходящий, а главное “рабочий” алгоритм.
![]()
Угол на клетчатой бумаге. В этой статье мы с вами рассмотрим задачу, суть которой заключается в том, чтобы найти синус, косинус, тангенс или котангенс угла, построенного на листе в клетку. Такие задания входят в состав экзамена по математике.
Способы решения существуют разные, их более трёх. Подход изложенный ниже можно было бы назвать универсальным. Если у вас найдутся задачи, которые вы таким способом решить не сможете, пришлите мне их, подберём другой. Углы могут быть построены следующим образом (примеры):
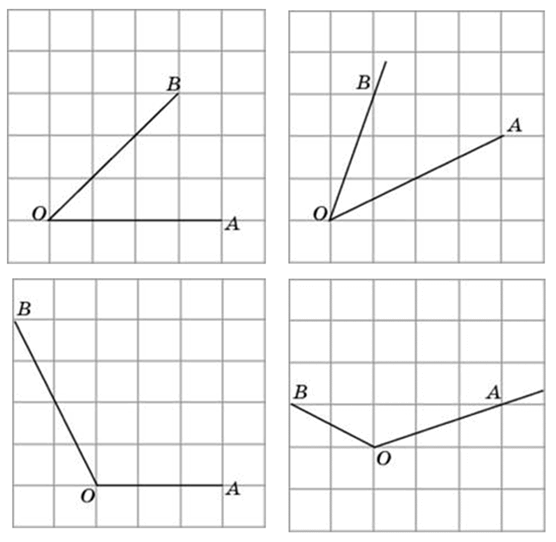
Итак, рассмотрим задание:

Найдите тангенс угла AOB. В ответе укажите значение тангенса, умноженное на 8.
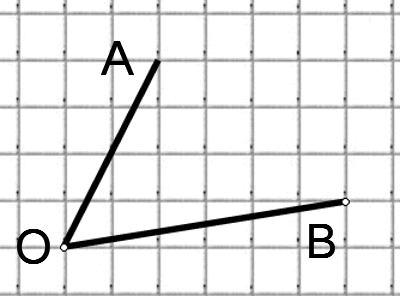
Соединим точки А и В. Получили треугольник АОВ. На сторонах полученного треугольника построим прямоугольные треугольники так, чтобы эти стороны являлись гипотенузами.
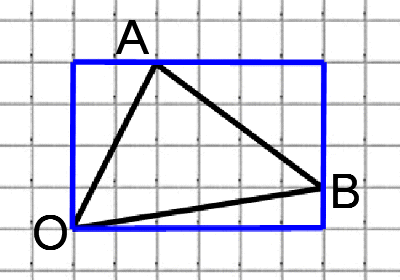
Суть подхода такова: находим все стороны треугольника (это можно сделать по теореме Пифагора); далее используя теорему косинусов, мы можем найти косинус угла; зная косинус мы без труда найдём остальные тригонометрические функции (синус, тангенс, котангенс).
АВ это гипотенуза в прямоугольном треугольнике с катетами 4 и 3,
![]()
ОВ это гипотенуза в прямоугольном треугольнике с катетами 6 и 1,
![]()
OА является гипотенузой в прямоугольном треугольнике с катетами 4 и 2,
![]()
По теореме косинусов: квадрат любой стороны треугольника равен сумме квадратов двух других сторон, без удвоенного произведения этих сторон на косинус угла между ними.
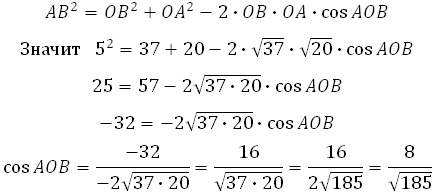
Из основного тригонометрического тождества можем найти sin AOB:
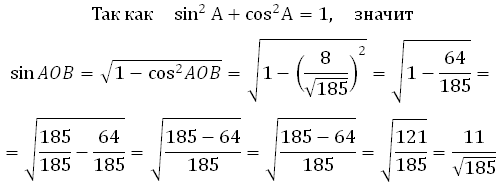
*Обратите внимание, что перед знаком корня у нас «+», так как угол острый (от 0 до 90 градусов). А синус острого угла имеет положительное значение.
Теперь можем найти тангенс:
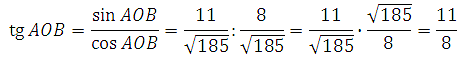
Умножим результат на 8 и запишем ответ:
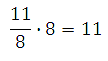
Ответ: 11
Ещё раз повторим: как бы не был построен угол, мы всегда можем достроить его до треугольника, найти стороны этого треугольника (используя теорему Пифагора), далее используя теорему косинусов найти косинус угла (заданного в условии). Затем не составит труда, используя основное тригонометрическое тождество, найти синус. Тангенс и котангенс далее не сложно найти по их формулам.
Ниже предложено самостоятельно решить задачи. При их решении на сайте использовались и другие способы (вы решите представленным выше):
Найдите синус угла AOB. В ответе укажите значение синуса, умноженное на два корня из двух.
Посмотреть решение
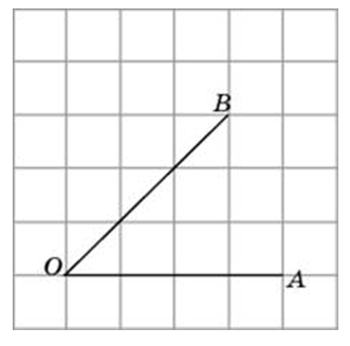
Найдите тангенс угла AOB.
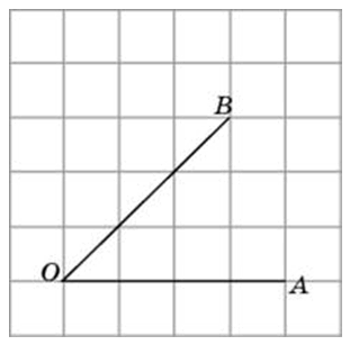
Посмотреть решение
Найдите синус угла AOB. В ответе укажите значение синуса, умноженное на половину корня из пяти.
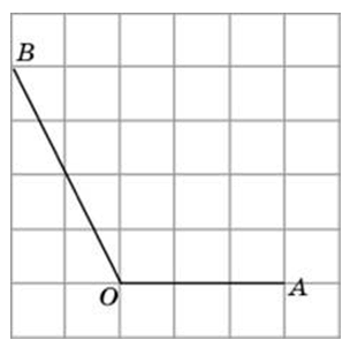
Посмотреть решение
Найдите косинус угла AOB. В ответе укажите значение косинуса, умноженное на два корня из пяти.
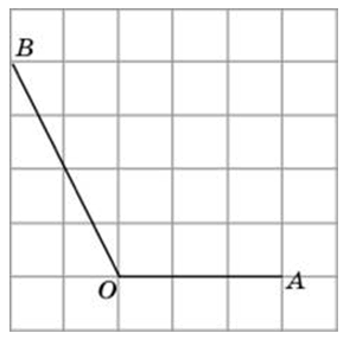
Посмотреть решение
Найдите синус угла AOB. В ответе укажите значение синуса, умноженное на два корня из двух.
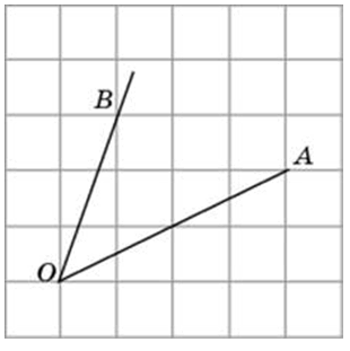
Посмотреть решение
Найдите синус угла AOB. В ответе укажите значение синуса, умноженное на 2 корня из двух.
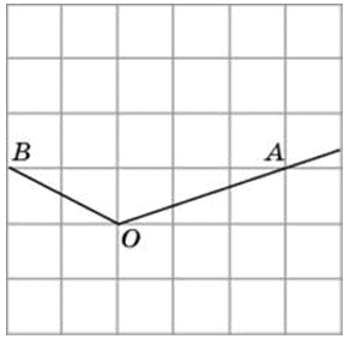
Посмотреть решение
Найдите тангенс угла AOB.
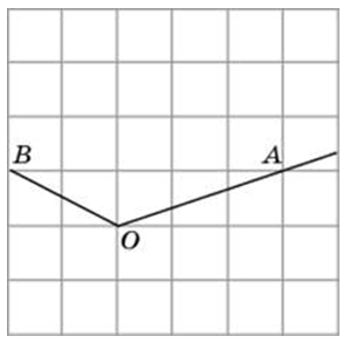
Посмотреть решение
В данной рубрике продолжим рассматривать задачи, не пропустите!
С уважением, Александр Крутицких.
*Делитесь информацией в социальных сетях )
Найдите тангенс угла, изображённого на клетчатой бумаге с размером клетки…
Условие задачи:
Найдите тангенс угла, изображённого на клетчатой бумаге с размером клетки 1 см X 1 см (рис. 112).
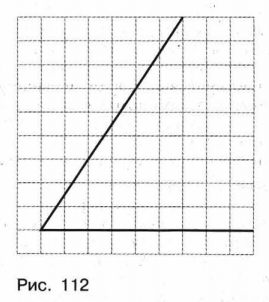
Решение:
Если построить прямоугольный треугольник, каждый из катетов которого измеряется целым числом делений сетки, так, чтобы данный угол был острым углом этого треугольника, то решить задачу удастся без труда. Для этого достаточно на наклонной стороне угла выбрать точку, являющуюся пересечением горизонтальной и вертикальной линий сетки (такие точки называют узлами сетки). Выберем одну из них, обозначим её буквой В, опустим из неё перпендикуляр ВН на горизонтальную сторону угла, а вершину угла обозначим буквой А (рис. 113).
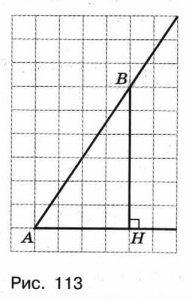
Искомый тангенс равен отношению противолежащего катета к прилежащему:
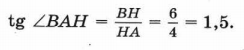
Ответ: 1,5
- 1
- 2
- 3
- 4
- 5
Оценка: 5.0 из 1
Комментарии
Всего комментариев
: 0
Обычно в задачах требуется найти тангенс именно острого угла, как, допустим, на этом примере:

Для этого мы строим прямоугольный треугольник, проведя линию (перпендикуляр) BD:

Далее вспоминаем определение тангенса, это отношение противолежащего катета к прилежащему.
То есть tg(BOA) = DB / DO.
Чтобы найти DO и DB достаточно будет посчитать количество клеточек.
DO = 2.
DB = 5.
Значит, tg(BOA) = 5 / 2 = 2,5.
Зная тангенс, мы можем легко найти и котангенс:
ctg(BOA) = 1 / tg(BOA) = 1 / 2,5 = 0,4.
_
А вот задача на нахождение тангенса угла по клеточкам немного другого плана (ищем тангенс угла AOB):

Если соединить точки A и B, то угол ABO будет прямым.

И тангенс можно вычислить как отношение BA к BO.
Как же нам их найти?

И BO, и BA будут гипотенузами 2 совершенно равных прямоугольных треугольников (для наглядности я их выделил красным).
Длина катетов их равна 2 и 8, а квадрат гипотенузы, как известно, равен сумме квадратов катетов.
Таким образом, у нас получится следующее:
tg(BOA) = BA / BO = √(2² + 8²) / √(2² + 8²) = 1.
И нетрудно догадаться, что треугольник этот равнобедренный с равными углами BOA и BAO по 45 градусов.

Онлайн калькуляторы
На нашем сайте собрано более 100 бесплатных онлайн калькуляторов по математике, геометрии и физике.

Справочник
Основные формулы, таблицы и теоремы для учащихся. Все что нужно, чтобы сделать домашнее задание!

Заказать решение
Не можете решить контрольную?!
Мы поможем! Более 20 000 авторов выполнят вашу работу от 100 руб!
![]() Asya Админ. спросил 5 лет назад
Asya Админ. спросил 5 лет назад
Здравствуйте!
Как найти тангенс угла по клеточкам? Дали задание, а к нему только рисунок. Не понимаю, как его можно решить. Помогите, пожалуйста.
Спасибо!
1 ответ
![]() Asix Админ. ответил 5 лет назад
Asix Админ. ответил 5 лет назад
Задание.
Найти тангенс угла АОВ, который изображен на данном рисунке.
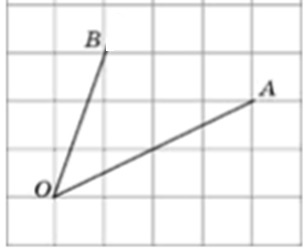
Решение.
Чтобы понять как найти тангенс угла по клеточкам данного рисунка вспомним, что тангенс можно найти из прямоугольного треугольника, длину катетов которого как раз и можно посчитать по клеточкам.
Рассмотрим рисунок, чтобы понять какой прямоугольный треугольник можно получить.
Построим прямоугольный треугольник таким образом, чтобы отрезок ОВ являлся его гипотенузой.
Обозначим новую точку буквой К. из полученного прямоугольного треугольника ОВК можно вычислить тангенс угла ВОК, который рассчитывается как отношение противолежащего катета к прилежащему. Из рисунка видно, что противолежащий катет к углу ВОК равен 3 клеточки, а прилежащий – 1 клеточка. Условно клеточки примем за единицы или сантиметры и рассчитаем:
tg BOK = BK / OK = 3 / 1 = 3
Аналогично поступим с отрезком ОА, который достроим до прямоугольного треугольника так, чтобы этот отрезок был гипотенузой нового треугольника.
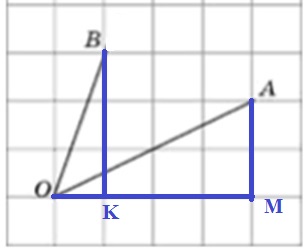
Из полученного треугольника ОАМ вычислим длины е5го катетов и найдем тангенс угла АОМ:
tg АOМ = АМ / OМ = 2 / 4 = 0,5
По условию нужно найти тангенс угла ВОА, который найдем как разницу:
tg BOA = tg BOK – tg АOМ = 3 – 0,5 = 2,5
Ответ. 2,5.
