tg(0°)=tg(360°)=0 точная, но чуть более сложная таблица ( с точностью до 1′) здесь.
|
Углы |
Углы |
Углы |
Углы |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
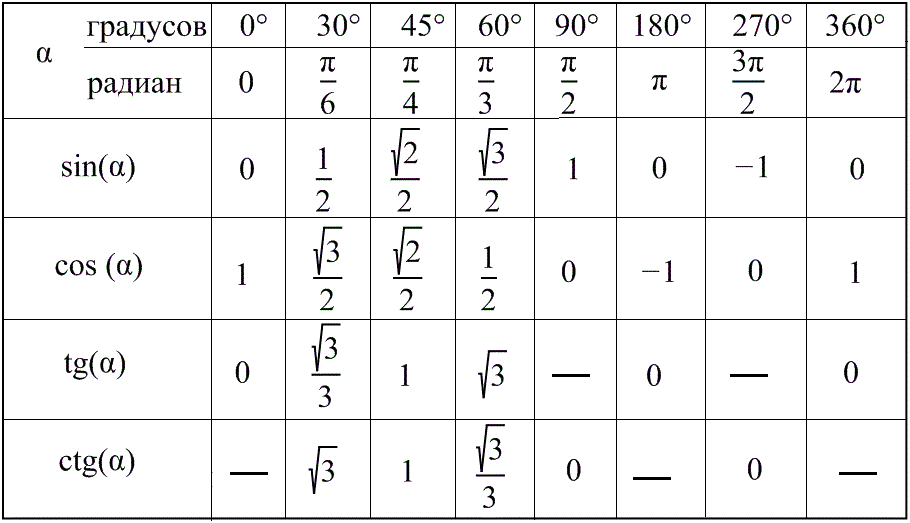
Углы 0°,30°,45°,60°,90°,180°,270°,360°,(π/6,π/4,π/3,π/2,π,3π/2,2π).
Синусы, косинусы, тангенсы и котангенсы. Таблица значений тригонометрических функций
Доп. Инфо:
- Таблица косинусов углов от 0° – 360°. Углы с шагом в 1°. Таблица значений косинусов.
- Таблица синусов углов от 0° – 360°. Углы с шагом в 1°. Таблица значений синусов.
- Таблица синусов, она-же косинусов точная.
- Таблица тангенсов углов углов от 0° – 360°. Углы с шагом в 1°. Таблица значений тангенса, tg
- Таблица котангенсов углов углов от 0° – 360°. Углы с шагом в 1°. Таблица значений котангенса, ctg
- Таблица тангенсов, она же котангенсов точная.
- Углы 0°,30°,45°,60°,90°,180°,270°,360°,(π/6,π/4,π/3,π/2,π,3π/2,2π).
Синусы, косинусы, тангенсы и котангенсы. Таблица значений тригонометрических функций. - Знаки тригонометрических функций синус, косинус, тангенс и котангенс по четвертям в тригонометрическом круге.
- Определение и численные соотношения между единицами измерения углов в РФ.
Тысячные, угловые градусы, минуты, секунды, радианы, обороты. - Таблица соответствия угловых градусов, радиан, оборотов, тысячных (артиллерийских РФ). 0-360 градусов, 0-2π радиан.
Свойства тригонометрических функций
Отсюда вытекает много интересных свойств и тригонометрических формул.
Во-первых, надеюсь, все знают, что в прямоугольном треугольнике самая большая сторона – это гипотенуза.
Поэтому из определения синуса и косинуса ((sin(alpha)=frac{a}{c}; quad cos(alpha)=frac{b}{c})) следует, что они всегда меньше единицы, ведь мы катет (меньшую сторону) делим на гипотенузу (большую сторону треугольника). И как мы узнаем позже, синус и косинус всегда больше минус единицы. То есть синус и косинус могут принимать только значения из промежутка:
$$ sin(alpha) in [-1;1];$$
$$ cos(alpha) in [-1;1];$$
Для тангенса и котангенса никаких ограничений нет, они могут принимать абсолютно любые значения.
Теперь выведем несколько формул, без которых нам точно потом не обойтись. Например, можно обратить внимание, что тангенс выражается через деление синуса на косинус, просто расписав их по определению:
$$frac{sin(alpha)}{cos(alpha)}=frac{frac{a}{c}}{frac{b}{c}}=frac{a}{c}*frac{c}{b}=frac{a}{b};$$
А последняя формула есть ни что иное, как определение тангенса:
$$ tg(alpha)=frac{a}{b};$$
Значит
$$ tg(alpha)=frac{sin(alpha)}{cos(alpha)}.$$
Аналогичные рассуждения можно провести для котангенса:
$$frac{cos(alpha)}{sin(alpha)}=frac{frac{b}{c}}{frac{a}{c}}=frac{b}{c}*frac{c}{a}=frac{b}{a};$$
А котангенс по определению:
$$ctg(alpha)=frac{b}{a};$$
Значит
$$ctg(alpha)=frac{cos(alpha)}{sin(alpha)}.$$
Кроме этого, легко заметить, что функции тангенса и котангенса взаимно обратны:
$$tg(alpha)*ctg(alpha)=frac{a}{b}*frac{b}{a}=1.$$
А теперь мы подобрались к не самой очевидной тригонометрической формуле, но одной из самых главных во всей тригонометрии. Основное тригонометрическое тождество:
$$sin^2(alpha)+cos^2(alpha)=1. qquad (1)$$
Выводится оно тоже из определений синуса и косинуса с использованием теоремы Пифагора (гипотенуза в прямоугольном треугольнике равна сумме квадратов катетов (c^2=a^2+b^2;)):
$$sin^2(alpha)+cos^2(alpha)=left(frac{a}{c}right)^2+left(frac{b}{c}right)^2=left(frac{a^2}{c^2}right)+left(frac{b^2}{c^2}right)=frac{a^2+b^2}{c^2}=frac{c^2}{c^2}=1.$$
С основным тригонометрическим тождеством вы будете сталкиваться постоянно и в 9-м и в 10-м классах.
И разберем еще две важные формулы:
$$1+tg^2(alpha)=frac{1}{cos^2(alpha)};$$
Выводится она очень легко, опять же, используя определения тангенса и косинуса. Рекомендую потренироваться и сделать это самим.
$$1+left(frac{a}{b}right)^2=frac{1}{frac{b^2}{c^2}};$$
$$left(frac{b^2}{b^2}right)+left(frac{a^2}{b^2}right)=1*frac{c^2}{b^2};$$
$$frac{b^2+a^2}{b^2}=frac{c^2}{b^2};$$
Используем теорему Пифагора:
$$frac{c^2}{b^2}=frac{c^2}{b^2};$$
Получили верное равенство, значит формула верна.
И вторая аналогичная формула для котангенса:
$$1+сtg^2(alpha)=frac{1}{sin^2(alpha)};$$
Вывод один в один, сделайте сами.
Для удобства соберем все формулы вместе.
$$sin^2(alpha)+cos^2(alpha)=1. qquad(1)$$
$$ tg(alpha)=frac{sin(alpha)}{cos(alpha)}. qquad(2)$$
$$ctg(alpha)=frac{cos(alpha)}{sin(alpha)}. qquad(3)$$
$$tg(alpha)*ctg(alpha)=1.qquad(4)$$
$$1+tg^2(alpha)=frac{1}{cos^2(alpha)}. qquad(5)$$
$$1+сtg^2(alpha)=frac{1}{sin^2(alpha)}. qquad(6)$$
Это далеко не все тригонометрические формулы, их гораздо больше. Но для начала и для 9-го класса этого вполне достаточно.
Зачем же они нужны? Оказывается, эти формулы помогают связать тригонометрические функции между собой. Посмотрите внимательно на первую формулу (1): зная, например, чему равен косинус, можно легко найти синус, и наоборот.
Пример 1
Пусть (cos(alpha) =frac{1}{2}), найдите (sin(alpha)=?)
Берем основное тригонометрическое тождество (формула (1)) и подставляем в него известный по условию задачи (cos(alpha)=frac{1}{2}:)
$$sin^2(alpha)+cos^2(alpha)=1;$$
$$sin^2(alpha)+left(frac{1}{2}right)^2=1;$$
А дальше просто решаем получившееся уравнение относительно синуса:
$$sin^2(alpha)=1-left(frac{1}{2}right)^2;$$
$$sin^2(alpha)=1-frac{1}{4};$$
Приводим к общему знаменателю:
$$sin^2(alpha)=frac{4}{4}-frac{1}{4};$$
$$sin^2(alpha)=frac{3}{4};$$
И здесь внимательно решаем квадратное уравнение:
$$sin(alpha)=pmfrac{sqrt{3}}{2};$$
Обратите внимание на (pm). Синус может быть как положительным, так и отрицательным, так как при подстановке и возведении в квадрат минус сгорает. Значит здесь получается два ответа.
Ответ:(sin(alpha)=pmfrac{sqrt{3}}{2}.)
Аналогично, зная хотя бы одну тригонометрическую функцию, можно найти все остальные, используя тригонометрические формулы. Рассмотрим еще пример:
Пример 2
Пусть (sin(alpha) =frac{1}{3}), найдите (ctg(alpha)=?)
Смотрим на наш список формул и находим такую, в которой есть и синус и котангенс – это формула (6):
$$1+сtg^2(alpha)=frac{1}{sin^2(alpha)}.$$
Подставляем известный из условия синус (sin(alpha) =frac{1}{3}):
$$1+сtg^2(alpha)=frac{1}{left(frac{1}{3}right)^2}.$$
Перевернем правую часть:
$$1+сtg^2(alpha)=left(frac{3}{1}right)^2.$$
$$1+сtg^2(alpha)=9.$$
Теперь решим уравнение и найдем котангенс:
$$сtg^2(alpha)=8.$$
$$сtg(alpha)=pmsqrt{8}=pmsqrt{4}*sqrt{2}=pm2sqrt{2}.$$
Ответ:(сtg(alpha)=pm2sqrt{2}).
Выглядит пугающе, но учить вам это НЕ НУЖНО! В некоторых школах есть изверги, которые заставляют учить такую таблицу, но в этом совершенно нет необходимости. В дальнейшем мы научимся сами выводить все значения тригонометрических функций только из маленькой таблицы.
Обратите внимание, что синус некоторого угла в треугольнике всегда положителен, неважно, тупой или острый угол. А вот косинус, тангенс и котангенс в треугольнике положительны только от острых углов и отрицательны от тупых.
Тут может возникнуть вопрос, как может существовать синус, косинус, тангенс или котангенс от тупого угла, большего чем (90^o), если мы давали определение всех тригонометрических функций через прямоугольный треугольник, в котором нет углов больших (90^o). Ну что ж, да тригонометрические функции существуют для любых углов и острых, и тупых, но для самого начала тригонометрии определения через прямоугольный треугольник нам более чем достаточно. Просто запомните выводы, которые мы сделали в предыдущем абзаце.
Рассмотрим пример на тригонометрию по типу схожий с заданиями ОГЭ. Обычно задачи сводятся просто к нахождению тригонометрической функции некоторого угла, нарисованного на рисунке:
Пример 2
По рисунку определить значение (sin(alpha)=?)
По определению синус в прямоугольном треугольнике – это отношение противолежащего катета к гипотенузе. Первым делом достроим наш синий угол (angle{ABC}) до прямоугольного треугольника, для этого опустим из точки (A) высоту (AH) к (BC). Получили прямоугольный треугольник (AHB). Теперь можем воспользоваться определением синуса:
$$sin(alpha)=frac{AH}{AB};$$
По клеточкам на рисунке найдем длину отрезка (AH=15). А гипотенузу (AB) найти по клеточкам не выйдет, так как она идет по диагонали. Но мы можем найти опять по клеточкам второй катет в прямоугольном треугольнике (BH=12) и применить теорему Пифагора:
$$AB^2=AH^2+BH^2;$$
$$AB^2=15^2+12^2=225+144=369;$$
$$AB=sqrt{369}=3sqrt{41};$$
Подставим в формулу для синуса и найдем его:
$$sin(alpha)=frac{AH}{AB}=frac{15}{3sqrt{41}};$$
Ответ: (sin(alpha)= frac{15}{3sqrt{41}}.)
Разберем еще примеры посложнее на нахождение тригонометрических функций друг через друга. Некоторые даже будут из реального ЕГЭ:
Пример 3
Пусть (tg(alpha)=sqrt{3}), найти (cos(alpha)=?), если известно, что (alpha<90^o).
Задание из ЕГЭ по профильной математике.
Условие аналогично условию в примерах №1 и 2, но появилось еще какое-то ограничение на угол (alpha), пока не будем обращать на него внимания, и решаем как обычно. Воспользуемся формулой (5), в ней есть и косинус, и тангенс, как раз одна из функций нам дана, а другую надо найти:
$$1+tg^2(alpha)=frac{1}{cos^2(alpha)};$$
$$1+(sqrt{3})^2=frac{1}{cos^2(alpha)};$$
$$1+3=frac{1}{cos^2(alpha)};$$
$$4=frac{1}{cos^2(alpha)};$$
$$cos^2(alpha)=frac{1}{4};$$
$$cos(alpha)=pmfrac{1}{2}.$$
У нас опять получилось два ответа из-за квадрата. В условии сказано, что задание из первой части ЕГЭ, а значит два ответа быть не может. Для этого нам и дано, что (alpha<90^o). Это означает, что угол (alpha) острый, а значит косинус у острого угла обязательно должен быть положительный.
Ответ: (cos(alpha)=frac{1}{2}.)
Пример 4
Пусть (tg(alpha) =-2), найти (sin(alpha)=?), при (90^o<alpha<180^o).
Опять обратимся к нашим формулам (1-6) и пытаемся найти такую, в которой есть и синус и тангенс. И тут оказывается, что такой формулы нет. Но нам никто не запрещает, зная тангенс и используя формулу (5), найти косинус:
$$1+tg^2(alpha)=frac{1}{cos^2(alpha)};$$
$$1+(-2)^2=frac{1}{cos^2(alpha)};$$
$$5=frac{1}{cos^2(alpha)};$$
$$cos^2(alpha)=frac{1}{5};$$
$$cos^2(alpha)=pmsqrt{frac{1}{5}};$$
Так как согласно условию (alpha>90^o), то значение косинуса должно быть отрицательным:
$$cos(alpha)=-sqrt{frac{1}{5}};$$
А потом, уже зная косинус, по основному тригонометрическому тождеству (1) можно найти требуемый в задаче синус:
$$sin^2(alpha)+cos^2(alpha)=1;$$
$$sin^2(alpha)+left(-sqrt{frac{1}{5}}right)^2=1;$$
$$sin^2(alpha)+frac{1}{5}=1;$$
$$sin^2(alpha)=-frac{1}{5}+1;$$
$$sin^2(alpha)=frac{4}{5};$$
$$sin(alpha)=pmsqrt{frac{4}{5}};$$
Синус у нас положительный и при острых ((alpha<90^o)) и при тупых углах ( (90<alpha<180) ):
$$sin(alpha)=sqrt{frac{4}{5}};$$
Ответ: (sin(alpha)=sqrt{frac{4}{5}}.)
Итак, зная значение хотя бы одной из четырех тригонометрических функций, при помощи формул (1-6) можно найти три оставшихся, именно для этого формулы и нужны.
Зная угол (angle{A}=60^o), мы знаем все тригонометрические функции от этого угла. Смотрите в таблицу (1):
$$sin(60^o)=frac{sqrt{3}}{2};$$
$$cos(60^o)=frac{1}{2};$$
$$tg(60^o)=sqrt{3};$$
$$ctg(60^o)=frac{1}{sqrt{3}};$$
С другой стороны, можно расписать функции по определению через отношение сторон в прямоугольном треугольнике:
$$sin(angle{A})=frac{BC}{AB};$$
$$cos(angle{A})=frac{AC}{AB};$$
$$tg(angle{A})=frac{BC}{AC};$$
$$ctg(angle{A})=frac{AC}{BC};$$
Не пугайтесь, все нам не понадобится. Воспользуемся пока формулами:
$$cos(60^o)=frac{1}{2};$$
$$cos(angle{A}=60^o)=frac{AC}{AB};$$
Нам известны косинус (angle{A}) и сторона (AC), а значит, мы можем найти гипотенузу (AB):
$$frac{1}{2}=frac{5}{AB};$$
$$AB=frac{5}{frac{1}{2}}=5*frac{2}{1}=10;$$
Нашли гипотенузу, теперь найдем последнюю сторону (BC). Для этого нам нужна любая формула с (BC), например:
$$sin(angle{A})=frac{BC}{AB};$$
Синус знаем, (AB) только что нашли – выражаем (BC):
$$BC=AB*sin(60^o)=10*frac{sqrt{3}}{2}=5*sqrt{3}.$$
Ответ: (AB=10;) (BC=5*sqrt{3}.)
Подведем итоги. Зная любую сторону в прямоугольном треугольнике и хотя бы один из острых углов, можно найти все остальные стороны при помощи тригонометрии.
Рассмотрим задачу посложнее.
Пример 6
Дан прямоугольный треугольник (bigtriangleup{ABC}), в котором угол (angle{C}=90^o), угол (tg(angle{A})=frac{1}{5}), сторона (AB=13). В треугольнике из прямого угла (angle{C}) проведена высота (CH). Найти (AH).
Первым делом обратите внимание на один очень важный факт. Если провести высоту в прямоугольном треугольнике из прямого угла, то она поделит треугольник еще на два прямоугольных. В нашем случае (bigtriangleup{ACH}) и (bigtriangleup{CHB}) тоже будут прямоугольными. А значит в них выполняются все соотношения для тригонометрических функций.
Например, в (bigtriangleup{ACH}) для угла (angle{A}) противолежащим катетом будет (CH), а прилежащим – сторона (AH), гипотенуза будет соответственно (AC). А значит можно записать формулы, следующие из определения тригонометрических функций:
$$sin(angle{A})=frac{CH}{AC};$$
$$cos(angle{A})=frac{AH}{AC};$$
$$tg(angle{A})=frac{CH}{AH};$$
$$ctg(angle{A})=frac{AH}{CH};$$
Аналогичные соотношения можно записать и для (bigtriangleup{CHB}) и (bigtriangleup{ABC}). Не буду нагромождать, запишите эти соотношения сами в качестве тренировки.
Следующий важный момент, на который следует обратить внимание – это углы в получившихся треугольниках. Обозначим угол (angle{CAB}=alpha). Тогда, так как (angle{CHA}=90^o), можно выразить угол:
$$angle{ACH}=180-angle{CAB}-angle{CHA}=180-alpha-90=90-alpha;$$
Напомню, что треугольник (bigtriangleup{ABC}) прямоугольный с прямым углом (angle{ACB}=90^o).
Значит
$$angle{HCB}=angle{ACB}-angle{ACH}=90-(90-alpha)=alpha=angle{CAB};$$
Важный факт: (angle{HCB}=angle{CAB})! А равенство этих углов само собой означает и равенство всех тригонометрических функций. То есть, например, (sin(angle{HCB})=sin(angle{ACB})). Точно так же у них равны и косинусы, и тангенсы, и даже котангенсы!
Аналогичные рассуждения можно провести для углов (angle{ACH}=angle{CBA}).
Запомните это!
А теперь приступим непосредственно к решению задачи. Нам известна гипотенуза (AB) и (tg(alpha)). По определению тангенса в (bigtriangleup{ABC}):
$$tg(angle{A})=frac{CB}{AC};$$
Либо из (bigtriangleup{ACH}):
$$tg(angle{A})=frac{CH}{AH};$$
В этих формулах есть проблема: нет известной нам стороны, гипотенузы (AB). А значит, у нас две неизвестные, и решить мы не можем.
Но зная тангенс, мы легко можем найти косинус по формуле:
$$1+tg(alpha)^2=frac{1}{cos^2(alpha)};$$
$$1+left(frac{1}{5}right)^2=frac{1}{cos^2(alpha)};$$
$$1+frac{1}{25}=frac{1}{cos^2(alpha)};$$
$$frac{26}{25}=frac{1}{cos^2(alpha)};$$
$$cos^2(alpha)=frac{1}{frac{26}{25}}=1*frac{25}{26}=frac{25}{26};$$
$$cos(alpha)=pmsqrt{frac{25}{26}}=pmfrac{5}{sqrt{26}};$$
Так как (anglealpha) это острый угол из прямоугольного треугольника, то его косинус точно будет положительным:
$$cos(alpha)=frac{5}{sqrt{26}}.$$
Не самый приятный косинус, но что делать, будем решать так, как есть.
С другой стороны, из (bigtriangleup{ABC}):
$$cos(alpha)=frac{AC}{AB};$$
Подставим известное (AB):
$$frac{5}{sqrt{26}}=frac{AC}{13};$$
$$AC=13*frac{5}{sqrt{26}}=frac{13*5}{sqrt{26}};$$
Либо косинус еще можно расписать в (bigtriangleup{ACH}):
$$cos(alpha)=frac{AH}{AC}=frac{5}{sqrt{26}};$$
Подставим найденное (AC):
$$frac{AH}{frac{13*5}{sqrt{26}}}=frac{5}{sqrt{26}};$$
$$AH=frac{5}{sqrt{26}}*frac{13*5}{sqrt{26}}=frac{5*13*5}{26}=frac{25}{2}=12,5.$$
Ответ: (AH=12,5.)
Таблица тангенсов
Таблица тангенсов – это записанные в таблицу посчитанные значения тангенсов углов от 0° до 360°. Используя таблицу тангенсов Вы сможете провести расчеты даже если под руками не окажется инженерного калькулятора. Чтобы узнать значение тангенса от нужного Вам угла достаточно найти его в таблице.
Калькулятор – тангенс угла
tg(°) = 0
Калькулятор – арктангенс угла
arctan() = 45°
Таблица тангенсов в радианах
| α | 0 | π6 | π4 | π3 | π2 | π | 3π2 | 2π |
| tg α | 0 | √33 | 1 | √3 | ∞ | 0 | ∞ | 0 |
Таблица тангенсов углов от 0° до 180°
| tg(0°) = 0 tg(1°) = 0.01746 tg(2°) = 0.03492 tg(3°) = 0.05241 tg(4°) = 0.06993 tg(5°) = 0.08749 tg(6°) = 0.1051 tg(7°) = 0.12278 tg(8°) = 0.14054 tg(9°) = 0.15838 tg(10°) = 0.17633 tg(11°) = 0.19438 tg(12°) = 0.21256 tg(13°) = 0.23087 tg(14°) = 0.24933 tg(15°) = 0.26795 tg(16°) = 0.28675 tg(17°) = 0.30573 tg(18°) = 0.32492 tg(19°) = 0.34433 tg(20°) = 0.36397 tg(21°) = 0.38386 tg(22°) = 0.40403 tg(23°) = 0.42447 tg(24°) = 0.44523 tg(25°) = 0.46631 tg(26°) = 0.48773 tg(27°) = 0.50953 tg(28°) = 0.53171 tg(29°) = 0.55431 tg(30°) = 0.57735 tg(31°) = 0.60086 tg(32°) = 0.62487 tg(33°) = 0.64941 tg(34°) = 0.67451 tg(35°) = 0.70021 tg(36°) = 0.72654 tg(37°) = 0.75355 tg(38°) = 0.78129 tg(39°) = 0.80978 tg(40°) = 0.8391 tg(41°) = 0.86929 tg(42°) = 0.9004 tg(43°) = 0.93252 tg(44°) = 0.96569 tg(45°) = 1 tg(46°) = 1.03553 tg(47°) = 1.07237 tg(48°) = 1.11061 tg(49°) = 1.15037 tg(50°) = 1.19175 tg(51°) = 1.2349 tg(52°) = 1.27994 tg(53°) = 1.32704 tg(54°) = 1.37638 tg(55°) = 1.42815 tg(56°) = 1.48256 tg(57°) = 1.53986 tg(58°) = 1.60033 tg(59°) = 1.66428 tg(60°) = 1.73205 |
tg(61°) = 1.80405 tg(62°) = 1.88073 tg(63°) = 1.96261 tg(64°) = 2.0503 tg(65°) = 2.14451 tg(66°) = 2.24604 tg(67°) = 2.35585 tg(68°) = 2.47509 tg(69°) = 2.60509 tg(70°) = 2.74748 tg(71°) = 2.90421 tg(72°) = 3.07768 tg(73°) = 3.27085 tg(74°) = 3.48741 tg(75°) = 3.73205 tg(76°) = 4.01078 tg(77°) = 4.33148 tg(78°) = 4.70463 tg(79°) = 5.14455 tg(80°) = 5.67128 tg(81°) = 6.31375 tg(82°) = 7.11537 tg(83°) = 8.14435 tg(84°) = 9.51436 tg(85°) = 11.43005 tg(86°) = 14.30067 tg(87°) = 19.08114 tg(88°) = 28.63625 tg(89°) = 57.28996 tg(90°) = ∞ tg(91°) = -57.28996 tg(92°) = -28.63625 tg(93°) = -19.08114 tg(94°) = -14.30067 tg(95°) = -11.43005 tg(96°) = -9.51436 tg(97°) = -8.14435 tg(98°) = -7.11537 tg(99°) = -6.31375 tg(100°) = -5.67128 tg(101°) = -5.14455 tg(102°) = -4.70463 tg(103°) = -4.33148 tg(104°) = -4.01078 tg(105°) = -3.73205 tg(106°) = -3.48741 tg(107°) = -3.27085 tg(108°) = -3.07768 tg(109°) = -2.90421 tg(110°) = -2.74748 tg(111°) = -2.60509 tg(112°) = -2.47509 tg(113°) = -2.35585 tg(114°) = -2.24604 tg(115°) = -2.14451 tg(116°) = -2.0503 tg(117°) = -1.96261 tg(118°) = -1.88073 tg(119°) = -1.80405 tg(120°) = -1.73205 |
tg(121°) = -1.66428 tg(122°) = -1.60033 tg(123°) = -1.53986 tg(124°) = -1.48256 tg(125°) = -1.42815 tg(126°) = -1.37638 tg(127°) = -1.32704 tg(128°) = -1.27994 tg(129°) = -1.2349 tg(130°) = -1.19175 tg(131°) = -1.15037 tg(132°) = -1.11061 tg(133°) = -1.07237 tg(134°) = -1.03553 tg(135°) = -1 tg(136°) = -0.96569 tg(137°) = -0.93252 tg(138°) = -0.9004 tg(139°) = -0.86929 tg(140°) = -0.8391 tg(141°) = -0.80978 tg(142°) = -0.78129 tg(143°) = -0.75355 tg(144°) = -0.72654 tg(145°) = -0.70021 tg(146°) = -0.67451 tg(147°) = -0.64941 tg(148°) = -0.62487 tg(149°) = -0.60086 tg(150°) = -0.57735 tg(151°) = -0.55431 tg(152°) = -0.53171 tg(153°) = -0.50953 tg(154°) = -0.48773 tg(155°) = -0.46631 tg(156°) = -0.44523 tg(157°) = -0.42447 tg(158°) = -0.40403 tg(159°) = -0.38386 tg(160°) = -0.36397 tg(161°) = -0.34433 tg(162°) = -0.32492 tg(163°) = -0.30573 tg(164°) = -0.28675 tg(165°) = -0.26795 tg(166°) = -0.24933 tg(167°) = -0.23087 tg(168°) = -0.21256 tg(169°) = -0.19438 tg(170°) = -0.17633 tg(171°) = -0.15838 tg(172°) = -0.14054 tg(173°) = -0.12278 tg(174°) = -0.1051 tg(175°) = -0.08749 tg(176°) = -0.06993 tg(177°) = -0.05241 tg(178°) = -0.03492 tg(179°) = -0.01746 tg(180°) = 0 |
Таблица тангенсов углов от 181° до 360°
| tg(181°) = 0.01746 tg(182°) = 0.03492 tg(183°) = 0.05241 tg(184°) = 0.06993 tg(185°) = 0.08749 tg(186°) = 0.1051 tg(187°) = 0.12278 tg(188°) = 0.14054 tg(189°) = 0.15838 tg(190°) = 0.17633 tg(191°) = 0.19438 tg(192°) = 0.21256 tg(193°) = 0.23087 tg(194°) = 0.24933 tg(195°) = 0.26795 tg(196°) = 0.28675 tg(197°) = 0.30573 tg(198°) = 0.32492 tg(199°) = 0.34433 tg(200°) = 0.36397 tg(201°) = 0.38386 tg(202°) = 0.40403 tg(203°) = 0.42447 tg(204°) = 0.44523 tg(205°) = 0.46631 tg(206°) = 0.48773 tg(207°) = 0.50953 tg(208°) = 0.53171 tg(209°) = 0.55431 tg(210°) = 0.57735 tg(211°) = 0.60086 tg(212°) = 0.62487 tg(213°) = 0.64941 tg(214°) = 0.67451 tg(215°) = 0.70021 tg(216°) = 0.72654 tg(217°) = 0.75355 tg(218°) = 0.78129 tg(219°) = 0.80978 tg(220°) = 0.8391 tg(221°) = 0.86929 tg(222°) = 0.9004 tg(223°) = 0.93252 tg(224°) = 0.96569 tg(225°) = 1 tg(226°) = 1.03553 tg(227°) = 1.07237 tg(228°) = 1.11061 tg(229°) = 1.15037 tg(230°) = 1.19175 tg(231°) = 1.2349 tg(232°) = 1.27994 tg(233°) = 1.32704 tg(234°) = 1.37638 tg(235°) = 1.42815 tg(236°) = 1.48256 tg(237°) = 1.53986 tg(238°) = 1.60033 tg(239°) = 1.66428 tg(240°) = 1.73205 |
tg(241°) = 1.80405 tg(242°) = 1.88073 tg(243°) = 1.96261 tg(244°) = 2.0503 tg(245°) = 2.14451 tg(246°) = 2.24604 tg(247°) = 2.35585 tg(248°) = 2.47509 tg(249°) = 2.60509 tg(250°) = 2.74748 tg(251°) = 2.90421 tg(252°) = 3.07768 tg(253°) = 3.27085 tg(254°) = 3.48741 tg(255°) = 3.73205 tg(256°) = 4.01078 tg(257°) = 4.33148 tg(258°) = 4.70463 tg(259°) = 5.14455 tg(260°) = 5.67128 tg(261°) = 6.31375 tg(262°) = 7.11537 tg(263°) = 8.14435 tg(264°) = 9.51436 tg(265°) = 11.43005 tg(266°) = 14.30067 tg(267°) = 19.08114 tg(268°) = 28.63625 tg(269°) = 57.28996 tg(270°) = ∞ tg(271°) = -57.28996 tg(272°) = -28.63625 tg(273°) = -19.08114 tg(274°) = -14.30067 tg(275°) = -11.43005 tg(276°) = -9.51436 tg(277°) = -8.14435 tg(278°) = -7.11537 tg(279°) = -6.31375 tg(280°) = -5.67128 tg(281°) = -5.14455 tg(282°) = -4.70463 tg(283°) = -4.33148 tg(284°) = -4.01078 tg(285°) = -3.73205 tg(286°) = -3.48741 tg(287°) = -3.27085 tg(288°) = -3.07768 tg(289°) = -2.90421 tg(290°) = -2.74748 tg(291°) = -2.60509 tg(292°) = -2.47509 tg(293°) = -2.35585 tg(294°) = -2.24604 tg(295°) = -2.14451 tg(296°) = -2.0503 tg(297°) = -1.96261 tg(298°) = -1.88073 tg(299°) = -1.80405 tg(300°) = -1.73205 |
tg(301°) = -1.66428 tg(302°) = -1.60033 tg(303°) = -1.53986 tg(304°) = -1.48256 tg(305°) = -1.42815 tg(306°) = -1.37638 tg(307°) = -1.32704 tg(308°) = -1.27994 tg(309°) = -1.2349 tg(310°) = -1.19175 tg(311°) = -1.15037 tg(312°) = -1.11061 tg(313°) = -1.07237 tg(314°) = -1.03553 tg(315°) = -1 tg(316°) = -0.96569 tg(317°) = -0.93252 tg(318°) = -0.9004 tg(319°) = -0.86929 tg(320°) = -0.8391 tg(321°) = -0.80978 tg(322°) = -0.78129 tg(323°) = -0.75355 tg(324°) = -0.72654 tg(325°) = -0.70021 tg(326°) = -0.67451 tg(327°) = -0.64941 tg(328°) = -0.62487 tg(329°) = -0.60086 tg(330°) = -0.57735 tg(331°) = -0.55431 tg(332°) = -0.53171 tg(333°) = -0.50953 tg(334°) = -0.48773 tg(335°) = -0.46631 tg(336°) = -0.44523 tg(337°) = -0.42447 tg(338°) = -0.40403 tg(339°) = -0.38386 tg(340°) = -0.36397 tg(341°) = -0.34433 tg(342°) = -0.32492 tg(343°) = -0.30573 tg(344°) = -0.28675 tg(345°) = -0.26795 tg(346°) = -0.24933 tg(347°) = -0.23087 tg(348°) = -0.21256 tg(349°) = -0.19438 tg(350°) = -0.17633 tg(351°) = -0.15838 tg(352°) = -0.14054 tg(353°) = -0.12278 tg(354°) = -0.1051 tg(355°) = -0.08749 tg(356°) = -0.06993 tg(357°) = -0.05241 tg(358°) = -0.03492 tg(359°) = -0.01746 tg(360°) = 0 |
Для того, чтобы определить значение угла α, необходимо воспользоваться подходящей функции из тригонометрии. Во время решения задач постоянно возникает необходимость в том, чтобы узнать значение углов. Для некоторых углов можно найти точные значения, для других сложно определить точную цифру и можно вывести только приблизительное значение.
В этой статье мы подробно поговорим о функциях из тригонометрии. Мы не только расскажем о свойствах синуса, тангенса и других функций, но и узнаем, как правильно вычислять значения для каждого отдельного случая.
Рассмотрим подробно каждый случай.
Приближенное число для каждой из известных функций можно найти по определению. Для одних можно указать точные значения, для других – только приблизительные.
Соотношения сторон и углов фигуры используются для того, чтобы определить значения для 30°, 45°, 60°. Если угол выходит за пределы 90°, то перед вычислением значения следует воспользоваться специальной формулой для того, чтобы привести угол к нужному виду.
Если известно значение синуса для α, можно быстро узнать значение косинуса для этого же угла. Это легко выполнить с помощью основных тождеств, которые представлены в геометрии.
В некоторых случаях для того, чтобы узнать sin или cos угла, можно использовать подходящую тригонометрическую формулу. Например, по известному значению синуса 45°, мы сможем определить значение синуса 30°, воспользовавшись правилом из тригонометрии.
Если для примера не подходит ни одно из приведенных выше решений, можно найти приближенное значение. В этом вам помогут таблицы основных тригонометрических функций, которые легко можно найти.
Если взять за основу определения, возможно определить значения для определенного угла α. Также можно вычислить значения тангенса и котангенса для определенного случая. Можно найти значений основных функций из тригонометрии для частных вариантов. Это углы 0°, 90°, 180°, 270°, 360°.
Разобьем эти углы на четыре группы: 360·z градусов (2π·z рад), 90+360·z градусов (π2+2π·z рад), 180+360·z градусов (π+2π·z рад) и 270+360·z градусов (3π2+2π·z рад), где z- любое целое число.
Изобразим данные формулы на рисунке:
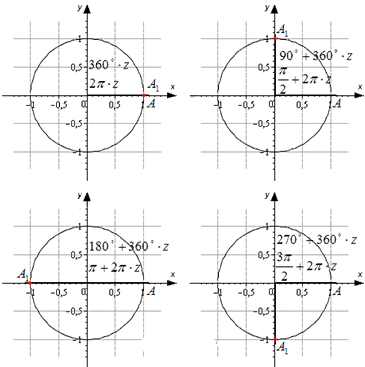
Для каждой группы соответствуют свои значения.
При повороте из точки A на 360·z°, она переходит в себя. А1(1, 0). Синус 0°, 360°, 720° равен 0, а косинус равен 1. Представим это в виде формулы: sin (360°·z)=0 и cos (360°·z)=1 .
Можно определить, что tg (360°·z)=01=0 , а котангенс не определен.
Если А(1, 0) повернуть на 90+360·z°, то она перейдет в А1 (0, 1). По определению: sin (90°+360°·z) =1 и cos (90°+360°·z) =0 . Мы не сможем определить значение тангенса, но котангенс рассчитывается по данной формуле: ctg (90°+360°·z) =01=0 .
Рассмотрим особенности для третьей группы углов. После поворота точки А(1, 0) на любой из углов 180+360·z°, она перейдет в A1(−1, 0). Мы находим значения функций кроме тангенса.
Рассмотрим правила для четвертой группы углов. При повороте точки на 270+360·z° мы попадем в A1(0, −1). Мы находим значения всех функций кроме тангенса.
Для углов, которые не относятся к перечню от 0 °, 90 °, 180 °, 270 °, 360 °…, точных значений нет. Мы можем найти лишь приближенные значения. Рассмотрим пример. Условия – найти основные значения для угла −52 °. Выполним построения.
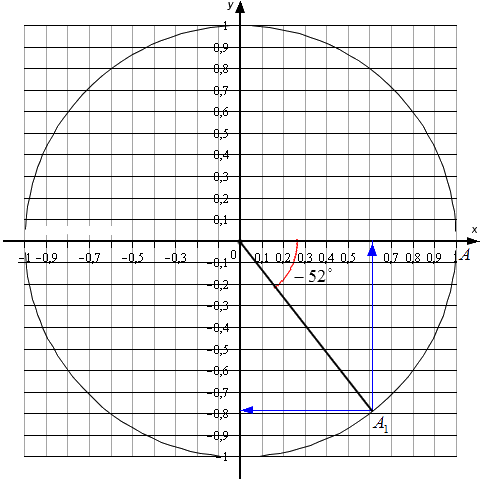
Согласно рисунку, абсцисса А1 ≈ 0,62, а ордината ≈ −0,78. Соответственно, sin(-52°)≈-0,78 и cos(-52°)≈0,62 . Осталось определиться с тангенсом и котангенсом.
Выполняем вычисления: tg(-52°)≈-0, 780, 62≈-1,26 и ctg(-52°)≈0,62-0,78≈-0,79.
Чем точнее выполняется чертеж, тем более точными будут значения для каждого индивидуального случая. Выполнять вычисления удобно только в теории, так как на практике довольно сложно и долго выполнять рисунки.
Линии тригонометрических функций
Линии тригонометрических функций – это линии, которые изображаются вместе с единичной окружностью. Они имеют точку отсчета и единичный отрезок, которая равна единице в координатной системе. Они используются для наглядного изображения значений.
Рассмотрим их на подробном рисунке
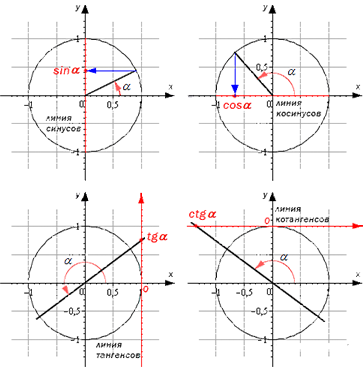
Как найти sin α, cos α, tg α, ctg α
Для тридцати-, сорокопяти-, шестидесятиградусных углов мы имеем определенные значения. Чтобы найти их, можно воспользоваться правилами о прямоугольном треугольнике с острыми углами. Для этого используется теорема Пифагора.
Для того, чтобы узнать значения для углов тридцати- и шестидесятиградусных углов изображаем прямоугольный треугольник с углами данной величины. Длина гипотенузы должна быть равна 1. Согласно теореме Пифагора, катет, лежащий напротив тридцатиградусного угла, равен половине гипотенузы. Воспользуемся теоремой: 12-122=32 . Так как синус угла – это катет, деленный на гипотенузу, вычисляем, что sin 30°=121=12 и sin 60°=321=32 .
Косинус можно найти по формуле, которая предполагает деление прилежащего катета на гипотенузу. Вычисляем: cos 30°=321=32 и cos 60°=121=12 .
Тангенс можно найти по формуле, которая предполагает деление противолежащего катета на прилежащий. Котангенс находим по такой же схеме – делим прилежащий катет на противолежащий.
Вычисляем: tg 30°=1232=13=33 и tg 60°=3212=3 . Находим котангенс по подобной схеме: сtg 30°=3212=3 и сtg 60°=1232=13=33 . После этого приступаем к вычислению значений основных тригонометрических функций для сорока пятиградусного угла. Используем равнобедренный треугольник с углами 45° и гипотенузой, которая равна 1. Используем теорему Пифагора. Согласно формуле, длины катетов равны 22 . Т
Теперь мы сможем найти значения для основных тригонометрических функций. Используем формулу, которая предполагает деление длин соответствующих сторон рассматриваемого треугольника.
Выводим формулу: ctg 45°=2222=1 .
Полученные значения для тридцати-, сорокапяти-, шестидесятиградусных углов будут использоваться для решения различных задач. Запишите их – они часто будут использоваться. Для удобства можно использовать таблицу значений.
Проиллюстрируем значения для тридцати-, сорокапяти-, шестидесятиградусных углов с использованием окружности и линий.
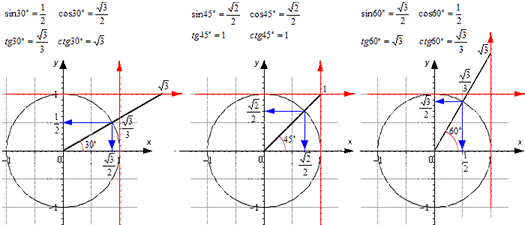
Значения основных функций тригонометрии
Основные тождества из геометрии связывают с собой sin α, cos α, tg α, ctg α для определенного угла. С помощью одной функции вы легко сможете найти другую.
Для того, чтобы найти синус по известному косинусу, sin2α+cos2α=1 .
Тангенс по известному косинусу tg2α+1=1cos2α .
Котангенс по известному синусу или наоборот 1+ctg2α= 1sin2α .
Тангенс через котангенс или наоборот можно найти благодаря удобной формуле: tg α·ctg α=1 .
Для того, чтобы закрепить полученные знания, рассмотрим их на подробном примере
Необходимо найти значение синуса угла π8, если tg π8=2-1 .
Сначала найдем котангенс угла: ctgπ8=1tgπ8=12-1=2+1(2-1)·(2+1)= 2+1(2)2-12=2+1 Воспользуемся формулой 1+ctg2α=1sin2α . Благодаря этому мы вычисляем значение синуса. Имеем
sin2π8=11+ctg2π8=11+(2+1)2=14+22=12·(2+2)=2-22·(2+2)·(2-2)==2-22·(22-(2)2)=2-24
Для завершения необходимо определить значение синуса. Угол π8 является углом первой четверти, то синус является положительным. Чтобы точно определить знак, вы можете воспользоваться таблицей, в которой определены знаки по четвертям координатной плоскости. Таким образом, sin π8=sin2π8=2-24=2-22 . sin π8=2-22.
Сведение к углу
Удобнее всего находить значения для угла от 0 до 90 °. Сведение к углу из интервала от 0 до 90 °. Если угол не соответствует заданному интервалу, можно использовать законы и тождества, которые мы учили на уроках геометрии. Тогда мы сможем найти значение, которое будет равно для угла указанных пределах.
Задача заключается в том, чтобы найти синус 210°. Представим 210 как разность или сумму, разложив число на несколько. Воспользуемся соответствующей формулой для приведения. Используем формулу для нахождения значения синуса 30°: sin 210°=sin(180°+30°)=-sin 30°=-12 , или косинуса 60 ° sin 210°=sin(270°-60°)=-cos 60°=-12.
Для того, чтобы решать задачи было намного проще, при нахождении значений переходите к углам из интервала от 0 до 90° с помощью формул приведения, если угол не находится в этих пределах.
Использование формул
Раннее мы рассмотрели подробности, касающиеся нахождению значений основных функций с использованием формул тригонометрии. Для того, чтобы определить значение для определенного угла, используйте формулы и значения основных функций для известных углов.
Для примера вычислим значение тангенса π8, который был использован в предыдущем примере. Возьмем за основу основные формулы тригонометрии.
Найдите значение tgπ8 .
Используя формулу тангенса, преобразуем уравнение до следующего равенства tg2π8=1-cosπ41+cosπ4 . Значения косинуса угла π4 известны из предыдущего примера. Благодаря этому мы быстро найдем значения тангенса.
tg2π8=1-cosπ41+cosπ4=1-221+22=2-22+2==(2-2)2(2+2)·(2-2)=(2-2)222-(2)2=(2-2)22
Угол π8 является углом первой четверти. Согласно таблице основных тригонометрических функций по четвертям координатной плоскости, тангенс этого угла положителен. Продолжаем вычисления для дальнейшего решения: tgπ8=tg2π8=(2-2)22=2-22=2-1
tgπ8=2-1.
Частные случаи
Тригонометрия – довольно сложная наука. Далеко не всегда можно найти формулы, используемые для вычисления. Существует множество уравнений, которые не поддаются стандартным формулам. Некоторые значения очень сложно обозначить точной цифрой. Это не так просто, как может показаться.
Однако точные значения не всегда нужны. Хватает и тех, что не претендуют на высокую точность. Благодаря существующим таблицам, которые можно найти в математических учебниках, можно найти любое приближенное значение основных функций. Благодаря справочным материалам вычислять формулы будет намного проще. В таблицах содержатся значения с высокой точностью.
В этой статье мы разберем такое понятие, как тангенс угла. Начнем с понятия прямого угла. Прямым углом называется угол равный 900. Угол в котором меньше 90 градусов – называется острым. Угол в котором больше 90 градусов – называется тупым. В развернутом угле 180 градусов.
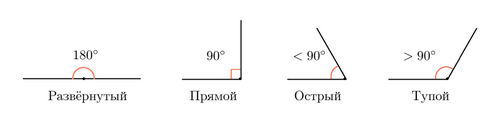
Изображаем треугольник с прямым углом С , при этом противолежащая сторона будет имеет такое же обозначение (с -будет гипотенузой), аналогично поступаем и с другими углами. Сторона находящаяся противоположно от острого угла – называется катетом.
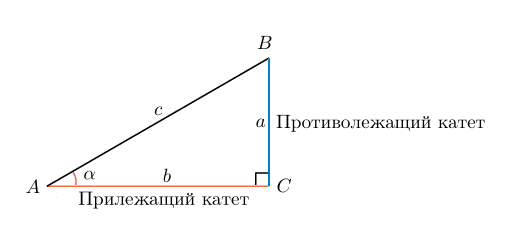
Синус и косинус находятся с помощью катета и гипотенузы, а именно:
sinA = a/c
cosA = b/c
Формула тангенса
tg A = a/b
другими словами определение тангенса – это деление противоположного катета на прилежащий
Существует ещё одна равносильная формула тангенса
tg A = sinA/cosA
расшифровывается как деление sin на cos.
Котангенс находится практически аналогично, лишь значения поменяются местами.
ctg A = cosA/sinA
Внимание! В помощь родителям и учителям гдз по математики 5 класс (http://spisaly.ru/gdz/5_klass/math). Все предложенные на сайте книги можно скачать или изучить онлайн. Перейдите по ссылке и узнайте подробнее.
Данные тригонометрические функции, значительно облегчают вычисление углов. Благодаря синусу, косинусу и тангенсу стало возможным, определение всех неизвестных углов в треугольнике, с одним известным.
Обозначения для основных углов:
тангенс 30 – 0,577
тангенс 45 – 1,000
тангенс 60 – 1,732
Существуют специальная таблица тангенсов, значения которой можно получить при помощи деления значений таблиц синуса и косинуса, но так как это достаточно трудоемкий процесс и нужна данная таблица тангенсов.
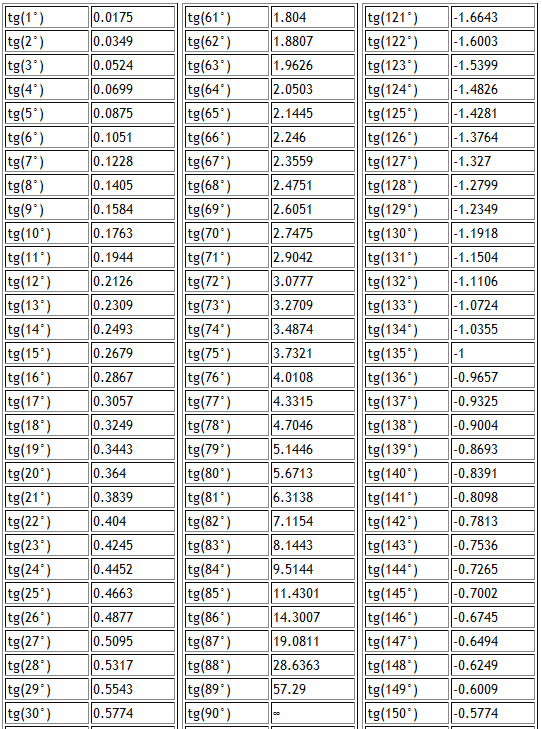
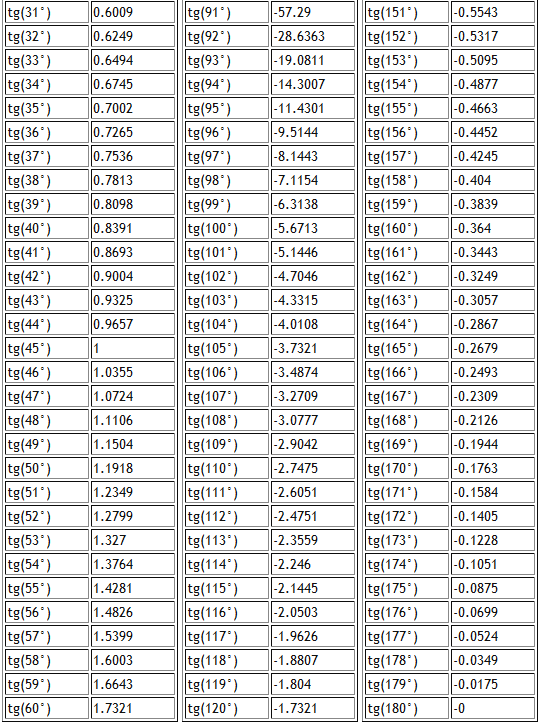
Есть очень много задач в которых у треугольника углы равны 90, 30, 60 градусам. либо 90, 45, 45 градусам. Для таких фигур лучше заучить их соотношение , что бы потом было проще.
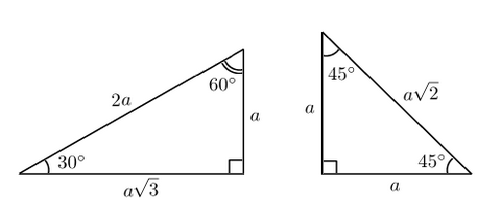
В первом случае катет противоположный 30 градусам равняется 1/2 от гипотенузы.
Во втором случае гипотенуза превышает катет в ?2 раз.
Если материал был полезен, вы можете отправить донат или поделиться данным материалом в социальных сетях:
