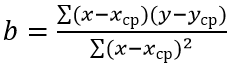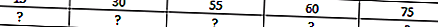Голосование за лучший ответ
Vikar
Мыслитель
(8884)
7 лет назад
Выбрать точку на графике и ее значение по оси Y разделить на значение по оси X (если график – прямая линия)
VikarМыслитель (8884)
7 лет назад
и проходит через начало координат…
Сикорский Роман
Ученик
(115)
7 лет назад
Подвести мышку к нужной точке графика. Появится окошко с значением
лиза мазулова
Профи
(615)
2 года назад
Если график не линейный, то через функцию ЛИНЕЙН (A1:А5;В1:В5), где A1:А5;В1:В5 диапазон координат
Функция TAN Excel (касательная)
Функция TAN Excel — это встроенная тригонометрическая функция в excel, которая используется для вычисления значения косинуса заданного числа или, с точки зрения тригонометрии, значения косинуса заданного угла, здесь угол — это число в Excel, и эта функция принимает только один аргумент. который является предоставленным входным номером.
Функция TAN Excel
Функция TAN Excel — это встроенная функция, относящаяся к категории Math / Trig function, которая возвращает значение тангенса угла. Формула для TAN всегда возвращает числовое значение.
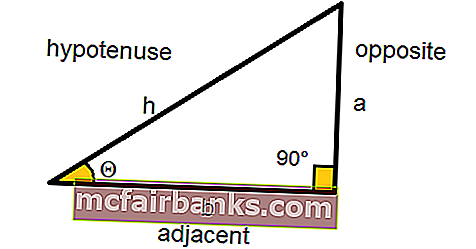
В тригонометрии тангенс угла эквивалентен отношению перпендикуляра к основанию прямоугольного треугольника.
TAN Θ = противоположная сторона / смежная сторона
Следовательно, TAN Θ = a / b
Формула TAN в Excel
Ниже приведена формула TAN в Excel.
Где число — это аргумент, передаваемый функции в радианах.
Угол, который мы указываем в качестве входных данных, распознается функцией Tangent, только если он указан как Radians.
Чтобы преобразовать угол в радианы, используйте функцию РАДИАНЫ или преобразуйте угол в радианы с помощью математического соотношения
Радиан = угол в градусах * (π / 180)
π в Excel представлена функцией PI ()
Следовательно, радиан = градус * (PI () / 180)
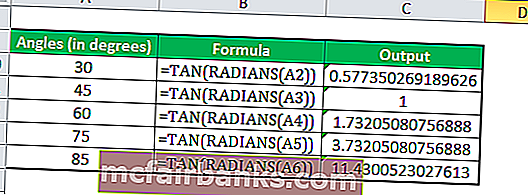
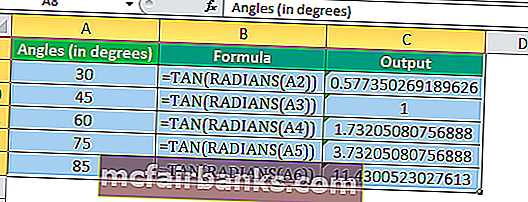
Расчет значения TAN с использованием функции TAN и RADIANS
Расчет значения TAN с использованием TAN и функции PI
У функции касательной есть много реальных приложений; он широко используется в архитектуре для расчета высоты и длины геометрических фигур. Функция касания, используемая в системах навигации и GPS, в аэронавтике.
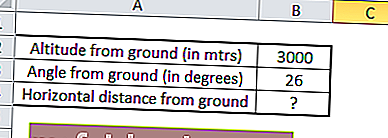
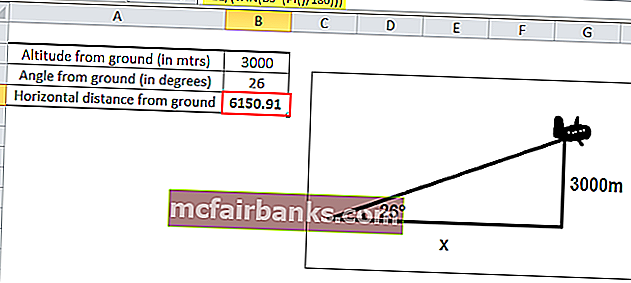
Например, если самолет летит на высоте 3000 м и делает угол к наблюдателю на земле 26 °, и мы хотим найти расстояние от самолета до наблюдателя.
Как мы знаем, TAN Θ = противоположная сторона / смежная сторона
Здесь противоположная сторона = высота самолета от земли, равная 3000 метров.
А соседняя сторона = горизонтальное расстояние самолета от земли, которое неизвестно, и нам нужно его вычислить.
Итак, используя формулу для TAN, мы имеем
TAN (26 °) = 3000 / x
Следовательно, x = 3000 / (TAN (26 °))
В Excel, взяв относительные контрольные значения, мы имеем
Икс = B2 / (TAN (B3 * (PI () / 180))))
X = 6150.91 метров
Как использовать TAN в Excel?
Функция Excel TAN очень проста и удобна в использовании. Позвольте мне понять, как работает формула TAN в Excel на нескольких примерах.
Касательная в Excel, пример # 1
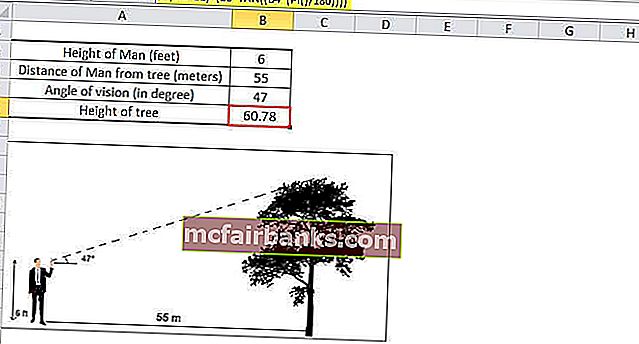
Мужчина ростом 6 футов находится в 55 метрах от дерева. Он делает угол обзора 47 ° параллельно земле. Мы хотим рассчитать высоту дерева.
Чтобы найти высоту дерева, мы будем использовать TAN Θ. В контексте Excel мы будем использовать функцию Tangent.
Высота дерева будет
Высота Человека + Расстояние Человека от дерева * TAN (47 °)
Поскольку рост человека указан в футах, мы переведем его в метры (1 фут = 0,30 метра).
Поместив все относительные значения в Excel, формула для высоты дерева будет
= (0,3 * B2) + (B3 * TAN ((B4 * (PI () / 180))))
Выходные данные TAN Excel:
Высота дерева 60,78 метра.
Касательная в Excel, пример # 2
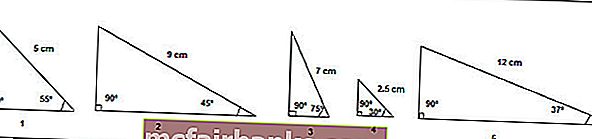
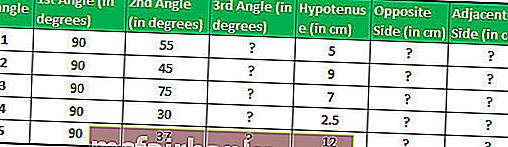
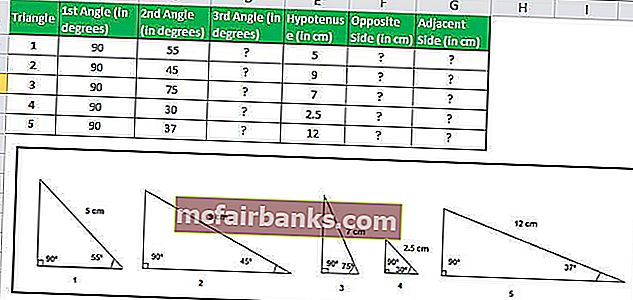
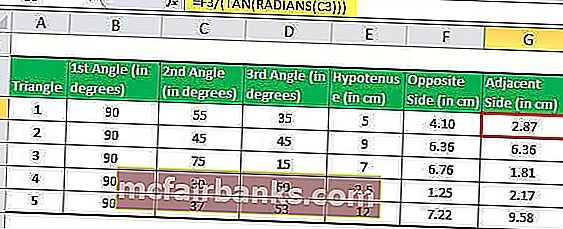
Предположим, у нас есть пять прямоугольных треугольников с указанием их углов и длины с одной стороны, и нам нужно вычислить длину двух других сторон.
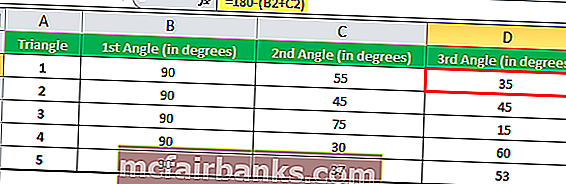
Сумма всех углов треугольника равна 180 °; следовательно, мы можем легко вычислить третий угол.
Мы знаем, Sin Θ = противоположное / гипотенуза
Таким образом, длина противоположной стороны будет Sin Θ * гипотенуза
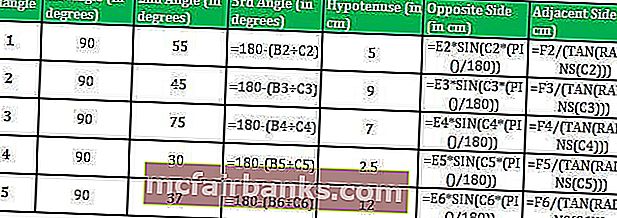
В Excel длина Противоположной стороны (перпендикулярной стороны) будет рассчитана по формуле TAN.
= E2 * SIN (C2 * (PI () / 180))
Применяя формулу TAN для пяти треугольников, мы можем получить длину перпендикуляров треугольников
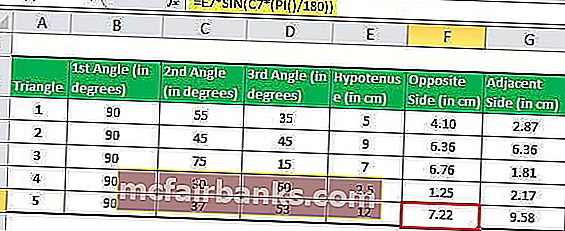
Теперь у нас есть две стороны треугольника: гипотенуза и перпендикулярная сторона. Мы можем легко вычислить третью сторону (основание), используя TAN в Excel.
Мы знаем, что TAN Θ = противоположная сторона / смежная сторона.
Таким образом, длина прилегающей стороны будет Обратная сторона/ТАН Θ.
В Excel длина прилегающей стороны (основания) будет рассчитываться по формуле TAN.
= F2 / (TAN (РАДИАНЫ (C2)))
Применяя формулу TAN для пяти треугольников, мы можем получить длину смежной стороны треугольника.
TAN в выводе Excel:
Касательная в Excel, пример №3
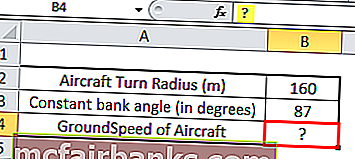
Самолет делает разворот радиусом 160 м и летит с постоянным углом крена 87 °, в идеальных условиях (без колебаний ветра) рассчитайте постоянную путевую скорость самолета.
Радиус поворота задается формулой.
Радиус поворота = V 2 / g * TAN Θ
Радиус поворота 160 метров; Постоянный угол крена 87 °, g — ускорение свободного падения, значение которого составляет 9,8 м / с. 2 , поэтому путевая скорость будет
V = (Радиус поворота * (g * TAN Θ)) 1/2
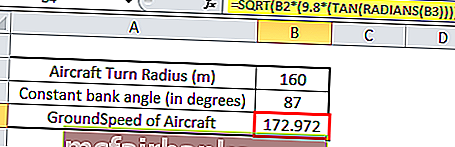
Применяя приведенную выше формулу TAN в Excel со справочными значениями, мы получаем формулу TAN.
= КОРЕНЬ (B2 * (9,8 * (TAN (РАДИАНЫ (B3)))))
SQRT — это встроенная функция Excel, которая вычисляет квадратный корень из числа.
TAN в выводе Excel:
Итак, путевая скорость самолета составляет 172,97 м / с.
Пример функции касания # 4
У нас есть формула для TAN, обозначенная f (x) = 2c * TAN2Θ, где c — постоянное значение, равное 0,988. Значение варианта — это значение, а формула для TAN зависит от значения. Нам нужно построить график заданной функции касания.
Используя функцию Excel TAN, мы затем вычислим значения функции, поэтому, взяв контрольные значения в качестве входных данных, мы получим формулу TAN,
Как можно провести касательную к графику в экселе?
Excel всё-таки не бумага, чтобы на ней что-то можно было провести.
Вы табулировали некую функцию и отобразили её график. Вам надо выбрать точку и табулировать функцию производной в некой заранее заданной точке.
Уравнение касательной к табулированной функции находят разными способами на выч. методах. В сети можно найти уже готовые формулы. Если хотите сами, то надо выбрать 3 точки, наиболее близкие к заданной, представить функцию параболой, проходящей через них, а потом построить касательную к этой параболе.
Как только у вас будет уравнение прямой, табулируйте её функцию и выведите на график результат.
ЗЫ
Табулировать функцию — найти множесто пар (аргумент, значение) и вывести их в табличном виде.
Как построить касательную в excel к точке
Тангенциальная линия — это прямая линия на графике, которая проходит по касательной к кривой линии, составленной из точек данных. В Excel есть возможность автоматически создавать линию тренда, или вы можете вручную нарисовать касательную линию на графике. Тангенциальная линия рисуется касаясь изогнутой линии, так что когда кривая отходит от линии, она равноудалена от линии. В то время как функция линии тренда в Excel покажет тренд всей линии, ручное рисование линии создаст истинную касательную.
Кредит: Драган Радоевич / iStock / Getty Images
Шаг 1
Откройте лист Excel, содержащий данные, которые вы хотите использовать для тангенциальной линии. Изогнутый линейный график основан на наборах двух точек данных, например времени и амплитуды.
Шаг 2
Нажмите и перетащите на электронную таблицу, чтобы выделить данные, которые вы хотите показать, включая метки в вашем выборе.
Шаг 3
Нажмите на вкладку «Вставить», а затем нажмите стрелку вниз рядом с кнопкой «Разброс» в области «Диаграмма». Выберите «Разброс с гладкими линиями». Диаграмма создана в вашей электронной таблице.
Шаг 4
Перейдите на вкладку «Инструменты диаграммы: макет», а затем нажмите кнопку «Линия тренда» справа. Выберите «Линейный», чтобы создать прямую линию, которая приближается к прогрессу изогнутой линии. Он будет пересекать кривую в некоторых точках.
Шаг 5
Нажмите на вкладку «Вставка», а затем нажмите «Фигуры». Выберите «Линия» и нарисуйте линию так, чтобы она просто касалась одной из точек на вашей кривой.
Шаг 6
Нажмите на вкладку «Инструменты рисования: Формат» и нажмите кнопку «Повернуть» справа. Выберите «Дополнительные параметры вращения». Нажмите стрелку «Вверх» или «Вниз» рядом с полем «Поворот» в диалоговом окне, которое появляется, чтобы повернуть линию на кривой. Когда линия будет равноудалена от обеих сторон кривой, нажмите «ОК».
Дубликаты не найдены
ЕСЛИ(условие;выполнить_если_истина;выполнить_если_ложь)
[в eng версии соответственно это IF(. )]
Условие — что угодно, что может интерпретироваться как булевская функция. Например, дано, что a=2, b=3. Тогда IF(a>b;”истина”;”ложь”) вернёт “ложь”.
Сделать разветвление на несколько вариантов — IF(условие1;действие1;IF(условие2;действие2;..))
В качетсве крайнего “ложь” блока ЕСЛИ можно писать что угодно [если уверены, что рассмотрели все возможные варианты].
Вообще, насколько помню, годная в экселе справка была.. Так что традиционное — RTFM.
В математике много задач связано с вычислением производных функций и использованием геометрической интерпретации первой производной функции. Рассмотрим методику построения касательной к заданной точке функции и определения параметров ее уравнения.
Если задана функция f(x), то первая производная функции в заданной точке с координатами хо и уо является угловым коэффициентом касательной в этой точке. Уравнение касательной, проходящей через точку с координатами хо и уо, имеет вид:
где к = /'(хо) — угловой коэффициент;
Требуется построить график функции /(х) и касательную в прямоугольной области диаграммы, ограниченной минимальными и максимальными значениями абсцисс (хмин и хмакс) и ординат (умин и умакс).
Так как касательная является прямой линией, проходящей через заданную точку, то ее можно построить по координатам двух точек: (х^у-^) и (х2,у2), которые располагаются на границах прямоугольника.
Рассмотрим расчет координат точек касательной с учетом значения углового коэффициента к = /'(х ) . Значения углового коэффициента
могут быть положительными, отрицательными, нулевыми или иметь бесконечно большие значения.
Пусть к > 0. Остановимся на всех возможных вариантах расположения точек. При хх = хмин с учетом формулы ух = к * (хмин — х ) + у .
Координаты второй точки касательной рассчитываются аналогичным образом. При этом задаем х2 = хмакс и у2 = к * (хмакс — х ) + у .
Если к Умэкс) П Р И предварительном построении графика заданной функции на основе табулированной функции (В5:С25)
Формируем таблицы начальных условий задачи.
координат заданной точки функции(х , у ) (F2 и G2);
углового коэффициента к = /'(х ) (Н2);
граничных значений диапазонов (хмин, хмакс, умин, умакс) (A2:D5).
Отступив одну ячейку от таблицы функции (В5:С25), рассчитываем координаты точек касательной (В27:С28) с учетом приведенных выше рассуждений (на рисунке в примечаниях отображены формулы расчетов). Предварительно для удобства вычисляем во вспомогательных ячейках значения уг при хг = хмин и у2 при х2 = хмакс (F8 и G8). Для отображения точки на графике функции добавляем ячейки с ее заданными координатами (ВЗО и СЗО).
Выделив диапазон ячеек (В5:С30), в который включаются ячейки таблицы функции и координат точек касательной, обращаемся к мастеру диаграмм для построения графика функции и касательной. Задаем тип диаграммы — Точечная, а вид — Точечная диаграмма со значениями, соединенными сглаживающими линиями без маркеров. Фиксируем минимальные и максимальные значения шкал осей х и у в диалоговом окне Формат оси.
Для заданной точки, к которой строится касательная, можно установить отличительный маркер и вывести ее координат. Чтобы установить цвет и толщину линии касательной нужно аккуратно щелкнуть по линии касательной. При появлении маркеров точек касательной вызвать контекстное меню и щелкнуть по пункту Формат точки данных. В диалоговом окне установить тип, цвет и толщину линии касательной.
Для наглядности одновременно вычисляем параметры уравнения касательной у = а * х + Ь, где из уравнения а = k, b = у — к * х . Эти параметры рассчитываем в соответствующих ячейках, которые соседствуют с ячейками, в которых занесены символы Y,=,* для представления уравнения касательной. Так как значение параметра b могут быть как отрицательными, так и положительными, то в соответствующей ячейке используем функцию ЕСЛИ для отображения символов + и -.
Изменяя значения координаты х , осуществляем исследование поведения касательной в заданной точке функции и изменения параметров уравнения касательной.
При необходимости можно дополнительно построить график производной заданной функции.
Функция НАКЛОН в Excel предназначена для определения угла наклона прямой, используемой для аппроксимации данных методом линейной регрессии, и возвращает значение коэффициента a из уравнения y=ax+b. Для определения наклона используются две любые точки на прямой. При этом вычисляется частное от деления длины отрезка, полученного при проецировании этих двух точек на ось Ординат (OY), на длину отрезка, образованного проекциями этих же двух точек на ось Абсцисс (OX).
Фактически, функция НАКЛОН вычисляет значение, которое характеризует скорость изменения данных вдоль линии регрессии. Зная наклон (коэффициент a) и значение коэффициента b можно рассчитать приближенные будущие значения какого-либо свойства y, которое меняется при изменении характеристики x.
Примеры использования функции НАКЛОН в Excel
Для расчета наклона линии регрессии используется уравнение:
где:
- x_ср – среднее значение для диапазона известных значений независимой переменной;
- y_ср – среднее значение для диапазона известных значений зависимой переменной.
Функция НАКЛОН не может быть использована для анализа коллинеарных данных и будет возвращать код ошибки #ДЕЛ/0! в отличие от функции ЛИНЕЙН, которая использует иной алгоритм расчета и возвращает как минимум одно полученное значение.
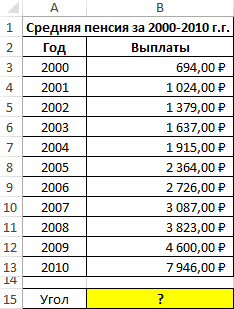
Пример 1. Определить наклон аппроксимирующей прямой для показателей средней пенсии на протяжении нескольких лет.
Вид исходной таблицы данных:
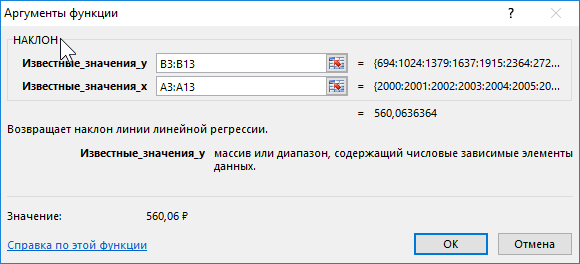
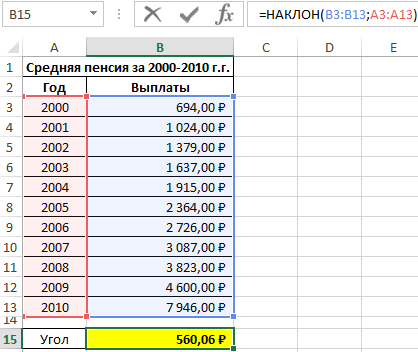
Для нахождения наклона используем следующую формулу:
Описание аргументов:
- B3:B13 – ссылка на диапазон ячеек, содержащих данные о средней пенсии, характеризующие зависимую переменную y;
- A3:A13 – диапазон ячеек с данными об отчетных периодах (годах), характеризующие независимую переменную x.
В результате вычислений получим:
Полученное значение свидетельствует о том, что на протяжении обозначенного периода размер пенсионных выплат в среднем увеличивался примерно на 560 рублей.
Прогноз объема продаж по линейно регрессии в Excel
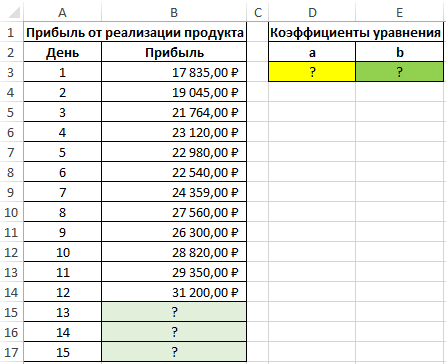
Пример 2. В таблице Excel содержатся данные о прибыли за продажи некоторого продукта компании на протяжении последних нескольких дней. Рассчитать коэффициенты a и b уравнения прямой y=ax+b, аппроксимирующей данные. На основе полученного уравнения спрогнозировать данные о продажах для трех последующих дней.
Вид таблицы с данными:
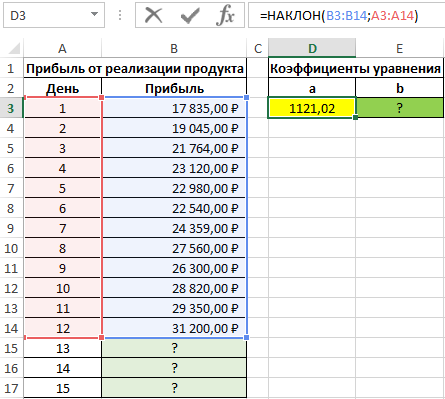
Для нахождения коэффициента a используем следующую формулу:
=НАКЛОН(B3:B14;A3:A14)
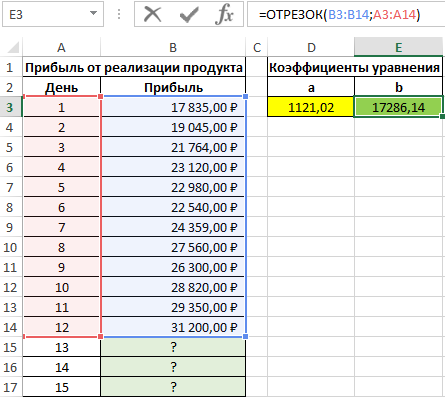
Коэффициент b рассчитывается с помощью следующей функции:
=ОТРЕЗОК(B3:B14;A3:A14)
Искомое уравнение имеет вид:
y=1121,02x+17286,14
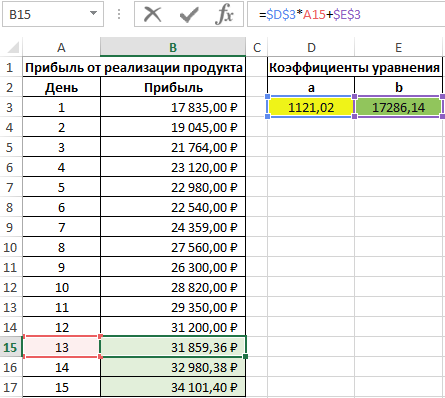
Для определения последующих значений y достаточно лишь подставить требуемое значение x. Выполним расчет предполагаемой прибыли для 13-го дня:
=$D$3*A15+$E$3
Описание аргументов:
- D3 – полученное значение коэффициента a;
- A15 – новое значение x;
- E3 – значение коэффициента b.
Используем функцию автозаполнения чтобы получить значения для остальных дней:
Анализ корреляции спроса и объема производства в Excel
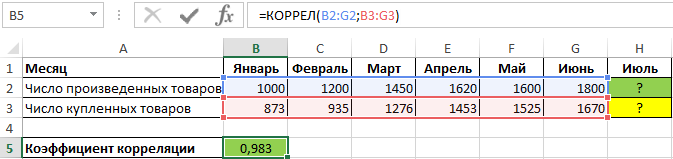
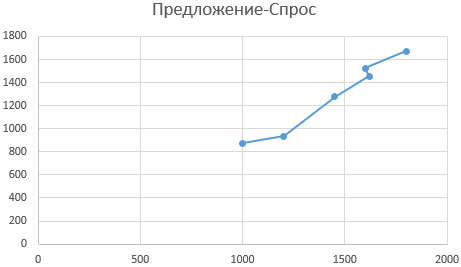
Пример 3. В таблице содержатся данные о количестве произведенной продукции за месяц, а также о числе приобретенных товаров данной марки покупателями. Отобразить взаимосвязь между данными графически, определить, целесообразно ли использовать уравнение линейно регрессии для описания корреляции между спросом и числом произведенных товаров.
Вид таблицы данных:
Для определения зависимости между двумя рядами числовых данных рассчитаем коэффициент корреляции по формуле:
=КОРРЕЛ(B2:G2;B3:G3)
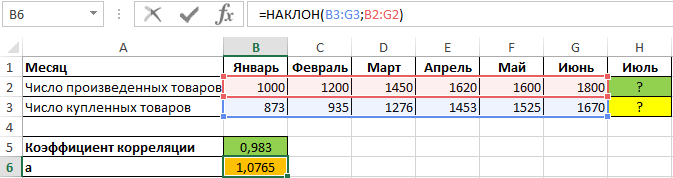
Полученное значение (0,983) свидетельствует о том, что между двумя числовыми диапазонами существует сильная прямая взаимосвязь. Поэтому целесообразно использовать аппроксимирующую прямую, для нахождения коэффициентов уравнения которой используем формулы:
=НАКЛОН(B3:G3;B2:G2)
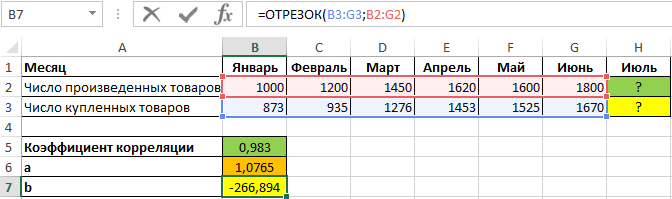
=ОТРЕЗОК(B3:G3;B2:G2)
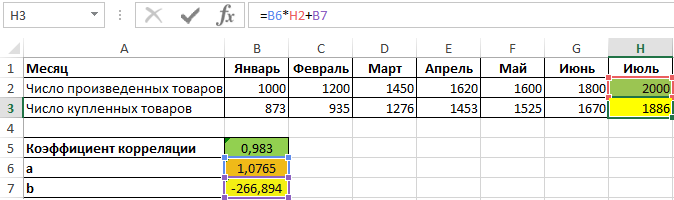
Для нахождения спроса на товары за июль при условии, что будет произведено, например, 2000 единиц продукции, используем полученное уравнение:
=B6*H2+B7
Полученное значение:
Альтернативным использованию функции НАКЛОН вариантом нахождения наклона в Excel является графический метод. Построим график на основе имеющихся данных, при этом для значений X выберем диапазон ячеек со значениями числа произведенных товаров, а для Y – с числом купленных товаров:
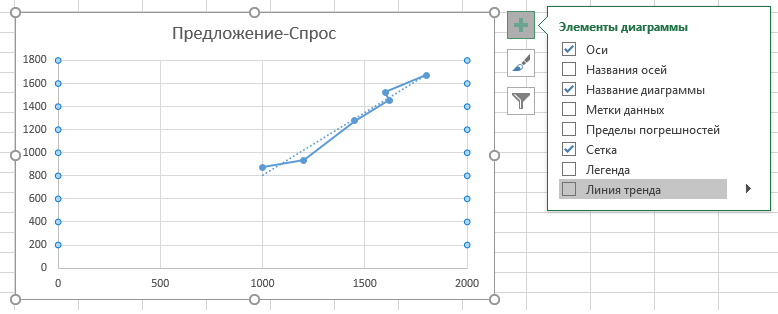
Отобразим на графике линию тренда:
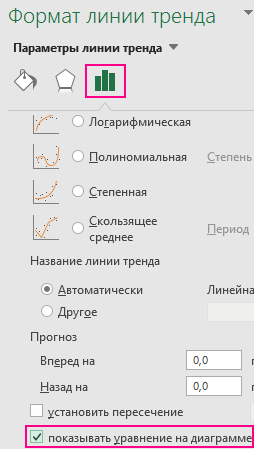
В меню «Формат линии тренда» установим флажок напротив пункта «показывать уравнение на диаграмме»:
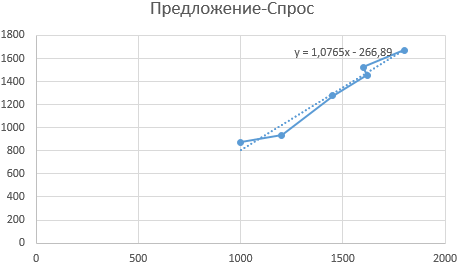
График примет следующий вид:
Как видно, найденные коэффициенты a и b соответствуют отображаемым на графике.
Особенности использования функции НАКЛОН в Excel
Функция имеет следующий синтаксис:
=НАКЛОН(известные_значения_y;известные_значения_x)
Описание аргументов (все являются обязательными для заполнения):
- известные_значения_y – аргумент, принимающий массив числовых значений или ссылку на диапазон ячеек, которые содержат числа, характеризующие значения зависимой переменной y, которые определены для известных значений x;
- известные_значения_x – аргумент, который может быть указан в виде массива чисел или ссылки на диапазон ячеек, содержащих числовые значения, которые характеризуют известные значения независимой переменной x.
Примечания:
- В качестве аргументов должны быть переданы массивы чисел либо ссылки на диапазоны ячеек с числовыми значениями или текстовыми строками, которые могут быть преобразованы к числам. Строки, не являющиеся текстовыми представлениями числовых данных, а также логические ИСТИНА и ЛОЖЬ в расчете не учитываются.
- Если в качестве аргументов были переданы массивы, содержащие разное количество элементов, или ссылки на диапазоны с разным количеством ячеек, функция НАКЛОН вернет код ошибки #Н/Д. Аналогичный код ошибки будет возвращен в случае, если оба аргумента принимают пустые массивы или ссылки на диапазоны пустых ячеек.
- Если оба аргумента ссылаются на нечисловые данные, функция НАКЛОН вернет код ошибки #ДЕЛ/0!.
- Если в диапазоне, переданном в качестве любого из аргументов, содержатся пустые ячейки, они игнорируются в расчете. Однако ячейки, содержащие значение 0 (нуль) будут учтены.
Функция TAN Excel (формула, примеры) | Как использовать касательную в Excel?
Функция TAN Excel — это встроенная тригонометрическая функция в Excel, которая используется для вычисления значения косинуса заданного числа или, в терминах тригонометрии, значения косинуса заданного угла, здесь угол — это число в Excel, и эта функция принимает только один аргумент. который является предоставленным входным номером.
Функция TAN Excel
Функция TAN Excel — это встроенная функция, относящаяся к категории математических / триггерных функций, которая возвращает значение тангенса угла. Формула для TAN всегда возвращает числовое значение.
В тригонометрии тангенс угла эквивалентен отношению перпендикуляра к основанию прямоугольного треугольника.
TAN Θ = противоположная сторона / смежная сторона
Следовательно, TAN Θ = a / b
Формула TAN в Excel
Ниже приведена формула TAN в Excel.
Где число — это аргумент, передаваемый функции в радианах.
Угол, который мы указываем в качестве входных данных, распознается функцией Tangent, только если указан как Radians.
Чтобы преобразовать угол в радианы, используйте функцию РАДИАНЫ или преобразуйте угол в радианы с помощью математического соотношения
Радиан = угол в градусах * (π / 180)
π в Excel представлена функцией PI ()
Следовательно, радиан = градус * (PI () / 180)
Расчет значения TAN с использованием функции TAN и RADIANS
Расчет значения TAN с использованием TAN и функции PI
Функция касания имеет множество реальных приложений; он широко используется в архитектуре для расчета высоты и длины геометрических фигур. Функция касания, используемая в системах навигации и GPS, в аэронавтике.
Например, если самолет летит на высоте 3000 м и делает угол к наблюдателю на земле 26 °, и мы хотим найти расстояние от самолета до наблюдателя.
Как мы знаем, TAN Θ = противоположная сторона / смежная сторона
Здесь противоположная сторона = высота самолета от земли, равная 3000 метров.
А прилегающая сторона = горизонтальное расстояние плоскости от земли, которое неизвестно, и нам нужно его вычислить.
Таким образом, используя формулу для TAN, мы имеем
TAN (26 °) = 3000 / x
Следовательно, x = 3000 / (TAN (26 °))
Если взять относительные контрольные значения, которые у нас есть,
X = B2 / (TAN (B3 * (PI () / 180)))
X = 6150,91 метра
Как использовать TAN в Excel?
Функция Excel TAN очень проста и удобна в использовании. Давайте разберемся, как работает формула TAN в Excel на нескольких примерах.
Вы можете скачать этот шаблон Excel с функцией TAN здесь — Шаблон Excel с функцией TAN
Касательная в Excel, пример # 1
Мужчина ростом 6 футов находится в 55 метрах от дерева. Он делает угол обзора 47 ° параллельно земле. Мы хотим рассчитать высоту дерева.
Чтобы найти высоту дерева, мы будем использовать TAN Θ, в контексте Excel мы будем использовать функцию Tangent.
Высота дерева будет
Высота Человека + Расстояние Человека от дерева * TAN (47 °)
Поскольку рост человека указан в футах, мы переведем его в метры (1 фут = 0,30 метра).
Помещая все относительные значения в Excel, формула для высоты дерева будет
= (0,3 * B2) + (B3 * TAN ((B4 * (PI () / 180))))
Выходные данные TAN Excel:
Высота дерева 60,78 метра.
Касательная в Excel, пример # 2
Предположим, у нас есть пять прямоугольных треугольников с указанием их углов и длины с одной стороны, и нам нужно вычислить длину двух других сторон.
Сумма всех углов на треугольнике равна 180 °, следовательно, мы можем легко вычислить третий угол.
Мы знаем, Sin Θ = противоположное / гипотенуза
Таким образом, длина противоположной стороны будет Sin Θ * гипотенуза
В Excel длина противоположной стороны (перпендикулярной стороны) будет рассчитана по формуле TAN.
= E2 * SIN (C2 * (PI () / 180))
Применяя формулу TAN для пяти треугольников, мы можем получить длину перпендикуляров треугольников
Теперь у нас есть две стороны треугольника, гипотенуза и перпендикулярная сторона, и мы можем легко вычислить третью сторону (основание), используя TAN в Excel.
Мы знаем, что TAN Θ = противоположная сторона / смежная сторона
Таким образом, длина соседней стороны будет Opposite Side / TAN Θ
В Excel длина прилегающей стороны (основания) будет рассчитываться по формуле TAN
= F2 / (TAN (РАДИАНЫ (C2)))
Применяя формулу TAN для пяти треугольников, мы можем получить длину смежной стороны треугольника
TAN в выводе Excel:
Касательная в Excel, пример №3
Самолет делает разворот радиусом 160 м и летит с постоянным углом крена 87 °, в идеальных условиях (без колебаний ветра) рассчитайте постоянную путевую скорость самолета.
Радиус поворота определяется формулой
Радиус поворота = V2 / g * TAN Θ
Радиус поворота 160 метров; Постоянный угол крена составляет 87 °, g — ускорение свободного падения, значение которого составляет 9,8 м / с2, поэтому путевая скорость будет равна
V = (Радиус поворота * (g * TAN Θ)) 1/2
Применяя приведенную выше формулу TAN в Excel с эталонными значениями, мы получаем формулу TAN
= КОРЕНЬ (B2 * (9,8 * (TAN (РАДИАНЫ (B3)))))
SQRT — это встроенная функция Excel, которая вычисляет квадратный корень из числа.
TAN в выводе Excel:
Итак, путевая скорость самолета составляет 172,97 м / с.
Пример функции касания # 4
У нас есть формула для TAN, обозначаемая f (x) = 2c * TAN2Θ, где c — постоянное значение, равное 0,988. Значение варианта — это значение, а формула для TAN зависит от значения Θ. Нам нужно построить график заданной функции касания.
Затем с помощью функции Excel TAN мы вычислим значения функции, поэтому взяв контрольные значения в качестве входных данных, мы получим формулу TAN,
Диаграммы и графики используются для анализа числовых данных, например, для оценки зависимости между двумя видами значений. С этой целью к данным диаграммы или графика можно добавить линию тренда и ее уравнение, прогнозные значения, рассчитанные на несколько периодов вперед или назад.
Линия тренда представляет собой прямую или кривую линию, аппроксимирующую (приближающую) исходные данные на основе уравнения регрессии или скользящего среднего. Аппроксимация определяется по методу наименьших квадратов. В зависимости от характера поведения исходных данных (убывают, возрастают и т.д.) выбирается метод интерполяции, который следует использовать для построения тренда.
Предусмотрено несколько вариантов формирования линии тренда.
Линейной функцией: y=mx+b
где m — тангенс угла наклона прямой, b — смещение.
Прямая линия тренда (линейный тренд) наилучшим образом подходит для величин, изменяющихся с постоянной скоростью. Применяется в случаях, когда точки данных расположены близко к прямой.
Логарифмической функцией: y=c*lnx+b
где с и b — константы.
Логарифмическая линия тренда соответствует ряду данных, значения которого вначале быстро растут или убывают, а затем постепенно стабилизируются. Может использоваться для положительных и отрицательных данных.
Полиномиальной функцией (до 6й степени включительно): y= b + c1*x + c2*x2 + c3*x3 + …+ c6*x6
где b, c1, c2 , … c6 — константы.
Полиномиальная линия тренда используется для описания попеременно возрастающих и убывающих данных. Степень полинома подбирают таким образом, чтобы она была на единицу больше количества экстремумов (максимумов и минимумов) кривой.
Степенной функцией: y = cxb
где c и b — константы.
Степенная линия тренда дает хорошие результаты для положительных данных с постоянным ускорением. Для рядов с нулевыми или отрицательными значениями построение указанной линии тренда невозможно.
Экспоненциальной функцией: y = cebx
где c и b — константы, е — основание натурального логарифма.
Экспоненциальный тренд используется в случае непрерывного возрастания изменения данных. Построение указанного тренда не возможно, если в множестве значений членов ряда присутствуют нулевые или отрицательные данные.
С использованием линейной фильтрации по формуле: Ft= (At+A(t-1)+⋯+A(t-n+1))/n
где n — общее число членов ряда, t — заданное число точек (2 ≤ t < n).
Тренд с линейной фильтрацией позволяет сгладить колебания данных, наглядно демонстрируя характер зависимостей. Для построения указанной линии тренда пользователь должен задать число — параметр фильтра. Если задано число 2, то первая точка линии тренда определяется как среднее значение из первых двух элементов данных, вторая точка — как среднее второго и третьего элементов данных и т.д.
Для некоторых типов диаграмм линия тренда в принципе не может быть построена — диаграмм с накоплением, объемных, лепестковых, круговых, поверхностных, кольцевых. При возможности к диаграмме можно добавить несколько линий с разными параметрами. Соответствие линии тренда фактическим значениям ряда данных устанавливается с помощью коэффициента достоверности аппроксимации:
Линия тренда, а также ее параметры добавляются к данным диаграммы следующими командами:
При необходимости параметры линии можно изменить, вызвав щелчком мыши по ряду данных диаграммы или линии тренда окно Формат линии тренда. Можно добавить (или удалить) уравнение регрессии, коэффициент достоверности аппроксимации, определить направление и прогноз изменения ряда данных, а также выполнить коррекцию оформительских элементов линии тренда. Выделенная линия тренда может быть также удалена.
На рисунке приведена таблица данных по изменению стоимости ценной бумаги. На основе этих условных данных построена точечная диаграмма, добавлена полиномиальная линия тренда третьего порядка (задана штриховой линией) и некоторые другие параметры. Полученное значение коэффициента достоверности аппроксимации R2на диаграмме близко к единице, что свидетельствует о близости расчетной линии тренда с данными задачи. Прогнозное значение изменения стоимости ценной бумаги направлено в сторону роста.