Всего: 13 1–13
Добавить в вариант
На рисунке изображён многогранник, все двугранные углы многогранника прямые. Найдите тангенс угла B2A2C2.
На рисунке изображён многогранник, все двугранные углы многогранника прямые. Найдите тангенс угла C2C3B2.
На рисунке изображён многогранник, все двугранные углы многогранника прямые. Найдите тангенс угла ABB3.
На рисунке изображён многогранник, все двугранные углы многогранника прямые. Найдите тангенс угла C3D3B3.
Найдите тангенс угла B2D2C2 многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые.
Найдите тангенс угла
многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые.
Найдите тангенс угла
многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые.
Найдите тангенс угла A2D3D2 многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые.
< Найдите тангенс угла
многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые.
Найдите тангенс угла DCD3 многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые.
Найдите тангенс угла
многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые.
Найдите тангенс угла B2C1C2 многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые.
Найдите тангенс угла
многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые.
Всего: 13 1–13
Здравствуйте, дорогие читатели. В этом выпуске поговорим о задании, которое иногда доставляет неожиданные неприятности на экзамене. Задания довольно простые, но бывают промахи. Это задания, которые сделаны как бы на тетрадном листочке в клеточку. Итак, давайте начнем.
Задание №1. УГЛЫ
Задача №1
Запомните, чтобы найти тангенс острого угла на таких картинках, обязательно нужно достроить до прямоугольного треугольника.
Вспомним, что такое тангенс острого угла прямоугольного треугольника?
Определение тангенса острого угла:
Тангенсом острого угла прямоугольного треугольника, называется отношение противолежащего катета к прилежащему. Катет BF- противолежащий угла FОВ, OF – прилежащий к углу FOB.
Задача №2
Чтобы найти тангенс угла АОВ на этой картинке, нужно достроить до прямоугольного треугольника, и найти стороны этого треугольника.
1. Достроим до треугольника ОВН и докажем, что он прямоугольный.
2. Для этого достроим на стороне ОН, ОВ и ВН прямоугольные треугольники ОСВ, ОНК и BDH. Докажем, что треугольник АВН прямоугольный.
Найдем гипотенузу ОВ прямоугольного треугольника ОСВ, гипотенузу ОН прямоугольного треугольника ОКН и гипотенузу ВН прямоугольного треугольника ВDH через теорему Пифагора: квадрат гипотенузы равен сумме квадратов катетов.
Теперь докажем, что треугольник ОВН прямоугольный. Воспользуемся обратной теоремой Пифагора: если квадрат одной стороны равен сумме квадратов двух других сторон, то треугольник прямоугольный.
Так как равенство верно, то треугольник ОВН прямоугольный.
Теперь найдем тангенс угла АОВ
Задание №2 Расстояние
Для выполнения этого задания, проведите отрезок ВС, найдите середину его и отметим точкой К. Проведите отрезок АК, который равен 4. Ответ 4
Задание №3 Площадь
Задача №1
Задание простое, но есть ошибки по невнимательности.
Задача №2
а) Площадь треугольника и параллелограмма
Запомните! Площадь треугольника от площади параллелограмма отличается только тем, что площадь треугольника нужно делить на 2, а площадь параллелограмма нет.
б) Площадь трапеции. Чтобы найти площадь трапеции, нужно сложить основания трапеции, умножить на высоту и поделить на 2.
в) Площадь ромба равна половине произведения диагоналей.
Это не все типы заданий, что встречаются на экзамене. Продолжение следует.
Спасибо что дочитали. Вы меня очень поддержите, если поставите лайк и подпишитесь на мой блог.
Для решения этой задачи нужно использовать теорему тангенсов, которая утверждает, что тангенс угла между прямыми, проходящими через вершину, равен отношению проекций векторов, соответствующих этим прямым, на плоскость, перпендикулярную им обеим.
Обозначим точки пересечения диагоналей многогранника как B и C, а точки D1 и D2 как D и D’. Также обозначим векторы, соответствующие прямым DA и DA’, как a и a’ соответственно. Тогда тангенс угла D1A1D2 можно выразить как отношение синуса угла между векторами B-a и B-a’ к косинусу этого угла:
tg(D1A1D2) = sin(∠(a, a’)) / cos(∠(a, a’)).
Заметим, что векторы a и a’ лежат в плоскостях, проходящих через B и перпендикулярных CD и C’D’ соответственно. Тогда проекции этих векторов на общую плоскость можно выразить как проекцию a на CD, умноженную на cos(∠(CD, C’D’)) и проекцию a’ на C’D’, умноженную на cos(∠(CD, C’D’)). Таким образом,
tg(D1A1D2) = sin(∠(a, a’)) / cos(∠(a, a’)) = (|a x a’| / |a| / |a’|) / (a * a’ / |a| / |a’|) = |a x a’| / (a * a’).
Здесь использовано скалярное произведение и векторное произведение векторов a и a’.
Осталось вычислить числитель и знаменатель.
Для нахождения векторного произведения векторов a и a’ можно воспользоваться определителем матрицы, составленной из компонент векторов:
a x a’ = det( |i j k |
|ax ay az|
|a’x a’y a’z| ) = (ay * a’z – az * a’y)i – (ax * a’z – az * a’x)j + (ax * a’y – ay * a’x)k.
Выражение для скалярного произведения векторов a и a’ можно получить из определения:
a * a’ = ax * a’x + ay * a’y + az * a’z.
Тогда искомый тангенс равен:
tg(D1A1D2) = |a x a’| / (a * a’) = ((ay * a’z – az * a’y)i – (ax * a’z – az * a’x)j + (ax * a’y – ay * a’x)k) / (ax * a’x + ay * a’y + az * a’z).
Значения компонент векторов a и a’ можно найти из координат вершин многогранника. Остается только подставить числовые значения и получить ответ.
На рисунке изображён многогранник, все двугранные углы многогранника прямые. Найдите тангенс угла ABB3.
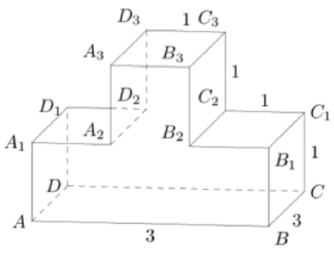
Источник: mathege
Решение:
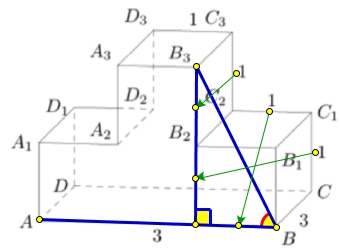
Тангенс острого угла прямоугольного треугольника – это отношение противолежащего катета к прилежащему катету.
tgangle ABB_{3}=frac{CC_{1}+C_{2}C_{3}}{C_{2}C_{1}}=frac{1+1}{1}=2
Ответ: 2.
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 0 / 5. Количество оценок: 0
Оценок пока нет. Поставь оценку первым.
Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️
Вступай в группу vk.com 😉
Расскажи, что не так? Я исправлю в ближайшее время!
В отзыве оставь любой контакт для связи, если хочешь, что бы я тебе ответил.
![]()
В данной статье хочу рассказать вам об определённом типе задач по стереометрии, одну из которых, возможно, предстоит решить именно вам на ЕГЭ по математике. Это задачи на решение составных многогранников:

Обычно требуется найти расстояние (или квадрат расстояния) между двумя точками; какой-либо угол, либо значение одной из тригонометрических функций обозначенного в условии угла.
Для решения необходимо знать совсем не много теории: теорему Пифагора; определения синуса, косинуса, тангенса и котангенса в прямоугольном треугольнике; значения углов тригонометрических функций.
Рассмотрим задачи:

Найдите расстояние между вершинами А и С2 многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые. Результат умножьте на корень из шести и запишите ответ.

Соединим точки А и С2 и рассмотрим прямоугольный треугольник АА2С2:

По теореме Пифагора:

Ответ: 6

Найдите угол САD2 многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые. Ответ дайте в градусах.

Соединим точки C, А, D2:

Рассмотрим треугольник CАD2: AC = CD2 = AD2, так как являются диагоналями квадратов со сторонами равными 8. Следовательно, треугольник CАD2 – равносторонний, то есть все его углы равны 60°.
Таким образом, угол CАD2 = 60°.
Ответ: 60

Найдите квадрат расстояния между вершинами В2 и D3 многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые.

Соединим точки B2, B3 и D3. Рассмотрим прямоугольный треугольник B2B3D3:

По теореме Пифагора:
![]()
Ответ: 12

Найдите тангенс угла АBB3 многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые.

Соединим точки В и B3, из точки B3 опустим перпендикуляр на ребро АВ, точку пересечения обозначим как К. Рассмотрим прямоугольный треугольник КВB3:

Ответ: 2

Найдите квадрат расстояния между вершинами D и C2 многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые.

Соединим точки В и C2, а так же C2 и С:

Рассмотрим прямоугольный треугольник СВС2. По теореме Пифагора:

Ответ: 46
![]()
245376. Найдите квадрат расстояния между вершинами В2 и D2 многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые.

Посмотреть решение
245380. Найдите тангенс угла AВB3 многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые.

Посмотреть решение
245382. Найдите квадрат расстояния между вершинами D и C2 многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые.

Посмотреть решение
При решении подобных заданий главное – это «увидеть» треугольник, в который входит искомый элемент (отрезок, угол) и построить этот треугольник. А далее уже использовать указанную в начале статьи теорию.
Есть ещё задачи с параллелепипедами:
245359 245360 245361 245362 245363
Процесс решения в них сводится к решению прямоугольного треугольника: нужно найти расстояние между вершинами (квадрат расстояния), либо заданный угол.
Мы продолжим рассматривать задачи по стереометрии? не пропустите! На этом всё. Как видите, ничего сложного. Успеха вам!
С уважением, Александр.
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.
