Как найти тангенс угла наклона к оси

Была ли эта статья полезной?

Как найти тангенс угла наклона

Под тангенсом угла наклона обычно понимают угловой коэффициент касательной прямой какой-либо функции. Однако вам может понадобиться также умение найти тангенс угла наклона обычной прямой, например, одной из сторон треугольника по отношению к другой. Определив, что вам надо найти, действуйте одним из следующих способов.

Инструкция

Если вам нужно посчитать угол наклона прямой к оси абсцисс, а вы не знаете уравнение прямой, опустите из любой точки этой прямой (кроме точки пересечения с осью) перпендикуляр на ось. Затем измерьте катеты полученного прямоугольного треугольника и найдите отношение прилежащего катета к противолежащему. Полученное число будет равно тангенсу угла наклона. Этот способ удобно использовать не только для изучения угла наклона прямой, но и для измерения любых углов, как на чертеже, так и в жизни (например, угол ската кровли).

Если вы знаете уравнение прямой, и вам нужно найти тангенс угла наклона этой прямой к оси абсцисс, выразите у через х. В результате вы получите выражение типа у=kх+b. Обратите внимание на коэффициент k – это и есть тангенс угла наклона между положительным направлением оси ох и лучом прямой, расположенным надо этой осью. Если же k=0, то тангенс также равен нулю, то есть прямая параллельна или совпадает с осью абсцисс.

Если вам дана сложная функция, например, квадратичная, и вам нужно найти тангенс угла наклона касательной к этой функции, или, по-другому, угловой коэффициент, вычислите производную. Затем вычислите значение производной в заданной точке, к которой будет проведена касательная. Полученное число и является тангенсом угла наклона касательной. Например, вам дана функция у=х^2+3х, посчитав ее производную, вы получите выражение у`=2х+3. Чтобы найти угловой коэффициент в точке х=3, подставьте это значение в уравнение. В результате несложных вычислений легко можно получить у=2*3+3=9, это и есть искомый тангенс.

Для того чтобы найти тангенс угла наклона одной из сторон треугольника к другой, поступите следующим образом. Найдите синус (sin) этого угла и разделите его на косинус (cos), в результате вы получите тангенс этого угла.

Источники:

• как найти тангенс по углу

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

Угол наклона прямой

Для построения графика линейной функции или определения координат точек пересечения прямой с осью Ох и Оy важно уметь находить угол наклона прямой.

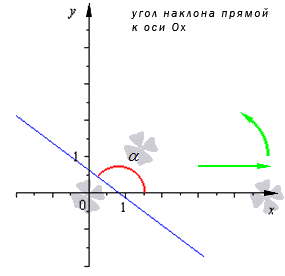
Углом наклона прямой к оси Ох является угол, который считают против часовой стрелки от положительного направления Ох к прямой.

В уравнении y = kх + b, где b — координата «у» — точки пересечения прямой с Оy, коэффициент k при х — коэффициент наклона прямой.
Этот коэффициент равняется тангенсу угла а, образованного между прямой и положительным направлением оси Ох: k = tg а.

Если прямая наклонена вправо, то угол, образованный между прямой и осью Ох, будет острым, тангенс угла (tgа) и коэффициент наклона k больше нуля. Угол определяем по формуле: a = arctg k.

Если наклон прямой влево, то угол между прямой и осью Ох будет тупым, а тангенс угла (tgа) и коэффициент k меньше нуля. Угол a = Пи — arctg |k|.

Угол наклона равняется 0, если прямая расположена параллельно Ох или совпадает с ней.

Зная координаты 2-х точек, расположенных на прямой, можно легко рассчитать угол наклона как отношение вертикального расстояния между двумя точками к горизонтальному расстоянию между ними.

Пусть координаты первой точки (х1,y1), координаты второй (х2,y2), тогда угловой коэффициент будет равняться: (y2 — y1): (х2 — х1),
где (y2 — y1) — величина изменения координаты «у», (х2 — х1) — изменение координаты «х». Из полученной величины возьмем арктангенс и определим угол наклона прямой.

Быстро определить угол наклона прямой, вам поможет онлайн калькулятор.

Уравнение прямой с угловым коэффициентом: теория, примеры, решение задач

Продолжение темы уравнение прямой на плоскости основывается на изучении прямой линии из уроков алгебры. Данная статья дает обобщенную информацию по теме уравнения прямой с угловым коэффициентом. Рассмотрим определения, получим само уравнение, выявим связь с другими видами уравнений. Все будет рассмотрено на примерах решений задач.

Угол наклона прямой и угловой коэффициент прямой

Перед записью такого уравнения необходимо дать определение угла наклона прямой к оси О х с их угловым коэффициентом. Допустим, что задана декартова система координат О х на плоскости.

Угол наклона прямой к оси О х , расположенный в декартовой системе координат О х у на плоскости, это угол, который отсчитывается от положительного направления О х к прямой против часовой стрелки.

Когда прямая параллельна О х или происходит совпадение в ней, угол наклона равен 0 . Тогда угол наклона заданной прямой α определен на промежутке [ 0 , π ) .

Угловой коэффициент прямой – это тангенс угла наклона заданной прямой.

Стандартное обозначение буквой k . Из определения получим, что k = t g α . Когда прямая параллельна Ох, говорят, что угловой коэффициент не существует, так как он обращается в бесконечность.

Угловой коэффициент положительный, когда график функции возрастает и наоборот. На рисунке показаны различные вариации расположения прямого угла относительно системы координат со значением коэффициента.

Для нахождения данного угла необходимо применить определение об угловом коэффициенте и произвести вычисление тангенса угла наклона в плоскости.

Посчитать угловой коэффициент прямой при угле наклона равном 120 ° .

Из условия имеем, что α = 120 ° . По определению необходимо вычислить угловой коэффициент. Найдем его из формулы k = t g α = 120 = – 3 .

Если известен угловой коэффициент, а необходимо найти угол наклона к оси абсцисс, тогда следует учитывать значение углового коэффициента. Если k > 0 , тогда угол прямой острый и находится по формуле α = a r c t g k . Если k 0 , тогда угол тупой, что дает право определить его по формуле α = π – a r c t g k .

Определить угол наклона заданной прямой к О х при угловом коэффициенте равном 3 .

Из условия имеем, что угловой коэффициент положительный, а это значит, что угол наклона к О х меньше 90 градусов. Вычисления производятся по формуле α = a r c t g k = a r c t g 3 .

Ответ: α = a r c t g 3 .

Найти угол наклона прямой к оси О х , если угловой коэффициент = – 1 3 .

Если принять за обозначение углового коэффициента букву k , тогда α является углом наклона к заданной прямой по положительному направлению О х . Отсюда k = – 1 3 0 , тогда необходимо применить формулу α = π – a r c t g k При подстановке получим выражение:

α = π – a r c t g – 1 3 = π – a r c t g 1 3 = π – π 6 = 5 π 6 .

Ответ: 5 π 6 .

Уравнение с угловым коэффициентом

Уравнение вида y = k · x + b , где k является угловым коэффициентом, а b некоторым действительным числом, называют уравнением прямой с угловым коэффициентом. Уравнение характерно для любой прямой, непараллельной оси О у .

Если подробно рассмотреть прямую на плоскости в фиксированной системе координат, которая задана уравнением с угловым коэффициентом, который имеет вид y = k · x + b . В данном случае значит, что уравнению соответствуют координаты любой точки прямой. Если подставить координаты точки М , M 1 ( x 1 , y 1 ) , в уравнение y = k · x + b , тогда в этом случае прямая будет проходить через эту точку, иначе точка не принадлежит прямой.

Задана прямая с угловым коэффициентом y = 1 3 x – 1 . Вычислить, принадлежат ли точки M 1 ( 3 , 0 ) и M 2 ( 2 , – 2 ) заданной прямой.

Необходимо подставить координаты точки M 1 ( 3 , 0 ) в заданное уравнение, тогда получим 0 = 1 3 · 3 – 1 ⇔ 0 = 0 . Равенство верно, значит точка принадлежит прямой.

Если подставим координаты точки M 2 ( 2 , – 2 ) , тогда получим неверное равенство вида – 2 = 1 3 · 2 – 1 ⇔ – 2 = – 1 3 . Можно сделать вывод, что точка М 2 не принадлежит прямой.

Ответ: М 1 принадлежит прямой, а М 2 нет.

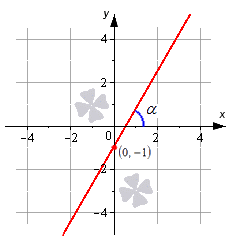
Известно, что прямая определена уравнением y = k · x + b , проходящим через M 1 ( 0 , b ) , при подстановке получили равенство вида b = k · 0 + b ⇔ b = b . Отсюда можно сделать вывод, что уравнение прямой с угловым коэффициентом y = k · x + b на плоскости определяет прямую, которая проходит через точку 0 , b . Она образует угол α с положительным направлением оси О х , где k = t g α .

Рассмотрим на примере прямую, определенную при помощи углового коэффициента, заданного по виду y = 3 · x – 1 . Получим, что прямая пройдет через точку с координатой 0 , – 1 с наклоном в α = a r c t g 3 = π 3 радиан по положительному направлению оси О х . Отсюда видно, что коэффициент равен 3 .

Уравнение прямой с угловым коэффициентом, проходящей через заданную точку

Необходимо решить задачу, где необходимо получить уравнение прямой с заданным угловым коэффициентом, проходящим через точку M 1 ( x 1 , y 1 ) .

Равенство y 1 = k · x + b можно считать справедливым, так как прямая проходит через точку M 1 ( x 1 , y 1 ) . Чтобы убрать число b, необходимо из левой и правой частей вычесть уравнение с угловым коэффициентом. Из этого следует, что y – y 1 = k · ( x – x 1 ) . Данное равенство называют уравнением прямой с заданным угловым коэффициентом k, проходящая через координаты точки M 1 ( x 1 , y 1 ) .

Составьте уравнение прямой, проходящей через точку М 1 с координатами ( 4 , – 1 ) , с угловым коэффициентом равным – 2 .

Решение

По условию имеем, что x 1 = 4 , y 1 = – 1 , k = – 2 . Отсюда уравнение прямой запишется таким образом y – y 1 = k · ( x – x 1 ) ⇔ y – ( – 1 ) = – 2 · ( x – 4 ) ⇔ y = – 2 x + 7 .

Ответ: y = – 2 x + 7 .

Написать уравнение прямой с угловым коэффициентом, которое проходит через точку М 1 с координатами ( 3 , 5 ) , параллельную прямой y = 2 x – 2 .

По условию имеем, что параллельные прямые имеют совпадающие углы наклона, отсюда значит, что угловые коэффициенты являются равными. Чтобы найти угловой коэффициент из данного уравнения, необходимо вспомнить его основную формулу y = 2 x – 2 , отсюда следует, что k = 2 . Составляем уравнение с угловым коэффициентом и получаем:

y – y 1 = k · ( x – x 1 ) ⇔ y – 5 = 2 · ( x – 3 ) ⇔ y = 2 x – 1

Переход от уравнения прямой с угловым коэффициентом к другим видам уравнений прямой и обратно

Такое уравнение не всегда применимо для решения задач, так как имеет не совсем удобную запись. Для этого необходимо представлять в другом виде. Например, уравнение вида y = k · x + b не позволяет записать координаты направляющего вектора прямой или координаты нормального вектора. Для этого нужно научиться представлять уравнениями другого вида.

Можем получить каноническое уравнение прямой на плоскости, используя уравнение прямой с угловым коэффициентом. Получаем x – x 1 a x = y – y 1 a y . Необходимо слагаемое b перенести в левую часть и поделить на выражение полученного неравенства. Тогда получим уравнение вида y = k · x + b ⇔ y – b = k · x ⇔ k · x k = y – b k ⇔ x 1 = y – b k .

Уравнение прямой с угловым коэффициентом стало каноническим уравнением данной прямой.

Привести уравнение прямой с угловым коэффициентом y = – 3 x + 12 к каноническому виду.

Вычислим и представим в виде канонического уравнения прямой. Получим уравнение вида:

y = – 3 x + 12 ⇔ – 3 x = y – 12 ⇔ – 3 x – 3 = y – 12 – 3 ⇔ x 1 = y – 12 – 3

Ответ: x 1 = y – 12 – 3 .

Общее уравнение прямой проще всего получить из y = k · x + b , но для этого необходимо произвести преобразования: y = k · x + b ⇔ k · x – y + b = 0 . Производится переход из общего уравнения прямой к уравнениям другого вида.

Дано уравнение прямой вида y = 1 7 x – 2 . Выяснить, является ли вектор с координатами a → = ( – 1 , 7 ) нормальным вектором прямой?

Для решения необходимо перейти к другому виду данного уравнения, для этого запишем:

y = 1 7 x – 2 ⇔ 1 7 x – y – 2 = 0

Коэффициенты перед переменными являются координатами нормального вектора прямой. Запишем это так n → = 1 7 , – 1 , отсюда 1 7 x – y – 2 = 0 . Понятно, что вектор a → = ( – 1 , 7 ) коллинеарен вектору n → = 1 7 , – 1 , так как имеем справедливое соотношение a → = – 7 · n → . Отсюда следует, что исходный вектор a → = – 1 , 7 – нормальный вектор прямой 1 7 x – y – 2 = 0 , значит, считается нормальным вектором для прямой y = 1 7 x – 2 .

Решим задачу обратную данной.

Необходимо перейти от общего вида уравнения A x + B y + C = 0 , где B ≠ 0 , к уравнению с угловым коэффициентом. для этого решаем уравнение относительно у. Получим A x + B y + C = 0 ⇔ – A B · x – C B .

Результат и является уравннием с угловым коэффициентом, который равняется – A B .

Задано уравнение прямой вида 2 3 x – 4 y + 1 = 0 . Получить уравнение данной прямой с угловым коэффициентом.

Исходя из условия, необходимо решить относительно у, тогда получим уравнение вида:

2 3 x – 4 y + 1 = 0 ⇔ 4 y = 2 3 x + 1 ⇔ y = 1 4 · 2 3 x + 1 ⇔ y = 1 6 x + 1 4 .

Ответ: y = 1 6 x + 1 4 .

Аналогичным образом решается уравнение вида x a + y b = 1 , которое называют уравнение прямой в отрезках, или каноническое вида x – x 1 a x = y – y 1 a y . Нужно решить его относительно у, только тогда получим уравнение с угловым коэффициентом:

x a + y b = 1 ⇔ y b = 1 – x a ⇔ y = – b a · x + b .

Каноническое уравнение можно привести к виду с угловым коэффициентом. Для этого:

x – x 1 a x = y – y 1 a y ⇔ a y · ( x – x 1 ) = a x · ( y – y 1 ) ⇔ ⇔ a x · y = a y · x – a y · x 1 + a x · y 1 ⇔ y = a y a x · x – a y a x · x 1 + y 1

Имеется прямая, заданная уравнением x 2 + y – 3 = 1 . Привести к виду уравнения с угловым коэффициентом.

Исходя из условия, необходимо преобразовать, тогда получим уравнение вида _formula_. Обе части уравнения следует умножить на – 3 для того, чтобы получить необходимо уравнение с угловым коэффициентом. Преобразуя, получим:

y – 3 = 1 – x 2 ⇔ – 3 · y – 3 = – 3 · 1 – x 2 ⇔ y = 3 2 x – 3 .

Ответ: y = 3 2 x – 3 .

Уравнение прямой вида x – 2 2 = y + 1 5 привести к виду с угловым коэффициентом.

Необходимо выражение x – 2 2 = y + 1 5 вычислить как пропорцию. Получим, что 5 · ( x – 2 ) = 2 · ( y + 1 ) . Теперь необходимо полностью его разрешить, для этого:

5 · ( x – 2 ) = 2 · ( y + 1 ) ⇔ 5 x – 10 = 2 y + 2 ⇔ 2 y = 5 x – 12 ⇔ y = 5 2 x

Ответ: y = 5 2 x – 6 .

Для решения таких заданий следует приводит параметрические уравнения прямой вида x = x 1 + a x · λ y = y 1 + a y · λ к каноническому уравнению прямой, только после этого можно переходить к уравнению с угловым коэффициентом.

Найти угловой коэффициент прямой, если она задана параметрическими уравнениями x = λ y = – 1 + 2 · λ .

Необходимо выполнить переход от параметрического вида к угловому коэффициенту. Для этого найдем каноническое уравнение из заданного параметрического:

x = λ y = – 1 + 2 · λ ⇔ λ = x λ = y + 1 2 ⇔ x 1 = y + 1 2 .

Теперь необходимо разрешить данное равенство относительно y , чтобы получить уравнение прямой с угловым коэффициентом. для этого запишем таким образом:

x 1 = y + 1 2 ⇔ 2 · x = 1 · ( y + 1 ) ⇔ y = 2 x – 1

Отсюда следует, что угловой коэффициент прямой равен 2 . Это записывается как k = 2 .

Уравнение прямой с угловым коэффициентом

Пусть на плоскости, где имеется прямоугольная декартова система координат, прямая l проходит через точку М₀ параллельно направляющему вектору а (рис. 96).

Если прямая l пересекает ось Ох (в точке N), то под углом прямой l с осью Ох будем понимать угол α, на который необходимо повернуть ось Ох вокруг точки N в направлении, обратном вращению часовой стрелки, чтобы ось Ох совпала с прямой l. (Имеется в виду угол, меньший 180°.)

Этот угол называют углом наклона прямой. Если прямая l параллельна оси Ох, то угол наклона принимается равным нулю (рис. 97).

Тангенс угла наклона прямой называется угловым коэффициентом прямой и обычно обозначается буквой k:

Если α = 0, то и k = 0; это означает, что прямая параллельна оси Ох и ее угловой коэффициент равен нулю.

Если α = 90°, то k = tg α не имеет смысла: это означает, что прямая, перпендикулярная оси Ох (т. е. параллельная оси Оу), не имеет углового коэффициента.

Угловой коэффициент прямой можно вычислить, если известны координаты двух каких-либо точек этой прямой. Пусть даны две точки прямой: M₁(x₁; у₁) и M₂(x₂; у₂) и пусть, например, 0 x₁, у₂ > у₁ (рис. 98).

Тогда из прямоугольного треугольника M₁РM₂ находим

Аналогично доказывается, что формула (2) верна и в случае 90° 3 х + 3у – 7 = 0.

Приведем данное уравнение к виду

Следовательно, k = tg α = – 1 /_{√ 3} , откуда α = 150°

Задача 5. Составить уравнение прямой, проходящей через точку Р(3; -4), с угловым коэффициентом k = 2 /₅

Задача 6. Составить уравнение прямой, проходящей через точку Q (-3; 4) и составляющей с положительным направлением оси Ох угол 30°.

Если α = 30°, то k = tg 30° = √ 3 /₃. Подставив в уравнение (4) значения x₁, y₁ и k, получим

[spoiler title=”источники:”]

http://zaochnik.com/spravochnik/matematika/prjamaja-ploskost/uravnenie-prjamoj-s-uglovym-koeffitsientom/

http://razdupli.ru/teor/100_uravnenie-pryamoj-s-uglovym-koefficientom.php

[/spoiler]

В декартовых координатах каждая прямая
определяется уравнением первой степени
и, обратно, каждое уравнение первой
степени определяет прямую.

Уравнение
вида

 (1)

называется
общим уравнением прямой.

Угол ,
определяемый, как показано на рис.,
называется углом наклона прямой к оси
Ох. Тангенс угла наклона прямой к оси
Ох называется угловым коэффициентом
прямой; его обычно обозначают буквой
k:

Уравнение  называется
уравнением прямой с угловым коэффициентом;
k – угловой коэффициент, b – величина
отрезка, который отсекает прямая на оси
Оу, считая от начала координат.

Если
прямая задана общим уравнением

,

то
ее угловой коэффициент определяется
по формуле

.

Уравнение  является
уравнением прямой, которая проходит
через точку  (, )
и имеет угловой коэффициент k.

Если
прямая проходит через точки (, ), (, ),
то ее угловой коэффициент определяется
по формуле

.

Уравнение

является
уравнением прямой, проходящей через
две точки (, )
и (, ).

Если
известны угловые коэффициенты  и  двух
прямых, то один из углов  между
этими прямыми определяется по формуле

.

Признаком
параллельности двух прямых является
равенство их угловых коэффициентов:.

Признаком
перпендикулярности двух прямых является
соотношение
,
или .

Иначе говоря, угловые коэффициенты
перпендикулярных прямых обратны по
абсолютной величине и противоположны
по знаку.

4.Общее уравнение прямой

Уравнение

Ах+Ву+С=0

(где А, В, Смогут иметь любые
значения, лишь бы коэффициентыА,
Вне были нулями оба сразу)
представляетпрямую
линию. Всякую прямую можно
представить уравнением этого вида.
Поэтому его называютобщим уравнением
прямой.

Если А=0, то есть уравнение не
содержитх, то оно представляет
прямую,параллельную
оси ОХ.

Если В=0, то есть уравнение не
содержиту, то оно представляет
прямую,параллельную
оси ОY.

Когла Вне равно нулю, то общее
уравнение прямой можноразрешить
относительно ординаты у,
тогда оно преобразуется к виду

y=ax+b

(где a=-A/B; b=-C/B).

Аналогично, при Аотличным от
нуля общее уравнение прямой можно
разрешить относительнох.

Если С=0, то есть общее уравнение
прямой не содержит свободного члена,
то оно представляет прямую, проходящую
через начало координат

5. Уравнение прямой, проходящей через данную точку с данным угловым коэффициентом

Уравнение прямой, проходящей
через данную точку A(x₁, y₁)
в данном направлении, определяемом
угловым коэффициентом k,

y – y₁ = k(x – x₁).     (1)

Это уравнение определяет
пучок прямых, проходящих через
точку A(x₁, y₁),
которая называется центром пучка.

6. уравнение прямой,
проходящей через две данные точки.

. Уравнение
прямой, проходящей через две точки: A(x₁, y₁)
и B(x₂, y₂),
записывается так:

     (2)

Угловой коэффициент прямой, проходящей
через две данные точки, определяется
по формуле

     (3)

7.
Уравнение прямой в отрезках

Если в общем уравнении
прямой  ,
то разделив (1) на  ,
получаем уравнение прямой в отрезках

,

где  ,  .
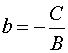
Прямая пересекает ось   в
точке  ,
ось   в
точке  .

8.
Формула: Угол между прямыми на плоскости

Уголα между
двумя прямыми, заданными
уравнениями: y=k₁x+b₁ (первая
прямая) и y=k₂x+b₂ (вторая
прямая), может быть вычислен по формуле
(угол отсчитывается от 1^й прямой
ко 2^й против
часовой стрелки):

tg(α)=(k2-k1)/(1+k1k2)

9. Взаимное
расположение двух прямых на плоскости.

  Пусть сейчас
оба уравнения прямых
записаны в общем виде.

Теорема. Пусть

    и 

– общие уравнения двух
прямых на координатной плоскости
Оху. Тогда

1) если ,
то прямые  и  совпадают;

2) если ,
то прямые   и 

    параллельные;

3) если ,
то прямые пересекаются.

   Доказательство.
Условие  равносильно
коллинеарности нормальных векторов данных
прямых:

.
Поэтому, если ,
то  и прямыепересекаются.

   Если же ,
то , ,  иуравнение прямой  принимает
вид:

 или ,
т.е. прямые совпадают.
Заметим, что коэффициент пропорциональности ,
иначе все коэффициенты общего уравнения были
бы равны нулю, что невозможно.

   Если же прямые не
совпадают и не пересекаются, то остается
случай ,
т.е. прямые параллельны.

Теорема доказана.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #