Как найти тангенс в физике

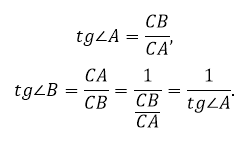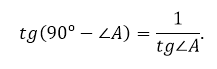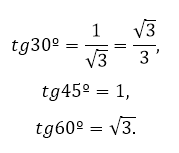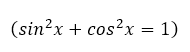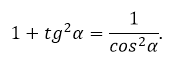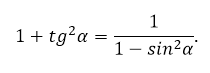
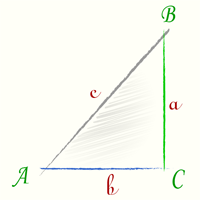
Тангенс угла tg(A) — есть отношение противолежащего катета a к прилежащему катету b [ tg(A) = frac{a}{b} ]

Тангенс угла — tg(A), таблица

0° Тангенс угла 0 градусов	$ tg(0°) = tg(0) = 0 $	0.000
30° Тангенс угла 30 градусов	$ tg(30°) = tgBig(Largefrac{pi}{6}normalsizeBig) = Largefrac{1}{sqrt{3}}normalsize $	0.577
45° Тангенс угла 45 градусов	$ tg(45°) = tgBig(Largefrac{pi}{4}normalsizeBig) = 1 $	1.000
60° Тангенс угла 60 градусов	$ tg(60°) = tgBig(Largefrac{pi}{3}normalsizeBig) = sqrt{3} $	1.732
90° Тангенс угла 90 градусов	$ tg(90°) = tgBig(Largefrac{pi}{2}normalsizeBig) = infin $	∞

Вычислить, найти тангенс угла tg(A) и угол, в прямоугольном треугольнике

Вычислить, найти тангенс угла tg(A) по углу A в градусах

Вычислить, найти тангенс угла tg(A) по углу A в радианах

Тангенс угла — tg(A)	стр. 224

Тангенс угла фи это отношение реактивной потребляемой мощности к активной.
КПД приблизительно равно отношению активной потребляемой мощности (она почти равна механической мощности на валу) к полной потребляемой. Тогда:

1-КПД=реактивная мощность/полная мощность

(реактивная мощность / полная мощность) / (активная мощность / полная мощность) =реактивная мощность / активная мощность=тангенс фи.

Очевидно :ехидно улыбаясь-} следующее:

тангенс фи=(1-КПД) / КПД

КПД у каждого двигателя написано на табличке, если табличка отсутствует, то по внешнему виду (монтажные и присоединительные размеры и количество ребер охлаждения статора) можно установить принадлежность двигателя к определенной серии, коих не так уж много. В спец справочниках можно по размерам установить тип двигателя и его КПД.

Если нет справочников, достаточно зайти на сайт любой фирмы, торгующей движками, серьезная фирма разместит полную инфу.

Эх, давно же учился, а все помню, хоть и теплосетями занимаюсь.

Тригонометрия в физике.

• Авторы
• Руководители
• Файлы работы
• Наградные документы

Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке “Файлы работы” в формате PDF

Введение

Многие из нас хотя бы раз в жизни задавались вопросом: зачем нужна тригонометрия? Впервые мы сталкиваемся с данным понятием в 8 классе при изучении  темы «Соотношения между сторонами и углами прямоугольного треугольника». На этом этапе мы узнаем, что такое синус, косинус и тангенс. Перейдя в 9 класс, мы вновь возвращаемся к тригонометрии. Здесь вводится понятие единичная окружность, с помощью которой определяются функции улов. Перейдя же в 10 класс, мы снова сталкиваемся с тригонометрией и понимаем, что она стала посложнее: ввелось понятие радианная мера угла,  появились тригонометрические уравнения и неравенства, а также стали изучаться  графики тригонометрических функций. Таким образом,  изучая весь этот материал, становится интересно посмотреть на практическую сторону тригонометрии. Для начала нужно сказать о том, что тригонометрия – это раздел математики, в котором изучаются тригонометрические функции и их использование в геометрии. Слово тригонометрия состоит из двух греческих слов: «trigwnon» – «треугольник» и «metrew» – «измерять», означает – «измерение треугольников». Именно эта задача – «измерение треугольников» или «решение треугольников», определение всех элементов треугольника по трем данным, с древнейших времен составила основу практических приложений тригонометрии. Сложно представить, но с этой наукой мы сталкиваемся не только на уроках математики, но и в нашей повседневной жизни. Многие из нас даже не подозревают, что тригонометрия нашла широкое применение в таких науках как физика, биология, химия, компьютерная графика, геодезия, океанология. Также большую роль тригонометрия играет в медицине и, на удивление, ее используют даже в музыке при описании звуковых волн.

Актуальность: Данная  тема, бесспорно, является актуальной. Тригонометрия использовалась людьми за много лет до нашей эры, уже тогда без знания этой науки было невозможно построить дом, а астрономам не удавалось провести различные расчеты. Спустя тысячелетия ничего не изменилось, тригонометрия по-прежнему остается одной из самых нужных наук, поэтому ее основы должен знать каждый человек, для того чтобы производить расчеты и иметь представление о самых элементарных функциях, так как тригонометрия заставляет думать логически и концентрирует наше внимание.

Цель: Определение связи  тригонометрии с окружающим миром.

Задачи:

1.Рассмотреть историю возникновения и развития тригонометрии.

2.Показать на примерах практическое применение тригонометрии в физике.

3.Раскрыть на примерах возможности использования тригонометрических функций.

Гипотеза: Большинство физических явлений природы, физиологических процессов, закономерностей в музыке и искусстве можно описать с помощью тригонометрии и тригонометрических функций.

Методы исследования:

1. Теоретический анализ
2. Проведение исследования

Практическая значимость: проект может использоваться в качестве теоретического курса в  качестве дополнения, закрепления уже пройденного материала или на внеурочных занятиях.

1.История возникновения тригонометрии

Зачатки тригонометрии можно найти в математических рукописях древнего Египта, Вавилона и древнего Китая. 56-я задача из папируса Ринда (II тысячелетие до н. э.) предлагает найти наклон пирамиды, высота которой равна 250 локтей, а длина стороны основания — 360 локтей.

От вавилонской математики ведёт начало привычное нам измерение углов градусами, минутами и секундами (введение этих единиц в древнегреческую математику обычно приписывают Гипсиклу, II век до н. э.).

Среди известных вавилонянам теорем была, например, такая: вписанный угол, опирающийся на диаметр круга — прямой. Главным достижением этого периода стало соотношение, позже получившее название теоремы Пифагора. Неизвестно, знали ли общую формулировку теоремы древние египтяне, но прямоугольный «египетский треугольник» со сторонами 3, 4 и 5 был там хорошо известен и широко использовался.

Общее и логически связное изложение тригонометрических соотношений появилось в древнегреческой геометрии. Греческие математики ещё не выделяли тригонометрию как отдельную науку, для них она была частью астрономии. Впервые само слово тригонометрия встречается в 1505 году в заглавии книги немецкого математика Питискуса.

Основным достижением античной тригонометрической теории стало решение в общем виде задачи «решения треугольников», то есть нахождения неизвестных элементов треугольника, исходя из трёх заданных его элементов (из которых хотя бы один является стороной).

В данном случае измерение треугольников следует понимать как решение треугольников, т. е. определение сторон, углов и других элементов треугольника, если даны некоторые из них.

Возникновение тригонометрии связано с землемерением, астрономией и строительным делом.

Значительный вклад в развитие тригонометрии внесли арабские ученые Аль-Батани (850-929) и Абу-ль-Вафа, Мухамед-бен Мухамед (940-998), который составил таблицы синусов и тангенсов через 10′ с точностью до 1/604. Теорему синусов уже знали индийский ученый Бхаскара (р. 1114, год смерти неизвестен) и азербайджанский астроном и математик Насиреддин Туси Мухамед (1201-1274). Кроме того, Насиреддин Туси в своей работе «Трактат о полном четырехстороннике» изложил плоскую и сферическую тригонометрию как самостоятельную дисциплину.

Дальнейшее развитие тригонометрия получила в трудах выдающихся астрономов Николая Коперника (1473-1543) – творца гелиоцентрической системы мира, Тихо Браге (1546-1601) и Иогана Кеплера (1571-1630), а также в работах математика Франсуа Виета (1540-1603), который полностью решил задачу об определениях всех элементов плоского или сферического треугольника по трем данным.

Долгое время тригонометрия носила чисто геометрический характер, т. е. Факты, которые мы сейчас формулируем в терминах тригонометрических функций, формулировались и доказывались с помощью геометрических понятий и утверждений. Такою она была еще в средние века, хотя иногда в ней использовались и аналитические методы, особенно после появления логарифмов. Пожалуй, наибольшие стимулы к развитию тригонометрии возникали в связи с решением задач астрономии, что представляло большой практический интерес.

Начиная с XVII в., тригонометрические функции начали применять к решению уравнений, задач механики, оптики, электричества, радиотехники, для описания колебательных процессов, распространения волн, движения различных механизмов, для изучения переменного электрического тока и т. д. Поэтому тригонометрические функции всесторонне и глубоко исследовались, и приобрели важное значение для всей математики.

Аналитическая теория тригонометрических функций в основном была создана выдающимся математиком XVIII веке Леонардом Эйлером (1707-1783) членом Петербургской Академии наук. Громадное научное наследие Эйлера включает блестящие результаты, относящиеся к математическому анализу, геометрии, теории чисел, механике и другим приложениям математики. Именно Эйлер первым ввел известные определения тригонометрических функций, стал рассматривать функции произвольного угла, получил формулы приведения. После Эйлера тригонометрия приобрела форму исчисления: различные факты стали доказываться путем формального применения формул тригонометрии, доказательства стали намного компактнее проще.

Таким образом, тригонометрия, возникшая как наука о решении треугольников, со временем развилась и в науку о тригонометрических функциях.

2.Тригонометрические функции

Тригонометрические функции представляют собой элементарные функции, аргументом которых является угол. С помощью тригонометрических функций описываются соотношения между сторонами и острыми углами в прямоугольном треугольнике. Области применения тригонометрических функций чрезвычайно разнообразны. Так, например, любые периодические процессы можно представить в виде суммы тригонометрических функций (ряда Фурье). Данные функции часто появляются при решении  дифференциальных и функциональных уравнений.

 К тригонометрическим функциям относятся следующие 6 функций: синус, косинус, тангенс, котангенс, секанс и косеканс. Для каждой из указанных функций существует обратная тригонометрическая функция.

 Геометрическое определение тригонометрических функций удобно ввести с помощью единичного круга. На приведенном ниже рисунке изображен круг радиусом r=1. На окружности обозначена точка M(x,y). Угол между радиус-вектором OМ и положительным направлением оси Ox равен α.

    Синусом угла α называется отношение ординаты y точки M(x,y) к радиусу r: 
sinα=y/r. 
Поскольку r=1, то синус равен ординате точки M(x,y).

      Косинусом угла α называется отношение абсциссы x точки M(x,y) к радиусу r: 
cosα=x/r 

      Тангенсом угла α называется отношение ординаты y точки M(x,y) к ee абсциссе x: 
tanα=y/x,x≠0 

      Котангенсом угла α называется отношение абсциссы x точки M(x,y) к ее ординате y: 
cotα=x/y,y≠0 

      Секанс угла α − это отношение радиуса r к абсциссе x точки M(x,y): 
secα=r/x=1/x,x≠0 

      Косеканс угла α − это отношение радиуса r к ординате y точки M(x,y): 
cscα=r/y=1/y,y≠0 

   В единичном круге проекции x, y точки M(x,y) и радиус r образуют прямоугольный треугольник, в котором x,y являются катетами, а r − гипотенузой. Поэтому, приведенные выше определения тригонометрических функций в приложении к прямоугольному треугольнику формулируются таким образом: 
Синусом угла α называется отношение противолежащего катета к гипотенузе. 
Косинусом угла α называется отношение прилежащего катета к гипотенузе. 
Тангенсом угла α называется противолежащего катета к прилежащему. 
Котангенсом угла α называется прилежащего катета к противолежащему. 
Секанс угла α представляет собой отношение гипотенузы к прилежащему катету. 
Косеканс угла α представляет собой отношение гипотенузы к противолежащему катету. 

  График функции синус 
y=sinx, область определения: x∈R, область значений: −1≤sinx≤1 

 График функции косинус 
y=cosx, область определения: x∈R, область значений: −1≤cosx≤1 

График функции тангенс  y=tanx, область определения: x∈R,x≠(2k+1)π/2, область значений: −∞<tanx<∞ 

График функции котангенс  y=cotx, область определения: x∈R,x≠kπ, область значений: −∞<cotx<∞ 

График функции секанс  y=secx, область определения: x∈R,x≠(2k+1)π/2, область значений:secx∈(−∞,−1]∪[1,∞) 

График функции косеканс  y=cscx, область определения: x∈R,x≠kπ, область значений: cscx∈(−∞,−1]∪[1,∞) 

3.Тригонометрия в физике

В технике и окружающем нас мире часто приходится сталкиваться с периодическими (или почти периодическими) процессами, которые повторяются через одинаковые промежутки времени. Такие процессы называют колебательными. Колебательные явления различной физической природы подчиняются общим закономерностям. Например, колебания тока в электрической цепи и колебания математического маятника могут описываться одинаковыми уравнениями. Общность колебательных закономерностей позволяет рассматривать колебательные процессы различной природы с единой точки зрения. Наряду с поступательными и вращательными движениями тел в механике значительный интерес представляют и колебательные движения.

Механические колебания

Механическими колебаниями называют движения тел, повторяющихся точно (или приблизительно) через одинаковые промежутки времени. Примерами простых колебательных систем могут служить груз на пружине или маятник. Возьмем, например, гирю, подвешенную на пружине (см. рис.) и толкнем ее вниз. Гиря начнет колебаться вниз и вверх. Как показывают расчеты, отклонение гири от положения равновесия выражается формулой

 s=  sinwt.

  Здесь v0-скорость, с которой мы толкнули гирю,  w= , где m-масса гири, k – жесткость пружины.

  Если мы сначала оттянем гирю на s0 см, а потом толкнем ее со скоростью v0, то она будет совершать колебания по более сложному закону:

s=Asin(wt+a).

  Расчеты показывают, что амплитуда А этого колебания равна ,а число таково, что tga= . Из-за слагаемого a это колебание отличается от колебания s=Asinwt.

  График колебания (2) получается из графика колебания(1) сдвигом влево

на  . Число a – начальная фаза.

  Колебания маятника

Колебания маятника тоже приближенно происходят по синусоидальному закону. Графическое изображение этой функции, дающее наглядное представление о протекании колебательного процесса во времени удобно рассмотреть с помощью модели маятника программы « Функции и графики»

Если эти колебания малы, то угол отклонения маятника приближенно выражается формулой: ,где l-длина маятника, а j0-начальный угол отклонения. Чем длиннее маятник, тем медленнее он качается. Измеряя период колебания маятника известной длины, можно вычислять ускорение земного тяготения g в различных точках земной поверхности.

Разряд конденсатора.

Не только многие механические колебания происходят по синусоидальному закону. И в электрических цепях возникают синусоидальные колебания. Так в цепи, изображенной в правом верхнем углу модели, заряд на обкладках конденсатора изменяется по закону

 q = CU + (q0 – CU) cos ωt, где С- емкость конденсатора, U –напряжение на источнике тока, L –индуктивность катушки,  – угловая частота колебаний в цепи.

  Благодаря модели конденсатора можно устанавливать параметры колебательного контура и строить, соответствующие графики g(t)и I(t). На графиках  хорошо видно как влияет напряжение на изменение силы тока и заряда конденсатора, при этом видно, что при положительном напряжении заряд также принимает положительные значения. На рисунке показано, что при изменении емкости конденсатора( при изменении индуктивности катушки) и сохранении неизменными остальных параметров меняется период колебаний, т. е. меняется частота колебаний силы тока в цепи и меняется частота заряда конденсатора.

          Баллистическое движение
          Баллистика – раздел механики, изучающий движение тел в поле тяжести Земли.

Пули снаряды и бомбы, так же как и теннисный, и футбольный мячи, и ядро легкоатлета, при полете движутся по баллистической траектории.

Закон баллистического движения в координатной форме: (1)

Уравнение траектории снаряда, или зависимость y(x), можно получить, исключая из уравнений системы время. Для этого из первого уравнения системы найдём:

t = .

Подставляя его во второе уравнение, получаем уравнение траектории снаряда:

y = x tg α – (2).

  Траектория баллистического движения.

Построим баллистическую траекторию (2).

Графиком квадратичной функции, как известно, является парабола. В рассматриваемом случае парабола проходит через начало координат,

так как из (2) следует, что у = 0 при х = 0.

Ветви параболы направлены вниз, так как коэффициент ( – ) при x меньше нуля.

Определим основные параметры баллистического движения: время подъема на максимальную высоту, максимальную высоту, время и дальность полета. Вследствие независимости движений по координатным осям подъем снаряда по вертикали определяется только проекцией начальной скорости на ось Y. В соответствии с формулой: полученной для тела, брошенного вверх с начальной скоростью , время подъема снаряда на максимальную высоту равно:

t = .

Максимальная высота подъема может быть рассчитана по формуле

, если  подставить вместо :

y = .

Как соединить две трубы.

Приведенные примеры могут создать впечатление, что синусоиды встречаются только в связи с колебаниями. Однако это не так. Например, синусоиды используются при соединении двух цилиндрических труб под углом друг к другу. Чтобы соединить две трубы таким образом, надо срезать их наискосок.

Если развернуть срезанную наискосок трубу, то она окажется ограниченной сверху синусоидой. В этом можно убедиться, обернув свечку бумагой, срезав ее наискосок и развернув бумагу. Поэтому, чтобы получить ровный срез трубы, можно сначала обрезать металлический лист сверху по синусоиде и свернуть его в трубу.

 Теория радуги.

Впервые теория радуги была дана в 1637 году Рене Декартом. Он объяснил радугу, как явление, связанное с отражением и преломлением света в дождевых каплях.

Радуга возникает из-за того, что солнечный свет испытывает преломление в капельках воды, взвешенных в воздухе по закону преломления:

где n1=1, n2≈1,33 – соответственно показатели преломления воздуха и воды, α – угол падения, а β – угол преломления света.

  Северное сияние

Проникновение в верхние слои атмосферы планет заряженных частиц солнечного ветра определяется взаимодействием магнитного поля планеты с солнечным ветром.

 Сила, действующая на движущуюся в магнитном поле заряженную частицу называется, силой Лоренца. Она пропорциональна заряду частицы и векторному произведению поля и скорости движения частицы

  Задачи по тригонометрии с практическим содержанием.

  Тело веса Р положено на наклонную плоскость с углом наклона a. Тело под действием своего собственного веса прошло ускоренно путь S в t секунд. Определить коэффициент трения k.

  Решение:

Сила давления тела на наклонную плоскость F =kPcosa.

Сила, которая тянет тело вниз равна F=Psina-kPcosa=P(sina-kcosa).(1)

Если тело движется по наклонной плоскости, то ускорение а= .

С другой стороны, ускорение а= = =gF ;следовательно,  .(2)

Из равенств (1) и (2) следует, что g(sina-kcosa)=  .

Отсюда: k= =gtga- .

4.Практическая часть

В качестве исследования, я решила провести измерения пандусов двух учреждения нашего города и выяснить, какой из них больше соответствует нормативным требованиям. Пандус –  (фр. pente douce — пологий скат), также рампа — пологая наклонная площадка, соединяющая две разновысокие горизонтальные поверхности, обычно для обеспечения перемещения колёсных транспортных средств с одной на другую. Среди часто встречающихся применений — обеспечение подъезда инвалидных колясок к расположенному над цоколем здания парадному входу.

Пандус магазина «Монетка» (см. приложение 1)

Измерения показали:

высота =40см=0,4м
        длина=240 см=2,4м

Пандус представляет собой прямоугольный треугольник, следовательно, имея данные измерения, можно рассчитать гипотенузу, обозначим ее за с.

с1= √2,42 +0,42 = 2,43 м
Зная гипотенузу, можно рассчитать синус угла наклона.

Синус- это отношение противолежащего катета к гипотенузе.
= = 0,164
Угол наклона пандуса равен 9°.

Рассмотрим пандус, принадлежащий магазину «Дикси» (см. приложение 2)

Высота = 80 см = 0,8 м

Длина=530 см=5,3 м

Соответственно первому решению, найдем гипотенузу (с)

с2=√5,32 +0,82=5,36 м

Найдем синус:  = =0,149
Угол наклона пандуса равен 8°.
           СНиП 35-01-2001

Требования СНиП (строительные нормы и правила) касательно пандусов для инвалидов содержат следующие пункты:

• Максимальная высота подъемного сооружения (одного марша) не должна превышать 0,8 м. Угол наклона при этом должен быть меньше 8%. Если перепад высоты менее 0,2 м, допустимый уклон составляет 10 %.

Таким образом, оба пандуса соответствуют строительным нормам и правилам. Данный пример также показал, что тригонометрия широко применима в жизни.

Заключение

Подводя итог всему выше сказанному, мы подтверждаем гипотезу, выдвинутую вначале проекта. Действительно, большинство физических явлений природы, закономерностей в архитектуре можно описать с помощью тригонометрии и тригонометрических функций. Сейчас в век инновационных технологий еще сложнее представить жизнь без использования тригонометрии. Как показал пример, даже для установления всем привычных пандусов нужно знать элементарную часть тригонометрии, изучаемую в школе.  На каждом шагу мы сталкиваемся с математикой. Однажды  Советский и российский математик Александр Данилович Александров сказал: «Окружающий нас мир – это мир геометрии» и я полностью с ним согласна.

Список литературы:

1. В.А.Косьянов «Физика 10 класс». Издательство «Дрофа», Москва, 2003 год.
2. Ш.А.Алимов «Алгебра и начала математического анализа». Издательство «Просвещение», Москва, 2017 год.
3. http://ya-znau.ru/znaniya/zn/78
4. Детская энциклопедия «Я познаю мир. Физика». Издательство «АСТ», Москва, 1997 год.
5. https://ru.wikipedia.org/wiki/История_тригонометрии
6. http://bouw.ru/article/uklon-pandusa-dlya-invalidov

Приложение:

1.  

Просмотров работы: 7372

Рассмотрим что означает понятие и значение слова тангенциальная сила (информация предоставлена intellect.icu).

ТАНГЕНЦИАЛЬНАЯ СИЛА

(от лат. tangens – касательный). 1) в астрономии: сила по касательной к орбите, вследствие которой двигаются планеты. 2) в механике: сила, действующая на тело по направлению касательной к кривой траектории.

ТАНГЕНЦИАЛЬНАЯ СИЛА

в физике, механике и астрономии – центробежная сила.

ТАНГЕНЦИАЛЬНАЯ СИЛА

от лат. tangens, касательный. Сила, вследствие которой планеты двигаются как бы по касательной.

ТАНГЕНЦИАЛЬНАЯ СИЛА

то же, что центробежная сила.

Цифровое произношение

Тангенциальная сила имеет soundex-Т525, metaphone-“тангинциалнаaсила”, double-metaphone primary : TNJN
secondary: TNKN.

См. также

… силой реакции опоры , где – нормальная составляющая силы реакции (сила . нормального давления ), а – тангенциальная составляющая силы реакции , то есть сила .трения ) Соответственно , уравнение второго закона Ньютона … … , в нее не включенных Внутренние силы будем обозначать как , где индексы показывают , что данная . сила действует на тело с номером со стороны тела с.номером Кроме того, на тело с номером действует … (Физические основы механики)

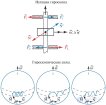
… . вокруг неподвижной оси 00 Элементарная работа по перемещению элемента массой равна :. где – тангенциальная составляющая внешней силы , действующей на элемент массой (рис . Рис Работа сил … … сил трения , показанные на. рис Таким образом , на груз действуют силы и , а на каток . – силы и Обозначим a ускорение груза и – ускорение катка Кроме того, каток вращается по часовой стрелке … (Физические основы механики)

… частицам воздуха за время , равен Из второго закона Ньютона следует , что средняя сила , действующая на. отбрасываемый вниз воздух равна . По третьему закону Ньютона такая же … … может испытывать . небольшие отклонения (флуктуации ) от положения равновесия При этом, естественно , возникают силы Если они возвращают частицу к положению равновесия , то такое равновесие . называется устойчивым Если … (Физические основы механики)

… ). В ведущих державах были разработаны мобилизационные планы развертывания в военное . время вооруженных сил на несколько миллионов человек Так накануне Первой мировой войны в вооруженных силах … … документом утвержденным в государстве , положения в. котором отражают систему взглядов на применения военной силы для достижения .политических целей , на характер военных задач и способов их осуществления , на. основные направления … (Военное дело)

… инерции (здесь . координата есть расстояние от оси вращения , а и – единичные орты ). Результирующая этих сил наклонена к вертикали под углом таким, что. Поверхность жидкости , описываемая функцией , всегда располагается ортогонально … … телами ., они являются следствием неинерциальности системы отсчета Для одного и того же тела эти силы различны и. имеют разные свойства в разных неинерциальных системах отсчета в зависимости .от характера … (Физические основы механики)

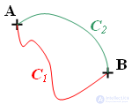
… тяготения , силы упругости ., силы электростатического взаимодействия заряженных тел Поле , работа сил которого по перемещению материальной точки вдоль произвольной . замкнутой траектории равна нулю , называется … … приложения и не зависит от выбора траектории , по.которой перемещается тело ; – работа консервативных сил по произвольному замкнутому контуру равна 0;. – ротор консервативных сил равен 0;. – консервативная сила … (Физические основы механики)

---

---

Что такое тангенс угла и как его найти

Живущим людям на Земле
всегда хотелось знать,
как путь найти в пустыне, море,
и можно к звёздам ли попасть.

Хотелось труд свой облегчить,
создать машины, чтоб летать.
И чтоб вопросы разрешить,
пришлось про тангенс всем узнать.

Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. Впервые встречаясь с тригонометрией в восьмом классе на геометрии, школьники оглядываются на свою жизнь, задавая вопрос, насколько пригодится им эта область науки в дальнейшем.

Редко кто задумывается, что раздел математики, позволяющий рассказать о заданном треугольнике всё (найти все его стороны и углы, выделить особенности), позволил в своё время сделать великие открытия.

Тригонометрия, дав возможность строить корабли и самолёты, отправлять человека в космос, создавать приборы для ориентирования на море, в лесу, в пустыне, определять расстояния, не измеряя их непосредственно линейкой, шагами или чем-то иным, помогла упростить жизнь человечества, раскрыть новые горизонты знаний.

Тангенс угла

Первые встречи с тангенсом происходят при изучении прямоугольных треугольников.

В них соотношения сторон, образующих прямой угол (катетов), и стороны, лежащей напротив угла в 90º (гипотенузы), задают важные параметры для изучения углов.

Для понимания связи между объектами рассматриваются отношения различных отрезков. Задавая связь между ними, вводят понятия синуса, косинуса (это что?), тангенса, котангенса.

Важно, что это отвлечённые понятия, не связанные с какими-либо единицами измерения.

Введя функции угла, определяют их свойства. Некоторые полученные формулы могут иметь довольно громоздкий вид. Чтобы избежать затруднённого чтения, вводятся другие объекты.

Так произошло и с тангенсом. Ему посчастливилось получить два определения. Каждое характеризует заданное отношение по-своему. С одной стороны, рассматривается связь между катетами и острыми углами прямоугольного треугольника, с другой – даётся возможность упростить формулы, содержащие синусы и косинусы.

Мало кто задумывается, изучая тангенс в школе, что первоначально он был необходим, чтобы найти касательные линии к заданной кривой. Само понятие возникло от латинского слова tangens, которое означает «трогающий», «касающийся» и является причастием настоящего времени от tangere («трогать», «касаться»).

Тангенс — это отношение…

Итак, есть два определения:

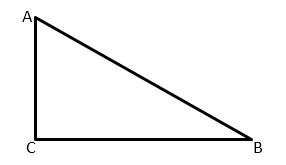
1. Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.

   Это определение удобно использовать при изучении геометрических фигур. Оно даёт возможность, минуя вычисления гипотенузы, находить углы или катеты. Выделяя прямоугольные треугольники в произвольных фигурах, задача по изучению свойств исследуемых объектов становится проще.

2. Тангенс – это отношение синуса к косинусу.

   Благодаря этому определению, многие тригонометрические формулы принимают более удобный вид, становятся легче воспринимаемыми.

Приняты обозначения:

Вместо «тангенс угла альфа» пишут: tgα. На калькуляторах, в различных программах ЭВМ и ПК закрепилось другое обозначение: tan⁡(α).

Как найти тангенс угла (формулы)

Первое свойство тангенса вытекает из его определения как отношения катетов.

Сумма двух непрямых углов прямоугольного треугольника равна 90º. Поэтому

Так как тангенс – это отношение катетов, то

Получается, что

Учитывая особенности некоторых треугольников (равностороннего, прямоугольного, равнобедренного), а также записанное свойство, была составлена таблица значений тангенса для углов 30º, 45º, 60º.

В частности,

Задача нахождения других углов по значению тангенса была решена с помощью составления более обширных таблиц. За счёт появления современных вычислительных средств необходимость применения табулированных значений уменьшилась.

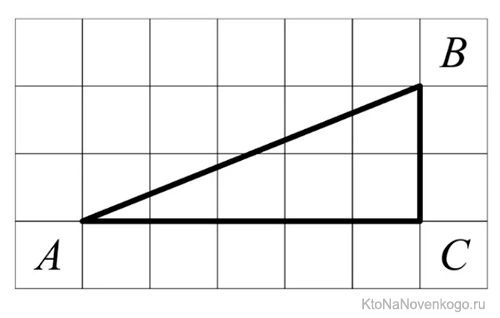
Как найти тангенс по клеточкам

Учитывая первое определение, можно определить, как найти его по клеточкам. Рисунок дополняется перпендикулярными линиями (строится высота), затем считается количество клеточек в полученном прямоугольном треугольнике на катетах, противолежащем и прилежащем искомому углу, а затем берётся их отношение.

Благодаря второму определению, задачу, как найти тангенс угла, можно решить, минуя таблицы и построение прямоугольных треугольников. Достаточно знать синус и косинус, связанные между собой основным тригонометрическим тождеством:

Из формулы тангенсов, записывающей кратко второе определение

и основного тригонометрического тождества можно понять, как найти тангенс, зная только косинус или синус угла.

Достаточно поделить основное тригонометрическое тождество на квадрат косинуса, подставить формулу тангенса. В результате получится его зависимость от косинуса:

Если выразить в последнем случае косинус, то запишется связь между тангенсом и синусом: