Как найти тангенс в геодезии

Расчет элементов кривой. Тангенсы, хорда, биссектриса, домер, длина кривой.

Опубликовано 6 лет назад. Просмотров с момента размещения на сайте 110729

Также, Вас может заинтересовать:

Для
построения профиля необходимо вычислить
элементы кривой: Т –
тангенс,
К – кривая, Д – домер, Б – биссектриса.

Элементы кривой
вычисляются по формулам:

Тангенс
; Кривая;

Домер
; Биссектриса

,

где R
– радиус
кривой, м; 
– угол
поворота трассы.

Пример вычисления
элементов кривой.

В
примере вершина угла поворота пк 4 + 33,
угол поворота 
= 43
26
и радиус кривой R
= 150 м.

Тангенс

м;

Кривая
м;

Домер
м;

Биссектриса
м.

2.7 Вычисление пикетажного значения главных точек кривой

Главные
точки кривой – это начало кривой (НК),
середина кривой (СК) и конец кривой (КК).
Пикетажное значение показывает расстояние
от начала трассы (НТ) до соответствующей
точки.

Вычисление
пикетажного значения главных точек
кривой выполняется по формулам:

пк НК = пк ВУ – Т;

пкКК = пкНК + К;

пкСК = пкНК +0,5К

Контроль: пкКК =
пкВУ + Т – Д;

пкКК = пкСК +0,5К.

Пример вычисления
пикетажных значений главных точек
кривой.

По
приведенным исходным данным пикетажные
значения главных точек кривой принимают
значения:

пк НК = пк ВУ – Т =
пк 4+33 – 59,74 = 3+73,26

пкКК
= пкНК + К = 373,26 + 113,65 = 486,91

пкСК
= пкНК +0,5К = пк 3+73,26 + 0,5 
113,65 = 430,08

Контроль:

пкКК
= пкВУ + Т – Д = пк 4 +33 +59,74 – 5,83 = 486,91

пкКК
= пкСК +0,5К = 430,08 + 0,5 
113,65 = 486,90

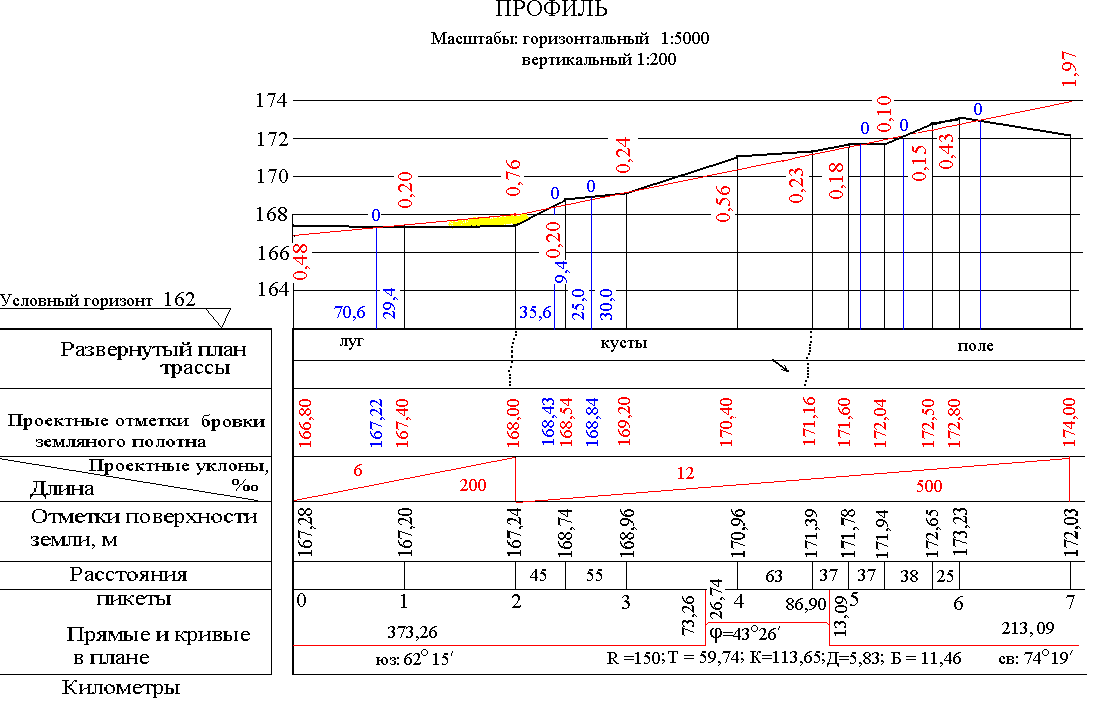
2.8 Построение продольного профиля

Профиль строится
на миллиметровой бумаге формата А3.
Масштаб для построения продольного
профиля по горизонтали и вертикали
различный. Для обеспечения наглядности
обычно вертикальный масштаб в 10 раз
крупнее горизонтального. В индивидуальном
задании указываются масштабы для
построения профиля. Профиль строится
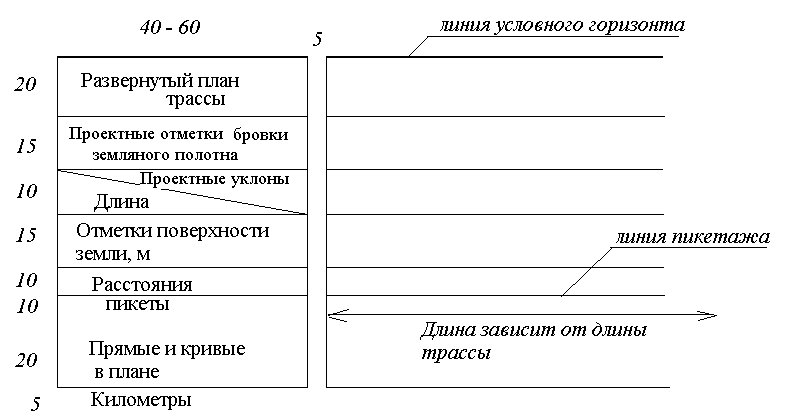
с использованием специальной таблицы
– сетки профиля. Ее размеры (в мм) и графы
приведены на рис.
7.

Рис 7. Сетка профиля

Профиль располагается
выше сетки профиля. При его построении
это необходимо учесть. Общий вид профиля
приведен на рис. 9.

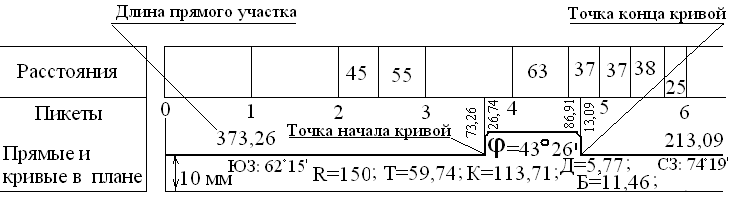
Построение профиля
начинается с графы «Расстояния».
В этой графе указываются пикетные и
плюсовые точки. С учетом горизонтального
масштаба строятся полные пикеты по 100
м. В графе они отмечаются вертикальными
линиями. Если между пикетами есть
плюсовые точки, они также наносятся в
эту графу и подписываются расстояния
между ними (рис. 8).

Рис. 8. Заполнение
графы «Расстояния» и «Пикеты»

В примере, между
пикетами 5 и 6 расположены две плюсовые
точки: +37 и +75. Расстояния подписываются
37и38(75 – 37 = 38 м) и25(100 – 75
м). Сумма отрезков 37 + 38 + 25 = 100 м (Рис.8).

Затем заполняется
графа «Пикеты».
В этой графе подписываются пикеты около
вертикальных линий, начиная с пикета 0
(пк0) (рис. 8).

Графа «Развернутый
план трассы»
заполняется по данным пикетажа
(пикетажной книжки). По середине графы
проводится ось дороги условно развернутая
в прямую линию. Вдоль линии наносится
план местности, прилегающий к трассе и
все объекты, которые находятся в полосе
25 м влево и вправо от оси трассы,
показываются границы между угодьями и
строения. В точках, соответствующих
вершинам углов поворота показывается
направление поворота трассы (вправо
или влево). Вместо условных знаков
допускается писать соответствующее
название: «луг», «лес» и т. д. (рис. 10).

Рис. 10. Заполнение
графы «Развернутый план трассы»

Графа «Прямые
и кривые в плане»
заполняется по результатам вычисления
пикетажных значений главных точек
кривых (Рис.11). В графе проводится прямая
линия на расстоянии 10 мм от нижней
границы. По пикетажному значению точки
«Начало кривой» она наносится на профиль
с учетом горизонтального масштаба на
линии пикетажа. От линии пикетажа
опускается перпендикуляр на ось дороги,
которая проводится вдоль графы. До точки
«Начало кривой» трасса показывается
прямой линией. Аналогично показывается
точка «Конец кривой». От нее трасса так
же показывается прямой. Между точками
«Начало кривой» и «Конец кривой» ось
дороги прерывается и кривая показывается
скобой. Если поворот правый, то скоба
направлена вверх, если поворот левый,
то скоба обращена вниз.

Рис. 11. Заполнение
графы «Прямые и кривые в плане»

Вдоль перпендикуляров
от пикетажной линии до оси дороги у
точек «Начало кривой» и «Конец кривой»
подписываются расстояния от заднего
пикета до точки и от точки до переднего
пикета.

Внутри кривой
выписываются угол поворота трассы ,
радиус R,
тангенс Т, кривая К, домер Д, биссектриса
Б.

Над
серединой каждой прямой вставки
записывают ее длину, а под ней дирекционный
угол или румб. Начальное направление
трассы выдается в задании. После поворота
трассы направление меняется. Ориентирующий
угол вычисляется по формулам зависимости
дирекционного угла и румба. В нашем
примере применяется формула второй
четверти:

_пк0-НК
= r
+ 180
= 6215
+ 180
= 24215;

_КК-ПК7
= _пк0-НК
+
= 43
26
= 285
41.
r
= 360
– 285
41
= 7419(сз).

Графа «Отметки
земли»
заполняется из «Ведомости геометрического
нивелирования». Отметки выписываются
к соответствующим пикетам и плюсовым
точкам с точностью 0,01 м.

ВНИМАНИЕ: «иксовые»
точки в построении не участвуют и их
отметки не
выписываются (рис.
2).

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

При решении геодезических и инженерных задач, очень часто приходиться вспоминать и искать необходимые формулы. В связи с этим хочется представить Вам шпаргалку (назовем её “геодезической шпаргалкой”:)), в которой приведены часто использующиеся формулы.
Конечно, ее содержание не охватывает всю высшую математику или сферическую геометрию, но что-нибудь должно пригодиться.
Зная из собственного опыта, неудобство восприятия формул без чисел, к каждой из них приводится пример вычисления.

---

Теорема Пифагора

Пример вычислений теорема Пифагора

---

Соотношения в прямоугольном треугольнике

Пример вычислений соотношения в прямоугольном треугольнике

---

Обратные тригонометрические функции арксинус (arcsin), арккосинус (arccos), арктангенс (arctg) и арккотангенс (arcctg)

— арксинус (arcsin) возвращает угол по его синусу

— арккосинус (arccos) возвращает угол по его косинусу

— арктангенс (arctg) возвращает угол по его тангенсу

— арккотангенс (arcctg) возвращает угол по его арктангенсу

Пример вычислений обратные тригонометрические функции

---

Сумма углов треугольника

Сумма углов в треугольнике равна 180 градусам

---

Теорема синусов

Для любого треугольника соблюдается выражение

Пример вычислений теорема синусов

---

Теорема косинусов

Квадрат любой стороны треугольника, равен сумме квадратов двух других его сторон, минус удвоенное произведение этих сторон на косинус угла между ними

Пример вычислений теорема косинусов

---

Площадь треугольника

Площадь треугольника можно определить по формулам

также удобно использовать формулу Герона ,
где p-полупериметр треугольника

Пример вычислений площадь треугольника

или по формуле Герона

---

Площадь круга

---

Длина дуги окружности

Длина дуги окружности вычисляется по формулам

если угол задан в угловых градусах минутах и секундах

если угол задан в радианах

Пример вычислений длина дуги окружности

угол задан в угловых градусах минутах и секундах

угол задан в радианах

---

Перевод градусов в угловые градусы минуты и секунды

Перевод угловых градусов минут и секунд в градусы выполняется согласно выражения

Пример вычислений
перевести в градусы угол, который задан в угловых градусах минутах и секундах

---

Перевод градусов в угловые градусы минуты и секунды

Перевод градусов в угловые градусы минуты и секунды выполняется согласно выражения

Пример вычислений
перевести в угловые градусы минуты и секунды угол, который задан в градусах

---

Перевод градусов в радианы

Перевод градусов в радианы выполняется по формуле

Пример вычислений
перевести в радианы угол, который задан в угловых градусах минутах и секундах

---

Перевод радианов в градусы

Перевод радианов в градусы выполняется по формуле

Пример вычислений
перевести в угловые градусы минуты и секунды угол, который задан в радианах

---

Определение наклона линии в градусах

Определение наклона линии в градусах выполняется с использованием соотношений в прямоугольном треугольнике
Пример вычислений
Определить наклон пандуса длиной 14м и высотой 3,5м

---

Определение уклона линии в долях, процентах и промилле

При инженерно-строительных работах, наклон линии задают не градусом наклона, а тангенсом этого градуса — безразмерной величиной, которая называется уклоном. Уклон может выражаться относительным числом, в процентах (сотые доли числа) и промилле (тысячные доли числа)

Пример вычислений
Определить уклон отмостки длиной 2,5м и высотой 0,30м

ПРАКТИЧЕСКАЯ РАБОТА № 2

По МДК 01.01. Технология производства полевых геодезических работ

Количество часов: 6

Тема занятия: «Определение элементов кривой и координат для детальной разбивки»

Наименование работы: расчетно-графическая работа.

Цель занятия:

-закрепление и развитие знаний, полученных при изучении теоретического материала по модулю;

– приобретение профессиональных навыков и умений по производству полевых геодезических работ;

– выполнить расчет элементов кривой и вычислить координаты для ее детальной разбивки, составить схему.

Приобретаемые умения и навыки:

– выполнения полевых геодезических работ на производственном участке;

– обрабатывать результаты полевых измерений;

– рассчитывать координаты опорных точек;

– осуществлять контроль производства геодезических работ;

Учебно-методическое оснащение рабочего места:

1. Инструкционно-технологическая карта.

2. Методические рекомендации.

3. Исходные данные (индивидуально).

Особые правила техники безопасности:

Инструкция по технике безопасности при выполнении камеральных работ.

Правила техники безопасности при выполнении чертежных работ.

Литература

Согласно пункта 4.2 рабочей программы ПМ 01

Исходные данные:

Вариант №__________

1. Пикетажное наименование вершины угла поворота ВУ ___________________

2. Измеренный угол поворота β = ______________

3. Радиус поворота R = _____________

Порядок выполнения практической работы

На всех линейных сооружениях, предназначенных для движения транспорта, в местах изменения направления трассы для сопряжения прямых участков с целью плавного и постепенного поворота движущего транспортного средства устраивают закругления или кривые. Закругления могут быть любыми. Простейшим является дуга окружности определенного радиуса, т.е. круговая кривая.

Конкретное решение о применении радиусов автомобильных, железнодорожных и других кривых принимают в соответствии с конкретными условиями и строительно-техническими нормами того или иного сооружения.

Разбивочные работы круговых кривых делятся на два этапа:

1. Разбивка главных точек круговой кривой выполняется одновременно с разбивкой пикетажа. Цель – определить пикетажное наименование конца кривой и затем продолжить разбивку пикетажа.

2. Детальная разбивка кривых – выполняется в период строительства.

Круговая кривая характеризуется четырьмя главными точками и шестью основными элементами.

Главными точками кривой, которые определяют положение кривой на местности, являются:

– вершина угла ВУ;

– начало кривой НК;

– середина кривой СК;

– конец кривой КК.

Рис.1 Главные точки кривой.

Основными элементами кривой, которые определяют положение главных точек, являются:

– угол поворота трассы – α;

– радиус закругления – R;

– длина кривой вставки – К;

– тангенсы – Т;

– биссектриса – Б;

– домер – Д.

Все линейные величины выражаются в метрах до сотых.

Во время изысканий угол α вычисляют, а радиус R назначают. Остальные элементы находят по формулам, вытекающим из прямоугольного треугольника с вершинами ВУ, НК, О (рис. 1).

Ход работы

1. Вычисляем угол поворота трассы – α:

α = 180⁰ – β

______________________________________________________________________________________

2. Вычисляем тангенс по формуле:

Т = R*tg*α/2

____________________________________________________________________________________

3. Вычисляем длину кривой по формуле:

K = α/180⁰*πR

_____________________________________________________________________________________

4. Вычисляем биссектрису по формуле:

Б = R(sek α/2 – 1) = (√R² + T² )– R

_____________________________________________________________________________________

5. Вычисляем домер по формуле:

D = 2T – K

__________________________________________________________________________________________

Все элементы кривой можно вычислить по вышеприведенным формулам. Но так как Т, K, Б и Д находятся в прямой зависимости от угла поворота и радиуса, то для их определения составлены специальные таблицы которыми пользуются для быстрой разбивки кривых.

6. Вычисляем пикетажные значения главных точек кривой, то есть определяем на каких пикетах и плюсовых точках они находятся. Для этого используем ниже следующие формулы:

НК = ВУ – Т =_______________________________________________________________________________

КК = НК + К=_______________________________________________________________________________

СК = НК + К/2=______________________________________________________________________________

Контроль:

КК = ВУ + Т – Д = ___________________________________________________________________________

КК = ВУ – Т + К =___________________________________________________________________________

СК = КК – К/2 =_____________________________________________________________________________

Расхождения в расчетах по двум формулам должны быть не более 0,01 м.

7. Вычерчиваем схему, на которую наносим все вычисленные величины и пикетажные наименования, необходимые для закрепления главных точек кривой и дальнейшей разбивки трассы.

Вывод:___________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

Выполнил:____________________________________________________________________________

Исходные данные к практической работе:

«Определение элементов кривой и координат для детальной разбивки»

2. Определение координат для детальной разбивки кривой.

По трем главным точкам НК, СК и КК точно построить кривую на местности невозможно, поэтому при строительстве трассы её обозначают рядом дополнительных точек. Данные работы называются детальной разбивкой кривой.

Расстояние между соседними точками на кривой  К  при детальной разбивке зависит от её радиуса R и характера сооружения, однако чем меньше R кривой, тем меньше значение К тем меньше промежутки k.

–  если R > 500 м, то  k = 20 м;

– если 500 > R > 100 м, то k = 10 м;

– если R ≤ 100 м, то k = 5 м.

Задание № 2 Определить координаты для детальной разбивки кривой применяя способ прямоугольных координат от тангенсов.

Ход работы:

1. За начало координат принимаем точку М – НК начало круговой кривой.

2. Тангенс МА принимаем за ось абсцисс (Х), а радиус МО за ось ординат (У).

3. Положение точки N, кривой в принятой системе  координат определяется абсциссой X₁ и ординатой Y₁.

4. Из прямоугольника ON1  находим Х₁ и У₁ используя формулы:

5. Угол φ находим в зависимости от длины дуги k, через которую производится разбивка кривой, используя формулу:

________________ φ = ______________________________________________

6. Для точек 2, 3 и т.д. координаты вычисляем, подставляя в вышеприведенные формулы углы 2φ, 3φ и т.д. до середины кривой:

7. На основании вычислений строим чертеж детальной разбивки круговой кривой способом прямоугольных координат. Масштаб подобран индивидуально:__1:_________

Вдоль тангенсов (ось абсцисс) откладываем длины х, восстанавливаем прямой угол в полученной точке. Точка 1 круговой кривой фиксируется расстоянием у, отмеренным по перпендикуляру. Так же получем другие точки круговой кривой. Вторую половину круговой кривой разбиваем от ее конца, выполняя аналогичные действия и используя значения х и у, полученные для первой половины.

Таблица 1 – Вычисление координат для детальной разбивки кривой

точки

Формула для Хп

Координаты по Х

Формула для Уп

Координаты по У

№ точки

1

Х₁=Rφ

У₁=2R ² φ/2

2

Х₂=R2φ

У₂=2R ² φ

3

Х₃=R3φ

У₃=2R ² 3φ/2

4

Х₄=R4φ

У₄=2R ² 4φ/2

5

Х₅=R5φ

У₅=2R ² 5φ/2

6

Х₆=R6φ

У₆=2R ² 6φ/2

7

Х₇=R7φ

У₇=2R ² 7φ/2

8

Х₈=R8φ

У₈=2R ² 8φ/2

9

Х₉=R9φ

У₉=2R ² 9φ/2

10

Х₁₀=R10φ

У₁₀=2R ² 10φ/2

11

Х₁₁=R11φ

У₁₁=2R ² 11φ/2

12

Х₁₂=R12φ

У₁₂=2R ² 12φ/2

13

Х₁₃=R13φ

У₁₃=2R ² 13φ/2

14

Х₁₄=R14φ

У₁₄=2R ² 14φ/2

Вывод:___________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

Выполнил:____________________________________________________________________________