Как найти тангенс внешнего угла в прямо

Как найти тангенс внешнего угла

Если продолжить любую сторону многоугольника, в точке примыкания к ней смежной стороны получится развернутый угол, разделенный примыкающей стороной на два – внешний и внутренний. Внешним называется тот из них, который лежит вне периметра геометрической фигуры. Его величина связана с размерами внутреннего определенным соотношением, а величина внутреннего, в свою очередь, связана с другими параметрами многоугольника. Такая взаимосвязь позволяет, в частности, рассчитать по параметрам многоугольника тангенс внешнего угла.

Инструкция

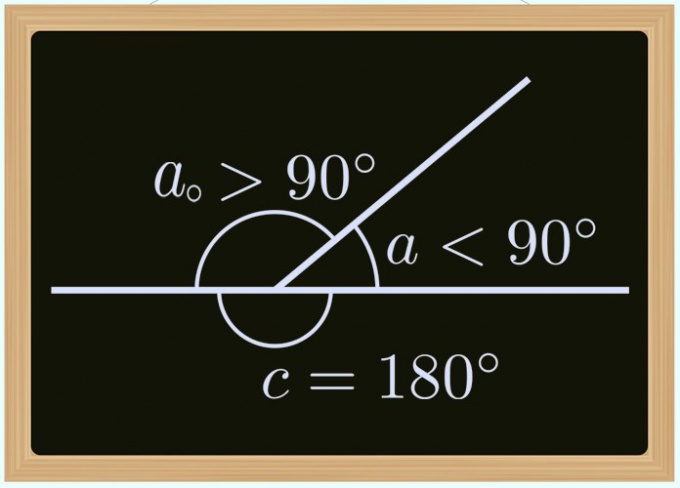
Если вам известна величина соответствующего внешнему углу (α₀) внутреннего (α), исходите из того, что вместе они всегда образуют развернутый угол. Величина развернутого равна 180° в градусах, что соответствует числу Пи в радианах. Из этого вытекает, что тангенс внешнего угла равен тангенсу разницы между 180° и величиной внутреннего угла: tg(α₀) = tg(180°-α₀). В радианах эту формулу надо записать так: tg(α₀) = tg(π-α₀).

Если в условиях задачи дана величина тангенса внутреннего угла (α), тангенс внешнего (α₀) приравнивайте к ней, но с измененным знаком: tg(α₀) = -tg(α).

Зная величину какой-нибудь другой тригонометрической функции, выражающей внутренний угол (α), проще всего для расчета тангенса внешнего (α₀) использовать обратную функцию, чтобы вычислить градусную меру внутреннего. Например, если известно значение косинуса, величину угла можно найти с использованием арккосинуса: α = arccos(cos(α)). Подставьте полученную величину в формулу из предыдущего шага: tg(α₀) = -tg(arccos(cos(α))).

В треугольнике величина любого внешнего угла (α₀) равна сумме величин двух внутренних углов (β и γ), лежащих в других вершинах фигуры. Если эти две величины известны, вычислите тангенс их суммы: tg(α₀) = tg(β+γ).

В прямоугольном треугольнике величину тангенса внешнего угла (α₀) можно рассчитать по длинам двух катетов. Разделите длину того из них, который лежит напротив вершины внешнего угла (a), на длину прилегающего к этой вершине (b). Результат надо брать с противоположным знаком: tg(α₀) = -a/b.

Если требуется вычислить тангенс внешнего угла (α₀) правильного многоугольника, вполне достаточно будет знания числа вершин (n) этой фигуры. По определению любой правильный многоугольник можно вписать в окружность, а любой внешний угол будет равен центральному углу круга, соответствующему длине стороны. Поскольку все стороны одинаковы, центральный угол можно рассчитать делением полного оборота – 360° – на количество сторон 360°/n. Значит, для получения искомого значения найдите тангенс от соотношения 360° и числа вершин: tg(α₀) = tg(360°/n).

Источники:

• рассчитать тангенс

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

Внешний угол треугольника. Синус и косинус внешнего угла

В некоторых
задачах ЕГЭ требуется найти синус,
косинус или тангенс внешнего
угла
треугольника. А что такое внешний
угол треугольника?

Давайте
вспомним сначала, что такое смежные
углы.
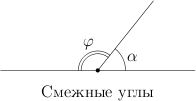
Вот они, на рисунке. У смежных углов
одна сторона общая, а две другие лежат
на одной прямой. Сумма смежных углов
равна

.

Возьмем
треугольник и продолжим одну из его
сторон. Внешний угол

при
вершине

 —
это угол, смежный с углом

. Если
угол 

острый, то смежный с ним угол —
тупой, и наоборот.

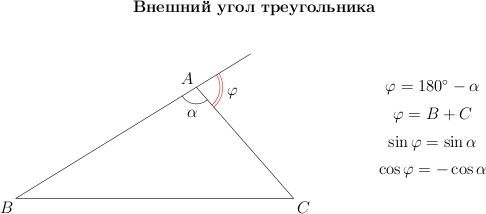
Обратите
внимание, что:

Запомните
эти важные соотношения. Сейчас мы берем
их без доказательств. В разделе
«Тригонометрия», в теме «Тригонометрический
круг»,
мы вернемся к ним.

Легко
доказать, что внешний
угол треугольника равен сумме двух
внутренних углов, не смежных с ним.

1.
В треугольнике

угол 

равен

,

.
Найдите тангенс внешнего угла при
вершине

.

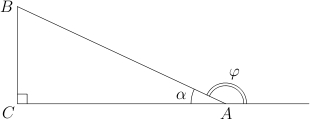
Пусть

—
внешний угол при вершине

.
Имеем:

Зная

,
найдем

 по формуле

Получим:

2.
В треугольнике

угол 

равен

,

.
Найдите синус внешнего угла при вершине

.

Задача
решается за четыре секунды. Поскольку
сумма углов 

и 

равна 
,

.
Тогда и синус внешнего угла при
вершине 

также равен

.

Высота в прямоугольном треугольнике

Вспомним,
что высота
треугольника —
это перпендикуляр, опущенный из его
вершины на противоположную сторону.

В
прямоугольном треугольнике катеты
являются высотами друг к другу. Главный
интерес представляет высота, проведённая
к гипотенузе.

Один
из типов экзаменационных задач В6 в
банке заданий ФИПИ — такие, где
в прямоугольном треугольнике высота
проведена из вершины прямого угла.
Посмотрим, что получается:

Высота
проведена к гипотенузе

.
Она делит треугольник

на два
прямоугольных треугольника —

и 
.
Смотрим внимательно на рисунок
и находим на нем равные
углы.
Это и есть ключ к задачам по геометрии,
в которых высота опущена на гипотенузу.

Мы помним,
что сумма двух острых углов прямоугольного
треугольника равна

.
Значит,

,
то есть угол

равен
углу

.
Аналогично, угол

.

Иными
словами, каждый из трех углов
треугольника

равен
одному из углов треугольника

и треугольника

.
Треугольники

,

и 

называются подобными.
Давайте нарисуем их рядом друг
с другом.

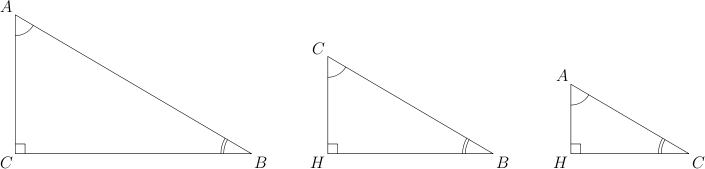
Они
отличаются только размерами. Стороны
подобных треугольников пропорциональны.
Что это значит?

Возьмем
треугольники

и 
.
Стороны треугольника

длиннее,
чем стороны треугольника

,
в  некоторое число

 раз:

При
решении задач нам пригодится равенство
углов треугольников

,

и 
,
а также пропорциональность их сторон.
Обратите также внимание, что площадь
треугольника

можно
записать двумя разными способами: как
половину произведения катетов и как
половину произведения гипотенузы
на проведенную к ней высоту.

1.
В треугольнике

угол 

равен

,

 —
высота,

,

.
Найдите

.

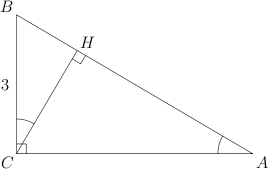
Рассмотрим
треугольник

.
В нем известны косинус угла 

и противолежащий катет

.
Зная синус угла 
,
мы могли бы найти гипотенузу

.
Так давайте найдем

:

(поскольку
значение синуса острого угла положительно).
Тогда:

Рассмотрим
прямоугольный треугольник

,

.
Имеем:

Отсюда,
поскольку

:

и
тогда

Ответ:

.

2.
В треугольнике

угол 

равен

,

,

.
Найдите высоту

.

Сделайте
чертеж и рассмотрите прямоугольный
треугольник

.

Ответ:

.

3.
В треугольнике

угол 

равен

,

,

.
К гипотенузе проведена высота

.
Найдите

.

Это
чуть более сложная задача. Ведь вам
неизвестны катеты

 и 
.

Зато
можно записать теорему Пифагора:

Нам
известно также, что

Решая
эту систему из двух уравнений, найдем:

Запишем
площадь треугольника

двумя
способами:

и найдем

.

Найти
высоту, проведенную из вершины прямого
угла, можно было и другим способом.
Мы выбрали самый короткий путь —
составили и решили систему уравнений.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #

  30.03.201540.15 Mб22спицын мартыненко.djvu

• #
• #
• #
• #
• #
• #
• #
• #

Внешний угол треугольника

Углы треугольника бывают внутренние и внешние. Что такое внешний угол треугольника? Как его найти?

Внешний угол треугольника при данной вершине — это угол, смежный с внутренним углом треугольника при этой вершине.

Как построить внешний угол треугольника? Нужно продлить сторону треугольника.

∠3 — внешний угол при вершине А,

∠2 — внешний угол при вершине С,

∠1 — внешний угол при вершине В.

Сколько внешних углов у треугольника?

При каждой вершине треугольника есть два внешних угла. Чтобы построить внешний угол при вершине треугольника, можно продлить любую из двух сторон, на которых лежит данная вершина. Таким образом получаем 6 внешних углов.

Внешние углы каждой пары при данной вершины равны между собой (как вертикальные):

Поэтому, когда говорят о внешнем угле треугольника, не важно, какую из сторон треугольника продлили.

Чему равен внешний угол?

Теорема (о внешнем угле треугольника)

Внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним.

Дано : ∆АВС, ∠1 — внешний угол при вершине С.

∠1 и ∠С (∠АСВ) — смежные, поэтому их сумма равна 180º, значит, ∠1=180º-∠С=180º-(180º-(∠А+∠В))=180º-180º+(∠А+∠В)=∠А+∠В.

Внешний угол треугольника. Синус и косинус внешнего угла

В некоторых задачах ЕГЭ требуется найти синус, косинус или тангенс внешнего угла треугольника. А что такое внешний угол треугольника?

Давайте вспомним сначала, что такое смежные углы. Вот они, на рисунке. У смежных углов одна сторона общая, а две другие лежат на одной прямой. Сумма смежных углов равна .

Возьмем треугольник и продолжим одну из его сторон. Внешний угол при вершине — это угол, смежный с углом . Если угол острый, то смежный с ним угол — тупой, и наоборот.

Обратите внимание, что:

Запомните эти важные соотношения. Сейчас мы берем их без доказательств. В разделе «Тригонометрия», в теме «Тригонометрический круг», мы вернемся к ним.

Легко доказать, что внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним.

Ты нашел то, что искал? Поделись с друзьями!

1. В треугольнике угол равен , . Найдите тангенс внешнего угла при вершине .

Пусть — внешний угол при вершине .

Зная , найдем по формуле

2. В треугольнике угол равен , . Найдите синус внешнего угла при вершине .

Задача решается за четыре секунды. Поскольку сумма углов и равна , . Тогда и синус внешнего угла при вершине также равен .

Внешний угол треугольника

Внешний угол треугольника — это угол, смежный с любым из внутренних углов треугольника.

При каждой вершине треугольника может быть построено по два равных внешних угла. Например, если продолжить все стороны треугольника ABC, то при каждой его вершине получится по два внешних угла, которые равны между собой, как вертикальные углы:

Из данного примера можно сделать вывод, что внешние углы, построенные при одной вершине, будут равны.

Внешний угол треугольника равен сумме двух внутренних углов треугольника, не смежных с ним.

Так как внешний угол (∠1) дополняет внутренний угол (∠4) до развёрнутого угла, то их сумма равна 180°:

Сумма внутренних углов углов любого треугольника тоже равна 180°, значит:

Из этого следует, что

Сократив обе части полученного равенства на одно и тоже число (∠4), получим:

Из этого можно сделать вывод, что внешний угол треугольника всегда больше любого внутреннего угла, не смежного с ним.

Сумма внешних углов

Сумма трёх внешних углов треугольника, построенных при разных вершинах, равна 360°

Рассмотрим треугольник ABC:

Каждая пара углов (внутренний и смежный с ним внешний) в сумме равны 180°. Все шесть углов (3 внутренних и 3 внешних) вместе равны 540°:

(∠1 + ∠4) + (∠2 + ∠5) + (∠3 + ∠6) = 180° + 180° + 180° = 540°.

Значит чтобы найти сумму внешних углов, надо из общей суммы вычесть сумму внутренних углов:

∠1 + ∠2 + ∠3 = 540° – (∠4 + ∠5 + ∠6) = 540° – 180° = 360°.

[spoiler title=”источники:”]

http://ege-study.ru/ru/ege/materialy/matematika/vneshnij-ugol-treugolnika/

http://izamorfix.ru/matematika/planimetriya/vneshnie_ugly_treug.html

[/spoiler]

Внешний угол треугольника. Продолжаем рассматривать задачи на решение прямоугольного треугольника. Такие типы заданий имеются в прототипах открытого банка заданий по математике. Некоторые примеры мы уже рассмотрели в статьях «Прямоугольный треугольник. Часть 1» и «Прямоугольный треугольник. Часть 2». В этой статье разберём задачи, в которых необходимо определить значения тригонометрических функций внешнего угла треугольника (или внутреннего, когда дано значение внешнего).

Внешний угол треугольника при данной вершине — это угол, смежный с внутренним углом треугольника при этой вершине

Угол DAB является внешним.

Стоит повторить определения синуса, косинуса, тангенса и котангенса в прямоугольном треугольнике, также основные тригонометрические формулы для решения прямоугольного треугольника.  Вспомним основные из них:

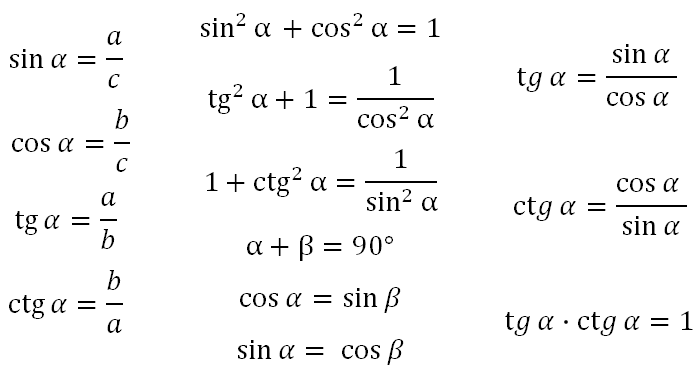
А также формулы приведения (не все). Отмечу одну типичную ошибку, которую допускают (из-за невнимательности). При решении подобных задач часто используется формула основного тригонометрического тождества:

Из  неё мы получаем:

*Запись с ошибкой (её часто допускают — теряют квадрат):

Будьте внимательны!

Рассмотрим задачи:

В треугольнике ABC угол C равен 90⁰, sin A = 0,27. Найдите синус внешнего угла при вершине А.

Углы ВАС и BAD смежные, значит:

По свойству синуса:

А лучше раз и навсегда запомнить сам факт того, что синусы смежных углов равны, и вам даже не будет необходимости что-то записывать при решении такой задачи, ответ вы озвучите сразу.

Ответ: 0,27

Решите самостоятельно:

Посмотреть решение 

В треугольнике ABC угол C равен 90⁰, . Найдите тангенс внешнего угла при вершине A.

Углы ВАС и BAD смежные, значит:

Значит по свойству тангенса (используем формулу приведения):

То есть необходимо найти тангенс угла ВАС.  Известно, что:

Синус угла ВАС нам известен. Найдём его косинус.

Из основного тригонометрического тождества:

Вычисляем тангенс:

Таким образом  tg BAD = – tg BAC = – 0,3

Ответ: – 0,3

Решите самостоятельно:

Посмотреть решение 

Посмотреть решение 

В треугольнике ABC угол C равен 90⁰, АВ = 6, .  Найдите косинус внешнего угла при вершине A.

Углы ВАС и BAD смежные, значит:

По свойству косинуса:

Найдём cos BAC   Для этого необходимо найти сторону АС. По теореме Пифагора:

Значит АС = 3.

По определению косинуса:

Таким образом, cos DAB = – cos BAC = – 0,5.   

Ответ: – 0,5

Решите самостоятельно:

Посмотреть решение 

Посмотреть решение 

В треугольнике ABC угол C равен 90⁰, косинус внешнего угла при вершине A равен  . Найдите sin A.

Углы ВАС и BAD смежные, значит:

В данной задаче можем найти косинус угла ВАС, а затем используя основное тригонометрическое тождество синус этого угла.

По свойству косинуса (используем формулу приведения):

Значит

Найдём sin BAC.  Из основного тригонометрического тождества получим:

Ответ: 0,9

В треугольнике ABC угол C равен 90⁰, тангенс внешнего угла при вершине A равен  –2/9.  Найдите tg = B.

Из свойств прямоугольного треугольника мы знаем, что tg ABC = ctg BAC.

Найдём ctg BAC. Известно, что tg BAC ∙ ctg BAC = 1, значит

Тангенс угла ВАС найти не сложно. Углы BAC и BAD смежные. Это  значит, что

По свойству тангенса:   

Значит

Таким образом:

Ответ: 4,5

В треугольнике ABC угол C равен 90⁰, косинус внешнего угла при вершине A  равен  – 0,7; АВ = 20. Найдите AC.

Найти АС мы сможем, если нам будет известен косинус угла ВАС. Так как по определению косинуса в прямоугольном треугольнике:

Найдём косинус. По его свойству:

*Использовали формулу приведения.

Значит

Таким образом:

Ответ: 14

Решите самостоятельно:

Посмотреть решение 

Посмотреть решение 

Посмотреть решение 

Посмотреть решение 

В треугольнике ABC АС = ВС, АВ = 12, тангенс внешнего угла при вершине A равен  . Найдите AC.

Построим  высоту CH.

Найдём  тангенс внутреннего угла.  По свойству тангенса:

Сторона АС является гипотенузой в прямоугольном треугольнике АСН. В этом треугольнике зная тангенс острого угла и один катет мы без труда можем найти второй катет.

Высота проведённая к основанию равнобедренного треугольника является медианой, то есть АН = ВН, a АВ = 2АН:

Рассмотрим прямоугольный треугольник ACH: по определению тангенса в прямоугольном треугольнике:

Следовательно:

В прямоугольном треугольнике  нам известны катеты АН и СН.

По теореме Пифагора мы можем найти гипотенузу АС:

Таким образом, АС = 9.

Ответ: 9

Решите самостоятельно:

Посмотреть решение

В будущем будем рассматривать другие задачи, не пропустите! Успехов Вам!

С уважением, Александр Крутицких.

P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.

Сайты, меню, вход, новости