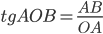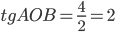Всего: 40 1–20 | 21–40
Добавить в вариант
Тип 18 № 40
i
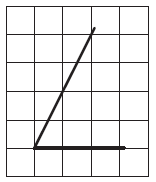
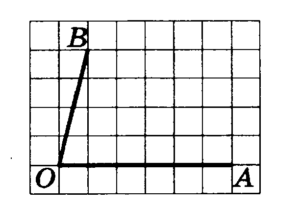
Найдите тангенс угла AOB, изображенного на рисунке.
Найдите тангенс угла AOB, изображённого на рисунке.
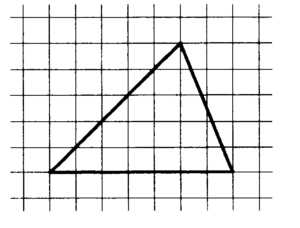
Найдите тангенс угла AOB.
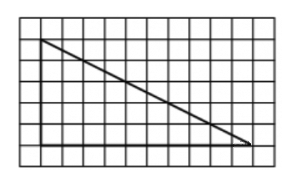
Найдите тангенс угла AOB, в треугольнике, изображённом на рисунке.
Найдите тангенс угла AOB, изображённого на рисунке.
Найдите тангенс угла AOB.
Найдите тангенс угла AOB, изображённого на рисунке.
Найдите тангенс угла AOB.
Найдите тангенс угла AOB, изображённого на рисунке.
Найдите тангенс угла AOB. Размер клетки 1 × 1.
Найдите тангенс угла AOB.
Найдите тангенс угла AOB, изображённого на рисунке.
Найдите тангенс угла AOB, изображённого на рисунке.
Найдите тангенс угла AOB
Найдите тангенс угла AOB, изображённого на рисунке.
Найдите тангенс угла AOB, изображённого на рисунке.
Найдите тангенс угла AOB, изображённого на рисунке.
Найдите тангенс угла AOB
Найдите тангенс угла AOB, изображённого на рисунке.
Найдите тангенс AOB
Всего: 40 1–20 | 21–40
2. Определение тангенса угла
Что нужно вспомнить:
• Тангенс угла в прямоугольном
треугольнике — отношение противолежащего катета к прилежащему.

прямоугольный треугольник.
Задача 1
Найдите тангенс угла А треугольника ABC,
изображённого на рисунке 1.
|
Решение:
Ответ: 0,4. |
Рис.1 |
Задача 2
Найдите тангенс угла B треугольника ABC,
изображённого на рисунке 2.
|
Решение:
Ответ: 3,5. |
Рис. 2 |
Задача 3
Найдите тангенс угла AOB, изображённого
на рисунке 3.
|
Решение: 1. 2. Ответ: 2. |
Рис. 3 |
Задача 4
На квадратной сетке изображён угол А
(рис.4). Найдите .
|
Решение: 1. 2. Ответ: 3. |
Рис. 4 |
Задача 5
Найдите тангенс угла, изображённого
на рисунке 5.
|
Решение: 1. 2. Значит,
Ответ: -3. |
Рис. 5 Рис. 5.1 |
Задача 6
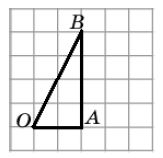
Найдите тангенс угла АОВ (рис. 6).
|
Решение: Найдём каждую из сторон треугольника АОВ, чтобы показать, что он прямоугольный: Таким образом Ответ: 0,5. |
Рис. 6 |
8. Определение градусной меры
вписанного угла
Что нужно вспомнить:
• Вписанный угол – угол, вершина которого
лежит на окружности, а стороны её пересекают.
• Центральный угол – угол, вершина которого
совпадает с центром окружности, а стороны её пересекают.
Вписанный угол равен половине дуги, на которую опирается.
Задача 1:
Найдите угол ABC (рис.
20). Ответ дайте в градусах.
|
Решение: Проведём вспомогательное Угол ABC — Ответ: 45. |
Рис. 20 |
Задача 2:
Найдите угол ABC (рис.
21). Ответ дайте в градусах.
|
Решение: Проведём вспомогательное Угол BAC — Треугольник ABC Ответ: 67,5. |
Рис. 21 |
Задача 3:
Найдите угол ABC (рис.22).
Ответ дайте в градусах.
|
Решение: Угол ABC – опирается на большую Проведём вспомогательное построение. Заметим, что дуга АC составляет Угол AВC — вписанный, поэтому он равен Ответ: 135. |
Рис. 22 |
Задача 4:
Найдите угол ABC (рис.
23). Ответ дайте в градусах.
|
Решение: Проведём вспомогательное Угол АВС опирается на ту же дугу, Ответ: 22,5. |
Рис. 23 |
9. Задачи для самостоятельно решения
I.
Определение
тангенса угла
1.

рисунке.
2.

на рисунке.
3.

4.

5.

6.
Найдите
тангенс угла AOB, изображённого на рисунке.
 |
7.

8.

9.

10.
Найдите
тангенс угла, изображённого на рисунке.

II.
Определение
площади фигуры (ромба, трапеции, параллелограмма, треугольника)
1.
На
клетчатой бумаге с размером клетки 1х1 изображён параллелограмм. Найдите его
площадь.
 |
2.

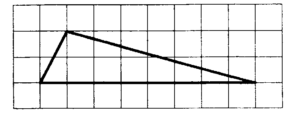
треугольник. Найдите его площадь.
3.
На
клетчатой бумаге с размером клетки 1х1 изображён прямоугольный треугольник.
 |
4.

ромб. Найдите его площадь.
5.

ромб. Найдите длину его большей диагонали.
6.

трапеция. Найдите её площадь.
7.

трапеция. Найдите её площадь.
III.
Определение
расстояния от точки до прямой (отрезка)
1.
На клетчатой
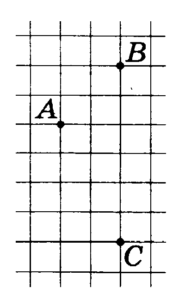
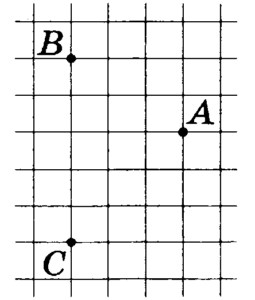
бумаге с размером клетки 1см x 1см отмечены точки А, В и С.
Найдите расстояние от точки А до прямой ВС. Ответ выразите
в сантиметрах.
 |
2.

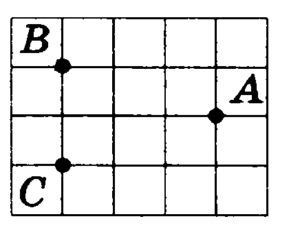
отмечены точки А, В и С. Найдите расстояние
от точки А до прямой ВС. Ответ выразите в
сантиметрах.
3.
На клетчатой
бумаге с размером клетки 1см x 1см отмечены точки А, В и С.
Найдите расстояние от точки А до середины отрезка ВС.
Ответ выразите в сантиметрах.
 |
4.

см отмечены точки А, В и С. Найдите
расстояние от точки А до середины отрезка ВС.
Ответ выразите в сантиметрах.
5.
На клетчатой
бумаге с размером клетки 1 см × 1 см отмечены точки А, В и С.
Найдите расстояние от точки А до прямой BC. Ответ выразите
в сантиметрах.
 |
IV.
Определение
длины средней линии треугольника и трапеции
1.

изображён треугольник ABC. Найдите длину его средней линии,
параллельной стороне AC.
2.

изображён треугольник ABC. Найдите длину его средней линии,
параллельной стороне AC.
3.

изображён треугольник ABC. Найдите длину его средней линии,
параллельной стороне AC.
4.

трапеция. Найдите длину её средней линии.
5.

трапеция. Найдите длину её средней линии.
6.

трапеция. Найдите длину её средней линии.
V.
Определение
длины большего катета, большей диагонали
1.

прямоугольный треугольник. Найдите длину его большего катета.
2.

прямоугольный треугольник. Найдите длину его большего катета.
3.

прямоугольный треугольник. Найдите длину его большего катета.
4.
На
клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите длину его
большей диагонали.
 |
5.

ромб. Найдите длину его большей диагонали.
VI.
Определение
площади сложных или составных фигур
1.

фигура. Найдите её площадь.
2.

фигура. Найдите её площадь.
3.
На
клетчатой бумаге с размером клетки 1х1 изображена фигура. Найдите её площадь.

4.
На клетчатой
бумаге с размером клетки 1х1 изображена фигура. Найдите её площадь.

5.

изображённой на рисунке.
6.

изображённой на рисунке.
VII.
Определение
площади сложных или составных фигур
1.
Найдите
угол ABC. Ответ дайте в градусах.
 |
2.

3.

4.
Найдите
угол ABC. Ответ дайте в градусах.
 |
5.
Найдите
угол ABC. Ответ дайте в градусах.
 |
6.
Найдите
угол ABC. Ответ дайте в градусах.
 |
II. Определение площади фигуры (ромба, трапеции, параллелограмма,
треугольника
III. Определение расстояния от
точки до прямой (отрезка)
IV. Определение расстояния от
точки до прямой (отрезка)
V. Определение длины большего катета,
большей диагонали
VII. Определение площади сложных
или составных фигур
№8. Найдите тангенс угла AOB, изображенного на рисунке.
Решение:
Опустим перпендикуляр AH на сторону OB.
Рассмотрим прямоугольный △ A O H :
Тангенс угла – отношение противолежащего катета к прилежащему.
tg ∠ A O H = A H O H = 4 2 = 2
Ответ: 2
№9. Найдите тангенс угла A треугольника ABCб изображённого на рисунке.
Решение:
Тангенс угла – это отношение противолежащего катета к прилежащему.
tg ∠ B A C = B C A C = 2 5 = 0,4
Ответ: 0,4
№10. На рисунке изображена трапеция ABCD. Используя рисунок, найдите sin ∠ B A H .
Решение:
Рассмотрим прямоугольный △ A B H :
Синус угла – отношение противолежащего катета к гипотенузе.
sin ∠ A = B H A B
Найдем AB по теореме Пифагора:
A B 2 = A H 2 + B H 2
A B 2 = 3 2 + 4 2
A B 2 = 9 + 16 = 25
A B = ± 25 = [ − 5 не подходит 5 подходит
A B = 5
sin ∠ A = B H A B = 4 5 = 0,8
Ответ: 0,8
№11. На рисунке изображен ромб ABCD. Используя рисунок, найдите tg ∠ O B C .
Решение:
Тангенс угла – это отношение противолежащего катета к прилежащему.
tg ∠ O B C = O C B O = 3 4 = 0,75
Ответ: 0,75
№12. На рисунке изображена трапеция ABCD. Используя рисунок, найдите cos ∠ H B A .
Решение:
Рассмотрим прямоугольный △ A B H :
Косинус угла – отношение прилежащего катета к гипотенузе.
cos ∠ A B H = B H A B
Найдем A B по теореме Пифагора:
A B 2 = A H 2 + B H 2
A B 2 = 6 2 + 8 2
A B 2 = 36 + 64 = 100
A B = ± 100 = [ − 10 не подходит 10 подходит
A B = 10
cos ∠ A B H = B H A B = 8 10 = 0,8
Ответ: 0,8
№13. Найдите тангенс угла, изображенного на рисунке.
Решение:
tg β = tg ( 180 ° − α ) = − tg α
Рассмотрим прямоугольный △ B C H .
Тангенс угла – отношение противолежащего катета к прилежащему.
tg α = C H B H = 3 1
tg β = − tg α = − 3
Ответ: -3
№14. Найдите тангенс угла AOB.
Решение:
Опустим высоту BH на сторону OA.
Рассмотрим прямоугольный △ O B H :
tg ∠ O = B H O H
Найдем B H и O H по теореме Пифагора:
B H 2 = 2 2 + 8 2 = = 4 + 64 = 68
B H = ± 68 = ± 4 ⋅ 17 = ± 4 ⋅ 17 = ± 2 17 = [ − 2 17 не подходит 2 17 подходит
B H = 2 17
O H 2 = 1 2 + 4 2 = 1 + 16 = 17
O H = ± 17 = [ − 17 не подходит 17 подходит
O H = 17
tg ∠ O = B H O H = 2 17 17 = 2
Ответ: 2
|
Объясните, пожалуйста, как можно проще, без дополнительных построений. Мы учим детей решать подобные задачи так. Нужно искать треугольники и использовать их свойства. Попробуем решать данную задачу именно таким способом. Ведь на ОГЭ нельзя пользоваться таблицами Брадиса, транспортиром, калькулятором. Да и в справочном материале имеются не все формулы, например, формулы разности тангенсов. Если рассмотреть треугольник ОАВ, то можно заметить, что это равнобедренный треугольник с вершиной в точке В. Действительно, рассчитаем длины сторон этого треугольника воспользовавшись теоремой Пифагора. Итак, ОА^2 = 2^2+8^2 = 4+64 = 68 (2 и 8 стороны прямоугольного треугольника по клеткам). Аналогично, ОВ^2 = 2^2+9^2 = 4+81 = 85, AB^2 = 6^2+7^2 = 36+49 = 85. То есть стороны АВ и ОВ равны между собой и равны соответственно корень из 85. Тогда медина ВМ проведенная к стороне ОА является одновременно и высотой. По рисунку видно, что ВМ = 2*ОМ, тогда тангенс угла АОВ равен 2 (отношению катетов треугольника ОВМ ВМ и ОМ). Ответ: 2. автор вопроса выбрал этот ответ лучшим Rafail 4 года назад Дополнительное построение потребуется, но только мысленное. Представьте, что из вершины заданного угла(О) проведён горизонтальный луч ОС (вправо). Тогда получается так: Угол АОВ равен разности углов СОВ и СОА. Вспоминаем формулу тангенса разности двух углов: tg(b-a)=[(tg(b)-tg(a)]/[1+tg(a)*tg(b)/ В данном случае, угол а – это угол СОА, а угол b – это угол СОВ. Непосредственно по рисунку находим, что tg(a)=2/8=0,25; tg(b)=9/2=4,5. Ну и осталось произвести арифметические вычисления: tg(BOA)=(4,5-0,25)/(1+4,5*0,25)=4,25/2,125=2. Но с дополнительными построениями проще. Из точки В проводим перпендикуляр к лучу ОА. Точку пересечения обозначим С. И непосредственно по чертежу видим, что отрезок ВС в 2 раза длиннее отрезка ОС. А тангенс угла АОВ как раз и есть ВС/ОС=2. Алеся Ясногорцева 4 года назад Как известно, величины тригонометрических функций – синуса, косинуса, тангенса, котангенса – зависят только от величины самого угла, несмотря на то, что представляют собой соотношения сторон прямоугольного треугольника между собой. Тангенс – это отношение противоположного углу катета к прилегающему катету. Вычислить его в данном случае можно, опустив перпендикуляр из любой точки луча ОВ на луч ОА, измерив получившиеся катеты и разделив длину противоположного катета на длину катета прилегающего. Но, если надо найти без дополнительных построений – можно просто измерить угол транспортиром и посмотреть значение тангенса для данного угла в таблице Брадиса. Знаете ответ? |
Основнóй госудáрственный экзáмен ОГЭ Математика задание №19 Демонстрационный вариант 2018 Найдите тангенс острого угла, изображённого на рисунке.
Решение:
тангенс = 2/1= 2
Ответ: 2
Демонстрационный вариант Основнóй госудáрственный экзáмен ОГЭ 2017 г. – задание №12 Модуль «Геометрия»
Найдите тангенс угла AOB треугольника, изображённого на рисунке.
Решение:
Ответ: 2
Демонстрационный вариант Основнóй госудáрственный экзáмен ОГЭ 2016 г. – задание №12 Модуль «Геометрия»
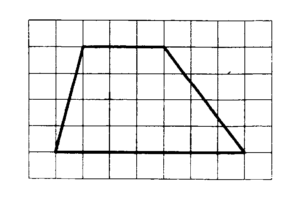
На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите её площадь.
Решение:
10
Ответ: 10
Демонстрационный вариант Основнóй госудáрственный экзáмен ОГЭ 2015 г. – задание №12
На клетчатой бумаге с размером клетки 1х1 изображён прямоугольный треугольник. Найдите длину его большего катета.
Решение:
посчитаем клеточки.
Ответ: 10
Источник: Основнóй госудáрственный экзáмен ОГЭ-2017.Математика.30 вар.ред.Ященко И.В.
1) На клетчатой бумаге с размером клетки 1 изображен угол. Найдите тангенс этого угла.
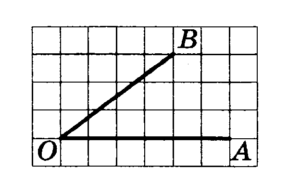
Ответ: 0,75.
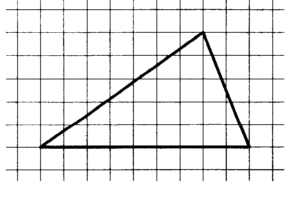
2) На клетчатой бумаге с размером клетки 1 изображен треугольник. Найдите его площадь.
Решение: S треугольника= 1/2a*h, где а – любая из сторон треугольника, h – высота , опущенная на эту сторону из противолежащей вершины треугольника.
Ответ: 15.
3) На клетчатой бумаге с размером клетки 1 изображен угол. Найдите тангенс этого угла.
Решение: Тангенс- отношение противоположного катета к прилежащему. Достраиваем прямой угол и считаем 4:1=4.
Ответ: 4.
4) На клетчатой бумаге с размером клетки 1 изображена трапеция. Найдите ее площадь.
Решение: Площадь трапеции находится по формуле: S = ½ abh
S= 4 (3+7):2=20.
Ответ: 20.
5) На клетчатой бумаге с размером клетки 1 отмечены три точки: А, В и С. Найдите расстояние от точки А до прямой ВС.
Решение: Проводим перпендикуляр от точки А к прямой ВС.
Ответ: 2.
6) На клетчатой бумаге с размером клетки 1 изображен треугольник. Найдите его площадь.
Решение: S треугольника= 1/2a*h, где а – любая из сторон треугольника, h – высота , опущенная на эту сторону из противолежащей вершины треугольника.
Ответ: 20.
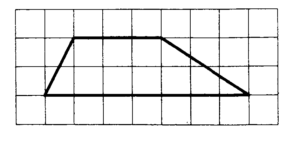
7) На клетчатой бумаге с размером клетки 1 изображена трапеция. Найдите ее площадь.
Решение: Площадь трапеции находится по формуле: S = ½ abh
S= 2 3+7):2=10.
Ответ: 10.
На клетчатой бумаге с размером клетки 1 отмечены три точки: А, В и С. Найдите расстояние от точки А до прямой ВС.
Решение: Проводим перпендикуляр от точки А к прямой ВС.
Ответ: 3
9) На клетчатой бумаге с размером клетки 1 отмечены три точки: А, В и С. Найдите расстояние от точки А середины отрезка ВС.
Решение: Проводим перпендикуляр от точки А к прямой ВС.
Ответ: 3.
10) На клетчатой бумаге с размером клетки 1 изображен треугольник. Найдите его площадь.
Решение: S треугольника= 1/2a*h, где а – любая из сторон треугольника, h – высота , опущенная на эту сторону из противолежащей вершины треугольника.
Ответ: 8.
Обычно в задачах требуется найти тангенс именно острого угла, как, допустим, на этом примере:
Для этого мы строим прямоугольный треугольник, проведя линию (перпендикуляр) BD:
Далее вспоминаем определение тангенса, это отношение противолежащего катета к прилежащему.
То есть tg(BOA) = DB / DO.
Чтобы найти DO и DB достаточно будет посчитать количество клеточек.
DO = 2.
DB = 5.
Значит, tg(BOA) = 5 / 2 = 2,5.
Зная тангенс, мы можем легко найти и котангенс:
ctg(BOA) = 1 / tg(BOA) = 1 / 2,5 = 0,4.
_
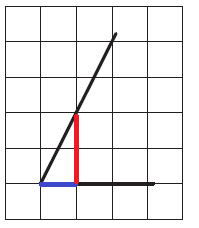
А вот задача на нахождение тангенса угла по клеточкам немного другого плана (ищем тангенс угла AOB):
Если соединить точки A и B, то угол ABO будет прямым.
И тангенс можно вычислить как отношение BA к BO.
Как же нам их найти?
И BO, и BA будут гипотенузами 2 совершенно равных прямоугольных треугольников (для наглядности я их выделил красным).
Длина катетов их равна 2 и 8, а квадрат гипотенузы, как известно, равен сумме квадратов катетов.
Таким образом, у нас получится следующее:
tg(BOA) = BA / BO = √(2² + 8²) / √(2² + 8²) = 1.
И нетрудно догадаться, что треугольник этот равнобедренный с равными углами BOA и BAO по 45 градусов.
Каталог заданий.
Углы
Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
Задание 18 № 40
Найдите тангенс угла AOB, изображенного на рисунке.
Аналоги к заданию № 40: 348424 348519 352779 357581 369740 369808 Все
Источник: Демонстрационная версия ГИА—2013 по математике., Демонстрационная версия ГИА—2014 по математике.
Раздел кодификатора ФИПИ: 5.1 Планиметрия. Нахождение геометрических величин.
Решение
·
·
Сообщить об ошибке · Помощь
2
Задание 18 № 311485
На квадратной сетке изображён угол A. Найдите .
Источник: ГИА-2013. Математика. Тренировочная работа № 4.(1 вар.)
Раздел кодификатора ФИПИ: 5.1 Планиметрия. Нахождение геометрических величин.
Решение
·
·
Сообщить об ошибке · Помощь
3
Задание 18 № 316348
Найдите тангенс угла, изображённого на рисунке.
Аналоги к заданию № 316348: 316374 323618 348622 348734 349410 349506 349517 349574 349593 340982 … Все
Раздел кодификатора ФИПИ: 5.1 Планиметрия. Нахождение геометрических величин.
Решение
·
·
Сообщить об ошибке · Помощь
4
Задание 18 № 316374
Найдите тангенс угла, изображённого на рисунке.
Аналоги к заданию № 316348: 316374 323618 348622 348734 349410 349506 349517 349574 349593 340982 … Все
Раздел кодификатора ФИПИ: 5.1 Планиметрия. Нахождение геометрических величин.
Решение
·
·
Сообщить об ошибке · Помощь
5
Задание 18 № 323618
Найдите тангенс угла AOB, изображённого на рисунке.
Аналоги к заданию № 316348: 316374 323618 348622 348734 349410 349506 349517 349574 349593 340982 … Все
Раздел кодификатора ФИПИ: 5.1 Планиметрия. Нахождение геометрических величин.
Решение
·
·
Сообщить об ошибке · Помощь
Пройти тестирование по этим заданиям
О проекте · Редакция · Правовая информация · О рекламе
© Гущин Д. Д., 2011—2022
Каталог заданий.
Треугольники общего вида
Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
Задание 18 № 341709
На клетчатой бумаге с размером клетки 1×1 изображён треугольник ABC. Найдите длину его высоты, опущенной на сторону AC.
Раздел кодификатора ФИПИ: 5.1 Планиметрия. Нахождение геометрических величин.
Решение
·
·
Сообщить об ошибке · Помощь
2
Задание 18 № 348403
На клетчатой бумаге с размером клетки 1×1 изображён треугольник. Найдите его площадь.
Аналоги к заданию № 348403: 348641 348678 349113 350279 350360 350458 350653 351131 351257 352262 … Все
Раздел кодификатора ФИПИ: 5.1 Планиметрия. Нахождение геометрических величин.
Решение
·
·
Сообщить об ошибке · Помощь
3
Задание 18 № 348480
На клетчатой бумаге с размером клетки 1х1 изображён треугольник ABC. Найдите длину его средней линии, параллельной стороне AC.
Аналоги к заданию № 348480: 348868 349105 349244 349561 351017 351461 351661 352049 352508 352659 … Все
Раздел кодификатора ФИПИ: 5.1 Планиметрия. Нахождение геометрических величин.
Решение
·
·
Сообщить об ошибке · Помощь
4
Задание 18 № 348641
На клетчатой бумаге с размером клетки 1х1 изображён треугольник. Найдите его площадь.
Аналоги к заданию № 348403: 348641 348678 349113 350279 350360 350458 350653 351131 351257 352262 … Все
Раздел кодификатора ФИПИ: 5.1 Планиметрия. Нахождение геометрических величин.
Решение
·
·
Сообщить об ошибке · Помощь
5
Задание 18 № 348678
На клетчатой бумаге с размером клетки 1х1 изображён треугольник. Найдите его площадь.
Аналоги к заданию № 348403: 348641 348678 349113 350279 350360 350458 350653 351131 351257 352262 … Все
Раздел кодификатора ФИПИ: 5.1 Планиметрия. Нахождение геометрических величин.
Решение
·
·
Сообщить об ошибке · Помощь
Пройти тестирование по этим заданиям