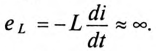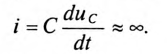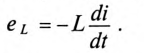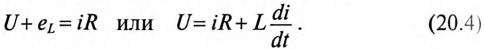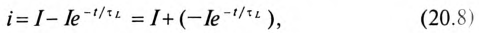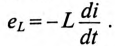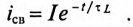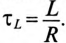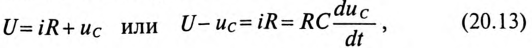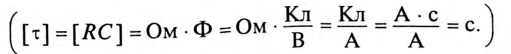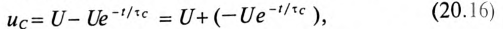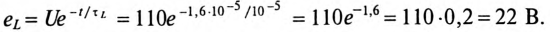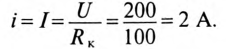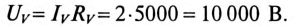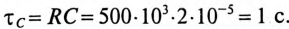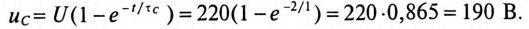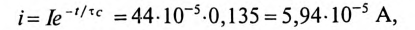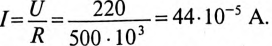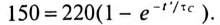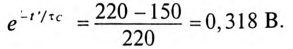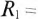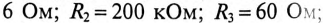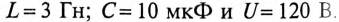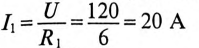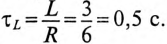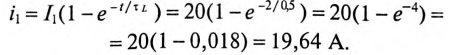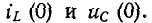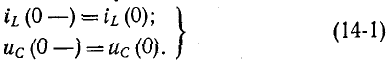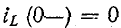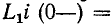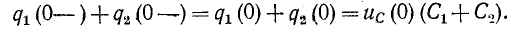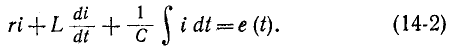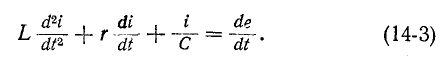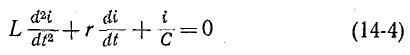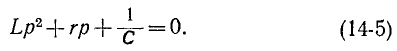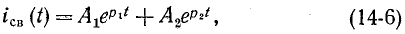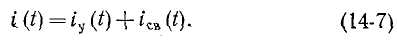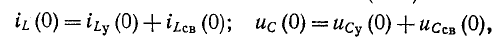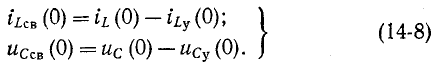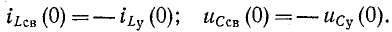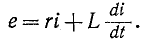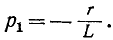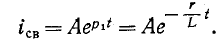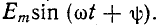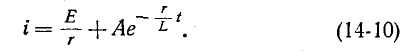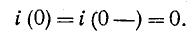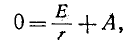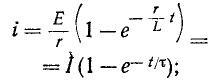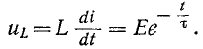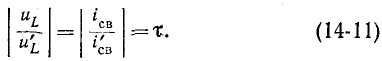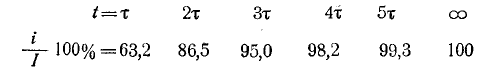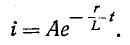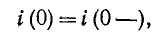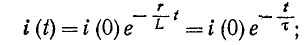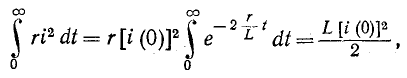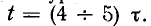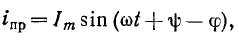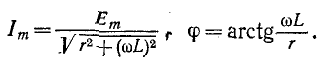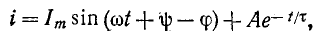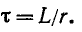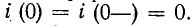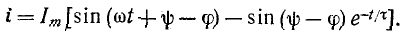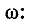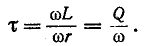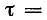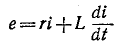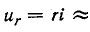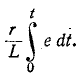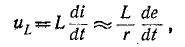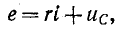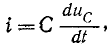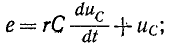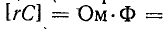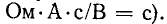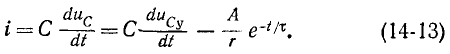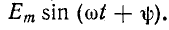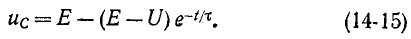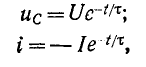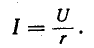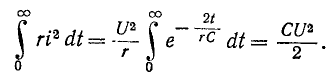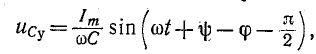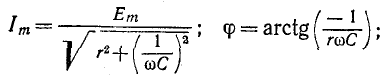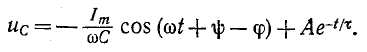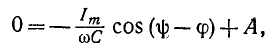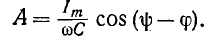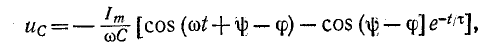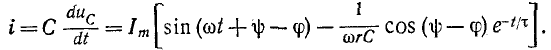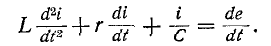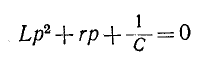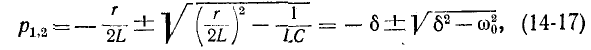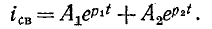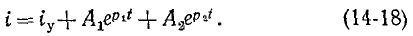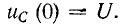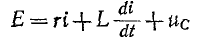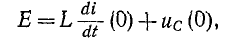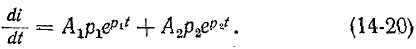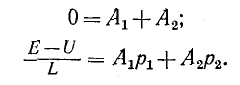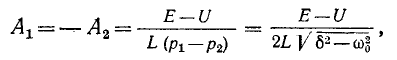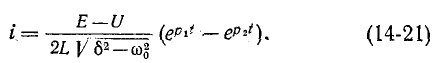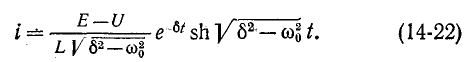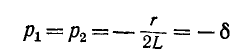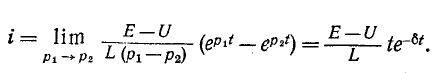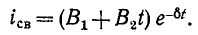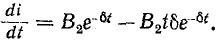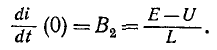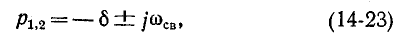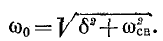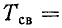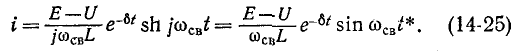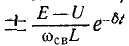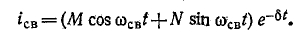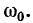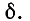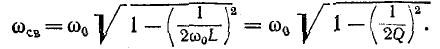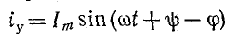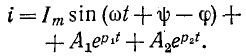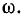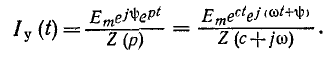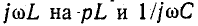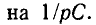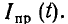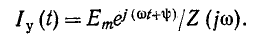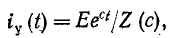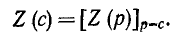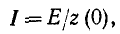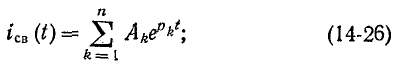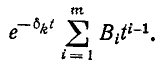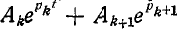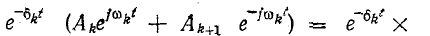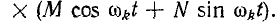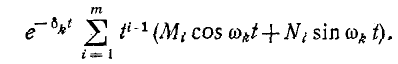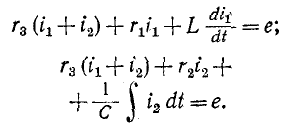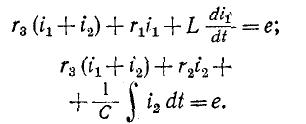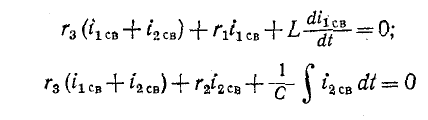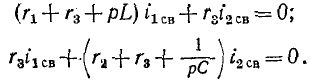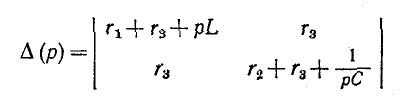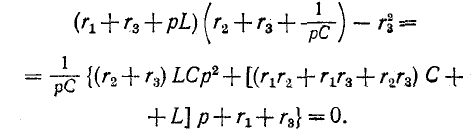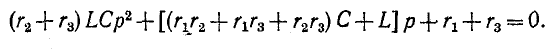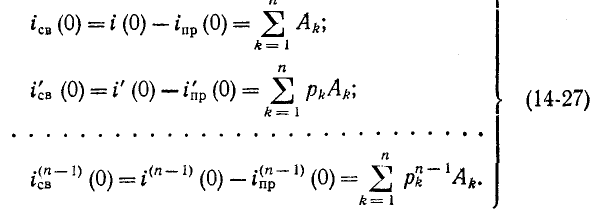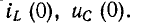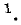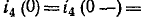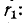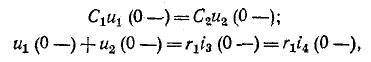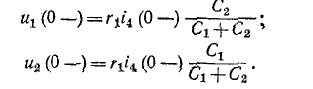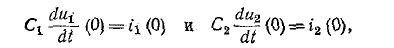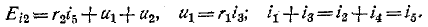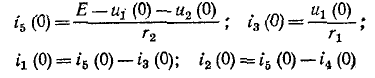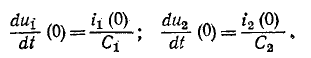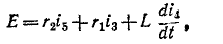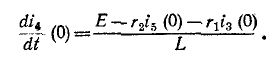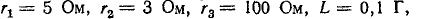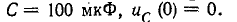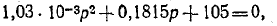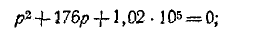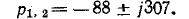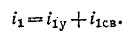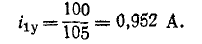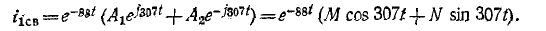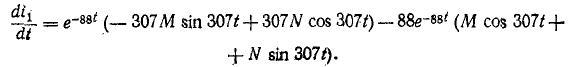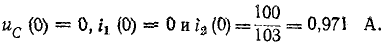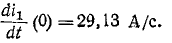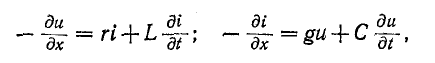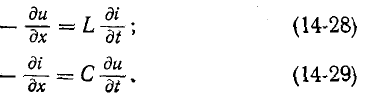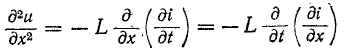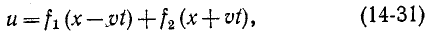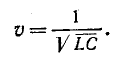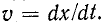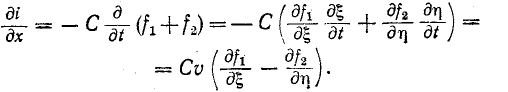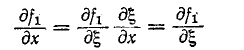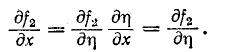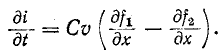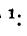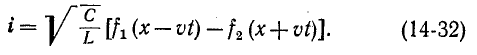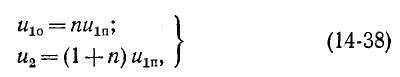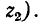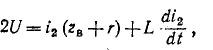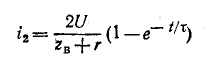Электрическая цепь RC
Рассмотрим ток в электрической цепи, состоящей из конденсатора ёмкостью C и резистора сопротивлением R, соединённых параллельно.
Значение тока заряда или разряда конденсатора определится выражением I = C(dU/dt), а значение тока в резисторе,
согласно закону Ома, составит U/R, где U – напряжение заряда конденсатора.
Из рисунка видно, что электрический ток I в элементах C и R цепи будет иметь одинаковое значение и
противоположное направление, согласно закону Кирхгофа. Следовательно, его можно выразить следующим образом:
Решаем дифференциальное уравнение C(dU/dt)= -U/R

Из таблицы интегралов здесь используем преобразование
Получаем общий интеграл уравнения: ln|U| = – t/RC + Const.
Выразим из него напряжение U потенцированием: U = e-t/RC * eConst.
Решение примет вид:
U = e-t/RC * Const.
Здесь Const – константа, величина, определяемая начальными условиями.
Следовательно, напряжение U заряда или разряда конденсатора будет меняться во времени по экспоненциальному закону
e-t/RC.
Экспонента – функция exp(x) = ex
e – Математическая константа, приблизительно равная 2.718281828…
Постоянная времени τ
Если конденсатор емкостью C последовательно с резистором сопротивлением R подключить к источнику постоянного напряжения U,
в цепи пойдёт ток, который за любое время t зарядит конденсатор до значения UC и определится выражением:

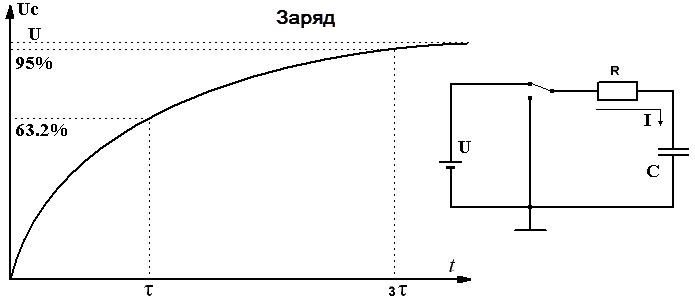
Тогда напряжение UC на выводах конденсатора будет увеличиваться от нуля до значения U по экспоненте:
UC = U(1 – e-t/RC)
При t = RC, напряжение на конденсаторе составит UC = U(1 – e-1) = U(1 – 1/e) .
Время, численно равное произведению RC, называется постоянной времени цепи RC и обозначается греческой буквой τ.
Постоянная времени τ = RC
За время τ конденсатор зарядится до (1 – 1/e)*100% ≈ 63,2% значения U.
За время 3τ напряжение составит (1 – 1/e3)*100% ≈ 95% значения U.
За время 5τ напряжение возрастёт до (1 – 1/e5)*100% ≈ 99% значения U.
Если к конденсатору емкостью C, заряженному до напряжения U, параллельно подключить резистор сопротивлением R,
тогда в цепи пойдёт ток разряда конденсатора.
Напряжение на конденсаторе при разряде будет составлять UC = Ue-t/τ = U/et/τ.
За время τ напряжение на конденсаторе уменьшится до значения U/e, что составит 1/e*100% ≈ 36.8% значения U.
За время 3τ конденсатор разрядится до (1/e3)*100% ≈ 5% от значения U.
За время 5τ до (1/e5)*100% ≈ 1% значения U.
Параметр τ широко применяется при расчётах RC-фильтров различных электронных цепей и узлов.
Замечания и предложения принимаются и приветствуются!
| Постоянная времени | |
|---|---|
 |
|
| Размерность | T |
| Единицы измерения | |
| СИ | Секунда |
См. также: Постоянная времени (нейрофизиология)
Постоя́нная вре́мени — характеристика экспоненциального процесса, определяющая время, через которое некоторый параметр процесса изменится в «е» раз (е≈2,718).
Содержание
- 1 В радиотехнике
- 1.1 Фильтры
- 2 См. также
- 3 Ссылки
В радиотехнике[править | править код]
Реакция апериодического звена 1-го порядка на единичное ступенчатое воздействие.
Реакция дифференцирующего звена 1-го порядка на единичное ступенчатое воздействие.
В радиотехнике постоянная времени 


Фильтры[править | править код]
Постоянная времени связана с граничной частотой, либо с частотой пропускания фильтра нижних частот:
См. также[править | править код]
- Время релаксации
- RC-цепь
- LR-цепь
Ссылки[править | править код]
- Постоянная времени — статья из Большой советской энциклопедии.
- Conversion of time constant τ to cutoff frequency fc and vice versa
- All about circuits — Voltage and current calculations
|
|
Эта статья слишком короткая. Пожалуйста, дополните её ещё хотя бы несколькими предложениями и уберите это сообщение. Если статья останется недописанной, она может быть выставлена к удалению. Для указания на продолжающуюся работу над статьёй используйте шаблон {{subst:Редактирую}}. (9 марта 2023) |
From Wikipedia, the free encyclopedia
The RC time constant, also called tau, the time constant (in seconds) of an RC circuit, is equal to the product of the circuit resistance (in ohms) and the circuit capacitance (in farads), i.e.
[seconds]
It is the time required to charge the capacitor, through the resistor, from an initial charge voltage of zero to approximately 63.2% of the value of an applied DC voltage, or to discharge the capacitor through the same resistor to approximately 36.8% of its initial charge voltage. These values are derived from the mathematical constant e, where 

- Charging toward applied voltage (initially zero voltage across capacitor, constant V0 across resistor and capacitor together)
[1]
- Discharging toward zero from initial voltage (initially V0 across capacitor, constant zero voltage across resistor and capacitor together)
Cutoff frequency[edit]
The time constant 
or, equivalently,
where resistance in ohms and capacitance in farads yields the time constant in seconds or the cutoff frequency in Hz.
Short conditional equations using the value for 
- fc in Hz = 159155 / τ in µs
- τ in µs = 159155 / fc in Hz
Other useful equations are:
- rise time (20% to 80%)
- rise time (10% to 90%)
In more complicated circuits consisting of more than one resistor and/or capacitor, the open-circuit time constant method provides a way of approximating the cutoff frequency by computing a sum of several RC time constants.
Delay[edit]
The signal delay of a wire or other circuit, measured as group delay or phase delay or the effective propagation delay of a digital transition, may be dominated by resistive-capacitive effects, depending on the distance and other parameters, or may alternatively be dominated by inductive, wave, and speed of light effects in other realms.
Resistive-capacitive delay, or RC delay, hinders the further increasing of speed in microelectronic integrated circuits. When the feature size becomes smaller and smaller to increase the clock speed, the RC delay plays an increasingly important role. This delay can be reduced by replacing the aluminum conducting wire by copper, thus reducing the resistance; it can also be reduced by changing the interlayer dielectric (typically silicon dioxide) to low-dielectric-constant materials, thus reducing the capacitance.
The typical digital propagation delay of a resistive wire is about half of R times C; since both R and C are proportional to wire length, the delay scales as the square of wire length. Charge spreads by diffusion in such a wire, as explained by Lord Kelvin in the mid nineteenth century.[2] Until Heaviside discovered that Maxwell’s equations imply wave propagation when sufficient inductance is in the circuit, this square diffusion relationship was thought to provide a fundamental limit to the improvement of long-distance telegraph cables. That old analysis was superseded in the telegraph domain, but remains relevant for long on-chip interconnects.[3][4][5]
See also[edit]
- Cutoff frequency and frequency response
- Emphasis, preemphasis, deemphasis
- Exponential decay
- Filter (signal processing) and transfer function
- High-pass filter, low-pass filter, band-pass filter
- RL circuit, and RLC circuit
- Rise time
References[edit]
- ^ “Capacitor Discharging”.
- ^ Andrew Gray (1908). Lord Kelvin. Dent. p. 265.
- ^ Ido Yavetz (1995). From Obscurity to Enigma. Birkhäuser. ISBN 3-7643-5180-2.
- ^ Jari Nurmi; Hannu Tenhunen; Jouni Isoaho & Axel Jantsch (2004). Interconnect-centric Design for Advanced SoC and NoC. Springer. ISBN 1-4020-7835-8.
- ^ Scott Hamilton (2007). An Analog Electronics Companion. Cambridge University Press. ISBN 978-0-521-68780-5.
External links[edit]
- RC Time Constant Calculator
- Conversion time constant
to cutoff frequency fc and back
- RC time constant
Термин: Постоянная времени RC-цепи
τ – постоянная времени RC-цепи – это временна́я характеристика простой электрической цепи, в которой происходит изменение заряда конденсатора С за счёт его разряда через сопротивление R. Постоянная времени вычисляется как τ=R*C [Ф*Ом], что эквивалентно размерности «секунда» [c].
Как показано на рисунке, постоянная времени τ входит в аналитическую функцию описания процесса изменения напряжения на конденсаторе U(t) при его заряде от источника напряжения через сопротивление R. На рисунке U(0) – это начальное напряжение на конденсаторе (в момент времени t=0), а U(∞) – это напряжение источника напряжения, к которому асимтотически стремится U(t).
За время, равное τ, напряжение на конденсаторе изменяется от U(0) до U(∞) + [U(0) — U(∞)]/e, где e=2,718. .
Экспоненциальный заряд конденсатора происходит для случая U(∞) > U(0), а экспоненциальный разряд – для случая U(∞) -t/τ ) в моменты времени t от t=0,001τ до t=10τ протекания экспоненциального процесса.
| Время процесса в единицах τ=RC | Доля неустановившейся величины напряжения e -t/τ | |
| *100, % | *10 6 , ppm | |
| 0,001τ | ≈99,9% | ≈999000 |
| 0,01τ | ≈99% | ≈990000 |
| 0,1τ | ≈90% | ≈900000 |
| 0,5τ | ≈61% | ≈610000 |
| τ | ≈37% | ≈370000 |
| 2τ | ≈14% | ≈140000 |
| 3τ | ≈5,0% | ≈50000 |
| 4τ | ≈1,8% | ≈1800 |
| 5τ | ≈0,67% | ≈6700 |
| 6τ | ≈0,25% | ≈2500 |
| 7τ | ≈0,091% | ≈910 |
| 8τ | ≈0,034% | ≈340 |
| 9τ | ≈0,012% | ≈120 |
| 10τ | ≈0,0045% | ≈45 |
Понятие постоянной времени RC-цепи помогает оценить время протекания процесса при анализе эквивалентных электрических схем, содержащих RC-цепи. Заметим только, что понятие постоянной времени не применимо для частного случая заряда-разряда конденсатора постоянным током, где закон изменения напряжения и заряда на конденсаторе имеет линейный характер, а не экспоненциальный.
Постоянные времени RC-цепей (в качестве величин с прозрачным физическим смыслом) участвуют в аналитических решениях дифференциальных уравнений, описывающих не только экспоненциальные процессы в электрических схемах, содержащих RC-цепи (например, пассивные и активные RC-фильтры).
Источник
Дифференциальное уравнение [ править ]
Основная статья: теория систем LTI
Системы LTI первого порядка характеризуются дифференциальным уравнением
τ d V d т + V знак равно ж ( т ) { Displaystyle тау { гидроразрыва {dV} {dt}} + V = f (t)}
где τ представляет собой экспоненциальную константу затухания, а V является функцией времени t
V знак равно V ( т ) . { Displaystyle V = V (t).}
Правая часть — это вынуждающая функция
f
(
t
), описывающая внешнюю движущую функцию времени, которую можно рассматривать как
вход
системы , на который
V
(
t
) является
ответом
или выходом системы. Классические примеры для
f
(
t
) :
Функция Хевисайда , часто обозначается U
(
т
) :
ты ( т ) знак равно { 0 , т < 0 1 , т ≥ 0 {displaystyle u(t)={begin{cases}0,&t<0\1,&tgeq 0end{cases}}}
импульсная функция , часто обозначается б
(
т
) , а также функция синусоидальной входного сигнала:
f ( t ) = A sin ( 2 π f t ) {displaystyle f(t)=Asin(2pi ft)}
или же
f ( t ) = A e j ω t , {displaystyle f(t)=Ae^{jomega t},}
где A — амплитуда вынуждающей функции, f — частота в герцах, а ω = 2 π f
— частота в радианах в секунду.
Пример решения [ править ]
Пример решения дифференциального уравнения с начальным значением V
0 и без функции принуждения:
V ( t ) = V o e − t / τ {displaystyle V(t)=V_{o}e^{-t/tau }}
куда
V o = V ( t = 0 ) {displaystyle V_{o}=V(t=0)}
это начальное значение V . Таким образом, отклик представляет собой экспоненциальный спад с постоянной времени τ .
Обсуждение [ править ]
Предполагать
V ( t ) = V 0 e − t / τ {displaystyle V(t)=V_{0}e^{-t/tau }} .
Такое поведение называется «убывающей» экспоненциальной функцией. Время τ (тау) называется «постоянной времени» и может использоваться (как в этом случае), чтобы указать, насколько быстро экспоненциальная функция затухает.
Здесь:
t = время (обычно
t
> 0 в технике управления)
V
0 = начальное значение (см. «Особые случаи» ниже).
Конкретные случаи [ править ]
1) Пусть ; тогда и так t = 0 {displaystyle t=0} V = V 0 e 0 {displaystyle V=V_{0}e^{0}} V = V 0 {displaystyle V=V_{0}} 2) Пусть ; тогда t = τ {displaystyle t=tau } V = V 0 e − 1 ≈ 0.37 V 0 {displaystyle V=V_{0}e^{-1}approx 0.37V_{0}} 3) Пусть , и так V = f ( t ) = V 0 e − t / τ {displaystyle V=f(t)=V_{0}e^{-t/tau }} lim t → ∞ f ( t ) = 0 {displaystyle lim _{tto infty }f(t)=0} 4) Пусть ; тогда t = 5 τ {displaystyle t=5tau } V = V 0 e − 5 ≈ 0.0067 V 0 {displaystyle V=V_{0}e^{-5}approx 0.0067V_{0}}
После периода в одну постоянную времени функция достигает e
−1 = примерно 37% от своего начального значения. В случае 4 после пяти постоянных времени функция достигает значения менее 1% от исходного. В большинстве случаев этот порог в 1% считается достаточным, чтобы предположить, что функция упала до нуля — как показывает опыт, в технике управления стабильной системой является система, которая демонстрирует такое общее затухающее поведение.
Переходные процессы в цепи с одним накопителем энергии и произвольным числом резисторов
Как отмечалось в предыдущей лекции, линейная цепь охвачена единым переходным процессом. Поэтому в рассматриваемых цепях с одним накопителем энергии (катушкой индуктивности или конденсатором) – цепях первого порядка – постоянная времени будет одной и той же для всех свободных составляющих напряжений и токов ветвей схемы, параметры которых входят в характеристическое уравнение.
Общий подход к расчету переходных процессов в таких цепях основан на применении теоремы об активном двухполюснике: ветвь, содержащую накопитель, выделяют из цепи, а оставшуюся часть схемы рассматривают как активный двухполюсник А (эквивалентный генератор) (см. рис.1, а) со схемой замещения на рис. 1,б.
Совершенно очевидно, что постоянная времени здесь для цепей с индуктивным элементом определяется, как:
и с емкостным, как:
где — входное сопротивление цепи по отношению к зажимам 1-2 подключения ветви, содержащей накопитель энергии.
Например, для напряжения на конденсаторе в цепи на рис. 2 можно записать
где в соответствии с вышесказанным
Переходные процессы при подключении последовательной R-L-C-цепи к источнику напряжения
Рассмотрим два случая:
Согласно изложенной в предыдущей лекции методике расчета переходных процессов классическим методом для напряжения на конденсаторе в цепи на рис. 3 можно записать
Тогда для первого случая принужденная составляющая этого напряжения
Характеристическое уравнение цепи
решая которое, получаем
В зависимости от соотношения параметров цепи возможны три типа корней и соответственно три варианта выражения для свободной составляющей:
1. или , где — критическое сопротивление контура, меньше которого свободный процесс носит колебательный характер.
В этом случае
2. — предельный случай апериодического режима.
В этом случае и
3. — периодический (колебательный) характер переходного процесса.
В этом случае и
где — коэффициент затухания; — угловая частота собственных колебаний; — период собственных колебаний.
Для апериодического характера переходного процесса после подстановки (2) и (3) в соотношение (1) можно записать
Для нахождения постоянных интегрирования, учитывая, что в общем случае и в соответствии с первым законом коммутации , запишем для t=0 два уравнения:
решая которые, получим
Тогда ток в цепи
и напряжение на катушке индуктивности
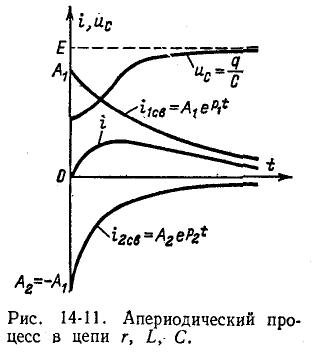
На рис. 4 представлены качественные кривые , и , соответствующие апериодическому переходному процессу при .
Для критического режима на основании (2) и (4) можно записать
Для колебательного переходного процесса в соответствии с (2) и (5) имеем
Для нахождения постоянных интегрирования запишем
На рис. 5представлены качественные кривые и , соответствующие колебательному переходному процессу при .
При подключении R-L-C-цепи к источнику синусоидального напряжения для нахождения принужденных составляющих тока в цепи и напряжения на конденсаторе следует воспользоваться символическим методом расчета, в соответствии с которым
Здесь также возможны три режима:
Наибольший интерес представляет третий режим, связанный с появлением во время переходного процесса собственных колебаний с частотой . При этом возможны, в зависимости от соотношения частот собственных колебаний и напряжения источника, три характерные варианта: 1 — ; 2 — ; 3 — , — которые представлены на рис. 6,а…6,в соответственно.
Литература
- Основы теории цепей: Учеб. для вузов /Г.В.Зевеке, П.А.Ионкин, А.В.Нетушил, С.В.Страхов. –5-е изд., перераб. –М.: Энергоатомиздат, 1989. -528с.
- Бессонов Л.А. Теоретические основы электротехники: Электрические цепи. Учеб. для студентов электротехнических, энергетических и приборостроительных специальностей вузов. –7-е изд., перераб. и доп. –М.: Высш. шк., 1978. –528с.
- Теоретические основы электротехники. Учеб. для вузов. В трех т. Под общ. ред. К.М.Поливанова. Т.1. К.М.Поливанов. Линейные электрические цепи с сосредоточенными постоянными. –М.: Энергия- 1972. –240с.
Контрольные вопросы
- Как можно определить постоянную времени в цепи с одним накопителем энергии по осциллограмме тока или напряжения в какой-либо ветви?
- Определить, какой процесс: заряд или разряд конденсатора в цепи на рис. 2 – будет происходить быстрее?
- Влияет ли на постоянную времени цепи тип питающего устройства: источник напряжения или источник тока?
- В цепи на рис. 2 , С=10 мкФ. Чему должна быть равна индуктивность L катушки, устанавливаемой на место конденсатора, чтобы постоянная времени не изменилась?
- Как влияет на характер переходного процесса в R-L-C-контуре величина сопротивления R и почему?
- Определить ток через катушку индуктивности в цепи на рис. 7, если ; ; ; ; .
Определить ток в ветви с конденсатором в цепи на рис. 8, если ; ; ; .Источник
RC-цепи, 5 самых ходовых схем фильтров и их простой рассчет
RC-цепь, такое частое явление радиоэлектроники. Такие фильтры стоят повсюду. Понимание того, как какой фильтр влияет на форму АЧХ сигнала во многом определяет правильность чтения всей электронной схемы. В статье собраны 5 основных RC-фильтров, приведены их АЧХ и упрощенные формулы расчета.
В ранние годы развития радиоэлектроники для воздействие на Амплитудно — Частотную Характеристику (АЧХ) сигнала в основном применялись LC — фильтры, т.е. фильтры состоящие из катушки индуктивности и конденсатора. Со временем им на смену пришла RC-цепь, которая была плотно взята в оборот радиоэлектроникой ввиду меньшей стоимости и габаритов.
Конечно, фильтры на RC-цепях не могут полностью вытеснить LC собратьев. Например в фильтрах для АС предпочтительнее использование LC-фильтров. Но практически во всей маломощной электронике главенствуют именно RC-цепи. Например двойная RC-цепь в фильтре RIAA-корректора.
Интересным вариантом избавления от катушек являются фильтры на гираторах, где посредством конденсатора и операционного усилителя эмитируется работа катушки.
Постоянная времени RC — RC time constant
Постоянная времени RC
, также называемая тау, постоянная времени (в секундах ) RC-цепи , равна произведению сопротивления цепи (в омах ) на емкость цепи (в фарадах ), т. Е.
τ знак равно р C [секунды]
Это время, необходимое для зарядки конденсатора через резистор от начального напряжения заряда, равного нулю, до примерно 63,2% от значения приложенного напряжения постоянного тока или для разряда конденсатора через тот же резистор примерно до 36,8% от его начального значения. напряжение заряда. (Эти значения получены из математической константы e
: и .) Следующие формулы используют ее, принимая постоянное напряжение, приложенное последовательно к конденсатору и резистору, для определения напряжения на конденсаторе в зависимости от времени: 63,2 % знак равно 1 — е — 1 >
Постоянная времени электрической цепи — что это такое и где используется
Природе свойственны периодические процессы: день сменяет ночь, теплое время года сменяется холодным и т. д. Период этих событий почти постоянен и поэтому может быть строго определен. Кроме того, мы вправе утверждать, что приведенные в качестве примера периодические природные процессы не являются затухающими, по крайней мере по отношению к продолжительности жизни одного человека.
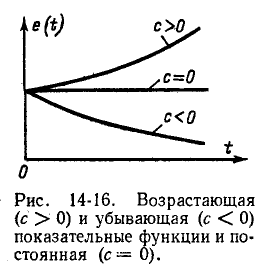
Однако в технике, а в электротехнике и в электронике — особенно, далеко не все процессы являются периодическими и незатухающими. Обычно какой-нибудь электромагнитный процесс сначала возрастает, а затем убывает. Часто дело ограничивается лишь фазой начала колебания, которое так и не успевает толком набрать размах.
Сплошь и рядом в электротехнике можно встретить так называемые экспоненциальные переходные процессы, суть которых заключается в том, что система просто стремится придти к какому-то равновесному состоянию, которое в конце концов выглядит как состояние покоя. Такой переходный процесс может быть как нарастающим, так и спадающим.
Внешняя сила сначала выводят динамическую систему из состояния равновесия, а затем не препятствует естественному возврату данной системы к ее исходному состоянию. Эта последняя фаза и есть так называемый переходный процесс, которому свойственна определенная длительность. Кроме того процесс выведения системы из равновесия также является переходным процессом с характерной длительностью.
Так или иначе, постоянной времени переходного процесса мы называем его временную характеристику, определяющую время, через которое некоторый параметр данного процесса изменится в «е» раз, то есть увеличится или уменьшится примерно в 2,718 раз по сравнению с состоянием, принятым за исходное.
Рассмотрим для примера электрическую цепь, состоящую из источника постоянного напряжения, конденсатора и резистора. Подобного рода цепь, где резистор включен последовательно с конденсатором, называется интегрирующей RC-цепью.
Если в начальный момент времени подать на такую цепь питание, то есть установить на входе некоторое постоянное напряжение Uвх, то Uвых — напряжение на конденсаторе, начнет по экспоненте нарастать.
Через время t1 напряжение на конденсаторе достигнет 63,2% от напряжения на входе. Так вот, промежуток времени от начального момента до t1 – это и будет постоянная времени данной RC-цепи.
Данную константу цепи называют «тау», она измеряется в секундах, а обозначают ее соответствующей греческой буквой. Численно для RC-цепи она равна R*C, где R выражается в омах, а С — в фарадах.
Содержание:
Переходные процессы в электрических цепях:
Переходный процесс в электрической цепи — это электромагнитный процесс, возникающий в электрической цепи при переходе от одного установившегося (принужденного) режима к другому. Установившимся (принужденным) называется режим работы электрической цепи, при котором напряжение и токи цепи в течение длительного времени остаются неизменными.
Такой режим в электрической цепи устанавливается при длительном действии источников постоянной или переменной ЭДС при неизменных параметрах этой цепи R, L и С.
Переходный процесс вызывается коммутацией в цепи. Коммутацией называется процесс замыкания или размыкания рубильников или выключателей. Переходный процесс может быть вызван изменением параметров электрической цепи R, L или С.
Переходный процесс базируется на двух законах коммутации:
- ток в индуктивности не может изменяться скачком;
- напряжение на емкости не может изменяться скачком.
Действительно, если ток в индуктивности L изменяется скачком, т. е. мгновенно, то ЭДС самоиндукции eL становится бесконечно большой (при
В реальных цепях ЭДС самоиндукции может иметь только конечные значения.
Если в цепи с емкостью С напряжение на ее обкладках изменяется скачком, т. е. мгновенно, то появляется бесконечно большой зарядный (или разрядный) ток (при 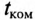
Ток в электрических цепях может иметь только конечные значения.
Переходный процесс является быстропротекающим процессом, длительность которого обычно составляет десятые, сотые и даже миллионные доли секунды и сравнительно редко — секунды и даже десятки секунд.
Таким образом, один установившийся режим цепи отделяется от другого некоторым промежутком времени, в течение которого происходит постепенный переход от прежнего состояния цепи к новому.
Переходный процесс в линейных цепях можно рассматривать как результат наложения двух процессов:
- нового установившегося режима, который наступает после коммутации;
- свободного процесса, обеспечивающего переход цепи от прежнего установившегося режима к новому установившемуся режиму.
Таким образом, ток i цепи в течение переходного процесса можно представить суммой двух токов: нового установившегося 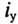
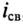
Аналогично напряжение в течение переходного процесса равно
В результате переходного процесса происходят изменения тока, напряжения, фазы, частоты и т.д.
Изучение переходных процессов очень важно, так как оно позволяет выявить возможные превышения напряжения на отдельных участках цепи, которые могут оказаться опасными для изоляции установки, позволяет выявить возможные броски токов, величина которых в десятки раз превышает установившийся. Изучение переходных процессов позволяет выявить ситуации, возникающие в электрических цепях при коротком замыкании, резком включении и выключении рубильников, и прочие режимы работы цепи.
Переходный процесс в электрической цепи
Переходный процесс в электрической цепи — это процесс, возникающий в электрической цепи при различных воздействиях, приводящих их из стационарного состояния в новое стационарное состояние, когда при действии различного рода коммутационной аппаратуры, например, ключей, переключателей для включения или отключения источника или приёмника энергии, при обрывах в цепи, при коротких замыканиях отдельных участков цепи и т. д.
Подключение катушки индуктивности к источнику с постоянным напряжением
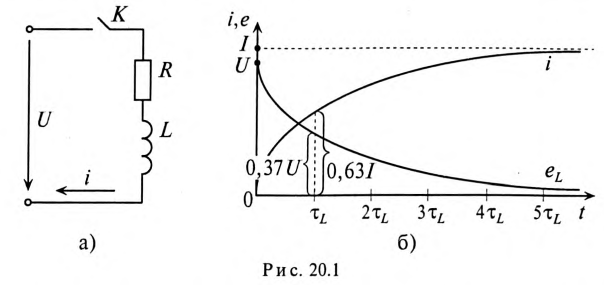
Если катушку индуктивности (RL) подключить к источнику с постоянным напряжением U (замыкание ключа К), то ток i в не-разветвленной цепи (рис. 20.1а) будет увеличиваться от нуля (в начале переходного процесса) до установившегося значения
Установившийся, т.е. постоянный, ток I не индуктирует в катушке ЭДС самоиндукции, поэтому индуктивное сопротивление в установившемся режиме при условии (20.3) отсутствует.
Этот увеличивающийся ток i индуктирует в индуктивности L катушки ЭДС самоиндукции (см. (9.11))
Следовательно, для любого момента времени переходного процесса по второму закону Кирхгофа можно записать
Разделив уравнение (20.4) на R, получают
В уравнении (20.5) 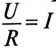
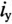
Отношение — 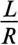
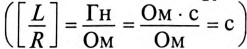
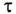
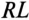
Тогда уравнение (20.5) можно записать в виде
Если это уравнение проинтегрировать, предварительно разделив переменные (ток и время), а затем спотенцировать, то получим выражение
где е — основание натурального логарифма (е=2,71); I — установившийся ток (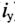
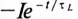
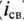
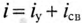
Таким образом, уравнение, которое позволяет определить вели-шу тока в цепи с индуктивностью L в любой момент переходно-процесса RL-цепи при подключении реальной катушки индук-1Вности к источнику с постоянным напряжением U, записывается в виде
Воспользовавшись Приложением 9, по выражению (20.10) можно определить, что за время t=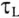
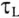
Теоретически переходный процесс происходит бесконечно долго. Практически переходный процесс в рассматриваемой цепи считается законченным, когда ток i увеличивается до 99 % установившегося тока I.
Как видим, чем больше xL, тем больше времени t длится перечный процесс.
Таким образом, постоянная времени xL определяет скорость греховного процесса или его длительность.
ЭДС самоиндукции в рассматриваемой цепи, вызванная свободным током 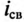
Таким образом, ЭДС самоиндукции в 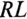
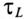
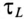
Увеличение тока и уменьшение ЭДС самоиндукции катушки при подключении катушки к источнику с постоянным напряжением U показаны на графике рис. 20.1б.
Отключение и замыкание RL-цепи
Если цепь с катушкой, в которой проходит установившийся ток I (рис. 20.1а), разомкнуть, то ток i в такой цепи с большой скоростью уменьшается до нуля и в катушке индуктируется большая ЭДС самоиндукции eL
Эта ЭДС полностью приложена к клеммам ключа, так как при размыкании сопротивление ключа становится бесконечно большим. Эта ЭДС вызывает значительное увеличение электрического поля между контактами ключа, а следовательно, и напряженности поля. Большая напряженность электрического поля может вызвать искровой и даже дуговой разряд между размыкающимися контактами ключа, в результате чего обгорают контакты ключа.
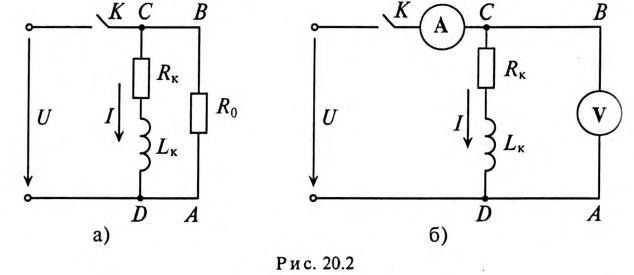
Поэтому рубильники в RL-цепях шунтируются специальными устройствами, которые обеспечивают гашение дугового разряда. Для гашения дугового разряда необходимо одновременно с отключением катушки индуктивности от источника замкнуть ее на разрядное сопротивление R0 (рис. 20.2а).
Уменьшение тока 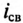
Наглядно это уменьшение можно наблюдать на рис. 20.1б, если кривую изменения eL считать кривой уменьшения тока 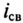
Постоянная времени при отключении катушки от источника с постоянным напряжением U определяется как и при включении катушки на это напряжение, т.е.
Если катушку с установившимся током I, зашунтированную сопротивлением Ro (рис. 20.2а), отключить от источника (разомкнуть ключ К), то в замкнутом контуре ABCD в начальный момент коммутации 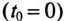
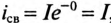
Для определения активного сопротивления катушки 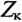
Как видно, за счет переходных процессов в цепях с индуктивностью возникают большие токи и напряжения. С этим необходимо считаться и учитывать при проектировании и эксплуатации цепей с индуктивностью.
Зарядка, разрядка и саморазрядка конденсатора
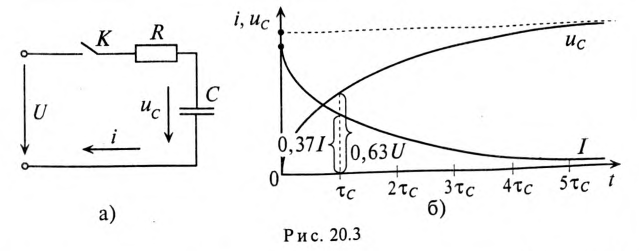
Если конденсатор с сопротивлением (утечки) R и емкостью С подключить к источнику с постоянным напряжением U (замыканием ключа К), то в цепи (рис. 20.3а) появится ток зарядки конденсатора (см. (11.16)):
где 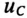
По второму закону Кирхгофа для цепи зарядки конденсатора (рис. 20.3а) можно записать уравнение
где произведение RC имеет размерность времени, обозначается буквой 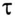
Уравнение (20.13) можно записать в виде
Если в уравнении (20.15) разделить переменные, проинтегрировать, а затем спотенцировать, то получится выражение
где U — установившееся напряжение 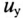
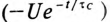
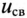
Следовательно, напряжение на заряжающемся конденсаторе в любой момент времени t переходного процесса определяется выражением
По (20.17), пользуясь Приложением 9, можно определить, что за время t= 
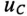

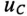
Теоретически зарядка конденсатора длится бесконечно долю а практически конденсатор считается заряженным, когда напряжение на нем достигает 99 % напряжения источника U.
Таким образом, и в RC-цепи, чем больше постоянная времени 

Ток i при зарядке конденсатора (см. (20.13)) уменьшается по за кону
(20. IS)
где 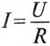
За время t=

Графики изменения напряжения на конденсаторе и тока в цепи арядки конденсатора изображены на рис. 20.36.
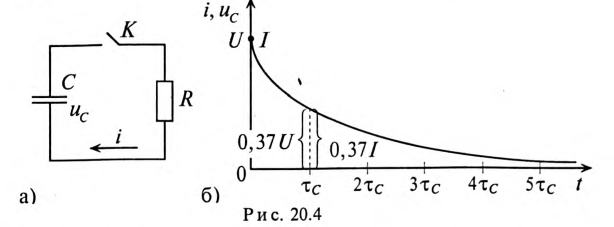
Если конденсатор емкостью С, заряженный предварительно до напряжения U, разряжать через резистор с сопротивлением R рис. 20.4а), то напряжение 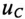
где U — напряжение на конденсаторе до начала разрядки (при t= 0), а 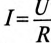

За время t= 
Если конденсатор емкостью С, заряженный до напряжения U, отсоединить от источника, то он будет разряжаться через свой диэлектрик. Напряжение на нем будет уменьшаться по закону 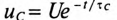
Постоянная времени саморазряда зависит от физических свойств диэлектрика
где р — удельное сопротивление диэлектрика; 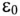
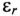
Для определения напряжения, тока, ЭДС в любой момент переходного процесса 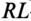
Пример 20.1
Катушка электромагнита с параметрами 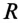
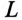
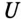
Решение
Установившийся ток
Постоянная времени для катушки
Подставляем значение величин в (20.10):
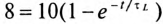
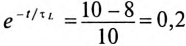
По Приложению 9 определяется 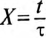
ЭДС самоиндукции за время 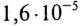
Пример 20.2
К зажимам катушки индуктивности с параметрами 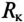
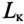
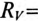
Определить напряжение на зажимах вольтметра и ток в обмотках прибора (обмотки соединены последовательно) при t=0, если размыкание рубильника К произойдет мгновенно и дуги не возникнет.
Решение
До размыкания рубильника через катушку проходил ток
В момент размыкания рубильника (t = 0) весь этот ток проходит обмоткам вольтметра. При этом на вольтметре напряжение cтанет равным
Такого напряжения (10 кВ) и такого тока (2 А) обмотка вольтметра (обычно подвижная обмотка электродинамического прибора рассчитана на ток порядка десятков, максимум, сотен миллиампер) не выдержит и сгорит.
При размыкании рубильника с конечной скоростью между расходящимися контактами рубильника К (рис. 20.26) возникнет электрическая дуга. Это приведет к тому, что увеличение напряжения на вольтметре и тока через обмотки вольтметра будет меньше, чем в рассмотренном выше случае (мгновенное размыкание рубильника). Однако меры предосторожности для сохранения вольтметра и рубильника, описанные выше, нужно соблюдать.
Пример 20.3
Конденсатор емкостью С= 2 мкФ через сопротивление R= 500 кОм подключается к источнику с постоянным напряжением U= 220 В.
Определить напряжение на конденсаторе 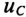
Решение
Постоянная времени заряда конденсатора
Напряжение на конденсаторе через 2 с от начала заряда
Ток в цепи заряда конденсатора через 2 с от начала заряда
так как
Время t’ заряда конденсатора до напряжения 150 В определяется по формуле (20.17):
Откуда
Из таблицы показательных функций (Приложение 9) находят t’= 1,14 с.
Пример 20.4
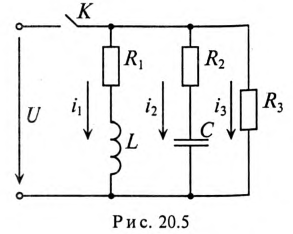
Параметры цепи, изображенной на рис. 20.5, следующие:
Определить значение токов в ветвях через время t= 2 с после замыкания ключа К.
Решение
Для ветви (1) с индуктивностью определяются:
установившийся ток
и постоянная времени
Тогда ток через 2 с будет равен
Для ветви (2) с емкостью определяются:
максимальный установившийся ток по окончании переходного процесса
и постоянная времени 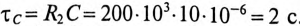
Тогда ток зарядки через 2 с будет равен
Для ветви (3) с активным сопротивлением 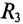
Постоянная времени 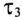
Через 2 с значение тока будет таким же, т. е.
Переходные процессы в электрических цепях. Классический метод расчета
Возникновение переходных процессов:
В предыдущих главах рассматривались установившиеся процессы в линейных электрических цепях, т. е. такие процессы, при которых напряжения и токи либо неизменны во времени (цепи постоянного тока), либо представляют собой периодические функции времени (цепи переменного тока).
Наступлению установившегося процесса, отличного от первоначального режима работы цепи, предшествует, как правило, переходный процесс, при котором напряжения и токи изменяются непериодически.
Переход от одного режима работы цепи к другому может быть вызван изменением параметров или схемы цепи, называемым в общем случае в электротехнике коммутацией.
Можно теоретически считать, что коммутация цепи производится мгновенно, т. е. на включение, выключение или переключение цепи время не расходуется. Тем не менее переход от исходного режима работы цепи к последующему установившемуся процессу происходит не мгновенно, а в течение некоторого времени. Объясняется это тем, что каждому состоянию цепи соответствует определенный запас энергии электрических и магнитных полей. Переход к новому режиму связан с нарастанием или убыванием энергии этих полей. Энергия 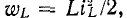
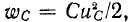
Если исключить случаи размыкания индуктивности и замыкания накоротко емкости и рассматривать цепи, в которых энергия, накапливаемая в магнитном или электрическом поле, может рассеиваться в виде теплоты в сопротивлениях, то, считая, что коммутация происходит мгновенно, можно искрообразование не учитывать.
Для завершения переходного и наступления установившегося процессов теоретически требуется бесконечно большое время. Практически, однако, время переходного процесса определяется малым интервалом, по истечении которого токи и напряжения настолько приближаются к установившимся значениям, что разница оказывается практически неощутимой. Чем интенсивнее происходит рассеяние энергии в сопротивлениях, тем быстрее протекает переходный процесс.
Если бы электрическая цепь состояла только из сопротивлений и не содержала индуктивностей и емкостей, то переход от одного установившегося состояния к другому совершался бы мгновенно, без затраты времени. В реальных электротехнических устройствах тепловые потери, обусловленные током, магнитные и электрические поля сопутствуют друг другу. Применяя специальные схемы и подбирая соответствующие параметры цепи, можно в зависимости от необходимости ускорить или замедлить переходный процесс.
В одних случаях переходные процессы в электрических цепях нежелательны и опасны (например, при коротких замыканиях в энергетических системах). В других случаях переходный процесс представляет собой естественный, нормальный режим работы цепи, как это, например, имеет место в радиопередающих и радиоприемных устройствах, системах автоматического регулирования и других цепях.
Существуют различные методы расчета переходных процессов в линейных электрических цепях. Настоящая глава посвящена классическому методу решения дифференциальных уравнений, описывающих переходные процессы.
Законы коммутации и начальные условия
Высказанные выше положения о том, что запас энергии магнитного или электрического поля может изменяться только плавно, без скачков, выражают принцип непрерывности во времени потокосцепления индуктивности и электрического заряда емкости и называются законами коммутации.
Невозможность скачкообразного изменения потокосцепления следует из того, что в противном случае на индуктивности появилось бы бесконечно большое напряжение 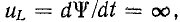
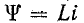
Аналогично невозможность скачкообразного изменения электрического заряда q следует из того, что в противном случае через емкость проходил бы бесконечно большой ток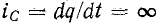
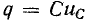
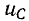
При этом следует отметить, что в цепях с идеализированными сосредоточенными параметрами скачкообразно могут изменяться: 1) токи в сопротивлениях и емкостях и 2) напряжения на сопротивлениях и индуктивностях.
Значения тока в индуктивности и напряжения на емкости в момент коммутации называются независимыми начальными условиями.
Обычно принимают, что коммутация происходит в момент времени t= 0; тогда ток в индуктивности и напряжение на емкости в момент времени непосредственно перед коммутацией обозначаются через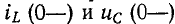
На основании законов коммутации:
Эти равенства выражают начальные условия цепи, в которых происходит коммутация.
При нулевых начальных условиях, т. е. косца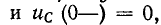
В случае ненулевых начальных условий, т. е. когда 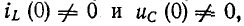
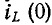
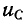
Независимые начальные условия характеризуют энергию магнитного и электрического полей, запасенную к моменту коммутации, и для расчета переходного процесса обязательно требуется знание этих начальных условий, причем совершенно безразлично, каким образом эти условия в цепи были созданы.
При расчете переходных процессов в разветвленных электрических цепях наряду с независимыми начальными условиями используются так называемые зависимые начальные условия, а именно: значения токов, напряжений и их производных в начальный момент времени (t = 0).
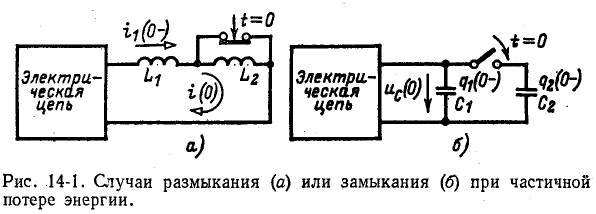
До сих пор нами исключались из рассмотрения случаи коммутации, при которых неизбежно между контактами возникает искра или дуга. Один из таких случаев показан на рис. 14-1, а. До коммутации ток проходит через индуктивность 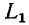
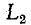
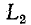
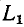
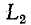
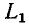
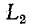
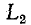
замкнуться и через межвитковую емкость. После быстрого погасания дуги токи в 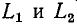
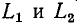
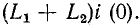
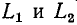
Найденный таким образом ток 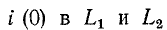
При коммутациях в цепях с емкостями при отсутствии сопротивлений также возможны весьма быстрые перераспределения зарядов, условно рассматриваемые как мгновенные. В этом случае применим принцип непрерывности суммарного заряда. Полученные при этом значения зарядов и напряжений на отдельных емкостях используются в расчете последующего переходного процесса как независимые начальные условия.
Например, в случае схемы на рис. 14-1, б принцип непрерывности суммарного заряда до и после коммутации выражается равенством
При сделанном допущении в остальной электрической цепи, соединенной с емкостями, не возникает бесконечно большого тока, так как суммарный заряд не изменяется скачкообразно при t=0.
В процессе рассматриваемой коммутации энергия электрического поля уменьшится, так как часть ее превратится в тепло в очень малом сопротивлении проводника при очень большом токе, а также сможет выделиться в искре и излучиться.
Установившийся и свободный режимы
В общем случае анализ переходного процесса в линейной цепи с сосредоточенными параметрами r, L, С и М сводится к решению обыкновенных линейных неоднородных дифференциальных уравнений, выражаюших законы Кирхгофа. Эти уравнения представляют собой линейную комбинацию напряжений, токов, их первых производных и интегралов по времени.
Например, если какая-нибудь э. д. с. е (t) включается в цепь, состоящую из последовательно соединенных r, L и С, то интегродифференциальное уравнение имеет вид:
Это уравнение после дифференцирования приводится к неоднородному дифференциальному уравнению второго
порядка
Как известно, общий интеграл такого^ уравнения равен сумме частного решения неоднородного уравнения и общего решения однородного уравнения.
Частное решение выражает установившийся режим, задаваемый источником.
Расчеты установившихся токов рассмотрены в предыдущих главах.
Общее решение физически определяет поведение цепи при отсутствии внешних источников электрической энергии и заданных начальных условиях. Функции, определяемые общим решением, называются свободными составляющими (токов, напряжений и пр.).
В случае, рассмотренном выше, однородное уравнение имеет вид:
и соответствующее ему характеристическое уравнение
Если корни характеристического уравнения обозначить через 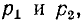
где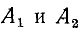
Полный переходный ток в цепи равен сумме установившегося и свободного токов:
Аналогично напряжение, заряд, магнитный поток и другие функции на любом участке цепи в переходном режиме состоят из установившейся и свободной составляющих.
На основании законов коммутации можно найти начальные независимые условия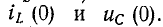
откуда
Итак, начальные значения свободных функций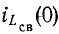
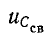
В частном случае при нулевых начальных условиях:
В зависимости от порядка дифференциальных уравнений, описывающих исследуемые переходные процессы, различают цепи первого, второго и более высокого порядков.
В цепях первого порядка накопление энергии происходит только в одном элементе, L или С в форме магнитной энергии, или электрической энергии . Одноконтурная цепь, содержащая элементы, в которых накапливается энергия обоих видов — магнитная « электрическая, представляет собой цепь второго порядка . Разветвленные цепи могут быть более высокого порядка.
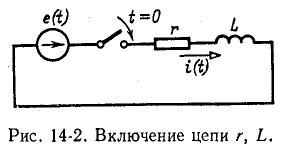
Переходный процесс в цепи r, L
Положим, что в момент t = 0 цепь, состоящая из сопротивления r и индуктивности L, включенных последовательно, присоединяется к источнику э. д. с. е (t) (рис. 14-2).
Дифференциальное уравнение для времени
Характеристическое уравнение имеет вид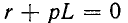
Отсюда свободный ток
Переходный ток в цепи определится суммой установившегося и свободного токов:
Установившийся ток может быть найден, если задана э. д. с. е (t).
Рассмотрим три случая:
1) включение в цепь г, L постоянной э. д. с. £;
2) короткое замыкание цепи г, L
3) включение в цепь г, L синусоидальной э. д. с.
1. Включение в цепь г, L постоянной э. д. с.
При включении в цепь г, L постоянной э. д. с. Е установившийся ток равен Е’/г. Поэтому согласно (14-9)
Постоянная интегрирования А находится по начальному условию
Согласно уравнению (14-10) при t — 0
откуда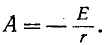
здесь 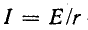
В начальный момент t = 0 э. д. с. самоиндукции 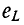
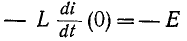
С течением времени э. д. с. самоиндукции убывает, а ток в цепи возрастает, асимптотически приближаясь к установившемуся значению.
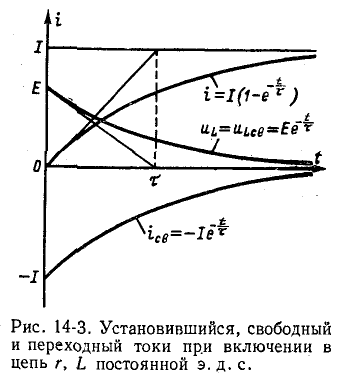
На рис. 14-3 показаны кривые установившегося, свободного и переходного токов; на том же рисунке изображена кривая напряжения на индуктивности
Из курса математического анализа известно, что если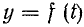
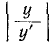
Величина 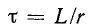
Выражение (14-11) показывает, что постоянная времени графически определяется длиной подкасательной к кривой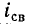
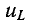
Нарастание тока происходит тем быстрее, чем меньше постоянная времени и соответственно чем быстрее убывает э. д. с. самоиндукции. Для различных моментов времени ток в цепи, выраженный в процентах конечного (установившегося) значения составляет:
Следовательно, постоянная времени цепи г, L равна промежутку времени, в течение которого свободная составляющая тока убывает в е = 2,718 раза и соответственно ток в этой цепи, включенной на постоянное напряжение, достигает 63,2% своего установившегося значения.
Как видно из рис. 14-3 и приведенной выше таблицы”, переходный процесс теоретически длится бесконечно долго. Практически же можно считать, что он заканчивается спустя
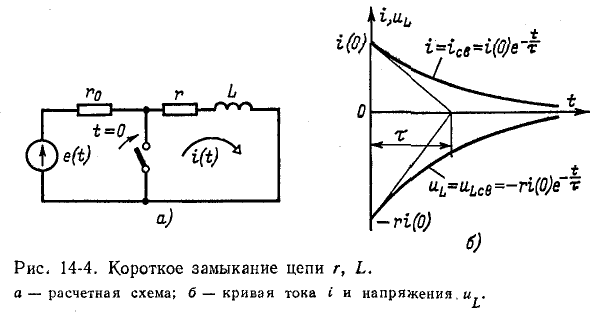
2. Короткое замыкание цепи r, L.
Положим, что цепь r, L, присоединенная к источнику постоянного или переменного напряжения, замыкается при t = 0 накоротко (рис. 14-4, а). В образовавшемся при этом контуре r, L благодаря наличию магнитного поля индуктивной катушки ток исчезает не мгновенно: э. д. с. самоиндукции, обусловленная убыванием магнитного потока, стремится поддержать ток в контуре за счет энергии исчезающего магнитного поля.
По мере того как энергия магнитного поля постепенно рассеивается, превращаясь в сопротивлении г в тепло, ток в контуре приближается к нулю.
Процесс, происходящий в короткозамкнутом контуре г, L, является свободным; установившийся ток в данном случае равен нулю.
Положив в (14-9)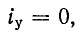
Постоянная интегрирования А находится из начального условия
откуда
здесь i (0—) — значение тока в индуктивности в момент, непосредственно предшествовавший короткому замыканию; оно может быть положительным или отрицательным.
На рис. 14-4, б изображены кривые спада тока в короткозамкнутом контуре и кривая напряжения на индуктивности

Постоянная времени контура 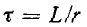
Переходный процесс в короткозамкнутом контуре заканчивается теоретически при 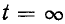
т. е. вся энергия, запасенная в магнитном поле катушки до коммутации.
Так же как и в предыдущем случае, переходный процесс в короткозамкнутом контуре можно практически считать законченным спустя
3. Включение в цепь r, L синусоидальной э. д. с.
При включении в цепь r, L синусоидальной э. д. с. 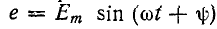
где
На основании (14-9)
где
Постоянная интегрирования определяется по начальному условию
Следовательно, 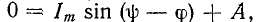
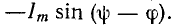
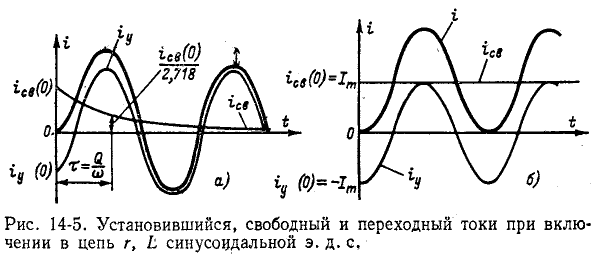
На рис. 14-5, а изображены кривые 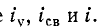
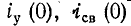
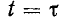
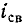
контура Q и обратно пропорциональна частоте
Если в момент коммутации (t = 0) ток 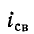
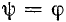
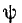
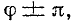
Если же коммутация происходит при 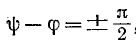
а именно 
гает экстремального значения (положительного или отрицательного) в конце первого полупёриода. Однако даже в предельном случае, когда r= 0 и, следовательно, 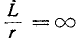
При достаточно большой постоянной времени 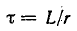
можно пренебречь по сравнению со вторым слагаемым, приняв приближенно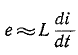
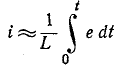
Следовательно, цепь с последовательно соединенными сопротивлением и индуктивностью при большой постоянной времени можно рассматривать как интегрирующее звено.
В свою очередь при достаточно малой постоянной времени, пренебрегая вторым слагаемым уравнения, приближенно получаем:
откуда
.
т. e. цепь с последовательно соединенными сопротивлением и индуктивностью при малой постоянной времени представляет собой дифференцирующее звено.
В обоих случаях функция е(t) может быть произвольной.
Интегрирующие и дифференцирующие звенья входят в качестве элементов в системы автоматического управления и регулирования.
Переходный процесс в цепи r, С
Положим, что в момент t = О цепь, состоящая из сопротивления г и емкости С, включенных последовательно, присоединяется к источнику э. д. с. е (t) (рис. 14-6).
На основании второго закона Кирхгофа уравнение для времени t
где 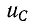
С учетом того, что
получим:
здесь искомой величиной является напряжение на емкости.
Характеристическое уравнение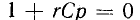
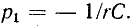
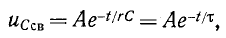
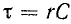
Переходное напряжение на емкости равно сумме принужденного и свободного напряжений:
В свою очередь ток в контуре
Рассмотрим три случая:
1) включение в цепь г, С постоянной э. д. с.
2) короткое замыкание цепи r, С
3) включение в цепь r, С синусоидальной э. д. с.
Включение в цепь r, С постоянной э. д. с.
Включим постоянную э. д. с. Е в цепь с сопротивлением г и предварительно заряженной емкостью С (полярности заряженной емкости указаны на рис. 14-6 знаками + и —); начальное напряжение на емкости
(0) обозначим для простоты через U.
Установившееся напряжение на емкости равно э. д. с. источника. Поэтому согласно (14-12)
Постоянная интегрирования А, входящая в (14-14), находится по начальному условию:
При t = 0 имеем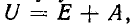
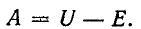
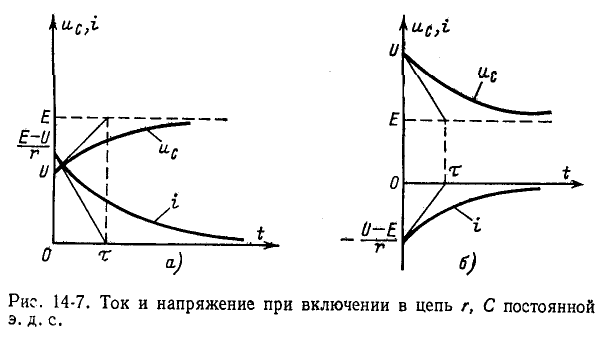
Согласно (14-13) ток в контуре
Если Е > U, то с течением времени напряжение на емкости возрастает, стремясь к установившемуся значению Е, а ток убывает, стремясь в пределе к нулю; на рис. 14-7, а изображены кривые нарастания 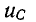
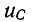
Если Е < U, то кривые 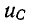
Постоянная времени 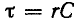
Закон изменения напряжения на емкости и тока в данной цепи аналогичен закону изменения тока и напряжения 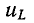
Короткое замыкание цепи r, С
Замыкание накоротко цепи, состоящей из последовательно соединенных г и С, равносильно принятию в предыдущем случае э. д. с., равной нулю. Предполагается, что емкость С заряжена, т. е. в момент включения на выводах имеется напряжение U.
Положив в (14-15) и (14-16) э. д. с. Е равной нулю, получим:
где
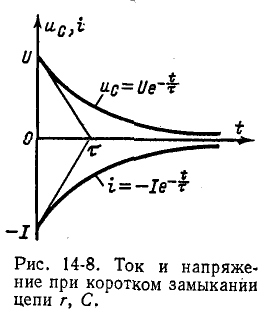
При коротком замыкании цепи r, С электрический ток идет от вывода + к выводу — Следовательно, при выбранной на рис. 14-6 полярности емкости ток проходит через сопротивление r в направлении, противоположном тому, которое принято на рис. 14-6 за положительное. Поэтому в выражении для тока стоит знак минус. На рис. 14-8 изображены кривые спала 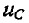
В отличие от напряжения на емкости, которое изменяется непрерывно, ток в контуре r, С, пропорциональный скорости изменения 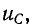
Энергия, рассеиваемая в сопротивлении г в течение всего переходного процесса, равна энергии, запасенной в электрическом поле до коммутации:
Так же как и в случае цепи r, L, переходный процесс может считаться законченным спустя 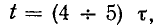
к этому времени емкость разрядится на 98,2—99,3% и напряжение на емкости снизится до 1,8—0,7% первоначального.
Включение в цепь г, С синусоидальной э. д. с.
При включении в цепь r, С синусоидальной э. д. с. установившееся напряжение на емкости
на основании (14-12)
Если предполагать, что конденсатор не был заряжен, то постоянная интегрирования определится по начальному условию 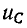
откуда
Тогда искомое напряжение на емкости будет:
а ток в цепи
Из написанных выражений видно, что если включение цепи r, С происходит в момент, когда установившийся ток должен достигать максимума — положительного или
отрицательного (т. е. 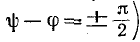
напряжение на емкости должно быть равно нулю, то свободной слагающей напряжения на емкости не возникает и в цепи сразу же без переходного процесса наступает установившийся режим.
Так как цепь г, С по протеканию переходного процесса подобна цепи г, L, то при соответствующем подборе параметров г и С она также может служить дифференцирующим и интегрирующим звеном.
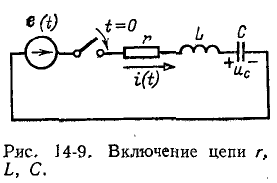
Переходный процесс в цепи r, L, С
При включении в цепь г, L, С э. д. с. е (t) (рис. 14-9) переходный процесс исследуется с помощью дифференциального уравнения (14-3):
Соответствующее ему характеристическое уравнение (14-5)
имеет корни
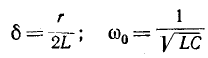
Свободный ток согласно (14-6) равен:
Ток в цепи определяется суммой установившегося и свободного токов:
Установившийся ток находится в соответствии с заданной э. д. с. е (t). Что касается свободного тока, то его характер зависит от знака подкоренного выражения (14-17).
Включение в цепь г, L, С постоянной э. д. с.
Рассмотрим сначала случай, когда э. д. с. источника постоянна: е = Е, и емкость имеет начальное напряжение
Ввиду наличия индуктивности начальное значение тока i (0) = 0.
Исходное уравнение
для начального момента записывается в виде
откуда находится начальное значение производной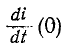
которое является зависимым начальным условием, необходимым для вычисления 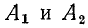
При установившемся режиме ток будет равен нулю, что следует как из физического смысла, так и из вида правой части дифференциального уравнения (14-3). Продифференцировав (14-18) с учетом того, что 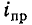
Подставляя в (14-18) и (14-20) t = 0 и используя (14-19), получаем:
Из этих уравнений следует:
поэтому
Рассмотрим возможные три случая.
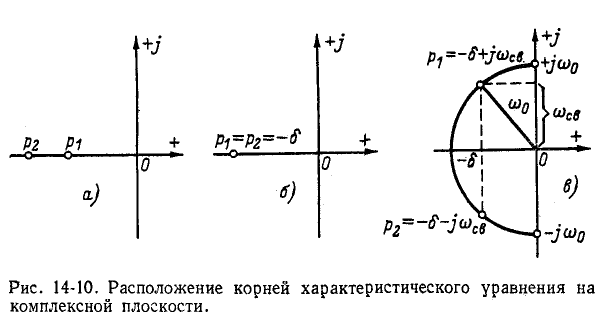
Случай 1. 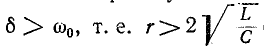
Согласно (14-17) корни характеристического уравнения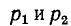
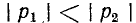
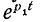
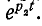
При больших значениях С влияние емкости мало и кривая тока приближается к кривой тока в цепи r, L (см. рис. 14-3); при малых значениях L влияние индуктивности незначительно и кривая тока близка к кривой тока в цепи г, С (рис. 14-7).
Выражение (14-21) может быть преобразовано в гиперболическую форму
Следует заметить, что при коротком замыкании цепи г, L, С, т. е. при Е = О, ток в цепи обусловливается разрядом емкости.
Случай 2.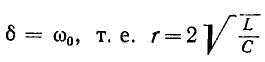
Согласно (14-17) корни характеристического уравнения одинаковы:
(см. рис. 14-10, б).
Выражение (14-21) приводит в этом случае к неопределенности вида 0/0.
Раскрывая неопределенность по правилу Лопиталя дифференцированием числителя и знаменателя по 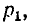
To же выражение получится, если воспользоваться общим решением однородного дифференциального уравнения с кратными корнями:
В рассматриваемом случае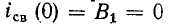
Следовательно,
Кривая тока аналогична кривой i на рис. 14-11.
Случай 3. 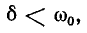
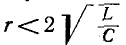
Корни характеристического уравнения комплексные и сопряженные:
Согласно (14-24)
Корни характеристического уравнения располагаются симметрично относительно действительной оси в левой полуплоскости, на полуокружности, центр которой совпадает с началом координат, а радиус равен 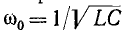
Сопоставление рис. 14-10, а, б к в показывает, что о характере переходного процесса в цени г, L, С можно судить по расположению корней характеристического уравнения, т. е. нулей функции Z (р), на комплексной плоскости.
Если расположенные в левой полуплоскости нули функции Z (р) лежат на действительной оси, то имеет место апериодический процесс: совмещению нулей в одной точке отвечает критический случай; наконец, если нули функции Z (р) являются комплексно-сопряженными, то имеет место колебательный процесс.
Величина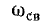
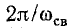
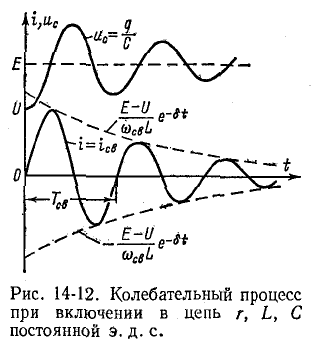
Полученное выражение показывает, что при включении цепи г, L, С на постоянное напряжение, когда 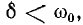
(рис. 14-12). Колебания возникают вследствие периодического преобразования энергии электрического поля в энергию
* Тот же результат получится, если исходить из общего решения однородного дифференциального уравнения с комплексно-сопряженными корнями:
магнитного поля и обратно, причем эти колебания сопровождаются потерей энергии в сопротивлении.
При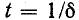
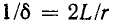
На рис. 14-12 показана также кривая напряжения 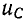
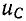
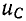
Как видно из (14-23) и рис. 14-10, в, угловая частота этих колебаний 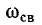
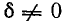
Чем меньше 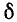
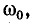
В пределе, при 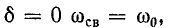
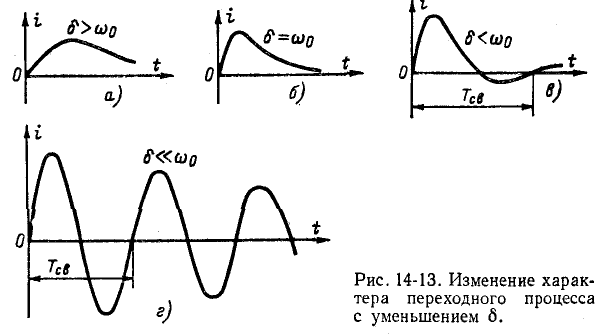
О быстроте затухания колебательного процесса судят по величине 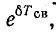
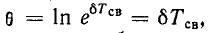
На рис. 14-13, а—г показано изменение характера переходного процесса при уменьшении
Приведенные выше величины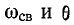
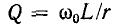
При достаточно высокой добротности 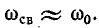
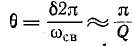
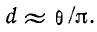
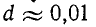
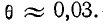
Включение в цепь г, L, С синусоидальной э. д. с.
Если цепь г, L, С присоединяется к источнику синусоидальной э. д. с.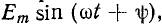
ток равен:
и переходный ток согласно (14-18) равен:
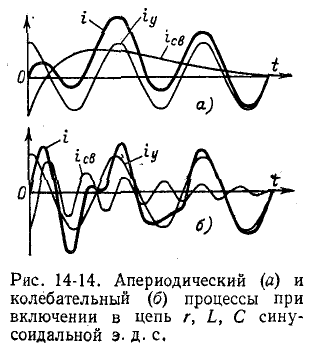
Кривые установившегося, свободного и- переходного токов при апериодическом и колебательном процессах показаны в виде примера на рис. 14-14.
Частота установившегося тока равна частоте источника синусоидального напряжения, свободный же ток при 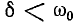
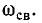
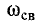
Свободные колебания тока накладываются на установившийся ток и затухают пропорционально множителю 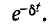
Та из двух слагающих тока i, частота которой меньше, служит как бы криволинейной осью для другой слагающей, колеблющейся относительно нее (рис. 14-14, б). При близком совпадении частот 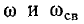
Расчет переходного процесса в разветвленной цепи
Переходный процесс в разветвленной линейной электрической цепи описывается системой линейных дифференциальных уравнений с постоянными коэффициентами, общее решение которых находится как сумма установившейся и свободной составляющих.
Рассмотрим сначала методику расчета установившегося режима.
Во многих случаях воздействующая функция, например
э. д. с. источника, может быть представлена в обобщенной форме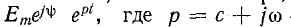
Условие 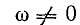
Условие 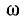
Задавшись э. д. с. 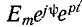
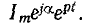
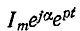
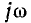
В зависимости от схемы и постановки задачи Z (р) означает обобщенное входное сопротивление или величину, обратную обобщенной передаточной проводимости;Z (р) получается из соответствующего комплексного сопротивления заменой
Мгновенные значения тока определяются мнимой или действительной частью
В случае синусоидальной э. д. с. (с = 0; р 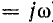
Если э. д. с. есть показательная функция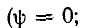
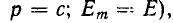
где
При постоянной э. д. с. 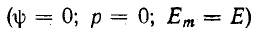
где z (0) — сопротивление при постоянном токе.
Перейдем теперь к рассмотрению свободного режима.
Свободные составляющие представляют собой общее решение системы однородных линейных дифференциальных уравнений. Для заданной цепи степень характеристического уравнения не зависит от выбора контуров, для которых составляются уравнения по второму закону Кирхгофа. Однако если выбрать контуры так, чтобы порядок дифференциальных уравнений был наименьшим, то степень характеристического уравнения не будет превышать суммы порядков исходных дифференциальных уравнений системы. При этом, как будет показано ниже, для получения характеристического уравнения отнюдь не обязательно приводить систему дифференциальных уравнений к одному уравнению относительно одной неизвестной функции.
Корни характеристического уравнения могут быть действительными или комплексными. Если корни комплексные, то они всегда образуют комплексно сопряженные пары. В связи с этим характеристическое уравнение нечетной степени всегда имеет хотя бы один действительный корень, остальные же корни могут быть действительными или комплексно-сопряженными; характеристическое уравнение четной степени имеет четное число действительных или комплексно-сопряженных корней. Действительные части всех корней характеристического уравнения всегда отрицательны, что физически обусловлено затуханием свободных составляющих в пассивных цепях с течением времени. При этом все коэффициенты характеристического уравнения должны быть действительными и положительными.
Корни единого характеристического уравнения используются для нахождения в данной цепи свободных составляющих как токов, так и напряжений.
Допустим, что характеристическое уравнение имеет п корней. Тогда свободный ток в любой ветви
здесь 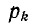
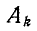
Аналогичная структура решения получается и для свободных составляющих напряжений.
В случае, когда 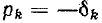
Если имеются сопряженные комплексные корни, например 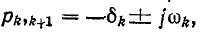
преобразуется в
Для m-кратных сопряженных комплексных корней решение принимает вид:
Методика получения характеристического уравнения иллюстрирована ниже на примере двухконтурной схемы, изображенной на рис. 14-17.
Первый контур содержит сопротивления 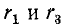
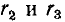
Соответственно степень характеристического уравнения равна 2.
Для получения характеристического уравнения применяется следующий прием. Система дифференциальных уравнений для свободных слагающих токов
записывается в символической алгебраической форме, при которой символ р заменяет операцию дифференцирования, а символ 1/р — операцию интегрирования:
Данная система уравнений имеет решение, отличное от нулевого, если определитель системы равен нулю, т. е.
или
Таким образом, получается характеристическое уравнение второй степени
Ввиду прямой пропорциональности, существующей между входным сопротивлением цепи Z (р) и определителем системы 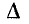
Операторное сопротивление Z (р) получается из комплексного сопротивления 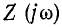
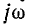
Если характеристическое уравнение имеет степень л, то искомыми являются п постоянных интегрирования 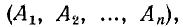
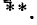
(n — 1)-кратного дифференцирования уравнения (14-26):
Значения свободного тока и его производных при t =0, входящие в (14-27), находятся предварительно на основании законов коммутациии уравнений Кирхгофа.
Для определения начальных значений токов и напряжений в цепи можно для наглядности воспользоваться схемой замещения, которая составляется из исходной схемы после коммутации, если заменить индуктивности идеальными источниками тока с токами, равными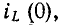
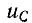
При нулевых начальных условиях индуктивность равносильна разрыву ветви, а емкость — короткому замыканию.
По этой схеме замещения можно найти другие токи и напряжения в момент t=0, если воспользоваться уравнениями Кирхгофа или правилами преобразования схем.
Итак, в соответствии со сказанным выше расчет переходного процесса классическим методом проводится в следующем порядке:
- Производится расчет режима до коммутации, из которого определяются конечные значения (т. е. при t=0—) функций, не меняющихся скачком (токов в индуктивностях, напряжений на емкостях). Далее с использованием законов коммутации находятся независимые начальные условия, т. е.
- Составляется система дифференциальных уравнений Кирхгофа, описывающая процесс в цепи после коммутации.
- Находится общее решение системы однородных дифференциальных уравнений.
- Находится тем или иным методом частное решение системы неоднородных дифференциальных уравнений, указанных в n. 2, соответствующее принужденному режиму цепи.
- Определяются зависимые начальные условия для искомых функций на основании найденных в п. 1 независимых начальных условий и уравнений Кирхгофа из п. 2, примененных для t = 0.
- По начальным условиям определяются постоянные интегрирования, содержащиеся в общем решении.
- Найденные установившиеся и свободные токи и напряжения складываются
Приведенный ниже пример 14-1 иллюстрирует нахождение начальных условий; в примере 14-2 дан численный расчет переходного процесса в цепи на рис. 14-17.
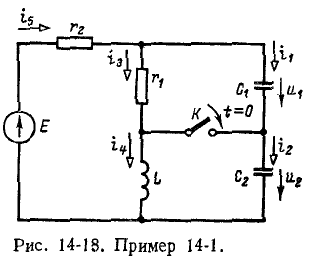
Пример 14-1. В цепи, изображенной на рис. 14-18, моменту t= 0 предшествовал установившийся режим постоянного тока. При t = 0 замкнулся контакт К. Найти начальные значения тока в.индук- is & тивности и напряжений на емкостях и их первых производных.
Независимыми начальными условиями будут ток в индуктивности 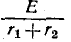
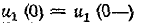
Напряжения на емкостях до коммутации находятся из условий равенства их зарядов (так как емкости соединены последовательно) и равенства суммарного напряжения на емкостях напряжению на сопротивлении
откуда
Требуемые зависимые начальные условия определятся из уравнений
1В случае, когда э. д. с. изменяется в виде импульса, имеющего кусочно-аналитическую форму, представляется часто целесообразным применять интеграл Дюамеля
токи же 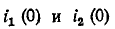
Подстановка в эти уравнения найденных значений 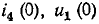
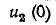
и далее
Начальное значение производной тока в индуктивности определяется также из уравнения Кирхгофа:
откуда при t = О
Пример (4-2. Определить ток i в иепи на рис. 14-17, если известно, что е = E = 100 В,
Подстановка заданных значений в приведенное выше характеристическое уравнение дает:
или
корни характеристического уравнения комплексные:
Искомый ток
Установившийся ток
Свободный ток
В начальный момент 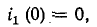
Производная тока по времени
В начальный момент
Следовательно, в начальный момент напряжение на ветви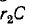
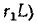
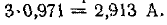
производной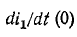
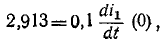
Следовательно, подставляя значение 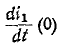
откуда
Итак,
Переходные процессы в цепях с распределенными параметрами
Переходные процессы в цепях с распределенными параметрами (в линиях, обмотках электрических машин и т. п.) возникают при коммутациях, передаче непериодических сигналов или под влиянием внешнего электромагнитного поля (например, при грозовых разрядах). Для исследования переходных процессов в однородных цепях с распределенными параметрами пользуются дифференциальными уравнениями (11-2) в частных производных:
где r, L, g и С — параметры цепи на единицу длины; х — координата рассматриваемой точки, отсчитываемая от начала цепи.
В общем виде решение этих дифференциальных уравнений достаточно сложно. Решение упрощается, если пренебречь потерями В этом случае
е. считать, что r и g равны нулю.
В этом случае
Дифференцируя (14-28) по х:
и используя (14-29), получаем:
Дифференциальное уравнение (14-30) известно в математической физике под названием уравнения ко–лебаний струны. Его решение дано Даламбером и имеет вид:
где
Первая слагающая представляет собой одиночную прямую волну напряжения, которая без изменения перемещается в сторону возрастающих х, т. е. от начала к концу цепи. Для всех значений х, при которых 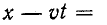
Вторая слагающая представляет собой одиночную о б -ратную волну напряжения, которая без изменения перемещается в противоположном направлении.
Для нахождения тока произведем замену переменных, обозначив 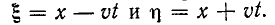
Но
и
Следовательно,
Интегрирование последнего уравнения дает
Выражения (14-31) и (14-32) записываются сокращенно:
здесь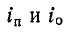
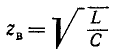
Следовательно, напряжение и ток прямой и соответственно обратной волн связаны законом
Аналогичный результат был получен для установившихся прямой и обратной волн при рассмотрении синусоидального режима в однородной линии. Физически установившиеся волны представляют собой бесконечные суммы прямых и обратных одиночных волн, отраженных от обоих концов линии.
Итак, при отсутствии потерь в однородной цепи с распределенными параметрами напряжение и ток могут быть представлены как сумма и разность двух волн, движущихся с одинаковой скоростью 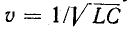
Если на пути распространения волны встречается неоднородность, например воздушная линия переходит в кабельную или волна достигает конца линии (разомкнутого или замкнутого через сопротивление или на короткое), происходит отражение волны. В зависимости от характера неоднородности отражение может быть частичным или полным. В первом случае наряду с отраженной волной возникает преломленная волна, распространяющаяся за место нарушения однородности; во втором случае преломленная волна отсутствует.
Обозначим 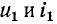
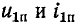
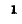
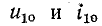
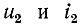
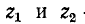
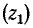
В месте неоднородности выполняется условие равенства
напряжений и токов:
Следовательно,
Подстановка в (14-36) значений 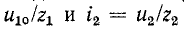
В результате совместного решения уравнений (14-35) — (14-37) находятся отраженная 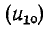
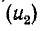
где 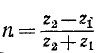
Соответственно ток отраженной волны
а ток преломленной волны
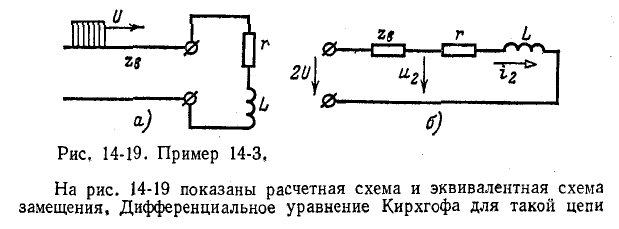
Последнее выражение показывает, что ток в конце линии после отражения можно найти как ток в эквивалентной цепи, в которую включается напряжение, равное двойному напряжению падающей волны, и которая состоит из волнового сопротивления первой линии 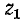
Опишем процесс включения однородной линии без потерь. После присоединения линии к источнику э. д. с. по линии начнет распространяться зарядная волна, создающая напряжение и ток. Если в конце линии присоединена нагрузка, равная волновому сопротивлению линии,
то падающая волна, достигнув ее, не отразится и в линии сразу наступит установившийся режим. Если же нагрузка с линией не согласована, то падающая зарядная волна, достигнув конца линии, претерпит отражение. Распространяясь в обратную сторону, отраженная волна сложится с падающей, причем напряжения волн суммируются, а токи вычитаются (алгебраически). Достигнув начала линии, обратная волна снова отразится от источника э. д. с., как от короткозамкнутого конца; появится новая прямая волна напряжения и тока, которая также отразится от конца, и т. д. Процесс будет продолжаться до наступления установившегося режима. Теоретически в идеальной линии без потерь при чисто реактивной нагрузке процесс колебаний будет продолжаться бесконечно долго. В реальной линии при наличии потерь волны напряжения и тока будут постепенно затухать в направлении распространения.
Напряжение и ток в линии в произвольный момент времени определятся как алгебраические суммы и соответственно разности напряжений и токов прямых и обратных волн.
Пользуясь формулами и схемой замещения, описанной выше, можно найти напряжение и ток, возникающие в месте присоединения сосредоточенной нагрузки или перехода одной линии в другую (см. пример 14-3).
Следует отметить что индуктивность, включенная последовательно в линию, или емкость, включенная параллельно проводам линии, сглаживает фронт преломленных волн; активное сопротивление, включенное в линию параллельно, уменьшает преломленную волну.
Пример 14-3. К концу линии, имеющей волновое сопротивление 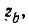
запишите так:
откуда
и
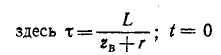
- Переходные процессы в линейных цепях
- Переходные процессы в нелинейных цепях
- Переходные процессы в электрических цепях с сосредоточенными параметрами
- Переходные процессы в колебательных контурах
- Цепи с взаимной индукцией
- Трехфазные цепи
- Периодические несинусоидальные напряжения и токи в линейных цепях
- Нелинейные цепи переменного тока