Как найти течение призмы - Сайт, где вы сможете решить свои вопросы

УДК 539.374

ПРОСТРАНСТВЕННАЯ ЗАДАЧА МАТЕМАТИЧЕСКОЙ ТЕОРИИ ПЛАСТИЧНОСТИ (КИНЕМАТИЧЕСКИЕ СООТНОШЕНИЯ, ОПРЕДЕЛЯЮЩИЕ ТЕЧЕНИЕ НА ГРАНИ И РЕБРЕ ПРИЗМЫ КУЛОНА-ТРЕСКА)

Ю.Н. Радаев

Самарский государственный университет, кафедра механики сплошных сред E-mail: radayev@ssu.samara.ru

В работе приводится вывод правильно определенной системы уравнений, описывающей кинематику пространственного идеально пластического течения на ребре призмы Кулона – Треска, и дано исследование основных кинематических уравнений (включая пространственные соотношения Коши и уравнения совместности для приращений деформаций) с помощью триортого-нальной изостатической системы координат. Устанавливаются правильная определенность и гиперболичность системы уравнений для приращений перемещений и находятся ее характеристические направления. Выводятся соотношения для приращений перемещений вдоль линий главных напряжений, обобщающие известные соотношения Гейрингер. Отдельно рассматриваются кинематические соотношения для случаев плоского деформированного и осесимметричного состояний. Исследована кинематика скольжения на поверхностях максимальной скорости сдвига. Показано, что скольжения на указанной поверхности происходят вдоль асимптотических направлений, если поверхность максимальной скорости сдвига имеет отрицательную Гауссову кривизну. Поэтому сдвиговое пластическое течение вблизи поверхности максимальной скорости сдвига (отрицательной Гауссовой кривизны) реализуется как результат микроскольжений в асимптотических направлениях. Получены интегрируемые соотношения для разрывов касательных составляющих приращений перемещений вдоль асимптотических линий поверхности максимальной скорости сдвига. Рассмотрены кинематические соотношения в областях эллиптичности, т.е. когда Гауссова кривизна положительна, поверхности максимальной скорости сдвига.

Three-Dimensional Problem of Perfect Plasticity (Kinematic Equations Determining Three-Dimensional Plastic Flow for a Facet and Edge of the Tresca Prism)

Yu.N. Radayev

In the present study a system of partial differential equations which describes kinematic of three-dimensional plastic flow for the states corresponding to an edge of the Tresca prism is obtained. The system includes the Cauchy equations and the compatibility equations formulated for the displacements and strains increments. These equations are then analysed by the aid of the triorthogonal isostatic co-ordinate net. The system of kinematic equations is shown correctly determines displacements increments and be of the hyperbolic type. Relations for the displacements increments valid along principal stress lines are derived. Kinematic of plane and axial symmetric plastic flow are separately considered for each case. Kinematic equations for states corresponding to a facet of the Tresca prism which are of the less importance are also examined. Slip kinematic on a surface of maximum shear strain rate in perfectly plastic continuous media is studied. Sliding on the surface is shown can be realized only along asymptotic directions and only within hyperbolic zones of the surface (wherein the Gaussian curvature of the surface is negative). Integrable equations along asymptotic lines of the maximum shear strain rate surface for the jumps of tangent velocities are obtained. Kinematic equations corresponding to elliptic zones on a maximum shear strain rate surface (i.e. if the Gaussian curvature of the surface is positive) are derived and analysed.

ВВЕДЕНИЕ

Проблема поиска такой математической теории идеальной пластичности, которая приводила бы в зоне пластического течения к соотношениям гиперболического типа для произвольных пространственных состояний, по-прежнему сохраняет свою актуальность, поскольку при использовании условий пластичности, отличных от условия пластичности Кулона – Треска, для подавляющего большинства пространственных состояний уравнения теории идеальной пластичности не имеют вещественных характеристических направлений. Так, пространственная задача математической теории пластичности в общем случае при условии пластичности Мизеса (R. von Mises) и ассоциированным с ним законом течения является статически неопределимой, и, кроме того, уравнения пространственной задачи не гиперболичны. Точнее говоря, уравнения пространственной задачи либо полностью эллиптичны (т.е. не существует действительных характеристических направлений), либо (если в рассматриваемой точке медианная скорость пластической деформации равна нулю) имеется только два характеристических элемента, совпадающих с площадками максимального касательного напряжения. Все это свидетельствует о том, что в подавляющем большинстве пространственных состояний, описываемых согласно условию пластичности Мизеса и ассоциированному с ним закону течения, действительные

характеристики отсутствуют. Не спасает положения учет упругих деформаций. Фактор упрочнения в принципе гарантирует эллиптичность уравнений. Аналогичное заключение остается справедливым и для теории малых упругопластических деформаций, и для редко применяемых в настоящее время неассоциированных законов пластического течения. После осмысления всех этих результатов в отчетливой форме и была сформулирована задача: найти такие определяющие зависимости, чтобы в области пластического течения всегда существовали, по меньшей мере, два семейства характеристических поверхностей, получив тем самым пространственные уравнения теории идеальной пластичности, адекватно описывающие скольжение.

Подытоживая почти полувековую дискуссию по указанной проблематике, можно сказать, что предельные состояния идеально пластических тел должны описываться статически определимыми уравнениями гиперболического типа. Именно такое положение дел имеет место в пространственной задаче теории идеальной пластичности при использовании критерия текучести Кулона – Треска. Здесь уравнения пластического равновесия в ряде важных случаев становятся статически определимыми и гиперболическими. Основополагающими работами этого важнейшего направления современной теории пластичности выступают статьи Д.Д. Ивлева [1], [2]. В монографии [3] с помощью изостатической координатной сетки были исследованы основные соотношения пространственной задачи математической теории пластичности для течения на ребре призмы Кулона – Треска.

Целью представляемой работы являются вывод правильно определенной системы уравнений, описывающей кинематику пространственного пластического течения на ребре призмы Кулона – Треска, и исследование кинематических уравнений с помощью триортогональной изостатической системы координат.

В первом параграфе статьи рассматриваются трехмерные уравнения равновесия для напряженных состояний, соответствующих ребру условия текучести Кулона – Треска, дается их классификация и с помощью геометрических условий совместности Адамара – Томаса определяются характеристические направления. Здесь же выводится ряд замечательных инвариантных форм указанных уравнений. Во втором параграфе исследуются уравнения обобщенного ассоциированного закона течения на ребре призмы Кулона – Треска и основные соотношения для приращений перемещений, следующие из него. Устанавливаются правильная определенность и гиперболичность системы уравнений для приращений перемещений и находятся ее характеристические направления. Затем (см. параграф 3 представляемой работы) анализируются уравнения математической теории пластичности для грани призмы Кулона – Треска и доказывается, что задача для приращений перемещений является неправильно определенной: три компоненты приращения вектора перемещений должны удовлетворять пяти независимым уравнениям. В следующем параграфе работы выводятся пространственные соотношения Коши в приращениях относительно триортогональной изостатической координатной сетки. Триортогональная изостатическая координатная сетка характеризуется тем, что ее координатные линии суть взаимно ортогональные траектории главных напряжений. В тех случаях, когда указанная координатная сетка существует, оказывается наиболее естественным рассматривать те или иные тензорные уравнения относительно именно таких криволинейных координат. Кинематические соотношения для пространственного пластического течения исследуются в пятом параграфе с помощью изостатических координат. Далее (параграф 6) приводятся уравнения совместности для приращений деформаций, а затем — вывод кинематических соотношений для случаев плоского деформированного и осесимметричного состояний (параграфы 7 и 8). Заканчивается работа параграфом 9, где дан анализ пластического скольжения на поверхности максимальной скорости сдвига и доказывается, что скольжения на указанной поверхности происходят вдоль асимптотических направлений.

1. УРАВНЕНИЯ РАВНОВЕСИЯ ДЛЯ СОСТОЯНИЙ, СООТВЕТСТВУЮЩИХ РЕБРУ ПРИЗМЫ КУЛОНА – ТРЕСКА

Условие текучести Треска, или условие максимального касательного напряжения, имеет следующий вид:

тах{о1 – о21, о1 – аз|, о2 – оз} = У, (1.1)

где о1, о2, о3 — собственные значения тензора напряжений (главные нормальные напряжения); У —

предел текучести при одноосном растяжении. Величины

02 — 03 03 — 01 01 — 02

Т1 = 2 ’ Т2 = 2 ’ Т3 = 2

называются главными касательными напряжениями и представляют собой экстремальные значения касательных напряжений для всех возможных площадок, проходящих через заданную точку. Пространственное напряженное состояние в данной точке весьма просто анализируется с помощью графического метода Мора (O.Mohr), который дает также простую схему для определения величины нормального и касательного напряжения в зависимости от ориентации площадки в пространстве [4].

Условие текучести Треска устанавливает, что величина Y связана с величиной k (пределом текучести при чистом сдвиге) простым соотношением Y = 2k.

Уравнение призмы Кулона – Треска (1.1), очевидно, можно также представить в форме

[(01 — 02)2 — Y2] [(03 — 0i)2 — Y2] [(02 — 03)2 — Y2] = 0. (1.2)

В пространстве главных напряжений поверхность текучести, определяемая уравнением (1.2), представляет собой правильную шестигранную призму (призма Кулона – Треска), ось которой равнона-клонена к декартовым осям этого пространства. Кривая текучести (сечение призмы Кулона – Треска девиаторной плоскостью 01 + 02 + 03 = 0) представляет собой правильный шестиугольник с центром в начале координат и стороной, равной 2/3Y.

Рассмотрим уравнения равновесия для напряженных состояний, соответствующих ребру призмы

Кулона – Треска. Обозначим через с тензор напряжений; l, m, n — ортонормированный базис из

собственных векторов тензора напряжений.

Спектральное разложение тензора напряжений имеет вид

с = 011 ® l + 02m ® m + 03n ® n. (1.3)

В пространстве главных напряжений ребра призмы Кулона – Треска определяются уравнениями

01 ± 2k = 02 = 03, 01 = 02 ± 2k = 03, 01 = 02 = 03 ± 2k.

Для данного напряженного состояния, соответствующего ребру призмы Треска, всегда можно перенумеровать главные оси тензора напряжений так, чтобы выполнялось равенство

01 = 02 = 03 ± 2k.

Последнее условие означает, что два главных напряжения равны по величине, а главное напряжение

03 является либо наименьшим, либо наибольшим главным нормальным напряжением.

Сделаем одно существенное для всего дальнейшего изложения замечание. Равенство двух главных напряжений 01 = 02 означает, что любое направление, расположенное в плоскости, ортогональной вектору n, является главным. Ясно поэтому, что при соответствии напряженного состояния ребру призмы Кулона – Треска имеется известная доля произвола при выборе собственных векторов l и m (они определены с точностью до поворотов в плоскости, ортогональной вектору n). Их преимущественное положение в упомянутой плоскости может быть указано только либо 1) после анализа тензора приращений пластических деформаций dsP, который в силу ассоциированного закона течения должен быть соосен тензору напряжений с и обладает, вообще говоря, уникальным триэдром

главных направлений; либо 2) условиями «подгонки» триэдра 1, m, n до триортогональной системы.

Все эти вопросы будут затронуты в параграфе 2.

Так как l, m, n — ортонормированный базис, то

1 ® 1 + m ® m + n ® n = I, (1.4)

где I — единичный тензор.

Учитывая (1.3), (1.4) и уравнение ребра призмы Кулона – Треска 01 = 02 = 03 ± 2k, получим

с = (03 ± 2k)I ^ 2kn ® n. (1.5)

Таким образом, тензор напряжений определяется скалярным полем аз и единичным векторным полем n.

Уравнение равновесия V ■ а = О после подстановки в него разложения (1.5) можно представить в следующем виде:

gradаз ^ 2kdiv(n ® n) = О (n ■ n = І). (1.6)

Следовательно, задача о равновесии тела, напряженное состояние которого соответствует ребру призмы Кулона – Треска, формально статически определима (поскольку имеется ровно три уравнения для определения трех неизвестных: собственного значения аз и, например, двух углов, задающих ориентацию единичного вектора n), если граничные условия заданы в напряжениях. Уравнения равновесия могут быть рассмотрены независимо от кинематических уравнений.

Обозначим через Е безразмерное отношение аз к ^2k и приведем уравнение (1.6) к виду:

gradE + div(n ® n) = О (n ■ n = І). (1.7)

В декартовых координатах векторное уравнение (1.7) эквивалентно системе трех скалярных уравнений (i, k = І, 2,3):

дЕ дп. дп^

т;—-+ nk—–+ Пі-— =0 (nfc nk = І).

дхі дх& дх&

Отметим также еще одну инвариантную форму уравнения (1.7):

VE + (n ■ V)n + n(V ■ n) = О, (1.В)

где V — пространственный оператор Гамильтона.

Для единичного векторного поля справедлива формулаІ

(n ■ V)n = —n x rot n, (1.9)

с помощью которой векторное уравнение (1.В) может быть также представлено в виде

VE — n x rot n + n div n = О. (1.10)

Исследуем характеристики уравнения (1.10). Для этого будем трактовать характеристические по-

верхности уравнения (1.10) как поверхности слабого разрыва Е и n и воспользуемся условиями совместности Адамара – Томаса [5]:

[VE] = BN, [V 0 n] = N 0 b, (1.11)

где [ ■ ] обозначает скачок при переходе через поверхность слабого разрыва; N — единичный вектор

нормали к поверхности слабого разрыва; B, b — некоторые поля, определенные на этой поверхности,

причем равенства B = 0 и b = О не могут выполняться одновременно ни в какой точке поверхности, если рассматриваемая поверхность есть действительно поверхность слабого разрыва.

На основании уравнения (1.10) имеем:

[VE] — n x [rot n] + n [div n] = О (1.12)

и, применяя условия совместности (І.ІІ), получим

BN — n x (N x b) + (N ■ b)n = О. (1.1З)

Кроме того, так как n ■ n = І, то n ■ (V 0 n)T = О и, следовательно, (b ■ n)N = О, что приводит к

следующему соотношению на поверхности слабого разрыва:

b ■ n = 0. (1.14)

ІПриводимая ниже формула является прямым следствием тождества

2 V(n • n) = (n • V)n + n X rot n

и условия нормировки n • n =1.

Замечая, что n х (N х b) = (n ■ b)N — (N ■ n)b, и учитывая (1.14), уравнение (1.13) приводим к виду

BN + (N ■ n)b + (N ■ b)n = 0. (1.15)

Умножим обе части этого уравнения скалярно на вектор N:

B + 2(N ■ n)(N ■ b) = 0. (1.16)

Умножая обе части уравнения (1.15) скалярно на вектор n, получим также

B(N ■ n) + N ■ b = 0. (1.17)

Подставляя в это уравнение выражение для B, полученное с помощью предыдущего уравнения, находим, что

(N ■ b)(1 — 2(N ■ n)2) = 0. (1.18)

Это уравнение распадается на два. Если N ■ b = 0, то необходимо

N ■ n = ±-1=. (1.19)

Если N ■ b = 0, то на основании (1.16) B = 0, и тогда уравнение (1.15) дает (N ■ n)b = 0, откуда в силу того, что равенства B = 0 и b = 0 не могут выполняться одновременно,

N ■ n = 0. (1.20)

Итак, уравнение (1.10) принадлежит к гиперболическому типу. Нормали к характеристическим поверхностям в силу (1.19) образуют конус с углом полураствора п/4 и осью, ориентированной вдоль вектора n. Ясно, что характеристические поверхности являются также и поверхностями максимального касательного напряжения (поверхностями скольжения). Характеристическими являются не только поверхности скольжения, но и согласно (1.20) интегральные поверхности поля n (т.е. поверхности, составленные из интегральных кривых поля n).

2. УРАВНЕНИЯ ОБОБЩЕННОГО АССОЦИИРОВАННОГО ЗАКОНА ТЕЧЕНИЯ НА РЕБРЕ ПРИЗМЫ

КУЛОНА – ТРЕСКА И СООТНОШЕНИЯ ДЛЯ ПРИРАЩЕНИЙ ПЕРЕМЕЩЕНИЙ

Ассоциированный закон течения является фундаментальным принципом математической теории пластичности и устанавливает, что в пространстве напряжений вектор, представляющий тензор приращений пластических деформаций dsP, ортогонален регулярной поверхности текучести f (с) = 0 в данном напряженном состоянии с:

dsP = f dA. (2.1)

д с

Величина dA, называемая неопределенным множителем, положительна при активном пластическом нагружении, признаком которого является выполнение условий f = 0, df = 0. Следует отметить, что множитель dA не может быть вычислен через определяющие функции, и его значение должно вычисляться в процессе решения краевой задачи.

Для изотропного тела критерий текучести f (с) = 0 связывает некоторой зависимостью главные нормальные напряжения

f (01,02,03) = 0, (2.2)

причем функция текучести f на самом деле зависит от трех независимых симметрических комбинаций главных нормальных напряжений; в качестве таковых могут быть выбраны линейная, квадратичная и кубическая симметрические формы главных нормальных напряжений

iНе можете найти то, что вам нужно? Попробуйте сервис подбора литературы.

J1 = 01 + 02 + 03,

J2 = —(0102 + 0103 + 0203),

J3 = 010203.

В теории идеальной пластичности обычно предполагается, что гидростатическое напряжение никак не влияет на текучесть, а поэтому функция текучести / в действительности зависит лишь от разностей главных нормальных напряжений, т.е. от двух независимых инвариантов девиатора тензора напряжений

^2 = – ^2)2 + (02 – 0э)2 + (03 – 01 )2),

J3 = т^(2а1 — а2 — а3 )(2а2 — а3 — а1)(2а3 — а1 — а2).

Ассоциированный закон течения (2.1) для изотропного тела устанавливает соосность тензоров dsP и а.

Действительно, если f = f (a1 ,a2,a3) — регулярная изотропная функция тензора напряжений а,

то

дf дЛ , дf дf

— = -— l 0 l + -— m 0 m + -— n 0 n, (2.З)

д а да1 даз да2

где l, m, n — ортонормированный базис из собственных векторов тензора напряжений.

Доказательство формулы (2.З) базируется на фундаментальных соотношениях дифференцирования собственных значений а1, а2, аз симметричного тензора второго ранга по самому тензору а

да1 , да2 даз

—— = l 0 l, —— = m 0 m, —— = n 0 n. (2.4)

да да да

Для доказательства этих соотношений продифференцируем спектральное разложение тензора напряжений

aij = ai li lj + a2 Ші mj + a3Ui nj по aks и в результате получим равенство (при дифференцировании не должна учитываться симметрия тензора напряжений, иначе необходимые частные производные будут вычислены неправильно)

с г да1 , , , д^ дlj

OikOjs = т; lilj + aij ———+ ail^—-+ … ,

^ks дaks дaks

сворачивая обе части которого сначала с li, а затем с lj, приходим (невыписанные слагаемые при этом дают нулевой вклад в силу взаимной ортогональности собственных векторов) к

да і , дli , дЬ

lkls = т;——-+ aili^–+ aij 0

дaks дaks дaks

Учитывая, что lj lj = І и поэтому

сразу же получаем

и аналогично

д^ д

да1 да ks

= lkls,

да2 доз

—-= тк ms, —-= Пк пв,

д°кв д°кв

что и доказывает (2.4).

Если два собственных значения равны (скажем, о = ст2), а третье с ними не совпадает, то частные до-! дст2

производные ——, —— становятся неопределенными. Однако в силу 1 ® 1 + т ® т + п ® п = I их да да

сумма будет вполне определенной, так как выполняется равенство

до1 до2

“5—-+ = I – п 0 п.

да да

В главных осях тензора напряжений ассоциированный закон течения изотропного тела (2.1) имеет следующий вид:

ЛеР = ^ А (2.5)

3 дО

где здесь и в дальнейшем йер — собственные значения тензора приращений пластических деформаций йер2, которые, вообще говоря, отличаются от приращений собственных значений ер тензора

2Или главные приращения пластических деформаций.

пластических деформаций ер. С учетом этого замечания спектральное разложение тензора dsp представляется как

dsp = l ® ldep + m ® mdep + n ® ndep.

Для изотропного тела в силу указанной выше формы критерия текучести и ассоциированного закона течения наиболее удобно геометрическое представление основных соотношений в трехмерном пространстве главных напряжений Хэя – Вестергарда (Haigh, 1920; Westergaard, 1920).

Ассоциированный закон течения однозначно определяет направление вектора, представляющего приращения пластических деформаций в пространстве главных напряжений, только в регулярных точках поверхности текучести. Если напряженное состояние соответствует ребру (угловой точке) или конической особенности на поверхности текучести, то необходимы дальнейшие предположения для вывода корректного определяющего закона. Обобщение ассоциированного закона на случай поверхности текучести с угловой точкой предложено Койтером (Koiter, 1953). Это обобщение основано на следующем принципе суперпозиции: особые точки поверхности текучести представляются как пересечение конечного числа p гладких поверхностей текучести /7 (ст) = 0.

Активное нагружение, сопровождающееся изменением пластических деформаций, определяется условиями

/ш = 0, d/w = 0,

/к = 0, d/к < 0 или /к < 0,

где индексы ш и к различны, и их значения в совокупности исчерпывают все значения индекса

Y = 1, 2, …,p, причем индекс ш пробегает непустое множество значений.

Полное приращение dsp есть сумма соответствующих всем индексам ш приращений dsp(ш):

ш)

dsp = £ dsp (ш),

где каждое приращение йврвычисляется согласно ассоциированному закону течения

dsp (ш) = dA„

а величины ^Аш должны быть положительными.

Окончательно обобщенный ассоциированный закон течения принимает следующий вид:

А д/

dsp = dA.

7=1

дст 7’

(2.6)

^А7 > 0 (/7 = 0, / = 0),

^А7 = 0 (/7 = 0, с/7 < 0 или /7 < 0).

Его следствием является соосность тензоров а и йвр в изотропном теле.

Геометрически обобщенный ассоциированный закон течения устанавливает, что в угловой точке поверхности текучести вектор, представляющий приращения пластических деформаций в пространстве главных напряжений, является линейной комбинацией нормальных к поверхностям /ш =0 в

указанной точке векторов, причем направление указанного вектора в угловой точке поверхности

нагружения обобщенным ассоциированным законом течения не фиксируется, а остается неопределенным.

Рассмотрим уравнения обобщенного ассоциированного закона течения применительно к условию текучести Треска. Обозначая, как обычно, через ть т2, т3 экстремальные (главные) касательные напряжения

О 2 — Оз Оз — О! О! — О 2

Т1 = 2 ’ Т2 = 2 ’ Т3 = 2 ’

имеем

дт

&р = sgn(т7)^А7 (7 = 1, 2, 3), (2.7)

где индекс 7 пробегает значения 1, 2, 3, однако суммирование в правой части (2.7) распространяется лишь на те значения 7, для которых sgn(т7) т7 = &, т.е. в правой части содержится не более двух слагаемых.

Частные производные в правой части (2.7) в главных осях тензора напряжений без труда вычисляются, если заметить, что (по г не суммировать)

д0;

д0у

В результате находим дті

дті 1

д0зз д022 2

= Ьц^ (м,1 = 1, 2, 3).

дт2 = дт2 = 1 д0іі д0зз 2

дтз = дтз = 1 д022 д0іі 2

(2.8)

(2.9)

Остальные частные производные равны нулю.

Непосредственный подсчет с помощью (2.7), (2.9) показывает, что в главных осях напряжений матрица тензора йвр диагональна

а = diag (о^, о2, о3), йвр = diag (йе15 йе2, йе3),

т.е. ориентации главных осей напряжений и главных осей приращений деформаций одинаковы.

Подсчет суммы главных приращений йер на основании (2.7), (2.9) позволяет заключить, что выполняется условие несжимаемости.

iНе можете найти то, что вам нужно? Попробуйте сервис подбора литературы.

Обратимся к более детальному исследованию уравнений обобщенного ассоциированного закона течения, предполагая, что напряженное состояние соответствует ребру призмы Кулона – Треска, а третье главное напряжение является максимальным: о3 — о1 = 2^, о3 — о2 = 2^. Ясно, что при этом имеет место равенство двух главных напряжений о1 = О2. В терминах главных касательных напряжений этот случай характеризуется выполнением условий Т1 = —&, т2 = &, т3 = 0.

Равенство двух главных напряжений о1 = о2 означает, что любое направление, расположенное в плоскости, ортогональной вектору п, является главным. Ясно поэтому, что при соответствии напряженного состояния ребру призмы Кулона – Треска, т.е. в состоянии полной пластичности, имеется известная доля произвола при выборе собственных векторов 1 и т (они определены с точностью до поворота в плоскости, ортогональной вектору п). Их преимущественное положение в упомянутой плоскости указывается ориентацией собственных векторов тензора приращений пластических деформаций йвр, который в силу ассоциированного закона течения должен быть соосен тензору напряжений а и обладает, поскольку, вообще говоря, йе1 = йе2, уникальным триэдром главных направлений. Следовательно, ассоциированный закон течения, сформулированный для ребра призмы Кулона – Треска, устанавливает совпадение только одной из трех главных осей тензора напряжений и тензора приращений пластических деформаций, накладывая тем самым минимум кинематических ограничений. Это обстоятельство мы будем характеризовать термином «1/3-соосность» тензоров йвр и а. Для течения на ребре призмы Кулона – Треска «1/3-соосность» тензоров йвр и а достаточна для их соосности в том смысле, что существует хотя бы одна тройка взаимно ортогональных направлений, которая будет главной как для тензора йвр, так и для тензора а. Итак, при исследовании течения на ребре призмы Кулона – Треска никогда не следует забывать об указанном обстоятельстве: триэдр главных направлений тензора приращений пластических деформаций йвр всегда будет и триэдром главных направлений тензора напряжений а, но не всякий триэдр главных направлений тензора напряжений будет триэдром главных направлений тензора приращений пластических деформаций.

Обозначая, как было оговорено выше, через йер собственные значения тензора приращений пластических деформаций, соотношения обобщенного ассоциированного закона течения для ребра призмы Кулона – Треска Т1 = — &, т2 = &, т3 = 0 представим в общих главных осях напряжений и приращений пластических деформаций в виде

^£Р — —ЙЛ2,

— —ЙЛ1,

^£Р — ЙЛі + ЙЛ2,

где dAe — неопределенные множители теории идеальной пластичности. Следовательно, обобщенный ассоциированный закон течения, сформулированный для ребра призмы Кулона – Треска, эквивалентен двум условиям: условию 1/3-соосности тензоров dsp и а и условию dep + dep + dep = 0, характеризующему несжимаемость пластического деформирования.

Таким образом, уравнения обобщенного ассоциированного закона течения, сформулированного для ребра призмы Треска, позволяют найти помимо условия соосности тензоров dsp и а (да и то с точностью до поворота триэдра главных осей в плоскости, ортогональной вектору n) еще только одно существенное соотношение, следующее из (2.10), — условие несжимаемости:

Его можно также представить в форме

или в инвариантной прямой записи

de-L + de2 + de3 =0. (2.11)

dj = 0 (2.12)

іг (йєР) — 0. (2.13)

Последнее обстоятельство имеет принципиально важное значение: для напряженных состояний, соответствующих ребру призмы Кулона – Треска, пластическое течение имеет наибольшую свободу и именно поэтому возрастает вероятность построить решения ряда важнейших прикладных задач, привлекая схему полной пластичности Хаара – Кармана3. Ясно, что напряженные состояния, соответствующие граням призмы Треска, могут реализовываться лишь в исключительных случаях, поскольку при этом имеется весьма сильное кинематическое ограничение: одна из главных скоростей пластических деформаций должна быть равна нулю4.

Условие соосности тензоров йєр и с в силу (1.3) может быть сформулировано как

йєр — 1 ® Ыер + т ® ш^єр + п ® п^єр. (2.14)

Здесь векторы 1 и т уже выступают как собственные векторы тензора йєр, и поэтому их ориентация в плоскости, ортогональной вектору п, уникальна. Если тензор напряжений с соответствует ребру призмы Кулона – Треска и задан, то ориентация вектора п известна, а ориентации векторов 1 и т не определены до тех пор, пока полностью не определены кинематические поля. Далее в кинематических уравнениях мы задействуем лишь вектор п.

Соотношение (2.14) позволяет заключить, что п ■ йєр — п^єр, или также п ■ йєр ■ п — йєр, и, кроме того (см. [6,с. 208]),

п ■ йєр — піг((п ® п) ■ йєр). (2.15)

Полученное уравнение устанавливает лишь только тот факт, что вектор п — собственный вектор тензора йєр. Проектируя векторное уравнение (2.15) на оси некоторой прямоугольной системы координат ж і, ж2, жз, можно получить три скалярных уравнения [7]

П^£р — ППкпгЙєрг. (2.16)

Только два из них будут независимыми. Действительно, свернутые с п соотношения (2.16) удовлетворяются тождественно, что указывает на их линейную зависимость.

Два независимых уравнения из (2.16) вместе с уравнением несжимаемости (2.12) образуют систему из трех независимых уравнений

dep- = 0, nj dej = Пі nk п dek1

П P j P (2.17)

которые после подстановки в них вместо приращений пластических деформаций трех приращений перемещений согласно

2^6 = (V 0 йи) + (V 0 йи)Т (2.18)

3Эта гипотеза принадлежит Д.Д. Ивлеву.

4В следующем параграфе приводится анализ общих соотношений математической теории идеальной пластичности для течения на грани призмы Кулона – Треска. Граням призмы соответствуют чисто сдвиговые течения, когда главные приращения пластических деформаций удовлетворяют условиям йер = 0, йер + <!гр = 0 (г = ], ] = 1,1 = г).

или, переходя к прямоугольной системе координат х1, х2, х3,

2йер” = дг (йИ” ) + д” (йиг ),

позволяют полностью исследовать кинематику пластического течения, если поле напряжений уже

определено5.

Система кинематических уравнений (2.17)

^ (йвр) = 0,

р Р (2.19)

п ■ = п tr((n 0 п) ■ ),

описывающая идеально пластическое течение на ребре призмы Кулона – Треска, правильно определенная и гиперболическая6. Характеристические направления этой системы, как показывает несложный расчет, совпадают с характеристическими направлениями системы трехмерных статических уравнений.

Действительно, будем трактовать характеристические поверхности системы уравнений (2.19) как поверхности слабого разрыва приращений перемещений йи и воспользуемся геометрическаими условиями совместности Адамара – Томаса (см., например [5]):

[V 0 йи] = N 0 а,

где [ ■ ] обозначает скачок при переходе через поверхность слабого разрыва, N — единичный вектор нормали к поверхности слабого разрыва, а — некоторое ненулевое векторное поле, определенное на этой поверхности. На основании соотношений Коши

2 [йер] = N 0 а + а 0 N

следовательно,

^ ([йвр]) = N ■ а.

Учитывая полученные формулы, из уравнений системы (2.19) находим следующие соотношения для вектора N

N ■ а = 0, (п ■ ^а + (п ■ а^ — 2(п ■ ^(п ■ а)п = 0.

Проектируя последнее из полученных уравнений на ортогональные друг другу направления N а, получаем

(п ■ а)(1 — 2(п ■ N)2) =0,

V л V ; ; , (2.20)

(п ■ N)(a ■ а — 2(п ■ а) ) = 0.

В зависимости от того, выполняется ли условие п ■ а = 0, имеем: п ■ N = 0 или 1 — 2(п ■ ^2 = 07.

Поэтому нормали к характеристическим поверхностям образуют конус с углом полураствора п/4

и осью, ориентированной вдоль вектора п. Конус нормалей к характеристическим площадкам для системы кинематических уравнений пространственной задачи математической теории пластичности (в случае течения на ребре призмы Треска) тот же самый, что и для системы уравнений равнове-сия8. На основании уравнения п ■ N = 0 можно заключить, что характеристическими поверхностями являются также и интегральные поверхности поля п (т.е. поверхности, составленные из интегральных кривых поля п). Все это указывает на гиперболичность системы уравнений (2.19), описывающей пространственное пластическое течение на ребре призмы Треска.

Если удается получить решение системы кинематических уравнений (2.17) относительно приращений перемещений йи, то затем можно найти тензор приращений пластических деформаций йбр, а вместе с ним и точную ориентацию собственных векторов 1 и т.

5В параграфе 5 будет дан анализ кинематических уравнений в случае пространственного течения на ребре призмы Кулона

– Треска в триортогональной криволинейной сетке линий главных напряжений.

6Далее будет установлено, что кинематические соотношения пространственной задачи для грани призмы Кулона – Треска не являются правильно определенными: три компоненты вектора приращения перемещений ёп^ должны удовлетворять пяти независимым уравнениям.

7Любопытно отметить, что во втором случае (т.е. когда п • а = 0) с помощью второго уравнения системы (2.20) можно установить, что вектор а, обладая произвольным модулем, должен составлять с вектором п угол ±п/4.

8Этот результат был получен в работе [2].

3. УРАВНЕНИЯ МАТЕМАТИЧЕСКОЙ ТЕОРИИ ПЛАСТИЧНОСТИ ДЛЯ ГРАНИ ПРИЗМЫ КУЛОНА-ТРЕСКА

Рассмотрим также основные уравнения теории идеальной пластичности для грани призмы Треска. Напряженные состояния, соответствующие граням призмы Треска, могут реализовываться лишь в исключительных случаях, поскольку ассоциированный закон течения в этом случае устанавливает весьма сильные кинематические ограничения на процесс пластического течения: одна из главных скоростей пластических деформаций должна быть равна нулю, и триэдр главных осей тензора приращений пластических деформаций жестко предписан тензором напряжений. Граням призмы соответствуют чисто сдвиговые течения, когда главные приращения пластических деформаций удовлетворяют условиям

dep = 0, dep + dep = 0 (i = j, j = l, l = i).

Совершенно иная ситуация наблюдается в случае, когда напряженное состояние соответствует ребру призмы Треска: ни одно из главных приращений пластических деформаций здесь принципиально определить нельзя9 а триэдр главных осей тензора приращений пластических деформаций не предписывается жестко триэдром главных напряжений (они могут отличаться друг от друга поворотами в плоскости, ортогональной вектору n).

Для грани призмы Треска, задаваемой уравнением а1 — 02 = 2k (в этом случае а1 — максимальное,

02 — минимальное, 03 — промежуточное главное напряжение), тензор напряжений имеет вид

a = 021 — (02 — 03)n ® n + 2kl ® l. (3.1)

Поэтому уравнения равновесия получаются в виде (ср. (1.7))

gradE2 + div(l ® l) + (Е3 — Е2)div(n ® n) + [n ■ grad(E3 — Е2)] n = 0, (3.2)

где введены безразмерные главные напряжения Е2 = 02/(2k), Е3 = 03/(2k), или

VE2 + (l ■ V)l + l(V ■ l) + (Е3 — Е2) ((n ■ V)n + n(V ■ n)) + n(n ■ V)(E3 — Е2) = 0 . (3.3)

К этому уравнению следует присоединить условия нормировки и ортогональности

l ■ l =1, n ■ n =1, l ■ n = 0.

Проектируя векторное уравнение (3.3) на главные оси тензора напряжений, определяемые ориентациями l, m, n, находим направление n:

(n ■ V)Eз + n ■ [(l ■ V)l] + (Е3 — Е2)(V ■ n) = 0; (3.4)

направление l:

(l ■ V)E2 + (V ■ l) + (Е3 — Е2) {l ■ [(n ■ V)n]} = 0; (3.5)

направление m:

(m ■ V)E2 + m ■ [(l ■ V)l] + (Е3 — Е2) {m ■ [(n ■ V)n]} = 0. (3.6)

Если оказывается возможным введение триортогональной координатной системы с координатными линиями, являющимися линиями главных напряжений, то полученные только что соотношения можно рассматривать как соотношения вдоль взаимно ортогональных изостат [3]. Тогда можно ввести кривизны Kj (Kj есть кривизна проекции изостаты с номером i, причем проектирование осуществляется параллельно направлению j на локальную координатную плоскость, ортогональную этому направлению), и, учитывая, что

V ■ l = K32 + K23, V ■ m = K13 + K31, V ■ n = K12 + K21,

9Главные приращения пластических деформаций связаны единственным уравнением (уравнением несжимаемости),

а также

1 ■ [(т ■ V)m] — -К2з, 1 ■ [(п ■ V)n] — -Кз2,

т ■ [(1 ■ V)1] — -кіз, т ■ [(п ■ V)n] — —кзі, п ■ [(1 ■ V)1] — —кі2, п ■ [(т ■ V)m] — —К2і,

привести уравнения равновесия для грани призмы Треска (3.4)-(3.6) к следующему виду:

(п ■ V)Ез — Кі2 + (кі2 + К2і)(Ез — Е2) — 0, (1 ■ ^Е2 + (кз2 + к2з) — кз2 (Ез — Е2) — 0, (т ■ V)Е2 — кіз — кзі(Ез — Е2) — 0.

(3.7)

Здесь дифференциальные операторы слева суть производные по направлениям линий главных напря-

Ассоциированный закон течения, сформулированный для грани призмы Треска аі — а2 — 2к, устанавливает жесткую (без неопределенности, характерной для ребра призмы Треска) соосность тензоров йєр и с и еще следующие соотношения для главных значений тензора приращений пластических деформаций

Видно, что характер пластического течения, если реализуется напряженное состояние на грани призмы Треска, оказывается чисто сдвиговым. Сдвиг происходит в плоскости, ортогональной вектору п. Направления максимальной скорости сдвига расположены в плоскости, ортогональной вектору п, и делят пополам прямые углы, образованные направленными вдоль векторов 1 и т пересекающимися прямыми.

Нетрудно видеть, что множитель йЛ вычисляется через главные приращения пластических деформаций в виде

Условие соосности тензоров йбр и с для течения на грани призмы Треска а1 — а2 = 2к принимает

где, в отличие от течения на ребре призмы Треска, векторы 1 и п жестко предписаны тензором напряжений и заданы, если задан тензор напряжений.

Таким образом, система кинематических уравнений для рассматриваемой грани может быть представлена в виде

жений:

п • V ——–— ——————

д$з ^ дСз ’

д 1 д

д^і ,/дГі д^’ д 1 д

iНе можете найти то, что вам нужно? Попробуйте сервис подбора литературы.

д 1 д

т • V

дА’2 У9І2 д£2 •

Йєр — ЙЛ, йєр — —ЙЛ, Йєр — 0,

откуда следует соотношение несжимаемости

Йєр + Йєр — 0.

форму

Йєр — (1 ® 1 — т ® т)^єр

или также

Йєр — —Ійєр + 21 ® 1^єр + п ® п^єр,

1 ■ Йєр — 1 іг((1 ® 1) ■ Йєр), п ■ Йєр — 0, іг(^єр) — 0.

Здесь содержится пять независимых скалярных уравнений, так как первое векторное уравнение дает только два независимых скалярных (скалярное умножение на вектор 1 приводит к тождеству), второе векторное уравнение — три независимых скалярных, но одно из них (которое получается скалярным умножением на вектор l) следует из первого векторного уравнения (точнее, из уравнения, которое получается скалярным умножением первого векторного уравнения на вектор n), а третье — одно скалярное уравнение.

Первое из уравнений (3.8) выражает просто тот факт, что вектор 1 есть собственный вектор тензора dsp, второе устанавливает, что вектор n — собственный вектор тензора dsp с нулевым собственным значением, третье — пластическую несжимаемость.

Проектируя уравнения (3.8) на оси некоторой прямоугольной системы координат, находим

lj dej — li lk lsdЄ/os,

nj deP = 0, (3.9)

dep- = 0.

Три компоненты приращения вектора перемещений duj, вводимые в (3.9) согласно

2de j = ді^и-) + д^- (dui),

должны, таким образом, удовлетворять пяти независимым уравнениям. Следовательно, полученная система кинематических уравнений при течении на грани призмы Треска не является правильно определенной10.

Тем не менее течение на грани призмы Треска реализуется в ряде важных случаев: в случае плоского деформированного состояния и в случае скольжений вдоль поверхностей максимальной скорости сдвига (кинематика таких течений будет исследована в заключительном параграфе статьи).

Итак, замкнутая система соотношений для состояний, соответствующих грани призмы Треска

a1 — a2 = 2k, имеет следующий вид:

VE2 + (1 ■ V)1 + 1(V ■ 1) + (E3 — E2) ((n ■ V)n + n(V ■ n)) + n(n ■ V)(E3 — E2) = О;

1 ■ dsp = 1 tr((l 0 1) ■ dsp),

n ■ dsp = О,

p (3.10)

tr(ds ) = 0;

2dsp = V 0 du + (V 0 du)T;

1 ■ 1 = І, n ■ n = І, 1 ■ n = 0.

4. СООТНОШЕНИЯ КОШИ В ТРИОРТОГОНАЛЬНОЙ ИЗОСТАТИЧЕСКОЙ СИСТЕМЕ КООРДИНАТ

Соотношения Коши, связывающие приращение вектора перемещений с приращением тензора полных деформаций, являются фундаментальными уравнениями механики деформируемого твердого тела. С их помощью наиболее просто могут быть выведены все кинематические уравнения теории идеальной пластичности.

Соотношения Коши, записанные для приращений перемещений, имеют форму прямого тензорного уравнения:

2^є — (V ® йи) + (V ® йи)т . (4.1)

Приращения перемещений можно представить в виде разложения по векторам локального орто-нормированного базиса в пространстве 1, т, п

йи — 1Йи<і> + тйи<2> + пйи<з>. (4.2)

10Состояния на грани призмы Треска, вообще говоря, статически неопределимы. Для состояний на грани необходимо совместное рассмотрение уравнений (3.3), (3.8), дополненных условиями нормировки и ортогональности собственных векторов

тензора напряжений

1 • 1 =1, п • п =1, 1 • п =0,

и соотношениями Коши

2dє = V ® du + (V ® du)T.

Только тогда получается правильно определенная система соотношений.

Здесь величины йи<,> не являются действительными приращениями, а служат для обозначения физических компонент вектора йи в триортогональной изостатической координатной сетке. Тем не менее о величинах йи<,> мы будем говорить как о приращениях перемещений, помня, однако, что они таковыми в действительности не являются.

Нетрудно видеть, что трехмерный оператор Гамильтона в триортогональной изостатической системе координат С1, С2, С3 есть (Л,,- — параметры Ламе рассматриваемой координатной системы)

„ ,1 д 1 д 1 д

V = 1———+ т———-+ п———-

V Лі дС1 + ^2 дС2 + дС3

(4.3)

Градиент приращения вектора перемещения V ® йи вычисляется в виде

V ® йи = 1 ® ‘Уй’и<1> + т ® + п ® У’«и<3> +

+ (йи<і>) V ® 1 + (йи<2>) V ® т + (йи<э>) V ® п.

(4.4)

Ясно, что

= 1 = 1 = 1

или (й1 = 1 ■ V, й2 = т ■ V, й3 = п ■ V)

1 дйи<і>

Лі дСі

1 д«и<2>

Лі дСі

1 дйи<3>

Лі дСі

+ т

1 дйи<і>

Л2 дС2

1 дйи<2>

Л2 дС2

1 д«и<3>

Л2 дС2

+ п

1 дйи<і>

Л3 дС 3

1 дйи<2>

Л3 дС 3

1 дйи<3>

Л3 дС 3

(4.5)

^7йи<і> — 1(сМи<і>) + т(^2^и<1>) + п(^3^и<і>), Vdu<2> = 1(йійи<2>) + т(^2^и<2>) + п(^3^и<2>), ^7йи<і> = 1(^и<3>) + т(^2^и<3>) + п(^3^и<3>).

(4.6)

Используя далее выражения для производных от базисных векторов

д1

1 д^4

а? = – д?т – п = -№Лі)т – (й3 Лі )п

д1 1 д^2 , .

дС2 = Лі дСіт = (<іі,!’2)т’

д1

дС3

1 дЛ

Лі дС

(4.7)

д т 1 дЛі

дСі = Л2 дС2 = ( ^ ’

дт

1 д^2

дС2 = – лі 5ёг 1 – л3 дС3 п = -(гііЛ’2)1 – (й3 Л2 )п

(4.8)

iНе можете найти то, что вам нужно? Попробуйте сервис подбора литературы.

дт

дС3

.1 дЛ

Л2 дС2

п = (^2 ^3 )п,

дп

1 дЛі

дСі Л3 дС3 1 (Й3Лі)1,

д п

дС2

1 дЛ2 , , ,

= 7Т т = («3 «2)

Л3 дС

(4.9)

д п

дС3

1 дЛя

1 дЛ

т = -(йіЛ3)1 – (^2^3)т,

приходим к следующим формулам:

V ® l = —-1 (d2hi) l ® m – -1 (d3hi) l ® n + -1 (dih2) m ® m + -1 (di) n ® n,

hi hi h2 h3

V ® m = -1 (d2hi) l ® l — -1 (dih2) m ® l — -1 (d3h2) m ® n + -1 (d2h3) n ® n,

hi h2 h2 h3

(4.10)

V ® n = -1(d3hi)l ® l + -1(d3h2)m ® m — -1(dih3)n ® l — -1(d2h3)n ® m.

hi h2 h3 h3

Используя (4.6) и (4.10), соотношение (4.4) можно представить следующим образом:

V ® du =l ® l

+ m ® m

-1(d2hi)du<2> + -1(d3hi)du<3> + didu hi hi

-1(dih2 )du + -1(d3 h2 )du<3> + d2 du<2> h2 h2

+ n ® n

+ l ® m

7—(di h3 )du + -1(d2h3)du<2> + d3du<3> h3 h3

— 7— (d2hi)du + d2du hi

+ l ® n

— 7— (d3 hi )du + d3 du hi

(4.11)

+ m ® l

— ^- (dih2)du<2> + didu<2> h2

+ m ® n

^ — (d3h2)du<2> + d3du<2> h2

+ n ® l

— 7—(di h3 )du<3> + di du<3> h3

+ n ® m

— — (d2 h3 )du<3> + d2 du<3> h3

Транспонировав уравнение (4.11), получаем V ® du)T =l ® l

+ m ® m

-1(d2 hi )du<2> + 7—(d3 hi )du<3> + di du hi hi

-1(di h2 )du + -1 (d3h2)du<3> + d2du<2> h2 h2

+ n ® n + m ® l + l ® m + l ® m

-1(dih3)du + -1(d2 h3 )du<2> + d3 du<3> h3 h3

—г—(d2 hi )du + d2 du hi

— “г- (di h2 )du<2> + di du<2> h2

T- (di h3)du<3> + didu<3> h3

+ n ® l

+ n ® m + m ® n

—

(4.12)

—г— (d3hi)du + d3du hi

— — (d3 h2 )du<2> + d3 du<2> h2

— 7—(d2 h3 )du<3> + d2 du<3> h3

Подставляя выражения (4.11) и (4.12) в соотношения Коши (4.1), получим

ds =l ® l

-1(d2hi )du<2> + -1(d3 hi )du<3> + di du hi hi

+ m ® m

— (di h2 )du + — (d3h2)du<3> + d2du<2> h2 h2

+ n ® n

-1(dih3)du + -1(d2h3 )du<2> + d3 du<3>

h3 h3

— “t (d2hi)du + d2du — (dih2)du<2> + didu<2>

hi h2

+ 2 m ® 1

— -г—(dзhl)du<l> + dзdu<l> — (dlhз)du<з> + dldu<з> +

hl Лз

— т— (d2 hl)du<l> + d2 du<l> — -т—(di h2 )du<2> + dl du<2> + hl h2

+ 2 m ® n

— — (dз h2 )du<2> + dз du<2> — — (d2 hз ^и<з> + d2 du<з> h2 hз

+ 2 n ® l

— t— (dзhl)du<l> + dзdu<l> — (dlhз)du<з> + dldu<з> +

hl hз

+ 2 n ® m

— t— ^з h2 )du<2> + dз du<2> — t-(d2 hз ^и<з> + d2 du<з> h2 hз

Тензор ds, как явствует из только что полученной формулы, симметричен, что и так ясно a priori. Указанную формулу можно несколько преобразовать, вводя нормальные кривизны Kj триортогональ-ной системы поверхностей = const (Kj есть кривизна проекции изостаты с номером i, причем проектирование осуществляется параллельно главному направлению j на плоскость, ортогональную этому направлению11 в соответствии с приводимыми ниже равенствами:

dlh-з = Лз Кз2, dlh2 = h2 К2з,

iНе можете найти то, что вам нужно? Попробуйте сервис подбора литературы.

d2 hз = ЛзКзі, d2 hi = ЛіКіз,

dзh2 = h2 К21, dзhl = hi К12 •

(4.13)

В результате получим следующие выражения для физических компонент тензора йе в триортогональ-ных координатах С1, С2, С3:

йє<ц> = кізйи<2> + Кі2^и<з> + йі йи<1>, йє<22> = К2зйи<1> + К21^и<з> + ^2 йи<2>,

йє<33> = к32йи<1> + к31йи<2> + й3 йи<3>, йє<12> = —К13^и<1> — К23 йи<2> + ^2^и<1> + ^1 йи<2>, йє<13> = —К12^и<1> — К32 йи<3> + ^3^и<1> + ^1 йи<3>, йє<23> = —К21^и<2> — К31 йи<3> + ^3^И<2> + ^2йи<3> .

Здесь ни ЙЄ<у>, ни йи<> действительными приращениями не являются; ЙЄ<у> — физические компоненты тензора йе в изостатической системе координат:

(4.14)

ds =1 ® lde<ii> + 1 ® mde<i2> + 1 ® ndє<lз> + m ® mde<22> + m ® lde<2i> + + m ® ndє<2з> + n ® ndє<зз> + n ® 1dє<зl> + n ® mdє<з2>•

(4.15)

Уравнения (4.14) можно преобразовать, используя величины 7^ (7^ — геодезическая кривизна изостатической траектории с номером і на поверхности, ортогональной главному направлению с номером ^), лишь знаком отличающиеся от 12. В итоге получаем

11Напомним, что справедливы следующие равенства:

l • [(m • V)m] = —к23, l • [(n • V)n] = —кз2, m • [(l • V)l] = —кіз, m • [(n • V)n] = — кзі, n • [(l • V)l] = —кі2, n • [(m • V)m] = —к2і.

Если имеется некоторая кривая на поверхности, параметризованная натуральным параметром в, 1 — единичный вектор, направленный по касательной к кривой в сторону возрастающих значений параметра в, 1* — единичный вектор, расположенный в касательной плоскости ортогонально вектору 1, п — единичный вектор, направленный по нормали к поверхности так, чтобы векторы 1, 1*, п образовывали правую тройку, то мы определяем

dt *

— • t*

соответственно как нормальную кривизну (кривизна проекции рассматриваемой кривой на плоскость, определяемую векторами 1, п) и геодезическую кривизну (кривизна проекции рассматриваемой кривой на касательную плоскость, определяемую векто-

de<ll> = — 7l3 du<2> — Yl2du<3> + dl du<l>, de<22> = —723 du<l> — Y2ldu<3> + d2 du<2>, de<33> = —732du<l> — Y3ldu<2> + d3du<3>,

(4.16)

de<l2> = Yl3du<l> + 723 du<2> + d2du<l> + dl du<2>,

de<l3> = Yl2du<l> + 732 du<3> + d3du<l> + dl du<3>,

de<23> = Y2ldu<2> + Y3l du<3> + d3du<2> + d2 du<3>.

5. КИНЕМАТИЧЕСКИЕ СООТНОШЕНИЯ ДЛЯ ПРОСТРАНСТВЕННОГО ТЕЧЕНИЯ В ТРИОРТОГОНАЛЬНЫХ

ИЗОСТАТИЧЕСКИХ КООРДИНАТАХ

В приближении жесткопластического анализа имеем ds = dsp. Ассоциированный закон течения, как известно, устанавливает соосность тензора напряжений ст и тензора приращений пластических деформаций dsp. При использовании критерия текучести Треска следует различать течение на грани (в этом случае уникальный триэдр l, m, n будет однозначно указывать также и главные оси тензора dsp) и течение на ребре, когда равны два главных напряжения al = а2 .В случае течения на ребре равенство двух главных напряжений al = а2 означает, что любое направление, расположенное в плоскости, ортогональной вектору n, является главным. При соответствии напряженного состояния ребру призмы Кулона – Треска сохраняется неопределенность в ориентации собственных векторов

l и m (они определены с точностью до поворотов в плоскости, ортогональной вектору n) и они уже, вообще говоря, могут и не быть собственными векторами тензора приращений пластических деформаций dsp.

Рассмотрим по отдельности каждый из двух указанных случаев.

1. Течение на грани призмы Кулона – Треска. Триэдр l, m, n есть также и триэдр главных направлений тензора ds. Полученная в предыдущем параграфе формула для ds приводит к шести соотношениям:

dep = — (d2 hl )du<2> + — (d3hl)du<3> + dldu<l>, (5.1)

hl hl

dep = 7—(dl h2 )du<l> + -1(d3h2)du<3> + d2du<2>, (5.2)

h2 h2

dep = -^(dl h3 )du<l> + -1(d2h3)du<2> + d3du<3>, (5.3)

h3 h3

— (d2hl)du<l> + d2du<l> — -1(dlh2)du<2> + dldu<2> = 0, (5.4)

hl h2

— -1(d3hl)du<l> + d3du<l> — -1(dlh3)du<3> + dldu<3> = 0, (5.5)

hl h3

— -1(d3h2)du<2> + d3du<2> — -1(d2h3)du<3> + d2du<3> = 0. (5.6)

h2 h3

Вводя кривизны в соотношения (5.1)-(5.6) согласно (4.13), получим (см. также (4.14))

dep = Kl3du<2> + Kl2 du<3> + dldu<l>, (5.7)

dep = K23du<l> + K2l du<3> + d2du<2>, (5.8)

dep = K32du<l> + K3l du<2> + d3du<3>, (5.9)

—Kl3 du<l> — K23du<2> + d2 du<l> + dl du<2> = 0, (5.10)

—Kl2 du<l> — K32du<3> + d3 du<l> + dl du<3> = 0, (5.11)

—K2l du<2> — K3ldu<3> + d3 du<2> + d2 du<3> = 0. (5.12)

рами 1, 1*) кривой на поверхности. В данном выше определении следует особо обратить внимание на знаки. Именно поэтому в применяемой нами терминологии 7^- — геодезическая кривизна изостатической траектории с номером і на поверхности, ортогональной главному направлению с номером ^’.

Эти соотношения компактно представляются в матричной форме:

deP

dep

d1 К13 К12

К2з d2 К21

К32 К31 d3

— К13 + d2 —К23 + d1

— К12 + d3

—К32 + di —К21 + d3 —К31 + d2

= О.

(5.13)

(5.14)

Второе из матричных соотношений выражает соосность тензора напряжений и тензора приращений пластических деформаций.

Как отмечалось выше (см. параграф ??), в случае пространственного течения на грани призмы Кулона – Треска ст — = 2к ассоциированный закон течения устанавливает жесткую (без неопре-

деленности, характерной для ребра призмы Треска) соосность тензоров йєр и а и еще следующие соотношения для главных значений тензора приращений пластических деформаций:

йер = ^А, &р = — ^А, &р = 0,

откуда сразу же следует соотношение несжимаемости

dep + dep = 0.

Следовательно, для анализа кинематики пространственного течения на грани призмы Кулона – Треска достаточно воспользоваться полученными только что матричными уравнениями (5.13), (5.14), положив в них dep = 0 и dep = —dep. В результате находим следующие уравнения, выражающие в изостатической координатной системе кинематическое ограничение dep = 0, условие несжимаемости и условие соосности:

К32 du<l> + K3l du<2> + d3du<3> = 0; (5.15)

dldu<l> + d2du<2> + K23 du<l> + Kl3du<2> + (ki2 + K2l)du<3> = 0; (5.16)

d2du<l> + dl du<2> — Kl3du<l> — K23 du<2> = 0,

d3du<l> + dl du<3> — Kl2du<l> — K32 du<3> = 0, (5.17)

d3du<2> + d2 du<3> — K2ldu<2> — K3l du<3> = 0.

Нетрудно видеть, что если напряженное состояние соответствует грани призмы Кулона – Треска и уже определено, то изостатическую координатную сетку (если таковая существует) можно считать известной. Но в таком случае три неизвестных величины du<j> должны удовлетворять пяти уравнениям (5.15), (5.16), (5.17)13. Ниже мы увидим, что подобной проблемы не возникает, например, в случае плоского деформированного состояния, поскольку тогда соотношение (5.15) и два из трех соотношений (5.17) удовлетворяются тождественно.

2. Течение на ребре призмы Кулона – Треска. Триэдр l, m, n, вообще говоря, не будет триэдром главных направлений тензора ds. Из ассоциированного закона течения можно вывести условие несжимаемости и лишь тот факт, что n есть собственный вектор тензора ds, т.е. соотношения

de<ll> + de<22> + de3 = 0; de<l3> = 0, de<23> = 0.

Полученная выше формула для ds позволяет представить приведенные выше соотношения в следующем виде:

dldu<l> + d2du<2> + d3du<3> + (K23 + K32)du<l> + (ki3 + K3l)du<2> + (ki2 + K2l)du<3> = 0; (5.18)

d3du<l> + dl du<3> — Kl2du<l> — K32 du<3> = ° (5 19)

d3du<2> + d2 du<3> — K2ldu<2> — K3l du<3> = 0.

Т.е. на приращения перемещений в триортогональной изостатической координатной сетке в случае пространствен-

ного пластического течения на грани призмы Кулона – Треска имеется слишком много ограничивающих соотношений. Поэтому, если в действительности реализуется течение на грани, то некоторые из приведенных соотношений (5.15), (5.16), (5.17) должны удовлетворяться тождественно, либо следовать из остальных соотношений.

Таким образом, в случае течения на ребре призмы Кулона – Треска три неизвестных величины du<j> должны удовлетворять трем уравнениям (5.18), (5.19), т.е. задача расчета приращений

перемещений по известному напряженному состоянию является правильно определенной.

Заметим, что уравнение несжимаемости (5.18) приобретает форму

dl + H(i) / du<l>

d2 + H(2) du<2> = 0, (5.20)

d3 + H(3) / V du<3> )

если ввести средние кривизны H(j) координатных поверхностей = const, учитывая, что

iНе можете найти то, что вам нужно? Попробуйте сервис подбора литературы.

2H(1) = К32 + к23,

2H(2) = к13 + К31,

2H(3) = Kl2 + K2l.

Докажем, что система, состоящая из уравнений (5.18), (5.19), гиперболична и определим ее характеристические направления. Обозначим через N<j> физические компоненты вектора N единичной нормали к характеристическому элементу относительно пространственного базиса l, m, n. Характеристическое уравнение

N N<2> N<3>

N<3> 0 N<l> =0

0 N<3> N<2>

или с учетом N<l> + N<2> + N<3> = 1

N<3> (2N<3> — 1) = 0

имеет три различных действительных корня

N<3> = 0, N<3> = ±^/2 ’

что указывает на гиперболичность системы уравнений (5.18), (5.19). Конус нормалей к характеристическим поверхностным элементам для системы кинематических уравнений пространственной задачи математической теории пластичности (в случае течения на ребре призмы Треска) тот же самый, что и для системы уравнений равновесия.

6. УРАВНЕНИЯ СОВМЕСТНОСТИ ПРИРАЩЕНИЙ МАЛЫХ ДЕФОРМАЦИЙ В ТРИОРТОГОНАЛЬНОЙ КРИВОЛИНЕЙНОЙ СЕТКЕ ИЗОСТАТ

Уравнения совместности деформаций наряду с соотношениями Коши, связывающими приращение вектора перемещений с приращением тензора полных деформаций, являются фундаментальными уравнениями механики деформируемого твердого тела. Их также можно применять для анализа кинематики идеально пластического течения. Сформулируем, следуя [3], уравнения совместности приращений малых деформаций в триортогональной криволинейной сетке линий главных напряжений

с1 , с2, с3.

Уравнение совместности малых деформаций в приращениях, как известно, имеет вид

—dS = V х dP = 0, (6.1)

где тензор второго ранга dP есть транспонированный вихрь тензора приращений полных деформаций

dP = (V х ds)T . (6.2)

Тензор несовместности dS симметричен:

Тензор йР антисимметричен, поскольку:

(V х йє)1 = – (йє х V)

(6.4)

Физические компоненты тензора несовместности ^8 относительно триортогональной криволинейной сетки линий главных напряжений С1, С2, С3 вычисляются в форме [8]:

д (І2йе<32>) д (І3ЙЄ<33>)

1 д ( 1 113 дёН 12 [. дС3 дС2

. йе<12> д^3 . йє<23> д^2 . йе<22> дІ3

дС1

д1

І2 І3 дС3 1^3

йе<32> д^3

І2 дС3

д (^2^Є<22> )

дС3

йе<13> д^2

І2 дС2 _

д(^3^Є<23>)

І3

дС2

дЫ3

1? Ы2 І3 дС1 1 дЫ3

І3 Ы1 дС1 1 д^2

ы2 Ы2 Ы3 дё1 1 д^2 ’

ЫН дС1

І1 дС1

д (І1 ЙЄ<21> )

дС2

ЙЄ<33> дІ2

І3 дС3 .

д(І2^Є<22>)

(6.5)

дС1

йє<31> дІ2 . йє<12> дІ1 . йє<11> дІ2

“”Т 7 7 ^ іО +

І213 дС 3 І112 дС 2 ‘ І1І2

д (І3йє<33>) д (І1^є<31>)

дС1

дС3

йє<21> дІ3 йє<13> дІ1 йє<11> дІ3

І213 дС І311 дС І311 дС1

сг&

<12>

1 д [1 113 дС2 111

^Є<21> дЇ3

д (Ї3 йє<33>) д (Ї1 йє<31>)

дС1

йє<13> дІ1

дС3 йє<11> дЇ3

Ї2 дС2

1 д Г І2

Ї1 дС3 Ї1 дС

д (Ї3^Є<23>) д (Ї1йє<21>)

Ї2 Ї3 дС3 І Ї1Ї3

1 д12

Ї112 Ї3 дТ 1 дІ2

дС1

1 дІ3

Ї112 Ї3 дС2

1 дІ3

дС1

дС3

iНе можете найти то, что вам нужно? Попробуйте сервис подбора литературы.

йє

<31>

дія

йє

<13>

дЇ1

Ї3 дС2

Ї1 дС2

д (Ї2йє<23>) д (І3^є<33>)

дС3

дС2

йє<12> дІ3 . йє<23> дІ2 . йє<22> дІ3

“”І- 7 7 “т

Ї3 Ї1 дС 1 Ї2 Ї3 дС 11Ї2 дС2

д (Ї1 йє<21>) д (І2^є<22>)

І312 дС 1 дІ2

Ї112 Ї3 дС3 1 д12

дС2 дС1

йє<31> дІ2 . йє<12> дІ1 . йє<11> дІ2

. , , ТГГп . , , дС1

І213 дС І112 дС 11І1

д (І1 йє<31>) д (І2^є<32>)

(6.6)

І2І3 дС3

йє

<12>

дС2

д11

дС1

ЙЄ<21> дІ2 “

І113 дС3 І213 де3.

где 1а — д/^аа (по а не суммировать) — параметры Ламе; й^<г^> ^8 в изостатической системе координат,

физические компоненты тензора

й8 —1 ® 1й^<11> . 1 ® шй^<12> . 1 ® пй^<13> . т ® тй$<22> . т ® 1й^<21>. . т ® пй^<23> . п ® пйє<33> . п ® 1й^<31> . п ® тй^<32>.

(6.7)

Компоненты й$<22>, й^<33> получаются циклической перестановкой индексов в (6.5). Компоненты й$<23>, й£<31> получаются циклической перестановкой индексов в (6.6). Здесь представляется уместным еще раз упомянуть о том, что ни ^$<у>, ни Й£<г7> не являются действительными приращениями величин, находящихся под знаком дифференциала.

Заметим также, что формулы (6.5), (6.6) справедливы для любой триортогональной координатной системы, хотя в дальнейшем нас будет интересовать лишь изостатическая координатная сетка.

В декартовой системе координат компоненты тензора несовместности ^8 вычисляются по следующим формулам:

где епгг — кососимметричные символы, или

Это известные формулы Сен-Венана, широко применяемые в механике деформируемого твердого тела. Их часто называют условиями сплошности. Сами уравнения были опубликованы в 1864 г. Сен-Венаном в издании одной книги Навье.

Компоненты тензора несовместности й8 в декартовой системе координат могут быть найдены также в виде

Сделаем ряд существенных замечаний, касающихся числа независимых уравнений совместности малых деформаций14. Обычно считается, что независимых уравнений совместности должно быть шесть (так как тензор —^8 = V х ^Р симметричен). И это неверное утверждение воспроизводится во всех руководствах по механике деформируемого твердого тела. На самом деле ситуация несколько сложнее. Действительно, тензор ^8 удовлетворяет, как это следует из его определения, уравнению15

Следовательно, независимых условий должно быть всего три. Используя приведенные выше выражения для компонент тензора й8 в декартовой системе координат, прямым подсчетом можно показать, что векторное уравнение (6.8) эквивалентно трем скалярным:

На первый взгляд может показаться, что три независимых условия в декартовой системе координат могут составить либо три уравнения й^11 = 0, й$22 = 0, й£33 = 0, либо три уравнения й$23 = 0, й$31 = 0, й$12 = 0. Однако ни три условия первой группы, ни три условия второй группы по отдельности использовать нельзя [9]. Известно [10], что если три условия первой группы удовлетворяются внутри некоторой односвязной области, а вторая тройка условий — на границе этой области, то все три условия второй группы будут удовлетворяться внутри области. Аналогичное утверждение будет справедливо, если поменять группы условий местами.

Опираясь на формулы (6.5), (6.6), запишем уравнение совместности для приращений пластических деформаций в изостатической сетке. Мы будем (как принято всюду в настоящей работе) пренебрегать упругими деформациями: ёе = .

14Хотя условия совместности деформаций были известны уже Сен-Венану, в настоящее время нет полной ясности в вопросе о числе независимых условий совместности.

15Приводимое ниже уравнение в тензорном анализе традиционно называется тождеством Бианки (Ь. Б1апсИ1) (см.: Схо-утен А.Я. Тензорный анализ для физиков. М.: Наука, 1965. С. 146, 147).

dSii = (д^д^defck – д^д^de^)&г I д^de^ I д^de^ – д^-д^-de^ – д^дгde^.

V ■ (dS) = 0.

(6.В)

д1 (dSn) I д2 (dSl2) I дз (dS3l) = О, д1 (dSl2) I д2 (dS22) I дз (dS23) = О, д1 (dS3l) I д2(dS23) I дз(dS33) = О.

Поскольку в силу ассоциированного закона течения тензоры с и йвр соосны, то в сетке изостат матрица тензора диагональна

del О О

О de2 О

О О de3

т.е.

ds = l ® ldel + m ® mde2 + n ® nde3, и в физических компонентах имеем

dS<n> = — d2d2de3 — d3d3de2 + (к2і — к3і) (de3 — de2) + d3 (К21 (de3 — de2)) —

– d2 (К31 (de3 — de2)) — К23К32 (de2 + de3 — 2del) — (б.9)

— K3ld2de3 — K2ld3de2 — К32 dl de2 — К23 dl de3,

dS<l2> = d2dlde3 + d2 [к32 (de3 — del)] + K3ldl (de3 — de2) —

(б.10)

К23d2de3 + К31 (de3 — del) (к32 — К23) ,

где, как и ранее, компоненты dS<22>, dS<33> получаются циклической перестановкой индексов в (б.9), а компоненты dS<23>, dS<3l> получаются циклической перестановкой индексов в (б. 1G).

Для ясного понимания условий применимости полученных выше выражений для физических компонент тензора несовместности еще раз повторим следующее. Ассоциированный закон течения устанавливает соосность тензора напряжений а и тензора приращений пластических деформаций dsP. При использовании критерия текучести Треска следует различать течение на грани (в этом случае уникальный триэдр l, m, n будет однозначно указывать также и главные оси тензора приращений пластических деформаций dsP) и течение на ребре, когда равны два главных напряжения а1 = а2. В случае течения на ребре равенство двух главных напряжений а1 = а2 означает, что любое направление, расположенное в плоскости, ортогональной вектору n, является главным. Поэтому при соответствии напряженного состояния ребру призмы Кулона – Треска есть известная доля произвола при выборе собственных векторов l и m (они определены с точностью до поворотов в плоскости, ортогональной вектору n). Следовательно, векторы l и m уже могут и не быть собственными векторами тензора приращений пластических деформаций dsP. Следовательно, возможно существование триортогональной сетки линий главных напряжений с локальным триэдром l, m, n, таким, что векторы l и m не являются собственными для тензора dsP, но тогда формулы (б.9), (б. 1G) подлежат модификации с целью учета недиагональности матрицы тензора ds = dsP в базисе l, m, n:

de<ll> de<l2> О

de<l2> de<22> О

О О de3

Подобного рода модификация без труда осуществляется с помощью полученных выше формул для физических компонент тензора несовместности (6.5), (6.6)16.

Сначала несколько упростим запись формул для физических компонент тензора несовместности (см. (6.5), (6.6))

^<іі> = 2к23 к32&<іі> +

+ [кзі — к2і — К32 К23 + К31) — (d3 К2і) + К31 d2 — К32 d1 — 2«2^з — ^^]^<22> +

+ [к21 — К31 — к32 к23 + (d3 К21) — (d2 к31) + К21 d3 — к23 ^ — 2к3^2 — ^^]^<33> +

+ [к31к32 + к23к31 + 2к32 к13 + (^2к32) + 2к32^]^<12> +

+ [к21к23 + к32к21 + 2к23 к12 + (d3 к23 ) + 2к23 d3 ]^<13> +

+ [4кзік21 + к21к23 + 2(^2к2і) + (d2 К31) + №кз0 +

+3к2і d2 + 2кз^з + К31 d2 + d2 dз + dз d2 ]dє<2з>,

16Она не требуется в плоском и осесимметричном случаях.

^<22> = 2кЗ1 к1З ^<22> +

+ [к12 — к32 — к1ЗкЗ1 + (^Зк12) — (d1 кЗ2 ) + к12^ — к1З d2 — 2к32 d1 — d1 d1 ]^<ЗЗ> +

+ [кЗ2 — к12 — к1ЗкЗ1 + №кЗ2) — (dЗ к12) + кЗ2^ — кЗ1 d2 — 2к12 dЗ — dЗ ^ ]^<11> +

+ [к12 к1З + кЗ1 к12 + 2к1Зк21 + ^З К1З) + 2к1З ^]^<2З> +

+[кз2кзі + К13К32 + 2кзі К2з + (dl КЗ1) + 2кзі dl ]dє<l2> +

+ [4кі2 КЗ2 + КЗ2 КЗ1 + 2^з К32) + №«і2 ) + ^1К12 ) +

+ЗК32 dз + 2к^і + к^з + dзdl + dldз]dє<lз>,

dS<зз> = 2кі2 К2і dє<зз> +

+ [к2З — к1З — к21к12 + (^1к2З) — № к1З) + к2З^ — к21 dЗ — 2к1З ^ — d2 d2 ]^<11> +

+ [к1З — к2З — к21к12 + (^2к1З) — (d1 к2З) + к1З^ — к12 ^ — 2к23 d1 — ^ d1 ]^<22> +

+ [к2З к21 + к12 к2З + 2к21к32 + (d1 к21) + 2к21 ^]^<1З> +

+ [к1Зк12 + к21к1З + 2к12 кЗ1 + (d2 к12 ) + 2к12 d2 ]^<2З> +

+ [4К2З Кіз + Кіз Кі2 + 2(dl Кіз) + ^іК23 ) + (d2 К2З ) +

+3кіз dl + 2к2зd2 + K2зdl + dld2 + d2dl]dє<l2>,

iНе можете найти то, что вам нужно? Попробуйте сервис подбора литературы.

dS<l2> = —Кзіdldє<22> + [кзі («23 — КЗ2) — ^«32) — КЗ2d2]dє<ll> +

+ [кзі(кз2 — К23) + №кз2) + «з^і + («З2 — «23 )d2 + d2 dl ^Є<зз> +

+ [к2З кЗ2 + 2кЗ1 к1З + 2к21к12 — КІ2і — «2і + — (d2 кЗ1) + к21^ +

+к12^ + dЗdЗ ]^<12> +

+ [к21 (кЗ1 + к1З) — 2кЗ1к12 + «21^ — кЗ1 dЗ — 2(d2 к12) — 2к12 d2 — ^ dЗ ]^<1З> + + [к21 (к23 + кЗ2) — (^ЗкЗ2) + (к2З — кЗ2 ^З — 2к21 d1 — ^ d1 ]^<2З>,

^<1З> = — к2З 4 ^<11> + [к2З (к12 — к21) — №«2^ — к21 d1 ]^<ЗЗ> +

+ [к2З(к21 — к12) + ^1к21) + к2З^ + (к21 — к12 )d1 + d1 ^ ]^<22> +

+ [Кі2 К2і + 2К2З К32 + 2кіз«зі — К2з — к2з + ^2«3і) — (dl К2З) + Klзd2 +

+«3^2 + d2d2 ]dє<lз> +

+ [к1З (к2З + кЗ2) — 2к2ЗкЗ1 + к1З^ — к2З d2 — 2(d1 кЗ1) — 2кЗ1 d1 — d1 d2 ]^<2З> + + [к1З (к12 + к21) — ^Зк2^ + (к12 — к21 ^2 — 2к1З dЗ — ^ dЗ ]dЄ<12>,

dS<2З> = —к12 ^ dЄ<ЗЗ> + [к12 (кЗ1 — к1З ) — — к1З dЗ ]dЄ<22> +

+ [к12(к1З — кЗ1) + (dЗк1З) + к12d2 + (к1З — кЗ1 )dЗ + dЗ ^ ]dЄ<11> +

+ [кЗ1 к1З + 2к12 к21 + 2кЗ2к2З — к252 — к22 + №к2З) — (dЗ к12) + кЗ2^ +

+K2зdl + dl dl ^Є<2З> +

+ [кз2 (кі2 + К2і) — 2кі2К23 + Kзldз — Кі2 dl — 2(dз К2З) — 2К2З dз — dз dl ]dє<l2> + +[кз2 («Зі + кіз) — ^іКіз) + (кзі — кіз )dl — 2КЗ2 d2 — dl d2 ]dє<lз>.

Затем положим в них dє<1З> = 0, dє<2З> = 0. В результате приходим к уравнениям:

^<11> = 2к23 кЗ2 ^<11> +

+ [кЗ1 — к2і — кЗ2 к2З + (d2кЗ1) — (dЗ к21) + «Зі ^ — кЗ2 ^ — 2к21dЗ — dЗdЗ]dЄ<22> +

+ [к2і — кЗ1 — кЗ2 к2З + (dЗк21) — (d2 «Зі) + к21 dЗ — к2З d1 — 2кЗ1d2 — d2d2]dЄ<ЗЗ> +

+ [кЗ1«З2 + к2ЗкЗ1 + 2к32 к1З + (d2кЗ2) + 2кЗ2d2 ]^<12>,

(б.11)

dS<22> = 2к31 К13 de<22> +

+[к22 — к32 — К13К31 + №кі2) — (dl К32) + Кl2dз — К13 d2 — 2К32 dl — dl dl ]de<33> +

+[к32 — Кі2 — К13К31 + (dlКз2) — (d3 К12) + Кз2dl — К31 d2 — 2кі2 d3 — d3 d3 ]de<n> +

+ [К32 К31 + Кіз К32 + 2К31К23 + (dl К31) + 2К31 dl ]de<i2>,

dS<33> = 2кі2 К2і de<33> +

+ [К23 — К13 — К21К12 + (d1К23) — (d2 К13) + К23d1 — К21 d3 — 2к13 d2 — d2 d2 ]de<11> +

+ [К13 — К23 — К21К12 + (d2К13) — (d1 К23) + К13d3 — К12 d3 — 2к23 d1 — d1 d1 ]de<22> +

+ [4к23 К13 + К13 К12 + 2(d1 К13) + (d1К23 ) + (d2 К23 ) +

+3кlзdl + 2к2з d2 + К23 di + di d2 + d2 di ]de<i2>,

^<12> = —кЗ1 ^ ^<22> + [кЗ1 (к2З — кЗ2) — (d2кЗ2) — кЗ2 ^ ]^<11> +

+ [кЗ1(кЗ2 — к2З) + (d2кЗ2) + кЗ^1 + (кЗ2 — к2З )d2 + d2 d1 ]^<ЗЗ> +

+ [к2З кЗ2 + 2кЗ1 к1З + 2к21К12 — к21 — «21 + (dЗ к12) — (d2кЗ1) + к21dЗ +

+к12 dЗ + dЗ dЗ ]^<12> 5

(6.12)

^<13> = — К23 4 ^<11> + [к23 (к12 — К21) — №к21) — К21 dl ]^в<33> +

+ [К23 (^21 — К12) + ^1«21) + К23 dз + (К21 — К12 )dl + dldз]de<22> +

+ [К13 (К12 + К21) — ^з«21) + (К12 — К21 )d2 — 2К13 dз — d2 dз ]de<l2>,

dS<23> = —К12 d2 de<зз> + [К12 («31 — К13 ) — ^з«1з) — К13 dз ]de<22> +

+ [К12 («13 — К31) + ^3 К13) + К12 d2 + («13 — К31 ^3 + dзd2]de<ll> +

+ [кз2 (К12 + К21) — 2К12К23 + Кз^з — К12dl — 2^3К23) — 2К23dз — dзdl]de<l2>.

Приведенные выражения должны использоваться, когда пластическое течение происходит на ребре призмы Кулона – Треска. Компоненты dS<22>, dS<33> нельзя получить циклической перестановкой индексов в уравнении (6.11). То же самое относится к компонентам dS<23>, dS<31> и уравнению (6.12). Вывод этих уравнений следует осуществлять, как это было сделано, исходя непосредственно из формул (6.5), (6.6) для физических компонент тензора несовместности.

В качестве примера применения уравнений совместности деформаций выясним аналитическую классификацию и найдем характеристики пространственных кинематических уравнений в случае течения на ребре призмы Кулона – Треска а1 = а2 = а3 ± 2к. Для этого выпишем главные части уравнений совместности деформаций

dS<ll> = —d2d2deз — dз dзde<22> + ••• = 0, dS<22> = —dldldeз — dз dзd£<ll> + … = 0,

dS<зз> = —d2d2de<ll> — dl dl de<22> + (dld2 + d2 dl )de<l2> + … = 0,

dS<l2> = d2 dl deз + dз dз de<l2> + … = 0,

dS<2з> = dз d2 de<ll> — dзdlde<l2> + … = 0, dS<lз> = dl dз de<22> — d2dзde<l2> + … = 0.

Пользуясь соотношением несжимаемости

de<ll> + de<22> + deз = 0, устраним из полученной системы уравнений de3. В результате приходим к системе dS<ll> = d2 d2 de<22> — dзdзde<22> + d2d2de<ll> + … = 0,

dS<22> = dl dl de<22> + dldlde<ll> — dзdзde<ll> + … = 0, (6.13)

dS<зз> = —d2d2de<ll> — dl dl de<22> + (dld2 + d2 dl )de<l2> + … = 0,

dS<l2> = —d2 dlde<ll> — d2dlde<22> + dзdз de<l2> + … = 0,

dS<2з> = dз d2 de<ll> — dз dl de<l2> + … = 0, (6.14)

dS<lз> = dl dз de<22> — d2 dз de<l2> + … = 0.

Только три из этих уравнений независимы, причем а рпоп неизвестно какие. Однако соображения симметрии позволяют быстро обнаружить нужные уравнения. Искомые уравнения есть dS<12> = 0, dS<11> = 0, dS<22> = 0, т.е. выбираются такие уравнения, чтобы индексы у компонент тензора несовместности dS не включали номер 3. Эти уравнения следует рассматривать как систему уравнений в частных производных относительно de<11>, de<22>, de<12>.

Найдем характеристики построенной системы. Составляя характеристический определитель, приходим к характеристическому уравнению (^<> — физические компоненты единичного вектора нормали к характеристике относительно ортонормированного базиса собственных векторов тензора напряжений 1, т, п):

— Ж<2>^<1> —^<2>^<1> ^<з>

^<2> ^<2> — Л<з> 0

^<1> — ^<з> ^<!> 0

или

Л<3> (Л<!> + Ж<2> — Ж<3>)=0.

Учитывая условие нормировки

^<1> + ^<2> + Ж<з> = 1,

преобразуем характеристическое уравнение к виду

Л<з> (1 — 2Ж<з>) = 0, откуда сразу же становится ясно, что оно имеет три различных вещественных корня:

^<3> = 0, ^<3> = ±^2,

причем кратность нулевого корня равна четырем, т.е. система дифференциальных уравнений в частных производных

dS<12> = 0, dS<11> = 0, dS<22> = 0 (6.16)

гиперболична, а ее характеристики идентичны характеристикам поля напряжений17.

Выясним, зависимы ли остальные уравнения совместности для приращений деформаций

dS<33> = ° ^<13> = 0, dS<23> = 0 (6.17)

от трех уравнений совместности (6.16). Для этого рассмотрим тождество Бианки для тензора несов-

местности dS. В изостатической координатной сетке оно представляется в форме

dl dS<ll> + К2з^6<11> — dS<22>) + К32 ^£<ц> — dS<зз>)+

+ (2к1з + К31 + d2 ^5<12> + (2К12 + К21 + dз ^5<1з> = 0,

(6.18)

^ ^<22> + К31 (^^<22> — ^<33> + К13 (^<22> — ^<11> ) +

+ (2к23 + К32 + d1 ^^<21> + (2к21 + К12 + 4 ^^<23> = 0,

d3 ^<33> + К12(^<33> — ^<11>) + К21 (^<33> — ^<22> ) +

+ (2к32 + К23 + d1 ^<31> + (2к31 + К13 + d2 ^£<32> = 0.

Учитывая (6.16), уравнения (6.18) приводим к виду (2К12 + К21 + dз)dS<lз> — кз2dS<зз> = 0,

(2К21 + К12 + dз)dS<2з> — Кз^5<зз> = 0, (6.19)

^^<33> + (к12 + К21^^<33> + (2к32 + К23 + d1 )^<13> + (2к31 + К13 + ^ ^^<23> = 0.

Отсюда видно, что эта система линейных уравнений в частных производных относительно трех компонент dS<33>, dS<13>, dS<23> тензора несовместности dS нормальна по изостатической переменной ^3, ибо приводится к нормальной форме Коши по этой переменной

ddS<i3> _

,3 _ … , (6.20)

дС3 ddS<23> дС3

ddS<33>

дС3

17Указанная система дифференциальных уравнений в частных производных, как нетрудно заметить, не является ^-гиперболической (или строго гиперболической относительно переменной £3), так как ее характеристическое уравнение имеет кратный корень. Поэтому проблема корректности постановки задачи Коши для системы дифференциальных уравнений в частных производных (6.16) с начальными данными на слое £3 = const векторного поля n нуждается в дополнительном исследовании. Заметим, что многие важные уравнения математической физики имеют характеристическую форму с кратными корнями. Можно даже сказать, что условие строгой гиперболичности очень редко выполняется для линейных систем первого порядка.

Следовательно, задача Коши для системы уравнений (б. 19) с начальными данными на слое С3 = const векторного поля n поставлена корректно. В частности, поставлена корректно задача Коши с нулевыми начальными данными на слое Сз = const

dS<33> = 0, dS<i3> = 0, dS<23> =0 (С3 = const).

(б.21)

Такая задача Коши имеет, очевидно, единственное нулевое решение. В случае, когда коэффициенты линейной системы дифференциальных уравнений в частных производных (6.19) являются аналитическими функциями изостатических координат С1, С2, С3 и слой С3 _ const векторного поля n есть аналитическая поверхность, единственность аналитического решения рассматриваемой задачи Коши прямо следует из теоремы Коши – Ковалевской (см., например, [11], с. 30-37), поскольку как мы покажем далее слой С3 _ const не является характеристической поверхностью для системы (6.19).

Единственность нулевого решения системы линейных дифференциальных уравнений (6.19) (если по-прежнему считать коэффициенты этой системы аналитическими функциями изостатических координат С1, С2, С3) с нулевыми начальными данными на слое С3 _ const в классе непрерывно дифференцируемых функций гарантируется теоремой Хольмгрена (Holmgren, 1901) (см., например, [12]-[15])18 поскольку слой С3 _ const не является характеристической поверхностью для системы

(6.19). Действительно, составляя характеристическое уравнение, имеем (N<j> — физические компоненты вектора нормали к плоскому характеристическому элементу относительно базиса l, m, n)

N<3> 0 0

0 N<3> 0

N N<2> N<3>

= О,

iНе можете найти то, что вам нужно? Попробуйте сервис подбора литературы.

т.е. находится корень N<3> _ 0 кратности 3, а сама характеристическая форма вырождается, что говорит о параболическом вырождении системы уравнений (6.19) и что нормали к характеристикам располагаются в плоскости, ортогональной вектору n19. Поэтому всюду в области достижимости слоя С3 _ const будут выполняться три оставшихся условия совместности (6.17), если они выполняются на слое.

Итак, если три уравнения совместности

dS.

<l2>

— О, dS<ii> — 0, dS<22> — О

выполнены, то три оставшихся

dS<33> _ ° dS<13> _ ° dS<23> _ 0

также выполняются, если они выполняются на каком-либо слое С3 _ const векторного поля n, причем гарантировать выполнение трех оставшихся условий совместности можно в области достижимости слоя С3 _ const или в более широком смысле в той области пространства, где начальные данные (6.21) однозначно определяют решение системы уравнений (6.20)20. Поскольку характеристические поверхности системы уравнений в частных производных (6.20) составляются из векторных линий

18Теорема Хольмгрена имеет весьма общий характер и применяется к линейным системам дифференциальных уравнений в частных производных любого аналитического типа (гиперболического, эллиптического, параболического). В условной части теоремы Хольмгрена можно не требовать аналитичности поверхности, на которой выставляются начальные данные. Теорема Хольмгрена указывает также и форму области, где решение задачи Коши единственным образом определяется начальными данными: это «линзообразная» область, ограниченная начальной поверхностью и частью пространства, заполненного семейством аналитических поверхностей, представляющим собой аналитическую деформацию начального слоя при фиксированном его крае, причем на всех поверхностях этого семейства характеристический определитель должен быть отделен от нуля одной и той же для всех поверхностей семейства постоянной. Насколько далеко удается продвинуться этим методом от начального слоя зависит от геометрии характеристических поверхностей.

19Поэтому поверхности, составленные из векторных линий поля n, будут характеристическими для системы дифференциальных уравнений в частных производных (6.19). Такие же поверхности являются характеристическими и для уравнений равновесия в случае состояний на ребре призмы Треска (см. уравнение (1.10)) VS — n х rot n + ndivn = 0.

20Этот важный результат проливает свет на отмеченную выше проблему о том, какие именно три уравнения составляют независимую систему условий совместности малых деформаций.

поля n, то область достижимости слоя = const будет, по-видимому, ограничена векторными линиями поля n, выпущенными из точек контура, являющегося краем слоя ^3 = const. Ясно, что в приведенных формулировках слой ^3 = const может быть заменен любой поверхностью, не являющейся характеристической для параболически вырожденной системы дифференциальных уравнений в частных производных (6.19).

Укажем еще на одно интересное обстоятельство. Если часть границы тела свободна от контактных усилий, то в качестве граничного условия здесь можно принять условие касания вектора n. Следовательно, указанная часть границы тела будет характеристической поверхностью для системы уравнений в частных производных (6.19). Если дополнить ее произвольной нехарактеристической поверхностью так, чтобы образовалась «линзообразная» пространственная область, то три условия совместности

dS<33> = 0, dS<i3> = 0, dS<23> = 0 (6.22)

будут выполнены всюду в образованной области, если они выполняются на дополняющей поверхности и если три других условия совместности выполняются всюду в указанной области.

Дальнейшие уточнения выполнимости условий (6.22) требует более детального анализа системы уравнений в частных производных

dS<i3>

dS<23>

dS<33>

0 0 0 / dS<i3>

0 0 0 1 dS<23>

-d1 -d2 0 V dS<33>

– (2к12 + K21) 0

– (2k21 + K12)

K32

K31

-(2K32 + K23 ) -(2K3i + K13) -(К21 + K12 )

dS<13>

dS<23>

dS<33>

7. КИНЕМАТИКА ПЛОСКОГО ПЛАСТИЧЕСКОГО ТЕЧЕНИЯ

Опираясь на полученные в предыдущем параграфе статьи результаты, можно исследовать кинематику плоского пластического течения.

Любое условие пластичности в случае плоского деформированного состояния приводится к виду

01 — 02 = 2к. В плоскости течения XI х2 имеется два взаимно ортогональных семейства изостатических траекторий. Одно из семейств будем идентифицировать номером 1, другое — номером 2. В условиях плоского деформированного состояния имеем ^3 = 0, йи<з> = 0, = 0, к31 = 0, к32 =0, к1 = к13,

К 2 = К23.

Обозначая через 9 угол наклона к оси х1 изостаты первого семейства, получаем

К1 = К13 = —^19, К 2 = К23 = ^2 9. (7.1)

Имеется всего одно деривационное соотношение, связывающее кривизны изостатических траекторий, которое имеет вид (см. [3])

^1К2 + ^2К1 + к2 + к2 = 0 (7.2)

и удовлетворяется тождественно в силу К1 = —Й19, К2 = й29.

Уравнения равновесия, сформулированные в изостатической координатной сетке, сводятся к двум соотношениям Ламе – Максвелла

^10-1 + К 2 (01 — 02) = 0, ^202 + К1 (<Г2 — 01) = 0, (7.3)

или

^101 + ——— = 0, ^202 + ——— = 0, (7.4)

Р2 Р1

где р1, р2 — радиусы кривизны линий главных напряжений, причем эти величины считаются положительными, если с возрастанием натурального параметра вдоль кривой касательная вращается против часовой стрелки, при этом положительное направление вдоль первой траектории выбирается

произвольно, а положительное направление вдоль второй траектории определяется вращением против хода часовой стрелки положительного направления первой траектории.

Так как в случае плоской пластической деформации 01 — 02 = 2к, то уравнения (7.4) приобретают следующий вид:

2к 2к _ч

^101 +——=0, й2 01 +—————————————–=0. (7.5)

Р2 Р1

Эта система гиперболична. Характеристики делят пополам угол между главными направлениями напряжений. Вводя в систему (7.5) производные вдоль характеристических направлений (примем, что первая характеристика отклоняется от первого главного направления напряжений, соответствующего наибольшему главному напряжению, на угол п/4 по ходу часовой стрелки)

— ^2 + ^2

тг’ й2 = “7Г’

складывая, а затем вычитая уравнения этой системы, получим интегрируемые соотношения Генки (Н.Иепеку) вдоль характеристик:

й1(а1 — 2к^) = 0, й2 (а1 + 2к$) = 0. (7.7)

Интересно заметить, что в случае плоской деформации единственная ненулевая компонента й£<зз> тензора несовместности й8 = V х йє х V может быть вычислена по формуле

й5<зз> = ^7 ■ (^7 ■ йє) — .

Поэтому в случае плоской деформации условия совместности в приращениях деформаций сводятся к одному уравнению (см. [3])

^5<зз> — — ^1 ^1 ^£2 — ^2 ^2 Й£1 — (^1К2 — ^2 К1 + К2 — К2 )(Й£2 — ^£1)—

— К2^(2^£2 — ^£1) — К1 ^2(2^£1 — ^£2) = 0.

Соотношения Коши в случае плоского деформированного состояния:

Й£р _ / Й1 К1 / йи<1>

й£р / V К2 й2 у V йи<2>

(7.8)

(7.9)

— К1 + ^2 —К2 + ^1 0 / Йи<1>

0 0 й1 I I йи<2> | = 0. (7.10)

0 0 ^2 У V 0

Следовательно, условие несжимаемости и соосности тензора напряжений и тензора скоростей

пластических деформаций в сетке линий главных напряжений можно представить в виде

(К2 + ^1 )^И<1> + (К1 + ^2)^И<2> = 0, (7 11)

(— К1 + ^2)^и<1> + (— К2 + ^1 )^и<2> = 0.

С помощью условия несжимаемости йе1 + йе2 =0 из уравнения (7.8) исключается йе2, поэтому

получается уравнение только относительно йе1. По главной части этого уравнения

^1 ^1^£1 — ^2 ^2 ^£1 + ■ ■ ■ =0

легко устанавливается, что кинематические уравнения принадлежат к гиперболическому типу, и характеристики являются линиями скольжения.

Ясно, что уравнение второго порядка для ^£1 может быть заменено системой двух уравнений первого порядка. С этой целью введем обозначения:

Переменная и — логарифмическое приращение деформации.

Принимая во внимание, что

didei = peu, d2dei_ = qeu, dididei = eudi p + eup2, d2d2 dei = eu d2 q + euq2, уравнение совместности деформаций представим в форме

d2 q — dip = p2 — q2 + 3(к2р — Ki q) + 2(di к2 — d2 Ki + к2 — к^). (7.13)

Заметим далее, что в силу

d2 di — di d2 = —Ki di + K2 d2 (7.14)

справедливо соотношение

d2p — di q = —Ki p + K2q. (7.15)

Следовательно, относительно величин p и q имеем систему уравнений первого порядка (7.13), (7.15).

Вводя обозначения P = di0, Q = d20, систему кинематических уравнений можно привести к следующему симметричному виду:

d2q — di p = p2 — q2 + 3(pQ + qP) + 2(di Q + d2P + Q2 — P2),

(7.16)

d2p — di q = pP + qQ.

Напомним, что здесь величины p и q — производные вдоль линий главных напряжений от логарифмического приращения деформации.

Уравнения статики также преобразуются к симметричной форме относительно величин P и Q. Действительно, уравнения равновесия (7.5) с помощью обозначений P* = diai/(2k), Q* = d2ai/(2fc) представляются как

P* = —Q, Q* = —P. (7.17)

На основании (7.14) находим

iНе можете найти то, что вам нужно? Попробуйте сервис подбора литературы.

d2P * — diQ* = — KiP * + к 2 Q* = PP * + QQ*

и в силу (7.17) —

di P — d2Q = —2PQ.

Переписывая в новых обозначениях деривационную формулу (7.2), имеем

d2P — di Q = P2 + Q2.

Таким образом, получаем систему статических уравнений плоской задачи в форме:

diP — d2 Q = —2PQ, d2P — di Q = P2 + Q2.

(7.18)

Последняя система уравнений позволяет сформулировать ряд новых результатов, касающихся геометрии поля изостат (см. также [16]).

Преобразуя систему уравнений (7.18) к характеристическим переменным (см. (7.6)), находим

^2 ^1(Р + ^) = —(Р + ^)2, ^2 й2(р — д) = (р — д)2,

или

і і

P + Q л/2

77 1 1

d2-

(7.19)

P — Q л/2

Вспоминая определение величин Р и получим следующие соотношения вдоль характеристик:

1 1

К2 — К1 f ‘ (7.20)

$2——– = — ,

К 2 + К1 л/2

т.е. обратная разность (сумма) кривизн изостатических линий при продвижении вдоль первой (второй) характеристики изменяется пропорционально пройденному пути21.

Не представляет труда и вывод соотношений для приращений перемещений вдоль характеристических направлений. Складывая уравнения (7.11), а затем вычитая одно из другого, с учетом (7.6) находим

—_ ^2(^и<1> + ^и<2>) + (К2 — К1)(^и<1> — ЙИ<2>) = 0, (7 21)

/_ ^1(^И<1> — $и<2>) + (К2 + К1)(^И<1> + $и<2> ) = 0.

Замечая далее, что при повороте осей главных напряжений 1, 2 на угол п/4 по ходу часовой стрелки

получаем характеристические оси 1, 2, так что физические компоненты вектора $и относительно ука-

занных осей вычисляются в виде (йи<1>, йи<2> — физические компоненты вектора $и относительно характеристических осей)

л/2йи<1> = йи<1> — $и<2>,

“/2Йи<2> = йи<1> + йи<2>.

Следовательно, для физических компонент22 приращения вектора перемещений имеем

^1^и<1> + — — йи<2> — 0,

^2^и<2> + ——-—=— йи<1> — 0.

<2> 2 <1>

(7.22)

Принимая во внимание, что

К2 — К1 $2 + $1 л “5 л К2 + К1 $2 — -} л

—^^— V — $2 V, ———–=– — —=— V — — а1 V,

л/_ л/_ л/_ л/_

из (7.22) получаем соотношения Гейрингера (Н. йеш^ег) вдоль характеристик

$1$и<1> — $и<2> $1V — 0,

$2$и<2> + $и<1> $2 V — 0

или на основании к1 — — $1и, к2 — $2$

$1$и<1> + К1 $и<2> — 0, $2$и<2> + К2 $и<1> — 0.

(7.23)

(7.24)

Напомним, что производные по характеристическим направлениям 1, 2 связаны с производными по главным направлениям 1, 2 следующими соотношениями:

— д д д

/_ $1 — л/_-^= — $1 — $2 — д”ё до-

д^1 до1 до2

21Этот результат — аналог второй теоремы Генки о геометрии поля скольжения в состоянии плоской деформации (см., например [17, с. 218]). Вторая теорема Генки непосредственно следует из (7.20). Действительно, применяя (7.6) к в, находим

К2 + К1 _ К2 — К1

К1 = ^Т” ’ К2 = ^Т” ’

где К1 = —^1 в, К2 = <12в — кривизны характеристических линий, что означает

dl^^ = 1, ^2 — = 1,

К2 К1

а эти соотношения как раз и составляют содержание второй теоремы Генки.

22Относительно характеристических направлений.

— д д д

V2 d2 = V^-= = d1 + d2 = + dS” ■

dS2 dSi ds2

Следовательно, соотношения Гейрингера (7.23) могут быть представлены в развернутой форме:

ddu<T> , д$

<т> — du<2^^= = О,

dSi wdSi (725)

ddu<2> , d9 ( )

—=<2> + du<T> -= =0. dS2 <т> dS2

Вводя в уравнения (7.23) вместо приращений перемещений du, du<2> физические компоненты скорости v<T>, v<2> относительно ортогональной сетки характеристических линий, имеем

dv v<2>d9 0 (7 26)

d2 v<2> + V<T> d2 9 = 0. ■

Соотношения Гейрингера (7.26) устанавливают, что скорости удлинений прямолинейных элементов, касающихся линий скольжения, равны нулю (см., например: Фрейденталь А., Гейрингер Х. Математические теории неупругой сплошной среды. М.: Физматгиз, 1962. С. 267, 272, 273). Если через £<тт>, ё<22>, £<т2> обозначить физические компоненты тензора скорости деформаций є в характеристической системе координат, то соотношения Гейрингера будут эквивалентны уравнениям

^<ТТ> = 0, ^<22> = °-

Связывая с помощью тензорного закона преобразования декартовы компоненты єТ1, є22, є12 тензора є с его компонентами относительно характеристической координатной системы є<тт>, є<22>, ^<Т2>, имеем

2 п п п 2 п

є<тт> = £ii cos (9 — 4) + 2єі2 sin(9 — 4) cos(9 — 4) + Є22 sin (9 — 4),

2 п п п 2 п

є<22> = £11 cos (9 + 4) + 2єі2 sin(9 + 4) cos(9 + 4) + Є22 sin (9 +4),

или

т п. (dvi п. dvi . пЛ

Е<тт> = cos(9 — 44 aXTcos(9 — 4) + aX2sin(9 — 4 V +

п. (dv2 п. dv2 пЛ

+sin(9 — 44dXTcos(9 — 4) + 5Ї2sin(9 — 44 ‘

п, (dvi п, dvi . пЛ

є<22> = cos(9 + 4^ dXTcos(9 + 4) + sin(9 + 4 V +

. пs (dv2 п, dv2 . пЛ

+sin(9 + 44dXTcos(9 + 4) + 5Ї2sin(9 + 4V .

Записывая полученные уравнения с помощью операторов дифференцирования по характеристическим направлениям, находим

П — П —

^<тт> = соэ(0 – 4)^1 VI + віп(0 – 4)^2,

П — П —

є<22> = соб(0 + 4)^2 VI + 8Іп($ + 4)^2, что при условиях є<тт> = 0, є<22> = 0 позволяет сразу же найти соотношения вдоль характеристик

П — П —

соб(0 — — )^т V1 + БІп(0 — — )^і^2 = 0,

П – П – <7-27)

СОб(0 + 4)^2 VI + 8Іп($ + 4 )d2V2 = 0.

Рассмотрим далее физические компоненты скорости v<т>, v<2> относительно характеристической координатной системы, связав их с декартовыми компонентами скорости с помощью тензорного закона преобразования

П П

iНе можете найти то, что вам нужно? Попробуйте сервис подбора литературы.

V<т> = V! СОБ(0 — 4) + V2 8Іп(0 — 4),

Дифференцируя последние уравнения вдоль первого и второго характеристических направлений соответственно и учитывая

и, принимая во внимание, что выражения в скобках в правых частях равны нулю на основании (7.27), снова приходим к соотношениям Гейрингера в форме (7.26).

Соотношения Гейрингера, как показывает внимательный анализ их вывода, остаются справедливыми при плоской несжимаемой деформации любого изотропного тела23. Их появление в рамках теории плоской задачи математической теории пластичности — не более чем дань традиции.

8. КИНЕМАТИКА ОСЕСИММЕТРИЧНОГО ТЕЧЕНИЯ

Осесимметричное пластическое течение, когда напряженное состояние соответствует ребру призмы Треска, можно разделить на следующие два типа24: 1) тангенциальное напряжение является наибольшим (наименьшим) главным напряжением, а меридиональные главные напряжения равны; 2) тангенциальное напряжение равно одному из меридиональных главных напряжений, а максимальное касательное напряжение в меридиональной плоскости равно пределу текучести &. Первый случай исследуется сравнительно элементарными средствами. Второй случай — состояние «полной пластичности» Хаара – Кармана. Если присвоить тангенциальному главному направлению второй номер и обозначить через аз наибольшее (наименьшее) из двух меридиональных главных напряжений, то приходим к соотношению, характеризующему состояние «полной пластичности»

В осесимметричном случае линии главных напряжений образуют триортогональную координатную сетку . При этом ^2 — угловая координата. Кроме того, имеем: й2 = 0, йи<2> = 0, кт3 = 0, к3т = 0. Поэтому приходим к более простым, по сравнению с общим пространственным случаем, соотношениям, описывающим распределения напряжений и скоростей.

Деривационные соотношения выражаются группой уравнений:

и при догружении вдоль ребра призмы Треска а = = а3 — 2& в этих уравнениях следует положить

0″1 — а2 = 0, а3 — а1 = 2^, а3 — а2 = 2^.

23Поскольку для их вывода в рамках теории плоского деформированного состояния достаточно условия несжимаемости и условия коориентированности главных осей тензора напряжений и тензора скоростей деформаций.

24Тангенциальное напряжение всегда будет главным напряжением при осесимметричном напряженном состоянии.

ПП

^ = ^т>йіп(9 + 4) — ^2>йіп(9 — 4).

ПП ^ = — *><т> сой(9 + 4) + ^2> С°8(0 — 4),

получаем

^2 “у<2> =

Г = £2 = Г3 ± 2к.

^К32 + ^3^2 + Кт2 + КЗ2 — 0, ^К23 + ^2з + = 0,

^зК^ + + К23К32 = 0,

^3^23 = К2т (К32 — К23).

Уравнения равновесия, сформулированные относительно изостатической сетки, есть

+ К23 (Г — 02) + К32 (Г — 73) = 0, ^303 + К2т (Г3 — Г2) + Кт2 (Г3 — г) = 0,

(8.1)

Условия совместности приращений деформаций выражаются тремя уравнениями относительно изостатических координат

= — ^3^3^£2 + К21 (^£э — ^£2) + ^3 [^21 (^£3 — ^£2)] — К23К32(^£2 + ^£3 — 2&1 ) —

— К21 ^3 ^£2 — К32 ^1 ^£2 — К23^1 ^£3 = 0,

Й5<22> = — ^3 ^3 ^£1 — ^1 ^1 ^£3 + (к^2 — К^2)(^£1 — ^£3) + ^1 [К32 (^£1 — ^£3)] —

— К12^3^£1 — К32^1 ^£3 — ^3 [^12(^£1 — ^£3)] = 0, (8-2)

^^<33> = — Й1Й1 Й£2 — к|3 (Й£2 — Й£1) — Й1 [К23 (Й£2 — Й£1)] — К21К12 (^£1 + ^£2 — 2^£3) —

— К23 ^1 ^£2 — К21 ^3 ^£1 — К12^3 ^£2 = 0,

из которых, в силу тождества Бианки V ■ ^8 = 0, независимы только два, например, первое и третье. Действительно, условия ^<12> = 0, ^<23> = 0, й^<31> = 0 удовлетворяются тождественно в силу к31 = 0, к13 =0, й2 = 0. Это означает, что тензор ^8 соосен тензору напряжений и й^<11> = ^51, ^^<22> = й£2, ^5<33> = й£3. Тождества Бианки при этом сводятся к двум уравнениям:

di dSi + к23 (dSi — dS2) + K32(dSi — dS3) — 0, d3 d$3 + K12 (dS3 — dSi) + K2i(dS3 — dS2) — 0.

(8.3)

Следовательно, если хотя бы одна из кривизн к23 или к21 отлична от нуля, то из условий dS1 = 0, dS3 = 0 необходимо dS2 = 0.

Независимыми можно также считать два условия dS<11> =0 и dS<22> = 0. Если кривизна к32 отлична от нуля, то из уравнений (8.3) необходимо следует dS<33> = 0.

Независимые условия совместности dS<11> =0 и dS<22> = 0 после исключения из них величины d£2 с помощью условия несжимаемости позволяют сформулировать систему двух уравнений второго порядка относительно d£1 и d£3. Главная часть этой системы есть

dзdзd£l + dзdзd£з + ■ ■ ■ = 0, —dз dз d£l — dl dl d£з + ■ ■ ■ =0.

Характеристическое уравнение

N<3> —N<3>

N 2

N<3>

N 2 N<1>

—0

где ^<> — физические компоненты вектора нормали N к характеристическому элементу относительно базиса 1, т, п при условии ^”<1> + ^”<3> = 1 приобретает вид

^<з> (^<з> — ^<1>) = 0

и имеет четыре действительных корня: ^<3> = 0 (корень кратности два), ^<3> = 1/л/2, ^<з> = —1/л/2, т.е. система уравнений dS<11> =0 и dS<22> = 0 принадлежит к гиперболическому типу; направления, ортогональные третьей главной оси напряжений, — характеристические, а остальные характеристические направления делят пополам углы между главными осями напряжений

1 и 3. Следовательно, характеристиками системы уравнений совместности приращений деформаций dS<11> =0 и dS<22> = 0 будут изостаты, ортогональные третьему главному направлению, и линии скольжения.

В осесимметричном случае соотношения Коши, связывающие приращения тензора малых деформаций с приращениями перемещений, в криволинейной ортогональной координатной сетке линий главных напряжений имеют следующий вид:

0 0 0

0 —К23 + di 0

—К12 + d3 0 — К32 + di

0 — K2i + d3 0

du

du<3>

du

— 0.

(8.4)

(8.5)

Следовательно, условие несжимаемости и соосности тензора напряжений и тензора скоростей пластических деформаций в сетке линий главных напряжений можно представить в виде

(к23 + К32 + ^і)^и<і> + (кі2 + К21 + ^3)^И<3> = 0, (8 ^

( —Кі2 + ^3 )^и<1> + ( — К32 + ^1 )^и<3> = 0.

Характеристическое уравнение этой системы

имеет два действительных различных корня, что указывает на гиперболичность приведенной выше системы уравнений. Характеристические линии являются линиями скольжения.

9. КИНЕМАТИКА ПРОСТРАНСТВЕННОГО ПЛАСТИЧЕСКОГО ТЕЧЕНИЯ НА ПОВЕРХНОСТЯХ СКОЛЬЖЕНИЯ

Рассмотрим, следуя [18] — [20], кинематику пространственного пластического течения на поверхности скольжения. Исключительный интерес здесь будут представлять соотношения, связывающие скачки тангенциальных приращений перемещений при переходе через линии сильного разрыва, расположенные на самой поверхности максимальной скорости сдвига. Указанные линии, как будет доказано, являются асимптотическими линиями поверхности максимальной скорости сдвига, а соотношения вдоль них, связывающие скачки, оказываются интегрируемыми. Изложение в основном следует статье: Радаев Ю.Н. Кинематика пространственного идеально пластического течения на поверхностях скольжения // Вестник Самарского гос. университета. Естественно-научная серия. 2006. №9(49).

Поверхность скольжения в идеально пластическом теле суть поверхность разрыва касательных составляющих приращений перемещений du.

Как показывает анализ, данный в [18], [19], на поверхности разрыва касательных составляющих приращений перемещений реализуется чисто сдвиговое течение, когда главные приращения пластических деформаций удовлетворяют условиям

Действительно, если считать, что поверхность сильного разрыва касательных составляющих приращений перемещений заменяется тонким слоем, внутри которого вектор du изменяется непрерывно (рис. 1), то можно получить ^ — единичный вектор, ортогональный рассматриваемой поверхности)

ds = ф(^и] 0 N + N 0 ^и]), где ф — некоторая функция, определенная на поверхности разрыва приращений перемещений.

при условии

С. 30-41.

= 0, йєР + = 0 (і = і, і = І, І = і).

(9.1)

Верхняя граница слоя

Нижняя граница слоя

Рис. 1. Слой скольжения внутри идеально пластического тела (касательная составляющая приращений перемещений ^и* непрерывно переходит внутри слоя из положения ^и- в положение ^и+)

Привлекая затем соотношение совместности для скачка вектора йи при переходе через поверхность разрыва приращений перемещений

N ■ [йи] = 0,

следующее из условия несжимаемости25, сразу же приходим к уравнению

N ■ йе = ф [йи], (9.2)

с помощью которого получаем следующее представление приращений деформаций на поверхности

разрыва касательных составляющих приращений перемещений:

йе = ^ ■ йе) 0 N + N 0 ^ ■ йе). (9.3)

Соотношения (9.1) без труда устанавливаются с помощью (9.3).

Ассоциированный закон течения, сформулированный для грани призмы Кулона – Треска

01 — 02 = 2к, устанавливает жесткую (без неопределенности, характерной для ребра призмы Треска) соосность тензоров йер и с и еще следующие соотношения для главных значений тензора приращений пластических деформаций:

= йЛ, = —йЛ, = 0,

откуда следует соотношение несжимаемости

def + dep = 0.

Видно, что характер пластического течения, если реализуется напряженное состояние на грани призмы Кулона – Треска, оказывается чисто сдвиговым. Сдвиг происходит в плоскости, ортогональной вектору п (рис. 2). Направления максимальной скорости сдвига расположены в плоскости, ортогональной вектору п, и делят пополам прямые углы, образованные направленными вдоль векторов 1 и т пересекающимися прямыми.

Направление максимальной скорости сдвига

Рис. 2. Положение направлений максимальной скорости сдвига относительно триэдра главных осей напряжений 1, т, п (течение на грани призмы Кулона – Треска о — о2 = 2к)

Чисто сдвиговое течение (9.1) характерно для состояний на грани призмы Треска, и тогда необходимо совместное рассмотрение уравнений (3.3), (3.8), дополненных соотношениями Коши. Однако чисто сдвиговое течение (9.1) возможно и на ребре призмы Треска тогда, когда вектор, представляющий приращения пластических деформаций в трехмерном пространстве главных напряжений Хэя

– Вестергарда, занимает одно из крайних своих возможных положений между нормалями к граням

25Последнее, поскольку речь идет о сильных разрывах приращений перемещений, следует брать в интегральной форме § ь • du =0, где Б — произвольная замкнутая поверхность, расположенная внутри тела и не изменяющаяся в процессе нагру-5

iНе можете найти то, что вам нужно? Попробуйте сервис подбора литературы.

жения, 1 — единичный вектор нормали к указанной поверхности.

призмы, пересечением которых образуется само ребро26. В любом случае в дальнейшем при анализе течения вдоль поверхностей скольжения мы будем, помимо (9.3), использовать лишь условия несжимаемости и соотношения Коши.

Деформация в нормальных сечениях поверхности скольжения представляет собой сдвиг одной стороны поверхности относительно другой. В одном из нормальных сечений поверхности скольжения скорость деформации сдвига максимальна27. Линия пересечения этого нормального сечения с касательной плоскостью указывает направление максимальной скорости сдвига28. Действительно, рассмотрим произвольную нормальную к поверхности скольжения плоскость, опирающуюся на единичные векторы 1, N. Вектор 1 касается поверхности скольжения. Согласно (9.2) скорость деформация сдвига в этой плоскости вычисляется как

N ■ ^е) ■ 1 = ф [^и] ■ 1. (9.4)

Ясно, что максимум эта величина достигает тогда, когда вектор 1 становится коллинеарным вектору [^и]. Проведенное рассуждение показывает также, что на поверхности максимальной скорости сдвига удобно ввести локальный ортогональный триэдр, состоящий из ортов 11, 12, N (орт 11 имеет направление [^и], орт 12 ортогонален [^и], а орт N нормален поверхности (рис. 3)).

В базисе 11, 12, N матрица тензора dе на основании (9.3) имеет вид

0 0 ^Є<13>

0 0 0

^е<13> 0 0

где йє<13> — единственная ненулевая физическая компонента тензора йе в указанном базисе. Следовательно, можно сразу же вычислить собственные значения тензора йе: 0, ±йє<13>.

Рис. 3. Ориентация локального репера її, , N на поверхности

скольжения

26Здесь мы говорим о ребре призмы Треска, хотя, по существу, сдвиговое течение (9.1) соответствует грани, с тем, чтобы оперировать с правильно определенной гиперболической системой кинематических уравнений (2.19) и ее решениями, подчиняющимися ограничениям (9.1). Мы пользуемся возможностью трактовать состояния на ребре как предельные случаи состояний на гранях, пересечением которых образовано ребро. Действительное течение на грани, помимо кинематических связей (9.1), ограничивается еще и жестким предписанием триэдра главных осей тензора приращений пластических деформаций (он предписан триэдром главных осей тензора напряжений). На ребре призмы Треска предписывается лишь одно из трех главных направлений тензора приращений пластических деформаций.

27Это нормальное сечение имеет направление вектора разности векторов тангенциальных приращений вектора перемещения с двух сторон поверхности.

28Именно поэтому поверхность скольжения мы будем называть также поверхностью максимальной скорости сдвига.

Из ассоциированного закона течения следует, что касательное напряжение на поверхности максимальной скорости сдвига также имеет максимальное значение29. Следовательно, если допускать отмеченную выше возможность реализации сдвигового течения вида (9.1) для состояний на ребре призмы Треска, то поверхность максимальной скорости сдвига — характеристическая для правильно определенной системы уравнений кинематики течения на ребре. Поясним сказанное примером. Рассмотрим грань призмы Треска о — ст2 = 2& и две ее крайние точки, расположенные в девиаторной плоскости, соответствующие ребрам (рис. 4)

Обобщенный ассоциированный закон течения допускает реализацию для таких состояний чисто сдвигового течения вида

Направления максимальной скорости сдвига для рассматриваемых состояний ортогональны вектору п и делят пополам угол между векторами 1 и т.

Вектор N (единичная нормаль к поверхности скольжения), поскольку он нормален характеристической площадке, должен для состояния сті = ст3 = + 2к удовлетворять соотношению

Учитывая еще, что вектор N ортогонален направлению максимальной скорости сдвига, удается однозначно определить его ориентацию относительно локального триэдра 1, т, п (рис. 5). Заметим, что в каждом из двух состояний о = = о2 + 2& и о2 = = о — 2^ вектор N ортогонален вектору

п, а вектор п касается поверхности скольжения.

29Можно показать (см. [19], с. 47-49), что только условие пластичности Треска обеспечивает существование в идеально пластических телах поверхностей разрыва касательных составляющих приращений перемещений с чисто сдвиговой картиной деформирования (9.1).

а1 = а3 = а2 + 2k, а2 = а3 = а1 – 2k.

Ребро СТ1 = 673 = сг2 + 2к

Грань о”|

Ребро <т2 —а3 = сг1 — 2к

Рис. 4. Крайние состояния для грани призмы Треска о — а2 = 2к в девиаторной плоскости пространства главных напряжений

de3 = 0, de1 = —de2.

m • N = ± —, л/2

а для состояния а2 = а3 = а1 — 2k —

l ■ N = ±—.

скорости сдвига

Рис. 5. Ориентация вектора N относительно локального репера 1, т, п для состояния 02 = оз = 01 — 2к (а) и 01 = оз = 02 + 2к (б)

Итак, поверхность максимальной скорости сдвига есть, вообще говоря, поверхность сильного разрыва приращений перемещений. Нормальная составляющая вектора du должна быть непрерывной при переходе через поверхность максимальной скорости сдвига, а касательная составляющая разрывна. Все последующие соотношения поэтому следует интерпретировать как выполняющиеся на каждой из двух сторон поверхности.

Как было установлено выше, на поверхности максимальной скорости сдвига выполняется соотношение

de = (К ■ de) 0 N + N 0 ^ ■ de),

т.е. сдвиги происходят в плоскостях, содержащих вектор К30, а в касательной плоскости сдвигов не происходит. Кроме него имеются также соотношение Коши и условие несжимаемости:

2dє = V 0 du + (V (0 du) ,

(9.5)

іт^є)=0. (9.6)

Введем на поверхности скольжения Гауссовы координаты т1, т2. Обозначим через іа локальные базисные векторы, соответствующие параметризации т1, т2. Разложим тензор V 0 du на рассматриваемой поверхности, используя триэдр і1, і2, N

V 0 du = N 0 (N ■ V)du + аавіа 0

дdu дтв ’

(9.7)

где аав — компоненты фундаментального тензора поверхности. В справедливости этого соотношения нетрудно убедиться, производя внутреннее умножение слева на векторы і1, і2, N.

Опираясь на условие несжимаемости и (9.5), (9.7), заключаем, что

дdu

а дтв •

N ■ (N ■ V)du = —ааві Умножая (9.5) слева на N и учитывая (9.7) и (9.8), находим

^ ■ V)du = 2N ■ dє + аа/3 ( (іа ■ N — і^ ( N

дdu дта )

(9.8)

(9.9)

Умножая тензорно обе части полученного уравнения справа и слева на вектор N складывая и используя (9.3),

N 0 ^ ■ V)du = V 0 du — аавіа 0

дdu дтв ’

30Точнее, в одной из нормальных плоскостей (опирающейся на векторы t2, N скорость деформации сдвига равна нулю, а во всех остальных нормальных плоскостях она будет отлична от нуля.

а также (9.5), приходим к

2““в (^ ■ ів) N 0 N + а“* (^ ® і* + і* в ^ = аав ^ ^ (^ 0 N + N в і„). (9.10)

дт а у дта у

_ в дйи .

Переходя в этом уравнении к следу, имеем аар—————- ■ 1в = 0, что позволяет несколько упростить

дт ;

уравнение (9.10)

«“* (^ в ів + і* 0 ^ = а“в ^ ^ (* 0 N + N 0 ів). (9-П)

Приращения перемещений на поверхности максимальной скорости сдвига должны удовлетворять тензорному уравнению (9.11). Оно дает лишь три независимых скалярных уравнения, так как умножение обеих его частей на вектор N приводит к тождеству. Независимые соотношения получаются умножением обеих частей уравнения (9.11) на вектор іи слева, что приводит к

Ши дйи / дйи

іи • іа + ТТГ7 = N • —- N

и дт “У ‘ дт и V дти )

а затем — на вектор ід, что дает

дйи дйи

дтЛ + Л дти

Поскольку уравнение (9.12) должно удовлетворяться на каждой из сторон поверхности макси мальной скорости сдвига, то для скачков приращений перемещений имеем следующее соотношение:

д [йи] д [йи]

іи ■ ^ +іЛ ■ ^ = °’

Для дальнейшего анализа разложим вектор йи по векторам локального триэдра іі, і2, N:

йи = (йи )N + йиа іа.

Ясно, что , йиа не являются действительными приращениями и служат для сокращенной записи проекций вектора йи на указанный триэдр.

дN

дт ^

ной формы поверхности максимальной скорости сдвига) можно получить следующие выражения для частных производных вектора йи по Гауссовым параметрам поверхности:

На основании формулы Вейнгартена = — сґаЬ^7 іа (Ь^7 — компоненты второй квадратич-

дйи , 1Тт. .. дйи;. ,, . тчтд^и

дт^ = -(йи)а ЬШ11а + дт7 1а + (йи )Га71а + N-7^ ,

да

внося которые в (9.12) и учитывая Гал „ + Га„ л = тг~^, приходим к уравнению

дт;

-%А (^) + а„« ^ + ала ^ ^ = 0. (9.13)

Поскольку уравнение (9.13) должно удовлетворяться на каждой из сторон поверхности максимальной скорости сдвига, а нормальная составляющая йи непрерывна при переходе через эту поверхность, то скачки касательных составляющих приращений перемещений связаны посредством следующего соотношения:

д 1 ,

+ аЛ;^Т-— + И;] (9.14)

д [^иа] + а д [^иа] + [ даДи иа дтд + ад« дти +[Йи ] “дт^

iНе можете найти то, что вам нужно? Попробуйте сервис подбора литературы.

Сворачивая обе части уравнения (9.13) с дЛи, имеем

4Н (йи) + 2 + аЛи даДи йиа =0, (9.15)

V ‘ дтЛ дта

где Н — средняя кривизна поверхности максимальной скорости сдвига:

Н = —1 ЬидаЛи.

Для скачков (принимая во внимание, что [йи] = 0) соответственно находим уравнение

2^ + алид0л^ [йи;] = 0. (9.16)

дтл дт;

Исключая затем с помощью соотношения (9.15) из (9.13) нормальную составляющую йи, получаем

дйи; дйи; , дйив ^ …

-На^а-дтт – Нал^“дт^ – (9 )

Это уравнение31 собственно и определяет пластическое скольжение вдоль поверхности максимальной скорости сдвига и должно удовлетворяться на каждой из двух ее сторон (касательные составляющие йи; могут иметь различные значения на разных сторонах поверхности; нормальная составляющая йи непрерывна при переходе через эту поверхность, если не допускать нарушения сплошности тела).

Для анализа кинематики течения на поверхности максимальной скорости сдвига исследуем уравнение (9.17) на предмет существования действительных характеристических направлений. Можно воспользоваться стандартной техникой Адамара – Томаса [5] геометрических условий совместности слабых разрывов касательных составляющих приращений перемещений. Слабый разрыв характеризуется скачками производных, в поперечных по отношению к характеристическим линиям направлениях, величина которых вычисляется согласно

дёис

тл

= ^л,

где ^л — единичный вектор нормали к характеристической линии на поверхности максимальной скорости сдвига32. Ясно, что

^л^л = 1, > 0.

Из уравнений (9.17) выводятся соотношения для скачков касательных составляющих приращений перемещений. В результате находим, что компоненты ^л должны определяться из условий нетривиальной разрешимости относительно Аа (АаАа > 0) системы уравнений

-Н(Аи^ + Ал) – (двV®)Ьил = (9Л8)

Несложные рассуждения показывают, что вещественные характеристические направления существуют, только когда главные нормальные кривизны поверхности максимальной скорости сдвига кь к2 имеют разный знак (т.е. Гауссова кривизна поверхности К отрицательна). При этом характеристики представляют собой асимптотические линии на поверхности максимальной скорости сдвига33. Действительно, система уравнений (9.18) в ортогональной Гауссовой сетке имеет вид

-2НД VI – (а11 А.1 VI + а22А2^)6ц = 0,

-2НА2V2 – (а11 А-1VI + а22ДV2)b22 = 0,

-Н(А^2 + А-2V!) – (а11А1 V! + а22ДV2)&12 = 0.

31Вместе с соответствующим уравнением, связывающим скачки касательных составляющих приращений перемещений

д [Аиа] д [ё,па] д йив]

-Яа^“~~дт^ – Ла~д^~ – »Л~дГ^ = °

32Вектор V расположен в касательной к поверхности плоскости ортогонально характеристической линии.

33Напомним, что асимпотическими линиями на поверхности называются линии, нормальная кривизна которых равна нулю. Если 1 есть касательный вектор к асимптотической линии, то

V л ^Л = о.

На поверхности отрицательной гауссовой кривизны асимптотические линии образуют координатную сетку. Угол 1 между асимптотическими линиями вычисляется по формуле

1 _ / к1 ‘*2 = V -К?

Известия Саратовского университета. 2008. Т.8. Сер. Математика. Механика. Информатика, вып.2 Характеристическое уравнение

2Н7/1 — а11 Ьи VI —а22Ьи«о 0

—2HVi — а11 611v1 —а22 6uv2

—Hv2 — аи612 v1 —Hv1 — а22 612v2

или

(2H1 + а11611 )(Hv1 + а22&12 V2 )v1 = а226и (Hv2 + а11&12 V1 )v2, принимает наиболее простую форму

622 V2 + 611 v| = 0,

когда криволинейная сетка на поверхности совпадает с сеткой линий кривизны (в этом случае а12 = 0, 612 = 0, —611/а11 = к1, —622/а22 = к2). Переходя в последнем уравнении к физическим компонентам v<1>, v<2> относительно локального базиса сетки линий кривизны согласно v1 = Л/а11v<1>, V2 = /a22 v<2>, получим

2 I 2 А 2 I 2 1

К 2 V<1> + K1 V<2> =0, V<1> + V<2> = 1,

откуда следует, что система уравнений (9.17) гиперболична, только если главные кривизны поверхности имеют разные знаки. Из этого же уравнения на основании формулы Эйлера для нормальной кривизны кривой на поверхности, составляющей угол и с первой линией кривизны,

22 Кп = К1 cos U + К2 sin и

заключаем, что нормальная кривизна характеристик системы уравнений (9.17) равна нулю, т.е. характеристики есть асимптотические линии поверхности максимальной скорости сдвига. Этот факт сразу же позволяет сделать вывод о том, что пластическое течение вблизи поверхности максимальной скорости сдвига (отрицательной Гауссовой кривизны) реализуется как результат микроскольжений в асимптотических направлениях. Поэтому результатом такого рода необратимого деформирования должны быть мозаичные узоры, составленные из отрезков линий микроскольжения, ориентированных в асимптотических направлениях. Даже локально поверхность отрицательной Гауссовой кривизны имеет довольно сложную форму. Любая окрестность точки поверхности отрицательной Гауссовой кривизны имеет седлообразную форму и делится асимптотическими направлениями на четыре части, причем две из них являются вогнутыми и две выпуклыми.

Предположим, что Гауссова кривизна поверхности максимальной скорости сдвига K отрицательна. Выберем параметризацию поверхности максимальной скорости сдвига так, чтобы координатные линии т1 = const, т2 = const были асимптотическими линиями. Поскольку в этом случае

611 =0, 622 = 0, K = — H ^H = Oil,

а а K 612

то из системы уравнений (9.17) можно получить два независимых уравнения34

ddu1 ddu2 ddu2 ddu1

O11 дт 1 + O12 дт 1 = 0, O22 дт2 + O12 дт2 = 0- (9.19)

Здесь а^л — компоненты метрического тензора поверхности, вычисленные в асимптотической координатной сетке. Система уравнений (9.19) записана в характеристических координатах. Каждое из уравнений этой системы есть соотношение вдоль характеристики.

В случае, когда система уравнений (9.17) эллиптична, в координатной сетке линий кривизны имеем

ddu1 (ddu1 ddu2

2 11 Тм + Ц атт + 7^) =°-

„тт ddu1 (ddu1 ddu2

2 22 атт + Ц этт + = 0

rr ddu2 rr ddu1 На22 дт 1 + На11 дт2 = 0’

4При ^ =1, Л =1 и ^ = 2, Л = 2. Уравнение, соответствующее ^ =1, Л = 2, не дает нового независимого соотношения.

откуда получаем два независимых уравнения

д^и1 д^и2 д^и1 д^и2 ^ … ….

К2_дт1—-К1 дт2 = 0 а11 дт2 + а22 дт 1 = °- (9.20)

Здесь, подчеркнем еще раз, координатная сетка т1, т2 совпадает с сеткой линий кривизны поверхности максимальной скорости сдвига. Второе уравнение приведенной системы можно преобразовать, переходя к физическим компонентам приращений перемещений и лонгальным параметрам 51, з2 вдоль линий кривизны. В результате имеем уравнение

д^и<1> д^и<2>

—о—–1 о-+ 71 ^и<1> + 72^и<2> = 0,

д^2 д^1

где 71, 72 — геодезические кривизны линий кривизны поверхности максимальной скорости сдвига

д 1п ^/оЦ д 1п ^/022

71 =——————————–о-, 72 =

ds2 ’ dsi ■

Заметим, что главные кривизны и геодезические кривизны линий кривизны связаны уравнениями Гаусса и Кодацци:

^ + (К1 – К2 )72 = 0, ds1

dKl – (К1 – К2 )yi = 0, dS2

dY1 + dY2 Y 2 Y 2 K

— 71 — 72 = K

В итоге главная часть системы дифференциальных уравнений (9.20) приобретет следующий вид:

ddu<1> ddu<2>

К2—^———-К1—^———+ … =0,

ds1 ds2

ddu<1> + ddu<2> + = о

ds2 + ds1 + ■” = ‘

Исследуем, наконец, соотношения для сильных разрывов касательных (по отношению к асимптотическим линиям поверхности максимальной скорости сдвига), составляющих приращения вектора перемещений. Поскольку уравнения (9.17) должны выполняться на поверхности максимальной скорости сдвига с каждой стороны соответствующей асмптотической линии, то для скачков имеем соотношения

д (“du1! д (“du2! д (“du2! д (“du1!

«11—д^л——-+ а12 дт 1 =0, «22 дт2——+ а12 дт2 =0.

Так как нормальные (по отношению к асимптотическим линиям поверхности максимальной скорости сдвига) составляющие приращения вектора перемещений непрерывны, то вдоль каждой из двух асимптотических линий справедливо соотношение

v1 [du1] + v2 [du2] = 0.

Принимая во внимание, что для ковариантных компонент нормалей к асимптотическим линиям

V1 = V ■ i1 =0, V2 = V ■ i2 = л/о22 sin i;

v2 = v ■ i2 =0, v1 = v ■ i1 = — a11 sin i,

приходим к следующим соотношениям вдоль асимптотических линий:

r 21 д [du1] ,

du =0, —1 = 0 вдоль т -линии;

l j дт1

r 11 д [du2] 2

du =0, —^ 0 = 0 вдоль т -линии;

l j дт2

интегрируя которые получаем четыре конечных соотношения:

,21 п .11 _ _1

[du2] =0, [du1] = const вдоль т1 -линии;

iНе можете найти то, что вам нужно? Попробуйте сервис подбора литературы.

[du1] = 0, [du2] = const вдоль т2-линии.

Таким образом, вдоль асимптотических линий поверхности максимальной скорости сдвига соотношения для скачков контравариантных (относительно локального базиса, который образует асимптотическая координатная сеть) компонент приращения вектора перемещений интегрируются. Два из четырех интегралов устанавливают непрерывность нормальных к асимптотическим линиям (и располагающихся в касательной плоскости к поверхности максимальной скорости сдвига) составляющих приращения вектора перемещений. Два других интеграла указывают на сохранение вдоль асимптотических линий одного семейства скачков тех контравариантных компонент приращения вектора перемещений, которые соответствуют базисным векторам, нормальным асимптотическим линиям другого семейства.

Библиографический список

1. Ивлев Д.Д. О соотношениях, определяющих пластическое течение при условии пластичности Треска, и его обобщениях // Докл. АН СССР. 1959. Т. 124, № 3. С. 546-549; Ивлев Д.Д. Механика пластических сред. Т. I. Теория идеальной пластичности. М.: Физматлит, 2001. С. 15-20.

2. Ивлев Д.Д. О выводе соотношений, определяющих пластическое течение при условии полной пластичности // Изв. АН СССР. ОТН. Механика и машиностроение. 1959. №3. С. 137; Ивлев Д.Д. Механика пластических сред. Т. I. Теория идеальной пластичности. М.: Физматлит, 2001. С. 20-21.

3. Радаев Ю.Н. Пространственная задача математической теории пластичности. Самара: Изд-во Самарск. гос. ун-та, 2004. 147 с.

4. Надаи А. Пластичность. Механика пластического состояния вещества. М.; Л.: ОНТИ, 1936. 280 с.; Ильюшин А.А. Пластичность. Ч.1. Упруго-пластические деформации. М.; Л.: Гостехтеоретиздат, 1948. 376 с.

5. Томас Т. Пластическое течение и разрушение в твердых телах. М.: Мир, 1964. 308 с.

6. Быковцев Г.И., Ивлев Д.Д. Теория пластичности. Владивосток: Дальнаука, 1998. 528 с.

7. Быковцев Г.И. Избранные проблемные вопросы механики деформируемых сред: Сб. статей. Владивосток: Дальнаука, 2002. С. 153.

8. Malvern L. Introduction to the Mechanics of Continuous Medium. Englewood Cliffs, N.J.: Prentice-Hall, 1969. 714 p.

9. Washizu K. A note on the conditions of compatibility// J. Math. Phys. 1958. V. 36. P. 306-312.

10. Moriguti S. Fundamental theory of dislocations of elastic bodies // Oyo Sugaku Rikigaku. 1947. V.1. P. 87-90.

11. Положий Г.Н. Уравнения математической физики. М.: Высш. шк., 1964. 560 с.

12. Мизохата С. Теория уравнений с частными производными. М.: Мир, 1977. С. 259-261.

13. Берс Л., Джон Ф., Шехтер М. Уравнения с частными производными. М.: Мир, 1966. С. 58-63.

14. Курант Р. Уравнения с частными производными. М.: Мир, 1964. С. 239-241.

15. Петровский И.Г. Лекции об уравнениях с частными производными. М.: Физматгиз, 1961. С. 49-54.

16. Радаев Ю.Н. Дополнительные теоремы теории плоской и осесимметричной задачи математической теории пластичности// Вестн. Самарск. гос. ун-та. Естественнонаучная сер. 2004. № 2(32). С. 41-61.

17. Соколовский В.В. Теория пластичности. М.: Высш. шк., 1969. 608 с.

18. Быковцев Г.И., Мяснянкин Ю.М. О поверхностях скольжения в трехмерных жесткопластических телах // Докл. АН СССР. 1966. Т. 167, № 6. С. 12601262.

19. Ивлев Д.Д. Теория идеальной пластичности. М.: Наука, 1966. 232 с.

20. Быковцев Г.И., Ивлев Д.Д., Мяснянкин Ю.М. О кинематических соотношениях на поверхностях скольжения в идеальных жесткопластических телах// При-кл. матем. и механика. 1968. Т. 32, вып. 4. С. 623-631.

Источник

Для цитирования:

Радаев Ю. Н. Пространственная задача математической теории пластичности (кинематические соотношения, определяющие течение на грани и ребре призмы Кулона – Треска) // Известия Саратовского университета. Новая серия. Серия : Математика. Механика. Информатика. 2008. Т. 8, вып. 2. С. 34-76. DOI: 10.18500/1816-9791-2008-8-2-34-76

Пространственная задача математической теории пластичности (кинематические соотношения, определяющие течение на грани и ребре призмы Кулона – Треска)

Аннотация:

В работе приводится вывод правильно определенной системы уравнений, описывающей кинематику пространственного идеально пластического течения на ребре призмы Кулона – Треска, и дано исследование основных кинематических уравнений (включая пространственные соотношения Коши и уравнения совместности для приращений деформаций) с помощью триортогональной изостатической системы координат. Устанавливаются правильная определенность и гиперболичность системы уравнений для приращений перемещений и находятся ее характеристические направления. Выводятся соотношения для приращений перемещений вдоль линий главных напряжений, обобщающие известные соотношения Гейрингер. Отдельно рассматриваются кинематические соотношения для случаев плоского деформированного и осесимметричного состояний. Исследована кинематика скольжения на поверхностях максимальной скорости сдвига. Показано, что скольжения на указанной поверхности происходят вдоль асимптотических направлений, если поверхность максимальной скорости сдвига имеет отрицательную Гауссову кривизну. Поэтому сдвиговое пластическое течение вблизи поверхности максимальной скорости сдвига (отрицательной Гауссовой кривизны) реализуется как результат микроскольжений в асимптотических направлениях. Получены интегрируемые соотношения для разрывов касательных составляющих приращений перемещений вдоль асимптотических линий поверхности максимальной скорости сдвига. Рассмотрены кинематические соотношения в областях эллиптичности, т.е. когда Гауссова кривизна положительна, поверхности максимальной скорости сдвига.

Список источников:

Ивлев Д.Д. О соотношениях, определяющих пластическое течение при условии пластичности Треска, и его обобщениях // Докл. АН СССР. 1959. Т. 124, No 3. С. 546–549; Ивлев Д.Д. Механика пластических сред. Т. I. Теория идеальной пластичности. М.: Физматлит, 2001. С. 15–20.
Ивлев Д.Д. О выводе соотношений, определяющих пластическое течение при условии полной пластичности // Изв. АН СССР. ОТН. Механика и машиностроение. 1959. No3. С. 137; Ивлев Д.Д. Механика пластических сред. Т. I. Теория идеальной пластичности. М.: Физматлит, 2001. С. 20–21.
Радаев Ю.Н. Пространственная задача математической теории пластичности. Самара: Изд-во Самарск. гос. ун-та, 2004. 147 с.
Надаи А. Пластичность. Механика пластического состояния вещества. М.; Л.: ОНТИ, 1936. 280 с.; Ильюшин А.А. Пластичность. Ч.1. Упруго-пластические деформации. М.; Л.: Гостехтеоретиздат, 1948. 376 с.
Томас Т. Пластическое течение и разрушение в твердых телах. М.: Мир, 1964. 308 с.
Быковцев Г.И., Ивлев Д.Д. Теория пластичности. Владивосток: Дальнаука, 1998. 528 с.
Быковцев Г.И. Избранные проблемные вопросы механики деформируемых сред: Сб. статей. Владивосток: Дальнаука, 2002. С. 153.
Malvern L. Introduction to the Mechanics of Continuous Medium. Englewood Cliffs, N.J.: Prentice–Hall, 1969. 714 p.
Washizu K. A note on the conditions of compatibility//J. Math. Phys. 1958. V. 36. P. 306–312.
Moriguti S. Fundamental theory of dislocations of elastic bodies // Oyo Sugaku Rikigaku. 1947. V.1. P. 87–90.
Положий Г.Н. Уравнения математической физики. М.: Высш. шк., 1964. 560 с.
Мизохата С. Теория уравнений с частными производными. М.: Мир, 1977. С. 259–261.
Берс Л., Джон Ф., Шехтер М. Уравнения с частными производными. М.: Мир, 1966. С. 58–63.
Курант Р. Уравнения с частными производными. М.: Мир, 1964. С. 239–241.
Петровский И.Г. Лекции об уравнениях с частными производными. М.: Физматгиз, 1961. С. 49–54.
Радаев Ю.Н. Дополнительные теоремы теорииплоской и осесимметричной задачи математической теории пластичности// Вестн. Самарск. гос. ун-та. Естественнонаучная сер. 2004. No 2(32). С. 41–61.
Соколовский В.В. Теория пластичности. М.: Высш.шк., 1969. 608 с.
Быковцев Г.И., Мяснянкин Ю.М. О поверхностях скольжения в трехмерных жесткопластических телах // Докл. АН СССР. 1966. Т. 167, No 6. С. 1260–1262.
Ивлев Д.Д. Теория идеальной пластичности. М.: Наука, 1966. 232 с.
Быковцев Г.И., Ивлев Д.Д., Мяснянкин Ю.М. О кинематических соотношениях на поверхностях скольжения в идеальных жесткопластических телах// Прикл. матем. и механика. 1968. Т. 32, вып. 4. С. 623–631.

690 просмотров

Источник

На этой странице вы узнаете

Чем упаковка стикеров похожа на призму?
Как можно попасть в призму в реальной жизни?
Как сложить игральные кости из листа бумаги?
Как найти объем воды в аквариуме?

Слышали такое выражение «смотреть сквозь призму чего-либо»? Оно значит ситуацию, в которой мы воспринимаем что-либо под влиянием каких-то убеждений или представлений. Замысловато, конечно… Возможно, потому что и сама призма — непростое понятие. Давайте разберемся с ней с точки зрения математики.

Определение призмы

Многие из нас пользуются стикерами. Для записи своих дел, для закладок, для пометок при ведении конспектов. Даже если мы ими не пользуемся, то наверняка видели их в магазинах или у родственников и друзей.

Один такой стикер можно принять за плоскость. Теперь вспомним, как выглядит упаковка с ними. Много-много стикеров накладываются друг на друга и получается небольшая объемная фигура, сверху и снизу которой лежат два абсолютно одинаковых листа. При этом сразу заметим, что нижний и верхний стикеры будут параллельны друг другу.

На самом деле, упаковка со стикерами является не чем иным, как призмой!

Призма — это многогранник, в котором две грани являются равными многоугольниками и лежат в параллельных плоскостях, а все остальные — параллелограммами.

Чем упаковка стикеров похожа на призму?

Упаковка стикеров является объемной фигурой, в основаниях которой лежат равные прямоугольники. А боковые стороны упаковки являются параллелограммом. Таким образом, упаковка стикеров полностью соответствует определению призмы.

Определение может показаться немного запутанным, но в нем нет ничего страшного. Разберемся, поближе взглянув на составные призмы.

Строение призмы

Представим себе обычную коробку. Ее дно и крышка равны между собой и лежат в параллельных плоскостях. Это и есть равные многоугольники. Также их называют основаниями призмы.

Посмотрим на стенки коробки. Они являются параллелограммами, просто с прямыми углами. Подробнее про параллелограммы можно прочитать в статье «Параллелограмм». Эти параллелограммы называются боковыми гранями призмы.

Возьмем линейку и измерим расстояние между основаниями призмы. Для этого из любой точки одного основания проведем перпендикуляр к другому.

Подробнее про расстояния между плоскостями можно узнать в статьях «Углы в пространстве» и «Расстояния между фигурами».

Может возникнуть вопрос, что мы сейчас нашли? Мы нашли высоту призмы.

Высота призмы — перпендикуляр, опущенный из любой точки одного основания на другое основание призмы.

В задачах намного удобнее опускать перпендикуляр не из произвольной точки, а из вершины призмы.

Рассмотрим элементы призмы.

Ребро — это линия пересечения двух плоскостей.

Представим, что вместо картонных стенок в нашей коробке ткань, которую нам нужно натянуть на каркас так, чтобы коробка не изменилась. В этом случае все прямые этого каркаса и будут ребрами.

Ребра бывают двух видов:

ребра оснований,
боковые ребра.

Отличить их также легко: ребра основания являются стороной многоугольника, который в нем лежит, в то время как боковые ребра не принадлежат основаниям.

У боковых ребер есть одно очень важное свойство: они равны между собой и параллельны.

Диагональ призмы — отрезок, соединяющий две вершины призмы, не принадлежащие одной грани.

Например, мы можем взять клетку попугая и от угла до угла сделать ему жердочку, чтобы птичке было весело жить. Эта жердочка и будет диагональю призмы.

Виды призм

Вернемся к рассуждениям о том, чем упаковка стикеров похожа на призму. Например, куб и параллелепипед будут отличаться. А если в основании призмы будет лежать треугольник или шестиугольник? Или двадцатиугольник? Разделим призмы на несколько видов.

Мы рассмотрим две классификации.

В первом случае будем рассматривать призмы по фигурам, которые лежат в основании. В многоугольнике может быть множество сторон, а значит, и в основании призмы может быть треугольник, четырехугольник, шестиугольник, десятиугольник и так далее.

В зависимости от фигуры в основании призмы могут называться по-разному. Вот три основных, которые чаще всего встречаются при решении заданий:

треугольная призма,

четырехугольная призма,

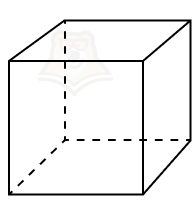
шестиугольная призма.

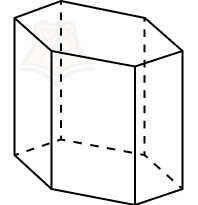
Аналогичным образом можно дать название любой призме, например, десятиугольная призма или стоугольная призма.

В определении призмы сказано, что в боковых гранях лежат параллелограммы. До этого мы чертили только прямоугольники, но в боковых гранях могут лежать не только они.

С этим связана вторая классификация призм. По этому признаку призмы делятся всего на два вида:

прямые,
наклонные.

Разберемся в них чуть подробнее.

Прямая призма — призма, боковые ребра которой перпендикулярны основаниям.

В этом случае боковые ребра и ребра оснований действительно образовывают прямоугольник.

Наклонная призма — призма, боковые ребра которой находятся под углом к основаниям.

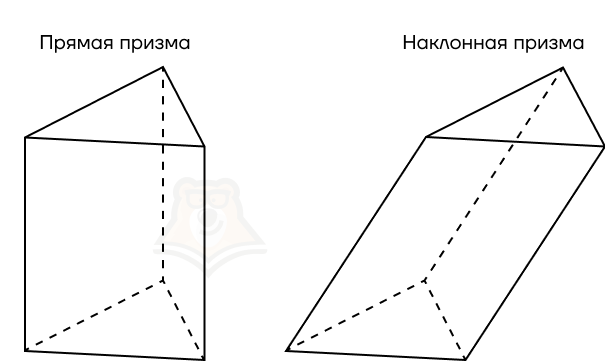
Где мы можем найти прямые и наклонные призмы? Оказывается, в архитектуре. Обычный жилой дом типовой застройки будет прямой призмой. А вот примером наклонной призмы может служить комплекс зданий “Ворота Европы” в Мадриде.

Чуть подробнее остановимся на прямых призмах. Они встречаются достаточно часто и обладают несколькими важными свойствами.

Посмотрите на свою комнату. Если по плану квартиры она будет многоугольником, то вы как бы сидите в призме. Теперь ответим на вопрос: как найти высоту комнаты?

Простой ответ: померить по стене. А если посмотреть на угол, то можно заметить, что ребро призмы совпадает с высотой. Таким образом, мы получаем первое свойство прямых призм.

Свойство 1. Высота прямой призмы совпадает с её боковым ребром.

Посмотрим на стены комнаты, на их форму. Они все являются прямоугольниками, верно?

Свойство 2. Все боковые грани прямой призмы — прямоугольники.

Как можно попасть в призму в реальной жизни?

Многие комнаты и помещения, особенно в типовой застройке, обладают формой призмы. Сидя в комнате, в классе, в столовой, даже в автобусе — мы как бы находимся внутри большой призмы.

Если мы в основании прямой призмы разместим правильный многоугольник, у нас получится правильная призма.

Правильная призма — прямая призма, в основании которой лежит правильный многоугольник.

Например, в правильной треугольной призме будет лежать равносторонний треугольник, а в правильной шестиугольной призме — правильный шестиугольник.

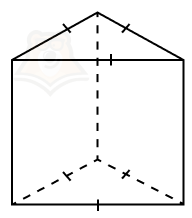
Определение параллелепипеда

Еще одной разновидностью прямоугольной призмы является параллелепипед.

Параллелепипед — это четырехугольная призма, все грани которой являются параллелограммами.

Параллелепипеды встречаются повсюду: коробки, мебель, комнаты, здания, склады, магазины. Поэтому изучить их не составит труда.

Свойство параллелепипеда, видимое невооруженным глазом: противоположные грани параллелепипеда равны. Как пример, вспомним ту же комнату: потолок и пол равны, так же как и стены, находящиеся напротив друг друга.

Нельзя не упомянуть про одно очень важное свойство параллелепипеда:

Все его диагонали пересекаются в одной точке и этой точкой делятся пополам. Это свойство справедливо для всех видов параллелепипеда.

Какие бывают параллелепипеды?

Параллелепипеды также бывают прямыми и наклонными. В этих случаях все определения такие же, как и для всех остальных призм.

Прямой параллелепипед

Рассмотрим несколько интересных свойств прямого параллелепипеда.

1 свойство. Боковые ребра прямого параллелепипеда перпендикулярны основаниям.

2 свойство. Высота прямоугольного параллелепипеда равна длине его бокового ребра.

3 свойство. Боковые грани, которые лежат напротив друг друга, равны между собой и являются прямоугольниками.

Прямые параллелепипеды можно разделить еще на два вида:

Прямой параллелепипед: в основании лежит параллелограмм;

Прямоугольный параллелепипед: в основании лежит прямоугольник.

Рассмотрим свойства прямоугольного параллелепипеда.

1 свойство. Все грани прямоугольного параллелепипеда являются прямоугольниками.

2 свойство. Все углы в прямоугольном параллелепипеде, образованные двумя гранями, равны 90°.

3 свойство. Квадрат длины диагонали прямоугольного параллелепипеда равен сумме квадратов длин его ширины, длины и высоты.

Таким образом, мы получаем важную формулу для параллелепипеда.

d² = a² + b² + c²

Пример 1. Дан прямоугольный параллелепипед. Два ребра, выходящие из одной его вершины, равны (sqrt{35}) и (sqrt{46}). Диагональ параллелепипеда равна 15. Найдите третье ребро параллелепипеда.

Решение. Пусть третье ребро параллелепипеда равняется х. Получаем уравнение:

(15^2 = (sqrt{35})^2 + (sqrt{46})^2 + x^2)
225 = 35 + 46 + x²
x² = 144
x = 12

Ответ: 12.

У прямоугольного параллелепипеда существует еще несколько видов. Прямоугольные параллелепипеды делятся на:

Произвольный прямоугольный параллелепипед. В основании может лежать прямоугольник.

Правильный прямоугольный параллелепипед. В основании лежит правильный четырехугольник, то есть квадрат.
При этом боковые ребра не равны ребрам основания. Следовательно, в основаниях будут лежать квадраты, а в боковых гранях прямоугольники.

Куб. В основании лежит квадрат, а боковые ребра равны ребрам основания.
В кубе все ребра равны, а все его грани будут квадратом.

Таким образом, мы рассмотрели все виды параллелепипеда.

Формулы для призмы

Однако ни одна задача не может быть решена без формул. Поэтому необходимо рассмотреть несколько основных формул, которые могут встретиться не только в задачах, но и в жизни.

Немного вспомним моделирование, а именно развертку кубика. Мы знаем, что из листа бумаги без труда можно сложить кубик, если правильно его вычертить.

Как сложить игральные кости из листа бумаги?

Задумали вы вечером сыграть с семьей или друзьями в настольную игру. Но вот незадача: игральные кости опять куда-то запропастились. Не беда.Достаточно вычертить на листе бумаги несколько квадратов, вырезать получившуюся фигуру, согнуть по ребрам и склеить между собой с помощью клея. В итоге получатся кубики для игры.

На рисунке оранжевым показаны основания, а желтым боковые грани нашего будущего кубика. А теперь представим, что нам нужно найти площадь боковой поверхности. Как это сделать?

Нужно найти площади желтых квадратиков и сложить их.

Площадь боковой поверхности призмы — сумма площадей всех боковых ее граней.

Единой формулы тут нет, поскольку призмы могут очень сильно отличаться друг от друга. В произвольных призмах придется считать площадь каждой боковой грани, а уже после их складывать.

Но есть один фокус! Правда, он работает только для прямой призмы. Если по условию дана прямая призма, то можно воспользоваться формулой

S_бок. = P * h

В этой формуле Р — периметр основания, h — высота призмы, которая совпадает с высотой боковой грани.

Пример 1. Найдите площадь боковой поверхности правильной шестиугольной призмы, сторона основания которой равняется 2, а высота 10.

Решение.

Шаг 1. Поскольку правильная призма по определению прямая, мы можем воспользоваться формулой S = Ph.

Шаг 2. В основании правильной призмы лежит правильный шестиугольник, следовательно, периметр основания будет равен 6 * 2 = 12.

Шаг 3. Осталось найти только площадь боковой поверхности. Подставляем данные в формулу и получаем: S = 12 * 10 = 120.

Ответ: 120.

Пример 2. Дана прямая треугольная призма, в основании которой лежит прямоугольный треугольник с катетами 12 и 5. Высота призмы равна 13. Найдите площадь ее боковой поверхности.

Решение.

Шаг 1. Поскольку призма прямая, можно воспользоваться формулой S = Ph.

Шаг 2. Найдем периметр основания. Для этого необходимо найти гипотенузу треугольника. Воспользуемся теоремой Пифагора: (sqrt{12^2 + 5^2} = sqrt{144 + 25} = sqrt{169} = 13).

Шаг 3. Найдем периметр основания: P = 12 + 5 + 13 = 30.

Шаг 4. Осталось найти только площадь боковой поверхности. Подставляем данные в формулу и получаем: S = 30 * 13 = 390.

Ответ: 390.

Мы научились находить площадь боковой поверхности. А как найти всю площадь призмы? Вспомним нашу развертку с кубиком. Чтобы найти всю площадь кубика, нужно найти площадь всех квадратов, из которых он состоит. То есть и площадь боковой поверхности, и площадь оснований.

Площадь полной поверхности призмы — сумма площадей всех граней.

Следовательно, нам нужно сложить площади всех боковых граней и дважды площадь основания. Получаем следующую формулу.

S = S_бок + 2S_осн

Вспомним обычный хлеб, черный или белый. Его форма очень приближена к параллелепипеду. Тогда его корочка будет площадью полной поверхности параллелепипеда. А все что внутри, то есть мякиш, можно принять за объем.

Пример 3. Дана прямая призма, в основании которой лежит ромб с диагоналями 12 и 16. Боковое ребро призмы равно 25. Найдите площадь поверхности призмы.

Решение.

Шаг 1. Найдем площадь основания. Площадь ромба можно найти по формуле (frac{1}{2} * D_1 * D_2). Следовательно, площадь ромба равна (frac{1}{2} * 12 * 16 = 96).

Шаг 2. Заметим, что диагонали ромба образуют четыре равных прямоугольных треугольника. Следовательно, чтобы найти сторону ромба, достаточно рассмотреть прямоугольный треугольник с катетами 6 и 8. По теореме Пифагора сторона ромба будет равна (sqrt{6^2 + 8^2} = sqrt{36 + 64} = sqrt{100} = 10).

Шаг 3. Периметр ромба будет равен 4 * 10 = 40. Тогда площадь боковой поверхности равна 40 * 25 = 1000.

Шаг 4. Площадь полной поверхности будет равняться 1000 + 2 * 96 = 1000 + 192 = 1192.

Ответ: 1192

Пример 4. Площадь поверхности правильной четырехугольной призмы равняется 1980. Сторона основания равна 5. Найдите боковое ребро этой призмы.

Решение.

Шаг 1. Воспользуемся формулой S = S_бок + 2S_осн. Площадь основания будет равняться площади квадрата, то есть 5 * 5 = 25.

Шаг 2. Подставим известные величины в формулу:

1980 = S_бок + 2 * 25
S_бок = 1930

Шаг 3. Площадь боковой поверхности равна произведению периметра основания на высоту призмы. Периметр равен 5 * 4 = 20. Тогда получаем уравнение:

20h = 1930
h = 96,5

Шаг 4. Поскольку по условию дана правильная призма, то высота совпадает с боковым ребром. Следовательно, боковое ребро равняется 96,5.

Ответ: 96,5.

Теперь рассмотрим, как найти объем призмы. Допустим, мы налили в прямоугольный аквариум немного воды. Как определить, сколько воды мы налили?

Для этого достаточно воспользоваться формулой объема призмы.

V = S_осн. * h

Эта формула общая, однако для каждой призмы она может принять свой вид в зависимости от того, какую формулу нужно использовать для поиска площади основания или высоты.

Например, чтобы найти объем воды в аквариуме, необходимо длину умножить на ширину и на высоту, а значит формула принимает вид V = abh.

Как найти объем воды в аквариуме?

Для этого достаточно перемножить ширину, длину аквариума и высоту воды. Тем самым мы найдем объем призмы, форму которой принимает вода в аквариуме.

Пример 5. Основанием прямой треугольной призмы является прямоугольный треугольник с катетами 12 и 15. Боковое ребро призмы равно 4. Найдите объем этой призмы.

Решение.

Шаг 1. Для начала найдем площадь основания. В этом случае мы можем воспользоваться формулой (frac{1}{2}ab). Площадь равна (frac{1}{2} * 12 * 15 = 90).

Шаг 2. Воспользуемся формулой объема призмы и подставим известные величины:

V = 90 * 4 = 360.

Ответ: 360.

Пример 6. Дан сосуд, в основании которого лежит правильный треугольник. В этот сосуд налили 3000 см³ воды. Высота жидкости оказалась равной 10 см. После этого в сосуд опустили шарик и высота изменилась с 10 см на 14 см. Найдите объем шарика.

Решение. Немного вспомним физику, а именно тот факт, что объем вытесненной жидкости равен объему тела. Значит, чтобы найти объем шарика, необходимо найти насколько изменился объем воды.

Шаг 1. Найдем площадь основания сосуда. Для этого немного преобразуем формулу объема:
(S = frac{V}{h})
Тогда:
(S = frac{3000}{10} = 300)

Шаг 2. А теперь найдем объем после того, как в воду погрузили шарик. Он будет равен 300 * 14 = 4200.

Шаг 3. Объем вытесненной жидкости равен 4200 — 3000 = 1200.

Ответ: 1200.

Мы рассмотрели основные формулы, которые применяются для решения задач. Стоит заметить, что они универсальны, и в каждой задаче их рационально преобразовывать под ситуацию.

Фактчек

Призма — это многогранник, в котором две грани являются равными многоугольниками и лежат в параллельных плоскостях, а все остальные — параллелограммами. Равные многоугольники называются основаниями призмы, а остальные стороны — боковыми гранями. В призме есть ребра — линии пересечения двух ее граней. Ребра как бы образуют каркас призмы.
Призмы можно разделить на несколько видов по тому, какая фигура лежит в основании: треугольник, четырехугольник, шестиугольник или любой другой многоугольник. Призмы бывают прямые и наклонные. В прямых призмах боковые ребра перпендикулярны основанию, а в наклонных — нет. Правильная призма — прямая призма, в основании которой лежит правильный многоугольник.
Параллелепипед — это четырехугольная призма, все грани которой являются параллелограммами. Параллелепипеды бывают наклонными и прямыми. Прямые параллелепипеды включают в себя прямоугольные параллелепипеды, которые, в свою очередь, делятся на произвольные, правильные и кубы.
В призме можно найти площадь боковой поверхности, площадь полной поверхности и объем. Для каждого из этих случаев необходимо пользоваться формулами.

Проверь себя

Задание 1.
Что такое диагональ призмы?

Отрезок, соединяющий две соседние вершины в призме.
Отрезок, соединяющий противоположные углы в боковой грани призмы.
Отрезок, соединяющий противоположные углы в основании призмы.
Отрезок, соединяющий две вершины призмы, не принадлежащие одной грани.

Задание 2.
Что такое прямая призма?

Призма, боковые ребра которой перпендикулярны основаниям.
Призма, боковые ребра которой расположены под острым углом относительно основания.
Призма, боковые ребра которой расположены под тупым углом относительно основания.
Призма, в основании которой лежит прямоугольник.

Задание 3.
Как найти высоту прямой призмы?

Высоту нужно найти с помощью оснований.
Высота совпадает с боковым ребром.
Необходимо найти расстояние между двумя вершинами, не принадлежащими одной грани.
В прямой призме невозможно найти высоту.

Задание 4.
Какая фигура лежит в основании прямоугольного параллелепипеда?

Параллелограмм с острыми углами.
Ромб с острыми углами.
Трапеция.
Прямоугольник.

Задание 5.
Как найти площадь полной поверхности призмы?

Нужно найти сумму площадей всех боковых граней.
Нужно сложить площадь боковой поверхности и площадь основания.
Нужно сложить площадь боковой поверхности и удвоенную площадь основания.
Нужно сложить площади оснований.

Ответы: 1. — 4 2. — 1 3. — 2 4. — 4 5. — 3

Источник

Монохроматический
свет падает на грань АВ стеклянной
призмы (рис.6), находящейся в воздухе.

Рис.
6

S₁O₁
– падающий луч,

α₁-угол
падения,

O₁O₂
– преломленный луч,

–
угол преломления.

Так
как свет переходит из среды оптически
менее плотной в более плотную (из воздуха
в стекло), то

<α₁.
Пройдя через призму, свет падает на ее
грань АС. Здесь он снова преломляется.
α₂
– угол падения,

–
угол преломления. На данной границе
свет переходит из среды более плотной
в менее плотную (из стекла в воздух). По
этому
>
.
Грани АВ и АС, на которых происходит
преломление света, называются
преломляющимися
гранями.

Угол

между
преломляющимися гранями называется
преломляющим
углом
призмы. Угол

–
называется углом
отклонения.
Грань (ВС), лежащая против преломляющего
угла, называется основанием
призмы.

Следовательно,
если оптическая плотность вещества
призмы больше чем окружающей среды, то
луч света, проходящий через призму,
отклоняется к основанию призмы.

Вопрос 5. Линзы. Фокусное расстояние линзы.

Важнейшая
деталь всех оптических приборов –
линза
(от нем. слова «Линзе» – чечевица).

Несмотря
на многочисленные исследования в
течение многих веков, до сих пор нельзя
сказать ни времени, ни места открытия
линз. Удалось лишь установить, что линзы
применялись как для увеличения, так и
для коррекции дальнозоркости.

Одно
из первых исторических свидетельств
рассмотрения линз в науке – это отрывок
Р. Бэкона: «Если человек будет рассматривать
буквы или другие мелкие предметы с
помощью кристалла или стекла, или
другого прозрачного тела, расположенного
над буквами, и если это тело будет
шаровым сегментом, выпуклость которого
обращена к глазу, находящемуся в воздухе,
то буквы видны лучше и кажутся больше….
И потому это приспособление полезно
людям старым и со слабым зрением, потому
что они могут видеть даже маленькую
букву достаточно большой».

Роджер
Бэкон – французский монах, родился
приблизительно в 1214г. в Ильчестере, в
графстве Самерсет. Умер в 1292г.

Известно
что Бэкон использовал линзы во многих
опытах и даже преподнес одну папе
Клименту IV, прося его попробовать
применить её.

К
середине 14 века очки уже получили
довольно широкое распространение. На
фреске 1352г. изображен монах в очках.

Линзами
называют прозрачные тела, ограниченные
двумя гладкими выпуклыми или вогнутыми
поверхностями (одна из них может быть
плоской).

Различают
линзы выпуклые и вогнутые (рис. 7)

Рис.
7

Выпуклые
линзы:

а)
двояковыпуклая,

б)
плосковыпуклая,

в)
вогнутовыпуклая.

Вогнутые
линзы:

г)
двояковогнутая,

д)
плосковогнутая,

е)
выпукловогнутая,

Выпуклую
линзу можно представить в виде
совокупности плоскопараллельной
пластинки (в середине) и усеченных
призм, расширяющихся к середине призмы
(рис. 8)

Рис.
8

Вогнутую
– как совокупность плоскопараллельной
пластинки и усеченных призм, расширяющихся
к краям (рис. 9)

Рис.
9

Если
призма сделана из материала оптически
более плотного, чем окружающая среда,
то она отклоняет лучи к основанию.

По
этому параллельный пучок после
преломления в выпуклой (вогнутой) линзе
станет сходящимся (расходящимся). Такие
линзы называются собирающими
(рассеивающими).

Двояковыпуклую
линзу можно представить как тело,
получившееся из двух пересекающихся
шаров (рис. 10)

Рис.
10

R₁,
R₂и
R₃
– радиусы шаров.

О₁
и О₂,
О₂и
О₃
– у тонких линз сливаются в одну О,
которая называется оптическим
центром линзы.

Оптический
центр линзы – точка, через которую лучи
идут, не преломляясь.

Любая
прямая, проходящая через оптический
центр О, называется оптической
осью.

Оптическая
ось, проходящая через центры сфер R₁
и R₂
называется – главной
оптической осью,
все остальные – побочными
оптическими осями.

Лучи,
параллельные главной оптической оси,
после преломления пересекаются в одной
точке F, лежащей на главной оптической
оси. Эта точка F – называется главным
фокусом
(или просто фокусом). У линзы 2 фокуса –
передний и задний (рис. 11)

Рис.
11

Вогнутая
линза, сделанная из материала оптически
более плотного, чем окружающая среда,
рассеивает свет. Условно такая линза
показана на рис. 12.

Рис.
12

У
такой призмы фокус F_м
– мнимый.

Мнимым
фокус называется потому, что в нем
пересекаются не сами параллельные
лучи, а их продолжения. Расстояние OF от
оптического центра до фокуса называется
фокусным
расстоянием F.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

В данной публикации мы рассмотрим определение, основные элементы, виды и возможные варианты сечения призмы. Представленная информация сопровождается наглядными рисунками для лучшего восприятия.

Определение призмы
Элементы призмы
Варианты сечения призмы
Виды призм

Определение призмы

Призма – это геометрическая фигура в пространстве; многогранник с двумя параллельными и равными гранями (многоугольниками), а другие грани при этом являются параллелограммами.

На рисунке ниже представлен один из самых распространенных видов призмы – четырехугольная прямая (или параллелепипед). Другие разновидности фигуры рассмотрены в последнем разделе данной публикации.

Элементы призмы

Для рисунка выше:

Основания – равные многоугольники. Это могут быть треугольники, четырех-, пяти-, шестиугольники и т.д. В нашем случае – это параллелограммы (или прямоугольники) ABCD и A₁B₁C₁D₁.
Боковые грани – это параллелограммы: AA₁B₁B, BB₁C₁C, CC₁D₁D и AA₁D₁D.
Боковое ребро – отрезок, соединяющий соответствующие друг другу вершины разных оснований (AA₁, BB₁, CC₁ и DD₁). Является общей стороной двух боковых граней.
Высота (h) – это перпендикуляр, проведенный от одного основания к другому, т.е. расстояние между ними. Если боковые ребра расположены под прямым углом к основаниям фигуры, значит они одновременно являются и высотами призмы.
Диагональ основания – отрезок, который соединяет две противолежащие вершины одного и того же основания (AC, BD, A₁C₁ и B₁D₁). У треугольной призмы данного элемента нет.
Диагональ боковой грани – отрезок, который соединяет две противолежащие вершины одной и той же грани. На рисунке изображены диагонали только одной грани (CD₁ и C₁D), чтобы не перегружать его.
Диагональ призмы – отрезок, соединяющий две вершины разных оснований, не принадлежащих одной боковой грани. Мы показали только две из четырех: AC₁ и B₁D.
Поверхность призмы – суммарная поверхность двух ее оснований и боковых граней. Формулы для расчета площади поверхности (для правильной фигуры) и объема призмы представлены в отдельных публикациях.

Развёртка призмы – разложение всех граней фигуры в одной плоскости (чаще всего, одного из оснований). В качестве примера – для прямоугольной прямой призмы:

Примечание: свойства призмы представлены в отдельной публикации.

Варианты сечения призмы

Диагональное сечение – секущая плоскость проходит через диагональ основания призмы и два соответствующих боковых ребра.Примечание: У треугольной призмы нет диагонального сечения, т.к. основанием фигуры является треугольник, у которого нет диагоналей.
Перпендикулярное сечение – секущая плоскость пересекает все боковые ребра под прямым углом.

Примечание: другие варианты сечения не так распространены, поэтому отдельно на них останавливаться не будем.

Виды призм

Рассмотрим разновидности фигуры с треугольным основанием.

Прямая призма – боковые грани расположены под прямым углом к основаниям (т.е. перпендикулярны им). Высота такой фигуры равняется ее боковому ребру.
Наклонная призма – боковые грани фигуры не перпендикулярны ее основаниям.
Правильная призма – основаниями являются правильные многоугольники. Может быть прямой или наклонной.
Усеченная призма – часть фигуры, оставшаяся после пересечения ее плоскостью, не параллельной основаниям. Также может быть как прямой, так и наклонной.