Если соединить
точки тела, имеющие одинаковую температуру,
получим поверхность равных температур,
называемую изотермической. Итак,
изотермической поверхностью называется
геометрическое место точек в температурном
поле, имеющих одинаковую температуру.
Так как одна и та
же точка тела не может одновременно
иметь различные температуры, то
изотермические поверхности не
пересекаются. Они либо оканчиваются
на поверхности тела, либо целиком
располагаются внутри самого тела.
Пересечение
изотермических поверхностей плоскостью
дает на этой плоскости семейство изотерм.
Они обладают теми же свойствами, что и
изотермические поверхности, т. е. не
пересекаются, не обрываются внутри
тела, оканчиваются на поверхности, либо
целиком располагаются внутри самого
тела.

Рисунок 1.1- Изотермы
На рисунке 1.1
приведены изотермы, температуры
которых отличаются на
![]() t.
t.
Температура в
теле изменяется только в направлениях,
пересекающих изотермические поверхности.
При этом наибольший перепад температуры
на единицу длины происходит в направления
нормали к изотермической поверхности.
Возрастание
температуры в направлении нормали к
изотермической поверхности характеризуется
градиентом температуры.
Градиент
температуры
есть вектор, направленный по нормали к
изотермической поверхности в сторону
возрастания температуры и численно
равный производной от температуры по
этому направлению, т. е.
grad t =
![]() ,
,
(1.6)
где nо—единичный
вектор, нормальный к изотермической
поверхности и направленный в сторону
возрастания температуры; dt/dn — производная
температура по нормали n.
Скалярная величина
температурного градиента dt/dn не одинакова
для различных точек изотермической
поверхности. Она больше там, где расстояние
![]() между изотермическими поверхностями
между изотермическими поверхностями
меньше. Скалярную величину температурного
градиента dt/dn мы будем также называтьтемпературным
градиентом.
Величина dt/dn в
направлении убывания температуры
отрицательна.
Проекции вектора
grad
t
на координатные оси Ох, Оу, Оz
будут равны:
(grad
t)x
=
![]()
(grad t)y
=
![]()
(1-7)
(grad
t)z
=
![]()
Лекция
3
Тема: ОСНОВНЫЕ
ПОЛОЖЕНИЯ УЧЕНИЯ О ТЕПЛОПРОВОДНОСТИ
План лекции
1.4 Тепловой поток.
Закон Фурье
1.5 Коэффициент
теплопроводности
1.4 Тепловой поток. Закон фурье
Необходимым
условием распространения теплоты
является неравномерность распределения
температуры в рассматриваемой среде.
Таким образом, для передачи теплоты
теплопроводностью необходимо неравенство
нулю температурного градиента в различных
точках тела.
Согласно гипотезе
Фурье количество теплоты dQ,
Дж, проходящее через элемент
изотермической поверхности dF за
промежуток времени d![]() ,
,
пропорционально температурному градиенту
dt/dn.
![]() .
.
(1.8)
Опытным путем
установлено, что коэффициент
пропорциональности в уравнении (1.8) есть
физический параметр вещества. Он
характеризует способность вещества
проводить теплоту и называется
коэффициентом
теплопроводности.
Количество теплоты,
проходящее в единицу времени через
единицу
площади изотермической
поверхности
![]() ,
,![]() Вт/м2,
Вт/м2,
называется плотностью
теплового п о т о к а.
Плотность теплового потока есть вектор,
определяемый соотношением
![]() .
.
(1.9)
Вектор плотности
теплового потока q направлен по нормали
к изотермической поверхности. Его
положительное направление совпадает
с направлением убывания температуры,
так как теплота всегда передается
от более горячих частей тела к холодным.
Таким образом, векторы q и grad t
лежат на одной прямой, но направлены в
противоположные стороны. Это и
объясняет наличие знака «минус» в правых
частях уравнений (1.9) и (1.8).
Линии, касательные
к которым совпадают с направлением
вектора
q, называются
линиями
теплового потока.
Линии теплового потока ортогональны
к изотермическим поверхностям (рисунок
1.2).

Рисунок 1.2 –
Изотермы и линии теплового потока
Скалярная величина
вектора плотности теплового потока q,
Вт/м2,
будет равна:
![]() , (1.10)
, (1.10)
Многочисленные
опыты подтвердили справедливость
гипотезы Фурье. Поэтому уравнение (1.8),
так же как и уравнение (1.9), является
математической записью основного закона
теплопроводности, который формируется
следующим образом: плотность
теплового потока пропорциональна
градиенту температуры.
Количество теплоты,
проходящее в единицу времени через
изотермическую поверхность F, называется
тепловым
потоком.
Если градиент температуры для
различных точек изотермической
поверхности различен, то количество
теплоты, которое пройдет через всю
изотермическую поверхность в единицу
времени, найдется как
![]() ,
,
(1.11)
где dF
—элемент изотермической поверхности.
Величина Q измеряется в ваттах.
Полное количество
теплоты Q, Дж, прошедшее за время т через
изотермическую поверхность F, равно:
![]()
![]() ,
,
(1.12)
Из сказанного
следует, что для определения количества
теплоты, проходящего через какую-либо
поверхность твердого тела, необходимо
знать температурное поле внутри
рассматриваемого тела. Нахождение
температурного поля и является главной
задачей аналитической теории
теплопроводности.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
From Wikipedia, the free encyclopedia
A temperature gradient is a physical quantity that describes in which direction and at what rate the temperature changes the most rapidly around a particular location. The temperature gradient is a dimensional quantity expressed in units of degrees (on a particular temperature scale) per unit length. The SI unit is kelvin per meter (K/m).
Temperature gradients in the atmosphere are important in the atmospheric sciences (meteorology, climatology and related fields).
Mathematical description[edit]
Assuming that the temperature T is an intensive quantity, i.e., a single-valued, continuous and differentiable function of three-dimensional space (often called a scalar field), i.e., that
where x, y and z are the coordinates of the location of interest, then the temperature gradient is the vector quantity defined as
Physical processes[edit]
Climatology[edit]
On a global and annual basis, the dynamics of the atmosphere (and the oceans) can be understood as attempting to reduce the large difference of temperature between the poles and the equator by redistributing warm and cold air and water, known as Earth’s heat engine.
Meteorology[edit]
Differences in air temperature between different locations are critical in weather forecasting and climate. The absorption of solar light at or near the planetary surface increases the temperature gradient and may result in convection (a major process of cloud formation, often associated with precipitation).
Meteorological fronts are regions where the horizontal temperature gradient may reach relatively high values, as these are boundaries between air masses with rather distinct properties.
Clearly, the temperature gradient may change substantially in time, as a result of diurnal or seasonal heating and cooling for instance. This most likely happens during an inversion. For instance, during the day the temperature at ground level may be cold while it’s warmer up in the atmosphere. As the day shifts over to night the temperature might drop rapidly while at other places on the land stay warmer or cooler at the same elevation. This happens on the West Coast of the United States sometimes due to geography.
Weathering[edit]
Expansion and contraction of rock, caused by temperature changes during a wildfire, through thermal stress weathering, may result in thermal shock and subsequent structure failure.
Indoor temperature[edit]
|
This section is empty. You can help by adding to it. (December 2022) |
See also[edit]
- Atmospheric temperature for gradient of earth’s atmosphere
- Geothermal gradient
- Gradient
- Lapse rate
References[edit]
- Edward N. Lorenz (1967). The Nature and Theory of the General Circulation of the Atmosphere. Publication No. 218. Geneva, Switzerland: World Meteorological Organization.
- M. I. Budyko (1978). Climate and Life. International Geophysics Series. Vol. 18. Academic Press. ISBN 0-12-139450-6.
- Robert G. Fleagle; Joost A. Businger (1980). An introduction to atmospheric physics. International Geophysics Series. Vol. 25. Academic Press. ISBN 0-12-260355-9.
- David Miller (1981). Energy at the surface of the earth : an introduction to the energetics of ecosystems. Academic Press. ISBN 978-0-08-095460-8.
- John M. Wallace; Peter V. Hobbs (2006). Atmospheric Science: An Introductory Survey. Elsevier. ISBN 978-0-08-049953-6.
External links[edit]
- IPCC Third Assessment Report
- Pictorial Representation of Temperature Gradient (Tools).
Стационарное поле – это когда температура в различных
точках тела постоянна во времени: ![]() ,
, 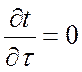 .
.
Нестационарное поле – это когда температура в различных
точках тела не постоянна, а изменяется во времени.
В зависимости температуры от числа пространственных
координат температурное поле может быть одномерным: ![]() ,
,
двухмерным: ![]() , трехмерным:
, трехмерным: ![]() .
.
Одномерное ![]() ,
, 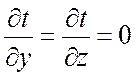 .
.
Двухмерное ![]() ,
, 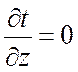 .
.
Трехмерное ![]() .
.
Для одномерного стационарного поля 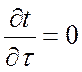 ,
,
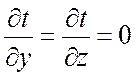 .
.
2.2. Температурный
градиент
Если соединить точки тела, имеющие одинаковую температуру,
получим поверхность равных температур, называемую изотермической. Отсюда определение.
Изотермической поверхностью называется совокупность точек,
имеющих равную температуру.
Поскольку одна и та же точка не может иметь в одно и то же
время различные температуры, то изотермические поверхности не пересекаются. Они
либо оканчиваются на граничных поверхностях тела, либо располагаются внутри
самого тела.
Сечение изотермических поверхностей плоскостью дает на
этой плоскости семейство изотерм. Они обладают теми же свойствами, что и
изотермические поверхности: не пересекаются, не обрываются внутри тела,
оканчиваются на границах тела либо располагаются внутри самого тела.
Изменение температуры в теле происходит в направлении
пересечения изотермических поверхностей. При этом наибольший перепад
температуры на единицу длины происходит в направлении нормали к изотермической
поверхности.
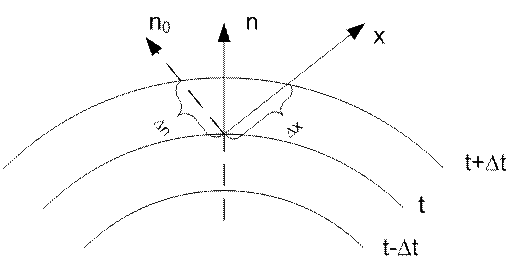
Рис. 1. Изотермы
Градиент температуры есть вектор, направленный по нормали
к изотермической поверхности в сторону возрастания температуры и численно
равный производной от температуры по этому направлению, т. е.
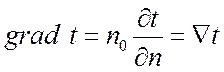 ,
,
где n0 – единичный
вектор, нормальный к изотермической поверхности и направленный в сторону
возрастания температур; n0 определяет
направление температурного градиента.
![]() – скалярная величина температурного
– скалярная величина температурного
градиента.
По физическому смыслу температурный градиент выражает
изменение температуры в градусах (K), приходящееся на 1 м расстояния между изотермическими поверхностями по нормали. Чем больше значение температурного
градиента, тем неравномернее распределение температуры в данном теле. Если все
точки тела имеют одинаковую температуру, то ![]() .
.
Величина ![]() в направлении убывания температуры
в направлении убывания температуры
отрицательна и называется падением температуры.
Проекции вектора ![]() на
на
координатные оси Ox, Oy, Oz равны:
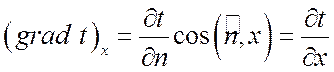 ,
,
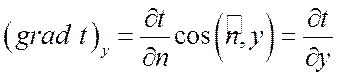 ,
,
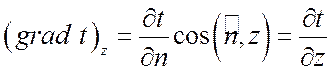 .
.
Размерность ![]() K/м
K/м
или °C/м.
2.3. Тепловой поток.
Закон Фурье
Количество тепла Q,
проходящее в единицу времени через изотермическую поверхность F, называется тепловым потоком.
Тепловой поток, приходящийся на 1 м2 поверхности, называется удельным тепловым потоком или плотностью теплового потока q (иногда его называют тепловой
нагрузкой поверхности).
Согласно гипотезе Фурье, количество тепла dQt,
проходящее через элемент изотермической поверхности dF
за промежуток времени dt, пропорционально температурному
градиенту Ñt:
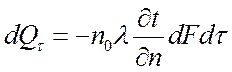 , Дж.
, Дж.
Коэффициент пропорциональности l называется коэффициентом теплопроводности, являющийся
физическим параметром вещества и указывающим способность вещества проводить
тепло.
l, Вт/(м·K).
Плотность теплового потока есть вектор, определяемый
выражением:
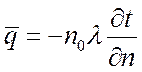 , Вт/м2.
, Вт/м2.
Вектор плотности теплового потока ![]() направлен
направлен
по нормали к изотермической поверхности в сторону убывания температуры, т. к.
тепло передается от более нагретых частей тела к более холодным, т. е.
противоположно вектору ![]() .
.
Линии, касательные к ![]() ,
,
являются векторами удельного теплового потока и называются линиями теплового
потока.
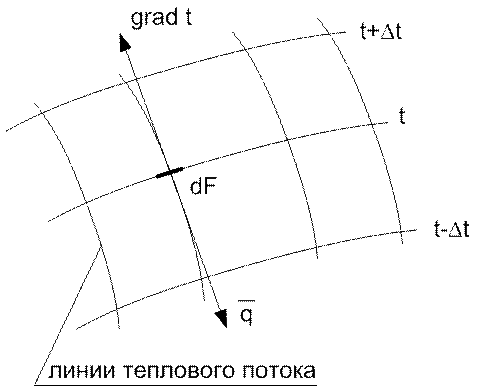
Рис. 2. Связь векторов теплового потока и градиента температуры
Скалярная величина вектора плотности теплового потока
равна
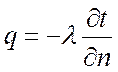 , Вт/м2.
, Вт/м2.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание – внизу страницы.

Рассмотрим две бесконечно близкие изотермические поверхностина одной из них (рис. 2.3).
Рис. 2.3
Перемещаясь из точки М вдоль любых направлений, можно обнаружить, что интенсивность изменения температуры по различным направлениям неодинакова. Если перемещаться вдоль какого либо направления l, пересекающего изотермические поверхности, то наблюдается изменение температуры. Используя понятие производной скалярного поля по заданному направлению, можно описать его локальные свойства, т. е. изменение температуры Т при переходе от точки М к близкой точке М’ по направлению l. Скорость изменения температуры Т в точке М в направлении l характеризуется производной функции Т
дТ/дl= lim[T(M’) – Т(М)]/?l. (2.3)
?l>0
Наибольшая разность температуры на единицу длины вектора перемещения [Т(М”)–Т(М)]/?l наблюдается в направлении нормали n к изотермической поверхности (рис. 2.3). В соответствии с (2.3) максимальная скорость изменения температуры при этом равна пределу отношения изменения температуры ?T к расстоянию между изотермическими поверхностями по нормали ?n, когда ?n стремится к нулю:
дТ/дп= lim [T(M”)–T(M)]/?n= lim ?T/?n. (2.4)
?n >0 ?n >0
Итак, в любой точке М изотермической поверхности можно построить некоторый вектор, направленный по нормали к этой поверхности в сторону увеличения температуры. Абсолютная величина этого вектора равна изменению температуры на единицу длины перемещения в рассматриваемом направлении — скорости возрастания температуры в этом направлении (т. е. производной от температурной функции Т по направлению нормали n). Такой вектор называют градиентом температуры в точке М или градиентом температурного поля и записывают в виде символа grad T:
в декартовых координатах (х, у, z)
grad T = ?T/?x i + ?T/?y j + ?T/?z k (2.5)
Для обозначения вектора (2.5) в теории поля иногда применяют символ gradT = T
Согласно сказанному выше, можно записать
|grad T| = ?T/?n (2.6)
длина вектора grad Т равна скорости возрастания Т в этом направлении. Здесь и всюду далее n — единичный вектор нормали.
Температурный градиент показывает, насколько интенсивно (резко) меняется температура внутри тела.
Производная от функции Т по направлению нормали n и вектор gradT связаны соотношением
дТ/дп = п grad Т. (2.7)
Вектор нормали n к поверхности T=const в точке М может иметь два противоположных направления, одно из которых можно считать внешним по отношению к данной поверхности, а другое внутренним.
Если нормаль n направить в сторону больших температур, то дТ/дп>0 и, как следует из (2.7), градиент температуры будет направлен в ту же сторону (угол между векторами n и grad T равен нулю). Если нормаль направить в сторону убывающей температуры, то производные дТ/дп < 0 и gradT окажутся направленными противоположно этому направлению, т. е. опять в сторону возрастающей температуры.
Тема 9.Теплопроводность
9.1. Температурное поле. Уравнение теплопроводности
Будем рассматривать только однородные и изотропные тела, т.е. такие тела,
которые обладают одинаковыми физическими свойствами по всем направлениям. При
передачи теплоты в твердом теле, температура тела будет изменяться по всему
объему тела и во времени. Совокупность значений температуры в данный момент
времени для всех точек изучаемого пространства называется температурным полем:
t = f(x,y,z,τ) ,
(9.1)
где:t –температура тела;
x,y,z -координаты точки;
τ – время.
Такое температурное поле называется
нестационарным
∂t/∂i ¹
0, т.е. соответствует неустановившемуся тепловому режиму теплопроводности
Если температура тела функция только координат и не изменяется с течением
времени, то температурное поле называется
стационарным
:
t = f(x,y,z) , ∂t/∂i
= 0 (9.2)
Уравнение двухмерного
температурного поля:
для нестационарного режима:
t = f(x,y,τ) ; ∂t/∂z = 0 (9.3)
для стационарного режима:
t = f(x,y) , ∂t/∂z = 0; ∂t/∂i
= 0 (9.4)
Уравнение одномерного
температурного поля:
для нестационарного режима:
t = f(x,τ) ; ∂t/∂y =
∂t/∂z = 0; ∂t/∂i
¹ 0 (9.5)
для стационарного режима:
t = f(x) ; ∂t/∂y = ∂t/∂z = 0;
∂t/∂i = 0 (9.6)
поверхностью
называется поверхность тела с одинаковыми
температурой.
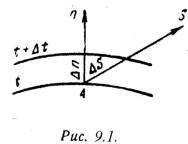
Рассмотрим две изотермические поверхности (Рис.9.1) с температурами t и
t + ∆t.
Градиентом температуры
называют предел отношения изменения температуры∆t к расстоянию между
изотермами по нормали ∆n, когда стремится к нулю:
gradt
= |gradt| = lim[∆t/∆n]∆n→0 = ∂t/∂n (9.7)
Температурный градиент-это вектор, направленной по нормали к
изотермической поверхности в сторону возрастания температуры и численно равный
производной температуры t по нормалиn:
gradt = ∂t/∂n no , (9.7*)
где:no – единичный
вектор.
Количество теплоты, проходящее через изотермическую поверхность F в единицу
времени называется
тепловым
потоком
– Q, [Вт=Дж/с].
Тепловой поток, проходящий через единицу площади называют
плотностью теплового потока
– q = Q /
F, [Вт/м2]
Для твердого тела уравнение теплопроводности подчиняется
закону Фурье
:
Тепловой поток,
передаваемая теплопроводностью, пропорциональна градиенту температуры и
площади сечения, перпендикулярного направлению теплового потока.
Q
= -λ∙F∙ ∂t/∂n, (9.8)
или
q = -λ ∙ ∂t/∂n
∙no =
-λ∙gradt , (9.9)
где: q – вектор плотности
теплового потока;
λ – κоэффициент теплопроводности, [Вт/(м∙К)].
Численное значение вектора плотности теплового потока равна:
q
= -λ∙ ∂t/∂n = -λ∙|gradt| , (9.10)


