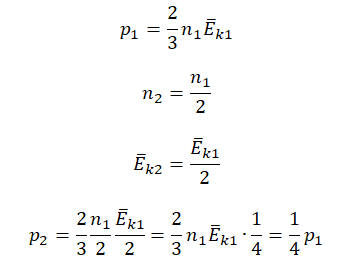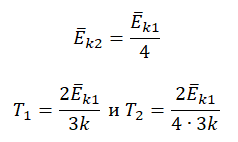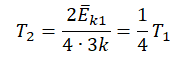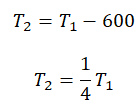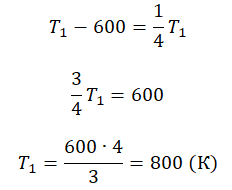Как найти температуру через скорость молекул

Определение

Идеальный газ — газ, удовлетворяющий трем условиям:

• Молекулы — материальные точки.
• Потенциальная энергия взаимодействия молекул пренебрежительно мала.
• Столкновения между молекулами являются абсолютно упругими.

Реальный газ с малой плотностью можно считать идеальным газом.

Измерение температуры

Температуру можно измерять по шкале Цельсия и шкале Кельвина. По шкале Цельсия за нуль принимается температура, при которой происходит плавление льда. По шкале Кельвина за нуль принимается абсолютный нуль — температура, при котором давление идеального газа равно нулю, и его объем тоже равен нулю.

Обозначение температуры

1. По шкале Цельсия — t. Единица измерения — 1 градус Цельсия (1 ^oC).
2. По шкале Кельвина — T. Единица измерения — 1 Кельвин (1 К).

Цена деления обеих шкал составляет 1 градус. Поэтому изменение температуры в градусах Цельсия равно изменению температуры в Кельвинах:

∆t = ∆T

При решении задач в МКТ используют значения температуры по шкале Кельвина. Если в условиях задачи температура задается в градусах Цельсия, нужно их перевести в Кельвины. Это можно сделать по формуле:

T = t + 273

Если особо важна точность, следует использовать более точную формулу:

T = t + 273,15

Пример №1. Температура воды равна ^oC. Определить температуру воды в Кельвинах.

T = t + 273 = 2 + 273 = 275 (К)

Основное уравнение МКТ идеального газа

Давление идеального газа обусловлено беспорядочным движением молекул, которые сталкиваются друг с другом и со стенками сосуда. Основное уравнение МКТ идеального газа связывает давление и другие макропараметры (объем, температуру и массу) с микропараметрами (массой молекул, скоростью молекул и кинетической энергией).

Основное уравнение МКТ

Давление идеального газа пропорционально произведению концентрации молекул на среднюю кинетическую энергию поступательного движения молекулы.

p=23n−Ek

p — давление идеального газа, n — концентрация молекул газа, −Ek — средняя кинетическая энергия поступательного движения молекул.

Выражая физические величины друг через друга, можно получить следующие способы записи основного уравнения МКТ идеального газа:

p=13m0n−v2	m0— масса одной молекулы газа; n — концентрация молекул газа; −v2 — среднее значение квадрата скорости молекул газа. Среднее значение квадрата скорости не следует путать со среднеквадратичной скоростью v, которая равна корню из среднего значения квадрата скорости: v=√−v2
p=13ρ−v2	ρ — плотность газа
p=nkT	k — постоянная Больцмана (k = 1,38∙10–3 Дж/кг) T — температура газа по шкале Кельвина

Пример №2. Во сколько раз уменьшится давление идеального одноатомного газа, если среднюю кинетическую энергию теплового движения молекул и концентрацию уменьшить в 2 раза?

Согласно основному уравнению МКТ идеального газа, давление прямо пропорционально произведению средней кинетической энергии теплового движения молекул и концентрации его молекул. Следовательно, если каждая из этих величин уменьшится в 2 раза, то давление уменьшится в 4 раза:

Следствия из основного уравнения МКТ идеального газа

Через основное уравнение МКТ идеального газа можно выразить скорость движения молекул (частиц газа):

v=√3kTm0=√3RTM

R — универсальная газовая постоянная, равная произведения постоянной Авогадро на постоянную Больцмана:

R=NAk=8,31 Дж/К·моль

Температура — мера кинетической энергии молекул идеального газа:

−Ek=32kT

T=2−Ek3k

Полная энергия поступательного движения молекул газа определяется формулой:

E=N−Ek

Пример №3. При уменьшении абсолютной температуры на 600 К средняя кинетическая энергия теплового движения молекул неона уменьшилась в 4 раза. Какова начальная температура газа?

Запишем формулу, связывающую температуру со средней кинетической энергией теплового движения молекул, для обоих случаев, с учетом что:

Следовательно:

Составим систему уравнений:

Отсюда:

Задание EF19012

На графике представлена зависимость объёма постоянного количества молей одноатомного идеального газа от средней кинетической энергии теплового движения молекул газа. Опишите, как изменяются температура и давление газа в процессах 1−2 и 2−3. Укажите, какие закономерности Вы использовали для объяснения.

---

Алгоритм решения

1.Указать, в каких координатах построен график.

2.На основании основного уравнения МКТ идеального газа и уравнения Менделеева — Клапейрона выяснить, как меняются указанные физические величины во время процессов 1–2 и 2–3.

Решение

График построен в координатах (V;E_k). Процесс 1–2 представляет собой прямую линию, исходящую из начала координат. Это значит, что при увеличении объема растет средняя кинетическая энергия молекул. Но из основного уравнения МКТ идеального газа следует, что мерой кинетической энергии молекул является температура:

T=2−Ek3

Следовательно, когда кинетическая энергия молекул растет, температура тоже растет.

Запишем уравнение Менделеева — Клапейрона:

pV=νRT

Так как количество вещества одинаковое для обоих состояния 1 и 2, запишем:

νR=p1V1T1=p2V2T2

Мы уже выяснили, что объем и температура увеличиваются пропорционально. Следовательно, давление в состояниях 1 и 2 равны. Поэтому процесс 1–2 является изобарным, давление во время него не меняется.

Процесс 2–3 имеет график в виде прямой линии, перпендикулярной кинетической энергии. Так как температуры прямо пропорциональна кинетической энергии, она остается постоянной вместе с этой энергией. Следовательно, процесс 2–3 является изотермическим, температура во время него не меняется. Мы видим, что объем при этом процессе уменьшается. Но так как объем и давление — обратно пропорциональные величины, то давление на участке 2–3 увеличивается.

Ответ:

• Участок 1–2 — изобарный процесс. Температура увеличивается, давление постоянно.

• Участок 2–3 — изотермический процесс. Температура постоянно, давление увеличивается.

pазбирался: Алиса Никитина | обсудить разбор

Задание EF17560

Первоначальное давление газа в сосуде равнялось р₁. Увеличив объём сосуда, концентрацию молекул газа уменьшили в 3 раза, и одновременно в 2 раза увеличили среднюю энергию хаотичного движения молекул газа. В результате этого давление р₂ газа в сосуде стало равным

Ответ:

а) 13p1

б) 2p1

в) 23p1

г) 43p1

---

Алгоритм решения

1.Записать исходные данные.

2.Записать основное уравнение МКТ идеального газа.

3.Составить уравнения для состояний 1 и 2.

4.Выразить искомую величину.

Решение

Исходные данные:

• Начальное давление: p₀.

• Начальная концентрация молекул: n₁ = 3n.

• Конечная концентрация молекул: n₂ = n.

• Начальная средняя энергия хаотичного движения молекул: E_k1 = E_k.

• Конечная средняя энергия хаотичного движения молекул: E_k2 = 2E_k.

Основное уравнение МКТ:

p=23n−Ek

Составим уравнения для начального и конечного состояний:

p1=23n1−Ek1=233n−Ek=2n−Ek

p2=23n2−Ek2=23n2−Ek=43n−Ek

Отсюда:

n−Ek=p12=3p24

p2=4p16=23p1

Ответ: в

pазбирался: Алиса Никитина | обсудить разбор

Задание EF18416

Цилиндрический сосуд разделён неподвижной теплоизолирующей перегородкой. В одной части сосуда находится кислород, в другой – водород, концентрации газов одинаковы. Давление кислорода в 2 раза больше давления водорода. Чему равно отношение средней кинетической энергии молекул кислорода к средней кинетической энергии молекул водорода?

---

Алгоритм решения

1.Записать исходные данные.

2.Записать основное уравнение МКТ идеального газа.

3.Составить уравнения для обоих газов.

4.Найти отношение средней кинетической энергии молекул кислорода к средней кинетической энергии молекул водорода.

Решение

Анализируя условия задачи, можно выделить следующие данные:

• Концентрации кислорода и водорода в сосуде равны. Следовательно, n₁ = n₂ = n.

• Давление кислорода вдвое выше давления водорода. Следовательно, p₁ = 2p, а p₂ = p.

Запишем основное уравнение идеального газа:

p=23n−Ek

Применим его для обоих газов и получим:

p1=23n1−Ek1 или 2p=23n−Ek1 

p2=23n2−Ek2 или p=23n−Ek2 

Выразим среднюю кинетическую энергию молекул газа из каждого уравнения:

−Ek1=3pn

−Ek2=3p2n

Поделим уравнения друг на друга и получим:

−Ek1−Ek2=3pn·2n3p=2

Ответ: 2

pазбирался: Алиса Никитина | обсудить разбор

Задание EF18824

В одном сосуде находится аргон, а в другом – неон. Средние кинетические энергии теплового движения молекул газов одинаковы. Давление аргона в 2 раза больше давления неона. Чему равно отношение концентрации молекул аргона к концентрации молекул неона?

---

Алгоритм решения

1.Записать исходные данные.

2.Записать основное уравнение МКТ идеального газа.

3.Составить уравнения для обоих газов.

4.Найти отношение концентрации молекул аргона к концентрации молекул неона.

Решение

Анализируя условия задачи, можно выделить следующие данные:

• Средние кинетические энергии теплового движения молекул газов одинаковы. Следовательно, −Ek1=−Ek2=−Ek.

• Давление аргона в 2 раза больше давления неона. Следовательно, p₁ = 2p, а p₂ = p.

Запишем основное уравнение идеального газа:

p=23n−Ek

Применим его для обоих газов и получим:

p1=23n1−Ek1 или 2p=23n1−Ek 

p2=23n2−Ek2 или p=23n2−Ek 

Выразим концентрации молекул газа из каждого уравнения:

n1=3p−Ek

n2=3p2−Ek

Поделим уравнения друг на друга и получим:

n1n2=3p−Ek·2−Ek3p=2

Ответ: 2

pазбирался: Алиса Никитина | обсудить разбор

Алиса Никитина | Просмотров: 10.6k

Основное уравнение МКТ идеального газа

теория по физике 🧲 молекулярная физика, МКТ, газовые законы

Идеальный газ — газ, удовлетворяющий трем условиям:

• Молекулы — материальные точки.
• Потенциальная энергия взаимодействия молекул пренебрежительно мала.
• Столкновения между молекулами являются абсолютно упругими.

Реальный газ с малой плотностью можно считать идеальным газом.

Измерение температуры

Температуру можно измерять по шкале Цельсия и шкале Кельвина. По шкале Цельсия за нуль принимается температура, при которой происходит плавление льда. По шкале Кельвина за нуль принимается абсолютный нуль — температура, при котором давление идеального газа равно нулю, и его объем тоже равен нулю.

Обозначение температуры

1. По шкале Цельсия — t. Единица измерения — 1 градус Цельсия (1 o C).
2. По шкале Кельвина — T. Единица измерения — 1 Кельвин (1 К).

Цена деления обеих шкал составляет 1 градус. Поэтому изменение температуры в градусах Цельсия равно изменению температуры в Кельвинах:

При решении задач в МКТ используют значения температуры по шкале Кельвина. Если в условиях задачи температура задается в градусах Цельсия, нужно их перевести в Кельвины. Это можно сделать по формуле:

Если особо важна точность, следует использовать более точную формулу:

Пример №1. Температура воды равна o C. Определить температуру воды в Кельвинах.

T = t + 273 = 2 + 273 = 275 (К)

Основное уравнение МКТ идеального газа

Давление идеального газа обусловлено беспорядочным движением молекул, которые сталкиваются друг с другом и со стенками сосуда. Основное уравнение МКТ идеального газа связывает давление и другие макропараметры (объем, температуру и массу) с микропараметрами (массой молекул, скоростью молекул и кинетической энергией).

Основное уравнение МКТ

Давление идеального газа пропорционально произведению концентрации молекул на среднюю кинетическую энергию поступательного движения молекулы.

p = 2 3 . . n − E k

p — давление идеального газа, n — концентрация молекул газа, − E k — средняя кинетическая энергия поступательного движения молекул.

Выражая физические величины друг через друга, можно получить следующие способы записи основного уравнения МКТ идеального газа:

p = 1 3 . . m 0 n − v 2

m 0 — масса одной молекулы газа;

n — концентрация молекул газа;

− v 2 — среднее значение квадрата скорости молекул газа.

Среднее значение квадрата скорости не следует путать со среднеквадратичной скоростью v, которая равна корню из среднего значения квадрата скорости:

p = 1 3 . . ρ − v 2

ρ — плотность газа

k — постоянная Больцмана (k = 1,38∙10 –3 Дж/кг)

T — температура газа по шкале Кельвина

Пример №2. Во сколько раз уменьшится давление идеального одноатомного газа, если среднюю кинетическую энергию теплового движения молекул и концентрацию уменьшить в 2 раза?

Согласно основному уравнению МКТ идеального газа, давление прямо пропорционально произведению средней кинетической энергии теплового движения молекул и концентрации его молекул. Следовательно, если каждая из этих величин уменьшится в 2 раза, то давление уменьшится в 4 раза:

Следствия из основного уравнения МКТ идеального газа

Через основное уравнение МКТ идеального газа можно выразить скорость движения молекул (частиц газа):

v = √ 3 k T m 0 . . = √ 3 R T M . .

R — универсальная газовая постоянная, равная произведения постоянной Авогадро на постоянную Больцмана:

R = N A k = 8 , 31 Д ж / К · м о л ь

Температура — мера кинетической энергии молекул идеального газа:

Полная энергия поступательного движения молекул газа определяется формулой:

Пример №3. При уменьшении абсолютной температуры на 600 К средняя кинетическая энергия теплового движения молекул неона уменьшилась в 4 раза. Какова начальная температура газа?

Запишем формулу, связывающую температуру со средней кинетической энергией теплового движения молекул, для обоих случаев, с учетом что:

Составим систему уравнений:

На графике представлена зависимость объёма постоянного количества молей одноатомного идеального газа от средней кинетической энергии теплового движения молекул газа. Опишите, как изменяются температура и давление газа в процессах 1−2 и 2−3. Укажите, какие закономерности Вы использовали для объяснения.

Алгоритм решения

Решение

График построен в координатах (V;E_k). Процесс 1–2 представляет собой прямую линию, исходящую из начала координат. Это значит, что при увеличении объема растет средняя кинетическая энергия молекул. Но из основного уравнения МКТ идеального газа следует, что мерой кинетической энергии молекул является температура:

Следовательно, когда кинетическая энергия молекул растет, температура тоже растет.

Запишем уравнение Менделеева — Клапейрона:

Так как количество вещества одинаковое для обоих состояния 1 и 2, запишем:

ν R = p 1 V 1 T 1 . . = p 2 V 2 T 2 . .

Мы уже выяснили, что объем и температура увеличиваются пропорционально. Следовательно, давление в состояниях 1 и 2 равны. Поэтому процесс 1–2 является изобарным, давление во время него не меняется.

Процесс 2–3 имеет график в виде прямой линии, перпендикулярной кинетической энергии. Так как температуры прямо пропорциональна кинетической энергии, она остается постоянной вместе с этой энергией. Следовательно, процесс 2–3 является изотермическим, температура во время него не меняется. Мы видим, что объем при этом процессе уменьшается. Но так как объем и давление — обратно пропорциональные величины, то давление на участке 2–3 увеличивается.

pазбирался: Алиса Никитина | обсудить разбор | оценить

Первоначальное давление газа в сосуде равнялось р₁. Увеличив объём сосуда, концентрацию молекул газа уменьшили в 3 раза, и одновременно в 2 раза увеличили среднюю энергию хаотичного движения молекул газа. В результате этого давление р₂ газа в сосуде стало равным

Идеальный газ

О чем эта статья:

Газ: агрегатное состояние

У веществ есть три агрегатных состояния — твердое, жидкое и газообразное.

Их характеристики — в таблице:

Агрегатные состояния

Свойства

Расположение молекул

Расстояние между молекулами

Движение молекулы

Твердое

сохраняет форму и объем

в кристаллической решетке

соотносится с размером молекул

колеблется около положения равновесия в кристаллической решетке

Жидкое

сохраняет объем и текучесть

близко друг к другу

молекулы малоподвижны, при нагревании скорость движения увеличивается

Газообразное

занимает весь предоставленный объем

больше размеров молекул

хаотичное и непрерывное

В жизни мы встречаем вещества в газообразном состоянии, когда чувствуем запахи. Запах очень легко распространяется, потому что газ не имеет ни формы, ни объема (занимает весь предоставленный объем) и состоит из хаотично движущихся молекул, расстояние между которыми больше, чем размеры молекул.

Агрегатных состояний точно три?

На самом деле есть еще четвертое — плазма. Звучит как что-то из научной фантастики, но это просто ионизированный газ — газ, в котором, помимо нейтральных частиц, есть еще и заряженные. Ионизаторы воздуха как раз строятся на принципе перехода из газообразного вещества в плазму.

Модель идеального газа

В физике есть такое понятие, как модель. Модель — это что-то идеализированное, она нужна в случаях, когда можно пренебречь некоторыми параметрами объекта или процесса.

Идеальный газ — это модель реального газа. Молекулы идеального газа представляют собой материальные точки, которые не взаимодействуют друг с другом на расстоянии, но взаимодействуют при столкновениях друг с другом или со стенками сосуда. При работе с идеальным газом можно пренебречь потенциальной энергией молекул (но не кинетической).

В повседневной жизни идеальный газ, конечно, не встречается. Но реальный газ может вести себя почти как идеальный. Такое случается, если среднее расстояние между молекулами во много раз больше их размеров, то есть если газ очень разреженный.

Свойства идеального газа

Расстояние между молекулами значительно больше размеров молекул.

Молекулы газа очень малы и представляют собой упругие шары.

Силы притяжения между молекулами пренебрежимо малы.

Молекулы взаимодействуют только при соударениях.

Молекулы движутся хаотично.

Молекулы движутся по законам Ньютона.

Среднеквадратичная скорость

Потенциальной энергией молекул газа пренебречь можно, а вот кинетической — никак нельзя. Потому что кинетическая энергия — это энергия движения, а мы не можем пренебрегать скоростью движения молекул.

На графике показано распределение Максвелла — то, как молекулы распределяются по скоростям. Судя по графику, большинство молекул движутся со средним значением скорости. Хотя есть и быстрые, и медленные молекулы, просто их значительно меньше.

Но наш газ идеальный, а в идеальном газе случаются чудеса. Одно из таких чудес — то, что все молекулы идеального газа двигаются с одинаковой скоростью. Эта скорость называется средней квадратичной.

Средняя квадратичная скорость

v_{ср. кв.} — средняя квадратичная скорость [м/с]

v₁, v₂, v_n — скорости разных молекул [м/с]

N — количество молекул [—]

Попробуйте курсы подготовки к ЕГЭ по физике с опытным преподавателем в онлайн-школе Skysmart!

Давление идеального газа

Молекулы газа беспорядочно движутся. Во время движения они сталкиваются друг с другом, а также со стенками сосуда, в котором этот газ находится. Поскольку молекул много, ударов тоже много.

Например, в комнате, в которой вы сейчас находитесь, за одну секунду на каждый квадратный сантиметр молекулы воздуха наносят столько ударов, что их количество выражается двадцатитрехзначным числом.

Хотя сила удара отдельной молекулы мала, действие всех молекул на стенки сосуда приводит к значительному давлению. Представьте, что комар пытается толкать машину — она не сдвинется с места. Но если за работу возьмется пара сотен миллионов комаров, то машину получится сдвинуть.

Эксперимент

Чтобы смоделировать давление газа, возьмите песок и лист бумаги, зажатый между двумя книгами. Песчинки будут выступать в роли молекул газа, а лист — в роли сосуда, в котором этот газ находится. Когда вы начинаете сыпать песок на лист бумаги, бумага отклоняется под воздействием множества песчинок. Так же и молекулы газа оказывают давление на стенки сосуда, в котором находятся.

Зависимость давления от других величин

Зависимость давления от объема

В механике есть формула давления, которая показывает, что давление прямо пропорционально силе и обратно пропорционально площади, на которую эта сила оказывается.

Давление

p = F/S

F — сила [Н]

S — площадь [м 2 ]

То есть если наши двести миллионов комаров будут толкать легковую машину, они распределятся по меньшей площади, чем если бы толкали грузовой автомобиль, — просто потому, что легковушка меньше грузовика. Из формулы давления следует, что давление на легковой автомобиль будет больше из-за его меньшей площади.

Рассмотрим аналогичный пример с двумя сосудами разной площади.

Давление в левом сосуде будет больше, чем во втором, потому что его площадь меньше. А раз меньше площадь сосуда, то меньше и его объем. Значит, давление зависит от объема следующим образом: чем больше объем, тем меньше давление, и наоборот.

При этом зависимость будет не линейная, а примет вот такой вид (при условии, что температура постоянна):

Зависимость давления от объема называется законом Бойля-Мариотта. Она экспериментально проверяется с помощью такой установки:

Объем шприца увеличивают с помощью насоса, а манометр измеряет давление. Эксперимент показывает, что при увеличении объема давление действительно уменьшается.

Зависимость давления от температуры

Рассмотрим зависимость давления газа от температуры при условии неизменного объема определенной массы газа. Исследования в этой области впервые провел французский изобретатель Жак Шарль в XVIII веке.

В ходе эксперимента газ нагревали в большой колбе, соединенной с ртутным манометром в виде узкой изогнутой трубки. Незначительным увеличением объема колбы при нагревании можно пренебречь, как и столь же незначительным изменением объема при смещении ртути в узкой манометрической трубке. Таким образом, объем газа можно считать неизменным.

Подогревая воду в сосуде, окружающем колбу, ученый измерял температуру газа термометром, а давление — манометром.

Эксперимент показал, что давление газа увеличивается с увеличением температуры. Это связано с тем, что при нагревании молекулы газа движутся быстрее, из-за чего чаще ударяются о стенки сосуда.

С температурой все проще. Зависимость давления от температуры при постоянных объеме и массе будет линейной:

Эта зависимость называется законом Шарля в честь ученого, открывшего ее.

Основное уравнение МКТ

Основная задача молекулярно-кинетической теории газа заключается в том, чтобы установить соотношение между давлением газа и его микроскопическими параметрами: массой молекул, их средней скоростью и концентрацией. Это соотношение называется основным уравнением молекулярно-кинетической теории газа или кратко — основным уравнением МКТ.

В основе молекулярно-кинетической теории лежат три положения.

Все вещества образованы из мельчайших частиц — молекул, которые состоят из атомов.

Молекулы химического вещества могут быть простыми и сложными, то есть состоять из одного или нескольких атомов. Молекулы и атомы представляют собой электрически нейтральные частицы. При определенных условиях молекулы и атомы могут приобретать дополнительный электрический заряд и превращаться в положительные или отрицательные ионы.

Атомы и молекулы находятся в непрерывном хаотическом движении.

Частицы взаимодействуют друг с другом силами, которые имеют электрическую природу. Гравитационное взаимодействие между частицами пренебрежимо мало.

Мы уже выяснили, что причина давления газа на стенки — это удары молекул. Давление напрямую зависит от количества молекул — чем их больше, тем больше ударов о стенки и тем больше давление. А количество молекул в единице объема — это концентрация. Значит, давление газа зависит от концентрации.

Также давление пропорционально квадрату скорости, так как чем больше скорость молекулы, тем чаще она бьется о стенку сосуда. Расчеты показывают, что основное уравнение молекулярно-кинетической теории для идеального газа имеет следующий вид.

Основное уравнение МКТ

p = nkT

p — давление газа [Па]

n — концентрация [м −3 ]

T — температура газа [К]

m 0 — масса одной молекулы [кг]

v — средняя квадратичная скорость [м/с]

Коэффициент 1/3 обусловлен трехмерностью пространства: во время хаотического движения молекул все три направления равноправны.

Важный нюанс: средняя квадратичная скорость сама по себе не в квадрате! Ее формула указана выше, а в основном уравнении МКТ (да и не только в нем) она возведена в квадрат. Это значит, что формулу средней квадратичной скорости нужно подставлять не вместо v 2 , а вместо v — и потом уже возводить эту формулу в квадрат. Это часто провоцирует путаницу.

Мы знаем, что кинетическая энергия вычисляется по следующей формуле:

Кинетическая энергия

Е_к = mv 2 /2

Е_к — кинетическая энергия [Дж]

m — масса тела [кг]

v — скорость [м/с]

Для молекулы газа формула примет вид:

Средняя кинетическая энергия поступательного движения молекулы

Е_к — средняя кинетическая энергия поступательного движения молекулы [Дж]

m₀ — масса молекулы [кг]

v — скорость молекулы [м/с]

Из этой формулы можно выразить m₀v 2 и подставить в основное уравнение МКТ. Подставим и получим, что давление идеального газа пропорционально произведению концентрации молекул на среднюю кинетическую энергию поступательного движения молекулы.

Основное уравнение МКТ

p — давление газа [Па]

n — концентрация [м −3 ]

E — средняя кинетическая энергия поступательного движения молекулы [Дж]

Хранение и транспортировка газов

Если нужно перевезти значительное количество газа из одного места в другое или если газ необходимо длительно хранить, его помещают в специальные прочные металлические сосуды. Из-за того, что при уменьшении объема увеличивается давление, газ можно закачать в небольшой баллон, но он должен быть очень прочным.

Сосуды, предназначенные для транспортировки газов, выдерживают высокие давления. Поэтому с помощью специальных насосов (компрессоров) туда можно закачать значительные массы газа, которые в обычных условиях занимали бы в сотни раз больший объем.

Поскольку давление газов в баллонах даже при комнатной температуре очень велико, их ни в коем случае нельзя нагревать. Например, держать под прямыми лучами солнца или пытаться сделать в них отверстие — даже после использования.

II. Молекулярная физика

Тестирование онлайн

Идеальный газ

Это несуществующая физическая модель газа, который состоит из большого числа молекул, размеры которых ничтожно малы по сравнению со средними расстояниями между ними. Молекулы такого газа можно считать материальными точками, это означает, что их вращательное и колебательное движения не принимаются во внимание. Движение молекул происходит без столкновений с другими молекулами, подчиняется законам Ньютона. Соударения молекул со стенками сосуда являются абсолютно упругими.

Параметры состояния газа

Давление, температура и объем – параметры состояния газа. Или их называют макропараметрами. Температура – внешняя характеристика скоростей частиц газа. Давление – внешняя характеристика соударений со стенками, например, сосуда. Объем – место, куда заключены частицы газа. Газ занимает весь предоставленный ему объем. Существуют еще внешние параметры, например тела или поля, действующие на газ из вне.

Микропараметры (маленькие, внутренние характеристики) газа – это параметры, которые мы не можем оценить без специальных экспериментов, например, скорость и направление движения каждой молекулы газа.

Состояние термодинамической системы, когда все ее параметры при неизменных внешних условиях не изменяются со временем, называют равновесным.

Основное уравнение молекулярно-кинетической теории

Уравнение связывает микропараметры и макропараметры (давление, объем и температуру) идеального газа.

Рассмотрим идеальный газ, который находится в кубическом сосуде. Каждая молекула упруго сталкивается со стенкой сосуда, при этом изменятся ее импульс. Столкновение всех молекул со стенкой на макроуровне ощущается как давление газа на сосуд. В формулах будут присутствовать средние значения, потому что какая-то молекула движется быстрее, какая-то помедленнее, для того, чтобы оценить примерную скорость, будем брать средние значения.

Основное уравнение мкт имеет вид

Средний квадрат скорости молекул

Средняя квадратичная скорость v_кв молекул это квадратный корень из среднего квадрата скорости

Средняя кинетическая энергия молекул

Можно вывести формулы

Температура

Это макропараметр, который характеризует способность тел к теплопередаче. Если два тела разной температуры контактируют, то произойдет переход энергии или передача теплоты от более горячего к холодному. Установится тепловое равновесие, все части будут одинаковой температуры.

Температура характеризует интенсивность движения частиц, поэтому связана со средней кинетической энергией частиц. Из опыта известно, что средняя кинетическая энергия молекул не зависит от вида газа и определяется температурой.

Связь между температурами по шкале Цельсия и по шкале Кельвина

[spoiler title=”источники:”]

http://skysmart.ru/articles/physics/idealnyj-gaz

http://fizmat.by/kursy/molekuljarnaja/uravnenie_mkt

[/spoiler]

Физика, 10 класс

Урок №19. Температура. Энергия теплового движения молекул

На уроке рассматриваются понятия: температура и тепловое равновесие; шкалы Цельсия и Кельвина; абсолютная температура как мера средней кинетической энергии теплового движения частиц вещества, зависимость давления от концентрации молекул и температуры.

Глоссарий по теме:

Макроскопические параметры – величины объём V, давление p и температура t, характеризующие состояние макроскопических тел без учёта их молекулярного строения.

Температура характеризует степень нагретости тела (холодное, тёплое, горячее).

Температура (от лат. temperatura — надлежащее смешение, соразмерность, нормальное состояние) – физическая величина, характеризующая состояние термодинамического равновесия макроскопической системы.

Тепловым равновесием называют – такое состояние тел, при котором температура во всех точках системы одинакова.

Тепловым или термодинамическим равновесием, изолированной системы тел, называют состояние, при котором все макроскопические параметры в системе остаются неизменными.

Термометр — это прибор для измерения температуры путём контакта с исследуемым телом. Различают жидкостные, газовые термометры, термопары, термометры сопротивления.

Абсолютная температура Т прямо пропорциональна температуре Θ (тета), выражаемой в энергетических единицах (Дж).

Абсолютный нуль – предельная температура, при которой давление идеального газа обращается в нуль при фиксированном объёме или объём идеального газа стремится к нулю при неизменном давлении.

Абсолютный нуль – температура, при которой прекращается тепловое движение молекул.

Абсолютная шкала температур (Шкала Кельвина) – здесь нулевая температура соответствует абсолютному нулю, а каждая единица температуры равна градусу по шкале Цельсия.

Кельвин – единица абсолютной температуры в Международной системе измерений (СИ).

Постоянная Больцмана – коэффициент, связывает температуру Θ энергетических единицах (Дж) с абсолютной температурой Т (К).

Абсолютная температура есть мера средней кинетической энергии молекул.

Давление газа прямо пропорционально концентрации его молекул и абсолютной температуре Т.

Закон Авогадро – в равных объёмах газов при одинаковых температурах и давлениях содержится одинаковое число молекул

Обязательная литература:

1. Мякишев Г.Я., Буховцев Б.Б., Сотский Н.Н. Физика.10 класс. Учебник для общеобразовательных организаций М.: Просвещение, 2017. – С. 195 – 203.

Дополнительная литература:

1. Смородинский Я.А. Температура. – 3-е издание. – М.: Бюро Квантум, 2007. (Библиотечка «Квант». Вып. 103. Приложение к журналу «Квант» № 5/2007.) С. 5— 25.
2. Кирик Л.А., Генденштейн Л.Э., Гельфгат И.М.. Задачи по физике. 10-11 классы для профильной школы. – М.: Илекса, 2010. – С. 111-115.
3. Рымкевич А.П. Физика. Задачник. 10-11 классы. – М.: Дрофа, 2013. – С. 65 – 67.
4. Орлов В.А., Сауров Ю.А. Практика решения физических задач. 10-11классы. – М.: Вентана-Граф, 2014. – С. 98-99.
5. http://kvant.mccme.ru/1991/09/idealnyj_gaz_-_universalnaya_f.htm

Теоретический материал для самостоятельного изучения

Измеряя расположение звёзд на небе, расстояния на земле, время, люди знали, для чего они это делают и изобретали, телескопы, часы, прототипы современных линеек. О температуре такого же сказать было нельзя. О том, что такое тепловое равновесие и что означает степень нагрева тела (температура), существовали разные мнения. Но человек с незапамятных времен точно знал, что, когда два тела плотно соприкасаются, между ними устанавливается, выражаясь современным языком, тепловое равновесие.

Любое макроскопическое тело или группа макроскопических тел при неизменных внешних условиях самопроизвольно переходят в состояние теплового равновесия.

Тепловым равновесием называют такое состояние тел, при котором температура во всех точках системы одинакова.

Температура (от лат. temperatura — надлежащее смешение, соразмерность, нормальное состояние) – физическая величина, характеризующая состояние термодинамического равновесия макроскопической системы.

К числу характеристик состояния макроскопических тел (твёрдых тел, жидкостей, газов) и процессов изменения их состояний, относят объём, давление и температуру. Эти величины описывают в целом тела, состоящие из большого числа молекул, а не отдельные молекулы. При этом микроскопические процессы внутри тела не прекращаются при тепловом равновесии: расположения молекул всё время меняются и меняются их скорости при столкновениях.

Величины объём, давление и температуру, характеризующие состояние макроскопических тел без учёта их молекулярного строения, называют макроскопическими параметрами.

Тепловым или термодинамическим равновесием, изолированной системы тел, называют состояние, при котором все макроскопические параметры в системе остаются неизменными.

Для точной характеристики нагретости тела, необходим прибор, способный измерить температуры тел и дать возможности их сравнения.

Термометр — это прибор для измерения температуры путём контакта с исследуемым телом. Различают жидкостные, газовые термометры, термопары, термометры сопротивления.

В 1597 году Галилей создал термоскоп, в собственных сочинениях учёного нет описания этого прибора, но его ученики засвидетельствовали этот факт. Аппарат представлял собой устройство для поднятия воды при помощи нагревания.

Изобретение термометра, данные которого не зависели бы от перепадов атмосферного давления, произошли благодаря экспериментам физика Э. Торричелли, ученика Галилея.

Во всех приборах, изобретённых в XVIII веке, измерение температуры было относительно расширению столбика воды, спирта или ртути и произвольности выбора начала отсчёта, т.е. нулевой температуры. Наполняющие их вещества замерзали или кипели и этими термометрами нельзя было измерять очень низкие или очень высокие температуры. Необходимо было изобрести такую шкалу, чтобы избавиться от зависимости выбранного вещества, на основе которого формировалось градуирование.

Шкала, предложенная шведским учёным Андерсом Цельсием в 1742 г., точно устанавливала положение двух точек: 0 и 100 градусов. По шкале Цельсия температура обозначается буквой t, измеряется в градусах Цельсия (ºС).

На территории Англии и США используется шкала Фаренгейта. Такая шкала была предложена немецким учёным Даниелем Габриелем Фаренгейтом в 1724 г.: 0 °F — температура смеси снега с нашатырём или поваренною солью, 96 °F —температура здорового человеческого тела, во рту или под мышкой.

Рене Антуан де Реомюр не одобрял применения ртути в термометрах вследствие малого коэффициента расширения ртути. В 1730 году изобрёл водно-спиртовой термометр и предложил шкалу от 0 до 80°.

Шкала Реомюра очень долго использовалась на родине учёного во Франции вплоть до настоящего времени.

Различные жидкости при нагревании расширяются не одинаково. Поэтому расстояния на шкале между нулевой отметкой 0 °C и 100 °C будут разными.

Однако существует способ создать тело, которое приближенно обладает нужными качествами. Это идеальный газ. Было замечено, что в отличие от жидкостей все разряжённые газы – водород, гелий, кислород – расширяются при нагревании одинаково и одинаково меняют своё давление при изменении температуры. Это свойство газов позволяет избавиться в термометрах от одного существенного недостатка шкалы Цельсия – произвольности выбора начала отсчёта, то есть нулевой температуры.

При тепловом равновесии, если давление и объём газа массой m постоянны, то средняя кинетическая энергия молекул газа должна иметь строго определённое значение, как и температура.

Практически такую проверку произвести непосредственно невозможно, но с помощью основного уравнения молекулярно-кинетической теории её можно выразить через макроскопические параметры:

; ; ; ;

Если кинетическая энергия действительно одинакова для всех газов в состоянии теплового равновесия, то и значение давления р должно быть тоже одинаково для всех газов при постоянном значении отношения объёма к числу молекул. Подтвердить или опровергнуть данное предположение может только опыт.

Возьмём несколько сосудов, заполненных различными газами, например, водородом, гелием и кислородом. Сосуды имеют определённые объёмы и снабжены манометрами, для измерения давления газов в сосудах. Массы газов известны, тем самым известно число молекул в каждом сосуде. Приведём газы в состояние теплового равновесия. Для этого поместим их в тающий лёд и подождём, пока не установится тепловое равновесие и давление газов перестанет меняться.

Здесь устанавливается тепловое равновесие и все газы имеют одинаковую температуру 0 °С. При этом показания манометра показывают разное давление р, объёмы сосудов V изначально были разными и число молекул N различно, так как газы, закаченные в баллоны разные. Найдём отношение для водорода всех параметров для одного моля вещества:

Такое значение отношения произведения давления газа на его объём к числу молекул получается для всех газов при температуре тающего льда. Обозначим это отношение через Θ₀ (тета нулевое):

Таким образом, предположение, что средняя кинетическая энергия, а также давление р в состоянии теплового равновесия одинаковы для всех газов, если их объёмы и количества вещества одинаковы или если отношение

Если же сосуды с газами поместить в кипящую воду при нормальном атмосферном давлении, то согласно эксперименту, отношение макроскопических параметров будет также одинаковым для всех газов, но значение будет больше предыдущего

Отсюда следует, что величина Θ растёт с повышением температуры и не зависит от других параметром, кроме температуры. Этот опытный факт позволяет рассматривать величину Θ тета как естественную меру температуры и измерять в энергетических единицах — джоулях.

А теперь вместо энергетической температуры введём температуру, которая будет измеряться в градусах. Будем считать величину тета Θ прямо пропорциональной температуре Т, где k- коэффициент пропорциональности

Так как , то тогда

По этой формуле вводится температура, которая даже теоретически не может быть отрицательной, так как все величины левой части этого равенства больше или равны нулю. Следовательно, наименьшим значением этой температуры является нуль, при любом другом параметре p, V, N равным нулю.

Предельную температуру, при которой давление идеального газа обращается в нуль при фиксированном объёме или при которой объём идеального газа стремится к нулю при неизменном давлении, называют абсолютным нулём температуры.

Тепловое движение молекул непрерывно и бесконечно, а при абсолютном нуле молекулы поступательно не двигаются. Следовательно, абсолютный нуль температур при наличии молекул вещества не может быть достигнут. Абсолютный нуль температур — это самая низкая температурная граница, верхней не существует, та «наибольшая или последняя степень холода», существование которой предсказывал М.В. Ломоносов.

В 1848 г. английскому физику Вильяму Томсону (лорд Кельвин) удалось построить абсолютную температурную шкалу (её в настоящее время называют шкалой Кельвина), которая имеет две основные точки 0 К (или абсолютный нуль) и 273К, точка в которой вода существует в трёх состояниях (в твёрдом, жидком и газообразном).

Абсолютная температурная шкала — шкала температур, в которой за начало отсчёта принят абсолютный нуль. Температура здесь обозначается буквой T и измеряется в кельвинах (К).

На шкале Цельсия, есть две основные точки: 0°С (точка, в которой тает лёд) и 100°С (кипение воды). Температура, которую определяют по шкале Цельсия, обозначается t. Шкала Цельсия имеет как положительные, так и отрицательные значения.

Из опыта мы определили значения величины Θ (тета) при 0 °С и 100 °С. Обозначим абсолютную температуру при 0 °С через Т₁, а при 100 °С через Т₂. Тогда согласно формуле:

Отсюда можно вычислить коэффициент k, который связывает температуру в Θ энергетических единицах (Дж) с абсолютной температурой Т (К)

k = 1,38 • 10^-23 Дж/К – постоянная Больцмана.

Зная постоянную Больцмана, можно найти значение абсолютного нуля по шкале Цельсия. Для этого найдём сначала значение абсолютной температуры, соответствующее 0°С:

значение абсолютной температуры.

Один кельвин и один градус шкалы Цельсия совпадают. Поэтому любое значение абсолютной температуры Т будет на 273 градуса выше соответствующей температуры t по Цельсию:

Теперь выведем ещё одну зависимость температуры от средней кинетической энергии молекул. Из основного уравнения молекулярно-кинетической теории и уравнения для определения абсолютной температуры

Здесь видно, что левые части этих уравнений равны, значит правые равны тоже.

Средняя кинетическая энергия хаотического поступательного движения молекул газа пропорциональна абсолютной температуре.

Абсолютная температура есть мера средней кинетической энергии движения молекул.

Из выведенных формул мы можем получить выражение, которое показывает зависимость давления газа от концентрации молекул и температуры

Из этой зависимости вытекает, что при одинаковых давлениях и температурах концентрация молекул у всех газов одна и та же. Отсюда следует закон Авогадро, известный нам из курса химии.

Закон Авогадро: в равных объёмах газов при одинаковых температурах и давлениях содержится одинаковое число молекул.

Рассмотрим задачи тренировочного блока урока.

1. При температуре _______ (37⁰C; 283⁰C; 27⁰C) средняя кинетическая энергия поступательного движения молекул равна 6,21·10^-21Дж.

Дано:

k = 1,38 • 10-23 Дж/К – постоянная Больцмана

t -?

Решение:

Запишем значение средней кинетической энергии хаотического поступательного движения молекул с зависимостью от абсолютной температуры:

Отсюда выразим Т:

Соотношение между абсолютной температурой и температурой в градусах Цельсия:

Подставим значение абсолютной температуры:

Правильный вариант ответа:

2. При температуре 290 К и давлении 0,8 МПа, средняя кинетическая энергия молекул равна __________ Дж, а концентрация составляет молекул ___________ м^-3.

Дано:

Т = 290К

р = 0,8 МПа =0,8·10⁶ Па

k = 1,38 • 10^-23 Дж/К – постоянная Больцмана

Е_к -? n – ?

Решение:

Значение средней кинетической энергии хаотического поступательного движения молекул:

Подставив значение абсолютной температуры, найдём ответ:

Определим концентрацию газа из соотношения:

Правильный вариант ответа: 6·10^-21; 2·10²⁶ м^-3.

Модель идеального газа считается самой простейшей относительно основных положений МКТ. Кинетическая модель идеального газа молекул говорит о том, что при взаимодействии между собой, шарики рассматриваются в качестве идеально упругих. Суммарный объем всех молекул достаточно мал по сравнению с объемом сосуда, в котором находится данный газ. Модель необходима для описания его поведения при различных давлениях и температурах.

Цель молекулярно-кинетической теории – установка связи между макроскопическими и макроскопическими параметрами.

После соударения  молекул между собой и стенками сосуда происходит изменение направления движения и времени между интервалами столкновений. Модель идеального газа основывается на законах механики Ньютона, то тесть столкновения соответствуют закону упругого удара.

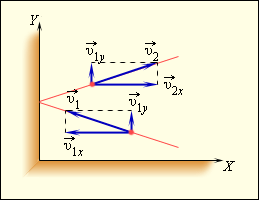
Чтобы определить давление газа на стенку сосуда, учитывается модель идеального газа. Исходя из этого, происходит возникновение сил, которые подчиняются 3 закону Ньютона. Отсюда получим, что проекция скорости υx перпендикулярна относительно стенки, а знак меняется на противоположный. Проекция υy параллельна и постоянна. Это показано на рисунке 3.2.1.

Рисунок 3.2.1. Упругое столкновение молекулы со стенкой.

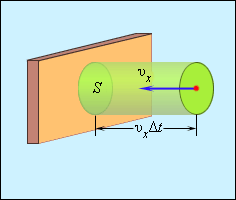
Отсюда следует, что изменение импульса можно записать в виде 2m0υx с массой молекулы, равной m0_. Необходимо выделить площадь S, как показано на рисунке 3.2.2. По прошествии времени Δt  с S поверхностью столкнутся молекулы с проекциями скорости υx_, которая направлена в сторону стены, и основанием цилиндра S с высотой υxΔt.

Рисунок 3.2.2. Определение числа столкновений молекул с поверхностью S.

Если за единицу объема брать сосуд с n-ым количеством молекул, тогда их число в объеме цилиндра нужно обозначить, как nSυxΔt. Очевидно, что происходит столкновение только половины имеющихся молекул. Тогда количество ударов о S за время Δt равняется 12nSvx∆t.

При столкновении происходит изменение импульса 2m0υx. Тогда формула nm0vx2S∆t говорит о полном его изменении за определенный промежуток времени. Исходя из закона механики, изменение импульса всех молекул записывается как FΔt. Силой F обозначается средняя сила, которая действует на молекулы. Но 3 закон Ньютона говорит о том, что аналогичная сила по модулю оказывает действие на поверхность S. Данное утверждение можно зафиксировать F∆t=nm0vx2S∆t.

Далее для упрощения следует разделить равенство на выражение SΔt. Формула примет вид p=FS=nm0vx2 со значением р, обозначаемым в качестве давления газа на стенку сосуда.

Все молекулы, находящиеся в сосуде на единицу объема, имеют разные проекции скоростей на ось Ох. При столкновениях прослеживалось статистическое их распределение по скоростям, причем с разными направлениями векторов их скоростей.

Распределением Максвелла называют распределение молекул газа по модулю скоростей.

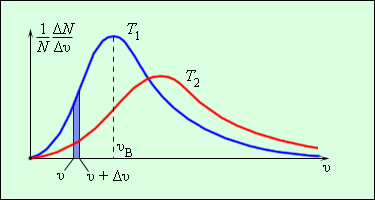
Еще в 1860 г Дж. Максвелл вывел закон распределения молекул газа по скоростям, основываясь на основных положениях молекулярно-кинетической теории молекулы. Рисунок 3.2.3. наглядно показывает распределения молекул по скоростям с помощью кривых. На оси Ох располагается модуль скорости, а на Оу – количество молекул, находящихся на интервале от υ до υ+Δυ. На рисунке 3.2.3. данное значение выделено в виде столбика.

Рисунок 3.2.3. Распределение молекул по скоростям. T2>T1.

Характерные параметры распределения Максвелла – это вероятная скорость υв,которая соответствует кривой распределения, и среднеквадратичная скорость υкв=υ2→, где υ2→обозначающие среднее значение квадрата скорости.

Если растет температура, тогда максимум кривой будет смещен в сторону больших скоростей, то есть υв и υкв увеличатся.

Распределение Максвелла

Для записи формулы давления газа необходимо предположить, что все молекулы разделены на n1, n2, n3 группы с проекциями υx1, υx2, υx3. Иначе говоря, записываем ∑ini=n. Можно зафиксировать, как nim0vxi2. Тогда суммарное давление примет вид p=m0∑inivxi2.

Данная сумма является суммой квадратов проекций υx всех n  молекул на единичном объеме газа. При делении выражения на n получим среднее значение квадратичной скорости проекции υx. Запишем в виде 1n∑niυxi2=vx2→i.

Другая интерпретация  формулы давления газа p=nm0vx2→. Все направления векторов различные, потому среднее значение квадратов проекций на координатные оси равняется vx2→=vy2→=vz2→=13v2→.

Формула для среднего давления газа на стенку сосуда обозначим, как p=p→=13nm0v2→=23nm0v2→2=23nEk→.

Из уравнения видна связь между р и m0 и количеством молекул n, средней квадратичной скоростью v2→ и средней кинетической энергией Ek→ молекул. Такое уравнение получило название уравнения молекулярно-кинетической уравнения теории газов.

Отсюда следует, что давление газа – это две трети средней кинетической энергии, которое имеется в единице объема. Основное уравнение молекулярно-кинетической теории газов или строения вещества содержит произведение количества молекул n на Ek→. Предположительно сосуд имеет газ неизменного объема V, тогда n=NV=const (N – число молекул в сосуде). Изменение давления происходит пропорционально изменению кинетической энергии.

Физика. Температура

Температура измеряется с помощью термометра. Для его создания выбирается термометрическое вещество и величину, которая его характеризует. Разные конструкции подразумевают отличия в их свойствах.

Каждый термометр должен быть откалиброван. Использование природных систем с неизменной температурой необходимо для хорошего теплообмена. Температура плавления льда равняется 0 градусов Цельсия, а точка кипения воды – 100 градусов. Одно маленькое деление из шкалы равняется  1 градусу. Существует обозначение замерзания воды по Фаренгейту, то есть 32 °F. Получаем, что формула примет вид TF=95TC+32 или TC=59(TF-32).

На рисунке 3.2.4. изображен газовый термометр, который чаще всего заполняют разряженным гелием, воздухом с неизменным объемом, обозначаемым V = const, и давлением р. Из опыта видно, что возрастание давления идет с повышением температуры по Цельсию.

Рисунок 3.2.4. Газовый термометр с постоянным объемом.

Температура кипения газов при давлении

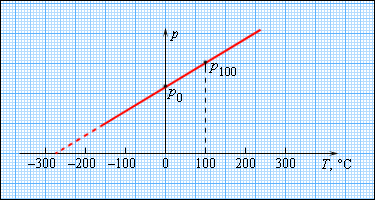
Чтобы произвести калибровку газового термометра, следует выполнить измерение состояния молекул при 0 и 100 градусах. Для этого мы наносим точки p0 и p100 на график, после чего проводим прямую линию, как изображено на рисунке 3.2.5. Получившийся калибровочный график способен определить температуру с разными значениями давления. При низких температурах возможно нахождение ее «гипотетической». Из опыта видно, что на свойства газа не влияет температура в-273,15 °С. При понижении температур газ переходит в жидкое или твердое состояние, поэтому получение охлажденного газа невозможно.

Рисунок 3.2.5. Зависимость давления газа от температуры при V = const.

В 1848 году У. Кельвин предлагает использовать точку нулевого давления газа для составления шкалы. Отличие от измерений температуры в Цельсиях в том, что нулевая точка сдвинута на TК =TС+273,15.

По системе СИ температура измеряется по Кельвину и обозначается К. Тогда комнатная температура запишется TС=20 °С, а по Кельвину – TК=293,15 К.

Температура кипения газов. Шкала Кельвина

Температурная шкала Кельвина считается абсолютной. Она наиболее приемлема для обозначения физических теорий.

Шкала Кельвина может быть не привязана двумя фиксированными точками, а именно: точка плавления льда и кипения воды с нормальным атмосферным давлением.

Нулевое давление называется абсолютным нулем температуры.

Шкала Кельвина имеет точку, в которой лед, вода и пар будут находиться  в тепловом равновесии. Для калибровки других термометров применяют газовые, так как для практики они не подходят в виду своих больших размеров. Отсюда следует, что давление разреженного газа в сосуде постоянного объема V изменяется прямо пропорционально его абсолютной температуре, то есть p~T. Из опыта видно, что неизменный объем V и температура давления T прямо пропорциональны количеству вещества в сосуде к его объему: p~υV=NNAV=nNA~n, где N принимает обозначение числа молекул в сосуде, а NА – постоянная Авогадро, n=NV – концентрации молекул.

После объединения соотношений получим, что запись примет вид p=nkT, где k считается универсальной постоянной величиной для всех газов, иначе говоря, постоянная Больцмана. Этот ученый являлся одним из создателей опытного обоснования основных положений молекулярно-кинетической теории. Ее обозначение в системе СИ k=1,38ċ10–23 Дж/К.

При сравнении соотношения p=nkT с уравнением МКТ газов, получим EK→.

Средняя кинетическая энергия беспорядочного движения молекул газа прямо пропорциональна абсолютной температуре.

Температура является мерой для кинетической энергии молекул, которая не зависит от ее величины. Броуновская частица из жидкости и газа обладает аналогичной средней кинетической энергией, как и другая отдельная молекула. Это суждение верно для разномассовых молекул, находящихся в одном сосуде. Состояние равновесия говорит о том, что на них действуют одинаковые средние кинетические энергии, которые определяются температурой смеси. Запись давления смеси газов запишется как сумма парциальных давлений каждого из них: p=p1+p2+p3+…=(n1+n2+n3+ …)kT.

Отсюда видно, что n1, n2, n3,… является концентрацией молекул газов в смеси. Выражение относят к молекулярно-кинетической теории, установленной Дальтоном: давление в смеси химически невзаимодействующих газов равняется сумме их парциальных давлений.