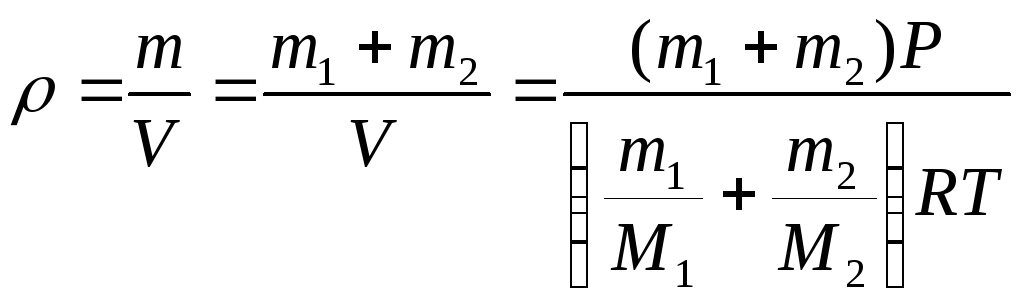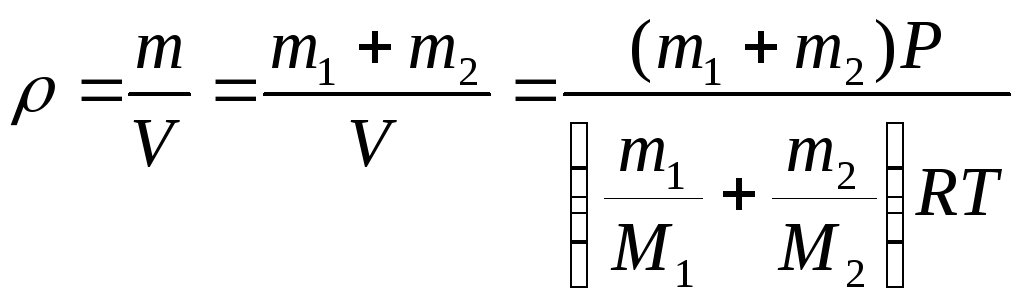Как найти температуру газа после расширения

План решения задач на газовые законы

1. Если
   в задаче рассматривается одно состояние
   газа и требуется найти какой-либо
   параметр этого состояния, нужно
   воспользоваться уравнением Менделеева
   – Клапейрона.

2. Если
   значения давления и объема явно не
   заданы, их нужно выразить через заданные
   величины, подставить в записанное
   уравнение и, решив его, найти неизвестный
   параметр.

3. В
   том случае, когда в задаче рассматриваются
   два различных состояния газа, нужно
   установить, изменяется ли масса газа
   при переходе из одного состояния в
   другое. Если масса остается постоянной,
   можно применить уравнение Клапейрона.
   Если же при постоянной массе в данном
   процессе не изменяется какой-либо из
   параметров ( р,V или Т), применяются
   уравнение соответствующего закона
   (Гей-Люссака, Шарля или Бойля-Мариотта).

4. Если
   в двух состояниях масса газа разная,
   то для каждого состояния записывают
   уравнение Менделеева-Клапейрона. Затем
   систему уравнений решают относительно
   искомой величины.

Примеры решения задач

Пример 3.1. Определите
число молекул воды в бутылке вместимостью
0,33л. Молярная масса воды М=18∙10^-3
кг/моль, плотность воды ρ=1г/см³.

Дано:
V=0,33л=0,33∙10^-3
м³;
М=18∙10^-3
кг/моль; ρ=1г/см³=
1∙10³
кг/м³;

Найти:
N.

Решение:
Масса
воды, занимающей объём V,

m=ρV,
(1)

где
ρ – плотность воды.

Масса
молекулы

,
(2)

где
М – молярная масса; N_A=6,02∙
10²³моль^-1
–
постоянная Авогадро.

Число
молекул в бутылке

(3)

Подставляя
в выражение (3) формулы (1) и (2), получим
искомое число молекул:

.

Ответ:
N=1,1∙10²⁵.

Пример 3.1. Узкая
цилиндрическая трубка, закрытая с одного
конца, содержит воздух, отделённый от
наружного воздуха столбиком ртути.
Когда трубка обращена закрытым концом
кверху, воздух внутри неё занимает длину
ℓ, когда же трубка обращена кверху
открытым концом, то воздух внутри неё
занимает длину ℓ’ < ℓ. Длина ртутного
столбика h мм. Определить атмосферное
давление.

Дано:
ℓ; ℓ’ < ℓ; h.

Найти:
Р.

Решение:
В данном процессе
изменяются давление и объём воздуха, а
температура остаётся постоянной.
Следовательно, если начальные параметры
воздуха обозначить Р₁
и V₁,
а конечные как Р₂
и V₂ получаем
следующее соотношение:

Р₁V₁
= Р₂V₂

Когда
трубка обращена закрытым концом кверху,
воздух в ней находится под давлением
Р₁=
Р_атм
– h ( здесь и далее измеряем в мм.рт. ст.).
Если же трубку перевернуть, давление
воздуха в ней будет равно Р₂
= Р_атм
+ h .

Учитывая,
что V₁ =
Sℓ₁,
V₂ =
Sℓ₂,
где S – площадь сечения трубки, получаем:

(Р_атм
– h) Sℓ =
(Р_атм
+ h) Sℓ’,

Отсюда
находим атмосферное давление

Ответ.

Пример
3.2. В сосуде находится
смесь m = 7 г азота и m = 11г углекислого
газа при температуре Т = 290 К и давлении
Р = 1 атм. Найти плотность этой смеси,
считая газа идеальными.

Дано:
m₁=7
г=7∙10^-3кг;
m₂=11
г=11∙10^-3кг;
Т=290К; Р=1атм=10⁵Па.

Найти:
ρ.

Решение:
Давление газов в сосуде
известно. Если через Р₁
обозначить давление
азота, если бы углекислого газа не было,
а через Р₂ давление
углекислого газа, если бы не было азота
(так называемые парциальными давления),
то давление смеси газов Р будет согласно
закону Дальтона Р =
Р₁ +
Р₂.
Учитывая, что температура каждого газа
Т запишем для азота и кислорода уравнение
Менделеева-Клапейрона:

Складывая
эти выражения, получаем:

Отсюда
находим объём, занимаемый смесью газов

Плотность
смеси газов вычисляется по формуле

Ответ:

Пример
3.3. Кислород массой
m=10г
находится под давлением 200кПа при
температуре 280К. В результате изобарного
расширения газ занял объём 9л. Определите:
1) объём газа V₁
до расширения; 2) температуру газа T₂
после расширения; 3) плотность газа ρ₂
после расширения.

Дано:
M=32∙10^-3кг/моль;
m=10г=10∙10^-3кг;
р=200кПа=2∙10⁵Па=const;
Т₁=280К;
V₂=9г=9∙10^-3м³.

Найти:
1) V₁;
2) Т₂;
3) ρ₂.

Решение:
Объём газа до расширения найдём, согласно
уравнению Клапейрона-Менделеева,

,

откуда

Записав уравнение Клапейрона-Менделеева
для конечного состояния газа:

,

найдём искомую температуру

Плотность газа после расширения газа

.

Ответ:
1) V₁=3,64
л; 2) Т₂=693
К; 3) ρ₂=1,11
кг/м³.

Пример 3.3. В
цилиндре с площадью основания 100 см²
находится воздух. Поршень расположен
на высоте 50 см от дна цилиндра. На поршень
кладут груз массой 50 кг, при этом он
опускается на 10 см. Найти температуру
воздуха после опускания поршня, если
до его опускания давление было равно
101 кПа, а температура 12С.

Дано: S=100см²=1∙10^-2м²;h₁=50см=0,5
м;m=50кг; Δh=10см=0,1
мt;P₁=101∙10³Па; Т₁=12С=285
К.

Найти:
Т₂.

Решение:

Рассмотрим два состояния воздуха под
поршнем: до опускания поршня и после
его опускания. До опускания поршня
состояние воздуха характеризуется
параметрами Р₁,
V₁,
T₁,
после опускания поршня – параметрами
Р₂,
V₂,
T₂,
где V₁=Sh₁,
Р₂=Р₀+Р,

,
V₂=Sh₂,
или, поскольку h₂=h₁–
Δh,

V₂=S(h₁–
Δh).

Применим
к этим двум состояниям формулу Клапейрона:

,

откуда

(1)

Подставим
в формулу (1) выражения для Р₁,
V₁,
Р₂
и V₂:

;

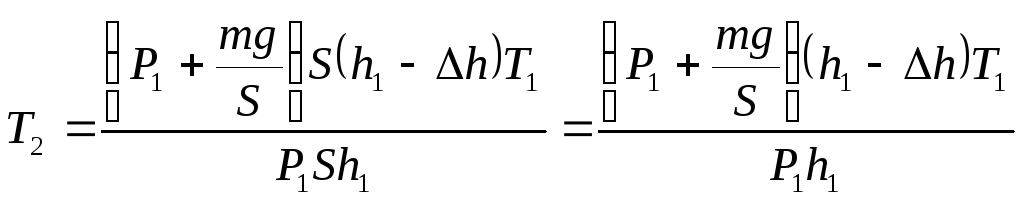
Ответ:
Т₂=338К

Пример 3.3. Имеются
два сосуда с газом: один вместимостью
3 л, другой 4 л. В первом сосуде газ
находится под давлением 202 кПа, а во
втором 101 кПа. Под каким давлением будет
находиться газ, если эти cосуды соединить
между собой? Считать, что температура
в сосудах одинакова и постоянна.

Дано: V₁=3л=3∙10^–3м³;V₂=4л=4∙10^–3м³;Р₁=202кПа=202∙10³Па; Р₂=101кПа=101∙10³Па.

Найти:
Р.

Решение:

По закону Дальтона,

Р
= Р₃
+ Р₄ (1)

Так
как процесс изотермический, то парциальное
давление газа в каждом сосуде можно
найти по закону Бойля-Мариотта:

Р₁V₁
=
Р₃V,
Р₂V₂
=
Р₄V,

где
V=V₁+V₂.
Тогда парциальное давление газа в каждом
из сосудов после их соединения

,

, (2)

Подставляем
выражения (2) в (1):

Ответ:
Р=141 Па

Пример 3.3. В
баллоне содержатся сжатый газ при
температуре t₁
= 27С
и давлении p₁
= 4 МПа. Каково будет давление, если из
баллона выпустить

Δm
= 0,4m
массы газа, а температуру понизить до
t₂
= 17С?

Дано: Т₁=27С
=300 К;Р₁=4МПа=4∙10⁶
Па;Δm
= 0,4m;
Т₂=17С
=290 К Найти:
Р.

Решение: Рассмотрим
два состояния газа: до разрежения и
после, когда осталось1-n массы m газа.
Параметры каждого из этих состояний
связаны уравнением Менделеева-Клапейрона:

,

где
Р₁,
Т₁,
Р₂,
Т₂
– соответственно давление и температура
газа до и после выпуска; m – масса газа;
М – молярная масса; V – объем.

Разделив
почленно первое равенство на второе,
получим:

,

oткуда

(1)

Ответ:
Р₂
= 2,310⁶
Па = 2,3 МПа.

Пример
3.3. Найти максимально
возможную температуру идеального газа
в процессе P = P₀
– αV²,
где P₀,
α – положительные постоянные.

Дано:
P = P₀
– αV²;
P₀, α
– const

Найти:
T_max.

Решение:
Для нахождения максимальной температуры
необходимо получить явную зависимость
последней от параметров и исследовать
эту зависимость на экстремум. Так как
газ является идеальным, выразим давление
из уравнения Менделеева-Клапейрона и
подставим его в уравнение процесса

Отсюда
выражаем температуру

Условие экстремума
,
которое сводится к выражению.

Решая
данное уравнение, получаем значение
объёма, при котором температура принимает
экстремальное значение
.
Исследуя знак второй производной, приходим к выводу, что при данном
значении объёма температура газа будет
идеальной. Подставляя выражение для
объёма в выражение для температуры при
данном процессе, получаем:

Ответ:

Пример
3.3. В сосуде
вместимостью V=5л
находится кислород массой m=15г.
определите: 1) концентрацию молекул
кислорода в сосуде; 2) число N
молекул газа в сосуде.

Дано:
V=5л=5∙10^-3м³;
M=32∙10^-3кг/моль;
m=15г=1,5∙10^-2кг.

Найти:
1) n; 2) N.

Решение:
Записав
уравнение Клапейрона-Менделеева

(1)

И
уравнение состояния идеального газа

Р=nkT
(2)

И
поделив (1) на (2), найдём искомую концентрацию
молекул кислорода в сосуде

.

Концентрация
молекул

,

Откуда
искомое число молекул газа в сосуде

N=nV.

Ответ:
1)
n=5,64∙10²⁵
м^-3;
2) N=2,82∙10²³.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Как изменяется температура газа при расширении

Зависимость температуры газа от изменения объема объясняется, прежде всего, изначальным физическим смыслом самого понятия температуры, которое связано с интенсивностью движения частиц газа.

Из курса молекулярной физики известно, что температура тела, несмотря на то что она является макроскопической величиной, связана, в первую очередь, с внутренним строением тела. Как известно, частицы любого вещества находятся в постоянном движении. Вид данного движения зависит от агрегатного состояния вещества.

Если это твердое тело, то частицы колеблются в узлах кристаллической решетки, а если это газ, то частицы свободно перемещаются в объеме вещества, соударяясь друг с другом. Температура вещества пропорциональна интенсивности движения. С точки зрения физики, это означает, что температура прямо пропорциональна кинетической энергии частиц вещества, которая, в свою очередь, определяется величиной скорости движения частиц и их массой.

Чем больше температура тела, тем больше средняя кинетическая энергия частиц. Этот факт отражается в формуле для кинетической энергии идеального газа, равной произведению концентрации частиц, постоянной Больцмана и температуры.

Представьте себе внутреннее строение газа. Газ можно считать идеальным, что означает абсолютную упругость столкновений молекул друг с другом. Газ имеет определенную температуру, то есть определенную величину кинетической энергии частиц. Каждая частица ударяется не только с другой частицей, но и со стенкой сосуда, ограничивающего объем вещества.

Если объем газа увеличивается, то есть газ расширяется, то количество столкновений частиц со стенками сосуда и друг с другом уменьшается из-за увеличения свободного пробега каждой молекулы. Уменьшение количества столкновений ведет к спаду давления газа, однако общая средняя кинетическая энергия вещества не меняется, ибо процесс соударения частиц никак не влияет ее величину. Таким образом, при расширении идеального газа температура не изменяется. Данный процесс называется изотермическим, то есть процессом с постоянной температурой.

Обратите внимание, что данный эффект постоянства температуры при расширении газа основан на предположении его идеальности, а также на том, что при соударении частиц со стенками сосуда частицы не теряют энергию. Если же газ не идеальный, то при его расширении уменьшается количество столкновений, приводящих к потере энергии, спад температуры становится менее резким. Практически данная ситуации соответствует термостатированию вещества газа, при котором снижаются энергетические потери, вызывающие уменьшение температуры.

Видео по теме