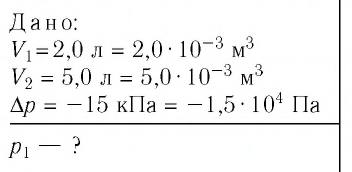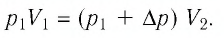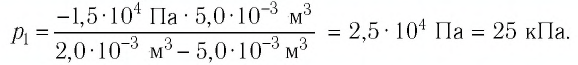Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 2 сентября 2021 года; проверки требуют 3 правки.
| Статья является частью одноименной серии. |
| Тепловые процессы |
|---|
 |
|
| См. также «Физический портал» |
Изохо́рный, или изохори́ческий проце́сс (от др.-греч. ἴσος — «равный» и χώρος — «место») — термодинамический изопроцесс, который происходит при постоянном объёме. Для осуществления изохорного процесса в газе или жидкости достаточно нагревать или охлаждать вещество в сосуде неизменного объёма.
При изохорическом процессе давление идеального газа прямо пропорционально его температуре (см. Закон Шарля). В реальных газах закон Шарля выполняется приближённо.
На графиках в координатах состояния (



История[править | править код]
Иллюстрация зависимости давления от температуры при постоянном объёме
Наиболее часто первые исследования изохорного процесса связывают с Гийомом Амонтоном. В своей работе «Парижские мемуары» в 1702 году он описал поведение газа в фиксированном объёме[Комм 1] внутри так называемого «воздушного термометра». Жидкость в нём находится в равновесии под воздействием давления газа в резервуаре и атмосферным давлением. При нагревании давление в резервуаре увеличивается, и жидкость вытесняется в выступающую трубку. Зависимость между температурой и давлением была установлена в виде[1][Комм 2]:
В 1801 году Джон Дальтон в двух своих эссе опубликовал эксперимент, в котором установил, что все газы и пары, исследованные им при постоянном давлении, одинаково расширяются при изменении температуры, если начальная и конечная температура одинакова[2][3][4]. Данный закон получил название закона Гей-Люссака, так как Гей-Люссак вскоре провёл самостоятельные эксперименты и подтвердил одинаковое расширение различных газов, причём получив практически тот же самый коэффициент, что и Дальтон[4]. Впоследствии он же объединил свой закон с законом Бойля — Мариотта[5], что позволило описывать в том числе и изохорный процесс.
Термодинамика процесса[править | править код]
График изохорного процесса на диаграмме в координатах
Из определения работы следует, что элементарная работа при термодинамическом процессе равна[6][Комм 3]:
Чтобы определить полную работу процесса проинтегрируем данное выражение[6]:
но, поскольку объём неизменен, то есть 
Это же можно показать на графике изохорного процесса. С математической точки зрения, работа процесса равна площади такого графика[6]. Но график изохорного процесса является прямой перпендикулярной к оси объёма. Таким образом, площадь под ним равна нулю.
Изменение внутренней энергии идеального газа можно найти по формуле[8]:
- где
— число степеней свободы, которое зависит от количества атомов в молекуле газа (3 — для одноатомной (например, неон), 5 — для двухатомной (например, кислород) и 6 — для трёхатомной и более (например, молекула углекислого газа)).
Из определения и формулы теплоёмкости формулу для внутренней энергии можно переписать в виде[8]:
- где
— молярная теплоёмкость при постоянном объёме.
Используя первое начало термодинамики можно найти количество теплоты при термодинамическом процессе[9]:
Но при изохорном процессе газ не выполняет работу[7]. То есть, имеет место равенство:
таким образом, вся теплота, которую получает газ, идёт на изменение его внутренней энергии.
Энтропия при изохорном процессе[править | править код]
Поскольку в системе при изохорном процессе происходит теплообмен с внешней средой, то происходит изменение энтропии. Из определения энтропии следует[10]:
- где
— элементарное количество теплоты[11][Комм 3].
Выше была выведена формула для определения количества теплоты. Если её переписать в дифференциальном виде[12][Комм 4]:
- где
— количество вещества,
— молярная теплоемкость при постоянном объёме.
Микроскопическое изменение энтропии при изохорном процессе можно определить по формуле[12]:
Или, если проинтегрировать последнее выражение, полное изменение энтропии в этом процессе[12]:
В данном случае выносить выражение молярной теплоемкости при постоянном объёме за знак интеграла нельзя, поскольку она является функцией, которая зависит от температуры.
Практическое применение теории изохорного процесса[править | править код]

При идеальном цикле Отто, который приближённо воспроизведён в бензиновом двигателе внутреннего сгорания, такты 2—3 и 4—1 являются изохорными процессами.
Работа, совершаемая на выходе двигателя, равна разности работ, которую произведёт газ над поршнем во время третьего такта (то есть рабочего хода), и работы, которую затрачивает поршень на сжатие газа во время второго такта. Так как в двигателе, работающем по циклу Отто используется система принудительного зажигания смеси, то происходит сжатие газа в 7—12 раз[13].
Анимация классического двигателя Стирлинга с конфигурацией бета-типа, при которой рабочий и вытеснительный поршни скомпонованы в одном цилиндре
В цикле Стирлинга также присутствуют два изохорных такта. Для его осуществления в двигателе Стирлинга добавлен регенератор. Газ, проходя через наполнитель в одну сторону, отдаёт тепло от рабочего тела к регенератору, а при движении в другую сторону отдаёт его обратно рабочему тему[14]. Идеальный цикл Стирлинга достигает обратимости и тех же величин КПД что и цикл Карно[15]. Изохорный процесс – также процесс, протекающий в автоклавах и пьезометрах
См. также[править | править код]
- Молекулярно-кинетическая теория
- Изотермический процесс
- Изобарный процесс
Примечания[править | править код]
Комментарии[править | править код]
Источники[править | править код]
- ↑ Кудрявцев, 1956, с. 292—293.
- ↑ J. Dalton, 1802, с. 550—574.
- ↑ J. Dalton, 1802, с. 595—602.
- ↑ 1 2 Кудрявцев, 1956, с. 393.
- ↑ Кудрявцев, 1956, с. 396.
- ↑ 1 2 3 Савельев, 2001, с. 19—21.
- ↑ 1 2 Савельев, 2001, с. 37.
- ↑ 1 2 Савельев, 2001, с. 61.
- ↑ Савельев, 2001, с. 17.
- ↑ Савельев, 2001, с. 93.
- ↑ Савельев, 2001, с. 18.
- ↑ 1 2 3 Сивухин, 1975, с. 128.
- ↑ Кириллин, 2008.
- ↑ Romanelli, 2017.
- ↑ Крестовников А. Н., Вигдорович В. Н., Химическая термодинамика, 1973, с. 63.
Список литературы[править | править код]
- Кириллин В. А., Сычёв В. В., Шейндлин А. Е. Техническая термодинамика: учебник для вузов. — М.: Издательство МЭИ, 2008. — 496 с. Архивная копия от 24 ноября 2011 на Wayback Machine
- Крестовников А. Н., Вигдорович В. Н. Химическая термодинамика. — 2-е изд., испр. и доп. — М.: Металлургия, 1973. — 256 с.
- Кудрявцев П. С. История физики. — М.: Гос. учебно-педагог. изд-во, 1956. — Т. 1. От античной физики до Менделеева. — 564 с. — 25 000 экз.
- Ландау Л. Д., Лифшиц Е. М. Статистическая физика. Часть 1. — Издание 5-е. — М.: Физматлит, 2005. — 616 с. — («Теоретическая физика», том V). — ISBN 5-9221-0054-8.
- Савельев И. В. Курс общей физики:Молекулярная физика и термодинамика. — М.: Астрель, 2001. — Т. 3. — 208 с. — 7000 экз. — ISBN 5-17-004585-9.
- Сивухин Д. В. Общий курс физики. — М.: Наука, 1975. — Т. II. Термодинамика и молекулярная физика. — 519 с.
- J. Dalton. 2 // Memoirs of the Literary and Philosophical Society of Manchester. — 1802. — Т. 5. — 701 с.
- Alejandro Romanelli. Alternative thermodynamic cycle for the Stirling machine. — Montevideo, Uruguay: Instituto de Física, Facultad de Ingeniería, 2017.
Печатать книгу
| Сайт: | Профильное обучение |
| Курс: | Физика. 10 класс |
| Книга: | § 6. Изотермический, изобарный и изохорный процессы |
| Напечатано:: | Гость |
| Дата: | Пятница, 19 Май 2023, 19:28 |
Оглавление
- Изотермический, изобарный и изохорный процессы
- Изотермический процесс
- Изобарный процесс
- Изохорный процесс
- Примеры решения задач
- Упражнение 5
Свойство газов существенно изменять предоставленный им объём широко используют в тепловых двигателях. Анализируя процессы, происходящие с газом в этих устройствах, важно знать, каким законам подчиняются газы и каковы условия применимости этих законов.
Процессы в газах часто происходят так, что изменяются только два параметра из пяти (p, V, T, m, M). Если при постоянных массе и молярной массе ещё один из макропараметров (p, V, T), входящих в уравнение состояния идеального газа, не изменяется, то такие процессы называют изопроцессами.
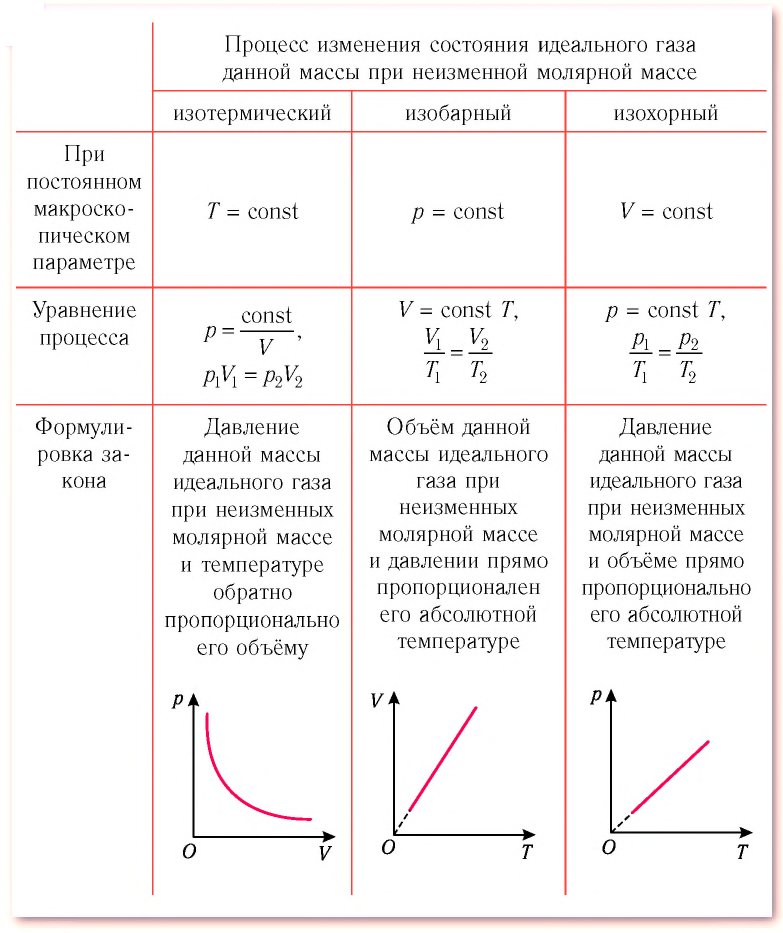
Изотермический процесс. Процесс изменения состояния физической системы при постоянной температуре (T = const) называют изотермическим.
Если при переходе из начального состояния в конечное масса и молярная масса идеального газа не изменяются, то из уравнения Клапейрона–Менделеева следует:
Давление данной массы газа при постоянных молярной массе и температуре обратно пропорционально его объёму.
Это утверждение называют законом Бойля–Мариотта.
Справедливость закона Бойля–Мариотта можно продемонстрировать экспериментально, используя установку, представленную на рисунке 18 в § 5.
Если медленно изменять объём газа, находящегося в сосуде, то вследствие теплообмена с окружающей средой можно поддерживать температуру газа в сосуде практически постоянной. При этом уменьшение объёма газа при вращении винта 3 повлечёт за собой увеличение его давления и некоторое незначительное увеличение температуры. И наоборот, увеличение объёма приведёт к уменьшению давления и некоторому незначительному уменьшению температуры газа*.
От теории к практике
1. Почему пузырьки воздуха, находящиеся в жидкости, поднимаясь вверх, увеличиваются в объёме?
2. Если, не отрываясь, выпить из пластиковой бутылки газированную воду, то можно обнаружить, что бутылка деформируется. Почему?
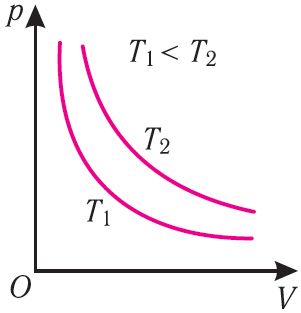
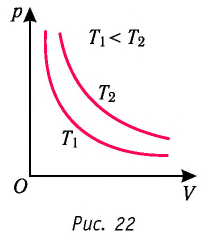
График изотермического процесса, совершаемого идеальным газом, в координатах (p, V) представляет собой гиперболу (рис. 22). В физике такую кривую называют изотермой. Разным значениям температуры газа соответствуют разные изотермы. Согласно соотношениям (6.1) для одинаковых объёмов газов с одинаковыми количествами вещества и разными температурами чем больше давление, тем выше температура (рис. 22).
Многочисленные опыты показали, что исследованные газы подчиняются закону Бойля–Мариотта тем точнее, чем меньше их плотность. При значительном увеличении давления газа этот закон перестаёт выполняться.
От теории к практике
Изобразите графики изотермического процесса в координатах (p, T) и (V, T).
Интересно знать
Лёгкие расположены в грудной клетке, объём которой при дыхании периодически изменяется благодаря работе межрёберных мышц и диафрагмы. К огда грудная клетка расширяется, давление воздуха в лёгких становится меньше атмосферного, и воздух через воздухоносные пути устремляется в лёгкие — происходит вдох. При выдохе объём грудной клетки уменьшается, что вызывает уменьшение объёма лёгких. Давление воздуха в них становится выше атмосферного, и воздух из лёгких устремляется в окружающую среду.
* Незначительное изменение температуры газа принципиально необходимо для теплообмена с термостатом — передача тепла возможна только при разных температурах тел. ↑
Изобарный процесс. Процесс изменения состояния газа при постоянном давлении (p = const) называют изобарным.
В 1802 г. французский учёный Жозеф Гей-Люссак (1778–1850) рассмотрел этот процесс для воздуха, водорода, кислорода и азота.
Если при переходе из начального состояния в конечное масса и молярная масса газа не изменяются, то объём газа, как следует из уравнения Клапейрона–Менделеева:
Объём данной массы газа при постоянных молярной массе и давлении прямо пропорционален абсолютной температуре.
Это утверждение называют законом Гей-Люссака.
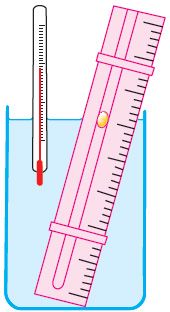
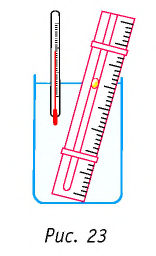
Справедливость закона Гей-Люссака можно продемонстрировать экспериментально, используя установку, представленную на рисунке 23. Жидкость в сосуде находится в тепловом равновесии с тонкой трубкой, заполненной воздухом, запертым капелькой масла. При увеличении температуры жидкости объём воздуха, находящегося в трубке под капелькой масла, возрастает и капелька движется вверх. При уменьшении температуры объём воздуха уменьшается — и капелька движется вниз.
От теории к практике
Можно ли считать расширение газа при медленном нагревании его в цилиндре с подвижным поршнем изобарным процессом?
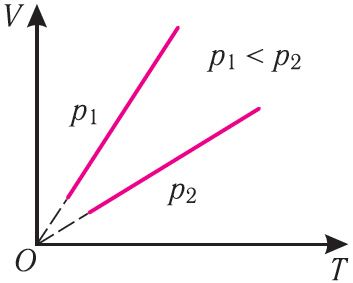
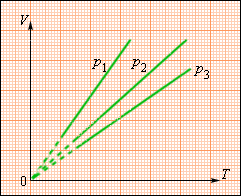
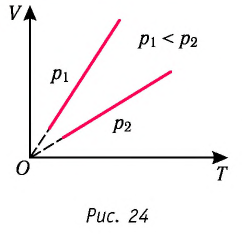
Поскольку V ~ T, то в координатах (V, T) график изобарного процесса, совершаемого идеальным газом, представляет собой прямую линию, продолжение которой проходит через начало координат (рис. 24). Эту линию называют изобарой.
Изобара реальных газов не может быть продлена до нулевого значения температуры (на графике пунктирная линия), потому что при низких температурах все газы существенно отличаются от модели «идеальный газ» и при дальнейшем уменьшении температуры превращаются в жидкости.
В одних и тех же координатах (V, T) можно построить несколько изобар, которые соответствуют разным давлениям данной массы идеального газа при неизменной молярной массе. Анализ соотношений (6.2) позволяет сделать вывод, что большему давлению соответствует меньший наклон изобары к оси температур (см. рис. 24).
От теории к практике
Изобразите графики изобарного процесса в координатах (p, V) и (p, T).
Изохорный процесс. Процесс изменения состояния газа при постоянном объёме (V = const) называют изохорным.
Впервые этот процесс рассмотрел в 1787 г. французский учёный Жак Шарль (1746–1823)*.
Если при переходе из начального состояния в конечное масса и молярная масса идеального газа не изменяются, то давление газа, как следует из уравнения Клапейрона–Менделеева:
Давление данной массы газа при постоянных молярной массе и объёме прямо пропорционально абсолютной температуре.
Это утверждение называют законом Шарля.
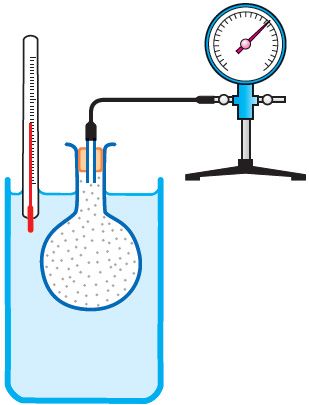
Справедливость закона Шарля можно продемонстрировать экспериментально, используя установку, представленную на рисунке 25. Колба, наполненная воздухом и соединённая с манометром, находится в тепловом равновесии с жидкостью в сосуде. При увеличении температуры жидкости давление воздуха в колбе возрастает, а при уменьшении температуры — давление воздуха уменьшается.
От теории к практике
Идеальный газ определённой массы изохорно охлаждают так, что его температура уменьшается от t1 = 327 °С до t2 = 7 °С. Во сколько раз уменьшается давление газа?
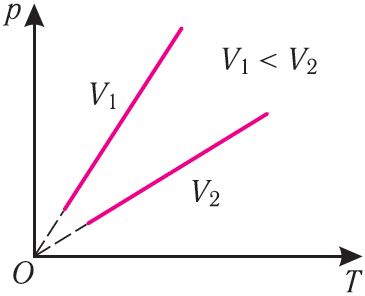
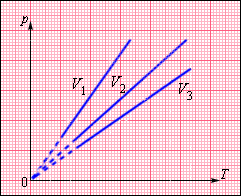
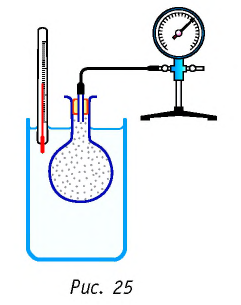
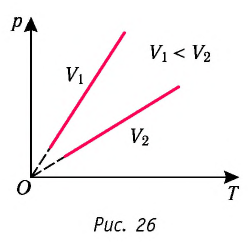
В координатах (p, T) график изохорного процесса, совершаемого идеальным газом, представляет собой прямую линию, продолжение которой проходит через начало координат (рис. 26). Эту линию называют изохорой.
Как и в случае изобарного процесса, изохора реальных газов не может быть продлена до нулевого значения температуры.
В одних и тех же координатах (p, T) можно построить несколько изохор, соответствующих разным объёмам данной массы газа при неизменной молярной массе. Анализ соотношений (6.3) показывает, что большему объёму соответствует меньший наклон изохоры к оси температур (см. рис. 26).
От теории к практике
Изобразите графики изохорного процесса в координатах (p, V) и (V, T).
1. Как связаны давление и объём идеального газа при изотермическом процессе?
2. Как связаны объём и абсолютная температура идеального газа при изобарном процессе?
3. Как связаны давление и абсолютная температура идеального газа при изохорном процессе?
4. При выполнении каких условий справедлив каждый из законов изопроцессов в реальном газе?
5. Объём идеального газа определённой массы и неизменного химического состава изобарно увеличили в b = 1,5 раза, а затем давление газа изохорно уменьшили в c = 3 раза.
а) Как изменилась абсолютная температура газа в результате первого процесса?
б) Как изменилась абсолютная температура газа в результате второго процесса?
в) Во сколько раз начальная абсолютная температура газа отличается от его конечной температуры?
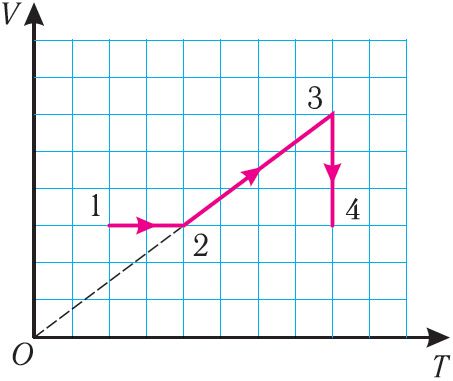
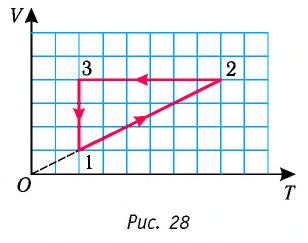
6. На рисунке 27 представлен график трёх процессов изменения состояния идеального газа определённой массы и неизменного химического состава.
а) Какому процессу соответствует участок 1 2 графика? Во сколько раз увеличилось давление газа в этом процессе?
б) Какому процессу соответствует участок 2 3 графика? Во сколько раз увеличились объём и абсолютная температура газа в этом процессе?
в) Какому процессу соответствует участок 3 4 графика? Как и во сколько раз изменились объём и давление газа в этом процессе?
г) Во сколько раз следует уменьшить температуру газа, чтобы изохорно перевести газ из состояния 4 в состояние 2?
* Несмотря на то что Шарль не опубликовал результаты своих исследований, история физики отдаёт приоритет открытия ему. ↑
Примеры решения задач
Решение. На участке 1 2 объём газа прямо пропорционален абсолютной температуре, следовательно, процесс перехода газа из состояния 1 в состояние 2 является изобарным. Из графика следует, что в состоянии 2 температура и объём газа больше в 4 раза, чем в состоянии 1. Следовательно, в процессе изобарного расширения некоторой массы газа из состояния 1 в состояние 2 температура и объём газа увеличились. Это можно записать таким образом:
переход ,
,
,
,
происходит изобарное нагревание газа.
В процессе перехода газа из состояния 2 в состояние 3 остаётся постоянным объём (процесс изохорный), а температура газа уменьшается в 4 раза. Из соотношения (6.3) следует, что при изохорном охлаждении давление газа уменьшается пропорционально его абсолютной температуре. Поэтому можно записать:
переход ,
,
,
происходит изохорное охлаждение газа.
Процесс перехода газа из состояния 3 в состояние 1 — изотермический. При этом объём газа уменьшается в 4 раза, что влечёт за собой, согласно закону Бойля–Мариотта, увеличение давления газа в 4 раза:
переход ,
,
происходит изотермическое сжатие газа.
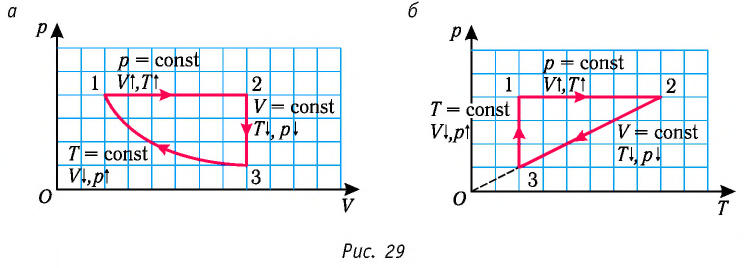
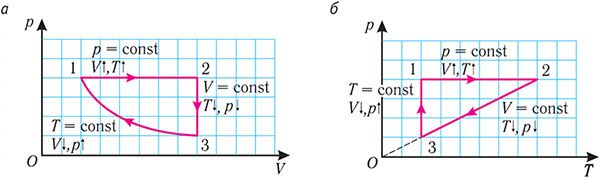
Опираясь на сделанные выводы, представим все три процесса в координатах (p, V) и (p, T) (рис. 29, а, б).
Пример 2. При изотермическом расширении идеального газа определённой массы его объём увеличился от V1 = 2,0 л до V2 = 5,0 л, а давление уменьшилось на Δp = –15 кПа. Определите первоначальное давление газа.
Дано:
V1 = 2,0 л = 2,0 · 10–3 м3
V2 = 5,0 л = 5,0 · 10–3 м3
Δp = –15 кПа = –1,5 · 104 Па
р1 — ?
Решение: Так как температура и масса газа не изменяются, то его начальное и конечное состояния связаны законом Бойля–Мариотта, т. е. . С учётом того, что
, получим:
.
Откуда .
.
Ответ: .
Пример 3. В двух сосудах вместимостью V1 = 20 л и V2 = 30 л находятся химически не реагирующие идеальные газы, давления которых p1 = 1,0 МПа и p2 = 0,40 МПа соответственно. Определите давление газов в сосудах после того, как их соединили тонкой короткой трубкой. Температура газов до и после соединения сосудов одинаковая.
Дано:
V1 = 20 л = 2,0 · 10-2 м3
V2 = 30 л = 3,0 · 10-2 м3
p1 = 1,0 МПа = 1,0 · 106 Па
p2 = 0,40 МПа = 4,0 · 105 Па
T = const
р — ?
Решение: Давление смеси газов равно сумме парциальных давлений (закон Дальтона): . Найдём парциальное давление каждого газа после соединения сосудов. Так как температура и массы газов не изменяются, то начальное и конечное состояния каждого газа связаны законом Бойля–Мариотта, т. е.
,
.
Следовательно, парциальные давления газов после соединения сосудов: ,
. Тогда
.
Ответ: p = 0,64 МПа.
Упражнение 5
1. При изобарном увеличении температуры идеального газа, находящегося в герметично закрытом цилиндре, на ΔT = 60,0 К его объём увеличился в β = 1,21 раза. Определите начальную абсолютную температуру газа.
2. Изобразите графически процесс изобарного охлаждения определённой массы идеального газа в координатах (p, T); (V, T); (V, p).
3. Идеальный газ определённой массы сначала изобарно расширили, а затем изотермически сжали до первоначального объёма. Изобразите графически эти процессы в координатах (V, T); (p, V).
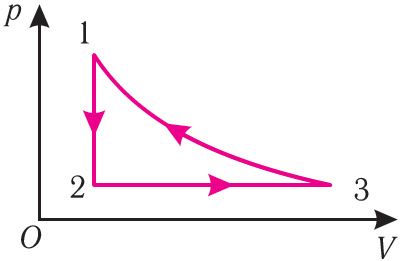
4. На рисунке 30 представлен график изменения состояния определённой массы идеального газа. (Переход 3 1 осуществляется при неизменной температуре.) Изобразите графически этот процесс в координатах (T, V) и (p, T).
5. При температуре t1 = –3,0 °С манометр на баллоне со сжатым кислородом показывал давление p1 = 1,8 · 106 Па, а при температуре t2 = 27 °С — давление p2 = 2,0 · 106 Па. Определите, была ли утечка газа из баллона.
6. В герметичном сосуде, заполненном воздухом (), лежит полый металлический шарик, диаметр которого d = 4,0 см, а масса m = 0,64 г. Определите минимальное значение давления воздуха, накачиваемого в сосуд, при котором бы шарик поднялся вверх, если температура t = 17 °С остаётся постоянной.
7. Идеальный газ, давление которого p1 = 4 · 105 Па, занимал объём V1 = 2 л. Сначала газ изотермически расширили до объёма V2 = 8 л, а затем изохорно нагрели, в результате чего его абсолютная температура увеличилась в α = 3 раза. Определите давление р3 газа в конце процесса, если при переходе из начального состояния в конечное масса газа оставалась неизменной.
Соотношение p=nkT – это формула, связывающая значение давления газа с его температурой и концентрацией молекул на единицу объема.
Они взаимодействуют со стенками сосуда посредствам упругих соударений. Данное выражение можно записать иначе, учитывая параметрические состояния объема V, давления p, температуры T и количества вещества ν. Применим неравенства:
n=NV=νNАV=mMNAV.
Значением N является количество молекул данного сосуда, NА – постоянной Авогадро, m – массой газа в емкости, М – молярной массой газа. Исходя из этого, формула примет вид:
pV=νNАkT=mMNАkT.
Произведение постоянной Авогадро NА на постоянную Больцмана k называют универсальной газовой постоянной и обозначают R.
По системе СИ имеет значение R=8,31 Дж/моль·К.
Соотношение pV=νRT=mMRT получило название уравнения состояния идеального газа.
Один моль газа обозначается pV=RT.
При температуре Tн=273,15 К (0 °C) и давлении ρн=1 атм=1,013·105 Па говорят о нормальных условиях состояния газа.
Из уравнения видно, что один моль газа при нормальных условиях занимает один и тот же объем, равный v0=0,0224 м3/моль=22,4 дм3/моль. Выражение получило название закона Авогадро.
Если имеется смесь невзаимодействующих газов, то формулу запишем как:
pV=ν1+ν2+ν3+…RT,
где ν1, v2, v3 обозначает количество вещества каждого из них.
Еще в ХХ веке Б. Клапейрон получил уравнение, показывающее связь между давлением и температурой:
pV=νRT=mMRT.
Впоследствии оно было записано Д.И. Менделеевым. Позже его назвали уравнением Клапейрона-Менделеева.
Задолго до получения уравнения состояния идеального газа на основе молекулярно-кинетической теории поведения газов изучались в различных условиях экспериментально. То есть уравнение pV=νRT=mMRT служит обобщением всех опытных фактов.
Газ принимает участие в процессах с постоянно изменяющимися параметрами состояния: (p, Vи T).
При протекании процессов медленно, система находится в состоянии, близком к равновесному. Процесс получил название квазистатического.
Соотнеся с происхождением процессов в нашем времени, то его протекания нельзя считать медленными.
Обычное время для разрежения и сжатия газа сотни раз в секунду. Это рассматривается как квазистатический процесс. Они изображаются с помощью диаграммы состояний параметров, где каждая из точек показывает равновесное состояние.
При неизменном одном параметре из (p, V или T) процесс принято называть изопроцессом.
Изотермический процесс (T=const)
При протекании квазипроцесса с постоянным параметром Т говорят об изотермическом процессе.
Из уравнения pV=νRT=mMRT имеем, что неизменные температура Т с количеством вещества ν – это постоянное состояние для произведения значения давления газа p на его объем V:
pV=const.
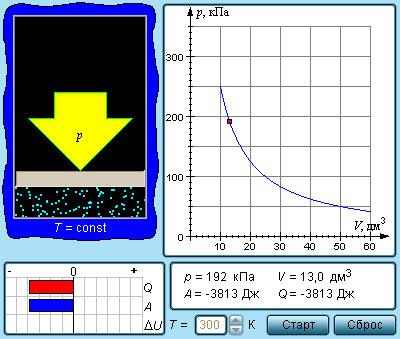
Рисунок 3.3.1. Модель изотермического процесса.
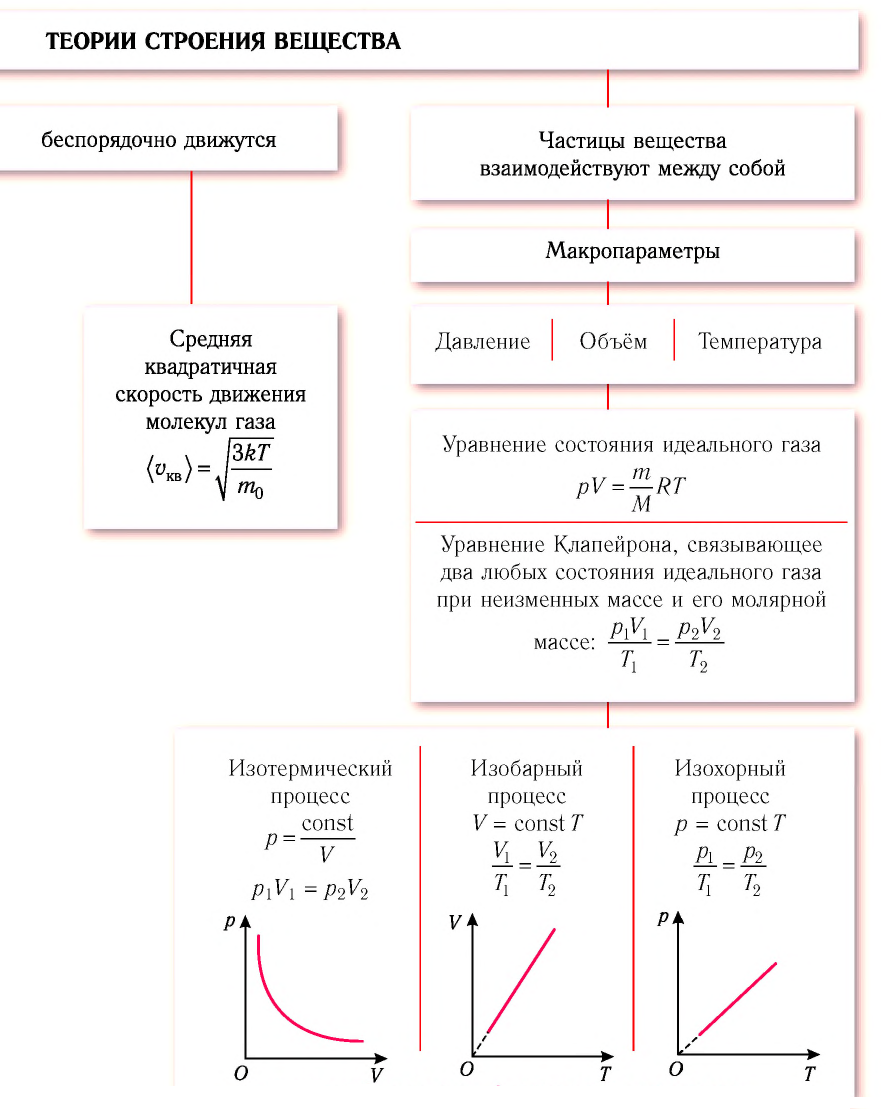
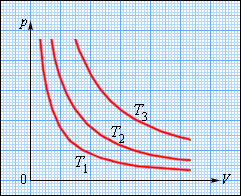
Изображение изотермических процессов на плоскости (p, V) предусматривает различные значения температур Т гипербол p~1V. Они получили название изотермов.
Коэффициент пропорциональности данного отношения увеличивается с ростом Т. Рисунок 3.3.2 показывает, что при меньшей Т подразумевает уменьшение V. В 1662 году было получено уравнение изотермического процесса Р. Бойлем, а позднее Э. Мариоттом в 1676 году. Отсюда и сложное его название – закон Бойля-Мариотта.
Рисунок 3.3.2. Семейство изотерм на плоскости (p, V). T3>T2>T1.
Изохорный процесс (V=const)
Изохорный процесс – это квазипроцесс нагревания или охлаждения газа с постоянным параметром V и неизменным количеством вещества ν емкости.
Уравнение состояния идеального газа говорит о том, что изменение p газа происходит прямо пропорционально абсолютной температуры, тогда p~T или pT=const.
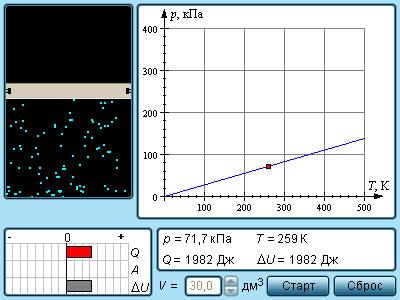
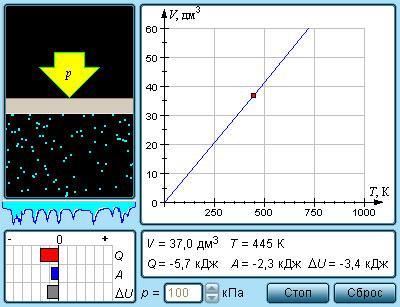
Рисунок 3.3.3. Модель изохорного процесса.
Изохорные процессы плоскости p, T с количеством вещества ν и различными значениями параметра V изображаются прямыми линиями – изохорами.
Рисунок 3.3.4 говорит о наличии меньшего наклона оси Т при увеличении параметра V.
Рисунок 3.3.4. Семейство изохор на плоскости p, T. V3>V2>V1.
Экспериментальную зависимость параметра p от Т довелось исследовать физику Ж. Шарлю в 1787 году. Позже уравнения изохорного процесса получило название закона Шарля.
Его запись принимает вид
p=p0T0T=p0αT с p0,
являющимся значением давления газа при T=T0=273,15 К (т.е. при температуре 0 °C). Температурный коэффициент давления обозначается α=1273,15К-1.
Изобарный процесс (p=const)
Изобарный процесс – это квазистатический процесс, протекающий с постоянным параметром p.
Уравнение такого состояния с неизменным количеством вещества ν запишется как
VT=const или V=V0αT, где V0 – объем газа при температуре 0 °C. Температурный коэффициент объемного расширения газов равняется α=1273,15К-1.
Рисунок 3.3.5. Модель изобарного процесса.
Изобарные процессы плоскости (V, T) имеют разные значения p и изображены прямыми линиями (изобарами), изображенными на рисунке 3.3.6.
Рисунок 3.3.6. Семейство изобар на плоскости (V, T). p3>p2>p1.
Данное уравнение с зависимостью параметра V от T с неизменным давлением довелось исследовать Ж. Гей-Люссаку в 1862 году. Оно получило название закона Гей-Люссака.
Законы Бойла-Мариотта, Шарля и Гей-Люссака объясняются с помощью молекулярно-кинетической теории газов, так как являются следствиями уравнения состояния идеального газа.
Содержание:
Изотермический, изобарный и изохорный процессы:
Свойство газов существенно изменять предоставленный им объём широко используют в тепловых двигателях. Анализируя процессы, происходящие с газом в этих устройствах, важно знать, каким законам подчиняются газы и каковы условия применимости этих законов.
Процессы в газах часто происходят так, что изменяются только два параметра из пяти
Изотермический процесс
Процесс изменения состояния физической системы при постоянной температуре 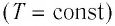
Если при переходе из начального состояния в конечное масса и молярная масса идеального газа не изменяются, то из уравнения Клапейрона—Менделеева следует:
Давление данной массы газа при постоянных молярной массе и температуре обратно пропорционально его объёму.
Это утверждение называют законом Бойля—Мариотта.
Справедливость закона Бойля—Мариотта можно продемонстрировать экспериментально, используя установку, представленную на рисунке 18 в § 5.
Если медленно изменять объём газа, находящегося в сосуде, то вследствие теплообмена с окружающей средой можно поддерживать температуру газа в сосуде практически постоянной. При этом уменьшение объёма газа при вращении винта 3 повлечёт за собой увеличение его давления и некоторое незначительное увеличение температуры. И наоборот, увеличение объёма приведёт к уменьшению давления и некоторому незначительному уменьшению температуры газа*.
* Незначительное изменение температуры газа принципиально необходимо для теплообмена с термостатом — передача тепла возможна только при разных температурах тел.
График изотермического процесса, совершаемого идеальным газом, в координатах 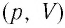
Многочисленные опыты показали, что исследованные газы подчиняются закону Бойля —Мариотта тем точнее, чем меньше их плотность. При значительном увеличении давления газа этот закон перестаёт выполняться.
Интересно знать:
Лёгкие расположены в грудной клетке, объём которой при дыхании периодически изменяется благодаря работе межрёберных мышц и диафрагмы. Когда грудная клетка расширяется, давление воздуха в лёгких становится меньше атмосферного, и воздух через воздухоносные пути устремляется в лёгкие — происходит вдох. При выдохе объём грудной клетки уменьшается, что вызывает уменьшение объёма лёгких. Давление воздуха в них становится выше атмосферного, и воздух из лёгких устремляется в окружающую среду.
Изобарный процесс
Процесс изменения состояния газа при постоянном давлении (р = const) называют изобарным.
В 1802 г. французский учёный Жозеф Гей-Люссак (1778-1850) рассмотрел этот процесс для воздуха, водорода, кислорода и азота.
Если при переходе из начального состояния в конечное масса и молярная масса газа не изменяются, то объём газа, как следует из уравнения Клапейрона—Менделеева:
Объём данной массы газа при постоянных молярной массе и давлении прямо пропорционален абсолютной температуре.
Это утверждение называют законом Гей-Люссака.
Справедливость закона Гей-Люссака можно продемонстрировать экспериментально, используя установку, представленную на рисунке 23. Жидкость в сосуде находится в тепловом равновесии с тонкой трубкой, заполненной воздухом, запертым капелькой масла. При увеличении температуры жидкости объём воздуха, находящегося в трубке под капелькой масла, возрастает и капелька движется вверх. При уменьшении температуры объём воздуха уменьшается — и капелька движется вниз.
Поскольку 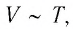
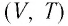
Изобара реальных газов не может быть продлена до нулевого значения температуры (на графике пунктирная линия), потому что при низких температурах все газы существенно отличаются от модели «идеальный газ» и при дальнейшем уменьшении температуры превращаются в жидкости.
В одних и тех же координатах 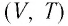
Изохорный процесс
Процесс изменения состояния газа при постоянном объёме (V = const) называют изохорным.
Впервые этот процесс рассмотрел в 1787 г. французский учёный Жак Шарль (1746-1823)*.
* Несмотря на то что Шарль не опубликовал результаты своих исследований, история физики отдаёт приоритет открытия ему.
Если при переходе из начального состояния в конечное масса и молярная масса идеального газа не изменяются, то давление газа, как следует из уравнения Клапейрона—Менделеева:
Давление данной массы газа при постоянных молярной массе и объёме прямо пропорционально абсолютной температуре.
Это утверждение называют законом Шарля.
Справедливость закона Шарля можно продемонстрировать экспериментально, используя установку, представленную на рисунке 25. Колба, наполненная воздухом и соединённая с манометром, находится в тепловом равновесии с жидкостью в сосуде. При увеличении температуры жидкости давление воздуха в колбе возрастает, а при уменьшении температуры — давление воздуха уменьшается.
В координатах 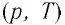
Как и в случае изобарного процесса, изохора реальных газов не может быть продлена до нулевого значения температуры.
В одних и тех же координатах 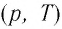
Пример №1
На рисунке 28 представлен график трёх процессов изменения состояния некоторой массы идеального газа. Как изменялись параметры газа на участках 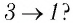
Решение. На участке 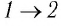
переход
происходит изобарное нагревание газа.
В процессе перехода газа из состояния 2 в состояние 3 остаётся постоянным объём (процесс изохорный), а температура газа уменьшается в 4 раза. Из соотношения (6.3) следует, что при изохорном охлаждении давление газа уменьшается пропорционально его абсолютной температуре. Поэтому можно записать:
переход
происходит изохорное охлаждение газа.
Процесс перехода газа из состояния 3 в состояние 1 — изотермический. При этом объём газа уменьшается в 4 раза, что влечёт за собой, согласно закону Бойля—Мариотта, увеличение давления газа в 4 раза:
- переход
происходит изотермическое сжатие газа.
Опираясь на сделанные выводы, представим все три процесса в координатах 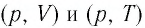
Пример №2
При изотермическом расширении идеального газа определённой массы его объём увеличился от 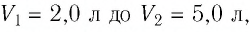
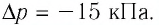
Решение. Так как температура и масса газа не изменяются, то его начальное и конечное состояния связаны законом Бойля—Мариотта, т. е. 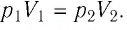
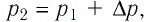
Откуда
Ответ:
Обобщение и систематизация определений:
- Твердые тела и их свойства в физике
- Строение и свойства жидкостей в физике
- Испарение и конденсация в физике
- Влажность воздуха в физике
- Уравнение состояния идеального газа
- Температура в физике
- Парообразование и конденсация
- Тепловое равновесие в физике
Мы продолжаем изучать наиболее распространенные газовые процессы. Сейчас мы рассмотрим изотермический, изохорный и адиабатный процессы.
Начнем с изотермического процесса. Одна из частей его названия – “термо” – сразу напоминает о термометре. Изотермический процесс – это процесс, происходящий при постоянной температуре.
Как такой процесс можно реализовать на практике, имея под рукой сосуд с газом? Сначала вспомним про первое начало термодинамики:
varDelta{U}=Q+A
Если мы намерены держать температуру на определенном уровне и не допускать каких-либо изменений этой величины, это означает, что также не будет меняться и внутренняя энергия. Посудите сами: нет изменений температуры – нет изменений средней кинетической энергии теплового движения молекул, которая как раз и определяет внутреннюю энергию системы, если речь идет об одноатомном идеальном газе. Таким образом, с левой стороны в приведенном выше уравнении окажется ноль:
0=Q+A
При изотермическом процессе вся работа, производимая над газом, должна быть равна количеству теплоты, которую система в итоге отдает окружающей среде:
boxed{-Q=A}
Ну и как это понимать? Передвигая поршень вниз, мы будем заставлять молекулы газа чаще соударяться друг с другом и со стенками сосуда, в связи с чем газ начнет нагреваться. Теплота, которую он будет генерировать, должна отдаваться окружающей среде, чтобы его температура все время оставалась постоянной.
Как же этого добиться на практике? Во-первых, поршень в сосуде нужно перемещать очень медленно, чтобы газ, действительно, успевал отдавать теплоту (если мы быстро передвинем поршень вниз, он не успеет это сделать и его температура изменится); во-вторых, нам следует поддерживать неизменную температуру окружающей среды. Если пространство вокруг сосуда сильно нагреется, газ уже не сможет отдавать теплоту как прежде и это опять же повлечет за собой изменение его температуры.
Чтобы этого не допустить, можно поместить контейнер с газом в водяной резервуар определенной температуры. Вода, как вы помните, обладает большой теплоемкостью, существенно нагреть ее очень трудно, поэтому она будет принимать теплоту от газа, практически не меняя свою температуру. А это-то нам и нужно.
Теперь посмотрим, как изотермический процесс будет выглядеть на pV-диаграмме. Мы можем воспользоваться уравнением Менделеева-Клапейрона, чтобы разобраться в этом:
pV=nu{RT}
p=dfrac{nu{RT}}{V}
Зависимость давления газа от его объема будет выражаться обратной пропорциональностью. При этом числитель дроби, стоящей справа, меняться никак не будет, поэтому его можно представить в виде константы (как уже упоминалось раньше, для всех изопроцессов важным условием является сохранение массы газа, а для изотермического процесса также не должна меняться и температура):
p=dfrac{const}{V}
Падение объема газа в какое-то количество раз при постоянной температуре будет означать рост его давления в такое же количество раз. Это еще одна формулировка закона Бойля-Мариотта, про который нам уже приходилось говорить. Так или иначе, подставляя разные значения в полученное выражение, мы можем построить график на pV-диаграмме, который будет выглядеть примерно так:
В математике такую кривую называют гиперболой. А физики от себя добавляют другое название – изотерма, так как на pV-диаграмме полученная кривая иллюстрирует именно изотермический процесс.
Мы переходим к следующему процессу – изохорному. Он сопровождается неизменным объемом газа.
На практике реализовать его не сложно, нужно лишь закрепить поршень в сосуде, не давая ему перемещаться вверх или вниз. Если поршень не будет двигаться, значит, газ не будет совершать никакой работы (ни положительной, ни отрицательной) и все количество теплоты, которую будут подводить к системе или, наоборот, отводить от нее, пойдет на изменение внутренней энергии тела:
boxed{varDelta{U}=Q}
В соответствии с уравнением Менделеева-Клапейрона температура и давление в таком случае должны будут меняться одинаково:
pV=nu{RT}
dfrac{p}{T}=dfrac{nu{R}}{V}
dfrac{p}{T}=const
На pV-диаграмме изохорный процесс будет выражаться изохорой – линией, перпендикулярной горизонтальной оси:
Если газ будет нагреваться, это приведет к росту его давления. Обратите внимание, что площадь под представленным графиком будет равна нулю: при изохорном процессе не совершается никакая работа.
Нам остается поговорить еще об одном наиболее распространенном процессе, проводимым над тем или иным газом, – адиабатном процессе.
Адиабатный процесс – это процесс, происходящий без теплообмена с окружающей средой. Заметьте: это не означает, что температура газа не меняется. Это означает, что количество теплоты, которое сообщают или, наоборот, отнимают у системы, равно нулю:
Q=0
В соответствии с первым началом термодинамики работа, производимая над газом, пойдет на изменение его внутренней энергии:
boxed{varDelta{U}=A}
Как адиабатный процесс выглядит на практике? Ну, нужно избавиться от передачи теплоты со стороны сосуда с газом, поэтому первая идея, которая приходит на ум, – добавить мощную теплоизоляцию, не пропускающую тепло. Есть такой вариант. Но можно поступить гораздо проще. При адиабатном процессе нужно, чтобы газ, нагреваясь, не успевал передавать эту энергию окружающей среде. Фактически здесь мы получаем ситуацию обратную изотермическому процессу: если там нужно было передвигать поршень как можно медленнее, чтобы температура оставалась неизменной, здесь нужно сделать это как можно скорее. Тогда газ не успеет передать значительное количество тепла окружающей среде, и мы будем наблюдать адиабатный процесс.
На pV-диаграмме адиабатный процесс выражается кривой под названием адиабата.
Смахивает на изотерму, но это все-таки не она: адиабата гораздо круче.























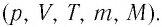
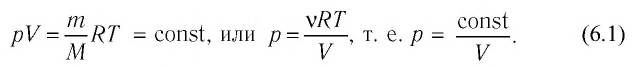
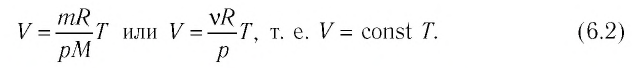
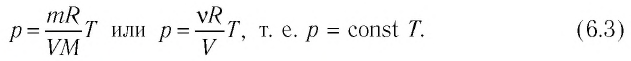
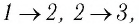
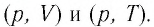
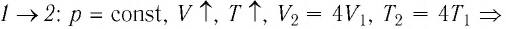
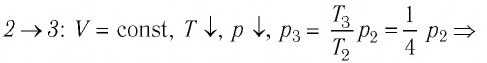
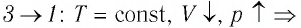 происходит изотермическое сжатие газа.
происходит изотермическое сжатие газа.