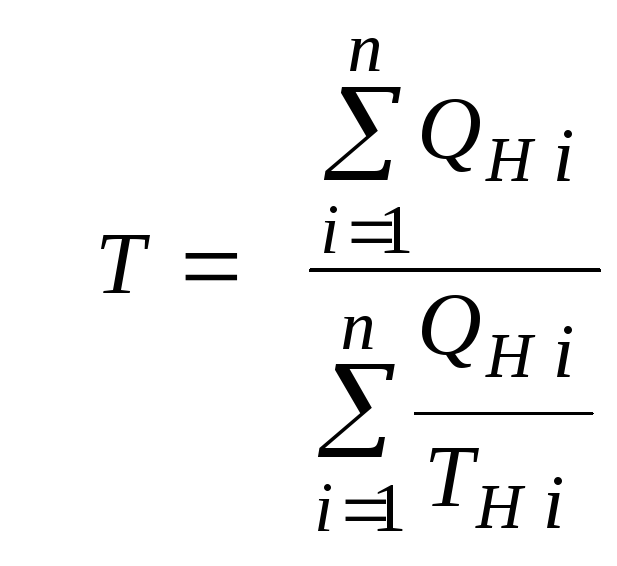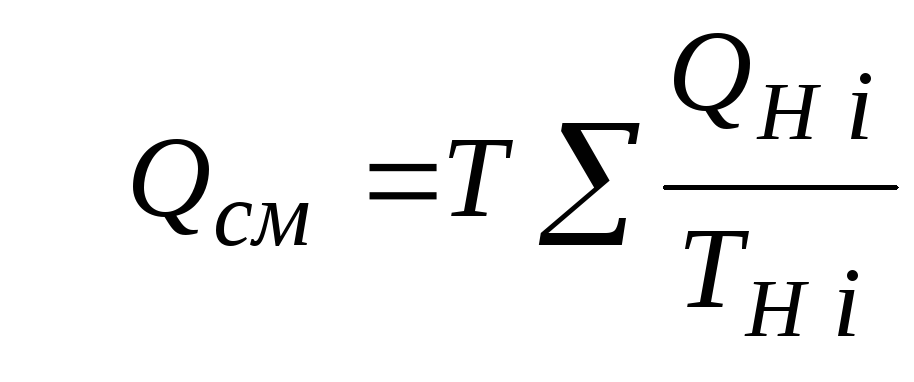Определение температуры смеси.
В технике часто приходится иметь дело с объектами или процессами, в которых смешиваются два или более потоков. Потоки могут состоять из разных веществ в разных агрегатных состояниях, иметь разные давления и температуры (например, смешивание воды и пара). Для лучшего перемешивания иногда используется перемешивающее устройство. В частности, для системы, изображенной на рис. 3.15, балансы массы и энергии можно записать так:
Рис. 3.15. Перемешивающее устройство
Пренебрегая изменением кинетической и потенциальной энергии, запишем
Если перемешивание происходит без теплообмена с окружающей средой и без совершения работы, то это выражение упрощается:
Это соотношение можно представить в виде
или, полагая, что теплоемкости постоянны,
Таким образом, зная температуры и потоки масс компонентов на входе, можно определить стационарную температуру потока на выходе.
Например, если два вещества с температурами tx и t2, с потоками масс щ, т2 и удельными теплоемкостями ср ср2 соответственно смешиваются при постоянном давлении, то приближенное значение температуры смеси можно найти по формуле
Если система состоит из нескольких таких фрагментов, то ее равновесную температуру приближенно можно рассчитать по формуле
Если выравнивание температур происходит при постоянном объеме, без теплообмена и совершения работы, то баланс энергии в стационарном режиме можно представить в виде равенства
где Е— энергия компонентов до смешения; Е2 — энергия после смешения,
В общем случае выполняется равенство
Если известны теплоемкости, температуры и массы компонентов, можно найти приближенное значение равновесной температуры смеси, полагая, что теплоемкости всех компонентов постоянны или используя средние значения теплоемкостей. Расчет температуры смеси в этом случае производится по формуле
В калориметре с адиабатными стенками находится mw = 800 г воды при температуре tw = 15°С, теплоемкость воды cw = 4,19 кДж/ (кг-К). Вода находится в серебряном стакане массой ms = 250 г, теплоемкость серебра cs = 0,23 кДж/ (кг-К). В воду бросают кусок алюминия массой тА = 200 г с температурой tA = 100°С. После выравнивания температур температура системы равна tm = 19,2°С. Чему равна теплоемкость алюминия?
Рассмотрим еще один пример.
Охлаждаемый объект находится в холодильнике, при этом из окружающей среды в холодильник за счет градиента температур направлен тепловой поток =50 Вт. Мощность, потребляемая холодильником, составляет W3J1 = -110 Вт. Чему равен тепловой поток, отводимый из холодильника в окружающую среду Qc q? Насколько изменится температура воздуха в помещении в течение часа работы холодильника, если объем помещения — 40 м 3 , плотность воздуха — 1,2 кг/м 3 , cv = 0,717 кДж/ (кг-К) и помещение полностью изолировано?
Баланс энергии для стационарного режима работы
В стационарном режиме суммарный поток энергии из холодильника в окружающую среду равен потребляемой мощности. При этом изменение внутренней энергии воздуха в единицу времени равно
Как найти температуру смеси газов
Простейшей моделью, рассматриваемой молекулярно-кинетической теорией, является модель идеального газа . В кинетической модели идеального газа молекулы рассматриваются как идеально упругие шарики, взаимодействующие между собой и со стенками только во время упругих столкновений. Суммарный объем всех молекул предполагается малым по сравнению с объемом сосуда, в котором находится газ. Модель идеального газа достаточно хорошо описывает поведение реальных газов в широком диапазоне давлений и температур. Задача молекулярно-кинетической теории состоит в том, чтобы установить связь между микроскопическими (масса, скорость, кинетическая энергия молекул) и макроскопическими параметрами (давление, объем, температура).
В результате каждого столкновения между молекулами и молекул со стенками скорости молекул могут изменяться по модулю и по направлению; на интервалах времени между последовательными столкновениями молекулы движутся равномерно и прямолинейно. В модели идеального газа предполагается, что все столкновения происходят по законам упругого удара, т. е. подчиняются законам механики Ньютона.
Используя модель идеального газа, вычислим давление газа на стенку сосуда . В процессе взаимодействия молекулы со стенкой сосуда между ними возникают силы, подчиняющиеся третьему закону Ньютона. В результате проекция скорости молекулы, перпендикулярная стенке, изменяет свой знак на противоположный, а проекция скорости, параллельная стенке, остается неизменной (рис. 3.2.1).
Поэтому изменение импульса молекулы будет равно , где – масса молекулы.
Выделим на стенке некоторую площадку (рис. 3.2.2). За время с этой площадкой столкнутся все молекулы, имеющие проекцию скорости , направленную в сторону стенки, и находящиеся в цилиндре с основанием площади и высотой .
Пусть в единице объема сосуда содержатся молекул; тогда число молекул в объеме цилиндра равно . Но из этого числа лишь половина движется в сторону стенки, а другая половина движется в противоположном направлении и со стенкой не сталкивается. Следовательно, число ударов молекул о площадку за время равно Поскольку каждая молекула при столкновении со стенкой изменяет свой импульс на величину , то полное изменение импульса всех молекул, столкнувшихся за время с площадкой , равно По законам механики это изменение импульса всех столкнувшихся со стенкой молекул происходит под действием импульса силы , где – некоторая средняя сила, действующая на молекулы со стороны стенки на площадке . Но по 3-му закону Ньютона такая же по модулю сила действует со стороны молекул на площадку . Поэтому можно записать:
Разделив обе части на , получим:
где – давление газа на стенку сосуда.
При выводе этого соотношения предполагалось, что все молекул, содержащихся в единице объема газа, имеют одинаковые проекции скоростей на ось . На самом деле это не так.
В результате многочисленных соударений молекул газа между собой и со стенками в сосуде, содержащем большое число молекул, устанавливается некоторое статистическое распределение молекул по скоростям. При этом все направления векторов скоростей молекул оказываются равноправными (равновероятными), а модули скоростей и их проекции на координатные оси подчиняются определенным закономерностям. Распределение молекул газа по модулю скоростей называется распределением Максвелла . Дж. Максвелл в 1860 г. вывел закон распределения молекул газа по скоростям, исходя из основных положений молекулярно-кинетической теории. На рис. 3.2.3 представлены типичные кривые распределения молекул по скоростям. По оси абсцисс отложен модуль скорости, а по оси ординат – относительное число молекул, скорости которых лежат в интервале от до . Это число равно площади выделенного на рис. 3.2.3 столбика.
Характерными параметрами распределения Максвелла являются наиболее вероятная скорость , соответствующая максимуму кривой распределения, и среднеквадратичная скорость где – среднее значение квадрата скорости.
С ростом температуры максимум кривой распределения смещается в сторону больших скоростей, при этом и увеличиваются.
Чтобы уточнить формулу для давления газа на стенку сосуда, предположим, что все молекулы, содержащиеся в единице объема, разбиты на группы, содержащие , , и т. д. молекул с проекциями скоростей , , и т. д. соответственно. При этом Каждая группа молекул вносит свой вклад в давление газа. В результате соударений со стенкой молекул с различными значениями проекций скоростей возникает суммарное давление
Входящая в это выражение сумма – это сумма квадратов проекций всех молекул в единичном объеме газа. Если эту сумму разделить на , то мы получим среднее значение квадрата проекции скорости молекул:
Теперь формулу для давления газа можно записать в виде
Так как все направления для векторов скоростей молекул равновероятны, среднее значение квадратов их проекций на координатные оси равны между собой:
Последнее равенство вытекает из формулы:
Формула для среднего давления газа на стенку сосуда запишется в виде
Это уравнение устанавливает связь между давлением идеального газа, массой молекулы , концентрацией молекул , средним значением квадрата скорости и средней кинетической энергией поступательного движения молекул. Его называют основным уравнением молекулярно-кинетической теории газов.
Таким образом, давление газа равно двум третям средней кинетической энергии поступательного движения молекул, содержащихся в единице объема .
В основное уравнение молекулярно-кинетической теории газов входит произведение концентрации молекул на среднюю кинетическую энергию поступательного движения. Если предположить, что газ находится в сосуде неизменного объема , то ( – число молекул в сосуде). В этом случае изменение давления пропорционально изменению средней кинетической энергии.
Возникают вопросы: каким образом можно на опыте изменять среднюю кинетическую энергию движения молекул в сосуде неизменного объема? Какую физическую величину нужно изменить, чтобы изменилась средняя кинетическая энергия Опыт показывает, что такой величиной является температура .
Понятие температуры тесно связано с понятием теплового равновесия . Тела, находящиеся в контакте друг с другом, могут обмениваться энергией. Энергия, передаваемая одним телом другому при тепловом контакте, называется количеством теплоты .
Тепловое равновесие – это такое состояние системы тел, находящихся в тепловом контакте, при котором не происходит теплопередачи от одного тела к другому, и все макроскопические параметры тел остаются неизменными. Температура – это физический параметр, одинаковый для всех тел, находящихся в тепловом равновесии. Возможность введения понятия температуры следует из опыта и носит название нулевого закона термодинамики .
Для измерения температуры используются физические приборы – термометры , в которых о величине температуры судят по изменению какого-либо физического параметра. Для создания термометра необходимо выбрать термометрическое вещество (например, ртуть, спирт) и термометрическую величину , характеризующую свойство вещества (например, длина ртутного или спиртового столбика). В различных конструкциях термометров используются разнообразные физические свойства вещества (например, изменение линейных размеров твердых тел или изменение электрического сопротивления проводников при нагревании).
Термометры должны быть откалиброваны. Для этого их приводят в тепловой контакт с телами, температуры которых считаются заданными. Чаще всего используют простые природные системы, в которых температура остается неизменной, несмотря на теплообмен с окружающей средой – это смесь льда и воды и смесь воды и пара при кипении при нормальном атмосферном давлении. По температурной шкале Цельсия точке плавления льда приписывается температура , а точке кипения воды – . Изменение длины столба жидкости в капиллярах термометра на одну сотую длины между отметками и принимается равным . В ряде стран (США) широко используется шкала Фаренгейта (F), в которой температура замерзающей воды принимается равной 32 °F, а температура кипения воды равной 212 °F. Следовательно,
Особое место в физике занимают газовые термометры (рис. 3.2.4), в которых термометрическим веществом является разреженный газ (гелий, воздух) в сосуде неизменного объема (), а термометрической величиной – давление газа . Опыт показывает, что давление газа (при ) растет с ростом температуры, измеренной по шкале Цельсия.
Чтобы проградуировать газовый термометр постоянного объема, можно измерить давление при двух значениях температуры (например, 0 °C и 100 °C), нанести точки и на график, а затем провести между ними прямую линию (рис. 3.2.5). Используя полученный таким образом калибровочный график, можно определять температуры, соответствующие другим значениям давления. Экстраполируя график в область низких давлений, можно определить некоторую «гипотетическую» температуру, при которой давление газа стало бы равным нулю. Опыт показывает, что эта температура равна и не зависит от свойств газа . На опыте получить путем охлаждения газ в состоянии с нулевым давлением невозможно, так как при очень низких температурах все газы переходят в жидкое или твердое состояние.
Английский физик У. Кельвин (Томсон) в 1848 г. предложил использовать точку нулевого давления газа для построения новой температурной шкалы ( шкала Кельвина ). В этой шкале единица измерения температуры такая же, как и в шкале Цельсия, но нулевая точка сдвинута:
В системе СИ принято единицу измерения температуры по шкале Кельвина называть кельвином и обозначать буквой K. Например, комнатная температура по шкале Кельвина равна .
Температурная шкала Кельвина называется абсолютной шкалой температур . Она оказывается наиболее удобной при построении физических теорий.
Нет необходимости привязывать шкалу Кельвина к двум фиксированным точкам – точке плавления льда и точке кипения воды при нормальном атмосферном давлении, как это принято в шкале Цельсия.
Кроме точки нулевого давления газа, которая называется абсолютным нулем температуры , достаточно принять еще одну фиксированную опорную точку. В шкале Кельвина в качестве такой точки используется температура тройной точки воды ), в которой в тепловом равновесии находятся все три фазы – лед, вода и пар. По шкале Кельвина температура тройной точки принимается равной .
Газовые термометры громоздки и неудобны для практического применения: они используются в качестве прецизионного стандарта для калибровки других термометров.
Сравнивая соотношения с основным уравнением молекулярно-кинетической теории газов, можно получить:
Средняя кинетическая энергия хаотического движения молекул газа прямо пропорциональна абсолютной температуре.
Таким образом, температура есть мера средней кинетической энергии поступательного движения молекул .
В этом соотношении , , , … – концентрации молекул различных газов в смеси. Это соотношение выражает на языке молекулярно-кинетической теории экспериментально установленный в начале XIX столетия закон Дальтона : давление в смеси химически невзаимодействующих газов равно сумме их парциальных давлений .
1.5. Смеси газов
Возникает естественный вопрос: какими уравнениями описываются смеси идеальных газов? Ведь с чистыми газами нам редко приходится встречаться в природе. Например, наша естественная среда обитания — воздух — состоит из азота N2 (78,08 %), кислорода O2 (20,95 %), инертных газов (0,94 %), углекислого газа СO2 (0,03 %).
Пусть в некотором объеме V при некоторой температуре Т содержится смесь газов (которые мы будем нумеровать
индексом i ). Роль каждого компонента смеси будем характеризовать массовой долей:
где mi — масса i-го компонента. Наша задача — написать уравнение, подобное уравнению Клапейрона — Менделеева, и разобраться с эффективным числом степеней свободы смеси, где могут содержаться и одноатомные, и многоатомные молекулы.
Прежде всего, заметим, что мы рассматриваем идеальные газы. Молекулы не взаимодействуют друг с другом, и потому каждый компонент не мешает любому другому «жить» в том же общем сосуде. Различные газы в сосуде, в силу их предполагаемой идеальности, просто «не замечают» друг друга. Поэтому для каждого из компонентов справедливо одно и то же уравнение Клапейрона — Менделеева:
где ni — число молей вещества в i -м компоненте. Полное число n молей в смеси равно сумме числа молей ni в каждом из компонентов:
Аналогично, полная масса смеси равна сумме масс каждого из компонентов
и естественно определить молярную массу смеси m как массу одного моля смеси:
Введем величину, называемую парциальным давлением.
Парциальное давление pi — это давление, оказываемое i-м компонентом газовой смеси.
Имеет место закон Дальтона для газовой смеси:
Полное давление газовой смеси равно сумме всех парциальных давлений
Суммируя левые и правые части (1.21), приходим к стандартной форме уравнения Клапейрона — Менделеева
где m, μ, n определяются из условия конкретной задачи. Например, если заданы массовые доли компонентов, то молярную массу смеси находим из соотношения
Внутренняя энергия Ui i-го компонента смеси определяется в соответствии с формулами (1.16) и (1.19):
С одной стороны, полная внутренняя энергия смеси равна сумме энергий каждого компонента:
С другой стороны, запишем стандартное выражение вида (1.25)
Сравнивая (1.26) и (1.27), получаем формулу для показателя адиабаты смеси
Найдя массу моля и показатель адиабаты смеси, мы можем пользоваться всеми формулами, полученными ранее для «чистых» идеальных газов.
Пример. Дана смесь кислорода O2 (компонент 1) и аргона Ar (компонент 2), причем количества вещества обоих компонентов одинаковы n1 = n2. Найдем показатель адиабаты смеси.
О, боже, неужели я настолько глуп? Помогите решить такую задачу:
Теплоизолированный сосуд разделен теплоизолирующей перегородкой на 2 равные части. В одной части находится 40 г газа аргона при температуре 300 К, а в другой – столько же газа неона при температуре 600 К. Найдите температуру смеси газов после удаления перегородки.
Что за бред, но я не могу составить дельное уравнение. То одно неизвестное, то другое тут вылазивает.
Записываю уравнение Менд.-Кл. для аргона:
1)[ p_1V=frac{m}{mu_1}RT_1; ]
Записываю уравнение Менд.-Кл. для неона:
2)[ p_2V=frac{m}{mu_2}RT_2; ]
Если поделить ур-ния друг на друга, то можно найти отношение давлений (1/4). Оно нам надо?
Затем если записать объединенный газовый закон для 1-го и для 2-го газа:
[ frac{p_1V}{T_1}=frac{2p^,_1V}{T^,} ] и [ frac{p_2V}{T_2}=frac{2p^,_2V}{T^,} ]
можно найти отношение установленных давлений каждым из газов (1/2).
И записав ур-ние Менд.-Кл. для смеси газов
[ p2V=frac{2m}{mu_c}RT^, ] где [ p=p_1^,+p_2^,=3p_1^,; ]
окончательно приходим в тупик
Помогите!
Полное условие задачи
Краткое условие задачи
Решение задачи
Запишем закон Дальтона для смеси газов:
Плотность смеси найдется следующим образом:
Запишем уравнение состояния идеального газа для гелия и кислорода:
Выразим массы гелия и кислорода:
Подставим массы в формулу для плотности смеси:
Из закона Дальтона имеем:
Тогда получаем:
Преобразуем последнее выражение:
Парциальное давление гелия определим через его концентрацию:
Подставляем это выражение вместо парциального давления гелия:
Подставляем данные и находим численный ответ:
Ответ: 300 К.
-
Смешение газовых потоков
-
Температура смеси газовых потоков
Пусть в проточной
смесительной камере смешиваются n
потоков, массовые расходы которых
равныGH1
,GH
2,…,GH
n
, объемные расходы –QH1,QH
2,… ,QH
n
, а начальные температуры и
давления –ТH
1,ТH
2,…,ТH
nи
РH
1,РH
2,…,РH
n
.
Давление газов в
смесителе Pсмявляется величиной задаваемой из
каких-либо соображений и устанавливаемой
за счет дросселерования газовых потоков
с помощью регулирующей арматуры
(задвижек, клапанов и т. п.), установленной
перед входом в смеситель. Это давление
не должно быть больше минимального изPH
i
, т. е. должно выполняться
условие:
Pсм
(PH
i) min
.
Здесь: i
= 1, 2, 3, …, n.
Если газы при
смешении не совершают технической
работы, то, полагая процесс смешенияадиабатным, т. е. идущим без
теплообмена с окружающей средой, ипренебрегая кинетической энергии
потока, первое начало термодинамикидля газового потока можно
записать в следующем виде:
Здесь: iсм– удельная энтальпия смеси газов;
iH
i– удельная энтальпияi-го
газа с начальной температуройТH
i
;
Gсм– массовый расход потока после смесителя.
Но, как известно,
di = Cp
dT, откуда:
и
Здесь: – средняя в диапазоне0 -Т0Кмассовая изобарная
теплоемкость
смеси газов;
– средняя в диапазоне0 -ТH
iмассовая изобарная
теплоемкость
i-го газа.
Дальнейший вывод
формул для температуры смеси потоков
газа аналогичен выводу для случая
смешения газов при сохранении постоянного
объема, но вместо изохорной теплоемкости
Сv
в уравнения подставляется изобарнаяСp.
Тогда по аналогии
с формулами предыдущего параграфа 2.1
можно сразу записать:

или
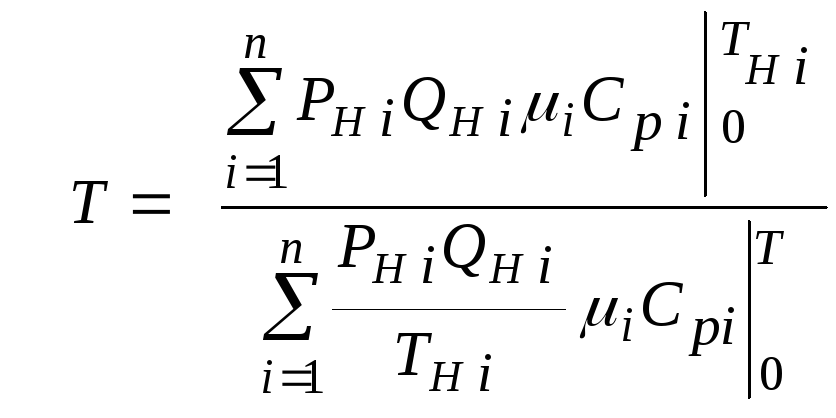
В тех случаях,
когда эмпирическая зависимость
теплоемкости от температуры дается для
температуры в градусах Цельсия,
формулы (2.2.1) и (2.2.2) приобретают
соответственно следующий вид:
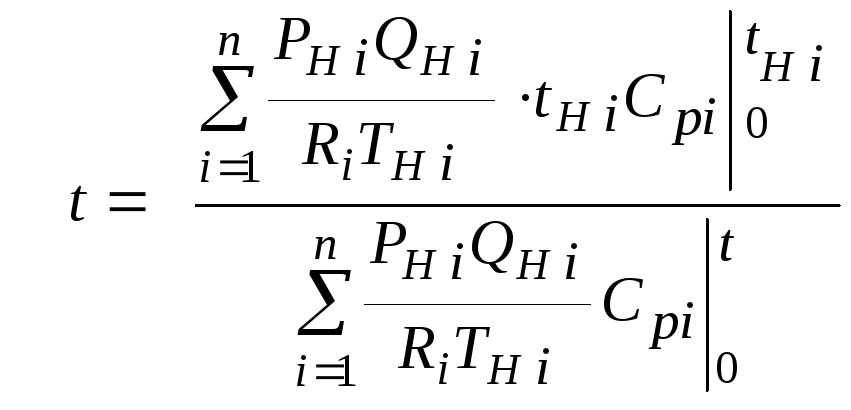
или
(2.2.6)
Значения температуры
смеси в формулах (2.2.1), (2.2.2), (2.2.5), (2.2.6)
определяются методом последовательных
приближений.
-
Объемный расход смеси газовых потоков
В отличие от
массового расхода Gсм
величина объемного расхода смесиQсмв общем случаене равна сумме
объемных расходов компонентов и
определяется из уравнения состояния
идеального газа, записанного для единицы
времени:
.
Т.
к..
, то
(2.2.3)
Если выразить Giчерез параметры начального состоянияi-го потока

то получим еще
одну формулу для объемного расхода
смеси:
(2.2.4)
2.2.3. Частные случаи смешения газовых потоков
Рассмотрим несколько
частных случаев формул (2.2.1) и (2.2.2).
-
Если приближенно
принять, что
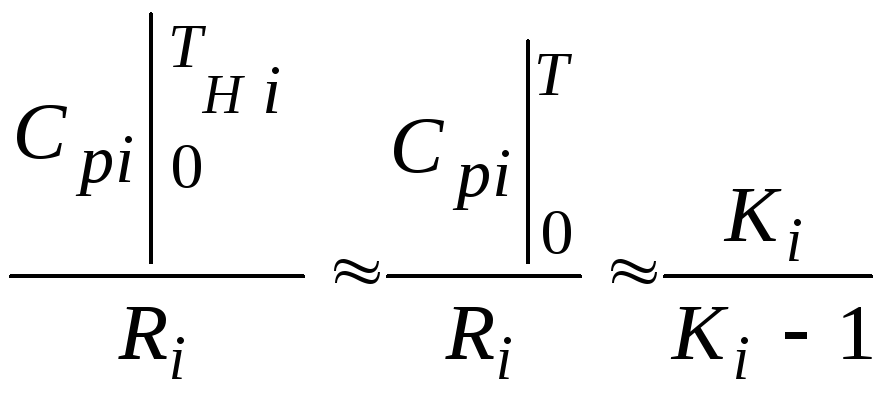
т. е. пренебречь
зависимостью показателей адиабаты Кiот температуры,
то формула (2.2.1)
запишется в следующем виде:

Эта формула может
быть использована в качестве первого
приближения для температуры смеси Т
в формулах (2.2.1) и (2.2.2).
-
Если все газы,
образующие смесь, имеют одинаковые и
постоянные (или близкие) во всем диапазоне
температур мольные теплоемкости, т.е.
,
то формула (2.2.2)
упрощается:

-
Если помимо
одинаковых мольных теплоемкостей (как
в частном случае 2) все газы имеют
одинаковое начальное давление, т. е.
,
то формула (2.2.8)
принимает следующий вид:
(2.2.9)
Формула 2.2.4 для
случая одинаковых начальных давлений
()
запишется как:
(2.2.10)
Если, кроме PH
i
равны между собой еще и начальные
температурыТH
i
, то
(2.2.11)
Литература.
1.
Берд Р., Стьюарт В., Лайтфут Е. Явления
переноса. Перевод с англ. – М.: Химия;
1974. –
2.
Розловский А. И. Научные основы техники
взрывобезопасности при работе с горючими
газами и парами. М.: Химия; 1972. – 90 с.
3.
Гиршфельдер Дж., Кертисс Ч., Берд Р.
Молекулярная теория газов и жидкостей.
– М.: ИИЛ; 1961. – 929 с.
4.
Рид Д., Праусниц, Шервуд. Свойства газов
и жидкости. – М.: Мир; 1984. – с.
5.
Стаскевич Н. Л., Северинец Г. Н., Вигдорчик
Д. Я. Справочник по газоснабжению и
использованию газа. – Л.: Недра, 1990. –
762 с.
Ижевский
государственный технический университет
Институт городского
хозяйства
Диденко В. Н.
Газовые смеси.
Смешение газов.
Ижевск 2002
Газовые смеси.
Смешение газов. Методическое пособие
к дисциплинам «Термодинамика»,
«Теплотехника», «Газоснабжение»,
«Химическая термодинамика и энергетика
топлива», «Физико-химические основы
горения топлива» специальностей 29.07.00
«Теплогазоснабжение и вентиляция» и
29.08.00 «Водоснабжение и водоотведение»
Составитель:
проф., д. т. н.
Диденко Валерий
Николаевич
Методическое
пособие содержит систематизированные
теоретические сведения, необходимые
для осознанного и грамотного использования
зависимостей, приводимых в технической
литературе, для расчета термодинамических
параметров и функций, а также теплофизических
характеристик газовых смесей.
Целью методического
пособия является устранение существующего
пробела в доказательной части содержания
разделов «газовые смеси» современных
учебников и справочников по термодинамике,
теплотехнике и газоснабжению.
Методическое
пособие предназначено для студентов
технических специальностей,
инженеров-теплотехников и аспирантов.
© Ижевский
государственный технический университет,
2002
© Институт городского
хозяйства, 2002
© Диденко Валерий
Николаевич, 2002.
После расширения газа и занятия всего объема между газами произойдет теплообмен. Считая молярную теплоемкость газов при постоянном объеме равной (i/2 + 1) R = cM, запишем уравнение теплового баланса (в конечном состоянии газ работу не совершает):
с1m (T − T1) + с2m (T − T2) = 0.
Умножим все уравнение на M1M2, получим:
с1M1M2(T − T1) + с2M1M2(T − T2) = 0.
Сократим одинаковую молярную теплоемкость при постоянном объеме:
с1M1 = с2M2 = (i/2 + 1) R,
M2(T − T1) + M1(T − T2) = 0.
Выразим искомую температуру:
T = (M2T1 + M1T2) / (M1 + M2).