Тела, температура которых отличается, могут обмениваться тепловой энергией. То есть, между телами будет происходить теплообмен. Самостоятельно тепловая энергия переходит от более нагретых тел к менее нагретым.
Что такое теплообмен и при каких условиях он происходит
Тела, имеющие различные температуры, будут обмениваться тепловой энергией. Этот процесс называется теплообменом.
Теплообмен – процесс обмена тепловой энергией между телами, имеющими различные температуры.
Рассмотрим два тела, имеющие различные температуры (рис. 1).
Тело, имеющее более высокую температуру, будет остывать и отдавать тепловую энергию телу, имеющему низкую температуру. А тело с низкой температурой будет получать количество теплоты и нагреваться.
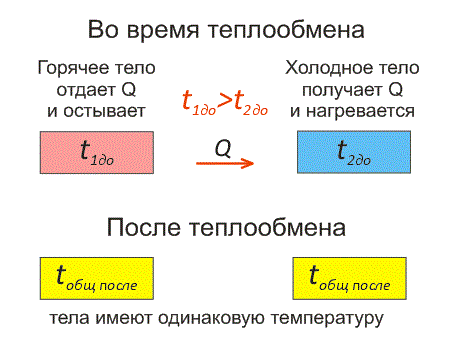
Рис.1. Два тела во время теплообмена и после
На рисунке, горячее тело имеет розовый оттенок, а холодное изображено голубым цветом.
Когда температуры тел выравниваются, теплообмен прекращается.
Чтобы теплообмен происходил, нужно, чтобы тела имели различные температуры.
Когда температура тел выравняется, теплообмен прекратится.
Тепловое равновесие — это состояние, при котором тела имеют одинаковую температуру.
Уравнение теплового баланса и сохранение тепловой энергии
Когда тело остывает, оно отдает тепловую энергию (теплоту). Утерянное количество теплоты Q имеет знак «минус».
А когда тело нагревается – оно получает тепловую энергию. Приобретенное количество теплоты Q имеет знак «плюс».
Эти факты отражены на рисунке 2.

Рис. 2. Полученное количество теплоты имеет знак «+», а отданное Q – знак «-»
Закон сохранения тепловой энергии: Количество теплоты, отданное горячим телом равно количеству теплоты, полученному холодным телом.
Примечание: Существует и другая формулировка закона сохранения энергии: Энергия не появляется сама собой и не исчезает бесследно. Она переходит из одного вида в другой.
Уравнение теплового баланса
Тот факт, что тепловая энергия сохраняется, можно записать с помощью математики в виде уравнения. Такую запись называют уравнением теплового баланса.
Запишем уравнение теплового баланса для двух тел, обменивающихся тепловой энергией:
[large boxed{ Q_{text{остывания горяч}} + Q_{text{нагревания холод}} = 0 }]
(large Q_{text{остывания горяч}} left( text{Дж} right) ) – это количество теплоты горячее тело теряет.
(large Q_{text{нагревания холод}} left( text{Дж} right) ) – это количество теплоты холодное тело получает.
В левой части уравнения складываем количество теплоты каждого из тел, участвующих в теплообмене.
Записываем ноль в правой части уравнения, когда теплообмен с окружающей средой отсутствует. То есть, теплообмен происходит только между рассматриваемыми телами.
В некоторых учебниках применяют сокращения:
[large Q_{1} + Q_{2} = 0 ]
Примечание: Складывая два числа мы получим ноль, когда эти числа будут:
- равными по модулю и
- имеют различные знаки (одно число — знак «плюс», а второе – знак «минус»).
Если несколько тел участвуют в процессе теплообмена
Иногда в процессе теплообмена участвуют несколько тел. Тогда, для каждого тела нужно записать формулу количества теплоты Q. А потом все количества теплоты подставить в уравнение для теплового баланса:
[large boxed{ Q_{1} + Q_{2} + Q_{3} + ldots + Q_{n} = 0 } ]
При этом:
- Q для каждого нагреваемого тела будет обладать знаком «+»,
- Q для каждого охлаждаемого тела — знаком «-».
Пример расчетов для теплообмена между холодным и горячим телом
К горячей воде, массой 200 грамм, имеющей температуру +80 градусов Цельсия, добавили холодную воду, в количестве 100 грамм при температуре +15 градусов Цельсия. Какую температуру будет иметь смесь после установления теплового равновесия? Считать, что окружающая среда в теплообмене не участвует.
Примечание: Здесь мы рассматриваем упрощенную задачу, для того, чтобы облегчить понимание закона сохранения энергии. Мы не учитываем в этой задаче, что вода содержится в емкости. И часть тепловой энергии будет затрачиваться на то, чтобы изменить температуру емкости.
При решении других задач обязательно учитывайте, что емкость, в которой будет содержаться вещество, имеет массу. И часть тепловой энергии будет затрачиваться на то, чтобы изменить температуру емкости.
Решение:
В условии сказано, что окружающая среда в теплообмене не участвует. Поэтому, будем считать рассматриваемую систему замкнутой. А в замкнутых системах выполняются законы сохранения. Например, закон сохранения энергии.
Иными словами, с сосудом и окружающим воздухом теплообмен не происходит и, все тепловая энергия, отданная горячей водой, будет получена холодной водой.
1). Запишем уравнение теплового баланса, в правой части которого можно записать ноль:
[large Q_{text{остывания горяч}} + Q_{text{нагревания холод}} = 0 ]
2). Теперь запишем формулу для каждого количества теплоты:
[large Q_{text{остывания горяч}} = c_{text{воды}} cdot m_{text{горяч}} cdot (t_{text{общ}} — t_{text{горяч}} ) ]
[large Q_{text{нагревания холодн}} = c_{text{воды}} cdot m_{text{холодн}} cdot (t_{text{общ}} — t_{text{холодн}} ) ]
Примечания:
- (large c_{text{воды}} ) – удельную теплоемкость воды находим в справочнике;
- Массу воды переводим в килограммы;
- Горячая вода остывает и отдает тепловую энергию. Поэтому, разность (large (t_{text{общ}} — t_{text{горяч}} ) ) будет иметь знак «минус», потому, что конечная температура горячей воды меньше ее начальной температуры;
- Холодная вода получает тепловую энергию и нагревается. Из-за этого, разность (large (t_{text{общ}} — t_{text{холодн}} ) ) будет иметь знак «плюс», потому, что конечная температура холодной воды больше ее начальной температуры;
3). Подставим выражения для каждого Q в уравнение баланса:
[large c_{text{воды}} cdot m_{text{горяч}} cdot (t_{text{общ}} — t_{text{горяч}} ) + c_{text{воды}} cdot m_{text{холодн}} cdot (t_{text{общ}} — t_{text{холодн}} ) = 0 ]
4). Для удобства, заменим символы числами:
[large 4200 cdot 0,2 cdot (t_{text{общ}} — 80 ) + 4200 cdot 0,1 cdot (t_{text{общ}} — 15 ) = 0 ]
Проведем упрощение:
[large 840 cdot (t_{text{общ}} — 80 ) + 420 cdot (t_{text{общ}} — 15 ) = 0 ]
Раскрыв скобки и решив это уравнение, получим ответ:
[large t_{text{общ}} = 58,33 ]
Ответ: Температура смеси после прекращения теплообмена будет равна 58,33 градуса Цельсия.
Задача для самостоятельного решения:
В алюминиевом калориметре массой 100 грамм находится керосин массой 250 грамм при температуре +80 градусов Цельсия. В керосин поместили свинцовый шарик, массой 300 грамм. Начальная температура шарика +20 градусов Цельсия. Найдите температуру тел после установления теплового равновесия. Внешняя среда в теплообмене не участвует.
Примечание к решению: В левой части уравнения теплового баланса теперь будут находиться три слагаемых. Потому, что мы учитываем три количества теплоты:
- (large Q_{1} ) – охлаждение алюминия от температуры +80 градусов до конечной температуры;
- (large Q_{2} ) – охлаждение керосина от температуры +80 градусов до конечной температуры;
- (large Q_{3} ) – нагревание свинца от температуры +20 градусов до конечной температуры;
А справа в уравнение теплового баланса запишем ноль. Так как внешняя среда в теплообмене не участвует.
Выводы
- Если тела имеют различную температуру, то между ними возможен обмен тепловой энергией, т. е. теплообмен;
- Когда тела будут иметь равную температуру, теплообмен прекратится;
- Тело с высокой температурой, отдает тепловую энергию (теплоту) и остывает. Отданное количество теплоты Q имеет знак «минус»;
- А тело с низкой температурой получает тепловую энергию и нагревается. Полученное количество теплоты Q имеет знак «плюс»;
- Количество теплоты, отданное горячим телом равно количеству теплоты, полученному холодным телом. Это – закон сохранения тепловой энергии;
- Сохранение тепловой энергии можно записать в виде уравнения теплового баланса;
- В левой части уравнения складываем количества теплоты (всех тел, участвующих в теплообмене);
- В правой части уравнения записываем ноль, когда теплообмен с окружающей средой отсутствует.
Определите, при какой температуре в реакционной системе
4НС1(г) + О2(г) ⇄ 2Н2О(г) + 2С12(г), ∆H0298 = -114,4 кДж наступит термодинамическое равновесие. Приведите соответствующие расчеты, принимая во внимание, что в состоянии термодинамического равновесия реализуется условие ∆G0 = 0.
Решение задачи
![]()
Термодинамическое равновесие — состояние системы, при котором ее параметры (температура, давление, объем, энтропия) остаются неизменными по времени в условиях изолированности от окружающей среды.
![]()
Отсюда при термодинамическом равновесии должно выполниться соотношение:
![]()
ΔH дано по условию задачи.
Используя справочные данные, определим изменение энтропии ΔS по формуле:
![]()
Получаем:
ΔSреакции =(2 ⋅ 188,7 + 2 ⋅ 223) – (4 ⋅ 187,6 + 205) = 377,4 + 446 – 750,4 -205 = -132 (Дж/моль).
T = -114400 / -132 = 867 (К)
Ответ:
термодинамическое равновесие наступает при температуре 867 К.
Температура
Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
Темы кодификатора ЕГЭ: тепловое равновесие, абсолютная температура.
Мы часто используем слово “температура” в повседневной речи. А что такое температура? В данной статье мы объясним физический смысл этого понятия.
В молекулярной физике и термодинамике рассматриваются макроскопические тела, т. е. тела, состоящие из огромного числа частиц. Например, в стакане воды содержится порядка молекул. Такое грандиозное число с трудом поддаётся осмыслению.
Термодинамическая система
Термодинамической системой называется макроскопическое тело или система тел, которые могут взаимодействовать друг с другом и с окружающими телами. Стакан с водой — пример термодинамической системы.
Термодинамическая система состоит из столь большого числа частиц, что совершенно невозможно описывать её поведение путём рассмотрения движения каждой молекулы в отдельности. Однако именно грандиозность числа молекул делает ненужным такое описание.
Оказывается, что состояние термодинамической системы можно характеризовать небольшим числом макроскопических параметров — величин, относящимся к системе в целом, а не к отдельным атомам или молекулам. Такими макроскопическими параметрами являются давление, объём, температура, плотность, теплоёмкость, удельное сопротивление и др.
Состояние термодинамической системы, при котором все макроскопические параметры остаются неизменными с течением времени, называется тепловым равновесием. В состоянии теплового равновесия прекращаются все макроскопические процессы: диффузия, теплопередача, фазовые переходы химические реакции и т. д.(Следует отметить, что тепловое равновесие является динамическим равновесием. Так, при тепловом равновесии жидкости и её насыщенного пара весьма интенсивно идут взаимные превращения жидкости и пара. Но это — процессы молекулярного масштаба, они происходят с одинаковыми скоростями и компенсируют друг друга. На макроскопическом уровне количество жидкости и пара со временем не меняется).
Термодинамическая система называется изолированной, если она не может обмениваться энергией с окружающими телами. Чай в термосе — типичный пример изолированной системы.
Тепловое равновесие
Фундаментальный постулат, вытекающий из многочисленных опытных данных, гласит: каково бы ни было начальное состояние тел изолированной системы, со временем в ней устанавливается тепловое равновесие. Таким образом, тепловое равновесие — это состояние, в которое любая система, изолированная от окружающей среды, самопроизвольно переходит через достаточно большой промежуток времени.
Температура как раз и является величиной, характеризующей состояние теплового равновесия термодинамической системы.
Температура — это макроскопический параметр, значения которого одинаковы для всех частей термодинамической системы, находящейся в состоянии теплового равновесия. Попросту говоря, температура — это то, что является одинаковым для любых двух тел, которые находятся в тепловом равновесии друг с другом. При тепловом контакте тел с одинаковыми температурами между ними не будет происходить обмен энергией (теплообмен).
В общем же случае при установлении между телами теплового контакта теплообмен начнётся. Говорят, что тело, которое отдаёт энергию, имеет более высокую температуру, а тело, которое получает энергию — более низкую температуру. Температура, таким образом, указывает направление теплообмена между телами. В процессе теплообмена температура первого тела начнёт уменьшаться, температура второго тела — увеличиваться; при выравнивании температур теплообмен прекратится — наступит тепловое равновесие.
Особенность температуры заключается в том, что она не аддитивна: температура тела не равна сумме температур его частей. Этим температура отличается от таких физических величин, как масса, длина или объём. И по этой причине температуру нельзя измерить путём сравнения с эталоном.
Измеряют температуру с помощью термометра.
Для создания термометра выбирают какое-либо вещество (термометрическое вещество), какую-либо характеристику этого вещества (термометрическую величину), и используют зависимость термометрической величины от температуры. При этом выбор термометрического вещества и термометрической величины может быть весьма произвольным.
Так, в бытовых жидкостных термометрах термометрическим веществом является ртуть (или спирт), а термометрической величиной — длина столбика жидкости. Здесь используется линейная зависимость объёма жидкости от температуры.
В идеально-газовых термометрах используется линейная зависимость давления разреженного газа (близкого по своим свойствам к идеальному) от температуры.
Действие электрических термометров (термометров сопротивления) основано на температурной зависимости сопротивления чистых металлов, сплавов и полупроводников.
В процессе измерения температуры термометр приводится в тепловой контакт(В области температур выше (раскалённые газы, расплавленные металлы) используются бесконтактные высокотемпературные термометры — пирометры. Их действие основано на измерении интенсивности теплового излучения в оптическом диапазоне.) с телом, температура которого определяется. Показания термометра после наступления теплового равновесия — это и есть температура тела. При этом термометр показывает свою температуру!
Температурная шкала. Абсолютная температура
При установлении единицы температуры чаще всего поступают следующим образом. Берут две температуры (так называемые реперные точки) — температуру таяния льда и температуру кипения воды при нормальном атмосферном давлении. Первой температуре приписывают значение , второй — значение
, а интервал между ними делят на
равных частей. Каждую из частей называют градусом (обозначают
), а полученную таким образом температурную шкалу — шкалой Цельсия.
При измерениях по шкале Цельсия с помощью жидкостных термометров возникает одна трудность: разные жидкости при изменении температуры изменяют свой объём по-разному. Поэтому два термометра с различными жидкостями, приведённые в тепловой контакт с одним и тем же телом, могут показать разные температуры. От данного недостатка свободны идеально-газовые термометры — зависимость давления разреженного газа от температуры не зависит от вещества самого газа.
Кроме того, для температурной шкалы идеально-газового термометра существует естественное начало отсчёта (исчезает произвол выбора реперной точки!): это та предельно низкая температура, при которой давление идеального газа постоянного объёма обращается в нуль. Эта температура называется абсолютным нулём температур.
Температурная шкала, началом отсчёта которой является абсолютный нуль, а единицей температуры — градус Цельсия, называется абсолютной температурной шкалой.
Температура, измеряемая по абсолютной шкале, называется абсолютной температурой и обозначается буквой . Единица абсолютной температуры называется кельвином (
).
Абсолютному нулю () соответствует температура
. Поэтому связь абсолютной температуры и температуры по шкале Цельсия даётся формулой:
В задачах достаточно использовать формулу
Благодарим за то, что пользуйтесь нашими материалами.
Информация на странице «Температура» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из данного раздела.
Публикация обновлена:
08.05.2023
Температура
является чисто термодинамической
величиной, не имеющей аналога в механике.
Температура определяется как некоторая
феноменологическая величина, позволяющая
численно описывать тепловое равновесие
между телами. Если два тела (или части
одного тела) имеют температуры Т1
и Т2,
то соотношение
Т1
= Т2
(2.4.1)
является
эмпирическим условием теплового
равновесия –
условием отсутствия потоков тепла.
Условие теплового термодинамического
равновесия можно также записать как
постоянство температуры в каждой точке
системы:
T(r)
= const.
(2.4.1)
Условие (2.4.1) открыто
экспериментально Дж. Блеком еще в XVIII
веке, до появления термодинамики как
науки, и часто называется нулевым
законом термодинамики.
Также чисто
эмпирически было установлено, что тепло
(тепловая энергия), всегда переходит
от тел с более высокой температурой к
телам с более низкой.
Это утверждение – одна из формулировок
второго
закона термодинамики.
Интересно, что второй закон термодинамики
был понят раньше первого (С. Карно, 1824
г.);
впервые этот закон был ясно математически
сформулирован Р. Клаузиусом (1850
г.),
которому мы обязаны и введением понятия
энтропии – важнейшей термодинамической
функции. Лорд Кельвин также открыл
второй закон термодинамики в 1851 г.,
независимо от Клаузиуса.
Температуру
измеряют, наблюдая за каким-либо
физическим свойством вещества: объемом
жидкости, давлением газа, электоросопротивлением
и др. Так определяется эмпирическая
температура.
Температура
исчисляется в градусах.
Абсолютная
шкала температуры,
которая используется в физике в настоящее
время, была предложена лордом Кельвином
(Вильямом Томсоном) в 1848 г. и поэтому
называется также шкалой
Кельвина.
Вначале
калибровка температурной шкалы Кельвина
производилась по двум фиксированным
точкам: точке плавления льда Т0
и точке кипения Т0
+
100° чистой воды при давлении в одну
атмосферу.
Учитывая то обстоятельство, что значение
тройной точки чистой воды очень близко
к 0,0098 °С, десятая Генеральная конференция
мер и весов в 1954 г. постановила считать
тройную точку воды фиксированной точкой,
которой соответствует температура
273,16 К. Эта конференция также следующим
образом определила термодинамическую
температурную шкалу Цельсия:
t°С
= Т
К
– 273,15
°С,
где
Т
К
— значение
абсолютной температуры, установленное
конференцией. Нуль новой термодинамической
температуры Цельсия отличается от точки
плавления льда примерно на 0,0001°. Для
обычных целей различием между новым и
старым определением шкалы можно
полностью пренебречь.
2.5. Уравнение состояния
В
классической термодинамике, изучающей
механические и химические явления,
внутренняя энергия зависит от четырех
и
только четырех первичных,
простейших физических параметров, или
факторов:
1)
температуры T,
которая характеризует энергию
поступательного, вращательного и
колебательного движения молекул;
2)
давления p,
от которого зависит расстояние между
частицами и, следовательно, энергия
межмолекулярного взаимодействия;
3)
объема V
системы, от
которого, также как и от давления, зависит
расстояние между частицами;
4)
количества n
образующих
систему веществ, определяющих энергию
как внутри-, так и межмолекулярного
взаимодействия.
Однако из
перечисленных четырех факторов
независимыми являются только три из
них. Связано это с тем, что для любого
тела, любой системы всегда существует
феноменологическое
уравнение связи
между ними, называемое уравнением
состояния. Например,
для идеального газа, состоящего из
частиц нескольких сортов (молекулярных
форм), уравнение состояния (другие
названия: объединенное уравнение
газового состояния; уравнение Менделеева
– Клапейрона) имеет вид:
pV
= RTni
,
(2.5.1)
где
ni
– количество
вещества сорта i
в молях, R –
коэффициент пропорциональности,
выравнивающий размерности правой и
левой части (2.5.1). Он называется газовой
постоянной,
ибо он одинаков для всех идеальных
газов.
Поскольку уравнение
состояния как уравнение связи существует
всегда, то величины p,T,V,n,
называемые обычно термодинамическими
переменными,
являются также и термодинамическими
функциями друг
от друга. Поскольку уравнение состояния
единственно, то каждой триаде значений
термодинамических переменных, описывающей
произвольное состояние системы,
соответствует единственное значение
четвертой величины как функции
состояния.
При достаточно
высоких температурах и низких
давлениях уравнение (2.5.1) является
хорошим приближением для любого газа.
Для реальных
тел (реальных газов, жидкостей, твердых
тел) уравнения состояния значительно
сложнее. В каждом конкретном случае и
вид уравнения состояния, и его параметры
устанавливаются экспериментально.
Уравнение состояния
можно иллюстрировать графически
различными способами. Если в уравнение
входят только три переменных и оно
записывается в виде f(p,
Т, V)
= 0,
то любые два
из них, скажем p
и V,
можно выбрать
в качестве осей декартовой системы
координат. Тогда, при любом фиксированном
значении третьей переменной Т,
уравнение
состояния определяет на этой плоскости
некоторую кривую, называемую изотермой.
В случае
идеального газа (теоретической модели),
как это видно из уравнения (2.5.1), изотермы
на плоскости p–V
при любой температуре представляют
собой равносторонние гиперболы (см.
верхнюю кривую на рис. 2.5.1). В действительности
для всех реальных газов существует
некоторая критическая
температура, выше
и ниже которой газ обладает принципиально
разными свойствами. Поэтому
реальные
газы при низких температурах и высоких
давлениях имеют изотермы более сложного
вида.
Если подвергнуть
изотермическому сжатию газ, находящийся
при температуре, меньше некоторой ТС
, называемой
критической температурой,
то давление будет сначала возрастать
(нижняя кривая до точки D
на рис. 2.5.1). Но, при некотором объеме Vs
наступит
насыщение: газ начинает конденсироваться
в жидкость. При дальнейшем сжатии, пока
весь газ не превратится в жидкость (при
объеме Vb,),
давление остается постоянным (прямая
D-А).
При дальнейшем
сжатии (теперь жидкости) изотерма снова
пойдет вверх, но более круто (верхняя
кривая после точки А
рис. 2.5.1), поскольку коэффициент сжимаемости
у жидкостей мал.
|
Рис. 2.5.1.
Изотермы
«Купол» |
До насыщения, т.
е. при V
> Vs,
экспериментальные
данные можно достаточно точно описывать
уравнением состояния, представляемым
в виде ряда по обратным степеням V:
![]() ,
,
в
котором вириальные
коэффициенты
Bi
зависят
от температуры. Эту форму записи уравнения
состояния ввел Камерлинг-Онесс в 1902 г.
Отметим, что в последствии такое
разложение по степеням плотности было
обосновано Дж. Майером (1937 г.) с теоретической
точки зрения. Вириальные коэффициенты
были
им непосредственно связаны с
межмолекулярными силами.
Уравнение
Ван-дер-Ваальса. При
температурах выше критической изотермы
представляют собой гладкие монотонные
кривые. В области же насыщения между
точками с абсциссами Vb
и Vs
(см. рис.
2.5.1) участки изотерм становятся прямыми:
p = const,
а производные дp/дV
в
этих точках
терпят разрыв. Описать все возможные
состояния равновесия реального газа
с помощью одного уравнения представляется
невозможным. Однако Ван-дер-Ваальсу в
его диссертации «О непрерывности
газообразного и жидкого состояний»
(1873 г.) удалось в известном смысле решить
эту задачу. Исходя из весьма простых
молекулярных соображений, он предложил
следующее уравнение состояния:
![]() .
.
(2.5.2)
Здесь
коэффициент а
учитывает
взаимное притяжение молекул газа,
коэффициент b
–
их конечные размеры. Это уравнение
сохранило свое значение до настоящего
времени и часто используется даже для
описания состояния жидкостей.
Уравнение (2.5.2)
дает изотермы, ниже определенной
температуры имеющие S-образный
участок (А-В-С-D
на рис. 2.5.1). Это свойство уравнения
Ван-дер-Ваальса особенно привлекательно
тем, что оно приближенно описывает и
неравновесные состояния: перегретую
жидкость (заштрихованный участок над
кривой А-В)
и переохлажденный пар (участок под
кривой C–D).
Прямая A–D
соответствует равновесной области
насыщенного пара.
С повышением
температуры изотермы поднимаются вверх,
точки А-D
и В-С сближаются
(см. «купол» на рис. 2.5.1). При некоторой
температуре Тс
максимум и
минимум на кривой изотермы сливаются
в точку, являющейся точкой
перегиба на
изотерме:
![]()
Эта
температура и является критической.
Точка перегиба на изотерме называется
критической
точкой, а
соответствующие ей температура, давление
и объем называются критическими
параметрами.
При температурах выше критической
реальный газ не переходит в жидкость
ни при каких давлениях. С дальнейшим
повышением температуры изотермы все
более приближаются к гиперболам (см.
рис. 2.5.1), отвечающим идеальному газу.
Соседние файлы в папке Samost_rabota
- #
22.08.2013280 б21.listing
- #
- #
- #
- #
Тепловое равновесие (или термодинамическое равновесие) – это такое состояние, при котором все макроскопические параметры сколь угодно долго остаются неизменными.
В состоянии термодинамического равновесия не происходит теплообмен с окружающими телами, не изменяются объём и давление тела, отсутствуют взаимные превращения жидкостей, газов и твёрдых тел.
Температура и её физический смысл
Любая термодинамическая система при неизменных внешних условиях самопроизвольно переходит в состояние термодинамического равновесия.
Температура тела – это физический параметр, одинаковый во всех частях системы тел, которая находится в состоянии термодинамического равновесия.
При тепловом равновесии микроскопические процессы внутри тела (движение частиц и взаимодействие частиц) не прекращаются. Термодинамическая система может находиться в различных состояниях теплового равновесия, каждому из которых соответствует определённое значение температуры. При теплообмене между телами происходит обмен энергией: тела с большей энергией передают свою энергию телам с меньшей энергией. Направление теплообмена между ними указывает разность температур тел. То есть энергия передаётся от более горячего тела к менее горячему.
Температура и её измерение
Для измерения температуры используется тот факт, что с изменением температуры тела изменяются почти все его физические свойства: длина, объём, плотность, электрическое сопротивление, упругие свойства и др. Основой для измерения температуры может являться изменение какого-либо свойства термометрического тела.
Термометрическое тело – это тело, для которого известна зависимость какого-либо свойства данного тела от температуры. Термометрическим телом может быть, например, жидкость или газ, для которого известна зависимость изменения его объёма от температуры.
Эмпирическая шкала – это температурная шкала, установленная с помощью термометрического тела.
Наиболее распространён способ измерения температуры с помощью жидкостного термометра, в котором используется расширение жидкости (изменение объёма) при нагревании.
При градуировке термометра отмечают опорные точки, расстояние между которыми на шкале делят на равные части, которые называются градусами.
Шкала температур Цельсия
Для практического употребления по решению IX Генеральной конференции по мерам и весам в 1948 году была принята международная стоградусная температурная шкала – шкала Цельсия.
Шведский физик и астроном Андерс Цельсий (1701 – 1744) в 1742 году предложил шкалу термометра, в которой за ноль градусов (начало отсчёта температуры) принял температуру таяния льда, а за сто градусов – температуру кипения воды при нормальном атмосферном давлении в 1,01325 * 105 Па. Изменение длины столба жидкости в термометре на одну сотую долю длины между отметками 0 и 100 °С соответствует изменению температуры на 1 °С. По данной шкале единица измерения температуры – градус Цельсия.
Однако, несмотря на указанную выше конференцию, в некоторых странах (например, в США) до сих пор активно используется другая шкала – шкала Фаренгейта. На шкале Фаренгейта точка таяния льда равна +32 °F, а точка кипения воды равна +212 °F. При этом один градус Фаренгейта равен 1/180 разности этих температур.
Перевести градусы из Цельсия в Фаренгейт можно так:
tF = tC * (9/5) + 32
Перевод из Фаренгейта в Цельсий:
tC = (tF — 32) * (5/9)
Здесь tF – температура по Фаренгейту, tC – температура по Цельсию
Перевести градусы по Цельсию в градусы по Фаренгейту и обратно вы можете ниже.

