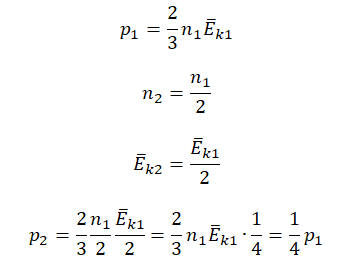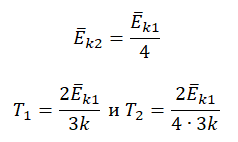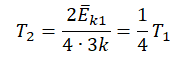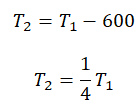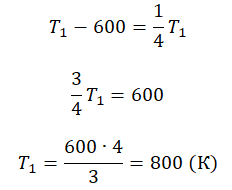Температуру газа можно найти, зная его давление, с помощью уравнения состояния для идеального и реального газа. В модели идеального газа потенциальной энергией взаимодействия молекул газа пренебрегают, считая ее малой по сравнению с кинетической энергией молекул. Такая модель достаточно точно может описывать газ при низких давлениях и низких температурах. В остальных случаях рассматривают модель реального газа, учитывающую межмолекулярные взаимодействия.

Вам понадобится
- Уравнение Клапейрона-Менделеева, уравнение Ван-дер-Ваальса
Инструкция
Рассмотрим для начала идеальный газ с давлением p, занимающий объем V. Температуру, давление и объем газа связывает уравнение состояния идеального газа или уравнение Клапейрона-Менделеева. Оно выглядит следующим образом: pV = (m/M)RT, где m – масса газа, M – его молярная масса, R – универсальная газовая постоянная (R ~ 8,31 Дж/(моль*K)). Таким образом, m/M – это количество вещества газа.
Следовательно, уравнение Клапейрона-Менделеева можно также записать в виде: p(Vm)=RT, где Vm – молярный объем газа, Vm = V/(m/M)= VM/m. Тогда температуру газа T можно выразить из этого уравнения: T = p(Vm)/R.
Если масса газа постоянна, то можно записать: (pV)/T = const. Отсюда мы можем найти изменение температуры газа при изменении других параметров. Если p = const, то V/T = const – закон Гей-Люссака. Если V = const, то p/T = const – закон Шарля.
Рассмотрим теперь модель реального газа. Уравнение состояния реального газа называется уравнением Ван-дер-Ваальса. Оно записывается в виде: (p+a*(v^2)/(V^2))((V/v)-b) = RT. Здесь поправка учитывает силы притяжения между молекулами, а поправка b – силы отталкивания. v – это количество вещества газа в молях. Остальные обозначения величин соответствуют обознанчениям в уравнении состояния идеального газа.
Следовательно, из уравнения Ван-дер-Ваальса температуру T можно выразить: T = (p+a*(v^2)/(V^2))((V/v)-b)/R
Видео по теме
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Модель идеального газа считается самой простейшей относительно основных положений МКТ. Кинетическая модель идеального газа молекул говорит о том, что при взаимодействии между собой, шарики рассматриваются в качестве идеально упругих. Суммарный объем всех молекул достаточно мал по сравнению с объемом сосуда, в котором находится данный газ. Модель необходима для описания его поведения при различных давлениях и температурах.
Цель молекулярно-кинетической теории – установка связи между макроскопическими и макроскопическими параметрами.
После соударения молекул между собой и стенками сосуда происходит изменение направления движения и времени между интервалами столкновений. Модель идеального газа основывается на законах механики Ньютона, то тесть столкновения соответствуют закону упругого удара.
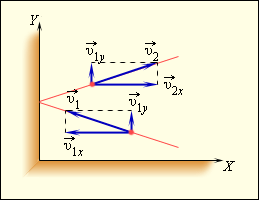
Чтобы определить давление газа на стенку сосуда, учитывается модель идеального газа. Исходя из этого, происходит возникновение сил, которые подчиняются 3 закону Ньютона. Отсюда получим, что проекция скорости υx перпендикулярна относительно стенки, а знак меняется на противоположный. Проекция υy параллельна и постоянна. Это показано на рисунке 3.2.1.
Рисунок 3.2.1. Упругое столкновение молекулы со стенкой.
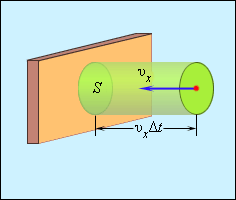
Отсюда следует, что изменение импульса можно записать в виде 2m0υx с массой молекулы, равной m0. Необходимо выделить площадь S, как показано на рисунке 3.2.2. По прошествии времени Δt с S поверхностью столкнутся молекулы с проекциями скорости υx, которая направлена в сторону стены, и основанием цилиндра S с высотой υxΔt.
Рисунок 3.2.2. Определение числа столкновений молекул с поверхностью S.
Если за единицу объема брать сосуд с n-ым количеством молекул, тогда их число в объеме цилиндра нужно обозначить, как nSυxΔt. Очевидно, что происходит столкновение только половины имеющихся молекул. Тогда количество ударов о S за время Δt равняется 12nSvx∆t.
При столкновении происходит изменение импульса 2m0υx. Тогда формула nm0vx2S∆t говорит о полном его изменении за определенный промежуток времени. Исходя из закона механики, изменение импульса всех молекул записывается как FΔt. Силой F обозначается средняя сила, которая действует на молекулы. Но 3 закон Ньютона говорит о том, что аналогичная сила по модулю оказывает действие на поверхность S. Данное утверждение можно зафиксировать F∆t=nm0vx2S∆t.
Далее для упрощения следует разделить равенство на выражение SΔt. Формула примет вид p=FS=nm0vx2 со значением р, обозначаемым в качестве давления газа на стенку сосуда.
Все молекулы, находящиеся в сосуде на единицу объема, имеют разные проекции скоростей на ось Ох. При столкновениях прослеживалось статистическое их распределение по скоростям, причем с разными направлениями векторов их скоростей.
Распределением Максвелла называют распределение молекул газа по модулю скоростей.
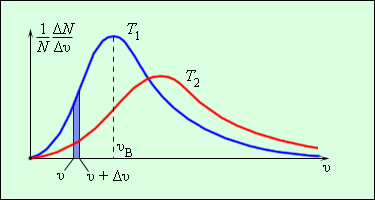
Еще в 1860 г Дж. Максвелл вывел закон распределения молекул газа по скоростям, основываясь на основных положениях молекулярно-кинетической теории молекулы. Рисунок 3.2.3. наглядно показывает распределения молекул по скоростям с помощью кривых. На оси Ох располагается модуль скорости, а на Оу – количество молекул, находящихся на интервале от υ до υ+Δυ. На рисунке 3.2.3. данное значение выделено в виде столбика.
Рисунок 3.2.3. Распределение молекул по скоростям. T2>T1.
Характерные параметры распределения Максвелла – это вероятная скорость υв,которая соответствует кривой распределения, и среднеквадратичная скорость υкв=υ2→, где υ2→обозначающие среднее значение квадрата скорости.
Если растет температура, тогда максимум кривой будет смещен в сторону больших скоростей, то есть υв и υкв увеличатся.
Распределение Максвелла
Для записи формулы давления газа необходимо предположить, что все молекулы разделены на n1, n2, n3 группы с проекциями υx1, υx2, υx3. Иначе говоря, записываем ∑ini=n. Можно зафиксировать, как nim0vxi2. Тогда суммарное давление примет вид p=m0∑inivxi2.
Данная сумма является суммой квадратов проекций υx всех n молекул на единичном объеме газа. При делении выражения на n получим среднее значение квадратичной скорости проекции υx. Запишем в виде 1n∑niυxi2=vx2→i.
Другая интерпретация формулы давления газа p=nm0vx2→. Все направления векторов различные, потому среднее значение квадратов проекций на координатные оси равняется vx2→=vy2→=vz2→=13v2→.
Формула для среднего давления газа на стенку сосуда обозначим, как p=p→=13nm0v2→=23nm0v2→2=23nEk→.
Из уравнения видна связь между р и m0 и количеством молекул n, средней квадратичной скоростью v2→ и средней кинетической энергией Ek→ молекул. Такое уравнение получило название уравнения молекулярно-кинетической уравнения теории газов.
Отсюда следует, что давление газа – это две трети средней кинетической энергии, которое имеется в единице объема. Основное уравнение молекулярно-кинетической теории газов или строения вещества содержит произведение количества молекул n на Ek→. Предположительно сосуд имеет газ неизменного объема V, тогда n=NV=const (N – число молекул в сосуде). Изменение давления происходит пропорционально изменению кинетической энергии.
Физика. Температура
Температура связана с понятием теплового равновесия. При контакте тела обмениваются энергией, которая передается и получает название количества теплоты.
Тепловым равновесием называют состояние системы тел, которые находятся в тепловом контакте с теплопередачей и с постоянными макроскопическими параметрами.
Температура – физический параметр, который находится в тепловом равновесии. Введение понятия температуры идет из нулевого закона термодинамики.
Температура измеряется с помощью термометра. Для его создания выбирается термометрическое вещество и величину, которая его характеризует. Разные конструкции подразумевают отличия в их свойствах.
Каждый термометр должен быть откалиброван. Использование природных систем с неизменной температурой необходимо для хорошего теплообмена. Температура плавления льда равняется 0 градусов Цельсия, а точка кипения воды – 100 градусов. Одно маленькое деление из шкалы равняется 1 градусу. Существует обозначение замерзания воды по Фаренгейту, то есть 32 °F. Получаем, что формула примет вид TF=95TC+32 или TC=59(TF-32).
На рисунке 3.2.4. изображен газовый термометр, который чаще всего заполняют разряженным гелием, воздухом с неизменным объемом, обозначаемым V = const, и давлением р. Из опыта видно, что возрастание давления идет с повышением температуры по Цельсию.
Рисунок 3.2.4. Газовый термометр с постоянным объемом.
Температура кипения газов при давлении
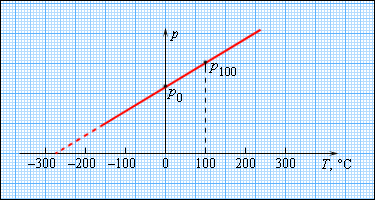
Чтобы произвести калибровку газового термометра, следует выполнить измерение состояния молекул при 0 и 100 градусах. Для этого мы наносим точки p0 и p100 на график, после чего проводим прямую линию, как изображено на рисунке 3.2.5. Получившийся калибровочный график способен определить температуру с разными значениями давления. При низких температурах возможно нахождение ее «гипотетической». Из опыта видно, что на свойства газа не влияет температура в-273,15 °С. При понижении температур газ переходит в жидкое или твердое состояние, поэтому получение охлажденного газа невозможно.
Рисунок 3.2.5. Зависимость давления газа от температуры при V = const.
В 1848 году У. Кельвин предлагает использовать точку нулевого давления газа для составления шкалы. Отличие от измерений температуры в Цельсиях в том, что нулевая точка сдвинута на TК =TС+273,15.
По системе СИ температура измеряется по Кельвину и обозначается К. Тогда комнатная температура запишется TС=20 °С, а по Кельвину – TК=293,15 К.
Температура кипения газов. Шкала Кельвина
Температурная шкала Кельвина считается абсолютной. Она наиболее приемлема для обозначения физических теорий.
Шкала Кельвина может быть не привязана двумя фиксированными точками, а именно: точка плавления льда и кипения воды с нормальным атмосферным давлением.
Нулевое давление называется абсолютным нулем температуры.
Шкала Кельвина имеет точку, в которой лед, вода и пар будут находиться в тепловом равновесии. Для калибровки других термометров применяют газовые, так как для практики они не подходят в виду своих больших размеров. Отсюда следует, что давление разреженного газа в сосуде постоянного объема V изменяется прямо пропорционально его абсолютной температуре, то есть p~T. Из опыта видно, что неизменный объем V и температура давления T прямо пропорциональны количеству вещества в сосуде к его объему: p~υV=NNAV=nNA~n, где N принимает обозначение числа молекул в сосуде, а NА – постоянная Авогадро, n=NV – концентрации молекул.
После объединения соотношений получим, что запись примет вид p=nkT, где k считается универсальной постоянной величиной для всех газов, иначе говоря, постоянная Больцмана. Этот ученый являлся одним из создателей опытного обоснования основных положений молекулярно-кинетической теории. Ее обозначение в системе СИ k=1,38ċ10–23 Дж/К.
При сравнении соотношения p=nkT с уравнением МКТ газов, получим EK→.
Средняя кинетическая энергия беспорядочного движения молекул газа прямо пропорциональна абсолютной температуре.
Температура является мерой для кинетической энергии молекул, которая не зависит от ее величины. Броуновская частица из жидкости и газа обладает аналогичной средней кинетической энергией, как и другая отдельная молекула. Это суждение верно для разномассовых молекул, находящихся в одном сосуде. Состояние равновесия говорит о том, что на них действуют одинаковые средние кинетические энергии, которые определяются температурой смеси. Запись давления смеси газов запишется как сумма парциальных давлений каждого из них: p=p1+p2+p3+…=(n1+n2+n3+ …)kT.
Отсюда видно, что n1, n2, n3,… является концентрацией молекул газов в смеси. Выражение относят к молекулярно-кинетической теории, установленной Дальтоном: давление в смеси химически невзаимодействующих газов равняется сумме их парциальных давлений.
Содержание:
Температура:
Перед тем как, например, пойти на пляж, многие интересуются прогнозом погоды. И если ожидается температура воздуха 10 °С, то, скорее всего, планы будут изменены. А стоит ли отказываться от прогулки, если прогнозируется температура 300 К (кельвинов)? И что на самом деле вкладывают физики в понятие «температура»?
Что такое температура
Эксперименты показывают, что макроскопическая система может переходить из одного состояния в другое. Например, если в морозный день занести в комнату шарик, наполненный гелием, то гелий в шарике будет нагреваться и при этом будут изменяться давление, объем и некоторые другие параметры газа. После того как шарик пробудет в комнате некоторое время, изменения прекратятся. Один из постулатов молекулярной физики и термодинамики — его еще называют нулевое начало термодинамики — гласит: любое макроскопическое тело или система тел при неизменных внешних условиях самопроизвольно переходит в термодинамическое равновесное состояние (состояние теплового равновесия), после достижения которого все части системы имеют одинаковую температуру. Нулевое начало термодинамики фактически вводит и определяет понятие температуры.
Температура — физическая величина, характеризующая состояние теплового равновесия макроскопической системы.
Состояние теплового равновесия — это такое состояние макроскопической системы, при котором все макроскопические параметры системы остаются неизменными сколь угодно долго.
В состоянии теплового равновесия все части системы имеют одинаковую температуру; другие макроскопические параметры неизменны, но могут быть разными. Вспомните пример с шариком: после того как установится тепловое равновесие, температура окружающего воздуха и температура гелия в шарике будут одинаковыми, а давление, плотность и объем — разными.
Как работают термометры
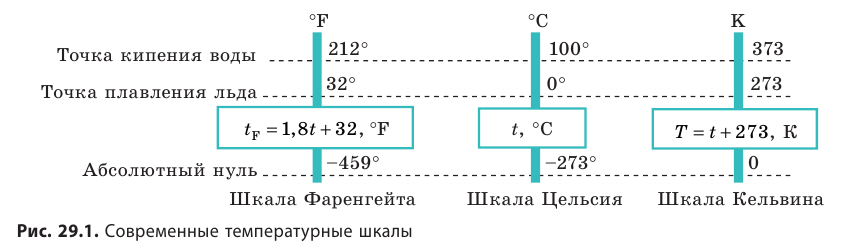
Температура — это физическая величина, и ее можно измерять. Для этого нужно установить шкалу температур. Самые распространенные температурные шкалы — шкалы Цельсия, Кельвина, Фаренгейта (рис. 29.1).
Построение шкалы температур начинается с выбора реперных (опорных) точек, которые должны быть однозначно связаны с какими-либо физическими процессами, которые легко воспроизвести. Например, за нулевую точку температурной шкалы Цельсия принята температура таяния льда при нормальном атмосферном давлении ( t = 0 °С). Температуре кипения воды при нормальном атмосферном давлении приписывают значение t =100 °С. Единица температуры по шкале Цельсия — градус Цельсия: 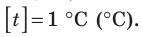
Рис. 29.2. различные виды термометров: а — жидкостный (принцип действия: изменение объема жидкости при изменении температуры); б — термометр сопротивления (изменение электрического сопротивления проводника при изменении температуры); в — биметаллический деформационный (изменение длин двух разных металлических пластин при изменении температуры)
Приборы для измерения температуры — термометры (рис. 29.2). Основные части любого термометра — термометрическое тело (ртуть или спирт в жидкостном термометре, биметаллическая пластина в металлическом деформационном термометре и т. д.) и шкала. Если термометрическое тело привести в контакт с телом, температуру которого нужно измерить, система придет в неравновесное состояние. При переходе в равновесное состояние будут изменяться некоторые параметры термометрического тела (объем, сопротивление и т. п.). Зная, как эти параметры зависят от температуры, определяют температуру тела.
Обратите внимание!
- Термометр фиксирует собственную температуру, равную температуре тела, с которым термометр находится в термодинамическом равновесии.
- Термометрическое тело не должно быть массивным, иначе оно существенно изменит температуру тела, с которым контактирует.
Температура и средняя кинетическая энергия молекул
То, что температура тела должна быть связана с кинетической энергией его молекул, следует из простых соображений. Например, с увеличением температуры увеличивается скорость движения броуновских частиц, ускоряется диффузия, повышается давление газа, а это значит, что молекулы движутся быстрее и их кинетическая энергия становится больше. Можно предположить: если газы находятся в состоянии теплового равновесия, средние кинетические энергии молекул этих газов одинаковы. Но как это доказать, ведь непосредственно измерить эти энергии невозможно?
Обратимся к основному уравнению МКТ идеального газа: 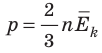
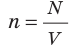
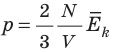
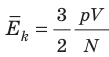
Таким образом, чтобы экспериментально убедиться в равенстве средних кинетических энергий молекул различных газов при одинаковой температуре, нужно измерить объемы (V), давления (p) и массы (m) газов и, зная их молярную массу (M), найти число молекул каждого газа (N) по формуле 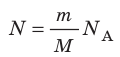
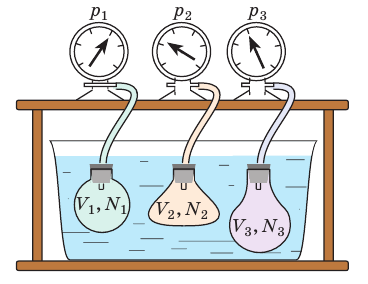
Чтобы обеспечить одинаковую температуру, можно, например, погрузить баллоны с различными газами в сосуд с водой и дождаться состояния теплового равновесия (рис. 29.3).
Рис. 29.3. опыт, позволяющий установить связь между температурой и средней кинетической энергией поступательного движения молекул газа. Газы в сосудах находятся в состоянии теплового равновесия со средой, а следовательно, и друг с другом
Эксперименты показывают, что для всех газов в состоянии теплового равновесия отношение 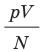
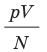
Например, при температуре 0 °С (сосуды с газами погрузили в тающий лед) 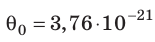
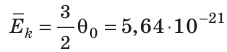
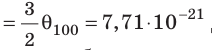
Абсолютная шкала температур
Понятно, что в джоулях представлять температуру неудобно (прежде всего потому, что значения θ очень малы), к тому же неудобно полностью отказываться от шкалы Цельсия. В 1848 г. английский физик Уильям Томсон (лорд Кельвин) (1824–1907) предложил абсолютную шкалу температур (сейчас ее называют шкалой Кельвина).
Температуру Т, измеренную по шкале кельвина, называют абсолютной температурой.
Единица абсолютной температуры — кельвин — основная единица СИ: [T] = 1 К (К).
Шкала Кельвина построена следующим образом:
- изменение температуры по шкале Кельвина равно изменению температуры по шкале Цельсия: ∆ = T t ∆ , то есть цена деления шкалы Кельвина равна цене деления шкалы Цельсия: 1 °С = 1 К; температуры, измеренные по шкалам Кельвина и Цельсия, связаны соотношениями:
- температура по шкале Кельвина связана с величиной
соотношением θ = kT, где k — постоянная Больцмана — коэффициент пропорциональности, не зависящий ни от температуры, ни от состава и количества газа:
- абсолютная температура имеет глубокий физический смысл: средняя кинетическая энергия поступательного движения молекул идеального газа прямо пропорциональна абсолютной температуре:
(1) То есть, если газ охладить до температуры T= 0 К, движение его молекул должно прекратиться (
). Таким образом, нулевая точка шкалы Кельвина — это самая низкая теоретически возможная температура. На самом деле движение молекул не прекращается никогда, поэтому достичь температуры 0 К (–273 °С) невозможно.
Абсолютный нижний предел температуры, при котором движение молекул и атомов должно прекратиться, называют абсолютным нулем температуры. Давление p газа полностью определяется его абсолютной температурой T и концентрацией n молекул газа: p=nkT (2).
Выводы:
- Физическая величина, характеризующая состояние теплового равновесия макроскопической системы, называется температурой. Абсолютный нижний предел температуры, при котором движение молекул и атомов должно прекратиться, называют абсолютным нулем температуры. Шкала, за нулевую точку которой взят абсолютный нуль температуры, называется абсолютной шкалой температур (шкалой Кельвина). Единица абсолютной температуры — кельвин (К) — основная единица СИ. Температуры по шкале Кельвина и Цельсия связаны соотношением: T=t + 273; t=T – 273.
- Средняя кинетическая энергия поступательного движения молекул идеального газа прямо пропорциональна абсолютной температуре, а давление газа определяется абсолютной температурой и концентрацией молекул газа:
— постоянная Больцмана.
- Парообразование и конденсация
- Тепловое равновесие в физике
- Изопроцессы в физике
- Твердые тела и их свойства в физике
- Механизмы, работающие на основе правила моментов
- Идеальный газ в физике
- Уравнение МКТ идеального газа
- Уравнение состояния идеального газа
Идеальный газ — газ, удовлетворяющий трем условиям:
- Молекулы — материальные точки.
- Потенциальная энергия взаимодействия молекул пренебрежительно мала.
- Столкновения между молекулами являются абсолютно упругими.
Реальный газ с малой плотностью можно считать идеальным газом.
Измерение температуры
Температуру можно измерять по шкале Цельсия и шкале Кельвина. По шкале Цельсия за нуль принимается температура, при которой происходит плавление льда. По шкале Кельвина за нуль принимается абсолютный нуль — температура, при котором давление идеального газа равно нулю, и его объем тоже равен нулю.
Обозначение температуры
- По шкале Цельсия — t. Единица измерения — 1 градус Цельсия (1 oC).
- По шкале Кельвина — T. Единица измерения — 1 Кельвин (1 К).
Цена деления обеих шкал составляет 1 градус. Поэтому изменение температуры в градусах Цельсия равно изменению температуры в Кельвинах:
∆t = ∆T
При решении задач в МКТ используют значения температуры по шкале Кельвина. Если в условиях задачи температура задается в градусах Цельсия, нужно их перевести в Кельвины. Это можно сделать по формуле:
T = t + 273
Если особо важна точность, следует использовать более точную формулу:
T = t + 273,15
Пример №1. Температура воды равна oC. Определить температуру воды в Кельвинах.
T = t + 273 = 2 + 273 = 275 (К)
Основное уравнение МКТ идеального газа
Давление идеального газа обусловлено беспорядочным движением молекул, которые сталкиваются друг с другом и со стенками сосуда. Основное уравнение МКТ идеального газа связывает давление и другие макропараметры (объем, температуру и массу) с микропараметрами (массой молекул, скоростью молекул и кинетической энергией).
Основное уравнение МКТ
Давление идеального газа пропорционально произведению концентрации молекул на среднюю кинетическую энергию поступательного движения молекулы.
p=23n−Ek
p — давление идеального газа, n — концентрация молекул газа, −Ek — средняя кинетическая энергия поступательного движения молекул.
Выражая физические величины друг через друга, можно получить следующие способы записи основного уравнения МКТ идеального газа:
|
p=13m0n−v2 |
m0— масса одной молекулы газа; n — концентрация молекул газа; −v2 — среднее значение квадрата скорости молекул газа. Среднее значение квадрата скорости не следует путать со среднеквадратичной скоростью v, которая равна корню из среднего значения квадрата скорости: v=√−v2 |
|
p=13ρ−v2 |
ρ — плотность газа |
|
p=nkT |
k — постоянная Больцмана (k = 1,38∙10–3 Дж/кг) T — температура газа по шкале Кельвина |
Пример №2. Во сколько раз уменьшится давление идеального одноатомного газа, если среднюю кинетическую энергию теплового движения молекул и концентрацию уменьшить в 2 раза?
Согласно основному уравнению МКТ идеального газа, давление прямо пропорционально произведению средней кинетической энергии теплового движения молекул и концентрации его молекул. Следовательно, если каждая из этих величин уменьшится в 2 раза, то давление уменьшится в 4 раза:
Следствия из основного уравнения МКТ идеального газа
Через основное уравнение МКТ идеального газа можно выразить скорость движения молекул (частиц газа):
v=√3kTm0=√3RTM
R — универсальная газовая постоянная, равная произведения постоянной Авогадро на постоянную Больцмана:
R=NAk=8,31 Дж/К·моль
Температура — мера кинетической энергии молекул идеального газа:
−Ek=32kT
T=2−Ek3k
Полная энергия поступательного движения молекул газа определяется формулой:
E=N−Ek
Пример №3. При уменьшении абсолютной температуры на 600 К средняя кинетическая энергия теплового движения молекул неона уменьшилась в 4 раза. Какова начальная температура газа?
Запишем формулу, связывающую температуру со средней кинетической энергией теплового движения молекул, для обоих случаев, с учетом что:
Следовательно:
Составим систему уравнений:
Отсюда:
Задание EF19012

Алгоритм решения
1.Указать, в каких координатах построен график.
2.На основании основного уравнения МКТ идеального газа и уравнения Менделеева — Клапейрона выяснить, как меняются указанные физические величины во время процессов 1–2 и 2–3.
Решение
График построен в координатах (V;Ek). Процесс 1–2 представляет собой прямую линию, исходящую из начала координат. Это значит, что при увеличении объема растет средняя кинетическая энергия молекул. Но из основного уравнения МКТ идеального газа следует, что мерой кинетической энергии молекул является температура:
T=2−Ek3
Следовательно, когда кинетическая энергия молекул растет, температура тоже растет.
Запишем уравнение Менделеева — Клапейрона:
pV=νRT
Так как количество вещества одинаковое для обоих состояния 1 и 2, запишем:
νR=p1V1T1=p2V2T2
Мы уже выяснили, что объем и температура увеличиваются пропорционально. Следовательно, давление в состояниях 1 и 2 равны. Поэтому процесс 1–2 является изобарным, давление во время него не меняется.
Процесс 2–3 имеет график в виде прямой линии, перпендикулярной кинетической энергии. Так как температуры прямо пропорциональна кинетической энергии, она остается постоянной вместе с этой энергией. Следовательно, процесс 2–3 является изотермическим, температура во время него не меняется. Мы видим, что объем при этом процессе уменьшается. Но так как объем и давление — обратно пропорциональные величины, то давление на участке 2–3 увеличивается.
Ответ:
• Участок 1–2 — изобарный процесс. Температура увеличивается, давление постоянно.
• Участок 2–3 — изотермический процесс. Температура постоянно, давление увеличивается.
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17560
Первоначальное давление газа в сосуде равнялось р1. Увеличив объём сосуда, концентрацию молекул газа уменьшили в 3 раза, и одновременно в 2 раза увеличили среднюю энергию хаотичного движения молекул газа. В результате этого давление р2 газа в сосуде стало равным
Ответ:
а) 13p1
б) 2p1
в) 23p1
г) 43p1
Алгоритм решения
1.Записать исходные данные.
2.Записать основное уравнение МКТ идеального газа.
3.Составить уравнения для состояний 1 и 2.
4.Выразить искомую величину.
Решение
Исходные данные:
• Начальное давление: p0.
• Начальная концентрация молекул: n1 = 3n.
• Конечная концентрация молекул: n2 = n.
• Начальная средняя энергия хаотичного движения молекул: Ek1 = Ek.
• Конечная средняя энергия хаотичного движения молекул: Ek2 = 2Ek.
Основное уравнение МКТ:
p=23n−Ek
Составим уравнения для начального и конечного состояний:
p1=23n1−Ek1=233n−Ek=2n−Ek
p2=23n2−Ek2=23n2−Ek=43n−Ek
Отсюда:
n−Ek=p12=3p24
p2=4p16=23p1
Ответ: в
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18416
Цилиндрический сосуд разделён неподвижной теплоизолирующей перегородкой. В одной части сосуда находится кислород, в другой – водород, концентрации газов одинаковы. Давление кислорода в 2 раза больше давления водорода. Чему равно отношение средней кинетической энергии молекул кислорода к средней кинетической энергии молекул водорода?
Алгоритм решения
1.Записать исходные данные.
2.Записать основное уравнение МКТ идеального газа.
3.Составить уравнения для обоих газов.
4.Найти отношение средней кинетической энергии молекул кислорода к средней кинетической энергии молекул водорода.
Решение
Анализируя условия задачи, можно выделить следующие данные:
• Концентрации кислорода и водорода в сосуде равны. Следовательно, n1 = n2 = n.
• Давление кислорода вдвое выше давления водорода. Следовательно, p1 = 2p, а p2 = p.
Запишем основное уравнение идеального газа:
p=23n−Ek
Применим его для обоих газов и получим:
p1=23n1−Ek1 или 2p=23n−Ek1
p2=23n2−Ek2 или p=23n−Ek2
Выразим среднюю кинетическую энергию молекул газа из каждого уравнения:
−Ek1=3pn
−Ek2=3p2n
Поделим уравнения друг на друга и получим:
−Ek1−Ek2=3pn·2n3p=2
Ответ: 2
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18824
В одном сосуде находится аргон, а в другом – неон. Средние кинетические энергии теплового движения молекул газов одинаковы. Давление аргона в 2 раза больше давления неона. Чему равно отношение концентрации молекул аргона к концентрации молекул неона?
Алгоритм решения
1.Записать исходные данные.
2.Записать основное уравнение МКТ идеального газа.
3.Составить уравнения для обоих газов.
4.Найти отношение концентрации молекул аргона к концентрации молекул неона.
Решение
Анализируя условия задачи, можно выделить следующие данные:
• Средние кинетические энергии теплового движения молекул газов одинаковы. Следовательно, −Ek1=−Ek2=−Ek.
• Давление аргона в 2 раза больше давления неона. Следовательно, p1 = 2p, а p2 = p.
Запишем основное уравнение идеального газа:
p=23n−Ek
Применим его для обоих газов и получим:
p1=23n1−Ek1 или 2p=23n1−Ek
p2=23n2−Ek2 или p=23n2−Ek
Выразим концентрации молекул газа из каждого уравнения:
n1=3p−Ek
n2=3p2−Ek
Поделим уравнения друг на друга и получим:
n1n2=3p−Ek·2−Ek3p=2
Ответ: 2
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 10.7k
- Подробности
- Обновлено 30.05.2018 20:17
- Просмотров: 639
Задачи по физике – это просто!
Вспомним
1). Если масса газа не меняется:
2). Формулы газовых законов:
3). Если в условиях задачи задан переход из состояния p1V1T1 в состояние p2V2T2, используем формулу:
При этом, если один из параметров const, его можно сократить, и тогда мы получаем одну из формул газовых законов.
3). Если в условиях задачи известны только 2 параметра из трех (p,V,T), используем формулу:
Не забываем
Решать задачи надо всегда в системе СИ!
А теперь к задачам!
Типовые задачи из курса школьной физики по термодинамике на вычисление макропараметров (p,V,T) газа.
Задача 1
Найти массу природного горючего газа объемом 64 м3, считая, что объем указан при нормальных условиях. Молярную массу природного газа считать равной молярной массе метана (СН4).
Задача 2
Воздух объемом 1,45 м3, находящийся при температуре 20oC и давлении 100 кПа, превратили в жидкое состояние. Какой объем займет жидкий воздух, если его плотность 861 кг/м3?
Задача 3
Какое количество вещества содержится в газе, если при давлении 200 кПа и температуре 240 К его объем равен 40 литров?
Задача 4
В одинаковых баллонах при одинаковой температуре находятся водород (H2) и углекислый газ (CO2). Массы газов одинаковы. Какой из газов и во сколько раз производит большее давление на стенки баллона?
Задача 5
Газ при давлении 0,2 МПа и температуре 15оС имеет объем 5 литров. Чему равен объем газа этой массы при нормальных условиях?
Задача 6
При температуре 27оС давление газа в закрытом сосуде было 75 кПа. Каким будет давление при температуре -13оС?
Задача 7
В баллоне находится газ под давлением.
Определить, какой объем занимал бы этот газ при нормальных условиях (t=0oC, давление 101 325 Па), если известны объем баллона – V1, температура газа в баллоне – t1, давление газа в баллоне – p1.
Задача 8
Определить давление сжатого воздуха в баллоне, если известны вместимость баллона, температура и масса газа.
Задача 9
В баллоне находится смесь газов (гелий и аргон). Определить давление смеси газов на стенки сосуда, если известны вместимость баллона, температура смеси и масса каждого газа.
Задача 10
Определить молярную массу газа, если известна его плотность и температура при нормальном атмосферном давлении.
Задача 11
Баллон заполнен газом, известны вместимость баллона – V1, температура газа – t1 и давление газа – p1. Какой объем занимал бы этот газ при нормальных условиях (температура t2=0oC, давление р2= 101 325 Па)?
Задача 12
Определить температуру газа по шкале Цельсия, если объем 4 молей газа при давлении 100 кПа составляет 20 литров.
Задача 13
Определить массу воздуха объемом 40 литров при нормальном атмосферном давлении (101325 Па) и температуре 20oC.



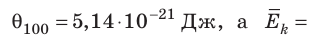
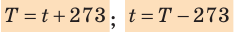
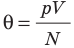 соотношением θ = kT, где k — постоянная Больцмана — коэффициент пропорциональности, не зависящий ни от температуры, ни от состава и количества газа:
соотношением θ = kT, где k — постоянная Больцмана — коэффициент пропорциональности, не зависящий ни от температуры, ни от состава и количества газа: 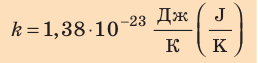
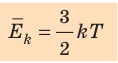 (1) То есть, если газ охладить до температуры T= 0 К, движение его молекул должно прекратиться (
(1) То есть, если газ охладить до температуры T= 0 К, движение его молекул должно прекратиться (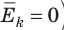 ). Таким образом, нулевая точка шкалы Кельвина — это самая низкая теоретически возможная температура. На самом деле движение молекул не прекращается никогда, поэтому достичь температуры 0 К (–273 °С) невозможно.
). Таким образом, нулевая точка шкалы Кельвина — это самая низкая теоретически возможная температура. На самом деле движение молекул не прекращается никогда, поэтому достичь температуры 0 К (–273 °С) невозможно.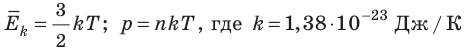 — постоянная Больцмана.
— постоянная Больцмана.