Содержание:
Температура:
Перед тем как, например, пойти на пляж, многие интересуются прогнозом погоды. И если ожидается температура воздуха 10 °С, то, скорее всего, планы будут изменены. А стоит ли отказываться от прогулки, если прогнозируется температура 300 К (кельвинов)? И что на самом деле вкладывают физики в понятие «температура»?

Что такое температура
Эксперименты показывают, что макроскопическая система может переходить из одного состояния в другое. Например, если в морозный день занести в комнату шарик, наполненный гелием, то гелий в шарике будет нагреваться и при этом будут изменяться давление, объем и некоторые другие параметры газа. После того как шарик пробудет в комнате некоторое время, изменения прекратятся. Один из постулатов молекулярной физики и термодинамики — его еще называют нулевое начало термодинамики — гласит: любое макроскопическое тело или система тел при неизменных внешних условиях самопроизвольно переходит в термодинамическое равновесное состояние (состояние теплового равновесия), после достижения которого все части системы имеют одинаковую температуру. Нулевое начало термодинамики фактически вводит и определяет понятие температуры.
Температура — физическая величина, характеризующая состояние теплового равновесия макроскопической системы.
Состояние теплового равновесия — это такое состояние макроскопической системы, при котором все макроскопические параметры системы остаются неизменными сколь угодно долго.
В состоянии теплового равновесия все части системы имеют одинаковую температуру; другие макроскопические параметры неизменны, но могут быть разными. Вспомните пример с шариком: после того как установится тепловое равновесие, температура окружающего воздуха и температура гелия в шарике будут одинаковыми, а давление, плотность и объем — разными.
Как работают термометры
Температура — это физическая величина, и ее можно измерять. Для этого нужно установить шкалу температур. Самые распространенные температурные шкалы — шкалы Цельсия, Кельвина, Фаренгейта (рис. 29.1).
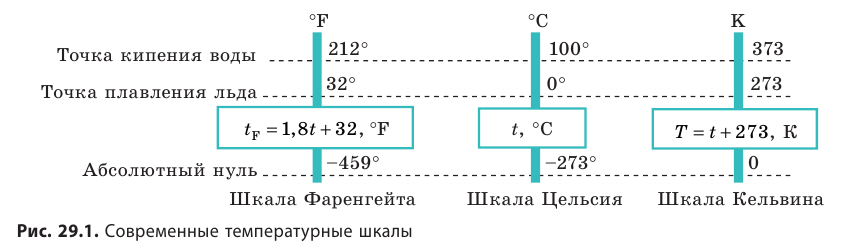
Построение шкалы температур начинается с выбора реперных (опорных) точек, которые должны быть однозначно связаны с какими-либо физическими процессами, которые легко воспроизвести. Например, за нулевую точку температурной шкалы Цельсия принята температура таяния льда при нормальном атмосферном давлении ( t = 0 °С). Температуре кипения воды при нормальном атмосферном давлении приписывают значение t =100 °С. Единица температуры по шкале Цельсия — градус Цельсия: 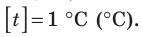 .
.

Рис. 29.2. различные виды термометров: а — жидкостный (принцип действия: изменение объема жидкости при изменении температуры); б — термометр сопротивления (изменение электрического сопротивления проводника при изменении температуры); в — биметаллический деформационный (изменение длин двух разных металлических пластин при изменении температуры)
Приборы для измерения температуры — термометры (рис. 29.2). Основные части любого термометра — термометрическое тело (ртуть или спирт в жидкостном термометре, биметаллическая пластина в металлическом деформационном термометре и т. д.) и шкала. Если термометрическое тело привести в контакт с телом, температуру которого нужно измерить, система придет в неравновесное состояние. При переходе в равновесное состояние будут изменяться некоторые параметры термометрического тела (объем, сопротивление и т. п.). Зная, как эти параметры зависят от температуры, определяют температуру тела.
Обратите внимание!
- Термометр фиксирует собственную температуру, равную температуре тела, с которым термометр находится в термодинамическом равновесии.
- Термометрическое тело не должно быть массивным, иначе оно существенно изменит температуру тела, с которым контактирует.
Температура и средняя кинетическая энергия молекул
То, что температура тела должна быть связана с кинетической энергией его молекул, следует из простых соображений. Например, с увеличением температуры увеличивается скорость движения броуновских частиц, ускоряется диффузия, повышается давление газа, а это значит, что молекулы движутся быстрее и их кинетическая энергия становится больше. Можно предположить: если газы находятся в состоянии теплового равновесия, средние кинетические энергии молекул этих газов одинаковы. Но как это доказать, ведь непосредственно измерить эти энергии невозможно?
Обратимся к основному уравнению МКТ идеального газа: 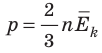 . По определению
. По определению 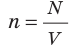 , поэтому
, поэтому 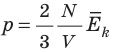 . После преобразований получим:
. После преобразований получим: 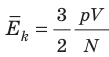 .
.
Таким образом, чтобы экспериментально убедиться в равенстве средних кинетических энергий молекул различных газов при одинаковой температуре, нужно измерить объемы (V), давления (p) и массы (m) газов и, зная их молярную массу (M), найти число молекул каждого газа (N) по формуле 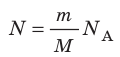 .
.
Чтобы обеспечить одинаковую температуру, можно, например, погрузить баллоны с различными газами в сосуд с водой и дождаться состояния теплового равновесия (рис. 29.3).
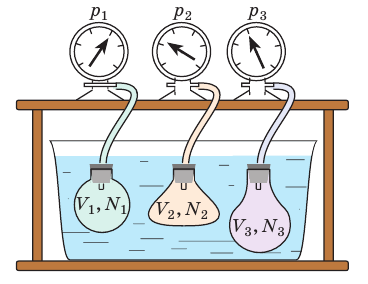
Рис. 29.3. опыт, позволяющий установить связь между температурой и средней кинетической энергией поступательного движения молекул газа. Газы в сосудах находятся в состоянии теплового равновесия со средой, а следовательно, и друг с другом
Эксперименты показывают, что для всех газов в состоянии теплового равновесия отношение 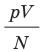 одинаково, а следовательно, одинаковыми являются и средние кинетические энергии молекул газов. (Отношение
одинаково, а следовательно, одинаковыми являются и средние кинетические энергии молекул газов. (Отношение 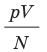 часто обозначают символом θ (тета).)
часто обозначают символом θ (тета).)
Например, при температуре 0 °С (сосуды с газами погрузили в тающий лед) 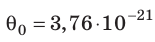 , Дж, то есть
, Дж, то есть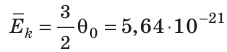 Дж; при температуре 100 °С (сосуды погрузили в кипящую воду)
Дж; при температуре 100 °С (сосуды погрузили в кипящую воду) 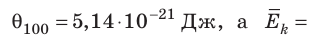
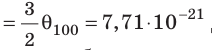 Дж. Так как в состоянии теплового равновесия значение θ для любых газов одинаково, то температуру можно измерять в джоулях.
Дж. Так как в состоянии теплового равновесия значение θ для любых газов одинаково, то температуру можно измерять в джоулях.
Абсолютная шкала температур
Понятно, что в джоулях представлять температуру неудобно (прежде всего потому, что значения θ очень малы), к тому же неудобно полностью отказываться от шкалы Цельсия. В 1848 г. английский физик Уильям Томсон (лорд Кельвин) (1824–1907) предложил абсолютную шкалу температур (сейчас ее называют шкалой Кельвина).
Температуру Т, измеренную по шкале кельвина, называют абсолютной температурой.
Единица абсолютной температуры — кельвин — основная единица СИ: [T] = 1 К (К).
Шкала Кельвина построена следующим образом:
- изменение температуры по шкале Кельвина равно изменению температуры по шкале Цельсия: ∆ = T t ∆ , то есть цена деления шкалы Кельвина равна цене деления шкалы Цельсия: 1 °С = 1 К; температуры, измеренные по шкалам Кельвина и Цельсия, связаны соотношениями:
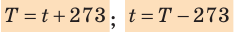
- температура по шкале Кельвина связана с величиной
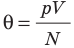 соотношением θ = kT, где k — постоянная Больцмана — коэффициент пропорциональности, не зависящий ни от температуры, ни от состава и количества газа:
соотношением θ = kT, где k — постоянная Больцмана — коэффициент пропорциональности, не зависящий ни от температуры, ни от состава и количества газа: 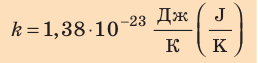
- абсолютная температура имеет глубокий физический смысл: средняя кинетическая энергия поступательного движения молекул идеального газа прямо пропорциональна абсолютной температуре:
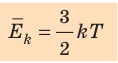 (1) То есть, если газ охладить до температуры T= 0 К, движение его молекул должно прекратиться (
(1) То есть, если газ охладить до температуры T= 0 К, движение его молекул должно прекратиться (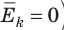 ). Таким образом, нулевая точка шкалы Кельвина — это самая низкая теоретически возможная температура. На самом деле движение молекул не прекращается никогда, поэтому достичь температуры 0 К (–273 °С) невозможно.
). Таким образом, нулевая точка шкалы Кельвина — это самая низкая теоретически возможная температура. На самом деле движение молекул не прекращается никогда, поэтому достичь температуры 0 К (–273 °С) невозможно.
Абсолютный нижний предел температуры, при котором движение молекул и атомов должно прекратиться, называют абсолютным нулем температуры. Давление p газа полностью определяется его абсолютной температурой T и концентрацией n молекул газа: p=nkT (2).
Выводы:
- Физическая величина, характеризующая состояние теплового равновесия макроскопической системы, называется температурой. Абсолютный нижний предел температуры, при котором движение молекул и атомов должно прекратиться, называют абсолютным нулем температуры. Шкала, за нулевую точку которой взят абсолютный нуль температуры, называется абсолютной шкалой температур (шкалой Кельвина). Единица абсолютной температуры — кельвин (К) — основная единица СИ. Температуры по шкале Кельвина и Цельсия связаны соотношением: T=t + 273; t=T – 273.
- Средняя кинетическая энергия поступательного движения молекул идеального газа прямо пропорциональна абсолютной температуре, а давление газа определяется абсолютной температурой и концентрацией молекул газа:
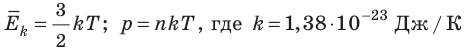 — постоянная Больцмана.
— постоянная Больцмана.
- Парообразование и конденсация
- Тепловое равновесие в физике
- Изопроцессы в физике
- Твердые тела и их свойства в физике
- Механизмы, работающие на основе правила моментов
- Идеальный газ в физике
- Уравнение МКТ идеального газа
- Уравнение состояния идеального газа
| Температура | |
|---|---|
 , ,  |
|
| Размерность | Θ |
| Единицы измерения | |
| СИ | К |
| СГС | К |
Температу́ра (от лат. temperatura — надлежащее смешение, нормальное состояние) — скалярная физическая величина, характеризующая термодинамическую систему и количественно выражающая интуитивное понятие о различной степени нагретости тел.
Живые существа способны воспринимать ощущения тепла и холода непосредственно, с помощью органов чувств. Однако точное определение температуры требует, чтобы температура измерялась объективно, с помощью приборов. Такие приборы называются термометрами и измеряют так называемую эмпирическую температуру. В эмпирической шкале температур устанавливаются одни реперные точки и число делений между ними — так были введены используемые ныне шкалы Цельсия, Фаренгейта и другие. Измеряемая в кельвинах абсолютная температура вводится по одной реперной точке[1] с учётом того, что в природе существует минимальное предельное значение температуры — абсолютный нуль. Верхнее значение температуры ограничено планковской температурой.
Если система находится в тепловом равновесии, то температура всех её частей одинакова. В противном случае в системе происходит передача энергии от более нагретых частей системы к менее нагретым, приводящая к выравниванию температур в системе, и говорят о распределении температуры в системе или скалярном поле температур. В термодинамике температура — интенсивная термодинамическая величина.
Наряду с термодинамическим, в других разделах физики могут вводиться и другие определения температуры. В молекулярно-кинетической теории показывается, что температура пропорциональна средней кинетической энергии частиц системы. Температура определяет распределение частиц системы по уровням энергии (см. Статистика Максвелла — Больцмана), распределение частиц по скоростям (см. Распределение Максвелла), степень ионизации вещества (см. Уравнение Саха), спектральную плотность излучения (см. Формула Планка), полную объёмную плотность излучения (см. Закон Стефана — Больцмана) и т. д. Температуру, входящую в качестве параметра в распределение Больцмана, часто называют температурой возбуждения, в распределение Максвелла — кинетической температурой, в формулу Саха — ионизационной температурой, в закон Стефана — Больцмана — радиационной температурой. Для системы, находящейся в термодинамическом равновесии, все эти параметры равны друг другу, и их называют просто температурой системы[2].
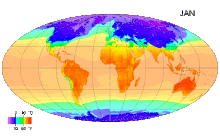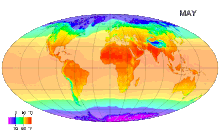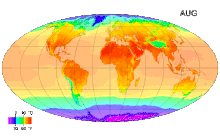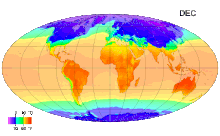
Среднемесячные температуры поверхности с 1961 по 1990 годы

Среднегодовая температура по всему миру

Тепловые колебания сегмента альфа-спирали белка: амплитуда колебаний увеличивается с повышением температуры.
В Международной системе величин (англ. International System of Quantities, ISQ) термодинамическая температура выбрана в качестве одной из семи основных физических величин системы. В Международной системе единиц (СИ), основанной на Международной системе величин, единица этой температуры — кельвин — является одной из семи основных единиц СИ[3]. В системе СИ и на практике используется также температура Цельсия, её единицей является градус Цельсия (°С), по размеру равный кельвину[4]. Это удобно, так как большинство климатических процессов на Земле и процессов в живой природе связаны с диапазоном от −50 до +50 °С.
Температура как локальный параметр. Температурное поле[править | править код]
Физика сплошных сред рассматривает температуру как локальную макроскопическую переменную, то есть величину, характеризующую мысленно выделяемую область (элементарный объём) сплошной среды (континуума), размеры которой бесконечно малы по сравнению с неоднородностями среды и бесконечно велики по отношению к размерам частиц (атомов, ионов, молекул и т. п.) этой среды[5]. Значение температуры может меняться от точки к точке (от одного элементарного объёма к другому); распределение температуры в пространстве в данный момент времени задаётся скалярным полем температуры (температурным полем)[6]. Температурное поле может быть как нестационарным (изменяющимся во времени), так и не зависящим от времени стационарным. Среду с одинаковыми во всех точках значениями температуры называют термически однородной. Математически температурное поле описывают уравнением зависимости температуры 

Термодинамическое определение[править | править код]
История термодинамического подхода[править | править код]
Слово «температура» возникло в те времена, когда люди считали, что в более нагретых телах содержится большее количество особого вещества — теплорода, чем в менее нагретых[источник не указан 3468 дней][7].
В равновесном состоянии температура имеет одинаковое значение для всех макроскопических частей системы. Если в системе два тела имеют одинаковую температуру, то между ними не происходит передачи кинетической энергии частиц (тепла). Если же существует разница температур, то тепло переходит от тела с более высокой температурой к телу с более низкой.
Температура связана также с субъективными ощущениями «тепла» и «холода», связанными с тем, отдаёт ли живая ткань тепло или получает его.
Некоторые квантовомеханические системы (например, рабочее тело лазера, в котором присутствуют инверсно заселённые уровни) могут находиться в состоянии, при котором энтропия не возрастает, а убывает при добавлении энергии, что формально соответствует отрицательной абсолютной температуре. Однако такие состояния находятся не «ниже абсолютного нуля», а «выше бесконечности», поскольку при контакте такой системы с телом, обладающим положительной температурой, энергия передаётся от системы к телу, а не наоборот (подробнее см. Отрицательная абсолютная температура).
Свойства температуры изучает раздел физики — термодинамика. Температура также играет важную роль во многих областях науки, включая другие разделы физики, а также химию и биологию.
Равновесная и неравновесная температуры[править | править код]
Система, находящаяся в состоянии термодинамического равновесия, имеет стационарное температурное поле. Если в такой системе отсутствуют адиабатические (энергонепроницаемые) перегородки, то все части системы имеют одну и ту же температуру. Иначе говоря, равновесная температура термически однородной системы не зависит явно от времени (но может меняться в квазистатических процессах). Неравновесная система в общем случае имеет нестационарное температурное поле, в котором каждый элементарный объём среды имеет собственную неравновесную температуру, в явном виде зависящую от времени.
Температура в феноменологической термодинамике[править | править код]
Определение температуры в феноменологической термодинамике зависит от способа построения математического аппарата данной дисциплины (см. Аксиоматика термодинамики).
Отличия в формальных определениях термодинамической температуры в различных системах построения термодинамики не означают большую наглядность некоторых из таких систем по сравнению с другими, ибо во всех этих системах, во-первых, в описательном определении температуру рассматривают как меру нагретости/охлаждённости тела, и, во-вторых, содержательные определения, устанавливающие связь между термодинамической температурой и используемыми для её измерения температурными шкалами, совпадают.
В рациональной термодинамике, изначально отвергающей деление этой дисциплины на термодинамику равновесную и термодинамику неравновесную (то есть не проводящей различия между равновесной и неравновесной температурами), температура есть первоначальная неопределяемая переменная, описываются только такими свойствами, которые можно выразить языком математики[8]. Понятия энергии, температуры, энтропии и химического потенциала вводятся в рациональной термодинамике одновременно; по отдельности определить их принципиально нельзя. Методика введения этих понятий показывает, что можно ввести в рассмотрение много различных температур, отвечающих разным энергетическим потокам. Например, можно ввести температуры трансляционных и спинорных движений, температуру радиационных излучений и т. д.[9].
Нулевое начало (закон) вводит в равновесную термодинамику понятие эмпирической температуры[10][11][12][13] как параметра состояния, равенство которого во всех точках есть условие термического равновесия в системе без адиабатических перегородок.
В подходе к построению термодинамики, используемом последователями Р. Клаузиуса[14], равновесные параметры состояния — термодинамическую температуру 


|
(Термодинамическая температура и энтропия по Клаузиусу) |
где 
В аксиоматике Каратеодори[15][16] 
В системе аксиом А. А. Гухмана[18][19] изменение внутренней энергии системы 



|
(Уравнение Гухмана) |
причём тепловым потенциалом служит термодинамическая температура 

В термодинамике Гиббса равновесную температуру выражают через внутреннюю энергию и энтропию[22][23][24]

|
(Термодинамическая температура по Гиббсу) |
где 
Аксиоматика Фалька и Юнга[25] при определении энтропии не делает различия между равновесными и неравновесными состояниями, и, следовательно, даваемое в этой системе аксиом определение температуры через энтропию и внутреннюю энергию одинаково применимо для любых термически однородных систем:
![Tequiv left[left({frac {partial S}{partial U}}right)_{{{x_{i}}}}right]^{{-1}},](https://wikimedia.org/api/rest_v1/media/math/render/svg/3199aedd04aecf0811bc8ef796f064be37d4cbac)
|
(Термодинамическая температура по Фальку и Юнгу) |
где 
Принцип локального равновесия разрешает для неравновесных систем заимствовать определение температуры из равновесной термодинамики и использовать данную переменную в качестве неравновесной температуры элементарного объёма среды[26].
В расширенной неравновесной термодинамике (РНТ), базирующейся на отказе от принципа локального равновесия, неравновесную температуру задают посредством соотношения, аналогичного используется в аксиоматике Фалька и Юнга (см. Термодинамическая температура по Фальку и Юнгу), но с другим набором независимых переменных для энтропии[27]. Локально-равновесная термодинамическая температура по Гиббсу также отличается от РНТ-неравновесной температуры выбором независимых переменных для энтропии[27].
В аксиоматике Н. И. Белоконя[28]. исходное определение температуры вытекает из постулата Белоконя, носящего название — постулат второго начала
термостатики. Температура есть единственная функция состояния тел, определяющая направление самопроизвольного теплообмена между этими телами, то есть тела, находящиеся в тепловом равновесии, имеют одинаковую температуру в любой температурной шкале. Отсюда следует, что два тела, не имеющие теплового контакта между собой, но каждое из которых находится в тепловом равновесии с третьим (измерительный прибор), имеют одинаковую температуру.
Эмпирическая, абсолютная и термодинамическая температуры[править | править код]
Температура не может быть измерена непосредственно. Об изменении температуры судят по изменению других физических свойств тел (объёма, давления, электрического сопротивления, ЭДС, интенсивности излучения и др.), однозначно с ней связанных (так называемых термометрических свойств). Количественно же температура определяется указанием способа её измерения с помощью того или иного термометра. Такое определение ещё не фиксирует ни начало отсчёта, ни единицу измерения температуры, поэтому любой метод измерения температуры связан с выбором температурной шкалы. Эмпирическая температура — это температура, измеренная в выбранной температурной шкале.
Даваемые феноменологической термодинамикой определения термодинамической температуры не зависят от выбора термометрического свойства, использованного для её измерения; единицу измерения температуры задают с помощью одной из термодинамических температурных шкал.
В термодинамике в качестве аксиомы принимается основанное на опыте положение о том, что равновесная термодинамическая температура есть величина, для всех систем ограниченная с одной стороны, причём температура, соответствующая этой границе, одинакова для всех термодинамических систем и, следовательно, может быть использована в качестве естественной реперной точки шкалы температур. Если этой реперной точке присвоить равное нулю значение температуры, то температуры в шкале, базирующейся на данном репере, всегда будут иметь один и тот же знак[29]. Приписывая второй реперной точке положительное значение температуры, получают абсолютную температурную шкалу с положительными температурами; температуру отсчитываемую от абсолютного нуля, называют абсолютной температурой[30]. Соответственно термодинамическую температуру, отсчитываемую от абсолютного нуля, называют абсолютной термодинамической температурой (см. Шкала температур Кельвина). Примером эмпирической температурной шкалы с отсчётом температуры от абсолютного нуля служит международная практическая температурная шкала.
Температурная шкала Цельсия не является абсолютной.
Некоторые авторы под абсолютностью температуры подразумевают не её отсчёт от абсолютного нуля, а независимость температуры от выбора термометрического свойства, используемого для её измерения[31][32].
Отрицательные абсолютные температуры[править | править код]
Равновесная термодинамическая абсолютная температура всегда положительна (см. Эмпирическая, абсолютная и термодинамическая температуры). Использование отрицательных (по шкале Кельвина) температур есть удобный математический приём описания неравновесных систем с особыми свойствами[33]. Приём этот состоит в мысленном выделении в самостоятельную подсистему объектов с особыми свойствами, входящих в состав физической системы, и сепаратном рассмотрении полученной парциальной подсистемы. Иными словами, один и тот же объём пространства рассматривается как одновременно занимаемый двумя и более парциальными подсистемами, слабо взаимодействующими друг с другом.
Примером использования данного подхода может служить рассмотрение ядерных спинов находящегося в магнитном поле кристалла как системы, слабо зависящей от тепловых колебаний кристаллической решётки. При быстром изменении направления магнитного поля на обратное, когда спины не успевают следовать за изменяющимся полем, система ядерных спинов некоторое время будет иметь отрицательную неравновесную температуру[34], то есть с формальной точки зрения в это время в одной и той же пространственной области будут находиться две слабо взаимодействующие системы с разными температурами[35]. В силу всё-таки имеющего место взаимодействия температуры обеих систем спустя какое-то время сравняются.
Формализм классической феноменологической термодинамики может быть дополнен представлениями об отрицательных абсолютных температурах[36][35]. В соответствии с постулатом Тиссы внутренняя энергия любой системы ограничена снизу, и эта граница соответствует абсолютному нулю температуры[37]. В системах, у которых имеется не только нижняя, но и верхняя граница внутренней энергии, с ростом температуры внутренняя энергия увеличивается и достигает своего предельного значения; дальнейшее повышение температуры 







Молекулярно-кинетическое определение[править | править код]
В молекулярно-кинетической теории (МКТ) температура определяется как величина, характеризующая приходящуюся на одну степень свободы среднюю кинетическую энергию частиц макроскопической системы, находящейся в состоянии термодинамического равновесия.
… мерилом температуры является не само движение, а хаотичность этого движения. Хаотичность состояния тела определяет его температурное состояние, и эта идея (которая впервые была разработана Больцманом), что определённое температурное состояние тела вовсе не определяется энергией движения, но хаотичностью этого движения, и является тем новым понятием в описании температурных явлений, которым мы должны пользоваться…П. Л. Капица[40]
Для одноатомного идеального газа температура может быть записана как
,
где 


Определение температуры в статистической физике[править | править код]
В статистической физике, как и в термодинамическом подходе, температура определяется производной от энергии системы по её энтропии:
(если объём и число частиц в системе неизменны, частная производная заменяется полной). В рамках статфизики существует конкретное выражение для энтропии, позволяющее выполнять вычисления:
,
где 


Введённая таким образом величина 

Измерение температуры[править | править код]

Типичный термометр со шкалой по Цельсию, показывающий −17 градусов
Для измерения термодинамической температуры выбирается некоторый термодинамический параметр термометрического вещества. Изменение этого параметра однозначно связывается с изменением температуры. Классическим примером термодинамического термометра может служить газовый термометр, в котором температуру определяют методом измерения давления газа в баллоне постоянного объёма. Известны также термометры абсолютные радиационные, шумовые, акустические.
Термодинамические термометры — это очень сложные установки, которые невозможно использовать для практических целей. Поэтому большинство измерений производится с помощью практических термометров, которые являются вторичными, так как не могут непосредственно связывать какое-то свойство вещества с температурой. Для получения функции интерполяции они должны быть отградуированы в реперных точках международной температурной шкалы.
Для измерения температуры какого-либо тела обычно измеряют какой-либо физический параметр, связанный с температурой, например, геометрические размеры (см. Дилатометр) для газов — объём или давление, скорость звука, электрическую проводимость, электромагнитные спектры поглощения или излучения (например, пирометры и измерение температуры фотосфер и атмосфер звёзд — в последнем случае по доплеровскому уширению спектральных линий поглощения или излучения).
В повседневной практике температуру обычно измеряют с помощью специальных приборов — контактных термометров. При этом термометр приводят в тепловой контакт с исследуемым телом, и, после установления термодинамического равновесия тела и термометра, — выравнивания их температур, по изменениям некоторого измеримого физического параметра термометра судят о температуре тела. Тепловой контакт между термометром и телом должен быть достаточным, чтобы выравнивание температур происходило быстрее, также, ускорение выравнивания температур достигается снижением теплоёмкости термометра по сравнению с исследуемым телом, обычно, уменьшением размеров термометра. Снижение теплоёмкости термометра также меньше искажает результаты измерения, так как меньшая часть теплоты исследуемого тела отбирается или передаётся термометру. Идеальный термометр имеет нулевую теплоёмкость[41].
Средства измерения температуры часто проградуированы по относительным шкалам — Цельсия или Фаренгейта.
На практике для измерения температуры также используют
- жидкостные и механические термометры,
- термопару,
- термометр сопротивления,
- газовый термометр,
- пирометр.
Самым точным практическим термометром является платиновый термометр сопротивления[42].
Разработаны новейшие методы измерения температуры, основанные на измерении параметров лазерного излучения[43].
Единицы и шкала измерения температуры[править | править код]
Поскольку температура — это мера средней кинетической энергии теплового движения частиц системы[44], наиболее естественно было бы измерять её в энергетических единицах (то есть в системе СИ в джоулях; см. также эВ). Исходя из соотношения температуры и энергии частиц в одноатомном идеальном газе Eкин = 3⁄2kТ[45]. В температурных единицах 1 эВ соответствует 11 604,518 12 К[46] (см. постоянная Больцмана)[47].
Однако измерение температуры началось задолго до создания молекулярно-кинетической теории, поэтому все практические шкалы измеряют температуру в условных единицах — градусах.
Абсолютная температура. Шкала температур Кельвина[править | править код]
Понятие абсолютной температуры было введено У. Томсоном (Кельвином), в связи с чем шкалу абсолютной температуры называют шкалой Кельвина или термодинамической температурной шкалой. Единица абсолютной температуры — кельвин (К).
Абсолютная шкала температуры называется так, потому что мера основного состояния нижнего предела температуры — абсолютный ноль, то есть наиболее низкая возможная температура, при которой в принципе невозможно извлечь из вещества тепловую энергию.
Абсолютный ноль определён как 0 K, что равно −273,15 °C и −459,67 °F.
Шкала температур Кельвина — это шкала, в которой начало отсчёта ведётся от абсолютного нуля.
Важное значение имеет разработка на основе термодинамической шкалы Кельвина Международных практических шкал, основанных на реперных точках — фазовых переходах чистых веществ, определенных методами первичной термометрии. Первой международной температурной шкалой являлась принятая в 1927 г. МТШ-27. С 1927 г. шкала несколько раз переопределялась (МТШ-48, МПТШ-68, МТШ-90): менялись реперные температуры, методы интерполяции, но принцип остался тот же — основой шкалы является набор фазовых переходов чистых веществ с определенными значениями термодинамических температур и интерполяционные приборы, градуированные в этих точках. В настоящее время действует шкала МТШ-90. Основной документ (Положение о шкале) устанавливает определение Кельвина, значения температур фазовых переходов (реперных точек)[48] и методы интерполяции.
Используемые в быту температурные шкалы — как Цельсия, так и Фаренгейта (используемая, в основном, в США), — не являются абсолютными и поэтому неудобны при проведении экспериментов в условиях, когда температура опускается ниже точки замерзания воды, из-за чего температуру приходится выражать отрицательным числом. Для таких случаев были введены абсолютные шкалы температур.
Одна из них называется шкалой Ранкина, а другая — абсолютной термодинамической шкалой (шкалой Кельвина); температуры по ним измеряются, соответственно, в градусах Ранкина (°Ra) и кельвинах (К). Обе шкалы начинаются при температуре абсолютного нуля. Различаются они тем, что цена одного деления по шкале Кельвина равна цене деления шкалы Цельсия, а цена деления шкалы Ранкина эквивалентна цене деления термометров со шкалой Фаренгейта. Температуре замерзания воды при стандартном атмосферном давлении соответствуют 273,15 K, 0 °C, 32 °F.
Масштаб шкалы Кельвина был привязан к тройной точке воды (273,16 К), при этом от неё зависела постоянная Больцмана. Это создавало проблемы с точностью интерпретации измерений высоких температур. Поэтому в 2018—2019 годах в рамках изменений в СИ было введено новое определение кельвина, основанное на фиксации численного значения постоянной Больцмана, вместо привязки к температуре тройной точки[49].
Шкала Цельсия[править | править код]
В технике, медицине, метеорологии и в быту в качестве единицы измерения температуры используется шкала Цельсия. В настоящее время в системе СИ термодинамическую шкалу Цельсия определяют через шкалу Кельвина[4]: t(°С) = Т(К) — 273,15 (точно), то есть цена одного деления в шкале Цельсия равна цене деления шкалы Кельвина. По шкале Цельсия температура тройной точки воды равна приблизительно 0,008 °C,[50] и, следовательно, точка замерзания воды при давлении в 1 атм очень близка к 0 °C. Точка кипения воды, изначально выбранная Цельсием в качестве второй реперной точки со значением, по определению равным 100 °C, утратила свой статус одного из реперов. По современным оценкам, температура кипения воды при нормальном атмосферном давлении в термодинамической шкале Цельсия составляет около 99,975 °C. Шкала Цельсия очень удобна с практической точки зрения, поскольку вода и её состояния распространены и крайне важны для жизни на Земле. Ноль по этой шкале является особой точкой для метеорологии, поскольку связан с замерзанием атмосферной воды. Шкала предложена Андерсом Цельсием в 1742 г.
Шкала Фаренгейта[править | править код]
В Англии и, в особенности, в США используется шкала Фаренгейта. Ноль градусов Цельсия — это 32 градуса Фаренгейта, а 100 градусов Цельсия — 212 градусов Фаренгейта.
В настоящее время принято следующее определение шкалы Фаренгейта: это температурная шкала, 1 градус которой (1 °F) равен 1/180 разности температур кипения воды и таяния льда при атмосферном давлении, а точка таяния льда имеет температуру +32 °F. Температура по шкале Фаренгейта связана с температурой по шкале Цельсия (t °С) соотношением t °С = 5/9 (t °F — 32), t °F = 9/5 t °С + 32. Предложена Г. Фаренгейтом в 1724 году.
Шкала Реомюра[править | править код]
Предложена в 1730 году Р. А. Реомюром, который описал изобретённый им спиртовой термометр.
Единица — градус Реомюра (°Ré), 1 °Ré равен 1/80 части температурного интервала между опорными точками — температурой таяния льда (0 °Ré) и кипения воды (80 °Ré)
1 °Ré = 1,25 °C.
В настоящее время шкала вышла из употребления, дольше всего она сохранялась во Франции, на родине автора.
Энергия теплового движения при абсолютном нуле[править | править код]
Когда материя охлаждается, многие формы тепловой энергии и связанные с ней эффекты одновременно уменьшаются по величине. Вещество переходит от менее упорядоченного состояния к более упорядоченному.
… современное понятие абсолютного нуля не есть понятие абсолютного покоя, наоборот, при абсолютном нуле может быть движение — и оно есть, но это есть состояние полного порядка …П. Л. Капица[40]
Газ превращается в жидкость и затем кристаллизуется в твёрдое тело (гелий и при абсолютном нуле остаётся в жидком состоянии при атмосферном давлении). Движение атомов и молекул замедляется, их кинетическая энергия уменьшается. Сопротивление большинства металлов падает из-за уменьшения рассеяния электронов на колеблющихся с меньшей амплитудой атомах кристаллической решётки. Таким образом даже при абсолютном нуле электроны проводимости движутся между атомами со скоростью Ферми порядка 106 м/с.
Температура, при которой частицы вещества имеют минимальное количество движения,
сохраняющееся только благодаря квантовомеханическому движению, — это температура абсолютного нуля (Т = 0К).
Температуры абсолютного нуля достичь невозможно. Наиболее низкая температура (450±80)⋅10−12К конденсата Бозе-Эйнштейна атомов натрия была получена в 2003 г. исследователями из МТИ[51]. При этом пик теплового излучения находится в области длин волн порядка 6400 км, то есть примерно радиуса Земли.
Температура и излучение[править | править код]
Излучаемая телом энергия пропорциональна четвёртой степени его температуры. Так, при 300 К с квадратного метра поверхности излучается до 450 ватт. Этим объясняется, например, ночное охлаждение земной поверхности ниже температуры окружающего воздуха. Энергия излучения абсолютно чёрного тела описывается законом Стефана — Больцмана
Переходы из разных шкал[править | править код]
| Шкала | Условное обозначение | из Цельсия (°C) | в Цельсий |
|---|---|---|---|
| Фаренгейт | (°F) | [°F] = [°C] × 9⁄5 + 32 | [°C] = ([°F] − 32) × 5⁄9 |
| Кельвин | (K) | [K] = [°C] + 273,15 | [°C] = [K] − 273,15 |
| Ранкин (Rankin) | (°R) | [°R] = ([°C] + 273,15) × 9⁄5 | [°C] = ([°R] − 491,67) × 5⁄9 |
| Делиль (Delisle) | (°Д или °De) | [°De] = (100 − [°C]) × 3⁄2 | [°C] = 100 − [°De] × 2⁄3 |
| Ньютон (Newton) | (°N) | [°N] = [°C] × 33⁄100 | [°C] = [°N] × 100⁄33 |
| Реомюр (Réaumur) | (°Re, °Ré, °R) | [°Ré] = [°C] × 4⁄5 | [°C] = [°Ré] × 5⁄4 |
| Рёмер (Rømer) | (°Rø) | [°Rø] = [°C] × 21⁄40 + 7,5 | [°C] = ([°Rø] − 7,5) × 40⁄21 |
Сравнение температурных шкал[править | править код]
| Описание | Кельвин | Цельсий | Фаренгейт | Ранкин | Делиль | Ньютон | Реомюр | Рёмер |
|---|---|---|---|---|---|---|---|---|
| Абсолютный нуль | 0 | −273,15 | −459,67 | 0 | 559,725 | −90,14 | −218,52 | −135,90 |
| Температура таяния смеси Фаренгейта (соль,лёд и хлорид аммония)[52] | 255,37 | −17,78 | 0 | 459,67 | 176,67 | −5,87 | −14,22 | −1,83 |
| Температура замерзания воды (Нормальные условия) | 273,15 | 0 | 32 | 491,67 | 150 | 0 | 0 | 7,5 |
| Средняя температура человеческого тела¹ | 309,75 | 36,6 | 98,2 | 557,9 | 94,5 | 12,21 | 29,6 | 26,925 |
| Температура кипения воды (Нормальные условия) | 373,15 | 100 | 212 | 671,67 | 0 | 33 | 80 | 60 |
| Плавление титана | 1941 | 1668 | 3034 | 3494 | −2352 | 550 | 1334 | 883 |
| Солнце² | 5800 | 5526 | 9980 | 10440 | −8140 | 1823 | 4421 | 2909 |
¹ Нормальная средняя температура человеческого тела — +36,6 °C ±0,7 °C, или +98,2 °F ±1,3 °F. Приводимое обычно значение +98,6 °F — это точное преобразование в шкалу Фаренгейта принятого в Германии в XIX веке значения +37 °C. Однако это значение не входит в диапазон нормальной средней температуры тела человека, поскольку температура разных частей тела разная.[53]
² Некоторые значения в этой таблице являются округлёнными. Например, температура поверхности Солнца равняется 5800 кельвинам очень приближённо. Однако для остальных температурных шкал уже дан точный результат перевода 5800 кельвинов в данную шкалу.
Характеристика фазовых переходов[править | править код]
Для описания точек фазовых переходов различных веществ используют следующие значения температуры:
- Температура плавления
- Температура кипения
- Температура отжига
- Температура спекания
- Температура синтеза
- Температура почвы
- Гомологическая температура
- Тройная точка
- Температура Дебая (Характеристическая температура)
- Температура Кюри
- Температура Нееля
Психология восприятия[править | править код]
Как показывают результаты многочисленных экспериментов, ощущение холода или тепла зависит не только от температуры и влажности окружающей среды, но и от настроения. Так, если испытуемый чувствует себя одиноким, например, находится в помещении с людьми, которые не разделяют его взглядов или ценностей, или просто находится далеко от других людей, то для него комната становится холоднее, и наоборот[54].
Интересные факты[править | править код]
|
|
Этот раздел представляет собой неупорядоченный список разнообразных фактов о предмете статьи. Пожалуйста, приведите информацию в энциклопедический вид и разнесите по соответствующим разделам статьи. Списки предпочтительно основывать на вторичных обобщающих авторитетных источниках, содержащих критерий включения элементов в список. (21 апреля 2021) |

- Самая высокая температура, созданная человеком, ~ 10⋅1012 К (что сравнимо с температурой Вселенной в первые секунды её жизни) была достигнута в 2010 году при столкновении ионов свинца, ускоренных до околосветовых скоростей. Эксперимент был проведён на Большом адронном коллайдере[55].
- Самая высокая теоретически возможная температура — планковская температура. Более высокая температура по современным физическим представлениям не может существовать, так как придание дополнительной энергии системе, нагретой до такой температуры, не увеличивает скорости частиц, а только порождает в столкновениях новые частицы, при этом число частиц в системе растёт, а также растёт и масса системы. Можно считать, что это температура «кипения» физического вакуума. Она примерно равна 1,41679(11)⋅1032 K (примерно 142 нониллиона K).
- Поверхность Солнца имеет температуры около 6000 K, а солнечное ядро — около 15 000 000 K.
- При очень низкой температуре, полученной в 1995 году Эриком Корнеллом и Карлом Виманом из США при охлаждении атомов рубидия удалось получить конденсат Бозе-Эйнштейна[56][57]. Температура была выше абсолютного нуля на 170 миллиардных долей кельвина (1,7⋅10−7 K).
- Самой низкой температурой, полученной в эксперименте, является температура в 50 пикокельвинов (5⋅10−11 K), полученная группой из Стенфордского университета в 2015 году[58].
- Рекордно низкая температура на поверхности Земли −89,2 °С была зарегистрирована на советской внутриконтинентальной научной станции Восток, Антарктида (высота 3488 м над уровнем моря) 21 июля 1983 года[59][60]. В июне 2018 года появилась информация о температуре −98 °С, зарегистрированной в Антарктиде[61].
- 9 декабря 2013 года на конференции Американского геофизического союза группа американских исследователей сообщила о том, что 10 августа 2010 года температура воздуха в одной из точек Антарктиды опускалась до −135,8 °F (−93,2 °С). Данная информация была выявлена в результате анализа спутниковых данных НАСА[62]. По мнению выступавшего с сообщением Т. Скамбоса (англ. Ted Scambos) полученное значение не будет зарегистрировано в качестве рекордного, поскольку определено в результате спутниковых измерений, а не с помощью термометра[63].
- Рекордно высокая температура воздуха вблизи поверхности земли +56,7 ˚C была зарегистрирована 10 июля 1913 года на ранчо Гринленд в долине Смерти (штат Калифорния, США)[64][65].
- Семена высших растений сохраняют всхожесть после охлаждения до −269 °C.[источник не указан 844 дня]
См. также[править | править код]
- Отрицательная абсолютная температура
- Цветовая температура
- Яркостная температура
- Антенная температура
- Тепловой насос
- Виртуальная температура
- Температура воздуха
- Температура тела
Примечания[править | править код]
- ↑ В качестве реперной точки 10-я Генеральная конференция по мерам и весам в 1954 году приняла тройную точку воды, приписав ей точное значение температуры 273,16 К по определению.
- ↑ Физика. Большой энциклопедический словарь / Гл. ред. А. М. Прохоров. — М.: Большая Российская энциклопедия, 1998. — С. 741. — 944 с.
- ↑ The SI brochure Архивная копия от 26 апреля 2006 на Wayback Machine Описание СИ на сайте Международного бюро мер и весов
- ↑ 1 2 ГОСТ 8.417-2002. Государственная система обеспечения единства измерений. Единицы величин. Дата обращения: 3 декабря 2018. Архивировано 20 сентября 2018 года.
- ↑ Жилин П. А., Рациональная механика сплошных сред, 2012, с. 84.
- ↑ Температурное поле. БСЭ, 3-е изд., 1976, т. 25. Дата обращения: 27 марта 2015. Архивировано 2 апреля 2015 года.
- ↑ Татьяна Данина. Механика тел. — Litres, 2017-09-05. — 163 с. — ISBN 9785457547490. Архивная копия от 26 апреля 2018 на Wayback Machine
- ↑ Трусделл К., Термодинамика для начинающих, 1970, с. 117.
- ↑ Жилин П. А., Рациональная механика сплошных сред, 2012, с. 48.
- ↑ Физика. Большой энциклопедический словарь, 1998, с. 751.
- ↑ Залевски К., Феноменологическая и статистическая термодинамика, 1973, с. 11–12.
- ↑ Вукалович М. П., Новиков И. И., Термодинамика, 1972, с. 11.
- ↑ Зоммерфельд А., Термодинамика и статистическая физика, 1955, с. 11.
- ↑ Клаузиус Р., Механическая теория тепла, 1934.
- ↑ Каратеодори К., Об основах термодинамики, 1964.
- ↑ Борн М., Критические замечания по поводу традиционного изложения термодинамики, 1964.
- ↑ Базаров И. П., Термодинамика, 2010, с. 57.
- ↑ Гухман А. А., Об основаниях термодинамики, 1986.
- ↑ Леонова В. Ф., Термодинамика, 1968.
- ↑ Базаров И. П., Термодинамика, 2010, с. 29, 58, 127, 171.
- ↑ Кубо Р., Термодинамика, 1970, с. 20–21.
- ↑ Гиббс Дж. В., Термодинамика. Статистическая механика, 1982, с. 93.
- ↑ Guggenheim E. A., Thermodynamics, 1986, p. 15.
- ↑ Callen H. B., Thermodynamics and an Introduction to Thermostatistics, 1986, p. 35.
- ↑ Falk G., Jung H., Axiomatik der Thermodynamik, 1959, p. 156.
- ↑ Дьярмати И., Неравновесная термодинамика, 1974, с. 26.
- ↑ 1 2 Jou D. e. a., Extended Irreversible Thermodynamics, 2010, p. 48.
- ↑ Белоконь Н. И., Основные принципы термодинамики, 1968, с. 10.
- ↑ Базаров И. П., Термодинамика, 2010, с. 62.
- ↑ Абсолютная температура. БСЭ, 3-е изд., 1969, т. 1. Дата обращения: 27 марта 2015. Архивировано 21 февраля 2015 года.
- ↑ Пригожин И., Кондепуди Д., Современная термодинамика, 2002, с. 23, 83, 86.
- ↑ Сорокин В. С., Макроскопическая необратимость и энтропия. Введение в термодинамику, 2004, с. 60.
- ↑ Отрицательная температура. БСЭ, 3-е изд., 1975, т. 19. Дата обращения: 27 марта 2015. Архивировано 2 апреля 2015 года.
- ↑ Ландау Л. Д., Лифшиц Е. М., Статистическая физика. Часть 1, 2002, с. 262.
- ↑ 1 2 3 4 Поулз Д., Отрицательные абсолютные температуры, 1964.
- ↑ Базаров И. П., Термодинамика, 2010, с. 136–148.
- ↑ Tisza L., Generalized Thermodynamics, 1966, p. 125.
- ↑ Ландау Л. Д., Лифшиц Е. М., Статистическая физика. Часть 1, 2002, с. 261.
- ↑ Базаров И. П., Термодинамика, 2010, с. 137–138.
- ↑ 1 2 Капица П. Л. Свойства жидкого гелия // Природа. — Наука, 1997. — № 12. Архивировано 21 февраля 2016 года.
- ↑ Шахмаев Н. М. и др. Физика: Учебник для 10 класса общеобразовательных учреждений. — М.: Просвещение, 1996. — С. 21. — 240 с. — ISBN 5090067937.
- ↑ Платиновый [[термометр сопротивления]] — основной прибор МТШ-90. Дата обращения: 5 мая 2010. Архивировано 8 июня 2010 года.
- ↑ Лазерная термометрия. Дата обращения: 5 мая 2010. Архивировано 8 июня 2010 года.
- ↑ Температура // Большая российская энциклопедия : [в 35 т.] / гл. ред. Ю. С. Осипов. — М. : Большая российская энциклопедия, 2004—2017.
- ↑ Электронвольт // Физическая энциклопедия / Гл. ред. А. М. Прохоров. — М.: Большая Российская энциклопедия, 1998. — Т. 5. Стробоскопические приборы — Яркость. — С. 545. — 760 с. — ISBN 5-85270-101-7.
- ↑ http://physics.nist.gov/cuu/Constants/Table/allascii.txt Архивная копия от 8 декабря 2013 на Wayback Machine Fundamental Physical Constants — Complete Listing
- ↑ Conversion factors for energy equivalents. Дата обращения: 17 февраля 2021. Архивировано 26 января 2021 года.
- ↑ Реперные точки МТШ-90. Дата обращения: 5 мая 2010. Архивировано 17 сентября 2011 года.
- ↑ Разработка нового определения кельвина. Дата обращения: 5 мая 2010. Архивировано 8 июня 2010 года.
- ↑ Д. А. Паршин, Г. Г. Зегря. Критическая точка. Свойства вещества в критическом состоянии. Тройная точка. Фазовые переходы II рода. Методы получения низких температур. Статистическая термодинамика. Лекция 11. Санкт-Петербургский академический университет. Дата обращения: 2 июня 2011. Архивировано из оригинала 3 декабря 2012 года.
- ↑ Belle Dumé. Bose-Einstein condensates break temperature record (англ.) (12 сентября 2003). Дата обращения: 24 июля 2013. Архивировано 25 июля 2013 года.
- ↑ Фаренгейта шкала // Большая российская энциклопедия : [в 35 т.] / гл. ред. Ю. С. Осипов. — М. : Большая российская энциклопедия, 2004—2017.
- ↑ О различных измерениях температуры тела Архивная копия от 26 сентября 2010 на Wayback Machine (англ.)
- ↑ Тальма Лобель, 2014, с. 24.
- ↑ BBC News — Large Hadron Collider (LHC) generates a ‘mini-Big Bang’. Дата обращения: 15 ноября 2010. Архивировано 15 ноября 2010 года.
- ↑ Всё про всё. Рекорды температуры. Дата обращения: 16 декабря 2009. Архивировано 25 сентября 2013 года.
- ↑ Чудеса науки. Дата обращения: 16 декабря 2009. Архивировано из оригинала 1 декабря 2012 года.
- ↑ Where is the coldest experiment on Earth? (англ.). Дата обращения: 23 февраля 2020. Архивировано 23 февраля 2020 года.
- ↑ Самая низкая температура на поверхности Земли. National Geographic Россия. Дата обращения: 9 декабря 2013. Архивировано из оригинала 13 декабря 2013 года.
- ↑ World: Lowest Temperature (англ.). Arizona State University. Дата обращения: 9 декабря 2013. Архивировано из оригинала 16 июня 2010 года.
- ↑ Учёные зафиксировали в Антарктиде самую низкую температуру на планете. Дата обращения: 27 июня 2018. Архивировано 27 июня 2018 года.
- ↑ NASA-USGS Landsat 8 Satellite Pinpoints Coldest Spots on Earth (англ.). NASA. Дата обращения: 10 декабря 2013. Архивировано 12 декабря 2013 года.
- ↑ Antarctica sets low temperature record of -135.8 degrees (англ.). FoxNews. Дата обращения: 10 декабря 2013. Архивировано 11 декабря 2013 года.
- ↑ Старый температурный рекорд оспорен. Компьюлента. Дата обращения: 30 ноября 2013. Архивировано из оригинала 3 декабря 2013 года.
- ↑ Press Release No. 956 (англ.). World Meteorological Organizayion. Дата обращения: 30 ноября 2013. Архивировано из оригинала 6 апреля 2016 года.
Литература[править | править код]
- Callen H. B. Thermodynamics and an Introduction to Thermostatistics (англ.). — 2nd ed. — N. Y. e. a.: John Wiley, 1986. — XVI + 493 p. — ISBN 0471862568, 9780471862567.
- Falk G., Jung H. Axiomatik der Thermodynamik (нем.) // Flügge S. (ed.). Encyclopedia of Physics / Flügge S. (Hrsg.). Handbuch der Physik. — Springer-Verlag, 1959. — Vol. III/2. Principles of Thermodynamics and Statistics / Band III/2. Prinzipien der Thermodynamik und Statistik, S. 119–175.
- Guggenheim E. A. Thermodynamics: An Advanced Treatment for Chemists and Physicists. — 8th ed. — Amsterdam: North-Holland, 1986. — XXIV + 390 p. — ISBN 0444869514, 9780444869517.
- Jou D., Casas-Vázquez J., Lebon G. Extended Irreversible Thermodynamics (англ.). — 4th ed. — N. Y.—Dordrecht—Heidelberg—London: Springer, 2010. — XVIII + 483 p. — ISBN 978-90-481-3073-3. — doi:10.1007/978-90-481-3074-0.
- Tisza Laszlo. Generalized Thermodynamics. — Cambridge (Massachusetts) — London (England): The M.I.T. Press, 1966. — XI + 384 p.
- Базаров И. П. Термодинамика. — 5-е изд. — СПб.—М.—Краснодар: Лань, 2010. — 384 с. — (Учебники для вузов. Специальная литература). — ISBN 978-5-8114-1003-3.
- Белоконь Н. И. Основные принципы термодинамики. — М.: Недра, 1968. — 112 с.
- Борн М. Критические замечания по поводу традиционного изложения термодинамики // Развитие современной физики. — М.: Наука, 1964. — С. 223—256.
- Вукалович М. П., Новиков И. И. Термодинамика. — М.: Машиностроение, 1972. — 671 с.
- Гиббс Дж. В. Термодинамика. Статистическая механика / Отв. ред. Д. Н. Зубарев. — М.: Наука, 1982. — 584 с. — (Классики науки).
- Гухман А. А. Об основаниях термодинамики. — Алма-Ата: Изд-во АН КазССР, 1947. — 106 с.
- Гухман А. А. Об основаниях термодинамики. — М.: Энергоатомиздат, 1986. — 384 с.
- Дьярмати И. Неравновесная термодинамика. Теория поля и вариационные принципы. — М.: Мир, 1974. — 304 с.
- Жилин П. А. Рациональная механика сплошных сред. — 2-е изд. — СПб.: Изд-во Политехн. ун-та, 2012. — 584 с. — ISBN 978-5-7422-3248-3.
- Залевски К. Феноменологическая и статистическая термодинамика: Краткий курс лекций / Пер. с польск. под. ред. Л. А. Серафимова. — М.: Мир, 1973. — 168 с.
- Зоммерфельд А. Термодинамика и статистическая физика / Пер. с нем.. — М.: Изд-во иностр. лит-ры, 1955. — 480 с.
- Каратеодори К. Об основах термодинамики // Развитие современной физики. — М.: Наука, 1964. — С. 3—22.
- Клаузиус Р. Механическая теория тепла // Второе начало термодинамики. — М.—Л.: Гостехиздат, 1934. — С. 70—158.
- Кубо Р. Термодинамика. — М.: Мир, 1970. — 304 с.
- Ландау Л. Д., Лифшиц Е. М. Статистическая физика. Часть 1. — 5-е изд. — М.: Физматлит, 2002. — 616 с. — (Теоретическая физика в 10 томах. Том 5). — ISBN 5-9221-0054-8.
- Леонова В. Ф. Термодинамика. — М.: Высшая школа, 1968. — 159 с.
- Поулз Д. Отрицательные абсолютные температуры и температуры во вращающихся системах координат // Успехи физических наук. — Российская академия наук, 1964. — Vol. 84, № 4. — С. 693—713.
- Пригожин И., Кондепуди Д. Современная термодинамика. От тепловых двигателей до диссипативных структур / Пер. с англ. — М.: Мир, 2002. — 462 с.
- Рудой Ю. Г. Математическая структура равновесной термодинамики и статистической механики. — М. — Ижевск: Институт компьютерных исследований, 2013. — 368 с. — ISBN 978-5-4344-0159-3.
- Сивухин Д. В. Термодинамика и молекулярная физика. — Москва: «Наука», 1990.
- Сорокин В. С. Макроскопическая необратимость и энтропия. Введение в термодинамику. — М.: ФИЗМАТЛИТ, 2004. — 174 с. — ISBN 5-9221-0507-8.
- Спасский Б. И. История физики Ч.I. — Москва: «Высшая школа», 1977.
- Тальма Лобель. Теплая чашка в холодный день: Как физические ощущения влияют на наши решения = Sensation The New Science of Physical Intelligence. — М.: Альпина Паблишер, 2014. — 259 с. — ISBN 978-5-9614-4698-2.
- Трусделл К. Термодинамика для начинающих // Механика. Периодический сборник переводов иностранных статей. — М.: Мир, 1970. — № 3 (121), с. 116—128.
- Физика. Большой энциклопедический словарь / Гл. ред. А. М. Прохоров. — М.: Большая Российская энциклопедия, 1998. — 944 с. — ISBN 5-85270-306-0.
Ссылки[править | править код]
- Current map of global surface temperatures (англ.)
- Miller, J. Cooling molecules the optoelectric way (англ.) // Physics Today : magazine. — 2013. — Vol. 66, no. 1. — P. 12—14. — doi:10.1063/pt.3.1840. — Bibcode: 2013PhT….66a..12M. Архивировано 15 мая 2016 года.
Физика, 10 класс
Урок №19. Температура. Энергия теплового движения молекул
На уроке рассматриваются понятия: температура и тепловое равновесие; шкалы Цельсия и Кельвина; абсолютная температура как мера средней кинетической энергии теплового движения частиц вещества, зависимость давления от концентрации молекул и температуры.
Глоссарий по теме:
Макроскопические параметры – величины объём V, давление p и температура t, характеризующие состояние макроскопических тел без учёта их молекулярного строения.
Температура характеризует степень нагретости тела (холодное, тёплое, горячее).
Температура (от лат. temperatura — надлежащее смешение, соразмерность, нормальное состояние) – физическая величина, характеризующая состояние термодинамического равновесия макроскопической системы.
Тепловым равновесием называют – такое состояние тел, при котором температура во всех точках системы одинакова.
Тепловым или термодинамическим равновесием, изолированной системы тел, называют состояние, при котором все макроскопические параметры в системе остаются неизменными.
Термометр — это прибор для измерения температуры путём контакта с исследуемым телом. Различают жидкостные, газовые термометры, термопары, термометры сопротивления.
Абсолютная температура Т прямо пропорциональна температуре Θ (тета), выражаемой в энергетических единицах (Дж).
Абсолютный нуль – предельная температура, при которой давление идеального газа обращается в нуль при фиксированном объёме или объём идеального газа стремится к нулю при неизменном давлении.
Абсолютный нуль – температура, при которой прекращается тепловое движение молекул.
Абсолютная шкала температур (Шкала Кельвина) – здесь нулевая температура соответствует абсолютному нулю, а каждая единица температуры равна градусу по шкале Цельсия.
Кельвин – единица абсолютной температуры в Международной системе измерений (СИ).
Постоянная Больцмана – коэффициент , связывает температуру Θ энергетических единицах (Дж) с абсолютной температурой Т (К).
, связывает температуру Θ энергетических единицах (Дж) с абсолютной температурой Т (К).
Абсолютная температура есть мера средней кинетической энергии молекул.
Давление газа прямо пропорционально концентрации его молекул и абсолютной температуре Т.
Закон Авогадро – в равных объёмах газов при одинаковых температурах и давлениях содержится одинаковое число молекул
Обязательная литература:
- Мякишев Г.Я., Буховцев Б.Б., Сотский Н.Н. Физика.10 класс. Учебник для общеобразовательных организаций М.: Просвещение, 2017. – С. 195 – 203.
Дополнительная литература:
- Смородинский Я.А. Температура. – 3-е издание. – М.: Бюро Квантум, 2007. (Библиотечка «Квант». Вып. 103. Приложение к журналу «Квант» № 5/2007.) С. 5— 25.
- Кирик Л.А., Генденштейн Л.Э., Гельфгат И.М.. Задачи по физике. 10-11 классы для профильной школы. – М.: Илекса, 2010. – С. 111-115.
- Рымкевич А.П. Физика. Задачник. 10-11 классы. – М.: Дрофа, 2013. – С. 65 – 67.
- Орлов В.А., Сауров Ю.А. Практика решения физических задач. 10-11классы. – М.: Вентана-Граф, 2014. – С. 98-99.
- http://kvant.mccme.ru/1991/09/idealnyj_gaz_-_universalnaya_f.htm
Теоретический материал для самостоятельного изучения
Измеряя расположение звёзд на небе, расстояния на земле, время, люди знали, для чего они это делают и изобретали, телескопы, часы, прототипы современных линеек. О температуре такого же сказать было нельзя. О том, что такое тепловое равновесие и что означает степень нагрева тела (температура), существовали разные мнения. Но человек с незапамятных времен точно знал, что, когда два тела плотно соприкасаются, между ними устанавливается, выражаясь современным языком, тепловое равновесие.
Любое макроскопическое тело или группа макроскопических тел при неизменных внешних условиях самопроизвольно переходят в состояние теплового равновесия.
Тепловым равновесием называют такое состояние тел, при котором температура во всех точках системы одинакова.
Температура (от лат. temperatura — надлежащее смешение, соразмерность, нормальное состояние) – физическая величина, характеризующая состояние термодинамического равновесия макроскопической системы.
К числу характеристик состояния макроскопических тел (твёрдых тел, жидкостей, газов) и процессов изменения их состояний, относят объём, давление и температуру. Эти величины описывают в целом тела, состоящие из большого числа молекул, а не отдельные молекулы. При этом микроскопические процессы внутри тела не прекращаются при тепловом равновесии: расположения молекул всё время меняются и меняются их скорости при столкновениях.
Величины объём, давление и температуру, характеризующие состояние макроскопических тел без учёта их молекулярного строения, называют макроскопическими параметрами.
Тепловым или термодинамическим равновесием, изолированной системы тел, называют состояние, при котором все макроскопические параметры в системе остаются неизменными.
Для точной характеристики нагретости тела, необходим прибор, способный измерить температуры тел и дать возможности их сравнения.
Термометр — это прибор для измерения температуры путём контакта с исследуемым телом. Различают жидкостные, газовые термометры, термопары, термометры сопротивления.
В 1597 году Галилей создал термоскоп, в собственных сочинениях учёного нет описания этого прибора, но его ученики засвидетельствовали этот факт. Аппарат представлял собой устройство для поднятия воды при помощи нагревания.
Изобретение термометра, данные которого не зависели бы от перепадов атмосферного давления, произошли благодаря экспериментам физика Э. Торричелли, ученика Галилея.
Во всех приборах, изобретённых в XVIII веке, измерение температуры было относительно расширению столбика воды, спирта или ртути и произвольности выбора начала отсчёта, т.е. нулевой температуры. Наполняющие их вещества замерзали или кипели и этими термометрами нельзя было измерять очень низкие или очень высокие температуры. Необходимо было изобрести такую шкалу, чтобы избавиться от зависимости выбранного вещества, на основе которого формировалось градуирование.
Шкала, предложенная шведским учёным Андерсом Цельсием в 1742 г., точно устанавливала положение двух точек: 0 и 100 градусов. По шкале Цельсия температура обозначается буквой t, измеряется в градусах Цельсия (ºС).
На территории Англии и США используется шкала Фаренгейта. Такая шкала была предложена немецким учёным Даниелем Габриелем Фаренгейтом в 1724 г.: 0 °F — температура смеси снега с нашатырём или поваренною солью, 96 °F —температура здорового человеческого тела, во рту или под мышкой.
Рене Антуан де Реомюр не одобрял применения ртути в термометрах вследствие малого коэффициента расширения ртути. В 1730 году изобрёл водно-спиртовой термометр и предложил шкалу от 0 до 80°.
Шкала Реомюра очень долго использовалась на родине учёного во Франции вплоть до настоящего времени.
Различные жидкости при нагревании расширяются не одинаково. Поэтому расстояния на шкале между нулевой отметкой 0 °C и 100 °C будут разными.
Однако существует способ создать тело, которое приближенно обладает нужными качествами. Это идеальный газ. Было замечено, что в отличие от жидкостей все разряжённые газы – водород, гелий, кислород – расширяются при нагревании одинаково и одинаково меняют своё давление при изменении температуры. Это свойство газов позволяет избавиться в термометрах от одного существенного недостатка шкалы Цельсия – произвольности выбора начала отсчёта, то есть нулевой температуры.
При тепловом равновесии, если давление и объём газа массой m постоянны, то средняя кинетическая энергия молекул газа должна иметь строго определённое значение, как и температура.
Практически такую проверку произвести непосредственно невозможно, но с помощью основного уравнения молекулярно-кинетической теории её можно выразить через макроскопические параметры:

 ;
;  ;
;  ;
;  ;
; 

Если кинетическая энергия действительно одинакова для всех газов в состоянии теплового равновесия, то и значение давления р должно быть тоже одинаково для всех газов при постоянном значении отношения объёма к числу молекул. Подтвердить или опровергнуть данное предположение может только опыт.

Возьмём несколько сосудов, заполненных различными газами, например, водородом, гелием и кислородом. Сосуды имеют определённые объёмы и снабжены манометрами, для измерения давления газов в сосудах. Массы газов известны, тем самым известно число молекул в каждом сосуде. Приведём газы в состояние теплового равновесия. Для этого поместим их в тающий лёд и подождём, пока не установится тепловое равновесие и давление газов перестанет меняться.
Здесь устанавливается тепловое равновесие и все газы имеют одинаковую температуру 0 °С. При этом показания манометра показывают разное давление р, объёмы сосудов V изначально были разными и число молекул N различно, так как газы, закаченные в баллоны разные. Найдём отношение для водорода всех параметров для одного моля вещества:

Такое значение отношения произведения давления газа на его объём к числу молекул получается для всех газов при температуре тающего льда. Обозначим это отношение через Θ0 (тета нулевое):

Таким образом, предположение, что средняя кинетическая энергия, а также давление р в состоянии теплового равновесия одинаковы для всех газов, если их объёмы и количества вещества одинаковы или если отношение

Если же сосуды с газами поместить в кипящую воду при нормальном атмосферном давлении, то согласно эксперименту, отношение макроскопических параметров будет также одинаковым для всех газов, но значение будет больше предыдущего

Отсюда следует, что величина Θ растёт с повышением температуры и не зависит от других параметром, кроме температуры. Этот опытный факт позволяет рассматривать величину Θ тета как естественную меру температуры и измерять в энергетических единицах — джоулях.
А теперь вместо энергетической температуры введём температуру, которая будет измеряться в градусах. Будем считать величину тета Θ прямо пропорциональной температуре Т, где k- коэффициент пропорциональности

Так как  , то тогда
, то тогда 
По этой формуле вводится температура, которая даже теоретически не может быть отрицательной, так как все величины левой части этого равенства больше или равны нулю. Следовательно, наименьшим значением этой температуры является нуль, при любом другом параметре p, V, N равным нулю.
Предельную температуру, при которой давление идеального газа обращается в нуль при фиксированном объёме или при которой объём идеального газа стремится к нулю при неизменном давлении, называют абсолютным нулём температуры.
Тепловое движение молекул непрерывно и бесконечно, а при абсолютном нуле молекулы поступательно не двигаются. Следовательно, абсолютный нуль температур при наличии молекул вещества не может быть достигнут. Абсолютный нуль температур — это самая низкая температурная граница, верхней не существует, та «наибольшая или последняя степень холода», существование которой предсказывал М.В. Ломоносов.
В 1848 г. английскому физику Вильяму Томсону (лорд Кельвин) удалось построить абсолютную температурную шкалу (её в настоящее время называют шкалой Кельвина), которая имеет две основные точки 0 К (или абсолютный нуль) и 273К, точка в которой вода существует в трёх состояниях (в твёрдом, жидком и газообразном).
Абсолютная температурная шкала — шкала температур, в которой за начало отсчёта принят абсолютный нуль. Температура здесь обозначается буквой T и измеряется в кельвинах (К).
На шкале Цельсия, есть две основные точки: 0°С (точка, в которой тает лёд) и 100°С (кипение воды). Температура, которую определяют по шкале Цельсия, обозначается t. Шкала Цельсия имеет как положительные, так и отрицательные значения.
Из опыта мы определили значения величины Θ (тета) при 0 °С и 100 °С. Обозначим абсолютную температуру при 0 °С через Т1, а при 100 °С через Т2. Тогда согласно формуле:



Отсюда можно вычислить коэффициент k, который связывает температуру в Θ энергетических единицах (Дж) с абсолютной температурой Т (К)
k = 1,38 • 10-23 Дж/К – постоянная Больцмана.
Зная постоянную Больцмана, можно найти значение абсолютного нуля по шкале Цельсия. Для этого найдём сначала значение абсолютной температуры, соответствующее 0°С:

 значение абсолютной температуры.
значение абсолютной температуры.
Один кельвин и один градус шкалы Цельсия совпадают. Поэтому любое значение абсолютной температуры Т будет на 273 градуса выше соответствующей температуры t по Цельсию:


Теперь выведем ещё одну зависимость температуры от средней кинетической энергии молекул. Из основного уравнения молекулярно-кинетической теории и уравнения для определения абсолютной температуры


Здесь видно, что левые части этих уравнений равны, значит правые равны тоже.

Средняя кинетическая энергия хаотического поступательного движения молекул газа пропорциональна абсолютной температуре.
Абсолютная температура есть мера средней кинетической энергии движения молекул.
Из выведенных формул мы можем получить выражение, которое показывает зависимость давления газа от концентрации молекул и температуры



Из этой зависимости вытекает, что при одинаковых давлениях и температурах концентрация молекул у всех газов одна и та же. Отсюда следует закон Авогадро, известный нам из курса химии.
Закон Авогадро: в равных объёмах газов при одинаковых температурах и давлениях содержится одинаковое число молекул.
Рассмотрим задачи тренировочного блока урока.
1. При температуре _______ (370C; 2830C; 270C) средняя кинетическая энергия поступательного движения молекул равна 6,21·10-21Дж.
Дано:

k = 1,38 • 10-23 Дж/К – постоянная Больцмана
t -?
Решение:
Запишем значение средней кинетической энергии хаотического поступательного движения молекул с зависимостью от абсолютной температуры:

Отсюда выразим Т:


Соотношение между абсолютной температурой и температурой в градусах Цельсия:

Подставим значение абсолютной температуры:

Правильный вариант ответа:
2. При температуре 290 К и давлении 0,8 МПа, средняя кинетическая энергия молекул равна __________ Дж, а концентрация составляет молекул ___________ м-3.
Дано:
Т = 290К
р = 0,8 МПа =0,8·106 Па
k = 1,38 • 10-23 Дж/К – постоянная Больцмана
Ек -? n – ?
Решение:
Значение средней кинетической энергии хаотического поступательного движения молекул:

Подставив значение абсолютной температуры, найдём ответ:

Определим концентрацию газа из соотношения:



Правильный вариант ответа: 6·10-21; 2·1026 м-3.
На протяжении школьного
курса физики, вы уже много раз слышали о том, что температура является мерой
средней кинетической энергии молекул. Но, как сказал Лев Ландау, «верховным
судьёй всякой физической теории является опыт». Поэтому, на сегодняшнем уроке мы
рассмотрим опыты, позволяющие нам дать определение температуре. Возьмем сосуд с
перегородкой и поместим в половинки сосуда два различных газа разной
температуры. Если перегородка сосуда проводит тепло, то через некоторое время
оба газа будут иметь одинаковую температуру.
Основываясь на нашем
начальном предположении о том, что температура является мерой средней
кинетической энергии молекул, мы попытаемся доказать, что средняя кинетическая
энергия молекул обладает таким же свойством, как и температура.
Как и было сказано в
предыдущих уроках, измерить кинетическую энергию отдельной молекулы крайне
сложно. Однако, мы можем выразить среднюю кинетическую энергию молекул газа
через макроскопические параметры. Воспользуемся основным уравнением
молекулярно-кинетической теории:
Заметим, что концентрация
молекул равна отношению числа молекул газа к его объёму:
Тогда
Итак, мы выразили среднюю
кинетическую энергию молекул через три величины, которые легко измеряются.
Объём можно задать, поместив газ в герметичный баллон, а давление измерим с
помощью манометра. Чтобы найти количество молекул, как вы знаете, нужно
количество вещества умножить на число Авогадро:
Вспомним теперь, что
количество вещества равно отношению массы к молярной массе:
Молярную массу, как вы
знаете, можно подсчитать, используя таблицу Менделеева.
Следовательно,
Для проведения опыта мы
можем использовать баллоны с водородом и кислородом, давление, объёмы и
количество молекул которых, различны.
Чтобы уравнять
температуру газов их необходимо привести в тепловое равновесие с одним и тем же
телом (как правило, используется тающий лед). Через некоторое время установится
тепловое равновесие, то есть температуры кислорода и водорода будут равны 0 оС.
Наша цель проверить — уравнялись ли при этом средние кинетические энергии
молекул газов, и если это так, то наше начальное предположение верно. Опыты и
сопутствующие расчеты говорят о том, что отношение произведения давления и
объёма к количеству молекул газа остается постоянным при постоянной температуре,
независимо от природы самого газа:
Это говорит нам о том,
что средняя кинетическая энергия молекул — это и есть температура.
Необходимо отметить, что
данное соотношение все же начинает зависеть от рода газа при очень большом
давлении, таком как несколько сотен атмосфер. Однако, мы с уверенностью можем
сказать, что до тех пор, пока газ может считаться идеальным, данное соотношение
строго определено.
Поскольку температура
фактически является мерой энергии, её иногда измеряют в энергетических единицах.
Но, дело в том, что в повседневной жизни подобные единицы измерения неудобны.
Например, если в баллоне объёмом 10 л находится 1 моль водорода при нормальном
давлении, то средняя кинетическая энергия его молекул будет равна 1,68 х 10−21
Дж. В связи с этим возникает вопрос: как перевести температуру из
энергетических единиц измерения в градусы, используемые в повседневной жизни?
Ведь, люди могут выбирать какую угодно температурную шкалу, но этот выбор не
может повлиять на кинетическую энергию молекул. Поэтому, вводится понятие абсолютной
температуры. Будем считать эту температуру прямо пропорциональной
температуре, выраженной в энергетических единицах:
В этой формуле мы
обозначили коэффициент пропорциональности буквой k.
Учитывая тот факт, что
такие величины, как объём, давление и число молекул, не могут быть
отрицательными, делаем вывод, что абсолютная температура тоже не может быть
отрицательной.
Как видно из формулы, абсолютный
ноль температуры — это такая температура, при которой давление газа равно нулю,
при постоянном объёме. Такое возможно только в случае, если молекулы газа
попросту остановились (это следует из основного уравнения
молекулярно-кинетической теории).
Абсолютную шкалу температур
предложил лорд Кельвин, в честь которого и названа единица измерения
температуры по абсолютной шкале. 1 К равен 1 оС, поэтому перевести
градусы Цельсия в кельвины довольно просто: нужно к температуре в градусах
Цельсия прибавить 273 градуса:
Таким образом, абсолютный
ноль температуры по шкале Цельсия равен −273 градуса. Необходимо
отметить, что абсолютный ноль недостижим.
Вернемся теперь к
уравнению, которое мы использовали в начале урока:
Также, мы выяснили, что
отношение произведения давления и объёма к числу молекул должно быть
пропорционально температуре:
Мы получили два
уравнения, левые части которых равны. Значит, должны быть равны и правые части:
Итак, мы вплотную подошли
к связи между средней кинетической энергией и температурой. Остается только
разобраться с коэффициентом пропорциональности.
Этот коэффициент получил
название постоянной Больцмана, в честь Людвига Больцмана.
Больцман был первым, кто
нашел соотношение между кинетической энергией и температурой. Постоянная
Больцмана определяет связь между температурой в энергетических единицах
измерения и температурой в кельвинах. Итак, средняя кинетическая энергия
молекул равна
Сегодня мы можем
повторить эксперимент, с помощью которого можно вычислить постоянную Больцмана.
Возьмем газ, который можно считать идеальным, и измерим среднюю кинетическую
энергию его молекул тем же способом, который мы использовали в начале урока —
то есть, выразив её через макроскопические параметры:
Проведем измерения для
двух случаев: в одном случае поместим сосуд в тающий лед, а во втором случае —
в кипящую воду.
Тогда, разность между
температурами в энергетических единицах измерения должна быть равна
произведению разности температуры в кельвинах и постоянной Больцмана:
Отсюда выразим постоянную
Больцмана:
Расчеты показывают, что
эта величина остается постоянной для любого газа, который можно считать
идеальным:
Несмотря на то, что
соотношение между температурой и кинетической энергией установлено для газов,
оно также выполняется для жидкостей и для твердых тел:
Данное соотношение не
выполняется только в том случае, если движение частиц не подчиняется законам
механики Ньютона. Это происходит при экстремальных условиях, например при
колоссальном давлении, огромной температуре или сильнейших электромагнитных
полях.
Пример решения задачи.
Задача. При
температуре 200 К средняя скорость молекул одного моля неизвестного газа равна
500 м/с. Считая этот газ идеальным, определите его молярную массу.
Что же такое температура?
Добавлено: 17 декабря 2021 в 17:49

Температура — базовое физическое понятие, которое понятно нам на бытовом уровне, но часто вызывает затруднения при решении задач ОГЭ по физике . Основная сложность состоит в том, что мы путаем тепло, температуру и процессы теплопередачи.
Попробуем разобраться в этих явлениях и закономерностях.
Шкалы температуры
Для восприятия температуры, то есть степени нагретости вещества у человека есть рецепторы, благодаря которым мы ощущаем: теплая вода или холодная, какая погода на улице и остыла ли уже кружка с чаем.
Понятия «холодный», «горячий», «теплый» хороши для повседневной жизни, но для науки требуется более совершенный инструмент, который позволяет однозначно понимать состояние материи или воспринимать условия проведения эксперимента.
Мы измеряем температуру веществ с помощью прибора, называемого термометром. Он имеет шкалу, которая показывает величину «нагрева» в градусах — единицах температуры. На этом этапе возникает первая проблема, потому что существует три распространенных единицы измерения температуры:
- градус Цельсия (°C)— 1/100 часть диапазона температур между точкой плавления льда и кипения воды, принятыми, соответственно за 0 °C и 100 °C;
- градус Кельвина (°K)— количественно равен градусу Цельсия (вернее, наоборот) и рассчитывается, как 1/273,16 доля тройной точки воды (что это такое, мы расскажем ниже);
- градус Фаренгейта (°F) — 1/180 часть диапазона температур между точкой плавления льда и кипения воды, которые равны, соответственно +32 °F и +212 °F.
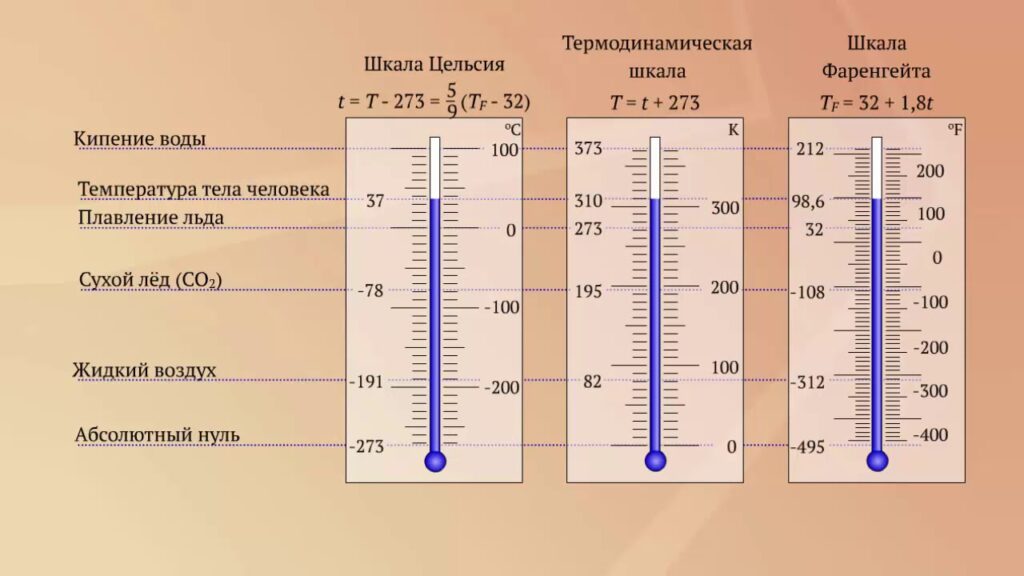
Единицы и шкала измерения температуры в физике
Внимание! Тройная точка — условия, при которых вода пребывает в равновесии между газообразным, жидким и твердым состоянием и может одновременно существовать в любом из них. При обычных условиях в природе такого не происходит — состояние равновесия достижимо лишь при понижении давления до 0,006 атм и температуре 0,01 °С.
Градус Фаренгейта используется, в основном, в США. Градус Цельсия распространен в остальном мире, но в науке базовой единицей является градус Кельвина.
Изначально все три параметра были привязаны к свойствам воды, но сейчас ситуация изменилась, поскольку в современной науке и технике важно очень точно знать состояние системы, поэтому градус Кельвина был переопределен через постоянную Больцмана.
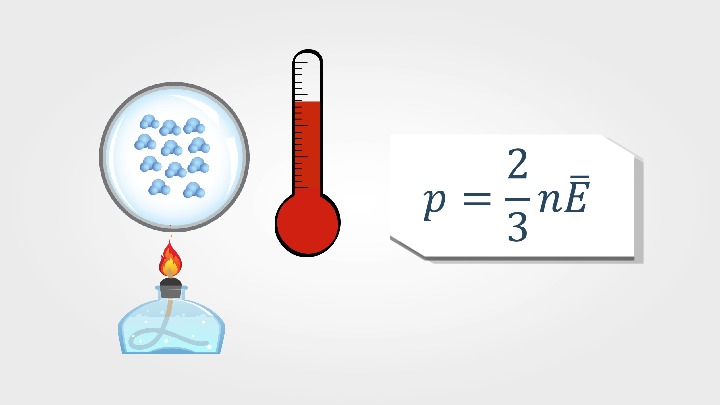
Единицы и шкала измерения температуры в физике
Перевод температуры
Для бытовых и школьных расчетов мы можем преобразовать результат измерения по шкале Цельсия в шкалу Кельвина или Фаренгейта и наоборот, используя следующее уравнение:
Пример: нормальная температура человеческого тела составляет 36,6 °C — она обозначена на наших медицинских градусниках. Определите, какая температура обозначена на американских термометрах и сколько это будет в Кельвинах.
Решение
- На американском термометре, как мы уже знаем, указана температура в Фаренгейтах. Чтобы найти соответствующее значение, составим пропорцию для перевода между двумя шкалами:
Подставим значение температуры в левую часть и решим пропорцию относительно °F:
°F = 97.88
- На термометре специалиста по термодинамике указана температура в Кельвинах. Чтобы найти соответствующее значение, составим пропорцию для перевода между двумя шкалами:
Подставим значение температуры в левую часть и решим пропорцию относительно °F:
Заметим, что обе части имеют одинаковый знаменатель, от которого можно избавиться, умножив каждую из них на 100. Проделаем этот маневр и одновременно решим относительно °K:
°K = 36,6 + 273 = 309,75
Вывод: Градусы Цельсия можно перевести в градусы Кельвина, просто прибавив 273.
Важно: 0 °K или -273,15 °C — самая низкая возможная температура или абсолютный ноль! На практике этой отметки достичь нельзя, хотя ученые и инженеры приблизились очень близко к этому значению, снизив температуру газовой среды до 38∙10-12 °К.

Единицы и шкала измерения температуры в физике
Что же такое температура?
Му уже знаем, как измерить температуру и как выразить ее количественно, но не знаем, что это такое. Заглянем внутрь материи: нам известно, что все вещества состоят из атомов и молекул.
О микромире мы знаем, что все частицы материи находятся в случайном движении, они колеблются, сталкиваясь случайным образом. Из механики мы знаем, что движущийся объект имеет кинетическую энергию. Таким образом, в объекте все частицы обладают кинетической энергией.
Температура — это величина, которая прямо пропорциональна средней кинетической энергии атомов вещества.
Важно! Будьте осторожны, это не энергия, это просто количество средней кинетической энергии одного атома или одной молекулы.
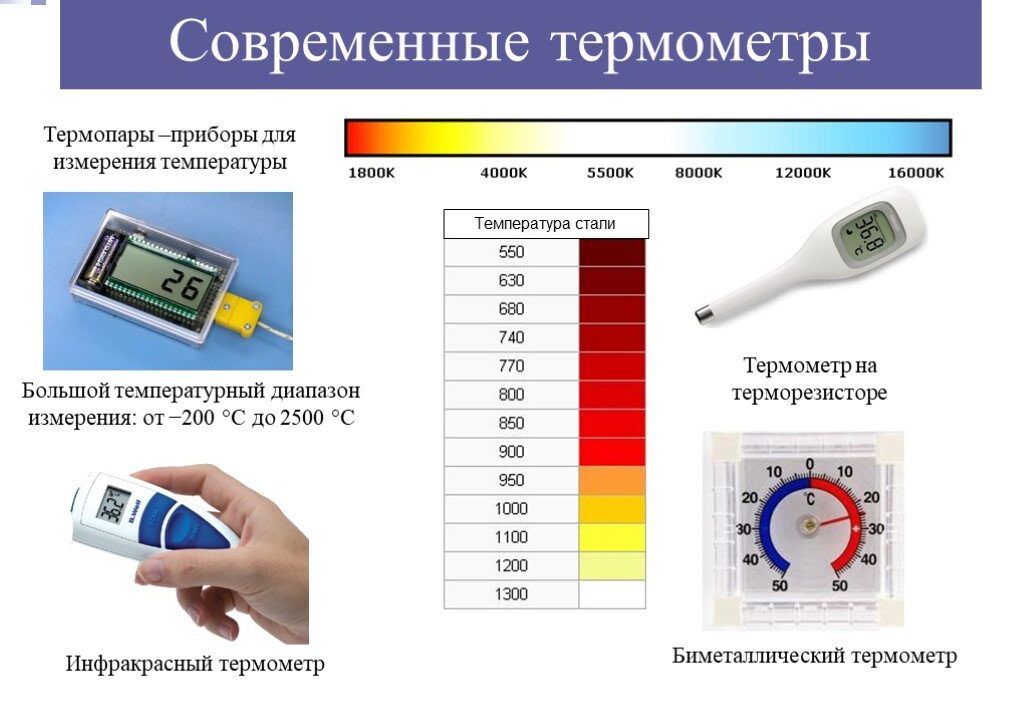
Единицы и шкала измерения температуры в физике
Тепло — это энергия, которую можно преобразовывать из одной формы в другую или передавать от одного объекта к другому.
Природный газ, сгорая, выделяет тепло и передает эту энергию через чайник воде. Это увеличивает кинетическую энергию молекул воды, заставляя их двигаться все быстрее и быстрее. При определенной температуре (точке кипения) атомы набирают достаточно энергии, чтобы разорвать молекулярные связи в жидкости и превратиться в пар.
Теплопередача — передача тепловой энергии от одного, более нагретого тела (участка) к другому, менее нагретому до момента достижения равновесия. Она может осуществляться по следующим механизмам:
- теплопроводность: холодная часть стены дома нагревается путем «перетекания» тепла от нагретой части;
- конвекция: воздух у батареи отопления нагревается и поднимается вверх, перенося тепловую энергию в пространстве комнаты;
- радиация или тепловое излучение: кусок раскаленного металла или инфракрасный обогреватель (вообще, любое тело) излучает электромагнитные волны, передавая тепловую энергию.
Занимайтесь на курсах ЕГЭ и ОГЭ в паре TwoStu и получите максимум баллов на экзамене:

Эксперт по подготовке к ЕГЭ, ОГЭ и ВПР
Задать вопрос
Закончил Московский физико-технический институт (Физтех) по специальности прикладная физика и математика. Магистр физико-математических наук. Преподавательский стаж более 13 лет. Соучредитель курсов ЕГЭ и ОГЭ в паре TwoStu.

