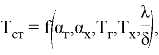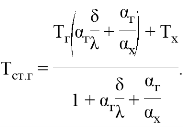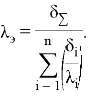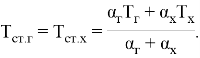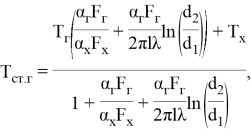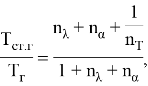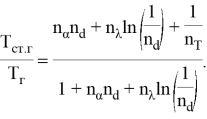В первом приближении
средняя температура стенки равна
среднему арифметическому между
температурами теплоносителей:
![]() , (1.4)
, (1.4)
где
![]() – средняя температура греющего
– средняя температура греющего
теплоносителя, °С;
![]() –средняя температура
–средняя температура
нагреваемого теплоносителя, °С.
![]() °С.
°С.
По
![]() выбираем критерии Прандтля для жидкостей,
выбираем критерии Прандтля для жидкостей,
движущихся в ТОА.
Prс1
= Prс2
= 1760,
где Prс1,
Prс2
– критерии Прандтля для греющей и
нагреваемой воды.
Коэффициент
теплопроводности медных труб λс
= 388,6 Вт/(м·К).
1.4 Определение коэффициента теплоотдачи со стороны греющего теплоносителя
При
турбулентном и переходном режимах Nu
зависит от Re и Pr, а при ламинарном еще и
от длины трубок. Поэтому перед расчетом
Nu1
зададимся некой “предполагаемой
длиной”, по которой будем вести расчет
трубного пространства. Формула для
расчета среднего значения критерия
Нуссельта имеет вид:
![]() , (1.5)
, (1.5)
где
Pr1
– критерий Прандтля теплоносителя при
его средней температуре;
Prc
– критерий Прандтля теплоносителя при
средней температуре стенки.
![]()
Т.к.
![]() ,
,
то можно записать формулу для определения
среднего коэффициента теплоотдачи для
греющего теплоносителя:
![]() , (1.6)
, (1.6)
где 1
– коэффициент теплопроводности греющего
теплоносителя при его средней температуре,
Вт/(мК).
![]() Вт/(м2К).
Вт/(м2К).
1.5 Определение коэффициента теплоотдачи со стороны нагреваемого теплоносителя
Выберем
шахматную компоновку трубного пучка.
Т.к.
в межтрубном пространстве режим течения
теплоносителя ламинарный, то формула
для расчета среднего значения критерия
Нуссельта для шахматного порядка имеет
вид:
![]() , (1.7)
, (1.7)
где Pr1
– критерий Прандтля теплоносителя при
его средней температуре;
Prc
– критерий Прандтля теплоносителя при
средней температуре стенки;
![]() .
.
Аналогично
формуле (1.6) можно записать:![]()
![]() , (1.8)
, (1.8)
![]() Вт/(м2К).
Вт/(м2К).
1.6 Определение
коэффициента теплопередачи
Т.к.
отношение наружного диаметра трубки к
внутреннему составляет 1,083, что меньше
1,6, то при расчете среднего коэффициента
теплопередачи можно пользоваться
формулой для плоской стенки.
Вычислим
средний коэффициент теплопередачи:
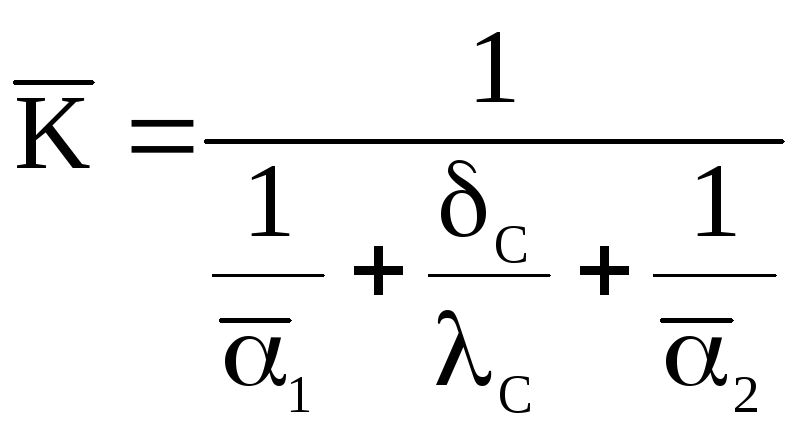 , (1.9)
, (1.9)
где С
– толщина стенок трубок, м;
С
– коэффициент теплопроводности материала
стенок при средней температуре стенки;
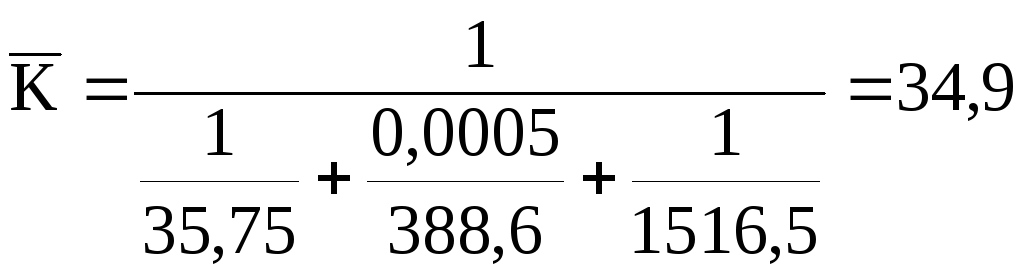 Вт/(м2К).
Вт/(м2К).
1.7 Уточнение температуры стенки
Средний
температурный напор для прямоточных и
противоточных ТОА с учетом перекрестного
тока вычисляется по формуле:
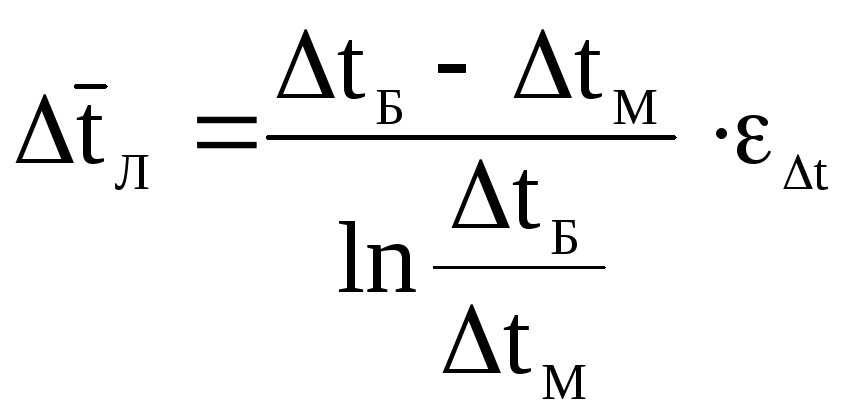 ,
,
(1.10)
где tБ
– большая разность температур между
теплоносителями;
tМ
– меньшая разность температур между
теплоносителями;
εΔt
= 0,75 – поправка на перекрестный ток.
tБ
и tМ
выбираются по разности температур
![]() и
и![]() ,
,
и разности температур![]() и
и![]() .
.
![]() –
–![]() = 100-60 = 40 °С,
= 100-60 = 40 °С,
![]() –
–![]() = 40-20 = 20 °С.
= 40-20 = 20 °С.
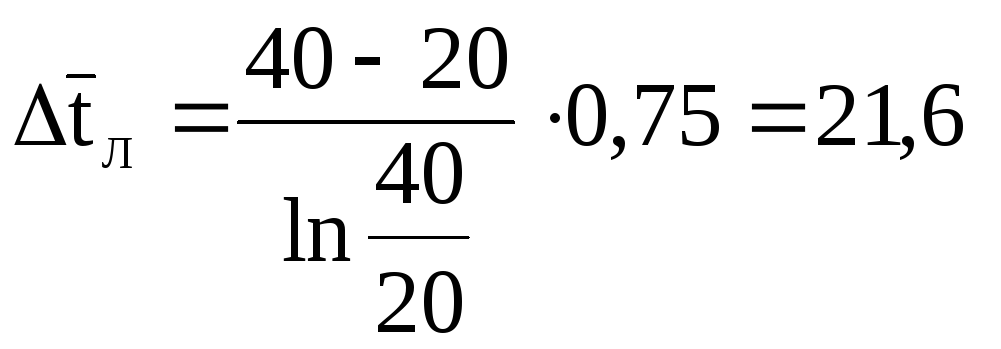 °С.
°С.
.
Температура стенки
труб со стороны греющего теплоносителя
находится по формуле:
![]() ,
,
(1.11)
![]()
Температура стенки
труб со стороны нагреваемого теплоносителя
находится по формуле:
![]() , (1.12)
, (1.12)
![]()
Найдем
уточненную среднюю температуру стенки:
![]() . (1.13)
. (1.13)
Определим
погрешность нахождения средней
температуры стенки:
 %. (1.14)
%. (1.14)
Т.к.
tc>5
%, то температура стенки определена с
недостаточной степенью точности.
Проведем аналогичный расчет, приняв за
среднюю температуру стенки значение,
полученное по формуле (1.13).
|
|
Макеты страниц
Из этих уравнений определяются частные температурные напоры, а именно:

Складывая их, получаем полный температурный напор:

из которого определяется значение плотности теплового потока

и значение коэффициента теплопередачи


Рис. 6-2. Теплопередача через однослойную плоскую стенку; характер изменения температуры в теплоносителях и разделяющей их стенке.
Таким образом, чтобы вычислить значение коэффициента теплопередачи k для плоской стенки, необходимо знать толщину этой стенки  , коэффициент теплопроводности
, коэффициент теплопроводности  и значения коэффициентов теплоотдачи
и значения коэффициентов теплоотдачи  .
.
Величина, обратная коэффициенту теплопередачи, называется общим термическим сопротивлением теплопередачи. Из уравнения (6-5) эта величина равна:

Из этого соотношения следует, что общее термическое сопротивление равно сумме частных:

где  — частное термическое сопротивление теплоотдачи со стороны горячего теплоносителя;
— частное термическое сопротивление теплоотдачи со стороны горячего теплоносителя;  — частное термическое сопротивление теплопроводности (стенки);
— частное термическое сопротивление теплопроводности (стенки);  — частное термическое сопротивление теплоотдачи со стороны холодного теплоносителя.
— частное термическое сопротивление теплоотдачи со стороны холодного теплоносителя.
2. Многослойная плоская стенка. Рассматривается стенка, состоящая из нескольких, например двух, слоев (рис. 6-3).
Толщины слоев  и
и  коэффициенты теплопроводности и
коэффициенты теплопроводности и  . С одной стороны находится горячая среда с температурой
. С одной стороны находится горячая среда с температурой  , с другой — холодная с температурой
, с другой — холодная с температурой  . Значение суммарного коэффициента теплоотдачи с горячей стороны
. Значение суммарного коэффициента теплоотдачи с горячей стороны  с холодной
с холодной  .
.
При установившемся тепловом состоянии системы плотность теплового потока постоянна и поэтому можно написать:

Из этих уравнений определяются частные температурные напоры:

Складывая раздельно левые и правые части уравнений, получаем полный температурный напор

из которого определяется значение плотности теплового потока

и значение коэффициента теплопередачи для двухслойной плоской стенки

Распределение температур при теплопередаче через плоскую одно- и многослойную стенки представлено соответственно на рис. 6-2 и 6-3.
Неизвестные температуры  могут быть определены из уравнений (е):
могут быть определены из уравнений (е):

Если стенка состоит из нескольких слоев толщиной  и коэффициенты теплопроводности их соответственно
и коэффициенты теплопроводности их соответственно  , то общее термическое сопротивление теплопередачи будет равно:
, то общее термическое сопротивление теплопередачи будет равно:

или

В этом случае уравнение (6-5) принимает вид:

или


Рис. 6-3. Теплопередача через многослойную плоскую стенку.
Температуры стенки можно определить и графически. Один из таких способов был описан в гл. 1. Поэтому мы здесь рассмотрим второй, который основан на замене термического сопротивления горячей и холодной среды термическим сопротивлением твердой стенки с таким же коэффициентом теплопроводности, как и действительная стенка.
Пусть температуры наружных поверхностей воображаемой стенки соответственно равны температурам горячей и холодной среды  (рис. 6-4). Количество передаваемой теплоты остается без изменения. Тогда общая толщина
(рис. 6-4). Количество передаваемой теплоты остается без изменения. Тогда общая толщина  этой воображаемой стенки определяется из соотношения
этой воображаемой стенки определяется из соотношения

откуда

Здесь величины  имеют размерность длины, м, они определяют собой эквивалентные толщины. При графическом построении сначала строится реальная стенка толщиной
имеют размерность длины, м, они определяют собой эквивалентные толщины. При графическом построении сначала строится реальная стенка толщиной  (в любом масштабе), затем по одну сторону от нее в том же масштабе откладывается значение
(в любом масштабе), затем по одну сторону от нее в том же масштабе откладывается значение  а по другую — значение
а по другую — значение  . Из крайних точек а и b по вертикали в некотором масштабе откладываются значения температур
. Из крайних точек а и b по вертикали в некотором масштабе откладываются значения температур  . Полученные точки А и С соединяются прямой линией. Точки пересечения этой прямой с поверхностями действительной стенки дают значения искомых температур
. Полученные точки А и С соединяются прямой линией. Точки пересечения этой прямой с поверхностями действительной стенки дают значения искомых температур  .
.

Рис. 6-4. Графический способ определения температур на поверхности стенки.

Рис. 6-5. Графическое определение температуры на поверхности и в плоскости соприкосновения слоев двухслойной стенки.
Действительно, из подобия треугольников АВС и ADE имеем, что  , откуда
, откуда

Согласно уравнению (б)  ; следовательно, отрезок
; следовательно, отрезок  . Таким же путем можно показать, что отрезок NG в выбранном масштабе температуры равен
. Таким же путем можно показать, что отрезок NG в выбранном масштабе температуры равен  .
.
Если стенка многослойная и требуется определить лишь температуру наружных поверхностей, то построение производят точно таким же образом, как и для однослойной стенки, имея дело лишь со средним коэффициентом теплопроводности  многослойной стенки (рис. 6-5).
многослойной стенки (рис. 6-5).
Температура же между слоями в точке А определяется по пересечению двух лучей (способ построения виден из рис. 6-5).
Пример 6-1. Определить потерю теплоты через 1 м2 кирпичной обмуровки котла толщиной  и температуры стенки
и температуры стенки  , если температура газов
, если температура газов  600° С, температура воздуха
600° С, температура воздуха  , коэффициент теплоотдачи со стороны газов
, коэффициент теплоотдачи со стороны газов  , коэффициент теплоотдачи со стороны воздуха
, коэффициент теплоотдачи со стороны воздуха  и коэффициент теплопроводности обмуровки
и коэффициент теплопроводности обмуровки  .
.
Согласно уравнению (6-5)

Подставляя это значение в уравнение (6-4), имеем:

Наконец, из уравнения (б)

3. Однородная цилиндрическая стенка. Пусть имеется цилиндрическая стенка (труба) с внутренним диаметром  внешним
внешним  и длиной l. Стенка трубы однородна; ее коэффициент теплопроводности
и длиной l. Стенка трубы однородна; ее коэффициент теплопроводности  . Внутри трубы горячая среда с температурой
. Внутри трубы горячая среда с температурой  , а снаружи — холодная с температурой
, а снаружи — холодная с температурой  . Температуры поверхностей стенки неизвестны, обозначим их через
. Температуры поверхностей стенки неизвестны, обозначим их через  (рис. 6-6). Со стороны горячей среды суммарный коэффициент теплоотдачи
(рис. 6-6). Со стороны горячей среды суммарный коэффициент теплоотдачи  а со стороны холодной
а со стороны холодной  .
.
При установившемся тепловом состоянии системы количество теплоты, отданное горячей и воспринятое холодной средой, одно и то же. Следовательно, можно написать:

Из этих соотношений определяем частные температурные напоры:

Складывая уравнения системы (к), получаем полный температурный напор


Рис. 6-6. Теплопередача через однослойную цилиндрическую стенку.

Рис. 6-7. Теплопередача через многослойную цилиндрическую стенку.
Из уравнения (л) определяется значение линейной плотности теплового потока 

откуда линейный коэффициент теплопередачи (на  длины трубы)
длины трубы)

Величина, обратная линейному коэффициенту теплопередачи,  называется линейным термическим сопротивлением теплопередачи.
называется линейным термическим сопротивлением теплопередачи.
Из уравнения (6-9) имеем:

Последнее означает, что общее термическое сопротивление равно сумме частных — термического сопротивления теплопроводности стенки  и термических сопротивлений теплоотдачи
и термических сопротивлений теплоотдачи  . Значения
. Значения  определяются из уравнений (к).
определяются из уравнений (к).
4. Многослойная цилиндрическая стенка. В этом случае рассматривается передача теплоты через многослойную, например двухслойную, цилиндрическую стенку. Диаметры и коэффициенты теплопроводности отдельных слоев известны (рис. 6-7). Температура горячей среды  холодной
холодной  Коэффициент теплоотдачи со стороны горячей среды
Коэффициент теплоотдачи со стороны горячей среды  а со стороны холодной
а со стороны холодной  . Температуры поверхностей
. Температуры поверхностей  а также температура в месте соприкосновения разнородных цилиндрических слоев
а также температура в месте соприкосновения разнородных цилиндрических слоев  неизвестны.
неизвестны.
При установившемся тепловом состоянии системы можно записать:

Определяем частные температурные напоры:

Складывая левые и правые части уравнений (н), получаем полный температурный напор

и значение линеинои плотности теплового потока

Распределение температур при теплопередаче через однослойную и многослойную цилиндрические стенки показано на рис. 6-6 и 6-7 соответственно.
Линейный коэффициент теплопередачи для двухслойной стенки

а общее термическое сопротивление  .
.
Для многослойной стенки трубы

и

Чтобы определить неизвестные температуры стенки  надо значение
надо значение  из уравнения (6-10) подставить в уравнения (н). Решая их, получаем:
из уравнения (6-10) подставить в уравнения (н). Решая их, получаем:


Способ определения температуры между слоями описан в гл. 1. Расчетные формулы теплопередачи для труб довольно громоздки, поэтому при практических расчетах применяются некоторые упрощения. Если толщина стенки не очень велика, то вместо формулы (6-8) в расчетах применяется формула для плоской стенки (6-4), которая в этом случае (в применении к трубе длиной 1 м) принимает вид:

где k — коэффициент теплопередачи для плоской стенки, рассчитанный по формуле (6-5), dx — средний диаметр стенки;  — ее толщина, равная полуразности диаметров.
— ее толщина, равная полуразности диаметров.
При этом если  , то погрешность расчета не превышает 4%. Эта погрешность снижается, если при выборе
, то погрешность расчета не превышает 4%. Эта погрешность снижается, если при выборе  соблюдать следующее правило:
соблюдать следующее правило:

т. е. при расчете теплопередачи по формуле (6-12) вместо  берется тот диаметр, со стороны которого коэффициент теплоотдачи имеет меньшее значение. Если же значения коэффициентов теплоотдачи
берется тот диаметр, со стороны которого коэффициент теплоотдачи имеет меньшее значение. Если же значения коэффициентов теплоотдачи  одного порядка, то
одного порядка, то  равно среднеарифметическому между внутренним
равно среднеарифметическому между внутренним  и внешним
и внешним  диаметрами трубы. При проведении расчетов как по формуле (6-8), так и по формуле (6-12) всегда следует иметь в виду, что в целях упрощения расчета относительно малыми сопротивлениями можно и следует пренебрегать.
диаметрами трубы. При проведении расчетов как по формуле (6-8), так и по формуле (6-12) всегда следует иметь в виду, что в целях упрощения расчета относительно малыми сопротивлениями можно и следует пренебрегать.
Пример 6-2. Паропровод диаметром 200/216 мм покрыт слоем совелитовой изоляции толщиной 120 мм, коэффициент теплопроводности которой  . Температура пара
. Температура пара  и окружающего воздуха
и окружающего воздуха  . Кроме того, заданы коэффициент теплопроводности стенки
. Кроме того, заданы коэффициент теплопроводности стенки  . Требуется определить линейный коэффициент теплопередачи, линейную плотность теплового потока и температуру в месте соприкосновения паропровода с изоляцией.
. Требуется определить линейный коэффициент теплопередачи, линейную плотность теплового потока и температуру в месте соприкосновения паропровода с изоляцией.
Согласно условию задачи  . Далее на основании формулы (6-9) имеем:
. Далее на основании формулы (6-9) имеем:

Первые два члена общего термического сопротивления по сравнению с остальными малы, при расчетах ими можно было бы пренебречь. На основании формулы (5-8)

И, наконец, согласно формуле (н):

5. Шар. Пусть внутренний диаметр шара равен  внешний
внешний  и коэффициент теплопроводности стенки
и коэффициент теплопроводности стенки  . Внутри шара находится горячая жидкость с температурой
. Внутри шара находится горячая жидкость с температурой  снаружи — холодная с температурой
снаружи — холодная с температурой  . Значения коэффициентов теплоотдачи соответственно
. Значения коэффициентов теплоотдачи соответственно  . Температуры поверхностей стенки неизвестны, обозначим их через
. Температуры поверхностей стенки неизвестны, обозначим их через  (рис. 6-8).
(рис. 6-8).
При стационарном тепловом состоянии системы количество теплоты, переданное от горячей жидкости к холодной, можно выразить тремя уравнениями:

Из этих уравнений определяется значение  :
:

Следовательно, коэффициент теплопередачи для шаровой стенки определяется оотношением

Обратная величина  называется общим термическим сопротивлением теплопередачи шаровой стенки:
называется общим термическим сопротивлением теплопередачи шаровой стенки:


Рис. 6-8. Теплопередача через шаровую стенку.
При практических расчетах надо проверять соотношение термических сопротивлений; относительно малыми из них всегда можно пренебречь.
Оглавление
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- ГЛАВА ПЕРВАЯ. ТЕПЛОПРОВОДНОСТЬ
- 1-1. ОСНОВНОЙ ЗАКОН ТЕПЛОПРОВОДНОСТИ
- 1-2. ТЕПЛОПРОВОДНОСТЬ ПЛОСКОЙ СТЕНКИ
- 1-3. ТЕПЛОПРОВОДНОСТЬ ЦИЛИНДРИЧЕСКОЙ СТЕНКИ
- 1-4. ТЕПЛОПРОВОДНОСТЬ ШАРОВОЙ СТЕНКИ И ТЕЛ НЕПРАВИЛЬНОЙ ФОРМЫ
- 1-5. ТЕПЛОПРОВОДНОСТЬ ТЕЛ С ВНУТРЕННИМИ ИСТОЧНИКАМИ ТЕПЛОТЫ
- ГЛАВА ВТОРАЯ. КОНВЕКТИВНЫЙ ТЕПЛООБМЕН
- 2-1. ОБЩИЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ
- 2-2. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ТЕПЛООБМЕНА
- 2-3. ОСНОВЫ ТЕОРИИ ПОДОБИЯ
- 2-4. ПОДОБИЕ ПРОЦЕССОВ КОНВЕКТИВНОГО ТЕПЛООБМЕНА
- 2-5. ОБОБЩЕНИЕ ОПЫТНЫХ ДАННЫХ НА ОСНОВЕ ТЕОРИИ ПОДОБИЯ
- ГЛАВА ТРЕТЬЯ. ТЕПЛООБМЕН В ЖИДКОСТЯХ И ГАЗАХ
- 3-1. ТЕПЛООТДАЧА ПРИ ОБТЕКАНИИ ПЛОСКОЙ ПОВЕРХНОСТИ (ПЛАСТИНЫ)
- 3-2. ТЕПЛООТДАЧА ПРИ ТЕЧЕНИИ ЖИДКОСТИ В ТРУБАХ
- 3-3. ТЕПЛООТДАЧА ПРИ СВОБОДНОЙ КОНВЕКЦИИ
- 3-4. ТЕПЛООТДАЧА ПРИ ПОПЕРЕЧНОМ ОБТЕКАНИИ ТРУБ
- ГЛАВА ЧЕТВЕРТАЯ. ТЕПЛООБМЕН ПРИ КИПЕНИИ И КОНДЕНСАЦИИ
- 4-1. ТЕПЛООБМЕН ПРИ КИПЕНИИ
- 4-2. ТЕПЛООБМЕН ПРИ КОНДЕНСАЦИИ ПАРА
- ГЛАВА ПЯТАЯ. ТЕПЛОВОЕ ИЗЛУЧЕНИЕ
- 5-1. ЗАКОНЫ ТЕПЛОВОГО ИЗЛУЧЕНИЯ
- 5-2. ЛУЧИСТЫЙ ТЕПЛООБМЕН МЕЖДУ ТЕЛАМИ
- 5-3. ТЕПЛОВОЕ ИЗЛУЧЕНИЕ ГАЗОВ
- ГЛАВА ШЕСТАЯ. ПРОЦЕССЫ ТЕПЛОПЕРЕДАЧИ
- 6-1. СЛОЖНЫЙ ТЕПЛООБМЕН И ТЕПЛОПЕРЕДАЧА
- 6-2. ТЕПЛОПЕРЕДАЧА ЧЕРЕЗ СТЕНКИ
- 6-3. ТЕПЛОПЕРЕДАЧА ЧЕРЕЗ СЛОЖНЫЕ СТЕНКИ
- 6-4. ИНТЕНСИФИКАЦИЯ ПРОЦЕССОВ ТЕПЛОПЕРЕДАЧИ
- 6-5. ТЕПЛОВАЯ ИЗОЛЯЦИЯ
- ГЛАВА СЕДЬМАЯ. НЕСТАЦИОНАРНАЯ ТЕПЛОПРОВОДНОСТЬ
- 7-1. ОПИСАНИЕ ПРОЦЕССА
- 7-2. АНАЛИТИЧЕСКОЕ РЕШЕНИЕ
- 7-3. ПРИБЛИЖЕННЫЕ МЕТОДЫ РЕШЕНИЯ
- 7-4. РЕГУЛЯРНЫЙ ТЕПЛОВОЙ РЕЖИМ
- ГЛАВА ВОСЬМАЯ. ТЕПЛООБМЕННЫЕ АППАРАТЫ
- 8-2. РЕКУПЕРАТИВНЫЕ АППАРАТЫ
- 8-3. ТЕПЛООБМЕННЫЕ РЕГЕНЕРАТИВНЫЕ И СМЕСИТЕЛЬНЫЕ АППАРАТЫ
- 8-4. ГИДРОМЕХАНИЧЕСКИЙ РАСЧЕТ ТЕПЛООБМЕННЫХ АППАРАТОВ
- ГЛАВА ДЕВЯТАЯ. МОДЕЛИРОВАНИЕ ТЕПЛОВЫХ УСТРОЙСТВ
- 9-2. УСЛОВИЯ МОДЕЛИРОВАНИЯ
- 9-3. ПРИМЕРЫ МОДЕЛИРОВАНИЯ
- ГЛАВА ДЕСЯТАЯ. ОТДЕЛЬНЫЕ ЗАДАЧИ ТЕПЛООБМЕНА
- 10-1. ГИДРОДИНАМИЧЕСКАЯ ТЕОРИЯ ТЕПЛООБМЕНА
- 10-2. ТЕПЛООБМЕН ПРИ ВЫСОКИХ СКОРОСТЯХ
- 10-3. ТЕПЛООБМЕН ПОВЕРХНОСТЕЙ С ИСКУССТВЕННОЙ ШЕРОХОВАТОСТЬЮ
- 10-4. ТЕПЛООТДАЧА РАСПЛАВЛЕННЫХ МЕТАЛЛОВ
- 10-5. ПЕРЕДАЧА ТЕПЛОТЫ ЧЕРЕЗ СТЕРЖЕНЬ
- 10-6. ПЕРЕДАЧА ТЕПЛОТЫ ЧЕРЕЗ РЕБРА
- ПРИЛОЖЕНИЯ
- СПИСОК ЛИТЕРАТУРЫ
Краткие сообщения
УДК 681.52.01
ВЫЧИСЛЕНИЕ СРЕДНЕЙ ТЕМПЕРАТУРЫ ^СЛОЙНОЙ СТЕНКИ
В.И. Панферов, А.Е. Милов
Южно-Уральский государственный университет, г. Челябинск
Рассмотрена задача вычисления средней температуры п-слойной ограждающей конструкции. С использованием метода математической индукции найдена формула, позволяющая определять среднюю температуру стенки по температурам ее внутренней и внешней поверхностей, а также по толщинам ее слоев и их термическим сопротивлениям теплопроводности. Формула рекомендуется для использования при построении математических моделей теплового режима зданий.
Ключевые слова: средняя температура, п-слойная ограждающая конструкция, метод математической индукции, термическое сопротивление, тепловой режим зданий.
В работе [1] при построении математической модели теплового режима здания (ТРЗ) полагалось, что средняя температура его наружной стены в квазистационарном приближении может быть вычислена по формуле
? = (1)
где £в – температура внутреннего воздуха, £н – температура наружного воздуха.
Однако данное допущение предполагает, что выполняются следующие условия:
1) коэффициенты теплоотдачи для внутренней и внешней поверхностей стенки ав, ан ^ да [2];
2) стенка однослойная.
В реальных условиях ав и ан имеют конечные значения, кроме того, наружные стены, как правило, многослойные. Поэтому возникает задача уточнения формулы для средней температуры наружной стены здания. Для решения этой задачи рассмотрим процесс теплопроводности в п-слойной ограждающей конструкции. Для иллюстрации последующих выкладок на рис. 1 приведена схема двухслойной стенки.
Здесь и далее через обозначим толщину всей стенки, имеющей в общем случае п слоев (в случае рис. 1 слоев 2), а через 5,- – толщину /’-го слоя, £ВП – температура внутренней поверхности стены, £НП – температура наружной поверхности
стены, £(¿-1)-! – температура на границе (/’-1)-го и /-го слоев, 11 – средняя температура /-го слоя, – термическое сопротивление теплопроводности всей стенки, а – ее /-го слоя.
Нетрудно показать, что температуры на внутренних границах слоев будут равны:
^1-2 = ¿ВП ‘ ^2-3 = ^ВП ‘ ^3-4 = ^ВП ‘
ОвП ‘
ОвП
Овп
ч Й1+Й2
cHnJ •
trn) •
Re
й1+Й2+Й3; Re ‘
(2)
(3)
(4)
t(n-l)-n = ^ВП (^ВП ^НП) X й1 + й2 + йз + …+йп-1
X ■
(5)
Обобщая полученные соотношения, запишем,
Re
что
^¿-(¿+1) = £вп ОВП W • k . (6)
При этом следует иметь в виду, что температура наружной поверхности формально может быть представлена следующим выражением:
¿НП = ^ВП — ОвП — W • к. (7)
Re
Так как температура по толщине каждого слоя распределяется по прямой, то его средняя температура будет равна полусумме температур на его границах, поэтому
= ^ВП — (^ВП — ¿НП) • (8)
^2 = ^ВП — (^ВП t-n = ^ВП — (^ВП X ‘
2RE 2й1+Й2i
2RE ‘
*НП) X
2й1 + 2Й2 + 2Й3 + …+ 2Йп_2+Йп-1 2RE .
(9)
(10)
Рис. 1. Двухслойная стенка
Вестник ЮУрГУ. Серия «Строительство и архитектура». 2015. Т. 15, № 2. С. 59-61
Краткие сообщения
Следовательно, общая формула для средней температуры /-го слоя будет такой:
Ч = £вп — (^ВП — ^НП) 1с~1п к 1 . (11)
Вычисляя среднюю температуру и-слойной стенки по известной формуле
1= ± + (12) получим следующее выражение:
х £?=15г( 2££:11Дк+Дг). (13)
Таким образом, найдена формула, позволяющая вычислять среднюю температуру и-слойной стенки по температурам ее внутренней и внешней поверхностей, а также по толщинам ее слоев и их термическим сопротивлениям теплопроводности.
Выясним, как отличаются значения средней температуры многослойной ограждающей конструкции, вычисленные по разным формулам. В качестве примера рассмотрим двухслойную стенку, состоящую из керамзитобетона (5Х=300 мм, R1 = = 0,46 м2 -°С/Вт) и минеральной ваты (52=100 мм, R2 = 1,78 м2 • °С/Вт). Примем наружную температуру равной ^ = -34 °С, а внутреннюю – 4 = 21 °С.
Тогда по формуле (1) получим, что I = 21+2 34 = = -6,5 °С. Заметим, что использование формулы (1) предполагает, что коэффициенты теплоотдачи для внутренней и внешней поверхности
ав, ан ^ да, но при практических расчетах их значениях принимаются согласно [3]: ав = 8,7 Вт/ (м2 °С), а ан = 23 Вт/ (м2- °С). С учетом этого, определены температуры внешней и внутренней поверхности стенки: tBn = 18,37 °С, а tHn = -33 °С. Тогда, условно полагая, что стенка однородная, получим,
что t =-= -7,315 °С. Если же вычисле-
2
ния проведем по формуле (13), то получим, что t= 6,67 °С.
Выводы
Получена формула, позволяющая вычислять среднюю температуру многослойной плоской стенки в соответствии с физикой процесса переноса теплоты. Показано, что погрешности использования ранее предложенных в литературе формул достаточно существенные.
Литература
1. Соколов, Е.Я. Теплофикация и тепловые сети: учебник для вузов / Е.Я. Соколов – 7-е изд., стер. – М.: Изд-во МЭИ, 2001. – 472 с.
2. Лыков, А.В. Теоретические основы строительной теплофизики / А.В. Лыков. -Минск: Издательство академии наук БССР, 1961. – 520 с.
3. СП 50.13330.2012. Тепловая защита зданий. Актуализированная редакция СНиП 23-02-2003.
Панферов Владимир Иванович, доктор технических наук, профессор, зав. кафедрой «Теплогазо-снабжение и вентиляция», Южно-Уральский государственный университет (Челябинск), tgsiv@mail.ru.
Милов Александр Евгеньевич, студент, архитектурно-строительный факультет, Южно-Уральский государственный университет (Челябинск), milovalexandr74@gmail.com.
Поступила в редакцию 12 января 2015 г.
CALCULATION OF THE AVERAGE TEMPERATURE FOR MULTILAYER WALL
V.I. Panferov, South Ural State University, Chelyabinsk, Russian Federation, tgsiv@mail.ru
A.E. Milov, South Ural State University, Chelyabinsk, Russian Federation, milovalexandr74@gmail.com
Calculation of the average temperature for multilayer enclosure structure is analyzed. With the help of mathematical induction method we have found a formula to calculate the average temperature of the wall using its boundary temperatures, thickness and thermal resistance of layers. This method is recommended for use with mathematical models of thermal conditions of buildings.
Keywords: average temperature, multilayer enclosure structure, mathematical induction method, thermal resistance, thermal conditions of buildings.
Bulletin of the South Ural State University. Ser. Construction Engineering and Architecture.
2015, vol. 15, no. 2, pp. 59-61
Панферов В.И., Милов А.Е.
Вычисление средней температуры n-слойной стенки
References
1. Sokolov E.Ya. Teplofikatsiya i teplovyie seti [District heating and heat networks]. Moscow, MEI Publ., 2001. 472 p.
2. Lyikov A.V. Teoreticheskie osnovyi stroitelnoy teplofiziki [Theoretical Foundations of Building Thermal Physics]. Minsk: Akademii nauk BSSR Publ., 1961. 520 p.
3. SP 50.13330.2012. Teplovaya zaschita zdaniy. Aktualizirovannaya redaktsiya SNiP 23-02-2003 [Thermal protection of buildings. The actualized edition Construction Norms and Regulations 23-02-2003]. Moscow, 2003.
Received 12 January 2015
БИБЛИОГРАФИЧЕСКОЕ ОПИСАНИЕ СТАТЬИ
Панферов, В.И. Вычисление средней температуры п-слойной стенки / В.И. Панферов, А.Е. Милов // Вестник ЮУрГУ. Серия «Строительство и архитектура». -2015. – Т. 15, № 2. – С. 59-61.
REFERENCE TO ARTICLE
Panferov V.I., Milov A.E. Calculation of the Average Temperature for Multilayer Wall. Bulletin of the South Ural State University. Ser. Construction Engineering and Architecture. 2015, vol. 15, no. 2, pp. 59-61. (in Russ.)
Вестник ЮУрГУ. Серия «Строительство и архитектура». 2015. Т. 15, № 2. С. 59-61
Теплота передается через ограждающие конструкции помещений, а также во всех непрерывно действующих нагревательных приборах — котлах, печах, водо- и воздухоподогревателях, сушилках, пропарочных камерах и других теплообменниках.
Расчет теплопередачи заключается обычно в определении количества теплоты, которая передается в единицу времени между теплоносителями через стенку, разделяющую их.
Может рассматриваться и обратная задача — определение требуемой площади поверхности стенки между жидкостями для передачи заданного количества теплоты от горячего теплоносителя к холодному.
Попутно с этими основными задачами при конструировании ограждений, разделяющих горячую и холодную жидкости (стенки печей, барабанов, кипятильных труб котла и т. п.), рассчитывают температуры на поверхности каждого слоя ограждения, с тем чтобы рабочая температура материала не превышала максимально допустимое для него значение.
В настоящей главе рассматривается теплопередача через плоскую, цилиндрическую, сферическую и ребристую стенки для условий стационарного режима, а также методика расчета теплообменных аппаратов.
Возможно эта страница вам будет полезна:

Теплопередача через плоскую стенку
Теплота передается от горячей жидкости с температурой 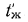 к холодной жидкости, имеющей температуру
к холодной жидкости, имеющей температуру  , через плоскую однородную стенку с теплопроводностью
, через плоскую однородную стенку с теплопроводностью 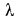 .
.
Стенка имеет толщину 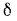 , которая значительно меньше линейных размеров ее площади поверхности S, что дает возможность пренебречь потерями теплоты с торцов стенки. Значения коэффициентов теплоотдачи, определяемые условиями движения жидкостей, считаем известными и соответственно равными на горячей стороне
, которая значительно меньше линейных размеров ее площади поверхности S, что дает возможность пренебречь потерями теплоты с торцов стенки. Значения коэффициентов теплоотдачи, определяемые условиями движения жидкостей, считаем известными и соответственно равными на горячей стороне 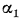 и на холодной
и на холодной 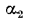 ,.
,.
Температуры поверхностей стенки неизвестны. Обозначим их соответственно через 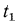 и
и 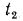 °С (рис. 16.1, а). Требуется определить плотность теплового потока, проходящего через стенку, и распределение температур в стенке. В условиях стационарного режима вся теплота, передаваемая горячей жидкостью стенке, проходит через нее и поглощается холодной средой. При этом плотность теплового потока q может быть выражена равенствами:
°С (рис. 16.1, а). Требуется определить плотность теплового потока, проходящего через стенку, и распределение температур в стенке. В условиях стационарного режима вся теплота, передаваемая горячей жидкостью стенке, проходит через нее и поглощается холодной средой. При этом плотность теплового потока q может быть выражена равенствами:
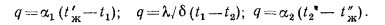
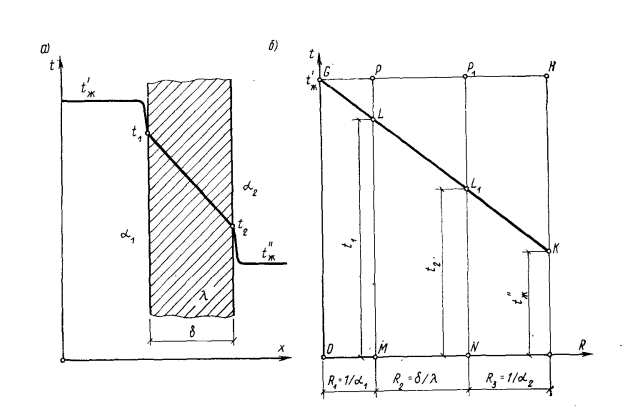
Из этих равенств определяем разности температур:

и, складывая их, получаем
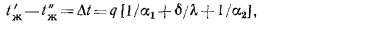
откуда искомая величина

а тепловой поток

где
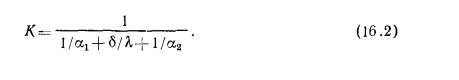
Коэффициент К носит название коэффициента теплопередачи. Он имеет ту же размерность, что и 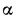 ; числовое значение его определяет мощность теплового потока, проходящего от одного теплоносителя к другому через единицу поверхности стенки, разделяющей эти теплоносители, при разности температур между ними 1°.
; числовое значение его определяет мощность теплового потока, проходящего от одного теплоносителя к другому через единицу поверхности стенки, разделяющей эти теплоносители, при разности температур между ними 1°.
В знаменателе формулы (16.2) слагаемое 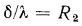 представляет собой термическое сопротивление теплопроводности (см. § 13.2), а слагаемые
представляет собой термическое сопротивление теплопроводности (см. § 13.2), а слагаемые 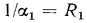 и
и  — термические сопротивления теплоотдачи (
— термические сопротивления теплоотдачи (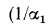 — от горячей жидкости к стенке, а
— от горячей жидкости к стенке, а 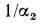 — от стенки к холодной жидкости). Сумма термических сопротивлений
— от стенки к холодной жидкости). Сумма термических сопротивлений 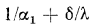
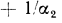 , представляющая собой величину, обратную коэффициенту теплопередачи, называется термическим сопротивлением теплопередачи и обозначается R, т. е.
, представляющая собой величину, обратную коэффициенту теплопередачи, называется термическим сопротивлением теплопередачи и обозначается R, т. е.
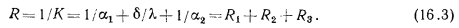
Единицами измерения для К и R служат соответственно 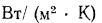 и
и 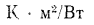 .
.
Для плоской стенки, состоящей из нескольких слоев толщиной 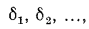
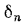 с соответствующими теплопроводностями
с соответствующими теплопроводностями 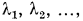
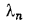 , термическое сопротивление теплопередачи составит
, термическое сопротивление теплопередачи составит
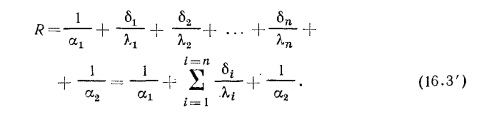
В этом случае выражение (16.2) для коэффициента теплопередачи К принимает вид
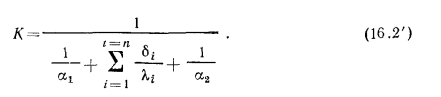
Из формулы видно, что величина К всегда меньше каждой из величин 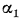 и
и 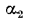 и если термические сопротивления слоев стенок малы по сравнению с
и если термические сопротивления слоев стенок малы по сравнению с 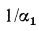 и
и 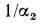 , то
, то
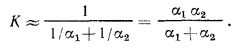
Полученное равенство показывает, что наибольшее влияние на К оказывает тот коэффициент теплоотдачи, который значительно меньше другого: например, при 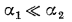
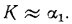
Для определения температуры 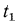 и
и 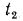 на поверхностях стенки достаточно подставить найденное значение плотности теплового потока q в равенство (а), тогда:
на поверхностях стенки достаточно подставить найденное значение плотности теплового потока q в равенство (а), тогда:
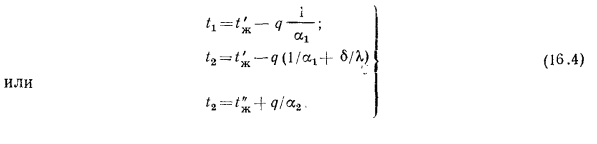
Графический способ определения температур
Эти температуры можно также определить графическим способом (рис. 16.1, б), суть которого состоит в том, что но оси абсцисс в одном масштабе откладывают последовательно все термические сопротивления, а на крайних ординатах от произвольного нуля откладывают температуры 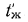 и
и  .
.
Соединяя полученные точки прямой линией GК , получаем в точке пересечения ее с остальными ординатами температуры на поверхностях слоев стенки 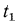 и
и 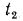 . Из рассмотрения подобия треугольников, например треугольников GPL и GHK, следует, что
. Из рассмотрения подобия треугольников, например треугольников GPL и GHK, следует, что
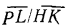 =
=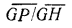 , откуда
, откуда
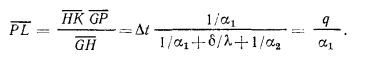
Согласно уравнению (16.4), 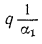
 следовательно, отрезок
следовательно, отрезок 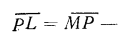
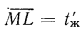

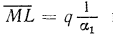 или
или 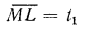 . Аналогично из подобия треугольников
. Аналогично из подобия треугольников 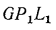 и GHK доказывается, что отрезок
и GHK доказывается, что отрезок 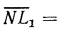
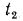
Возможно эта страница вам будет полезна:
Теплопередача через цилиндрическую стенку
Мощность теплового потока, передаваемого от горячей жидкости к холодной через цилиндрическую стенку, находят по той же методике, что и для плоской стенки.
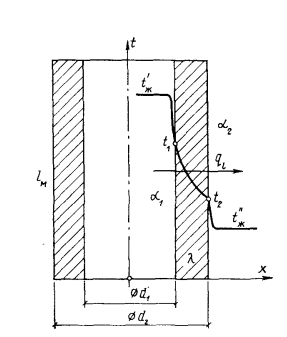
Пусть внутри трубы, диаметр которой достаточно мал по сравнению с ее длиной (это позволяет пренебречь потерями теплоты через торцы стенки), протекает горячая жидкость с постоянной температурой 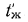 — Снаружи трубы находится холодная среда, температура которой также неизменна и равна
— Снаружи трубы находится холодная среда, температура которой также неизменна и равна . Стенка грубы однородна, ее теплопроводность равна
. Стенка грубы однородна, ее теплопроводность равна 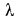 , внутренний диаметр
, внутренний диаметр 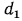 наружный
наружный 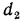
Суммарные коэффициенты теплоотдачи соответственно равны 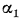 и
и 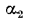 . Неизвестные температуры на внутренней поверхности стенки обозначим
. Неизвестные температуры на внутренней поверхности стенки обозначим 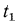 и на наружной
и на наружной 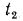 (рис. 16.2). В условиях стационарного режима линейная плотность теплового потока, т. е. количество теплоты, переданной от нагретой среды стенке, прошедшего через стенку и. переданного от стенки к более холодной среде, будет постоянным и соответственно равным:
(рис. 16.2). В условиях стационарного режима линейная плотность теплового потока, т. е. количество теплоты, переданной от нагретой среды стенке, прошедшего через стенку и. переданного от стенки к более холодной среде, будет постоянным и соответственно равным:
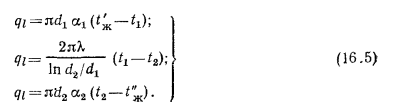
Определяя по этим уравнениям разности температур:
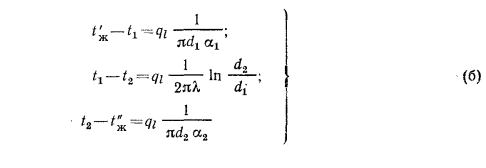
и суммируя, можем написать
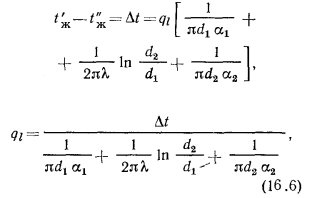
или

где
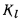 — линейный коэффициент теплопередачи, числовое значение которого определяет мощность теплового потока , проходящего от одного теплоносителя к другому через 1 м длинны трубы при разности температур между теплоносителями, равной 1°.
— линейный коэффициент теплопередачи, числовое значение которого определяет мощность теплового потока , проходящего от одного теплоносителя к другому через 1 м длинны трубы при разности температур между теплоносителями, равной 1°.
Величину 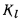 находят по формуле
находят по формуле
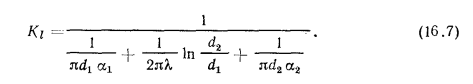
Мощность теплового потока, переданного через трубу длиной l, составляет 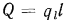

Величина, обратная линейному коэффициенту теплопередачи, 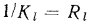 называется линейным термическим сопротивлением теплопередачи, т. е.
называется линейным термическим сопротивлением теплопередачи, т. е.
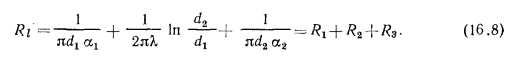
В этом уравнении среднее слагаемое 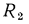 является термическим сопротивлением теплопроводности стенки (см. § 13.2), а крайние слагаемые
является термическим сопротивлением теплопроводности стенки (см. § 13.2), а крайние слагаемые 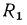 и
и 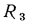 — термическими сопротивлениями теплоотдачи от горячей жидкости к внутренней поверхности цилиндрической стенки и от наружной поверхности к холодной жидкости.
— термическими сопротивлениями теплоотдачи от горячей жидкости к внутренней поверхности цилиндрической стенки и от наружной поверхности к холодной жидкости.
Единица измерения линейного коэффициента теплопередачи
Единица измерения линейного коэффициента теплопередачи — 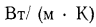 , единица измерения линейного термического сопротивления теплопередачи — м • К/Вт.
, единица измерения линейного термического сопротивления теплопередачи — м • К/Вт.
Для многослойной цилиндрической стенки в состав выражения для вычисления линейного термического сопротивления 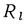 вместо одного слагаемого, определяющего сопротивление теплопроводности стенки,
вместо одного слагаемого, определяющего сопротивление теплопроводности стенки,
должен входить ряд однотипных слагаемых в соответствии с числом слоев, т. е.
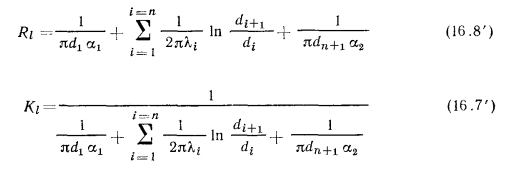
Неизвестные значения температур поверхностей стенки 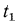 и
и 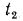 находят из равенств (б), если подставить в них полученное значение
находят из равенств (б), если подставить в них полученное значение 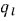 по уравнению (16.6). Решая эти равенства, можем написать:
по уравнению (16.6). Решая эти равенства, можем написать:
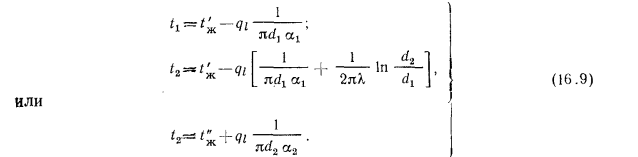
Температуры между слоями у многослойной цилиндрической стенки могут быть определены или графическим способом аналогично определению температур у плоской многослойной стенки, или аналитическим путем, рассмотренным.
Плотность теплового потока, отнесенного к внутренней или наружной поверхности трубы, определяется по известным соотношениям:
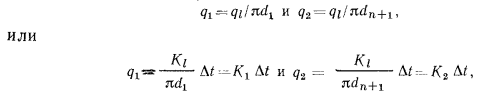
где  — коэффициенты теплопередачи цилиндрической стенки, отнесенные соответственно к единице внутренней или наружной ее поверхности, определяемые по формулам:
— коэффициенты теплопередачи цилиндрической стенки, отнесенные соответственно к единице внутренней или наружной ее поверхности, определяемые по формулам:
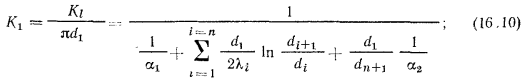
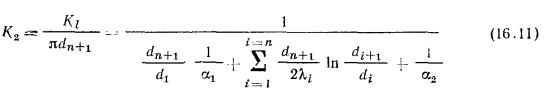
dn+1 1 lyn dn+1 di+l
При 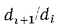
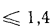 в соответствии с уравнением (13.12′)
в соответствии с уравнением (13.12′) 
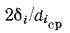 , что позволяет упростить расчетные формулы, которые, например, для
, что позволяет упростить расчетные формулы, которые, например, для 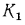 и
и 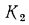 принимают вид:
принимают вид:
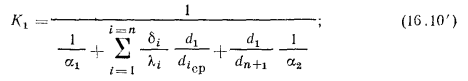
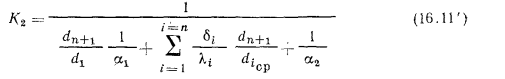
В случае использования тонких цилиндрических стенок значения 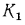 и
и 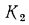 определяют по тем же уравнениям, что и для плоской многослойной стенки формула (16.2), так как отношения
определяют по тем же уравнениям, что и для плоской многослойной стенки формула (16.2), так как отношения 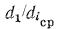 и
и 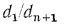 практически можно принять равными единице.
практически можно принять равными единице.
Этим, в частности, объясняется то положение, что при расчете теплообменных аппаратов, имеющих обычно трубчатую конструкцию (конденсаторы, котлы, подогреватели), теоретический коэффициент теплопередачи рассчитывают по формуле для плоской многослойной стенки.
Рассмотрим более подробно формулу (16.8), определяющую линейное термическое сопротивление теплопередачи трубы. Из этой формулы следует, что с увеличением наружного диаметра трубы 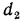 возрастает термическое сопротивление теплопроводности стенки
возрастает термическое сопротивление теплопроводности стенки 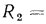
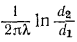 и уменьшается термическое сопротивление теплоотдачи от стенки к холодной жидкости
и уменьшается термическое сопротивление теплоотдачи от стенки к холодной жидкости 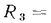
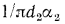 . Поэтому в зависимости от толщины стенки трубы
. Поэтому в зависимости от толщины стенки трубы 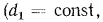
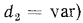 ее термическое сопротивление теплопередаче будет увеличиваться или уменьшаться.
ее термическое сопротивление теплопередаче будет увеличиваться или уменьшаться.
Для этого нужно взять производную термического сопротивления грубы при переменном 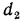 и приравнять ее к нулю. В результате получим:
и приравнять ее к нулю. В результате получим:
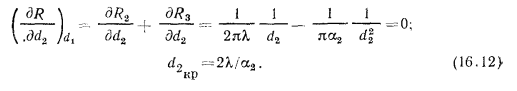
Исследование полученной формулы показывает, что, например, для стальной трубы при 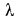 = 46 Вт/ (м • К) и
= 46 Вт/ (м • К) и 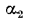 = 14
= 14 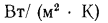


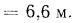 Таким образом, предельное значение диаметра металлических труб, после увеличения которого количество передаваемой через трубу теплоты
Таким образом, предельное значение диаметра металлических труб, после увеличения которого количество передаваемой через трубу теплоты
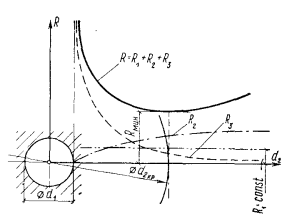
будет падать, весьма велико и измеряется метрами. В границах этого диаметра чем толще стенка металлической трубы, тем больше теплоты через нее будет передаваться от горячей жидкости к холодной. Если труба изготовлена из теплоизоляционного материала, например асбестовой массы с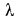 = 0,167 Вт/ (м • К ), то при том же значении
= 0,167 Вт/ (м • К ), то при том же значении 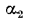 = 14
= 14 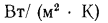
 2 • 0,167 : 14 = 0,024 м, т. е. для труб с наружным диаметром более 24 мм при увеличении толщины изоляции теплопередача будет снижаться.
2 • 0,167 : 14 = 0,024 м, т. е. для труб с наружным диаметром более 24 мм при увеличении толщины изоляции теплопередача будет снижаться.
У бетонных труб при 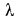 = 1,17Вт/ (м • К) и
= 1,17Вт/ (м • К) и 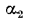 =14
=14 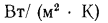 )
)  160 мм. При наружных диаметрах этих труб, которые меньше или больше 160 мм, количество теплоты, передаваемой от внутренней ■среды к наружной, снижается.
160 мм. При наружных диаметрах этих труб, которые меньше или больше 160 мм, количество теплоты, передаваемой от внутренней ■среды к наружной, снижается.
Это означает, что если металлическую трубу покрыть слоем бетона, теплопередача через такую двухслойную цилиндрическую стенку может оказаться больше, чем через чистую металлическую трубу.
Действительно, если наружный диаметр стальной трубы принять равным 40 мм, толщину ее стенки 2 мм, а наружный диаметр бетонной рубашки на этой трубе 120 мм, то при 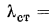 46 Вт/ (м • К),
46 Вт/ (м • К), 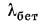 = 1,17 Вт/ (м • К),
= 1,17 Вт/ (м • К), 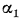 = 2800
= 2800 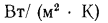 и
и 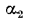 = 14
= 14 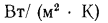 термическое сопротивление чистой металлической трубы составит
термическое сопротивление чистой металлической трубы составит
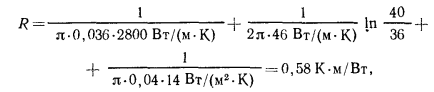
а трубы с бетонной рубашкой —
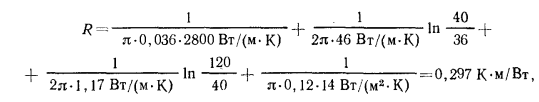
т. е. почти в 2 раза меньше, чем стальной трубы без слоя бетона. Это свидетельствует о том, что при диаметре цилиндрической оболочки меньше 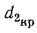 тепловая изоляция теряет свою роль.
тепловая изоляция теряет свою роль.
Поэтому при конструировании нагревательных приборов целесообразно использовать бетон, а также керамику для частичной замены металла.
В частности, в промышленности строительных материалов широкое применение находят керамические рекуператоры, состоящие из блоков различного фасонного сечения, образующих при укладке взаимно перекрещивающиеся каналы, по одной стороне которых движется воздух, подругой — продукты горения топлива.
Теплопередача через сферическую и ребристую стенки
При установившемся тепловом состоянии системы количество теплоты Q, переданной через однородную сферическую стенку от горячей жидкости к холодной, так же как количество теплоты, переданной плоской и цилиндрической стенками, может быть выражено тремя следующими уравнениями:
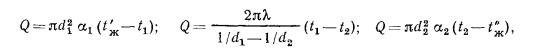
где 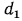 ,
,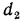 — внутренний и наружный диаметры сферической стенки;
— внутренний и наружный диаметры сферической стенки; 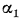 ,
,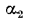 — коэффициенты теплоотдачи от горячей жидкости к стенке и от стенки холодной жидкости;
— коэффициенты теплоотдачи от горячей жидкости к стенке и от стенки холодной жидкости; 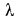 — теплопроводность материала стенки;
— теплопроводность материала стенки; 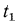 ,
,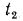 — температуры поверхностей стенки.
— температуры поверхностей стенки.
Из этих уравнений определяют искомое значение
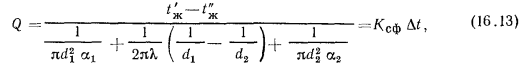
где 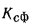 — коэффициент теплопередачи для сферической стенки, равный:
— коэффициент теплопередачи для сферической стенки, равный:
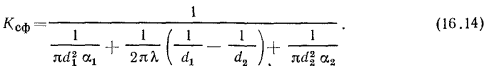
Величина, обратная 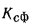 называется термическим сопротивлением теплопередачи сферической стенки и выражается соотношением
называется термическим сопротивлением теплопередачи сферической стенки и выражается соотношением
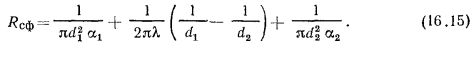
Единицей измерения для 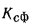 служит Вт/К, для термического сопротивления теплопередачи сферической стенки — К/Вт.
служит Вт/К, для термического сопротивления теплопередачи сферической стенки — К/Вт.
Анализ формул (16.3), (16.8) и (16.15) для термических сопротивлений стенок различной конфигурации показывает, что чем больше площадь внешней поверхности стенки отличается от площади внутренней, тем меньше при прочих равных условиях термические сопротивления теплоотдачи таких стенок.
Например, у плоской стенки 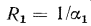 у цилиндрической
у цилиндрической 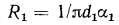 а для сферической стенки
а для сферической стенки 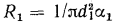 . Поэтому для понижения термического сопротивления системы в целом достаточно увеличить площадь поверхности стенки, сделав ее ребристой с той стороны, где меньше теплоотдача.
. Поэтому для понижения термического сопротивления системы в целом достаточно увеличить площадь поверхности стенки, сделав ее ребристой с той стороны, где меньше теплоотдача.
Ребра увеличивают площадь поверхности теплообмена и таким образом при том же
способствуют повышению количества передаваемой теплоты.
В последнем нетрудно убедиться, если проанализировать, как передается теплота через ребристую стенку (рис. 16.4).
Пусть площадь поверхности этой стенки с гладкой стороны 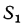 с ребристой —
с ребристой — 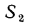 , температуры жидкостей, омывающих стенку,
, температуры жидкостей, омывающих стенку, 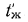 и
и 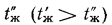 коэффициенты теплоотдачи
коэффициенты теплоотдачи 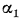 и
и 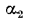 при этом
при этом 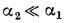 , температуры поверхностей стенки
, температуры поверхностей стенки 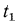 и
и 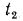 теплопроводность стенки
теплопроводность стенки 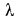 , а ее толщина
, а ее толщина 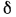 .
.
Процесс передачи теплоты через стенку соответственно трем
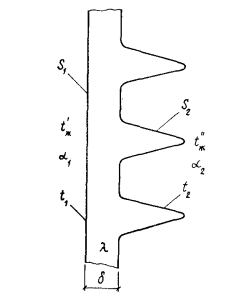
составляющим его звеньям может быть выражен следующими тремя уравнениями:
Q
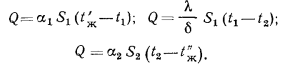
Решая эти уравнения относительно частных температурных напоров и складывая их, получим
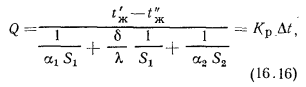
гдe Kp — коэффициент теплопередачи я ребристой стенки, равный:

При расчете плотности теплового потока на единицу гладкой поверхности стенки имеем
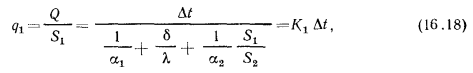
где 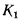 — коэффициент теплопередачи, отнесенный к плоской поверхности ребристой стенки и равный:
— коэффициент теплопередачи, отнесенный к плоской поверхности ребристой стенки и равный:

Если определяют тепловой поток на единицу ребристой поверхности стенки, то расчетная формула принимает вид
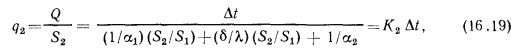
- где
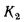 — коэффициент теплопередачи, отнесенный к ребристой поверхности стенки и равный:
— коэффициент теплопередачи, отнесенный к ребристой поверхности стенки и равный:
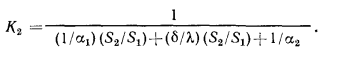
Расчет теплопередачи через тела неправильной формы можно приближенно сводить к трем рассмотренным случаям. С этой целью стенку сложного очертания мысленно деформируют, придавая ей правильную форму плоской стенки, цилиндра или шара в зависимости от того, к какому типу тел ее можно отнести.
При этом расчетную толщину такой деформированной стенки определяют из условия равенства ее объема и объема правильной стенки, а расчетный коэффициент теплоотдачи для поверхности деформированной стенки находят из равенства:

где индекс «д» относится к деформированной стенке, а величины без индекса характеризуют стенку правильной формы.
Все приведенные формулы по расчету теплопередачи могут быть использованы и для расчета тепловой изоляции.
Для этого с учетом допустимых тепловых потерь объекта, возможности осуществления технологического процесса, а также соблюдения техники безопасности выбирают вид изоляции, температуру на ее поверхности и рассчитывают требуемую толщину слоя изоляции. Основные темы теории из учебников тут, надеюсь она вам поможет.
При выборе изоляции немаловажное значение имеют и такие факторы, как масса, гигиеничность, удобство монтажа и срок службы изоляции.

Библиографическое описание:
Годорожа, Д. В. Исследование температурного состояния стенки конструкции при изменении режимов нагрева и охлаждения / Д. В. Годорожа. — Текст : непосредственный // Молодой ученый. — 2019. — № 23 (261). — С. 87-95. — URL: https://moluch.ru/archive/261/60252/ (дата обращения: 17.05.2023).
Теплообменные установки (ТУ) широко применяются в энергетике, транспортной, химической и других отраслях промышленности и имеют разнообразные конструкции, зависящие от условий работы и предъявляемых к ним требований. Интенсивное развитие техники, в том числе ракетно-космической, в настоящее время характеризуется выдвижением современных требований к ТУ. Для решения новых задач необходимо создание усовершенствованных ТУ, обеспечивающих оптимальное сочетание тепловой эффективности, технологичности, удобства эксплуатации и минимальной стоимости.
Проблема разработки эффективной теплоэнергетической установки или аппарата обычно связана с необходимостью проведения огневых испытаний зачастую при достаточно высоких температурах. В связи с этим актуальной становится оценка температурного состояния поверхности теплообмена при различных режимах нагрева и охлаждения.
Целью настоящей работы является прогнозирование состояния объекта испытания и системы измерения и планирование режимов безаварийного испытания теплообменных трактов.
Задачи исследования:
- на основании теории тепломассообмена изучить методы определения температур поверхности теплообмена;
- получить расчетные зависимости для исследования температуры стенки;
- проанализировать степень влияния различных режимных и конструктивных параметров тракта на температурное состояние стенки.
Согласно известным закономерностям теплопереноса, температура стенки, как целевая функция исследования, представляется в виде зависимости, отражающей режимы нагрева и охлаждения.
|
|
(1) |
где ![]() температуры горячего и холодного теплоносителей соответственно, К;
температуры горячего и холодного теплоносителей соответственно, К; ![]() температура поверхности стенки, К;
температура поверхности стенки, К; ![]() коэффициент теплоотдачи от горячего теплоносителя к стенке, Вт/(м2
коэффициент теплоотдачи от горячего теплоносителя к стенке, Вт/(м2![]() К);
К); ![]() коэффициент теплоотдачи от стенки к холодному теплоносителю, Вт/(м2
коэффициент теплоотдачи от стенки к холодному теплоносителю, Вт/(м2![]() К);
К); ![]() коэффициент теплопроводности стенки, Вт/(м
коэффициент теплопроводности стенки, Вт/(м![]() К);
К); ![]() толщина стенки, м.
толщина стенки, м.
На основании закона Ньютона-Рихмана и закона Био-Фурье для стенки можно записать следующие расчетные формулы:
где ![]() плотность теплового потока, Вт/м2;
плотность теплового потока, Вт/м2; ![]() температура горячей поверхности стенки, К;
температура горячей поверхности стенки, К; ![]() температура холодной поверхности стенки, К.
температура холодной поверхности стенки, К.
На основании баланса тепловых потоков получена следующая зависимость для температуры горячей поверхности теплообмена, например, плоской стенки, при граничных условиях III рода [1]:
|
|
(5) |
Полученные формулы справедливы для расчета температур и на многослойной поверхности теплообмена. В этом случае для плоских стенок в формулу (5) подставляется ![]() — полная толщина многослойной стенки и
— полная толщина многослойной стенки и ![]() эквивалентный коэффициент теплопроводности многослойной стенки,
эквивалентный коэффициент теплопроводности многослойной стенки,
|
|
(6) |
Если тепловым сопротивлением стенки можно пренебречь (![]() ), то формула (5) принимает вид:
), то формула (5) принимает вид:
|
|
(7) |
Аналогично, как и для плоской стенки, находится температура горячей поверхности цилиндрической стенки:
|
|
(8) |
где ![]() поверхности, непосредственно соприкасающиеся с теплоносителями,
поверхности, непосредственно соприкасающиеся с теплоносителями, ![]()
Методика исследования построена на использовании параметрического расчетного эксперимента, где целевой функцией является температура горячей стенки (точнее, отношение температуры горячей поверхности стенки к температуре горячего теплоносителя).
С целью обобщения полученных результатов исследование ведется в безразмерных параметрах.
Введем следующие безразмерные параметры:
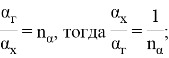
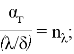
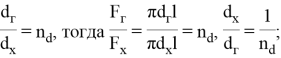
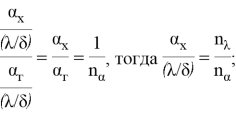
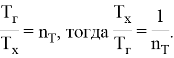
Таким образом, целевая функция в параметрической форме представляется в виде:
а) для плоской стенки
|
|
(9) |
б) для цилиндрической поверхности
|
|
(10) |
Характер исследования — двухпараметрический, т. е. предполагается, что нужно выбрать два из вышеперечисленных параметров, а остальные зафиксировать.
Диапазоны исследования выбраны на основании диапазонов натуральных переменных реальных задач и предстоящих испытаний и составляют:
![]()
![]()
![]()
Расчет и анализ результатов производится по приоритетным параметрам. Результаты эксперимента представляются в графическом виде.
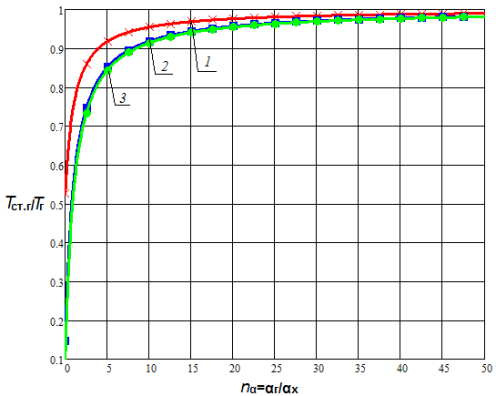
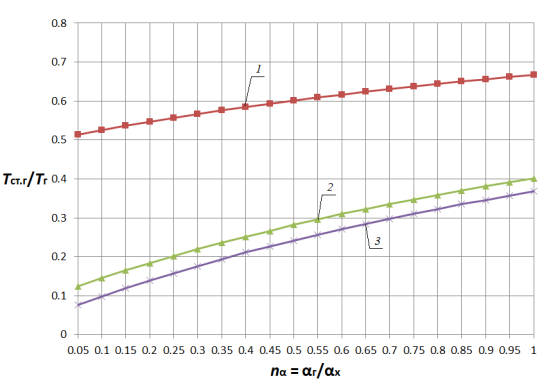
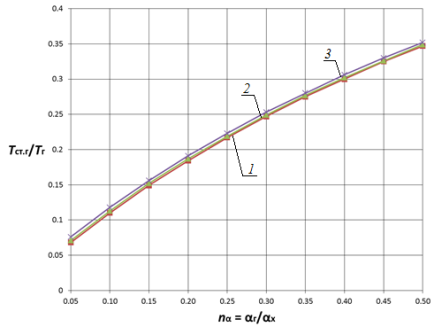
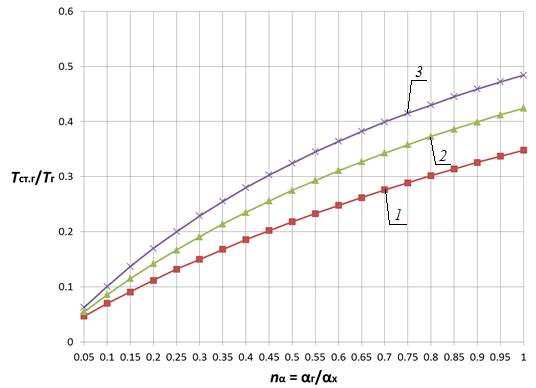
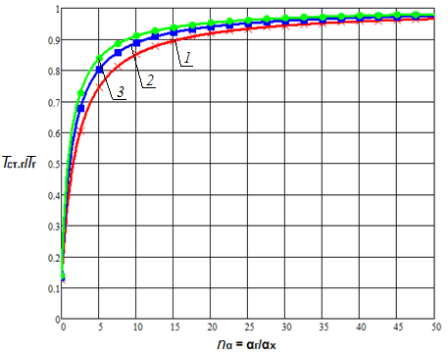
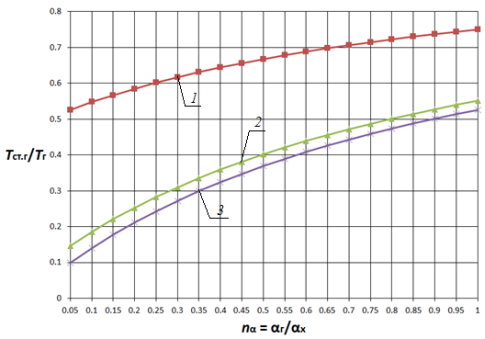
Анализ влияния отношения коэффициентов теплоотдачи показывает, что в диапазоне nα = 0,05…1,0 с увеличением отношения ![]() в 20 раз температура стенки монотонно возрастает приблизительно в 1,4…5,3 раз для плоской стенки и в 1,3…4,6 раз для цилиндрической поверхности теплообмена (рис. 1 (а), рис. 2 (а)) в зависимости от параметров
в 20 раз температура стенки монотонно возрастает приблизительно в 1,4…5,3 раз для плоской стенки и в 1,3…4,6 раз для цилиндрической поверхности теплообмена (рис. 1 (а), рис. 2 (а)) в зависимости от параметров ![]() и
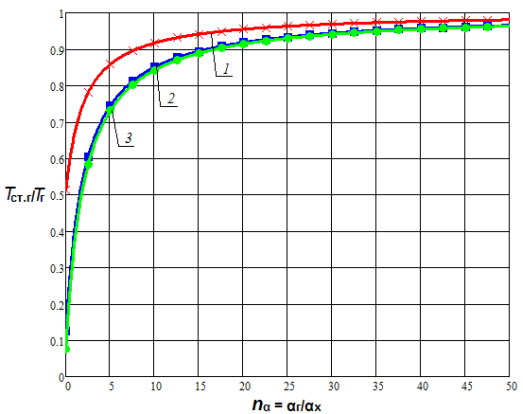
и ![]() при прочих равных условиях. При этом очевидна тенденция снижения этого роста по мере увеличения nα. Увеличение диапазона исследования (рис. 1 (б), рис. 2 (б)) показывает, что наиболее существенное влияние на температуру стенки nα оказывает в диапазоне nα< 5, что существует область значений параметра nα (nα > 15), при которой данный параметр не оказывает существенного влияния на температурное состояние стенки. При этом зависимости температуры плоской и цилиндрической поверхностей теплообмена от одноименных параметров имеют сходственный характер.
при прочих равных условиях. При этом очевидна тенденция снижения этого роста по мере увеличения nα. Увеличение диапазона исследования (рис. 1 (б), рис. 2 (б)) показывает, что наиболее существенное влияние на температуру стенки nα оказывает в диапазоне nα< 5, что существует область значений параметра nα (nα > 15), при которой данный параметр не оказывает существенного влияния на температурное состояние стенки. При этом зависимости температуры плоской и цилиндрической поверхностей теплообмена от одноименных параметров имеют сходственный характер.
|
а) |
|
|
|
б) |
|
Рис. 1. Зависимость Tст.г/Tг от nα и nT при nλ = 0,005 для плоской стенки 1 — Tг/Тх = 2; 2 — Tг/Тх = 10; 3 — Tг/Тх = 20 |
|
|
|
а) |
|
|
|
б) |
|
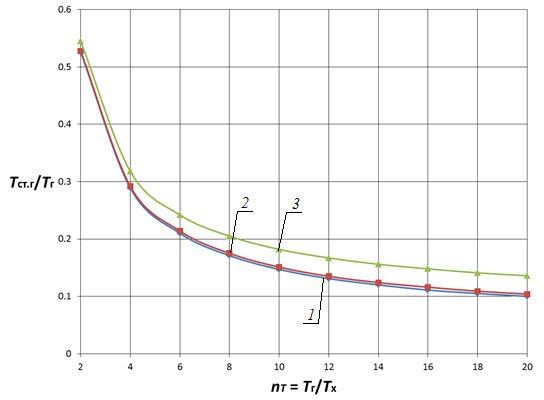
Рис. 2. Зависимость Tст.г/Tг от nα и nT при nλ = 0,005 и nd = 0,5 для цилиндрической стенки |
|
1 — Tг/Тх = 2; 2 — Tг/Тх = 10; 3 — Tг/Тх = 20 |
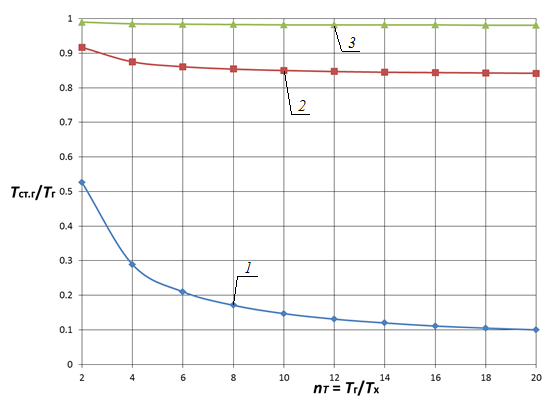
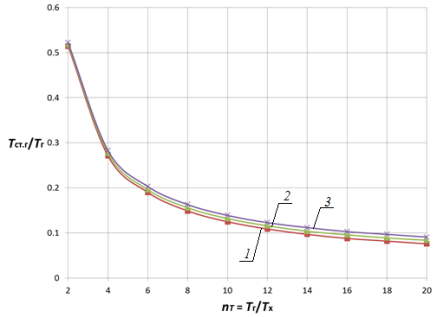
Анализ влияния отношения температур горячего и холодного теплоносителей![]() в исследованном диапазоне показывает следующее. При малых значениях nα увеличение температурного напора
в исследованном диапазоне показывает следующее. При малых значениях nα увеличение температурного напора ![]() ведет к существенному снижению температуры стенки, тогда как при больших значениях параметра (nα > 1) во всем диапазоне
ведет к существенному снижению температуры стенки, тогда как при больших значениях параметра (nα > 1) во всем диапазоне ![]() существенного снижения температуры стенки не наблюдается и ее относительное значение приближается к своему максимуму, т. е. Tст/Tг ≈ 1. Так, с ростом отношения температур горячего и холодного теплоносителей
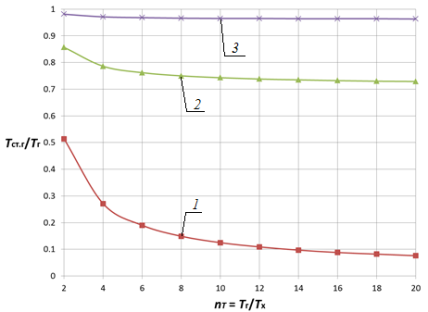
существенного снижения температуры стенки не наблюдается и ее относительное значение приближается к своему максимуму, т. е. Tст/Tг ≈ 1. Так, с ростом отношения температур горячего и холодного теплоносителей![]() в 10 раз (рис. 3 и 4) температура стенки уменьшается в 5,3…1,1 раза для плоской стенки и в 6,4…1,2 раз для цилиндрической поверхности теплообмена на границах области nα = 0,05…50.
в 10 раз (рис. 3 и 4) температура стенки уменьшается в 5,3…1,1 раза для плоской стенки и в 6,4…1,2 раз для цилиндрической поверхности теплообмена на границах области nα = 0,05…50.
|
|
|
Рис. 3. Зависимость Tст.г/Tг от nT и nα при nλ = 0,005 для плоской стенки 1 — nα = 0,05; 2 — nα = 5; 3 — nα = 50 |
|
|
|
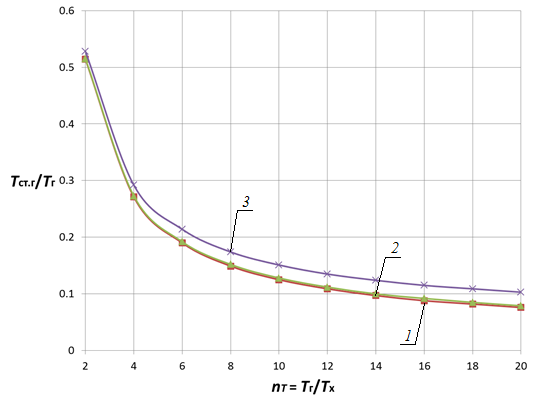
Рис. 4. Зависимость Tст.г/Tг от nT и nα при nλ = 0,005и nd = 0,5 для цилиндрической стенки |
|
1 — nα = 0,05; 2 — nα = 5; 3 — nα = 50 |
Исследование влияния проводимости стенки ![]() показывает ее слабое (до ничтожного) влияние на температурное состояние стенки в широком диапазоне исследованных параметров nλ, nα, nT (рис. 5–7).
показывает ее слабое (до ничтожного) влияние на температурное состояние стенки в широком диапазоне исследованных параметров nλ, nα, nT (рис. 5–7).
|
|
|
Рис. 5. Зависимость Tст.г/Tг от nα и nλ при nT = 20 для плоской стенки |
|
1 — nλ = 0,001; 2 — nλ = 0,005; 3 — nλ = 0,01 |
Анализ исследования влияния кривизны ![]() цилиндрической стенки (рис. 8 и 9) показывает следующее. Характер влияния кривизны на температуру стенки подобен влиянию nα и
цилиндрической стенки (рис. 8 и 9) показывает следующее. Характер влияния кривизны на температуру стенки подобен влиянию nα и ![]() . Так с увеличением степени кривизны (уменьшением
. Так с увеличением степени кривизны (уменьшением ![]() ) как и с увеличением
) как и с увеличением ![]() (рис. 1) и уменьшением nα (рис. 3, 4) температура стенки уменьшается. Количественная мера влияния
(рис. 1) и уменьшением nα (рис. 3, 4) температура стенки уменьшается. Количественная мера влияния ![]() на температуру стенки уменьшается с увеличением степени кривизны до 30 % в диапазоне nα = 0,05…1,0, особенно с ростом nα до 1,0, с дальнейшим ростом nα влияние уменьшается до 3…6 %.
на температуру стенки уменьшается с увеличением степени кривизны до 30 % в диапазоне nα = 0,05…1,0, особенно с ростом nα до 1,0, с дальнейшим ростом nα влияние уменьшается до 3…6 %.
|
|
|
Рис. 6. Зависимость Tст.г/Tг от nT и nλ при nα = 0,05 для плоской стенки 1 — nλ = 0,001; 2 — nλ = 0,005; 3 — nλ = 0,01 |
|
|
|
Рис. 7. Зависимость Tст.г/Tг от nT и nλ при nα = 0,05 и nd = 0,5 для цилиндрической стенки |
|
1 — nλ = 0,001; 2 — nλ = 0,005; 3 — nλ = 0,01 |
|
|
|
а) |
|
|
|
б) |
|
Рис. 8. Зависимость Tст.г/Tг от nα и nd при nT = 50 и nλ = 0,005 для цилиндрической стенки 1 — nd = 0,5; 2 — nd = 0,7; 3 — nd = 0,9 |
|
|
|
Рис. 9. Зависимость Tст.г/Tг от nT и nd при nα = 0,05 и nλ = 0,005 для цилиндрической стенки 1 — nd = 0,5; 2 — nd = 0,7; 3 — nd = 0,9 |
На основании полученных результатов сделаны следующие выводы:
1) Наиболее существенное влияние на температуру горячей поверхности стенки оказывают параметры nα и nT в диапазонах: nα < 1,0…5,0 и nT < 10…15.
2) Влияние степени кривизны цилиндрической стенки на температуру стенки значительно менее существенно и составляет по величине от 3 до 30 % в исследованном диапазоне параметров.
3) Влиянием относительной проводимости стенки в исследованном диапазоне параметров можно с достаточной точностью пренебрегать.
Литература:
- В. П. Исаченко, В. А. Осипова. А. С. Сукомел. Теплопередача. Учебник для вузов, Изд. 4-е перераб. и доп. — М.: «Энергоиздат», 1981. — 415 с.
Основные термины (генерируются автоматически): плоская стенка, температура стенки, цилиндрическая стенка, зависимость, холодный теплоноситель, горячая поверхность стенки, параметр, существенное влияние, температурное состояние стенки, целевая функция.