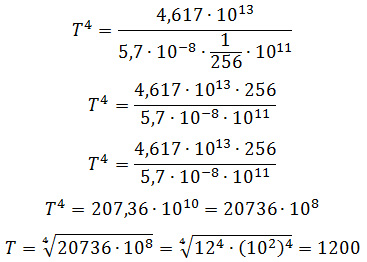Как найти температуру звезды в кельвинах

Как найти температуру звезды в кельвинах

1

Тип 8 № 41841

i

Для определения эффективной температуры звёзд используют закон Стефана–Больцмана, согласно которому P = sigma ST в степени 4 дробь: числитель: Вт, знаменатель: м в квадрате умножить на К в степени 4 конец дроби , где P  — мощность излучения звезды (в ваттах), sigma = 5,7 умножить на 10 в степени левая круглая скобка минус 8 правая круглая скобка   — постоянная, S  — площадь поверхности звезды (в квадратных метрах), а T  — температура (в кельвинах). Известно, что площадь поверхности не-которой звезды равна дробь: числитель: 1, знаменатель: 125 конец дроби умножить на 10 в степени левая круглая скобка 20 правая круглая скобка м2, а мощность её излучения равна 2,85 умножить на 10 в степени левая круглая скобка 25 правая круглая скобка Вт. Найдите температуру этой звезды в кельвинах.

Аналоги к заданию № 27969: 41841 41845 500914 … Все

Решение

·

Видеокурс

·

Помощь

2

Тип 8 № 41845

i

Для определения эффективной температуры звёзд используют закон Стефана–Больцмана, согласно которому P = sigma ST в степени 4 дробь: числитель: Вт, знаменатель: м в квадрате умножить на К в степени 4 конец дроби , где P  — мощность излучения звезды (в ваттах), sigma = 5,7 умножить на 10 в степени левая круглая скобка минус 8 правая круглая скобка   — постоянная, S  — площадь поверхности звезды (в квадратных метрах), а T  — температура (в кельвинах). Известно, что площадь поверхности не-которой звезды равна дробь: числитель: 1, знаменатель: 81 конец дроби умножить на 10 в степени левая круглая скобка 21 правая круглая скобка м2, а мощность её излучения равна 9,12 умножить на 10 в степени левая круглая скобка 26 правая круглая скобка Вт. Найдите температуру этой звезды в кельвинах.

Аналоги к заданию № 27969: 41841 41845 500914 … Все

Решение

·

Видеокурс

·

Помощь

3

Тип 8 № 500914

i

Для определения эффективной температуры звёзд используют закон Стефана–Больцмана, согласно которому P = sigma ST в степени 4 , где P  — мощность излучения звезды (в ваттах), sigma = 5,7 умножить на 10 в степени левая круглая скобка минус 8 правая круглая скобка дробь: числитель: Вт, знаменатель: м в квадрате умножить на К в степени 4 конец дроби ,   — постоянная, S  — площадь поверхности звезды (в квадратных метрах), а T  — температура (в кельвинах). Известно, что площадь поверхности не-которой звезды равна дробь: числитель: 1, знаменатель: 8 конец дроби умножить на 10 в степени левая круглая скобка 20 правая круглая скобка м2, а мощность её излучения равна 9,234 умножить на 10 в степени левая круглая скобка 26 правая круглая скобка Вт. Найдите температуру этой звезды в кельвинах.

Аналоги к заданию № 27969: 41841 41845 500914 … Все

Решение

·

Видеокурс

·

Помощь

4

Тип 8 № 518908

i

Для определения эффективной температуры звёзд используют закон Стефана—Больцмана, согласно которому P = sigma ST в степени 4 , где P  — мощность излучения звезды (в ваттах), sigma =5,7 умножить на 10 в степени левая круглая скобка минус 8 правая круглая скобка дробь: числитель: Вт, знаменатель: м в квадрате умножить на К в степени левая круглая скобка 4 правая круглая скобка конец дроби   — постоянная, S  — площадь поверхности звезды (в квадратных метрах), а T  — температура (в кельвинах). Известно, что площадь поверхности некоторой звезды равна дробь: числитель: 1, знаменатель: 729 конец дроби умножить на 10 в степени левая круглая скобка 20 правая круглая скобка м в квадрате , а мощность её излучения равна5,13 умножить на 10 в степени левая круглая скобка 25 правая круглая скобка Вт. Найдите температуру этой звезды в кельвинах.

Аналоги к заданию № 27969: 41841 41845 500914 … Все

Решение

·

Видеокурс

·

Помощь

5

Тип 8 № 518955

i

Для определения эффективной температуры звёзд используют закон Стефана—Больцмана, согласно которому P = sigma ST в степени 4 , где P  — мощность излучения звезды (в ваттах), sigma =5,7 умножить на 10 в степени левая круглая скобка минус 8 правая круглая скобка дробь: числитель: Вт, знаменатель: м в квадрате умножить на К в степени левая круглая скобка 4 правая круглая скобка конец дроби   — постоянная, S  — площадь поверхности звезды (в квадратных метрах), а T  — температура (в кельвинах). Известно, что площадь поверхности некоторой звезды равна дробь: числитель: 1, знаменатель: 729 конец дроби умножить на 10 в степени левая круглая скобка 20 правая круглая скобка м в квадрате , а мощность её излучения равна5,13 умножить на 10 в степени левая круглая скобка 25 правая круглая скобка Вт. Найдите температуру этой звезды в кельвинах.

Аналоги к заданию № 27969: 41841 41845 500914 … Все

Решение

·

Видеокурс

·

Помощь

6

Тип 8 № 525374

i

Для определения эффективной температуры звёзд используют закон Стефана–Больцмана, согласно которому P = sigma ST в степени 4 дробь: числитель: Вт, знаменатель: м в квадрате умножить на К в степени 4 конец дроби , где P  — мощность излучения звезды (в ваттах), sigma = 5,7 умножить на 10 в степени левая круглая скобка минус 8 правая круглая скобка   — постоянная, S  — площадь поверхности звезды (в квадратных метрах), а T  — температура (в кельвинах). Известно, что площадь поверхности некоторой звезды равна дробь: числитель: 1, знаменатель: 9 конец дроби умножить на 10 в степени левая круглая скобка 20 правая круглая скобка м2, а мощность её излучения равна 5,13 умножить на 10 в степени левая круглая скобка 25 правая круглая скобка Вт. Найдите температуру этой звезды в кельвинах.

Аналоги к заданию № 27969: 41841 41845 500914 … Все

Источник: ЕГЭ по ма­те­ма­ти­ке 10.04.2019. До­сроч­ная волна, ре­зерв­ный день

Решение

·

Видеокурс

·

Помощь

7

Тип 8 № 530452

i

Для определения эффективной температуры звёзд используют закон Стефана—Больцмана, согласно которому P = sigma ST в степени 4 , где P  — мощность излучения звезды (в ваттах), sigma =5,7 умножить на 10 в степени левая круглая скобка минус 8 правая круглая скобка дробь: числитель: Вт, знаменатель: м в квадрате умножить на К в степени левая круглая скобка 4 правая круглая скобка конец дроби   — постоянная, S  — площадь поверхности звезды (в квадратных метрах), а T  — температура (в кельвинах). Известно, что площадь поверхности некоторой звезды равна дробь: числитель: 1, знаменатель: 2 конец дроби умножить на 10 в степени левая круглая скобка 18 правая круглая скобка м в квадрате , а мощность её излучения равна2,85 умножить на 10 в степени левая круглая скобка 26 правая круглая скобка Вт. Найдите температуру этой звезды в кельвинах.

Аналоги к заданию № 27969: 41841 41845 500914 … Все

Решение

·

Видеокурс

·

Помощь

8

Тип 8 № 530554

i

Для определения эффективной температуры звёзд используют закон Стефана—Больцмана, согласно которому P = sigma ST в степени 4 , где P  — мощность излучения звезды (в ваттах), sigma =5,7 умножить на 10 в степени левая круглая скобка минус 8 правая круглая скобка дробь: числитель: Вт, знаменатель: м в квадрате умножить на К в степени левая круглая скобка 4 правая круглая скобка конец дроби   — постоянная, S  — площадь поверхности звезды (в квадратных метрах), а T  — температура (в кельвинах). Известно, что площадь поверхности некоторой звезды равна дробь: числитель: 1, знаменатель: 64 конец дроби умножить на 10 в степени левая круглая скобка 20 правая круглая скобка м в квадрате , а мощность её излучения равна2,28 умножить на 10 в степени левая круглая скобка 25 правая круглая скобка Вт. Найдите температуру этой звезды в кельвинах.

Аналоги к заданию № 27969: 41841 41845 500914 … Все

Решение

·

Видеокурс

·

Помощь

9

Тип 8 № 560134

i

Для определения эффективной температуры звёзд используют закон Стефана–Больцмана, согласно которому P = sigma ST в степени 4 дробь: числитель: Вт, знаменатель: м в квадрате умножить на К в степени 4 конец дроби , где P  — мощность излучения звезды (в ваттах),sigma = 5,7 умножить на 10 в степени левая круглая скобка минус 8 правая круглая скобка   — постоянная, S   — площадь поверхности звезды (в квадратных метрах), а T  — температура (в кельвинах). Известно, что площадь поверхности некоторой звезды равна дробь: числитель: 1, знаменатель: 18 конец дроби умножить на 10 в степени левая круглая скобка 21 правая круглая скобка м в квадрате , а мощность её излучения равна 4,104 умножить на 10 в степени левая круглая скобка 27 правая круглая скобка Вт. Найдите температуру этой звезды в кельвинах.

Аналоги к заданию № 27969: 41841 41845 500914 … Все

Решение

·

Видеокурс

·

Помощь

10

Тип 8 № 560653

i

Для определения эффективной температуры звёзд используют закон Стефана–Больцмана, согласно которому P = sigma ST в степени 4 дробь: числитель: Вт, знаменатель: м в квадрате умножить на К в степени 4 конец дроби , где P  — мощность излучения звезды (в ваттах),sigma = 5,7 умножить на 10 в степени левая круглая скобка минус 8 правая круглая скобка   — постоянная, S   — площадь поверхности звезды (в квадратных метрах), а T  — температура (в кельвинах). Известно, что площадь поверхности некоторой звезды равна дробь: числитель: 1, знаменатель: 8 конец дроби умножить на 10 в степени левая круглая скобка 20 правая круглая скобка м в квадрате , а мощность её излучения равна 2,9184 умножить на 10 в степени левая круглая скобка 27 правая круглая скобка Вт. Найдите температуру этой звезды в кельвинах.

Аналоги к заданию № 27969: 41841 41845 500914 … Все

Решение

·

Видеокурс

·

Помощь

11

Тип 8 № 28193

i

Для определения эффективной температуры звёзд используют закон Стефана–Больцмана, согласно которому P = sigma ST в степени 4 дробь: числитель: Вт, знаменатель: м в квадрате умножить на К в степени 4 конец дроби , где P  — мощность излучения звезды (в ваттах), sigma = 5,7 умножить на 10 в степени левая круглая скобка минус 8 правая круглая скобка   — постоянная, S  — площадь поверхности звезды (в квадратных метрах), а T  — температура (в кельвинах). Известно, что площадь поверхности не-которой звезды равна дробь: числитель: 1, знаменатель: 125 конец дроби умножить на 10 в степени левая круглая скобка 20 правая круглая скобка м2, а мощность её излучения равна 4,56 умножить на 10 в степени левая круглая скобка 26 правая круглая скобка Вт. Найдите температуру этой звезды в кельвинах.

Аналоги к заданию № 27969: 41841 41845 500914 … Все

Видеокурс

12

Тип 8 № 28195

i

Для определения эффективной температуры звёзд используют закон Стефана–Больцмана, согласно которому P = sigma ST в степени 4 дробь: числитель: Вт, знаменатель: м в квадрате умножить на К в степени 4 конец дроби , где P  — мощность излучения звезды (в ваттах), sigma = 5,7 умножить на 10 в степени левая круглая скобка минус 8 правая круглая скобка   — постоянная, S  — площадь поверхности звезды (в квадратных метрах), а T  — температура (в кельвинах). Известно, что площадь поверхности не-которой звезды равна дробь: числитель: 1, знаменатель: 228 конец дроби умножить на 10 в степени левая круглая скобка 20 правая круглая скобка м2, а мощность её излучения равна 1,5625 умножить на 10 в степени левая круглая скобка 25 правая круглая скобка Вт. Найдите температуру этой звезды в кельвинах.

Аналоги к заданию № 27969: 41841 41845 500914 … Все

Видеокурс

13

Тип 8 № 28197

i

Для определения эффективной температуры звёзд используют закон Стефана–Больцмана, согласно которому P = sigma ST в степени 4 дробь: числитель: Вт, знаменатель: м в квадрате умножить на К в степени 4 конец дроби , где P  — мощность излучения звезды (в ваттах), sigma = 5,7 умножить на 10 в степени левая круглая скобка минус 8 правая круглая скобка   — постоянная, S  — площадь поверхности звезды (в квадратных метрах), а T  — температура (в кельвинах). Известно, что площадь поверхности не-которой звезды равна дробь: числитель: 1, знаменатель: 128 конец дроби умножить на 10 в степени левая круглая скобка 20 правая круглая скобка м2, а мощность её излучения равна 1,14 умножить на 10 в степени левая круглая скобка 25 правая круглая скобка Вт. Найдите температуру этой звезды в кельвинах.

Аналоги к заданию № 27969: 41841 41845 500914 … Все

Видеокурс

14

Тип 8 № 28199

i

Для определения эффективной температуры звёзд используют закон Стефана–Больцмана, согласно которому P = sigma ST в степени 4 дробь: числитель: Вт, знаменатель: м в квадрате умножить на К в степени 4 конец дроби , где P  — мощность излучения звезды (в ваттах), sigma = 5,7 умножить на 10 в степени левая круглая скобка минус 8 правая круглая скобка   — постоянная, S  — площадь поверхности звезды (в квадратных метрах), а T  — температура (в кельвинах). Известно, что площадь поверхности не-которой звезды равна дробь: числитель: 1, знаменатель: 2 конец дроби умножить на 10 в степени левая круглая скобка 18 правая круглая скобка м2, а мощность её излучения равна 2,85 умножить на 10 в степени левая круглая скобка 26 правая круглая скобка Вт. Найдите температуру этой звезды в кельвинах.

Аналоги к заданию № 27969: 41841 41845 500914 … Все

Видеокурс

15

Тип 8 № 28201

i

Для определения эффективной температуры звёзд используют закон Стефана–Больцмана, согласно которому P = sigma ST в степени 4 дробь: числитель: Вт, знаменатель: м в квадрате умножить на К в степени 4 конец дроби , где P  — мощность излучения звезды (в ваттах), sigma = 5,7 умножить на 10 в степени левая круглая скобка минус 8 правая круглая скобка   — постоянная, S  — площадь поверхности звезды (в квадратных метрах), а T  — температура (в кельвинах). Известно, что площадь поверхности не-которой звезды равна дробь: числитель: 1, знаменатель: 64 конец дроби умножить на 10 в степени левая круглая скобка 20 правая круглая скобка м2, а мощность её излучения равна 2,28 умножить на 10 в степени левая круглая скобка 25 правая круглая скобка Вт. Найдите температуру этой звезды в кельвинах.

Аналоги к заданию № 27969: 41841 41845 500914 … Все

Видеокурс

16

Тип 8 № 28203

i

Для определения эффективной температуры звёзд используют закон Стефана–Больцмана, согласно которому P = sigma ST в степени 4 дробь: числитель: Вт, знаменатель: м в квадрате умножить на К в степени 4 конец дроби , где P  — мощность излучения звезды (в ваттах), sigma = 5,7 умножить на 10 в степени левая круглая скобка минус 8 правая круглая скобка   — постоянная, S  — площадь поверхности звезды (в квадратных метрах), а T  — температура (в кельвинах). Известно, что площадь поверхности не-которой звезды равна дробь: числитель: 1, знаменатель: 625 конец дроби умножить на 10 в степени левая круглая скобка 20 правая круглая скобка м2, а мощность её излучения равна 9,12 умножить на 10 в степени левая круглая скобка 25 правая круглая скобка Вт. Найдите температуру этой звезды в кельвинах.

Аналоги к заданию № 27969: 41841 41845 500914 … Все

Видеокурс

17

Тип 8 № 41793

i

Для определения эффективной температуры звёзд используют закон Стефана–Больцмана, согласно которому P = sigma ST в степени 4 дробь: числитель: Вт, знаменатель: м в квадрате умножить на К в степени 4 конец дроби , где P  — мощность излучения звезды (в ваттах), sigma = 5,7 умножить на 10 в степени левая круглая скобка минус 8 правая круглая скобка   — постоянная, S  — площадь поверхности звезды (в квадратных метрах), а T  — температура (в кельвинах). Известно, что площадь поверхности не-которой звезды равна дробь: числитель: 1, знаменатель: 8 конец дроби умножить на 10 в степени левая круглая скобка 20 правая круглая скобка м2, а мощность её излучения равна 2,9184 умножить на 10 в степени левая круглая скобка 27 правая круглая скобка Вт. Найдите температуру этой звезды в кельвинах.

Аналоги к заданию № 27969: 41841 41845 500914 … Все

Видеокурс

18

Тип 8 № 41795

i

Для определения эффективной температуры звёзд используют закон Стефана–Больцмана, согласно которому P = sigma ST в степени 4 дробь: числитель: Вт, знаменатель: м в квадрате умножить на К в степени 4 конец дроби , где P  — мощность излучения звезды (в ваттах), sigma = 5,7 умножить на 10 в степени левая круглая скобка минус 8 правая круглая скобка   — постоянная, S  — площадь поверхности звезды (в квадратных метрах), а T  — температура (в кельвинах). Известно, что площадь поверхности не-которой звезды равна дробь: числитель: 1, знаменатель: 2 конец дроби умножить на 10 в степени левая круглая скобка 20 правая круглая скобка м2, а мощность её излучения равна 3,6936 умножить на 10 в степени левая круглая скобка 27 правая круглая скобка Вт. Найдите температуру этой звезды в кельвинах.

Аналоги к заданию № 27969: 41841 41845 500914 … Все

Видеокурс

19

Тип 8 № 41797

i

Для определения эффективной температуры звёзд используют закон Стефана–Больцмана, согласно которому P = sigma ST в степени 4 дробь: числитель: Вт, знаменатель: м в квадрате умножить на К в степени 4 конец дроби , где P  — мощность излучения звезды (в ваттах), sigma = 5,7 умножить на 10 в степени левая круглая скобка минус 8 правая круглая скобка   — постоянная, S  — площадь поверхности звезды (в квадратных метрах), а T  — температура (в кельвинах). Известно, что площадь поверхности не-которой звезды равна дробь: числитель: 1, знаменатель: 128 конец дроби умножить на 10 в степени левая круглая скобка 21 правая круглая скобка м2, а мощность её излучения равна 1,14 умножить на 10 в степени левая круглая скобка 26 правая круглая скобка Вт. Найдите температуру этой звезды в кельвинах.

Аналоги к заданию № 27969: 41841 41845 500914 … Все

Видеокурс

20

Тип 8 № 41799

i

Для определения эффективной температуры звёзд используют закон Стефана–Больцмана, согласно которому P = sigma ST в степени 4 дробь: числитель: Вт, знаменатель: м в квадрате умножить на К в степени 4 конец дроби , где P  — мощность излучения звезды (в ваттах), sigma = 5,7 умножить на 10 в степени левая круглая скобка минус 8 правая круглая скобка   — постоянная, S  — площадь поверхности звезды (в квадратных метрах), а T  — температура (в кельвинах). Известно, что площадь поверхности не-которой звезды равна дробь: числитель: 1, знаменатель: 216 конец дроби умножить на 10 в степени левая круглая скобка 21 правая круглая скобка м2, а мощность её излучения равна 3,42 умножить на 10 в степени левая круглая скобка 26 правая круглая скобка Вт. Найдите температуру этой звезды в кельвинах.

Аналоги к заданию № 27969: 41841 41845 500914 … Все

Видеокурс

21

Тип 8 № 41801

i

Для определения эффективной температуры звёзд используют закон Стефана–Больцмана, согласно которому P = sigma ST в степени 4 дробь: числитель: Вт, знаменатель: м в квадрате умножить на К в степени 4 конец дроби , где P  — мощность излучения звезды (в ваттах), sigma = 5,7 умножить на 10 в степени левая круглая скобка минус 8 правая круглая скобка   — постоянная, S  — площадь поверхности звезды (в квадратных метрах), а T  — температура (в кельвинах). Известно, что площадь поверхности не-которой звезды равна дробь: числитель: 1, знаменатель: 8 конец дроби умножить на 10 в степени левая круглая скобка 20 правая круглая скобка м2, а мощность её излучения равна 1,824 умножить на 10 в степени левая круглая скобка 26 правая круглая скобка Вт. Найдите температуру этой звезды в кельвинах.

Аналоги к заданию № 27969: 41841 41845 500914 … Все

Видеокурс

22

Тип 8 № 41803

i

Для определения эффективной температуры звёзд используют закон Стефана–Больцмана, согласно которому P = sigma ST в степени 4 дробь: числитель: Вт, знаменатель: м в квадрате умножить на К в степени 4 конец дроби , где P  — мощность излучения звезды (в ваттах), sigma = 5,7 умножить на 10 в степени левая круглая скобка минус 8 правая круглая скобка   — постоянная, S  — площадь поверхности звезды (в квадратных метрах), а T  — температура (в кельвинах). Известно, что площадь поверхности не-которой звезды равна дробь: числитель: 1, знаменатель: 2 конец дроби умножить на 10 в степени левая круглая скобка 20 правая круглая скобка м2, а мощность её излучения равна 7,296 умножить на 10 в степени левая круглая скобка 26 правая круглая скобка Вт. Найдите температуру этой звезды в кельвинах.

Аналоги к заданию № 27969: 41841 41845 500914 … Все

Видеокурс

23

Тип 8 № 41805

i

Для определения эффективной температуры звёзд используют закон Стефана–Больцмана, согласно которому P = sigma ST в степени 4 дробь: числитель: Вт, знаменатель: м в квадрате умножить на К в степени 4 конец дроби , где P  — мощность излучения звезды (в ваттах), sigma = 5,7 умножить на 10 в степени левая круглая скобка минус 8 правая круглая скобка   — постоянная, S  — площадь поверхности звезды (в квадратных метрах), а T  — температура (в кельвинах). Известно, что площадь поверхности не-которой звезды равна дробь: числитель: 1, знаменатель: 36 конец дроби умножить на 10 в степени левая круглая скобка 21 правая круглая скобка м2, а мощность её излучения равна 2,052 умножить на 10 в степени левая круглая скобка 27 правая круглая скобка Вт. Найдите температуру этой звезды в кельвинах.

Аналоги к заданию № 27969: 41841 41845 500914 … Все

Видеокурс

24

Тип 8 № 41807

i

Для определения эффективной температуры звёзд используют закон Стефана–Больцмана, согласно которому P = sigma ST в степени 4 дробь: числитель: Вт, знаменатель: м в квадрате умножить на К в степени 4 конец дроби , где P  — мощность излучения звезды (в ваттах), sigma = 5,7 умножить на 10 в степени левая круглая скобка минус 8 правая круглая скобка   — постоянная, S  — площадь поверхности звезды (в квадратных метрах), а T  — температура (в кельвинах). Известно, что площадь поверхности не-которой звезды равна дробь: числитель: 1, знаменатель: 24 конец дроби умножить на 10 в степени левая круглая скобка 21 правая круглая скобка м2, а мощность её излучения равна 3,078 умножить на 10 в степени левая круглая скобка 27 правая круглая скобка Вт. Найдите температуру этой звезды в кельвинах.

Аналоги к заданию № 27969: 41841 41845 500914 … Все

Видеокурс

25

Тип 8 № 41809

i

Для определения эффективной температуры звёзд используют закон Стефана–Больцмана, согласно которому P = sigma ST в степени 4 дробь: числитель: Вт, знаменатель: м в квадрате умножить на К в степени 4 конец дроби , где P  — мощность излучения звезды (в ваттах), sigma = 5,7 умножить на 10 в степени левая круглая скобка минус 8 правая круглая скобка   — постоянная, S  — площадь поверхности звезды (в квадратных метрах), а T  — температура (в кельвинах). Известно, что площадь поверхности не-которой звезды равна дробь: числитель: 1, знаменатель: 5 конец дроби умножить на 10 в степени левая круглая скобка 20 правая круглая скобка м2, а мощность её излучения равна 7,125 умножить на 10 в степени левая круглая скобка 26 правая круглая скобка Вт. Найдите температуру этой звезды в кельвинах.

Аналоги к заданию № 27969: 41841 41845 500914 … Все

Видеокурс

26

Тип 8 № 41811

i

Для определения эффективной температуры звёзд используют закон Стефана–Больцмана, согласно которому P = sigma ST в степени 4 дробь: числитель: Вт, знаменатель: м в квадрате умножить на К в степени 4 конец дроби , где P  — мощность излучения звезды (в ваттах), sigma = 5,7 умножить на 10 в степени левая круглая скобка минус 8 правая круглая скобка   — постоянная, S  — площадь поверхности звезды (в квадратных метрах), а T  — температура (в кельвинах). Известно, что площадь поверхности не-которой звезды равна дробь: числитель: 1, знаменатель: 1024 конец дроби умножить на 10 в степени левая круглая скобка 21 правая круглая скобка м2, а мощность её излучения равна 2,28 умножить на 10 в степени левая круглая скобка 26 правая круглая скобка Вт. Найдите температуру этой звезды в кельвинах.

Аналоги к заданию № 27969: 41841 41845 500914 … Все

Видеокурс

27

Тип 8 № 41813

i

Для определения эффективной температуры звёзд используют закон Стефана–Больцмана, согласно которому P = sigma ST в степени 4 дробь: числитель: Вт, знаменатель: м в квадрате умножить на К в степени 4 конец дроби , где P  — мощность излучения звезды (в ваттах), sigma = 5,7 умножить на 10 в степени левая круглая скобка минус 8 правая круглая скобка   — постоянная, S  — площадь поверхности звезды (в квадратных метрах), а T  — температура (в кельвинах). Известно, что площадь поверхности не-которой звезды равна дробь: числитель: 1, знаменатель: 7 конец дроби умножить на 10 в степени левая круглая скобка 20 правая круглая скобка м2, а мощность её излучения равна 1,9551 умножить на 10 в степени левая круглая скобка 27 правая круглая скобка Вт. Найдите температуру этой звезды в кельвинах.

Аналоги к заданию № 27969: 41841 41845 500914 … Все

Видеокурс

28

Тип 8 № 41815

i

Для определения эффективной температуры звёзд используют закон Стефана–Больцмана, согласно которому P = sigma ST в степени 4 дробь: числитель: Вт, знаменатель: м в квадрате умножить на К в степени 4 конец дроби , где P  — мощность излучения звезды (в ваттах), sigma = 5,7 умножить на 10 в степени левая круглая скобка минус 8 правая круглая скобка   — постоянная, S  — площадь поверхности звезды (в квадратных метрах), а T  — температура (в кельвинах). Известно, что площадь поверхности не-которой звезды равна дробь: числитель: 1, знаменатель: 32 конец дроби умножить на 10 в степени левая круглая скобка 21 правая круглая скобка м2, а мощность её излучения равна 7,296 умножить на 10 в степени левая круглая скобка 27 правая круглая скобка Вт. Найдите температуру этой звезды в кельвинах.

Аналоги к заданию № 27969: 41841 41845 500914 … Все

Видеокурс

29

Тип 8 № 41817

i

Для определения эффективной температуры звёзд используют закон Стефана–Больцмана, согласно которому P = sigma ST в степени 4 дробь: числитель: Вт, знаменатель: м в квадрате умножить на К в степени 4 конец дроби , где P  — мощность излучения звезды (в ваттах), sigma = 5,7 умножить на 10 в степени левая круглая скобка минус 8 правая круглая скобка   — постоянная, S  — площадь поверхности звезды (в квадратных метрах), а T  — температура (в кельвинах). Известно, что площадь поверхности не-которой звезды равна дробь: числитель: 1, знаменатель: 54 конец дроби умножить на 10 в степени левая круглая скобка 21 правая круглая скобка м2, а мощность её излучения равна 1,368 умножить на 10 в степени левая круглая скобка 27 правая круглая скобка Вт. Найдите температуру этой звезды в кельвинах.

Аналоги к заданию № 27969: 41841 41845 500914 … Все

Видеокурс

30

Тип 8 № 41819

i

Для определения эффективной температуры звёзд используют закон Стефана–Больцмана, согласно которому P = sigma ST в степени 4 дробь: числитель: Вт, знаменатель: м в квадрате умножить на К в степени 4 конец дроби , где P  — мощность излучения звезды (в ваттах), sigma = 5,7 умножить на 10 в степени левая круглая скобка минус 8 правая круглая скобка   — постоянная, S  — площадь поверхности звезды (в квадратных метрах), а T  — температура (в кельвинах). Известно, что площадь поверхности не-которой звезды равна дробь: числитель: 1, знаменатель: 108 конец дроби умножить на 10 в степени левая круглая скобка 21 правая круглая скобка м2, а мощность её излучения равна 6,84 умножить на 10 в степени левая круглая скобка 26 правая круглая скобка Вт. Найдите температуру этой звезды в кельвинах.

Аналоги к заданию № 27969: 41841 41845 500914 … Все

Видеокурс

31

Тип 8 № 41821

i

Для определения эффективной температуры звёзд используют закон Стефана–Больцмана, согласно которому P = sigma ST в степени 4 дробь: числитель: Вт, знаменатель: м в квадрате умножить на К в степени 4 конец дроби , где P  — мощность излучения звезды (в ваттах), sigma = 5,7 умножить на 10 в степени левая круглая скобка минус 8 правая круглая скобка   — постоянная, S  — площадь поверхности звезды (в квадратных метрах), а T  — температура (в кельвинах). Известно, что площадь поверхности не-которой звезды равна дробь: числитель: 1, знаменатель: 2048 конец дроби умножить на 10 в степени левая круглая скобка 21 правая круглая скобка м2, а мощность её излучения равна 1,14 умножить на 10 в степени левая круглая скобка 26 правая круглая скобка Вт. Найдите температуру этой звезды в кельвинах.

Аналоги к заданию № 27969: 41841 41845 500914 … Все

Видеокурс

32

Тип 8 № 41823

i

Для определения эффективной температуры звёзд используют закон Стефана–Больцмана, согласно которому P = sigma ST в степени 4 дробь: числитель: Вт, знаменатель: м в квадрате умножить на К в степени 4 конец дроби , где P  — мощность излучения звезды (в ваттах), sigma = 5,7 умножить на 10 в степени левая круглая скобка минус 8 правая круглая скобка   — постоянная, S  — площадь поверхности звезды (в квадратных метрах), а T  — температура (в кельвинах). Известно, что площадь поверхности не-которой звезды равна дробь: числитель: 1, знаменатель: 6 конец дроби умножить на 10 в степени левая круглая скобка 20 правая круглая скобка м2, а мощность её излучения равна 1,2312 умножить на 10 в степени левая круглая скобка 27 правая круглая скобка Вт. Найдите температуру этой звезды в кельвинах.

Аналоги к заданию № 27969: 41841 41845 500914 … Все

Видеокурс

33

Тип 8 № 41825

i

Для определения эффективной температуры звёзд используют закон Стефана–Больцмана, согласно которому P = sigma ST в степени 4 дробь: числитель: Вт, знаменатель: м в квадрате умножить на К в степени 4 конец дроби , где P  — мощность излучения звезды (в ваттах), sigma = 5,7 умножить на 10 в степени левая круглая скобка минус 8 правая круглая скобка   — постоянная, S  — площадь поверхности звезды (в квадратных метрах), а T  — температура (в кельвинах). Известно, что площадь поверхности не-которой звезды равна дробь: числитель: 1, знаменатель: 4096 конец дроби умножить на 10 в степени левая круглая скобка 22 правая круглая скобка м2, а мощность её излучения равна 5,7 умножить на 10 в степени левая круглая скобка 26 правая круглая скобка Вт. Найдите температуру этой звезды в кельвинах.

Аналоги к заданию № 27969: 41841 41845 500914 … Все

Видеокурс

34

Тип 8 № 41827

i

Для определения эффективной температуры звёзд используют закон Стефана–Больцмана, согласно которому P = sigma ST в степени 4 дробь: числитель: Вт, знаменатель: м в квадрате умножить на К в степени 4 конец дроби , где P  — мощность излучения звезды (в ваттах), sigma = 5,7 умножить на 10 в степени левая круглая скобка минус 8 правая круглая скобка   — постоянная, S  — площадь поверхности звезды (в квадратных метрах), а T  — температура (в кельвинах). Известно, что площадь поверхности не-которой звезды равна дробь: числитель: 1, знаменатель: 3 конец дроби умножить на 10 в степени левая круглая скобка 20 правая круглая скобка м2, а мощность её излучения равна 1,539 умножить на 10 в степени левая круглая скобка 26 правая круглая скобка Вт. Найдите температуру этой звезды в кельвинах.

Аналоги к заданию № 27969: 41841 41845 500914 … Все

Видеокурс

35

Тип 8 № 41829

i

Для определения эффективной температуры звёзд используют закон Стефана–Больцмана, согласно которому P = sigma ST в степени 4 дробь: числитель: Вт, знаменатель: м в квадрате умножить на К в степени 4 конец дроби , где P  — мощность излучения звезды (в ваттах), sigma = 5,7 умножить на 10 в степени левая круглая скобка минус 8 правая круглая скобка   — постоянная, S  — площадь поверхности звезды (в квадратных метрах), а T  — температура (в кельвинах). Известно, что площадь поверхности не-которой звезды равна дробь: числитель: 1, знаменатель: 162 конец дроби умножить на 10 в степени левая круглая скобка 21 правая круглая скобка м2, а мощность её излучения равна 4,56 умножить на 10 в степени левая круглая скобка 26 правая круглая скобка Вт. Найдите температуру этой звезды в кельвинах.

Аналоги к заданию № 27969: 41841 41845 500914 … Все

Видеокурс

36

Тип 8 № 41831

i

Для определения эффективной температуры звёзд используют закон Стефана–Больцмана, согласно которому P = sigma ST в степени 4 дробь: числитель: Вт, знаменатель: м в квадрате умножить на К в степени 4 конец дроби , где P  — мощность излучения звезды (в ваттах), sigma = 5,7 умножить на 10 в степени левая круглая скобка минус 8 правая круглая скобка   — постоянная, S  — площадь поверхности звезды (в квадратных метрах), а T  — температура (в кельвинах). Известно, что площадь поверхности не-которой звезды равна дробь: числитель: 1, знаменатель: 9 конец дроби умножить на 10 в степени левая круглая скобка 20 правая круглая скобка м2, а мощность её излучения равна 8,208 умножить на 10 в степени левая круглая скобка 26 правая круглая скобка Вт. Найдите температуру этой звезды в кельвинах.

Аналоги к заданию № 27969: 41841 41845 500914 … Все

Видеокурс

37

Тип 8 № 41833

i

Для определения эффективной температуры звёзд используют закон Стефана–Больцмана, согласно которому P = sigma ST в степени 4 дробь: числитель: Вт, знаменатель: м в квадрате умножить на К в степени 4 конец дроби , где P  — мощность излучения звезды (в ваттах), sigma = 5,7 умножить на 10 в степени левая круглая скобка минус 8 правая круглая скобка   — постоянная, S  — площадь поверхности звезды (в квадратных метрах), а T  — температура (в кельвинах). Известно, что площадь поверхности не-которой звезды равна дробь: числитель: 1, знаменатель: 9 конец дроби умножить на 10 в степени левая круглая скобка 20 правая круглая скобка м2, а мощность её излучения равна 5,13 умножить на 10 в степени левая круглая скобка 25 правая круглая скобка Вт. Найдите температуру этой звезды в кельвинах.

Аналоги к заданию № 27969: 41841 41845 500914 … Все

Видеокурс

38

Тип 8 № 41835

i

Для определения эффективной температуры звёзд используют закон Стефана–Больцмана, согласно которому P = sigma ST в степени 4 дробь: числитель: Вт, знаменатель: м в квадрате умножить на К в степени 4 конец дроби , где P  — мощность излучения звезды (в ваттах), sigma = 5,7 умножить на 10 в степени левая круглая скобка минус 8 правая круглая скобка   — постоянная, S  — площадь поверхности звезды (в квадратных метрах), а T  — температура (в кельвинах). Известно, что площадь поверхности не-которой звезды равна дробь: числитель: 1, знаменатель: 4 конец дроби умножить на 10 в степени левая круглая скобка 20 правая круглая скобка м2, а мощность её излучения равна 3,648 умножить на 10 в степени левая круглая скобка 26 правая круглая скобка Вт. Найдите температуру этой звезды в кельвинах.

Аналоги к заданию № 27969: 41841 41845 500914 … Все

Видеокурс

39

Тип 8 № 41837

i

Для определения эффективной температуры звёзд используют закон Стефана–Больцмана, согласно которому P = sigma ST в степени 4 дробь: числитель: Вт, знаменатель: м в квадрате умножить на К в степени 4 конец дроби , где P  — мощность излучения звезды (в ваттах), sigma = 5,7 умножить на 10 в степени левая круглая скобка минус 8 правая круглая скобка   — постоянная, S  — площадь поверхности звезды (в квадратных метрах), а T  — температура (в кельвинах). Известно, что площадь поверхности не-которой звезды равна дробь: числитель: 1, знаменатель: 256 конец дроби умножить на 10 в степени левая круглая скобка 21 правая круглая скобка м2, а мощность её излучения равна 9,12 умножить на 10 в степени левая круглая скобка 26 правая круглая скобка Вт. Найдите температуру этой звезды в кельвинах.

Аналоги к заданию № 27969: 41841 41845 500914 … Все

Видеокурс

40

Тип 8 № 41839

i

Для определения эффективной температуры звёзд используют закон Стефана–Больцмана, согласно которому P = sigma ST в степени 4 дробь: числитель: Вт, знаменатель: м в квадрате умножить на К в степени 4 конец дроби , где P  — мощность излучения звезды (в ваттах), sigma = 5,7 умножить на 10 в степени левая круглая скобка минус 8 правая круглая скобка   — постоянная, S  — площадь поверхности звезды (в квадратных метрах), а T  — температура (в кельвинах). Известно, что площадь поверхности не-которой звезды равна дробь: числитель: 1, знаменатель: 32 конец дроби умножить на 10 в степени левая круглая скобка 20 правая круглая скобка м2, а мощность её излучения равна 4,56 умножить на 10 в степени левая круглая скобка 25 правая круглая скобка Вт. Найдите температуру этой звезды в кельвинах.

Аналоги к заданию № 27969: 41841 41845 500914 … Все

Видеокурс

41

Тип 8 № 41843

i

Для определения эффективной температуры звёзд используют закон Стефана–Больцмана, согласно которому P = sigma ST в степени 4 дробь: числитель: Вт, знаменатель: м в квадрате умножить на К в степени 4 конец дроби , где P  — мощность излучения звезды (в ваттах), sigma = 5,7 умножить на 10 в степени левая круглая скобка минус 8 правая круглая скобка   — постоянная, S  — площадь поверхности звезды (в квадратных метрах), а T  — температура (в кельвинах). Известно, что площадь поверхности не-которой звезды равна дробь: числитель: 1, знаменатель: 27 конец дроби умножить на 10 в степени левая круглая скобка 20 правая круглая скобка м2, а мощность её излучения равна 1,71 умножить на 10 в степени левая круглая скобка 25 правая круглая скобка Вт. Найдите температуру этой звезды в кельвинах.

Аналоги к заданию № 27969: 41841 41845 500914 … Все

Видеокурс

Источник

Как вычислить температуру звезды на основе данных о её светимости и размерах?

Формула зависимости температуры T, светимости L и радиуса звезды R выводится из формулы закона Стефана-Больцмана:

J = σ*T^4, где J – энергетическая светимость на единицу площади, σ – постоянная Стефана-Больцмана, Т – абсолютная температура.

Поскольку площадь поверхности сферы определяется как S=4ПR^2, то полную светимость можно вычислить по формуле:

L=4*П*R^2*σ*T^4, где L – светимость звезды, R – радиус звезды, σ – постоянная Стефана-Больцмана, Т – абсолютная температура.

Из этой формулы находим температуру:

Т = ∜(L/(4*П*R^2*σ))

916

Комментировать ответ…Комментировать…

Здравствуйте! Методов определения температуры очень много вообще есть…
Для начала напомню, что температура характеризует среднюю кинетическую энергию одной частицы вещества. Вернее сказать, кинетическая температура, потому что температур есть много – и яркостная, и цветовая, и эффективная… много их.  Сейчас объясню.
Ваш вопрос сводится к методам определения температуры… Читать далее

1,8 K

Комментировать ответ…Комментировать…

Инженер-радиофизик, преподаватель физической культуры и спорта  · 24 июл 2022

По законам физики и довольно точно, Юля Воротынцева подробно описала методы, однако, температура звезды – понятие бессмысленное, так как она в разных местах сильно различается. Строение звёзд, их эволюция и классификация уже давно известны, и можно говорить о температуре фотосферы (тысячи кельвин) и температуре ядра (многие десятки миллионов кельвин), исходя из её… Читать далее

314

Комментировать ответ…Комментировать…

О сообществе

Источник

Как вы измеряете температуру своего тела? Самый простой ответ – “с помощью термометра”. Но так ли это и со звездами? Ответ – большое НЕТ. Как известно, температура звезды может достигать нескольких тысяч Кельвинов. Но на сегодняшний день нет такого термометра, который выдерживал бы такие высокие температуры. Более того, даже если такой термометр со сверхмощными способностями существует, кто будет использовать его на звездах в миллионы световых лет от нас? Итак, как мы измеряем температуру звезд?

Здесь нам на помощь приходят косвенные методы. Чтобы преодолеть вышеупомянутые проблемы, астрофизики используют ряд косвенных методов измерения температуры. Давайте посмотрим на некоторые из них по очереди!

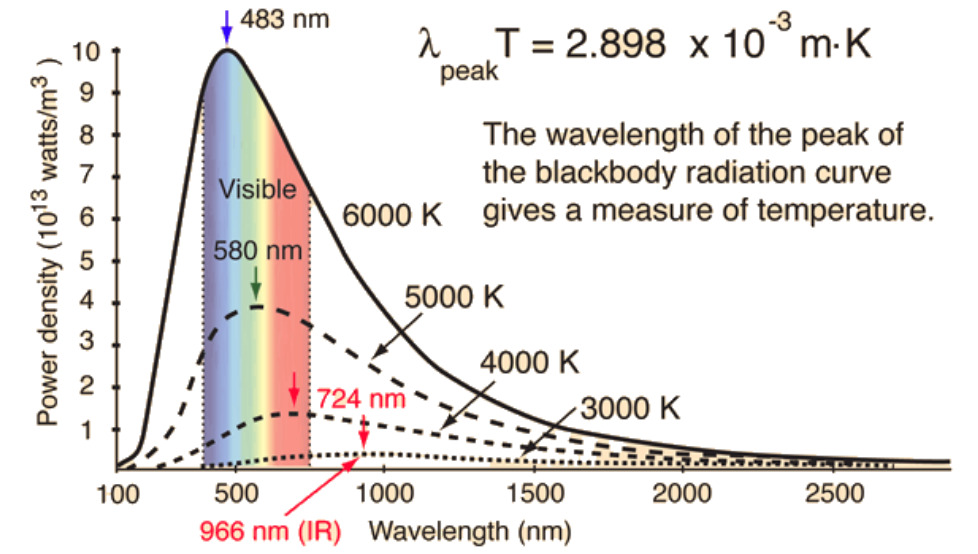
Закон смещения Вина

Закон смещения Вина касается спектра излучения черного тела. В соответствии с этим кривая излучения черного тела для разных температур будет иметь пик на разных длинах волн, которые обратно пропорциональны температуре. Используя эту обратную зависимость между длиной волны и температурой, можно оценить температуры звезд.

Однако это применимо только к звездам, у которых спектр очень близок к спектру черного тела. Более того, должны быть доступны также спектры, откалиброванные по потоку рассматриваемой звезды. Однако этот метод не дает очень точных результатов, поскольку звезды, как правило, не являются черными телами.

Закон Стефана — Больцмана

Еще один закон, который можно использовать для измерения температуры звезд, – это закон Стефана — Больцмана. Закон Стефана – Больцмана описывает мощность, излучаемую черным телом, с точки зрения его температуры. Согласно этому закону, общая лучистая тепловая мощность, излучаемая поверхностью, пропорциональна четвертой степени ее абсолютной температуры. L = 4πR2 σT4. Здесь σ – постоянная Стефана-Больцмана, L – светимость, R и T – радиус и температура рассматриваемой звезды.

Сначала мы измеряем полный поток света, исходящего от звезды. Объединив эти факторы, ученые оценивают светимость. А с помощью интерферометров можно определить радиус звезды. В конце концов, температура измеряется путем включения всех этих членов в формулу Стефана — Больцмана. Ограничивающим фактором здесь является сложность измерения радиусов самых больших или ближайших звезд. Таким образом, измерения существуют только для нескольких гигантов и нескольких десятков ближайших звезд главной последовательности. Однако они действуют как фундаментальные калибраторы, с которыми астрофизики сравнивают и калибруют другие методы.

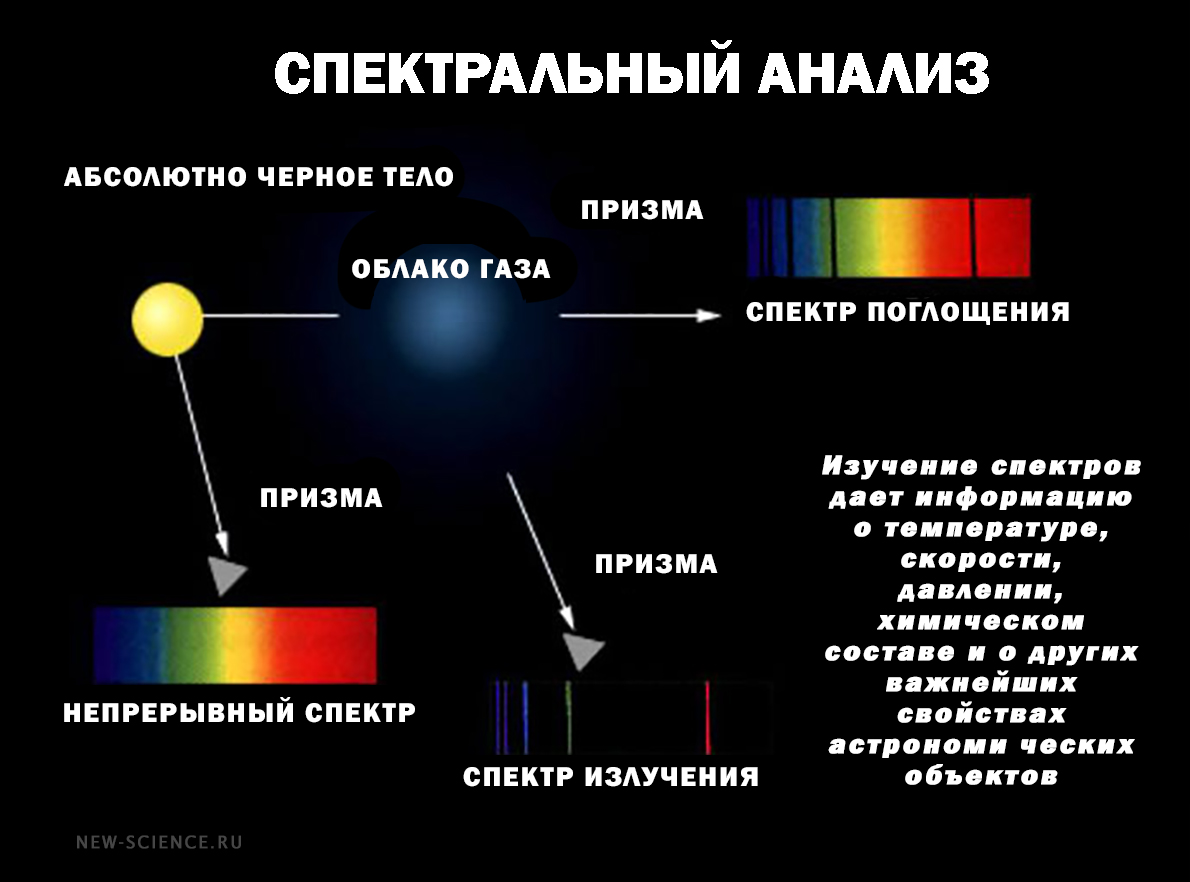
По спектральному анализу звезды

Мы знаем, что атомы/ионы имеют разные уровни энергии. И численность этих уровней зависит от температуры. И население этих уровней зависит от температуры. Более высокие уровни заняты при более высоких температурах и наоборот – при более низких. Переходы между уровнями могут привести к излучению или поглощению света на определенной длине волны в зависимости от разницы в энергии между соответствующими уровнями. Как правило, звезда горячее внутри и холоднее снаружи. Более холодные вышележащие слои поглощают излучение, исходящее из центра звезды. Это приводит к появлению линий поглощения в полученном нами спектре.

Спектральный анализ состоит из измерения силы этих линий поглощения для различных химических элементов и разных длин волн. Сила линии поглощения зависит в первую очередь от температуры звезды и количества конкретного химического элемента. Однако на нее могут влиять и некоторые другие параметры, такие как гравитация, турбулентность, структура атмосферы и т.д. Этот метод дает температурные измерения с точностью до +/-50 Кельвинов.

Взаимосвязь цвета и температуры

Еще один метод измерения температуры звезд – анализ их цвета. Хотя все звезды кажутся белыми, при внимательном рассмотрении они имеют разные цвета. Вариации являются результатом их температуры. Холодные звезды кажутся красными, а горячие – синими. Мы измеряем цвет звезды с помощью прибора, называемого фотоэлектрическим фотометром.

Это включает в себя пропускание света через различные фильтры и определение количества, которое проходит через каждый фильтр. Измерения фотометра преобразуются в температуру с использованием стандартных шкал. Этот метод очень полезен, когда хороший спектр звезды недоступен. Результаты, полученные этим методом, имеют точность до +/- 100-200 К. Однако этот метод дает плохие результаты для более холодных звезд.

Каждый из вышеупомянутых методов имеет свои преимущества и недостатки. Тем не менее астрофизики во всем мире широко используют эти методы, и в конечном итоге дают удовлетворительные результаты.

Источник

Задание 10. ЕГЭ. Для определения эффективной температуры звезд используют закон Стефана-Больцмана

Задание. Для определения эффективной температуры звезд используют закон Стефана-Больцмана, согласно которому P = σST4, где P – мощность излучения звезды (в Вт), σ = 5,7·10-8 Вт/м2К4 – постоянная, S – площадь поверхности звезды (в м2), а T – температура (в К). Известно, что площадь поверхности некоторой звезды равна (1/256)·1011 м2, а мощность ее излучения равна 4,617·1013 Вт. Найдите температуру этой звезды. Ответ дайте в кельвинах.

Решение:

Из закона Стефана-Больцмана P = σST4, выразим температуру:

Подставим необходимые данные в формулу, получим

Ответ: 1200

Оставить комментарий

Рубрики

  • Демоверсия ЕГЭ по информатике
  • Демоверсия ЕГЭ по математике
  • Демоверсия ОГЭ по информатике
  • Демоверсия ОГЭ по математике
  • Материалы по аттестации
  • Решаем ЕГЭ по математике
    • Задание 1
    • Задание 10
    • Задание 11
    • Задание 12
    • Задание 13
    • Задание 14
    • Задание 15
    • Задание 16
    • Задание 2
    • Задание 3
    • Задание 4
    • Задание 5
    • Задание 6
    • Задание 7
    • Задание 8
    • Задание 9
  • Решаем ОГЭ по математике
    • Задание 21
    • Задание 22
    • Задание 24
  • Скачать экзаменационные варианты по информатике
    • ЕГЭ по информатике
    • ОГЭ по информатике
  • Скачать экзаменационные варианты по математике
    • ЕГЭ по математике
    • ОГЭ по математике
  • Тематическое планирование

Яндекс.Метрика

Источник

Как известно, температура внутри звезд очень высокая. Ведь благодаря ей и запускаются термоядерные реакции. При сжатии молекулярного облака гравитационными силами происходит нагрев, который при достаточной массе молекул всё увеличивается и увеличивается. Так, начинается синтез гелия из водорода или, проще говоря, рождается звезда.

Рождение звезды

Рождение звезды

Несмотря на то, что все облака состоят из молекул водорода, они отличаются друг от друга количеством его частиц. В итоге получается разная масса протозвезд. Хотя процесс формирования светил примерно одинаковый.

Главным образом, температура звезд повышается при их начальном образовании, а затем при реакциях, происходящих в их ядре. В свою очередь, тепло, производимое в центральной части светила, поднимается и в его верхние слои (то есть на поверхность). А так как у разных тел она разная в недрах, соответственно, она отличается и на поверхности.

Стоит отметить, что внутри и снаружи нагрев светила не может быть одинаковым. Что интересно, звёздная корона (внешняя часть атмосферы) во много раз горячее нижних атмосферных слоёв, но, разумеется, ядерный жар самый высокий.

Структура звезды

Структура звезды

От чего зависит температура звезды

В действительности, она обуславливается двумя основными факторами.
Во-первых, уровнем производимой ядром энергии. По данным учёных, ядро разогревается до 15 млн градусов. Однако излучается только тепло, полученное в результате термоядерных реакций. А вот энергия от гравитационного сжатия остаётся в самом центре.

Температура поверхности звезд напрямую зависит от силы внутренних процессов, а также какие элементы в них задействованы. Например, если происходит синтез не только гелия из водорода, но и синтез с участием тяжёлых элементов, то и излучающая энергия будет в разы больше. Как следствие, поверхностный нагрев увеличится.

А во-вторых, важное значение имеет площадь поверхности, которая излучает внутреннюю энергию. Дело в том, что звёздные объекты производят и в то же время отдают энергию в космическое пространство. И сколько они её отдадут, зависит от внешней оболочки, то есть от излучаемой поверхности.

Когда у звёзд расширяются внешние границы, увеличивается и ядро. А чем оно плотнее, тем горячее. Но так лишь внутри, а снаружи (в фотосфере) такие звезды имеют низкую температуру. Проще говоря, чем больше площадь, тем больше энергетический расход.

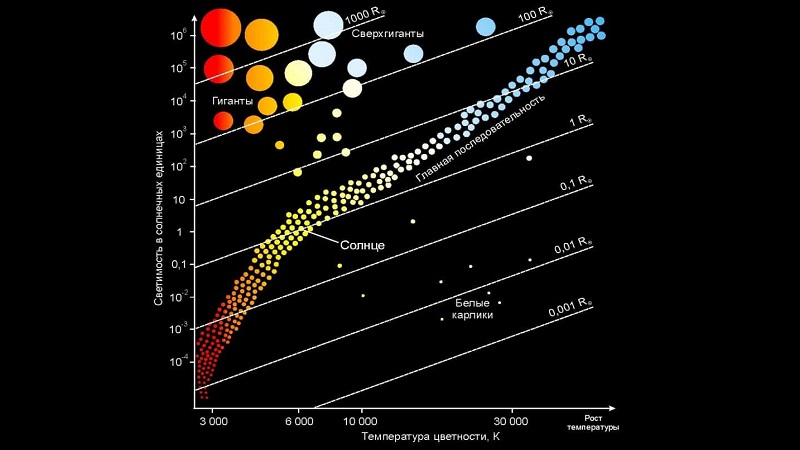
Помимо этого, прослеживается связь размеров, масс, светимостей и температур звёздных объектов. К примеру, чем массивнее звёздное тело, тем выше его светимость, а значит и нагрев. Стоит отметить, что температура звезды определяет её цвет. Взаимосвязь характеристик светил отображена на диаграмме Герцшпрунга-Расела.

Диаграмма Герцшпрунга - Рассела

Диаграмма Герцшпрунга — Рассела

Как видно, спектральные классы отличаются между собой набором характеристик.

Как определить и в чем измеряется температура звезд

Стоит отметить, что для данной характеристики используют эффективную величину нагретости тела. Другими словами, насколько горячий объект, настолько он излучает энергию. В случае со звёздными телами, их накал даёт характеристику светимости.

А вот для определения эффективной температуры звезд применяют закон Стефана-Больцмана. Он гласит, что мощность излучения нагретого тела прямо пропорциональна площади поверхности и температуры четвёртой степени.

P=σST⁴

где σ — это постоянный коэффициент 5,7*10-8,
S — площадь, а P — излучаемая мощность.

На самом деле, определяется температура звезд в Кельвинах (К). Правда, можно перевести в градусы Цельсия (С).

Какие температуры поверхности могут иметь звезды

По оценке учёных, показатели отдельных светил разные. Более холодные обладают теплом 2000-5000 К, средняя температура (у жёлтых и оранжевых) тел составляет 5000-7500 К, а горячие представители достигают значений 7500-80000 К.

Наос (самая горячая звезда)

Наос (самая горячая звезда)

Какие звезды имеют самую низкую температуру

Наименьшую температуру поверхности имеют звезды красных цветов. Правда, называть их холодными не совсем точно. Потому как их нагретость равняется 2000-3000К.

Звезда Барнарда (одна из самых холодных звёзд)

Звезда Барнарда (одна из самых холодных звёзд)

У какого типа звезд наибольшая температура

Как вы думаете, какая температура на поверхности самых горячих звезд?
Между прочим, наиболее жаркие светила имеют голубой или белый цвет. Хотя самый высокий уровень у синих. Только вдумайтесь, их уровень тепла может достигать 40000К.

Итак, мы выяснили, что температура и размеры звёзд могут быть разными. Вдобавок их характеристики связаны между собой.

Также очевидно, что температура в центре звезды отличается от температуры поверхности, которые они могут иметь. Это лишний раз доказывает, что каждый небесный объект уникален. Даже если одни его свойства схожи с другими телами, обязательно будет отличие в каком-либо другом параметре.

Источник

Добавить комментарий