Содержание:
Проекционные чертежи архитектурных объектов выполненные в одних линиях, не дают достаточно полного представления о запроектированном объекте.
Для придания объемности и наглядности ортогональным чертежам зданий и сооружений выполняется построение теней.
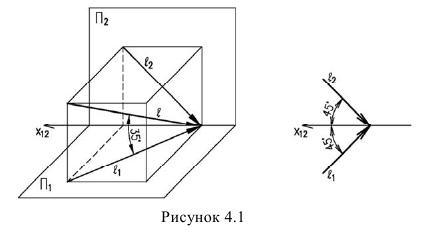
Тени строятся от естественного освещения, т.е. солнца. Так как солнце практически бесконечно удаленная точка, то лучи принимаются параллельными. За направление лучей принимается диагональ куба грани которого совпадают с плоскостями проекций, а её проекции являются диагоналями граней куба, т.е. квадратов (см. рисунок 4.1). Истинный угол наклона будет равен 35°, а проекции лучей располагаются под углом 45° к оси (см. рисунок 4.1).
Тень точки – способ следа луча, способ выноса
Тенью точки на плоскости является точка пересечения светового луча, проведенного через данную точку, с плоскостью. Если тень точки падает на плоскость проекций, то для её построения используется способ следа луча. Т.е. через проекции точки проводим проекции лучей и строим след. На рисунке 4.2 след луча фронтальный, следовательно тень падает на фронтальную плоскость —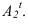
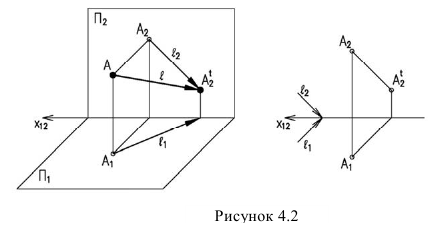
Кроме этого может быть использован метод выноса. Особенно важен этот метод при построении теней на фасадах зданий.
Вынос – это расстояние от точки до фронтальной плоскости или плоскости фасада, если тень строится на фасаде. На рисунке 4.3 у – эго вынос.
Тень примой общего положении
Тенью прямой на плоскость является линия пересечения лучевой плоскости, проведенной через прямую с заданной плоскостью. Т.е. тенью прямой на плоскость является прямая линия. Поэтому для построения тени прямой на плоскость, достаточно построить тени двух ее точек.
Если же тень от прямой падает на две плоскости, то она имеет точку излома, лежащую на линии пересечения плоскостей. В данном случае точка излома лежит на оси (рисунок 4.4). Для ее нахождения, необходимо строить мнимую тень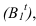 т.е. определить горизонтальный след луча проведенного через точку В.
т.е. определить горизонтальный след луча проведенного через точку В.
Тени прямых частного положении
Тени прямых частного положения на плоскостях проекций располагаются всегда определенно и часто служат «опорными» при построении теней различных деталей, включающих такие прямые. Рассмотрим эти случаи.
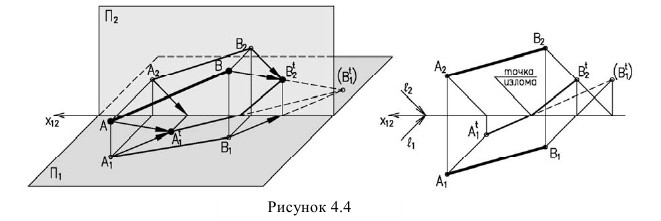
Тень от прямой, на плоскость ей параллельную, располагается параллельно прямой, т.е. параллельно проекции прямой на эту плоскость и равна ей по величине (рисунок 4.5).
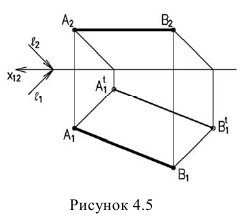
Тень от прямой на плоскость, ей перпендикулярную, располагается по проекции луча, т.е. под углом 45° (рисунок 4.6).
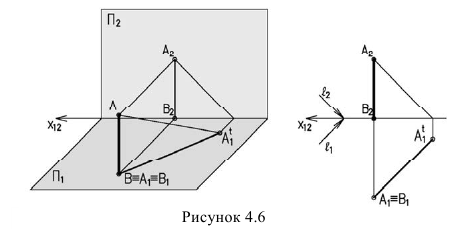
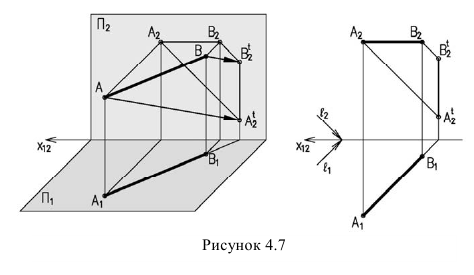
Если точка лежит на плоскости, то тень совпадает с самой точкой и такая точка называется сама себе тень. В нашем случае это точка В. Тень на фронтальной плоскости от горизонтальной прямой, расположенной под углом 45° к ней, вертикальна (рисунок 4.7)
Тени плоских фигур
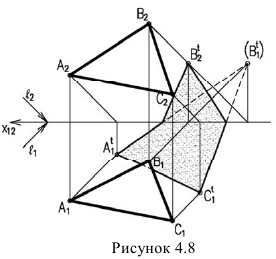
Чтобы построить тень от плоской фигуры, например треугольника, падающую на плоскости проекций достаточно построить тени от вершин (рисунок 4.8). Т.к. тень падает на две плоскости необходимо определять линию излома тени, а, следовательно, построить мнимую тень от вершины В.
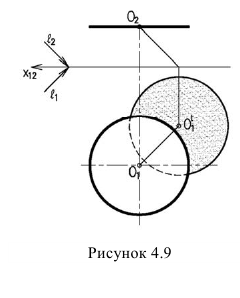
Тень от плоской фигуры, на плоскость ей параллельную, изображается фигурой равной ей по величине. Поэтому достаточно построить тень от одной точки и вычертить тень в виде той же фигуры. Так, для построения тени от окружности (рисунок 4.9) достаточно определить тень от центра и вычертить тень в виде такой же окружности.
Тень окружности
Тень окружности обычно строится по восьми точкам. Из них четыре -точки касания окружности к сторонам описанного около окружности квадрата, и четыре – точки пересечения окружности с диагоналями этого квадрата (рисунок 4.10).
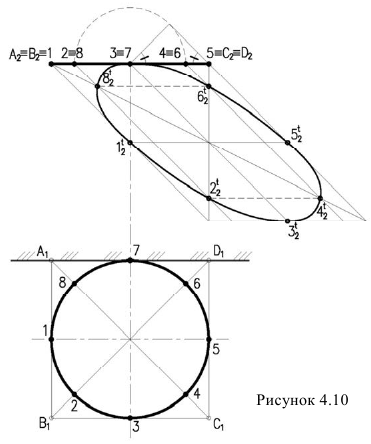
Тень от квадрата – параллелограмм, диагональ которого BD вертикальна. Точки 1,3,5,7 точки касания к параллелограмму. Точки, лежащие на диагоналях, делят радиус в отношении 0,707. Они могут быть получены без горизонтальной проекции. Для этого на
радиусе строим равнобедренный треугольник с углами при основании 45° и дугой окружности определяем положение точек 2,8 и 4,6. Проведем из них лучи до пересечения с диагоналями. Полученные восемь точек соединяем плавной линией, которая будет эллипсом. Практически тень окружности по восьми точкам строят без горизонтальной проекции, которая здесь приведена только для пояснения.
Тени поверхностей. Понятие собственной и падающей тени
Для поверхностей характерны следующие понятия: Собственная тень (ф) – неосвещенна часть поверхности (предмета) рисунок 4.11.
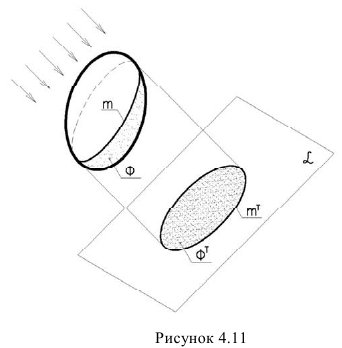
Контур собственной тени (ш)-граница между освещенной и неосвещенной частью поверхности (предмета).
Падающая тень – тень падающая от одного предмета на другой, или на плоскость.
– тень падающая от одного предмета на другой, или на плоскость.
Контур падающей тени – контур, ограничивающий падающую тень.
– контур, ограничивающий падающую тень.
Фактически контур падающей тени -это тень от контура собственной тени. Поэтому, обычно, сначала определяют контур собственной тени, а затем уже строят падающую.
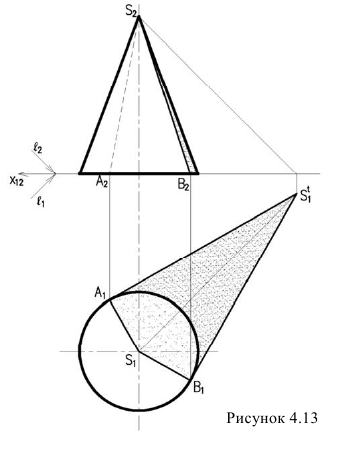
Рассмотрим примеры построения теней трехгранной призмы (рисунок 4.12) и прямого кругового конуса (рисунок 4.13).
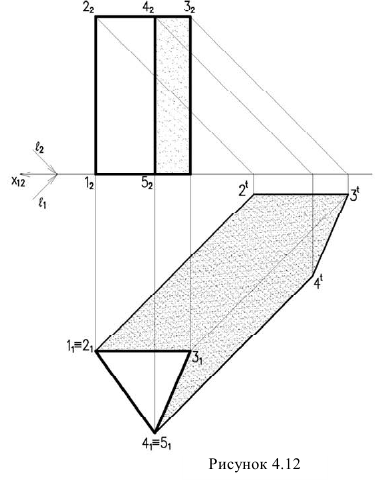
Проведя лучи на горизонтальной проекции касательные к крайним ребрам призмы, определяем контур собственной тени. Она является пространственной ломаной 1,2,3,4,5. Т.к. точки 1 и 5 лежат на плоскости  они являются тенями.
они являются тенями.
Поэтому для построения контура падающей тени, достаточно построить тени точек 2,3,4.
Проанализировав построенную тень, мы видим, что тени от ребер 1,2 и 5,4 совпадают с направлением лучей, т.к. они перпендикулярны к плоскости  А тени от ребер 2,3 и 3,4 параллельны этим ребрам и равны но величине, т.к. они параллельны плоскости.
А тени от ребер 2,3 и 3,4 параллельны этим ребрам и равны но величине, т.к. они параллельны плоскости.
Учитывая это, построение контуров падающих теней многогранников может быть значительно упрощено.
Для конуса логично сначала построить падающую тень, а затем собственную (рисунок 4.13). Для построения падающей тени, строим тень от вершины конуса 
Из полученной точки проводим касательные к окружности основания. Эти касательные образуют, контур падающей тени (она является тенями от образующих конуса). Поэтому, соединив точки А и В с вершиной конуса S получим границы собственной тени конуса. А затем уже строим фронтальную проекцию контура собственной тени. Аналогично строятся тени пирамидальных поверхностей.
Тени в ортогональных проекциях. Метод лучевых сечений, метод обратных лучей. Тени фрагментов зданий
Тень точки и прямой на плоскость общего положения (способ лучевых сечений, способ обратных лучей).
Тени схематизированного здания, состоящего из призматических форм.
Тени фрагментов зданий.
Тень точки на плоскость общего положения. Способ лучевых сечений
Для построения тени точки М на плоскость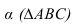 (рисунок 5.1), проведем через точку М луч и определим точку пересечения луча с плоскостью а. Задача сводится к нахождению точки пересечения прямой (луча) с плоскостью.
(рисунок 5.1), проведем через точку М луч и определим точку пересечения луча с плоскостью а. Задача сводится к нахождению точки пересечения прямой (луча) с плоскостью.
Через луч проводим горизонтально-проецирующую лучевую плоскость о. Строим линию пересечения 1-2 плоскости а и заданной плоскости Определяем точку пересечения луча с полученной линией пересечения. Эта точка
Определяем точку пересечения луча с полученной линией пересечения. Эта точка  и будет тенью точки М на плоскости а.
и будет тенью точки М на плоскости а.
Способ обратного луча
Рассмотрим построение тени от двух прямых SF и SB на непрозрачную пластинку ECDF. (рисунок 5.2).
Тень от проецирующей прямой SA строится, аналогично предыдущему примеру (рисунок 5.1), методом лучевых сечений. На горизонтальной проекции тень совпадает с направлением луча, на фронтальной – идет по лучевому сечению. Тень от точки S на пластину ESDF не надает. Для построения тени от наклонной прямой SB на пластину ESDF, необходимо построить сначала тень падающую на плоскость 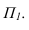 Для чего строим тень от точки S падающую на
Для чего строим тень от точки S падающую на 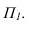 и полученную точку
и полученную точку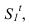 соединяем с точкой
соединяем с точкой 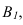 т.к. точка В лежит на плоскости
т.к. точка В лежит на плоскости 
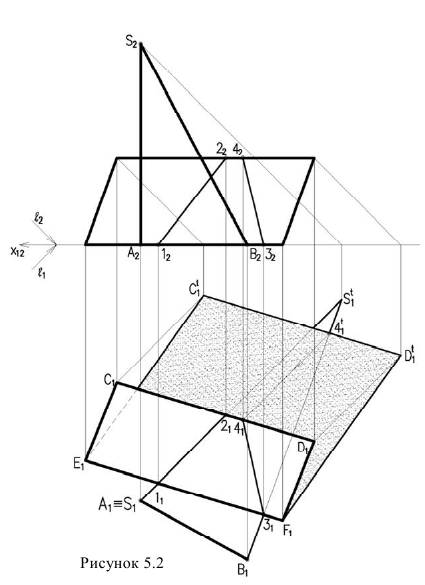
Далее строим тень от пластины ESDF на плоскость для чего строим тени точек С и D и соединяем их с точками
для чего строим тени точек С и D и соединяем их с точками лежащими на плоскости
лежащими на плоскости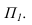 Полученные тени пересекаются
Полученные тени пересекаются 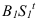
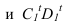 в точке
в точке 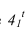 . Из точки пересечения теней проводим обратный луч под углом 45° на прямую
. Из точки пересечения теней проводим обратный луч под углом 45° на прямую 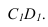 По вертикальной линии связи находим фронтальную проекцию этой точки. Обратите внимание, что точки 1 и 3, являются точками излома теней падающих на горизонтальную плоскость и на наклонную плоскость а.
По вертикальной линии связи находим фронтальную проекцию этой точки. Обратите внимание, что точки 1 и 3, являются точками излома теней падающих на горизонтальную плоскость и на наклонную плоскость а.
Необходимо отметить что данную задачу можно решить используя построение мнимой тени от точки S на пластину ESDF (рисунок 5.3).
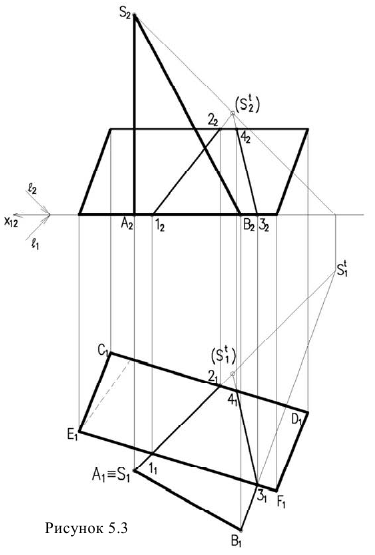
Тени схематизированною здании, состоящею из призматических форм
Здание состоит из двух призматических форм (рисунок 5.4). Обычно сначала строятся тени от двух этих форм падающие на плоскость  (т.е. на землю).
(т.е. на землю).
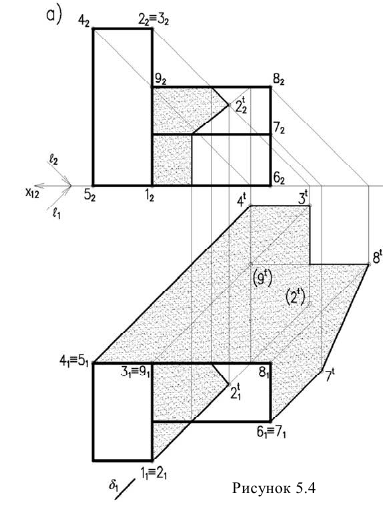
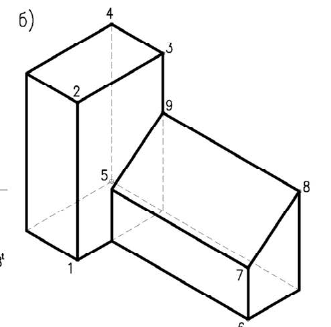
Дли построении падающих теней определяем контур собственной тени каждой из призм (рисунок 5.46). Высотная часть здания представляет прямую призму, контур собственной тени которой 1,2,3,4,5, причем точки 1 и 5 лежат на плоскости, поэтому тени строим от трех точек 2,3,4. Контур собственной тени второй призмы – 6,7,8,9. Точка 6 лежит на 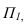 , поэтому строим тени от точек 7,8,9 (рисунок 5.4а). Т.к. две полученные тени пересекаются, определяем общий контур тени. Видим, что точки
, поэтому строим тени от точек 7,8,9 (рисунок 5.4а). Т.к. две полученные тени пересекаются, определяем общий контур тени. Видим, что точки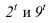 являются мнимыми. Поэтому тень от точки 2 очевидно упадет на пристройку, а точка 9 будет в тени и фактически тень не отбросит.
являются мнимыми. Поэтому тень от точки 2 очевидно упадет на пристройку, а точка 9 будет в тени и фактически тень не отбросит.
Для построения тени падающей от высотной части здания на пристройку используем метод лучевых сечений. Заключаем луч, проведенный через точку 2 в плоскость  Строим сечение призмы – пристройки плоскостью
Строим сечение призмы – пристройки плоскостью 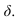 Луч, проведенный из точки 2, пересекает линию сечения в точке
Луч, проведенный из точки 2, пересекает линию сечения в точке 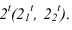 Т.е. тень падает на наклонную плоскость. Тень от вертикальной прямой 1,2, на горизонтальной проекции совпадает с направлением луча, на фронтальной идет по сечению. Тень от прямой 2,3 на фронтальной проекции совпадает с направлением луча, на горизонтальной идет по сечению.
Т.е. тень падает на наклонную плоскость. Тень от вертикальной прямой 1,2, на горизонтальной проекции совпадает с направлением луча, на фронтальной идет по сечению. Тень от прямой 2,3 на фронтальной проекции совпадает с направлением луча, на горизонтальной идет по сечению.
При построении теней зданий очень важно помнить положение теней прямых частного положения, это значительно упрощает процесс построения.
Тени фрагментов зданий
К фрагментам зданий относятся ниши, козырьки, трубы, лестницы и т.п. Рассмотрим построение теней некоторых из них.
Тени в нишах
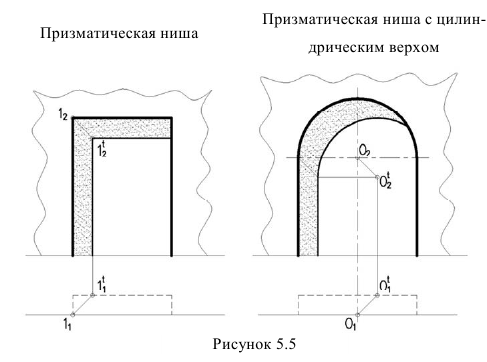
Две изображенные ниши относятся к нишам с плоским днищем, т.е. контур ниши отбрасывает тень на плоскость днища ниши параллельной контуру. Поэтому тени в нишах с – плоским днищем повторяют контур ниши. Для построения таких теней достаточно построить тень одной точки, как показано на примере (рисунок 5.5). Если дан лишь фасад здания, необходимо знать глубину ниши и тень построить методом выноса.
В цилиндрической нише (рисунок 5.6) сначала определяем собственную тень. Для чего удобнее провести нормаль (т.е. радиус под углом 45°). Получим контурную образующую собственной тени.
Падающую тень будет отбрасывать две прямые кромки ниши – вертикальная и продольная. Тень от вертикальной прямой надает на ось ниши. Тень от продольной прямой будет представлять четверть окружности.
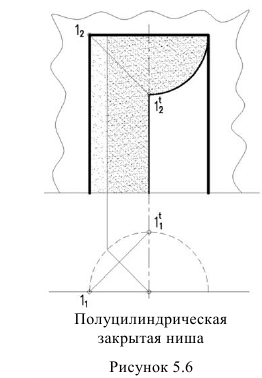
Из этого чертежа можно сделать вывод: тень от продольной прямой на фасаде с вертикальными образующими зеркально повторяется план. Этот вывод позволяет построить тень на фасаде от свеса крыши, построив тень одной точки (тень точки 1 на рисунке 5.7). Остальной контур тени зеркально повторяет план.
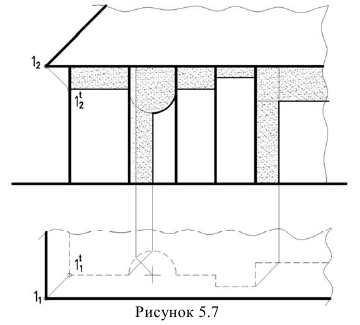
Тень падающая от трубы на крышу
На рисунке 5.8 дана труба призматической формы.
Тень строится методом лучевых сечений. Если отсутствует план здания, то нужно иметь ввиду, что тени от вертикальных прямых на фасаде имеют угол наклона равный углу наклона ската крыши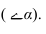
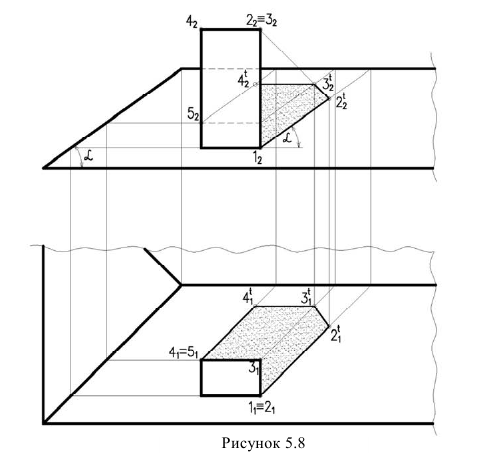
Тень от барьера на ступенях лестницы
Контур собственной тени барьера (рисунок 5.9), отбрасывающий тень на ступени представляет собой две прямые – горизонтально-проецирующую 1,2 и фронтально-проецирующую 2,3. Из точек 1 и 3 начинается тень. Следовательно, необходимо построить тень точки 2. Для построения падающей тени используется метод лучевых секущих плоскостей. 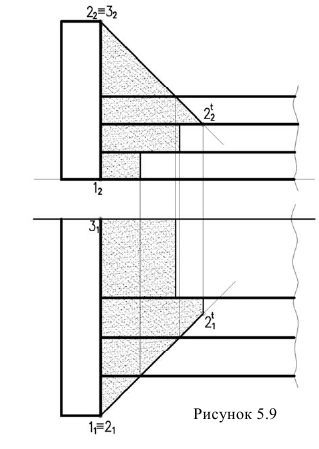
Тени в ортогональных проекциях
Строительство зданий и сооружений ведется по чертежам, выполненным в ортогональных проекциях. Представление о внешнем виде здания, в основном, создается по изображению фасада. Это изображение имеет существенный недостаток – в нем отсутствует объемность. Тени, построенные на ортогональных чертежах, дают возможность представить по чертежу расположение отдельных элементов, их освещенность, а также помогают находить наилучшие пропорции проектируемых зданий и сооружений.
При освещении лучами света каких-либо объектов на них образуются тени. Для образования тени необходим источник света и плоскость, на которую падает тень.
Освещение может быть центральным (факельным) или параллельным (солнечным). Освещение называется центральным в случае, когда световые лучи идут из одной точки (лампа, свеча); параллельным, если источник света (солнце) удален в бесконечность, и световые лучи практически будут параллельны между собой.
Основной геометрической задачей построения теней является определение контуров собственных и падающих теней (рис. 17.1).
Неосвещенная часть поверхности тела 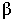 называется собственной тенью. Линия
называется собственной тенью. Линия 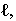 разграничивающая освещенную часть поверхности тела
разграничивающая освещенную часть поверхности тела 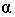 и собственную тень
и собственную тень 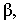 называется контуром собственной тени. Пространственное тело, преграждая путь световым лучам, образует на некоторой поверхности
называется контуром собственной тени. Пространственное тело, преграждая путь световым лучам, образует на некоторой поверхности 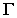 падающую тень
падающую тень 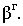 Линия
Линия 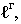 ограничивающая падающую тень
ограничивающая падающую тень 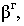 называется контуром падающей тени. Контур падающей тени
называется контуром падающей тени. Контур падающей тени 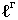 есть тень от контура собственной тени
есть тень от контура собственной тени 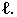
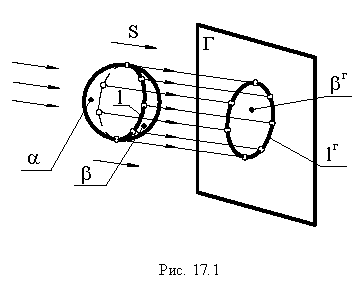
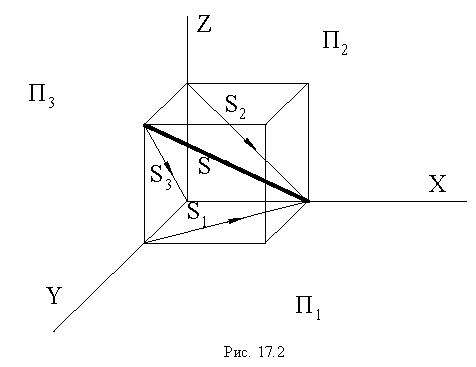
Для построения падающей тени необходимо знать направление лучей света. Направление световых лучей 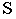 принимается параллельным диагонали куба, прислоненного своими гранями к плоскостям проекций. Проекции такого светового луча на плоскости проекций
принимается параллельным диагонали куба, прислоненного своими гранями к плоскостям проекций. Проекции такого светового луча на плоскости проекций 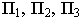 составляют угол
составляют угол 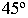 с соответствующими координатными осями
с соответствующими координатными осями 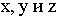 (рис. 17.2).
(рис. 17.2).
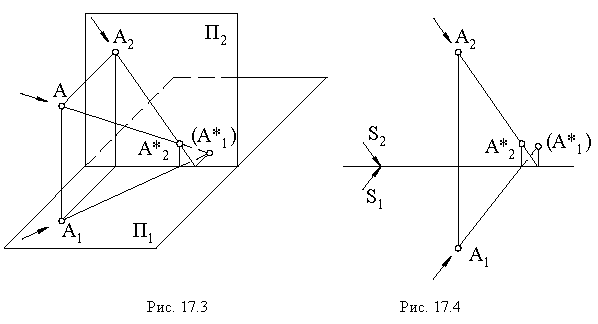
Тень от точки на плоскость проекций
Тенью от точки 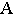 на плоскость проекций является след светового луча
на плоскость проекций является след светового луча 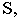 проходящего через точку
проходящего через точку 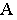 на этой плоскости. Поэтому построение проекций тени от точки на чертеже аналогично построению следов прямой На рис. 17.3 плоскость проекций
на этой плоскости. Поэтому построение проекций тени от точки на чертеже аналогично построению следов прямой На рис. 17.3 плоскость проекций 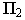 пересекается лучом в точке
пересекается лучом в точке 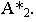 Точка
Точка 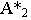 для луча является фронтальным следом, а для точки
для луча является фронтальным следом, а для точки 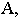 через которую проходит этот луч, – тенью её на плоскость проекций
через которую проходит этот луч, – тенью её на плоскость проекций 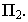 Аналогично, точка
Аналогично, точка 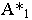 для луча служит горизонтальным следом, а для точки
для луча служит горизонтальным следом, а для точки 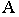 – тенью на
– тенью на 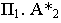 – реальная тень,
– реальная тень, 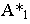 – мнимая тень точки
– мнимая тень точки 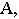 так как луч пересекает плоскость
так как луч пересекает плоскость 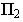 раньше, чем
раньше, чем 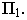 На рис. 17.4 показано построение тени точки на эпюре.
На рис. 17.4 показано построение тени точки на эпюре.
Тень от точки на плоскую фигуру
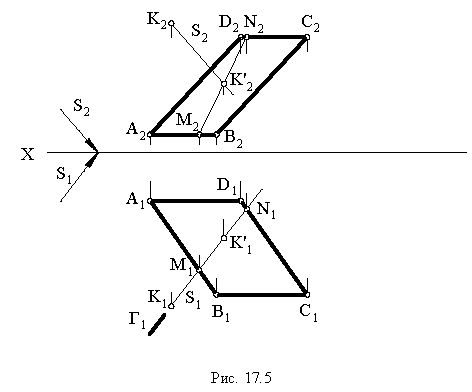
Чтобы построить тень от точки на плоскость общего положения (рис. 17.5), необходимо найти точку пересечения луча света, проходящего через заданную точку  с плоскостью
с плоскостью 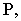 заданной четырехугольником
заданной четырехугольником 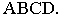 Для этой цели через проекции точки
Для этой цели через проекции точки 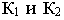 проводятся проекции светового луча, световой луч заключается в горизонтально-проецирующую плоскость
проводятся проекции светового луча, световой луч заключается в горизонтально-проецирующую плоскость 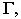 определяется линия пересечения
определяется линия пересечения 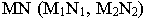 плоскости
плоскости 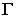 с плоскостью
с плоскостью 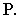 Точка пересечения светового луча
Точка пересечения светового луча 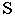 с линией
с линией 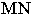 определяет точку пересечения светового луча
определяет точку пересечения светового луча 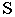 с плоскостью
с плоскостью 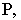 т.е. тень от точки
т.е. тень от точки 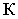 на плоскость четырехугольника
на плоскость четырехугольника  – точка
– точка 
- Заказать чертежи
Тень от прямой линии
Построение тени от отрезка прямой линии сводится к определению тени двух или нескольких его точек. Тень от прямой можно рассматривать как след лучевой плоскости, проходящей через данную прямую. В зависимости от положения прямой, лучевая плоскость может быть общего и частного положения. Линия пересечения её с плоскостями или поверхностями определит форму тени от отрезка прямой.
Тени на плоскости проекций от прямые частного положения
Построение тени от отрезка прямой  перпендикулярной плоскости проекций
перпендикулярной плоскости проекций 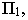 показано на рис. 17.6.
показано на рис. 17.6.
Тень 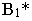 от точки
от точки 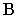 совпадает с самой точкой, т.к. точка
совпадает с самой точкой, т.к. точка 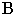 расположена на плоскости проекций
расположена на плоскости проекций 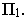 Следовательно, для построения тени отрезка
Следовательно, для построения тени отрезка 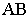 достаточно построить тень
достаточно построить тень 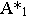 от точки
от точки 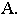 Соединив точки
Соединив точки 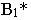 и
и 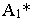 прямой линией, получим тень от отрезка
прямой линией, получим тень от отрезка 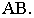
Вывод. Тень от прямой, перпендикулярной плоскости проекций, совпадает с проекцией светового луча на эту плоскость.
На рис. 17.7 показано построение тени от отрезка прямой 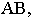 параллельной плоскости проекций
параллельной плоскости проекций 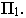
Вывод. Тень от отрезка прямой, параллельной плоскости проекций, на этой плоскости равна и параллельна самому отрезку.
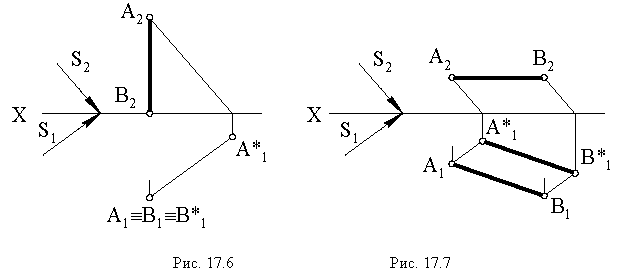
Тени на плоскости проекций от прямых общего положения
На рис. 17.8 показано построение тени от отрезка прямой 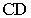 общего положения. Строим падающие тени
общего положения. Строим падающие тени 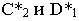 от точек
от точек 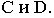 Тень от точки
Тень от точки 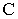 падает на фронтальную плоскость проекций, а тень от точки
падает на фронтальную плоскость проекций, а тень от точки 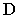 – на горизонтальную. Следовательно, тень отрезка прямой будет преломляться в точке на оси проекций. Эта точка называется точкой перелома тени. Для нахождения точки перелома тени построим тень от отрезка прямой
– на горизонтальную. Следовательно, тень отрезка прямой будет преломляться в точке на оси проекций. Эта точка называется точкой перелома тени. Для нахождения точки перелома тени построим тень от отрезка прямой 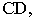 предположив, что тень от него падает только на горизонтальную плоскость. Мысленно уберем плоскость проекций
предположив, что тень от него падает только на горизонтальную плоскость. Мысленно уберем плоскость проекций 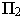 и построим мнимую тень
и построим мнимую тень 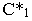 от точки
от точки 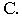 Соединив точки
Соединив точки 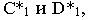 получим на оси
получим на оси 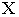 точку перелома
точку перелома 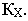 Таким образом, тень от отрезка будет ломаная линия
Таким образом, тень от отрезка будет ломаная линия 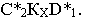 Точку перелома можно получить также, если взять на отрезке какую-нибудь дополнительную точку и построить от неё тень. На рис. 17.8 это будет точка 1.
Точку перелома можно получить также, если взять на отрезке какую-нибудь дополнительную точку и построить от неё тень. На рис. 17.8 это будет точка 1.
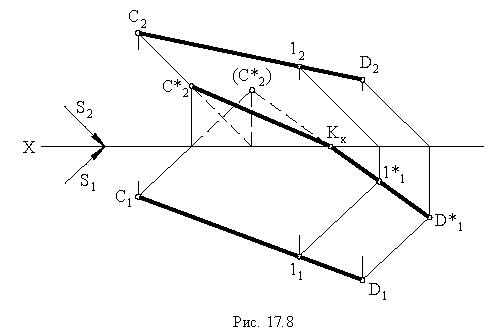
Тень от прямой на произвольную плоскость
Для построения тени от прямой на плоскость общего положения достаточно определить тени на эту плоскость от двух любых точек прямой (см. построение тени от точки на плоскую фигуру, рис. 17.5).
Тень от плоской фигуры
Падающая тень от плоской фигуры на плоскости проекций может быть построена как совокупность теней от её вершин и сторон. Таким образом, построение тени от плоской фигуры на плоскость проекций может быть сведено к известному определению теней от точек и прямых.
На рис. 17.9 показано построение тени от треугольника 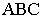 на плоскости проекций. Известным способом построены тени от вершин треугольника
на плоскости проекций. Известным способом построены тени от вершин треугольника 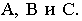 Тени от вершин падают на разные плоскости, и для определения действительной тени треугольника построена мнимая тень
Тени от вершин падают на разные плоскости, и для определения действительной тени треугольника построена мнимая тень 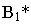 вершины
вершины 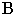 (см. рис. 17.9).
(см. рис. 17.9).
На рис. 17.10 построена тень от круглой пластины, перпендикулярной плоскости проекций  Вокруг заданной пластины опишем квадрат и проведем в нём диагонали. Построим тени от сторон, диагоналей и вспомогательных прямых
Вокруг заданной пластины опишем квадрат и проведем в нём диагонали. Построим тени от сторон, диагоналей и вспомогательных прямых 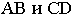 этого квадрата. Точки
этого квадрата. Точки  делят тени каждой стороны пополам, а точки
делят тени каждой стороны пополам, а точки  располагаются на пересечении теней от диагоналей и вспомогательных прямых
располагаются на пересечении теней от диагоналей и вспомогательных прямых 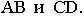
Соединив полученные точки, получим контур падающей тени круглой пластины, перпендикулярной плоскости 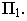
Метод обратных лучей
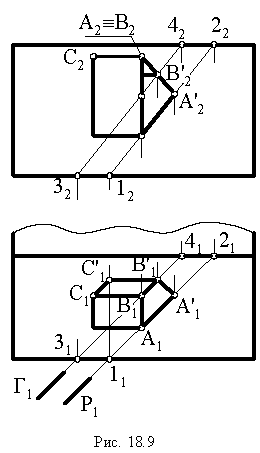
Метод обратных лучей применяется при построении теней, падающих от одного предмета на другой. Суть метода заключается в том, что строят тени заданных геометрических фигур на одну из плоскостей проекций и определяют точки пересечения теней. Через отмеченные точки проводят луч, направление которого противоположно световым лучам. Каждый из обратных лучей, пересекая данные геометрические фигуры, определяет нужные для построения тени точки.
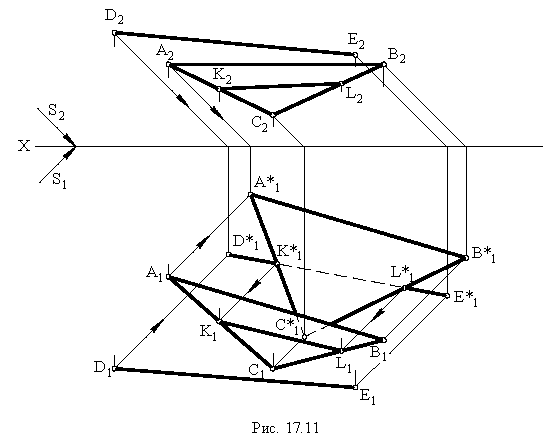
На рис. 17.11 показано применение этого метода на примере построения тени прямой на плоскость треугольника. Построены падающие тени треугольника 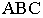 и отрезка
и отрезка 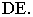 Обе тени падают на горизонтальную плоскость проекций и пересекаются в точках
Обе тени падают на горизонтальную плоскость проекций и пересекаются в точках 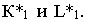 Проведем обратные лучи из точек
Проведем обратные лучи из точек 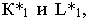 до пересечения с горизонтальными проекциями сторон
до пересечения с горизонтальными проекциями сторон 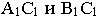 треугольника
треугольника 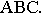 Прямая
Прямая 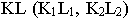 является тенью отрезка
является тенью отрезка 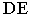 на плоскости треугольника
на плоскости треугольника 
Вывод. Если падающие тени двух геометрических образов пересекаются, то тень от одного из них будет падать на другой
Тени геометрических тел
При построении теней геометрических тел вначале определяют контур собственной тени, затем находят контур падающей тени путем построения падающих теней от вершин и сторон ломаной линии (или точек кривой линии), являющейся контуром собственной падающей тени
В отдельных случаях бывает целесообразно определять контур собственной тени по уже построенной падающей тени.
Рассмотрим процесс построения теней от основных геометрических тел.
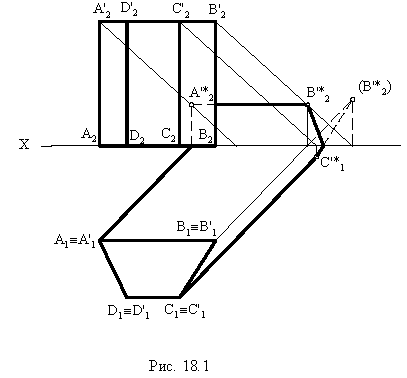
Тени призмы
Контур тени от призмы определяется тенями от рёбер (рис. 18.1). Освещенность призмы легко определить по горизонтальной проекции, где видно, что обращенными к свету являются две грани  – и верхнее основание призмы. Следовательно, контуром собственной тени будет ломаная линия
– и верхнее основание призмы. Следовательно, контуром собственной тени будет ломаная линия  Тень, построенная от этой линии, представляет собой падающую тень призмы.
Тень, построенная от этой линии, представляет собой падающую тень призмы.
Тени пирамиды
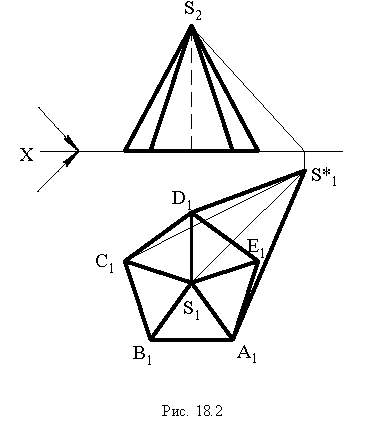
Построим тени пятиугольной пирамиды (рис. 18.2). Строим падающую тень  от вершины
от вершины  и определяем падающую тень от боковых ребер. Соединим точки
и определяем падающую тень от боковых ребер. Соединим точки  с точкой
с точкой 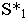 (на чертеже прямые
(на чертеже прямые 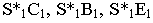 не показаны). Линиями контура падающей тени оказались прямые
не показаны). Линиями контура падающей тени оказались прямые 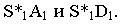 Поэтому в собственной тени будут находиться грани
Поэтому в собственной тени будут находиться грани 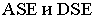 и основание пирамиды
и основание пирамиды
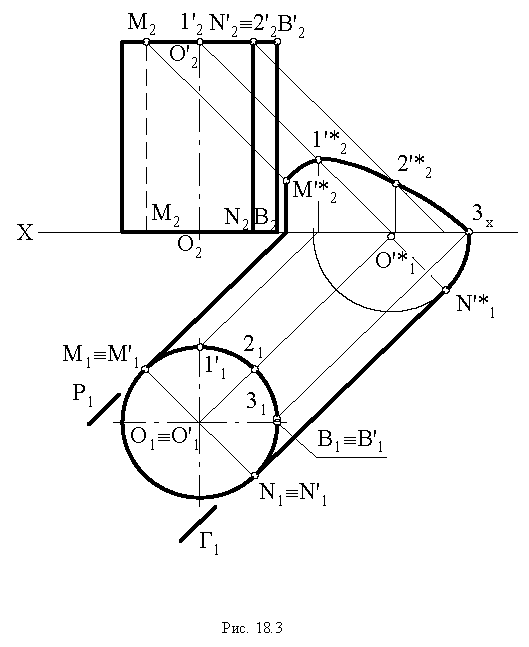
Тени цилиндра
Для определения контура собственной тени прямого кругового цилиндра необходимо провести две горизонтально-проецирующие лучевые плоскости  касательные к поверхности цилиндра и составляющие с плоскостью проекций
касательные к поверхности цилиндра и составляющие с плоскостью проекций  угол
угол  Образующие
Образующие 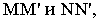 по которым плоскости
по которым плоскости 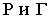 касаются цилиндра, и полуокружности
касаются цилиндра, и полуокружности 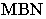 нижнего и верхнего оснований определяют контур собственной тени Контур падающей тени от цилиндра состоит из падающих теней от образующих
нижнего и верхнего оснований определяют контур собственной тени Контур падающей тени от цилиндра состоит из падающих теней от образующих 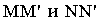 и полуокружностей
и полуокружностей  (рис. 18.3). Цилиндр расположен так, что тень от него одновременно падает на обе плоскости проекций, и тень от полуокружности
(рис. 18.3). Цилиндр расположен так, что тень от него одновременно падает на обе плоскости проекций, и тень от полуокружности  на плоскость проекций
на плоскость проекций  строится по произвольно выбранным на этой полуокружности точкам 1, 2.
строится по произвольно выбранным на этой полуокружности точкам 1, 2.
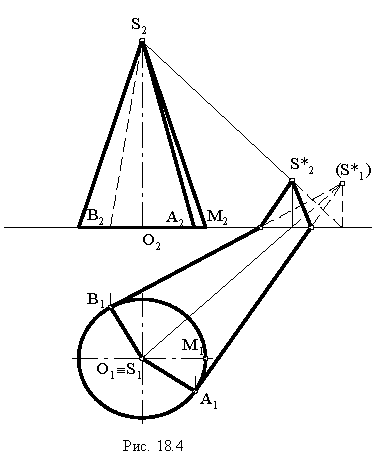
Тени конуса
На рнс. 18.4 показано построение собственной и падающей теней прямого кругового конуса. Вначале определяем мнимую тень от вершины конуса 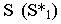 на плоскости его основания
на плоскости его основания 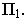 Затем из точки
Затем из точки 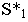 проводим прямые, касательные к основанию конуса, и определяем точки касания
проводим прямые, касательные к основанию конуса, и определяем точки касания 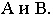 Через точки касания
Через точки касания 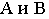 проводим образующие конуса
проводим образующие конуса 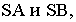 которые вместе с дугой основания
которые вместе с дугой основания 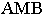 образуют контур собственной тени конуса. Падающая тень конуса имеет точки излома на оси
образуют контур собственной тени конуса. Падающая тень конуса имеет точки излома на оси 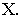
Тени элементов зданий
При построении проекций теней на фасадах зданий используются те же приемы, что и при построении теней геометрических тел.
Рассмотрим примеры построения теней некоторых частей здания
На рис. 18.5 показан пример построения теней в плоской нише. Определение границы падающей тени заключается в построении тени от ломаной линии  на заднюю плоскость ниши. От вертикального ребра
на заднюю плоскость ниши. От вертикального ребра  тень падает на горизонтальную плоскость проекций
тень падает на горизонтальную плоскость проекций  и на фронтальную плоскость задней стенки ниши. От горизонтального ребра
и на фронтальную плоскость задней стенки ниши. От горизонтального ребра 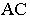 тень падает частично на заднюю фронтальную стенку ниши в виде прямой, параллельной ребру
тень падает частично на заднюю фронтальную стенку ниши в виде прямой, параллельной ребру 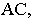 и частично – на правую боковую грань ниши (на чертеже не изображена).
и частично – на правую боковую грань ниши (на чертеже не изображена).
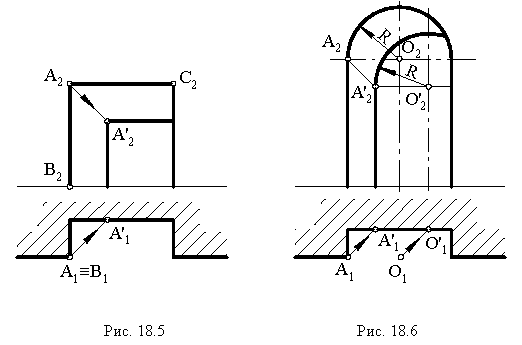
На рис. 18.6 приведен пример построения тени в прямоугольной нише с цилиндрической аркой В этом примере надо найти тень от точки 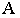 (пяты арки) и от центра
(пяты арки) и от центра  Из полученной точки (тени)
Из полученной точки (тени)  центра арки проводим дугу в пределах ниши радиусом, равным радиусу самой арки.
центра арки проводим дугу в пределах ниши радиусом, равным радиусу самой арки.
На рис. 18.7 построена тень от козырька (или балкона) здания Построения понятны из чертежа.
На рис. 18.8 показано построение теней на лестнице (крыльце). В собственной тени находятся правые грани вертикальных стенок. Падающая тень от правой стенки лестницы на плоскость стены здания и на землю строится как тень от плоской фигуры на плоскости проекций  Падающая тень от левой стенки на ступени лестницы строится методом секущих лучевых плоскостей. Этот способ заключается в том, что через заданную прямую проводится лучевая плоскость. Линия пересечения этой лучевой плоскости с произвольной поверхностью будет падающей тенью от прямой на поверхность. Через отрезок
Падающая тень от левой стенки на ступени лестницы строится методом секущих лучевых плоскостей. Этот способ заключается в том, что через заданную прямую проводится лучевая плоскость. Линия пересечения этой лучевой плоскости с произвольной поверхностью будет падающей тенью от прямой на поверхность. Через отрезок  параллельно световому лучу
параллельно световому лучу 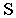 проводим лучевую плоскость
проводим лучевую плоскость 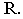 Так как отрезок
Так как отрезок 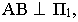 то плоскость
то плоскость 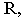 проходящая через него, будет горизонтально-проецирующей
проходящая через него, будет горизонтально-проецирующей 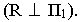 Горизонтальный след этой плоскости
Горизонтальный след этой плоскости 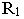 параллелен горизонтальной проекции светового луча:
параллелен горизонтальной проекции светового луча: 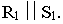 Ломаная линия
Ломаная линия 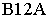 является линией пересечения многогранной поверхности лестницы плоскостью
является линией пересечения многогранной поверхности лестницы плоскостью 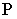 и тенью от прямой
и тенью от прямой 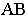 на ступени лестницы Через отрезок
на ступени лестницы Через отрезок 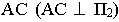 проводим фронтально-проецирующую плоскость
проводим фронтально-проецирующую плоскость 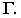 Фронтальный след этой плоскости
Фронтальный след этой плоскости 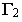 параллелен фронтальной проекции светового луча:
параллелен фронтальной проекции светового луча: 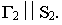 Ломаная линия
Ломаная линия 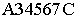 является линией пересечения многогранной поверхности лестницы плоскостью
является линией пересечения многогранной поверхности лестницы плоскостью 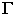 и тенью от прямой
и тенью от прямой 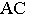 на ступени лестницы
на ступени лестницы
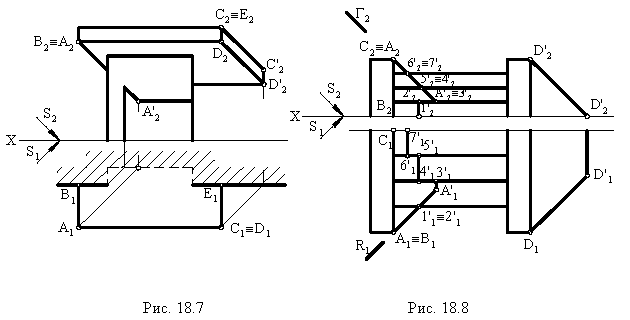
На рис. 1S.9 показано построение контура падающей тени от трубы на скат крыши здания Задача сводится к определению теней от точек и прямых на произвольно расположенную плоскость (скат крыши). Построения выполнены способом вспомогательных секущих лучевых плоскостей  которые пересекают скат крыши по прямым 12 и 34.
которые пересекают скат крыши по прямым 12 и 34.
Тени в перспективе
При построении теней в перспективе в качестве источника света рассматривается естественный источник – солнце. Правила построения теней в перспективе точно такие же, как и в ортогональных проекциях.
Для упрощения построения считают, что световые лучи параллельны плоскости картины, тогда на картине перспективы оснований лучей будут параллельны основанию картины
Если на картине задана перспектива 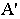 точки
точки 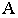 и перспектива
и перспектива 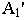 ее основания
ее основания 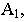 то для построения тени от точки
то для построения тени от точки 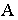 на предметной плоскости (рис. 18.10) необходимо на картине через перспективу
на предметной плоскости (рис. 18.10) необходимо на картине через перспективу 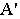 точки
точки 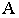 провести перспективу луча света, а через перспективу
провести перспективу луча света, а через перспективу 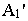 ее основания – перспективу основания луча. В месте пересечения луча и его основания получим точку, которая и будет искомой тенью
ее основания – перспективу основания луча. В месте пересечения луча и его основания получим точку, которая и будет искомой тенью 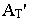 от точки
от точки 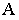 на предметной плоскости.
на предметной плоскости.
Построение тени от прямой сводится к построению тени от двух ее точек. При этом, если прямая перпендикулярна предметной плоскости (рис. 18.11), то тень от нее на этой плоскости совпадает с основанием луча, проведенного через основание прямой.
Тень от вертикальной прямой на вертикальной плоскости вертикальна.
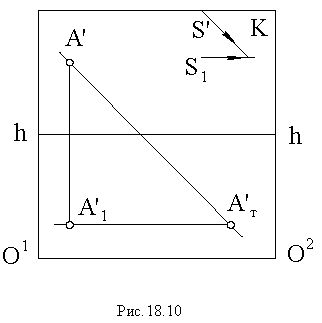
Если прямая параллельна предметной плоскости (горизонтальная прямая), то тень от нее на этой плоскости будет параллельна данной прямой (рис. 18.12) и направлена в точку схода.
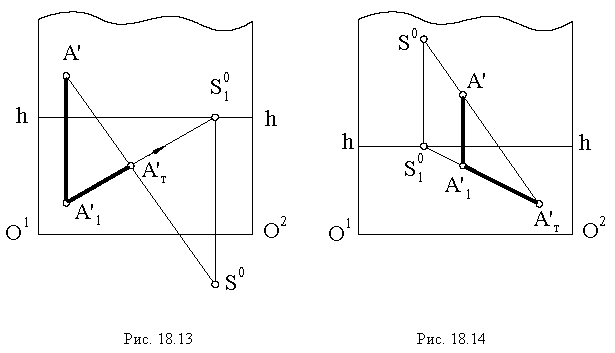
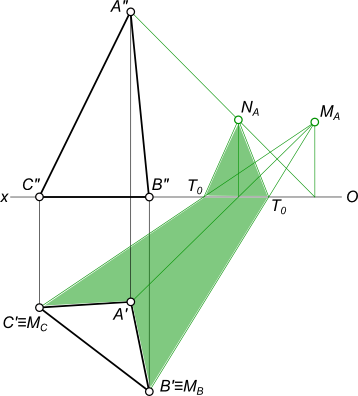
Тени в перспективе могут быть построены с различных точек расположения источника света. Направление лучей света может быть выбрано в зависимости от характера объекта и от желания показать его освещенным с той или другой стороны. Так, например, если источник света будет находиться позади предмета (рис. 18.13) или перед зрителем, но позади предмета (рис. 18.14), то для построения перспективы тени 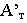 точки
точки 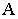 на плоскость
на плоскость 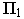 необходимо выполнить следующие действия: через точку
необходимо выполнить следующие действия: через точку 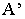 и точку схода лучей
и точку схода лучей 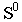 провести перспективу луча (прямую
провести перспективу луча (прямую 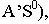 а через ее вторичную проекцию
а через ее вторичную проекцию 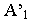 – вторичную проекцию луча (прямую
– вторичную проекцию луча (прямую 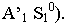 Пересечение перспективы луча его вторичной проекцией определит тень
Пересечение перспективы луча его вторичной проекцией определит тень  точки
точки  на плоскость
на плоскость 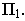
- Кривые поверхности
- Пересечения криволинейных поверхностей
- Пересечения поверхностей с прямой и плоскостью
- Взаимное пересечение поверхностей
- Развертки поверхностей
- Способы преобразования проекций
- Взаимное положение прямой и плоскости
- Решение метрических задач
-
Построение теней
План:
7.1. Основы теории теней
7.2. Тени от точки, линии и плоской фигуры
7.3. Тень, падающая от одной фигуры на
другую
7.4. Тени геометрических тел
7.5. Тени пересекающихся многогранников
(от здания)
7.6. Тени на фасадах зданий
-
Основы теории теней
Нанесением теней
пользуются для придания проекционным
чертежам большей наглядности. Особенно
широко используются тени при оформлении
архитектурных проектов, а также для
решения ряда практических задач
(например, для выявления освещенности
наружных или внутренних частей сооружения
при определенных условиях, для определения
размеров сооружения по отбрасываемой
им тени и т.п.).
Различают
собственные и падающие тени.
СОБСТВЕННОЙ
называется тень, которая получается
на неосвещенной поверхности предмета
(или объекта) при освещении его каким-либо
источником света (рис. 72).
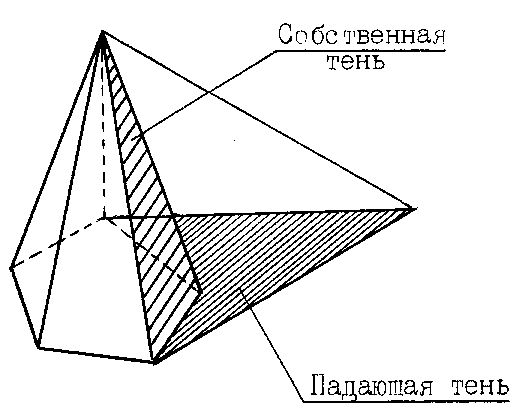
Рис.
72
ПАДАЮЩЕЙ
называется тень, отбрасываемая
предметом на плоскости проекций, или
возникающая на поверхности предмета
из-за того, что на пути лучей света
расположен другой предмет.
Если предмет
освещается источником света, находящимся
на конечном расстоянии от него (факелом,
лампой, свечой), то совокупность световых
лучей, падающих на предмет, образует
конус или пирамиду. Такая тень называется
ФАКЕЛЬНОЙ.
Если же источник
света находится в бесконечности, то
совокупность световых лучей образует
цилиндр или призму. Тень при этих
условиях называется СОЛНЕЧНОЙ.
НАПРАВЛЕНИЕ
СВЕТОВЫХ ЛУЧЕЙ. При построении теней
в ортогональных проекциях, направление
lлучей света обычно принимают
параллельным диагонали куба, грани
которого параллельны плоскостям
проекций (рис. 73).
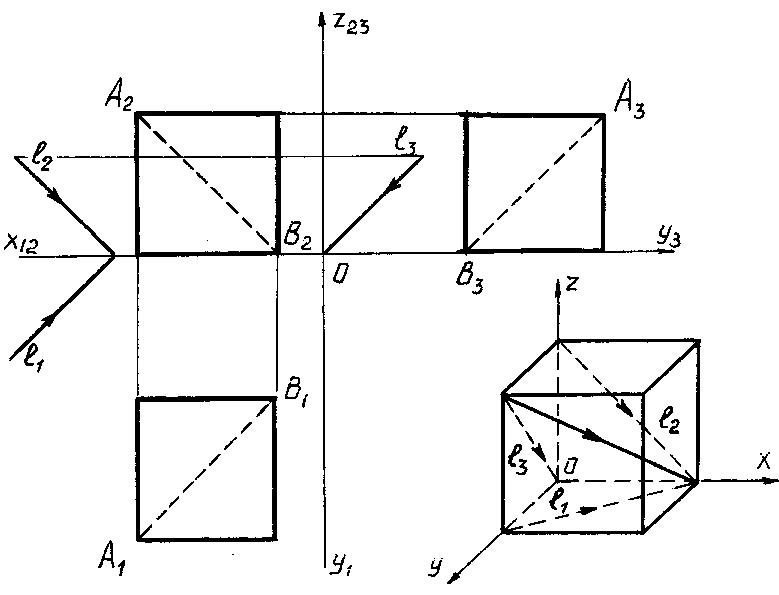
Рис.
73
Диагональ куба
АВобразует с плоскостями проекций
углы, равные 35о16′, а проекции ее
наклонены к плоскостям H, V, и W под углом
45o.
При построении
теней в аксонометрии, направление лучей
света, параллельное диагонали куба, не
всегда дает удачное расположение
светотеней; в таких случаях следует
выбрать другое направление, обеспечивающее
выразительность чертежа.
-
Тени от точки, линии и плоской фигуры
ПАДАЮЩАЯ ТЕНЬ ОТ
ТОЧКИ
Представим себе
материальную точку А(рис. 74),
расположенную в пространстве над
плоскостью Н, которая освещается
световыми лучами, идущими из бесконечности
параллельно заданному направлениюl.
ТочкаАзадержит один из них и
отбросит теневой луч, который пересечет
плоскость Н в точкеАТ‘. Эта
точка и будет являться тенью точкиА.
Иными словами,
тень точки является следом теневого
луча.
Итак, чтобы
построить тень, падающую от точки на
какую-либо плоскость или поверхность,
необходимо через данную точку провести
прямую, параллельную направлению лучей
света, и определить точку пересечения
этой прямой с плоскостью или поверхностью,
на которую падает тень.
На рис. 75а в
ортогональных проекциях и на рис. 75б
в аксонометрии построены тени, падающие
на плоскости Н, V и P(nm) от точекА,ВиС.
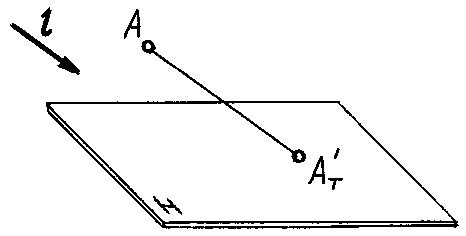
Рис.
74
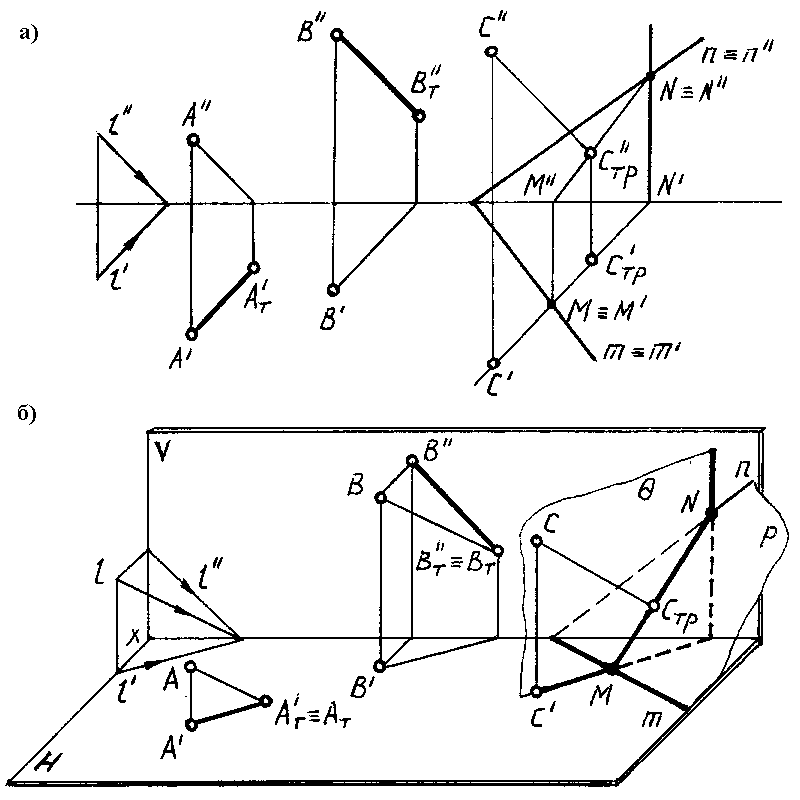
Рис.
75
Тень от точки
Ападает на плоскость Н в точкеАТ‘ (эта точка является
горизонтальным следом лучаААТ).
Тень от точки Впадает на плоскость V в точкеBТ”
(эта точка является фронтальным
следом лучаАВТ).
Тень от точки в
аксонометрииопределяется в результате
пересечения луча с его вторичной
проекцией.
Тень ВT”
(в аксонометрии) можно построить как
точку пересечения лучаВВТ с
его фронтальной проекциейВ”BT”или при помощи горизонтальной проекции
луча.
Тень от точки
Спадает на плоскость P (nm) в точкеСTP (СTP‘, СTP”),
которая определяется в результате
пересечения лучаССT с заданной
плоскостью Р при помощи
горизонтально-проецирующей плоскости.
ПАДАЮЩАЯ ТЕНЬ ОТ
ПРЯМОЙ ЛИНИИ
Тень, падающая от
прямой линии, состоит из падающих теней
от всех ее точек. Лучи, проходящие через
все точки прямой, образуют лучевую
плоскость, а тень от прямой линии есть
линия пересечения лучевой плоскости
с плоскостью или поверхностью, на
которую падает тень (то есть след лучевой
плоскости).
Тенью, падающей
от прямой на плоскость, является прямая
линия, поэтому для ее построения
достаточно построить тени от двух
точек, принадлежащих этой прямой
(рис. 76).
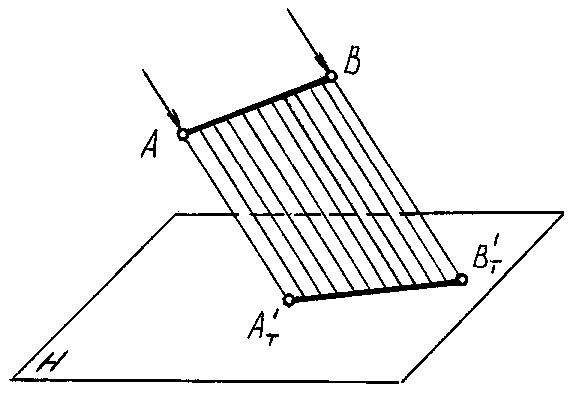
Рис.
76
На рис. 77
построена тень на плоскости проекций
от отрезка АВ на комплексном чертеже.

Рис.
77
Тени от точек А
и B
в этом
примере падают на одну плоскость
проекций V, поэтому для построения тени
отрезкаАВдостаточно соединить
между собой полученные точкиАT”
иВT” прямой линией.
ПРИМЕР.
Построить падающую тень на H и V от
отрезка прямойСD(рис. 78, 79).


Рис. 78 Рис.
79
Решение. Тень от
отрезка СDпадает на две плоскости
проекций и представляет собой ломаную
линиюCT”KXDT‘.
Точку переломаКX можно
определить двумя способами:
1) при помощи
мнимой тени(рис. 78, 79).
Для этого строят
тень отрезка на одну из плоскостей
проекций, предполагая, что второй не
существует. На рисунке сначала построена
тень отрезка на плоскость Н (СT‘DT‘).
Построенная тень пересекает осьОХв точкеКX, в этой точке тень
переломится и с одной плоскости перейдет
на другую (в точкуСT”).
2) при помощи
тени от промежуточной точки(рис.
80).
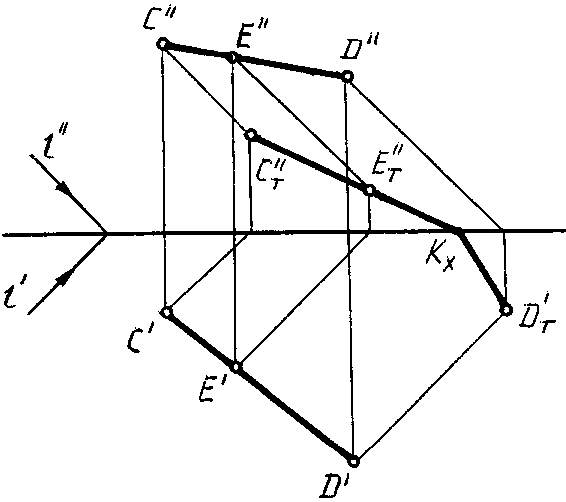
Рис.
80
На чертеже точка
перелома КX определяется при
помощи тени от произвольной промежуточной
точкиЕ (ЕT”).
Тени от прямых,
находящихся в частных положениях
ПРИМЕР. В
ортогональных проекциях заданы отрезки
частного положенияАВ,СDиEF.
Построить тени, падающие от этих отрезков
на плоскости проекций H и V (рис. 81).
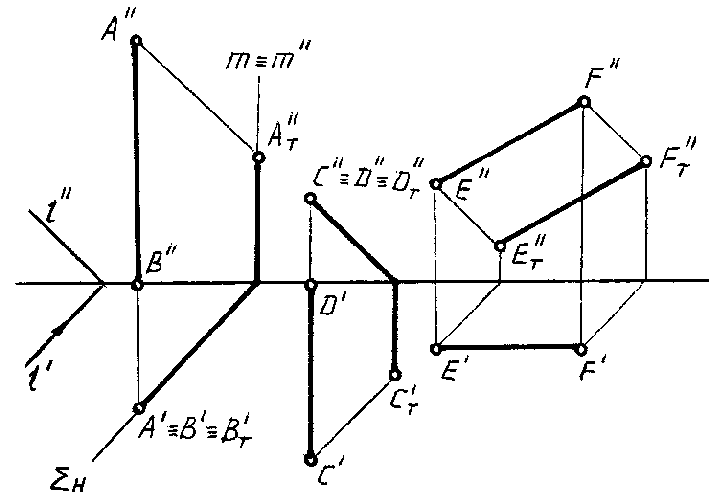
Рис.
81
Решение.
1. Отрезок АВ
занимает вертикальное положение,
поэтому лучи, проходящие через все его
точки, образуют вертикальную
(горизонтально-проецирующую) лучевую
плоскость , которая
пересечет плоскость Н по линииH,
а плоскость V — по вертикальной
прямойm=m”. Следовательно,
тень от вертикальной прямой линии на
горизонтальной плоскости совпадает с
горизонтальной проекцией (следом)
лучевой плоскости.
Но, так как
горизонтальная проекция лучевой
плоскости параллельна горизонтальной
проекции луча света, то для построения
тени на горизонтальной плоскости
проекций (от вертикальной прямой)
достаточно через горизонтальную
проекцию прямой (точку) провести
горизонтальную проекцию луча света.
2. Отрезок CDперпендикулярен плоскости V, поэтому
проходящая через него лучевая плоскость
является фронтально-проецирующей
плоскостью.
В ортогональных
проекциях тень от прямой СDна
плоскости V совпадает с проекцией
лучевой плоскости.
3. Отрезок EFпараллелен плоскости V. Его теньET”FT”
параллельна и равна данному отрезку.
В ЫВОДЫ:
1. Тень от
прямой, перпендикулярной к плоскости,
совпадает с ортогональной проекцией
светового луча на эту плоскость.
2. Тень, падающая
на плоскость от отрезка прямой,
параллельной этой плоскости, параллельна
и равна отрезку прямой. На комплексном
чертеже проекция тени равна и параллельна
проекции отрезка.
ТЕНЬ ОТ ПЛОСКОЙ
ФИГУРЫ
(непрозрачной
пластинки)
Чтобы построить
падающую тень от плоской фигуры,
ограниченной многоугольником, достаточно
построить тени, падающие от всех сторон
многоугольника.
На рисунке 82
построена тень, падающая от треугольника
АВСна плоскости проекций H и V.
Тень от вершиныАпадает на плоскость
V, а от вершиныВи вершиныС— на
плоскость Н. Следовательно, тень от
стороныВСпадает на одну плоскость
Н и представляет прямую линию, а тени
от сторонАВиАСпадают на две
плоскости и представляют ломаные линии.
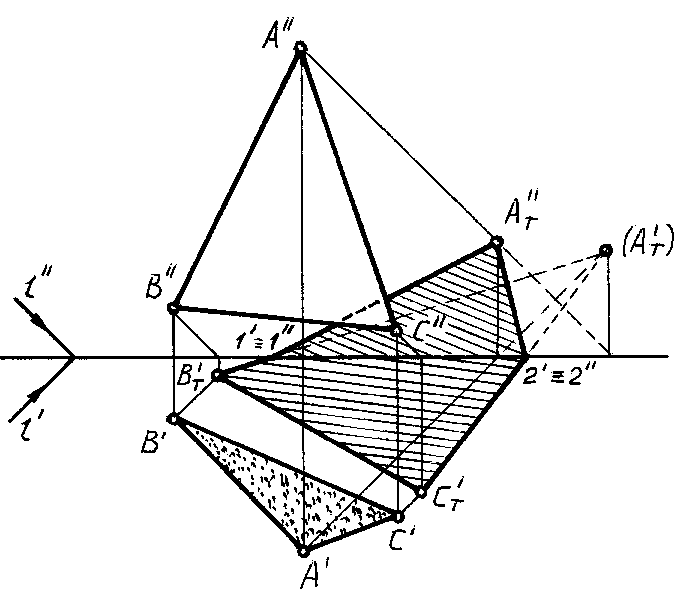
Рис.
82
Падающие тени от
сторон АВиАСможно построить
при помощи промежуточных точек (как на
чертеже 81) или при помощи мнимой тени
(АT‘), падающей от точкиАна заднюю полуплоскость Н. Получив
треугольникАTHВTHСTH,
определяем на осиОХточки перелома
1 и 2 падающей тени и соединяем их
с действительной теньюАTV от
точкиАна плоскости V. Сторона
плоской фигуры, обращенная к теневому
столбу, находится в тени, то есть у
плоских фигур следует различать
освещенную и неосвещенную стороны.
Иначе говоря, плоская фигура всегда
имеет собственную тень.
Для выяснения
освещенности сторон плоскости
треугольника применяем следующий
прием: обходя на исследуемой проекции
периметр треугольника по часовой
стрелке, замечаем порядок букв,
обозначающих вершины, и сопоставляем
с порядком букв, который получается
при обходе по часовой стрелке контура
падающей тени. Совпадение порядка букв
обозначает, что на данной проекции
видима освещенная сторона треугольника,
несовпадение — что видима
неосвещенная сторона плоскости.
На рисунке контур
падающей тени при его обходе по часовой
стрелке дает порядок букв АT”СT”ВT”.
Такой же порядок (А”є”)
получается на фронтальной проекции.
Следовательно, на V видима освещенная
сторона. Горизонтальная проекция имеет
обратный порядок букв (А‘‘ё).
Это значит, что на горизонтальной
проекции к нам обращена неосвещенная
сторона плоскости треугольника (сторона,
находящаяся в собственной тени).
Этим же приемом
можно пользоваться в аксонометрии
(рис. 83).
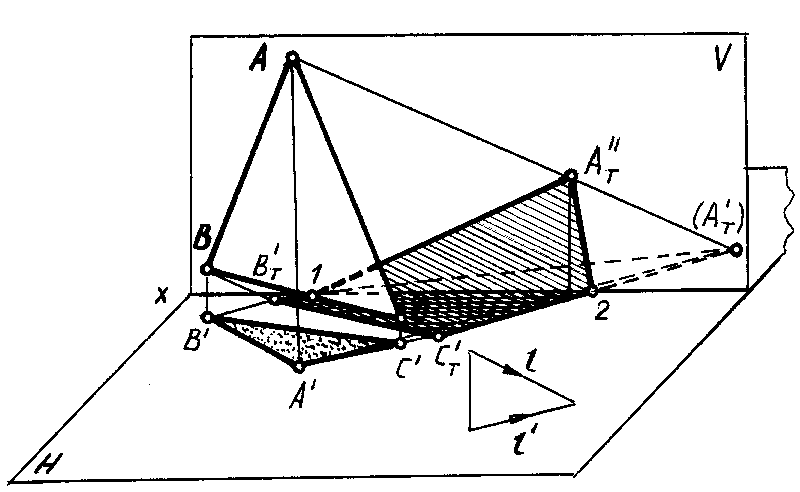
Рис.
83
ТЕНЬ ОТ ДИСКА
(окружности)
Если плоская
фигура, бросающая тень, ограничена
кривой линией, то лучи, проходящие через
точки этой кривой, образуют цилиндрическую
лучевую поверхность. В пересечении с
плоскостью, на которую падает тень, эта
поверхность дает контур падающей тени
данной фигуры.
Если плоскость
фигуры параллельна плоскости, на которую
падает тень, то тень равна самой фигуре
(так как равны параллельные между собой
основания цилиндра).
На рис. 84 показано
построение тени от круга, параллельного
плоскости H, на плоскость H. Контуром
тени является окружность тог же радиуса.
Для построения тени достаточно найти
тень от центра С.
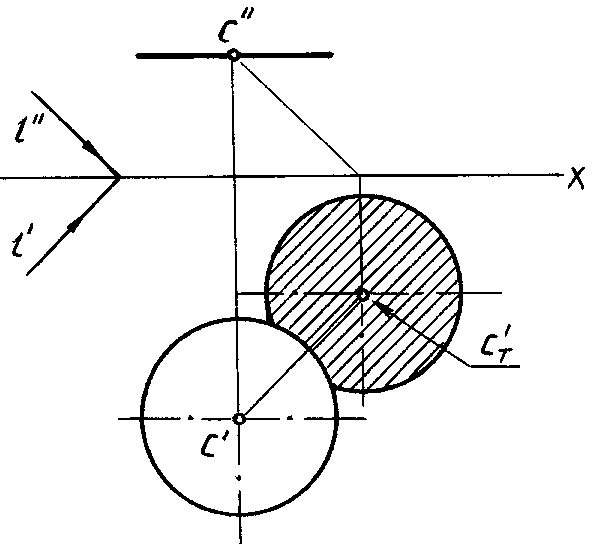
Рис.
84
Для построения
тени, падающей от кривой линии на
произвольно расположенную плоскость,
можно применить один из двух способов.
1. На кривой
линии намечается достаточно большое
число точек, от которых строится падающая
тень. Полученные точки (падающей тени)
соединяются между собой плавной кривой
линией.
2. Около кривой
линии описывается многоугольник,
строится падающая тень от многоугольника
и в нее вписывается тень кривой линии.
На рис. 85 для
построения падающей тени от круга,
параллельного плоскости V, на плоскость
Н использован описанный около него
квадрат АBCD. Сначала строится
падающая тень от сторон квадрата, его
диагоналей и линий, проходящих через
центрСпараллельно сторонам
квадрата, а затем вписывается в полученный
параллелограмм кривая (эллипс). На
рисунке эллипс проходит через восемь
точек, принадлежащих одновременно
падающим теням от окружности, сторон
и диагоналей квадрата.
Если тень от кривой
линии падает на две пересекающиеся
плоскости, то она будет иметь излом на
линии пересечения плоскостей.
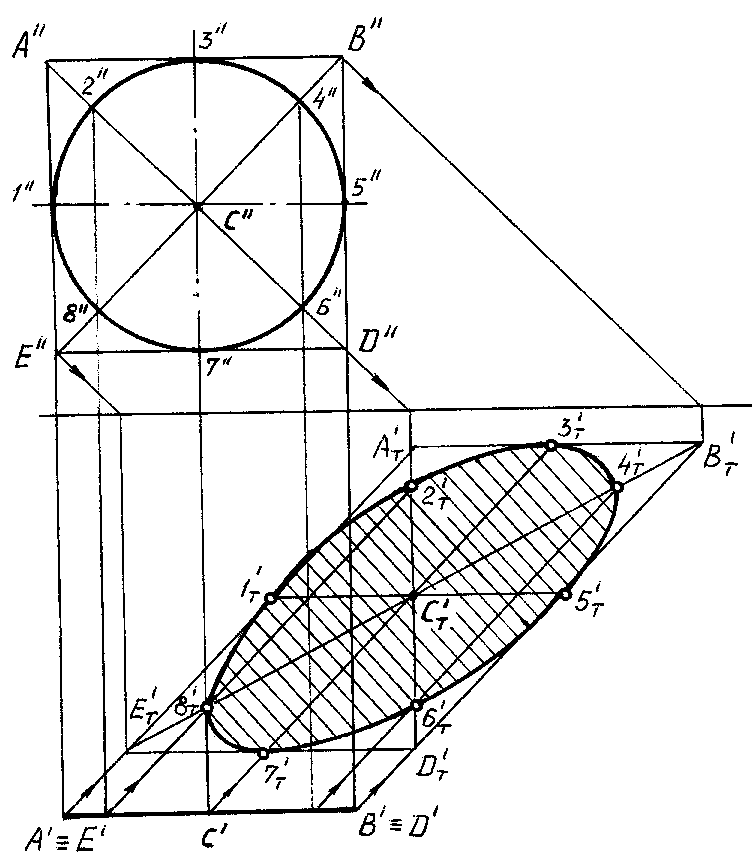
Рис.
85
Тень плоской фигуры
Тень плоской фигуры в тех случаях, когда точка или прямая принадлежащая ей расположена в плоскости проекций
Тень плоской фигуры
Здесь построение теней упрощается потому, что точки B и C или прямая BC совпадают с своей тенью.
Тень плоской фигуры четырехугольника занимающего общее положение, когда его вершины и стороны не принадлежат плоскостям проекций
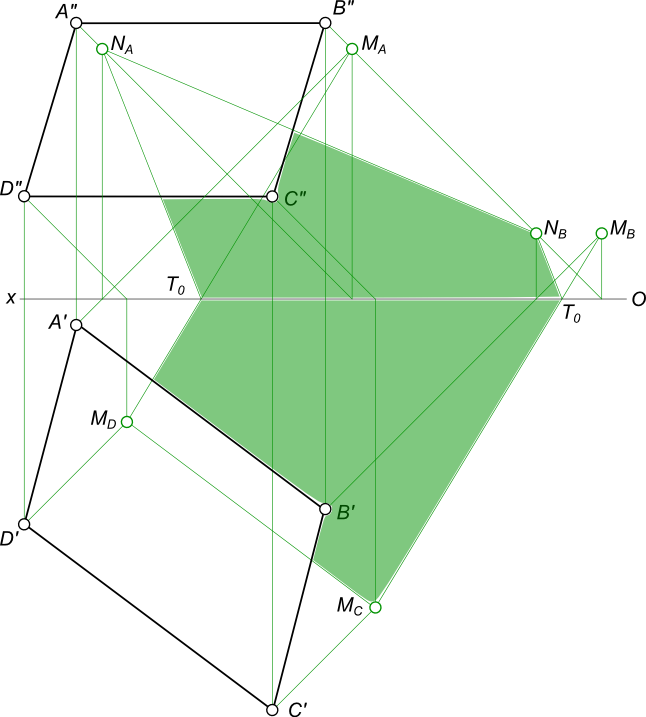
Тень плоской фигуры
Чтобы построить падающую тень плоской фигуры – четырехугольника ABCD на плоскостях проекций находим тени от каждой его вершины.
Одноименные тени точек соединяем между собой прямыми линиями.
Тень плоской фигуры – тень круга или тень диска, расположенного параллельно фронтальной плоскости проекций
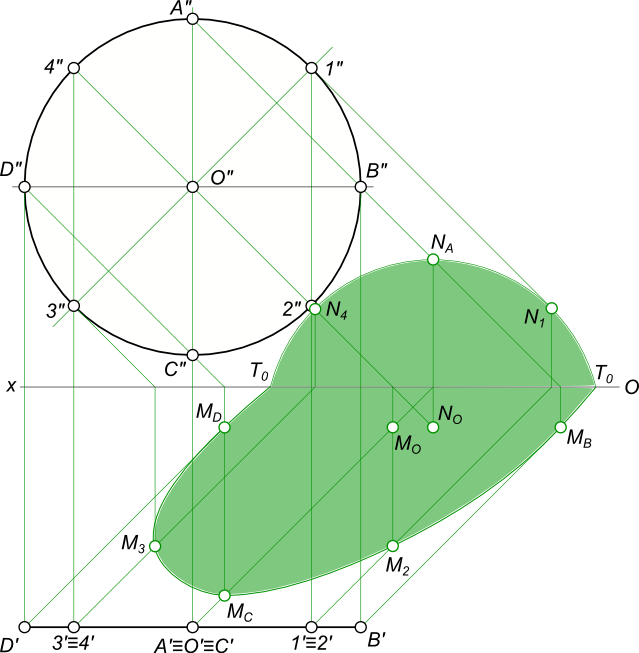
Тень плоской фигуры
Здесь для построение тени:
– на горизонтальной плоскости проекций разделяем круг на 8 или 12 равных частей и находим тени всех этих точек, которые соединяем плавной кривой;
– на фронтальной плоскости проекций достаточно найти тень от центра круга, которая послужит центром для проведения окружности, служащей контуром падающей тени от круга.
+
Рисование теней является важной частью трехмерного рисунка. Вам нужно понять геометрию этого процесса. Это не так сложно, как кажется. Тень – это форма, созданная объектом на поверхности (или нескольких поверхностей) путем блокировки света. Чтобы увидеть тень, вам нужен источник света.
Существует два типа источников света: натуральный (солнце, луна) и искусственный (лампа, свеча, вспышка и т. д.).
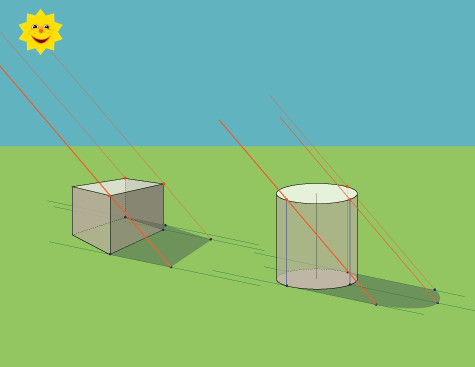
Естественный свет
Естественные источники света (Солнце и Луна) находятся от нас довольно далеко. Таким образом, световые лучи, которые исходят от них на объект, считаются параллельными (из-за расстояния).
Искусственный (точечный) свет
Точечный свет намного ближе к нам. Мы можем позиционировать его более точно в нашей среде – мы можем точно сказать, насколько далеко и насколько высоко он находится от объекта.
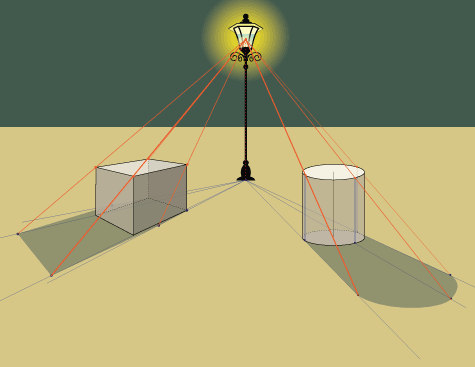
Надо знать:
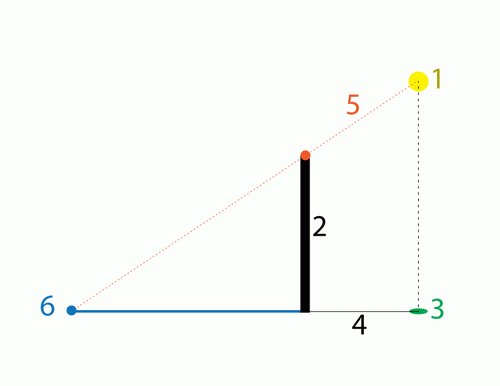
1 – Источник света (желтая точка)
2 – Объект
3 – Точка заземления источника света – положение источника света на поверхности (зеленая точка)
4 – Линия, соединяющая точку заземления источника света и нижнюю часть объекта (черная линия)
5 – Линия, соединяющая источник света (1) и верхнюю часть объекта (красная точка), служит для определения конечной точки тени (6)
6 – Конечная точка тени на поверхности
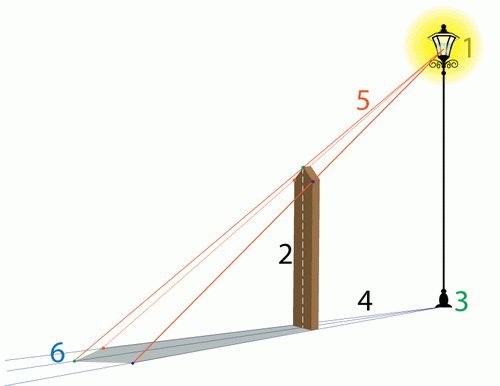
Это правило применяется для обоих типов источника света и для всех форм и объектов. Существует только одно отличие:
Естественный свет
Линии (4) параллельны, поскольку источник света находится очень далеко, поэтому нам не нужно рисовать желтую точку (1). Линии (5) также параллельны по той же причине.
Прожектор
Каждая угловая точка соответствует приведенному выше правилу, чтобы сформировать точную форму тени.
Тень точки

Представьте, что вам нужно нарисовать тень маленького круглого объекта, почти точку. Давайте нарисуем одну из мух. Почему нет?
Итак, здесь у нас есть комната с одним источником света и мухой. Поверхность – коричневый пол – здесь мы собираемся разместить тень.
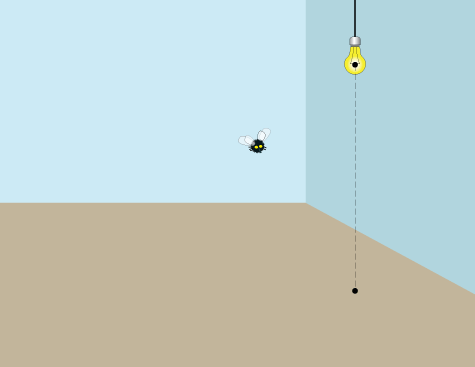
Первое, что нужно сделать, это отметить положение источника света на полу (черная точка).
Проводим прямую вертикальную линию вниз до пола и отмечаем точку на полу, которая находится точно под светом.
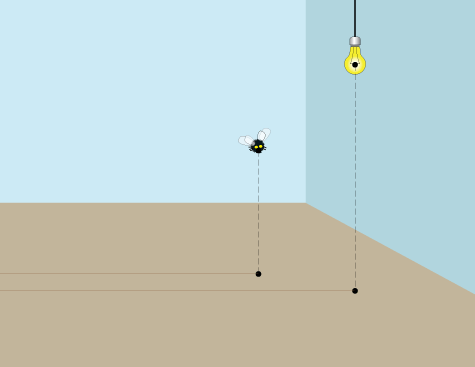
Отмечаем положение мухи на полу. Обратите внимание на положение света и мухи в отношении друг друга – в этом случае свет ближе к нам, чем муха (вам не нужно рисовать коричневые горизонтальные линии – они просто для справки).
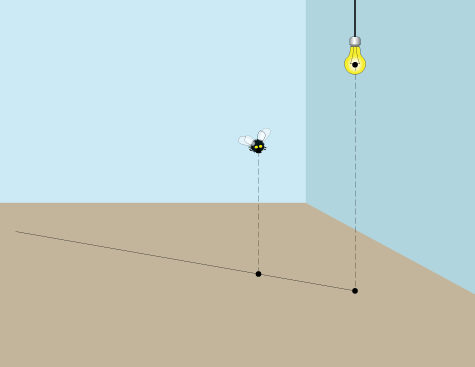
Соединим точки от источника света и объекта линией – она будет определять направление к тени.
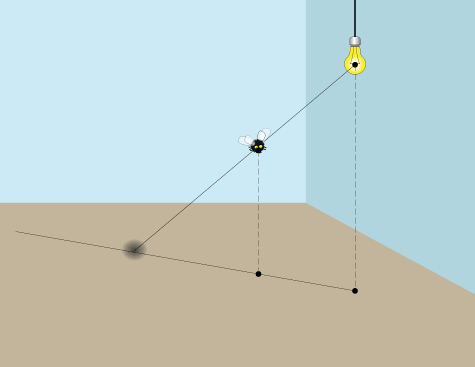
Создадим линию от источника света через муху до плоскости пола. Точка пересечения двух линий покажет положение тени.
Тень от карандаша (плоская тень)
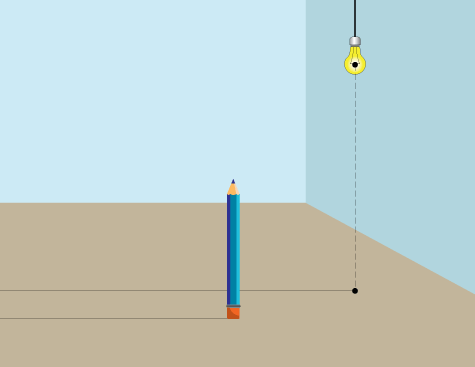
Начните, опять же, с определения положения вашего источника света на поверхности пола. Обратите внимание, что в этом случае объект (карандаш) ближе к нам, чем источник света.
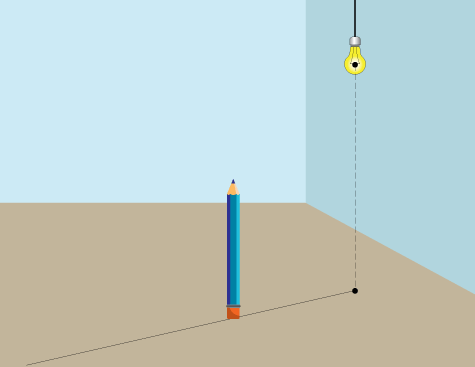
Соедините точку источника света на полу с нижней плоскостью объекта.
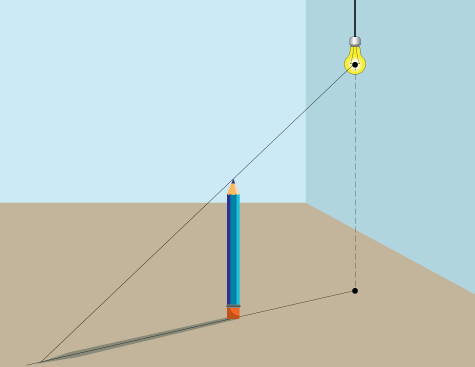
Теперь нарисуйте линию (луч света) от источника света через верхний кончик карандаша. Это определит длину тени.
Тень от карандаша (согнутая тень)

В случае, если вам нужно нарисовать тень, которая падает на несколько поверхностей (пол и стены), используйте те же самые шаги, просто слегка подкорректируйте их. Скажем, ваш карандаш находится рядом со стеной. Тень падает как на пол, так и на стену. Вот как вы это делаете:

Просто согните линию, когда она попадает на стену.
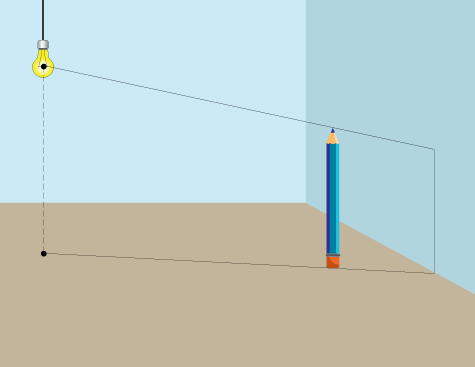
Нарисуйте линию от света через верхнюю часть карандаша, как показано.
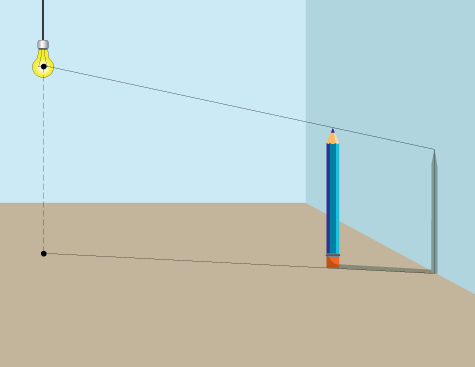
Конечный результат.
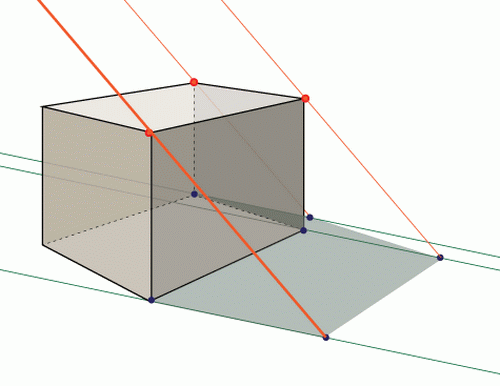
Тень от куба
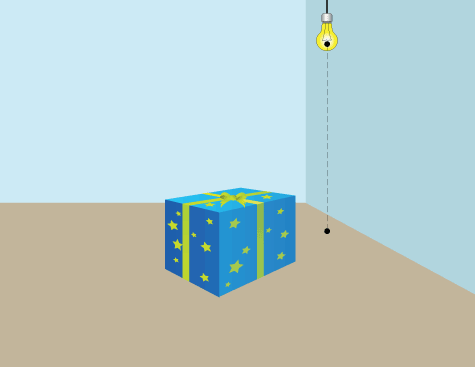
Рисование тени от куба (ящика) – это повторное использование той же технологии, что и в случае создания тени от карандаша. Вам придется повторить те же шаги со всеми углами куба, которые образуют тень.
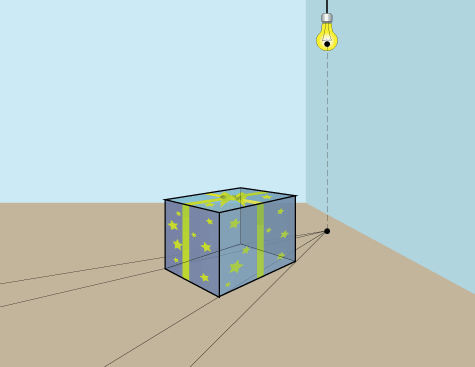
Известно, лучший способ рисовать трехмерные формы – это рисовать их с «прозрачными сторонами» – как будто форма сделана из стекла.
Проведите линии от точки источника света на полу через все угловые точки нижней плоскости объекта.
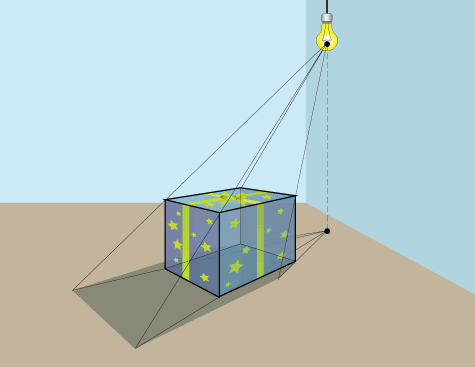
Нарисуйте линии от источника света через верхние угловые точки объекта. Точки пересечения образуют теневую форму.
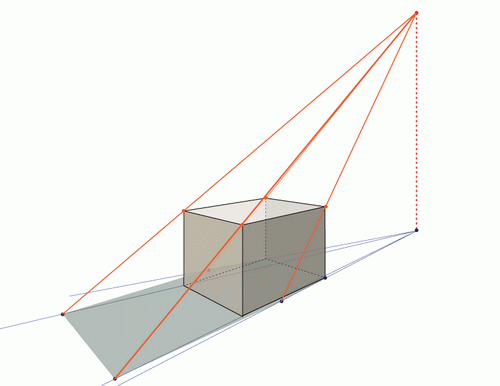
Тени других геометрических форм
Получите востребованную профессию дизайнера
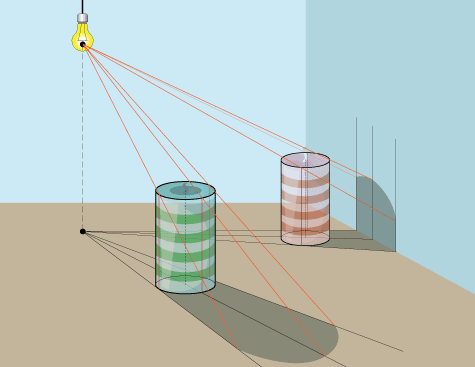
Тень цилиндра
Тот же метод используется для создания тени цилиндра с небольшими корректировками.
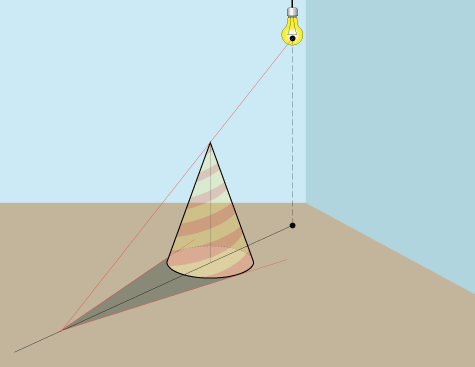
Тень конуса
Julianna Kunstler
Понравилась статья? Поделитесь с друзьями.
Твитнуть
Поделиться
Поделиться
Отправить
Класснуть
Линкануть
Светотенью называется распределение света и тени на поверхностях предметов. Законами светотени — принципы этого распределения.
Благодаря правильному распределению света и тени, мы можем показать на рисунке форму предмета и характер освещения.
Помимо этого, светотень мощное выразительное средство. Творческий метод таких мастеров как Караваджо, Рембрандт, Сурбаран основан на работе со светотенью. Уводя в тень второстепенное и освещая главное они создавали удивительно точные, цельные и лаконичные образы.

Светотень в рисунке.
Распределение света и тени в рисунке мы делаем на глаз, без точных построений.
При этом, если мы хотим создать реалистичное изображение, необходимо соблюдать ряд правил:
- На поверхности каждого освещенного предмета есть:
- свет с бликом
- полутон
- тень
- рефлекс (участки, освещенные отраженным светом)
И этот предмет отбрасывает падающую тень.

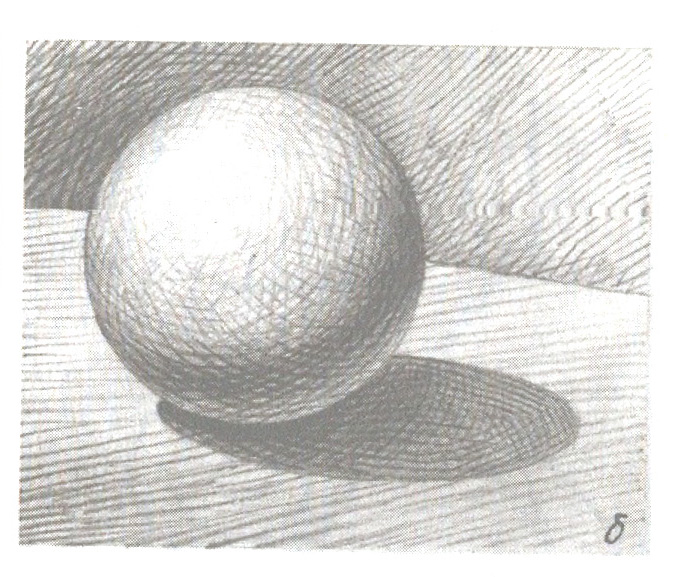
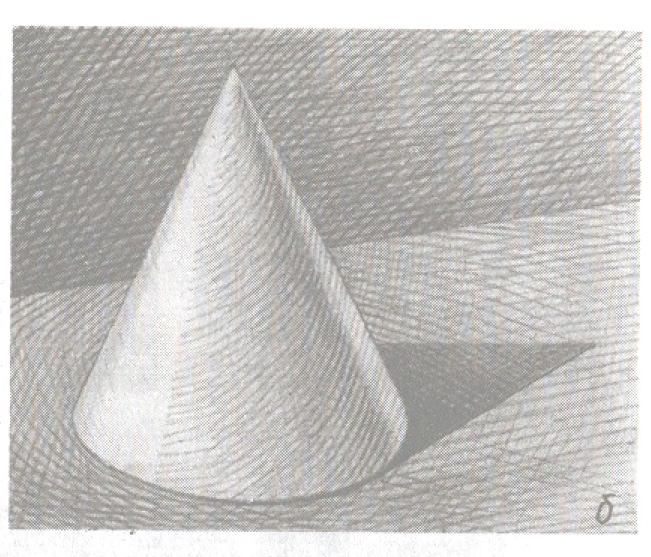
- Границы между этими участками ( светом и тенью и.т.д.) проходят по поверхности предмета, а значит, должны соответствовать ее форме. Например, на шаре граница между светом и собственной тенью не может иметь углов, а на боковой поверхности Цилиндра- не может быть дугообразной. Если предмет сложной формы, границы меняют направление вместе с изменением формы поверхности. Рисуя шар, обратите внимание, что границы на нем — эллипсы или линии.

- Свет находится на поверхности предмета обращенной к источнику света, собственная и падающая тень находятся с противоположной стороны.
- Рефлекс всегда темнее полутона.
- Выявляя светотень мы пользуемся штрихом по форме, то есть штрихи должны повторять форму поверхности, например, на шаре они дугообразные, а на кубе — прямые.


- Тень более светлого предмета светлее тени более темного, свет более светлого предмета светлее света более темного.

- Падающая тень по очертаниям напоминает предмет. Но ее границы менее четкие.
- Детали тщательно прорабатываются либо на светах, либо в тенях.Чаще на светах. Если мы выявляем фактуру и детали в светах, нормально и правильно, что тени сливаются и деталей в них не видно

- Мы не изображаем предметы в вакууме, пространство вокруг предмета так же заполнено другими поверхностями, имеющими тон и освещенными тем же источником света. Даже если фон в постановке белый, мы не воспринимаем и не изображаем его как белый. Исключение — некоторые типы набросков и зарисовок.
Давайте отработаем эти правила на практике.
Упражнение 1.
Светотень как выразительное средство. Прежде чем учиться делать светотеневую моделировку, давайте поймем какие огромные выразительные возможности дает нам ее применение.
Возьмите интересный для вас предмет. Сфотографируйте его при разном освещении:
- Прямые солнечные лучи.

- Рассеянный свет (когда не четко видны границы между светом и тенью)

- Тусклый свет, полумрак.

- Направленный свет лампы. Поэкспериментируйте с направлением света и расстоянием до натуры. Попробуйте снять против света, с источником света совсем близко к натуре и т. д.

Отберите три самые выразительные фотографии.
Упражнение 2.
Есть только два способа научиться штриховать по форме: копирование и практика. Давайте начнем с первого. Скопируйте рисунки, приведенные ниже. Ваша задача — сделать это максимально точно, вплоть до штриха.
Упражнение 3.
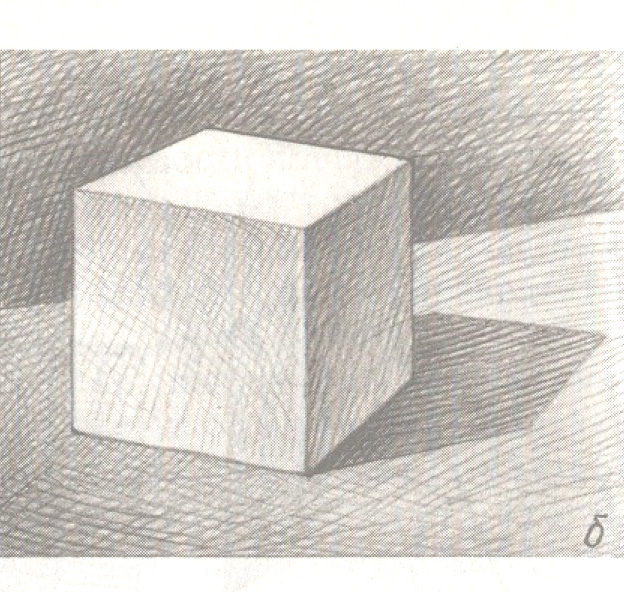
Тональный рисунок коробки с натуры.
- Ставим натуру либо с боковым дневным светом, либо с направленным светом лампы так, чтобы было ясно, какие стороны на свету, а какие — в тени.
- Компонуем изображение на листе. Определяем, какого размера оно будет и где будет расположено.

- Строим на просвет
- Убираем линии поведения и невидимые линии. Оставшиеся линии должны быть тонкими и ровными.
- Смотрим на натуру и определяем, что темнее, что светлее. Можно сделать небольшой набросок и на нем обозначить тона цифрами (от самого светлого до самого темного)
- Штриховку я советую начать с того, что закрыть тоном все тени. Расстояние между штрихами небольшое, тон не очень темный.
- Разбираем по тону тени
- Разбираем света. Обратите внимание, что чем ближе к нам, тем темнее тень и тем светлее свет. Белая бумага остается только в самой ближней части самой светлой грани.

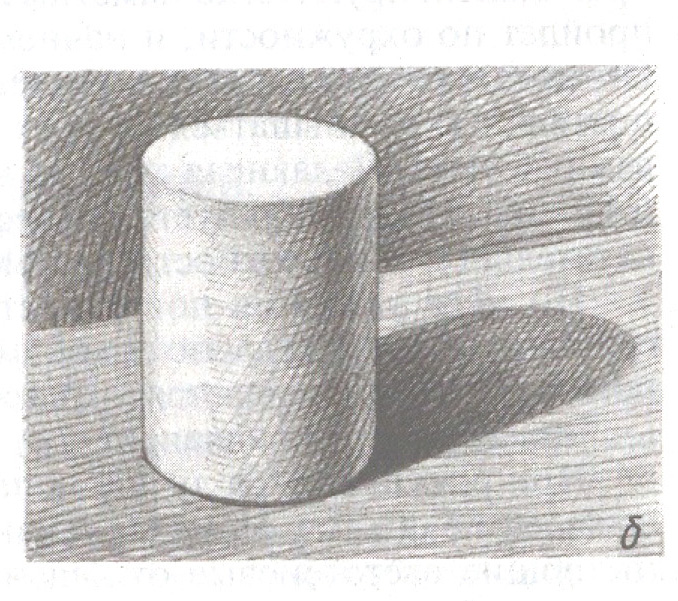
Упражнение 4.
Тональный рисунок чашки с натуры. Делаем в той же последовательности, как в предыдущем задании.
Рисунок темного и светлого предмета с натуры. Если у вас нет опыта, не изображайте ткани, стекло или металл. Помним, что тень более светлого предмета светлее тени более темного, свет более светлого предмета светлее света более темного.

Упражнение 6.
Зарисовки предметов сложной формы с натуры. Натуру ставим с контрастным освещением, чтобы граница света и тени была видна. в рисунках можно использовать линии. Строим форму, по возможности, подробно и напросвет. Определяем границу тени, штрихуем тень. СВЕТА НЕ НУЖНО ПРОРАБАТЫВАТЬ.
Дополнительное упражнение 1.
Тональный рисунок предмета сложной формы с натуры. Выполняем в той же последовательности, что и рисунок коробочки.

Дополнительное упражнение 2.
Натюрморт, черно-белая графика. У вас есть только два тона — черный и белый. Задача — передать объем и форму. Тени могут и должны сливаться, линии стараемся не использовать.

Основы построения падающих теней в перспективе.
Когда мы рисуем с натуры, мы изображаем падающие тени на глаз. Но для того чтобы изображать их более достоверно, полезно понимать, как они образуются и как их можно построить.
Для построения теней мы пользуемся проекциями. Чтобы получить проекцию точки на плоскость, нам нужно опустить перпендикуляр из этой точки на эту плоскость.
Чтобы получить проекцию прямой на плоскость, нам нужно из двух точек прямой опустить перпендикуляры на плоскость и соединить их между собой.
Грубо говоря, проекция на горизонтальную плоскость — это то место, над которым находится прямая или точка.
Чтобы построить тень точки, нам нужно через точку провести луч, а через проекцию точки — проекцию луча. На месте их пересечения и будет тень точки.

На этом видео я простыми словами объясняю логику этого построения.
Есть два типа построения теней: от естественного источника света (солнце, луна) и от искусственного (лампа, свеча и т.д. ).
Но какой бы ни был источник света, алгоритм построения не меняется: проводим луч через точку и проекцию луча через ее проекцию. На месте пересечения получаем тень точки. Строем тени основных точек объекта, соединяем и получаем тень объекта.
Построение тени от естественного источника света.
Так как естественные источники света бесконечно удалены от нас, мы условно считаем, что их лучи параллельны.
Из этого следует, что проекции лучей естественных источников света также параллельны между собой.
Возьмем самый простой случай — естественный источник света находится строго сбоку, то есть проекции его лучей параллельны картинной плоскости. Построим тени от всех его вершин и, соединив их между собой, получим тень от прямоугольника. Обратите внимание, что тени вершин, лежащих на горизонтальной плоскости, совпадают с этими вершинами.

Дополнительное упражнение 3
Постройте тень от прямоугольного параллелепипеда при естественном освещении.

Построение тени от искусственного источника света.
При построении теней от искусственного источника света, мы условно считаем, что все лучи исходят из одной точки — источника света, и, соответственно, проекции лучей — из проекции источника света.
Когда мы рисуем по представлению, чтобы построить тени от предмета при искусственном освещении, мы произвольно, в соответствии с нашим замыслом, задаём положение источника света и его проекции.
Дальше действуем по общему алгоритму: проводим луч через точку и проекцию луча через проекцию этой точки. На месте пересечения получаем тень точки.
Найдя тени основных точек предмета, соединяем их в той же последовательности, как они соединены в самом предмете и получаем тень предмета.
На рисунке разобрано построение тени от прямоугольника при искусственном освещении.

Дополнительное упражнение 3
Постройте тень от прямоугольного параллелепипеда при искусственном освещении.

