Представление о внешнем виде здания в
основном создается по чертежу фасада.
Поэтому рассмотрим примеры построения
теней от различных элементов фасада,
используя те же приемы, что и при
построении теней геометрических тел
(см. раздел 12.6).
Рассмотрим сначала примеры построения
теней некоторых частей здания.
На рис.12.25а в аксонометрии (построение
теней в аксонометрии см. главу 11.6), а на
рис.12.25б в прямоугольных проекциях
показано построение падающих теней от
козырька (или балкончика) здания. Для
построения теней в аксонометрии
использована вторичная проекция
козырька.

Рис. 12.25
Тени в нишах. Ниши это
углубление в стене. Если задняя грань
ниши параллельна фронтальной плоскости
проекций, ниши называют плоскими
Тень, падающая от фронтального обрамления
ниши, повторит его форму на задней грани.

Рис. 12.26
На рис. 12.26а в аксонометрии, а рис. 12.26б
на ортогональном чертеже дано построение
проекций собственной и падающей теней
прямоугольной ниши. Изучив чертеж, можно
установить, что строить нужно проекции
лишь падающей тени от ребер АВ и ВС. От
вертикального ребра АВ (проекции А1В1,
А2В2)тень падает на горизонтальную
плоскость П1 и на фронтальную плоскость
задней стенки ниши (рис. 12.26б). Как
известно, тень, падающая от вертикальной
прямой на горизонтальную плоскость,
совпадает с горизонтальной проекцией
светового луча, а тень, падающая от
вертикальной прямой на фронтальную
плоскость, параллельна этой прямой (см.
раздел 12.3).
От горизонтальной прямой ВС (В1С1, В2С2)
тень падает частично на заднюю фронтальную
стенку ниши в виде прямой, параллельной
ребру ВС, и частично на правую боковую
грань ниши (на чертеже не изображена),
где она параллельна профильной проекции
луча света, так как ребро ВС занимает
профильно – проецирующее положение.
На рис. 12.27а показано построение тени в
нише, перекрытой полуциркульной аркой.

Рис. 12.27
Для построения тени в нише необходимо
построить тень от прямой АВ и от дуги
окружности, проходящей через точки В и
С. Тень от дуги окружности будет окружность
того же с центром в точке От. На рис.
12.27б построения выполнены в системе
прямоугольных проекций.
На рис. 12.28а показано построение тени
аналогичное построению теней в
прямоугольной нише. Здесь тени от
отрезков АВ, ВС, СД параллельны самим
отрезкам.

Рис. 12.28
В цилиндрической нише (рис.12.28 б) падающая
тень ограничена прямой линией, делящей
нишу пополам, и четвертью окружности.
Падающие тени от выступающих частей
здания. Рассмотрим как строятся
падающие тени от нависающих карнизов
зданий.
Тень от карниза на рис. 12.29 падает
от прямых АВ, ВС и СД. Тень от прямой АВ
будет параллельна самой прямой, так как
прямая параллельна той плоскости, на
которую падает тень. Тень от прямой ВС
ложится на фронтальную плоскость
параллельно самой прямой, а тень от
прямой СД, как от прямой, перпендикулярной
фронтальной плоскости, пройдет по
направлению светового луча. Ребро
выступа Е дает тень, параллельную самому
себе на фронтальной плоскости проекций.

Рис. 12.29
На рис. 12.30а показано построение тени
от полуколонны на стене и от абака
(прямоугольной плиты) на колонну и
на стену, а также собственная тень
колонны. Полуколонна имеет форму
полуцилиндра. Построение падающей тени
от колонны и абака на стену основано на
том, что линии, от которых падает тень,
занимают частное положение. Через тень
точки С на стене проходит три линии,
поэтому строятся три тени. Тень от СД
вертикальна, тень от АС горизонтальна,
тень от прямой, проходящей через точку
С перпендикулярно к стене, параллельна
фронтальной проекции луча света. Тень
от последней прямой расположена внутри
тени от абака. Через точку Д также
проходят три линии. Тень от одной из них
(СД) построена, тень от горизонтальной
прямой, параллельной стене, не нужна,
так как она находится внутри тени от
абака, тень от прямой, перпендикулярной
стене, параллельна фронтальной проекции
световых лучей. Тень падающая от
колонны найдена по собственной тени
колонны, как показано на рисунке. Эта
тень будет вертикальна, так как вертикальна
граница собственной тени.

Рис. 12.30
Через точку А проходит три линии. Тень
от вертикальной прямой не нужна, так
как эта прямая не принадлежит границе
собственной тени абака. Тень от прямой
АС – в натуре дуга эллипса – проецируется
на плоскость П2 в дугу окружности. Тень
от АВ параллельна фронтальной проекции
светового луча.
Если абак полуцилиндр (рис. 12.30 б), то
нужно взять на нижнем основании цилиндра
некоторое количество точек и, проведя
через них лучи света, определить тени
точек на поверхности колонны. Точка С
пересечения границы собственной тени
колонны с границей тени, падающей от
абака на колонну, построена методом
обратных лучей (см. раздел 12.5) (через
точку С2т* проведен обратный луч до
пересечения с границей собственной
тени в точке С2т). Так же с помощью
обратного луча построена точка А*, в
которой граница падающей тени пересекается
с левой контурной образующей колонны;
вначале построена точка А1, затем
найдена точка А2. Через точку А2 проведена
фронтальная проекция луча света, которая
пересекается с фронтальной проекцией
образующей в точке А2*.Граница тени,
падающей от абака на стену, представляет
собой две дуги эллипсов и отрезок прямой,
касательной к ним.
Тень на лестнице. На рис. 12.31 и
12.32 дан фрагмент лестницы и входа в
здание в виде прямоугольной ниши. На
рис 12.31 показано построение в аксонометрии,
а на рис. 12.32 в прямоугольных проекциях
собственных и падающих теней элементов
крыльца. Тень на земле от вертикальной
прямой АВ параллельна горизонтальной
проекции светового луча. Строится точка
1 пересечения этой тени с вертикальной
гранью первой ступени и проводится тень
на этой грани параллельно АВ. Через
точку 2 проходит тень от прямой АВ
параллельно тени той же прямой на земле.
Проведя луч света через точку А строим
тень Ат от этой точки на горизонтальной
грани первой ступени. Тень от прямой АС
на первой ступени Ат3 параллельна самой
прямой АС.

Рис. 12.31
Тень от прямой АС на вертикальную грань
второй ступени и плоскость стены проходит
параллельно фронтальной проекции
светового луча. Построение тени от
боковой части лестницы на земле и стене
ясно из чертежа.

Рис. 12.32
Аналогичная задача в ортогональных
проекциях показана на рис. 12.32.
горизонтальная проекция тени от прямой
АВ на плоскости земли и на горизонтальной
грани первой ступени по направлению
совпадают с горизонтальной проекцией
луча света. Тень от прямой АС на
горизонтальные плоскости ступеней
параллельна горизонтальной проекции
самой прямой АС. Тень на плоскость стены
и вертикальную грань второй ступени
совпадает по направлению с фронтальной
проекцией светового луча.
Тени на крышах зданий. Скат крыши
это наклонная плоскость. Трубы, антенны,
смотровые окна и т.д. отбрасывают тень
на плоскость ската. На рис. 12.33 показано
построение тени от трубы на скат крыши
и от одного ската на другой.
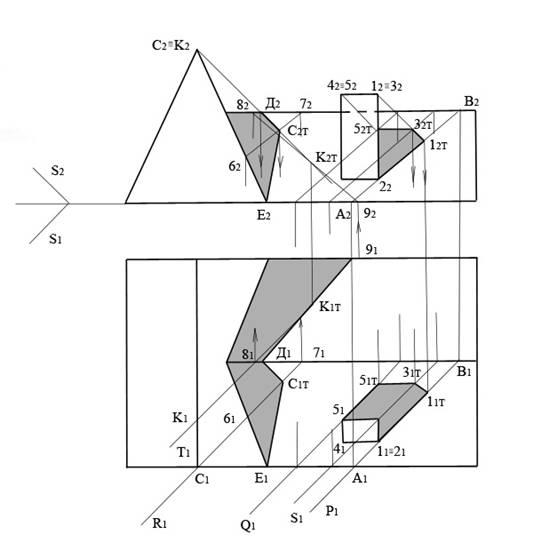
Рис. 12.33
При построении этих теней используется
метод секущих плоскостей (см. раздел
12.2). Проведем через ребро трубы 1-2
горизонтально проецирующую плоскость
Р параллельно горизонтальной проекции
светового луча и найдем линию пересечения
АВ пересечения этой плоскости со скатом
крыши. Точку 12т получим, проведя
фронтальную проекцию светового луча
до пересечения с фронтальной проекцией
прямой АВ. Тени точек 3 и 5 найдены
аналогично. При построении тени от
одного ската на другой проводим
через точку С горизонтально проецирующую
плоскость R и находим
линию пересечения 6-7 этой плоскости со
скатом крыши. На фронтальной проекции
определяем тень точки С2т и тут же
отмечаем точку Д тени на коньке. Контур
тени замыкается точкой Е, так как она
лежит на скате крыши. Тень на противоположном
скате крыши определяется по произвольной
точке К.
На рис.12.34 приведен пример построения
теней на фасаде и плане здания. Собственные
тени элементов здания на чертеже не
видимы, кроме тени на крыше, которая
будет видимой на горизонтальной
проекции. Начинают построения с
определения падающей на горизонтальную
плоскость проекций тени здания,
используя для этого характерные точки
здания: углы карниза, конек карниза.
Затем строят тени от трубы на скат крыши
и от одного ската на другой, используя
при этом метод секущих плоскостей (см.
раздел 12.2) и метод обратного луча (см.
раздел (12.5). Построение ведется в следующей
последовательности:
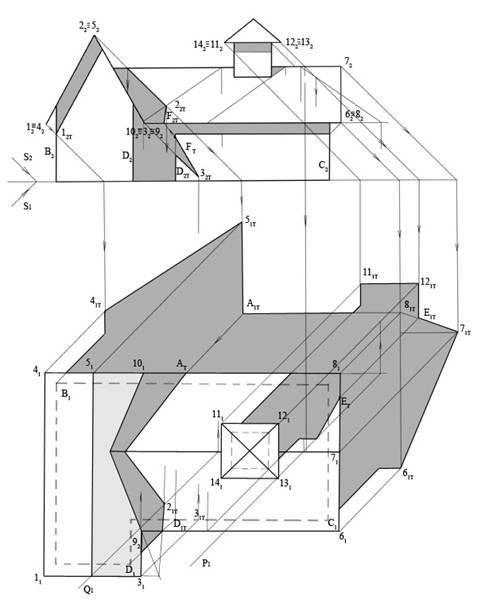
Рис. 12.34
1.
Строим тени точек 4, 5, 6, 7 и 8 на
горизонтальную плоскость проекций П1;
2.
Соединяем тени точек 4 – 5 и 6 –7
– 8;
3.
Т. к. свесы 1-4, 6-9, 8-10 и конек крыши
2-5 прямые, параллельные плоскости
проекций П1, то их тени на эту плоскость
будут параллельны самим прямым (см.
раздел 12.3);
4.
Тени от углов В и С будут совпадать
с горизонтальной проекцией световых
лучей (см. раздел 12.3);
5.
Тень от трубы на плоскость П1
строится аналогично по точкам 11 и 12;
6.
Точки пересечения теней от свеса
8 –10 и конька 5 – 2, а также от свеса трубы
12 – 13 и свеса крыши 7 – 8 методом обратного
луча (см раздел 12.5) возвращаем на скат
крыши;
7.
Тень от трубы на скат крыши и от
более высокого ската строиться методом
секущих плоскостей (см. раздел 12.2) так,
как было описано в рис. 12.33;
8.
Тень свеса 1 – 2 на передней
плоскости здания
на фронтальной проекции будет параллельна
самому свесу, т.к. 1 – 2 // П2;
9.
Тени от выступа стены и свеса
крыши 3 – 9 на стену получены:
а) от вертикального отрезка Д тень
Д2Т будет параллельна самому отрезку;
б) от горизонтальной прямой 3 – 9 тень
на плоскость
будет совпадать с направлением светового
луча и проходить через точку 32Т;
в) от свеса 2 – 3 тень будет проходить
через точку 32Т и /параллельно самому
свесу, т.к. прямая 2 – 3 //П2;
г) точку пересечения теней FТ
методом обратного луча
возвращаем на свес 6 -9 и соединяем
точкой 22Т.
10.Тень от свеса 6 – 9 на плоскость стены
будет проходить
параллельно самому свесу.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #

Лекция 24 Построение теней в интерьере • • Положение источника света Построение теней геометрических тел Метод обратного луча Метод лучевых сечений

Построение теней в интерьере представляет собой довольно сложную задачу. Это объясняется, во-первых, наличием различных источников освещения- солнечного, рассеянного и искусственного света и, во-вторых, в условиях освещения искусственными источниками света большое их число, разнообразие форм и расположения в современном интерьере делают задачу точного построения контуров теней довольно сложной.

Три случая построения контуров теней В зависимости от вида источников освещения интерьера возможны три случая построения контуров теней: • При солнечном освещении, проникающем через оконные проемы; • При точечных источниках света ; • При рассеянном (диффузном) дневном освещении

Построение теней при солнечном освещении Задача 4. 2 стр. 34: Построить солнечное пятно от контура оконного проема прямоугольной формы (толщина стен задана и учитывается при построении) Солнце находится перед зрителем
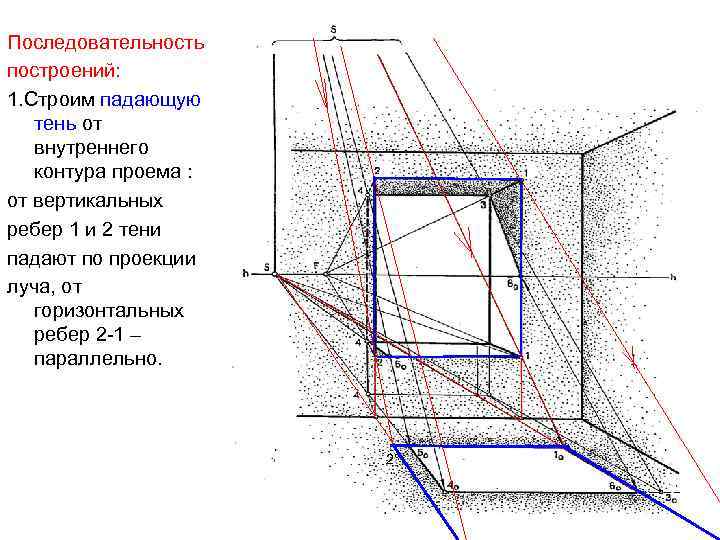
Последовательность построений: 1. Строим падающую тень от внутреннего контура проема : от вертикальных ребер 1 и 2 тени падают по проекции луча, от горизонтальных ребер 2 -1 – параллельно. 2°
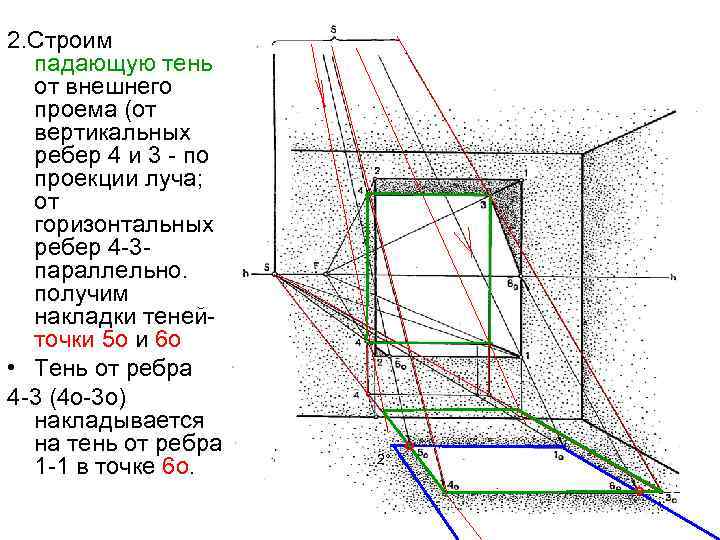
2. Строим падающую тень от внешнего проема (от вертикальных ребер 4 и 3 – по проекции луча; от горизонтальных ребер 4 -3 параллельно. получим накладки тенейточки 5 о и 6 о • Тень от ребра 4 -3 (4 о-3 о) накладывается на тень от ребра 1 -1 в точке 6 о. 2° ° °
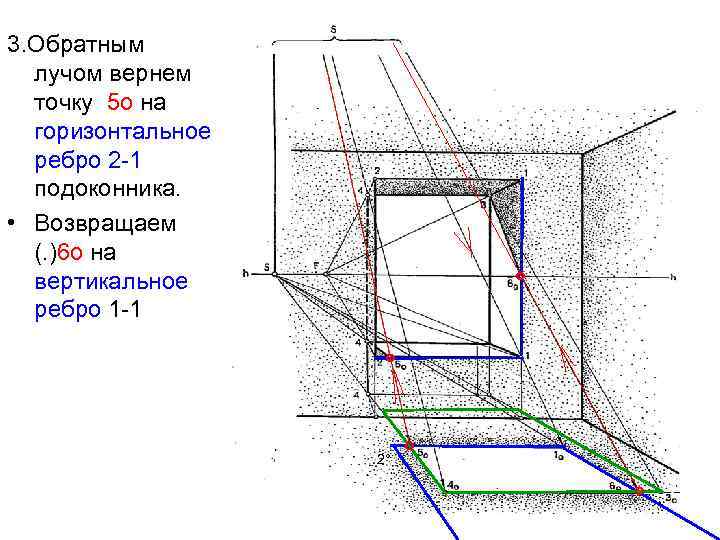
3. Обратным лучом вернем точку 5 о на горизонтальное ребро 2 -1 подоконника. • Возвращаем (. )6 о на вертикальное ребро 1 -1 ° ° 2° ° °

4. Ребро 4 -3 упирается в правый боковой простенок в точке 3 – тень замыкается. Тень на подоконник от ребра 4 -4 падает по направлению вторичной проекции луча. ° ° 2° Солнечный «зайчик» ° °

Построение теней при солнечном освещении • Солнечный свет, проникающий через оконный проем прямоугольной формы образует на полу четкий и контрастный четырехугольник.

Построение теней при точечном источнике света • При точечном источнике света лучевые прямые не параллельны между собой и и не имеют точек схода, они пересекаются в «светящейся» точкеисточнике света • Падающие тени строят при помощи вторичной проекции светового луча
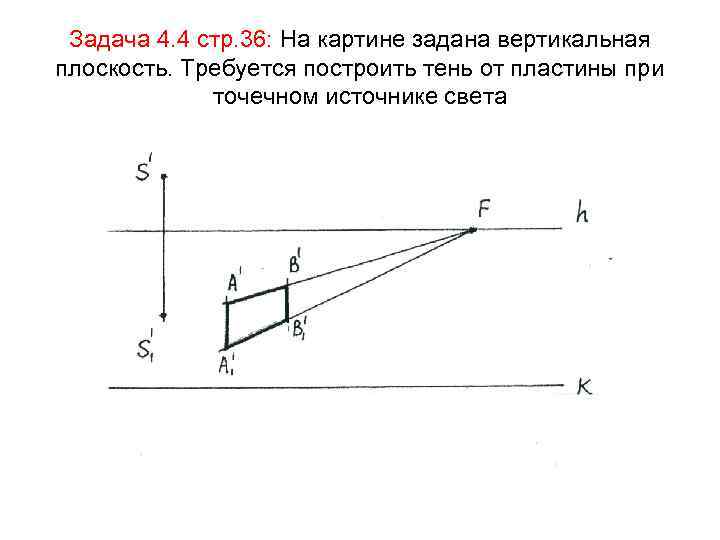
Задача 4. 4 стр. 36: На картине задана вертикальная плоскость. Требуется построить тень от пластины при точечном источнике света
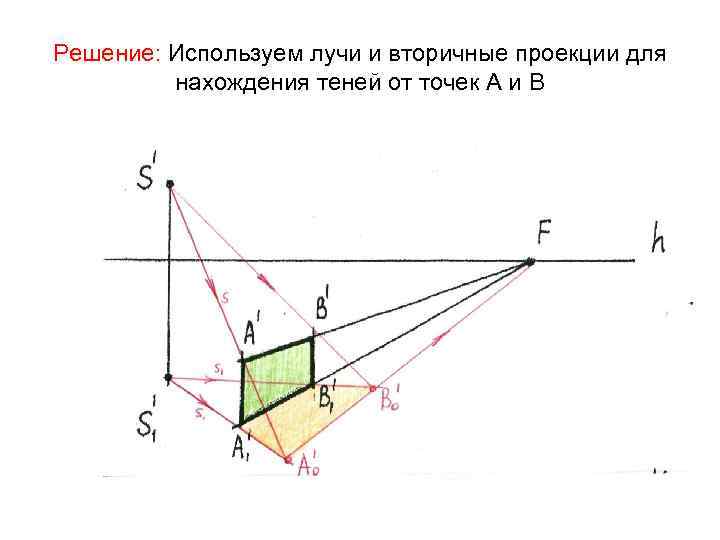
Решение: Используем лучи и вторичные проекции для нахождения теней от точек А и В
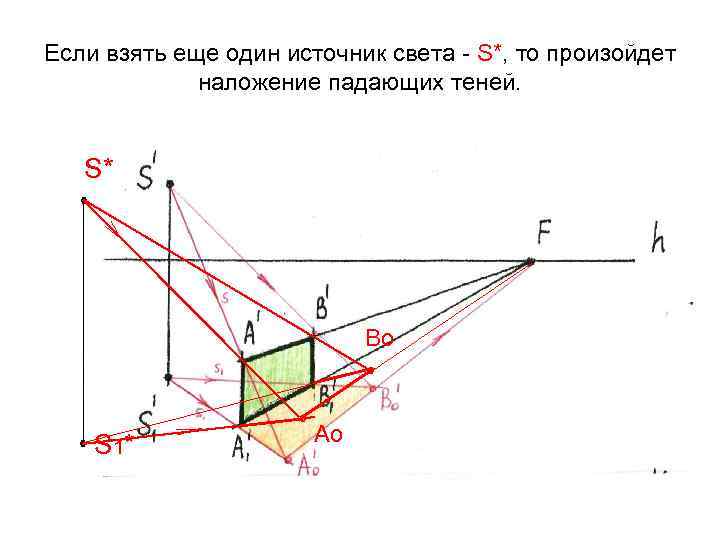
Если взять еще один источник света – S*, то произойдет наложение падающих теней. S* ° Во ° ° S 1* ° Ао
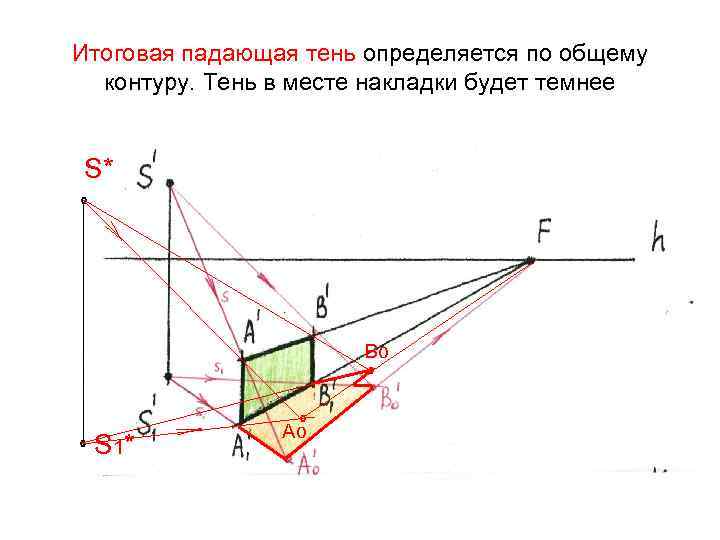
Итоговая падающая тень определяется по общему контуру. Тень в месте накладки будет темнее S* ° Во ° ° S 1* ° Ао
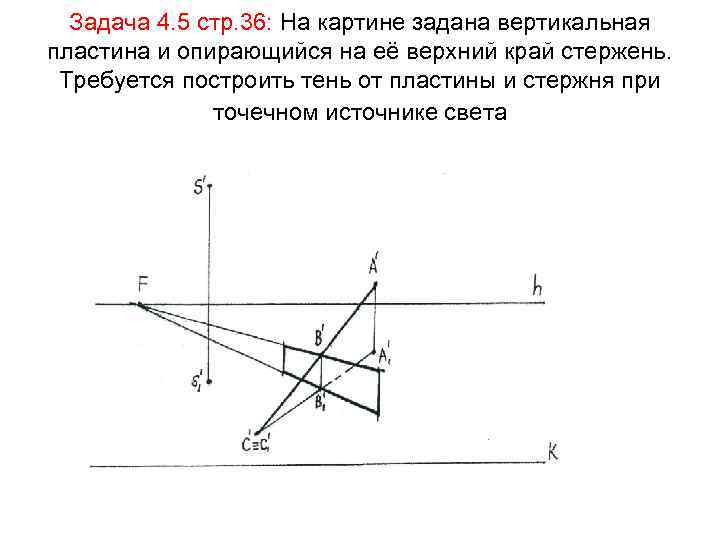
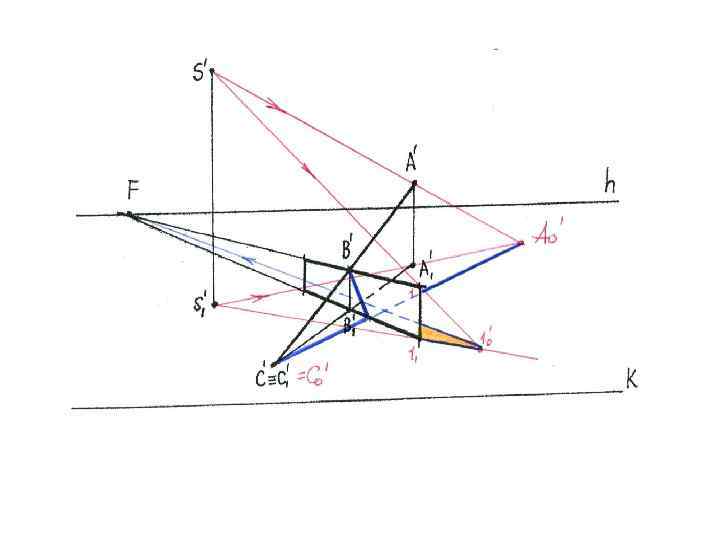
Задача 4. 5 стр. 36: На картине задана вертикальная пластина и опирающийся на её верхний край стержень. Требуется построить тень от пластины и стержня при точечном источнике света
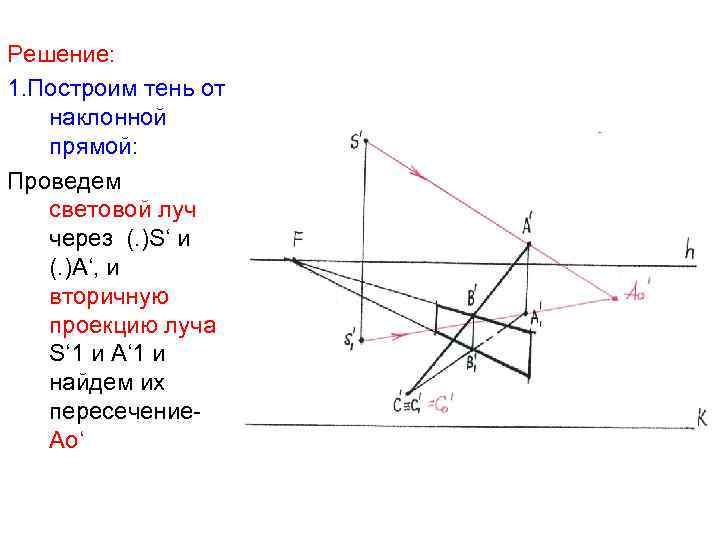
Решение: 1. Построим тень от наклонной прямой: Проведем световой луч через (. )S‘ и (. )А‘, и вторичную проекцию луча S‘ 1 и А‘ 1 и найдем их пересечение. Ао‘
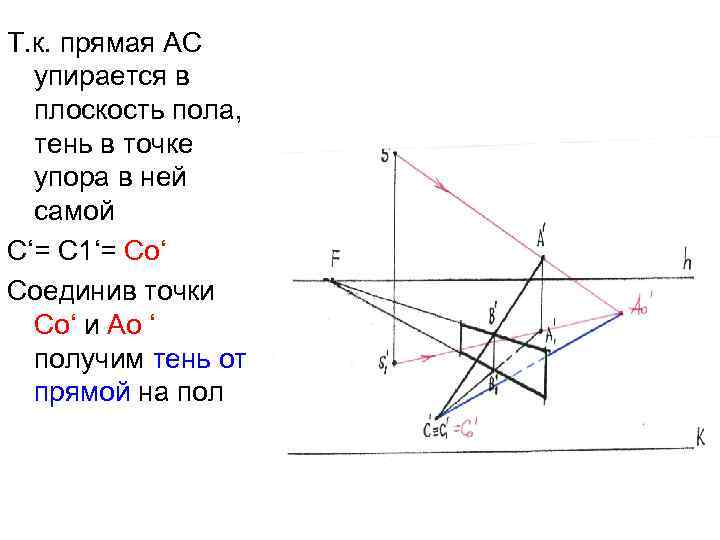
Т. к. прямая АС упирается в плоскость пола, тень в точке упора в ней самой С‘= С 1‘= Со‘ Соединив точки Со‘ и Ао ‘ получим тень от прямой на пол
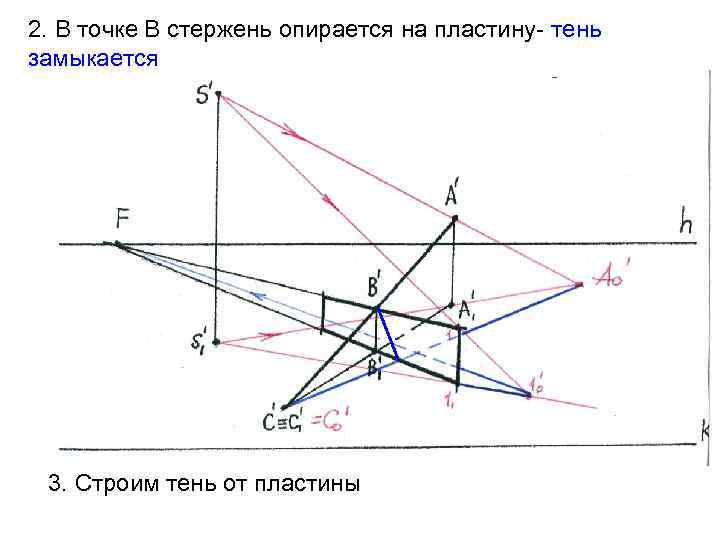
2. В точке В стержень опирается на пластину- тень замыкается 3. Строим тень от пластины
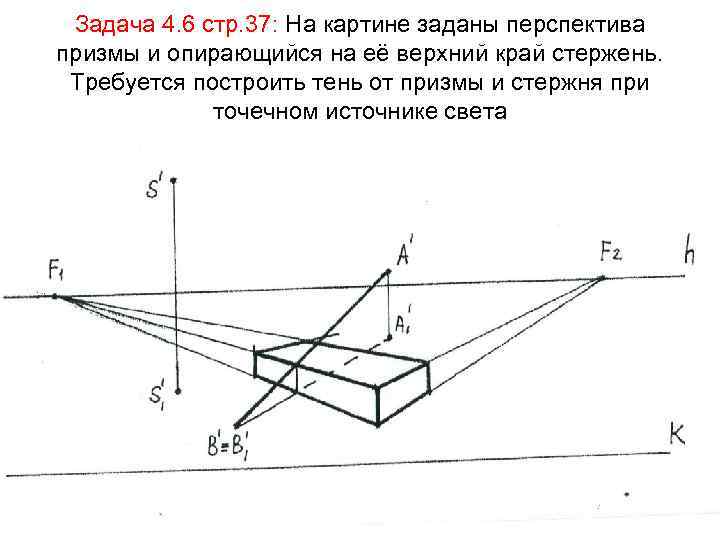
Задача 4. 6 стр. 37: На картине заданы перспектива призмы и опирающийся на её верхний край стержень. Требуется построить тень от призмы и стержня при точечном источнике света
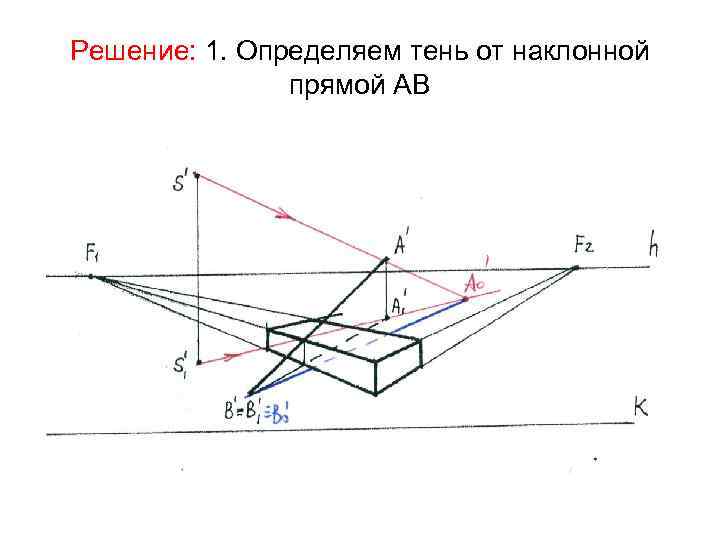
Решение: 1. Определяем тень от наклонной прямой АВ
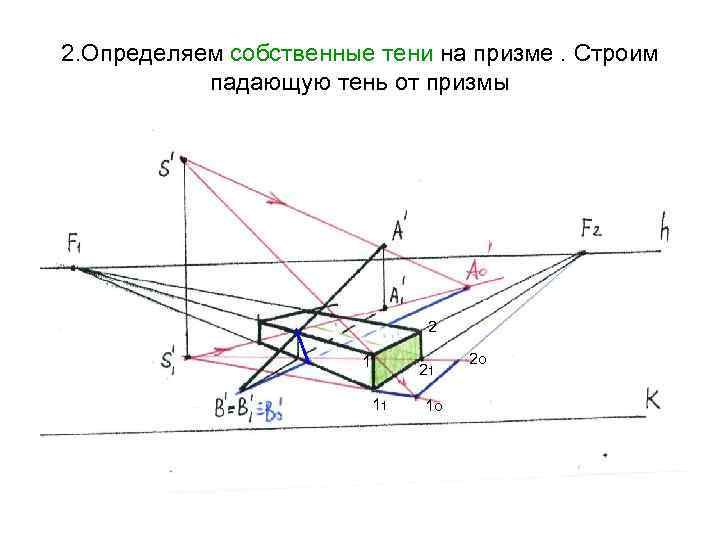
2. Определяем собственные тени на призме. Строим падающую тень от призмы 2 1 21 11 1 о 2 о
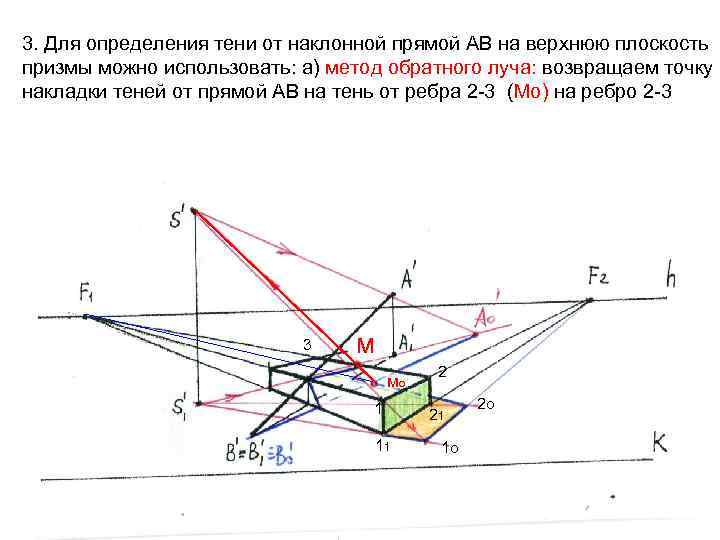
3. Для определения тени от наклонной прямой АВ на верхнюю плоскость призмы можно использовать: а) метод обратного луча: возвращаем точку накладки теней от прямой АВ на тень от ребра 2 -3 (Мо) на ребро 2 -3 3 м мо 1 11 2 21 1 о 2 о
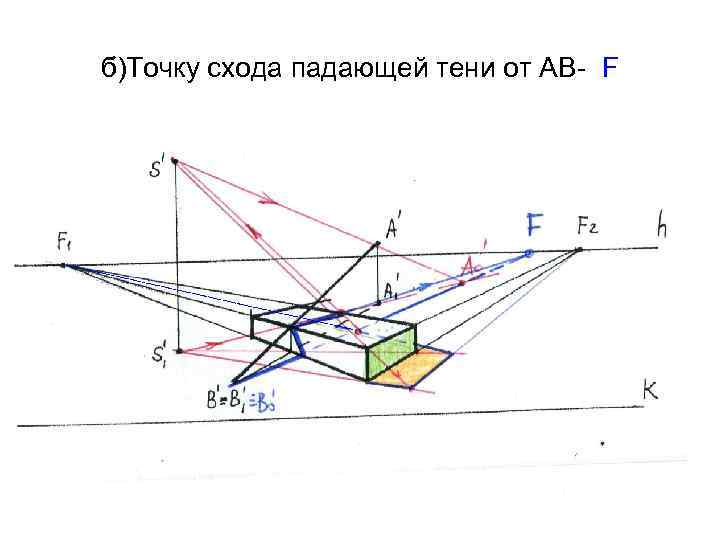
б)Точку схода падающей тени от АВ- F
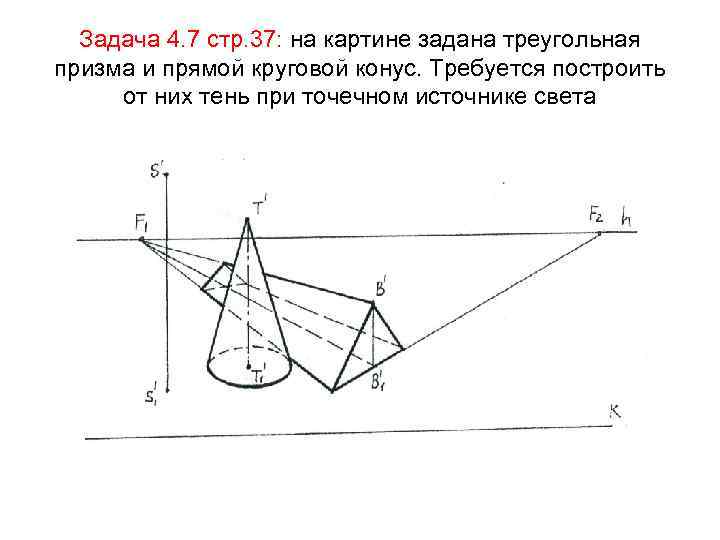
Задача 4. 7 стр. 37: на картине задана треугольная призма и прямой круговой конус. Требуется построить от них тень при точечном источнике света
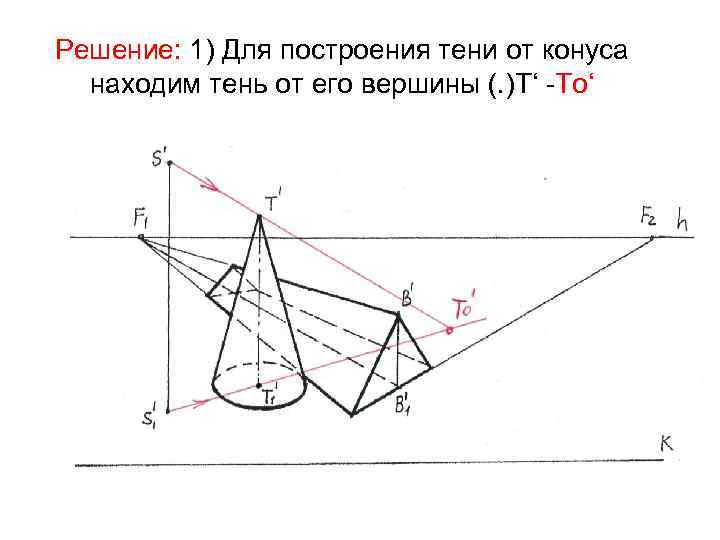
Решение: 1) Для построения тени от конуса находим тень от его вершины (. )T‘ -То‘
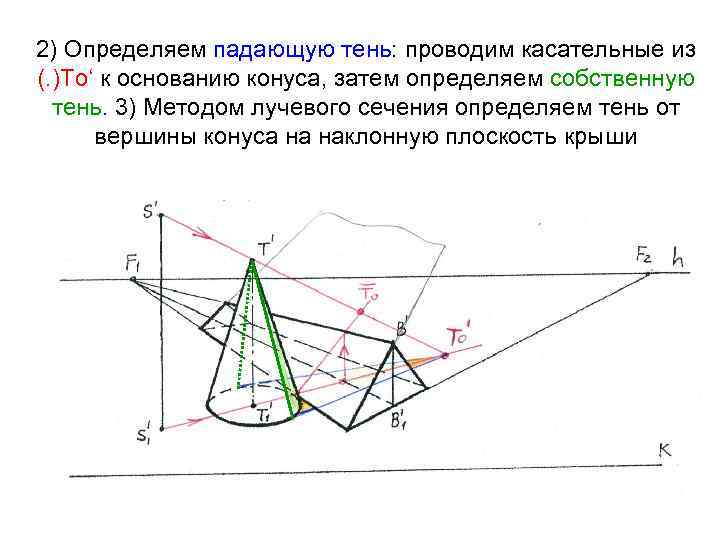
2) Определяем падающую тень: проводим касательные из (. )То‘ к основанию конуса, затем определяем собственную тень. 3) Методом лучевого сечения определяем тень от вершины конуса на наклонную плоскость крыши
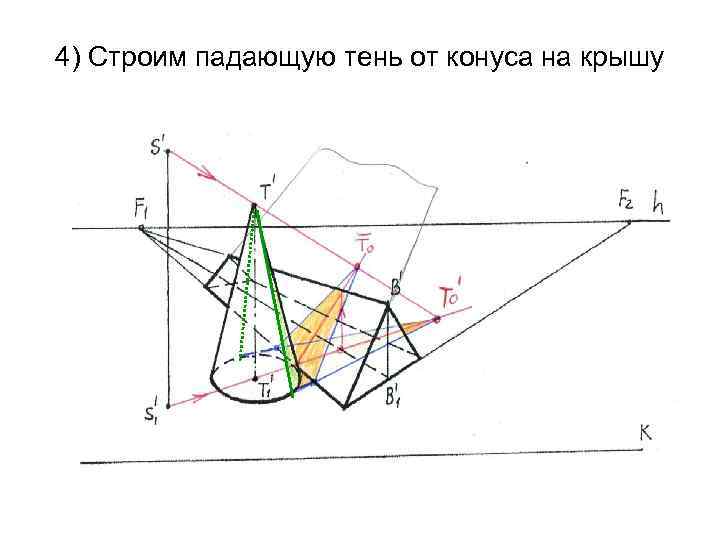
4) Строим падающую тень от конуса на крышу
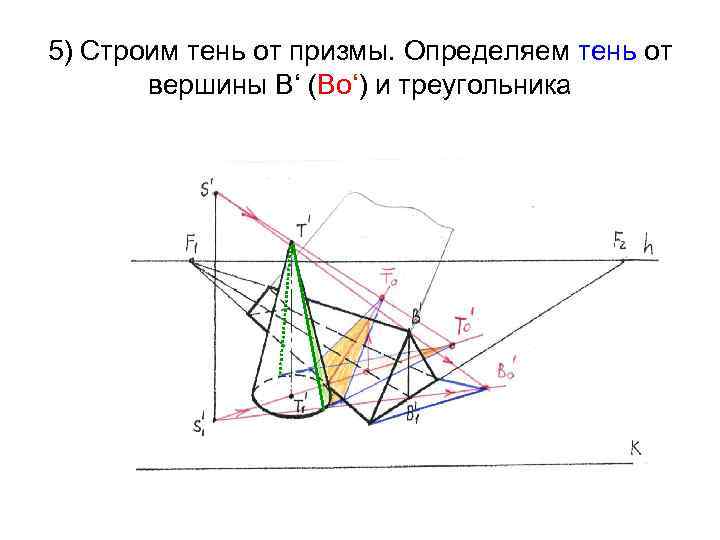
5) Строим тень от призмы. Определяем тень от вершины В‘ (Во‘) и треугольника
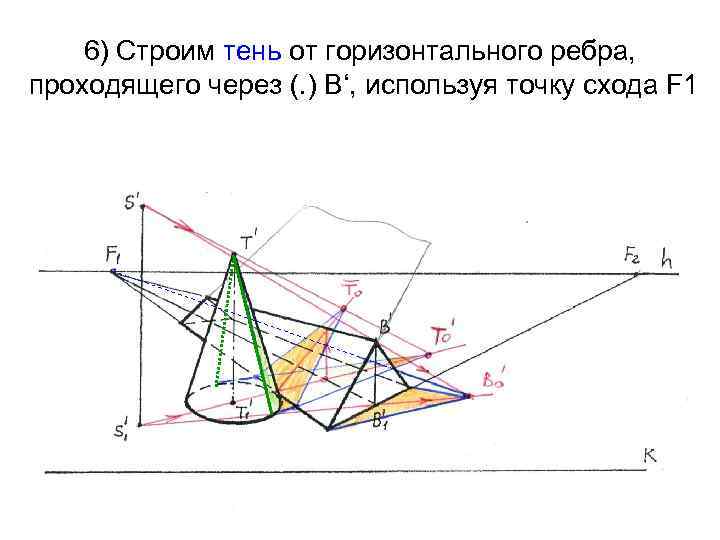
6) Строим тень от горизонтального ребра, проходящего через (. ) В‘, используя точку схода F 1
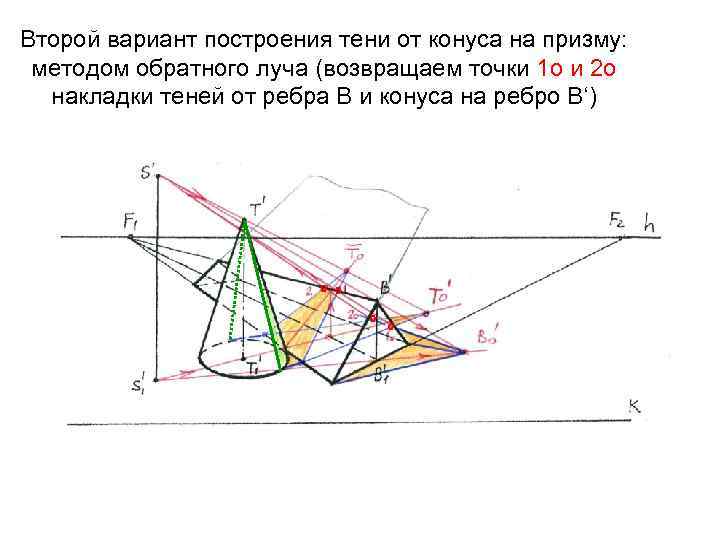
Второй вариант построения тени от конуса на призму: методом обратного луча (возвращаем точки 1 о и 2 о накладки теней от ребра В и конуса на ребро В‘) °° ° °

• При построении теней в перспективе интерьера следует построить сначала проекции источника света на те ограждающие плоскости интерьера, на которые надо будет строить тени : пол, потолок, стены
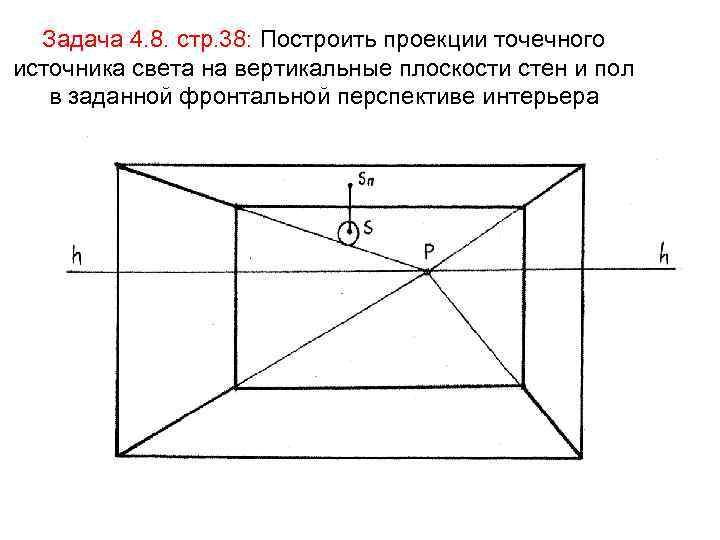
Задача 4. 8. стр. 38: Построить проекции точечного источника света на вертикальные плоскости стен и пол в заданной фронтальной перспективе интерьера
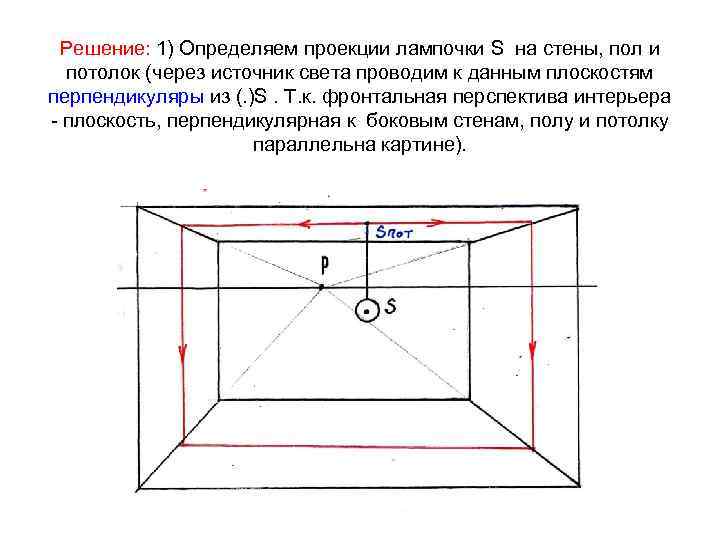
Решение: 1) Определяем проекции лампочки S на стены, пол и потолок (через источник света проводим к данным плоскостям перпендикуляры из (. )S. Т. к. фронтальная перспектива интерьера – плоскость, перпендикулярная к боковым стенам, полу и потолку параллельна картине).
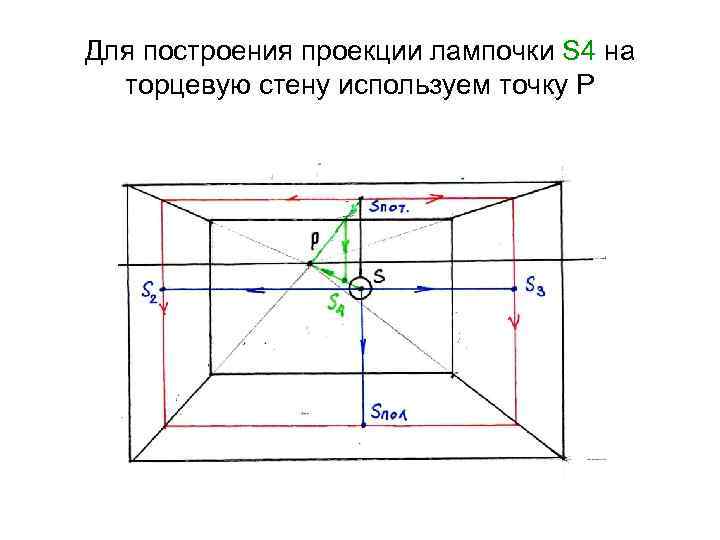
Для построения проекции лампочки S 4 на торцевую стену используем точку Р
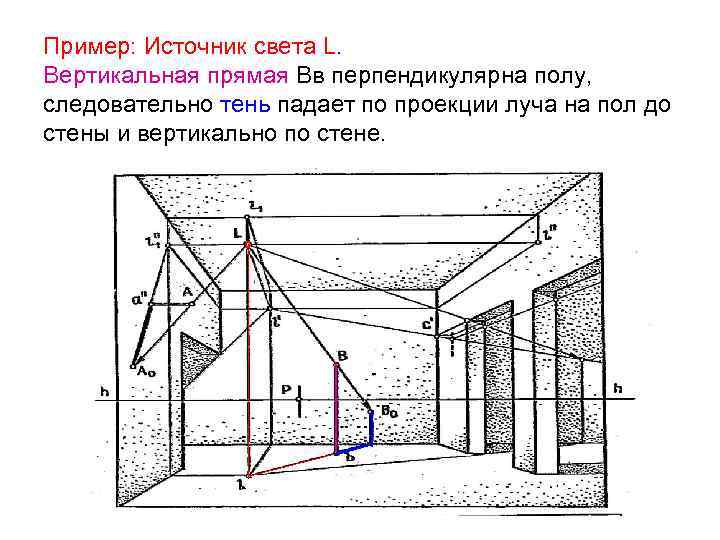
Пример: Источник света L. Вертикальная прямая Вв перпендикулярна полу, следовательно тень падает по проекции луча на пол до стены и вертикально по стене. °
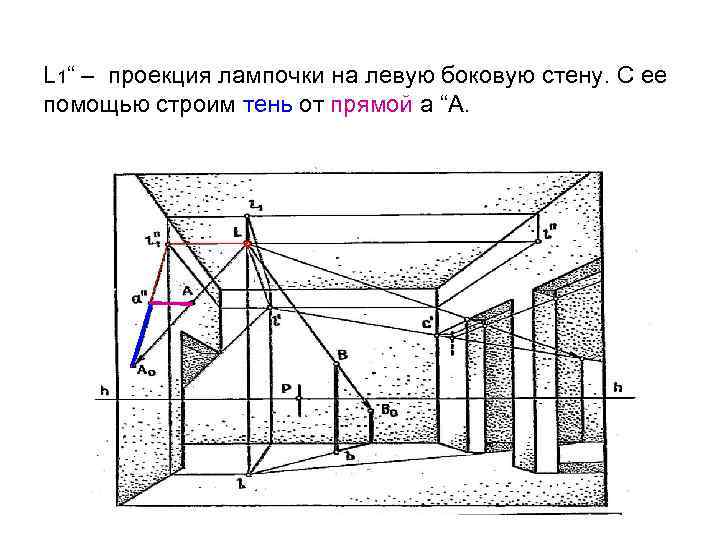
L 1“ – проекция лампочки на левую боковую стену. С ее помощью строим тень от прямой а “А. °
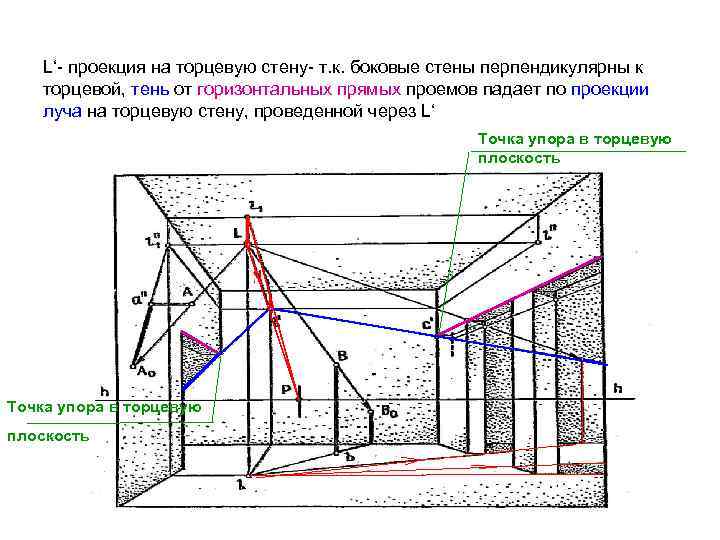
L‘- проекция на торцевую стену- т. к. боковые стены перпендикулярны к торцевой, тень от горизонтальных прямых проемов падает по проекции луча на торцевую стену, проведенной через L‘ Точка упора в торцевую плоскость ° ° Точка упора в торцевую плоскость
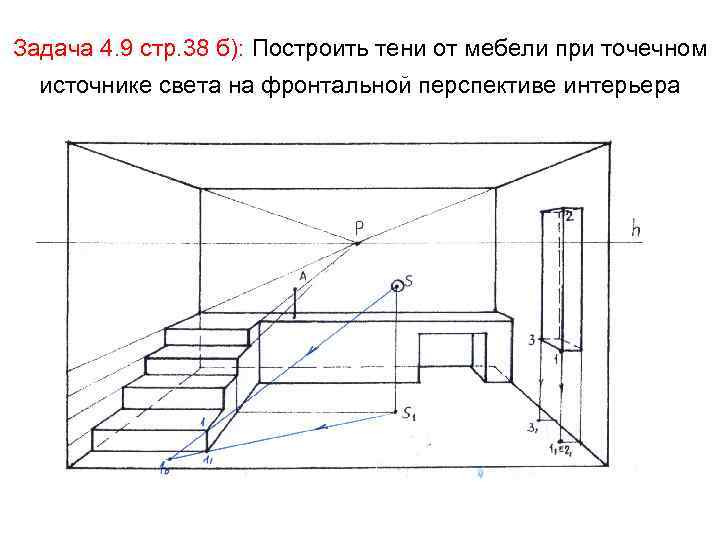
Задача 4. 9 стр. 38 б): Построить тени от мебели при точечном источнике света на фронтальной перспективе интерьера
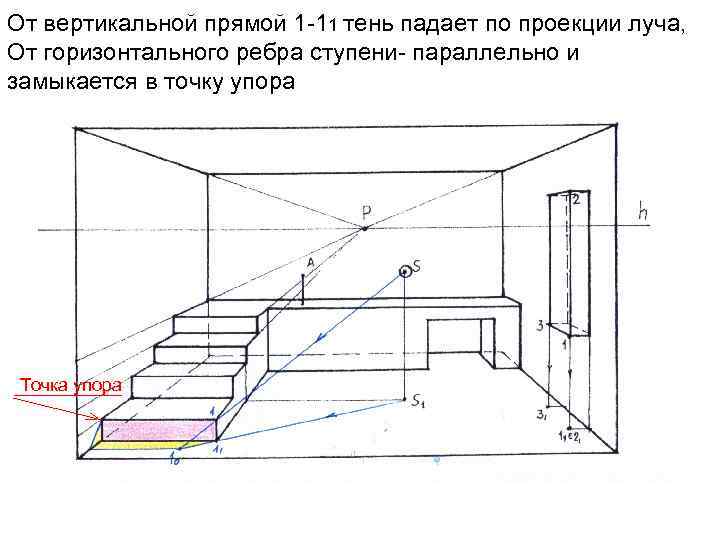
От вертикальной прямой 1 -11 тень падает по проекции луча, От горизонтального ребра ступени- параллельно и замыкается в точку упора Точка упора
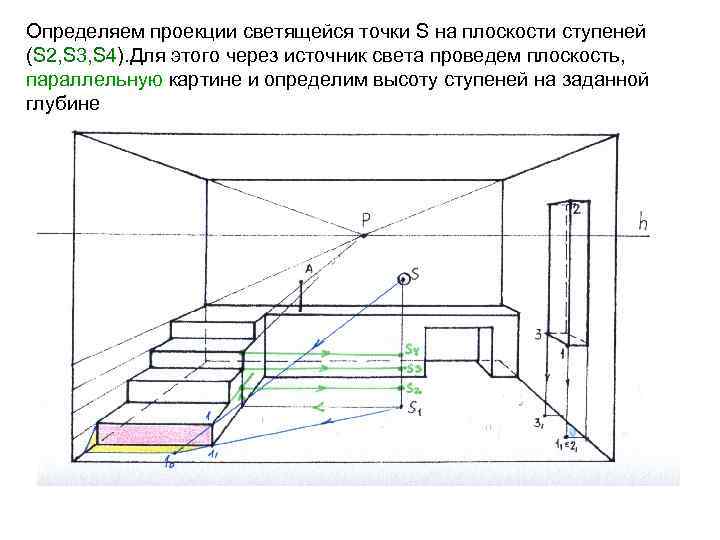
Определяем проекции светящейся точки S на плоскости ступеней (S 2, S 3, S 4). Для этого через источник света проведем плоскость, параллельную картине и определим высоту ступеней на заданной глубине
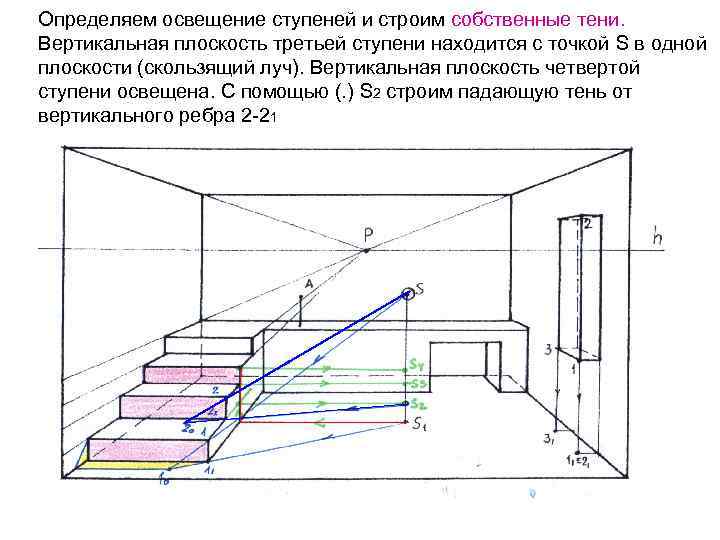
Определяем освещение ступеней и строим собственные тени. Вертикальная плоскость третьей ступени находится с точкой S в одной плоскости (скользящий луч). Вертикальная плоскость четвертой ступени освещена. С помощью (. ) S 2 строим падающую тень от вертикального ребра 2 -21
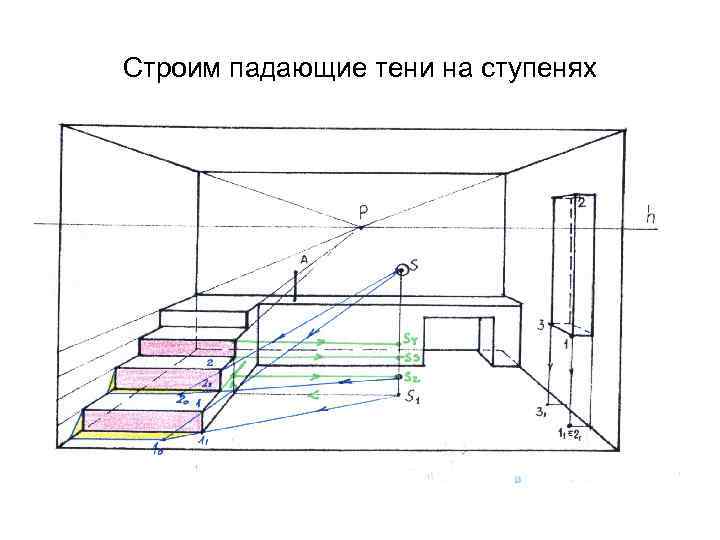
Строим падающие тени на ступенях
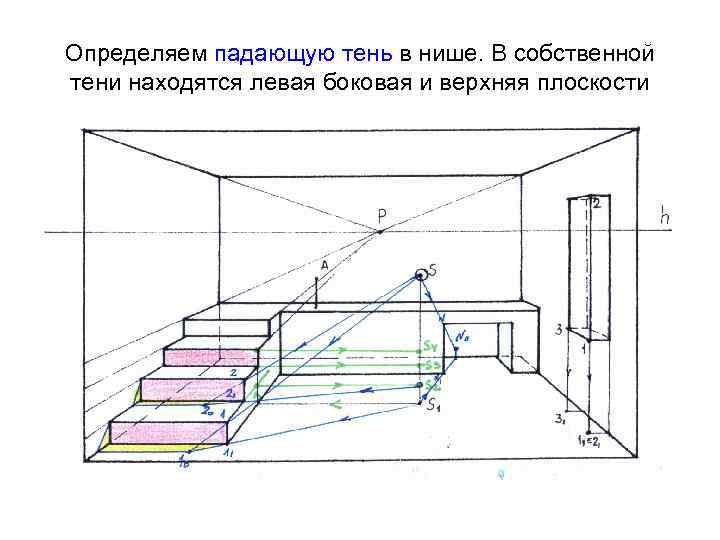
Определяем падающую тень в нише. В собственной тени находятся левая боковая и верхняя плоскости
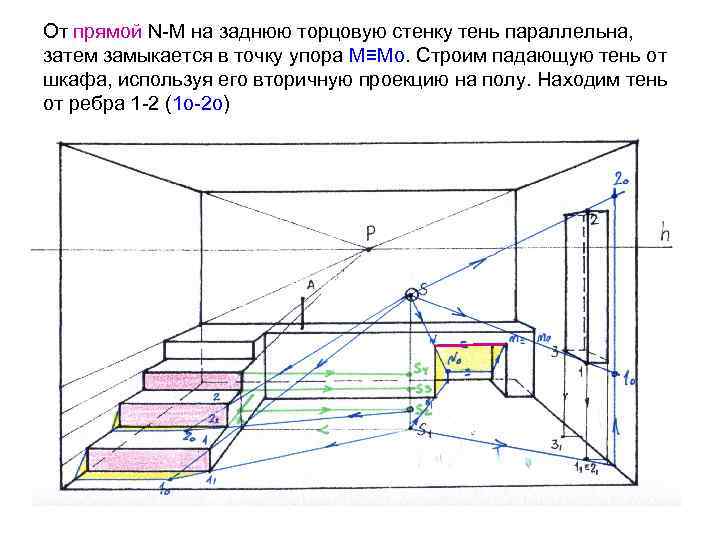
От прямой N-M на заднюю торцовую стенку тень параллельна, затем замыкается в точку упора М≡Мо. Строим падающую тень от шкафа, используя его вторичную проекцию на полу. Находим тень от ребра 1 -2 (1 о-2 о) •
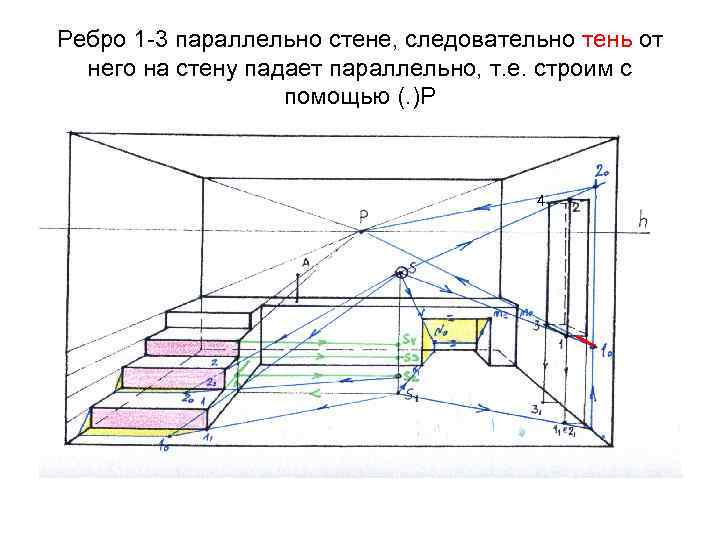
Ребро 1 -3 параллельно стене, следовательно тень от него на стену падает параллельно, т. е. строим с помощью (. )Р 4
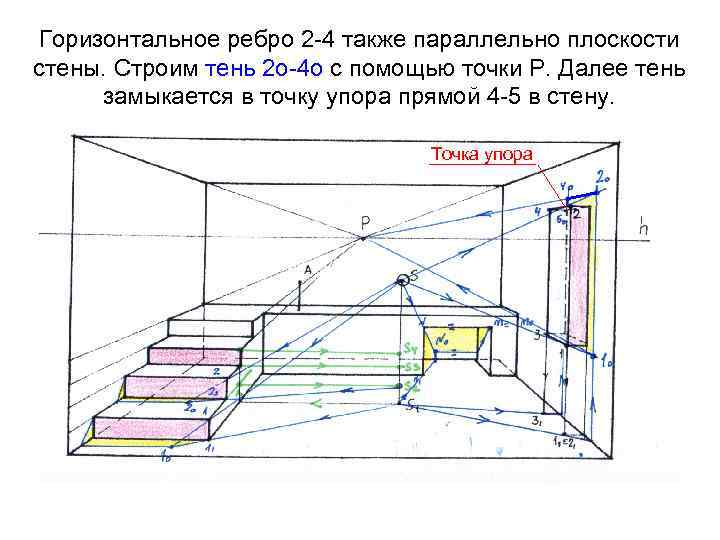
Горизонтальное ребро 2 -4 также параллельно плоскости стены. Строим тень 2 о-4 о с помощью точки Р. Далее тень замыкается в точку упора прямой 4 -5 в стену. Точка упора
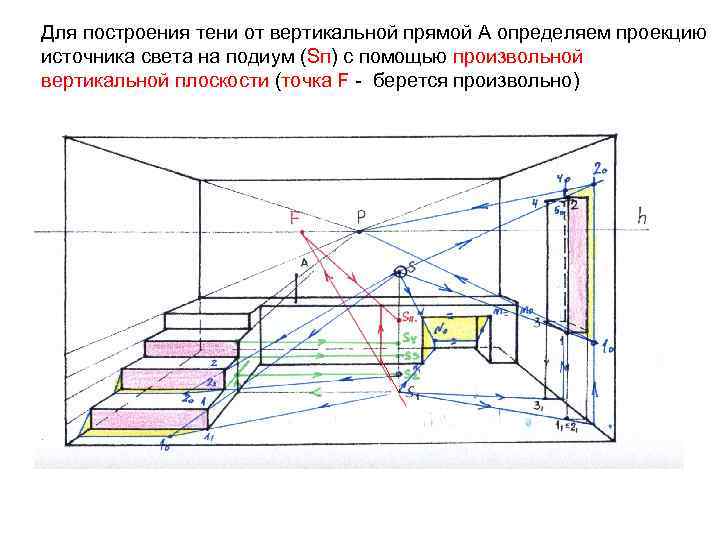
Для построения тени от вертикальной прямой А определяем проекцию источника света на подиум (Sп) с помощью произвольной вертикальной плоскости (точка F – берется произвольно)
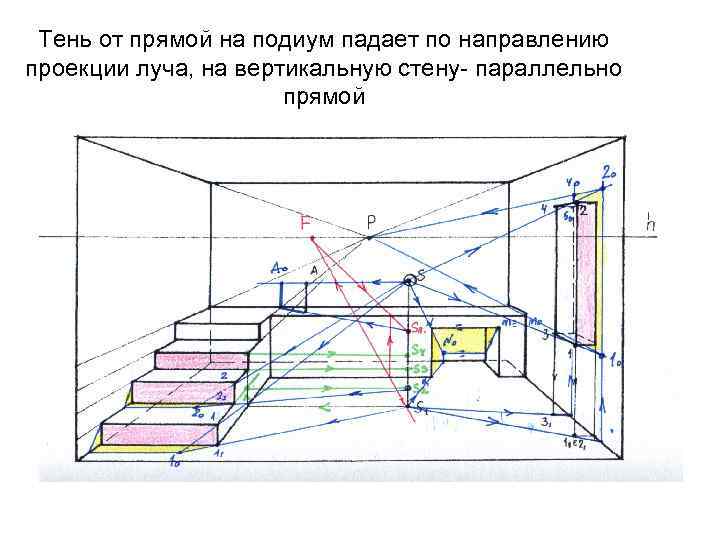
Тень от прямой на подиум падает по направлению проекции луча, на вертикальную стену- параллельно прямой
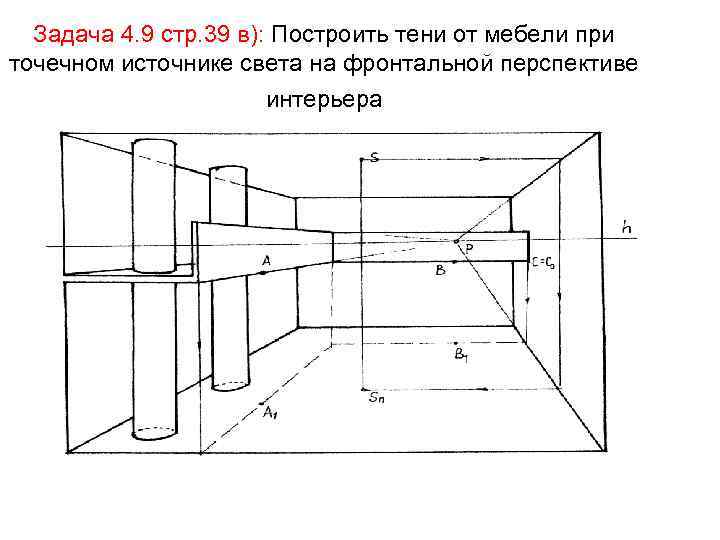
Задача 4. 9 стр. 39 в): Построить тени от мебели при точечном источнике света на фронтальной перспективе интерьера
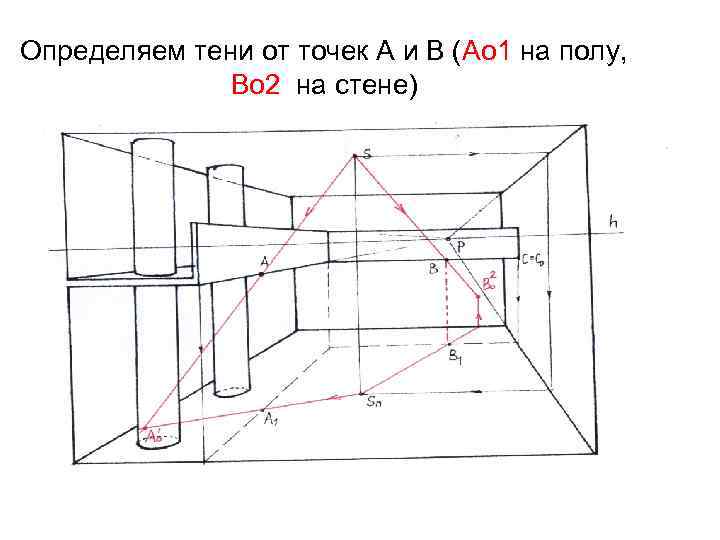
Определяем тени от точек А и В (Ао 1 на полу, Во 2 на стене)
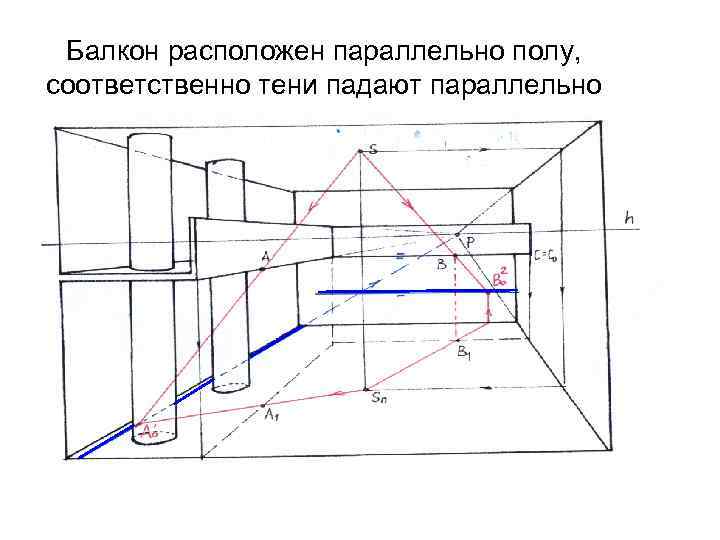
Балкон расположен параллельно полу, соответственно тени падают параллельно
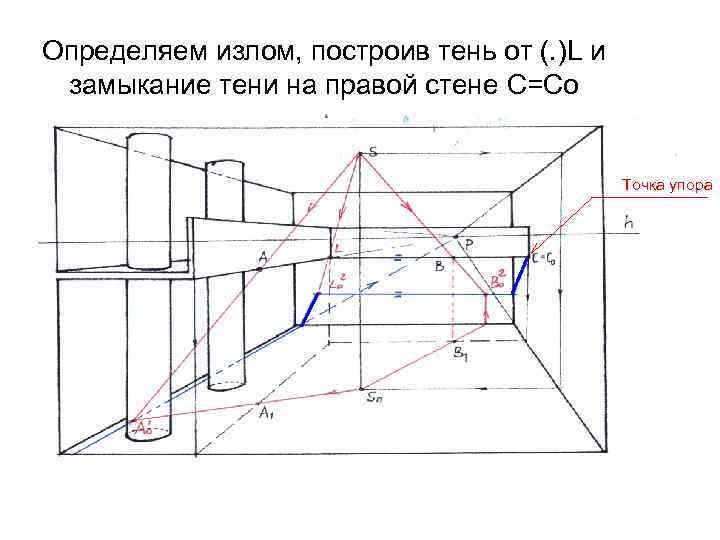
Определяем излом, построив тень от (. )L и замыкание тени на правой стене С=Со Точка упора
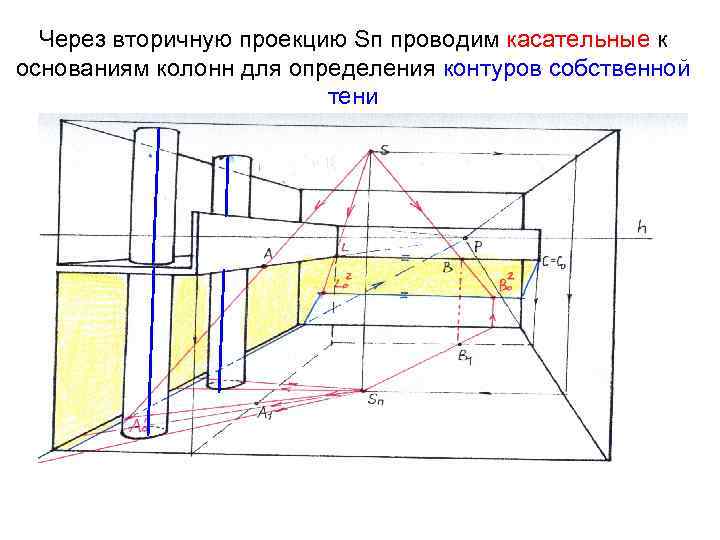
Через вторичную проекцию Sп проводим касательные к основаниям колонн для определения контуров собственной тени
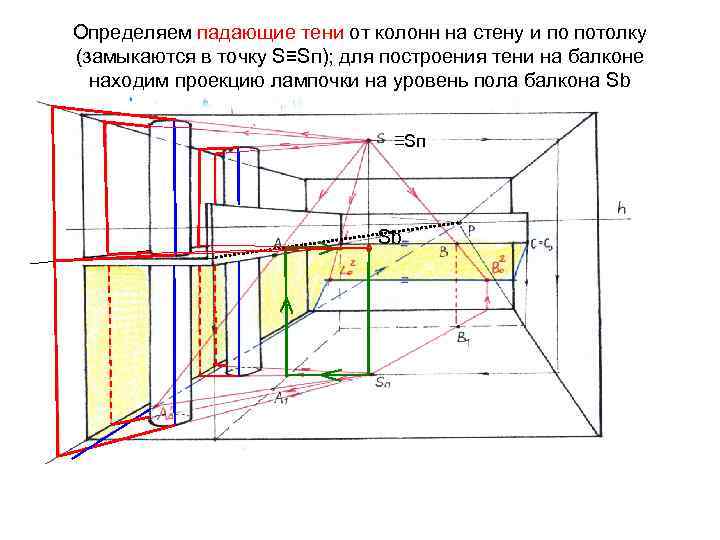
Определяем падающие тени от колонн на стену и по потолку (замыкаются в точку S≡Sп); для построения тени на балконе находим проекцию лампочки на уровень пола балкона Sb ≡Sп ° Sb
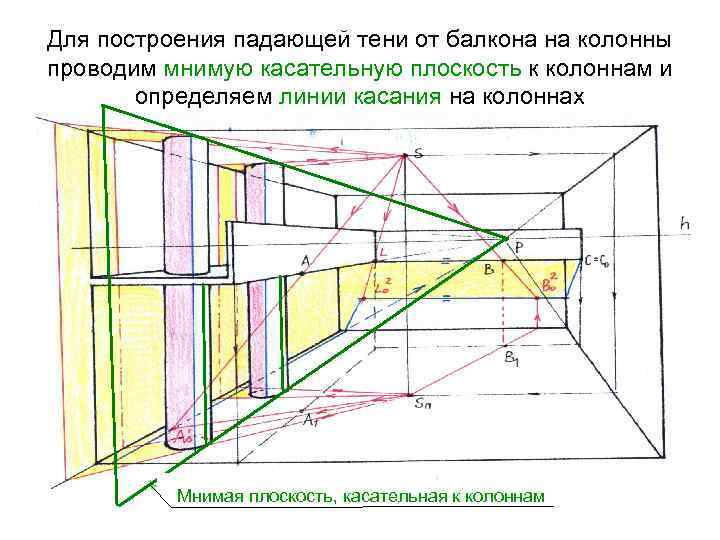
Для построения падающей тени от балкона на колонны проводим мнимую касательную плоскость к колоннам и определяем линии касания на колоннах Мнимая плоскость, касательная к колоннам
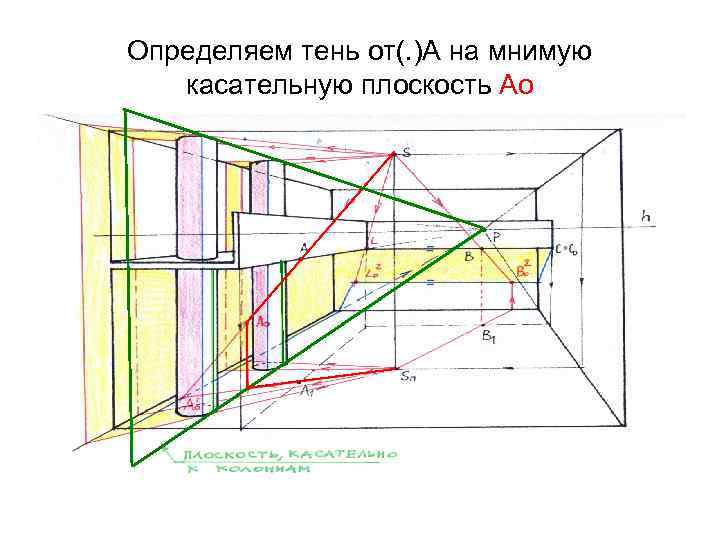
Определяем тень от(. )А на мнимую касательную плоскость Ао
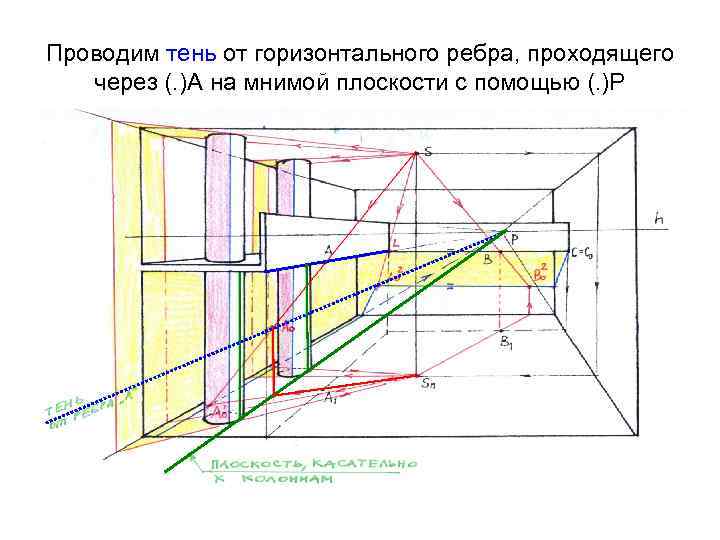
Проводим тень от горизонтального ребра, проходящего через (. )А на мнимой плоскости с помощью (. )Р
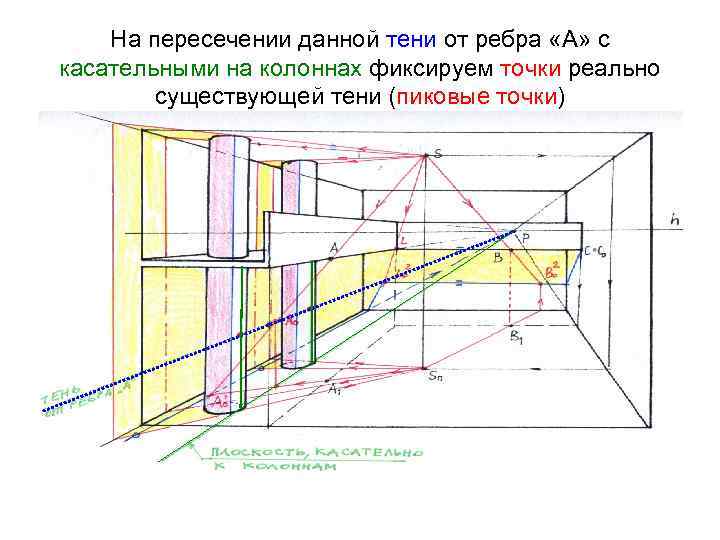
На пересечении данной тени от ребра «А» с касательными на колоннах фиксируем точки реально существующей тени (пиковые точки)
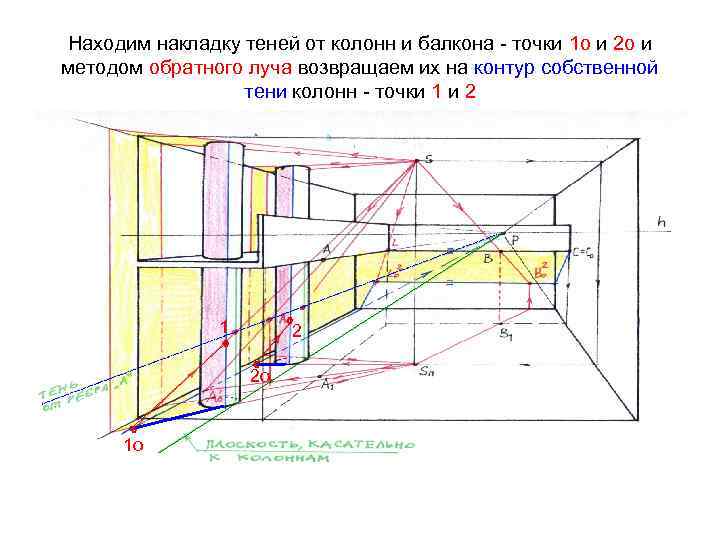
Находим накладку теней от колонн и балкона – точки 1 о и 2 о и методом обратного луча возвращаем их на контур собственной тени колонн – точки 1 и 2 ° 2 1 ° ° 1 о ° 2 о
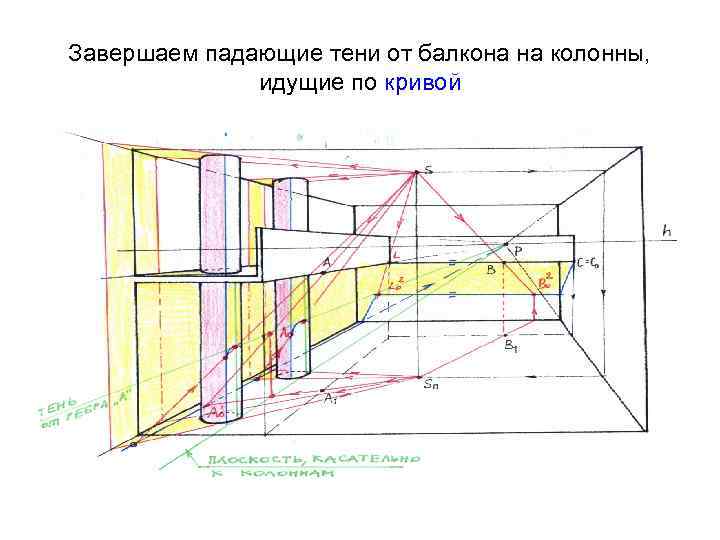
Завершаем падающие тени от балкона на колонны, идущие по кривой
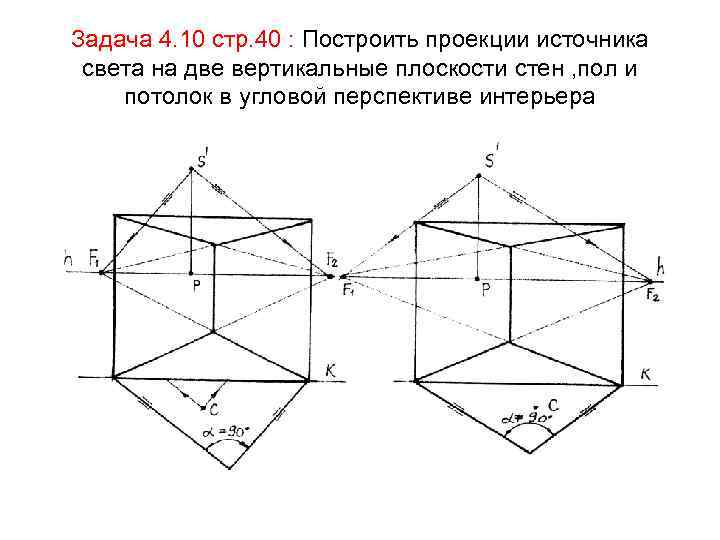
Задача 4. 10 стр. 40 : Построить проекции источника света на две вертикальные плоскости стен , пол и потолок в угловой перспективе интерьера
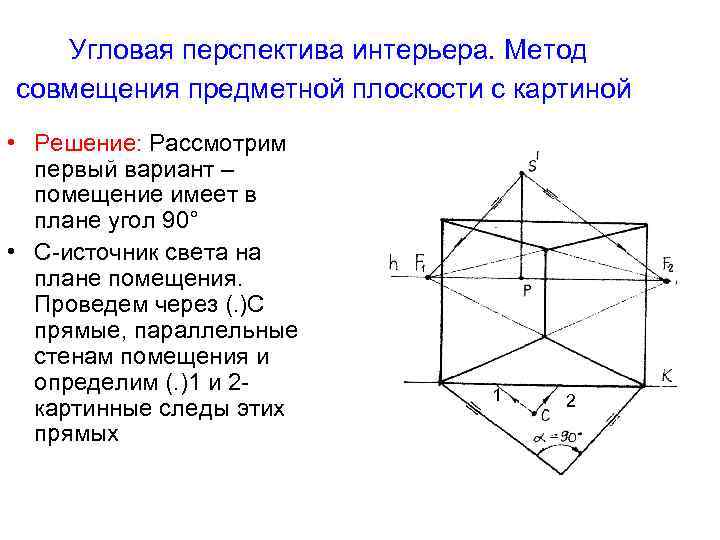
Угловая перспектива интерьера. Метод совмещения предметной плоскости с картиной • Решение: Рассмотрим первый вариант – помещение имеет в плане угол 90° • С-источник света на плане помещения. Проведем через (. )С прямые, параллельные стенам помещения и определим (. )1 и 2 картинные следы этих прямых 1 2
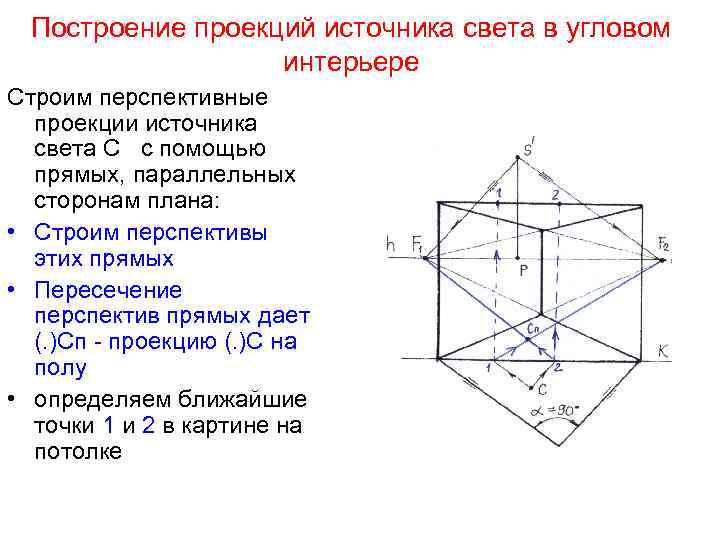
Построение проекций источника света в угловом интерьере Строим перспективные проекции источника света С с помощью прямых, параллельных сторонам плана: • Строим перспективы этих прямых • Пересечение перспектив прямых дает (. )Сп – проекцию (. )С на полу • определяем ближайшие точки 1 и 2 в картине на потолке
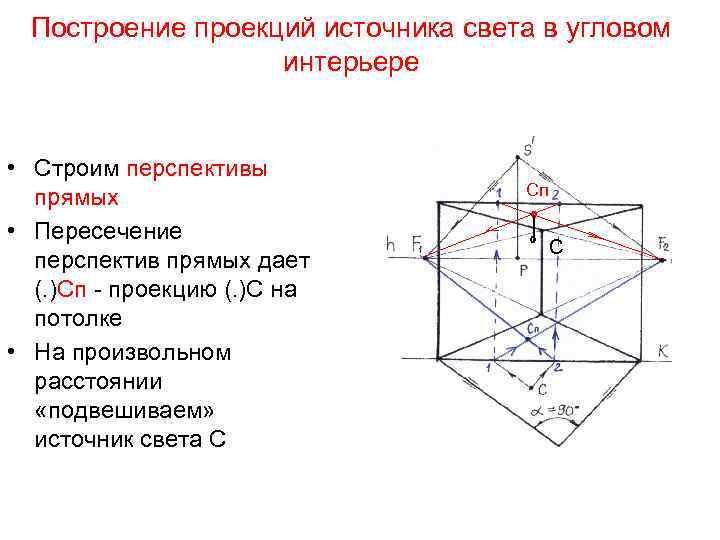
Построение проекций источника света в угловом интерьере • Строим перспективы прямых • Пересечение перспектив прямых дает (. )Сп – проекцию (. )С на потолке • На произвольном расстоянии «подвешиваем» источник света С Сп ° ° С
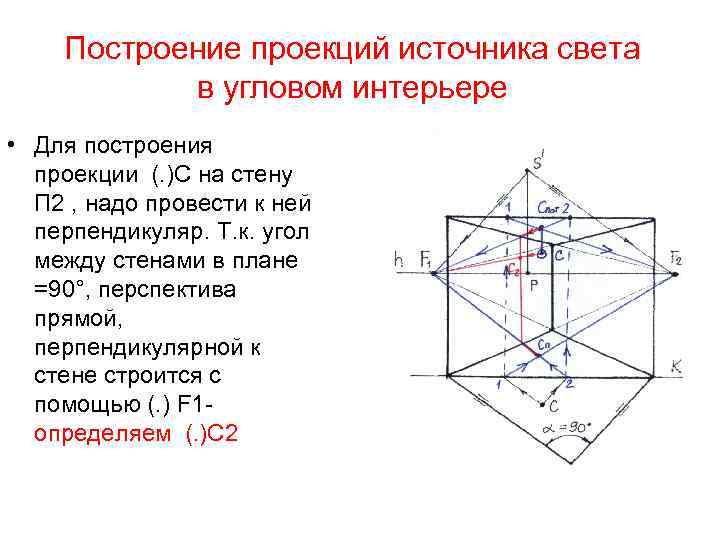
Построение проекций источника света в угловом интерьере • Для построения проекции (. )С на стену П 2 , надо провести к ней перпендикуляр. Т. к. угол между стенами в плане =90°, перспектива прямой, перпендикулярной к стене строится с помощью (. ) F 1 определяем (. )С 2
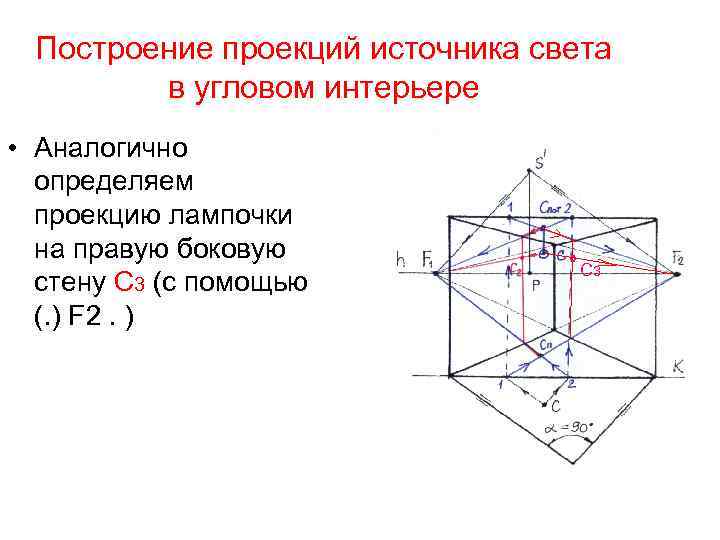
Построение проекций источника света в угловом интерьере • Аналогично определяем проекцию лампочки на правую боковую стену С 3 (с помощью (. ) F 2. ) ° С 3
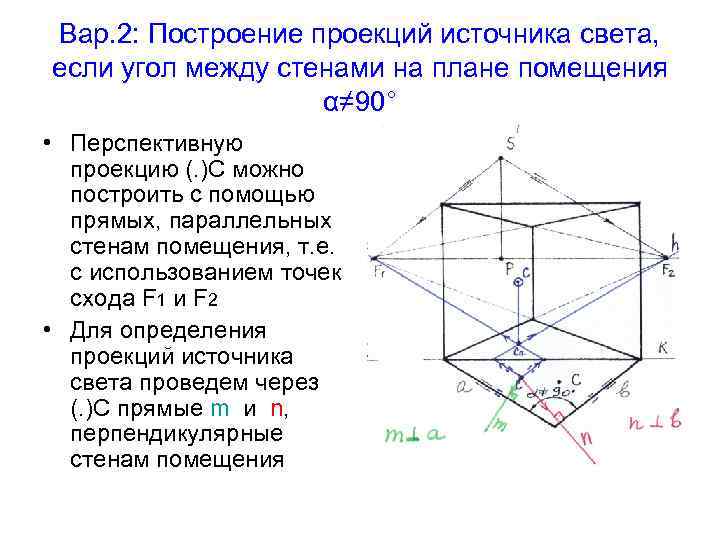
Вар. 2: Построение проекций источника света, если угол между стенами на плане помещения α≠ 90° • Перспективную проекцию (. )С можно построить с помощью прямых, параллельных стенам помещения, т. е. с использованием точек схода F 1 и F 2 • Для определения проекций источника света проведем через (. )С прямые m и n, перпендикулярные стенам помещения
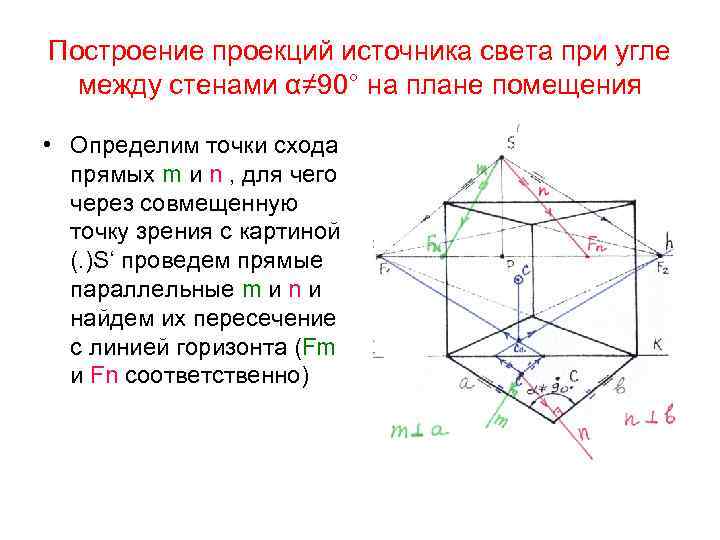
Построение проекций источника света при угле между стенами α≠ 90° на плане помещения • Определим точки схода прямых m и n , для чего через совмещенную точку зрения с картиной (. )S‘ проведем прямые параллельные m и n и найдем их пересечение с линией горизонта (Fm и Fn соответственно)
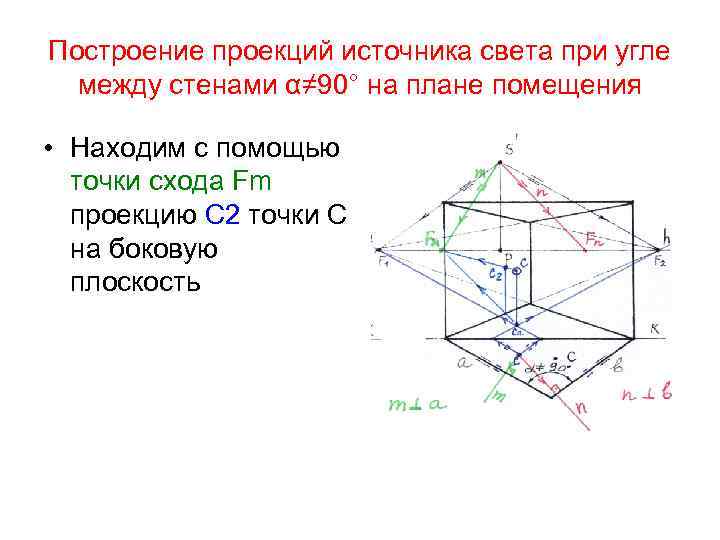
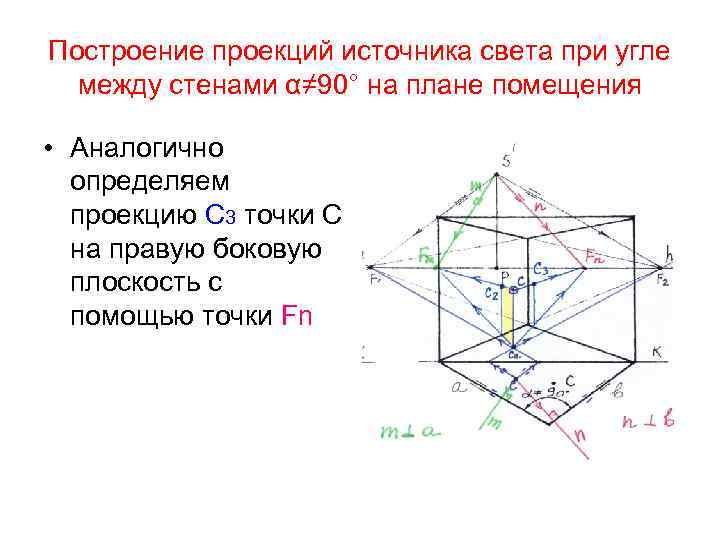
Построение проекций источника света при угле между стенами α≠ 90° на плане помещения • Находим с помощью точки схода Fm проекцию С 2 точки С на боковую плоскость
Построение проекций источника света при угле между стенами α≠ 90° на плане помещения • Аналогично определяем проекцию С 3 точки С на правую боковую плоскость с помощью точки Fn
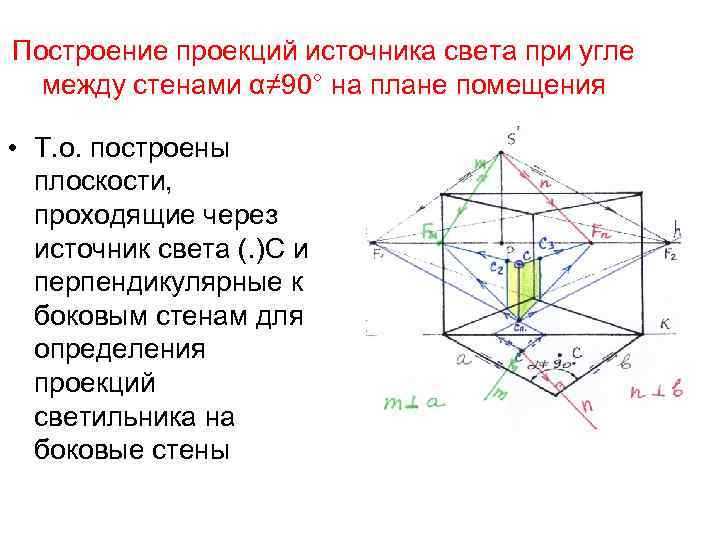
Построение проекций источника света при угле между стенами α≠ 90° на плане помещения • Т. о. построены плоскости, проходящие через источник света (. )С и перпендикулярные к боковым стенам для определения проекций светильника на боковые стены
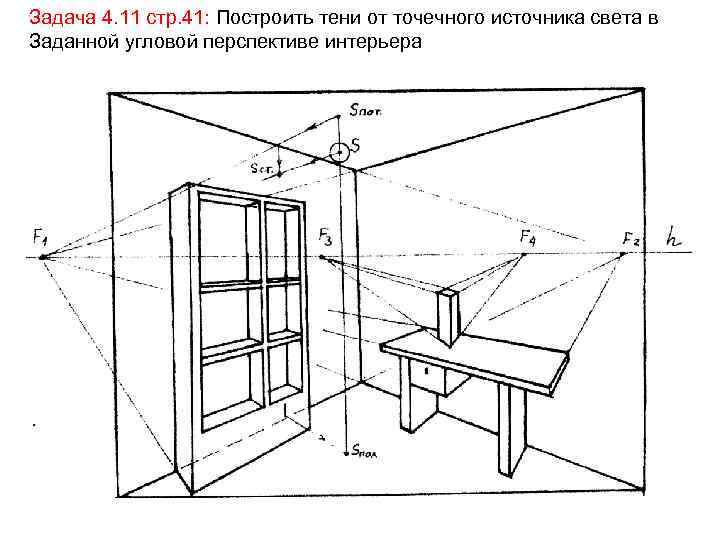
Задача 4. 11 стр. 41: Построить тени от точечного источника света в Заданной угловой перспективе интерьера
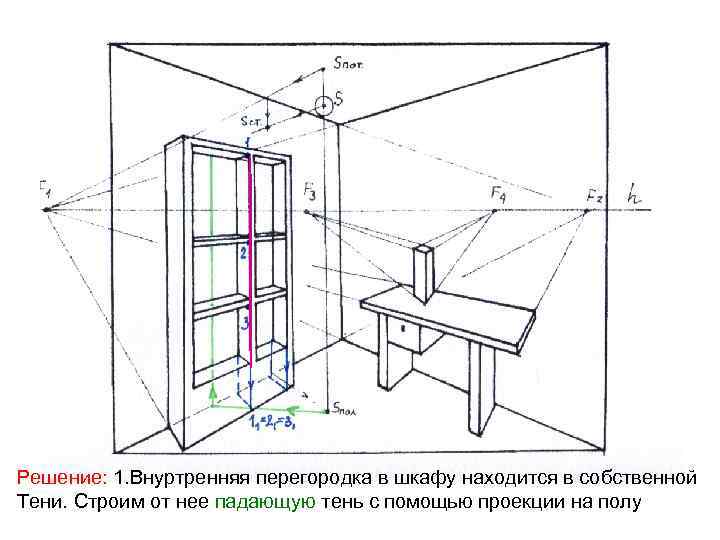
Решение: 1. Внуртренняя перегородка в шкафу находится в собственной Тени. Строим от нее падающую тень с помощью проекции на полу
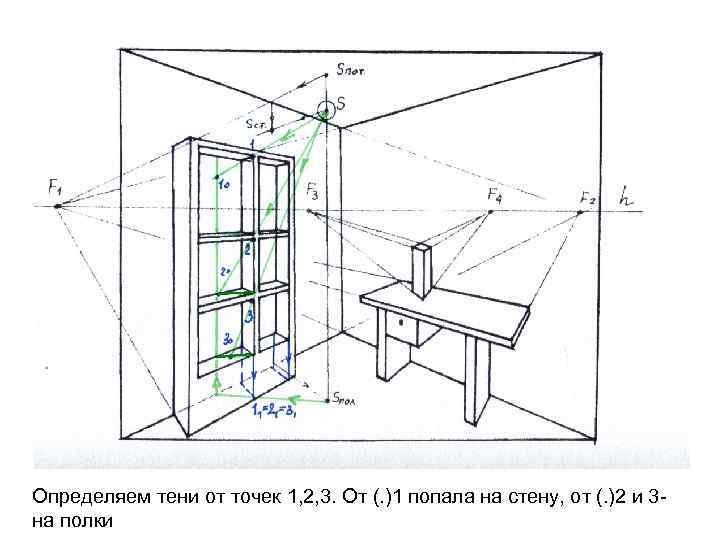
Определяем тени от точек 1, 2, 3. От (. )1 попала на стену, от (. )2 и 3 на полки
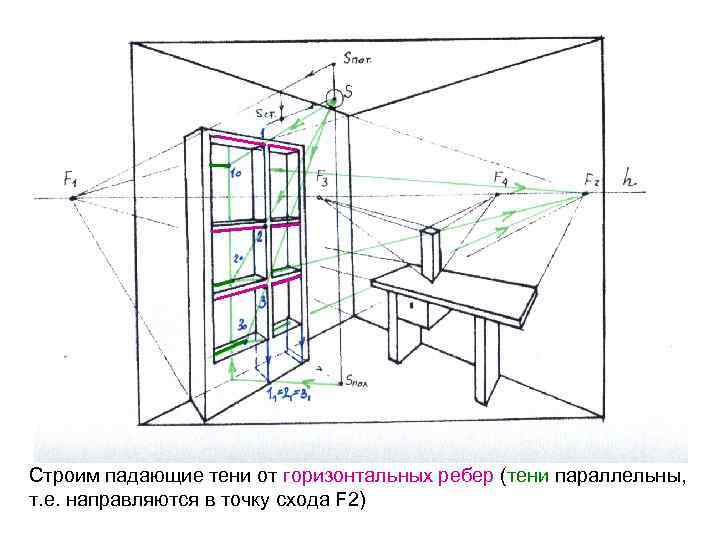
Строим падающие тени от горизонтальных ребер (тени параллельны, т. е. направляются в точку схода F 2)
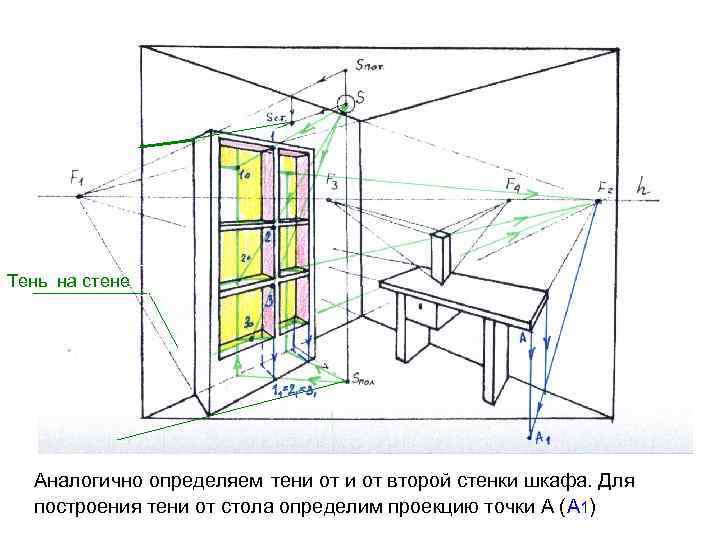
Тень на стене Аналогично определяем тени от второй стенки шкафа. Для построения тени от стола определим проекцию точки А (А 1)
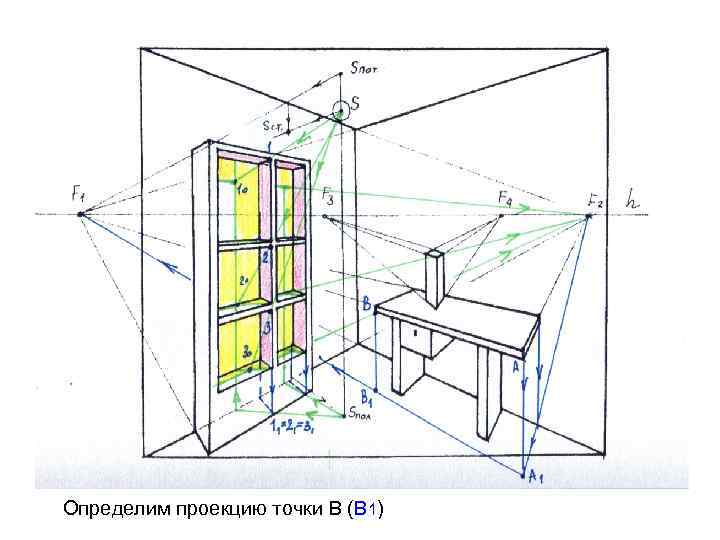
Определим проекцию точки В (В 1)
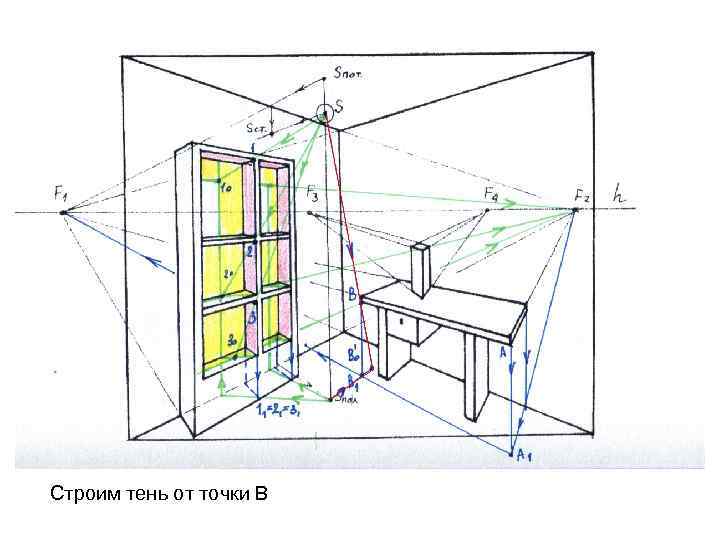
Строим тень от точки В
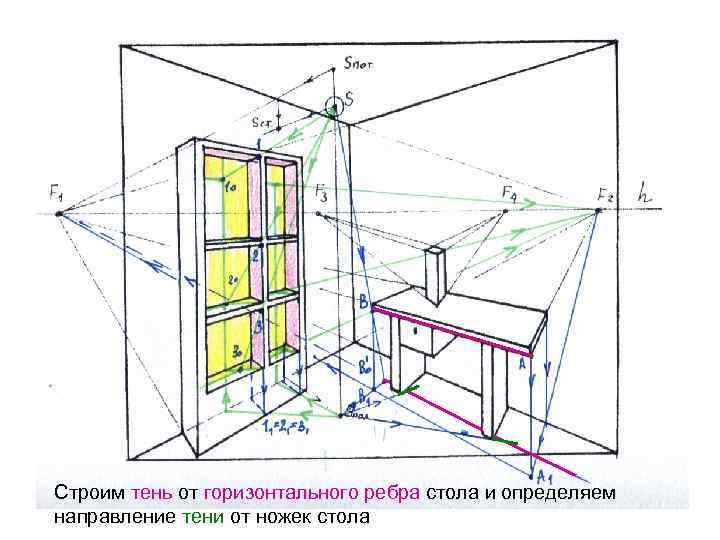
Строим тень от горизонтального ребра стола и определяем направление тени от ножек стола
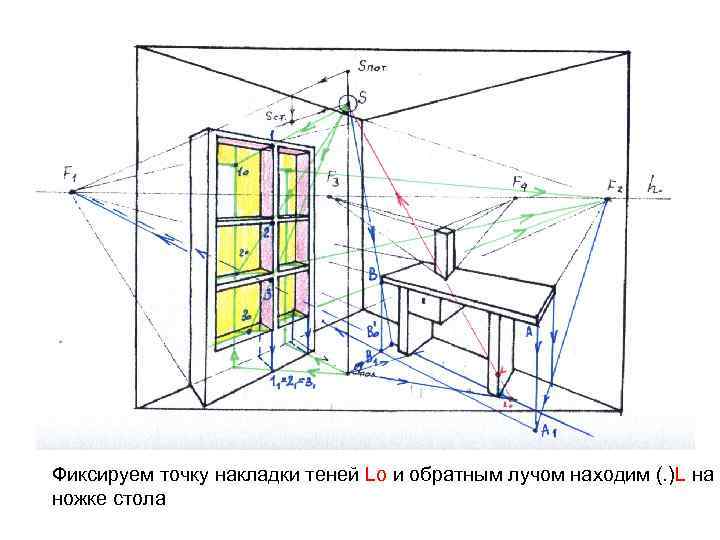
Фиксируем точку накладки теней Lo и обратным лучом находим (. )L на ножке стола
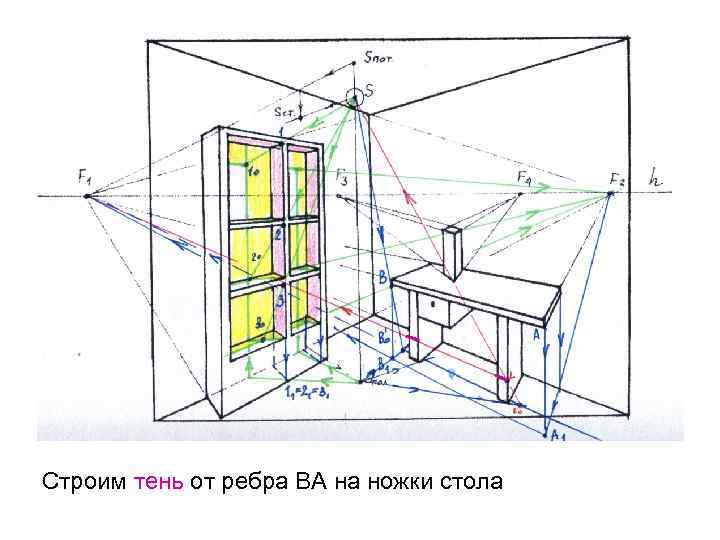
Строим тень от ребра ВА на ножки стола
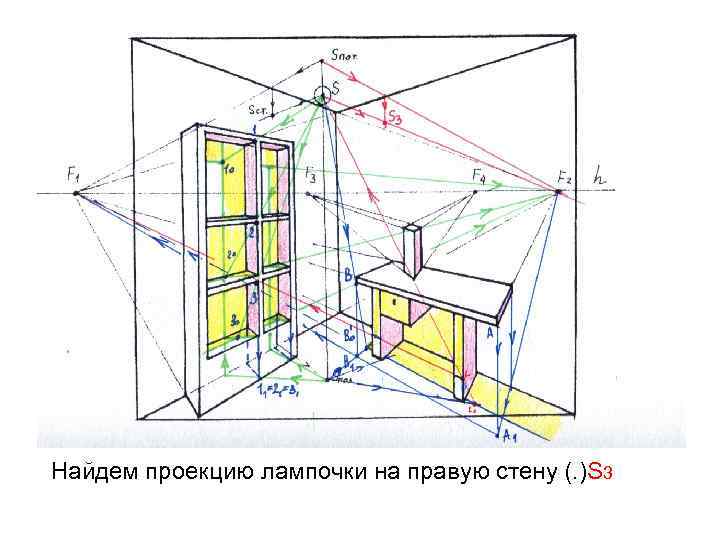
Найдем проекцию лампочки на правую стену (. )S 3
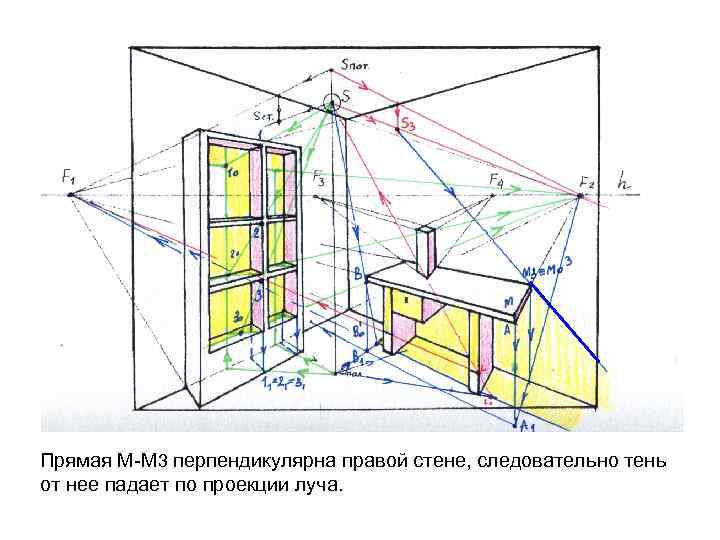
Прямая М-М 3 перпендикулярна правой стене, следовательно тень от нее падает по проекции луча.
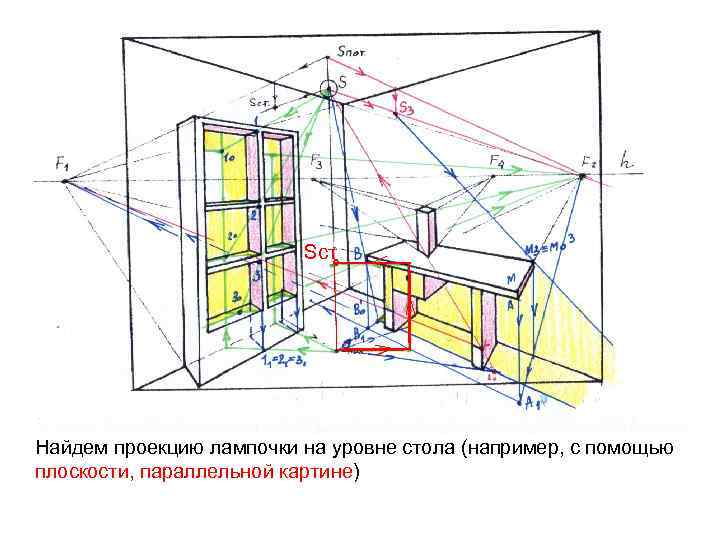
Sст ° Найдем проекцию лампочки на уровне стола (например, с помощью плоскости, параллельной картине)
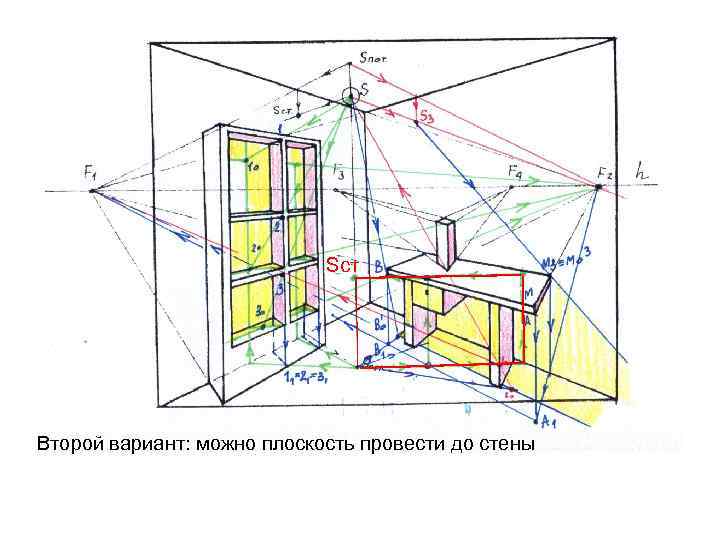
Scт Второй вариант: можно плоскость провести до стены
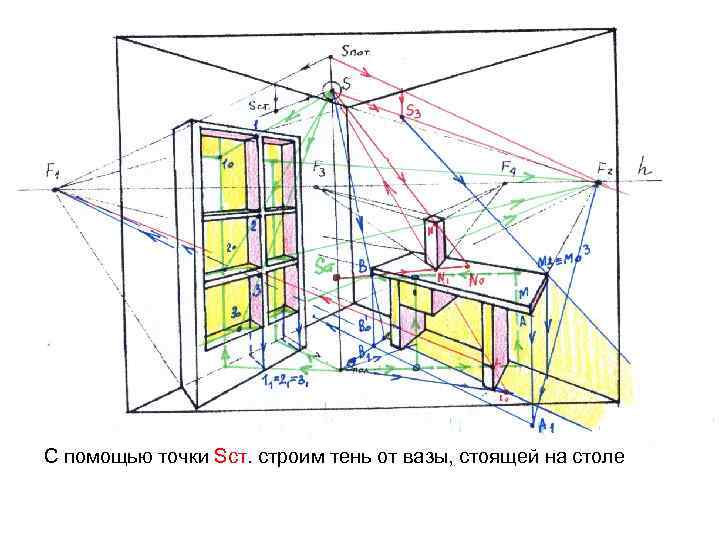
С помощью точки Sст. строим тень от вазы, стоящей на столе
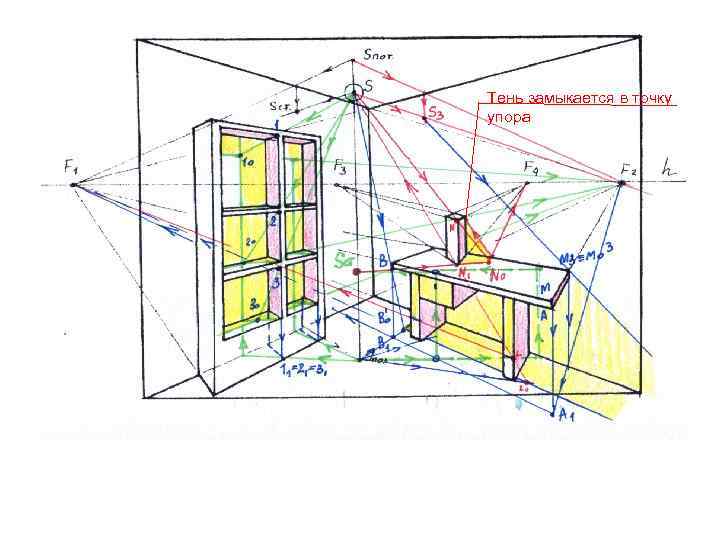
Тень замыкается в точку упора

Построение теней при рассеянном освещении При диффузном, рассеянном свете, проникающем через оконный проем, излучение света происходит по всей площади проема. Контуры теней как бы накладываются один на другой, их границы оказываются все более «размытыми» по мере удаления от светового проема. Плоскости откосов освещены, поэтому вертикальные и горизонтальные ребра откосов проема, обращенные внутрь помещения, являются тенеобразующими.

Построение теней при рассеянном освещении Из множества «светящихся» точек в проеме выделяют точки, расположенные в углах проема(1, 2, 4, 5). С помощью точек 1, 2 и 3 строят падающие тени на полу, а с помощью точек 4 и 5 – на потолке. Для построения теней необходимо спроецировать эти точки на те плоскости помещения, на которые должны быть построены тени: на пол (точки 1, 2), на потолок(точки 4 и 5) и боковую стену (5″). Затем проводят из «светящихся» точек перспективы лучевых прямых через тенеобразующие точки объекта до пересечения с вторичными проекциями этих лучей
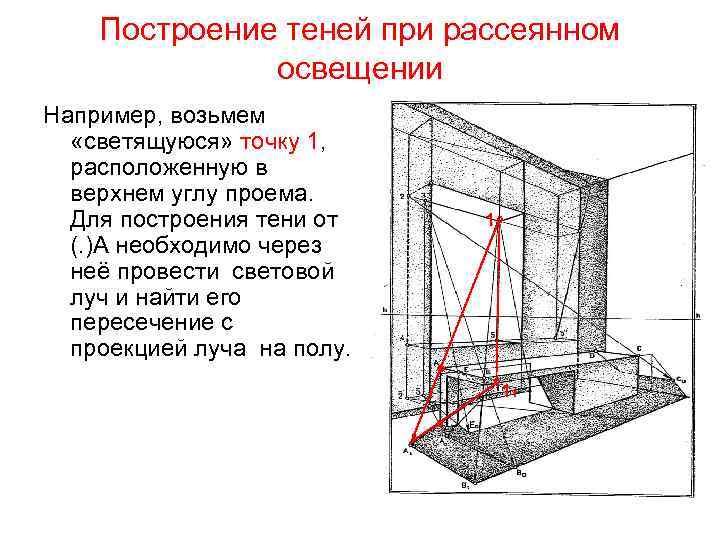
Построение теней при рассеянном освещении Например, возьмем «светящуюся» точку 1, расположенную в верхнем углу проема. Для построения тени от (. )А необходимо через неё провести световой луч и найти его пересечение с проекцией луча на полу. 1° ° 11
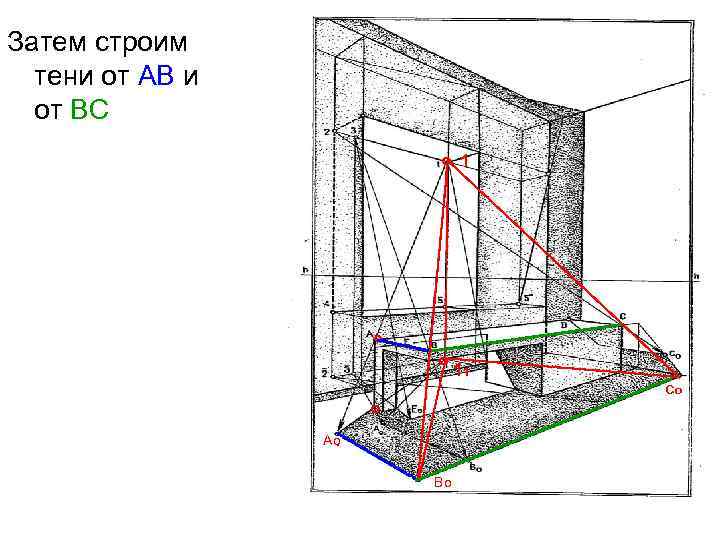
Затем строим тени от АВ и от ВС ° 1 ° ° 11 Со ° Ао Во
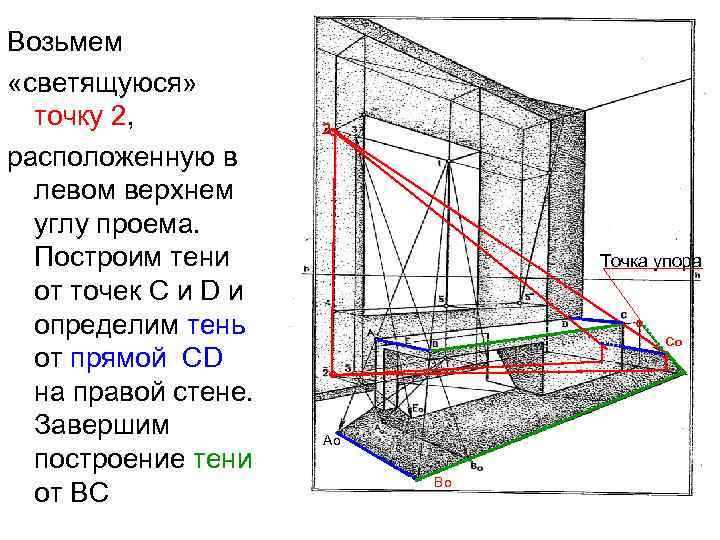
Возьмем «светящуюся» точку 2, расположенную в левом верхнем углу проема. Построим тени от точек С и D и определим тень от прямой СD на правой стене. Завершим построение тени от ВС 2 ° Точка упора ° Со ° ° Ао Во
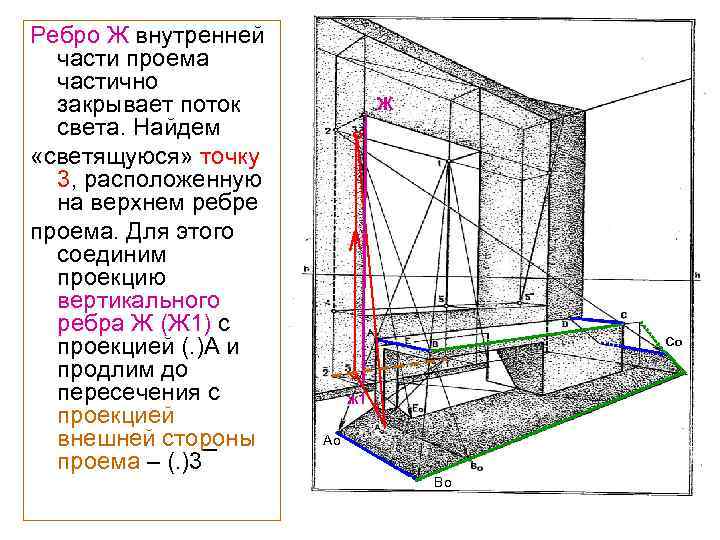
Ребро Ж внутренней части проема частично закрывает поток света. Найдем «светящуюся» точку 3, расположенную на верхнем ребре проема. Для этого соединим проекцию вертикального ребра Ж (Ж 1) с проекцией (. )А и продлим до пересечения с проекцией внешней стороны проема – (. )3¯ Ж ° Со ° ж 1 ° Ао Во
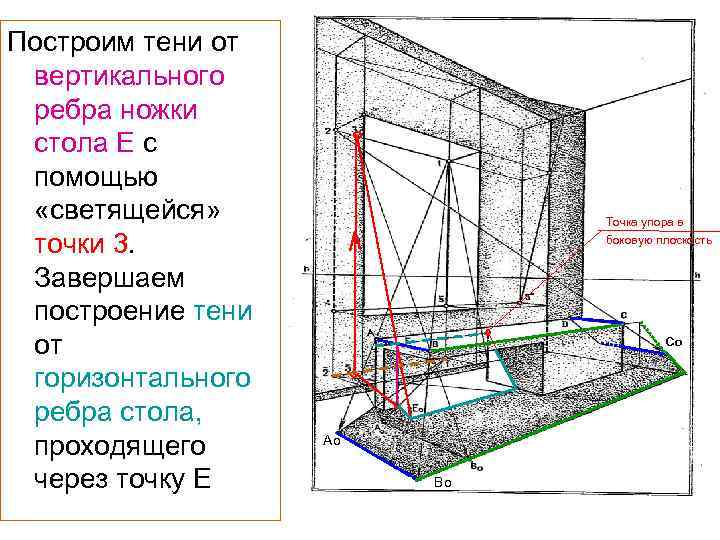
Построим тени от вертикального ребра ножки стола Е с помощью «светящейся» точки 3. Завершаем построение тени от горизонтального ребра стола, проходящего через точку Е ° Точка упора в боковую плоскость ° ° ° Ао Во Со
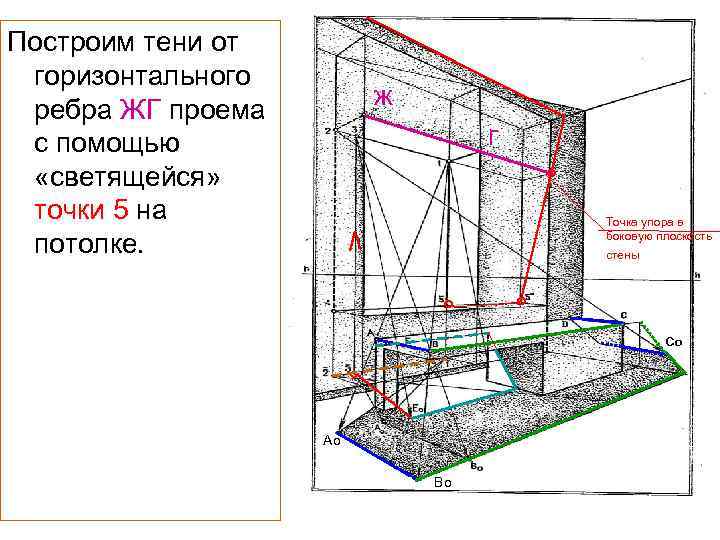
Построим тени от горизонтального ребра ЖГ проема с помощью «светящейся» точки 5 на потолке. ж г ° Точка упора в боковую плоскость стены ° ° Со ° Ао Во
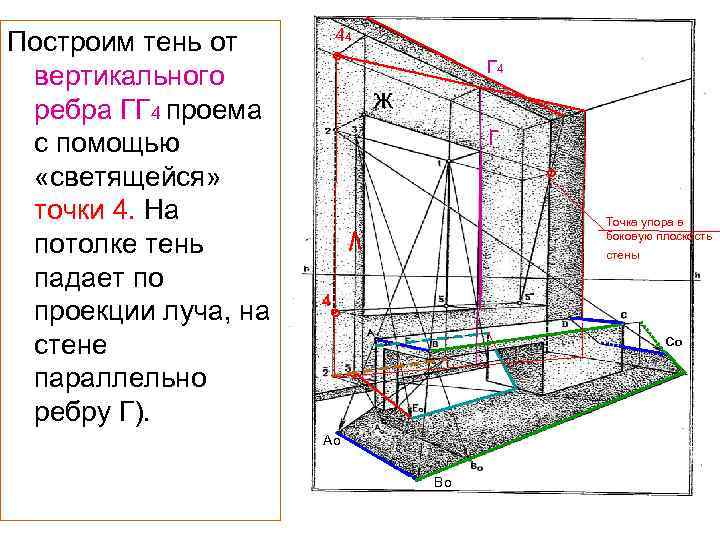
Построим тень от вертикального ребра ГГ 4 проема с помощью «светящейся» точки 4. На потолке тень падает по проекции луча, на стене параллельно ребру Г). 44 ° Г 4 ж г ° Точка упора в боковую плоскость стены 4 ° Со ° Ао Во
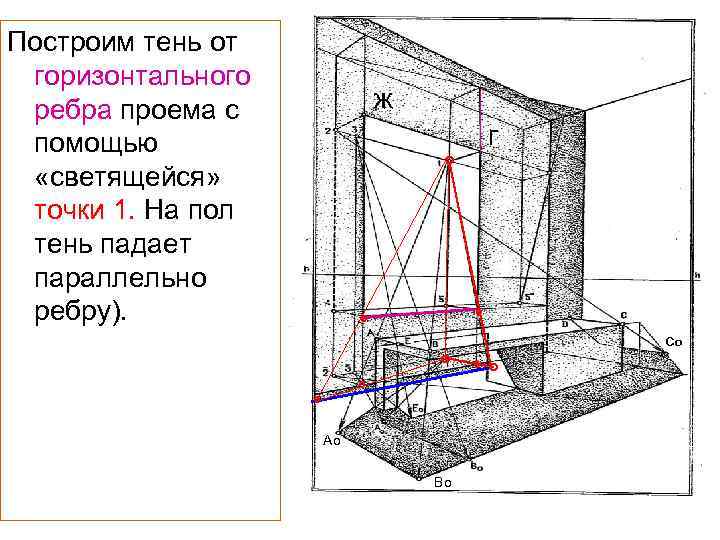
Построим тень от горизонтального ребра проема с помощью «светящейся» точки 1. На пол тень падает параллельно ребру). ж г ° ° ° Со ° ° ° Ао Во ° °
Библиографическое описание:
Тошев, И. И. Построение теней в перспективе / И. И. Тошев, Н. Т. Очилова, Н. Ш. Солиева. — Текст : непосредственный // Молодой ученый. — 2014. — № 11 (70). — С. 118-122. — URL: https://moluch.ru/archive/70/11940/ (дата обращения: 17.05.2023).
При построении теней на перспективных чертежах за источник света принимается солнце, которое по отношению к картине может занимать различные положения:
1. солнце расположено позади предмета и тень падает в сторону наблюдателя (рис.1);
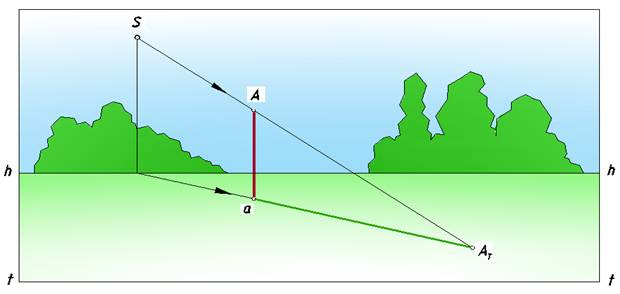
Рис. 1. Солнце позади предмета
2. солнце расположено позади зрителя, тень падает в сторону линии горизонта от основания предмета (рис. 2);
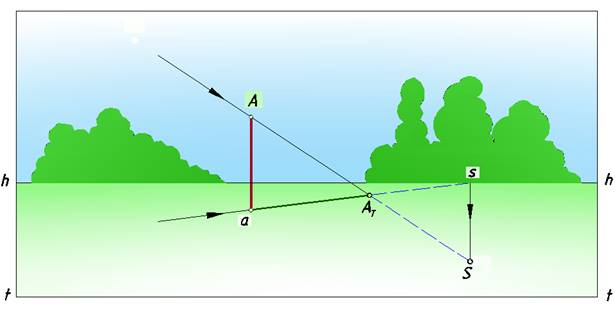
Рис. 2. Солнце позади зрителя
3. солнце расположено сбоку так, что лучи идут параллельно картине (рис. 3).
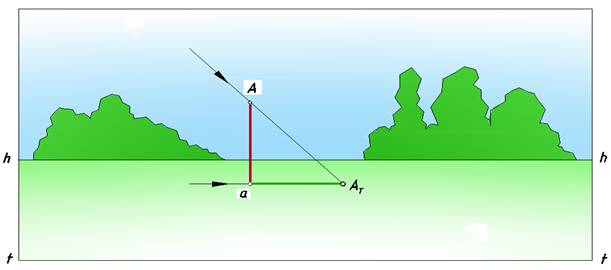
Рис. 3. Солнце сбоку предмета
Последний случай чаще других применяется инженерами при построении перспективных изображениях зданий и сооружений, поэтому остановимся на нем более подробно.
Рассмотрим построение точки в перспективе. Будем считать, что объект освещается слева (или справа), лучи идут параллельно картине, составляя угол 45° с предметной плоскостью. Запишем эти условия символически:
1. S∥K;
2. S^T= 45°.
Проведем через точку A (рис. 4) перспективу луча, а через ее вторичную проекцию (точку a) — вторичную проекцию луча. Поскольку луч параллелен картине, его вторичная проекция параллельна основанию картины t — t. Точка пересечения перспективы луча с его вторичной проекцией определит действительную тень точки А на земле — точку АТ.
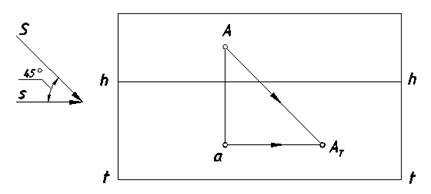
Рис. 4. Тень точки в перспективе
Построим собственные и падающие тени параллелепипеда, стоящего на земле (рис. 5).
Заметим, что те выводы, которые были сформулированы ранее для построения теней в ортогональных проекциях, справедливы и для центральных.
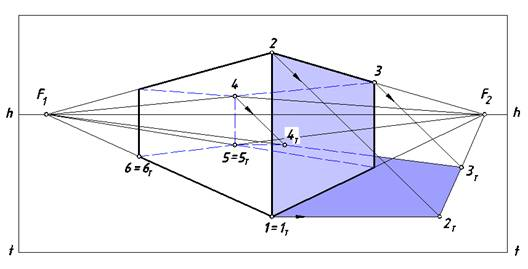
Рис. 5. Построение теней параллелепипеда
Проанализируем освещенность граней параллелепипеда. При заданном направлении лучевого потока освещенными будут верхняя, левая видимая и невидимая на чертеже грани объекта. Остальные грани окажутся в собственной тени. Определим контур собственной тени данного тела. В его состав войдут ребра (12) — (23) — (34) — (45) — (56) — (61), составляющие замкнутую цепочку в виде пространственной ломаной линии. От выявленного контура строим падающую тень. Поскольку точка 1 лежит на земле 1 = 1Т. Проведем через точку 2 перспективу луча, а через ее вторичную проекцию (точку 1) — его вторичную проекцию. На пересечении этих линий находим точку 2Т. Поскольку ребро [23] параллельно предметной плоскости, его падающая тень равна и параллельна ему. Точка схода ребра (23) находится на линии горизонта (точка F1). Соединяем точку 2Т с этой точкой (т. е. проводим через нее прямую, параллельную этому ребру). На этой же прямой находится тень точки 3. Проведем через точку 3 перспективу луча до пересечения с построенной прямой — определим точку 3Т. Вторичную проекцию луча в этом случае строить не следует, поскольку искомая точка уже установлена пересечением двух линий. Ребро (34) также параллельно плоскости T, его тень параллельна ребру.
Точкой схода этих прямых — фокус F1. Проведя перспективу луча через точку 4 до пересечения с отрезком (3Т F1), определим точку 4Т. Точки 5 и 6 расположены на предметной плоскости T, поэтому 5 = 5Т и 6 = 6Т. Очертание контура падающей тени параллелепипеда состоит из совокупности отрезков (1Т 2T) — (2Т 3T) — (3Т 4T) — (4Т 5T) — (5Т 6T) — (3Т 4T), представляющих собой замкнутый контур.
Задача
Построить тени от прямых барьеров на лестнице, земле и стене
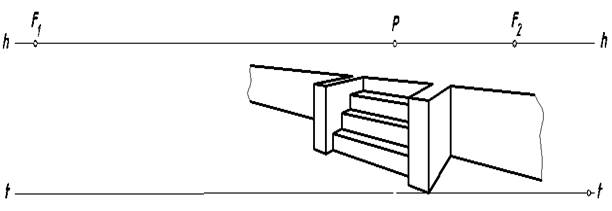
Рис. 6. Лестница с прямыми барьерами
Вначале построим тени правого барьера (рис.49). Поскольку при заданном направлении светового потока правая грань барьера находится в собственной тени легко видеть, что ребра, находящиеся на границе света и тени войдут в состав контура собственной тени. Определим падающую тень вертикального ребра. Точка А принадлежит Т, поэтомуможно отметить, что А = АТ. Проведем через точку В перспективу луча, а через ее вторичную проекцию — точку А перспективу вторичной проекции луча. На пересечении построенных линий определим тень ВТ.Другое ребро BC параллельно предметной плоскости, следовательно, его тень параллельна ребру и имеет ту же точку схода F2. Реальная часть этой тени на земле — отрезок ВТ1Т. Поскольку точка 1Т находится на границе земли и стены 1Т = 1Т‘. С помощью обратного луча можно определить точку на ребре BC, которая отбросила эту тень. Точка С горизонтального ребра находится на стене, поэтому С = СТ‘. Тень отрезка 1C падает на стену. Его тенью является отрезок 1Т‘ СТ‘.
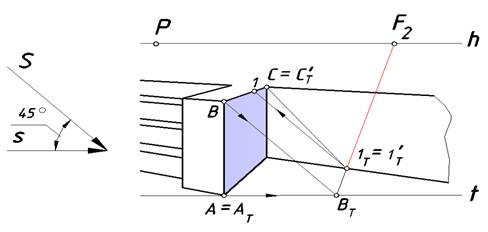
Рис.7. Построение контура падающей тени правого барьера
Контур собственной тени всегда замкнут. Рассуждения по его определению приводились во многих задачах. Элемент контура может совпадать со своей тенью (если, например, он находится на земле, стене или примыкает к другому объекту). Этот фактор следует учитывать при построении падающей тени.
У левого барьера правая грань находится в собственной тени, следовательно, ребра LN и LM входят в состав определяемого контура (рис. 8). Построим падающие тени этих ребер.
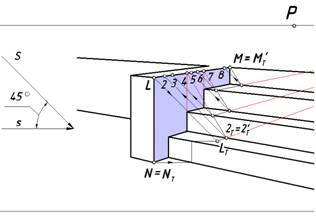
Рис.8. Построение контура падающей тени левого барьера
Лучевая плоскость (фронтальная плоскость уровня), проходящая через ребро LN пересекает землю и нижнюю ступеньку по параллельным прямым, оставляя на них теневые следы, а подступенок по вертикальной прямой. Верхняя точка L этого ребра отбрасывает тень на первую ступеньку и определяется пересечением луча с его вторичной проекцией. Ребро LM параллельно плоскости нижней ступеньки, поэтому его тень параллельна ребру. Соединяет точку LТсточкой схода F2иотмечаем реальную часть тени этого ребра на нижней ступеньке до точки 2Т = 2Т‘. Заметим, что это ребро является гвоздем по отношению ко всем подступенкам. Проведем вспомогательные линии для нахождения общих точек для ребра LM и граней всех подступенков. Эти построения позволят определить падающие тени на подступенки. На рис. 8 на ребре LM отмечены все его участки, отбросившие тени на конкретные фрагменты лестницы, землю и стену.
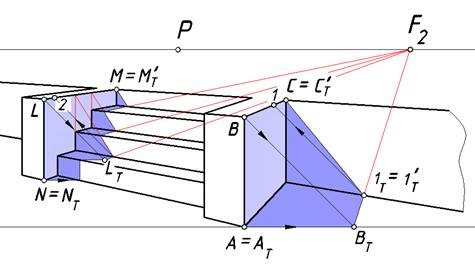
Рис. 9. Собственные и падающие тени от прямых барьеров
На рис. 9. представлен окончательный вариант решения задачи. Тени ребер LM и BC на стене и подступенках параллельны и представляют собой пример восходящих прямых. Их точка схода расположена выше линии горизонта, а точка схода их вторичных проекций лежит на линии горизонта.
Литература:
1. Макарова М. Н. Перспектива / М. Н. Макарова. — М.: Академический проект,2002.–512 с.
2. Яблонский А. Г. Начертательная геометрия (перспектива) / А. Г. Яблонский. — М.: из-во «Просвещение», 1966. — 176 с.
Основные термины (генерируются автоматически): тень, вторичная проекция, ребро, падающая тень, перспектива луча, предметная плоскость, вторичная проекция луча, земля, линия горизонта, нижняя ступенька.
Содержание:
Проекционные чертежи архитектурных объектов выполненные в одних линиях, не дают достаточно полного представления о запроектированном объекте.
Для придания объемности и наглядности ортогональным чертежам зданий и сооружений выполняется построение теней.
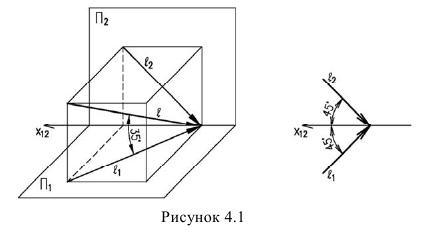
Тени строятся от естественного освещения, т.е. солнца. Так как солнце практически бесконечно удаленная точка, то лучи принимаются параллельными. За направление лучей принимается диагональ куба грани которого совпадают с плоскостями проекций, а её проекции являются диагоналями граней куба, т.е. квадратов (см. рисунок 4.1). Истинный угол наклона будет равен 35°, а проекции лучей располагаются под углом 45° к оси (см. рисунок 4.1).
Тень точки – способ следа луча, способ выноса
Тенью точки на плоскости является точка пересечения светового луча, проведенного через данную точку, с плоскостью. Если тень точки падает на плоскость проекций, то для её построения используется способ следа луча. Т.е. через проекции точки проводим проекции лучей и строим след. На рисунке 4.2 след луча фронтальный, следовательно тень падает на фронтальную плоскость —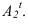
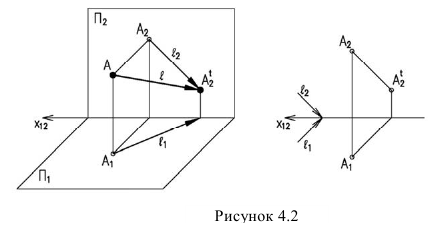
Кроме этого может быть использован метод выноса. Особенно важен этот метод при построении теней на фасадах зданий.
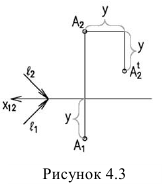
Вынос – это расстояние от точки до фронтальной плоскости или плоскости фасада, если тень строится на фасаде. На рисунке 4.3 у – эго вынос.
Тень примой общего положении
Тенью прямой на плоскость является линия пересечения лучевой плоскости, проведенной через прямую с заданной плоскостью. Т.е. тенью прямой на плоскость является прямая линия. Поэтому для построения тени прямой на плоскость, достаточно построить тени двух ее точек.
Если же тень от прямой падает на две плоскости, то она имеет точку излома, лежащую на линии пересечения плоскостей. В данном случае точка излома лежит на оси (рисунок 4.4). Для ее нахождения, необходимо строить мнимую тень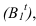 т.е. определить горизонтальный след луча проведенного через точку В.
т.е. определить горизонтальный след луча проведенного через точку В.
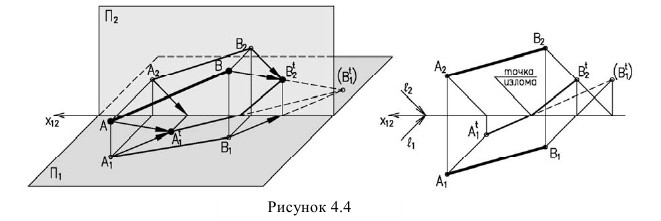
Тени прямых частного положении
Тени прямых частного положения на плоскостях проекций располагаются всегда определенно и часто служат «опорными» при построении теней различных деталей, включающих такие прямые. Рассмотрим эти случаи.
Тень от прямой, на плоскость ей параллельную, располагается параллельно прямой, т.е. параллельно проекции прямой на эту плоскость и равна ей по величине (рисунок 4.5).
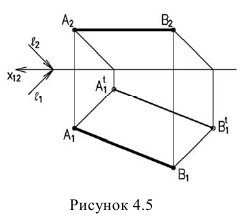
Тень от прямой на плоскость, ей перпендикулярную, располагается по проекции луча, т.е. под углом 45° (рисунок 4.6).
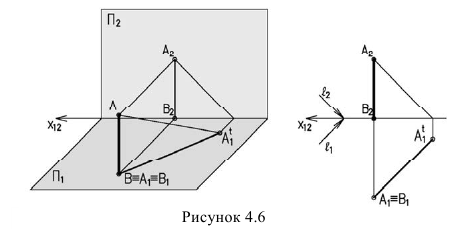
Если точка лежит на плоскости, то тень совпадает с самой точкой и такая точка называется сама себе тень. В нашем случае это точка В. Тень на фронтальной плоскости от горизонтальной прямой, расположенной под углом 45° к ней, вертикальна (рисунок 4.7)
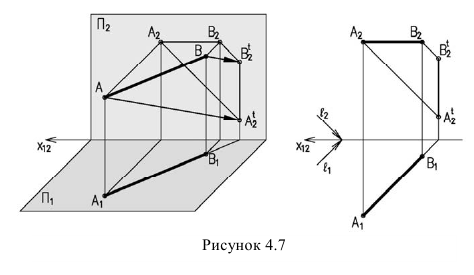
Тени плоских фигур
Чтобы построить тень от плоской фигуры, например треугольника, падающую на плоскости проекций достаточно построить тени от вершин (рисунок 4.8). Т.к. тень падает на две плоскости необходимо определять линию излома тени, а, следовательно, построить мнимую тень от вершины В.
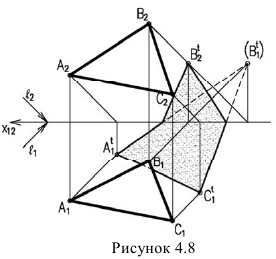
Тень от плоской фигуры, на плоскость ей параллельную, изображается фигурой равной ей по величине. Поэтому достаточно построить тень от одной точки и вычертить тень в виде той же фигуры. Так, для построения тени от окружности (рисунок 4.9) достаточно определить тень от центра и вычертить тень в виде такой же окружности.
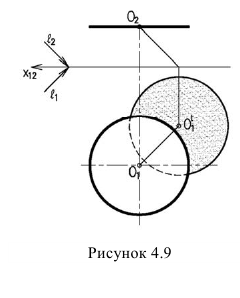
Тень окружности
Тень окружности обычно строится по восьми точкам. Из них четыре -точки касания окружности к сторонам описанного около окружности квадрата, и четыре – точки пересечения окружности с диагоналями этого квадрата (рисунок 4.10).
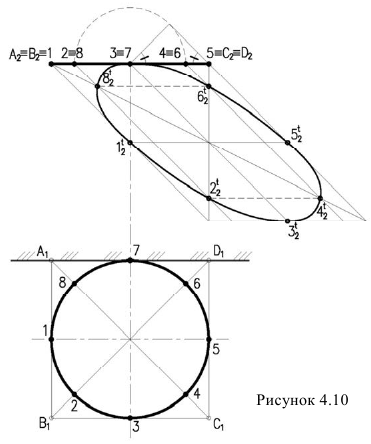
Тень от квадрата – параллелограмм, диагональ которого BD вертикальна. Точки 1,3,5,7 точки касания к параллелограмму. Точки, лежащие на диагоналях, делят радиус в отношении 0,707. Они могут быть получены без горизонтальной проекции. Для этого на
радиусе строим равнобедренный треугольник с углами при основании 45° и дугой окружности определяем положение точек 2,8 и 4,6. Проведем из них лучи до пересечения с диагоналями. Полученные восемь точек соединяем плавной линией, которая будет эллипсом. Практически тень окружности по восьми точкам строят без горизонтальной проекции, которая здесь приведена только для пояснения.
Тени поверхностей. Понятие собственной и падающей тени
Для поверхностей характерны следующие понятия: Собственная тень (ф) – неосвещенна часть поверхности (предмета) рисунок 4.11.
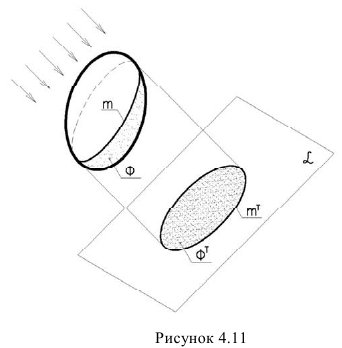
Контур собственной тени (ш)-граница между освещенной и неосвещенной частью поверхности (предмета).
Падающая тень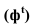 – тень падающая от одного предмета на другой, или на плоскость.
– тень падающая от одного предмета на другой, или на плоскость.
Контур падающей тени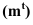 – контур, ограничивающий падающую тень.
– контур, ограничивающий падающую тень.
Фактически контур падающей тени -это тень от контура собственной тени. Поэтому, обычно, сначала определяют контур собственной тени, а затем уже строят падающую.
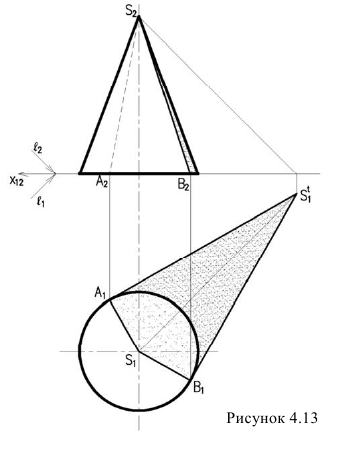
Рассмотрим примеры построения теней трехгранной призмы (рисунок 4.12) и прямого кругового конуса (рисунок 4.13).
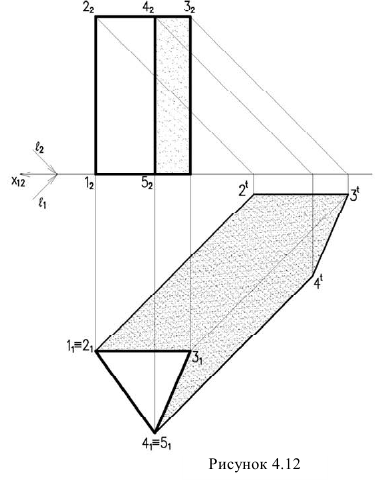
Проведя лучи на горизонтальной проекции касательные к крайним ребрам призмы, определяем контур собственной тени. Она является пространственной ломаной 1,2,3,4,5. Т.к. точки 1 и 5 лежат на плоскости 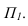 они являются тенями.
они являются тенями.
Поэтому для построения контура падающей тени, достаточно построить тени точек 2,3,4.
Проанализировав построенную тень, мы видим, что тени от ребер 1,2 и 5,4 совпадают с направлением лучей, т.к. они перпендикулярны к плоскости 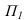 А тени от ребер 2,3 и 3,4 параллельны этим ребрам и равны но величине, т.к. они параллельны плоскости.
А тени от ребер 2,3 и 3,4 параллельны этим ребрам и равны но величине, т.к. они параллельны плоскости.
Учитывая это, построение контуров падающих теней многогранников может быть значительно упрощено.
Для конуса логично сначала построить падающую тень, а затем собственную (рисунок 4.13). Для построения падающей тени, строим тень от вершины конуса 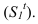
Из полученной точки проводим касательные к окружности основания. Эти касательные образуют, контур падающей тени (она является тенями от образующих конуса). Поэтому, соединив точки А и В с вершиной конуса S получим границы собственной тени конуса. А затем уже строим фронтальную проекцию контура собственной тени. Аналогично строятся тени пирамидальных поверхностей.
Тени в ортогональных проекциях. Метод лучевых сечений, метод обратных лучей. Тени фрагментов зданий
Тень точки и прямой на плоскость общего положения (способ лучевых сечений, способ обратных лучей).
Тени схематизированного здания, состоящего из призматических форм.
Тени фрагментов зданий.
Тень точки на плоскость общего положения. Способ лучевых сечений
Для построения тени точки М на плоскость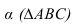 (рисунок 5.1), проведем через точку М луч и определим точку пересечения луча с плоскостью а. Задача сводится к нахождению точки пересечения прямой (луча) с плоскостью.
(рисунок 5.1), проведем через точку М луч и определим точку пересечения луча с плоскостью а. Задача сводится к нахождению точки пересечения прямой (луча) с плоскостью.
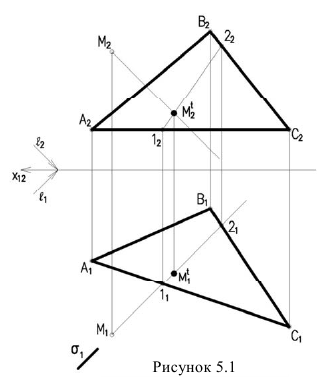
Через луч проводим горизонтально-проецирующую лучевую плоскость о. Строим линию пересечения 1-2 плоскости а и заданной плоскости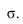 Определяем точку пересечения луча с полученной линией пересечения. Эта точка
Определяем точку пересечения луча с полученной линией пересечения. Эта точка 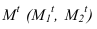 и будет тенью точки М на плоскости а.
и будет тенью точки М на плоскости а.
Способ обратного луча
Рассмотрим построение тени от двух прямых SF и SB на непрозрачную пластинку ECDF. (рисунок 5.2).
Тень от проецирующей прямой SA строится, аналогично предыдущему примеру (рисунок 5.1), методом лучевых сечений. На горизонтальной проекции тень совпадает с направлением луча, на фронтальной – идет по лучевому сечению. Тень от точки S на пластину ESDF не надает. Для построения тени от наклонной прямой SB на пластину ESDF, необходимо построить сначала тень падающую на плоскость 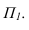 Для чего строим тень от точки S падающую на
Для чего строим тень от точки S падающую на 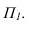 и полученную точку
и полученную точку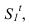 соединяем с точкой
соединяем с точкой 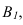 т.к. точка В лежит на плоскости
т.к. точка В лежит на плоскости 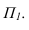
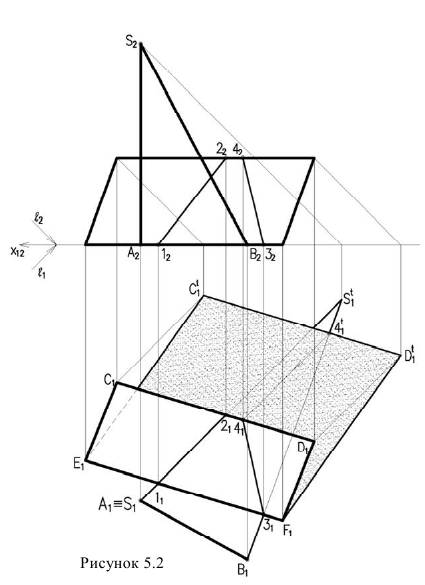
Далее строим тень от пластины ESDF на плоскость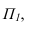 для чего строим тени точек С и D и соединяем их с точками
для чего строим тени точек С и D и соединяем их с точками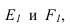 лежащими на плоскости
лежащими на плоскости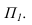 Полученные тени пересекаются
Полученные тени пересекаются 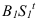
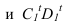 в точке
в точке 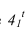 . Из точки пересечения теней проводим обратный луч под углом 45° на прямую
. Из точки пересечения теней проводим обратный луч под углом 45° на прямую 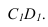 По вертикальной линии связи находим фронтальную проекцию этой точки. Обратите внимание, что точки 1 и 3, являются точками излома теней падающих на горизонтальную плоскость и на наклонную плоскость а.
По вертикальной линии связи находим фронтальную проекцию этой точки. Обратите внимание, что точки 1 и 3, являются точками излома теней падающих на горизонтальную плоскость и на наклонную плоскость а.
Необходимо отметить что данную задачу можно решить используя построение мнимой тени от точки S на пластину ESDF (рисунок 5.3).
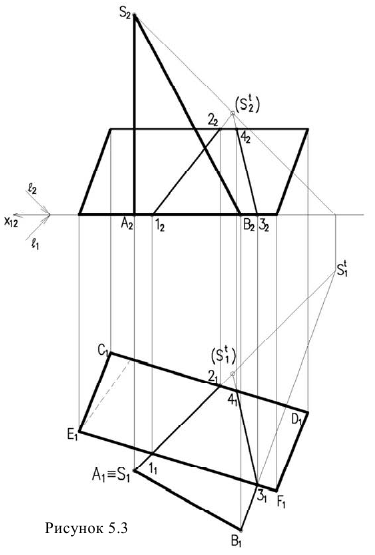
Тени схематизированною здании, состоящею из призматических форм
Здание состоит из двух призматических форм (рисунок 5.4). Обычно сначала строятся тени от двух этих форм падающие на плоскость 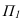 (т.е. на землю).
(т.е. на землю).
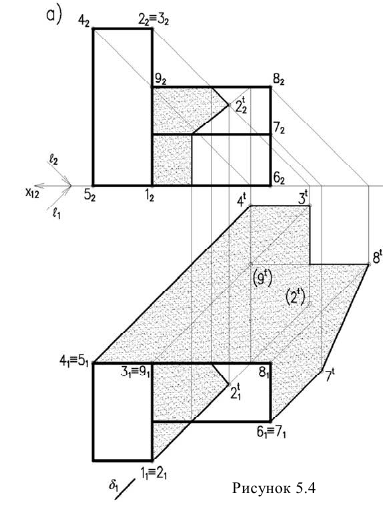
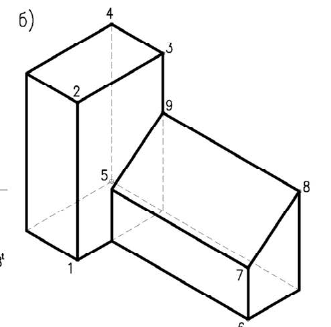
Дли построении падающих теней определяем контур собственной тени каждой из призм (рисунок 5.46). Высотная часть здания представляет прямую призму, контур собственной тени которой 1,2,3,4,5, причем точки 1 и 5 лежат на плоскости, поэтому тени строим от трех точек 2,3,4. Контур собственной тени второй призмы – 6,7,8,9. Точка 6 лежит на 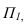 , поэтому строим тени от точек 7,8,9 (рисунок 5.4а). Т.к. две полученные тени пересекаются, определяем общий контур тени. Видим, что точки
, поэтому строим тени от точек 7,8,9 (рисунок 5.4а). Т.к. две полученные тени пересекаются, определяем общий контур тени. Видим, что точки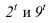 являются мнимыми. Поэтому тень от точки 2 очевидно упадет на пристройку, а точка 9 будет в тени и фактически тень не отбросит.
являются мнимыми. Поэтому тень от точки 2 очевидно упадет на пристройку, а точка 9 будет в тени и фактически тень не отбросит.
Для построения тени падающей от высотной части здания на пристройку используем метод лучевых сечений. Заключаем луч, проведенный через точку 2 в плоскость 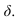 Строим сечение призмы – пристройки плоскостью
Строим сечение призмы – пристройки плоскостью 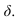 Луч, проведенный из точки 2, пересекает линию сечения в точке
Луч, проведенный из точки 2, пересекает линию сечения в точке 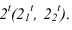 Т.е. тень падает на наклонную плоскость. Тень от вертикальной прямой 1,2, на горизонтальной проекции совпадает с направлением луча, на фронтальной идет по сечению. Тень от прямой 2,3 на фронтальной проекции совпадает с направлением луча, на горизонтальной идет по сечению.
Т.е. тень падает на наклонную плоскость. Тень от вертикальной прямой 1,2, на горизонтальной проекции совпадает с направлением луча, на фронтальной идет по сечению. Тень от прямой 2,3 на фронтальной проекции совпадает с направлением луча, на горизонтальной идет по сечению.
При построении теней зданий очень важно помнить положение теней прямых частного положения, это значительно упрощает процесс построения.
Тени фрагментов зданий
К фрагментам зданий относятся ниши, козырьки, трубы, лестницы и т.п. Рассмотрим построение теней некоторых из них.
Тени в нишах
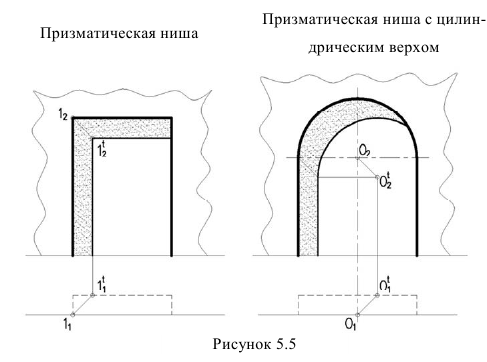
Две изображенные ниши относятся к нишам с плоским днищем, т.е. контур ниши отбрасывает тень на плоскость днища ниши параллельной контуру. Поэтому тени в нишах с – плоским днищем повторяют контур ниши. Для построения таких теней достаточно построить тень одной точки, как показано на примере (рисунок 5.5). Если дан лишь фасад здания, необходимо знать глубину ниши и тень построить методом выноса.
В цилиндрической нише (рисунок 5.6) сначала определяем собственную тень. Для чего удобнее провести нормаль (т.е. радиус под углом 45°). Получим контурную образующую собственной тени.
Падающую тень будет отбрасывать две прямые кромки ниши – вертикальная и продольная. Тень от вертикальной прямой надает на ось ниши. Тень от продольной прямой будет представлять четверть окружности.
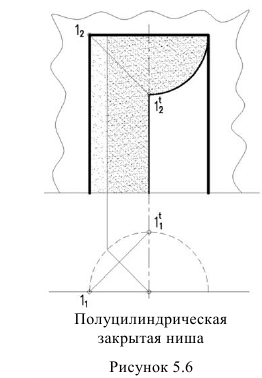
Из этого чертежа можно сделать вывод: тень от продольной прямой на фасаде с вертикальными образующими зеркально повторяется план. Этот вывод позволяет построить тень на фасаде от свеса крыши, построив тень одной точки (тень точки 1 на рисунке 5.7). Остальной контур тени зеркально повторяет план.
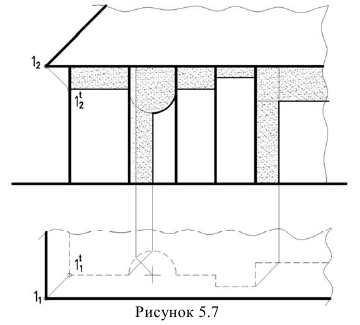
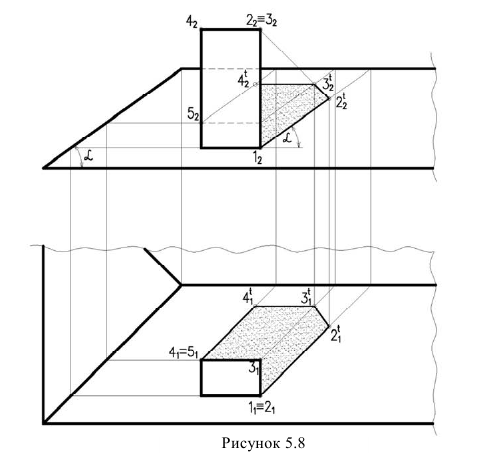
Тень падающая от трубы на крышу
На рисунке 5.8 дана труба призматической формы.
Тень строится методом лучевых сечений. Если отсутствует план здания, то нужно иметь ввиду, что тени от вертикальных прямых на фасаде имеют угол наклона равный углу наклона ската крыши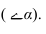
Тень от барьера на ступенях лестницы
Контур собственной тени барьера (рисунок 5.9), отбрасывающий тень на ступени представляет собой две прямые – горизонтально-проецирующую 1,2 и фронтально-проецирующую 2,3. Из точек 1 и 3 начинается тень. Следовательно, необходимо построить тень точки 2. Для построения падающей тени используется метод лучевых секущих плоскостей. 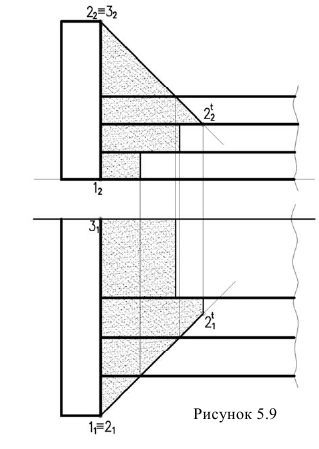
Тени в ортогональных проекциях
Строительство зданий и сооружений ведется по чертежам, выполненным в ортогональных проекциях. Представление о внешнем виде здания, в основном, создается по изображению фасада. Это изображение имеет существенный недостаток – в нем отсутствует объемность. Тени, построенные на ортогональных чертежах, дают возможность представить по чертежу расположение отдельных элементов, их освещенность, а также помогают находить наилучшие пропорции проектируемых зданий и сооружений.
При освещении лучами света каких-либо объектов на них образуются тени. Для образования тени необходим источник света и плоскость, на которую падает тень.
Освещение может быть центральным (факельным) или параллельным (солнечным). Освещение называется центральным в случае, когда световые лучи идут из одной точки (лампа, свеча); параллельным, если источник света (солнце) удален в бесконечность, и световые лучи практически будут параллельны между собой.
Основной геометрической задачей построения теней является определение контуров собственных и падающих теней (рис. 17.1).
Неосвещенная часть поверхности тела 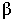 называется собственной тенью. Линия
называется собственной тенью. Линия 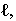 разграничивающая освещенную часть поверхности тела
разграничивающая освещенную часть поверхности тела 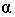 и собственную тень
и собственную тень 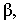 называется контуром собственной тени. Пространственное тело, преграждая путь световым лучам, образует на некоторой поверхности
называется контуром собственной тени. Пространственное тело, преграждая путь световым лучам, образует на некоторой поверхности 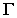 падающую тень
падающую тень 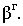 Линия
Линия 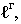 ограничивающая падающую тень
ограничивающая падающую тень 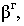 называется контуром падающей тени. Контур падающей тени
называется контуром падающей тени. Контур падающей тени 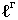 есть тень от контура собственной тени
есть тень от контура собственной тени 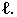
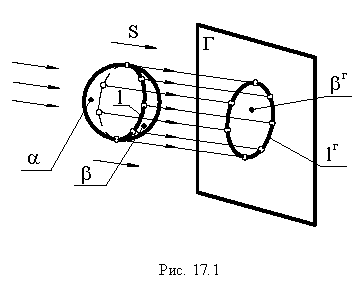
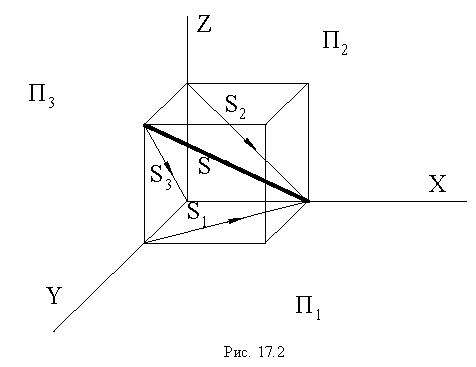
Для построения падающей тени необходимо знать направление лучей света. Направление световых лучей 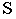 принимается параллельным диагонали куба, прислоненного своими гранями к плоскостям проекций. Проекции такого светового луча на плоскости проекций
принимается параллельным диагонали куба, прислоненного своими гранями к плоскостям проекций. Проекции такого светового луча на плоскости проекций 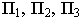 составляют угол
составляют угол 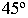 с соответствующими координатными осями
с соответствующими координатными осями 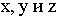 (рис. 17.2).
(рис. 17.2).
Тень от точки на плоскость проекций
Тенью от точки 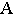 на плоскость проекций является след светового луча
на плоскость проекций является след светового луча 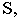 проходящего через точку
проходящего через точку 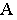 на этой плоскости. Поэтому построение проекций тени от точки на чертеже аналогично построению следов прямой На рис. 17.3 плоскость проекций
на этой плоскости. Поэтому построение проекций тени от точки на чертеже аналогично построению следов прямой На рис. 17.3 плоскость проекций 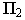 пересекается лучом в точке
пересекается лучом в точке 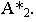 Точка
Точка 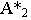 для луча является фронтальным следом, а для точки
для луча является фронтальным следом, а для точки 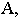 через которую проходит этот луч, – тенью её на плоскость проекций
через которую проходит этот луч, – тенью её на плоскость проекций 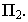 Аналогично, точка
Аналогично, точка 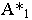 для луча служит горизонтальным следом, а для точки
для луча служит горизонтальным следом, а для точки 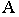 – тенью на
– тенью на 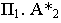 – реальная тень,
– реальная тень, 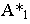 – мнимая тень точки
– мнимая тень точки 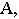 так как луч пересекает плоскость
так как луч пересекает плоскость 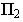 раньше, чем
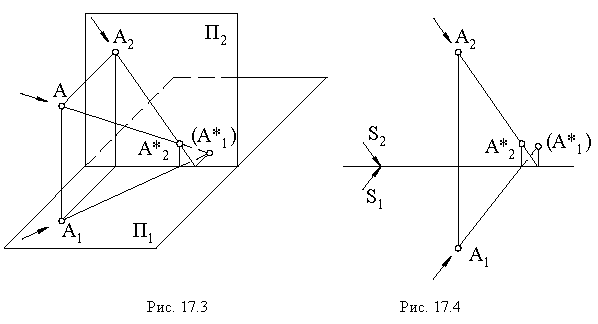
раньше, чем 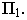 На рис. 17.4 показано построение тени точки на эпюре.
На рис. 17.4 показано построение тени точки на эпюре.
Тень от точки на плоскую фигуру
Чтобы построить тень от точки на плоскость общего положения (рис. 17.5), необходимо найти точку пересечения луча света, проходящего через заданную точку  с плоскостью
с плоскостью 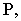 заданной четырехугольником
заданной четырехугольником 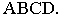 Для этой цели через проекции точки
Для этой цели через проекции точки 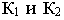 проводятся проекции светового луча, световой луч заключается в горизонтально-проецирующую плоскость
проводятся проекции светового луча, световой луч заключается в горизонтально-проецирующую плоскость 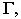 определяется линия пересечения
определяется линия пересечения 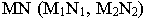 плоскости
плоскости 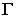 с плоскостью
с плоскостью 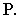 Точка пересечения светового луча
Точка пересечения светового луча 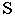 с линией
с линией 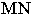 определяет точку пересечения светового луча
определяет точку пересечения светового луча 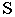 с плоскостью
с плоскостью 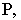 т.е. тень от точки
т.е. тень от точки 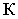 на плоскость четырехугольника
на плоскость четырехугольника 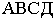 – точка
– точка 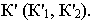
- Заказать чертежи
Тень от прямой линии
Построение тени от отрезка прямой линии сводится к определению тени двух или нескольких его точек. Тень от прямой можно рассматривать как след лучевой плоскости, проходящей через данную прямую. В зависимости от положения прямой, лучевая плоскость может быть общего и частного положения. Линия пересечения её с плоскостями или поверхностями определит форму тени от отрезка прямой.
Тени на плоскости проекций от прямые частного положения
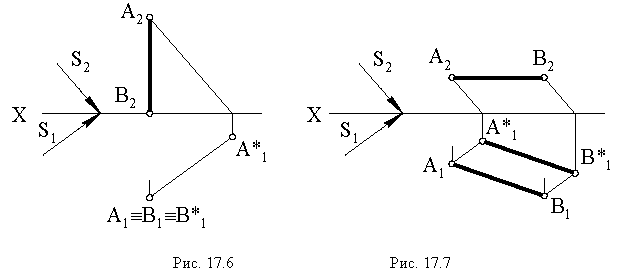
Построение тени от отрезка прямой 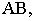 перпендикулярной плоскости проекций
перпендикулярной плоскости проекций 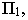 показано на рис. 17.6.
показано на рис. 17.6.
Тень 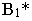 от точки
от точки 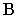 совпадает с самой точкой, т.к. точка
совпадает с самой точкой, т.к. точка 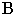 расположена на плоскости проекций
расположена на плоскости проекций 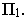 Следовательно, для построения тени отрезка
Следовательно, для построения тени отрезка 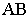 достаточно построить тень
достаточно построить тень 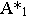 от точки
от точки 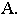 Соединив точки
Соединив точки 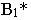 и
и 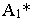 прямой линией, получим тень от отрезка
прямой линией, получим тень от отрезка 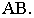
Вывод. Тень от прямой, перпендикулярной плоскости проекций, совпадает с проекцией светового луча на эту плоскость.
На рис. 17.7 показано построение тени от отрезка прямой 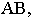 параллельной плоскости проекций
параллельной плоскости проекций 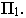
Вывод. Тень от отрезка прямой, параллельной плоскости проекций, на этой плоскости равна и параллельна самому отрезку.
Тени на плоскости проекций от прямых общего положения
На рис. 17.8 показано построение тени от отрезка прямой 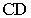 общего положения. Строим падающие тени
общего положения. Строим падающие тени 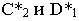 от точек
от точек 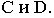 Тень от точки
Тень от точки 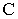 падает на фронтальную плоскость проекций, а тень от точки
падает на фронтальную плоскость проекций, а тень от точки 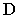 – на горизонтальную. Следовательно, тень отрезка прямой будет преломляться в точке на оси проекций. Эта точка называется точкой перелома тени. Для нахождения точки перелома тени построим тень от отрезка прямой
– на горизонтальную. Следовательно, тень отрезка прямой будет преломляться в точке на оси проекций. Эта точка называется точкой перелома тени. Для нахождения точки перелома тени построим тень от отрезка прямой 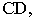 предположив, что тень от него падает только на горизонтальную плоскость. Мысленно уберем плоскость проекций
предположив, что тень от него падает только на горизонтальную плоскость. Мысленно уберем плоскость проекций 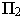 и построим мнимую тень
и построим мнимую тень 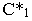 от точки
от точки 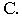 Соединив точки
Соединив точки 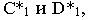 получим на оси
получим на оси 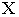 точку перелома
точку перелома 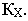 Таким образом, тень от отрезка будет ломаная линия
Таким образом, тень от отрезка будет ломаная линия 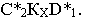 Точку перелома можно получить также, если взять на отрезке какую-нибудь дополнительную точку и построить от неё тень. На рис. 17.8 это будет точка 1.
Точку перелома можно получить также, если взять на отрезке какую-нибудь дополнительную точку и построить от неё тень. На рис. 17.8 это будет точка 1.
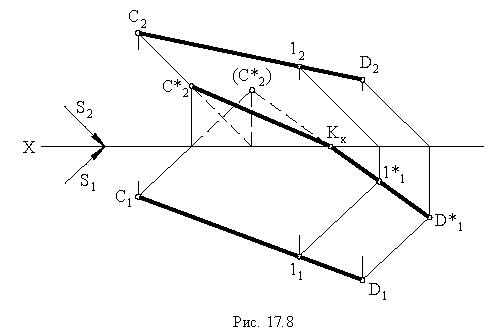
Тень от прямой на произвольную плоскость
Для построения тени от прямой на плоскость общего положения достаточно определить тени на эту плоскость от двух любых точек прямой (см. построение тени от точки на плоскую фигуру, рис. 17.5).
Тень от плоской фигуры
Падающая тень от плоской фигуры на плоскости проекций может быть построена как совокупность теней от её вершин и сторон. Таким образом, построение тени от плоской фигуры на плоскость проекций может быть сведено к известному определению теней от точек и прямых.
На рис. 17.9 показано построение тени от треугольника 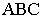 на плоскости проекций. Известным способом построены тени от вершин треугольника
на плоскости проекций. Известным способом построены тени от вершин треугольника 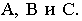 Тени от вершин падают на разные плоскости, и для определения действительной тени треугольника построена мнимая тень
Тени от вершин падают на разные плоскости, и для определения действительной тени треугольника построена мнимая тень 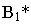 вершины
вершины 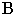 (см. рис. 17.9).
(см. рис. 17.9).
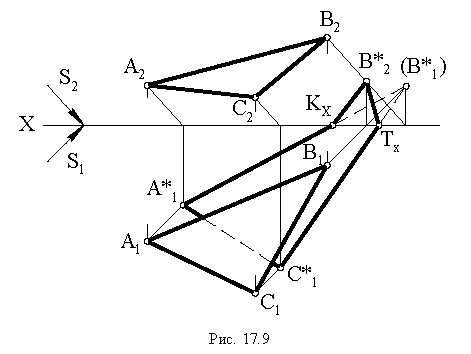
На рис. 17.10 построена тень от круглой пластины, перпендикулярной плоскости проекций 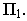 Вокруг заданной пластины опишем квадрат и проведем в нём диагонали. Построим тени от сторон, диагоналей и вспомогательных прямых
Вокруг заданной пластины опишем квадрат и проведем в нём диагонали. Построим тени от сторон, диагоналей и вспомогательных прямых 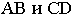 этого квадрата. Точки
этого квадрата. Точки 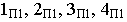 делят тени каждой стороны пополам, а точки
делят тени каждой стороны пополам, а точки 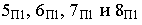 располагаются на пересечении теней от диагоналей и вспомогательных прямых
располагаются на пересечении теней от диагоналей и вспомогательных прямых 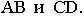
Соединив полученные точки, получим контур падающей тени круглой пластины, перпендикулярной плоскости 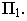
Метод обратных лучей
Метод обратных лучей применяется при построении теней, падающих от одного предмета на другой. Суть метода заключается в том, что строят тени заданных геометрических фигур на одну из плоскостей проекций и определяют точки пересечения теней. Через отмеченные точки проводят луч, направление которого противоположно световым лучам. Каждый из обратных лучей, пересекая данные геометрические фигуры, определяет нужные для построения тени точки.
На рис. 17.11 показано применение этого метода на примере построения тени прямой на плоскость треугольника. Построены падающие тени треугольника 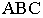 и отрезка
и отрезка 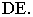 Обе тени падают на горизонтальную плоскость проекций и пересекаются в точках
Обе тени падают на горизонтальную плоскость проекций и пересекаются в точках 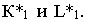 Проведем обратные лучи из точек
Проведем обратные лучи из точек 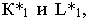 до пересечения с горизонтальными проекциями сторон
до пересечения с горизонтальными проекциями сторон 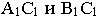 треугольника
треугольника 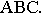 Прямая
Прямая 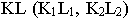 является тенью отрезка
является тенью отрезка 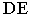 на плоскости треугольника
на плоскости треугольника 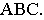
Вывод. Если падающие тени двух геометрических образов пересекаются, то тень от одного из них будет падать на другой
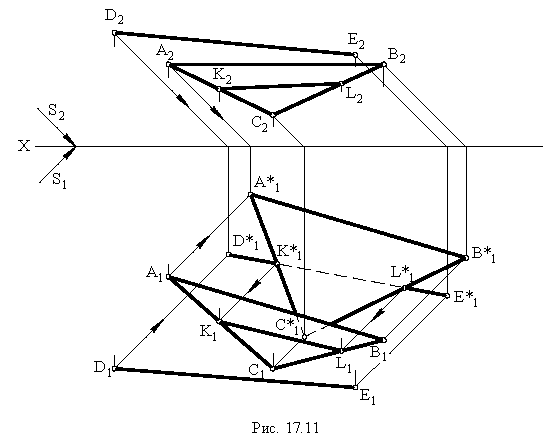
Тени геометрических тел
При построении теней геометрических тел вначале определяют контур собственной тени, затем находят контур падающей тени путем построения падающих теней от вершин и сторон ломаной линии (или точек кривой линии), являющейся контуром собственной падающей тени
В отдельных случаях бывает целесообразно определять контур собственной тени по уже построенной падающей тени.
Рассмотрим процесс построения теней от основных геометрических тел.
Тени призмы
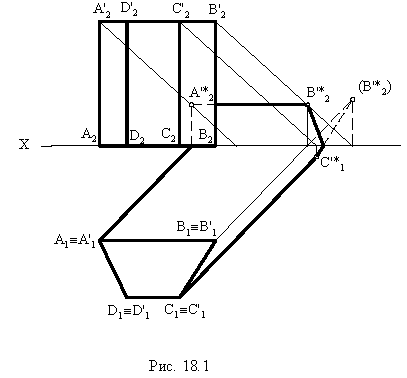
Контур тени от призмы определяется тенями от рёбер (рис. 18.1). Освещенность призмы легко определить по горизонтальной проекции, где видно, что обращенными к свету являются две грани 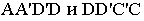 – и верхнее основание призмы. Следовательно, контуром собственной тени будет ломаная линия
– и верхнее основание призмы. Следовательно, контуром собственной тени будет ломаная линия 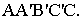 Тень, построенная от этой линии, представляет собой падающую тень призмы.
Тень, построенная от этой линии, представляет собой падающую тень призмы.
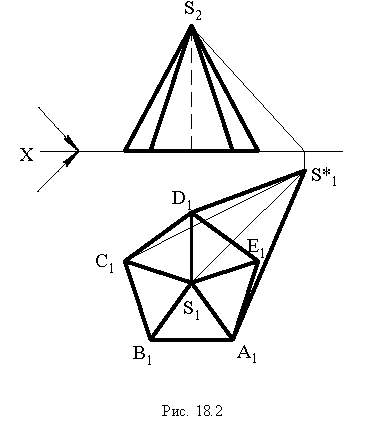
Тени пирамиды
Построим тени пятиугольной пирамиды (рис. 18.2). Строим падающую тень 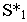 от вершины
от вершины 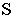 и определяем падающую тень от боковых ребер. Соединим точки
и определяем падающую тень от боковых ребер. Соединим точки 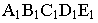 с точкой
с точкой 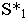 (на чертеже прямые
(на чертеже прямые 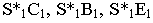 не показаны). Линиями контура падающей тени оказались прямые
не показаны). Линиями контура падающей тени оказались прямые 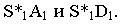 Поэтому в собственной тени будут находиться грани
Поэтому в собственной тени будут находиться грани 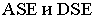 и основание пирамиды
и основание пирамиды
Тени цилиндра
Для определения контура собственной тени прямого кругового цилиндра необходимо провести две горизонтально-проецирующие лучевые плоскости 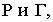 касательные к поверхности цилиндра и составляющие с плоскостью проекций
касательные к поверхности цилиндра и составляющие с плоскостью проекций 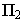 угол
угол 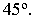 Образующие
Образующие 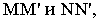 по которым плоскости
по которым плоскости 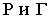 касаются цилиндра, и полуокружности
касаются цилиндра, и полуокружности 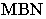 нижнего и верхнего оснований определяют контур собственной тени Контур падающей тени от цилиндра состоит из падающих теней от образующих
нижнего и верхнего оснований определяют контур собственной тени Контур падающей тени от цилиндра состоит из падающих теней от образующих 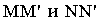 и полуокружностей
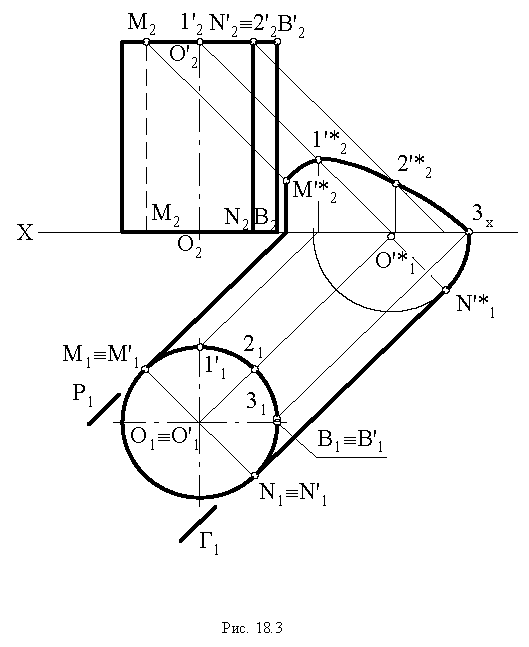
и полуокружностей 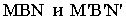 (рис. 18.3). Цилиндр расположен так, что тень от него одновременно падает на обе плоскости проекций, и тень от полуокружности
(рис. 18.3). Цилиндр расположен так, что тень от него одновременно падает на обе плоскости проекций, и тень от полуокружности 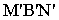 на плоскость проекций
на плоскость проекций 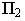 строится по произвольно выбранным на этой полуокружности точкам 1, 2.
строится по произвольно выбранным на этой полуокружности точкам 1, 2.
Тени конуса
На рнс. 18.4 показано построение собственной и падающей теней прямого кругового конуса. Вначале определяем мнимую тень от вершины конуса 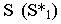 на плоскости его основания
на плоскости его основания 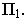 Затем из точки
Затем из точки 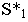 проводим прямые, касательные к основанию конуса, и определяем точки касания
проводим прямые, касательные к основанию конуса, и определяем точки касания 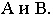 Через точки касания
Через точки касания 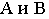 проводим образующие конуса
проводим образующие конуса 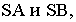 которые вместе с дугой основания
которые вместе с дугой основания 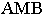 образуют контур собственной тени конуса. Падающая тень конуса имеет точки излома на оси
образуют контур собственной тени конуса. Падающая тень конуса имеет точки излома на оси 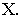
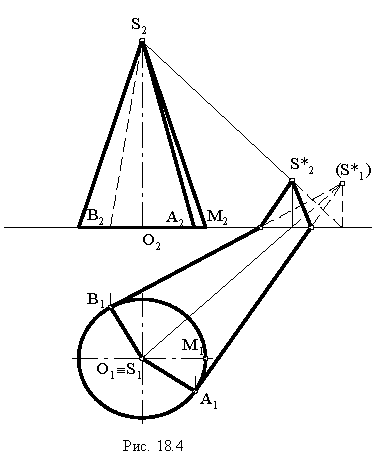
Тени элементов зданий
При построении проекций теней на фасадах зданий используются те же приемы, что и при построении теней геометрических тел.
Рассмотрим примеры построения теней некоторых частей здания
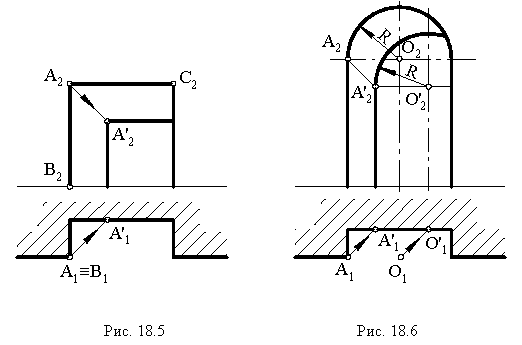
На рис. 18.5 показан пример построения теней в плоской нише. Определение границы падающей тени заключается в построении тени от ломаной линии 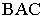 на заднюю плоскость ниши. От вертикального ребра
на заднюю плоскость ниши. От вертикального ребра 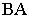 тень падает на горизонтальную плоскость проекций
тень падает на горизонтальную плоскость проекций 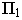 и на фронтальную плоскость задней стенки ниши. От горизонтального ребра
и на фронтальную плоскость задней стенки ниши. От горизонтального ребра 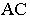 тень падает частично на заднюю фронтальную стенку ниши в виде прямой, параллельной ребру
тень падает частично на заднюю фронтальную стенку ниши в виде прямой, параллельной ребру 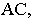 и частично – на правую боковую грань ниши (на чертеже не изображена).
и частично – на правую боковую грань ниши (на чертеже не изображена).
На рис. 18.6 приведен пример построения тени в прямоугольной нише с цилиндрической аркой В этом примере надо найти тень от точки 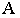 (пяты арки) и от центра
(пяты арки) и от центра 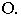 Из полученной точки (тени)
Из полученной точки (тени) 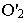 центра арки проводим дугу в пределах ниши радиусом, равным радиусу самой арки.
центра арки проводим дугу в пределах ниши радиусом, равным радиусу самой арки.
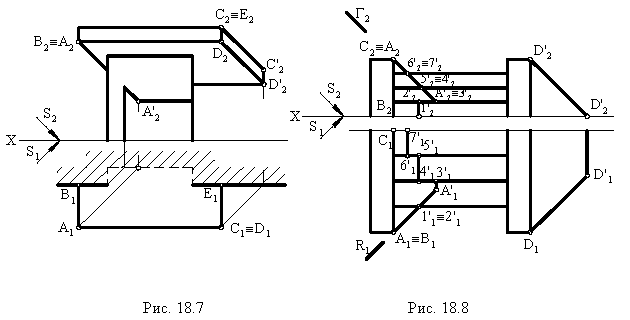
На рис. 18.7 построена тень от козырька (или балкона) здания Построения понятны из чертежа.
На рис. 18.8 показано построение теней на лестнице (крыльце). В собственной тени находятся правые грани вертикальных стенок. Падающая тень от правой стенки лестницы на плоскость стены здания и на землю строится как тень от плоской фигуры на плоскости проекций  Падающая тень от левой стенки на ступени лестницы строится методом секущих лучевых плоскостей. Этот способ заключается в том, что через заданную прямую проводится лучевая плоскость. Линия пересечения этой лучевой плоскости с произвольной поверхностью будет падающей тенью от прямой на поверхность. Через отрезок
Падающая тень от левой стенки на ступени лестницы строится методом секущих лучевых плоскостей. Этот способ заключается в том, что через заданную прямую проводится лучевая плоскость. Линия пересечения этой лучевой плоскости с произвольной поверхностью будет падающей тенью от прямой на поверхность. Через отрезок  параллельно световому лучу
параллельно световому лучу  проводим лучевую плоскость
проводим лучевую плоскость 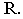 Так как отрезок
Так как отрезок 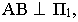 то плоскость
то плоскость 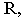 проходящая через него, будет горизонтально-проецирующей
проходящая через него, будет горизонтально-проецирующей 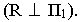 Горизонтальный след этой плоскости
Горизонтальный след этой плоскости 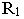 параллелен горизонтальной проекции светового луча:
параллелен горизонтальной проекции светового луча: 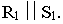 Ломаная линия
Ломаная линия 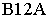 является линией пересечения многогранной поверхности лестницы плоскостью
является линией пересечения многогранной поверхности лестницы плоскостью 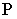 и тенью от прямой
и тенью от прямой 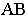 на ступени лестницы Через отрезок
на ступени лестницы Через отрезок 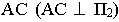 проводим фронтально-проецирующую плоскость
проводим фронтально-проецирующую плоскость 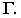 Фронтальный след этой плоскости
Фронтальный след этой плоскости 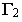 параллелен фронтальной проекции светового луча:
параллелен фронтальной проекции светового луча: 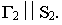 Ломаная линия
Ломаная линия 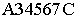 является линией пересечения многогранной поверхности лестницы плоскостью
является линией пересечения многогранной поверхности лестницы плоскостью 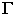 и тенью от прямой
и тенью от прямой 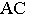 на ступени лестницы
на ступени лестницы
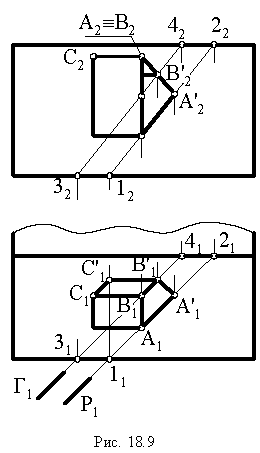
На рис. 1S.9 показано построение контура падающей тени от трубы на скат крыши здания Задача сводится к определению теней от точек и прямых на произвольно расположенную плоскость (скат крыши). Построения выполнены способом вспомогательных секущих лучевых плоскостей 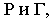 которые пересекают скат крыши по прямым 12 и 34.
которые пересекают скат крыши по прямым 12 и 34.
Тени в перспективе
При построении теней в перспективе в качестве источника света рассматривается естественный источник – солнце. Правила построения теней в перспективе точно такие же, как и в ортогональных проекциях.
Для упрощения построения считают, что световые лучи параллельны плоскости картины, тогда на картине перспективы оснований лучей будут параллельны основанию картины
Если на картине задана перспектива  точки
точки 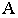 и перспектива
и перспектива 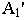 ее основания
ее основания 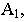 то для построения тени от точки
то для построения тени от точки 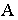 на предметной плоскости (рис. 18.10) необходимо на картине через перспективу
на предметной плоскости (рис. 18.10) необходимо на картине через перспективу 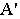 точки
точки 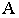 провести перспективу луча света, а через перспективу
провести перспективу луча света, а через перспективу 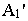 ее основания – перспективу основания луча. В месте пересечения луча и его основания получим точку, которая и будет искомой тенью
ее основания – перспективу основания луча. В месте пересечения луча и его основания получим точку, которая и будет искомой тенью 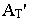 от точки
от точки 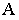 на предметной плоскости.
на предметной плоскости.
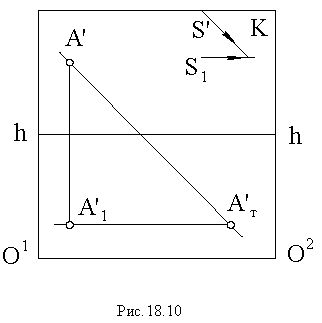
Построение тени от прямой сводится к построению тени от двух ее точек. При этом, если прямая перпендикулярна предметной плоскости (рис. 18.11), то тень от нее на этой плоскости совпадает с основанием луча, проведенного через основание прямой.
Тень от вертикальной прямой на вертикальной плоскости вертикальна.
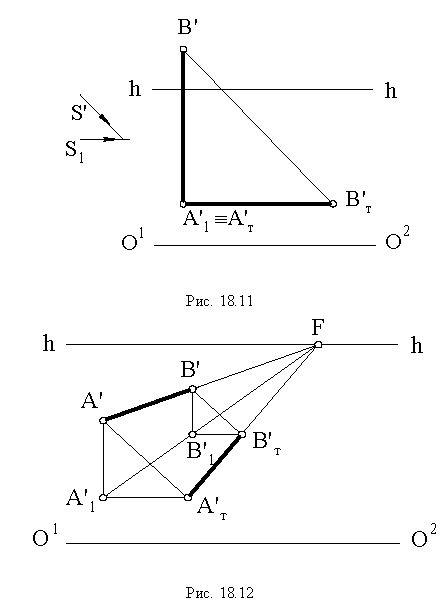
Если прямая параллельна предметной плоскости (горизонтальная прямая), то тень от нее на этой плоскости будет параллельна данной прямой (рис. 18.12) и направлена в точку схода.
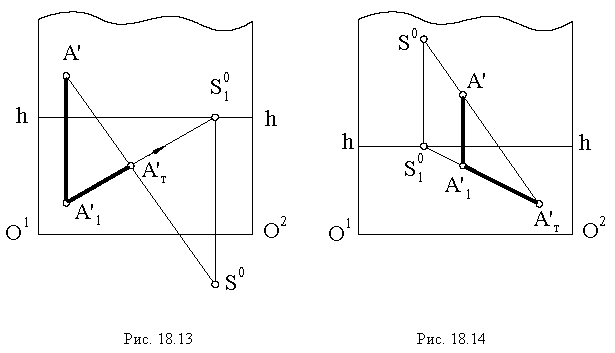
Тени в перспективе могут быть построены с различных точек расположения источника света. Направление лучей света может быть выбрано в зависимости от характера объекта и от желания показать его освещенным с той или другой стороны. Так, например, если источник света будет находиться позади предмета (рис. 18.13) или перед зрителем, но позади предмета (рис. 18.14), то для построения перспективы тени 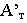 точки
точки 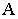 на плоскость
на плоскость 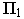 необходимо выполнить следующие действия: через точку
необходимо выполнить следующие действия: через точку 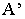 и точку схода лучей
и точку схода лучей 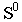 провести перспективу луча (прямую
провести перспективу луча (прямую 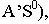 а через ее вторичную проекцию
а через ее вторичную проекцию 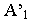 – вторичную проекцию луча (прямую
– вторичную проекцию луча (прямую 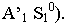 Пересечение перспективы луча его вторичной проекцией определит тень
Пересечение перспективы луча его вторичной проекцией определит тень 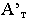 точки
точки  на плоскость
на плоскость 
- Кривые поверхности
- Пересечения криволинейных поверхностей
- Пересечения поверхностей с прямой и плоскостью
- Взаимное пересечение поверхностей
- Развертки поверхностей
- Способы преобразования проекций
- Взаимное положение прямой и плоскости
- Решение метрических задач
