Как найти тень у шара

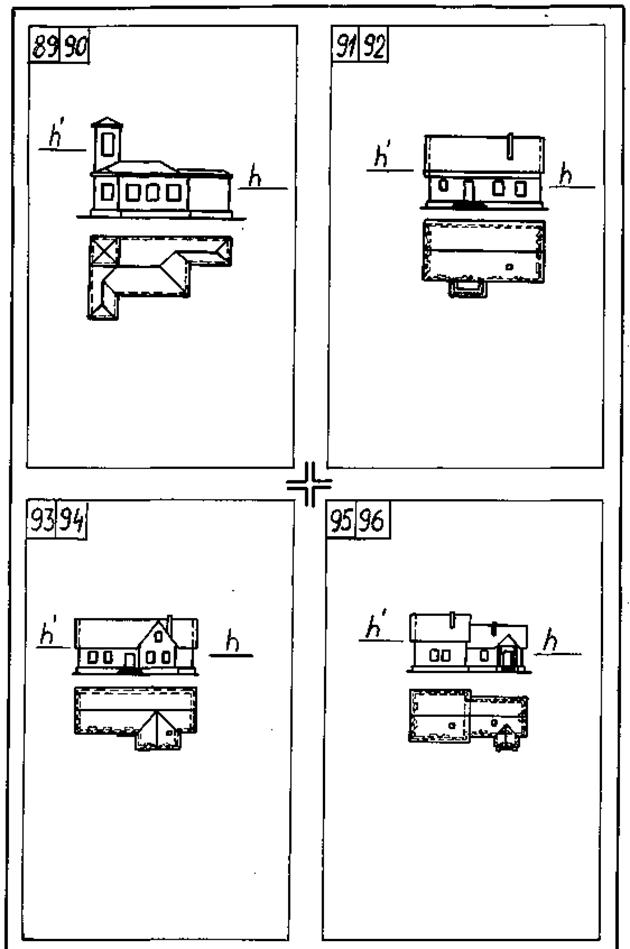
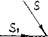Множество лучей,
падающих на шар (рис. 37), образует световой
цилиндр,
соосный с его поверхностью, поэтому
общим элементом для двух поверхностей
(на основании леммы о пересечении соосных
поверхностей) будет окружность,
представляющая собой контур
собственной тени шара.
Теневой цилиндр пересекает плоскость
H
по эллипсу, который является падающей
тенью шара.
При нахождении очертаний этих теней
можно использовать преобразование
чертежа, например, метод перемены
плоскостей проекций. Проведем плоскость
V₁,
параллельную направлению S,
и построим
новые фронтальные проекции шара и луча.
Контур собственной тени шара отобразится
на этой плоскости отрезком прямой [а₁‘
b₁‘].
Поскольку аппликаты всех точек контура
в старой и новой системе плоскостей
проекций одинаковы, можно найти множество
точек, принадлежащих очертанию контура
на обеих проекциях. Вначале определим
с помощью характерных точек размеры
осей эллипсов, в которые проецируется
контур, а затем аналогичным образом
построим необходимое количество
случайных точек. Соединив плавной кривой
линией одноименные проекции найденных
точек с учетом видимости, получим
проекции очертания контура собственной
тени.

Построение падающей
тени шара начнем с нахождения тени точки
O(o,
o’)
(центра шара) – точки о_Т.
Искомая тень на плоскости V₁
отобразится
прямолинейным отрезком, равным большой
оси искомого эллипса

Размер малой оси
эллипса [m_1Т
n_1Т]
равен диаметру шара. Нахождение случайных
точек очертания контура выполняется
следующим образом:

На
построенном контуре собственной тени
берется произвольная точка
и
определяется ее падающая тень. По
множеству найденных падающих теней
случайных точек завершаем построение
эллипса (нахождение случайных точек на
чертеже не показаны для удобства
восприятия изображений).

Рис. 37. Построение
теней на шаре

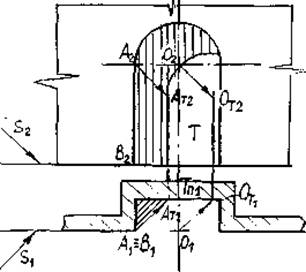
На рис. 38 показан
другой способ нахождения теней шара.
Как отмечалось выше, контурами собственных
теней шара
являются эллипсы. Большие оси этих
эллипсов – отрезки [ab]
и [c‘d‘]
равны диаметру шара. Точки A
A(a,
a’)
и B
(b,
b’)
расположены на экваторе сферы, а C(c,
c’)

и D(d,
d’)
на главном меридиане, плоскость которого
параллельна V.
Учитывая симметрию эллипса относительно
его большой и малой осей, можно получить
точки, симметричные точкам c
и d,
и а‘
и b‘
на соответствующих проекциях. После
этого по восьми полученным точкам
выполнить очертание эллипсов с учетом
видимости.

Построение падающей
тени шара как и в предыдущем случае
начинаем с нахождения точки о_Т.
Малая ось эллипса, представляющего
собой падающую тень, равна отрезку [a_Т
b_Т].
Большая полуось – высоте правильного
треугольника, построенного на отрезке
[a_Т
b_Т]
Определив точку n_Т,
строим
точку, ей симметричную относительно
оси [a_Т
b_Т].
По большой
и малой оси можно построить
эллипс различными способами (их около
шестисот!), один из которых показан на
рис. 38 в правом нижнем углу – способ
родственного соответствия. Ввиду того,
что этот раздел не изучается студентами
в курсе начертательной геометрии,
приведем только порядок нахождения
случайных точек искомого эллипса.

Рис.
38. Второй способ нахождения теней шара

С центром в точке
о_Т
построим
две окружности, диаметры которых равны
большой и малой осям эллипса. Затем
через точку о_Т
проведем
какой-либо луч и отметим точки его
пересечения с каждой окружностью.

Из полученных
точек проведем прямые, параллельные
большой
и малой осям и на их пересечении
зафиксируем одну из искомых точек
эллипса, На рисунке ниже показано
построение одной из таких точек – точки
1_Т.
Остальные точки определяются аналогично
и соединяются плавной кривой.

В том случае, когда
требуется определить собственную тень
шара на одном изображении, можно
воспользоваться приемом, показанным
на рис. 39.

Рис.
39. Построение собственной тени
шара по 8-ми
точкам

Точки 1,2,…, 8
указывают на последовательность
нахождения восьми точек искомого
эллипса.

Аналитическое
обоснование этому приему существует,
но в данной работе не приводится.

Рассмотрим некоторые
задачи, связанные с построением теней
на поверхности шара.

З а д а ч а 1

Определить тень
точки А
на поверхности шара (рис. 40).

Решение данной
задачи сводится к нахождению точки
пересечения светового луча, проведенного
через точку А,
с поверхностью шара.

Поскольку в задаче
не ставится вопрос о нахождении
собственных и падающих теней шара, то
достаточно определить только точки
пересечения светового луча с поверхностью
шара.

Задачи такого рода
решаются по известному алгоритму:

1. луч заключается
в какую-либо плоскость (или поверхность);

2. строится линия
пересечения данной поверхности с
проведенной плоскостью (или поверхностью)
– фигура сечения;

3. определяются
искомые точки пересечения луча с
построенной фигурой сечения.

Поскольку луч
занимает в пространстве общее положение,
авторы учебников по начертательной
геометрии обычно рекомендуют применять
в
этом случае преобразование чертежа
(например, метод замены плоскостей
проекций), для того чтобы луч или прямая
линия заняли в пространстве частное
положение, поскольку только в этом
случае можно получить точное решение
задачи.

Рис.
40. Решение задачи 1

Заметим, что
преобразованные чертежи имеют большие
достоинства: они легко читаются, их
применение позволяет избежать построения
лекальных кривых по множеству точек и
получить точное решение задачи. Но, к
сожалению, преобразованные чертежи
занимают большую площадь на поле листа
бумаги и потому являются довольно
громоздкими.

Известно, что любую
задачу по начертательной геометрии
можно решить, не прибегая к преобразованию
чертежа. Покажем, как в данной задаче
обойтись без последнего и в то же время
получить точное решение.

Воспользуемся
приведенным выше алгоритмом нахождения
точки пересечения прямой линии с
поверхностью:

1.заключим световой
луч, проходящий через точку А,
в коническую поверхность вращения,
соосную со сферой. За вершину этой
поверхности примем точку T
(t,
t‘),
лежащую в плоскости главного меридиана
сферы. Ось конической поверхности
определится парой точек O
(o,
o‘)
и T
(t,
t‘).

Для построения
главного меридиана конической поверхности,
параллельного плоскости V,
применим способ прямоугольного
треугольника

(рис.
40), который реализован на графическом
условии данной задачи,
а необходимые
пояснения к нему приведены на этом же
рисунке справа.

После построения
очертания конической поверхности
перейдем
к выполнению второго пункта
алгоритма:

2. найдем линию
пересечения данной сферы с проведенной
вспомогательной поверхностью;

Обе поверхности
сосны по построению, поэтому согласно
лемме
о пересечении соосных поверхностей
они пересекутся по окружностям столько
раз, сколько раз пересекутся их главные
полумеридианы. В данном случае пересечение
произошло по двум окружностям, которые
на фронтальной проекции отобразились
отрезками прямых линий (на
рис. 40
показана только одна из них, которая
задействована в задаче).

3. Определяем
искомые точки пересечения светового
луча, принадлежащего конической
поверхности, с построенными фигурами
сечения (окружностями).

На эпюре зафиксирована
только одна точка а_Т‘
поскольку она является действительной
тенью точки А
на фронтальной проекции. Горизонтальную
проекцию а_Т
определим с помощью линии связи на
горизонтальной проекции луча, пользуясь
свойством принадлежности.

З а д а ч а 2

Построить тень
отрезка [AB]
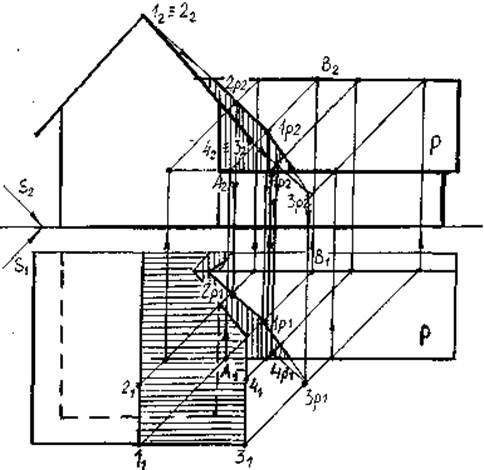
на поверхности шара (рис. 41).

Наличие собственной
тени для решения поставленной задачи
необходимо. Способ ее нахождения изложен
ранее. Применять способ обратных лучей
для этой задачи нерационально, поскольку
по условию не требуется определение
падающих теней шара.

Подойдем к решению
задачи следующим образом. Из аналитической
геометрии известно, что любая плоскость
пересекает сферу по окружности. Лучевая
плоскость, проходящая через отрезок
[AB]
– горизонтально-проецирующая, поэтому
пересекает сферу по окружности, которая
на горизонтальной проекции отобразится
отрезком прямой [12].

Рис.
41. Нахождение тени отрезка [AB]
на поверхности шара

Поскольку окружность
одновременно принадлежит лучевой
плоскости и данной сфере ее фронтальная
проекция (представляющая собой эллипс)
может быть построена по точкам, исходя
из условия их принадлежности поверхности
сферы. Точке обеспечивается принадлежность
сфере с помощью параллели, заведомо на
ней лежащей. Горизонтальная проекция
параллели отобразится окружностью,
фронтальная – отрезком прямой, на
котором определяется фронтальная
проекция точки. На рис. 41 показаны
построения всех характерных точек
кривой линии и нескольких случайных,
затем все точки соединены плавной
кривой.

Точка пересечения
светового луча с построенным по точкам
эллипсом является действительной тенью
точки А
на поверхности шара, от которой идет
дальнейшее отбрасывание тени отрезка
[AB]
вплоть до точки
K
(k,
k‘),
построенной на этом отрезке способом
обратного луча, после того как на
фронтальной проекции определена точка
k_Т‘
пересечением
контура собственной тени с дугой эллипса.
Отрезок [KB]
частично отбрасывает тень на поверхность
шара в области его собственной тени и
на землю (плоскость H)
в виде горизонтального следа лучевой
плоскости.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Шар, в рисунке становится объемным во многом благодаря светотени. Но с начала его, как и другие объемные фигуры, нужно построить.

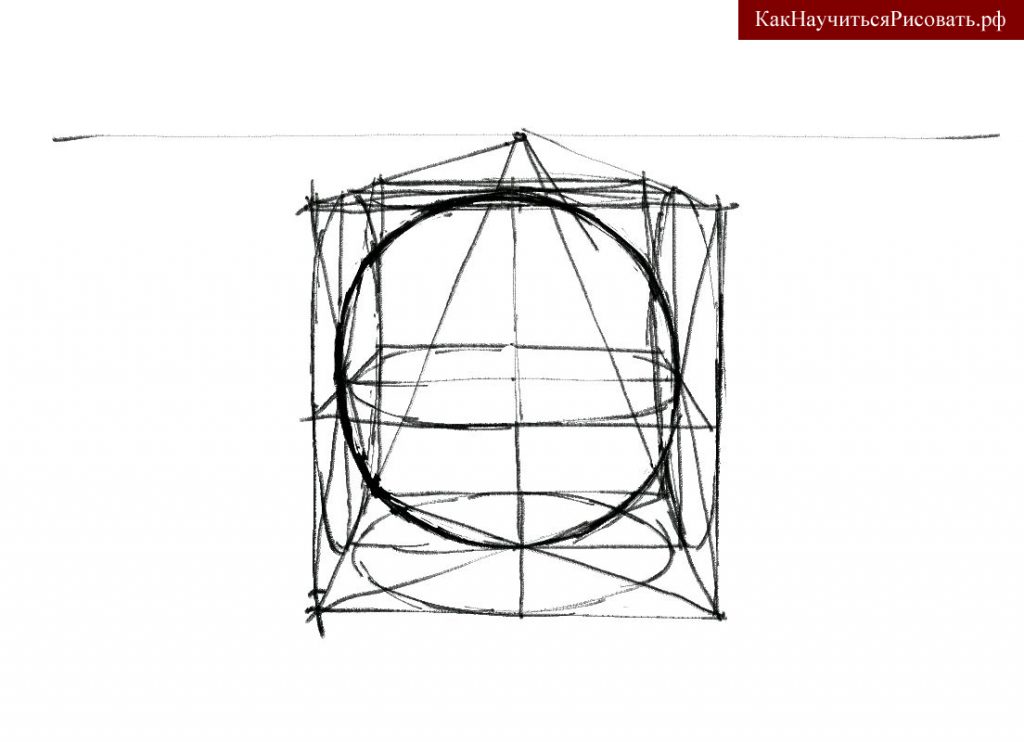
Построение шара

В отличии от других объемных фигур контурный рисунок шара не демонстрирует его объема. Например, в кубе контуры граней своим расположением и направлением указывают на наличие в кубе объема. Чтобы выявить объем в шаре, его нужно мысленно построить, а затем отобразить построение в рисунке. Без этого построения нанести грамотно тени будет затруднительно. Итак приступим.

Учебное построение шара

Определяем размер шара и вписываем его композиционно в рисунок. Следим за тем, чтобы контуры фигуры были максимально приближены к кругу. Далее, точно по центру проводим через весь круг горизонталь и вертикаль. Круг вписываем в квадрат. Этот квадрат будет центральным вертикальный срезом будущего куба, в который будет вписан будущий шар. Теперь строим тот самый куб во фронтальной проекции с одной точкой схода, срез которого только что нарисовали, и в который, в свою очередь, будет вписан будущий шар. Действие это умозрительное, так как в реальности куба не существует.

В учебных целях на всех сторонах куба делаем следующий рисунок. Соединяем диагоналями углы стороны куба. Пересечение диагоналей указывает на центры сторон куба. Через эти центры на всех сторонах куба проводим центральные вертикальные и горизонтальные линии, соединяющие противолежащие грани сторон куба. Следующее действие требует понимания того как строится круг в перспективе. На каждой из сторон куба рисуем эллипсы (круг, изображенный с учетом перспективных сокращений), которые являются проекциями будущего шара на поверхности куба. Еще один эллипс вписываем в центральный горизонтальный срез куба. Этот эллипс является центральным горизонтальным срезом шара.

Проверим правильность выполнения предыдущих действий. Изначально нарисованный круг своим контуром должен проходить по центральным точкам четырех сторон куба: правой, левой, нижней, верхней. Если есть неточности, то их нужно устранить. Всех выше перечисленных манипуляций вполне достаточно для полного представления об объемном строении шара и дальнейшего нанесения на него светотени.

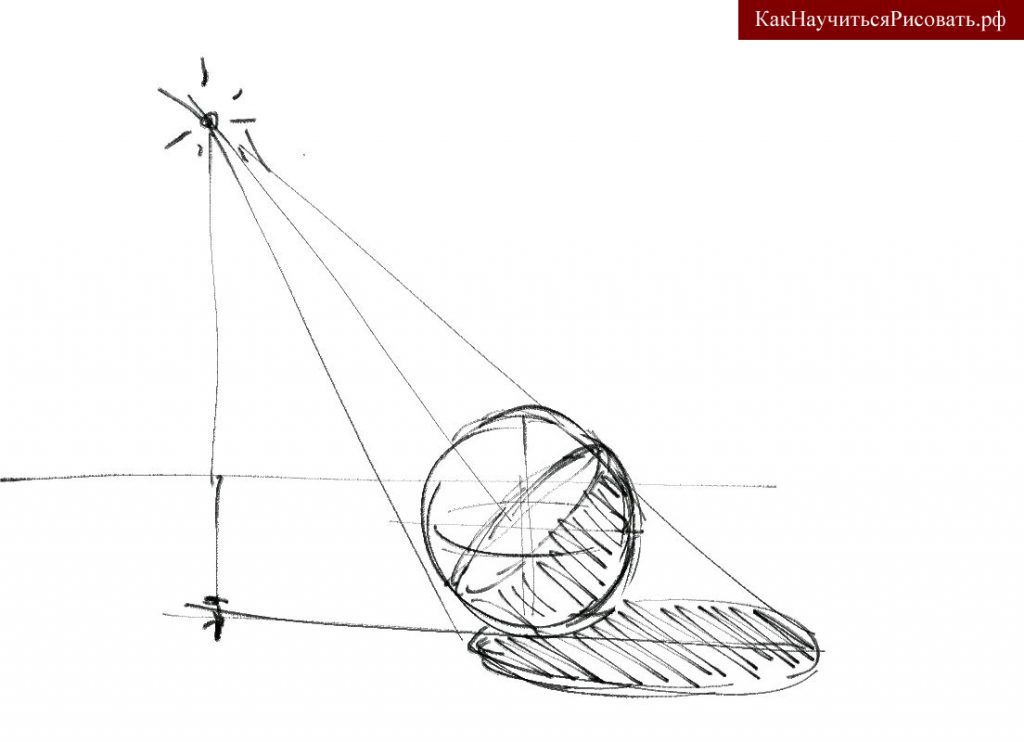
Светотеневой рисунок шара

Построение падающей тени от шара

Для начала отмечаем на рисунке источник света и проводим от него вертикаль. Проводим лучи от источника света через верх шара, от нижней точки вертикали, опущенной от источника света, через низ шара. Определяем точку пересечения лучей. Далее рисуем контуры падающей тени через полученную точку. В отличии от тех объектов, где есть грани, у шара контуры падающей тени следует рисовать путем измерений ее направлений и размеров на натуре.

Собственные свет и тень шара

Нарисовать собственную тень шара можно путем построения дополнительного сечения шара, которое будет перпендикулярно, падающим от источника света, лучам. Контуры данного сечения шара фактически будут указывать на границу светотени. В области этой границы будет самое темное пятно на шаре. От границы светотени в сторону света будет освещенная часть шара и блик, который располагается в той части шара, которая ближе всего к источнику света. С противоположной от света стороны располагается собственная тень шара и рефлексы от окружающих объектов, в том числе от поверхности, на которой расположен шар.

Окружающая атмосфера

При рисовании шара с использованием тона большое значение играет фон. Правильно оттененный фоном шар будет смотреться на рисунке действительно объемным. Единственный рецепт хорошего фона здесь — это наблюдать за натурой и стараться, как можно точнее передать увиденные тональные пятна и контрасты между ними. В дополнение лишь стоит смягчить контрасты на фоне, чтобы они смотрелись размытыми относительно главного объекта на переднем плане, то есть шара.

Тени от шара Тени от шара Тени от шара Тени от шара в ортогональных проекциях строим исходя из представления, что шар в лучах света формирует цилиндр, пересечение образующих которого с плоскостями проекций дает их линии пересечения или границы тени. На основании данного представления образования тени от шара выполняем для их построения следующее: – через центр шара O проводим луч сета и находим его следы MO и NO на плоскостях проекций; – через центр шара O, перпендикулярно световым лучам, проводим плоскость β, задав ее следами. Смотри Построение следов плоскости; – находим линию пересечения поверхности шара с плоскостью β, которая определяет границы собственной тени шара α, применяя для этого Перемена плоскости проекции; – приступаем к построению падающей тени от шара на горизонтальную плоскость проекции: – отмечаем на горизонтальной плоскости проекции G` и проведя через точку G вспомогательную горизонтально проецирующую плоскость δΗ находим ее недостающую проекцию G”, применяя при этом Конкурирующие точки и Определение видимости; – проводим лучи света через центр шара O и точку G находим их следы MO и MG на горизонтальной плоскости проекции, определяющие большую полуось эллипса; – проводим луч света через F находим ее след на горизонтальной плоскости проекции MF. Отрезок MO MF определяет малую полуось эллипса; – выполняем построение эллипса до точек перелома тени; – аналогично выполняем построение падающей тени от шара на фронтальную плоскость проекции. Тени от шара Тени от шара Световые лучи, касаясь поверхности шара, образуют обёртывающий лучевой цилиндр, который касается поверхности по окружности большого круга. Эта окружность является контуром собственной тени. Проекции её на H и V изображаются в виде одинаковых эллипсов. Большие оси эллипсов равны диаметру шара и направлены перпендикулярно проекциям светового луча. Малые оси эллипсов могут быть определены построением. Определение большой NM и малой AB оси эллипса, являющегося фронтальной проекцией контура собственной тени шара, а также точек C”, E”, D”, F” этого эллипса. Построение выполнено с помощью равностороннего треугольника с вершиной в точке M”, вписанного в окружность. Обёртывающий лучевой цилиндр пересекается с плоскостями проекций по эллипсам, являющимися контурами падающей тени. На горизонтальной плоскости проекций: малая ось этого эллипса MCMD равна диаметру шара и проходит через точку MO – тень центра, а большая ось MGMK может быть построена, как тень от оси GK эллипса, являющегося контуром собственной тени. На фронтальной плоскости проекций построение выполняется аналогично. +

Падающие тени от точки, прямой и плоской фигуры. Способ следа луча.

ТЕНИ В ОРТОГОНАЛЬНЫХ ПРОЕКЦИЯХ

При построении теней в ортогональных проекциях направление лучей света принимают параллельным диагонали куба, грани которого параллельны плоскостям проекций (рис. 1). Все три проекции диагонали наклонены к осям проекций под углом 45º.

Падающие тени от точки, прямой и плоской фигуры. Способ следа луча.

Чертёж любого сооружения состоит из отрезков прямых или кривых линий, которые в совокупности могут представлять различные геометрические формы.

Тень от точки на какую-либо поверхность (см. рис. 2) является точкой пересечения с этой поверхностью луча света, проведённого через данную точку. От точки, расположенной в пространстве тень может падать или на пл. π1 или π2 . На рис.2 показано построение тени точек А и В на эпюре. Из двух теней А_т и А т _у, В_т и В т _у, первые — А_т и В_т будут реальными и действительными, вторые — А т _у и В т _у будут мнимыми.

Тень от прямой линии на поверхность — это есть линия пересечения лучевой плоскости с этой поверхностью. Плоскость, проходящая через заданную прямую линию параллельно световому лучу называется лучевой плоскостью. Тень от прямой линии может быть точкой, прямой, ломаной или кривой.

Построение тени отрезка прямой на две плоскости проекций ведется в следующей последовательности:

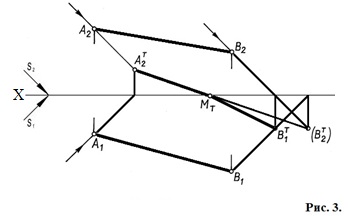
1. Тень отрезка на одну из плоскостей строят, предполагая, что второй не существует. В примере на рис. 3 сначала построена тень отрезка на фронтальную плоскость проекций.

2. Если построенная тень пересекает ось проекций, то в этой точке тень преломляется и с одной плоскости проекций переходит на другую. В эту точку и будет направлена преломившаяся тень отрезка прямой. На рис. 3 такой точкой является реальная тень точки В на горизонтальной плоскости проекций.

Закономерности расположения теней отрезков прямых частного положения:

· Если отрезок прямой параллелен плоскости, то тень от него на эту плоскость параллельна отрезку и равна ему по величине.

· Если прямая перпендикулярна к плоскости, то тень, падающая от неё на эту плоскость, совпадает с проекцией светового луча на этой плоскости.

· Если прямая параллельна направлению светового луча, то тень от неё – точка.

· Параллельные прямые имеют параллельные тени.

Тень плоских фигур

Построение теней плоской фигуры упрощается в тех случаях (см. рис. 4), когда точка или принадлежащая ей прямая, расположена в плоскости проекций, потому, что точки B и C или прямая BC совпадают со своей тенью.

Тень четырехугольника, занимающего общее положение.

Чтобы построить падающую тень плоской фигуры четырехугольника ABCD, занимающего общее положение (см. рис. 5), когда его вершины и стороны не принадлежат плоскостям проекций, нужно найти тени от каждой его вершины, соединив между собой прямыми линиями одноименные тени точек.

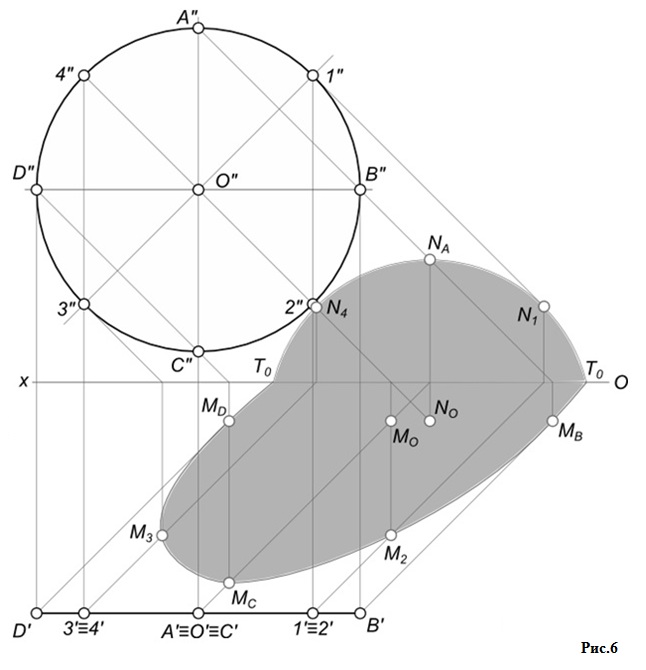
При построении тени круга, расположенного параллельно фронтальной плоскости проекций (см. рис. 6), разделяем круг на 8 равных частей и находим тени всех этих точек, которые соединяем плавной кривой. На фронтальной плоскости проекций достаточно найти тень от центра круга, которая послужит центром для проведения окружности, служащей контуром падающей тени от круга.

Тени геометрических тел

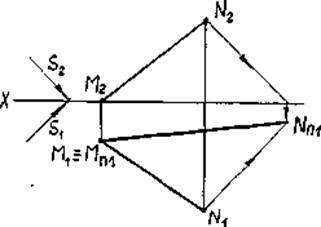
Построение тенипрямого параллелепипеда, стоящего на горизонтальной плоскости проекций (см. рис. 7).

Построение тенипрямого кругового цилиндра, стоящего на горизонтальной плоскости проекции.

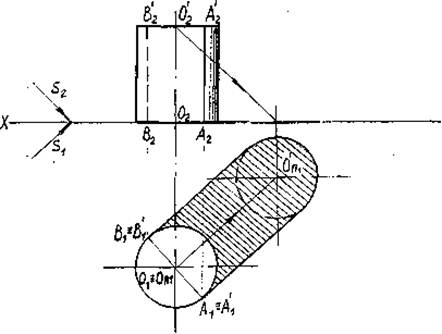
Чтобы построить контур собственной тени поверхности цилиндра (см. рис. 8), необходимо провести к этой поверхности касательные лучевые плоскости, параллельные направлению лучей света, и найти линии касания (образующие цилиндра). Вдоль этих образующих пройдет контур собственной тени.

Контур падающей тени от цилиндра состоит из падающих теней от образующих 2 и 4 и падающей тени от полуокружности DAB.

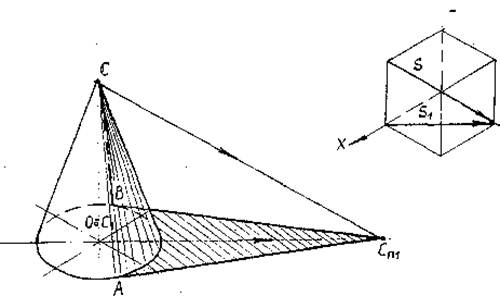
Построение тенипрямого кругового конуса, стоящего на горизонтальной плоскости проекций.

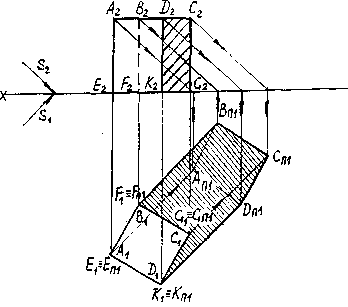
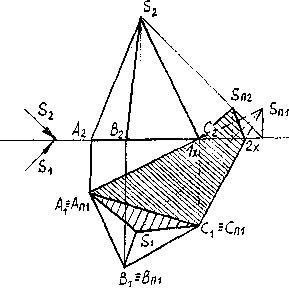
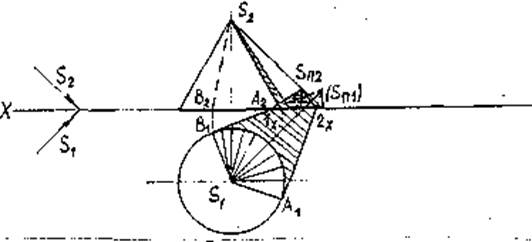
В данном случае (см. рис. 9), тень основания конуса совпадает с ним, остается найти тени только от вершины конуса, которые падают на фронтальную плоскость проекции в точку N_S и горизонтальную плоскость проекции в точку M_S. Из точки M_S проводим прямые касательные окружности основания и находим на ней точки A`≡M<sub>A</sub> и B`≡M_B, соединив которые с вершиной конуса S`, получим падающую тень конуса на горизонтальной плоскости проекций.

Падающую тень конуса на фронтальную плоскость проекции получим, соединив точки преломления T₀ и N_S.

Тени от шара в ортогональных проекциях строят исходя из представления, что шар в лучах света формирует цилиндр, пересечение образующих которого с плоскостями проекций дает их линии пересечения или границы тени, основываясь на этом представлении, выполняем следующее (см. рис. 10):

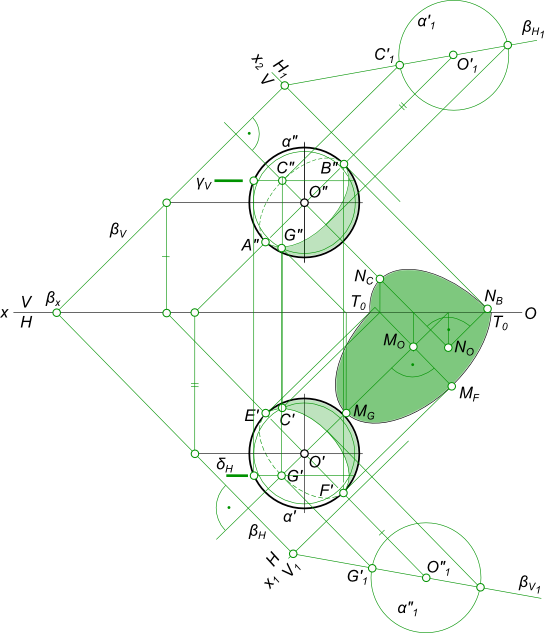
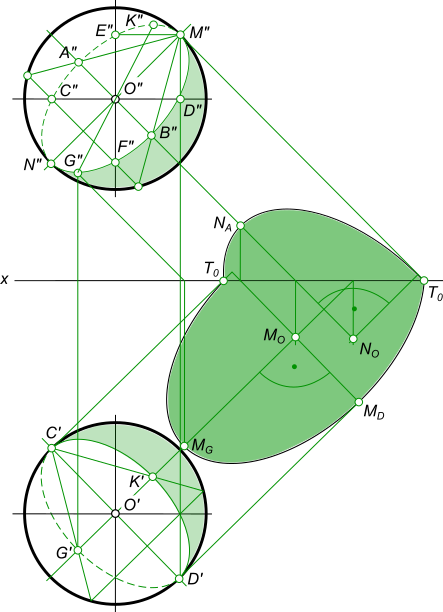
· через центр шара O проводим луч света и находим его следы M_O и N_O на плоскостях проекций;

· через центр шара O, перпендикулярно световым лучам, проводим плоскость β, задав ее следами;

· находим линию пересечения поверхности шара с плоскостью β, которая определяет границы собственной тени шара α, применяя для этого перемену плоскости проекции;

· отмечаем на горизонтальной плоскости проекции G` и проведя через точку G вспомогательную горизонтально проецирующую плоскость δ_Η находим ее недостающую проекцию G», применяя при этом конкурирующие точки и определение видимости;

· проводим лучи света через центр шара O и точку G находим их следы M_O и M_G на горизонтальной плоскости проекции, определяющие большую полуось эллипса;

· проводим луч света через точку F, находим ее след на горизонтальной плоскости проекции M_F. Отрезок M_O M_F определяет малую полуось эллипса; выполняем построение эллипса до точек перелома тени;

· аналогично выполняем построение падающей тени от шара на фронтальную плоскость проекции.

Построение теней разновысотных объектов

Источник

Тени в ортогональных проекциях и перспективе

На архитектурно-строительных чертежах изображают падающие и собственные тени. Тени придают чертежам наглядность.

Расположенный на пути света предмет отбрасывает на находящуюся за ним поверхность падающую тень. Неосвещенная часть поверхности предмета также находится в тени, которая называется собственной.

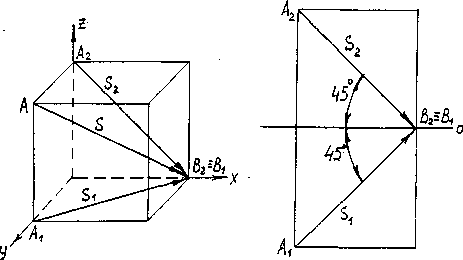
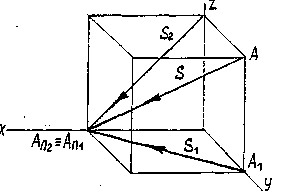
При построении теней направление лучей в ортогональных проекциях на архитектурных чертежах принято брать по диагонали куба (рис.9).

такое направление лучей света удобно при построении теней на фасадах зданий.1

Тень от точки и прямой.

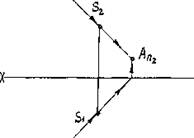
Тень от точки.

Тень от точки будет там, где луч света, проходящий через точку, пересекает поверхность, на которую падает тень.

Для получения тени от точки А через проекции A₁ и А₂ проводим проекции S₁ и S₂ луча S под углом 45 ° к оси проекций. Затем находим следы лучей как следы прямых линий, т.е. находим точку пересечения луча с плоскость проекций.

Для получения тени от точки А на плоскость П₁ продолжим фронтальную проекцию луча S₂ до пересечения с осью ОХ, далее проводим линию связи до пересечения с горизонтальной проекцией луча S₁. Получим тень от точки А на плоскость П₁ – A_П1 (рис.10).

Рис.10

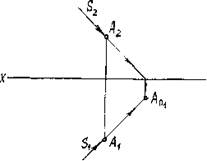
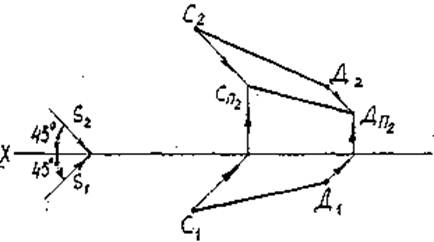
Для получения тени от точки А на плоскость П₂ продолжим S₁ до пересечения с осью ОХ, далее проводим линию связи до пересечения с фронтальной проекцией луча S₂. Получим тень от точки А на плоскость П₂ – А_П2 (рис.11).

1.2 Тень от отрезка прямой.

Тень от прямой на плоскость в общем случае прямая. Следовательно, чтобы построить тень от отрезка прямой, достаточно построить тень от двух его точек. Например, тень от отрезка АВ на плоскость П₁. Сначала строим тень А_П1 от точки А на плоскость П₁ (см. п. 1.1), затем тень В_П1 от точки В на плоскость П₁. Соединив тени точек A_П1 и В_П1 получим тень отрезка АВ на плоскость П₁ (рис.12).

Рис.12

Аналогично строим тень от отрезка CD на плоскость П₂ (рис13).

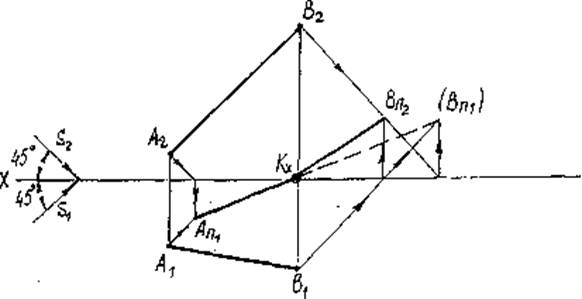
Если тень от прямой падает одновременно на две или несколько плоскостей, то она будет преломляться на линиях пересечения этих плоскостей (рис 14).

Построение тени будем производить в следующей последовательности:

1) Строим тень отрезка на одну из плоскостей проекций, предполагая, что другой не суще­ствует. Например, строим тень от отрезка АВ на плоскость П₁. Получим тень от точки А – А_П1 — действительная тень. Получим тень от точки В — (В_П1) — мнимая тень.

2) Построенная тень пересекает ось ОХ в точке К_X — точка перелома.

3) Так как тень от точки В на плоскость П₁ получилась мнимой, строим действительную тень от точки В на плоскость П₂ — получим В_П2.

4) Соединив последовательно A_П1, К_X, В_П2 — получим тень от отрезка АВ.

Тени от прямых частного положения.

Отрезок АВ параллелен горизонтальной плоскости проекций П₁. Тень А_П1 В_П1 параллельна прямой АВ (рис.15).

Рис.15

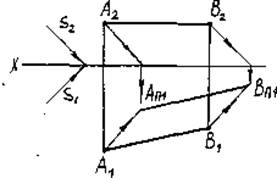
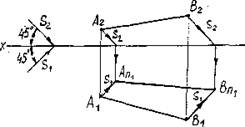
Отрезок CD параллелен фронтальной плоскости проекций П_П2. Тень С_П2D_П2 параллельна прямой CD (рис.16).

Рис.16

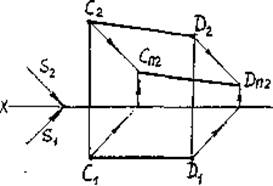
Вывод: Падающие тени от прямых, параллельных плоскостям проекций, будут параллельны самим прямым на той же плоскости, которой данные прямые параллельны.

Рис.17

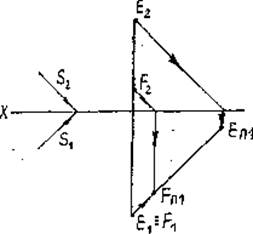
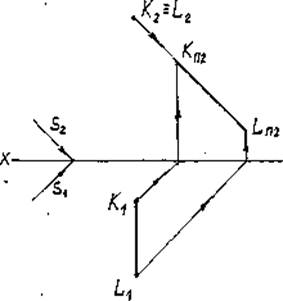
Отрезок EF перпендикулярен к горизонтальной плоскости проекций П₁. Тень E_П1 F_П1 совпадает с горизонтальной проекцией луча (рис.17).

Отрезок KL перпендикулярен к фронтальной плоскости проекций П₂. Тень К_П2L_П2 совпадает с фронтальной проекцией луча (рис.18).

Отрезок MN расположен так, что точка М, находится в плоскости П₁. Тень M_П1N_П1 проходит через точку М = M_П1 (рис.19)

Тени от плоских фигур.

Тень от многоугольника.

Построение тени от многоугольника сводится к построению тени от всех его сторон. Рассмотрим тень от четырехугольника ABCD. Строим тени от всех вершин четырехугольника на плоскость П₁. Получим A_П1, B_П1, C_П1, D_П1. Соединив их последовательно получим тень от четырехугольника на плоскость П₁ (рис.20).

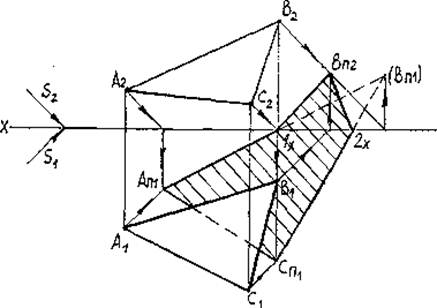
Рассмотрим пример построения тени треугольника ABC на две плоскости проекций (рис.21). Прежде всего строим тень от треугольника на плоскость П₁ предполагая, что плоскости П₂ нет. Для этого строим тени от точек А, В, С на плоскость П₁.Получаем действительные тени A_П1 и С_П1. Тень от точки В получилась мнимая — (В_П1). Соединяем тени точек А_П1 (В_П1), С_П1. Тень от стороны АВ — А_П1(В_П1) пересекает ось X в точке 1_х. Тень от стороны СВ — C_П1(B_П1) пересекает ось X в точке 2_Х. Точки 1_Х и 2_Х -точки перегиба.

Так как тень от точки получилась мнимой — строим действительную тень от точки В — В_П2-Соединяя действительные тени от точек А, В, С и точки перегиба, получим тень от треугольника ABC.

Тень от окружности.

Для построения тени от окружности необходимо разделить ее на несколько частей, например, на 8 или 12, и найти тень от каждой точки.

Рассмотрим тень от окружности, параллельной фронтальной плоскости проекций (рис.22). Для той части тени, которая ложится на фронтальную плоскость проекций, достаточно найти тень от центра окружности О_П2 и из нее радиусом равным радиусу окружности провести круг. Часть тени, которая будет находиться ниже оси X — будет мнимая тень от части окружности. Точки 1_Х и 2_x — точки перегиба. Та тень, которая падает на горизонтальную плоскость проекций, будет изображаться в виде эллипса. Для его изображения строим тени от точек на П₁.

Тени от геометрических тел.

Тени от многогранников.

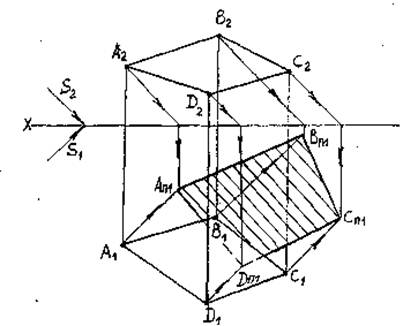
Для построения тени от многогранника необходимо найти тени от каждой из вершин данной фигуры. Например, построим тень от призмы (рис 23) .

Так как призма стоит на плоскости П₁ — тень от нижнего основания строить не нужно. Т.е. тени от точек нижнего основания: Е_П1 = E₁ ; F_П1 = F₁ ; G_П1 = G₁ ; K_П1= K₁ (совпадут с проекциями этих точек на плоскость П₁).

Строим тени от точек верхнего основания. Получим А_П1; В_П1; C_П1; D_П1 — Соединив E_П1 с A_П1; F_П1 с В_П1; G_П1 с C_П1; K_П1 с D_П1 получим тени от ребер ЕА, FB, DK, CG. Соединив точки A_П1, В_П1, С_П1 и D_П1 получим тень от верхнего основания.

Линию, ограничивающую падающую тень, называют контуром падающей тени. Грани призмы, к которым примыкает падающая тень, окажется в тени собственной . В нашем примере это грани DCGKD и BCGFB.

Тень от пирамиды (рис.24).

Для построения тени от пирамиды строим тень основания и вершины пирамиды. Соединив тени от точек основания с тенью от вершины — получим тени от ребер пирамид

Рассуждаем как в предыдущем примере, получим контур падающей тени: A_П11_X S_П22_XC_П1B_П1. Точки 1 _X и 2_Х — точки перегиба. В собственной тени находится грань ASC.

Тени от тел вращения.

Тень от цилиндра (рис 25).

Для построения тени от цилиндра строим тень от его верхнего и. нижнего оснований. Для получения падающей тени от боковой поверхности цилиндра проводим касательные к окружностям-контурам падающих теней верхнего и нижнего оснований. Контур собственной тени ограничен образующими АА’ и ВВ’, проходящими через точки касания А и В.

Тень от конуса (рис.26).

Для построения тени от конуса, строим тень от вершины конуса. Контур падающей тени ко­нуса ограничен прямыми, проведенными через точку (S_П1) касательно к основанию. Эти прямые представляют собой тени от образующих конуса SA и SB, ограничивающих контур собственной тени.

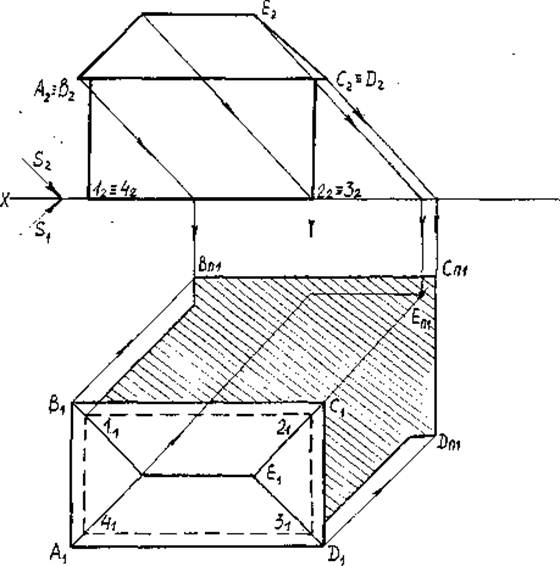
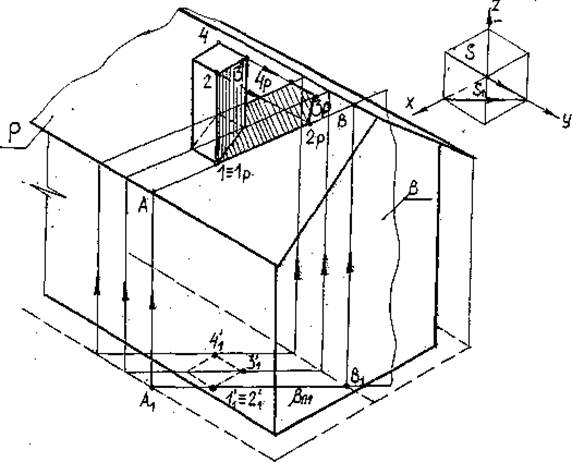
4. Построение падающей тени от здания.

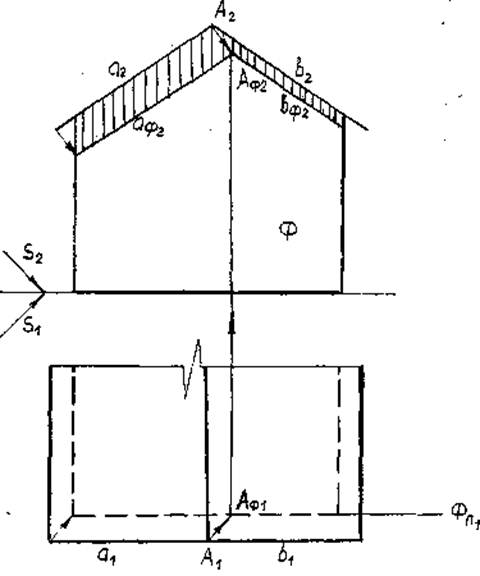
Через характерные точки здания: углы карниза D, С, В и границу конька крыши (линии пересечения ее скатов) — точку Е-проводим проекции лучей. Определяем горизонтальные тени точек — D_П1; С_П1;В_П1;Е_П1 (рис.27).

Тени от углов здания (от прямых перпендикулярных к плоскости П₁) совпадут с горизонтальной проекцией луча. Лучи выходят из точек 1₁; 2₁; 3₁; 4₁ (горизонтальные проекции ребер здания). В результате получим контур падающей тени 1₁B_П1 C_П1 и т.д. Часть здания, примыкающая к падающей тени, будет находиться в собственной тени. В тени находится правая и задняя стены здания. Крыша освещена полностью, т.к. контур собственной тени проходит по свесам карнизов (ВС и CD), тень от точки Е — E_П1 попала внутрь контура падающей тени.

Тени на фасаде здания.

При построении тени на фасаде здания нужно:

1) Уметь строить точку пересечения прямой с плоскостью частного положения и с плоскостью общего положения. Т.е. определять точки пересечения лучей с вертикальными плоскостями фасада или с наклонными скатами крыши.

2) Пользоваться следующими правилами:

Если прямая перпендикулярна некоторой плоскости. то тень прямой на эту плоскость совпадет с направлением проекций луча на ту же плоскость. Если прямая параллельна некоторой плоскости. то тень прямой на эту плоскость будет параллельна самой прямой.

Для построения теней на чертежах фасадов зданий необходимо кроме чертежа фасада иметь также план здания в том же масштабе.

Тени элементов зданий.

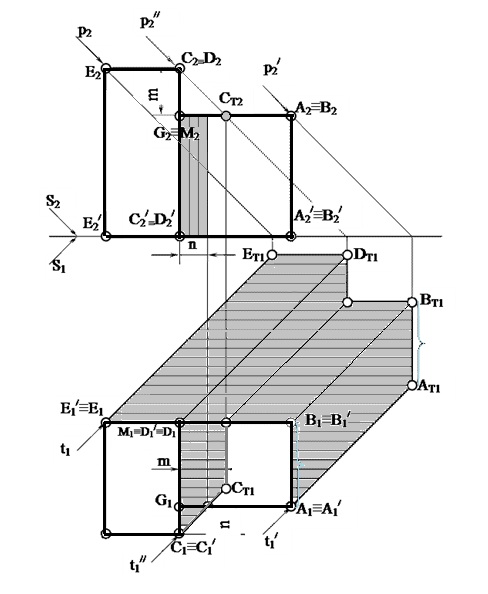
Построение тени в нише (дверных и оконных проемов (рис.28 и рис.29).

Рис.28

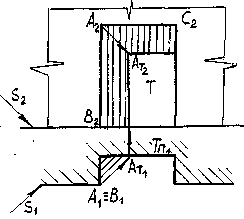
Тень в нише, если ниша прямоугольная, будут давать прямые АВ и АС (рис28). Тени от этих прямых ограничивают падающую тень на плоскость ниши Т. Тень от АВ пойдет через точку А_Т параллельно АВ, а тень от АС — через точку А_Т параллельно АС, т.к. АВ и ВС параллельны плоскости Т. Получим тень от точки А на плоскость Т. Через проекцию точки А на П₁ (А₁) проведем горизонтальную проекцию луча S₁ до пересечения с плоскостью Т.

Плоскость Т — горизонтально — проецирующая. Луч, пересекая плоскость Т в точке A_Т1 (см. построение точки пересечения прямой с проецирующей плоскостью). Через проекцию точки А на плоскость П₂ (А₂) проведем фронтальную проекцию луча S_2. Из точки А_Т1 проведем линию связи до пересечения с S₂. Получим А_Т2 — тень от точки А на плоскость Т. Через точку А_Т2 проведем прямые параллельные прямым А₂В₂ и А₂С₂.

Если в нише арка полукруглая (рис.29), построение проводим аналогично. Построив тень от точки Ана плоскость ниши Т (как в предыдущем примере) проводим прямую параллельную вертикальному ребру ниши АВ. Чтобы построить тень верхней части арки, нужно построить тень от центра окружности на плоскость ниши Т.Для этого через точку О₁ (проекция центра окружности на П₁) проведем S₁, через точку О₂ проведем S₂. Луч S₁ пересечет плоскость ниши в точке О_Т1. Далее по линии связи до пересечения с S₂. Получили О_Т2 — тень от центра окружности на плоскость ниши. Далее из точки О_Т2 радиусом, равным радиусу самой арки, проводим окружность.

Тень от козырька (рис.30).

Через проекции точек АВС на плоскость П₁ и П₂ проведем проекции лучей S₁ на плоскость П₁ и проекции лучей S₂ на плоскость П₂. Точки Е, F, В лежат на плоскости фасада, тень от этих точек на фасад, будет совпадать с проекциями этих точек. Строим тень от остальных точек. Луч S₁, проходящий через точку D₁, пересечет плоскость фасада в точке D_Ф2. Далее проводим линию связи до пересечения с S₂, проходящему через точку D₂. Получим тень от точки D на плоскость фасада — D_ф2. Аналогично строим остальные точки. Получим падающую тень от козырька на фасад здания.

Рис.30

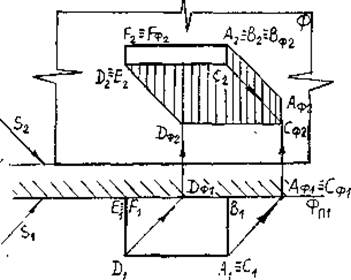
Тень от козырька над входом (рис.31).

1. Строим тень в дверном проеме (см. построение тени в нише).

2. Строим тень от козырька на плоскость фасада (см. построение тени от козырька).

3. Строим тень от козырька на плоскость ниши Т. Проецирующие лучи проводим до пересечения с плоскостью Т.

Обводим контур падающей тени козырька. Тень от козырька перегнется, т.к. она падает на разные плоскости.

Построение теней лестницы (рис.32).

Построим тень от стенок крыльца на ступени. Ребро крыльца АВ перпендикулярно плоскости П₁ и горизонтальным плоскостям ступеней. Таким образом тень от АВ на П₁ пойдет по лучу S₁.

Ребро АС перпендикулярно плоскости П₂ и перпендикулярно вертикальным плоскостям ступеней. Таким образом тень от ребра АС на плоскость П₂ пойдет по лучу S₂. Находим точки пересечения лучей S₁ и S₂ с соответствующими плоскостями ступеней.

Тень от крыши на плоскость стены (рис.33).

Для построения тени от фронтального свеса крыши, ограниченного спереди линиями а и b, достаточно найти тень от произвольной точки, принадлежащей этим линиям. Например, возьмем точку А (А₁, А₂), расположенную на коньке крыши.

Через точки A₁ и А₂ проведем проекции луча S₁ и S₂. Луч S₁ пересечет плоскость фасада в точке А_Ф1. Проведем линию связи до пересечения с S₂. Получим тень от точки А на плоскость фасада А_ф2.

Через точку А_ф2 проведем прямые параллельные ребрам свеса крыши а и b (т.к. а и b параллельны фасаду). Получим падающие тени от ребер свеса крыши а_ф2 и b_ф2.

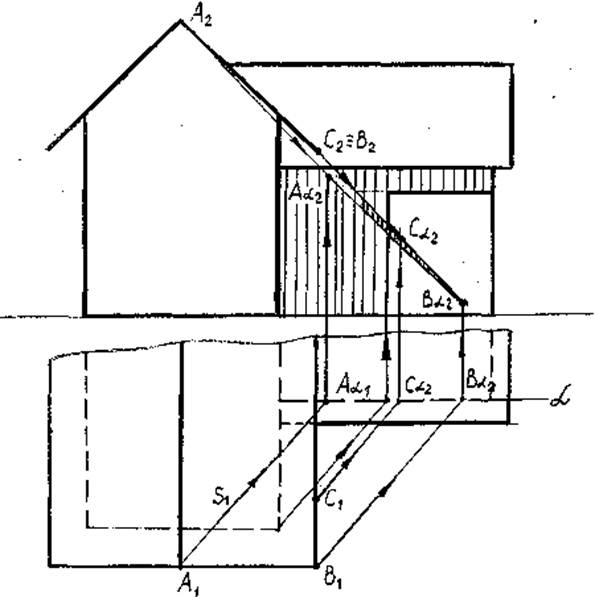
Тень от свеса крыши основного здания на пристройку (рис.34).

Возьмем точку А, расположенную на коньке крыши и точки В и С на ребре крыши. Через проекции этих точек на П₁ и П₂ проведем проекции лучей S₁ и S₂. Луч, проходящий через точку А пересечет плоскость стены пристройки в точке A_α1. Из этой точки проведем линию связи до пересечения с S_2. Получим тень от точки А на плоскость стены пристройки α – А_α2. Аналогично получили тень от точки В – В_α2. Соединив точки А_α2 и В_α2 получим тень от кромки крыши АВ. Тень от прямой ВС пойдет по лучу, т.к. прямая ВС перпендикулярна плоскости стены пристройки, т.е. из точки С₂ проводим проекцию луча S₂ – это и будет тень прямой ВС.

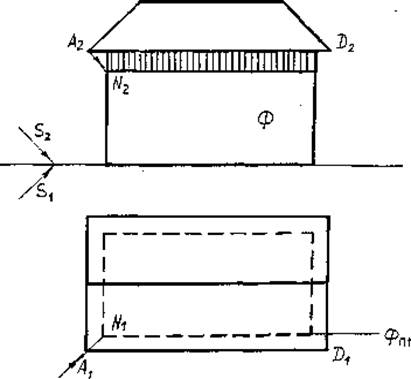
Тень от свеса крыши (рис.35).

Для построения падающей тени от свеса крыши AD на плоскость Ф (стены) направим через угол свеса А луч света, который пересечет плоскость Ф в точке N₁. По линии связи найдем точку N₂. Через эту точку проведем прямую параллельную AD (т.к. свес крыши AD параллелен плоскости стены).

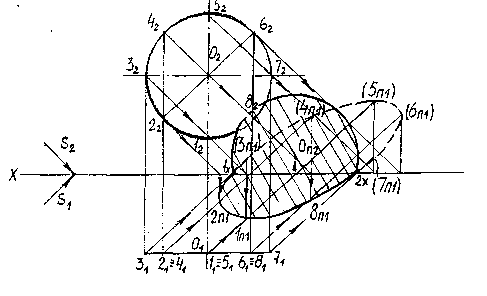
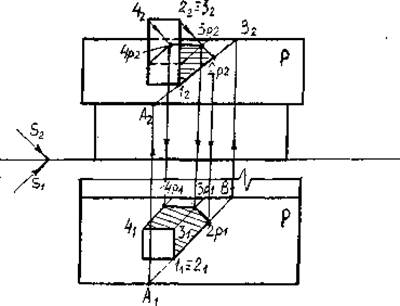
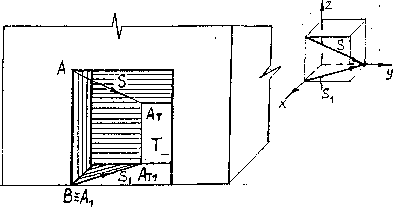
Тень от трубы на крышу (рис.36).

Плоскость ската крыши, на которую падает тень от трубы обозначим Р. Находим тень от вертикального ребра трубы 1-2. Тень от точки 1 будет в той же точке, так как она принадлежит плоскости Р. Для построения тени от точки 2 проведем через эту точку луч света и определим точку пересечения его с плоскостью Р.

С этой целью через луч проведем горизонтально проецирующую плоскость S, которая пересекает скат крыши Р по прямой АВ. В пересечении прямой АВ и луча, проведенного через точку 2, находится тень от точки 2-2_Р. Рассуждаем так же, как при построении точки пересечения прямой с плоскостью общего положения.

Построение начнем с плоскости П₁. Через точку 2₁ проведем S₁. Получим точки А₁и В₁. По линии связи находим А₂ и В₂. Через точку 2₂проводим S₂. При пересечении прямой А₂В₂ с S₂ получим точку 2_Р2. Проведем линию связи из точки 2_Р2 до пересечения с A₁В₁. Получим тень отточки 2 на П₁, т.е. 2_Р1

Аналогично строим тени от точек 3 и 4. Тень 4_Р-3_Р параллельна прямой 4-3, т.к. эта прямая параллельна плоскости

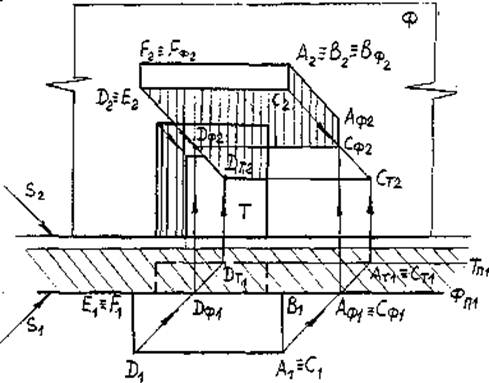
Тень от крыши основного здания на крышу пристройки (рис.37).

Плоскость ската крыши обозначим Р. На крыше возьмем точки 1,2,3. Построение проводим аналогично построению тени от точки 2 на плоскость крыши (см. тень от трубы на крышу).

Тени в аксонометрии.

Основные правила построения теней остаются в силе и при построении теней в аксонометрических проекция.

Направление светового луча рекомендуется определять диагональю куба (рис.38), грани которого совмещены с координатными плоскостями, а ребра построены с учетом коэффициента искажения.

Построение тени в аксонометрии проводим следующим образом. Построив аксонометрию сооружения, строим куб в той же аксонометрии, что и сооружение, например в косоугольной диметрии (рис.38).

Луч по П₁ — S₁ (вторичная проекция луча) пойдет по диагонали нижней грани куба. Луч в пространстве (S) будет проходить по диагонали куба.

Чтобы построить тень от точки А:

1) Находим ее проекцию на П₁ (ее вторичную проекцию). В нашем примере А₁.

3) Через точку А в пространстве проводим S (луч в пространстве).

4) На пересечении S₁ и S получим А_П1 – тень от точки А на плоскость П₁.

1. Построим тень в аксонометрии от параллелепипеда. Параллелепипед построен в косоугольной диметрии (рис.39).

Рис.39

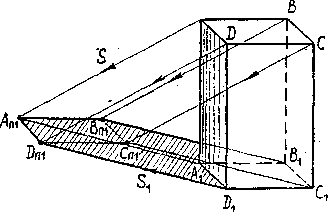
Параллелепипед стоит на плоскости П₁ .Поэтому строить тень от нижнего основания мы не будем. Построим тень от верхнего основания. Найдем проекции точек А, В, С, D на плоскость П₁. Затем через проекции точек на П₁ (A₁, B₁, C₁, D₁) — проведем S₁ (перенесем параллельно из построенного в косоугольной диметрии куба). Через точки в пространстве проведем S (S перенесем параллельно из построенного в косоугольной диметрии куба). На пересечении S и S₁, проведенных через каждую точку, получим А_П1, В_П1, С_П1, D_П1.

Соединив Е_П1 и А_П1 В_П1 и G_П1, C_П1 и К_П1, D_П1 и L_П1, получим тени от вертикальных ребер. Ребра АЕ; BG; СК и DL перпендикулярны плоскости П₁, таким образом тени от этих ребер пойдут по проекции луча на П₁. AD, ВС, АВ и CD параллельны П₁, таким образом тени от этих ребер A_П1D_П1; В_П1С_П1; А_П1В_П1; D_П1C_П1 параллельны самим прямым. Обведем контур падающей тени – L_П1D_П1A_П1B_П1G_П1. Грани ADLE, ABGE параллелепипеда, прилегающие к падающей тени, будут находиться в собственной тени.

2. Тень от конуса в изометрии (рис.40).

1) Строим аксонометрию конуса.

2) Строим куб в изометрии.

3) Определяем направление лучей S₁ и S.

4) Находим вторичную проекцию вершины конуса (C₁)

5) Через проекцию вершины на П₁ через точку C₁ проводим S₁ (берем параллельно S₁ в кубе).

6) Через вершину конуса С проводим S.

7) На пересечении S и S₁ получим С_П1 — тень от вершины конуса на горизонтальную плоскость.

8) Тень от основания не строим, т.к. конус стоит на плоскости П₁.

1. Из точки С_П1 проводим касательные к основанию. Получим тень от конуса на П₁.

9) Собственная тень будет ограничиваться образующими СА и ВС.

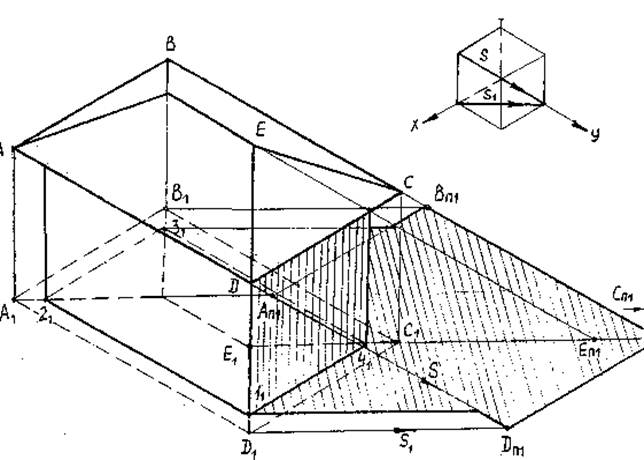
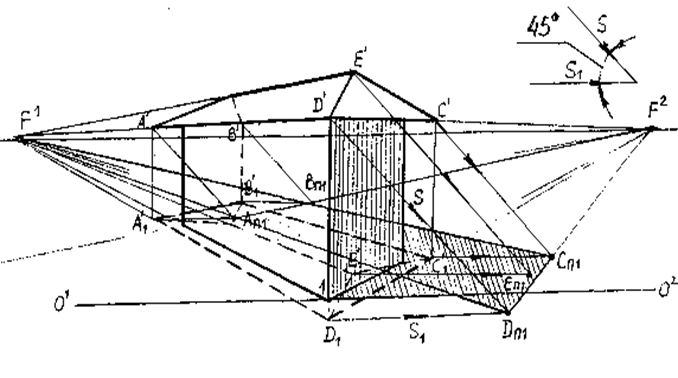
3. Построение падающей тени от здания (рис.41).

Здание построено в изометрии.

1) Строим куб в изометрии, для выбора направлений луча S₁ и S₂.

2) Через вторичные проекции точек A, D, С, В, Е — A₁, D_1,С₁ ,В₁, E₁ проведем S₁.

3) Через точки D, С, В, Е – проведем S.

4) На пересечении S₁S — выходящих из точек, получим тени точек A, D, С, В, Е на плоскость П₁.

5) Тени от углов зданий (от прямых перпендикулярных к плоскости П₁) совпадут со вторичной проекцией луча S₁, выходящего из точек 1₁; 3₁; 4₁.

6) Обведем контур падающей тени.

Тень от прямой АВ — А_П1В_П1 параллельна самой прямой, т.к. АВ параллельна П₁. Аналогично ВС параллельна B_П1C_П1; AD параллельна A_П1D_П1; ED параллельна E_П1D_П1.

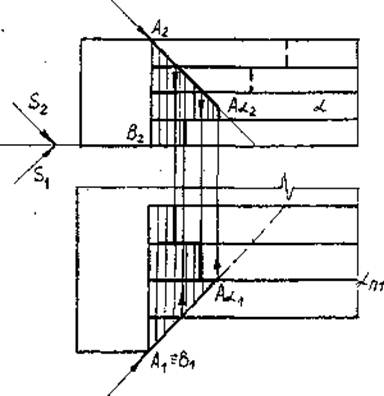
4. Тень в нише (рис.42).

Тень от левого откоса АВ на плоскость П₁ пойдет по S₁, т.к. АВ перпендикулярна П₁. Пройдя по плоскости П₁ тень от АВ перегнется на плоскость Т в точке А_Т1. Далее, т.к. АВ параллельна плоскости ниши Т, тень от АВ пойдет параллельно самому откосу АВ. Тень А_Т от точки А на плоскость Т находится в точке пересечения луча света S, проведенного через А, с плоскостью Т.

Через точку А_Т проведем тень от прямой АС. Тень от прямой АС параллельна самой прямой, т.к. АС параллельна плоскости Т.

Тень от козырька (рис.43).

Через проекции точек D, А, С на плоскость П₁ проведем лучи S₁. Луч, проходящий через точку D₁, пересечет плоскость стены Ф в точке D_Ф1 через точку А — в точке А_Ф1 через точку С — в точке C_Ф1. Далее по линии связи до пересечения с лучами S, выходящими из точек D, А, С получим точки D_Ф, А_Ф, С_Ф. Тени от точек Е, F, В не строим, т.к. они лежат в плоскости стены, т.е. Е = Е_Ф; F = F_Ф, В = В_Ф. Соединив Е_Ф, D_Ф, С_Ф, А_Ф — получим тень от козырька.

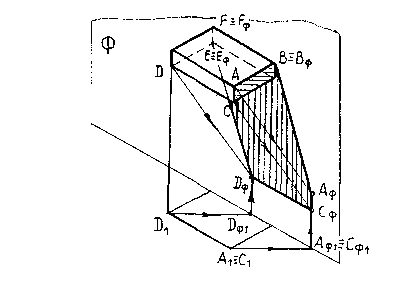
6. Тень от крыши на плоскость стены (рис.44).

Для построения тени от фронтального свеса крыши, ограниченного спереди линиями а и b находим тень от точки А, расположенную на коньке крыши. Через точку А₁ проводим S₁, далее по линии связи до пересечения с S, выходящим из точки А. Через точку А_Ф проведем прямые а_Ф и b_Ф, параллельные ребрам свеса крыши а и b, получим тень от ребер свеса крыши а и b.

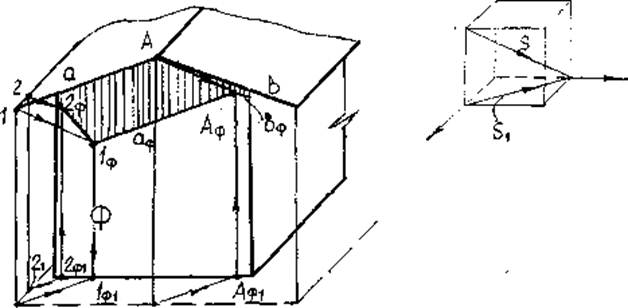
7. Тень от трубы на крышу (рис.45)

Для построения тени необходимо построить вторичные проекции как крыши, так и трубы. Затем проводим лучевые плоскости. Проведем лучевую плоскость β через ребро трубы 1-2. След плоскости β на предметной плоскости совпадает со вторичной проекцией луча S₁ (прямая A₁B₁, проходящая через точку 1₁ = 2₁). Далее построена линия пересечения плоскости β и заданного ската Р. Это прямая АВ. Из точки 2 проведем луч S до пересечения с прямой АВ. Получим тень от точки 2 на плоскость Р. Тень от точки 1будет в той же точке, т.к. она принадлежит плоскости Р, т.е. 1 = 1_Р. Соединим 1_Р и 2_Р получим тень от ребра трубы 1-2. Аналогично строим и тени от остальных ребер трубы.

Рассмотрев ряд примеров мы видим, что при построении тени в ортогональных проекциях и в аксонометрии в принципе выполняются одни и те же построения.

7. Тени в перспективе от естественного источника освещения.

Для удобства построения рекомендуется угол наклона лучей к предметной плоскости принимать равным 45°. Световые лучи параллельны плоскости картины. Принцип построения теней в перспективе такой же, как в ортогональных проекциях и в аксонометрии . Тень от точки, падающая на поверхность, будет в точке пересечения луча света с поверхностью, например: А’ — перспектива точки A, A₁‘ — вторичная проекция точки А. Через точку А’ проводим луч света (под углом 45° к основанию картины) через точку А₁‘ проведем S₁ — параллельно основанию картины. Место пересечения луча и его вторичной проекции определит тень A_П1 на предметную плоскость (рис.46).

Далее рассмотрим пример построения тени в перспективе. Рассуждать будем так же, как при построений тени в аксонометрии. Отличие в том, что направление лучей S и S₁ в аксонометрии зависит от типа аксонометрии, а в перспективе мы проводим S₁ параллельно основанию картины, a S под углом 45° к основанию картины.

Построение падающей тени от здания.

Построение падающей тени от здания проводим аналогично построению тени от здания в аксонометрии (п. 3).

Рекомендуемая литература.

1. Анисимов Н. Н., Кузнецов Н. С.Ю., Кириллов А. Ф. Черчение и рисование. — М. : Стройиздат, 1983.

2. Балягин С. Н. Брилинг Н. С, Симонин С. И. Справочник по строительному черчению. — М. : Стройиздат, 1987.

3. БудасовБ. В. Строительное черчение. -М.: Стройиздат, 1990.

4. Короев Ю. П. Инжерно — строительное черчение и рисование, — М.: Высшая школа, 1983.

5. Крылов Н.Н. Начертательная геометрия. — М. : Высшая школа, 2000.

6. Кузнецов Н.С. Начертательная геометрия . — М.: Высшая школа, 1981.

Приложение

Понравилась статья? Добавь ее в закладку (CTRL+D) и не забудь поделиться с друзьями:

Самое популярное на сайте:

Недостатки речного транспорта РЕЧНОЙ ТРАНСПОРТ Речной транспорт (внутренний водный транспорт) — транспорт.
Типовые звенья автоматических систем При исследовании автоматических систем первостепенное значение приобретает характер преобразования сигналов в отдельных звеньях.
Задание 1. 1. Создайте таблицу расчета заработной платы по образцу Введите исходные данные — Табельный номер, ФИО и Оклад 1. Создайте таблицу расчета заработной платы по образцу Введите исходные данные — Табельный номер.
Краткий словарь философских терминов Философия — это культура разумного мышления, которое осуществляется в рационально-понятийной форме.
Современные тенденции развития образования в России Начало XXI века многими учеными связывается с наступлением эпохи инноваций.

Источник