Как найти тензор напряжений

Полный тензор механического напряжения элементарного объёма тела.

Те́нзор напряже́ний (иногда тензор напряжений Коши, тензор натяжений) — тензор второго ранга, описывающий механические напряжения в произвольной точке нагруженного тела, возникающих в этой точке при его (тела) малых деформациях. В случае объёмного тела, тензор часто записывается в виде матрицы 3×3:

${displaystyle {boldsymbol {sigma }}=left[{begin{matrix}mathbf {T} ^{(mathbf {e} _{1})}\mathbf {T} ^{(mathbf {e} _{2})}\mathbf {T} ^{(mathbf {e} _{3})}\end{matrix}}right]=left[{begin{matrix}sigma _{11}&sigma _{12}&sigma _{13}\sigma _{21}&sigma _{22}&sigma _{23}\sigma _{31}&sigma _{32}&sigma _{33}\end{matrix}}right]equiv left[{begin{matrix}sigma _{xx}&sigma _{xy}&sigma _{xz}\sigma _{yx}&sigma _{yy}&sigma _{yz}\sigma _{zx}&sigma _{zy}&sigma _{zz}\end{matrix}}right]equiv left[{begin{matrix}sigma _{x}&tau _{xy}&tau _{xz}\tau _{yx}&sigma _{y}&tau _{yz}\tau _{zx}&tau _{zy}&sigma _{z}\end{matrix}}right]}$

а в случае двумерного тела (см. пример ниже) матрицей 2×2:

${displaystyle {boldsymbol {sigma }}=left[{begin{matrix}mathbf {T} ^{(mathbf {e} _{1})}\mathbf {T} ^{(mathbf {e} _{2})}\end{matrix}}right]=left[{begin{matrix}sigma _{11}&sigma _{12}\sigma _{21}&sigma _{22}\end{matrix}}right]equiv left[{begin{matrix}sigma _{xx}&sigma _{xy}\sigma _{yx}&sigma _{yy}\end{matrix}}right]equiv left[{begin{matrix}sigma _{x}&tau _{xy}\tau _{yx}&sigma _{y}\end{matrix}}right]}$

где ${displaystyle mathbf {T} ^{(e_{n})}}$ — вектор механического напряжения, действующий на поверхность ${displaystyle e_{n}}$ .

В случае матричной записи (в декартовой системе координат) величины $sigma_{ij}$ (компоненты тензора напряжений), описывают напряжения испытываемые телом в какой-то заданной точке. В данной точке проводятся умозрительные плоскости с нормалями ${displaystyle color {Red}e_{1}}$ , ${displaystyle color {Red}e_{2}}$ , … Нормальные компоненты сил, действующих на данные плоскости, записываются на главной диагонали $sigma_{11}$ , $sigma_{22}$ , …, а в остальных позициях стоят касательные компоненты ${displaystyle tau _{yx}}$ , $tau_{xy}$ , … векторов напряжений на этих плоскостях.

В случае больших деформаций (конечные деформации), приходится использовать такие подходы как тензор напряжений Пиолы — Кирхгофа, тензор Биота или тензор напряжения Кирхгофа.

Физический смысл тензора напряжений на примере в двумерном случае[править | править код]

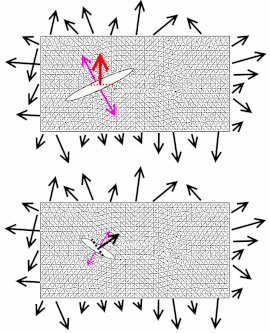
Рис. Б. Различный отклик ткани на разнонаправленные разрезы , совершённые в одной и той же точке.

Простейшей иллюстрацией, позволяющей понять физический смысл тензора напряжений, будет, вероятно, не рассмотрение случая напряжения в некотором объёмном теле, а, наоборот, рассмотрение напряжения в плоском двумерном теле. Для этого рассмотрим напряжение отрезка ткани под внешней нагрузкой (см. рис. А).

На рисунке изображен прямоугольный кусок ткани под внешней нагрузкой, которая изображена чёрными стрелками по периметру прямоугольника. В данном случае нагрузкой может служить растяжение её руками в разные стороны, или натягивание ткани на какую-то сложную форму.

Интуитивно понятно, что из-за формы, ориентации молекул, атомных слоёв и разного плетения волокон (на рис.А расположение волокон схематично изображено мелкой серой сеткой) в разных точках ткани напряжение будет разным: где-то будут области, которые подвергаются вертикальному растяжению, а в других областях волокна будут испытывать напряжение сдвига.

Каждой точке на поверхности отрезка ткани соответствует своё уникальное значение напряжения. Это значит, что каждой точке $(x_{0},y_{0})$ ткани соответствует свой математический объект — — тензор второго ранга.

Чтобы понять, как тензор показывает состояние напряжения в какой-нибудь точке ткани, можно сделать маленький разрез в данной точке и понаблюдать, в каком направлении будут расходиться данные разрезы. Так, на рис. А мы сделали два разреза в разных точках ткани: направление одного разреза показано красной пунктирной линией, направление другого — синей пунктирной линией. Чтобы математически описать направление данных разрезов, используется вектор нормали (вектор, перпендикулярный плоскости разреза). Так, у разреза вектор нормали красный и направлен перпендикулярно плоскости разреза, у разреза ситуация похожая. Направление роста разрыва в ткани обозначено фиолетовыми векторами .

Для предсказания того, куда будет развиваться разрез, как раз и используется тензор напряжений. Математически данное предсказание выглядело бы так:

Определить «тензорную функцию» ${displaystyle f(x,y)=mathbf {T_{x,y}} ,}$ аргументами которой являются координаты точек внутри тела, а значением является тензор, описывающий состояние напряжения в заданной точке тела.
Выбрать точку в теле, например, ${displaystyle (x_{0},y_{0}),}$ и из получить тензор, который описывает состояние напряжения в точке ${displaystyle mathbf {T_{x_{0},y_{0}}} .}$
Определить направление плоскости , в которой будет проводиться разрез тела.
Умножить направление разреза в точке $(x_{0},y_{0})$ на тензор напряжения в данной точке ${displaystyle mathbf {T_{x_{0},y_{0}}} }$ , что в математической записи выглядит как ${displaystyle {mathbf {T_{x_{0},y_{0}}} color {red}{vec {c}}}=color {RedViolet}{vec {t}}.}$
Вектор и покажет, куда будет распространяться разрез в точке $(x_{0},y_{0})$ .

Разрезы и — это вектора, а напряжение в точке — это тензор.

Следует понимать, что разнонаправленные разрезы, совершённые в одной и той же точке тела, повлекут за собой различный отклик ткани. Данное явление показано на рис. Б, где разрастание разрыва ткани происходит по разным направлениям и с разной интенсивностью , в ответ на различные направления первоначальных разрезов и , совершённых в одной и той же точке.

Как раз для описания такого сложного поведения и используются тензоры, которые в данном случае служат векторными функциями ${displaystyle f_{x_{0},y_{0}}({vec {c}})=mathbf {T_{x_{0},y_{0}}} {vec {c}}={vec {t}}}$ , определёнными в каждой точке $(x_{0},y_{0})$ куска ткани, которые ставят все возможные направления разрезов в соответствие со всеми возможными направлениями дальнейшего разрыва ткани.

Вывод компонентов тензора[править | править код]

Компоненты тензора напряжений $sigma_{ij}$ в декартовой системе координат Ox_i (то есть Oxyz ) вводят следующим образом. Рассматривают бесконечно малый объём тела (сплошной среды) в виде прямоугольного параллелепипеда, грани которого ортогональны координатным осям и имеют площади $dS_{i}$ . На каждой грани $dS_{i}$ параллелепипеда действуют поверхностные силы $dF_{i}$ . Если обозначить проекции этих сил на оси $Ox_{j}$ как $dF_{ij}$ , то компонентами тензора напряжений называют отношение проекций силы к величине площади грани, на которой действует эта сила:

$sigma_{ij} = frac{ d F_{ij}}{dS_{i}}$

По индексу здесь суммирования нет. Компоненты $sigma_{11}$ , $sigma_{22}$ , $sigma_{33}$ , обозначаемые также как $sigma_{xx}$ , $sigma_{yy}$ , $sigma_{zz}$ — это нормальные напряжения, они представляют собой отношение проекции силы $dF_{i}$ на нормаль к площади рассматриваемой грани $dS_{i}$ :

$sigma_{11} = frac{ d F_{11}}{dS_{1}}$

и т. д.

Компоненты $sigma_{12}$ , $sigma_{23}$ , $sigma_{31}$ , обозначаемые также как $tau_{xy}$ , $tau_{yz}$ , $tau_{zx}$ — это касательные напряжения, они представляют собой отношение проекции силы $dF_{i}$ на касательные направления к площади рассматриваемой грани $dS_{i}$ :

$sigma_{12} = frac{ d F_{12}}{dS_{1}}$

и т. д.

При отсутствии собственного момента импульса сплошной среды, а также объёмных и поверхностных пар тензор напряжений симметричен (так называемый закон парности касательных напряжений), что является следствием уравнения баланса момента импульса. В частности, тензор напряжений симметричен в классической теории упругости и в гидродинамике идеальной и линейно-вязкой жидкостей.

Тензор напряжений в релятивистской физике[править | править код]

С точки зрения теории относительности, компоненты тензора напряжений являются девятью пространственными компонентами тензора энергии-импульса.

Тензор напряжений в классической электродинамике[править | править код]

В классической электродинамике тензор напряжений электромагнитного поля (максвелловский тензор напряжений^[1], тензор натяжений Максвелла^[2]) в Международной системе единиц (СИ) имеет вид:

$T_{ij} = E_i D_j + B_i H_j - frac{1}{2}delta_{ij}(mathbf E cdot mathbf D + mathbf B cdot mathbf H) = E_i D_j + B_i H_j - delta_{ij}W,$

где — плотность энергии электромагнитного поля.

См. также[править | править код]

Тензор энергии-импульса
Теория упругости
Тензор деформации
Тензор упругости
Закон Гука

Примечания[править | править код]

↑ Ландау Л. Д., Лифшиц Е. М. Теория поля. — Издание 7-е, исправленное. — М.: Наука, 1988. — С. 115. — («Теоретическая физика», том II). — ISBN 5-02-014420-7.
↑ Степановский Ю. П. Максвелла тензор натяжений // Физическая энциклопедия : [в 5 т.] / Гл. ред. А. М. Прохоров. — М.: Большая российская энциклопедия, 1992. — Т. 3: Магнитоплазменный — Пойнтинга теорема. — С. 32—33. — 672 с. — 48 000 экз. — ISBN 5-85270-019-3.

Литература[править | править код]

Седов Л. И. Механика сплошной среды. Том 1. М.: Наука, 1970. 492 c.
Трусделл К. Первоначальный курс рациональной механики сплошных сред. М.: Наука, 1975. 592 с.
Димитриенко Ю. И. Нелинейная механика сплошной среды. М.: Физматлит, 2010.

Источник

Выше показано,
используя метод сечений и представление
материальной точки в виде элементарного
параллелепипеда, имеем либо три вектора
разложения, либо девять векторов
разложения полного напряжения

,
рис.3.3

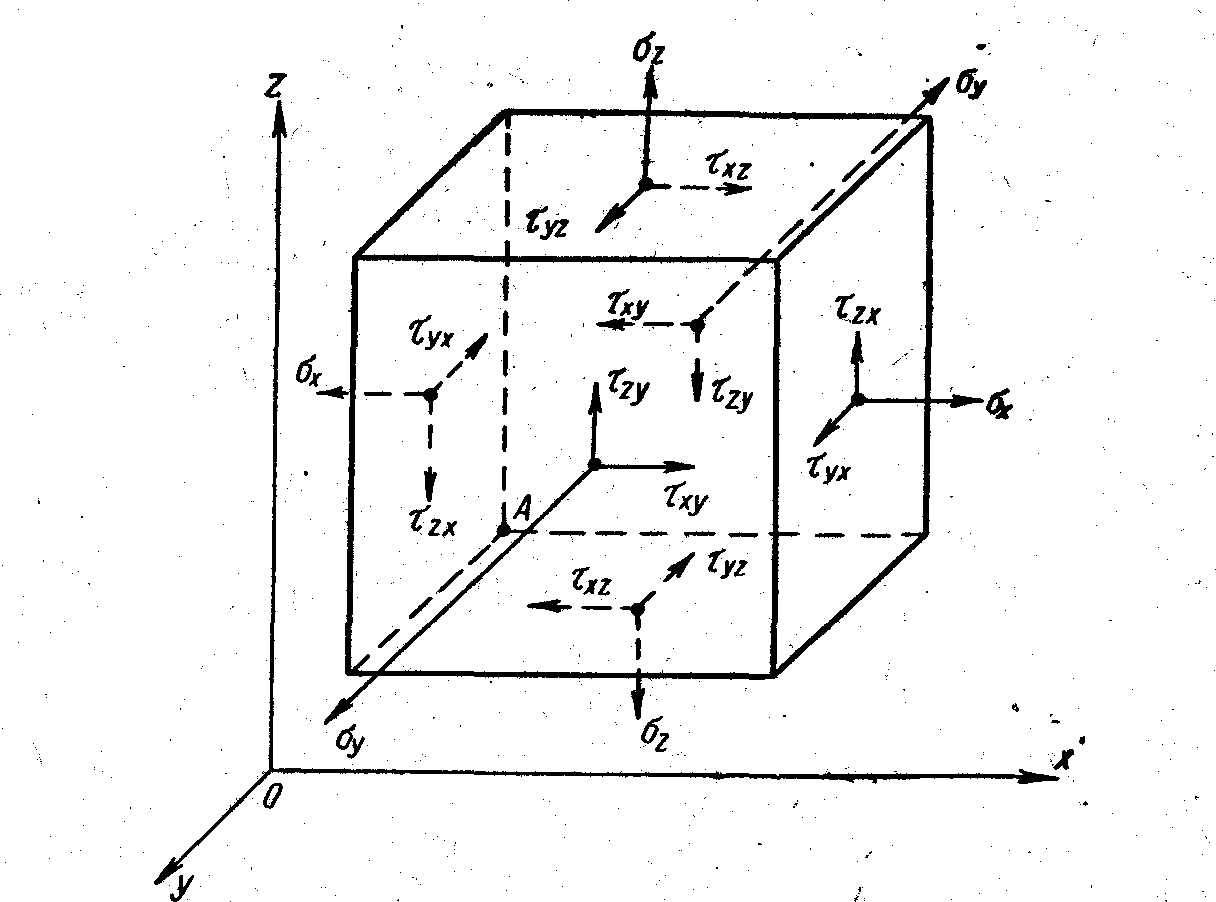
Рис.3.3. Схема
действия напряжений на элементарный
объем

Запишем проекции
полного напряжения в произвольных
координатах в виде таблицы

– направление

X
Y
Z

Большие буквы
X,Y,Z – показывают адреса площадок, нормали
которых совпадают с направлениями

.
Нижние индексы имеют определенное
функциональное назначение. Первый
индекс показывает направление действия
вектора напряжения, второй индекс
указывает адрес площадки. Если первый
индекс

,
следовательно, напряжение направлено
параллельно оси

.
Если второй индекс

,
следовательно, площадка действия
напряжения перпендикулярна оси

,
а ее нормаль параллельна этой оси. Два
одинаковых нижних индекса заменяется
одним.

Совокупность
девяти величин называется тензором
второго ранга. В общем случае тензор
характеризует вектор в многомерном
пространстве. В соответствии с
характеристикой вектора он должен быть
задан своими проекциями и по величине
и по направлению. Величина напряжения
характеризуется совокупностью всех
проекций и определяется последовательным
применением теоремы Пифагора, а
направление – направляющими косинусами,
или же направляющим тензором. Вектор в
трехмерном пространстве представляется
тремя составляющими (проекциями) и
называется тензором первого ранга.
Скалярная величина – это тензор нулевого
ранга. Тензор второго ранга или тензор
напряжений

Если элементарный
объем находится в равновесии, то следует
закон парности касательных напряжений,
т.е.

касательные
напряжения с одинаковыми нижними
индексами равны.

С учетом последних
соотношений, тензор напряжений
записывается

Тензор напряжений
полностью характеризует напряженное
состояние в точке.

3.3. Напряжения на наклонной площадке

Составляющие
тензора напряжений, исходя из геометрических
соотношений, определяют напряжение

(напряженное состояние) в данной точке
и по модулю и по направлению. Однако
этого может оказаться недостаточным,
если необходимо определить напряжение
по заданному направлению, т.е. на наклонной
площадке. Докажем, если заданы напряжения
в трёх взаимно перпендикулярных
площадках, проходящих через заданную
точку, то напряженное состояние по
любому направлению будет известно,
следовательно будет известным и
наряженное состояние в точке.

Проведём через
данную точку

,
рис.3.4, плоскость наклона к осям
координат. Фигура тетраэдр, сливающаяся
с точкой

.
Нормаль

перпендикуляра к наклонной плоскости.
Ее площадь

,
площади остальных граней

.
На взаимно перпендикулярные грани
действуют составляющие тензора
напряжений.

На наклонной грани
действует полное напряжение

.
Напряжение может быть разложено по
разным направлениям. В данном случае

.

Если тетраэдр
находится в равновесии, то имеем условия
равновесия по координатным осям всех
действующих сил

;

Из построения

,

где

направляющие косинусы

;

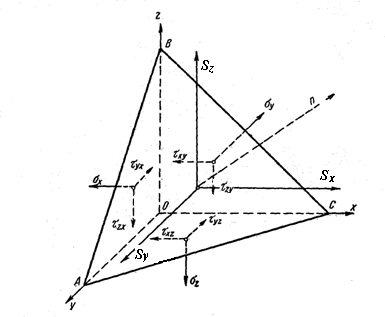
Рис. 3.4. Напряжения
на наклонной площадке.

После преобразований
и сокращений на

,
имеем

;

Проекции полного
напряжения

на наклонной площадке содержат все
компоненты тензора напряжений. По
правилу параллелепипеда полное напряжение

.
Направляющие косинусы

;

Если известны
проекции вектора на координатные оси

,

,

,
можно определить этот вектор по величине
и направлению. В теории упругости и
пластичности удобно вектор напряжений
разложить не только по координатным
направлениям

,
но и по другим, связанных с направлением
наклонной площадки. Это нормальное и
касательное направление к площадке.
Используя теорему о проекции суммы,
получим нормальное напряжение к наклонной
площадке

Подставляя значения

Полное касательное
напряжение в наклонной площадке по
теореме Пифагора

По формулам можно
определить напряжения в любой наклонной
площадке. Если заданы шесть напряжений,
действующих в точке по трём взаимно
перпендикулярным, то её напряженное
состояние определено.

Следует добавить,
что выражения могут быть использованы
для вычисления внешней силы. Это уравнения
связи между внешними силами на контакте
и компонентами тензора напряжений или
внутренними силами. Ещё их называют
условиями на контуре, которые должны
входить в математическую постановку
задачи теории упругости или пластичности.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Встречавшиеся
до сих пор симметричные тензоры возникали как коэффициенты, связывающие один
вектор с другим. Сейчас я познакомлю вас с тензором, имеющим совершенно другой
физический смысл, – это тензор напряжений. Предположим, что на твердое тело
действуют различные внешние силы. Мы говорим, что внутри тела возникают
различные «напряжения», имея при этом в виду внутренние силы между смежными частями
материала. Мы уже говорили немного о подобных напряжениях в двумерном случае,
когда рассматривали поверхностное натяжение напряженной диафрагмы (см. гл. 12,
§ 3, вып. 5). А теперь вы увидите, что внутренние силы в материале трехмерного
тела записываются в виде тензора.

Рассмотрим
тело из какого-то упругого материала, например брусок из желе. Если мы разрежем
этот брусок, то материал на каждой стороне разреза будет, вообще говоря,
претерпевать перемещение под действием внутренних сил. До того как был сделан
разрез, между двумя этими частями должны были действовать силы, которые
удерживали обе части в едином куске; мы можем выразить напряжение через эти
силы. Представьте себе, что мы смотрим на воображаемую плоскость,
перпендикулярную оси , подобную плоскости на фиг. 31.5, и
интересуемся силами, действующими на маленькой площадке , расположенной в этой
плоскости. Материал, находящийся слева от площадки, действует на материал с
правой стороны с силой (фиг. 31.5,б). Есть, конечно, и
обратная реакция, т.е. на материал слева от поверхности действует сила . Если площадка
достаточно мала, то мы ожидаем, что сила пропорциональна площади .

Фиг. 31.5. Материал, находящийся
слева от плоскости на площади , действует на материал, находящийся
справа, с силой .

Вы
уже знакомы с одним видом напряжений – статическим давлением жидкости. Там сила
была равна давлению, умноженному на площадь, и направлена под прямым углом к
элементу поверхности. Для твердого тела, а также движущейся вязкой жидкости
сила не обязательно перпендикулярна поверхности: помимо давления
(положительного или отрицательного), появляется еще и сдвигающая сила. (Под
«сдвигающей» силой мы подразумеваем тангенциальные компоненты сил, действующих
на поверхности.) Для этого нужно учитывать все три компоненты силы. Заметьте
еще, что если разрез мы сделаем по плоскости с какой-то другой ориентацией, то
действующие на ней силы тоже будут другими. Полное описание внутренних
напряжений требует применения тензоров.

Определим
тензор напряжений следующим образом. Вообразите сначала разрез, перпендикулярный
оси и
разложите силу ,
действующую на разрезе, на ее компоненты: , , (фиг. 31.6). Отношение этих сил к
площади мы
назовем ,
и . Например,

Первый
индекс относится
к направлению компоненты силы, а второй – к направлению нормали к плоскости.
Если угодно, площадь можно записать как , имея в виду
элемент площади, перпендикулярный оси , т. е.

А
теперь представьте себе разрез, перпендикулярный оси . Пусть на маленькую
площадку действует
сила .
Разлагая снова эту силу на три компоненты, как показано на фиг. 31.7, мы
определяем три компоненты напряжения , , как силы, действующие на единичную
площадь в этих трех направлениях. Наконец, проведем воображаемый разрез,
перпендикулярный оси , и определим три компоненты , и . Таким образом,
получается девять чисел:

. (31.23)

Фиг. 31.6. Сила , действующая на
элементе площади , перпендикулярной оси , разлагается на
три компоненты: ,
и .

Фиг. 31.7. Сила, действующая на
элемент площади, перпендикулярной оси , разлагается на три взаимно
перпендикулярные компоненты.

Я
хочу теперь показать, что этих девяти величин достаточно, чтобы полностью
описать внутреннее напряженное состояние, и что – действительно тензор. Предположим,
что мы хотим знать силу, действующую на поверхность, наклоненную под некоторым
произвольным углом. Можно ли найти ее, исходя из ? Можно, и это делается следующим
образов. Вообразите маленькую призму, одна грань которой наклонна, а другие –
параллельны осям координат. Если окажется, что грань параллельна оси , то получается
картина, изображенная на фиг. 31.8. (Это, конечно, частный случай, но он
достаточно хорошо иллюстрирует общий метод.) Дальше, напряжения, действующие на
эту призмочку, должны быть такими, чтобы она находилась в равновесии (по
крайней мере в пределе бесконечно малого размера), так что действующая на нее
полная сила должна быть равна нулю. Силы, действующие на грани, параллельные
осям координат, известны нам непосредственно из тензора . А их векторная сумма
должна равняться силе, действующей на грань , так что эту силу можно выразить
через .

Фиг. 31.8. Разложение на
компоненты силы ,
действующей на грани (с единичной нормалью ).

Наше
допущение, что поверхностные силы, действующие на малый объем, находятся в
равновесии, предполагает отсутствие объемных сил, подобных силе тяжести или
псевдосилам, которые тоже могут присутствовать, если наша система координат не
инерциальна. Заметьте, однако, что такие объемные силы будут пропорциональны
объему призмочки и поэтому пропорциональны , , , тогда как поверхностные силы
пропорциональны ,
и т. п.
Итак, если размер призмочки взять достаточно малым, то объемные силы будут
пренебрежимо малы по сравнению с поверхностными.

А
теперь сложим силы, действующие на нашу призмочку. Возьмемся сначала за -компоненту,
которая состоит из пяти частей, по одной от каждой грани. Но если достаточно мало,
то силы от треугольных граней (перпендикулярные оси ) будут равны друг другу и
противоположны по направлению, поэтому о них можно забыть. На основание призмы
действует компонента силы, равная

а
-компонента
силы, действующей на вертикальную прямоугольную грань, равна

Сумма
этих двух сил должна быть равна -компоненте силы, действующей извне
на грань .
Обозначим через единичный
вектор нормали к грани , а через – действующую на нее силу,
тогда получим

Составляющая
напряжения по оси , действующего в этой плоскости,
равна силе ,
деленной на площадь, т. е. , или

Но,
как видно из фиг. 31.8, отношение – это косинус угла между и осью и может быть
записан как ,
т. е. -компонента
вектора .
Аналогично, равно
.
Поэтому мы можем написать

Если
теперь обобщить это на произвольный элемент поверхности, то мы получим

или
в еще более общей форме:

. (31.24)

Так
что мы действительно можем выразить силу, действующую на произвольную площадь,
через элементы и
полностью описать внутреннее напряжение.

Уравнение
(31.24) говорит, что тензор связывает силу с единичным вектором точно так же, как
связывает
с . Но поскольку и – векторы, то
компоненты при
изменении осей координат должны преобразовываться как тензор. Так что действительно
тензор.

Можно
также доказать, что – симметричный тензор. Для этого
нужно обратить внимание на силы, действующие на маленький кубик в материале.
Возьмем кубик, грани которого параллельны осям координат, и посмотрим на его
разрез (фиг. 31.9). Если допустить, что ребра куба равны единице, то – и -компоненты сил на
гранях, перпендикулярных к осям и , должны быть такими, как показано на
рисунке. Если взять достаточно маленький кубик, можно надеяться, что напряжение
на его противоположных гранях будет отличаться ненамного, а поэтому компоненты
сил должны быть равны и противоположны, как это показано на рисунке. Заметьте
теперь, что на кубик не должен действовать никакой момент сил, иначе кубик
начал бы вращаться. Но полный момент относительно центра равен произведению на единичную
длину ребра куба, а поскольку полный момент равен нулю, то должно быть равно и тензор
напряжений, таким образом, оказывается симметричным.

Фиг. 31.9. – и -компоненты сил,
действующих на четыре грани маленького единичного кубика.

Благодаря
этой симметрии тензора можно тоже описывать эллипсоидом с
тремя главными осями. Напряжение имеет особенно простой вид на площадках,
нормальных к этим осям: оно соответствует чистому сжатию или растяжению в
направлении главных осей. Вдоль этих площадок нет никаких сдвиговых сил, причем
такие оси, для которых отсутствуют сдвиговые силы, можно выбрать для любого
напряжения. Если эллипсоид превращается в сферу, то в любом направлении
действуют только нормальные силы. Это соответствует гидростатическому давлению
(положительному или отрицательному). Таким образом, для гидростатического
давления тензор диагоналей, причем все три компоненты его равны друг другу
(фактически они просто равны давлению ). В этом случае мы можем написать

. (31.25)

Вообще
говоря, тензор напряжений в куске твердого тела, а также его эллипсоид
изменяются от точки к точке, поэтому для описания всего куска мы должны задать
каждую компоненту как функцию положения. Тензор
напряжений, таким образом, является полем. Мы уже имели примеры скалярных
полей, подобных температуре , и векторных полей, подобных , которые в каждой
точке задавались тремя числами. А теперь перед нами пример тензорного поля,
задаваемого в каждой точке пространства девятью числами, из которых для
симметричного тензора реально остается только шесть.
Полное описание внутренних сил в произвольном твердом теле требует знания шести
функций координат , и .

Источник

Полный тензор механического напряжения элементарного объёма тела.

[math]displaystyle{ boldsymbol{sigma}=left[{begin{matrix} mathbf{T}^{(mathbf{e}_1)} \
mathbf{T}^{(mathbf{e}_2)} \
mathbf{T}^{(mathbf{e}_3)} \
end{matrix}}right] =
left[{begin{matrix}
sigma _{11} & sigma _{12} & sigma _{13} \
sigma _{21} & sigma _{22} & sigma _{23} \
sigma _{31} & sigma _{32} & sigma _{33} \
end{matrix}}right]

equiv left[{begin{matrix}
sigma _{xx} & sigma _{xy} & sigma _{xz} \
sigma _{yx} & sigma _{yy} & sigma _{yz} \
sigma _{zx} & sigma _{zy} & sigma _{zz} \
end{matrix}}right]
equiv left[{begin{matrix}
sigma _x & tau _{xy} & tau _{xz} \
tau _{yx} & sigma _y & tau _{yz} \
tau _{zx} & tau _{zy} & sigma _z \
end{matrix}}right]
}[/math]

а в случае двумерного тела (см. пример ниже) матрицей 2×2:

[math]displaystyle{ boldsymbol{sigma}=left[{begin{matrix} mathbf{T}^{(mathbf{e}_1)} \
mathbf{T}^{(mathbf{e}_2)} \
end{matrix}}right] =
left[{begin{matrix}
sigma _{11} & sigma _{12} \
sigma _{21} & sigma _{22} \
end{matrix}}right]

equiv left[{begin{matrix}
sigma _{xx} & sigma _{xy} \
sigma _{yx} & sigma _{yy} \
end{matrix}}right]
equiv left[{begin{matrix}
sigma _x & tau _{xy} \
tau _{yx} & sigma _y \
end{matrix}}right]
}[/math]

где [math]displaystyle{ mathbf{T}^{(e_n)} }[/math] — вектор механического напряжения, действующий на поверхность [math]displaystyle{ e_n }[/math].

В случае матричной записи (в декартовой системе координат) величины [math]displaystyle{ sigma_{ij} }[/math](компоненты тензора напряжений), описывают напряжения испытываемые телом в какой-то заданной точке. В данной точке проводятся умозрительные плоскости с нормалями [math]displaystyle{ color{Red}e_{1} }[/math], [math]displaystyle{ color{Red}e_{2} }[/math], … Нормальные компоненты сил, действующих на данные плоскости, записываются на главной диагонали [math]displaystyle{ sigma_{11} }[/math], [math]displaystyle{ sigma_{22} }[/math], …, а в остальных позициях стоят касательные компоненты [math]displaystyle{ tau_{yx} }[/math], [math]displaystyle{ tau_{xy} }[/math], … векторов напряжений на этих плоскостях.

Физический смысл тензора напряжений на примере в двумерном случае

Рис. А. Модель ткани под сложной внешней нагрузкой (чёрные стрелки), в теле которой было совершено два разреза [math]displaystyle{ color{red}c }[/math] и [math]displaystyle{ color{blue}c }[/math] (пунктирные линии), на которой изображены нормали к плоскости разрезов [math]displaystyle{ color{red}vec{c} }[/math], [math]displaystyle{ color{blue}vec{c} }[/math] и реакция ткани [math]displaystyle{ color{RedViolet}vec{t} }[/math](фиолетовые стрелки) на осуществление данных разрезов в виде дальнейшего разрастания разрыва.

Рис. Б. Различный отклик ткани на разнонаправленные разрезы [math]displaystyle{ color{red}vec{c} }[/math], [math]displaystyle{ color{black}vec{c} }[/math] совершённые в одной и той же точке.

Каждой точке на поверхности отрезка ткани соответствует своё уникальное значение [math]displaystyle{ mathbf{T} }[/math] напряжения. Это значит, что каждой точке [math]displaystyle{ (x_0,y_0) }[/math] ткани соответствует свой математический объект — [math]displaystyle{ mathbf{T} }[/math] — тензор второго ранга.

Чтобы понять, как тензор [math]displaystyle{ mathbf{T} }[/math] показывает состояние напряжения в какой-нибудь точке ткани, можно сделать маленький разрез в данной точке и понаблюдать, в каком направлении будут расходиться данные разрезы. Так, на рис. А мы сделали два разреза в разных точках ткани: направление одного разреза [math]displaystyle{ color{red}c }[/math] показано красной пунктирной линией, направление другого [math]displaystyle{ color{blue}c }[/math] — синей пунктирной линией. Чтобы математически описать направление данных разрезов, используется вектор нормали (вектор, перпендикулярный плоскости разреза). Так, у разреза [math]displaystyle{ color{red}c }[/math] вектор нормали [math]displaystyle{ color{red}vec{c} }[/math] красный и направлен перпендикулярно плоскости разреза, у разреза [math]displaystyle{ color{blue}c }[/math] ситуация похожая. Направление роста разрыва в ткани обозначено фиолетовыми векторами [math]displaystyle{ color{RedViolet}vec{t} }[/math].

Определить «тензорную функцию» [math]displaystyle{ f(x,y)=mathbf {T_{x,y}}, }[/math] аргументами которой являются координаты точек внутри тела, а значением является тензор, описывающий состояние напряжения в заданной точке тела.
Выбрать точку в теле, например, [math]displaystyle{ (x_0,y_0), }[/math] и из [math]displaystyle{ f(x,y) }[/math] получить тензор, который описывает состояние напряжения в точке [math]displaystyle{ mathbf {T_{x_0,y_0}}. }[/math]
Определить направление плоскости [math]displaystyle{ color{red}vec{c} }[/math], в которой будет проводиться разрез тела.
Умножить направление разреза [math]displaystyle{ color{red}vec{c} }[/math] в точке [math]displaystyle{ (x_0,y_0) }[/math] на тензор напряжения в данной точке [math]displaystyle{ mathbf {T_{x_0,y_0}} }[/math], что в математической записи выглядит как [math]displaystyle{ {mathbf{T_{x_0,y_0}} color{red}vec{c}} = color{RedViolet}vec{t}. }[/math]
Вектор [math]displaystyle{ color{RedViolet}vec{t} }[/math] и покажет, куда будет распространяться разрез [math]displaystyle{ color{red}vec{c} }[/math] в точке [math]displaystyle{ (x_0,y_0) }[/math].

Разрезы [math]displaystyle{ color{red}vec{c} }[/math] и [math]displaystyle{ color{blue}vec{c} }[/math] — это вектора, а напряжение в точке [math]displaystyle{ mathbf {T} }[/math] — это тензор.

Следует понимать, что разнонаправленные разрезы, совершённые в одной и той же точке тела, повлекут за собой различный отклик ткани. Данное явление показано на рис. Б, где разрастание разрыва ткани происходит по разным направлениям [math]displaystyle{ color{RedViolet}vec{t} }[/math] и с разной интенсивностью [math]displaystyle{ ||{color{RedViolet}vec{t}}|| }[/math], в ответ на различные направления первоначальных разрезов [math]displaystyle{ color{red}vec{c} }[/math] и [math]displaystyle{ vec{c} }[/math], совершённых в одной и той же точке.

Как раз для описания такого сложного поведения и используются тензоры, которые в данном случае служат векторными функциями [math]displaystyle{ f_{x_0,y_0}(vec{c}) =mathbf {T_{x_0,y_0}} vec{c}=vec{t} }[/math], определёнными в каждой точке [math]displaystyle{ (x_0,y_0) }[/math] куска ткани, которые ставят все возможные направления [math]displaystyle{ vec{c} }[/math] разрезов в соответствие со всеми возможными направлениями [math]displaystyle{ vec{t} }[/math] дальнейшего разрыва ткани.

Вывод компонентов тензора

Компоненты тензора напряжений [math]displaystyle{ sigma_{ij} }[/math] в декартовой системе координат [math]displaystyle{ Ox_i }[/math] (то есть [math]displaystyle{ Oxyz }[/math]) вводят следующим образом. Рассматривают бесконечно малый объём тела (сплошной среды) в виде прямоугольного параллелепипеда, грани которого ортогональны координатным осям и имеют площади [math]displaystyle{ dS_{i} }[/math]. На каждой грани [math]displaystyle{ dS_{i} }[/math] параллелепипеда действуют поверхностные силы [math]displaystyle{ dF_{i} }[/math]. Если обозначить проекции этих сил на оси [math]displaystyle{ Ox_{j} }[/math] как [math]displaystyle{ dF_{ij} }[/math], то компонентами тензора напряжений называют отношение проекций силы к величине площади грани, на которой действует эта сила:

[math]displaystyle{ sigma_{ij} = frac{ d F_{ij}}{dS_{i}} }[/math]

По индексу [math]displaystyle{ i }[/math] здесь суммирования нет. Компоненты [math]displaystyle{ sigma_{11} }[/math], [math]displaystyle{ sigma_{22} }[/math],[math]displaystyle{ sigma_{33} }[/math], обозначаемые также как [math]displaystyle{ sigma_{xx} }[/math], [math]displaystyle{ sigma_{yy} }[/math],[math]displaystyle{ sigma_{zz} }[/math] — это нормальные напряжения, они представляют собой отношение проекции силы [math]displaystyle{ dF_{i} }[/math] на нормаль к площади рассматриваемой грани [math]displaystyle{ dS_{i} }[/math]:

[math]displaystyle{ sigma_{11} = frac{ d F_{11}}{dS_{1}} }[/math] и т. д.

Компоненты [math]displaystyle{ sigma_{12} }[/math], [math]displaystyle{ sigma_{23} }[/math],[math]displaystyle{ sigma_{31} }[/math], обозначаемые также как [math]displaystyle{ tau_{xy} }[/math], [math]displaystyle{ tau_{yz} }[/math],[math]displaystyle{ tau_{zx} }[/math] — это касательные напряжения, они представляют собой отношение проекции силы [math]displaystyle{ dF_{i} }[/math] на касательные направления к площади рассматриваемой грани [math]displaystyle{ dS_{i} }[/math]:

[math]displaystyle{ sigma_{12} = frac{ d F_{12}}{dS_{1}} }[/math] и т. д.

Тензор напряжений в релятивистской физике

Тензор напряжений в классической электродинамике

[math]displaystyle{ T_{ij} = E_i D_j + B_i H_j – frac{1}{2}delta_{ij}(mathbf E cdot mathbf D + mathbf B cdot mathbf H) = E_i D_j + B_i H_j – delta_{ij}W, }[/math]

где [math]displaystyle{ W }[/math] — плотность энергии электромагнитного поля.

См. также

Тензор энергии-импульса
Теория упругости
Тензор деформации
Тензор упругости
Закон Гука

Примечания

↑ Шаблон:Ландафшиц
↑ Степановский Ю. П. Максвелла тензор натяжений // Физическая энциклопедия : [в 5 т.] / Гл. ред. А. М. Прохоров. — М.: Большая российская энциклопедия, 1992. — Т. 3: Магнитоплазменный — Пойнтинга теорема. — С. 32—33. — 672 с. — 48 000 экз. — ISBN 5-85270-019-3.

Литература

Седов Л. И. Механика сплошной среды. Том 1. М.: Наука, 1970. 492 c.
Трусделл К. Первоначальный курс рациональной механики сплошных сред. М.: Наука, 1975. 592 с.
Димитриенко Ю. И. Нелинейная механика сплошной среды. М.: Физматлит, 2010.

Источник

Figure 2.3 Components of stress in three dimensions

In continuum mechanics, the Cauchy stress tensor , true stress tensor,^[1] or simply called the stress tensor is a second order tensor named after Augustin-Louis Cauchy. The tensor consists of nine components $sigma _{ij}$ that completely define the state of stress at a point inside a material in the deformed state, placement, or configuration. The tensor relates a unit-length direction vector e to the traction vector T^(e) across an imaginary surface perpendicular to e:

${displaystyle mathbf {T} ^{(mathbf {e} )}=mathbf {e} cdot {boldsymbol {sigma }}quad {text{or}}quad T_{j}^{(e)}=sigma _{ij}e_{i},}$

or,

${displaystyle left[{begin{matrix}T_{1}^{(mathbf {e} )}&T_{2}^{(mathbf {e} )}&T_{3}^{(mathbf {e} )}end{matrix}}right]=left[{begin{matrix}e_{1}&e_{2}&e_{3}end{matrix}}right]cdot left[{begin{matrix}sigma _{11}&sigma _{12}&sigma _{13}\sigma _{21}&sigma _{22}&sigma _{23}\sigma _{31}&sigma _{32}&sigma _{33}\end{matrix}}right].}$

The SI units of both stress tensor and traction vector are N/m², corresponding to the stress scalar. The unit vector is dimensionless.

The Cauchy stress tensor obeys the tensor transformation law under a change in the system of coordinates. A graphical representation of this transformation law is the Mohr’s circle for stress.

The Cauchy stress tensor is used for stress analysis of material bodies experiencing small deformations: It is a central concept in the linear theory of elasticity. For large deformations, also called finite deformations, other measures of stress are required, such as the Piola–Kirchhoff stress tensor, the Biot stress tensor, and the Kirchhoff stress tensor.

According to the principle of conservation of linear momentum, if the continuum body is in static equilibrium it can be demonstrated that the components of the Cauchy stress tensor in every material point in the body satisfy the equilibrium equations (Cauchy’s equations of motion for zero acceleration). At the same time, according to the principle of conservation of angular momentum, equilibrium requires that the summation of moments with respect to an arbitrary point is zero, which leads to the conclusion that the stress tensor is symmetric, thus having only six independent stress components, instead of the original nine. However, in the presence of couple-stresses, i.e. moments per unit volume, the stress tensor is non-symmetric. This also is the case when the Knudsen number is close to one, ${displaystyle K_{n}rightarrow 1}$ , or the continuum is a non-Newtonian fluid, which can lead to rotationally non-invariant fluids, such as polymers.

There are certain invariants associated with the stress tensor, whose values do not depend upon the coordinate system chosen, or the area element upon which the stress tensor operates. These are the three eigenvalues of the stress tensor, which are called the principal stresses.

Euler–Cauchy stress principle – stress vector[edit]

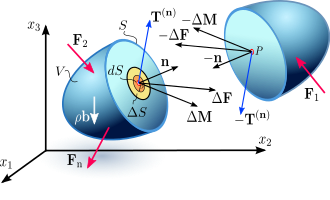
Figure 2.1a Internal distribution of contact forces and couple stresses on a differential of the internal surface in a continuum, as a result of the interaction between the two portions of the continuum separated by the surface

Figure 2.1b Internal distribution of contact forces and couple stresses on a differential of the internal surface in a continuum, as a result of the interaction between the two portions of the continuum separated by the surface

Figure 2.1c Stress vector on an internal surface S with normal vector n. Depending on the orientation of the plane under consideration, the stress vector may not necessarily be perpendicular to that plane, i.e. parallel to , and can be resolved into two components: one component normal to the plane, called normal stress $sigma _{{mathrm {n}}}$ , and another component parallel to this plane, called the shearing stress tau .

The Euler–Cauchy stress principle states that upon any surface (real or imaginary) that divides the body, the action of one part of the body on the other is equivalent (equipollent) to the system of distributed forces and couples on the surface dividing the body,^[2] and it is represented by a field $mathbf{T}^{(mathbf{n})}$ , called the traction vector, defined on the surface and assumed to depend continuously on the surface’s unit vector .^[3]^[4]^{: p.66–96}

To formulate the Euler–Cauchy stress principle, consider an imaginary surface passing through an internal material point dividing the continuous body into two segments, as seen in Figure 2.1a or 2.1b (one may use either the cutting plane diagram or the diagram with the arbitrary volume inside the continuum enclosed by the surface ).

Following the classical dynamics of Newton and Euler, the motion of a material body is produced by the action of externally applied forces which are assumed to be of two kinds: surface forces and body forces .^[5] Thus, the total force applied to a body or to a portion of the body can be expressed as:

Only surface forces will be discussed in this article as they are relevant to the Cauchy stress tensor.

When the body is subjected to external surface forces or contact forces , following Euler’s equations of motion, internal contact forces and moments are transmitted from point to point in the body, and from one segment to the other through the dividing surface , due to the mechanical contact of one portion of the continuum onto the other (Figure 2.1a and 2.1b). On an element of area Delta S containing , with normal vector , the force distribution is equipollent to a contact force exerted at point P and surface moment . In particular, the contact force is given by

$Deltamathbf F= mathbf T^{(mathbf n)},Delta S$

where $mathbf {T} ^{(mathbf {n} )}$ is the mean surface traction.

Cauchy’s stress principle asserts^[6]^{: p.47–102} that as Delta S becomes very small and tends to zero the ratio becomes and the couple stress vector vanishes. In specific fields of continuum mechanics the couple stress is assumed not to vanish; however, classical branches of continuum mechanics address non-polar materials which do not consider couple stresses and body moments.

The resultant vector is defined as the surface traction,^[7] also called stress vector,^[8] traction,^[4] or traction vector.^[6] given by ${displaystyle mathbf {T} ^{(mathbf {n} )}=T_{i}^{(mathbf {n} )}mathbf {e} _{i}}$ at the point associated with a plane with a normal vector :

$T^{(mathbf{n})}_i= lim_{Delta S to 0} frac {Delta F_i}{Delta S} = {dF_i over dS}.$

This equation means that the stress vector depends on its location in the body and the orientation of the plane on which it is acting.

This implies that the balancing action of internal contact forces generates a contact force density or Cauchy traction field ^[5] that represents a distribution of internal contact forces throughout the volume of the body in a particular configuration of the body at a given time . It is not a vector field because it depends not only on the position of a particular material point, but also on the local orientation of the surface element as defined by its normal vector .^[9]

Depending on the orientation of the plane under consideration, the stress vector may not necessarily be perpendicular to that plane, i.e. parallel to , and can be resolved into two components (Figure 2.1c):

one normal to the plane, called normal stress

$mathbf{sigma_mathrm{n}}= lim_{Delta S to 0} frac {Delta F_mathrm n}{Delta S} = frac{dF_mathrm n}{dS},$

where ${displaystyle dF_{mathrm {n} }}$

is the normal component of the force

to the differential area

and the other parallel to this plane, called the shear stress

$mathbf tau= lim_{Delta S to 0} frac {Delta F_mathrm s}{Delta S} = frac{dF_mathrm s}{dS},$

where ${displaystyle dF_{mathrm {s} }}$

is the tangential component of the force

to the differential surface area

. The shear stress can be further decomposed into two mutually perpendicular vectors.

Cauchy’s postulate[edit]

According to the Cauchy Postulate, the stress vector $mathbf{T}^{(mathbf{n})}$ remains unchanged for all surfaces passing through the point and having the same normal vector at ,^[7]^[10] i.e., having a common tangent at . This means that the stress vector is a function of the normal vector only, and is not influenced by the curvature of the internal surfaces.

Cauchy’s fundamental lemma[edit]

A consequence of Cauchy’s postulate is Cauchy’s Fundamental Lemma,^[1]^[7]^[11] also called the Cauchy reciprocal theorem,^[12]^{: p.103–130} which states that the stress vectors acting on opposite sides of the same surface are equal in magnitude and opposite in direction. Cauchy’s fundamental lemma is equivalent to Newton’s third law of motion of action and reaction, and is expressed as

${displaystyle -mathbf {T} ^{(mathbf {n} )}=mathbf {T} ^{(-mathbf {n} )}.}$

Cauchy’s stress theorem—stress tensor[edit]

The state of stress at a point in the body is then defined by all the stress vectors T⁽ⁿ⁾ associated with all planes (infinite in number) that pass through that point.^[13] However, according to Cauchy’s fundamental theorem,^[11] also called Cauchy’s stress theorem,^[1] merely by knowing the stress vectors on three mutually perpendicular planes, the stress vector on any other plane passing through that point can be found through coordinate transformation equations.

Cauchy’s stress theorem states that there exists a second-order tensor field σ(x, t), called the Cauchy stress tensor, independent of n, such that T is a linear function of n:

${displaystyle mathbf {T} ^{(mathbf {n} )}=mathbf {n} cdot {boldsymbol {sigma }}quad {text{or}}quad T_{j}^{(n)}=sigma _{ij}n_{i}.}$

This equation implies that the stress vector T⁽ⁿ⁾ at any point P in a continuum associated with a plane with normal unit vector n can be expressed as a function of the stress vectors on the planes perpendicular to the coordinate axes, i.e. in terms of the components σ_ij of the stress tensor σ.

To prove this expression, consider a tetrahedron with three faces oriented in the coordinate planes, and with an infinitesimal area dA oriented in an arbitrary direction specified by a normal unit vector n (Figure 2.2). The tetrahedron is formed by slicing the infinitesimal element along an arbitrary plane with unit normal n. The stress vector on this plane is denoted by T⁽ⁿ⁾. The stress vectors acting on the faces of the tetrahedron are denoted as T^(e₁), T^(e₂), and T^(e₃), and are by definition the components σ_ij of the stress tensor σ. This tetrahedron is sometimes called the Cauchy tetrahedron. The equilibrium of forces, i.e. Euler’s first law of motion (Newton’s second law of motion), gives:

${displaystyle mathbf {T} ^{(mathbf {n} )},dA-mathbf {T} ^{(mathbf {e} _{1})},dA_{1}-mathbf {T} ^{(mathbf {e} _{2})},dA_{2}-mathbf {T} ^{(mathbf {e} _{3})},dA_{3}=rho left({frac {h}{3}}dAright)mathbf {a} ,}$

Figure 2.2. Stress vector acting on a plane with normal unit vector n.
A note on the sign convention: The tetrahedron is formed by slicing a parallelepiped along an arbitrary plane n. So, the force acting on the plane n is the reaction exerted by the other half of the parallelepiped and has an opposite sign.

where the right-hand-side represents the product of the mass enclosed by the tetrahedron and its acceleration: ρ is the density, a is the acceleration, and h is the height of the tetrahedron, considering the plane n as the base. The area of the faces of the tetrahedron perpendicular to the axes can be found by projecting dA into each face (using the dot product):

${displaystyle dA_{1}=left(mathbf {n} cdot mathbf {e} _{1}right)dA=n_{1};dA,}$

${displaystyle dA_{2}=left(mathbf {n} cdot mathbf {e} _{2}right)dA=n_{2};dA,}$

${displaystyle dA_{3}=left(mathbf {n} cdot mathbf {e} _{3}right)dA=n_{3};dA,}$

and then substituting into the equation to cancel out dA:

${displaystyle mathbf {T} ^{(mathbf {n} )}-mathbf {T} ^{(mathbf {e} _{1})}n_{1}-mathbf {T} ^{(mathbf {e} _{2})}n_{2}-mathbf {T} ^{(mathbf {e} _{3})}n_{3}=rho left({frac {h}{3}}right)mathbf {a} .}$

To consider the limiting case as the tetrahedron shrinks to a point, h must go to 0 (intuitively, the plane n is translated along n toward O). As a result, the right-hand-side of the equation approaches 0, so

${displaystyle mathbf {T} ^{(mathbf {n} )}=mathbf {T} ^{(mathbf {e} _{1})}n_{1}+mathbf {T} ^{(mathbf {e} _{2})}n_{2}+mathbf {T} ^{(mathbf {e} _{3})}n_{3}.}$

Assuming a material element (Figure 2.3) with planes perpendicular to the coordinate axes of a Cartesian coordinate system, the stress vectors associated with each of the element planes, i.e. T^(e₁), T^(e₂), and T^(e₃) can be decomposed into a normal component and two shear components, i.e. components in the direction of the three coordinate axes. For the particular case of a surface with normal unit vector oriented in the direction of the x₁-axis, denote the normal stress by σ₁₁, and the two shear stresses as σ₁₂ and σ₁₃:

$mathbf{T}^{(mathbf{e}_1)}= T_1^{(mathbf{e}_1)}mathbf{e}_1 + T_2^{(mathbf{e}_1)} mathbf{e}_2 + T_3^{(mathbf{e}_1)} mathbf{e}_3 = sigma_{11} mathbf{e}_1 + sigma_{12} mathbf{e}_2 + sigma_{13} mathbf{e}_3,$

$mathbf{T}^{(mathbf{e}_2)}= T_1^{(mathbf{e}_2)}mathbf{e}_1 + T_2^{(mathbf{e}_2)} mathbf{e}_2 + T_3^{(mathbf{e}_2)} mathbf{e}_3=sigma_{21} mathbf{e}_1 + sigma_{22} mathbf{e}_2 + sigma_{23} mathbf{e}_3,$

$mathbf{T}^{(mathbf{e}_3)}= T_1^{(mathbf{e}_3)}mathbf{e}_1 + T_2^{(mathbf{e}_3)} mathbf{e}_2 + T_3^{(mathbf{e}_3)} mathbf{e}_3=sigma_{31} mathbf{e}_1 + sigma_{32} mathbf{e}_2 + sigma_{33} mathbf{e}_3,$

In index notation this is

$mathbf{T}^{(mathbf{e}_i)}= T_j^{(mathbf{e}_i)} mathbf{e}_j = sigma_{ij} mathbf{e}_j.$

The nine components σ_ij of the stress vectors are the components of a second-order Cartesian tensor called the Cauchy stress tensor, which can be used to completely define the state of stress at a point and is given by

$boldsymbol{sigma}= sigma_{ij} = left[{begin{matrix} mathbf{T}^{(mathbf{e}_1)} \ mathbf{T}^{(mathbf{e}_2)} \ mathbf{T}^{(mathbf{e}_3)} \ end{matrix}}right] = left[{begin{matrix} sigma _{11} & sigma _{12} & sigma _{13} \ sigma _{21} & sigma _{22} & sigma _{23} \ sigma _{31} & sigma _{32} & sigma _{33} \ end{matrix}}right] equiv left[{begin{matrix} sigma _{xx} & sigma _{xy} & sigma _{xz} \ sigma _{yx} & sigma _{yy} & sigma _{yz} \ sigma _{zx} & sigma _{zy} & sigma _{zz} \ end{matrix}}right] equiv left[{begin{matrix} sigma _x & tau _{xy} & tau _{xz} \ tau _{yx} & sigma _y & tau _{yz} \ tau _{zx} & tau _{zy} & sigma _z \ end{matrix}}right],$

where σ₁₁, σ₂₂, and σ₃₃ are normal stresses, and σ₁₂, σ₁₃, σ₂₁, σ₂₃, σ₃₁, and σ₃₂ are shear stresses. The first index i indicates that the stress acts on a plane normal to the X_i -axis, and the second index j denotes the direction in which the stress acts (For example, σ₁₂ implies that the stress is acting on the plane that is normal to the 1_st axis i.e.;X₁ and acts along the 2_nd axis i.e.;X₂). A stress component is positive if it acts in the positive direction of the coordinate axes, and if the plane where it acts has an outward normal vector pointing in the positive coordinate direction.

Thus, using the components of the stress tensor

$begin{align} mathbf{T}^{(mathbf{n})} &= mathbf{T}^{(mathbf{e}_1)}n_1 + mathbf{T}^{(mathbf{e}_2)}n_2 + mathbf{T}^{(mathbf{e}_3)}n_3 \ & = sum_{i=1}^3 mathbf{T}^{(mathbf{e}_i)}n_i \ &= left( sigma_{ij}mathbf{e}_j right)n_i \ &= sigma_{ij}n_imathbf{e}_j end{align}$

or, equivalently,

$T_j^{(mathbf n)}= sigma_{ij}n_i.$

Alternatively, in matrix form we have

$left[{begin{matrix} T^{(mathbf n)}_1 & T^{(mathbf n)}_2 & T^{(mathbf n)}_3end{matrix}}right]=left[{begin{matrix} n_1 & n_2 & n_3 end{matrix}}right]cdot left[{begin{matrix} sigma _{11} & sigma _{12} & sigma _{13} \ sigma _{21} & sigma _{22} & sigma _{23} \ sigma _{31} & sigma _{32} & sigma _{33} \ end{matrix}}right].$

The Voigt notation representation of the Cauchy stress tensor takes advantage of the symmetry of the stress tensor to express the stress as a six-dimensional vector of the form:

${displaystyle {boldsymbol {sigma }}={begin{bmatrix}sigma _{1}&sigma _{2}&sigma _{3}&sigma _{4}&sigma _{5}&sigma _{6}end{bmatrix}}^{textsf {T}}equiv {begin{bmatrix}sigma _{11}&sigma _{22}&sigma _{33}&sigma _{23}&sigma _{13}&sigma _{12}end{bmatrix}}^{textsf {T}}.}$

The Voigt notation is used extensively in representing stress–strain relations in solid mechanics and for computational efficiency in numerical structural mechanics software.

Transformation rule of the stress tensor[edit]

It can be shown that the stress tensor is a contravariant second order tensor, which is a statement of how it transforms under a change of the coordinate system. From an x_i-system to an x_i‘ -system, the components σ_ij in the initial system are transformed into the components σ_ij‘ in the new system according to the tensor transformation rule (Figure 2.4):

${displaystyle sigma '_{ij}=a_{im}a_{jn}sigma _{mn}quad {text{or}}quad {boldsymbol {sigma }}'=mathbf {A} {boldsymbol {sigma }}mathbf {A} ^{textsf {T}},}$

where A is a rotation matrix with components a_ij. In matrix form this is

$left[{{begin{matrix}sigma '_{{11}}&sigma '_{{12}}&sigma '_{{13}}\sigma '_{{21}}&sigma '_{{22}}&sigma '_{{23}}\sigma '_{{31}}&sigma '_{{32}}&sigma '_{{33}}\end{matrix}}}right]=left[{{begin{matrix}a_{{11}}&a_{{12}}&a_{{13}}\a_{{21}}&a_{{22}}&a_{{23}}\a_{{31}}&a_{{32}}&a_{{33}}\end{matrix}}}right]left[{{begin{matrix}sigma _{{11}}&sigma _{{12}}&sigma _{{13}}\sigma _{{21}}&sigma _{{22}}&sigma _{{23}}\sigma _{{31}}&sigma _{{32}}&sigma _{{33}}\end{matrix}}}right]left[{{begin{matrix}a_{{11}}&a_{{21}}&a_{{31}}\a_{{12}}&a_{{22}}&a_{{32}}\a_{{13}}&a_{{23}}&a_{{33}}\end{matrix}}}right].$

Figure 2.4 Transformation of the stress tensor

Expanding the matrix operation, and simplifying terms using the symmetry of the stress tensor, gives

${displaystyle {begin{aligned}sigma _{11}'={}&a_{11}^{2}sigma _{11}+a_{12}^{2}sigma _{22}+a_{13}^{2}sigma _{33}+2a_{11}a_{12}sigma _{12}+2a_{11}a_{13}sigma _{13}+2a_{12}a_{13}sigma _{23},\sigma _{22}'={}&a_{21}^{2}sigma _{11}+a_{22}^{2}sigma _{22}+a_{23}^{2}sigma _{33}+2a_{21}a_{22}sigma _{12}+2a_{21}a_{23}sigma _{13}+2a_{22}a_{23}sigma _{23},\sigma _{33}'={}&a_{31}^{2}sigma _{11}+a_{32}^{2}sigma _{22}+a_{33}^{2}sigma _{33}+2a_{31}a_{32}sigma _{12}+2a_{31}a_{33}sigma _{13}+2a_{32}a_{33}sigma _{23},\sigma _{12}'={}&a_{11}a_{21}sigma _{11}+a_{12}a_{22}sigma _{22}+a_{13}a_{23}sigma _{33}\&+(a_{11}a_{22}+a_{12}a_{21})sigma _{12}+(a_{12}a_{23}+a_{13}a_{22})sigma _{23}+(a_{11}a_{23}+a_{13}a_{21})sigma _{13},\sigma _{23}'={}&a_{21}a_{31}sigma _{11}+a_{22}a_{32}sigma _{22}+a_{23}a_{33}sigma _{33}\&+(a_{21}a_{32}+a_{22}a_{31})sigma _{12}+(a_{22}a_{33}+a_{23}a_{32})sigma _{23}+(a_{21}a_{33}+a_{23}a_{31})sigma _{13},\sigma _{13}'={}&a_{11}a_{31}sigma _{11}+a_{12}a_{32}sigma _{22}+a_{13}a_{33}sigma _{33}\&+(a_{11}a_{32}+a_{12}a_{31})sigma _{12}+(a_{12}a_{33}+a_{13}a_{32})sigma _{23}+(a_{11}a_{33}+a_{13}a_{31})sigma _{13}.end{aligned}}}$

The Mohr circle for stress is a graphical representation of this transformation of stresses.

Normal and shear stresses[edit]

The magnitude of the normal stress component σ_n of any stress vector T⁽ⁿ⁾ acting on an arbitrary plane with normal unit vector n at a given point, in terms of the components σ_ij of the stress tensor σ, is the dot product of the stress vector and the normal unit vector:

$begin{align} sigma_mathrm{n} &= mathbf{T}^{(mathbf{n})}cdot mathbf{n} \ &=T^{(mathbf n)}_i n_i \ &=sigma_{ij}n_i n_j. end{align}$

The magnitude of the shear stress component τ_n, acting orthogonal to the vector n, can then be found using the Pythagorean theorem:

$begin{align} tau_mathrm{n} &=sqrt{ left( T^{(mathbf n)} right)^2-sigma_mathrm{n}^2} \ &= sqrt{T_i^{(mathbf n)}T_i^{(mathbf n)}-sigma_mathrm{n}^2}, end{align}$

where

$left( T^{(mathbf n)} right)^2 = T_i^{(mathbf n)} T_i^{(mathbf n)} = left( sigma_{ij} n_j right) left(sigma_{ik} n_k right) = sigma_{ij} sigma_{ik} n_j n_k.$

Balance laws – Cauchy’s equations of motion[edit]

Figure 4. Continuum body in equilibrium

Cauchy’s first law of motion[edit]

${displaystyle sigma _{ji,j}+F_{i}=0}$

where ${displaystyle sigma _{ji,j}=sum _{j}partial _{j}sigma _{ji}}$ following Einstein notations.

For example, for a hydrostatic fluid in equilibrium conditions, the stress tensor takes on the form:

${displaystyle {sigma _{ij}}=-p{delta _{ij}},}$

where is the hydrostatic pressure, and ${delta_{ij}}$ is the kronecker delta.

Derivation of equilibrium equations
Consider a continuum body (see Figure 4) occupying a volume , having a surface area , with defined traction or surface forces ${displaystyle T_{i}^{(n)}}$ per unit area acting on every point of the body surface, and body forces $F_{i}$ per unit of volume on every point within the volume . Thus, if the body is in equilibrium the resultant force acting on the volume is zero, thus: ${displaystyle int _{S}T_{i}^{(n)}dS+int _{V}F_{i}dV=0}$ By definition the stress vector is ${displaystyle T_{i}^{(n)}=sigma _{ji}n_{j}}$ , then ${displaystyle int _{S}sigma _{ji}n_{j},dS+int _{V}F_{i},dV=0}$ Using the Gauss’s divergence theorem to convert a surface integral to a volume integral gives ${displaystyle int _{V}sigma _{ji,j},dV+int _{V}F_{i},dV=0}$ ${displaystyle int _{V}(sigma _{ji,j}+F_{i},)dV=0}$ For an arbitrary volume the integral vanishes, and we have the equilibrium equations ${displaystyle sigma _{ji,j}+F_{i}=0}$

Derivation of equilibrium equations

Consider a continuum body (see Figure 4) occupying a volume

, having a surface area

, with defined traction or surface forces ${displaystyle T_{i}^{(n)}}$

per unit area acting on every point of the body surface, and body forces $F_{i}$

per unit of volume on every point within the volume

. Thus, if the body is in equilibrium the resultant force acting on the volume is zero, thus:

${displaystyle int _{S}T_{i}^{(n)}dS+int _{V}F_{i}dV=0}$

By definition the stress vector is ${displaystyle T_{i}^{(n)}=sigma _{ji}n_{j}}$ , then

${displaystyle int _{S}sigma _{ji}n_{j},dS+int _{V}F_{i},dV=0}$

Using the Gauss’s divergence theorem to convert a surface integral to a volume integral gives

${displaystyle int _{V}sigma _{ji,j},dV+int _{V}F_{i},dV=0}$

${displaystyle int _{V}(sigma _{ji,j}+F_{i},)dV=0}$

For an arbitrary volume the integral vanishes, and we have the equilibrium equations

${displaystyle sigma _{ji,j}+F_{i}=0}$

Cauchy’s second law of motion[edit]

According to the principle of conservation of angular momentum, equilibrium requires that the summation of moments with respect to an arbitrary point is zero, which leads to the conclusion that the stress tensor is symmetric, thus having only six independent stress components, instead of the original nine:

${displaystyle sigma _{ij}=sigma _{ji}}$

Derivation of symmetry of the stress tensor
Summing moments about point O (Figure 4) the resultant moment is zero as the body is in equilibrium. Thus, ${displaystyle {begin{aligned}M_{O}&=int _{S}(mathbf {r} times mathbf {T} )dS+int _{V}(mathbf {r} times mathbf {F} )dV=0\0&=int _{S}varepsilon _{ijk}x_{j}T_{k}^{(n)}dS+int _{V}varepsilon _{ijk}x_{j}F_{k}dV\end{aligned}}}$ where is the position vector and is expressed as ${displaystyle mathbf {r} =x_{j}mathbf {e} _{j}}$ Knowing that ${displaystyle T_{k}^{(n)}=sigma _{mk}n_{m}}$ and using Gauss’s divergence theorem to change from a surface integral to a volume integral, we have ${displaystyle {begin{aligned}0&=int _{S}varepsilon _{ijk}x_{j}sigma _{mk}n_{m},dS+int _{V}varepsilon _{ijk}x_{j}F_{k},dV\&=int _{V}(varepsilon _{ijk}x_{j}sigma _{mk})_{,m}dV+int _{V}varepsilon _{ijk}x_{j}F_{k},dV\&=int _{V}(varepsilon _{ijk}x_{j,m}sigma _{mk}+varepsilon _{ijk}x_{j}sigma _{mk,m})dV+int _{V}varepsilon _{ijk}x_{j}F_{k},dV\&=int _{V}(varepsilon _{ijk}x_{j,m}sigma _{mk})dV+int _{V}varepsilon _{ijk}x_{j}(sigma _{mk,m}+F_{k})dV\end{aligned}}}$ The second integral is zero as it contains the equilibrium equations. This leaves the first integral, where ${displaystyle x_{j,m}=delta _{jm}}$ , therefore ${displaystyle int _{V}(varepsilon _{ijk}sigma _{jk})dV=0}$ For an arbitrary volume V, we then have ${displaystyle varepsilon _{ijk}sigma _{jk}=0}$ which is satisfied at every point within the body. Expanding this equation we have ${displaystyle sigma _{12}=sigma _{21}}$ , ${displaystyle sigma _{23}=sigma _{32}}$ , and ${displaystyle sigma _{13}=sigma _{31}}$ or in general ${displaystyle sigma _{ij}=sigma _{ji}}$ This proves that the stress tensor is symmetric

Derivation of symmetry of the stress tensor

Summing moments about point O (Figure 4) the resultant moment is zero as the body is in equilibrium. Thus,

${displaystyle {begin{aligned}M_{O}&=int _{S}(mathbf {r} times mathbf {T} )dS+int _{V}(mathbf {r} times mathbf {F} )dV=0\0&=int _{S}varepsilon _{ijk}x_{j}T_{k}^{(n)}dS+int _{V}varepsilon _{ijk}x_{j}F_{k}dV\end{aligned}}}$

where is the position vector and is expressed as

${displaystyle mathbf {r} =x_{j}mathbf {e} _{j}}$

Knowing that ${displaystyle T_{k}^{(n)}=sigma _{mk}n_{m}}$ and using Gauss’s divergence theorem to change from a surface integral to a volume integral, we have

${displaystyle {begin{aligned}0&=int _{S}varepsilon _{ijk}x_{j}sigma _{mk}n_{m},dS+int _{V}varepsilon _{ijk}x_{j}F_{k},dV\&=int _{V}(varepsilon _{ijk}x_{j}sigma _{mk})_{,m}dV+int _{V}varepsilon _{ijk}x_{j}F_{k},dV\&=int _{V}(varepsilon _{ijk}x_{j,m}sigma _{mk}+varepsilon _{ijk}x_{j}sigma _{mk,m})dV+int _{V}varepsilon _{ijk}x_{j}F_{k},dV\&=int _{V}(varepsilon _{ijk}x_{j,m}sigma _{mk})dV+int _{V}varepsilon _{ijk}x_{j}(sigma _{mk,m}+F_{k})dV\end{aligned}}}$

The second integral is zero as it contains the equilibrium equations. This leaves the first integral, where ${displaystyle x_{j,m}=delta _{jm}}$ , therefore

${displaystyle int _{V}(varepsilon _{ijk}sigma _{jk})dV=0}$

For an arbitrary volume V, we then have

${displaystyle varepsilon _{ijk}sigma _{jk}=0}$

which is satisfied at every point within the body. Expanding this equation we have

${displaystyle sigma _{12}=sigma _{21}}$

, ${displaystyle sigma _{23}=sigma _{32}}$

, and ${displaystyle sigma _{13}=sigma _{31}}$

or in general

${displaystyle sigma _{ij}=sigma _{ji}}$

This proves that the stress tensor is symmetric

However, in the presence of couple-stresses, i.e. moments per unit volume, the stress tensor is non-symmetric. This also is the case when the Knudsen number is close to one, ${displaystyle K_{n}rightarrow 1}$ , or the continuum is a non-Newtonian fluid, which can lead to rotationally non-invariant fluids, such as polymers.

Principal stresses and stress invariants[edit]

Stress components on a 2D rotating element. Example of how stress components vary on the faces (edges) of a rectangular element as the angle of its orientation is varied. Principal stresses occur when the shear stresses simultaneously disappear from all faces. The orientation at which this occurs gives the principal directions. In this example, when the rectangle is horizontal, the stresses are given by ${displaystyle left[{begin{matrix}sigma _{11}&sigma _{12}\sigma _{21}&sigma _{22}end{matrix}}right]=left[{begin{matrix}-10&10\10&15end{matrix}}right].}$

At every point in a stressed body there are at least three planes, called principal planes, with normal vectors , called principal directions, where the corresponding stress vector is perpendicular to the plane, i.e., parallel or in the same direction as the normal vector , and where there are no normal shear stresses $tau _{{mathrm {n}}}$ . The three stresses normal to these principal planes are called principal stresses.

The components $sigma _{ij}$ of the stress tensor depend on the orientation of the coordinate system at the point under consideration. However, the stress tensor itself is a physical quantity and as such, it is independent of the coordinate system chosen to represent it. There are certain invariants associated with every tensor which are also independent of the coordinate system. For example, a vector is a simple tensor of rank one. In three dimensions, it has three components. The value of these components will depend on the coordinate system chosen to represent the vector, but the magnitude of the vector is a physical quantity (a scalar) and is independent of the Cartesian coordinate system chosen to represent the vector (so long as it is normal). Similarly, every second rank tensor (such as the stress and the strain tensors) has three independent invariant quantities associated with it. One set of such invariants are the principal stresses of the stress tensor, which are just the eigenvalues of the stress tensor. Their direction vectors are the principal directions or eigenvectors.

A stress vector parallel to the normal unit vector is given by:

${displaystyle mathbf {T} ^{(mathbf {n} )}=lambda mathbf {n} =mathbf {sigma } _{mathrm {n} }mathbf {n} }$

where lambda is a constant of proportionality, and in this particular case corresponds to the magnitudes $sigma _{{mathrm {n}}}$ of the normal stress vectors or principal stresses.

Knowing that ${displaystyle T_{i}^{(n)}=sigma _{ij}n_{j}}$ and ${displaystyle n_{i}=delta _{ij}n_{j}}$ , we have

${displaystyle {begin{aligned}T_{i}^{(n)}&=lambda n_{i}\sigma _{ij}n_{j}&=lambda n_{i}\sigma _{ij}n_{j}-lambda n_{i}&=0\left(sigma _{ij}-lambda delta _{ij}right)n_{j}&=0\end{aligned}}}$

This is a homogeneous system, i.e. equal to zero, of three linear equations where $n_{j}$ are the unknowns. To obtain a nontrivial (non-zero) solution for $n_{j}$ , the determinant matrix of the coefficients must be equal to zero, i.e. the system is singular. Thus,

${displaystyle left|sigma _{ij}-lambda delta _{ij}right|={begin{vmatrix}sigma _{11}-lambda &sigma _{12}&sigma _{13}\sigma _{21}&sigma _{22}-lambda &sigma _{23}\sigma _{31}&sigma _{32}&sigma _{33}-lambda \end{vmatrix}}=0}$

Expanding the determinant leads to the characteristic equation

${displaystyle left|sigma _{ij}-lambda delta _{ij}right|=-lambda ^{3}+I_{1}lambda ^{2}-I_{2}lambda +I_{3}=0}$

where

${displaystyle {begin{aligned}I_{1}&=sigma _{11}+sigma _{22}+sigma _{33}\&=sigma _{kk}={text{tr}}({boldsymbol {sigma }})\[4pt]I_{2}&={begin{vmatrix}sigma _{22}&sigma _{23}\sigma _{32}&sigma _{33}\end{vmatrix}}+{begin{vmatrix}sigma _{11}&sigma _{13}\sigma _{31}&sigma _{33}\end{vmatrix}}+{begin{vmatrix}sigma _{11}&sigma _{12}\sigma _{21}&sigma _{22}\end{vmatrix}}\&=sigma _{11}sigma _{22}+sigma _{22}sigma _{33}+sigma _{11}sigma _{33}-sigma _{12}^{2}-sigma _{23}^{2}-sigma _{31}^{2}\&={frac {1}{2}}left(sigma _{ii}sigma _{jj}-sigma _{ij}sigma _{ji}right)={frac {1}{2}}left[left({text{tr}}({boldsymbol {sigma }})right)^{2}-{text{tr}}left({boldsymbol {sigma }}^{2}right)right]\[4pt]I_{3}&=det(sigma _{ij})=det({boldsymbol {sigma }})\&=sigma _{11}sigma _{22}sigma _{33}+2sigma _{12}sigma _{23}sigma _{31}-sigma _{12}^{2}sigma _{33}-sigma _{23}^{2}sigma _{11}-sigma _{31}^{2}sigma _{22}\end{aligned}}}$

The characteristic equation has three real roots $lambda _{i}$ , i.e. not imaginary due to the symmetry of the stress tensor. The ${displaystyle sigma _{1}=max left(lambda _{1},lambda _{2},lambda _{3}right)}$ , ${displaystyle sigma _{3}=min left(lambda _{1},lambda _{2},lambda _{3}right)}$ and ${displaystyle sigma _{2}=I_{1}-sigma _{1}-sigma _{3}}$ , are the principal stresses, functions of the eigenvalues $lambda _{i}$ . The eigenvalues are the roots of the characteristic polynomial. The principal stresses are unique for a given stress tensor. Therefore, from the characteristic equation, the coefficients $I_{1}$ , $I_{2}$ and $I_{3}$ , called the first, second, and third stress invariants, respectively, always have the same value regardless of the coordinate system’s orientation.

For each eigenvalue, there is a non-trivial solution for $n_{j}$ in the equation ${displaystyle left(sigma _{ij}-lambda delta _{ij}right)n_{j}=0}$ . These solutions are the principal directions or eigenvectors defining the plane where the principal stresses act. The principal stresses and principal directions characterize the stress at a point and are independent of the orientation.

A coordinate system with axes oriented to the principal directions implies that the normal stresses are the principal stresses and the stress tensor is represented by a diagonal matrix:

${displaystyle sigma _{ij}={begin{bmatrix}sigma _{1}&0&0\0&sigma _{2}&0\0&0&sigma _{3}end{bmatrix}}}$

The principal stresses can be combined to form the stress invariants, $I_{1}$ , $I_{2}$ , and $I_{3}$ . The first and third invariant are the trace and determinant respectively, of the stress tensor. Thus,

${displaystyle {begin{aligned}I_{1}&=sigma _{1}+sigma _{2}+sigma _{3}\I_{2}&=sigma _{1}sigma _{2}+sigma _{2}sigma _{3}+sigma _{3}sigma _{1}\I_{3}&=sigma _{1}sigma _{2}sigma _{3}\end{aligned}}}$

Because of its simplicity, the principal coordinate system is often useful when considering the state of the elastic medium at a particular point. Principal stresses are often expressed in the following equation for evaluating stresses in the x and y directions or axial and bending stresses on a part.^[14]^{: p.58–59} The principal normal stresses can then be used to calculate the von Mises stress and ultimately the safety factor and margin of safety.

${displaystyle sigma _{1},sigma _{2}={frac {sigma _{x}+sigma _{y}}{2}}pm {sqrt {left({frac {sigma _{x}-sigma _{y}}{2}}right)^{2}+tau _{xy}^{2}}}}$

Using just the part of the equation under the square root is equal to the maximum and minimum shear stress for plus and minus. This is shown as:

${displaystyle tau _{max },tau _{min }=pm {sqrt {left({frac {sigma _{x}-sigma _{y}}{2}}right)^{2}+tau _{xy}^{2}}}}$

Maximum and minimum shear stresses[edit]

The maximum shear stress or maximum principal shear stress is equal to one-half the difference between the largest and smallest principal stresses, and acts on the plane that bisects the angle between the directions of the largest and smallest principal stresses, i.e. the plane of the maximum shear stress is oriented 45^circ from the principal stress planes. The maximum shear stress is expressed as

${displaystyle tau _{max }={frac {1}{2}}left|sigma _{max }-sigma _{min }right|}$

Assuming ${displaystyle sigma _{1}geq sigma _{2}geq sigma _{3}}$ then

${displaystyle tau _{max }={frac {1}{2}}left|sigma _{1}-sigma _{3}right|}$

When the stress tensor is non zero the normal stress component acting on the plane for the maximum shear stress is non-zero and it is equal to

${displaystyle sigma _{text{n}}={frac {1}{2}}left(sigma _{1}+sigma _{3}right)}$

Derivation of the maximum and minimum shear stresses^[8]^{: p.45–78}^[11]^: p.1–46^[13]^[15]^{: p.111–157}^[16]^: p.9–41^[17]^{: p.33–66}^[18]^{: p.43–61}
The normal stress can be written in terms of principal stresses ${displaystyle (sigma _{1}geq sigma _{2}geq sigma _{3})}$ as ${displaystyle {begin{aligned}sigma _{mathrm {n} }&=sigma _{ij}n_{i}n_{j}\&=sigma _{1}n_{1}^{2}+sigma _{2}n_{2}^{2}+sigma _{3}n_{3}^{2}\end{aligned}}}$ Knowing that $left( T^{(n)} right)^2=sigma_{ij}sigma_{ik}n_jn_k$ , the shear stress in terms of principal stresses components is expressed as ${displaystyle {begin{aligned}tau _{text{n}}^{2}&=left(T^{(n)}right)^{2}-sigma _{text{n}}^{2}\&=sigma _{1}^{2}n_{1}^{2}+sigma _{2}^{2}n_{2}^{2}+sigma _{3}^{2}n_{3}^{2}-left(sigma _{1}n_{1}^{2}+sigma _{2}n_{2}^{2}+sigma _{3}n_{3}^{2}right)^{2}\&=left(sigma _{1}^{2}-sigma _{2}^{2}right)n_{1}^{2}+left(sigma _{2}^{2}-sigma _{3}^{2}right)n_{2}^{2}+sigma _{3}^{2}-left[left(sigma _{1}-sigma _{3}right)n_{1}^{2}+left(sigma _{2}-sigma _{2}right)n_{2}^{2}+sigma _{3}right]^{2}\&=(sigma _{1}-sigma _{2})^{2}n_{1}^{2}n_{2}^{2}+(sigma _{2}-sigma _{3})^{2}n_{2}^{2}n_{3}^{2}+(sigma _{1}-sigma _{3})^{2}n_{1}^{2}n_{3}^{2}\end{aligned}}}$ The maximum shear stress at a point in a continuum body is determined by maximizing ${displaystyle tau _{mathrm {n} }^{2}}$ subject to the condition that ${displaystyle n_{i}n_{i}=n_{1}^{2}+n_{2}^{2}+n_{3}^{2}=1}$ This is a constrained maximization problem, which can be solved using the Lagrangian multiplier technique to convert the problem into an unconstrained optimization problem. Thus, the stationary values (maximum and minimum values)of ${displaystyle tau _{text{n}}^{2}}$ occur where the gradient of ${displaystyle tau _{text{n}}^{2}}$ is parallel to the gradient of . The Lagrangian function for this problem can be written as ${displaystyle {begin{aligned}Fleft(n_{1},n_{2},n_{3},lambda right)&=tau ^{2}+lambda left(gleft(n_{1},n_{2},n_{3}right)-1right)\&=sigma _{1}^{2}n_{1}^{2}+sigma _{2}^{2}n_{2}^{2}+sigma _{3}^{2}n_{3}^{2}-left(sigma _{1}n_{1}^{2}+sigma _{2}n_{2}^{2}+sigma _{3}n_{3}^{2}right)^{2}+lambda left(n_{1}^{2}+n_{2}^{2}+n_{3}^{2}-1right)\end{aligned}}}$ where is the Lagrangian multiplier (which is different from the use to denote eigenvalues). The extreme values of these functions are ${displaystyle {frac {partial F}{partial n_{1}}}=0qquad {frac {partial F}{partial n_{2}}}=0qquad {frac {partial F}{partial n_{3}}}=0}$ thence ${displaystyle {frac {partial F}{partial n_{1}}}=n_{1}sigma _{1}^{2}-2n_{1}sigma _{1}left(sigma _{1}n_{1}^{2}+sigma _{2}n_{2}^{2}+sigma _{3}n_{3}^{2}right)+lambda n_{1}=0}$ ${displaystyle {frac {partial F}{partial n_{2}}}=n_{2}sigma _{2}^{2}-2n_{2}sigma _{2}left(sigma _{1}n_{1}^{2}+sigma _{2}n_{2}^{2}+sigma _{3}n_{3}^{2}right)+lambda n_{2}=0}$ ${displaystyle {frac {partial F}{partial n_{3}}}=n_{3}sigma _{3}^{2}-2n_{3}sigma _{3}left(sigma _{1}n_{1}^{2}+sigma _{2}n_{2}^{2}+sigma _{3}n_{3}^{2}right)+lambda n_{3}=0}$ These three equations together with the condition ${displaystyle n_{i}n_{i}=1}$ may be solved for ${displaystyle lambda ,n_{1},n_{2},}$ and $n_{3}$ By multiplying the first three equations by ${displaystyle n_{1},,n_{2},}$ and $n_{3}$ , respectively, and knowing that ${displaystyle sigma _{text{n}}=sigma _{ij}n_{i}n_{j}=sigma _{1}n_{1}^{2}+sigma _{2}n_{2}^{2}+sigma _{3}n_{3}^{2}}$ we obtain ${displaystyle n_{1}^{2}sigma _{1}^{2}-2sigma _{1}n_{1}^{2}sigma _{text{n}}+n_{1}^{2}lambda =0}$ ${displaystyle n_{2}^{2}sigma _{2}^{2}-2sigma _{2}n_{2}^{2}sigma _{text{n}}+n_{2}^{2}lambda =0}$ ${displaystyle n_{3}^{2}sigma _{3}^{2}-2sigma _{1}n_{3}^{2}sigma _{text{n}}+n_{3}^{2}lambda =0}$ Adding these three equations we get ${displaystyle {begin{aligned}left[n_{1}^{2}sigma _{1}^{2}+n_{2}^{2}sigma _{2}^{2}+n_{3}^{2}sigma _{3}^{2}right]-2left(sigma _{1}n_{1}^{2}+sigma _{2}n_{2}^{2}+sigma _{3}n_{3}^{2}right)sigma _{mathrm {n} }+lambda left(n_{1}^{2}+n_{2}^{2}+n_{3}^{2}right)&=0\left[tau _{mathrm {n} }^{2}+left(sigma _{1}n_{1}^{2}+sigma _{2}n_{2}^{2}+sigma _{3}n_{3}^{2}right)^{2}right]-2sigma _{mathrm {n} }^{2}+lambda &=0\left[tau _{mathrm {n} }^{2}+sigma _{mathrm {n} }^{2}right]-2sigma _{mathrm {n} }^{2}+lambda &=0\lambda &=sigma _{mathrm {n} }^{2}-tau _{mathrm {n} }^{2}end{aligned}}}$ this result can be substituted into each of the first three equations to obtain ${displaystyle {begin{aligned}{frac {partial F}{partial n_{1}}}=n_{1}sigma _{1}^{2}-2n_{1}sigma _{1}left(sigma _{1}n_{1}^{2}+sigma _{2}n_{2}^{2}+sigma _{3}n_{3}^{2}right)+left(sigma _{text{n}}^{2}-tau _{text{n}}^{2}right)n_{1}&=0\n_{1}sigma _{1}^{2}-2n_{1}sigma _{1}sigma _{text{n}}+left(sigma _{text{n}}^{2}-tau _{text{n}}^{2}right)n_{1}&=0\left(sigma _{1}^{2}-2sigma _{1}sigma _{text{n}}+sigma _{text{n}}^{2}-tau _{text{n}}^{2}right)n_{1}&=0\end{aligned}}}$ Doing the same for the other two equations we have ${displaystyle {frac {partial F}{partial n_{2}}}=left(sigma _{2}^{2}-2sigma _{2}sigma _{text{n}}+sigma _{text{n}}^{2}-tau _{text{n}}^{2}right)n_{2}=0}$ ${displaystyle {frac {partial F}{partial n_{3}}}=left(sigma _{3}^{2}-2sigma _{3}sigma _{text{n}}+sigma _{text{n}}^{2}-tau _{text{n}}^{2}right)n_{3}=0}$ A first approach to solve these last three equations is to consider the trivial solution ${displaystyle n_{i}=0}$ . However, this option does not fulfill the constraint ${displaystyle n_{i}n_{i}=1}$ . Considering the solution where ${displaystyle n_{1}=n_{2}=0}$ and ${displaystyle n_{3}neq 0}$ , it is determine from the condition ${displaystyle n_{i}n_{i}=1}$ that ${displaystyle n_{3}=pm 1}$ , then from the original equation for ${displaystyle tau _{text{n}}^{2}}$ it is seen that ${displaystyle tau _{text{n}}=0}$ . The other two possible values for ${displaystyle tau _{text{n}}}$ can be obtained similarly by assuming ${displaystyle n_{1}=n_{3}=0}$ and ${displaystyle n_{2}neq 0}$ ${displaystyle n_{2}=n_{3}=0}$ and ${displaystyle n_{1}neq 0}$ Thus, one set of solutions for these four equations is: ${displaystyle {begin{aligned}n_{1}&=0,&n_{2}&=0,&n_{3}&=pm 1,&tau _{text{n}}&=0\n_{1}&=0,&n_{2}&=pm 1,&n_{3}&=0,&tau _{text{n}}&=0\n_{1}&=pm 1,&n_{2}&=0,&n_{3}&=0,&tau _{text{n}}&=0end{aligned}}}$ These correspond to minimum values for $tau _{{mathrm {n}}}$ and verifies that there are no shear stresses on planes normal to the principal directions of stress, as shown previously. A second set of solutions is obtained by assuming ${displaystyle n_{1}=0,,n_{2}neq 0}$ and ${displaystyle n_{3}neq 0}$ . Thus we have ${displaystyle {frac {partial F}{partial n_{2}}}=sigma _{2}^{2}-2sigma _{2}sigma _{text{n}}+sigma _{text{n}}^{2}-tau _{text{n}}^{2}=0}$ ${displaystyle {frac {partial F}{partial n_{3}}}=sigma _{3}^{2}-2sigma _{3}sigma _{text{n}}+sigma _{text{n}}^{2}-tau _{text{n}}^{2}=0}$ To find the values for $n_{2}$ and $n_{3}$ we first add these two equations ${displaystyle {begin{aligned}sigma _{2}^{2}-sigma _{3}^{2}-2sigma _{2}sigma _{text{n}}+2sigma _{3}sigma _{text{n}}&=0\sigma _{2}^{2}-sigma _{3}^{2}-2sigma _{text{n}}left(sigma _{2}-sigma _{3}right)&=0\sigma _{2}+sigma _{3}&=2sigma _{text{n}}end{aligned}}}$ Knowing that for $n_{1}=0$ ${displaystyle sigma _{text{n}}=sigma _{1}n_{1}^{2}+sigma _{2}n_{2}^{2}+sigma _{3}n_{3}^{2}=sigma _{2}n_{2}^{2}+sigma _{3}n_{3}^{2}}$ and ${displaystyle n_{1}^{2}+n_{2}^{2}+n_{3}^{2}=n_{2}^{2}+n_{3}^{2}=1}$ we have ${displaystyle {begin{aligned}sigma _{2}+sigma _{3}&=2sigma _{text{n}}\sigma _{2}+sigma _{3}&=2left(sigma _{2}n_{2}^{2}+sigma _{3}n_{3}^{2}right)\sigma _{2}+sigma _{3}&=2left(sigma _{2}n_{2}^{2}+sigma _{3}left(1-n_{2}^{2}right)right)=0end{aligned}}}$ and solving for $n_{2}$ we have ${displaystyle n_{2}=pm {frac {1}{sqrt {2}}}}$ Then solving for $n_{3}$ we have ${displaystyle n_{3}={sqrt {1-n_{2}^{2}}}=pm {frac {1}{sqrt {2}}}}$ and ${displaystyle {begin{aligned}tau _{text{n}}^{2}&=(sigma _{2}-sigma _{3})^{2}n_{2}^{2}n_{3}^{2}\tau _{text{n}}&={frac {sigma _{2}-sigma _{3}}{2}}end{aligned}}}$ The other two possible values for ${displaystyle tau _{text{n}}}$ can be obtained similarly by assuming ${displaystyle n_{2}=0,,n_{1}neq 0}$ and ${displaystyle n_{3}neq 0}$ ${displaystyle n_{3}=0,,n_{1}neq 0}$ and ${displaystyle n_{2}neq 0}$ Therefore, the second set of solutions for ${displaystyle {frac {partial F}{partial n_{1}}}=0}$ , representing a maximum for ${displaystyle tau _{text{n}}}$ is ${displaystyle n_{1}=0,,,n_{2}=pm {frac {1}{sqrt {2}}},,,n_{3}=pm {frac {1}{sqrt {2}}},,,tau _{text{n}}=pm {frac {sigma _{2}-sigma _{3}}{2}}}$ ${displaystyle n_{1}=pm {frac {1}{sqrt {2}}},,,n_{2}=0,,,n_{3}=pm {frac {1}{sqrt {2}}},,,tau _{text{n}}=pm {frac {sigma _{1}-sigma _{3}}{2}}}$ ${displaystyle n_{1}=pm {frac {1}{sqrt {2}}},,,n_{2}=pm {frac {1}{sqrt {2}}},,,n_{3}=0,,,tau _{text{n}}=pm {frac {sigma _{1}-sigma _{2}}{2}}}$ Therefore, assuming ${displaystyle sigma _{1}geq sigma _{2}geq sigma _{3}}$ , the maximum shear stress is expressed by ${displaystyle tau _{max }={frac {1}{2}}left\|sigma _{1}-sigma _{3}right\|={frac {1}{2}}left\|sigma _{max }-sigma _{min }right\|}$ and it can be stated as being equal to one-half the difference between the largest and smallest principal stresses, acting on the plane that bisects the angle between the directions of the largest and smallest principal stresses.

Derivation of the maximum and minimum shear stresses^[8]^{: p.45–78}^[11]^: p.1–46^[13]^[15]^{: p.111–157}^[16]^: p.9–41^[17]^{: p.33–66}^[18]^{: p.43–61}

The normal stress can be written in terms of principal stresses ${displaystyle (sigma _{1}geq sigma _{2}geq sigma _{3})}$

${displaystyle {begin{aligned}sigma _{mathrm {n} }&=sigma _{ij}n_{i}n_{j}\&=sigma _{1}n_{1}^{2}+sigma _{2}n_{2}^{2}+sigma _{3}n_{3}^{2}\end{aligned}}}$

Knowing that $left( T^{(n)} right)^2=sigma_{ij}sigma_{ik}n_jn_k$ , the shear stress in terms of principal stresses components is expressed as

${displaystyle {begin{aligned}tau _{text{n}}^{2}&=left(T^{(n)}right)^{2}-sigma _{text{n}}^{2}\&=sigma _{1}^{2}n_{1}^{2}+sigma _{2}^{2}n_{2}^{2}+sigma _{3}^{2}n_{3}^{2}-left(sigma _{1}n_{1}^{2}+sigma _{2}n_{2}^{2}+sigma _{3}n_{3}^{2}right)^{2}\&=left(sigma _{1}^{2}-sigma _{2}^{2}right)n_{1}^{2}+left(sigma _{2}^{2}-sigma _{3}^{2}right)n_{2}^{2}+sigma _{3}^{2}-left[left(sigma _{1}-sigma _{3}right)n_{1}^{2}+left(sigma _{2}-sigma _{2}right)n_{2}^{2}+sigma _{3}right]^{2}\&=(sigma _{1}-sigma _{2})^{2}n_{1}^{2}n_{2}^{2}+(sigma _{2}-sigma _{3})^{2}n_{2}^{2}n_{3}^{2}+(sigma _{1}-sigma _{3})^{2}n_{1}^{2}n_{3}^{2}\end{aligned}}}$

The maximum shear stress at a point in a continuum body is determined by maximizing ${displaystyle tau _{mathrm {n} }^{2}}$ subject to the condition that

${displaystyle n_{i}n_{i}=n_{1}^{2}+n_{2}^{2}+n_{3}^{2}=1}$

This is a constrained maximization problem, which can be solved using the Lagrangian multiplier technique to convert the problem into an unconstrained optimization problem. Thus, the stationary values (maximum and minimum values)of ${displaystyle tau _{text{n}}^{2}}$ occur where the gradient of ${displaystyle tau _{text{n}}^{2}}$ is parallel to the gradient of .

The Lagrangian function for this problem can be written as

${displaystyle {begin{aligned}Fleft(n_{1},n_{2},n_{3},lambda right)&=tau ^{2}+lambda left(gleft(n_{1},n_{2},n_{3}right)-1right)\&=sigma _{1}^{2}n_{1}^{2}+sigma _{2}^{2}n_{2}^{2}+sigma _{3}^{2}n_{3}^{2}-left(sigma _{1}n_{1}^{2}+sigma _{2}n_{2}^{2}+sigma _{3}n_{3}^{2}right)^{2}+lambda left(n_{1}^{2}+n_{2}^{2}+n_{3}^{2}-1right)\end{aligned}}}$

where lambda is the Lagrangian multiplier (which is different from the lambda use to denote eigenvalues).

The extreme values of these functions are

${displaystyle {frac {partial F}{partial n_{1}}}=0qquad {frac {partial F}{partial n_{2}}}=0qquad {frac {partial F}{partial n_{3}}}=0}$

thence

${displaystyle {frac {partial F}{partial n_{1}}}=n_{1}sigma _{1}^{2}-2n_{1}sigma _{1}left(sigma _{1}n_{1}^{2}+sigma _{2}n_{2}^{2}+sigma _{3}n_{3}^{2}right)+lambda n_{1}=0}$

${displaystyle {frac {partial F}{partial n_{2}}}=n_{2}sigma _{2}^{2}-2n_{2}sigma _{2}left(sigma _{1}n_{1}^{2}+sigma _{2}n_{2}^{2}+sigma _{3}n_{3}^{2}right)+lambda n_{2}=0}$

${displaystyle {frac {partial F}{partial n_{3}}}=n_{3}sigma _{3}^{2}-2n_{3}sigma _{3}left(sigma _{1}n_{1}^{2}+sigma _{2}n_{2}^{2}+sigma _{3}n_{3}^{2}right)+lambda n_{3}=0}$

These three equations together with the condition ${displaystyle n_{i}n_{i}=1}$ may be solved for ${displaystyle lambda ,n_{1},n_{2},}$ and $n_{3}$

By multiplying the first three equations by ${displaystyle n_{1},,n_{2},}$ and $n_{3}$ , respectively, and knowing that ${displaystyle sigma _{text{n}}=sigma _{ij}n_{i}n_{j}=sigma _{1}n_{1}^{2}+sigma _{2}n_{2}^{2}+sigma _{3}n_{3}^{2}}$ we obtain

${displaystyle n_{1}^{2}sigma _{1}^{2}-2sigma _{1}n_{1}^{2}sigma _{text{n}}+n_{1}^{2}lambda =0}$

${displaystyle n_{2}^{2}sigma _{2}^{2}-2sigma _{2}n_{2}^{2}sigma _{text{n}}+n_{2}^{2}lambda =0}$

${displaystyle n_{3}^{2}sigma _{3}^{2}-2sigma _{1}n_{3}^{2}sigma _{text{n}}+n_{3}^{2}lambda =0}$

Adding these three equations we get

${displaystyle {begin{aligned}left[n_{1}^{2}sigma _{1}^{2}+n_{2}^{2}sigma _{2}^{2}+n_{3}^{2}sigma _{3}^{2}right]-2left(sigma _{1}n_{1}^{2}+sigma _{2}n_{2}^{2}+sigma _{3}n_{3}^{2}right)sigma _{mathrm {n} }+lambda left(n_{1}^{2}+n_{2}^{2}+n_{3}^{2}right)&=0\left[tau _{mathrm {n} }^{2}+left(sigma _{1}n_{1}^{2}+sigma _{2}n_{2}^{2}+sigma _{3}n_{3}^{2}right)^{2}right]-2sigma _{mathrm {n} }^{2}+lambda &=0\left[tau _{mathrm {n} }^{2}+sigma _{mathrm {n} }^{2}right]-2sigma _{mathrm {n} }^{2}+lambda &=0\lambda &=sigma _{mathrm {n} }^{2}-tau _{mathrm {n} }^{2}end{aligned}}}$

this result can be substituted into each of the first three equations to obtain

${displaystyle {begin{aligned}{frac {partial F}{partial n_{1}}}=n_{1}sigma _{1}^{2}-2n_{1}sigma _{1}left(sigma _{1}n_{1}^{2}+sigma _{2}n_{2}^{2}+sigma _{3}n_{3}^{2}right)+left(sigma _{text{n}}^{2}-tau _{text{n}}^{2}right)n_{1}&=0\n_{1}sigma _{1}^{2}-2n_{1}sigma _{1}sigma _{text{n}}+left(sigma _{text{n}}^{2}-tau _{text{n}}^{2}right)n_{1}&=0\left(sigma _{1}^{2}-2sigma _{1}sigma _{text{n}}+sigma _{text{n}}^{2}-tau _{text{n}}^{2}right)n_{1}&=0\end{aligned}}}$

Doing the same for the other two equations we have

${displaystyle {frac {partial F}{partial n_{2}}}=left(sigma _{2}^{2}-2sigma _{2}sigma _{text{n}}+sigma _{text{n}}^{2}-tau _{text{n}}^{2}right)n_{2}=0}$

${displaystyle {frac {partial F}{partial n_{3}}}=left(sigma _{3}^{2}-2sigma _{3}sigma _{text{n}}+sigma _{text{n}}^{2}-tau _{text{n}}^{2}right)n_{3}=0}$

A first approach to solve these last three equations is to consider the trivial solution ${displaystyle n_{i}=0}$ . However, this option does not fulfill the constraint ${displaystyle n_{i}n_{i}=1}$ .

Considering the solution where ${displaystyle n_{1}=n_{2}=0}$ and ${displaystyle n_{3}neq 0}$ , it is determine from the condition ${displaystyle n_{i}n_{i}=1}$ that ${displaystyle n_{3}=pm 1}$ , then from the original equation for ${displaystyle tau _{text{n}}^{2}}$ it is seen that ${displaystyle tau _{text{n}}=0}$ .
The other two possible values for ${displaystyle tau _{text{n}}}$ can be obtained similarly by assuming

${displaystyle n_{1}=n_{3}=0}$

and ${displaystyle n_{2}neq 0}$

${displaystyle n_{2}=n_{3}=0}$

and ${displaystyle n_{1}neq 0}$

Thus, one set of solutions for these four equations is:

${displaystyle {begin{aligned}n_{1}&=0,&n_{2}&=0,&n_{3}&=pm 1,&tau _{text{n}}&=0\n_{1}&=0,&n_{2}&=pm 1,&n_{3}&=0,&tau _{text{n}}&=0\n_{1}&=pm 1,&n_{2}&=0,&n_{3}&=0,&tau _{text{n}}&=0end{aligned}}}$

These correspond to minimum values for $tau _{{mathrm {n}}}$ and verifies that there are no shear stresses on planes normal to the principal directions of stress, as shown previously.

A second set of solutions is obtained by assuming ${displaystyle n_{1}=0,,n_{2}neq 0}$ and ${displaystyle n_{3}neq 0}$ . Thus we have

${displaystyle {frac {partial F}{partial n_{2}}}=sigma _{2}^{2}-2sigma _{2}sigma _{text{n}}+sigma _{text{n}}^{2}-tau _{text{n}}^{2}=0}$

${displaystyle {frac {partial F}{partial n_{3}}}=sigma _{3}^{2}-2sigma _{3}sigma _{text{n}}+sigma _{text{n}}^{2}-tau _{text{n}}^{2}=0}$

To find the values for $n_{2}$ and $n_{3}$ we first add these two equations

${displaystyle {begin{aligned}sigma _{2}^{2}-sigma _{3}^{2}-2sigma _{2}sigma _{text{n}}+2sigma _{3}sigma _{text{n}}&=0\sigma _{2}^{2}-sigma _{3}^{2}-2sigma _{text{n}}left(sigma _{2}-sigma _{3}right)&=0\sigma _{2}+sigma _{3}&=2sigma _{text{n}}end{aligned}}}$

Knowing that for $n_{1}=0$

${displaystyle sigma _{text{n}}=sigma _{1}n_{1}^{2}+sigma _{2}n_{2}^{2}+sigma _{3}n_{3}^{2}=sigma _{2}n_{2}^{2}+sigma _{3}n_{3}^{2}}$

and

${displaystyle n_{1}^{2}+n_{2}^{2}+n_{3}^{2}=n_{2}^{2}+n_{3}^{2}=1}$

we have

${displaystyle {begin{aligned}sigma _{2}+sigma _{3}&=2sigma _{text{n}}\sigma _{2}+sigma _{3}&=2left(sigma _{2}n_{2}^{2}+sigma _{3}n_{3}^{2}right)\sigma _{2}+sigma _{3}&=2left(sigma _{2}n_{2}^{2}+sigma _{3}left(1-n_{2}^{2}right)right)=0end{aligned}}}$

and solving for $n_{2}$ we have

${displaystyle n_{2}=pm {frac {1}{sqrt {2}}}}$

Then solving for $n_{3}$ we have

${displaystyle n_{3}={sqrt {1-n_{2}^{2}}}=pm {frac {1}{sqrt {2}}}}$

and

${displaystyle {begin{aligned}tau _{text{n}}^{2}&=(sigma _{2}-sigma _{3})^{2}n_{2}^{2}n_{3}^{2}\tau _{text{n}}&={frac {sigma _{2}-sigma _{3}}{2}}end{aligned}}}$

The other two possible values for ${displaystyle tau _{text{n}}}$ can be obtained similarly by assuming

${displaystyle n_{2}=0,,n_{1}neq 0}$

and ${displaystyle n_{3}neq 0}$

${displaystyle n_{3}=0,,n_{1}neq 0}$

and ${displaystyle n_{2}neq 0}$

Therefore, the second set of solutions for ${displaystyle {frac {partial F}{partial n_{1}}}=0}$ , representing a maximum for ${displaystyle tau _{text{n}}}$ is

${displaystyle n_{1}=0,,,n_{2}=pm {frac {1}{sqrt {2}}},,,n_{3}=pm {frac {1}{sqrt {2}}},,,tau _{text{n}}=pm {frac {sigma _{2}-sigma _{3}}{2}}}$

${displaystyle n_{1}=pm {frac {1}{sqrt {2}}},,,n_{2}=0,,,n_{3}=pm {frac {1}{sqrt {2}}},,,tau _{text{n}}=pm {frac {sigma _{1}-sigma _{3}}{2}}}$

${displaystyle n_{1}=pm {frac {1}{sqrt {2}}},,,n_{2}=pm {frac {1}{sqrt {2}}},,,n_{3}=0,,,tau _{text{n}}=pm {frac {sigma _{1}-sigma _{2}}{2}}}$

Therefore, assuming ${displaystyle sigma _{1}geq sigma _{2}geq sigma _{3}}$ , the maximum shear stress is expressed by

${displaystyle tau _{max }={frac {1}{2}}left|sigma _{1}-sigma _{3}right|={frac {1}{2}}left|sigma _{max }-sigma _{min }right|}$

and it can be stated as being equal to one-half the difference between the largest and smallest principal stresses, acting on the plane that bisects the angle between the directions of the largest and smallest principal stresses.

Stress deviator tensor[edit]

The stress tensor $sigma _{ij}$ can be expressed as the sum of two other stress tensors:

a mean hydrostatic stress tensor or volumetric stress tensor or mean normal stress tensor, ${displaystyle pi delta _{ij}}$ , which tends to change the volume of the stressed body; and
a deviatoric component called the stress deviator tensor, $s_{ij}$ , which tends to distort it.

${displaystyle sigma _{ij}=s_{ij}+pi delta _{ij},,}$

where is the mean stress given by

${displaystyle pi ={frac {sigma _{kk}}{3}}={frac {sigma _{11}+sigma _{22}+sigma _{33}}{3}}={frac {1}{3}}I_{1}.,}$

Pressure () is generally defined as negative one-third the trace of the stress tensor minus any stress the divergence of the velocity contributes with, i.e.

${displaystyle p=lambda ,nabla cdot {vec {u}}-pi =lambda ,{frac {partial u_{k}}{partial x_{k}}}-pi =sum _{k}lambda ,{frac {partial u_{k}}{partial x_{k}}}-pi ,}$

where lambda is a proportionality constant, is the divergence operator, $x_{k}$ is the k:th Cartesian coordinate, is the velocity and $u_{k}$ is the k:th Cartesian component of .

The deviatoric stress tensor can be obtained by subtracting the hydrostatic stress tensor from the Cauchy stress tensor:

${displaystyle {begin{aligned}s_{ij}&=sigma _{ij}-{frac {sigma _{kk}}{3}}delta _{ij},,\left[{begin{matrix}s_{11}&s_{12}&s_{13}\s_{21}&s_{22}&s_{23}\s_{31}&s_{32}&s_{33}end{matrix}}right]&=left[{begin{matrix}sigma _{11}&sigma _{12}&sigma _{13}\sigma _{21}&sigma _{22}&sigma _{23}\sigma _{31}&sigma _{32}&sigma _{33}end{matrix}}right]-left[{begin{matrix}pi &0&0\0&pi &0\0&0&pi end{matrix}}right]\&=left[{begin{matrix}sigma _{11}-pi &sigma _{12}&sigma _{13}\sigma _{21}&sigma _{22}-pi &sigma _{23}\sigma _{31}&sigma _{32}&sigma _{33}-pi end{matrix}}right].end{aligned}}}$

Invariants of the stress deviator tensor[edit]

As it is a second order tensor, the stress deviator tensor also has a set of invariants, which can be obtained using the same procedure used to calculate the invariants of the stress tensor. It can be shown that the principal directions of the stress deviator tensor $s_{ij}$ are the same as the principal directions of the stress tensor $sigma _{ij}$ . Thus, the characteristic equation is

${displaystyle left|s_{ij}-lambda delta _{ij}right|=lambda ^{3}-J_{1}lambda ^{2}-J_{2}lambda -J_{3}=0,}$

where $J_{1}$ , $J_{2}$ and J_3 are the first, second, and third deviatoric stress invariants, respectively. Their values are the same (invariant) regardless of the orientation of the coordinate system chosen. These deviatoric stress invariants can be expressed as a function of the components of $s_{ij}$ or its principal values $s_{1}$ , $s_{2}$ , and $s_{3}$ , or alternatively, as a function of $sigma _{ij}$ or its principal values $sigma _{1}$ , $sigma _{2}$ , and sigma_3 . Thus,

${displaystyle {begin{aligned}J_{1}&=s_{kk}=0,\[3pt]J_{2}&={frac {1}{2}}s_{ij}s_{ji}={frac {1}{2}}operatorname {tr} left({boldsymbol {s}}^{2}right)\&={frac {1}{2}}left(s_{1}^{2}+s_{2}^{2}+s_{3}^{2}right)\&={frac {1}{6}}left[(sigma _{11}-sigma _{22})^{2}+(sigma _{22}-sigma _{33})^{2}+(sigma _{33}-sigma _{11})^{2}right]+sigma _{12}^{2}+sigma _{23}^{2}+sigma _{31}^{2}\&={frac {1}{6}}left[(sigma _{1}-sigma _{2})^{2}+(sigma _{2}-sigma _{3})^{2}+(sigma _{3}-sigma _{1})^{2}right]\&={frac {1}{3}}I_{1}^{2}-I_{2}={frac {1}{2}}left[operatorname {tr} left({boldsymbol {sigma }}^{2}right)-{frac {1}{3}}operatorname {tr} ({boldsymbol {sigma }})^{2}right],\[3pt]J_{3}&=det(s_{ij})\&={frac {1}{3}}s_{ij}s_{jk}s_{ki}={frac {1}{3}}{text{tr}}left({boldsymbol {s}}^{3}right)\&={frac {1}{3}}left(s_{1}^{3}+s_{2}^{3}+s_{3}^{3}right)\&=s_{1}s_{2}s_{3}\&={frac {2}{27}}I_{1}^{3}-{frac {1}{3}}I_{1}I_{2}+I_{3}={frac {1}{3}}left[{text{tr}}({boldsymbol {sigma }}^{3})-operatorname {tr} left({boldsymbol {sigma }}^{2}right)operatorname {tr} ({boldsymbol {sigma }})+{frac {2}{9}}operatorname {tr} ({boldsymbol {sigma }})^{3}right].,end{aligned}}}$

Because ${displaystyle s_{kk}=0}$ , the stress deviator tensor is in a state of pure shear.

A quantity called the equivalent stress or von Mises stress is commonly used in solid mechanics. The equivalent stress is defined as

${displaystyle sigma _{text{vM}}={sqrt {3,J_{2}}}={sqrt {{frac {1}{2}}~left[(sigma _{1}-sigma _{2})^{2}+(sigma _{2}-sigma _{3})^{2}+(sigma _{3}-sigma _{1})^{2}right]}},.}$

Octahedral stresses[edit]

Figure 6. Octahedral stress planes

Considering the principal directions as the coordinate axes, a plane whose normal vector makes equal angles with each of the principal axes (i.e. having direction cosines equal to ) is called an octahedral plane. There are a total of eight octahedral planes (Figure 6). The normal and shear components of the stress tensor on these planes are called octahedral normal stress ${displaystyle sigma _{text{oct}}}$ and octahedral shear stress ${displaystyle tau _{text{oct}}}$ , respectively. Octahedral plane passing through the origin is known as the π-plane (π not to be confused with mean stress denoted by π in above section) . On the π-plane, ${textstyle s_{ij}={frac {1}{3}}I}$ .

Knowing that the stress tensor of point O (Figure 6) in the principal axes is

${displaystyle sigma _{ij}={begin{bmatrix}sigma _{1}&0&0\0&sigma _{2}&0\0&0&sigma _{3}end{bmatrix}}}$

the stress vector on an octahedral plane is then given by:

${displaystyle {begin{aligned}mathbf {T} _{text{oct}}^{(mathbf {n} )}&=sigma _{ij}n_{i}mathbf {e} _{j}\&=sigma _{1}n_{1}mathbf {e} _{1}+sigma _{2}n_{2}mathbf {e} _{2}+sigma _{3}n_{3}mathbf {e} _{3}\&={frac {1}{sqrt {3}}}(sigma _{1}mathbf {e} _{1}+sigma _{2}mathbf {e} _{2}+sigma _{3}mathbf {e} _{3})end{aligned}}}$

The normal component of the stress vector at point O associated with the octahedral plane is

${displaystyle {begin{aligned}sigma _{text{oct}}&=T_{i}^{(n)}n_{i}\&=sigma _{ij}n_{i}n_{j}\&=sigma _{1}n_{1}n_{1}+sigma _{2}n_{2}n_{2}+sigma _{3}n_{3}n_{3}\&={frac {1}{3}}(sigma _{1}+sigma _{2}+sigma _{3})={frac {1}{3}}I_{1}end{aligned}}}$

which is the mean normal stress or hydrostatic stress. This value is the same in all eight octahedral planes.
The shear stress on the octahedral plane is then

${displaystyle {begin{aligned}tau _{text{oct}}&={sqrt {T_{i}^{(n)}T_{i}^{(n)}-sigma _{text{oct}}^{2}}}\&=left[{frac {1}{3}}left(sigma _{1}^{2}+sigma _{2}^{2}+sigma _{3}^{2}right)-{frac {1}{9}}(sigma _{1}+sigma _{2}+sigma _{3})^{2}right]^{frac {1}{2}}\&={frac {1}{3}}left[(sigma _{1}-sigma _{2})^{2}+(sigma _{2}-sigma _{3})^{2}+(sigma _{3}-sigma _{1})^{2}right]^{frac {1}{2}}={frac {1}{3}}{sqrt {2I_{1}^{2}-6I_{2}}}={sqrt {{frac {2}{3}}J_{2}}}end{aligned}}}$

References[edit]

^ ^a ^b ^c
Fridtjov Irgens (2008), “Continuum Mechanics”. Springer. ISBN 3-540-74297-2
^
Truesdell, C.; Toupin, R.A. (1960), “The Classical Field Theories”, in Flügge, Siegfried (ed.), Principles of Classical Mechanics and Field Theory/Prinzipien der Klassischen Mechanik und Feldtheorie, Handbuch der Physik (Encyclopedia of Physics), vol. III/1, Berlin–Heidelberg–New York: Springer-Verlag, pp. 226–793, Bibcode:1960HDP…..2…..F, doi:10.1007/978-3-642-45943-6, ISBN 978-3-540-02547-4, MR 0118005, Zbl 0118.39702.
^
Peter Chadwick (1999), “Continuum Mechanics: Concise Theory and Problems”. Dover Publications, series “Books on Physics”. ISBN 0-486-40180-4. pages
^ ^a ^b
Yuan-cheng Fung and Pin Tong (2001) “Classical and Computational Solid Mechanics”. World Scientific. ISBN 981-02-4124-0
^ ^a ^b Smith & Truesdell p.97
^ ^a ^b
G. Thomas Mase and George E. Mase (1999), “Continuum Mechanics for Engineers” (2nd edition). CRC Press. ISBN 0-8493-1855-6
^ ^a ^b ^c
I-Shih Liu (2002), “Continuum Mechanics”. Springer ISBN 3-540-43019-9
^ ^a ^b
Han-Chin Wu (2005), “Continuum Mechanics and Plasticity”. CRC Press. ISBN 1-58488-363-4
^ Lubliner
^ Basar
^ ^a ^b ^c
Teodor M. Atanackovic and Ardéshir Guran (2000), “Theory of Elasticity for Scientists and Engineers”. Springer. ISBN 0-8176-4072-X
^
Keith D. Hjelmstad (2005), “Fundamentals of Structural Mechanics” (2nd edition). Prentice-Hall. ISBN 0-387-23330-X
^ ^a ^b
Wai-Fah Chen and Da-Jian Han (2007), “Plasticity for Structural Engineers”. J. Ross Publishing ISBN 1-932159-75-4
^
Bernard Hamrock (2005), “Fundamentals of Machine Elements”. McGraw–Hill. ISBN 0-07-297682-9
^
Rabindranath Chatterjee (1999), “Mathematical Theory of Continuum Mechanics”. Alpha Science. ISBN 81-7319-244-8
^
John Conrad Jaeger, N. G. W. Cook, and R. W. Zimmerman (2007), “Fundamentals of Rock Mechanics” (4th edition). Wiley-Blackwell. ISBN 0-632-05759-9
^
Mohammed Ameen (2005), “Computational Elasticity: Theory of Elasticity and Finite and Boundary Element Methods” (book). Alpha Science, ISBN 1-84265-201-X
^
William Prager (2004), “Introduction to Mechanics of Continua”. Dover Publications. ISBN 0-486-43809-0

Источник

Физический смысл тензора напряжений на примере в двумерном случае[править | править код]

Вывод компонентов тензора[править | править код]

Тензор напряжений в релятивистской физике[править | править код]

Тензор напряжений в классической электродинамике[править | править код]

См. также[править | править код]

Примечания[править | править код]

Литература[править | править код]

3.3. Напряжения на наклонной площадке

Физический смысл тензора напряжений на примере в двумерном случае

Вывод компонентов тензора

Тензор напряжений в релятивистской физике

Тензор напряжений в классической электродинамике

См. также

Примечания

Литература

Euler–Cauchy stress principle – stress vector[edit]

Cauchy’s postulate[edit]

Cauchy’s fundamental lemma[edit]

Cauchy’s stress theorem—stress tensor[edit]

Transformation rule of the stress tensor[edit]

Normal and shear stresses[edit]

Balance laws – Cauchy’s equations of motion[edit]

Cauchy’s first law of motion[edit]

Cauchy’s second law of motion[edit]

Principal stresses and stress invariants[edit]

Maximum and minimum shear stresses[edit]

Stress deviator tensor[edit]

Invariants of the stress deviator tensor[edit]

Octahedral stresses[edit]

See also[edit]

References[edit]

Добавить комментарий Отменить ответ

Физический смысл тензора напряжений на примере в двумерном случае[править | править код]

Вывод компонентов тензора[править | править код]

Тензор напряжений в релятивистской физике[править | править код]

Тензор напряжений в классической электродинамике[править | править код]

См. также[править | править код]

Примечания[править | править код]

Литература[править | править код]

3.3. Напряжения на наклонной площадке

Физический смысл тензора напряжений на примере в двумерном случае

Вывод компонентов тензора

Тензор напряжений в релятивистской физике

Тензор напряжений в классической электродинамике

См. также

Примечания

Литература

Euler–Cauchy stress principle – stress vector[edit]

Cauchy’s postulate[edit]

Cauchy’s fundamental lemma[edit]

Cauchy’s stress theorem—stress tensor[edit]

Transformation rule of the stress tensor[edit]

Normal and shear stresses[edit]

Balance laws – Cauchy’s equations of motion[edit]

Cauchy’s first law of motion[edit]

Cauchy’s second law of motion[edit]

Principal stresses and stress invariants[edit]

Maximum and minimum shear stresses[edit]

Stress deviator tensor[edit]

Invariants of the stress deviator tensor[edit]

Octahedral stresses[edit]

See also[edit]

References[edit]

Вам также может понравиться

Как найти все картинки в папке

Как найти координаты вершин шестиугольной призмы

Как найти индукцию магнитного поля через радиус

Добавить комментарий Отменить ответ