Как найти теоретический уровень

Расчет теоретических уровней линейного тренда

Год	Производство мяса, млн. т.	Условное обозначение времени, t	t2	yt		(y- )2
1991 1992 1993 1994 1995	9,4 8,3 7,5 6,8 5,9	1 2 3 4 5	1 4 9 16 25	9,4 16,6 22,5 27,2 29,5	9,28 8,43 7,58 6,73 5,88	0,0144 0,0169 0,0064 0,0049 0,0004
n=5						0,043

Приняв в качестве
гипотетической функции теоретических
уровней прямую

,
определим параметры последней:

Решение этой
системы можно осуществить по формулам:

.

Отсюда искомое
уравнение тренда:

.
Подставляя в полученное уравнении
значения 1, 2, 3, 4, 5, определяем теоретические
уровни ряда (см. предпоследнюю графу
табл. 4.3). Сравнивая значения эмпирических
и теоретических уровней, видим, что они
близки, т.е. можно сказать, что найденное
уравнение весьма удачно характеризует
основную тенденцию изменения уровней
именно как линейную функцию.

Система нормальных
уравнений упрощается, если отсчет
времени ведется от середины ряда.
Например, при нечетном
числе уровней
серединная точка (год, месяц) принимается
за нуль. Тогда предшествующие периоды
обозначаются соответственно -1, -2, -3 и
т.д., а следующие за средним – соответственно
+1, +2, +3 и т.д. При четном числе уровней
два срединных момента (периода) времени
обозначают −1 и +1, а все последующие и
предыдущие, соответственно, через два
интервала:

и т.д.

При таком порядке
отсчета времени (от середины ряда)

,
система нормальных
уравнений упрощается до следующих двух
уравнений, каждое из которых решается
самостоятельно:

Важное значение
при построении модели временного ряда
имеет учет сезонных и циклических
колебаний. Простейшим подходом,
позволяющим учесть в модели сезонные
и циклические колебания, является расчет
значений сезонной/циклической компоненты
и построение аддитивной и мультипликативной
модели временного ряда.

Общий вид аддитивной
модели следующий: Y=T+S+E.
Эта модель предполагает, что каждый
уровень временного уровня ряда может
быть представлен как сумма трендовой
T,
сезонной S
и случайной компонент. Общий вид
мультипликативной модели выглядит как:
Y=T∙S∙E.

Выбор одной из
двух моделей проводится на основе
анализа структуры сезонных колебаний.
Если амплитуда колебаний приблизительно
постоянна, строят аддитивную модель
временного ряда, в которой значения
сезонной компоненты предполагаются
постоянными для различных циклов. Если
амплитуда сезонных колебаний возрастает
или уменьшается, строят мультипликативную
модель временного ряда, которая ставит
уровни ряда в зависимость от значений
сезонной компоненты.

Построение
аддитивной и мультипликативной моделей
сводится к расчету T,
S,
E
для каждого уровня ряда. Этапы построения
модели включают в себя следующие шаги:

1. Выравнивание
   исходного ряда методом скользящей
   средней

2. Расчет значений
   сезонной компоненты S.

3. Устранение сезонной
   компоненты из исходных уровней ряда и
   получение выровненных данных в аддитивной
   (T+E)
   или мультипликативной (T∙E)
   модели.

4. Аналитическое
   выравнивание уровней (T+E)
   или (T∙E)
   и расчет значений T
   с использованием полученного уравнения
   тренда.

5. Расчет полученных
   по модели значений (T+E)
   или (T∙E).

6. Расчет абсолютных
   и/или относительных ошибок. Если
   полученные значения не содержат
   автокорреляции, ими можно заменить
   исходные уровни ряда и в дальнейшем
   использовать временной ряд ошибок
   E
   для анализа взаимосвязи исходного ряда
   и других временных рядов.

Рассмотрим другие
методы анализа взаимосвязи, предположив
что изучаемые временные ряды не содержат
периодических колебаний. Допустим, что
изучается зависимость между рядами х
и у.
Для количественной характеристики этой
зависимости используется линейный
коэффициент корреляции. Если рассматриваемые
временные ряды имеют тенденцию,
коэффициент корреляции по абсолютной
величине будет высоким. Однако это не
говорит о том, что х
причина у.
Высокий коэффициент корреляции в данном
случае – это результат того, что х
и у
зависят от времени, или содержат
тенденцию. При этом одинаковую или
противоположную тенденцию могут иметь
ряды, совершенно не связанные друг с
другом причинно-следственной зависимостью.
Например, коэффициент корреляции между
численностью выпускников вузов и числом
домов отдыха в РФ в период с 1970-1990 г.
составил 0,8. Однако, это не говорит о
том, что количество домов отдыха
способствует росту числа выпускников
или наоборот.

Для того чтобы
получить коэффициенты корреляции,
характеризующие причинно-следственную
связь между изучаемыми рядами, следует
избавиться от так называемой ложной
корреляции, вызванной наличием тенденции
в каждом ряду, которую устраняют одним
из методов.

Предположим, что
по двум временным рядам х_t
и у_t
строится уравнение парной регрессии
линейной регрессии вида:

.
наличие тенденции в каждом из этих
временных рядов означает, что на зависимую
у_t
и независимую х_t
переменные модели оказывает воздействие
фактор времени, который непосредственно
в модели не учтен. Влияние фактора
времени будет выражено в корреляционной
зависимости между значениями остатков

за текущий и предыдущие моменты времени,
которая получила название автокорреляции
в остатках.

Автокорреляция в
остатках – это нарушение одной из
основных предпосылок МНК – предпосылки
о случайности остатков, полученных по
уравнению регрессии. Один из возможных
путей решения этой проблемы состоит в
применении обобщенного МНК.

Для устранения
тенденции используются две группы
методов:

– методы, основанные
на преобразовании уровней исходного
ряда в новые переменные, не содержащие
тенденции (метод последовательных
разностей и метод отклонения от трендов);

– методы, основанные
на изучении взаимосвязи исходных уровней
временных рядов при элиминировании
воздействия фактора времени на зависимую
и независимую переменные модели
(включение в модель регрессии по временным
рядам фактора времени).

Пусть имеются два
временных ряда

и

,
каждый из которых содержит трендовую
компоненту Т
и случайную составляющую

.
Аналитическое выравнивание каждого из
этих рядов позволяет найти параметры
соответствующих уравнений трендов и
определить расчетные по тренду уровни

и

соответственное. Эти расчетные значения
можно принять за оценку трендовой
компоненты Т
каждого ряда. Поэтому влияние тенденции
можно устранить путем вычитания расчетных
значений уровней ряда из фактических.
Эту процедуру проделывают для каждого
временного ряда в модели. Дальнейший
анализ взаимосвязи рядов проводят с
использованием не исходных уровней, а
отклонений от тренда

и

.
Именно в этом и заключается
метод отклонений от тренда.

В ряде случаев
вместо аналитического выравнивания
временного ряда с целью устранения
тенденции можно применить более простой
метод – метод
последовательных разностей.
Если временной ряд содержит ярко
выраженную линейную тенденцию, ее можно
устранить путем замены исходных уровней
ряда цепными абсолютными приростами
(первыми разностями).

Пусть

,

.

Тогда

.

Коэффициент b
– константа, которая не зависит от
времени. При наличии сильной линейной
тенденции отставки достаточно малы и
в соответствии с предпосылками МНК
носят случайный характер. Поэтому первые
разности уровней ряда

не зависят от переменной времени, их
можно использовать для дальнейшего
анализа.

Если временной
ряд содержит тенденцию в форме параболы
второго порядка, то для ее устранения
можно заменить исходные уровни ряда на
вторые разности:

.

Если тенденции
временного ряда соответствует
экспоненциальной, или степенной, тренд,
метод последовательных разностей
следует применять не к исходным уровням
ряда, а к их логарифмам.

Модель вида:

также относится к группе моделей,
включающих фактор времени. Преимущество
данной модели перед методами отклонений
от трендов и последовательных разностей
состоит в том, что она позволяет учесть
всю информацию, содержащуюся в исходных
данных, поскольку значения

и

– это уровни исходных временных рядов.
Кроме того, модель строится по всей
совокупности данных за рассматриваемый
период в отличие от метода последовательных
разностей, который приводит к потере
числа наблюдений. Параметры этой модели
определяются обычным МНК.

Пример. Построим
уравнение тренда по исходным данным
таблицы 4.4.

Таблица 4.4

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Динамические ряды — краткое руководство по анализу изменений явлений во времени

Даная статья понятными и простыми терминами объяснит, что же такое динамические ряды, для чего они нужны, как производится анализ полученных данных и какие возможности открываются перед теми, кто владеет методикой данного анализа. Любое явление в области здравоохранения нуждается в тщательной оценке, и здесь знания анализа динамических рядов неоценимы. С помощью динамического ряда можно оценить и спрогнозировать проблематику любой нозологической единицы, сформировать дальнейшую тактику лечения и меры профилактики заболеваний.

Динамический ряд — ряд однородных величин, характеризующих изменение явления во времени.

Целью анализа динамических рядов является:

• выявление закономерности изменения изучаемого явления во времени;
• прогнозирование (экстраполирование) полученных данных на последующие
  годы.

Числовые значения, составляющие динамический ряд, называются уровнями ряда (у).

Типы динамических рядов:

1. В зависимости от вида уровня ряда:

а) простые (уровень ряда выражен абсолютными числами);

б) сложные (уровень ряда выражен обобщающими коэффициентами).

1. В зависимости от способа формирования временного интервала:

а) моментные (данные собираются на определенный момент времени);

б) интервальные (данные собираются за определенный период времени).

1. В зависимости от выраженности изменений явления во времени (определя­ется по коэффициенту корреляции между временем и изучаемым явлением).

а) с выраженной тенденцией (r =0,7 — 1,0);

б) с неустойчивой тенденцией (r =0,3 — 0,69);

в) с отсутствием тенденции ( r = 0 — 0,29).

Основное требование, предъявляемое к анализируемым динамическим ря­дам, заключается в сопоставимости их уровней. Для оценки сопоставимости прово­дят предварительный анализ полученных данных по следующим критериям:

• единство территории, на которой проводился сбор данных;
• единая методология учета данных;
• единые временные интервалы, в течение которых проводилась регистрация
  данных.

Методика анализа динамических рядов

Методика аналитики предусматривает выполнение последовательных действий:

1. Представить полученные данные графически и выявить форму зависимости изучаемого явления от времени.
2. Оценить наличие и силу корреляции изучаемого явления от времени.
3. Если установлено, что ряд обладает выраженной тенденцией, проводят анализ компонентов динамики ряда: основной тенденции (эволюции, тренда), кратковременных систематических движений и случайных колебаний. Основная задача анализа — разделить эти компоненты и выявить основную закономерность изменения явления во времени. Для выявления и описания тренда динамический ряд подвергают обработке — выравниванию.

Способы выравнивания динамических рядов

Чтобы произвести выравнивание динамических рядов потребуются следующие действия:

• Укрупнение временных интервалов (периодов), в течение которых изучается явление.
• Сглаживание ряда методом скользящей средней.
• Аналитический способ.

При этом способе на основании фактических данных подбирается наиболее подходящее для отражения тенденции развития явления математическое уравнение (аппроксимирующая функция), которое принимается за модель развития явления во времени. Т.е. уровни ряда рассматриваются как функция времени, и задача выравнивания сводится к определению вида функции, отысканию ее параметров по эмпирическим данным и расчету по найденной формуле теоретических выравненных уровней. Наиболее часто используются следующие функции:

а) линейная зависимость:

б) экспоненциальная зависимость:

в) показательная зависимость:

г)  параболическая зависимость:

и др.

где  a₀, a₁, а₂ — параметры уравнения;

у – теоретический уровень;

t – временной интервал.

В качестве примера возьмем линейную зависимость и проведем выравнивание, используя для нахождения параметров уравнения а₀ ,а₁  способ наименьших квадратов. Способ наименьших квадратов позволяет найти теоретическую кривую, максимально приближенную к эмпирической, а условие минимума суммы квадратов отклонений теоретических данных от фактических позволяет свести математическое решение задачи к системе нормальных уравнений:

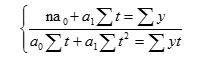
где  у — уровни фактического ряда;

n — количество уровней;

t — порядковый номер временного периода.

Эта система уравнений легко упрощается, если «t» присвоить ранги (порядковые номера), ведя отсчет времени от середины ряда. При нечетном ряде середина обозначается через 0, а отсчет рангов ведется через единицу с соответствующим знаком в ту или иную сторону от середины (например: -5,-4,-3,-2,-1, 0,+1.+2,+3,->:4,+5). При четном ряде две средние временные точки обозначаются через +1 и -1, а остальные ранги присваиваются через две единицы (например: -5,-3,-1,+1,+3,+5).

При отсчете времени от середины ряда   St = 0  и система нормальных уравнений принимает вид:

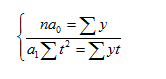
Отсюда находим параметры уравнения:

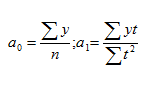
Подставляя в уравнение у = а₀ + а₁t  вместо «t» его ранги, находим выравненные (теоретические) значения уровней ряда и строим теоретическую кривую выравненного динамического ряда.

При использовании аналитического способа всегда отмечается отклонение теоретических уровней от фактических уровней ряда, которое может быть обуслов­лено как случайными колебаниями, так и неправильно подобранным аппроксими­рующим уравнением. В связи с этим заключительным этапом выравнивания динамического ряда аналитическим способом является оценка точности аппроксимации с определенным уровнем значимости.

Оценка точности аппроксимации возможна с помощью нахождения

Для получения точной оценки необходимо найти такие величины:

а) коэффициент вариации:

 

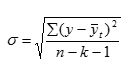
где  у- фактический уровень ряда;

y_t — теоретический уровень ряда;

k- число параметров уравнения;

n- число уровней ряда.

Аппроксимация считается точной при C_v не более 15%.

б) коэффициент расхождения Тейла:

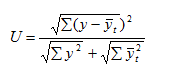
где      у — фактический уровень ряда;

y_t — теоретический уровень ряда.

Аппроксимация считается точной при U не более 5%

После аналитического выравнивания динамического ряда и описания тренда возможно экстраполировать полученные данные. Экстраполяция — предположение о сохранении тренда, базирующееся на допущении неизменности влияющих факто­ров и предшествующей тенденции. Осуществляется путем подставления в найденное уравнение аппроксимации не фактического значения временного интервала, а предполагаемого порядкового номера (ранг) того периода, на который прогнозируется результат.

 Вычисление основных показателей динамического ряда

Алгоритм вычислений ведущих параметров динамических рядов:

Условные обозначения:

yi- текущий уровень (сравниваемый);

у_i-1— базисный уровень (с каким сравнивают);

t- период времени, в течение которого уровень предполагается неизменным.

1.Абсолютный прирост (убыль) :

2.Темп роста (убыли):

3.Темп прироста (относительная скорость), темп убыли :

4.Средний темп прироста (убыли):

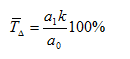
где      а₀; а₁ — параметры уравнения;

k = 1 при нечетном ряде;

k = 2 при четном ряде.

5.1% прироста (убыли): используются при сравнении динамических рядов с уровнями, выраженными различными обобщающими коэффициентами.

Таким образом, с помощью данного руководства по определению и расчетам такого понятия, как, динамические ряды, специалисты различных отраслей медицины, ученые могут эффективно и быстро оценить изменение различных величин в течение времени.

Благодарим за интерес, проявленный к нашей статье, оставайтесь с нами!

В настоящее время принято различать следующие уровни научного познания: эмпирический и теоретический.

Эмпирический уровень научного познания

Эмпирический уровень научного познания отвечает за изучение определенных явлений (иначе говоря, средств и вариантов отражения специфики наблюдаемых предметов, явлений и паттернов), который, в свою очередь, благодаря использованию методов наблюдения, измерения и эксперимента.

В качестве основных форм реализации эмпирического уровня знания выступают такие факторы, как группирование, классифицирование, описание и систематизирование, совместно с обобщением полученных показателей в наблюдении и эксперименте. 

В эмпирическом знании существует сложная структура, которая включает в себя четыре определенных уровня: 

1. Первый уровень, который представлен единичными эмпирическими высказываниями, в содержании которых содержатся зафиксированные результаты от отдельного наблюдения; вместе с тем, принято отмечать точные показатели времени, места с условий, в которых реализовывалось наблюдение.
2. В качестве второго уровня эмпирического познания выступают научные факты, а именно – характеристика определенных фактов окружающей реальности с помощью использования научного языка. Благодаря этим средствам констатируется наличие, либо отсутствие определенных явлений, паттернов и взаимодействий в наблюдаемой отрасли, совместно с их интенсивностью (количественной определенностью). В качестве их символических представлений выступают диаграммы, графики, классификации, статистические модели и таблицы. 
3. Третий уровень эмпирического знания представлен различного рода эмпирическими закономерностями: функциональными, причинными, структурными, динамическими, статистическими и прочими. 
4. На четвертом уровне научного эмпирического знания располагаются различные теории феноменологии, которые выступают в качестве логически взаимосвязанного множества определенных доказанных на практике фактов и аксиом (к ним относят феноменологическую термодинамику, небесную механику. Которую разработал Д. И. Менделеев и прочее). Отличие эмпирических теорий от теорий заключается в том, что они не направлены на исследование сущности изучаемых явлений, а являются некоторого рода эмпирическим обобщением того процесса и воспринимаемого паттерна, который можно изучить наглядным путем. 

Теоретический уровень научного познания

На теоретическом уровне научного познания происходит изучение сущности определенных явлений, паттернов, и взаимосвязей, опорой которого выступает эмпирическое познание. Теоретическое познание является результатом работы разума – одной из конструктивных частей сознания.

Ведущая логическая операция, наблюдаемая в теоретическом мышлении представлена идеализацией, в качестве цели и результата которой выступает формирование особого предмета – «идеального объекта» научных теорий (материальные точки и «абстрактные черные тела» физики, «идеальные типы» социологического знания и прочие).

Взаимосвязанные общности данного типа явлений составляет общую базу в теоретическом научном знании. 

На данном уровне научного знания происходит постановка научной проблемы, формулирование научной гипотезы и теории; определение логической последовательности из законов; формирование взаимосвязи между отдельными гипотезами и теориями; создание теорий, совместно с процедурой разъяснений, предсказаний, обобщений, приводящих к пониманию. 

Структура теоретического уровня представлена целым рядом составляющих: законами, теориями, моделями, концепциями, учениями, принципами и совокупностью методов. Дадим короткое описание части из них.

Законы науки являются отражением объективных, регулярных, повторяющихся, существенных и нужных связей явлений и объективно существующих процессов. В качестве примера можно привести закон теплового расширения тел: «При нагревании расширяются все три тела».

В частных законах представлены связями, которые или выведены благодаря универсальным законам, или отражают закономерность в событиях, которая характеризуется определенной частной сферой сущего. Например, вторичным, либо исходящим из универсального закона теплового расширения всех физических тел, является закон теплового расширения металлов, который описывает свойства частных групп в химических элементах. 

Законы детерминизма и статистические (стохастические) законы. Такой тип законов формулируют предсказания, которые обладают весьма точным и достоверным характером. Статистические законы, в отличие от них, являются вероятностными, так как отражают некоторую повторяющуюся регулярность, возникающую из-за связей массового случайного, либо повторяющегося события. 

Законы эмпирики и теории. Законы эмпирики отражают регулярность, которая обнаруживается в рамках явлений в контексте эмпирических форм познания. В теоретических законах отражены связи-повторения, которые действуют на мыслительном уровне. Самые распространенные из них – причинные (каузальные) законы, они отражают необходимые отношения двух связанных явлений. 

В общем смысле, научная теория является единой и целостной системой знаний, элементами которой выступают: обобщение, закон и аксиома, которые связаны некоторой логической содержательной связью. Теория, которая отражает и выражает смысл объектов исследования, является высшей формой, организующей научные знания. 

Структура научных теорий: 

1. Исходный фундаментальный принцип.
2. Основное системообразующее понятие.
3. Языковые тезаурусы, выраженные в нормах выстраивания верных смысловых фраз, подходящих данной концепции.
4.  Интерпретационная база, позволяющая реализовать переход из фундаментального утверждения в широкое поле наблюдений и фактов. 

Современная наука представлена типами научных теорий, которые классифицированы на различных основаниях:

1. Согласно адекватному отражению в исследуемых областях паттернов выделяют феноменологический аналитический типы теорий. Первые их них содержат описания действительности в рамках событий, либо явлений, без раскрытия их природы. Например, в геометрической оптике были изучены паттерны светового распространения, отражения и преломления, без раскрытия сущности самого света. При этом, в аналитических теориях раскрывается природа исследуемого явления. Так, в теории электромагнитных полей раскрывается смысл оптического явления. 
2. Согласно уровням достоверности, принято выделять детерминистический и стохастических виды научных теорий и законов. Детерминистический тип способствует точному и достоверному предсказанию, однако из-за неоднозначности, существующей в большинстве процессов и явлений, совместно со значительной долей неопределенности и случайности, данные теории применяют нечасто. В стохастических теориях делают предсказания, которые основаны на исследовании случайных законов.

Данный тип теорий применяется во всех типах наук: и точных, и гуманитарных, в ситуациях, когда необходимо дать предсказание, либо прогноз некоторым процессам, у которых большая часть паттернов подвержена неопределенности, стечению факторов, которые связаны с выражением случайностей в массовых событиях. 

Значительную роль научного познания в рамках теоретического уровня играют методы, в рамках которых отражены аксиоматические, гипотетико-дедуктивные, формализирующие, идеализирующие, системные и прочие.

Тема: ИЗУЧЕНИЕ ДИНАМИЧЕСКИХ ПРОЦЕССОВ

Методика анализа динамических рядов

1. Представить полученные данные графически и выявить форму зависимости изучаемого явления от времени.

2. Оценить наличие и силу корреляции изучаемого явления от времени.

3. Если установлено, что ряд обладает выраженной тенденцией, проводят анализ компонентов динамики ряда: основной тенденции (эволюции, тренда), кратковременных систематических движений и случайных колебаний. Основная задача анализа – разделить эти компоненты и выявить основную закономерность изменения явления во времени.

Для выявления и описания тренда динамический ряд подвергают обработке – выравниванию.

Способы выравнивания динамических рядов:

1. Укрупнение временных интервалов (периодов), в течение которых изучается явление.

2. Сглаживание ряда методом скользящей средней.

3. Аналитический способ.

При этом способе на основании фактических данных подбирается наиболее подходящее для отражения тенденции развития явления математическое уравнение (аппроксимирующая функция), которое принимается за модель развития явления во времени.

То есть, уровни ряда рассматриваются как функция времени, и задача выравнивания сводится к определению вида функции, отысканию ее параметров по эмпирическим данным и расчету по найденной формуле теоретических выравненных уровней.

Наиболее часто используются следующие функции:

а) линейная зависимость

б) экспоненциальная зависимость

в) показательная зависимость

г) параболическая зависимость

Чаще всего стремятся выравнивать ряд по прямой, используя для нахождения параметров уравнения а0 и а1 способ наименьших квадратов.

Способ наименьших квадратов позволяет найти теоретическую кривую, максимально приближенную к эмпирической, а условие минимума суммы квадратов отклонений теоретических данных от фактических позволяет свести математическое решение задачи к системе нормальных уравнений:

где

у – уровни фактического ряда;

n – количество уровней;

t – порядковый номер временного периода.

Эта система уравнений легко упрощается, если « t » присвоить ранги (порядковые номера), ведя отсчет времени от середины ряда.

При нечетном ряде середина обозначается через 0 , а отсчет рангов ведется через единицу с соответствующим знаком в ту или иную сторону от середины.

Например: -5,-4,-3,-2,-1, 0,+1.+2,+3,+4,+5 .

При четном ряде две средние временные точки обозначаются через +1 и -1 , а остальные ранги присваиваются через две единицы

Например: -5,-3,-1,+1,+3,+5.

При отсчете времени от середины ряда Σt = 0 и система нормальных уравнений принимает вид:

Отсюда находим параметры уравнения:

Подставляя в уравнение

вместо « t » его ранги, находим выравненные (теоретические) значения уровней ряда и строим теоретическую кривую выравненного динамического ряда.

При использовании аналитического способа всегда отмечается отклонение теоретических уровней от фактических уровней ряда, которое может быть обусловлено как случайными колебаниями, так и неправильно подобранным аппроксимирующим уравнением.

В связи с этим заключительным этапом выравнивания динамического ряда аналитическим способом является оценка точности аппроксимации с определенным уровнем значимости.

Оценка точности аппроксимации возможна с помощью нахождения:

а) коэффициента вариации:

где

у – фактический уровень ряда;

y t – теоретический уровень ряда;

k – число параметров уравнения;

n – число уровней ряда.

Аппроксимация считается точной при Cv не более 15%.

б) коэффициент расхождения Тейла:

где

у – фактический уровень ряда;

y t – теоретический уровень ряда.

Аппроксимация считается точной при U не более 5%

После аналитического выравнивания динамического ряда и описания тренда возможно экстраполировать полученные данные.

Экстраполяция – предположение о сохранении тренда, базирующееся на допущении неизменности влияющих факторов и предшествующей тенденции. Осуществляется путем подставления в найденное уравнение аппроксимации не фактического значения временного интервала, а тех лет, на которые прогнозируется результат.

Пример решения

Выравнивание аналитическим способом

В качестве модели (аппроксимирующей функции) выбираем линейную зависимость:

Показатели выравненного ряда

Общественное здоровье и здравоохранение, экономика здравоохранения. Занятия 4-5 курса

Содержание канала

Целью исследовательской деятельности являются научные знания, которые в свою очередь могут существовать лишь в виде организованной системы – теории. Предшествующие формированию теории действия заключаются в понятие – научное познание, т.е. производство знаний путём постановки проблемы, сбора информации и её дальнейшего преобразования. Процессу познания характерно деление на этапы, они представлены в виде двух уровней – эмпирический и теоретический, которые отличаются своими методами.

Эмпирический уровень научного познания

На этом этапе происходит фиксация информации об изучаемом объекте или явлении на уровне восприятия. Описываются очевидные факты, выявленные методом ощущения, и представления исследователя, а также соответствующими измерительными приборами. Информация, описанная в процессе наблюдения, структурируется путём её классифицирования, группирования и систематизируется по выбранному принципу. Финалом эмпирического познания выступает создание эмпирической теории.

Подробная структура процесса эмпирического познания

Единичные высказывания. Уточняется место и условия, а также дата и время, полученные результаты в ходе отдельного наблюдения (эксперимента) фиксируются исследователем.

Научные факты. На этой ступени эмпирического познания единичные протоколы (высказывания) обобщаются индуктивным методом. Представляя в виде таблиц и графиков, диаграмм и моделей, исследователь утверждает или отрицает наличие явлений, закономерностей, свойств относительно объекта изучения.

Эмпирические закономерности. Третий этап познания характеризуется выявлением зависимости от каких-либо факторов в количественном показателе. Результат такой зависимости обычно выражается в формулах или коэффициентах, в перспективе позволяющих упрощать расчеты и измерения.

Эмпирическая теория. Представляет собой логическую связь практически доказанных фактов и закономерностей, обобщая результаты наглядного изучения объекта или явления. Особенность эмпирической теории в том, что она не противоречит, но и не вытекает из фундаментальной. Теория феномена (эмпирическая) не затрагивает сущность и механизм явления, а лишь обобщает сухие факты. Например, вода меняет агрегатные состояния, но как происходит этот процесс, в рамках эмпирической теории не описывается.

Эмпирическое познание носит пассивный характер и сопровождается использованием ряда методик, которые в перспективе и приводят к созданию эмпирической теории. Исследующий человек не вмешивается в происходящее явление, а только фиксирует замеченные изменения.

Методы эмпирического познания

Наблюдение. Это отправная точка в эмпирическом познании, основанная на восприятии через чувственные способности человека. Исследователь намеренно следит за изменениями научного объекта или явления;

Эксперимент. Исследователь создаёт определённые условия, в которых явление изменяет свои характеристики. Схож с понятием опыта, являясь его разновидностью;

Описание. Метод раскрывает себя в воплощении чувственного восприятия в символы, понятные другому человеку. Отображается информация, полученная через ощущения, путём рисунков, схем, письменной речи и т.д.;

Измерение. Этот метод посредством различных приборов придаёт свойствам явления числовые характеристики;

Сравнение. Представляет процесс поиска общих признаков и отличий между объектами, паттернами, объективно обобщённых между собой одной областью действительности. Найденные общие признаки определяют начало познания закона.

По факту создания эмпирической теории процесс научного исследования на эмпирическом уровне завершается. Изучение объекта или явления выходит на второй уровень – теоретический. Сухие факты, полученные на первом уровне познания, подвергнутся изучению с точки зрения их сущности и механизма происхождения.

Теоретический уровень научного познания

Получение знаний на этом уровне является результатом активной работы разума с применением специальных логических операций – идеализации (формируя в сознании некий идеальный объект, например, известные нам абстрактные чёрные тела из области физики), аналогии, моделирования и прочего. Теоретическое познание, будучи конструктивной работой разума, обусловлено лишь мысленными экспериментами без взаимодействия с самим объектом. Созерцание познаваемого объекта маловажно на этом уровне. Как и эмпирическое, теоретическое познание в исследовании имеет свою структуру.

Подробная структура процесса теоретического познания

Постановка проблемы. Представляет собой некую подвижную форму знания, которая отражает потребность познать ещё не познанное явление и само продвижение к её решению;

Выдвижение гипотезы. Являясь предположением, которое направлено на объяснение того или иного явления, требует теоретического объяснения и проверки посредством эксперимента;

Создание научной теории. Являясь синтезом противоположностей, эмпирического и умозрительного знания, а также высшей формой познания, она полностью раскрывает сущность объекта, явления или их системы.

Двигаясь от этапа к этапу теоретического познания человек, проводящий исследование, пользуется рядом методов обобщения и преобразования эмпирических фактов. Полученный на эмпирическом уровне объём информации обрабатывается путём логики и анализа мышления, помогая достичь преследуемых результатов, уже внутри теоретического уровня.

Методы теоретического научного познания

Идеализация. Представляет собой приём, когда исследователь мысленно изменяет свойства явления, исходя из поставленных задач. В реальности этот процесс не возможен;

Моделирование. Специфика метода в том, что познание явления осуществляется через его созданную модель, которая замещает реальное явление или объект;

Формализация. Применяя специально заданную символику, исследователь воспроизводит явление в тех случаях, когда исследование с применением оригинала невозможно или затруднительно;

Мысленный эксперимент. Является суммой моделирования и идеализации. Представленная мысленно идеальная модель объекта погружается в воображаемые условия, и в уме проигрывается дальнейшее развитие эксперимента. Метод необходим как для утверждения имеющихся знаний, так и для получения новых;

Аналогия. Суть в том, что, если объект, который исследуется в данный момент по удовлетворяющим цели исследователя признакам схож с прежде изученным, то имеющиеся знания переносятся на менее изученный объект;

Дедукция. Это метод овладевания знанием путём распространения общих свойств класса на частное явление;

Индукция. Метод, обратный дедукции. Получение знания происходит посредством распространения свойств частого явления на весь класс;

Анализ. Метод нарушает целостность объекта, разбивая его на части – свойства, признаки, отношения и прочее. Анализ приводит к углубленному изучению объекта, паттерна;

Синтез. Метод, обратный анализу. Представляет собой соединение отдельных частей явления с целью объединить знания, полученные аналитическим методом;

Абстрагирование. Исследователь в рамках эксперимента выделяет важные для него свойства явления и отвлекается от несущественных, получая в результате этих действий абстракцию;

Аксиоматизация. Метод, при котором познание явления, объекта осуществляется путём логического выведения из истинного утверждения (аксиомы) нового знания и его доказательства;

Экстраполяция. Смысл метода в распространении устоявшейся тенденции и закономерности на развитие паттерна, если условия будут сохранены;

Классификация. Суть метода в систематизации знания с помощью организации объектов или явлений из разных областей в классы, основываясь на общие признаки;

Сравнение. Операция познания, где за основу берётся суждение о сходствах сущности двух однородных явлений (изученного и не изученного) или их отличиях.

Полученные теоретические знания о явлении, выраженные в высшей форме, определяются понятием научная теория, состоящим из логически связанных аксиом, обобщений и законов. Научная теория, организующая собой знания, является выражением сущности, смысла явления и его механизма, а также определяет конечную точку исследования явления. Однако она имеет свойство ограниченности, не исключая перспективу создания на своей основе новой более обобщённой теории.

Типы научных теорий, выделенные на различных основаниях

Феноменологические и аналитические. Первая теория описывает исследованный паттерн с точки зрения его действительности без раскрытия его природы. Вторая теория раскрывает сущность паттерна;

Детерминистические и стохастические. Эти типы теорий выделяются по признаку достоверности. Первый тип характеризуется точностью предсказания, но неоднозначность и неопределённость явлений ограничивает его применение в науке. Второй тип основан на предсказании, базой которому служит исследование случайных законов.

Для лучшего понимания рассмотрим примеры знаменитых теорий.

Теория	Суть теории
Феноменологическая теория Роджерса	Самоосознавая себя, и, видя свою концепцию в личностном росте, человек ищет своё место в мире. Другими словами, поведение человека зависит от его внутренних элементов, являющихся тенденцией к оценке опыта и развития.
Аналитическая теория Юнга	Личность человека определяется как совокупность и врождённых и реализованных архетипов, а структура личности – это своеобразное соотношение свойств архетипов, установок личности экстравертированной и интравертированной, а также определённых участков сознательного и бессознательного.
Детерминистическая теория Томаса Гоббса	Основываясь на механический детерминизм, возможно приравнять друг к другу живые существа и автоматы, так как все тела – вещи, способные двигаться, имеют ощущения и другие одинаковые способности.
Стохастическая теория Слуцкого	Распространение колебания циклического характера в экономике происходит по схеме «импульс – распространение», надолго сохраняя эффект после ликвидации причины цикла. Случайным импульсом служит изменения в предпочтениях потребителя, в фискальной или монетарной политике.

Выявленные наукой теории, законы и закономерности складывают общую картину мира, основанную только на естественных причинах существования того или иного явления. Научное мировоззрение конфликтует с религиозным, где принято объяснять всякие явления произвольными причинами. Характерная научной картине мира постепенность вызревания, обусловлена непрерывным получением наукой новых знаний на основе уже полученных.

Почвой для такой рациональности является одна из задач науки – изменять и совершенствовать мир.