§ 19. Закон Джоуля-Ленца. Энергетические превращения в электрической цепи
Для любого участка цепи, даже содержащего ЭДС, справедлив закон Джоуля – Ленца:
количество теплоты, выделяемое на участке цепи с сопротивлением $$ R$$ при прохождении постоянного тока $$ I$$ в течение времени $$ t$$, есть $$ W={I}^{2}Rt$$.
Отсюда мощность выделяемого тепла `P=W//t=I^2R`.
Пусть на участке `1-2` идёт постоянный ток $$ I$$, перенося за время $$ t$$ от т. `1` к т. `2` заряд $$ q=It$$.
Работой тока на участке `1-2` называется работа сил электростатического поля по перемещению $$ q$$ из т. `1` в т. `2:` $$ {A}_{mathrm{Т}}=q({varphi }_{1}-{varphi }_{2})$$.
Обозначим разность потенциалов (напряжение) $$ {varphi }_{1}-{varphi }_{2}=U$$. Тогда $$ {A}_{T}=qU=UIt$$. В зависимости от знака $$ U$$ получается и знак $$ {A}_{mathrm{T}}$$.
Мощность тока:
$$ {P}_{mathrm{T}}={A}_{mathrm{T}}/t=UI$$.
Работой источника с ЭДС $$ mathcal{E}$$ при прохождении через него заряда $$ q$$ называется работа сторонних сил над зарядом `q:`
Aист=±qE{A}_{mathrm{ист}}=pm qmathcal{E}.
Если заряд переносится постоянным током $$ I$$, то $$ {A}_{mathrm{ист}}=pm mathcal{E}It$$.
Когда заряд (ток) через источник идёт в направлении действия сторонних сил, то работа источника положительна (он отдаёт энергию). Аккумулятор в таком режиме разряжается. При обратном направлении тока работа источника отрицательна (он поглощает энергию). В этом режиме аккумулятор заряжается, запасая энергию. Мощность источника:
$$ {P}_{mathrm{ист}}={A}_{mathrm{ист}}/t=pm mathcal{E}I$$.
Для участка цепи `1-2`, содержащего ЭДС (источник), работа тока $$ {A}_{mathrm{Т}}$$, работа источника $$ {А}_{mathrm{ист}}$$ и выделяемое количество теплоты $$ W$$ связаны равнением закона сохранения энергии: $$ {A}_{mathrm{T}}+{A}_{mathrm{ист}}=W$$.
Для участка цепи без ЭДС $$ {A}_{mathrm{ист}}=0$$, $$ {А}_{mathrm{Т}}=W$$ и количество теплоты равно работе тока. В этом случае количество теплоты можно выразить, используя закон Ома $$ I=U/R$$, через любые две из трёх величин: $$ I$$, $$ U$$ и $$ R$$:
$$ W={A}_{mathrm{T}}={I}^{2}Rt=UIt={displaystyle frac{{U}^{2}}{R}}t$$.
Аналогичное соотношение и для мощностей:
$$ {P}_{mathrm{T}}={I}^{2}R=UI={displaystyle frac{{U}^{2}}{R}}$$.
Найти количество теплоты, выделяющееся на внутреннем сопротивлении каждого аккумулятора и на резисторе $$ R$$ за время $$ t=10$$ c в схеме на рис. 17.1. Какие работы совершают аккумуляторы за это время?
$$ {mathcal{E}}_{1}=12$$ B, $$ {mathcal{E}}_{2}=3$$ B, $$ {r}_{1}=1$$ Ом, $$ {r}_{2}=2$$ Ом, $$ R=6$$ Ом.
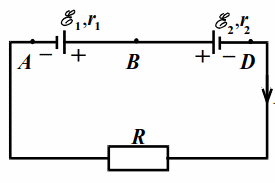 |
| Рис. 17,1 |
Ток: $$ I=left({mathcal{E}}_{1}-{mathcal{E}}_{2}right)/(R+{r}_{1}+{r}_{2})=1$$ A.
Количество теплоты на аккумуляторах и на резисторе:
$$ {W}_{1}={I}^{2}{r}_{1}t=10$$ Дж,
$$ {W}_{2}={I}^{2}{r}_{2}t=20$$ Дж,
$$ W={I}^{2}Rt=60$$ Дж.
Направление действия ЭДС первого аккумулятора совпадает с направлением тока, он разряжается, его работа положительна: $$ {A}_{1}={mathcal{E}}_{1}It=120$$ Дж.
ЭДС второго аккумулятора направлена против тока, он заряжается, поглощая энергию, его работа отрицательна: $$ A2=-{mathcal{E}}_{2}It=-30$$ Дж.
Заметим, что `A_1+A_2=W_1+W_2+W`, что согласуется с законом сохранения энергии.
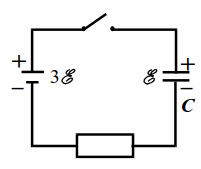 |
| Рис. 19.1 |
Конденсатор ёмкости $$ C$$, заряженный до напряжения $$ mathcal{E}$$, подключается к батарее с ЭДС $$ 3mathcal{E}$$ (рис. 19.1). Какое количество теплоты выделится в цепи после замыкания ключа?
После замыкания ключа ток в цепи скачком достигает некоторого значения и затем спадает до нуля, пока конденсатор не зарядится до напряжения $$ 3mathcal{E}$$. Энергия конденсатора увеличится на
$$ ∆{W}_{C}=C{left(3mathcal{E}right)}^{2}/2-c{mathcal{E}}^{2}/2=4C{mathcal{E}}^{2}$$.
Через батарею пройдёт заряд $$ Q$$, равный изменению заряда не верхней обкладке конденсатора: $$ ∆q=3Cmathcal{E}-Cmathcal{E}=2Cmathcal{E}$$.
Работа батареи: $$ A=∆q3mathcal{E}=6C{mathcal{E}}^{2}$$. По закону сохранения энергии:
$$ A=∆{W}_{C}+W$$.
В цепи выделится теплоты: $$ W=A-∆{W}_{C}=2C{mathcal{E}}^{2}$$.
Тепловая мощность, выделяемая на резисторе
Электрический ток, проходящий по проводнику, нагревает его. Это объясняется тем, что свободные электроны, перемещаясь под действием электрического поля, взаимодействуют с ионами или атомами вещества и передают им свою энергию. В результате работы электрического тока внутренняя энергия вещества увеличивается, повышается его температура. Нагретый проводник передает свою энергию окружающим телам. Если проводник не движется, то вся энергия электрического тока переходит во внутреннею энергию проводника. Работа тока определяется
(A = U*I*T)
Количество теплоты, выделяемое на резисторе, обозначим через Q Так как Q = A, то
(Q = U*I*R*t)
или используя закон Ома (U = I*R), получим
(Q = {I^2}Rt)
Количество теплоты, выделяемое проводником с током, равно произведению квадрата силы тока, сопротивления и времени.
Эта формулировка называется законом Джоуля — Ленца
Перезаряд емкости и выделившееся при этом количество теплоты
Задачи на количество выделившегося тепла в цепи почему-то вызывают у моих учеников страх и неприязнь. Так бывает всегда, когда нет понимания вопроса. Поэтому, чтобы все расставить по полкам, пишу эту статью, где подробно постараюсь объяснить, как же эти задачи решаются.
Задача 1.
Какое количество тепла выделится на резисторе сопротивлением после замыкания ключа К в цепи, показанной на рисунке? Внутренним сопротивлением батареи пренебречь.
Задача 1
Проанализируем состояние цепи до замыкания ключа. Имеем цепь с двумя конденсаторами, включенными последовательно. Оба они заряжены, общая эквивалентная их емкость равна
А их общий заряд тогда
Этот заряд будет одинаковым на обоих конденсаторах. Напряжение на конденсаторах распределится согласно их емкостям:
Теперь рассмотрим цепь после замыкания ключа. Конденсатор будет разряжаться через резистор и напряжение на нем будет уменьшаться, а напряжение на конденсаторе
будет расти, пока не достигнет
. Таким образом, энергия, запасенная обоими конденсаторами до замыкания ключа, равна:
Суммарная энергия, запасенная конденсаторами, равна:
А после замыкания ключа энергия сосредоточена только в , и равна:
То есть изменениe внутренней энергии:
Определим изменение заряда конденсатора : был
, стал
, следовательно,
Ответ:
Задача 2.
Какое количество тепла выделится на резисторе сопротивлением после переключения ключа К из положения 1 в положение 2 в цепи, показанной на рисунке?
Задача 2
Вначале в цепи действовала суммарная ЭДС, равная , а затем, после переключения ключа, стала действовать такая же по модулю, но обратная по знаку ЭДС. Следовательно, Сначала заряд конденсатора был равен
, а потом стал таким же по модулю, но пластины поменяли знаки зарядов, то есть
Тогда энергия конденсатора была вначале
А потом стала
Таким образом, энергия не изменилась, следовательно, вся работа источника пошла на тепло, выделившееся в резисторе:
Ответ:
Задача 3.
Конденсатор емкостью , заряженный до напряжения
, разряжается через резистор с большим сопротивлением
и батарею с
. Найдите количество теплоты, выделившееся при разрядке конденсатора.
Задача 3
Энергия, запасенная конденсатором до разряда:
После того, как произойдет разряд, напряжение на конденсаторе станет равно , а энергия, запасенная им, станет равна
Изменение внутренней энергии тогда равно:
Заряд конденсатора вначале был равен:
А после разряда
Тогда заряд, протекший через источник, равен
И работа источника равна:
Теперь можем определить и количество теплоты:
Ответ:
Задача 4.
При разомкнутом ключе К один конденсатор в цепи был заряжен до напряжения , а второй – нет. Найдите количество теплоты, выделившееся на каждом из сопротивлений
и
после замыкания ключа К.
Задача 4
Эквивалентная емкость обоих конденсаторов равна , поэтому энергия, запасенная в цепи, равна
Количество теплоты, выделившееся в цепи, в силу отсутствия источника равно запасенной энергии, а на каждом из резисторов, так как ток через них протекает один и тот же, выделится количество теплоты, пропорциональное их сопротивлениям:
Подставим выраженное из второго уравнения в первое:
А количество теплоты :
Ответ: ,
Задача 5. В цепи, изображенной на рисунке, ЭДС батареи равна В, сопротивления резисторов равны
Ом и
Ом, а емкости конденсаторов
мкФ и
мкФ. В начальном состоянии ключ К разомкнут, а конденсаторы не заряжены. Какое количество теплоты выделится в цепи после замыкания ключа? Ответ выразить в Дж, округлив до десятых.
Задача 5
Сначала, при разомкнутом ключе, напряжения на обоих конденсаторах равны 0 и заряды также нулевые. После замыкания ключа начнется перераспределение заряда, но в конце, когда переходной процесс завершится, токи во всех ветвях будут равны нулю, следовательно, на конденсаторе нулевое напряжение (напряжение на нем равно напряжению на резисторе, а так как тока нет, то оно равно 0). По этой же причине вся ЭДС источника будет падать на
(ведь при нулевом токе на резисторе ничего не падает). То есть энергия конденсатора
по окончании процесса равна
Заряд будет равен
И, следовательно, работа источника
Таким образом, в виде тепла выделилось
Ответ: 0,3 Дж
На чтение 6 мин. Просмотров 2.9k. Опубликовано 27.07.2021
Практически все электроприборы содержат в своих схемах резисторы. Это объясняется тем, что для каждого прибора или проводника избирается своя сила тока для функционирования. Для того чтобы компенсировать значение между напряжением и движением заряженных частиц, в схемы вводят сопротивление. Основной параметр – это его мощность.
Что такое тепловая мощность резистора
Другое название – рассеивание. Этим понятием называют максимальные токи, которые без вреда могут протекать через него для осуществления работы и образования ЭДС в контактах и т.п.
Важно! Для каждой электрической схемы параметры рассеивания подбираются индивидуально.
Вычисляется по физической формуле с алгебраическими значениями: P = I * R.
В СИ:
- I – сила тока, Ампер.
- R – сопротивление, Ом.
- Р – мощность, Вт.
В физическом плане рассеивание – это способность проводника отдавать тепло в окружающую среду в том количестве, которое не вредит составным частям самого элемента. Это очень важный параметр, так как от него зависит исправность и долговечность электроприбора.
Важно! Все компоненты работают, подчиняясь закону Ома, но сам нагрев происходит из-за разности величин напряжения на входе и выходе. Это и является основным условием движения заряженных частиц через проводник.
Как определить и подобрать мощность
Данный параметр избирается от максимального значения силы заряженных частиц, которые будут протекать через проводник.
Для того чтобы подбирать тепловое рассеивание участков сопротивления для конкретных электроприборов, необходимо изучить параметры входного и выходного напряжения, а также силу электроцепи.
Важно! Необходимо понимать, что городские и промышленные цепи различаются по нагрузке и напряжению. Для бытовых используется 220V, для промышленных часто применяется значение в 380V.
Далее будет представлен стандартный ряд с графическим изображением мощностного отбора резистантов. Абсолютное большинство фабричных электроприборов оснащаются схемами, где указан конкретный диапазон элементов. Такие схемы незаменимы при ремонте и позволяют быстро подбирать необходимое.
Стандартный ряд мощностей и их обозначение на схемах
| Вт | Условное обозначение на электросхемах |
| 0,05 Вт |  |
| 0,125 Вт |  |
| 0,025 Вт |  |
| 0,5 Вт |  |
| 1 Вт |  |
| 2 Вт |  |
| 5 Вт |  |
В качестве графических обозначений используются римские цифры и черточки, раскрывающие диапазон от 0,05 до 25
Важно! Очень важно запомнить то, что слабые устройства обозначается косыми линиями.
Формула для расчета мощности тока в активном сопротивлении, как узнать сколько ватт
Как уже было упомянуто, классическая формула для расчета формируется так: квадрат силы движущихся заряженных частиц, помноженный на величину резистента.
Так показатели работоспособности напрямую зависят от напряжения. При работе и возникновении ЭДС частицы протекают через элемент, «осаживаясь» сопротивлением, и происходит нагрев элемента. Нагрев – это выделение тепла, который может быть измерен в Вт.
Важно! Что будет, если неправильно подобрать изделие? Если величина рассеивания слишком маленькая, то сопротивление перегорит, а если установить слишком «сильный» резистант, то движение заряженных частиц не начнется, и произойдет замыкание. Если из строя вышел элемент в 0,5 Вт, то он заменяется точным аналогом с соответствующими параметрами.
Действует еще одно правило подбора – оно касается не графических изображений на схеме, а самого типоразмера устройства. Чем больше элемент по габаритам, тем выше характеристика его параметров.
Как рассчитать рассеивание для сопротивления
Рассеиванием в физике и электромеханике называется процесс образования тепловой энергии, при чем это касается не только резисторов, но и прочих электрических элементов: кабелей, проводов, штекеров и катушек.
Главное не допускать перегрева, так как это кратно снижает долговечность электроприборов и их отдельных элементов. Следующий ряд является типовым в отборе характеристик зависимости производительности от напряжения:
- 0,125
- 0,25
- 0,5
- 1
- 2
- Более 2 Ватт.
Им соответствует значение для сопротивлений, Ом: 10, 20, 25, 50, 60, 100.
Приведем конкретный пример алгебраического вычисления.
Мы имеем изделие с параметром в 10 Ом и пропускаем через него поток заряда в 0,1 А. Используем значения для того, чтобы подставить их в известную формулу с переменными. Получаем P = 1
P(Ватт) – теплота, выделяемая на резисторе;
R(Ом) – сопротивление цепочки;
I(А) – движение заряженных частиц.
Как определить по внешнему виду
Если на схеме имеется конкретное обозначение, то тепловая мощность на резисторе определяется по символам, но как определить параметр по внешнему виду элементов на плате?
Известно, что чем больше площадь поверхности, тем больше она может поглощать или отдавать количества теплоты на резисторе.
Кроме того, существуют буквенные обозначения для российских и импортных устройств.
Для отечественных:
В – Маломощные от 0,125 до 0,25
Для импортных:
W — Маломощные от 0,125 до 0,25
V – Средний диапазон.
SW – Более 2
Важно! Существуют миниатюрные устройства, на корпусе которых невозможно нанести маркировку. Такие сопротивления окрашиваются в белый, желтый или красный цвет. Цвета в соответствии с диапазонами по возрастающей. В частности, это касается импортных изделий.
Как рассчитать мощность в схеме
Для схем также обязательны знания о силе тока и сопротивлении, без знания этих параметров расчет будет невозможен. Тепловые потери на резисторе формируются из квадрата силы тока, помноженного на сопротивление: P = I² * R (количество теплоты на резисторе формула). Актуальна только при расчетах готовой и известной схемы, во всех случаях предварительного расчета используется прямое значение силы тока, а не ее квадрат.
Величина указывается исключительно в Омах, если используются значения в кило- или мегаомах, то их необходимо округлять до классического значения в одну единицу сопротивления – Ом.
Схема с последовательным соединением элементов
Последовательное соединение означает тот факт, что через все элементы схемы проходит одно и то же значение силы тока. Это означает, что и рассеивание будет тождественным на всех резистантах. Для подсчета необходимо:
- Суммировать значения на всех участках, то есть: 200 Ом + 100 Ом + 51 Ом + 39 Ом = 390 Ом. Сила тока рассчитывается по закону: I = U/R. Алгебраически значение формируется в следующем виде: I = 100 В / 390 Ом = 0,256 А.
- Рассчитать параметр: P = 0,256² * 390 Ом = 25,549
Это ответ на вопрос о том, какая тепловая мощность будет выделяться на резисторе r1 в схеме.
Таким образом становится возможным подсчитать индивидуальное рассеивание на каждом участке, указанном в схеме.
Как подобрать резистор на замену
Для замены всегда подбирается точно такой же элемент. Допускается временное использование сопротивлений с параметром на 1 порядок выше, чем у перегоревшего или вышедшего из строя по другим причинам. Это основное условие замкнутого контура в цепи. Установить неисправный участок цепи – означает разомкнуть цепь.
Определить параметры можно приблизительно по маркировке и размерам.
Элементы для замены оснащены выводами с обоих концов – их паяют на плату. Рекомендуется не подрезать выводы, так как они тоже обладают дополнительным сопротивлением.
На резисторе внешней цепи аккумулятора выделяется тепловая мощность 10 Вт
Этот параметр и условие являются актуальными при последовательном подключении трех аккумуляторов. Если к концам подведена внешняя цепь с аккумулятором, то для каждого следующего аккумулятора значение будет увеличиваться в 2 раза. Но поскольку мощность зависит от напряжения через силу тока, то для третьего аккумулятора возрастание мощности составит значение в 25%. Тепловые потери составят 26,9Вт.
Используя сведения, которые были представлены в данной статье, можно самостоятельно и быстро подобрать необходимые элементы электроцепи в электроприборе для замены. Для этого в настоящее время существует множество магазинов электроники, которые удовлетворят запросы самых претенциозных клиентов.
Данную статью можно использовать в качестве конкретного руководства по выбору резисторов не только в бытовые электроприборы, но и в промышленные установки.
Резистор – это один из главных радиоэлементов, у которого есть целый ряд важнейших параметров. Сегодня речь пойдет о мощности рассеивания, ведь этот параметр отвечает за надежную и стабильную работу любого резистора.
Что такое мощность и рассеиваемая мощность
Для начала давайте освежим в памяти, что такое мощность постоянного тока, для этого следует вспомнить очень простую формулу:
Из выше представленного выражения вполне ясно, что мощность зависит от таких величин как напряжение и ток.
Если мы рассмотрим реальную схему, то в процессе ее работы через резисторы, расположенные в схеме, будет протекать ток определенной величины, а так как они (резисторы) обладают определенным сопротивлением, то под действием тока на резисторе будет выделяться тепло. Это тепло и есть та мощность, которая рассеивается на резисторе.
Так вот, если мы в схему установим резистор с меньшей мощностью рассеивания, чем это требуется, то резистор будет перегреваться. Это приведет к его быстрому выходу из строя.
Поэтому очень важно соблюдать следующее правило: заменяемый резистор должен соответствовать по мощности рассеивания сгоревшему резистору, либо этот параметр должен быть больше, но никак не меньше.
Все выпускаемые резисторы соответствуют стандартному ряду, который выглядит так:
1. 0,125 Вт, 0,25 Вт, 0,5 Вт, 1 Вт, 2 Вт, и более
Обычно, соблюдается следующее правило: чем больший размер у резистора, тем на большую рассеиваемую мощность он рассчитан.
Давайте рассмотрим пример. Допустим нам нужно установить резистор с сопротивлением 100 Ом, а ток через него будет протекать 0,1 Ампер.
Для того, чтобы рассчитать требуемую мощность рассеивания нашего резистора воспользуемся следующей формулой:
Итак, получается, что в данном примере нам потребуется резистор с мощностью рассеивания в один Ватт.
Примечание. Для стабильной и надежной работы следует обязательно брать резистор с запасом по мощности рассеивания. Это позволит обеспечить требуемую надежность и долговечность работы схемы.
Но что делать, если вы не знаете, какой ток будет протекать через резистор. Для расчета требуемой мощности рассеивания можно воспользоваться уже другой формулой:
Все вышеперечисленное справедливо для того случая, когда нужно заменить единичный резистор, но довольно часто в схемах можно найти так называемой составной резистор (несколько резисторов соединены параллельно, последовательно или же смешанно).
Итак, давайте для начала рассмотрим последовательное соединение.
При последовательном соединении через резисторы будет протекать одинаковый ток. И получается если нам нужно найти замену резистору на 100 Ом, через который протекает ток в 0,1 А и он рассчитан на мощность рассеивания в 1 Вт, его можно заменить двумя последовательно соединенными резисторами на 80 Ом и 20 Ом.
Если воспользоваться выше представленными формулами и рассчитать на какую мощность должен быть рассчитан каждый резистор, то получим следующий результат:
R1 – 20 Ом (0,2 Вт)
R2 – 80 Ом (0,8 Вт)
Теперь смотрим таблицу со стандартным рядом и выбираем ближайший наибольший номинал. Получается, что в нашем случае подойдут резисторы с мощностью рассеивания R1 – 0.5 Вт, R2 – 1 Вт.
При параллельном же соединении учитывайте тот факт, что через резистор с меньшим сопротивлением будет течь больший ток.
Смешанное соединение на практике практически не используется.
Как обойтись без расчетов
В принципе можно обойтись без формул и подсчетов, достаточно следовать следующему правилу:
Мощность каждого резистора, который входит в составляемую цепь (параллельную или последовательную) должен быть равен мощности рассеивания заменяемого резистора. Проще говоря, если вы хотите заменить резистор на 1 Вт составным резистором, то каждый из них должен быть не менее 1 Вт по мощности рассеивания.
Это все, что я хотел вам рассказать о расчете мощности рассеивания резистора и правилах его замены. Если статья оказалась вам полезна, то оцените ее лайком и спасибо за ваше внимание!







