Как найти тепло при изотермическом

Что такое изотермический процесс

Изотермический процесс – процесс изменения состояния идеального газа при постоянной температуре. 

Главное условие: T=const

С разницей в 14 лет закон открыли Роберт Бойль (1662 г.) и Эдм Мариотт (1676 г.) Название дано в честь обоих ученых.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Закон Бойля-Мариотта

При постоянной температуре и массе идеального газа произведение его давления и объёма постоянно.

(T-const\P_1V_1=P_2V_2\\\)

Или соотношение:

(frac{p_1}{p_2}=frac{V_2}{V_1}\\\)

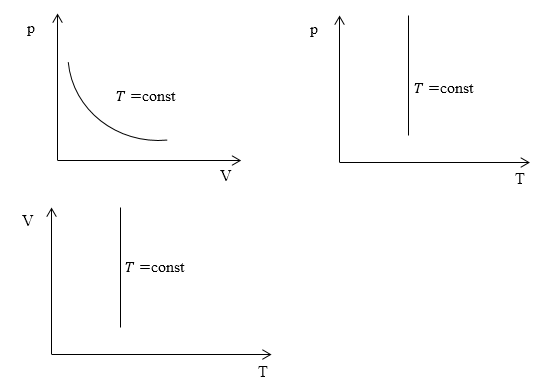
Закон выражается графиками:

1. Зависимость давления от объема:

2. Зависимость давления от температуры:

3. Зависимость объема от температуры:

Как изменяется внутренняя энергия при изотермическом процессе

Внутренняя энергия изменяется вместе с температурой. Отличительной чертой изотермического процесса является его протекание с постоянной температурой. Из этого следует, что внутренняя энергия не изменяется. 

Формула количества теплоты в изотермическом процессе

Запишем первый закон термодинамики:

(Q=triangle U+A\\\ )

(Q-количество;теплоты;(Дж)\triangle U-изменение;внутренней;энергии;(Дж)\А-работа;(Дж)\\\)

Поскольку температура постоянна, то изменение внутренней энергии равно нулю. Уравнение принимает вид:

(triangle Q=A\\\)

Все тепло расходуется на работу газа.

Для изотермического процесса характерен определенный процесс, который происходит с газовым веществом, который в свою очередь имеет неизменную массу и постоянную неизменяемую температуру вещества.

Изотермический процесс для температуры газа, основные формулы и величины

Изотермический процесс для системы координат

Характерные изотермические процессы   зачастую отражают на термодинамических графиках и диаграммах.

Если рассмотреть подробно график можно увидеть линию, именно ее и принято называть изотермой. Она непосредственно является основной характеристикой процесса.

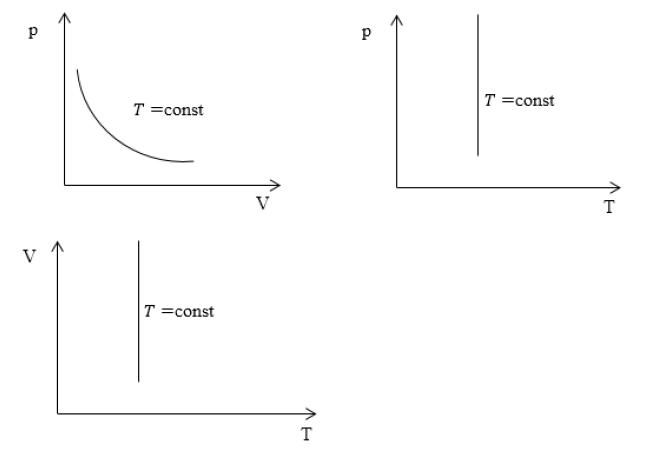
Изотермический процесс — закон Бойля-Мариотта

Разделим уравнение для второго состояния газа на выражение первого состояния и получим основное уравнение изотермического процесса.

[frac{p_{2} V_{2}}{p_{1} V_{1}}=1] или [p V=mathrm{const}] (постоянное значение)

Полученное уравнение и будет называться законом Бойля-Мариотта.

Данный процесс осуществляется с использованием тепловой энергии.

В случае, когда объем увеличивается, или отводится, для его уменьшения.

Составим первое значение термодинамики.

Затем постепенно получим уравнение для определения работы.

А также вычисления внутренней энергии и количества теплоты тела при изотермическом процессе.

[delta Q=d cup+d A=frac{i}{2} v R d T+p d V]

Температура является неизменной, поэтому, изменение значения внутренней энергии будет равняться нулевому значению. [(d cup=0)].

Из этого следует, что для изотермического процесса все подводимое тепло направлено  на работу, которую совершает газ:

[ Delta Q=int_{V_{1}}^{V_{2}} d A ]

где:

• [delta Q] — тепло элементарного характера, которое подводится ко всей системе;
• dA  — работа элементарного типа, совершаемая газом  в изотермическом процессе; 
• i —  количество  свободных степеней  газовых молекул; 
• R —   газовое значение постоянной; 
• d —   значение молей для газа;
• V₁— первоначальное значение объема газа;
• V₂— окончательное значение объема газа.

[A=int_{V_{1}}^{V_{2}} p d V]

Давление газа, которое зависит от уравнения газа в идеальном состоянии.

[p V=v R T rightarrow p=frac{v R T}{V}]

Подставим вышеуказанное выражение в подынтегральное выражение:

[A=int_{V_{1}}^{V_{2}} frac{v R T}{V}=v R T int_{V_{1}}^{V_{2}} frac{d V}{V}=mathrm{u} R T ln left(frac{V_{2}}{V_{1}}right)]

Составленное уравнение необходимо  определения значения работы, которую совершает газ  в изотермическом процессе.

[ A=v R T ln left(frac{p_{1}}{p_{2}}right) ]

[ Delta Q=A ]

Как найти изотермический процесс — примеры решения задач

Пример №1

Основное содержание задания: газ идеального состояния, имеет способность расширяется, имея постоянную температуру, от объема.

[V_{1}=0.2 mathrm{~m}^{3}]

[V_{2}=0.6 mathrm{~m}^{3}]

Известно  сила давления во втором состоянии и  оно равняется [p_{2}=1 cdot 10^{5} mathrm{Pi a}].

Определить:

• Величину изменения внутренней энергии газа;
• Значение работы, которую совершает газовое вещество в данном процессе;
• Какое необходимое количество теплоты получает газ в процессе работы.

Методика решения:

Внутренняя энергия газа неизменна, так как процесс который рассматривается в задаче, является изотермическим:

[Delta mathrm{U}=0]

Из основного закона термодинамики можно определить:

[Delta cup=A]

[A=v R T ln left(frac{V_{2}}{V_{1}}right)]

Составим и запишем уравнение, которое отражает окончательное (конечное) состояние газа:

[p_{2} V_{2}=v R T rightarrow T=frac{p_{2} V_{2}}{v R}]

Подставим в уравнение для температуры вышеизложенные формулы и получим решение:

[A=v R frac{p_{2} V_{2}}{v R} ln left(frac{V_{2}}{V_{1}}right)=p_{2} V_{2} ln left(frac{V_{2}}{V_{1}}right) .]

Следовательно, все величины расположены в международной системе единиц (СИ), можно провести вычисления и определить неизвестные значения:

[A=0.6 cdot 10^{5} ln left(frac{0.6}{0.2}right)=0.6 cdot 10^{5} cdot 1.1=6.6 cdot 10^{4} text { (Дж) }]

Ответ задачи:

• значение изменения внутренней энергии газа в рассматриваемой процессе равно нулевому значению.
• работа, которая совершается в процессе газовым веществом равняется  [6,6 cdot 10^{4} text { Дж }].
• Необходимое количество тепловой энергии равно: [6,6 cdot 10^{4} text { Дж }].

---

Пример №2

Задание: изображен график, где изменяется идеальное состояние массы газа равное m в координатных осях p (V).

Нужно перенесите данный процесс на координатные оси в p(T).

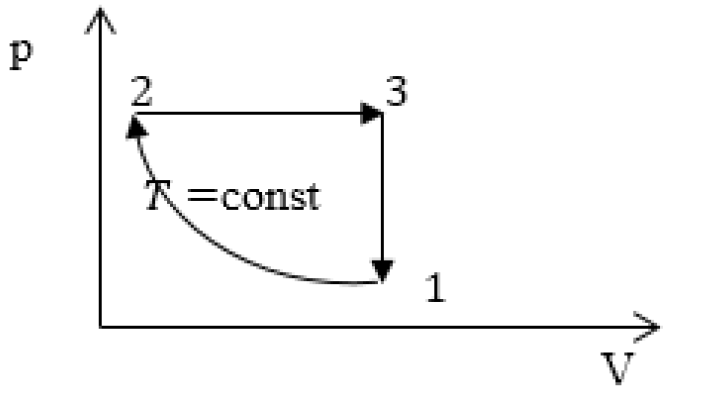
На данном графике изображен круговой процесс.

Где:

1. Прямая 1-2  является изотермическим процессом с константой [(T=text { cons } t)].  Следовательно  значение объема будет уменьшается [(mathrm{V} downarrow)],  а давления соответственно расти [(p uparrow)].
2. Прямая 2-3  отражает изобарический процесс [(p=text { const })]

const). Для данного процесса характерно увеличение объема  [mathrm{V} uparrow] и  применяя закон Гей-Люссака,  увеличение [Т uparrow]

• Прямая (отрезок) 3-1  является изохорным процессом объем будет постоянной величиной  [(mathrm{V}=text { const })], а  [p downarrow],а исходя из  закона Шарля [T downarrow].

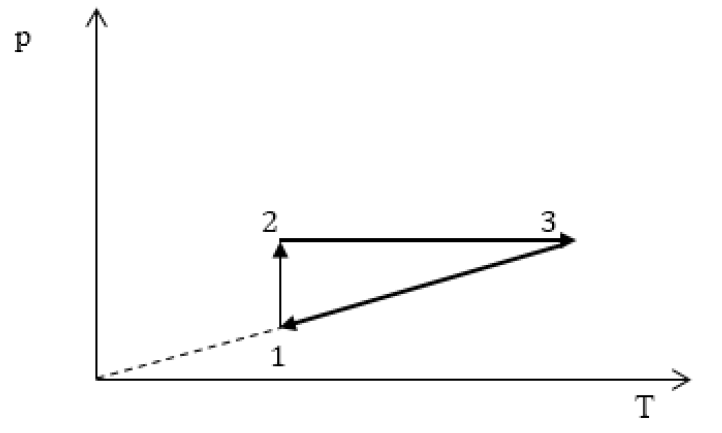
Все перечисленные процессы изобразим на координатных осях  p(T).

Изотермическим
называется процесс, протекающий при
постоянной температуре.

Рис. 2.7. График изотермического процесса	Рис. 2.8. К определению внутренней энергии газа

1. Уравнение процесса –

.

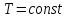
2. График процесса.
Из уравнения состояния следует, что
, так как.
Следовательно, графиком процесса вр,υ
– координатах является
равнобокая
гипербола
(рис. 2.7).

3. Связь между
параметрами состояния газа. Для этого
запишем уравнение состояния для точек
2 и 1 и разделим их друг на друга

,
.

Так как в
изотермическом процессе
,
то

.
(2.20)

4.
Теплоемкость газа в изотермическом
процессе
,
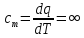
так как в этом процессе,
а.

5. Определение
количества теплоты q,
подведенной к газу, совершенной им
работы l
и изменения его внутренней энергии Δu:

.
(2.21)

Если
,
то, согласно равенству (2.21),.
Значит, при подводе теплоты к газу его
удельный объем возрастает и наоборот
(рис. 2.7).

Таким образом,
в изотермическом процессе теплота,
сообщаемая газу, идет на совершение им
работы расширения против внешних сил.

Используя график
изотермического процесса (рис. 2.8), можно
показать, что изменение внутренней
энергии газа в любом процессе
.
Действительно, во всех процессахa,
b
и c,
начинающихся в точке 0 и заканчивающихся
на изотерме, изменение внутренней
энергии будет одинаково, т.е.
,
так как начальное и конечное значение
температуры в этих процессах одно и то
же.

Но согласно первому
закону термодинамики в изохорном
процессе a
теплота, подведенная к газу, идет только
на увеличение его внутренней энергии,
т.к. в этом процессе газ не совершает
работу, т.е.
.
Как установлено выше, в изохорном
процессе.
Отсюда следует, что в любом процессе

.

Рис. 2.9. Графики адиабатного и изотермического процессов

2.9. Адиабатный процесс

Адиабатным
называется процесс, протекающий при
отсутствии теплообмена с окружающей
средой
(т.е. при q =
0).

1. Уравнение
процесса.

Для вывода уравнения
процесса запишем уравнение первого
закона термодинамики в двух формах:

и

или в виде

и.

Разделив второе
уравнение на первое, получим

или,

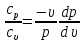
где
– показатель адиабаты.

Проинтегрировав
последнее уравнение, получим

или
.

Откуда следует
выражение для уравнения адиабатного
процесса в виде

.
(2.22) 2. График процесса. Из
уравнения процесса (2.22) следует, что
. Вр,υ
– координатах – это
неравнобокая
гипебла.

Так как k
>1, то адиабата протекает круче изотермы
(рис. 2.9).

3. Связь между
параметрами состояния газа. Для этого
запишем уравнение адиабаты для точек
2 и 1 и разделим их друг на друга

,
.

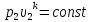
Тогда получим

.
(2.23)

Из уравнения
состояния, записанного для точек 1 и 2
(рис. 2.9), следует, что
. Используя соотношение (2.23), получим

.
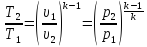
(2.24)

4.
Теплоемкость газа в адиабатном процессе.
Так как в этом процессе
, а, то

.

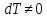
5. Определение
количества теплоты q,
подведенной к газу, совершенной им
работы l
и изменения его внутренней энергии Δu:

• количество тепла,
  подведенного к газу
  ;

• изменение внутренней
  энергии газа

;

• для адиабатного
  процесса по определению q
  = 0. Тогда из
  первого закона термодинамики следует,
  что при q
  = 0 работа
  расширения газа

,
(2.25)

т.
е. в адиабатном процессе работа газа
совершается за счет убыли его внутренней
энергии.Поэтому, как видно из
формулы (2.25), адиабатное расширение газа
(т.е. присопровождается уменьшением его
температуры, а сжатиеповышением.

Из уравнения Майера
и выражения для показателя адиабатыследует, что,a

,
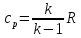
тогда

. (2.26)

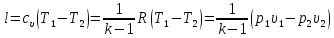
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Основными процессами в термодинамике являются:

• изохорный, протекающий при постоянном объеме;
• изобарный, протекающий при постоянном давлении;
• изотермический, происходящий при постоянной температуре;
• адиабатный, при котором теплообмен с окружающей средой отсутствует;
• политропный, удовлетворяющий уравнению pvⁿ= const.

Изохорный, изобарный, изотермический и адиабатный процессы являются частными случаями политропного процесса.

При исследовании термодинамических процессов определяют:

• уравнение процесса в p—v иT—s координатах;
• связь между параметрами состояния газа;
• изменение внутренней энергии;
• величину внешней работы;
• количество подведенной теплоты на осуществление процесса или количество отведенной теплоты.

Изохорный процесс

 

Изохорный процесс в p, v— , T, s— и i, s-координатах (диаграммах)

При изохорном процессе выполняется условие v = const.

Из уравнения состояния идеального газа (pv = RT) следует:

 p/T = R/v = const,

т. е. давление газа прямо пропорционально его абсолютной температуре:

 p₂/p₁ = T₂/T₁.

Работа расширения в изохорном процессе равна нулю (l = 0), так как объем рабочего тела не меняется (Δv = const).

Количество теплоты, подведенной к рабочему телу в процессе 1-2 при c_v = const определяется по формуле:

q= c_v(T₂ —  T₁). 

Т. к.l = 0, то на основании первого закона термодинамики Δu = q, а значит изменение внутренней энергии можно определить по формуле:

Δu = c_v(T₂ — T₁).

Изменение энтропии в изохорном процессе определяется по формуле:

s₂ – s₁= Δs = c_vln(p₂/p₁) = c_vln(T₂/T₁).

Изобарный процесс

Изобарный процесс в p, v— , T, s— и i, s-координатах (диаграммах)

Изобарным называется процесс, протекающий при постоянном давлении p = const. Из уравнения состояния идеального газа слуедует:

v/T = R/p = const

или

 v₂/v₁ = T₂/T₁,

т. е. в изобарном процессе объем газа пропорционален его абсолютной температуре.

Работа будет равна:

l = p(v₂ – v₁). 

Т. к. pv₁ = RT₁ и pv₂ = RT₂, то

l = R(T₂ – T₁).

Количество теплоты при c_p = const определяется по формуле:

q = c_p(T₂ – T₁).

Изменение энтропии будет равно: 

s₂ – s₁= Δs = c_pln(T₂/T₁).

Изотермический процесс

Изотермический процесс в p, v— , T, s— и i, s-координатах (диаграммах)

При изотермическом процессе температура рабочего тела остается постоянной T = const, следовательно:

pv = RT = const

или

p₂/p₁ = v₁/v₂,

т. е. давление и объем обратно пропорциональны друг другу, так что при изотермическом сжатии давление газа возрастает, а при расширении – снижается.

Работа процесса будет равна:

l  = RTln (v₂ – v₁) = RTln (p₁ – p₂).

Так как температура остается неизменной, то и внутренняя энергия идеального газа в изотермическом процессе остается постоянной (Δu = 0) и вся подводимая к рабочему телу теплота полностью превращается в работу расширения:

q = l.

При изотермическом сжатии от рабочего тела отводится теплота в количестве, равном затраченной на сжатие работе.

Изменение энтропии равно:

s₂ – s₁= Δs = Rln(p₁/p₂) = Rln(v₂/v₁).

Адиабатный процесс

Адиабатный процесс в p, v— , T, s— и i, s-координатах (диаграммах)

Адиабатным называется процесс изменения состояния газа, который происзодит без теплообмена с окружающей средой. Так как dq = 0, то уравнение первого закона термодинамики для адиабатного процесса будет иметь вид:

du + pdv = 0

или

Δu+ l = 0,

следовательно

Δu= —l. 

В адиабатном процессе работа расширения совершается только за счет расходования внутренней энергии газа, а при сжатии, происходящем за счет действия внешних сил, вся совершаемая ими работа идет на увеличение внутренней энергии газа.

Обозначим теплоемкость в адиабатном процессе через c_ад, и условие dq = 0 выразим следующим образом:

dq = c_адdT = 0. 

Это условие говорит о том, что теплоемкость в адиабатном процессе равна нулю (c_ад = 0).

Известно, что

с_p/c_v = k

и уравнение кривой адиабатного процесса (адиабаты) в p, v-диаграмме имеет вид:

pv^k = const. 

В этом выражении k носит название показателя адиабаты (так же ее называют коэффициентом Пуассона).

Значения показателя адиабаты k для некоторых газов:

k_{воздуха} = 1,4

k_{перегретого пара} = 1,3

k_{выхлопных газов ДВС} = 1,33

k_{насыщенного влажного пара} = 1,135

Из предыдущих формул следует:

l= — Δu = c_v(T₁ – T₂);

i₁ – i₂= c_p(T₁ – T₂).

Техническая работа адиабатного процесса (l_техн) равна разности энтальпий начала и конца процесса (i₁ – i₂).

Адиабатный процесс, происходящий без внутреннего  трения в рабочем теле, называется изоэнтропийным. В T, s-диаграмме он изображается вертикальной линией.

Обычно реальные адиабатные процессы протекают при наличии внутреннего трения в рабочем теле, в результате чего всегда выделяется теплота, которая сообщается самому рабочему телу. В таком случае ds > 0, и процесс называется реальным адиабатным процессом.

Политропный процесс

Политропным называется процесс, который описывается уравнением:

pvⁿ= const.

Показатель политропы n может принимать любые значения в пределах от -∞ до +∞, но для данного процесса он является постоянной величиной.

Из уравнения политропного процесса и уравнения Клайперона можно получить выражение, устанавливающее связь между p, vи Tв любых двух точках на политропе:

p₂/p₁ = (v₁/v₂)ⁿ; T₂/T₁ = (v₁/v₂)^n-1; T₂/T₁ = (p₂/p₁)^(n-1)/n. 

Работа расширения газа в политропном процессе равна:

В случае идеального газа эту формулу можно преобразовать:

  

Количество подведенной или отведенной в процессе теплоты определяется с помощью первого закона термодинамики:

q = (u₂ – u₁) + l.

Поскольку

представляет собой теплоемкость идеального газа в политропном процессе.

При c_v, k и n = const c_n = const, поэтому политропный процесс иногда определят как процесс с постоянной теплоемкостью.

Политропный процесс имеет обобщающее значение, ибо охватывает всю совокупность основных термодинамических процессов.

Графическое представление политропа в p, v координатах в зависимости от показателя политропа n.

pv⁰ = const (n = 0) – изобара;

pv = const (n = 1) – изотерма;

p⁰v = const, p^1/∞v = const, pv^∞ = const – изохора;

pv^k = const (n = k) – адиабата.

n > 0 – гиперболические кривые,

n < 0 – параболы.

По материалам моего конспекта лекций по термодинамике и учебника «Основы энергетики». Автор Г. Ф. Быстрицкий. 2-е изд., испр. и доп. — М. :КНОРУС, 2011. — 352 с.

Запишем уравнение для двух состояний идеального газа:

[p_1V_1=nu RTleft(1right),]

[p_2V_2=nu RT left(2right).]

Закон Бойля-Мариотта

Разделим уравнение (2) на уравнение (1), получим уравнение изотермического процесса:

[frac{p_2V_2}{p_1V_1}=1 (3)]

или

[pV=const left(4right).]

Уравнение (4) называют законом Бойля-Мариотта.

Этот процесс происходит с подводом тепла, если объем увеличивается, или его отводом, чтобы уменьшать объем. Запишем первое начало термодинамики, последовательно получим выражения для работы, внутренней энергии и количества теплоты изотермического процесса:

[delta Q=dU+dA=frac{i}{2}nu RdT+pdV, left(5right).]

Температура не изменяется, следовательно, изменение внутренней энергии равно нулю ($dU=0$). Получается, что в изотермическом процессе все подводимое тепло идет на совершение газом работы:

[triangle Q=intlimits^{V_2}_{V_1}{dA}left(6right),]

где $delta Q $- элементарное тепло, подводимое к системе, $dA$- элементарная работа, которую совершает газ в процессе, i – число степеней свободы молекулы газа, R — универсальная газовая постоянная, d -количество молей газа, $V_1$- начальный объем газа, $V_2$- конечный объем газа.

[A=intlimits^{V_2}_{V_1}{pdV}left(7right).]

Используем уравнение состояния идеального газа, выразим из него давление:

[pV=nu RTto p=frac{nu RT}{V}left(8right).]

Подставим уравнение (8) в подынтегральное выражение уравнения (7):

[A=intlimits^{V_2}_{V_1}{frac{nu RT}{V}dV}=nu RTintlimits^{V_2}_{V_1}{frac{dV}{V}}=nu RTlnleft(frac{V_2}{V_1}right)left(9right).]

Уравнение (9) — выражение для работы газа в изотермическом процессе. Уравнение (9) можно записать через отношение давлений, если использовать закон Бойля-Мариотта, в таком случае:

[A=nu RTlnleft(frac{p_1}{p_2}right)left(10right)]

[triangle Q=A (11),]

Уравнение (11) определяет количество теплоты, сообщаемое газу массы m в изотермическом процессе$.

Изопроцессы очень часто изображают на термодинамических диаграммах. Так, линия, изображающая на такой диаграмме изотермический процесс, называется изотермой (рис.1).

Рис. 1

Пример 1