§ 19. Закон Джоуля-Ленца. Энергетические превращения в электрической цепи
Для любого участка цепи, даже содержащего ЭДС, справедлив закон Джоуля – Ленца:
количество теплоты, выделяемое на участке цепи с сопротивлением $$ R$$ при прохождении постоянного тока $$ I$$ в течение времени $$ t$$, есть $$ W={I}^{2}Rt$$.
Отсюда мощность выделяемого тепла `P=W//t=I^2R`.
Пусть на участке `1-2` идёт постоянный ток $$ I$$, перенося за время $$ t$$ от т. `1` к т. `2` заряд $$ q=It$$.
Работой тока на участке `1-2` называется работа сил электростатического поля по перемещению $$ q$$ из т. `1` в т. `2:` $$ {A}_{mathrm{Т}}=q({varphi }_{1}-{varphi }_{2})$$.
Обозначим разность потенциалов (напряжение) $$ {varphi }_{1}-{varphi }_{2}=U$$. Тогда $$ {A}_{T}=qU=UIt$$. В зависимости от знака $$ U$$ получается и знак $$ {A}_{mathrm{T}}$$.
Мощность тока:
$$ {P}_{mathrm{T}}={A}_{mathrm{T}}/t=UI$$.
Работой источника с ЭДС $$ mathcal{E}$$ при прохождении через него заряда $$ q$$ называется работа сторонних сил над зарядом `q:`
Aист=±qE{A}_{mathrm{ист}}=pm qmathcal{E}.
Если заряд переносится постоянным током $$ I$$, то $$ {A}_{mathrm{ист}}=pm mathcal{E}It$$.
Когда заряд (ток) через источник идёт в направлении действия сторонних сил, то работа источника положительна (он отдаёт энергию). Аккумулятор в таком режиме разряжается. При обратном направлении тока работа источника отрицательна (он поглощает энергию). В этом режиме аккумулятор заряжается, запасая энергию. Мощность источника:
$$ {P}_{mathrm{ист}}={A}_{mathrm{ист}}/t=pm mathcal{E}I$$.
Для участка цепи `1-2`, содержащего ЭДС (источник), работа тока $$ {A}_{mathrm{Т}}$$, работа источника $$ {А}_{mathrm{ист}}$$ и выделяемое количество теплоты $$ W$$ связаны равнением закона сохранения энергии: $$ {A}_{mathrm{T}}+{A}_{mathrm{ист}}=W$$.
Для участка цепи без ЭДС $$ {A}_{mathrm{ист}}=0$$, $$ {А}_{mathrm{Т}}=W$$ и количество теплоты равно работе тока. В этом случае количество теплоты можно выразить, используя закон Ома $$ I=U/R$$, через любые две из трёх величин: $$ I$$, $$ U$$ и $$ R$$:
$$ W={A}_{mathrm{T}}={I}^{2}Rt=UIt={displaystyle frac{{U}^{2}}{R}}t$$.
Аналогичное соотношение и для мощностей:
$$ {P}_{mathrm{T}}={I}^{2}R=UI={displaystyle frac{{U}^{2}}{R}}$$.
Найти количество теплоты, выделяющееся на внутреннем сопротивлении каждого аккумулятора и на резисторе $$ R$$ за время $$ t=10$$ c в схеме на рис. 17.1. Какие работы совершают аккумуляторы за это время?
$$ {mathcal{E}}_{1}=12$$ B, $$ {mathcal{E}}_{2}=3$$ B, $$ {r}_{1}=1$$ Ом, $$ {r}_{2}=2$$ Ом, $$ R=6$$ Ом.
 |
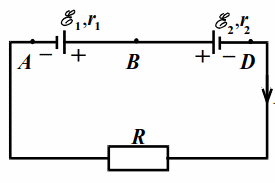| Рис. 17,1 |
Ток: $$ I=left({mathcal{E}}_{1}-{mathcal{E}}_{2}right)/(R+{r}_{1}+{r}_{2})=1$$ A.
Количество теплоты на аккумуляторах и на резисторе:
$$ {W}_{1}={I}^{2}{r}_{1}t=10$$ Дж,
$$ {W}_{2}={I}^{2}{r}_{2}t=20$$ Дж,
$$ W={I}^{2}Rt=60$$ Дж.
Направление действия ЭДС первого аккумулятора совпадает с направлением тока, он разряжается, его работа положительна: $$ {A}_{1}={mathcal{E}}_{1}It=120$$ Дж.
ЭДС второго аккумулятора направлена против тока, он заряжается, поглощая энергию, его работа отрицательна: $$ A2=-{mathcal{E}}_{2}It=-30$$ Дж.
Заметим, что `A_1+A_2=W_1+W_2+W`, что согласуется с законом сохранения энергии.
 |
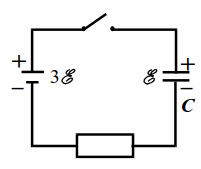| Рис. 19.1 |
Конденсатор ёмкости $$ C$$, заряженный до напряжения $$ mathcal{E}$$, подключается к батарее с ЭДС $$ 3mathcal{E}$$ (рис. 19.1). Какое количество теплоты выделится в цепи после замыкания ключа?
После замыкания ключа ток в цепи скачком достигает некоторого значения и затем спадает до нуля, пока конденсатор не зарядится до напряжения $$ 3mathcal{E}$$. Энергия конденсатора увеличится на
$$ ∆{W}_{C}=C{left(3mathcal{E}right)}^{2}/2-c{mathcal{E}}^{2}/2=4C{mathcal{E}}^{2}$$.
Через батарею пройдёт заряд $$ Q$$, равный изменению заряда не верхней обкладке конденсатора: $$ ∆q=3Cmathcal{E}-Cmathcal{E}=2Cmathcal{E}$$.
Работа батареи: $$ A=∆q3mathcal{E}=6C{mathcal{E}}^{2}$$. По закону сохранения энергии:
$$ A=∆{W}_{C}+W$$.
В цепи выделится теплоты: $$ W=A-∆{W}_{C}=2C{mathcal{E}}^{2}$$.
Перезаряд емкости и выделившееся при этом количество теплоты
Задачи на количество выделившегося тепла в цепи почему-то вызывают у моих учеников страх и неприязнь. Так бывает всегда, когда нет понимания вопроса. Поэтому, чтобы все расставить по полкам, пишу эту статью, где подробно постараюсь объяснить, как же эти задачи решаются.
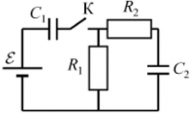
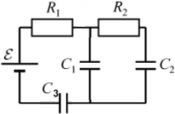
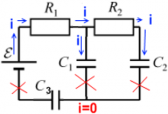
Задача 1.
Какое количество тепла выделится на резисторе сопротивлением 
после замыкания ключа К в цепи, показанной на рисунке? Внутренним сопротивлением батареи пренебречь.
Задача 1
Проанализируем состояние цепи до замыкания ключа. Имеем цепь с двумя конденсаторами, включенными последовательно. Оба они заряжены, общая эквивалентная их емкость равна
А их общий заряд тогда
Этот заряд будет одинаковым на обоих конденсаторах. Напряжение на конденсаторах распределится согласно их емкостям:
Теперь рассмотрим цепь после замыкания ключа. Конденсатор будет разряжаться через резистор и напряжение на нем будет уменьшаться, а напряжение на конденсаторе будет расти, пока не достигнет . Таким образом, энергия, запасенная обоими конденсаторами до замыкания ключа, равна:
Суммарная энергия, запасенная конденсаторами, равна:
А после замыкания ключа энергия сосредоточена только в , и равна:
То есть изменениe внутренней энергии:
Определим изменение заряда конденсатора : был , стал , следовательно,
Ответ:
Задача 2.
Какое количество тепла выделится на резисторе сопротивлением после переключения ключа К из положения 1 в положение 2 в цепи, показанной на рисунке?
Задача 2
Вначале в цепи действовала суммарная ЭДС, равная , а затем, после переключения ключа, стала действовать такая же по модулю, но обратная по знаку ЭДС. Следовательно, Сначала заряд конденсатора был равен , а потом стал таким же по модулю, но пластины поменяли знаки зарядов, то есть
Тогда энергия конденсатора была вначале
А потом стала
Таким образом, энергия не изменилась, следовательно, вся работа источника пошла на тепло, выделившееся в резисторе:
Ответ:
Задача 3.
Конденсатор емкостью , заряженный до напряжения , разряжается через резистор с большим сопротивлением и батарею с . Найдите количество теплоты, выделившееся при разрядке конденсатора.
Задача 3
Энергия, запасенная конденсатором до разряда:
После того, как произойдет разряд, напряжение на конденсаторе станет равно , а энергия, запасенная им, станет равна
Изменение внутренней энергии тогда равно:
Заряд конденсатора вначале был равен:
А после разряда
Тогда заряд, протекший через источник, равен
И работа источника равна:
Теперь можем определить и количество теплоты:
Ответ:
Задача 4.
При разомкнутом ключе К один конденсатор в цепи был заряжен до напряжения , а второй – нет. Найдите количество теплоты, выделившееся на каждом из сопротивлений и после замыкания ключа К.
Задача 4
Эквивалентная емкость обоих конденсаторов равна , поэтому энергия, запасенная в цепи, равна
Количество теплоты, выделившееся в цепи, в силу отсутствия источника равно запасенной энергии, а на каждом из резисторов, так как ток через них протекает один и тот же, выделится количество теплоты, пропорциональное их сопротивлениям:
Подставим выраженное из второго уравнения в первое:
А количество теплоты :
Ответ: ,
Задача 5. В цепи, изображенной на рисунке, ЭДС батареи равна В, сопротивления резисторов равны Ом и Ом, а емкости конденсаторов мкФ и мкФ. В начальном состоянии ключ К разомкнут, а конденсаторы не заряжены. Какое количество теплоты выделится в цепи после замыкания ключа? Ответ выразить в Дж, округлив до десятых.
Задача 5
Сначала, при разомкнутом ключе, напряжения на обоих конденсаторах равны 0 и заряды также нулевые. После замыкания ключа начнется перераспределение заряда, но в конце, когда переходной процесс завершится, токи во всех ветвях будут равны нулю, следовательно, на конденсаторе нулевое напряжение (напряжение на нем равно напряжению на резисторе, а так как тока нет, то оно равно 0). По этой же причине вся ЭДС источника будет падать на (ведь при нулевом токе на резисторе ничего не падает). То есть энергия конденсатора по окончании процесса равна
Заряд будет равен
И, следовательно, работа источника
Таким образом, в виде тепла выделилось
Ответ: 0,3 Дж
Содержание
- Теплота цепи с конденсатором
- § 19. Закон Джоуля-Ленца. Энергетические превращения в электрической цепи
- Определить количество электрической энергии, перешедшей в тепло при соединении одноименно
- Условие задачи:
- Решение задачи:
- Ответ: 0,5 мДж.
- Перезаряд емкости и выделившееся при этом количество теплоты
- 35. Электродинамика Читать 0 мин.
- 35.441. Цепи
Теплота цепи с конденсатором
§ 19. Закон Джоуля-Ленца. Энергетические превращения в электрической цепи
Для любого участка цепи, даже содержащего ЭДС, справедлив закон Джоуля – Ленца:
количество теплоты, выделяемое на участке цепи с сопротивлением $$ R$$ при прохождении постоянного тока $$ I$$ в течение времени $$ t$$, есть $$ W=^<2>Rt$$.
Отсюда мощность выделяемого тепла `P=W//t=I^2R`.
Пусть на участке `1-2` идёт постоянный ток $$ I$$, перенося за время $$ t$$ от т. `1` к т. `2` заряд $$ q=It$$.
Работой тока на участке `1-2` называется работа сил электростатического поля по перемещению $$ q$$ из т. `1` в т. `2:` $$ _<mathrm<Т>>=q(<varphi >_<1>—<varphi >_<2>)$$.
Работой источника с ЭДС $$ mathcal$$ при прохождении через него заряда $$ q$$ называется работа сторонних сил над зарядом `q:`
Если заряд переносится постоянным током $$ I$$, то $$ _<mathrm<ист>>=pm mathcalIt$$.
Когда заряд (ток) через источник идёт в направлении действия сторонних сил, то работа источника положительна (он отдаёт энергию). Аккумулятор в таком режиме разряжается. При обратном направлении тока работа источника отрицательна (он поглощает энергию). В этом режиме аккумулятор заряжается, запасая энергию. Мощность источника:
Источник
Определить количество электрической энергии, перешедшей в тепло при соединении одноименно
Условие задачи:
Определить количество электрической энергии, перешедшей в тепло при соединении одноименно заряженных обкладок конденсаторов электроемкостью 2 и 0,5 мкФ, заряженных до напряжений 100 и 50 В, соответственно.
Задача №6.4.57 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
(C_1=2) мкФ, (C_2=0,5) мкФ, (U_1=100) В, (U_2=50) В, (Q-?)
Решение задачи:
Обратимся к закону сохранения энергии, согласно которому количество теплоты (Q) можно определить как разность начальной (W_1) и конечной (W_2) суммарной электрической энергии конденсаторов, то есть:
Начальную энергию (W_1) двух заряженных конденсаторов легко определить по такой формуле (это просто сумма двух энергий заряженных конденсаторов):
Чтобы найти конечную энергию двух конденсаторов (W_2), нужно воспользоваться законом сохранения заряда. Пусть (q_<01>) и (q_<02>) – начальные заряды первого и второго конденсаторов соответственно, а (q_<1>) и (q_<2>) – конечные заряды. Тогда должно выполняться равенство:
После соединения одноименно заряженных обкладок напряжение на конденсаторах станет одинаковым и равным некоторому (U). Последнее равенство можно записать в ином виде, если заряд выразить как произведение электроемкости на напряжение:
Конечную энергию конденсаторов можно найти по формуле:
Подставим (4) в (3), тогда:
Подставим теперь (2) и (5) в (1), тогда получим:
В принципе задача уже решена, но хочется привести ответ к более красивому виду, поэтому приведем под общий знаменатель:
Раскроем скобки в числителе:
Смотрите какую замечательную формулу мы поучили! Пришло время посчитать ответ:
Ответ: 0,5 мДж.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Источник
Перезаряд емкости и выделившееся при этом количество теплоты
03.07.2016 12:50:13 | Автор: Анна
Задачи на количество выделившегося тепла в цепи почему-то вызывают у моих учеников страх и неприязнь. Так бывает всегда, когда нет понимания вопроса. Поэтому, чтобы все расставить по полкам, пишу эту статью, где подробно постараюсь объяснить, как же эти задачи решаются.
Задача 1.
Какое количество тепла выделится на резисторе сопротивлением после замыкания ключа К в цепи, показанной на рисунке? Внутренним сопротивлением батареи пренебречь.
Проанализируем состояние цепи до замыкания ключа. Имеем цепь с двумя конденсаторами, включенными последовательно. Оба они заряжены, общая эквивалентная их емкость равна
А их общий заряд тогда
Этот заряд будет одинаковым на обоих конденсаторах. Напряжение на конденсаторах распределится согласно их емкостям:
Теперь рассмотрим цепь после замыкания ключа. Конденсатор будет разряжаться через резистор и напряжение на нем будет уменьшаться, а напряжение на конденсаторе будет расти, пока не достигнет . Таким образом, энергия, запасенная обоими конденсаторами до замыкания ключа, равна:
Суммарная энергия, запасенная конденсаторами, равна:
А после замыкания ключа энергия сосредоточена только в , и равна:
То есть изменениe внутренней энергии:
Определим изменение заряда конденсатора : был , стал , следовательно,
Ответ:
Задача 2.
Какое количество тепла выделится на резисторе сопротивлением после переключения ключа К из положения 1 в положение 2 в цепи, показанной на рисунке?
Вначале в цепи действовала суммарная ЭДС, равная , а затем, после переключения ключа, стала действовать такая же по модулю, но обратная по знаку ЭДС. Следовательно, Сначала заряд конденсатора был равен , а потом стал таким же по модулю, но пластины поменяли знаки зарядов, то есть
Тогда энергия конденсатора была вначале
Таким образом, энергия не изменилась, следовательно, вся работа источника пошла на тепло, выделившееся в резисторе:
Ответ:
Задача 3.
Конденсатор емкостью , заряженный до напряжения , разряжается через резистор с большим сопротивлением и батарею с . Найдите количество теплоты, выделившееся при разрядке конденсатора.
Энергия, запасенная конденсатором до разряда:
После того, как произойдет разряд, напряжение на конденсаторе станет равно , а энергия, запасенная им, станет равна
Изменение внутренней энергии тогда равно:
Заряд конденсатора вначале был равен:
А после разряда
Тогда заряд, протекший через источник, равен
И работа источника равна:
Теперь можем определить и количество теплоты:
Ответ:
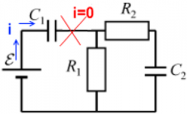
Задача 4.
При разомкнутом ключе К один конденсатор в цепи был заряжен до напряжения , а второй — нет. Найдите количество теплоты, выделившееся на каждом из сопротивлений и после замыкания ключа К.
Эквивалентная емкость обоих конденсаторов равна , поэтому энергия, запасенная в цепи, равна
Количество теплоты, выделившееся в цепи, в силу отсутствия источника равно запасенной энергии, а на каждом из резисторов, так как ток через них протекает один и тот же, выделится количество теплоты, пропорциональное их сопротивлениям:
Подставим выраженное из второго уравнения в первое:
А количество теплоты :
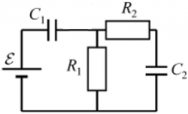
Задача 5. В цепи, изображенной на рисунке, ЭДС батареи равна В, сопротивления резисторов равны Ом и Ом, а емкости конденсаторов мкФ и мкФ. В начальном состоянии ключ К разомкнут, а конденсаторы не заряжены. Какое количество теплоты выделится в цепи после замыкания ключа? Ответ выразить в Дж, округлив до десятых.
Сначала, при разомкнутом ключе, напряжения на обоих конденсаторах равны 0 и заряды также нулевые. После замыкания ключа начнется перераспределение заряда, но в конце, когда переходной процесс завершится, токи во всех ветвях будут равны нулю, следовательно, на конденсаторе нулевое напряжение (напряжение на нем равно напряжению на резисторе, а так как тока нет, то оно равно 0). По этой же причине вся ЭДС источника будет падать на (ведь при нулевом токе на резисторе ничего не падает). То есть энергия конденсатора по окончании процесса равна
Источник
35. Электродинамика Читать 0 мин.
Читать 0 мин.35.441. Цепи
Через конденсатор постоянный ток не течёт.
Напряжение на параллельных участках цепи одинаково.
В системе отключенных конденсаторов заряд всегда остаётся постоянным. Напряжение и ёмкость может меняться.
Выделившееся количество теплоты равно разности начальной и конечной энергии:
Eн ― начальная энергия системы [Дж];
Ек ― конечная энергия системы [Дж].
Начальные и конечные энергии определяются энергиями конденсаторов и катушек индуктивности входящих в цепь.
После установления равновесия, напряжение есть только на конденсаторах, не подключенных параллельно к резисторам.
Конденсатор в цепи постоянного тока
Плоский конденсатор представляет собой пластинки, на которых может скапливаться заряд. Между пластинками находится пространство, заполненное диэлектриком (или воздухом в роли диэлектрика). Поскольку диэлектрики ― вещества, плохо проводящие ток, от одной пластины конденсатора через слой диэлектрика на другую пластину заряд перейти не может, а значит, через конденсатор ток не проходит. Если на участке цепи находится такой конденсатор ― этот участок «заблокирован», тока в нем нет.
Если на участке цепи находится конденсатор не заряженный, или заряженный частично, а цепь подключают к источнику тока ― на обкладках конденсатора начинает скапливаться заряд. Это означает, что на этом участке цепи до конденсатора есть ток ― до тех пор, пока конденсатор не заряжен полностью.
Если цепь от источника тока отключить, и в ней есть заряженный конденсатор ― конденсатор начинает разряжаться. Заряды с одной обкладки конденсатора пытаются перейти на другую, по «длинному пути» ― через всю цепь, создавая, таким образом, ток. Ток в такой цепи будет до тех пор, пока конденсатор не разрядится.
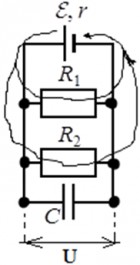
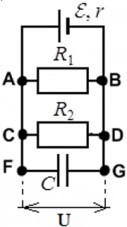
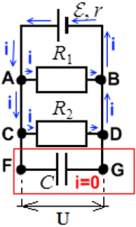
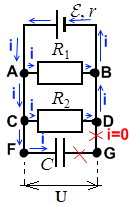
Пример: Пусть в цепи есть два резистора с сопротивлениями R1 и R2, источник ЭДС ε, и конденсатор емкостью C:
Конденсатор C полностью заряжен. В этом случае токи в цепи не проходят через участок цепи FG ― его словно нет в цепи, и в расчетах параметров цепи он не учитывается. Ток считается выходящим из положительно заряженной клеммы источника ЭДС (тонкая и длинная) к входящим в отрицательно заряженную клемму (жирная короткая черта):
Конденсатор разряжен или заряжен не док конца. В этом случае конденсатор только заряжается, и ток в цепи через точку F проходит — вплоть до обкладки конденсатора – но дальше, в точку G ток не проходит.
Конденсатор заряжен, но от источника ЭДС цепь отключена. В этом случае ток идет через всю цепь ― пока конденсатор может служить источником зарядов и пока полностью не разрядится. Когда конденсатор разрядится ― ток в цепи прекратится.
Напряжения на всех параллельных участках цепи равны ― это основное свойство параллельного подключения. Вне зависимости от того, находится на ветви резистор, или конденсатор. Таким образом, во всех случаях для примера выше, напряжение на конденсаторе C равно напряжению на резисторе R1, и равно напряжению на резисторе R2. Благодаря этому свойству, зная, например, энергию, скопившуюся на заряженном конденсаторе, или его заряд, можно вычислить напряжение на резисторах.
Заряженный конденсатор, отключенный от цепи. У заряженного конденсатора на обкладках находится определенное количество заряда. Если конденсатор отключить от цепи ― заряду некуда переместиться, и он остается на конденсаторе неизменным. Получить дополнительный заряд, если он заряжен не до конца, конденсатору тоже неоткуда. Заряд конденсатора, отключенного от цепи, постоянен.
Электроемкость конденсатора ― это его физико-геометрическая характеристика, показывающая, как много заряда он может скопить. Электроемкость конденсатор не зависит ни от заряда на его обкладках, ни от напряжения в цепи.
Электроемкость конденсатора равна C = $frac <varphi_2 – varphi_1>= frac
$ , где
C ― электроемкость конденсатора, [Ф];
(φ2 – φ1) ― разность потенциалов на обкладках конденсатора, [В];
U ― напряжение на обкладках конденсатора [В].
Электроемкость плоского конденсатора зависит от размеров его пластин, расстояния между ними, а также типа диэлектрика, который заполняет пространство между пластинами.
Электроемкость плоского конденсатора равна C = $frac<varepsilonvarepsilon_0 S>$ , где
C ― ёмкость конденсатора [Ф];
ε ― диэлектрическая проницаемость;
ε0 ― электрическая постоянная;
S ― площадь обкладок конденсатора [м2];
d ― расстояние между обкладками [м].
В электрической цепи за счет сопротивления, которое преодолевают движущиеся в материале заряды, выделяется тепло. Количество теплоты, которая выделяется в цепи, равно разности начальной и конечной энергии всей системы Q = Eн – Eк¸ где
Eн ― начальная энергия системы [Дж];
Eк ― конечная энергия системы [Дж].
В цепи энергия скапливается на конденсаторах (энергия электрического поля) и на катушках индуктивности (энергия магнитного поля). Поэтому энергия электромагнитных сил в цепи в любой момент равна сумме энергий на конденсаторах и на катушках, которые входят в цепь.
Энергия электрического поля заряженного конденсатора равна We = $frac <2>= frac <2>= frac<2c>$ , где
We ― энергия электрического поля конденсатора, [Дж];
C ― электроемкость конденсатора, [Ф];
U ― напряжение на обкладках конденсатора, [В];
q ― заряд на обкладках конденсатора, [Кл].
Энергия магнитного поля катушки индуктивности равна E = $frac<2>$ , где
E ― энергия магнитного поля катушки [Дж];
L ― индуктивность катушки [Гн];
I ― сила тока в катушке [А].
Состояние равновесия и зарядка конденсаторов
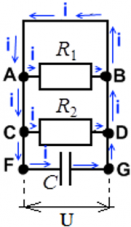
Пример 1: в цепи, изображенной на рисунке, есть ЭДС и резисторы с сопротивлениями R1 и R2, оба конденсатора емкостями C1 и C2 разряжены.
Ток от источника ЭДС до конденсатора C1 будет идти до тех пор, пока конденсатор C1 не будет полностью заряжен. При этом от конденсатора C1 дальше заряды не проходят ― ни на резисторы R1 и R2, ни на конденсаторC2. Как только конденсатор C1 полностью заряжается, в системе наступает состояние равновесия ― напряжение на конденсаторе становится равным ЭДС, весь возможный заряд конденсатор принял. Поскольку ток через него не прошел до конденсатора C2 ― этот конденсатор так и остался незаряженным. Напряжение есть лишь на конденсаторе C1, а на конденсаторе C2напряжение равно нулю. Зарядка конденсатораC1:
После того, как конденсатор C1 заряжен, ток в цепи прекращается.
Пример 2: в цепи, изображенной на рисунке, есть ЭДС и резисторы с сопротивлениями R1 и R2, все три конденсатора емкостями C1, C2 и C3 разряжены.
Ток, выходя из источника ЭДС, разделяется на два тока ― один питает подзарядку конденсатораC1, а другой ― конденсатораC2. Состояние равновесия наступает, когда оба конденсатора полностью заряжены ― в цепи ток больше не проходит. Но так как ток дальше конденсаторов не проходит ― конденсатор C3 не получает заряд, и остается разряженным. Напряжение на конденсаторе C3 равно нулю.
Зарядка конденсаторов C1 иC2:
После того, как конденсаторыC1 и C2 заряжены, ток в цепи прекращается.
Источник
Проходя по проводнику, ток может оказывать некоторые действия: тепловое, химическое и магнитное.
Тепловое действие тока обусловлено тем, что свободные электроны, двигаясь с большой скорость, взаимодействуют с ионами металлов, ионами солей в растворах кислот и щелочей. Ионы начинают усиленно колебаться, двигаться, вращаться, то есть их энергия тоже повышается. Проводник или электролит нагревается.
Например, спираль лампочки раскаляется до такой температуры, что начинает излучать свет.
Электрическая энергия превращается в тепловую энергию проводника; часть рассеивается, часть используется в бытовых целях (для нагревания).
Работа, которую совершает электрический ток, определяется количеством теплоты, выделяемой проводником:
Q = A
, где (A) — работа тока, (Q) — количество теплоты.
Работу тока рассчитывают по формуле:
A = U⋅I⋅t
. Тогда количество теплоты, исходя из закона сохранения энергии, также будет равно:
Q = U⋅I⋅t
.
Согласно закону Ома
U = IR
. Подставляя эту формулу в предыдущую, получим:
Q = I2⋅R⋅t
.
Количество теплоты, которое выделяется в проводнике с током, прямо пропорционально квадрату силы тока, сопротивлению проводника и времени протекания тока.
В процессе своих экспериментов получили такой же результат Джеймс Джоуль в Англии и Эмилий Христианович Ленц в России. В их честь закон имеет двойное название: закон Джоуля-Ленца.
Джоуль Джеймс Прескотт ((1818—1889)) — английский физик, член Лондонского королевского общества. Он внёс значительный вклад в исследование электромагнетизма и тепловых явлений, в создание физики низких температур, в обоснование закона сохранения и превращения энергии. Именем Джоуля назвали единицу измерения работы и энергии в системе СИ.
Эмилий Христианович Ленц ((1804—1865)) — российский физик и электротехник, академик Петербургской Академии наук ((1830)), ректор Санкт-Петербургского университета (с (1863)). Результатом его исследований стало открытие взаимосвязей (на «языке математики») между электрическими и термодинамическими параметрами, между электрическими и магнитными параметрами при протекании тока в проводнике.
Преобразование электрической энергии в тепловую широко используется в электрических печах и различных электронагревательных приборах.
Состояние сети, когда по проводам и приборам проходит ток больше допустимого значения, называется перегрузкой. Опасность этого явления в тепловом действии тока, ведь при большой перегрузке изоляция проводников легко воспламеняется. Перегрузка может возникнуть при подключении устройств большой мощности через удлинитель (смотри рисунок и никогда так не делай!).
Для примера, перегрузка проводов на (25)% приводит к сокращению срока их службы где-то с (20) лет до (3—5) месяцев, а перегрузка проводов на (50)% — до нескольких часов.
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 31 октября 2021 года; проверки требуют 4 правки.
Закон Джоуля — Ле́нца — физический закон, дающий количественную оценку теплового действия электрического тока. Установлен в 1841 году Джеймсом Джоулем и независимо от него в 1842 году Эмилием Ленцем[1].
Определения[править | править код]
В словесной формулировке звучит следующим образом[2]:
Мощность тепла, выделяемого в единице объёма среды при протекании постоянного электрического тока, равна произведению плотности электрического тока на величину напряженности электрического поля.
Математически может быть выражен в следующей форме:
где 
— мощность выделения тепла в единице объёма, 
— плотность электрического тока, 
— напряжённость электрического поля, σ — проводимость среды, а точкой обозначено скалярное произведение.
Закон также может быть сформулирован в интегральной форме для случая протекания токов в тонких проводах[3]:
Количество теплоты, выделяемое в единицу времени в рассматриваемом участке цепи, пропорционально произведению квадрата силы тока на этом участке и сопротивления участка.
В интегральной форме этот закон имеет вид
где 
— количество теплоты, выделяемое за промежуток времени 
, 
— сила тока, 
— сопротивление, 
— полное количество теплоты, выделенное за промежуток времени от 
до 
. В случае постоянных силы тока и сопротивления:
Применяя закон Ома, можно получить следующие эквивалентные формулы:
Практическое значение[править | править код]
Снижение потерь энергии[править | править код]
При передаче электроэнергии тепловое действие тока в проводах является нежелательным, поскольку ведёт к потерям энергии. Подводящие провода и нагрузка соединены последовательно — значит, ток в сети на проводах и нагрузке одинаков. Мощность нагрузки и сопротивление проводов не должны зависеть от выбора напряжения источника. Выделяемая на проводах и на нагрузке мощность определяется следующими формулами
Откуда следует, что 
. Так как в каждом конкретном случае мощность нагрузки и сопротивление проводов остаются неизменными и выражение 
является константой, то тепло, выделяемое на проводе, обратно пропорционально квадрату напряжения на потребителе. Повышая напряжение, мы снижаем тепловые потери в проводах. Это, однако, снижает электробезопасность линий электропередачи.
Выбор проводов для цепей[править | править код]
Тепло, выделяемое проводником с током, в той или иной степени выделяется в окружающую среду. В случае, если сила тока в выбранном проводнике превысит некоторое предельно допустимое значение, возможен столь сильный нагрев, что проводник может спровоцировать возгорание находящихся рядом с ним объектов или расплавиться сам. Как правило, при выборе проводов, предназначенных для сборки электрических цепей, достаточно следовать принятым нормативным документам, которые регламентируют выбор сечения проводников.
По этой причине для передачи необходимой мощности через современные магистральные воздушные линии электропередач, их проектируют под сверхвысокое напряжение (до 1150 кВ), чтобы обеспечить сверхнизкие токи в ЛЭП.
Электронагревательные приборы[править | править код]
Если сила тока одна и та же на всём протяжении электрической цепи, то в любом выбранном участке будет выделять тепла тем больше, чем выше сопротивление данного участка.
За счёт сознательного увеличения сопротивления участка цепи можно добиться локализованного выделения тепла в этом участке. По этому принципу работают электронагревательные приборы. В них используется нагревательный элемент — проводник с высоким сопротивлением. Повышение сопротивления достигается (совместно или по отдельности) выбором сплава с высоким удельным сопротивлением (например, нихром, константан), увеличением длины проводника и уменьшением его поперечного сечения. Подводящие провода имеют обычное низкое сопротивление и поэтому их нагрев, как правило, незаметен.
Плавкие предохранители[править | править код]
Для защиты электрических цепей от протекания чрезмерно больших токов используется отрезок проводника со специальными характеристиками. Это проводник относительно малого сечения и из такого сплава, что при допустимых токах нагрев проводника не перегревает его, а при чрезмерно больших перегрев проводника столь значителен, что проводник расплавляется и размыкает цепь.
См. также[править | править код]
- Закон Ома
Примечания[править | править код]
- ↑ Джоуля — Ленца закон // Дебитор — Евкалипт. — М. : Советская энциклопедия, 1972. — (Большая советская энциклопедия : [в 30 т.] / гл. ред. А. М. Прохоров ; 1969—1978, т. 8).
- ↑ Сивухин Д. В. Общий курс физики. — М.: Наука, 1977. — Т. III. Электричество. — С. 186. — 688 с.
- ↑ Сивухин Д. В. Общий курс физики. — М.: Наука, 1977. — Т. III. Электричество. — С. 197—198. — 688 с.
